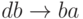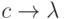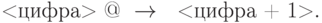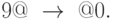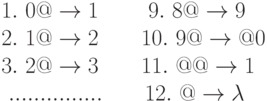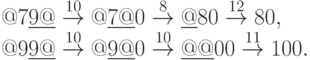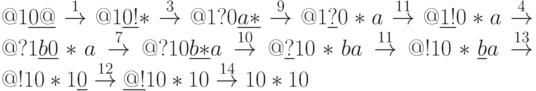Как составить алгоритм маркова

Норма́льный алгори́тм (алгори́фм) Ма́ркова (НАМ, также марковский алгоритм) — один из стандартных способов формального определения понятия алгоритма (другой известный способ — машина Тьюринга). Понятие нормального алгоритма введено А. А. Марковым (младшим) в конце 1940-х годов в работах по неразрешимости некоторых проблем теории ассоциативных вычислений. Традиционное написание и произношение слова «алгорифм» в этом термине также восходит к его автору, многие годы читавшему курс математической логики на механико-математическом факультете МГУ.

Нормальный алгоритм описывает метод переписывания строк, похожий по способу задания на формальные грамматики. НАМ — полный по Тьюрингу язык, что делает его по выразительной силе эквивалентным машине Тьюринга и, следовательно, современным языкам программирования. На основе НАМ был создан функциональный язык программирования Рефал.

Описание[править | править код]

Нормальные алгоритмы вербальны, то есть предназначены для применения к словам в различных алфавитах.

Определение всякого нормального алгоритма состоит из двух частей: определения алфавита алгоритма (к словам, из символов которого алгоритм будет применяться) и определения его схемы. Схемой нормального алгоритма называется конечный упорядоченный набор так называемых формул подстановки, каждая из которых может быть простой или заключительной. Простыми формулами подстановки называются слова вида , где и  — два произвольных слова в алфавите алгоритма (называемые, соответственно, левой и правой частями формулы подстановки). Аналогично, заключительными формулами подстановки называются слова вида , где и  — два произвольных слова в алфавите алгоритма. При этом предполагается, что вспомогательные буквы и не принадлежат алфавиту алгоритма (в противном случае на исполняемую ими роль разделителя левой и правой частей следует избрать другие две буквы).

Примером схемы нормального алгоритма в пятибуквенном алфавите может служить схема

Процесс применения нормального алгоритма к произвольному слову в алфавите этого алгоритма представляет собой дискретную последовательность элементарных шагов, состоящих в следующем. Пусть  — слово, полученное на предыдущем шаге работы алгоритма (или исходное слово , если текущий шаг — первый). Если среди формул подстановки нет такой, левая часть которой входила бы в , то работа алгоритма считается завершённой, и результатом этой работы считается слово . Иначе среди формул подстановки, левая часть которых входит в , выбирается самая первая. Если эта формула подстановки имеет вид , то из всех возможных представлений слова в виде выбирается такое, при котором  — самое короткое, после чего работа алгоритма считается завершённой с результатом . Если же эта формула подстановки имеет вид , то из всех возможных представлений слова в виде выбирается такое, при котором  — самое короткое, после чего слово считается результатом текущего шага, подлежащим дальнейшей переработке на следующем шаге.

Например, в ходе процесса применения алгоритма с указанной выше схемой к слову последовательно возникают слова , , , , , , , , , и , после чего алгоритм завершает работу с результатом . Другие примеры смотрите ниже.

Любой нормальный алгоритм эквивалентен некоторой машине Тьюринга, и наоборот — любая машина Тьюринга эквивалентна некоторому нормальному алгоритму. Вариант тезиса Чёрча — Тьюринга, сформулированный применительно к нормальным алгоритмам, принято называть «принципом нормализации».

Нормальные алгоритмы оказались удобным средством для построения многих разделов конструктивной математики. Кроме того, заложенные в определении нормального алгоритма идеи используются в ряде ориентированных на обработку символьной информации языков программирования — например, в языке Рефал.

Примеры[править | править код]

Пример 1[править | править код]

Использование алгоритма Маркова для преобразований над строками.

Алфавит:

{ а…я, А…Я, «пробел», «точка» }

Правила:

1. А → апельсин
2. кг → килограмм
3. М → магазинчике
4. Т → том
5. магазинчике →. ларьке (заключительная формула)
6. в том ларьке → на том рынке

Исходная строка:

Я купил кг Аов в Т М.

При выполнении алгоритма строка претерпевает следующие изменения:

1. Я купил кг апельсинов в Т М.
2. Я купил килограмм апельсинов в Т М.
3. Я купил килограмм апельсинов в Т магазинчике.
4. Я купил килограмм апельсинов в том магазинчике.
5. Я купил килограмм апельсинов в том ларьке.

На этом выполнение алгоритма завершится (так как будет достигнута формула № 5, которую мы сделали заключительной).

Пример 2[править | править код]

Данный алгоритм преобразует двоичные числа в «единичные» (в которых записью целого неотрицательного числа N является строка из N палочек). Например, двоичное число 101 преобразуется в 5 палочек: |||||.

Алфавит:

{ 0, 1, | }

Правила:

1. 1 → 0|
2. |0 → 0||
3. 0 → “” (пустая строка)

Исходная строка:

101

Выполнение:

1. 0|01
2. 0|00|
3. 00||0|
4. 00|0|||
5. 000|||||
6. 00|||||
7. 0|||||
8. |||||

См. также[править | править код]

Прочие абстрактные исполнители и формальные системы вычислений[править | править код]

• Машина Тьюринга (автоматное программирование)
• Машина Поста (автоматное программирование)
• Рекурсивная функция (теория вычислимости)
• Лямбда-исчисление (функциональное программирование)
• Brainfuck (императивное программирование)

Языки, основанные на нормальных алгоритмах[править | править код]

• РЕФАЛ
• Thue

Прочие алгоритмы[править | править код]

• Операторный алгоритм

Ссылки[править | править код]

• Yad Studio — IDE и интерпретатор для Нормальных Алгоритмов Маркова (Open Source)
• Javascript-эмулятор нормальных алгорифмов Маркова (работает on-line)

Определение нормального алгоритма и его выполнение

В середине прошлого века выдающийся русский математик А.А. Марков ввел понятие нормального алгоритма (алгорифма) с целью уточнения понятия “алгоритм“, что позволяет решать задачи по определению алгоритмически неразрешимых проблем. Позже это понятие получило название нормального алгоритма Маркова (НАМ). Язык НАМ, с одной стороны, намеренно беден, что необходимо для цели введения понятия “алгоритм“. Однако, с другой стороны, идеи НАМ положены в основу большой группы языков программирования, получивших название языки логического программирования, которые являются темой данного пособия.

Для определения НАМ вводится произвольный алфавит – конечное непустое множество символов, при помощи которых описывается алгоритм и данные. В алфавит также включается пустой символ, который мы будем обозначать греческой буквой . Под словом понимается любая последовательность непустых символов алфавита либо пустой символ, который обозначает пустое слово.

Всякий НАМ определяется конечным упорядоченным множеством пар слов алфавита, называемых подстановками . В паре слов подстановки левое (первое) слово непустое, а правое (второе) слово может быть пустым символом. Для наглядности левое и правое слово разделяются стрелкой. Например,

1. 
2. 
3. 
4. 

В качестве данных алгоритма берется любая непустая строка символов. Работа НАМ состоит из последовательности совершенно однотипных шагов. Шаг работы алгоритма может быть описан следующим образом:

1. В упорядоченной последовательности подстановок ищем самую первую подстановку, левое слово которой входит в строку данных.
2. В строке данных ищем самое первое (левое) вхождение левого слова найденной подстановки.
3. Это вхождение в строке данных заменяем на правое слово найденной подстановки (преобразование данных).

Шаг работы алгоритма повторяется до тех пор, пока

• либо не возникнет ситуация, когда шаг не сможет быть выполнен из-за того, что ни одна подстановка не подходит ( левое слово любой подстановки уже не входит в строку данных ) – правило остановки ;
• либо не будет установлено, что процесс подстановок не может остановиться.

В первом случае строка данных, получившаяся при остановке алгоритма, является выходной (результатом) и алгоритм применим к входным данным, а во втором случае алгоритм не применим к входным данным.

Так, определенный выше в примере нормальный алгоритм Маркова преобразует слово в слово следующим образом (над стрелкой преобразования мы пишем номер применяемой подстановки, а в преобразуемой строке подчеркиваем левое слово применяемой подстановки ):

а при преобразовании слова abbc этот же алгоритм будет неограниченно работать, так как имеет место цикличное повторение данных:

Таким образом, всякий нормальный алгоритм Маркова определяет функцию, которую мы назовем нормальной (или вычислимой по Маркову), которая может быть частичной и которая в области определения входному слову ставит в соответствие выходное слово.

Возможности нормальных алгоритмов и тезис Маркова

Прежде всего рассмотрим возможности реализации арифметических операций с помощью нормальных алгоритмов Маркова. Сначала обратим внимание на одно обстоятельство, связанное с работой любого НАМ: нужно либо вводить дополнительное правило остановки работы нормального алгоритма (иначе в примере увеличения числа на 1 алгоритм продолжит работу и снова будет увеличивать полученный результат еще на 1 и т.д. неограниченное число раз), либо перед началом работы нормального алгоритма добавлять к входной строке специальные символы, отличные от других символов строки, которые учитываются подстановками алгоритма в начале его работы и которые удаляются в конце работы алгоритма. Мы будем придерживаться второго способа, как и одна из наиболее успешных реализаций нормальных алгоритмов Маркова в виде языка программирования Рефал. В качестве добавляемого символа возьмем символ “@”.

Пример 1. Рассмотрим простейшую операцию увеличения десятичного числа на 1. В этом случае почти всегда необходимо увеличить последнюю цифру на 1, а последняя цифра отличается тем, что после нее идет символ “@”. Поэтому первыми подстановками должны быть подстановки типа

Но если это цифра 9, то ее нужно заменить 0 и увеличение на 1 перенести в предыдущий разряд. Этому отвечает подстановка

Наконец, если число начинается с 9 и перед этой цифрой нужно поставить 1, то этому будет отвечать подстановка

а если это не так, то в конце работы алгоритма символы @ надо стереть, что выполнит подстановка

Таким образом, мы получаем следующий НАМ увеличения десятичного числа на 1:

Приведем работу построенного алгоритма для чисел 79 и 99:

Аналогичным образом разрабатывается нормальный алгоритм Маркова для уменьшения числа на 1 (см. упражнение 1.3.1).

Пример 2. Прежде, чем перейти к другим арифметическим операциям, рассмотрим как довольно типичный пример, используемый часто в других алгоритмах, алгоритм копирования двоичного числа. В этом случае прежде всего исходное и скопированное числа разделим символом “*”. В разрабатываемом алгоритме мы будем копировать разряды числа по очереди, начиная с младшего, но нужно решить 2 проблемы: как запоминать значение символа, который мы копируем, и как запоминать место копируемого символа. Для решения второй проблемы используем символ “!”, которым мы будем определять еще не скопированный разряд числа, после которого и стоит этот символ. Для запоминания значения копируемого разряда мы будем образовывать для значения 0 символ “a”, а для значения 1 – символ “b”. Меняя путем подстановок эти символы “a” или “b” с последующими, мы будем передвигать разряды “a” или “b” в начало копируемого числа (после “*”), но для того, чтобы пока не происходило копирование следующего разряда справа, мы перед передвижением разряда временно символ “!” заменим на символ “?”, а после передвижения сделаем обратную замену. После того как все число окажется скопированным в виде символов “a” и “b”, мы заменим эти символы на 0 и 1 соответственно. В результате нормальный алгоритм копирования двоичного числа можно определить следующей последовательностью подстановок:

Продемонстрируем работу алгоритма для числа 10:

Для построения алгоритма сложения двух чисел можно использовать идею уменьшения одного числа на 1 с последующим увеличением другого числа на 1 и повторением этого до тех пор, пока уменьшаемое число не исчезнет после того, как станет равным 0. Но можно использовать и более сложную идею поразрядного сложения с переносом 1 в разряд слева. Построение этих алгоритмов, а также алгоритмов вычитания, умножения и деления выделено для самостоятельной работы в упражнениях 2 – 9 (см. 1.3).

Приведенные примеры показывают также возможности аппарата нормальных алгоритмов Маркова по организации ветвления и цикличных процессов вычисления. Это показывает, что всякий алгоритм может быть нормализован
т. е. задан нормальным алгоритмом Маркова. В этом и состоит тезис Маркова, который следует понимать как определение алгоритма.

Вместе с тем построение алгоритма в последнем приведенном примере подсказывает следующую методику разработки НАМ:

1. Произвести декомпозицию (разбиение на части) строящегося алгоритма. В примере это следующие части:
   1. разделение исходного числа и копии;
   2. копирование разряда;
   3. повторение предыдущей части до полного копирования всех разрядов.
2. Решение проблем реализации каждой части. В примере это следующие проблемы:
   1. запоминание копируемого разряда – разряд 1 запоминается как символ “a”, а разряд 0 – как символ “b”;
   2. запоминание места копируемого разряда – пометка еще не скопированного символа дополнительным символом “!” с заменой его на символ “?” при передвижении копируемого разряда и обратной заменой после передвижения.
3. Если часть для реализации является сложной, то она также подвергается декомпозиции.
4. Сборка реализации в единый алгоритм.

Упражнения

1. Определите нормальный алгоритм, который уменьшает число на единицу.
2. Определите нормальный алгоритм сложения двух двоичных чисел методом уменьшения одного числа на 1 и увеличением другого числа на 1 до тех пор, пока уменьшаемое число не станет равным 0.
3. Определите нормальный алгоритм логического сложения двух двоичных чисел.
4. Определите нормальный алгоритм логического умножения двух двоичных чисел.
5. Определите нормальный алгоритм сложения по модулю 2 двух двоичных чисел.
6. Определите нормальный алгоритм поразрядного сложения двух двоичных чисел.
7. Определите нормальный алгоритм вычитания двоичных чисел.
8. Определите нормальный алгоритм умножения двух двоичных чисел столбиком.
9. Определите нормальный алгоритм деления двух двоичных чисел с определением частного и остатка.
10. Определите нормальный алгоритм вычисления наибольшего общего делителя двух двоичных чисел.
11. Определите нормальный алгоритм вычисления наименьшего общего кратного двух двоичных чисел.

Нормальные алгоритмы Маркова

Теория нормальных алгоритмов (или алгорифмов, как называл их создатель теории) была разработана советским математиком А. А. Марковым (1903–1979) в конце 1940-х — начале 1950-х гг. XX в. Эти алгоритмы представляют собой некоторые правила по переработке слов в каком-либо алфавите, так что исходные данные и искомые результаты для алгоритмов являются словами в некотором алфавите.

Марковские подстановки

Алфавитом (как и прежде) называется любое непустое множество. Его элементы называются буквами, а любые последовательности букв — словами в данном алфавите. Для удобства рассуждений допускаются пустые слова (они не имеют в своем составе ни одной буквы). Пустое слово будем обозначать . Если и — два алфавита, причем , то алфавит называется расширением алфавита .

Слова будем обозначать латинскими буквами: (или этими же буквами с индексами). Одно слово может быть составной частью другого слова. Тогда первое называется подсловом второго или вхождением во второе. Например, если — алфавит русских букв, то можем рассмотреть такие слова: . Слово является подсловом слова , а — подсловом и , причем в оно входит дважды. Особый интерес представляет первое вхождение.

Определение 34.1. Марковской подстановкой называется операция над словами, задаваемая с помощью упорядоченной пары слов , состоящая в следующем. В заданном слове находят первое вхождение слова (если таковое имеется) и, не изменяя остальных частей слова , заменяют в нем это вхождение словом . Полученное слово называется результатом применения марковской подстановки к слову . Если же первого вхождения в слово нет (и, следовательно, вообще нет ни одного вхождения в ), то считается, что марковская подстановка неприменима к слову .

Частными случаями марковских подстановок являются подстановки с пустыми словами:

Пример 34.2. Примеры марковских подстановок рассмотрены в таблице, в каждой строке которой сначала дается преобразуемое слово, затем применяемая к нему марковская подстановка и, наконец, получающееся в результате словно:

Преобразуемое слово	Марковская подстановка	Результат
138 578 926	(8 578 9, 00)	130 026
тарарам	(ара, Λ)	трам
шрам	(ра, ар)	шарм
функция	(Λ, ζ-)	ζ-функция
логика	(ика, Λ)	лог
книга	(Λ, Λ)	книга
поляна	(пор, т)	[неприменима]

Для обозначения марковской подстановки используется запись . Она называется формулой подстановки . Некоторые подстановки будем называть заключительными (смысл названия станет ясен чуть позже). Для обозначения таких подстановок будем использовать запись , называя ее формулой заключительной подстановки. Слово называется левой частью, а — правой частью в формуле подстановки.

---

Нормальные алгоритмы и их применение к словам

Упорядоченный конечный список формул подстановок

в алфавите называется схемой (или записью) нормального алгоритма в . (Запись точки в скобках означает, что она может стоять в этом месте, а может отсутствовать.) Данная схема определяет (детерминирует) алгоритм преобразования слов, называемый нормальным алгоритмом Маркова. Дадим его точное определение.

Определение 34.3. Нормальным алгоритмом (Маркова) в алфавите называется следующее правило построения последовательности слов в алфавите , исходя из данного слова в этом алфавите. В качестве начального слова последовательности берется слово . Пусть для некоторого слово построено и процесс построения рассматриваемой последовательности еще не завершился. Если при этом в схеме нормального алгоритма нет формул, левые части которых входили бы в , то полагают Равным , и процесс построения последовательности считается завершившимся. Если же в схеме имеются формулы с левыми частями, входящими в , то в качестве берется результат марковской подстановки правой части первой из таких формул вместо первого вхождения ее левой части в слово ; процесс построения последовательности считается завершившимся, если на данном шаге была применена формула заключительной подстановки) и продолжающимся — в противном случае. Если процесс построения упомянутой последовательности обрывается, то говорят, что рассматриваемый нормальный алгоритм применим к слову . Последний член последовательности называется результатом применения нормального алгоритма к слову . Говорят, что нормальный алгоритм перерабатывает и .

Последовательность будем записывать следующим образом:

, где и .

Мы определили понятие нормального алгоритма в алфавите . Если же алгоритм задан в некотором расширении алфавита , то говорят, что он есть нормальный алгоритм над .

Рассмотрим примеры нормальных алгоритмов.

Пример 34.4. Пусть — алфавит. Рассмотрим следующую схему нормального алгоритма в

Нетрудно понять, как работает определяемый этой схемой нормальный алгоритм. Всякое слово в алфавите , содержащее хотя бы одно вхождение буквы , он перерабатывает в слово, получающееся из вычеркиванием в нем самого левого (первого) вхождения буквы а. Пустое слово он перерабатывает в пустое. (Алгоритм не применим к таким словам, которые содержат только букву .) Например,

Пример 34.5. Пусть — алфавит. Рассмотрим схему

Она определяет нормальный алгоритм, перерабатывающий всякое слово (в алфавите ) в пустое слово. Например,

---

Нормально вычислимые функции и принцип нормализации Маркова

Как и машины Тьюринга, нормальные алгоритмы не производят собственно вычислений: они лишь производят преобразования слов, заменяя в них одни буквы другими по предписанным им правилам. В свою очередь, мы предписываем им такие правила, результаты применения которых мы можем интерпретировать как вычисления. Рассмотрим два примера.

Пример 34.6. В алфавите схема определяет нормальный алгоритм, который к каждому слову в алфавите (все такие слова суть следующие: и т.д.) приписывает слева 1. Следовательно, алгоритм реализует (вычисляет) функцию .

Пример34.7. Дана функция где — число единиц в слове . Рассмотрим нормальный алгоритм в алфавите со следующей схемой:

Этот алгоритм работает по такому принципу: пока число букв 1 а слове не меньше 3, алгоритм последовательно стирает по три буквы. Если число букв меньше 3, но больше 0, то оставшиеся буквы 1 или 11 стираются заключительно; если слово пусто, оно заключительно переводится в слово 1. Например:

Таким образом, рассмотренный алгоритм реализует (или вычисляет) данную функцию.

Сформулируем теперь точное определение такой вычислимости функций.

Определение 34.8. Функция , заданная на некотором множестве слов алфавита , называется нормально вычислимой, если найдется такое расширение данного алфавита и такой нормальный алгоритм в , что каждое слово (в алфавите ) из области определения функции этот алгоритм перерабатывает в слово .

Таким образом, нормальные алгоритмы примеров 34.6 и 34.7 показывают, что функции и нормально вычислимы. Причем соответствующие нормальные алгоритмы удалось построить в том же самом алфавите , на словах которого были заданы рассматривавшиеся функции, т.е. расширять алфавит не потребовалось . Следующий пример демонстрирует нормальный алгоритм в расширенном алфавите, вычисляющий данную функцию.

Пример 34.9. Построим нормальный алгоритм для вычисления Функции не в одноичной системе (как сделано в примере 34.6), а в десятичной. В качестве алфавита возьмем перечень арабских цифр , а нормальный алгоритм будем строить в его расширении . Вот схема этого нормального алгоритма (читается по столбцам):

Попытаемся применить алгоритм к пустому слову . Нетрудно понять, что на каждом шаге должна будет применяться самая последняя формула данной схемы. Получается бесконечный процесс:

Это означает, что к пустому слову данный алгоритм не применим.

Если применить теперь алгоритм к слову 499, получим следующую последовательность слов: (применена последняя формула) (формула из середины второго столбца) (дважды применена формула из конца второго столбца) (предпоследняя формула) (дважды применена предпоследняя формула первого столбца) (применена формула из середины первого столбца).

Таким образом, слово 499 перерабатывается данным нормальным алгоритмом в слово 500. Предлагается проверить, что .

В рассмотренном примере нормальный алгоритм построен в алфавите , являющемся существенным расширением алфавита (т.е. и ), но данный алгоритм слова в алфавите перерабатывает снова в слова в алфавите . В таком случае говорят, что алгоритм задан над алфавитом .

Создатель теории нормальных алгоритмов советский математик А. А. Марков выдвинул гипотезу, получившую название “Принцип нормализации Маркова”. Согласно этому принципу, для нахождения значений функции, заданной в некотором алфавите, тогда и только тогда существует какой-нибудь алгоритм, когда функция нормально вычислима.

Сформулированный принцип, как и тезисы Тьюринга и Чёрча, носит внематематический характер и не может быть строго доказан. Он выдвинут на основании математического и практического опыта.

Все, что в предыдущих параграфах было сказано о тезисах Тьюринга и Чёрча, можно с полным правом отнести к принципу нормализации Маркова. Косвенным подтверждением этого принципа служат теоремы следующего пункта, устанавливающие эквивалентность и этой теории алгоритмов теориям машин Тьюринга и рекурсивных функций.

---

Совпадение класса всех нормально вычислимых функций с классом всех функций, вычислимых по Тьюрингу

Это совпадение будет означать, что понятие нормально вычислимой функции равносильно понятию функции, вычислимой по Тьюрингу, а вместе с ним и понятию частично рекурсивной функции.

Теорема 34.10. Всякая функция, вычислимая по Тьюрингу, будет также и нормально вычислимой.

Доказательство

Верно и обратное утверждение.

Теорема 34.11. Всякая нормально вычислимая функция вычислима по Тьюрингу.

---

Эквивалентность различных теорий алгоритмов

Итак, в двух последних параграфах мы познакомились с тремя теориями, каждая из которых уточняет понятие алгоритма, и доказали, что все эти теории равносильны между собой. Другими словами, они описывают один и тот же класс функций, т. е. справедлива следующая теорема.

Теорема 34.12. Следующие классы функций {заданных на натуральных числах и принимающих натуральные значения) совпадают:
а) класс всех функций, вычислимых по Тьюрингу;
б) класс всех частично рекурсивных функций;
в) класс всех нормально вычислимых функций.

Полезно уяснить смысл и значение этого важного результата. В разное время в разных странах ученые независимо друг от друга, изучая интуитивное понятие алгоритма и алгоритмической вычислимости, создали теории, описывающие данное понятие, которые оказались равносильными. Этот факт служит мощным косвенным подтверждением адекватности этих теорий опыту вычислений, справедливости каждого из тезисов Тьюринга, Чёрча и Маркова. В самом деле, ведь если бы один из этих классов оказался шире какого-либо другого класса, то соответствующий тезис Тьюринга, Чёрча или Маркова был бы опровергнут. Например, если бы класс нормально вычислимых функций оказался шире класса рекурсивных функций, то существовала бы нормально вычислимая, но не рекурсивная функция. В силу ее нормальной вычислимости она была бы алгоритмически вычислима в интуитивном понимании алгоритма, и предположение о ее нерекурсивности опровергало бы тезис Чёрча. Но классы Тьюринга, Чёрча и Маркова совпадают, и таких функций не существует. Это и служит еще одним косвенным подтверждением тезисов Тьюринга, Маркова и Чёрча.

Можно отметить, что существуют еще и другие теории алгоритмов, и для всех них также доказана их равносильность с рассмотренными теориями.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Нормальный алгоритм Маркова для деления чисел

Добрый день. Хотелось бы поделиться с Вами очень интересным вариантом ненормального прграммирования — составлением нормальных алгоритмов Маркова. Этот вариант программирования может служить великолепным умственным отдыхом от привычных языков и сред программирования.
Студенты, которых я имею возможность учить, кричат криком, что это сложно, но только до первого собственными руками сделанного рабочего алгоритма, потом это перетекает в очень интересные алгоритмические задачки.
Собственно, к теме этого поста: наша задача написать нормальный алгоритм Маркова для деления двух целых чисел с точностью 4 знака после запятой(для задания чисел пользуемся унарной системой исчисления). Например, вход: |/||||, выход: 0.25.
При этом у нас есть только одна операция — замена одной подстроки в исходной строке на другую. Кому интересно что это такое и как это работает — добро пожаловать под кат.

Нормальный алгоритм Маркова

Под нормальным алгоритмом Маркова будем понимать некий упорядоченный набор продукций(замен подстрок). Продукции могут быть как и обыкновенными(выполняться столько раз, сколько это возможно) так и финальными(выполняются только 1 раз и после них работа алгоритма заканчивается). Продукции выполняются начиная с первой. Если первую выполнить нельзя — делаем вторую итд. Если же после какой-либо продукции можно опять выполнить какую-то из предудущих — выполняем. Работа алгоритма закнчивается тогда, когда нет следующей для выполнения продукции и все предыдущие нельзя выполнить или после выполнения какой-нибудь финальной продукции.

Собственно решение поставленной задачи

Список замен:
%* на *%
%| на %*
*| на **
|* на t
t* на *t
t% на %t
%t на %v|
t на |
%v на ?d
?d на d?
|d на d|
? на %
*d на h
h* на oh
h% наh
h на «пустая строка»
* на «пустая строка»
d на |_
/| на -k
k| на kk
k на |+
+| на |+
- на ey
|e на e|
y на %
eo на 0o
e на «пустая строка»
|_ на .a
a. на .a
.. на .
.aaaaaaaaaa на a,.
,a на a,
.aaaaaaaaa на 9
.aaaaaaaa на 8
.aaaaaaa на 7
.aaaaaa на 6
.aaaaa на 5
.aaaa на 4
.aaa на 3
.aa на 2
.a на 1
. на 0
, на «пустая строка»
a на .a
o на p||||||||||
|p на p|
pp на p
% на u
u+ на u
u на _
|+ на |)+
) на (>
>+ на +>
+ на {
{ на |
>>>>> на =
|= на =
(= на =
( на /
p= на =<
<0 на 0<
<1 на 1<
<2 на 2<
<3 на 3<
<4 на 4<
<5 на 5<
<6 на 6<
<7 на 7<
<8 на 8<
<9 на 9<
<<<<< на$
0$ на $0
1$ на $1
2$ на $2
3$ на $3
4$ на $4
5$ на $5
6$ на $6
7$ на $7
8$ на $8
9$ на $9
=$ на .FIN
0= на =0
1= на =1
2= на =2
3= на =3
4= на =4
5= на =5
6= на =6
7= на =7
8= на =8
9= на =9
_> на «пустая строка»
0> на >0
1> на >1
2> на >2
3> на >3
4> на >4
5> на >5
6> на >6
7> на >7
8> на >8
9> на >9
p> на «пустая строка»
p на .FIN
_ на .FIN

FIN после подстроки на которую заменяем означает, что такая продукция финальная.

Написать эмулятор, который позволит эмулировать работу такого алгоритма не составит никакого труда на любом из языков программирования.

В результате для входа |/|||| путем строковых преобразований получим 0.25. Кто не верит — проверьте. (Записываем на бумажке вход, например те же |/|||| и выполняем указанные выше подстановки до тех пор пока алгоритм не закончит свою работу(условие завершения работы см. еще выше))
P.S.Вот такой элегантный и непривычный вариант составления программ и выноса мозга.

P.P.S.Уважаемые господа программисты предлагаю конкурс из серии «А вам слабо?»(Позволит понапрягать мозг и отдохнуть от привычного программирования). Задание простое — составить алгоритм Маркова для умножения двух обыкновенных дробей.
Пример: Вход: (1/2)*(2/5)
Результат должен получиться 1/5
Если это будет кому-нибудь интересно — дерзайте.

From Wikipedia, the free encyclopedia

In theoretical computer science, a Markov algorithm is a string rewriting system that uses grammar-like rules to operate on strings of symbols. Markov algorithms have been shown to be Turing-complete, which means that they are suitable as a general model of computation and can represent any mathematical expression from its simple notation. Markov algorithms are named after the Soviet mathematician Andrey Markov, Jr.

Refal is a programming language based on Markov algorithms.

Description[edit]

Normal algorithms are verbal, that is, intended to be applied to strings in different alphabets.

The definition of any normal algorithm consists of two parts: the definition of the alphabet of the algorithm (the algorithm will be applied to strings of these alphabet symbols), and the definition of its scheme. The scheme of a normal algorithm is a finite ordered set of so-called substitution formulas, each of which can be simple or final. Simple substitution formulas are represented by strings of the form , where and are two arbitrary strings in the alphabet of the algorithm (called, respectively, the left and right sides of the formula substitution). Similarly, final substitution formulas are represented by strings of the form , where and are two arbitrary strings in the alphabet of the algorithm. This assumes that the auxiliary characters and do not belong to the alphabet of the algorithm (otherwise two other characters to perform their role as the dividers of the left and right sides, which are not in the algorithm’s alphabet, should be selected).

Here is an example of a normal algorithm scheme in the five-letter alphabet :

The process of applying the normal algorithm to an arbitrary string in the alphabet of this algorithm is a discrete sequence of elementary steps, consisting of the following. Let’s assume that is the word obtained in the previous step of the algorithm (or the original word , if the current step is the first). If of the substitution formulas there is no left-hand side which is included in the , then the algorithm terminates, and the result of its work is considered to be the string . Otherwise, the first of the substitution formulae whose left sides are included in is selected. If the substitution formula is of the form , then out of all of possible representations of the string of the form (where and are arbitrary strings) the one with the shortest is chosen. Then the algorithm terminates and the result of its work is considered to be . However, if this substitution formula is of the form , then out of all of the possible representations of the string of the form of the one with the shortest is chosen, after which the string is considered to be the result of the current step, subject to further processing in the next step.

For example, the process of applying the algorithm described above to the word results in the sequence of words , , , , , , , , , and , after which the algorithm stops with the result .

For other examples, see below.

Any normal algorithm is equivalent to some Turing machine, and vice versa – any Turing machine is equivalent to some normal algorithm. A version of the Church-Turing thesis formulated in relation to the normal algorithm is called the “principle of normalization.”

Normal algorithms have proved to be a convenient means for the construction of many sections of constructive mathematics. Moreover, inherent in the definition of a normal algorithm are a number of ideas used in programming languages aimed at handling symbolic information – for example, in Refal.

Algorithm[edit]

The Rules are a sequence of pairs of strings, usually presented in the form of pattern → replacement. Each rule may be either ordinary or terminating.

Given an input string:

1. Check the Rules in order from top to bottom to see whether any of the patterns can be found in the input string.
2. If none is found, the algorithm stops.
3. If one (or more) is found, use the first of them to replace the leftmost occurrence of matched text in the input string with its replacement.
4. If the rule just applied was a terminating one, the algorithm stops.
5. Go to step 1.

Note that after each rule application the search starts over from the first rule.

Example[edit]

The following example shows the basic operation of a Markov algorithm.

Rules[edit]

1. “A” -> “apple”
2. “B” -> “bag”
3. “S” -> “shop”
4. “T” -> “the”
5. “the shop” -> “my brother”
6. “a never used” -> .“terminating rule”

Symbol string[edit]

“I bought a B of As from T S.”

Execution[edit]

If the algorithm is applied to the above example, the Symbol string will change in the following manner.

1. “I bought a B of As from T S.”
2. “I bought a B of apples from T S.”
3. “I bought a bag of apples from T S.”
4. “I bought a bag of apples from T shop.”
5. “I bought a bag of apples from the shop.”
6. “I bought a bag of apples from my brother.”

The algorithm will then terminate.

Another example[edit]

These rules give a more interesting example. They rewrite binary numbers to their unary counterparts. For example, 101 will be rewritten to a string of 5 consecutive bars.

Rules[edit]

1. “|0” -> “0||”
2. “1” -> “0|”
3. “0” -> “”

Symbol string[edit]

“101”

Execution[edit]

If the algorithm is applied to the above example, it will terminate after the following steps.

1. “101”
2. “0|01”
3. “00||1”
4. “00||0|”
5. “00|0|||”
6. “000|||||”
7. “00|||||”
8. “0|||||”
9. “|||||”

See also[edit]

• Thue (programming language)
• Formal grammar

References[edit]

• Caracciolo di Forino, A. String processing languages and generalized Markov algorithms. In Symbol manipulation languages and techniques, D. G. Bobrow (Ed.), North-Holland Publ. Co., Amsterdam, The Netherlands, 1968, pp. 191–206.
• Andrey Andreevich Markov (1903-1979) 1960. The Theory of Algorithms. American Mathematical Society Translations, series 2, 15, 1-14. (Translation from the Russian, Trudy Instituta im. Steklova 38 (1951) 176-189^[1])

External links[edit]

• Yad Studio – Markov algorithms IDE and interpreter (Open Source)
• Markov algorithm interpreter
• Markov algorithm interpreter
• Markov algorithm interpreters at Rosetta-Code