Как составить алгоритм нахождения наибольшего общего делителя

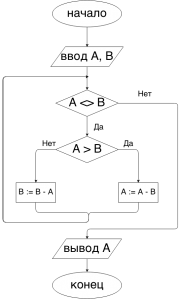
Алгоритм Евклида – нахождение наибольшего общего делителя

Алгоритм Евклида – это алгоритм нахождения наибольшего общего делителя (НОД) пары целых чисел.

Наибольший общий делитель (НОД) – это число, которое делит без остатка два числа и делится само без остатка на любой другой делитель данных двух чисел. Проще говоря, это самое большое число, на которое можно без остатка разделить два числа, для которых ищется НОД.

Решение задачи на языке программирования Python

Алгоритм нахождения НОД делением

Большее число делим на меньшее.
Если делится без остатка, то меньшее число и есть НОД (следует выйти из цикла).
Если есть остаток, то большее число заменяем на остаток от деления.
Переходим к пункту 1.

Пример:
Найти НОД для 30 и 18.
30 / 18 = 1 (остаток 12)
18 / 12 = 1 (остаток 6)
12 / 6 = 2 (остаток 0)
Конец: НОД – это делитель 6.
НОД (30, 18) = 6

a = int(input())
b = int(input())
 
while a != 0 and b != 0:
    if a > b:
        a = a % b
    else:
        b = b % a
 
print(a + b)

В цикле в переменную a или b записывается остаток от деления. Цикл завершается, когда хотя бы одна из переменных равна нулю. Это значит, что другая содержит НОД. Однако какая именно, мы не знаем. Поэтому для определения НОД находим сумму этих переменных. Поскольку в одной из переменных ноль, он не оказывает влияние на результат.

Если условием завершения цикла является равенство хотя бы одной из переменных нулю (a == 0 or b == 0), то условием продолжения его работы является обратное этому условие – обе переменные должны иметь отличные от нуля значения (a != 0 and b != 0).

Блок-схема алгоритма Евклида

Для того, чтобы вышеприведенная программа могла обрабатывать отрицательные числа, в логическом выражении при if должны сравниваться модули значений переменных: if abs(a) > abs(b):. Иначе большим числом может оказаться меньшее по модулю. В этом случае интерпретатор Питона в качестве остатка от деления выдает вещественное число. В результате это приводит к зацикливанию, так как низвести переменные до нуля становится как минимум маловероятным.

Алгоритм нахождения НОД вычитанием

Из большего числа вычитаем меньшее.
Если получается 0, значит, числа равны друг другу и являются НОД (следует выйти из цикла).
Если результат вычитания не равен 0, то большее число заменяем на результат вычитания.
Переходим к пункту 1.

Пример:
Найти НОД для 30 и 18.
30 – 18 = 12
18 – 12 = 6
12 – 6 = 6
6 – 6 = 0
Конец: НОД – это уменьшаемое или вычитаемое.
НОД (30, 18) = 6

a = int(input())
b = int(input())
 
while a != b:
    if a > b:
        a = a - b
    else:
        b = b - a
 
print(a)

Функция, вычисляющая НОД

def gcd(m, n):
    while m != n:
        if m > n:
            m = m - n
        else:
            n = n - m
    return n
 
 
a = int(input())
b = int(input())
 
print(gcd(a, b))

Функция `gcd` модуля `math`

В модуле math языка программирования Python есть функция gcd, вычисляющая наибольший общий делитель двух чисел.

>>> import math
>>> math.gcd(30, 18)
6

Больше задач в PDF

Источник

Алгори́тм Евкли́да — эффективный алгоритм для нахождения наибольшего общего делителя двух целых чисел (или общей меры двух отрезков). Алгоритм назван в честь греческого математика Евклида (III век до н. э.), который впервые описал его в VII^[1] и X^[2] книгах «Начал». Это один из старейших численных алгоритмов, используемых в наше время^[3].

В самом простом случае алгоритм Евклида применяется к паре положительных целых чисел и формирует новую пару, которая состоит из меньшего числа и разницы между большим и меньшим числом. Процесс повторяется, пока числа не станут равными. Найденное число и есть наибольший общий делитель исходной пары. Евклид предложил алгоритм только для натуральных чисел и геометрических величин (длин, площадей, объёмов). Однако в XIX веке он был обобщён на другие типы математических объектов, включая целые числа Гаусса и полиномы от одной переменной. Это привело к появлению в современной общей алгебре такого понятия, как евклидово кольцо. Позже алгоритм Евклида был обобщён на другие математические структуры, такие как узлы и многомерные полиномы.

Для данного алгоритма существует множество теоретических и практических применений. В частности, он является основой для криптографического алгоритма с открытым ключом RSA^[4], широко распространённого в электронной коммерции. Также алгоритм используется при решении линейных диофантовых уравнений^[5], при построении непрерывных дробей^[6], в методе Штурма^[7]. Алгоритм Евклида является основным инструментом для доказательства теорем в современной теории чисел, например таких как теорема Лагранжа о сумме четырёх квадратов^[8] и основная теорема арифметики^[9].

История[править | править код]

Древнегреческие математики называли этот алгоритм ἀνθυφαίρεσις или ἀνταναίρεσις — «взаимное вычитание». Этот алгоритм не был открыт Евклидом, так как упоминание о нём имеется уже в Топике Аристотеля (IV век до н. э.)^[3]. В «Началах» Евклида он описан дважды — в VII книге для нахождения наибольшего общего делителя двух натуральных чисел^[1] и в X книге для нахождения наибольшей общей меры двух однородных величин^[2]. В обоих случаях дано геометрическое описание алгоритма, для нахождения «общей меры» двух отрезков.

Историками математики было выдвинуто предположение, что именно с помощью алгоритма Евклида (процедуры последовательного взаимного вычитания) в древнегреческой математике впервые было открыто существование несоизмеримых величин (стороны и диагонали квадрата, или стороны и диагонали правильного пятиугольника)^[10]. Впрочем, это предположение не имеет достаточных документальных подтверждений. Алгоритм для поиска наибольшего общего делителя двух натуральных чисел описан также в I книге древнекитайского трактата Математика в девяти книгах.

Описание[править | править код]

Алгоритм Евклида для целых чисел[править | править код]

Пусть и — целые числа, не равные одновременно нулю, и последовательность чисел

${displaystyle a>b>r_{1}>r_{2}>r_{3}>r_{4}> dots >r_{n}}$

определена тем, что каждое $r_{k}$ — это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, то есть:

$a=bq_{0}+r_{1},$

$b=r_{1}q_{1}+r_{2},$

$r_{1}=r_{2}q_{2}+r_{3},$

$r_{k-2}=r_{k-1}q_{k-1}+r_{k},$

$r_{n-2}=r_{n-1}q_{n-1}+r_{n},$

$r_{n-1}=r_{n}q_{n}.$

Тогда НОД(a, b), наибольший общий делитель a и b, равен r_n, последнему ненулевому члену этой последовательности^[11].

Существование таких r₁, r₂, …, r_n, то есть возможность деления с остатком m на n для любого целого m и целого n ≠ 0, доказывается индукцией по m.

Корректность этого алгоритма вытекает из следующих двух утверждений^[12]:

I. Пусть a = b⋅q + r, тогда НОД (a, b) = НОД (b, r).

Доказательство

Пусть k — любой общий делитель чисел a и b, не обязательно наибольший, тогда a = t₁⋅k и b = t₂⋅k, где t₁ и t₂ — целые числа из определения.
Тогда k является также общим делителем чисел b и r, так как b делится на k по определению, а ${displaystyle r=a-bcdot q=(t_{1}-t_{2}cdot q)cdot k}$ (выражение в скобках есть целое число, следовательно, k делит r без остатка).
Обратное также верно и доказывается аналогично пункту 2: любой делитель b и r так же является делителем a и b.
Следовательно, все общие делители пар чисел (a, b) и (b, r) совпадают. Другими словами, нет общего делителя у чисел (a, b), который не был бы также делителем (b, r), и наоборот.
В частности, наибольший общий делитель остаётся тем же самым, так как в предположении, что НОД (a, b) > НОД (b, r) или НОД (a, b) < НОД (b, r) получаются противоречия, следовательно, НОД (a, b) = НОД (b, r). Что и требовалось доказать.

II. НОД(r, 0) = r для любого ненулевого r (так как 0 делится на любое целое число).

Геометрический алгоритм Евклида[править | править код]

Пусть даны два отрезка длины a и b. Вычтем из большего отрезка меньший и заменим больший отрезок полученной разностью. Повторяем эту операцию, вычитая из большего отрезка меньший, пока отрезки не станут равны. Если это произойдёт, то исходные отрезки соизмеримы, и последний полученный отрезок есть их наибольшая общая мера. Если общей меры нет, то процесс бесконечен. В таком виде алгоритм описан Евклидом^[2] и реализуется с помощью циркуля и линейки.

Пример[править | править код]

Для иллюстрации алгоритм Евклида будет использован, чтобы найти НОД a = 1071 и b = 462. Для начала от 1071 отнимем кратное значение 462, пока не получим разность меньше, чем 462. Мы должны дважды отнять 462, (q₀ = 2), оставаясь с остатком 147:

1071 = 2 × 462 + 147.

Затем от 462 отнимем кратное значение 147, пока не получим разность меньше, чем 147. Мы должны трижды отнять 147 (q₁ = 3), оставаясь с остатком 21:

462 = 3 × 147 + 21.

Затем от 147 отнимем кратное значение 21, пока не получим разность меньше, чем 21. Мы должны семь раз отнять 21 (q₂ = 7), оставаясь без остатка:

147 = 7 × 21 + 0.

Таким образом последовательность a > b > r₁ > r₂ > r₃ > … > r_n в данном конкретном случае будет выглядеть так:

1071 > 462 > 147 > 21.

Так как последний остаток равен нулю, алгоритм заканчивается числом 21 и НОД(1071, 462) = 21.

В табличной форме шаги были следующие:

Шаг k	Равенство	Частное и остаток
0	1071 = q₀ 462 + r₀	q₀ = 2 и r₀ = 147
1	462 = q₁ 147 + r₁	q₁ = 3 и r₁ = 21
2	147 = q₂ 21 + r₂	q₂ = 7 и r₂ = 0; алгоритм заканчивается

Если требуется найти НОД для более чем двух чисел, алгоритм аналогичен, на каждом шаге все числа, кроме
наименьшего, заменяются остатками по модулю наименьшего. Нулевые остатки, если получатся, вычёркиваются. Алгоритм завершается, когда остаётся одно ненулевое число, это и есть НОД.

Применения[править | править код]

Расширенный алгоритм Евклида и соотношение Безу[править | править код]

Формулы для $r_{i}$ могут быть переписаны следующим образом:

$r_{1}=a+b(-q_{0})$

$r_{2}=b-r_{1}q_{1}=a(-q_{1})+b(1+q_{1}q_{0})$

НОД $(a,b)=r_{n}=as+bt$

Здесь s и t целые. Это представление наибольшего общего делителя называется соотношением Безу, а числа s и t — коэффициентами Безу^[13]. Соотношение Безу является ключевым в доказательстве леммы Евклида и основной теоремы арифметики.

Цепные дроби[править | править код]

Алгоритм Евклида достаточно тесно связан с цепными дробями^[6]. Отношение a/b допускает представление в виде цепной дроби:

${frac {a}{b}}=[q_{0};q_{1},q_{2},cdots ,q_{n}]$

При этом цепная дробь без последнего члена равна отношению коэффициентов Безу t/s, взятому со знаком минус:

$[q_{0};q_{1},q_{2},cdots ,q_{n-1}]=-{frac {t}{s}}$

Последовательность равенств, задающая алгоритм Евклида, может быть переписана в форме:

${begin{aligned}{frac {a}{b}}&=q_{0}+{frac {r_{0}}{b}}\{frac {b}{r_{0}}}&=q_{1}+{frac {r_{1}}{r_{0}}}\{frac {r_{0}}{r_{1}}}&=q_{2}+{frac {r_{2}}{r_{1}}}\&{} vdots \{frac {r_{k-2}}{r_{k-1}}}&=q_{k}+{frac {r_{k}}{r_{k-1}}}\&{} vdots \{frac {r_{N-2}}{r_{N-1}}}&=q_{N}end{aligned}}$

Последнее слагаемое в правой части равенства всегда равно обратному значению левой части следующего уравнения. Поэтому первые два уравнения могут быть объединены в форме:

${frac {a}{b}}=q_{0}+{cfrac {1}{q_{1}+{cfrac {r_{1}}{r_{0}}}}}$

Третье равенство может быть использовано, чтобы заменить знаменатель выражения r₁/r₀, получим:

${frac {a}{b}}=q_{0}+{cfrac {1}{q_{1}+{cfrac {1}{q_{2}+{cfrac {r_{2}}{r_{1}}}}}}}$

Последнее отношение остатков r_k/r_k−1 всегда может быть заменено с использованием следующего равенства в последовательности, и так до последнего уравнения. Результатом является цепная дробь:

${frac {a}{b}}=q_{0}+{cfrac {1}{q_{1}+{cfrac {1}{q_{2}+{cfrac {1}{ddots +{cfrac {1}{q_{N}}}}}}}}}=[q_{0};q_{1},q_{2},ldots ,q_{N}]$

В приведённом выше примере НОД(1071, 462) был посчитан и были найдены частные q_k, равные 2, 3 и 7 соответственно. Поэтому 1071/462 может быть записана как:

${displaystyle {frac {1071}{462}}=2+{cfrac {1}{3+{cfrac {1}{7}}}}=[2;3;7]}$

Линейные диофантовы уравнения[править | править код]

Диофантово уравнение — это уравнение с целочисленными коэффициентами и с одним или несколькими переменными, причём ставится задача поиска лишь его целых корней. Такое уравнение может иметь бесконечно много решений, конечное число решений или не иметь их вовсе. Простейшее диофантово уравнение — линейное с двумя неизвестными:

где a, b, c — целые числа. С помощью алгоритма Евклида может быть найдено полное решение уравнения такого типа^[5]. Сначала с помощью этого алгоритма можно определить d = НОД(a, b). Затем, используя расширенный алгоритм Евклида, определяются такие k и l, что:

То есть x = k и y = l — это частное решение уравнения при c = d. Получается, что если c = q⋅d, то x = q⋅k, y = q⋅l — частное решение исходного уравнения, так как:

Обратно, если существует хотя бы одно решение уравнения, то c кратно d. Это следует из того, что d делит и a, и b (а значит, и всю левую часть), поэтому должно делить и c (правую часть). Таким образом, линейное диофантово уравнение имеет хотя бы одно решение тогда и только тогда, когда c кратно НОД(a, b).

Вариации и обобщения[править | править код]

Евклидово кольцо[править | править код]

Кольца, в которых применим алгоритм Евклида, называются евклидовыми кольцами^[14]. К ним относятся, в частности, кольца целых чисел и кольца многочленов.

Обобщённый алгоритм Евклида для многочленов[править | править код]

Алгоритм Евклида и расширенный алгоритм Евклида естественным образом обобщается на кольцо многочленов k[x] от одной переменной над произвольным полем k, поскольку для таких многочленов определена операция деления с остатком. При выполнении алгоритма Евклида для многочленов аналогично алгоритму Евклида для целых чисел получается последовательность полиномиальных остатков (PRS)^[15].

Пример для кольца Z[x]

Пусть cont(f) по определению — НОД коэффициентов многочлена f(x) из — содержание многочлена. Частное от деления f(x) на cont(f) называется примитивной частью многочлена f(x) и обозначается primpart(f(x)). Эти определения понадобятся для нахождения НОД двух многочленов p₁(x) и p₂(x) в кольце . Для многочленов над целыми числами верно следующее:

cont( НОД ${p_{1}(x),p_{2}(x)})=$ НОД ${cont(p_{1}(x)),cont(p_{2}(x))},$

НОД ${p_{1}(x),p_{2}(x)})=$ НОД ${primpart(p_{1}(x)),primpart(p_{2}(x))}.$

Таким образом, задача поиска НОД двух произвольных многочленов сводится к задаче поиска НОД примитивных полиномов.

Пусть есть два примитивных многочлена p₁(x) и p₂(x) из Z[x], для которых выполняется соотношение между их степенями: deg(p₁(x)) = m и deg(p₂(x)) = n, m > n. Деление многочленов с остатком предполагает точную делимость старшего коэффициента делимого на старший коэффициент делителя, в общем случае деление с остатком выполнить невозможно. Поэтому вводят алгоритм псевдоделения, который всё же позволяет получить псевдочастное и псевдоостаток (prem), которые будут сами по себе принадлежать множеству многочленов над целыми числами.

Под псевдоделением будем понимать, что самому делению предшествует умножение полинома $p_{1}(x)$ на $(lc(p_{2}(x)))^{m-n+1}$ , то есть

$lc(p_{2}(x))^{m-n+1}p_{1}(x)=p_{2}(x)q(x)+r_{2}(x),deg(r(x))<deg(p_{2}(x)),$

где q(x) и r(x) — соответственно псевдочастное и псевдоостаток.

Итак, $p_{1}(x),p_{2}(x)in Z[x]$ , причём $deg(p_{1})=n_{1}geq deg(p_{2})=n_{2}$ . Тогда алгоритм Евклида состоит из следующих шагов:

1. Вычисление НОД содержаний:

c:= НОД ${cont(p_{1}),cont(p_{2})}$ .

2. Вычисление примитивных частей:

$p_{1}'(x):=primpart(p_{1}(x));$

$p_{2}'(x):=primpart(p_{2}(x)).$

3. Построение последовательности полиномиальных остатков:

$p_{1}'(x),$

$p_{2}'(x),$

$p_{3}(x):=prem(p_{1}'(x),p_{2}'(x)),$

$p_{4}(x):=prem(p_{2}'(x),p_{3}(x)),$

$p_{5}(x):=prem(p_{3}(x),p_{4}(x)),$

$p_{h}(x):=prem(p_{h-2}(x),p_{h-1}(x)).$

4. Возврат результата:

Если $deg(p_{h}(x))=0$ , то вернуть , иначе вернуть $ccdot primpart(p_{h}(x))$ .

Ускоренные версии алгоритма[править | править код]

Одним из методов ускорения целочисленного алгоритма Евклида является использование симметричного остатка^[16]:

$r_{i}equiv r_{i-2}{pmod {r_{i-1}}},$

где

$-{frac {r_{i-1}}{2}}leq r_{i}leq {frac {r_{i-1}}{2}}.$

Одна из версий ускоренного алгоритма Евклида для полиномов основывается на том, что промежуточные значения алгоритма в основном зависят от высоких степеней. Применение стратегии «разделяй и властвуй» позволяет уменьшить асимптотическую сложность алгоритма^[16].

Вычислительная сложность алгоритма[править | править код]

Число шагов в алгоритме Евклида для НОД(x,y). Более светлые точки (красные и жёлтые) указывают на относительно меньшее количество шагов, тогда как более тёмные точки (фиолетовые и синие) на большее количество шагов. Самая большая тёмная область следует за прямой y = Φx, где Φ — золотое сечение.

Вычислительная сложность алгоритма Евклида изучена полностью.^[17] Эта сложность может быть описана произведением количества шагов деления, требуемых алгоритмом, на вычислительную сложность одного шага. Первый известный анализ алгоритма Евклида был предложен Рейнаудом в 1811.^[18] Он показал, что число шагов алгоритма для пары чисел (u, v) ограничено v. Позже он улучшил оценку до v/2 + 2. Эмиль Леже в 1837 году изучил наихудший случай, когда для вычисления НОД подаются последовательные числа Фибоначчи.^[19] Затем, в 1841 году, Пьер Джосеф Финк показал,^[20] что количество шагов алгоритма не превышает 2 log₂ v + 1. Следовательно, алгоритм работает за полиномиальное время от размера меньшего из пары чисел (u, v).^[19] Анализ Финка был уточнён Габриэлем Ламе в 1844 году.^[21] Он показал, что количество шагов, необходимых для завершения алгоритма, не более чем в пять раз превышает h — количество цифр в десятичном представлении меньшего из пары чисел (u, v).^[22]^[23]

Когда НОД вычисляется для чисел, которые вписываются в одно машинное слово, каждый шаг алгоритма занимает постоянное время. В данном случае анализ Ламе предполагает, что вычислительная сложность оценивается как O(h). Однако в модели расчёта, подходящей для вычислений с числами больше одного машинного слова, оценка сложности вычисления одного остатка может быть O(h²).^[24] В этом случае общее время для всех этапов алгоритма можно проанализировать с помощью телескопического ряда, показав, что это также O(h²). Для ускорения алгоритма Евклида могут быть использованы современные алгоритмические методы, основанные на методе Шёнхаге — Штрассена для быстрого целочисленного умножения. Это приводит к квазиполиномиальному времени.^[25]

Количество шагов[править | править код]

Число шагов для вычисления НОД двух натуральных чисел a и b обозначим как T(a, b). Если g — это наибольший общий делитель a и b, тогда a = mg и b = ng для двух взаимно простых чисел m и n. Тогда T(a, b) = T(m, n), что можно заметить, если разделить уравнения, полученные при вычислении НОД для пары (a, b), на g.^[26] Используя тот же принцип, число шагов алгоритма остаётся неизменным, если a и b умножаются на общий множитель w, что эквивалентно равенству T(a, b) = T(wa, wb). Следовательно, количество шагов T может сильно различаться между соседними парами чисел, такими как (a, b) и (a, b+1), так как данная величина зависит от НОД.

Рекурсивный характер алгоритма Евклида даёт следующее уравнение T(a, b) = 1 + T(b, r₀) = 2 + T(r₀, r₁) = … = N + T(r_N−2, r_N−1) = N + 1, где T(x, 0) = 0 по предположению.^[17]

Наихудший случай[править | править код]

Если для алгоритма Евклида требуются N шагов для пары натуральных чисел a > b > 0, наименьшие значения a и b, для которых это выполняется — числа Фибоначчи F_N+2 и F_N+1 соответственно.^[27] Тогда, если алгоритм Евклида требует N шагов для пары чисел (a,b), где a > b, выполняются следующие неравенства a ≥ F_N+2 и b ≥ F_N+1. Доказать это можно по математической индукции. Если N = 1, тогда a делится на b без остатка. Наименьшие натуральные числа, для которых это верно, равны b = 1 и a = 2, соответственно F₂ и F₃. Предположим теперь, что результат выполняется для всех значений N до M − 1. Первый шаг алгоритма Евклида с M шагами a = q₀b + r₀, и алгоритм Евклида для пары чисел (b,r₀), где b > r₀, требует M − 1 шагов. По предположению индукции имеем b ≥ F_M+1 и r₀ ≥ F_M. Следовательно, a = q₀b + r₀ ≥ b + r₀ ≥ F_M+1 + F_M = F_M+2, что является искомым неравенством. Это доказательство, опубликованное Габриэлем Ламе в 1844 году, представляет собой начало теории сложности вычислений,^[28] а также первое практическое применение чисел Фибоначчи.^[27]

Теорема Ламе[править | править код]

Число делений с остатком в процессе применения алгоритма Евклида не превосходит упятеренного количества цифр меньшего числа , записанного в десятичной системе^[29].

Среднее[править | править код]

Существуют различные способы вычисления среднего количества шагов алгоритма. Первый способ вычисления — среднее время T(a), необходимое для вычисления НОД заданного числа a и меньшего натурального числа b, выбранного с равной вероятностью из целых чисел от 0 до a − 1.^[17]

${displaystyle T(a)={frac {1}{a}}sum _{0leq b<a}T(a,b).}$

Однако, поскольку T(a, b) сильно колеблется в зависимости от НОД двух чисел, усреднённая функция T(a) также является «шумной».^[30] Для того, чтобы уменьшить этот шум, второе среднее τ(a) берётся по всем числам, взаимно простым с a.

${displaystyle tau (a)={frac {1}{varphi (a)}}sum _{begin{smallmatrix}0leq b<a\gcd(a,b)=1end{smallmatrix}}T(a,b)}$

где φ(a) функция Эйлера. Это среднее плавно растёт с ростом a.^[31]

${displaystyle tau (a)={frac {12}{pi ^{2}}}ln 2ln a+C+O(a^{-1/6-varepsilon })}$

Константа (константа Портера^[32]) в этой формуле , а ε является бесконечно малым.

Третье среднее значение Y(n) определяется как среднее число шагов, требуемых, когда a и b выбираются случайным образом (с равномерным распределением) от 1 до n.

${displaystyle Y(n)={frac {1}{n^{2}}}sum _{a=1}^{n}sum _{b=1}^{n}T(a,b)={frac {1}{n}}sum _{a=1}^{n}T(a).}$

Вычислительная сложность шага[править | править код]

На каждом шаге алгоритма Евклида вычисляется коэффициент q_k и остаток r_k для заданной пары целых чисел r_k−2 и r_k−1. Эти величины связаны следующим соотношением:

r_k−2 = q_k r_k−1 + r_k

Вычислительная сложность каждого шага связана главным образом с нахождением q_k, так как остаток r_k можно быстро вычислить, используя r_k−2, r_k−1, и q_k

r_k = r_k−2 − q_k r_k−1

Вычислительная сложность операции деления чисел размером h бит оценивается как O(h(ℓ+1)), где ℓ размер частного.^[24]

Для сравнения, исходный алгоритм Евклида, с использованием вычитания, может быть намного медленнее. В большинстве случаев коэффициент q_k является малым числом. Вероятность данного частного q примерно равна ln|u/(u − 1)|, где u = (q + 1)².^[33] Для иллюстрации вероятность частного 1, 2, 3 или 4 составляет примерно 41,5 %, 17,0 %, 9,3 % и 5,9 % соответственно. Так как операция вычитания быстрее, чем деление, особенно для чисел больше одного машинного слова,^[34] алгоритм Евклида с использованием вычитания может быть более конкурентоспособным в сравнении с алгоритмом, использующим деление.^[35] Это используется в бинарном алгоритме вычисления НОД.^[36]

Оценка сложности алгоритма вычисляется как произведение количества шагов на время выполнения одного шага. Она показывает, что алгоритм Евклида растёт квадратично O(h²), где h — среднее число цифр в двух начальных числах a и b в десятичной записи. Пусть h₀, h₁, …, h_N−1 представляют число цифр в последовательных остатках r₀, r₁, …, r_N−1. Так как число шагов N растёт линейно с h, время работы ограничено следующим выражением:

${displaystyle O{Big (}sum _{i<N}h_{i}(h_{i}-h_{i+1}+2){Big )}subseteq O{Big (}hsum _{i<N}(h_{i}-h_{i+1}+2){Big )}subseteq O(h(h_{0}+2N))subseteq O(h^{2}).}$

Примечания[править | править код]

↑ ¹ ² Мордухай-Болтовской, 1949, с. 11—13.
↑ ¹ ² ³ Мордухай-Болтовской, 1949, с. 103—105.
↑ ¹ ² Кнут, 2001, с. 378.
↑ Menezes, 1996, с. 286.
↑ ¹ ² Курант, 2001, с. 74—76.
↑ ¹ ² Виноградов, 1952, с. 14—18.
↑ Энгелер, 1987, с. 24—31.
↑ Тихомиров, 2003, с. 11—14.
↑ Калужин, 1969, с. 6—14.
↑ Цейтен, 1932, с. 112—114.
↑ Виноградов, 1952, с. 9—10.
↑ Курант, 2001, с. 67—70.
↑ Хассе, 1953, с. 29—30.
↑ Курош, 1973, с. 91—92.
↑ Панкратьев, 2007, с. 54—58.
↑ ¹ ² Gathen, 2013, с. 313—326.
↑ ¹ ² ³ Knuth, 1997, с. 344.
↑ Shallit, 1994, с. 414.
↑ ¹ ² Shallit, 1994, с. 401—419.
↑ Shallit, 1994, с. 413.
↑ Lame, 1844, с. 867—870.
↑ Grossman, 1924, с. 443.
↑ Абрамов С. А. Математические построения и программирование. — М., Наука, 1978. — Тираж 100 000 экз. — c. 170
↑ ¹ ² Knuth, 1997, с. 257—261.
↑ Moeller, 2005, с. 1.
↑ Ore, 1948, с. 45.
↑ ¹ ² Knuth, 1997, с. 343.
↑ LeVeque, 1996, с. 3.
↑ Абрамов С. А. Математические построения и программирование. — М., Наука, 1978. — Тираж 100 000 экз. — c. 170
↑ Knuth, 1997, с. 353.
↑ Tonkov, 1974, с. 47—57.
↑ Weisstein, Eric W. Porter’s Constant (англ.) на сайте Wolfram MathWorld.
↑ Knuth, 1997, с. 352.
↑ Wagon, 1999, с. 335—336.
↑ Cohen, 1993, с. 14.
↑ Cohen, 1993, с. 14—15, 17-18.

Литература[править | править код]

Абрамов С. А. Самый знаменитый алгоритм // Квант / под ред. И. К. Кикоин, Ю. А. Осипьян, В. В. Козлов, А. Л. Семёнов, А. А. Гайфуллин — МИАН, 1985. — вып. 11. — С. 44—46. — ISSN 0130-2221
Виноградов И. М. Основы теории чисел. — М.—Л.: ГИТТЛ, 1952. — 180 с. — ISBN 978-5-811-40535-0.
Калужин Л. А. Основная теорема арифметики. — Популярные лекции по математике. — М.: Наука, 1969. — 33 с.
Кнут Д. Э. Искусство программирования. — Вильямс, 2001. — Т. 2. — 829 с. — ISBN 5-8459-0081-6.
Курант Р., Роббинс Г. Дополнение к главе I, § 4. // Что такое математика? — 3-e изд., испр. и доп. — М., 2001. — 568 с. — ISBN 5-900916-45-6.
Курош А. Г. Лекции по общей алгебре / под ред. О. Н. Головин — 2-е изд. — М.: Наука, 1973. — 400 с. — ISBN 978-5-8114-0617-3
Начала Евклида / пер.с греч. и комм. Д. Д. Мордухая-Болтовского под ред. Выгодского М. Я. и Веселовского И. Н.. — ГИТТЛ, 1949. — Т. 2. — 511 с.
Панкратьев Е. В. Элементы компьютерной алгебры. — ИНТУИТ, 2007. — 217 с. — ISBN 978-5-955-60099-4.
Тихомиров В. М. Великие математики прошлого и их великие теоремы. — 2-е изд., испр. — МЦНМО, 2003. — 16 с. — ISBN 5-94057-110-7.
Хассе Г. Лекции по теории чисел. — Изд. иностранной литературы, 1953. — 527 с.
Цейтен Г. Г. История математики в Древности и в Средние века. — ГТТИ, 1932. — 232 с.
Энгелер Э. Метаматематика элементарной математики. — М.: Мир, 1987. — 128 с.
Cohen H. A Course in Computational Algebraic Number Theory. — Springer-Verlag, 1993. — ISBN 0-387-55640-0.
von zur Gathen J., Gerhard J. Modern Computer Algebra. — Cambridge University Press, 2013. — 808 с. — ISBN 978-1-107-03903-2.
Grossman H. On the Number of Divisions in Finding a G.C.D. (англ.) // The American Mathematical Monthly. — 1924. — Vol. 31, iss. 9. — P. 443. — doi:10.2307/2298146. — JSTOR 2298146.
Knuth D. E. The Art of Computer Programming. — 3. — Addison–Wesley, 1997. — Т. 2: Seminumerical Algorithms. — ISBN 0-201-89684-2.
Lamé G. Note sur la limite du nombre des divisions dans la recherche du plus grand commun diviseur entre deux nombres entiers (фр.). — Comptes Rendus Acad. Sci., 1844. — N^o 19.
LeVeque W. J. Fundamentals of Number Theory (англ.). — Dover, 1996. — ISBN 0-486-68906-9.
Menezes A., van Oorschot P., Vanstone S. Handbook of Applied Cryptography. — CRC-Press, 1996. — 816 с. — (Discrete Mathematics and Its Applications). — ISBN 0-8493-8523-7.
Moeller Niels. Mathematics of Computation (англ.). — 2005.
Ore O. Number Theory and Its History (англ.). — McGraw–Hill, 1948.
Shallit J. Origins of the analysis of the Euclidean algorithm (англ.) // Historia Math.. — 1994. — Vol. 21. — doi:10.1006/hmat.1994.1031.
Tonkov T. On the average length of finite continued fractions (англ.) // Acta Arithmetica. — 1974. — Vol. 26.
Wagon S. Mathematica in Action (англ.). — Springer-Verlag, 1999. — ISBN 0-387-98252-3.

Ссылки[править | править код]

Реализация алгоритма Евклида на языке Pascal

Алгоритм Евклида на e-maxx.ru
Реализация расширенного алгоритма Евклида на языке C

Источник

Алгоритм Евклида

Для начала разберемся, что это и как это работает. Алгоритм Евклида позволяет найти нам наибольший общий делитель чисел. Как это работает:
Пусть a = 18, b = 30.
Цикл: a!=0 and b!=0
Если a > b, то a = a % b, если меньше, то b = b % a, таким образом мы сначала находим остаток деления, а потом повторяем действия. У нас a < b, значит, ищем остаток деления b % a (30 % 18) = 12, присваиваем b = 12, повторяем цикл но теперь у нас уже a > b(b = 12)
значит выполняем a % b (18 % 12) = 6? снова переходим к циклу, теперь снова b > a, значит выполняем b % a (30 % 6), остаток от деления 0, на этом мы прекращаем наш цикл и узнаем, что наибольший общий делитель 18 и 30 = 6. и выводим a + b (b = 0, a = 6).

Python

#!/usr/bin/env python
a = 18
b = 30
 
while a!=0 and b!=0:
    if a > b:
        a = a % b
    else:
        b = b % a
 
print (a+b)

Perl:

 sub nod
 {
 return  $_[0] != 0  ?  nod ( ( $_[1] % $_[0] ), $_[0] )  :  $_[1];
 }

C:

 int gcd(int a, int b) {
   int c;
   while (b) {
      c = a % b;
      a = b;
      b = c;        
   }
   return abs(a);
 }

Pascal:

  function nod( a, b: longint): longint; 
  begin
   while (a <> 0) and (b <> 0) do
     if a >= b then 
       a:= a mod b 
     else 
       b:= b mod a;
   nod:= a + b;
  end;

Java:

public class GCD {
    public static int gcd(int a,int b) {
        while (b !=0) {
            int tmp = a%b;
            a = b;
            b = tmp;
        }
        return a;
    }
}

C#:

int gcd(int a, int b)
{
    while (b != 0)
        b = a % (a = b);
    return a;
}

Источник

Приветствуем читателей и посетителей нашего сайта! Сегодня на learnpascal.ru открывается новая рубрика — Алгоритмы. В этой рубрике мы с вами будем разбирать различные алгоритмы, а также их реализацию на Паскале.

Для освоения материала сегодняшнего урока вам понадобится знание циклов и ветвлений.

Сегодня мы рассмотрим три алгоритма(из пяти) на нахождение наибольшего общего делителя двух целых чисел, два из которых непосредственно связывают с именем Евклида. Еще два мы рассмотрим в следующей части.
Наибольший общий делитель (НОД) двух чисел a и b — наибольшее целое число, которое делит их оба.
Пример: НОД(25, 5) = 5; НОД(12, 18) = 6.

Переборный алгоритм

Начинаем перебор с d — наименьшего из двух чисел. Это первый, очевидный кандидат на роль их наибольшего общего делителя. А затем, пока d не делит оба числа, уменьшаем его на единицу. Как только такое деление будет обеспечено, останавливаем уменьшение d.

var
  a, b, d: integer;

begin
  write('Введите два числа: ');
  readln(a, b);
  if a < b then d := a + 1 else d := b + 1; 
  {так как мы используем цикл с постусловием, 
  необходимо минимальное значение увеличить на один,
  иначе цикл repeat, в силу своих конструктивных особенностей,
  не учтет это минимальное число  
  и не сделает его кандидатом в НОД. Например, 5 и 25.}
  repeat d := d - 1
  until (a mod d = 0) and (b mod d = 0);
  write('NOD = ', d)
end.

Обратимся к этой программе, например, с числами 30 и 18. Тогда на пути к ответу(числу 6) ей придется перебрать числа: 18, 17, 16, 15, 14, 13, 12, 11, 10, 9, 8, 7, 6.

Алгоритм Евклида «с вычитанием»

Пусть a и b — целые числа, тогда верны следующие утверждения:

Все общие делители пары a и b являются также общими делителями пары a — b, b;
И наоборот, все общие делители пары a — b и b являются также общими делителями пары a и b;
НОД(A, B) = НОД(A — B, B), если A > B;
НОД(A, 0) = A.

Доказательство:

Если t — произвольный общий делитель a и b, то он делит и разность a — b. Действительно, из a = t * u и b = t * v следует, что a — b = t * u — t * v = t * (u — v). То есть t — также общий делитель а — b и b.
Обратно, если t — произвольный делитель общий делитель a — b и b, то он делит и их сумму a — b + b = a. Это можно доказать аналгично предыдущему. Поэтому t — также общий делитель a и b.
Делаем вывод, что множество общих делителей a и b совпадает с множеством делителей a — b и b. В частности, совпадают и наибольшие общие делители этих пар.
Наибольшее целое, на которое делится число a, есть само число а. Число 0 делится на любое число. Отсюда наибольший общий делитель а и 0 равен а.

Доказанная формула(3) позволяет свести вычисление наибольшего делителя одной пары к вычислению наибольшего общего делителя другой пары, в которой числа уже меньше. Очевидная же формула (4) дает нам понять, когда надо остановиться.

Вкратце алгоритм Евклида «с вычитанием» будет таким. Вычитаем из большего числа меньшее и заменяем большее на разность до тех пор, пока одно из чисел не обратится в нуль. Тогда оставшееся ненулевое число — наибольший общий делитель.

Пример. Пусть а = 82 и b = 60. НОД(82, 60) = НОД(22, 60) = НОД(22, 38) = НОД(22, 16) = НОД(6, 16) = НОД(6, 10) = НОД(6, 4) = НОД(2, 4) = НОД(2, 2) = НОД(2, 0) = 2.

На предпоследнем шаге алгоритма, перед появлением 0, оба числа равны, иначе не мог возникнуть 0. Поэтому мы будем извлекать НОД именно в этот момент.

Блок — схема алгоритма Евклида «с вычитанием»

Программа

var
  a, b: integer;

begin
  write('a = '); 
  readln(a);
  write('b = ');
  readln(b);
  while a <> b do 
    if a > b then 
      a := a - b 
    else 
      b := b - a;
  writeln('NOD = ', a);
end.

Алгоритм Евклида с «делением»

Пусть a и b — целые числа, а r — остаток от деления a на b. Тогда НОД(a, b) = НОД(b, r).

Эта формула также позволяет свести вычисление наибольшего общего делителя одной пары чисел к вычислению наибольшего обшего делителя другой пары чисел.

Пример. НОД(82, 60) = НОД(22, 60) = НОД(22, 16) = НОД(6, 16) = НОД(6, 4) = НОД(2, 4) = НОД(0, 2) = 2.

var
  a, b: integer;

begin
  write('a = ');
  readln(a);
  write('b = ');
  readln(b);
  while (a <> 0) and (b <> 0) do
    if a >= b 
    then 
      a := a mod b 
    else 
      b := b mod a;
  write(a + b)
end.

На сегодня все! Еще несколько модификаций алгоритма Евклида и способов нахождения НОД вы узнаете на следующих уроках.

Источник

Министерство
образования, науки и молодежи Республики Крым

Конкурс
проектных и исследовательских работ

«Мои
первые шаги в науку – 2017»

Направление
математика

Различные
алгоритмы нахождения НОД

Работу выполнила:

Андрусенко
Диана Анатольевна,

ученица
7 класса

муниципального
бюджетного

общеобразовательного
учреждения

«Сакская
средняя школа № 2»

города
Саки Республики Крым

Научный
руководитель:

Куртмаметова Эльмара Айдаровна,

учитель математики

муниципального бюджетного

общеобразовательного
учреждения

«Сакская
средняя школа № 2»

города
Саки Республики Крым

г.
Саки, 2017

Оглавление

Введение
3

Глава 1. «Прадедушка»
всех алгоритмов 5

Глава 2. Алгоритмы
вычисления НОД

2.1. Алгоритм
простого перебора
6

2.2. Алгоритм разложения
на множители
6

2.3. Алгоритм
Евклида 6

2.4. Бинарный алгоритм Евклида. 7

2.5. Геометрический метод нахождения наибольшего общего делителя 8

2.6. Вычисление НОД трех и более чисел.
8

2.7. Нахождение НОД отрицательных чисел
9

Глава 3 Оценка эффективности применения алгоритмов

3.1. Сравнение
алгоритмов Евклида вычитанием и делением.
10

3.2. Сравнение
алгоритмов вычисления НОД
10

Заключение 12

Литература
13

Приложение 14

Введение.

Мы с вами, можем удивляться, узнав, что
всю жизнь мы исполняем огромное число всякого рода алгоритмов.

В каждодневной жизни человеку приходится
решать большое число разного рода задач, в широком смысле этого слова, не
только математических или физических, которые требуют применения определённых
алгоритмов.

Когда мы переходим улицу на регулируемом
светофором перекрёстке, мы выполняем определённый алгоритм, когда же переходим
улицу в месте, не регулируемом светофором, выполняем другой алгоритм (эти
алгоритмы заданы правилами уличного движения). И когда мы берём книги в
библиотеке, мы выполняем определённые правила пользования библиотечными
книгами, т.е. тоже определенный алгоритм.

Разве можно перечислить все задачи, при
решении которых мы используем определённые алгоритмы?

Слово алгоритм стало широко употребляться
в последнее время. Оно означает описание совокупности действий, составляющих
некоторый процесс. Обычно здесь подразумевают процесс решения некоторой задачи,
но и кулинарный рецепт, и инструкция по пользованию стиральной машиной, и ещё
многие другие правила, не имеющие отношения к математике, являются алгоритмами.

Данная работа
знакомит с алгоритмами вычисления НОД. Знакомство с ними не только дополняет и
углубляет знания, но и развивает интерес к предмету, любознательность и
логическое мышление. Предлагаемая работа помогает увидеть красоту
математических выкладок и эстетику алгоритма Евклида, а так же помочь нам не
бояться громоздких и очень трудных с виду задач с НОД, помня пословицу: «Волков
бояться, в лес не ходить!».

Например,
это может пригодиться, если мы захотим представить какое-нибудь рациональное
число в виде дроби, имеющей по возможности меньший числитель и знаменатель. Или
позволит найти красивые способы решения нестандартных текстовых задач.

Мне стало
интересно, а есть ли другие способы нахождения НОД и, если есть, то, может быть
они интереснее или рациональнее уже известных нам. Я заинтересовалась этим и
решила разобраться в этом вопросе подробнее

Гипотеза: Если
алгоритм Евклида является удобным и быстрым способом вычисления НОД, то нужно знакомить
с ним учащихся и чаще использовать.

Цель
исследования:
изучить разные алгоритмы вычисления НОД, выявить наиболее рациональные способы
решения, красиво и сравнительно просто приводящие к ответу.

Достижение
поставленной цели требует решения следующих основных задач:

1. Рассмотреть
несколько алгоритмов вычисления НОД

2. Сравнить
алгоритмы вычисления НОД

3. Провести
анкетирование

4. Составить
список рекомендаций

Предмет
исследования: Алгоритмы вычисления НОД

Объект
исследования: умения и навыки вычисления НОД

Методы
исследования:

·
Изучение специальной литературы по данному
вопросу: энциклопедии, справочники и учебные пособия.

·
Сравнение и анализ.

·
Обработка полученных данных

·
Работа в компьютерных программах Microsoft Word,
Microsoft PowerPoint

Глава 1. «Прадедушка»
всех алгоритмов

Алгоритм Евклида —
эффективный алгоритм для нахождения наибольшего общего делителя двух целых
чисел. Алгоритм назван в честь греческого математика Евклида, который впервые
описал его в VII и X книгах «Начал».

Первое описание алгоритма находится в
«Началах Евклида» (около 300 лет до н. э.), что делает его одним из старейших
численных алгоритмов, используемых в наше время. Оригинальный алгоритм был
предложен только для натуральных чисел и геометрических длин (вещественных
чисел). Однако в 19 веке он был обобщён на другие типы чисел, такие как целые
числа Гаусса и полиномы от одной переменной.

Для данного алгоритма существует множество
теоретических и практических применений. В частности он широко распространён в
электронной коммерции. Также алгоритм используется при решении диофантовых
уравнений, при построении непрерывных дробей. Алгоритм Евклида является
основным инструментом для доказательства теорем в современной теории чисел.

Долгое время алгоритм Евклида был самым
эффективным способом отыскания наибольшего общего делителя, однако с появлением
электронно-вычислительных машин ситуация изменилась (алгоритм Евклида, как
нетрудно понять, появился задолго до вычислительных машин). Учет специфических
особенностей выполнения арифметических операций компьютером позволил построить
более эффективную (для программной реализации) версию алгоритма Евклида.

Глава 2. Алгоритмы
вычисления НОД

2.1 Алгоритм
простого перебора

Чтобы найти
наибольший общий делитель двух данных натуральных чисел можно действовать по
определению: выписать все делители этих чисел, выделить среди них общие и
выбрать среди всех общих делителей наибольший.

Пример.

Найдем все
делители чисел 54 и 36.

54 делится на
1; 2; 3; 6; 9; 18; 27; 54.

36 делится на
1; 2; 3; 4; 6; 9; 18; 36.

Общими делителями
являются числа: 1, 2, 3, 6, 9, 18.

Значит НОД(54;
36)=18

2.2. Нахождение НОД с помощью разложения
чисел на простые множители

Рассмотрим еще
один способ нахождения НОД. Наибольший общий делитель может быть найден по
разложениям чисел на простые множители.

Сформулируем
правило: НОД двух целых положительных чисел a и b равен произведению всех общих
простых множителей, находящихся в разложениях чисел a и b на простые множители.

Приведем пример
для пояснения правила нахождения НОД.

Пусть нам известны
разложения чисел 220 и 600 на простые множители, они имеют вид 220=2·2·5·11 и
600=2·2·2·3·5·5. Общими простыми множителями, участвующими в разложении чисел
220 и 600, являются 2, 2 и 5. Следовательно, НОД(220, 600)=2·2·5=20.

Таким образом,
если разложить числа a и b на простые множители и найти произведение всех их
общих множителей, то будет найден наибольший общий делитель чисел a и b.

Пример.

Найдите
наибольший общий делитель чисел 72 и 96.

Решение.

Разложим числа 72
и 96 на простые множители.

72=2·2·2·3·3 и
96=2·2·2·2·2·3. Общими простыми множителями являются 2, 2, 2 и 3. Таким
образом, НОД(72, 96)=2·2·2·3=24.

Ответ: НОД(72,
96)=24.

В заключение
этого пункта заметим, что справедливость приведенного правила нахождения НОД
следует из свойства наибольшего общего делителя, которое утверждает, что
НОД(m·a, m·b)=m·НОД(a, b), где m – любое целое положительное число.

2.3. Алгоритм
Евклида

Одним из
простейших алгоритмов нахождения наибольшего общего делителя является Алгоритм
Евклида. Он может быть реализован, как при помощи вычитания, так и деления. Рассмотрим
каждый из этих двух способов.

а) Описание
алгоритма нахождения НОД вычитанием:

Из большего числа
вычитаем меньшее.

Если получается 0,
то значит, что числа равны друг другу и являются НОД (следует выйти из цикла).

Если результат
вычитания не равен 0, то большее число заменяем на результат вычитания.

Переходим к пункту
1.

Пример:

Найти НОД для 30
и 18.

30 – 18 = 12

18 – 12 = 6

12 – 6 = 6

6 – 6 = 0 Конец:
НОД – это уменьшаемое или вычитаемое. НОД (30, 18) = 6

б) Описание
алгоритма нахождения НОД делением:

Большее число
делим на меньшее.

Если делится без
остатка, то меньшее число и есть НОД (следует выйти из цикла).

Если есть остаток,
то большее число заменяем на остаток от деления.

Переходим к пункту
1.

Пример.

Пусть
требуется найти НОД(102;84). Разделим одно число на другое и определим остаток.

102=84*1+18
0 <18<84

Теперь
проделаем такую же операцию для чисел 84 и 18:

84=18*4+
12 0 <12<18

Следующий
шаг – для 18 и 12:

18=12*1+6
0 <6<12

Теперь
– для 12 и 6:

12=6*2+0
0-остаток. Процесс закончился.

2.4. Бинарный алгоритм Евклида.

Бинарный
алгоритм вычисления наибольшего общего делителя, как понятно из названия,
находит наибольший общий делитель двух целых чисел. Данный
алгоритм быстрее обычного алгоритма
Евклида, т.к. вместо медленных операций деления и умножения используются сдвиги.
Алгоритм был известен еще в Китае 1-го века, но опубликован был лишь в 1967
году израильским физиком и программистом Джозефом Стайном. Он основан на
использовании следующих свойств НОД:

НОД(2a; 2b) = 2 НОД(a; b),

НОД(2a; 2b+1) = НОД(a; 2b+1),

НОД(-a; b) = НОД(a; b)

Сам
алгоритм выглядит так:

1. Если
a, b чётные, то НОД(a; b)
= 2*НОД(a/2; b/2);

2. Если
a чётное, b нечётное, то НОД(a; b)
= НОД(a/2; b);

3. Если
b чётное, a нечётное, то НОД(a; b)
= НОД(a; b/2);

4. Если
a, b нечётные и b > a, то НОД(a; b) = НОД((b–a)/2; a);

5. Если
a, b нечётные и b < a, то НОД(a; b) = НОД((a–b)/2; b);

2.5. Геометрический метод
нахождения наибольшего общего делителя (НОД) натуральных чисел с помощью
квадратов.

Этот алгоритм – геометрическая иллюстрация
алгоритма Евклида, описанного в 5-ом способе.

Например: Найти НОД(162;48).

Построим прямоугольник со сторонами 162мм и 48
мм.

От прямоугольника отрежем несколько квадратов со
стороной 48 мм – таких квадратов три.

Остался прямоугольник со сторонами 48
мм и 162-3*48=18 мм.

От полученного прямоугольника снова отрезаем
квадраты, у которых сторона равна 18 мм – таких квадратов получится два.

Остался прямоугольник со сторонами 18
мм и 48-2*18=12 мм.

От полученного прямоугольника снова отрезаем
квадраты, у которых сторона равна 12 мм – такой квадрат будет единственный.

Остался прямоугольник со сторонами 12
мм и 18-12=6 мм, который , в свою очередь состоит из двух квадратов 6мм х 6
мм.

Длина стороны последнего полученного квадрата и
есть наибольший общий делитель чисел 162 и 48.

Ответ: НОД(162; 48)=6.

Этот способ мне кажется нерациональным:
вычерчивая прямоугольники и квадраты, легко ошибиться в построениях и получится
неверный ответ. Но все же я попробовала решить этим способом несколько примеров
нахождения наибольшего общего делителя двух натуральных чисел (см. приложение).

2.6. Нахождение НОД трех и большего
количества чисел

Нахождение
наибольшего общего делителя трех и большего количества чисел может быть сведено
к последовательному нахождению НОД двух чисел. Теорема: наибольший общий
делитель нескольких чисел a₁, a₂, …, a_k равен
числу d_k, которое находится при последовательном вычислении НОД(a₁,
a₂)=d₂, НОД(d₂, a₃)=d₃,

НОД(d₃,
a₄)=d₄, …, НОД(d_k-1,
a_k)=d_k.

Давайте разберемся, как
выглядит процесс нахождения НОД нескольких чисел, рассмотрев решение примера.

Пример.

Найдите
наибольший общий делитель четырех чисел 78, 294, 570 и 36.

Решение. В этом
примере a₁=78, a₂=294, a₃=570, a₄=36.

Сначала по
алгоритму Евклида определим наибольший общий делитель d₂двух первых
чисел 78 и 294. При делении получаем равенства 294=78·3+60; 78=60·1+18;
60=18·3+6 и 18=6·3. Таким образом, d₂=НОД(78, 294)=6.

Теперь вычислим d₃=НОД(d₂,
a₃)=НОД(6, 570). Опять применим алгоритм Евклида: 570=6·95,
следовательно, d₃=НОД(6, 570)=6.

Осталось
вычислить d₄=НОД(d₃, a₄)=НОД(6, 36). Так как
36 делится на 6, то d₄=НОД(6, 36)=6.

Таким образом,
наибольший общий делитель четырех данных чисел равен d₄=6, то есть,

НОД(78, 294, 570,
36)=6.

Ответ: НОД(78,
294, 570, 36)=6.

Разложение чисел на простые множители
также позволяет вычислять НОД трех и большего количества чисел. В этом случае
наибольший общий делитель находится как произведение всех общих простых
множителей данных чисел.

Пример.

Вычислите НОД чисел из предыдущего
примера, используя их разложения на простые множители.

Решение.

Разложим числа 78, 294, 570 и 36 на
простые множители, получаем 78=2·3·13, 294=2·3·7·7, 570=2·3·5·19, 36=2·2·3·3.
Общими простыми множителями всех данных четырех чисел являются числа 2 и 3.
Следовательно, НОД(78, 294, 570, 36)=2·3=6.

Ответ: НОД(78, 294, 570, 36)=6.

2.7. Нахождение НОД отрицательных чисел

Если одно, несколько или все числа,
наибольший делитель которых нужно найти, являются отрицательными числами, то их
НОД равен наибольшему общему делителю модулей этих чисел. Это связано с тем,
что противоположные числа a и −a имеют одинаковые делители.

Пример.

Найдите НОД отрицательных целых чисел
−231 и −140.

Решение.

Модуль числа −231 равен 231, а модуль
числа −140 равен 140, и НОД(−231, −140) = НОД(231, 140). Алгоритм Евклида дает
нам следующие равенства: 231=140·1+91; 140=91·1+49; 91=49·1+42; 49=42·1+7 и
42=7·6. Следовательно, НОД(231, 140)=7. Тогда искомый наибольший общий делитель
отрицательных чисел −231 и −140 равен 7.

Ответ: НОД(−231, −140)=7.

Глава 3 Оценка эффективности применения алгоритмов

3.1. Сравнение
алгоритмов Евклида вычитанием и делением.

Возьмем два числа: 112 и 32. Первое больше
второго – присвоим ему остаток от деления 112 на 32. Теперь у нас имеются числа
16 и 32. Второе больше, поэтому присвоим ему остаток отделения 32 на 16, т. е.
0. Так выглядят эти действия в виде таблицы:

Начальные данные 112 32

Шаг 1
16 32

Шаг 2
16 0

А теперь снова, используя те же самые
числа, составим таблицу, но на этот раз при помощи алгоритма вычитания.

Начальные данные
112 32

Шаг 1
80 32

Шаг 2
48 32

Шаг 3
16 32

Шаг 4
16 0

Из примера видно, что Алгоритм Евклида,
реализуемый делением эффективней метода вычитания.

3.2. Сравнение
алгоритмов вычисления НОД

Сравним
алгоритмы вычисления НОД на двух примерах:

I.
Сколько шагов потребуется, чтобы вычислить НОД (1980; 390)

1) алгоритм простого перебора – 360 шагов

2) алгоритм разложения на простые множители – 14 шагов

3) бинарный алгоритм Евклида – 4 шага

4) алгоритм Евклида – 2 шага

II.
Найти НОД (20451; 3065)

1) алгоритм простого перебора – 6018 шагов

2) алгоритм разложения на простые множители – 25 шагов

3) бинарный алгоритм Евклида – 7 шагов

4) алгоритм Евклида – 7 шагов

Чтобы
убедится в преимуществе приема последовательного деления над приемами
разложения на простые множители, когда имеем дело с большими числами,
рассмотрим следующий пример. Найти НОД (4847, 4181).

Разложение
данных чисел на простые множители является делом нелегким, так как ни одно из
чисел 2, 3, 4, 5, 6, 9, для которых устанавливаются в школе признаки делимости,
не является делителем данных чисел. Алгоритм же Евклида легко и быстро приводит
к результату: НОД (4847, 4181) = НОД(4181,666)=НОД(666,185)=НОД(185,111)=

НОД(111,74)=НОД(74,37)=37

Другой пример:
сократить дробь .

Решение.
Выполним деление с остатком. Разделим 833 на 714:

833 714

714
1

119

Здесь
делимое а = 833, делитель в = 714 и остаток r = 119.

НОД
(833,714) = НОД (714, 119). Теперь разделим 714 на 119:

714
119

714 6

0 Таким образом, НОД (833 и 714) = 119. Тогда = = !

Заключение.

В
процессе проделанной работы в соответствии с ее целями и задачами были получены
следующие выводы и результаты:

–
я поняла самое главное, что при глубоком изучении данной темы мы получаем
большие вычислительные навыки, навыки устного и быстрого счета, которые потом в
дальнейшем пригодятся нам для решения более сложных задач математики, для
решения практических задач, для успешной сдачи ЕГЭ.

Для
поиска НОД натуральных чисел существуют различные алгоритмы:

Если
данные числа сравнительно невелики, то лучший алгоритм – непосредственный
перебор.
Если
числа достаточно большие, то нахождение НОД(а;b)
путем перечисления всех делителей чисел а и b –
процесс трудоемкий и ненадежный и тогда НОД(а;b)
находится с помощью разложения чисел на простые множители. Этот алгоритм
наиболее распространенный.

·
Алгоритм отыскания НОД(а, b) с помощью разложения
чисел на простые множители прост, понятен и удобен, но у него есть
существенный недостаток: если данные числа велики, да еще не очень легко
раскладываются на множители, то задача отыскания НОД(а, b) становится довольно
трудной. К тому же может оказаться, что, основательно потрудившись, мы
убедимся, что НОД (а, b)=1 и вроде вся работа проделана зря.

·
Большинство древних алгоритмов со временем
вытеснялось из вычислительной практики более новыми алгоритмами. Алгоритм
Евклида избежал этой участи прежде всего благодаря своей экономности. Тем более
удивительно, что хотя почтенный алгоритм Евклида и применяется в течение столь
многих столетий, он не всегда является наилучшим способом для нахождения НОД!

Основной вывод, который я
сделала, состоит в том, что научиться быстро и правильно вычислять НОД чисел не
так уж сложно. Вышеперечисленные алгоритмы рассчитаны на ум
“обычного” человека и не требуют уникальных способностей. Главное –
более или менее продолжительная тренировка.

«Математика
– царица всех наук. Ее возлюбленный – истина, ее наряд – простота и ясность.
Дворец этой владычицы окружен тернистыми зарослями, и, чтобы достичь его,
каждому приходится продираться сквозь чащу. Случайный путник не обнаружит во
дворце ничего привлекательного. Красота его открывается лишь разуму, любящему
истину, закаленному в борьбе с трудностями, свидетельствующему о незаурядности
и непреодолимой склонности человека к необычайно запутанным, но неиссякаемым и
возвышенным наслаждениям ума, свойственным самой природе людей» (Снядецкий Ян)

Литература

[1].//Учебник для
общеобразовательных учреждений Математика 6 класс под ред. Н.Я Зубаревой.,
Москва, Мнемозина,2013 г.

[2].//За
страницами учебника алгебры. Л.Ф Пичурин, Москва, Просвещение, 1990г.

[3].//Сборник примеров
и задач по математике, Н.А Терешин, Т.Н.Терешина Москва, Аквариум, 1997 г.

Интернет-ресурсы.

[1]. //Википедия
(свободная энциклопедия), http://ru.wikipedia.org

[ 2]. //Сайт
“Единая коллекция цифровых образовательных ресурсов”.

[ 3]. //
bymath.net — сайт «Вся элементарная математика», раздел «Общий делитель.
Наибольший общий делитель»

Приложение
.

Мои
примеры нахождения НОД двух натуральных чисел.

1способ:
1) НОД(81;243) 2) НОД(195;156)

D(81)={1,3,9,81}
D(195)={1,3,5,15,65,195}

D(243)={1,3,9,27,81,243}
D(156)={1,2,3,4,6,12,52,78,156}

НОД(81;243)=81
НОД(156;192)=3

______________________________________________________________

2способ:
1)НОД(81;243) 2)НОД(195;156)

D(81)={1,3,9,27,81}
D(156)={1,2,3,4,6,12,52,78,156}

81 является делителем
243 156 не является делителем 195

НОД(81;243)=81
78не является делителем 195

52 не является делителем 195

12 не является делителем 195

6 не является делителем 195

3 является делителем 195

НОД(195;156)=3

________________________________________________________________

3 способ:1)
НОД(585;360) 2) НОД(680,612)

585=13*3*3*5
612=17*2*2*3*3*3

360=2*2*3*3*5*2
680=17*2*2*2*5

5*3*3=45
17*2*2=68

НОД(585;360)=45
НОД(612;680)=68

_________________________________________________________________

4 способ:1)
НОД(612,680) 2) НОД(585,360)

680-612=68
585-360=225

612-68=476 360-225=135

476-68=408
225-135=90

408-68=340
135-90=45

340-68=272 90-45=45

272-68=204
45-45=0

204-68=136
НОД(585,360)=45

136-68=68

НОД(612,680)=68

______________________________________________________________________________
5 способ: НОД(7875,4725)
НОД(7920,594)

7875:4725=1(ост.3150)
7920:594=13(ост.153)

4725:3150=1(ост.1575)
594:153=3(ост.135)

3150:1575=2
153:135=1(ост.18)

НОД(7875,4725)=1575
135:18=7(ост.9)

18:9=2       НОД(7920,594)=9
                __________________________________________________________________

6 способ:
1) НОД(825;675)

НОД(825;675) = НОД((825-675):2;675) =
НОД((625-75) :2);75) =

НОД((275-75):2;75) = НОД((100:2);75) =
НОД(50;75) = НОД(25;75) = 25 НОД(825;675)=25

2) НОД(7875;4725)

НОД(7875;4725)=НОД((7875-4725);2)=НОД(1575;4725)=НОД((4725-1575);2,1575)=НОД(1575;1575)=1575

НОД(7875;4725)=1575

7 способ:
1) НОД(160;40)

160 мм

мм

1. Построим прямоугольник со сторонами
160мм и 40 мм.

2. От прямоугольника отрежем несколько
квадратов со стороной 40 мм – таких квадратов четыре.

3. Длина стороны последнего полученного
квадрата и есть наибольший общий делитель чисел 160 и 40.

НОД(160;40)=40

2) НОД(85,125)

1. Построим прямоугольник со сторонами
125мм и 85 мм.

5
мм

40 мм

40мм

125мм

2. От прямоугольника отрежем квадрат со
стороной 85 мм – такой квадрат один.

3. Остался
прямоугольник со сторонами 85 мм и 125-85=40 мм. От полученного прямоугольника
снова отрезаем квадраты, у которых сторона равна 40
мм – таких квадратов получится два.

4. Остался
прямоугольник со сторонами 40 мм и 85-2*40=5 мм. От полученного прямоугольника
снова отрезаем квадраты, у которых сторона равна 8
мм – таких квадратов получится восемь.

5. Длина стороны последнего
полученного квадрата и есть наибольший общий делитель чисел 125 и
8. НОД(85,125)=5

Приложение

Каждый из нас в школе изучал, что такое
наибольший общий делитель (далее НОД) двух чисел a и b. Конечно же, это
наибольшее целое число d, на которое a и b делятся без остатка. Без труда
каждый ученик может сказать, например, что НОД(12, 18) = 6. Но что если одно из
чисел равно 0? А если a или b отрицательно? Над этим вопросом на школьных
уроках, наверное, не каждый из нас задумывался. Для того чтобы ответить на
поставленные вопросы, приведем определение – что же такое наибольший общий
делитель.

Определение 1. Наибольшим общим
делителем (далее НОД) двух целых чисел a и b, одновременно не равных нулю,
называется такое наибольшее целое число d, на которое a и b делятся без
остатка. Этот факт обозначается так: d = НОД(a, b). Если оба числа равны нулю,
то положим НОД(0, 0) = 0.

Исходя из определения, имеют место
следующие равенства:

НОД(a,
b) = НОД(b, a),

НОД(a,
b) = НОД(-a, b)

НОД(a,
0) = |a|

Источник

Алгоритм Евклида – нахождение наибольшего общего делителя

Алгоритм нахождения НОД делением

Алгоритм нахождения НОД вычитанием

Функция, вычисляющая НОД

Функция gcd модуля math

История[править | править код]

Описание[править | править код]

Алгоритм Евклида для целых чисел[править | править код]

Геометрический алгоритм Евклида[править | править код]

Пример[править | править код]

Применения[править | править код]

Расширенный алгоритм Евклида и соотношение Безу[править | править код]

Цепные дроби[править | править код]

Линейные диофантовы уравнения[править | править код]

Вариации и обобщения[править | править код]

Евклидово кольцо[править | править код]

Обобщённый алгоритм Евклида для многочленов[править | править код]

Ускоренные версии алгоритма[править | править код]

Вычислительная сложность алгоритма[править | править код]

Количество шагов[править | править код]

Наихудший случай[править | править код]

Теорема Ламе[править | править код]

Среднее[править | править код]

Вычислительная сложность шага[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Алгоритм Евклида

Python

Perl:

C:

Pascal:

Java:

C#:

Переборный алгоритм

Алгоритм Евклида «с вычитанием»

Блок — схема алгоритма Евклида «с вычитанием»

Программа

Алгоритм Евклида с «делением»

Вам также может понравиться

Как найти ответы на вопросы кроссворда

Как найти плейстейшен на телевизоре

В документе все слова написаны слитно как исправить

Добавить комментарий Отменить ответ

Функция `gcd` модуля `math`