Учитель математики МБОУ «Шеморданский лицей Сабинского муниципального района РТ» А.С. Галиахметова, 1 кв.категория
Алгоритм сокращения рациональных дробей
1. Представить числитель и знаменатель дроби в виде произведений, содержащих один и тот же множитель, применяя способы разложения на множители (либо вынесение общего множителя за скобки, либо способ группировки, либо применение формул сокращенного умножения).
2. Сократить и числитель, и знаменатель этой дроби на этот множитель.
Алгоритм приведения рациональных дробей к новому знаменателю
1. Или умножить числитель и знаменатель дроби на дополнительный множитель, т.е. 
2. Или изменить знак числителя (или знак знаменателя) дроби и знак перед дробью. Например:  .
.
Алгоритм сложения и вычитания рациональных дробей с одинаковыми знаменателями
1. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тем же.
При с ≠ 0 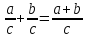
2. Чтобы выполнить вычитание дробей с одинаковыми знаменателями, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тем же.
При с ≠ 0 
Алгоритм сложения и вычитания рациональных дробей с разными знаменателями
1. При сложении и вычитании рациональных дробей с разными знаменателями, нужно эти дроби привести к общему знаменателю.
Способы приведения к общему знаменателю:
– в качестве общего знаменателя можно выбрать выражение, равное произведению знаменателей данных дробей (не всегда является наиболее удобным общим знаменателем);
– если знаменатели дробей представляют собой одночлены, то общим знаменателем является одночлен, у которого коэффициент равен наименьшему общему кратному коэффициентов знаменателей дробей, а каждая переменная взята с наибольшим показателем, с которым она входит в знаменатели дробей;
– если знаменатели дробей представляют собой многочлены, то нужно по мере возможности разложить их на множители, применяя способы разложения на множители многочленов. Тогда общим знаменателем будет выражение, состоящее из произведения разных множителей.
2. Воспользоваться правилом сложения и вычитания дробей с одинаковыми знаменателями.
Алгоритм умножения и деления рациональных дробей
1. Произведением рациональных дробей является рациональная дробь, числитель которой равен произведению числителей данных дробей, а знаменатель – произведению их знаменателей.
2. Частным двух рациональных дробей является рациональная дробь, числитель которой равен произведению числителя делимого и знаменателя делителя, а знаменатель – произведению знаменателя делимого и числителя делителя.
Алгоритм возведения рациональной дроби в степень
Чтобы возвести рациональную дробь в степень, нужно возвести в эту степень числитель и знаменатель. Первый результат записать как числитель, а второй – как знаменатель дроби.
Алгоритм решения дробных рациональных уравнений вида 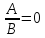
1. Решить уравнение А = 0;
2. Проверить, какие из найденных корней удовлетворяют условию В ≠ 0.
3. Корни, удовлетворяющие условию В ≠ 0, включить в ответ.
Алгоритм решения дробных рациональных уравнений
1. Найти общий знаменатель дробей, входящих в уравнение.
2. Умножить обе части уравнения на общий знаменатель.
3. Решить получившееся целое уравнение.
4. Исключить из его корней те, которые обращают в нуль общий знаменатель.
Алгоритм решения задач на движение с помощью рациональных уравнений
Алгоритм решения задач на движение подразумевает выполнение двух больших этапов:
Основные формулы:
s = v ∙ t;

-
В задачах на движение обязательно необходимо рисовать чертеж. Тела могут двигаться навстречу друг другу, в противоположные стороны и догонять друг друга, по течению или против течения, или по озеру.
-
Все числа нужно привести в единой размерности – только км или только м; только часы или минуты, и т.д.
-
Решая задачи, удобно записывать данные в виде таблицы с обязательными графами – путь, скорость и время.
-
За x можно брать как то, что нужно найти в задаче, так и другое неизвестное.
-
Внимательно читай, что спрашивается в задаче! x – не всегда ответ. Кроме этого, в ответе могут попросить указать величину в другой единице измерения (не в той, которая вышла у тебя, решая уравнение).
-
Составить уравнение задачи, обосновав его условием задачи.
-
Решить уравнение.
-
Сделать проверку корней на соответствие смысла задачи.
-
Выписать ответ.
Алгоритм решения задач на работу и производительность с помощью рациональных уравнений
Для решения необходимо знать одну-единственную формулу:
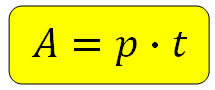
Здесь A — работа, t — время, а величина p, которая по смыслу является скоростью работы, носит специальное название — производительность. Она показывает, сколько работы сделано в единицу времени. Например, Вася красит забор. Количество метров, которые он красит за час — это и есть его производительность.
Правила решения задач на работу:
1. А = р∙t, из этой формулы легко найти t или p.
2. Если объем работы не важен в задаче и нет никаких данных, позволяющих его найти — работа принимается за единицу. Построен дом (один), покрашен забор (один), наполнен резервуар. А вот если речь идет о количестве кирпичей, количестве деталей, литрах воды — работа как раз и равна этому количеству.
3. Все числа нужно привести в единой размерности – только л или только м3; только часы или минуты, и т.д.
4. Если трудятся двое рабочих (два экскаватора, два мастера, Даша и Маша…) или трое (не важно) — их производительности складываются. Очень логичное правило.
5. В качестве переменной х удобно взять (в абсолютном большинстве задач) именно производительность. Так же, как в задах на движение мы за х принимаем скорость.
6. Внимательно читай, что спрашивается в задаче! x – не всегда ответ. Кроме этого, в ответе могут попросить указать величину в другой единице измерения (не в той, которая вышла у тебя, решая уравнение).
7. Решая задачи, удобно записывать данные в виде таблицы с обязательными графами – производительность, время, работа.
Например:

8. Составить уравнение задачи, обосновав его условием задачи.
9. Решить уравнение.
10. Сделать проверку корней на соответствие смысла задачи.
11. Выписать ответ.
Алгоритм решения линейных неравенств
-
Раскрыть скобки.
-
Перенести все слагаемые с х влево, а числа вправо, меняя при этом знак на противоположный.
-
Привести подобные слагаемые.
-
Разделить обе части неравенства на число, стоящее перед х (если это число положительное, то знак неравенства не меняется; если это число отрицательное, то знак неравенства меняется на противоположный).
-
Перейти от аналитической модели к геометрической модели.
-
Указать множество решений данного неравенства, записав ответ.
Алгоритм решения систем неравенств
1. Решаем каждое неравенство отдельно.
2. Изображаем решение каждого неравенства системы на одной числовой прямой (штриховкой). Промежуток на оси, где штриховки «пересекутся» и будет решением системы; если общих точек нет, то система не имеет решения.
3. Ответ записываем в виде неравенства или в виде числового промежутка.
«Алгоритм решения задач с помощью уравнения»:
1) Обозначить буквой х неизвестную величину, записав ответ на вопрос задачи (Пусть…).
2) Составить уравнение по условию задачи.
3) Решить это уравнение.
- Записать краткий ответ на вопрос задачи.
«Алгоритм решения задач на применение теоремы Пифагора»:
1)Выделить на чертеже прямоугольный треугольник, стороной которого является искомый отрезок.
2)Определить катет это или гипотенуза.
3)Записать для этого треугольника теорему Пифагора (для гипотенузы) или следствие из нее (для катета) в обозначениях данной задачи.
4)Подставив в формулу известные величины, найти неизвестную величину.
Как решать задачи.
- Прочитай задачу и представь себе то, о чем говорится в задаче.
- Запиши задачу кратко или выполни чертеж.
- Поясни, что показывает каждое число, повтори вопрос задачи.
- Подумай, можно ли сразу ответить на вопрос задачи. Если нет, то почему. Что
нужно узнать сначала, что потом.
- Составь план решения.
- Выполни решение.
- Проверь решение и ответь на вопрос задачи.
- Не забудь записать ответ к задаче, проверь правильно ли записаны пояснения к
действиям.
Рекомендации по решению нестандартных задач:
1. Сделать к задаче рисунок или чертеж; подумай, может быть, нужно сделать на них дополнительные построения или изменить чертеж в процессе решения задачи.
2. Ввести вспомогательный элемент (часть).
3. Использовать для решения задачи способ подбора.
4. Переформулировать задачу другими словами, чтобы она стала более понятной и знакомой.
5. Разделить условие или вопрос задачи на части и решить ее по частям.
6. Начать решение задачи «с конца».
Алгоритм решения задач на переливание:
В задачах на переливание разрешены следующие операции:
- заполнение жидкостью одного сосуда до краев;
- переливание жидкости в другой сосуд или выливание жидкости;
При решении таких задач необходимо учитывать следующие замечания:
- разрешается наливать в сосуд ровно столько жидкости, сколько в нем помещается;
- разрешается переливать всю жидкость из одного сосуда в другой, если она в него вся помещается;
- разрешается отливать из одного сосуда в другой столько жидкости, сколько необходимо, чтобы второй сосуд стал полным.
Каждую задачу на переливание таким методом можно решать двумя способами:
а) начать переливания с большего сосуда;
б) начать переливания с меньшего сосуда.
При решении задач первого типа («Водолей») можно использовать такой алгоритм:
- Наполнить большую емкость жидкостью из бесконечного источника.
- Перелить из большей емкости в меньшую емкость.
- Вылить жидкость из меньшей емкости.
- Повторить действия 1-3 до тех пор, пока не будет получено обозначенное в условии задачи количество жидкости.
При решении задач второго типа («Переливашка») можно использовать следующий алгоритм:
- Из большей емкости наполнить емкость промежуточного объема.
- Перелить жидкость из промежуточной емкости в самую маленькую емкость.
- Перелить жидкость из самой маленькой емкости в большую емкость.
- Повторять действия 2-3 до тех пор, пока емкость промежуточного объема не станет пустой.
- Если емкость промежуточного объема опустела, то повторить действия 1-5 до тех пор, пока не будет получено обозначенное в условии задачи количество жидкости.
Алгоритм решения задач :
- Читаем условие задачи. Условие – это та часть текста, где содержатся сведения об известных и неизвестных значениях величин, об отношениях между ними.
- Определяем требование, т.е. указание на то, что надо найти. Требование обычно выражается вопросом, начинающимся словом «Сколько…?» и заканчивающимся знаком вопроса.
- Находим данные задачи. Данные – это известные числа.
- Определяем искомое. Это конечная цель процесса решения арифметической задачи.
- Если что-то непонятно, необходимо обратиться за разъяснением к учителю. Могут встретиться непонятные слова и обороты.
- Ищем пути решения задачи и составляем план решения.
- Можно использовать графическую модель (схема в «отрезках») или составить таблицу.
- Записываем решение и ответ.
Современные формы обучения, инновации в преподавании, введение новых
технологий диктуют учителю необходимость постигать секреты мастерства, а значит,
и совершенствовать методы обучения и воспитания учащихся.
Исследования психологов и педагогов, опыт коллег показывают: чтобы научить
детей самостоятельно учиться и проявлять творчество необходимо применение
деятельностного подхода в обучении. Для этого учащихся нужно замотивировать и
обучить их приемам и способам учебной деятельности, которые помогут сформировать
необходимые знания, умения и навыки.
Курс школьной математики имеет достаточно широкие возможности для применения
различных приемов, методов и технологий. В последние годы в содержание школьного
курса естественным образом закладывается алгоритмическая линия. Так как
применение алгоритмов является приоритетным в моей работе, то нужно отметить
что, между понятиями “прием” и “алгоритм” существует много общего, ни и есть
принципиальные отличия, а именно:
– прием – это рациональный способ работы, который состоит из отдельных
действий, он может быть выражен в виде правил или инструкций, его можно
перестроить и на его основе создать новый прием. Приемы деятельности допускают
самостоятельный выбор учениками конкретных действий по решению учебных задач;
– алгоритм – это общепонятное и однозначное предписание, которое определяет
последовательность действий, позволяющее достичь искомый результат. Алгоритм
предполагает жесткое выполнение шагов, а прием дает общее направление
деятельности по решению учебных задач, не регламентируя каждый шаг. Поэтому я в
своей работе выделяю два подхода: 1) обучение алгоритмам; 2) формирование
приемов решения задач. Школьные задачи делятся на: алгоритмические,
полуалгоритмические, полуэвристические и эвристические. Каждый тип задачи
предполагает свои схемы решения, подходы, применение логики и изобретательности.
На начальном этапе обучения математике применение алгоритмов способствует
формированию и прочному усвоению навыков владения математическими методами.
Также осуществляется подготовка к формированию первоначальных представлений о
математическом моделировании. Уже в начальных классах прослеживается применение
простейших алгоритмов выполнения арифметических операций, дети овладевают
навыками выполнения последовательных действий. Решают задачи с составлением схем
и кратких записей. Это можно рассматривать как пропедевтику операционного стиля
мышления.
Следующий уровень алгоритмической культуры учащихся – введение понятия
алгоритма и формирование его основных свойств. Это происходит в среднем звене
школы. Именно в этот период необходимо сочетания алгоритма и образца ответа, что
дает возможность ученику, верно, ответить на поставленный вопрос, сопроводив его
правильной речью. У учителя появляется возможность предлагать задачи с
элементами творчества. А материал, предлагаемый в наших школьных учебниках,
является хорошей базой для обучения составлению простейших алгоритмов и
дальнейшей их записи в разных формах. Мы применяем табличную, графическую
(блок-схема), словесную и формульную форму записи алгоритмов.
В качестве примера, иллюстрирующего процесс алгоритмизации как средство
обучения, можно указать на решение задач методом уравнений. Примером
графического алгоритма является блок-схема для отыскания количества решений
системы двух линейных уравнений с двумя неизвестными (см. Рисунок 1).
Отыскания числа решений системы двух линейных уравнений (блок-схема)
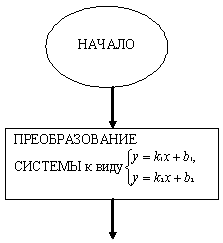
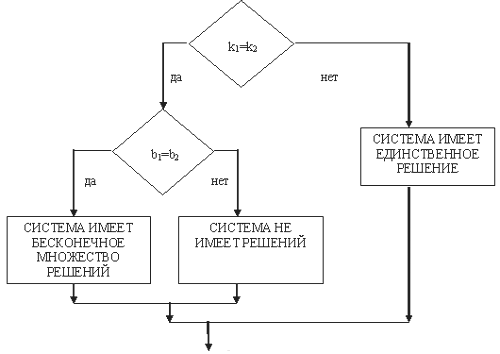

Рис. 1
Графические алгоритмы
Табличную форму алгоритма можно продемонстрировать на примере таблицы,
составляемой для исследования функций и дальнейшего построения графиков (см.
рис. 2).
Исследование функции и построение графика
Функция задана уравнением у = f(x). Исследовать
функцию и построить ее график.
1. Таблица исследования функции

2. Построение графика
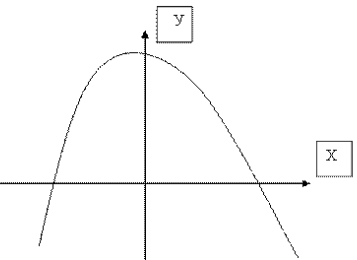
Рис. 2
Табличный алгоритм
Пример формульного способа – последовательность нахождения компонентов при
составлении уравнения касательной к графику той или иной функции (см. рис. 3).
Уравнение касательной к графику функции

Рис. 3
Формульный способ
Словесный алгоритм используется практически во всех правилах выполнения
действий, например, правило сложения чисел с разными знаками (см. рис. 4).
Алгоритм сложения чисел с разными знаками

Рис. 4
Словесный алгоритм
В старших классах работа становится разнообразней и содержательней,
появляется возможность включать упражнения разного типа и уровня сложности,
предполагающее, что приемы деятельности могут быть разной степени сложности и
обобщенности. Они состоят из большого числа действий, выполнение которых
приводит к применению алгоритмов на отдельных этапах работы.
Такой подход к преподаванию математики в основной школе определяет условия
для формирования у учащихся навыков, позволяющих в старших классах успешно
изучать базовый курс “Информатики и ИКТ”. Применение алгоритмов в старших
классах, по мнению некоторых учителей, отбивает творческий подход к решению
задач, но с другой стороны, твердое знание основных задач курса и умение их
решать, является твердым фундаментом для активизации самостоятельной и
творческой работы учащихся.
Список литературы
- Кухарев Н.В. На пути к профессиональному совершенству. – М.:
Просвещение, 1990. - Епишева О.Б. Крутич В.И. Учить школьников учиться математике. –
М.: Просвещение, 1990. - Сост. Глейзер Г.Д. Повышение эффективности обучения математике в
школе. – М.: Просвещение, 1991. - Груденов Я.И. Совершенствование методики работы учителя
математики. – М.: Просвещение, 1990. - Байдак В.А. и др. Формирование алгоритмической культуры у
учащихся. – М.: Просвещение, 1989.
Основные алгоритмические конструкции
Алгоритм применительно к вычислительной машине — точное предписание, т.е. набор операций и правил их чередования, при помощи которого, начиная с некоторых исходных данных, можно решить любую задачу фиксированного типа.
Алгоритмы в зависимости от цели, начальных условий задачи, путей ее решения, определения действий исполнителя подразделяются следующим образом:
Линейный алгоритм — набор команд (указаний), выполняемых последовательно друг за другом.
Основным элементарным действием в линейных алгоритмах является присваивание значения переменной величине. Если значение константы определено видом ее записи, то переменная величина получает конкретное значение только в результате присваивания. Присваивание может осуществляться двумя способами: с помощью команды присваивания и с помощью команды ввода.
Рассмотрим пример. В школьном учебнике математики правила деления обыкновенных дробей описаны так:
- Числитель первой дроби умножить на знаменатель второй дроби.
- Знаменатель первой дроби умножить на числитель второй дроби.
- Записать дробь, числитель которой есть результат выполнения пункта 1, а знаменатель — результат выполнения пункта 2.
В алгебраической форме это выглядит следующим образом:

Построим алгоритм деления дробей для ЭВМ. В этом алгоритме сохраним те же обозначения для переменных, которые использованы в записанной выше формуле. Исходными данными являются целочисленные переменные а, Ь, с, d. Результатом — также целые величины m и n. Блок-схема и текст алгоритма на языке программирования (ЯП) Kotlin приведены ниже.

namespace oap { class Program { static void Main(string[] args) { Console.WriteLine("Enter a, b, c, d: "); var a = int.Parse(Console.ReadLine()); var b = int.Parse(Console.ReadLine()); var c = int.Parse(Console.ReadLine()); var d = int.Parse(Console.ReadLine()); var m = a * d; var n = b * c; Console.WriteLine($"m={m}, n={n}"); } } }
Формат команды присваивания следующий:
Знак «=» нужно читать как «присвоить».
Команда присваивания обозначает следующие действия, выполняемые компьютером:
- Вычисляется выражение.
- Полученное значение присваивается переменной.
В приведенном выше алгоритме присутствуют две команды присваивания. В блок-схемах команда присваивания записывается в прямоугольнике. Такой блок называется вычислительным блоком.
В описаниях алгоритмов необязательно соблюдать строгие правила в записи выражений. Их можно писать в обычной математической форме. Это еще не язык программирования со строгим синтаксисом.
В приведенном алгоритме присутствуют команды ввода:
var a = int.Parse(Console.ReadLine()); var b = int.Parse(Console.ReadLine()); var c = int.Parse(Console.ReadLine()); var d = int.Parse(Console.ReadLine());
В блок-схеме команда ввода записывается в параллелограмме — блоке ввода-вывода. При выполнении данной команды процессор прерывает работу и ожидает действий пользователя. Пользователь должен набрать на устройстве ввода (клавиатуре) значения вводимых переменных и нажать на клавишу ввода Enter. Обычно с помощью команды ввода присваиваются значения исходных данных, а команда присваивания используется для получения промежуточных и конечных величин.
Полученные компьютером результаты решения задачи должны быть сообщены пользователю. Для этих целей предназначена команда вывода:
Console.WriteLine($"m={m}, n={n}");
С помощью этой команды результаты выводятся на экран или на устройство печати на бумагу.
Поскольку присваивание является важнейшей операцией в вычислительных алгоритмах, обсудим ее более подробно.
Рассмотрим последовательное выполнение четырех команд присваивания, в которых участвуют две переменные величины a и b.
В приведенной ниже таблице напротив каждой команды присваивания указываются значения переменных, которые устанавливаются после ее выполнения.
| Команда | a | b |
|---|---|---|
| a=1 | 1 | – |
| b=a*2 | 1 | 2 |
| a=b | 2 | 2 |
| b=a+b | 2 | 4 |
Этот пример иллюстрирует три основных свойства команды присваивания:
- пока переменной не присвоено значение, она остается неопределенной;
- значение, присвоенное переменной, сохраняется в ней вплоть до выполнения следующей команды присваивания этой переменной;
- новое значение, присваиваемое переменной, заменяет ее предыдущее значение.
Рассмотрим один очень полезный алгоритм, который приходится часто использовать при программировании. Даны две величины: Х и Y. Требуется произвести между ними обмен значениями. Например, если первоначально было Х=1, Y=2, то после обмена должно стать: Х=2, Y=1.
Хорошей моделью для решения этой задачи является следующая ситуация: имеются два стакана — один с молоком, другой с водой. Требуется произвести обмен их содержимым. Всякому ясно, что в этом случае нужен дополнительный третий пустой стакан. Последовательность действий будет следующей: 1) перелить из первого стакана в третий; 2) перелить из второго в первый;
3) перелить из третьего во второй. Цель достигнута!
По аналогии для обмена значениями двух переменных нужна третья дополнительная переменная. Назовем ее Z. Тогда задача обмена решается последовательным выполнением трех команд присваивания:
| Команда | X | Y | Z |
|---|---|---|---|
| ввод X, Y | 1 | 2 | – |
| Z = X | 1 | 2 | 1 |
| X = Y | 2 | 2 | 1 |
| Y = Z | 2 | 1 | 1 |
Аналогия со стаканами не совсем точна в том смысле, что при переливании из одного стакана в другой первый становится пустым. В результате же присваивания (Х = Y) переменная, стоящая справа (Y), сохраняет свое значение.
Алгоритм для деления дробей имеет линейную структуру. В нем все команды выполняются в строго однозначной последовательности, каждая по одному разу. Линейный алгоритм составляется из команд присваивания, ввода, вывода и обращения к вспомогательным алгоритмам (об этом позже).
При описании алгоритмов в блок-схемах типы, как правило, не указываются (но подразумеваются). В алгоритмах для всех переменных типы указываются явно. В них используются следующие обозначения типов: Int — целый тип, Float — вещественный тип, String — символьный (литерный) тип, Boolean — логический тип. В алгоритме для деления дробей для всех переменных указан тип Int.
Разветвляющийся алгоритм — алгоритм, содержащий хотя бы одно условие, в результате проверки которого ЭВМ обеспечивает переход на один из двух возможных шагов.
Циклический алгоритм — алгоритм, предусматривающий многократное повторение одного и того же действия (одних и тех же операций) над новыми исходными данными. К циклическим алгоритмам сводится большинство методов вычислений, перебора вариантов. Цикл программы — последовательность команд (серия, тело цикла), которая может выполняться многократно (для новых исходных данных) до удовлетворения некоторому условию.
Составим алгоритм решения квадратного уравнения: ax2+bx+c=0
Задача хорошо знакома из математики. Исходными данными здесь являются коэффициенты а, b, с. Решением в общем случае будут два корня х1 и х2, которые вычисляются по формуле:

namespace oap { class Program { static void Main(string[] args) { Console.WriteLine("Введите a, b, c: "); var a = int.Parse(Console.ReadLine()); var b = int.Parse(Console.ReadLine()); var c = int.Parse(Console.ReadLine()); var d = b * b - 4 * a * c; var x1 = (-b + Math.Sqrt(d)) / (2 * a); var x2 = (-b - Math.Sqrt(d)) / (2 * a); Console.WriteLine($"x1={x1}, x2={x2}"); } } }
Введите a, b, c:
3
2
1
x1=NaN, x2=NaN
Слабость такого алгоритма видна невооруженным глазом. Он не обладает важнейшим свойством, предъявляемым к качественным алгоритмам, — универсальностью по отношению к исходным данным. Какими бы ни были значения исходных данных, алгоритм должен приводить к определенному результату и завершать работу. Результатом может быть число, но может быть и сообщение о том, что при определенных данных задача решения не имеет. Недопустимы остановки в середине алгоритма из-за невозможности выполнить какую-то операцию. Упомянутое свойство называют результативностью алгоритма (в любом случае должен быть получен какой-то результат).
Чтобы построить универсальный алгоритм, сначала требуется тщательно проанализировать математическое содержание задачи.
Решение уравнения зависит от значений коэффициентов а, b, с. Вот анализ рассмотренной выше задачи (ограничиваемся только поиском вещественных корней):
если а = 0, b = 0, с = 0, то любое х — решение уравнения;
если а = 0, b = 0, с <> О, то уравнение действительных решений не имеет;
если а = 0, b <> О, то это линейное уравнение, которое имеет одно решение х = -c/b;
если а<>0 и d=b2-4ac >= 0, то уравнение имеет два вещественных корня (формулы приведены выше);
если a<>0 и d<0, то уравнение не имеет вещественных корней.

Этот же алгоритм на Kotlin:
fun main(){ println("Введите a, b, c:") val a = readLine()!!.toInt() val b = readLine()!!.toInt() val c = readLine()!!.toInt() var x1: Float if(a==0){ if(b==0){ if(c==0) println("любое X") else println("нет решений") } else { x1 = -c.toFloat()/b println("X=$x1") } } else { val d = b*b-4*a*c if(d<0) println("нет вещественных корней") else{ x1 = (-b+sqrt(d.toFloat()))/(2*a) val x2 = (-b-sqrt(d.toFloat()))/(2*a) println("x1=$x1, x2=$x2") } } }
В этом алгоритме многократно использована структурная команда ветвления. Общий вид команды ветвления в блок-схемах и на ЯП следующий:

if (условие) {серия1} else {серия2}
Вначале проверяется условие (вычисляется отношение, логическое выражение). Если условие истинно, то выполняется серия 1 — последовательность команд, на которую указывает стрелка с надписью «да» (положительная ветвь). В противном случае выполняется серия 2 (отрицательная ветвь). В языке Kotlin условие записывается после служебного слова if, положительная ветвь — сразу после условия, отрицательная — после слова else.
Если на ветвях одного ветвления содержатся другие ветвления, то такой алгоритм имеет структуру вложенных ветвлений. Именно такую структуру имеет алгоритм «Корни квадратного уравнения».
Рассмотрим следующую задачу: дано целое положительное число n. Требуется вычислить n! (n-факториал). Вспомним определение факториала:

Ниже приведена блок-схема алгоритма. В нем используются три переменные целого типа: n — аргумент; i — промежуточная переменная; F — результат. Для проверки правильности алгоритма построена трассировочная таблица. В такой таблице для конкретных значений исходных данных по шагам прослеживается изменение переменных, входящих в алгоритм. Данная таблица составлена для случая п = 3.

| Шаг | n | F | i | Условие |
|---|---|---|---|---|
| 1 | 3 | |||
| 2 | 1 | |||
| 3 | 1 | |||
| 4 | 1<=3, да | |||
| 5 | 1 | |||
| 6 | 2 | |||
| 7 | 2<=3, да | |||
| 8 | 2 | |||
| 9 | 3 | |||
| 10 | 3<=3, да | |||
| 11 | 6 | |||
| 12 | 4 | |||
| 13 | 4<=3, нет | |||
| 14 | вывод |
Трассировка доказывает правильность алгоритма. Теперь запишем этот алгоритм на ЯП.
fun main(){ println("Введите n:") val n = readLine()!!.toInt() var F = 1 var i = 1 while (i<=n){ F *= i // F = F*i i++ // i = i+1 } println("F=$F") }
Этот алгоритм имеет циклическую структуру. В алгоритме использована структурная команда цикл-пока, или цикл с предусловием. Общий вид команды цикл-пока в блок-схемах и в ЯП следующий:

while (условие) { //серия }
Выполнение серии команд (тела цикла) повторяется, пока условие цикла истинно. Когда условие становится ложным, цикл заканчивает выполнение.
Цикл с предусловием — это основная, но не единственная форма организации циклических алгоритмов. Другим вариантом является цикл с постусловием. Вернемся к алгоритму решения квадратного уравнения. К нему можно подойти с такой позиции:
если а = 0, то это уже не квадратное уравнение и его можно не рассматривать. В таком случае будем считать, что пользователь ошибся при вводе данных, и следует предложить ему повторить ввод. Иначе говоря, в алгоритме будет предусмотрен контроль достоверности исходных данных с предоставлением пользователю возможности исправить ошибку. Наличие такого контроля — еще один признак хорошего качества программы.

fun main(){ var a: Int do { println("Введите a:") a = readLine()!!.toInt() } while(a!=0) val d = b*b-4*a*c if(d<0) println("нет вещественных корней") else{ val x1 = (-b+sqrt(d.toFloat()))/(2*a) val x2 = (-b-sqrt(d.toFloat()))/(2*a) println("x1=$x1, x2=$x2") } }
В общем виде структурная команда цикл с постусловием или цикл — до представляется так:

do { //серия } while (условие)
Здесь используется условие окончания цикла. Когда оно становится истинным, цикл заканчивает работу.
Составим алгоритм решения следующей задачи: даны два натуральных числа М и N. Требуется вычислить их наибольший общий делитель — НОД(M, N).
Эта задача решается с помощью метода, известного под названием алгоритма Евклида. Его идея основана на том свойстве, что если M>N, то НОД(М, N) = НОД(М-N,N). Другой факт, лежащий в основе алгоритма, тривиален — НОД(М, М) = М. Для «ручного» выполнения этот алгоритм можно описать в форме следующей инструкции:
- Если числа равны, то взять их общее значение в качестве ответа; в противном случае продолжить выполнение алгоритма
- Определить большее из чисел
- Заменить большее число разностью большего и меньшего значений
- Вернуться к выполнению пункта 1

fun main(){ println("Введите m, n: ") var m = readLine()!!.toInt() var n = readLine()!!.toInt() while (m!=n){ if(m>n) m = m-n else n = n-m } println("НОД = $m") }
Алгоритм имеет структуру цикла с вложенным ветвлением. Проделайте самостоятельно трассировку этого алгоритма для случая М = 18, N = 12. В результате получится НОД = 6, что, очевидно, верно.
Вспомогательные алгоритмы и процедуры
В теории алгоритмов известно понятие вспомогательного алгоритма. Вспомогательным называется алгоритм решения некоторой подзадачи из основной решаемой задачи. В таком случае алгоритм решения исходной задачи называется основным алгоритмом.
В качестве примера рассмотрим следующую задачу: требуется составить алгоритм вычисления степенной функции с целым показателем у = хк, где к — целое число, х<>0. В алгебре такая функция определена следующим образом:

Для данной задачи в качестве подзадачи можно рассматривать возведение числа в целую положительную степень.
Учитывая, что 1/х-n = (1/х)-n, запишем основной алгоритм решения этой задачи.
fun main(){ println("Введите x, n: ") var x = readLine()!!.toFloat() var n = readLine()!!.toInt() var y: Float if(n==0) y = 1F else { if(n>0) y = stepen(x, n) else y = stepen(1/x, -n) } println("y = $y") }
Здесь дважды присутствует команда обращения к вспомогательному алгоритму с именем stepen. Это алгоритм возведения вещественного основания в целую положительную степень путем его многократного перемножения. Величины, стоящие в скобках в команде обращения к вспомогательному алгоритму, называются фактическими параметрами.
В котлине вспомогательные алгоритмы оформляются в виде функций. Запишем функцию stepen.
fun stepen(x: Float, n: Int): Float { var res = 1F var i = 1 while(i<=n){ res = res * x i++ } return res }
Заголовок вспомогательного алгоритма начинается с ключевого слова fun, после которого следует имя функции, в скобках — список формальных параметров и после скобок тип результата (не обязателен). В списке параметров перечисляются переменные-аргументы с указанием их типов. Здесь x и n — формальные параметры-аргументы. Следовательно, процедура stepen производит вычисления по формуле ак. В основном алгоритме «Степенная функция» обращение к процедуре производится путем указания ее имени с последующим в скобках списком фактических параметров. Между формальными и фактическими параметрами процедуры должны выполняться следующие правила соответствия:
- по количеству (сколько формальных, столько и фактических параметров)
- по последовательности (первому формальному соответствует первый фактический параметр, второму — второй и т.д.)
- по типам (типы соответствующих формальных и фактических параметров должны совпадать)
Фактические параметры-аргументы могут быть выражениями соответствующего типа.
Обращение к процедуре инициирует следующие действия:
- Значения параметров-аргументов присваиваются соответствующим формальным параметрам.
- Выполняется тело процедуры (команды внутри процедуры).
- Значение результата возвращается командой return, и происходит переход к выполнению следующей команды основного алгоритма.
В функции stepen нет команд ввода исходных данных и вывода результатов. Здесь присваивание начальных значений аргументам (x, n) производится через передачу параметров-аргументов. А получение результата происходит командой return. Таким образом, передача значений параметров процедур — это третий способ присваивания (наряду с командой присваивания и командой ввода).
Использование процедур позволяет строить сложные алгоритмы методом последовательной детализации.
Программы для графического отображения алгоритмов
https://draw.io (онлайн)
Microsoft Visio
Dia (бесплатная)
КОНТРОЛЬНЫЕ ВОПРОСЫ
- Линейный алгоритм
- Разветвляющийся алгоритм
- Циклический алгоритм
- Вспомогательные алгоритмы и процедуры
