Как составить алгоритм пути

Часть 1. Общий алгоритм поиска

Введение

Поиск пути — это одна из тех тем, которые обычно представляют самые большие сложности для разработчиков игр. Особенно плохо люди понимают алгоритм A*, и многим кажется, что это какая-то непостижимая магия.

Цель данной статьи — объяснить поиск пути в целом и A* в частности очень понятным и доступным образом, положив таким образом конец распространённому заблуждению о том, что эта тема сложна. При правильном объяснении всё достаточно просто.

Учтите, что в статье мы будем рассматривать поиск пути для игр; в отличие от более академических статей, мы опустим такие алгоритмы поиска, как поиск в глубину (Depth-First) или поиск в ширину (Breadth-First). Вместо этого мы постараемся как можно быстрее дойти от нуля до A*.

В первой части мы объясним простейшие концепции поиска пути. Разобравшись с этими базовыми концепциями, вы поймёте, что A* на удивление очевиден.

Простая схема

Хотя вы сможете применять эти концепции и к произвольным сложным 3D-средам, давайте всё-таки начнём с чрезвычайно простой схемы: квадратной сетки размером 5 x 5. Для удобства я пометил каждую ячейку заглавной буквой.

Простая сетка.

Самое первое, что мы сделаем — это представим эту среду в виде графа. Я не буду подробно объяснять, что такое граф; если говорить просто, то это набор кружков, соединённых стрелками. Кружки называются «узлами», а стрелки — «рёбрами».

Каждый узел представляет собой «состояние», в котором может находиться персонаж. В нашем случае состояние персонажа — это его позиция, поэтому мы создаём по одному узлу для каждой ячейки сетки:

Узлы, обозначающие ячейки сетки.

Теперь добавим рёбра. Они обозначают состояния, которых можно «достичь» из каждого заданного состояния; в нашем случае мы можем пройти из любой ячейки в соседнюю, за исключением заблокированных:

Дуги обозначают допустимые перемещения между ячейками сетки.

Если мы можем добраться из A в B, то говорим, что B является «соседним» с A узлом.

Стоит заметить, что рёбра имеют направление; нам нужны рёбра и из A в B, и из B в A. Это может показаться излишним, но не тогда, когда могут возникать более сложные «состояния». Например, персонаж может упасть с крыши на пол, но не способен допрыгнуть с пола на крышу. Можно перейти из состояния «жив» в состояние «мёртв», но не наоборот. И так далее.

Пример

Допустим, мы хотим переместиться из A в T. Мы начинаем с A. Можно сделать ровно два действия: пройти в B или пройти в F.

Допустим, мы переместились в B. Теперь мы можем сделать два действия: вернуться в A или перейти в C. Мы помним, что уже были в A и рассматривали варианты выбора там, так что нет смысла делать это снова (иначе мы можем потратить весь день на перемещения A → B → A → B…). Поэтому мы пойдём в C.

Находясь в C, двигаться нам некуда. Возвращаться в B бессмысленно, то есть это тупик. Выбор перехода в B, когда мы находились в A, был плохой идеей; возможно, стоит попробовать вместо него F?

Мы просто продолжаем повторять этот процесс, пока не окажемся в T. В этот момент мы просто воссоздадим путь из A, вернувшись по своим шагам. Мы находимся в T; как мы туда добрались? Из O? То есть конец пути имеет вид O → T. Как мы добрались в O? И так далее.

Учтите, что на самом деле мы не движемся; всё это было лишь мысленным процессом. Мы продолжаем стоять в A, и не сдвинемся из неё, пока не найдём путь целиком. Когда я говорю «переместились в B», то имею в виду «представьте, что мы переместились в B».

Общий алгоритм

Этот раздел — самая важная часть всей статьи. Вам абсолютно необходимо понять его, чтобы уметь реализовывать поиск пути; остальное (в том числе и A*) — это просто детали. В этом разделе вы будете разбираться, пока не поймёте смысл.

К тому же этот раздел невероятно прост.

Давайте попробуем формализовать наш пример, превратив его в псевдокод.

Нам нужно отслеживать узлы, которых мы знаем как достичь из начального узла. В начале это только начальный узел, но в процессе «исследования» сетки мы будем узнавать, как добираться до других узлов. Давайте назовём этот список узлов reachable:

reachable = [start_node]

Также нам нужно отслеживать уже рассмотренные узлы, чтобы не рассматривать их снова. Назовём их explored:

explored = []

Дальше я изложу ядро алгоритма: на каждом шаге поиска мы выбираем один из узлов, который мы знаем, как достичь, и смотрим, до каких новых узлов можем добраться из него. Если мы определим, как достичь конечного (целевого) узла, то задача решена! В противном случае мы продолжаем поиск.

Так просто, что даже разочаровывает? И это верно. Но из этого и состоит весь алгоритм. Давайте запишем его пошагово псевдокодом.

Мы продолжаем искать, пока или не доберёмся до конечного узла (в этом случае мы нашли путь из начального в конечный узел), или пока у нас не закончатся узлы, в которых можно выполнять поиск (в таком случае между начальным и конечным узлами пути нет).

while reachable is not empty:

Мы выбираем один из узлов, до которого знаем, как добраться, и который пока не исследован:

    node = choose_node(reachable)

Если мы только что узнали, как добраться до конечного узла, то задача выполнена! Нам просто нужно построить путь, следуя по ссылкам previous обратно к начальному узлу:

    if node == goal_node:
       path = []
       while node != None:
            path.add(node)
            node = node.previous
        
        return path

Нет смысла рассматривать узел больше одного раза, поэтому мы будем это отслеживать:

    reachable.remove(node)
    explored.add(node)

Мы определяем узлы, до которых не можем добраться отсюда. Начинаем со списка узлов, соседних с текущим, и удаляем те, которые мы уже исследовали:

    new_reachable = get_adjacent_nodes(node) - explored

Мы берём каждый из них:

    for adjacent in new_reachable:

Если мы уже знаем, как достичь узла, то игнорируем его. В противном случае добавляем его в список reachable, отслеживая, как в него попали:

        if adjacent not in reachable:
            adjacent.previous = node  # Remember how we got there.
            reachable.add(adjacent)

Нахождение конечного узла — это один из способов выхода из цикла. Второй — это когда reachable становится пустым: у нас закончились узлы, которые можно исследовать, и мы не достигли конечного узла, то есть из начального в конечный узел пути нет:

return None

И… на этом всё. Это весь алгоритм, а код построения пути выделен в отдельный метод:

function find_path (start_node, end_node):
    reachable = [start_node]
    explored = []

    while reachable is not empty:
        # Choose some node we know how to reach.
        node = choose_node(reachable)

        # If we just got to the goal node, build and return the path.
        if node == goal_node:
            return build_path(goal_node)

        # Don't repeat ourselves.
        reachable.remove(node)
        explored.add(node)

        # Where can we get from here?
        new_reachable = get_adjacent_nodes(node) - explored
        for adjacent in new_reachable:
            if adjacent not in reachable
                adjacent.previous = node  # Remember how we got there.
                reachable.add(adjacent)

    # If we get here, no path was found :(
    return None

Вот функция, которая строит путь, следуя по ссылкам previous обратно к начальному узлу:

function build_path (to_node):
    path = []
    while to_node != None:
        path.add(to_node)
        to_node = to_node.previous
    return path

Вот и всё. Это псевдокод каждого алгоритма поиска пути, в том числе и A*.

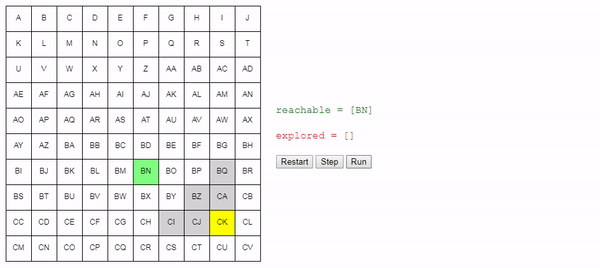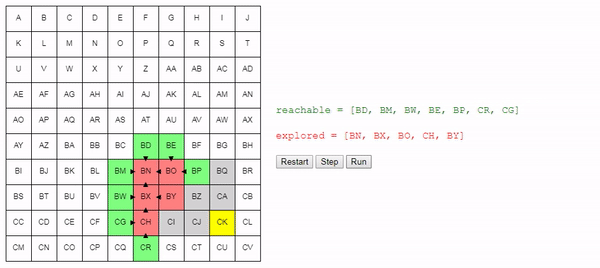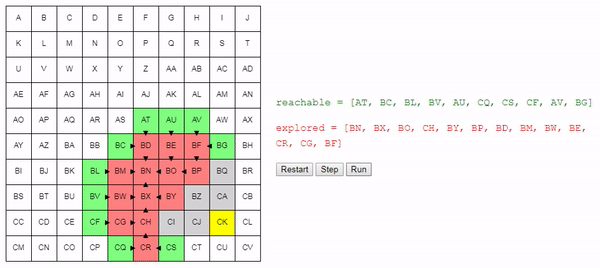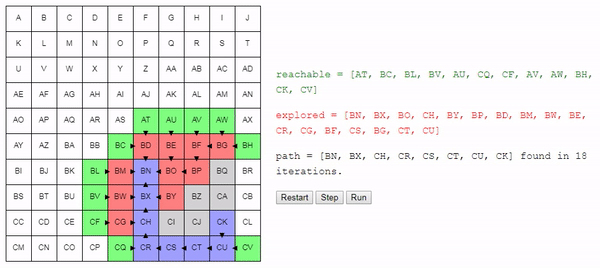
Перечитывайте этот раздел, пока не поймёте, как всё работает, и, что более важно, почему всё работает. Идеально будет нарисовать пример вручную на бумаге, но можете и посмотреть интерактивное демо:

Интерактивное демо

Вот демо и пример реализации показанного выше алгоритма (запустить его можно на странице оригинала статьи). choose_node просто выбирает случайный узел. Можете запустить алгоритм пошагово и посмотреть на список узлов reachable и explored, а также на то, куда указывают ссылки previous.

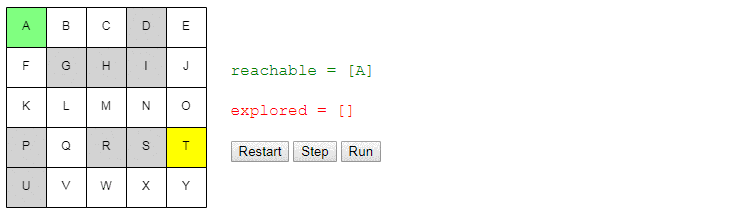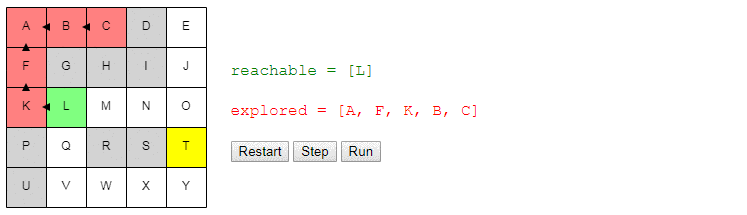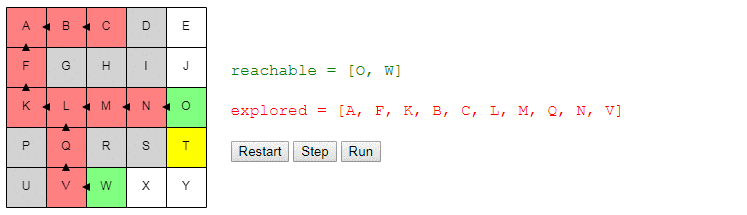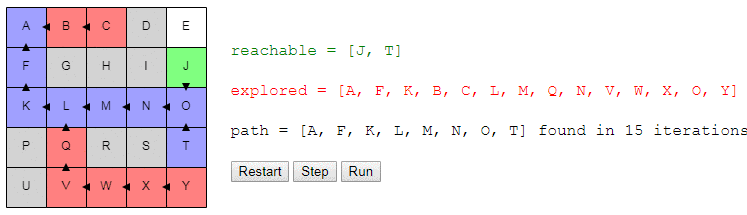
Заметьте, что поиск завершается, как только обнаруживается путь; может случиться так, что некоторые узлы даже не будут рассмотрены.

Заключение

Представленный здесь алгоритм — это общий алгоритм для любого алгоритма поиска пути.

Но что же отличает каждый алгоритм от другого, почему A* — это A*?

Вот подсказка: если запустить поиск в демо несколько раз, то вы увидите, что алгоритм на самом деле не всегда находит один и тот же путь. Он находит какой-то путь, и этот путь необязательно является кратчайшим. Почему?

Часть 2. Стратегии поиска

Если вы не полностью поняли описанный в предыдущем разделе алгоритм, то вернитесь к нему и прочтите заново, потому что он необходим для понимания дальнейшей информации. Когда вы в нём разберётесь, A* покажется вам совершенно естественным и логичным.

Секретный ингредиент

В конце предыдущей части я оставил открытыми два вопроса: если каждый алгоритм поиска использует один и тот же код, почему A* ведёт себя как A*? И почему демо иногда находит разные пути?

Ответы на оба вопроса связаны друг с другом. Хоть алгоритм и хорошо задан, я оставил нераскрытым один аспект, и как оказывается, он является ключевым для объяснения поведения алгоритмов поиска:

node = choose_node(reachable)

Именно эта невинно выглядящая строка отличает все алгоритмы поиска друг от друга. От способа реализации choose_node зависит всё.

Так почему же демо находит разные пути? Потому что его метод choose_node выбирает узел случайным образом.

Длина имеет значение

Прежде чем погружаться в различия поведений функции choose_node, нам нужно исправить в описанном выше алгоритме небольшой недосмотр.

Когда мы рассматривали узлы, соседние с текущим, то игнорировали те, которые уже знаем, как достичь:

if adjacent not in reachable:
    adjacent.previous = node  # Remember how we got there.
    reachable.add(adjacent)

Это ошибка: что если мы только что обнаружили лучший способ добраться до него? В таком случае необходимо изменить ссылку previous узла, чтобы отразить этот более короткий путь.

Чтобы это сделать, нам нужно знать длину пути от начального узла до любого достижимого узла. Мы назовём это стоимостью (cost) пути. Пока примем, что перемещение из узла в один из соседних узлов имеет постоянную стоимость, равную 1.

Прежде чем начинать поиск, мы присвоим значению cost каждого узла значение infinity; благодаря этому любой путь будет короче этого. Также мы присвоим cost узла start_node значение 0.

Тогда вот как будет выглядеть код:

if adjacent not in reachable:
    reachable.add(adjacent)

# If this is a new path, or a shorter path than what we have, keep it.
if node.cost + 1 < adjacent.cost:
    adjacent.previous = node
    adjacent.cost = node.cost + 1

Одинаковая стоимость поиска

Давайте теперь рассмотрим метод choose_node. Если мы стремимся найти кратчайший возможный путь, то выбирать узел случайным образом — не самая лучшая идея.

Лучше выбирать узел, которого мы можем достичь из начального узла по кратчайшему пути; благодаря этому мы в общем случае будем предпочитать длинным путям более короткие. Это не значит, что более длинные пути не будут рассматриваться вовсе, это значит, что более короткие пути будут рассматриваться первыми. Так как алгоритм завершает работу сразу после нахождения подходящего пути, это должно позволить нам находить короткие пути.

Вот возможный пример функции choose_node:

function choose_node (reachable):
    best_node = None

    for node in reachable:
        if best_node == None or best_node.cost > node.cost:
            best_node = node
    
    return best_node

Интуитивно понятно, что поиск этого алгоритма расширяется «радиально» от начального узла, пока не достигнет конечного. Вот интерактивное демо такого поведения:

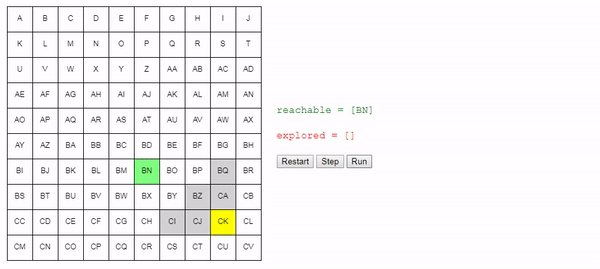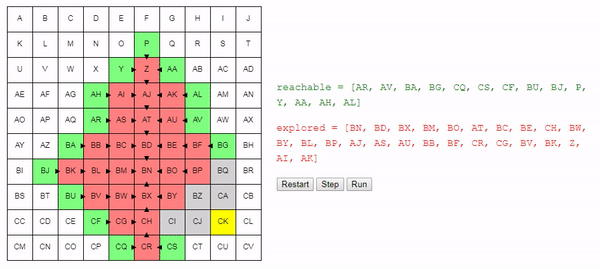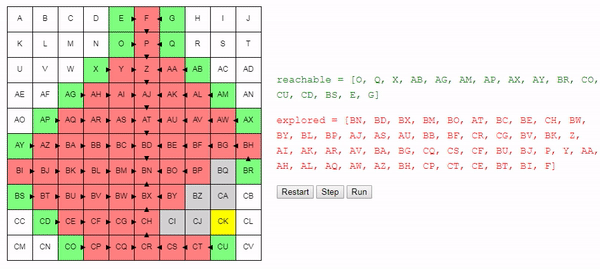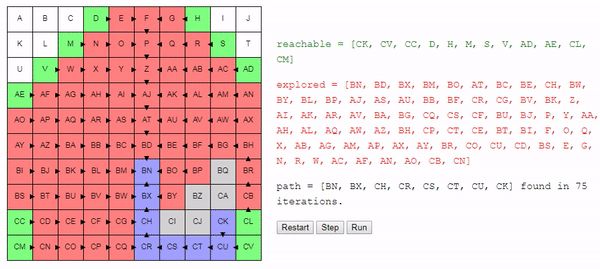
Заключение

Простое изменение в способе выбора рассматриваемого следующим узла позволило нам получить достаточно хороший алгоритм: он находит кратчайший путь от начального до конечного узла.

Но этот алгоритм всё равно в какой-то степени остаётся «глупым». Он продолжает искать повсюду, пока не наткнётся на конечный узел. Например, какой смысл в показанном выше примере выполнять поиск в направлении A, если очевидно, что мы отдаляемся от конечного узла?

Можно ли сделать choose_node умнее? Можем ли мы сделать так, чтобы он направлял поиск в сторону конечного узла, даже не зная заранее правильного пути?

Оказывается, что можем — в следующей части мы наконец-то дойдём до choose_node, позволяющей превратить общий алгоритм поиска пути в A*.

Часть 3. Снимаем завесу тайны с A*

Полученный в предыдущей части алгоритм достаточно хорош: он находит кратчайший путь от начального узла до конечного. Однако, он тратит силы впустую: рассматривает пути, которые человек очевидно назовёт ошибочными — они обычно удаляются от цели. Как же этого можно избежать?

Волшебный алгоритм

Представьте, что мы запускаем алгоритм поиска на особом компьютере с чипом, который может творить магию. Благодаря этому потрясающему чипу мы можем выразить choose_node очень простым способом, который гарантированно создаст кратчайший путь, не теряя времени на исследование частичных путей, которые никуда не ведут:

function choose_node (reachable):
    return magic(reachable, "любой узел, являющийся следующим на кратчайшем пути")

Звучит соблазнительно, но магическим чипам всё равно требуется какой-то низкоуровневый код. Вот какой может быть хорошая аппроксимация:

function choose_node (reachable):
    min_cost = infinity
    best_node = None

    for node in reachable:
        cost_start_to_node = node.cost
        cost_node_to_goal = magic(node, "кратчайший путь к цели")
        total_cost = cost_start_to_node + cost_node_to_goal

        if min_cost > total_cost:
            min_cost = total_cost
            best_node = node

    return best_node

Это отличный способ выбора следующего узла: вы выбираем узел, дающий нам кратчайший путь от начального до конечного узла, что нам и нужно.

Также мы минимизировали количество используемой магии: мы точно знаем, какова стоимость перемещения от начального узла к каждому узлу (это node.cost), и используем магию только для предсказания стоимости перемещения от узла к конечному узлу.

Не магический, но довольно потрясающий A*

К сожалению, магические чипы — это новинка, а нам нужна поддержка и устаревшего оборудования. БОльшая часть кода нас устраивает, за исключением этой строки:

# Throws MuggleProcessorException
cost_node_to_goal = magic(node, "кратчайший путь к цели")

То есть мы не можем использовать магию, чтобы узнать стоимость ещё не исследованного пути. Ну ладно, тогда давайте сделаем прогноз. Будем оптимистичными и предположим, что между текущим и конечным узлами нет ничего, и мы можем просто двигаться напрямик:

cost_node_to_goal = distance(node, goal_node)

Заметьте, что кратчайший путь и минимальное расстояние разные: минимальное расстояние подразумевает, что между текущим и конечным узлами нет совершенно никаких препятствий.

Эту оценку получить достаточно просто. В наших примерах с сетками это расстояние городских кварталов между двумя узлами (то есть abs(Ax - Bx) + abs(Ay - By)). Если бы мы могли двигаться по диагонали, то значение было бы равно sqrt( (Ax - Bx)^2 + (Ay - By)^2 ), и так далее. Самое важное то, что мы никогда не получаем слишком высокую оценку стоимости.

Итак, вот немагическая версия choose_node:

function choose_node (reachable):
    min_cost = infinity
    best_node = None

    for node in reachable:
        cost_start_to_node = node.cost
        cost_node_to_goal = estimate_distance(node, goal_node)
        total_cost = cost_start_to_node + cost_node_to_goal

        if min_cost > total_cost:
            min_cost = total_cost
            best_node = node

    return best_node

Функция, оценивающая расстояние от текущего до конечного узла, называется эвристикой, и этот алгоритм поиска, леди и джентльмены, называется … A*.

Интерактивное демо

Пока вы оправляетесь от шока, вызванного осознанием того, что загадочный A* на самом деле настолько прост, можете посмотреть на демо (или запустить его в оригинале статьи). Вы заметите, что в отличие от предыдущего примера, поиск тратит очень мало времени на движение в неверном направлении.

Заключение

Наконец-то мы дошли до алгоритма A*, который является не чем иным, как описанным в первой части статьи общим алгоритмом поиска с некоторыми усовершенствованиями, описанными во второй части, и использующим функцию choose_node, которая выбирает узел, который по нашей оценке приближает нас к конечному узлу. Вот и всё.

Вот вам для справки полный псевдокод основного метода:

function find_path (start_node, end_node):
    reachable = [start_node]
    explored = []

    while reachable is not empty:
        # Choose some node we know how to reach.
        node = choose_node(reachable)

        # If we just got to the goal node, build and return the path.
        if node == goal_node:
            return build_path(goal_node)

        # Don't repeat ourselves.
        reachable.remove(node)
        explored.add(node)

        # Where can we get from here that we haven't explored before?
        new_reachable = get_adjacent_nodes(node) - explored
        for adjacent in new_reachable:
            # First time we see this node?
            if adjacent not in reachable:
                reachable.add(adjacent)
        
            # If this is a new path, or a shorter path than what we have, keep it.
            if node.cost + 1 < adjacent.cost:
                adjacent.previous = node
                adjacent.cost = node.cost + 1

    # If we get here, no path was found :(
    return None

Метод build_path:

function build_path (to_node):
    path = []
    while to_node != None:
        path.add(to_node)
        to_node = to_node.previous
    return path

А вот метод choose_node, который превращает его в A*:

function choose_node (reachable):
    min_cost = infinity
    best_node = None

    for node in reachable:
        cost_start_to_node = node.cost
        cost_node_to_goal = estimate_distance(node, goal_node)
        total_cost = cost_start_to_node + cost_node_to_goal

        if min_cost > total_cost:
            min_cost = total_cost
            best_node = node

    return best_node

Вот и всё.

А зачем же нужна часть 4?

Теперь, когда вы поняли, как работает A*, я хочу рассказать о некоторых потрясающих областях его применения, которые далеко не ограничиваются поиском путей в сетке ячеек.

Часть 4. A* на практике

Первые три части статьи начинаются с самых основ алгоритмов поиска путей и заканчиваются чётким описанием алгоритма A*. Всё это здорово в теории, но понимание того, как это применимо на практике — совершенно другая тема.

Например, что будет, если наш мир не является сеткой?

Что если персонаж не может мгновенно поворачиваться на 90 градусов?

Как построить граф, если мир бесконечен?

Что если нас не волнует длина пути, но мы зависим от солнечной энергии и нам как можно больше нужно находиться под солнечным светом?

Как найти кратчайший путь к любому из двух конечных узлов?

Функция стоимости

В первых примерах мы искали кратчайший путь между начальным и конечным узлами. Однако вместо того, чтобы хранить частичные длины путей в переменной length, мы назвали её cost. Почему?

Мы можем заставить A* искать не только кратчайший, но и лучший путь, причём определение «лучшего» можно выбирать, исходя из наших целей. Когда нам нужен кратчайший путь, стоимостью является длина пути, но если мы хотим минимизировать, например, потребление топлива, то нужно использовать в качестве стоимости именно его. Если мы хотим по максимуму увеличить «время, проводимое под солнцем», то затраты — это время, проведённое без солнца. И так далее.

В общем случае это означает, что с каждым ребром графа связаны соответствующие затраты. В показанных выше примерах стоимость задавалась неявно и считалась всегда равной 1, потому что мы считали шаги на пути. Но мы можем изменить стоимость ребра в соответствии с тем, что мы хотим минимизировать.

Функция критерия

Допустим, наш объект — это автомобиль, и ему нужно добраться до заправки. Нас устроит любая заправка. Требуется кратчайший путь до ближайшей АЗС.

Наивный подход будет заключаться в вычислении кратчайшего пути до каждой заправки по очереди и выборе самого короткого. Это сработает, но будет довольно затратным процессом.

Что если бы мы могли заменить один goal_node на метод, который по заданному узлу может сообщить, является ли тот конечным или нет. Благодаря этому мы сможем искать несколько целей одновременно. Также нам нужно изменить эвристику, чтобы она возвращала минимальную оцениваемую стоимость всех возможных конечных узлов.

В зависимости от специфики ситуации мы можем и не иметь возможности достичь цели идеально, или это будет слишком много стоить (если мы отправляем персонажа через половину огромной карты, так ли важна разница в один дюйм?), поэтому метод is_goal_node может возвращать true, когда мы находимся «достаточно близко».

Полная определённость не обязательна

Представление мира в виде дискретной сетки может быть недостаточным для многих игр. Возьмём, например, шутер от первого лица или гоночную игру. Мир дискретен, но его нельзя представить в виде сетки.

Но есть проблема и посерьёзней: что если мир бесконечен? В таком случае, даже если мы сможем представить его в виде сетки, то у нас просто не будет возможности построить соответствующий сетке граф, потому что он должен быть бесконечным.

Однако не всё потеряно. Разумеется, для алгоритма поиска по графам нам определённо нужен граф. Но никто не говорил, что граф должен быть исчерпывающим!

Если внимательно посмотреть на алгоритм, то можно заметить, что мы ничего не делаем с графом, как целым; мы исследуем граф локально, получая узлы, которых можем достичь из рассматриваемого узла. Как видно из демо A*, некоторые узлы графа вообще не исследуются.

Так почему бы нам просто не строить граф в процессе исследования?

Мы делаем текущую позицию персонажа начальным узлом. При вызове get_adjacent_nodes она может определять возможные способы, которыми персонаж способен переместиться из данного узла, и создавать соседние узлы на лету.

За пределами трёх измерений

Даже если ваш мир действительно является 2D-сеткой, нужно учитывать и другие аспекты. Например, что если персонаж не может мгновенно поворачиваться на 90 или 180 градусов, как это обычно и бывает?

Состояние, представляемое каждым узлом поиска, не обязательно должно быть только позицией; напротив, оно может включать в себя произвольно сложное множество значений. Например, если повороты на 90 градусов занимают столько же времени, сколько переход из одной ячейки в другую, то состояние персонажа может задаваться как [position, heading]. Каждый узел может представлять не только позицию персонажа, но и направление его взгляда; и новые рёбра графа (явные или косвенные) отражают это.

Если вернуться к исходной сетке 5×5, то начальной позицией поиска теперь может быть [A, East]. Соседними узлами теперь являются [B, East] и [A, South] — если мы хотим достичь F, то сначала нужно скорректировать направление, чтобы путь обрёл вид [A, East], [A, South], [F, South].

Шутер от первого лица? Как минимум четыре измерения: [X, Y, Z, Heading]. Возможно, даже [X, Y, Z, Heading, Health, Ammo].

Учтите, что чем сложнее состояние, тем более сложной должна быть эвристическая функция. Сам по себе A* прост; искусство часто возникает благодаря хорошей эвристике.

Заключение

Цель этой статьи — раз и навсегда развеять миф о том, что A* — это некий мистический, не поддающийся расшифровке алгоритм. Напротив, я показал, что в нём нет ничего загадочного, и на самом деле его можно довольно просто вывести, начав с самого нуля.

Дальнейшее чтение

У Амита Патела есть превосходное «Введение в алгоритм A*» [перевод на Хабре] (и другие его статьи на разные темы тоже великолепны!).

%saved0% Граф — это (упрощенно) множество точек, называемых вершинами, соединенных какими-то линиями, называемыми рёбрами (необязательно все вершины соединены). Можно представлять себе как города, соединенные дорогами.

Любое клетчатое поле можно представить в виде графа. Вершинами будут являться клетки, а ребрами — смежные стороны клеток.

Наглядное представление о работе перечисленных далее алгоритмов можно получить благодаря визуализатору PathFinding.js.

Поиск в ширину (BFS, Breadth-First Search)

Алгоритм был разработан независимо Муром и Ли для разных приложений (поиск пути в лабиринте и разводка проводников соответственно) в 1959 и 1961 годах. Этот алгоритм можно сравнить с поджиганием соседних вершин графа: сначала мы зажигаем одну вершину (ту, из которой начинаем путь), а затем огонь за один элементарный промежуток времени перекидывается на все соседние с ней не горящие вершины. В последствие то же происходит со всеми подожженными вершинами. Таким образом, огонь распространяется «в ширину». В результате его работы будет найден кратчайший путь до нужной клетки.

Алгоритм Дейкстры (Dijkstra)

Этот алгоритм назван по имени создателя и был разработан в 1959 году. В процессе выполнения алгоритм проверит каждую из вершин графа, и найдет кратчайший путь до исходной вершины. Стандартная реализация работает на взвешенном графе — графе, у которого каждый путь имеет вес, т.е. «стоимость», которую надо будет «заплатить», чтобы перейти по этому ребру. При этом в стандартной реализации веса неотрицательны. На клетчатом поле вес каждого ребра графа принимается одинаковым (например, единицей).

А* (А «со звездочкой»)

Впервые описан в 1968 году Питером Хартом, Нильсом Нильсоном и Бертрамом Рафаэлем. Данный алгоритм является расширением алгоритма Дейкстры, ускорение работы достигается за счет эвристики — при рассмотрении каждой отдельной вершины переход делается в ту соседнюю вершину, предположительный путь из которой до искомой вершины самый короткий. При этом существует множество различных методов подсчета длины предполагаемого пути из вершины. Результатом работы также будет кратчайший путь. О реализации алгоритма читайте в здесь.

Поиск по первому наилучшему совпадению (Best-First Search)

Усовершенствованная версия алгоритма поиска в ширину, отличающаяся от оригинала тем, что в первую очередь развертываются узлы, путь из которых до конечной вершины предположительно короче. Т.е. за счет эвристики делает для BFS то же, что A* делает для алгоритма Дейкстры.

IDA* (A* с итеративным углублением)

Расшифровывается как Iterative Deeping A*. Является измененной версией A*, использующей меньше памяти за счет меньшего количества развертываемых узлов. Работает быстрее A* в случае удачного выбора эвристики. Результат работы — кратчайший путь.

Jump Point Search

Самый молодой из перечисленных алгоритмов был представлен в 2011 году. Представляет собой усовершенствованный A*. JPS ускоряет поиск пути, «перепрыгивая» многие места, которые должны быть просмотрены. В отличие от подобных алгоритмов JPS не требует предварительной обработки и дополнительных затрат памяти.

---

Материалы по более интересным алгоритмам мы обозревали в подборке материалов по продвинутым алгоритмам и структурам данных.

Когда вы пользуетесь навигатором, вы указываете точку А и точку Б, и дальше навигатор как-то сам строит маршрут. Сегодня посмотрим, что лежит в основе алгоритма, который это делает. Просто ради интереса. 

Графы и «задача коммивояжёра»

Ещё до появления навигаторов у людей была такая же проблема: как найти кратчайший путь из одного места в другое, если есть ограниченное количество промежуточных точек? Или как объехать ограниченное количество точек, затратив минимальные усилия. В общем виде это называется «задачей коммивояжёра», и мы уже рассказывали, в чём там идея:

Если взять просто города и расстояния между ними, то с точки зрения математики это называется графом: города будут вершинами графа, а дороги между ними — рёбрами графа. Если мы знаем длину каждой дороги, то это будет значением (весом) рёбер графа. Этой теории нам уже хватит, чтобы понять, как работает навигатор в машине.

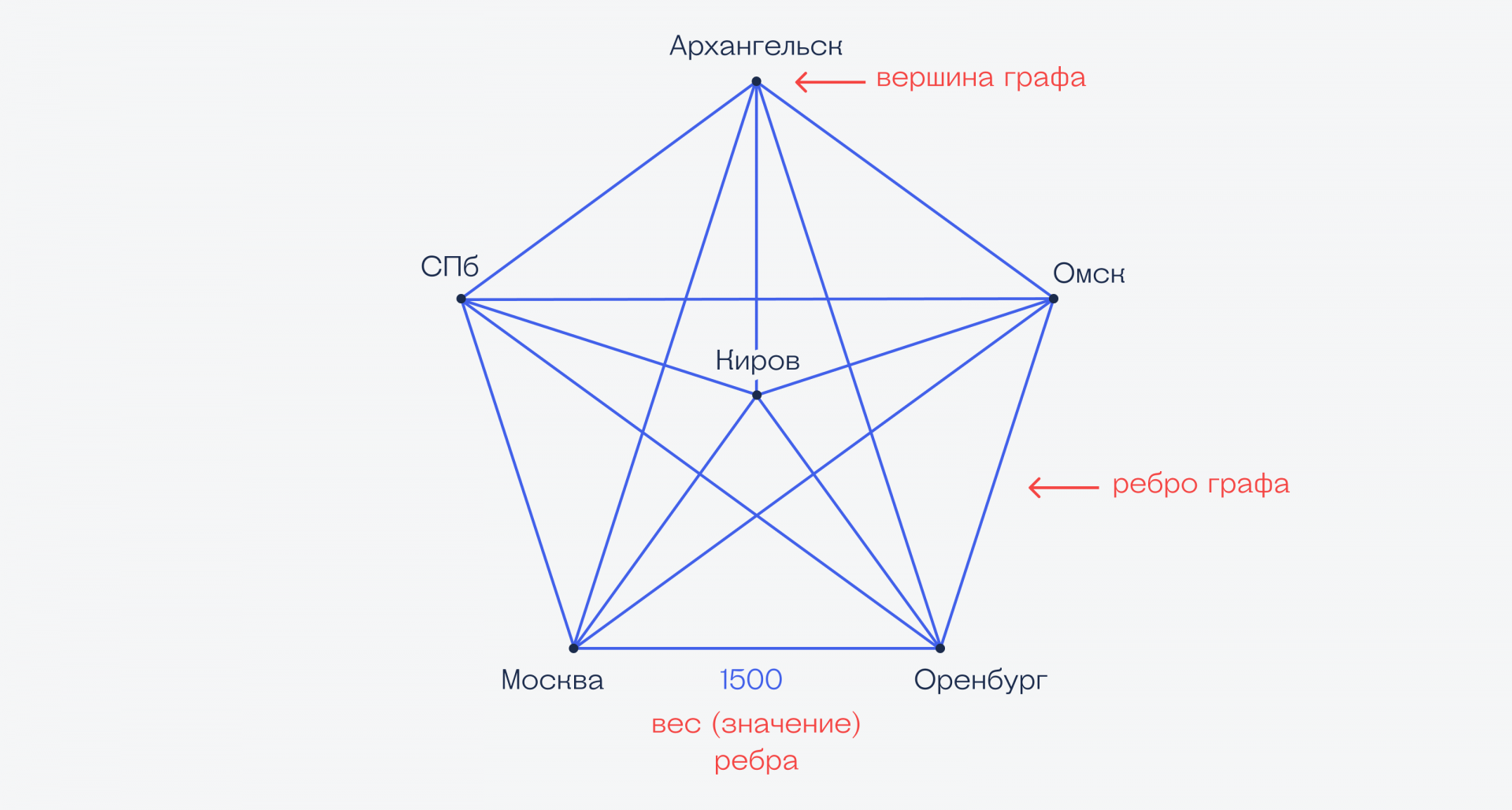
Алгоритм Дейкстры — ищем самый быстрый путь

Как только появилось решение полным перебором, математики стали искать другой подход, который работал бы гораздо быстрее и не требовал бы вычисления такого огромного объёма данных. В 1959 году Эдсгер Дейкстра придумал свой алгоритм, которым пользуются до сих пор. Идея его в том, чтобы не перебирать все варианты, а находить самый короткий путь только между соседними графами — и так, шаг за шагом, продвигаться к конечной точке.

Допустим, у нас есть улицы, перекрёстки и мы знаем время пути между ними. Нарисуем это в виде графа, а чтобы было проще ориентироваться — сделаем визуально всё одинаковой длины:

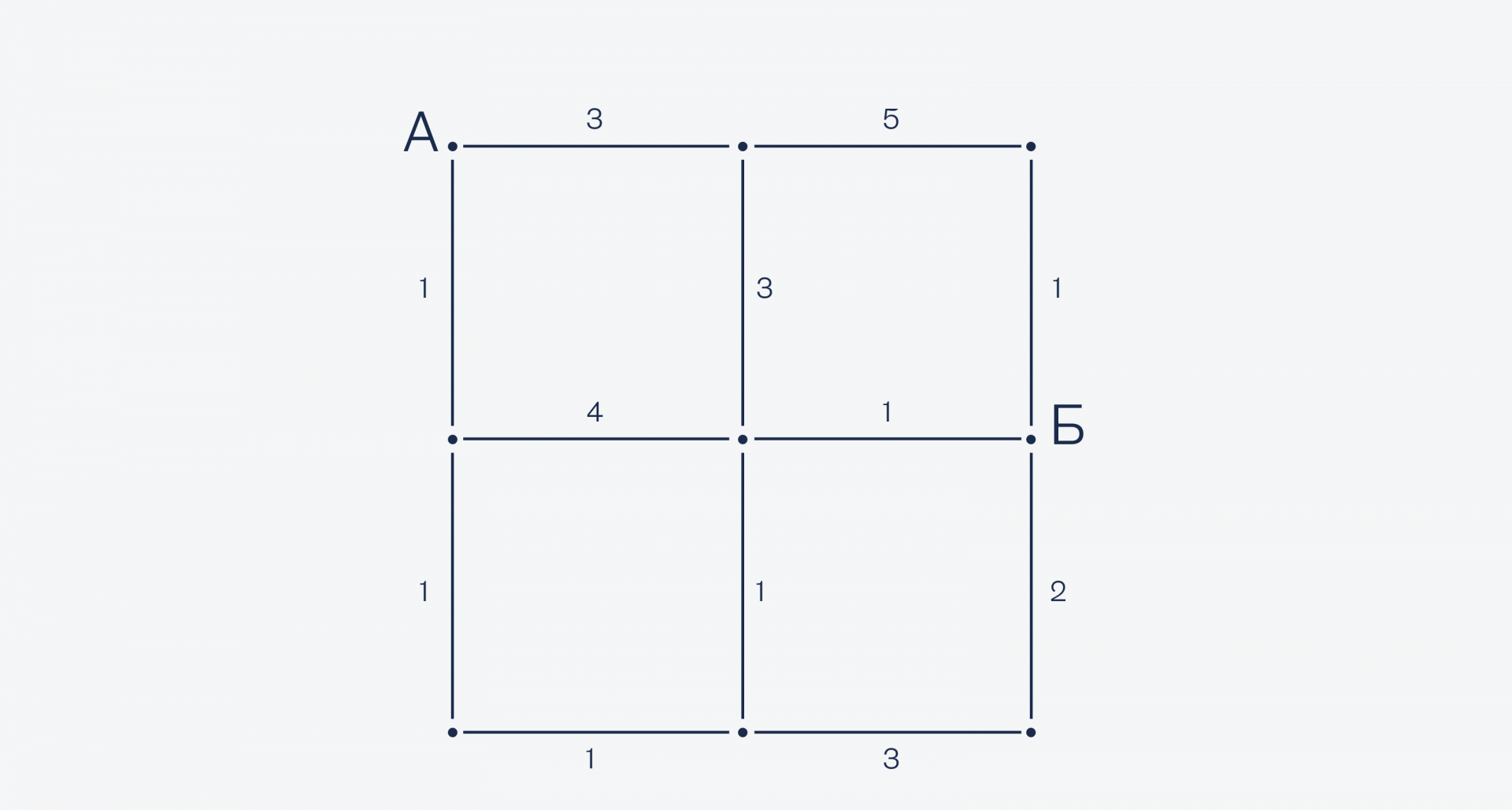
Чтобы найти самый быстрый путь из А в Б, мы смотрим сначала, какие пути у нас выходят из точки А. Видно, что поехать вниз будет быстрее, чем поехать направо:

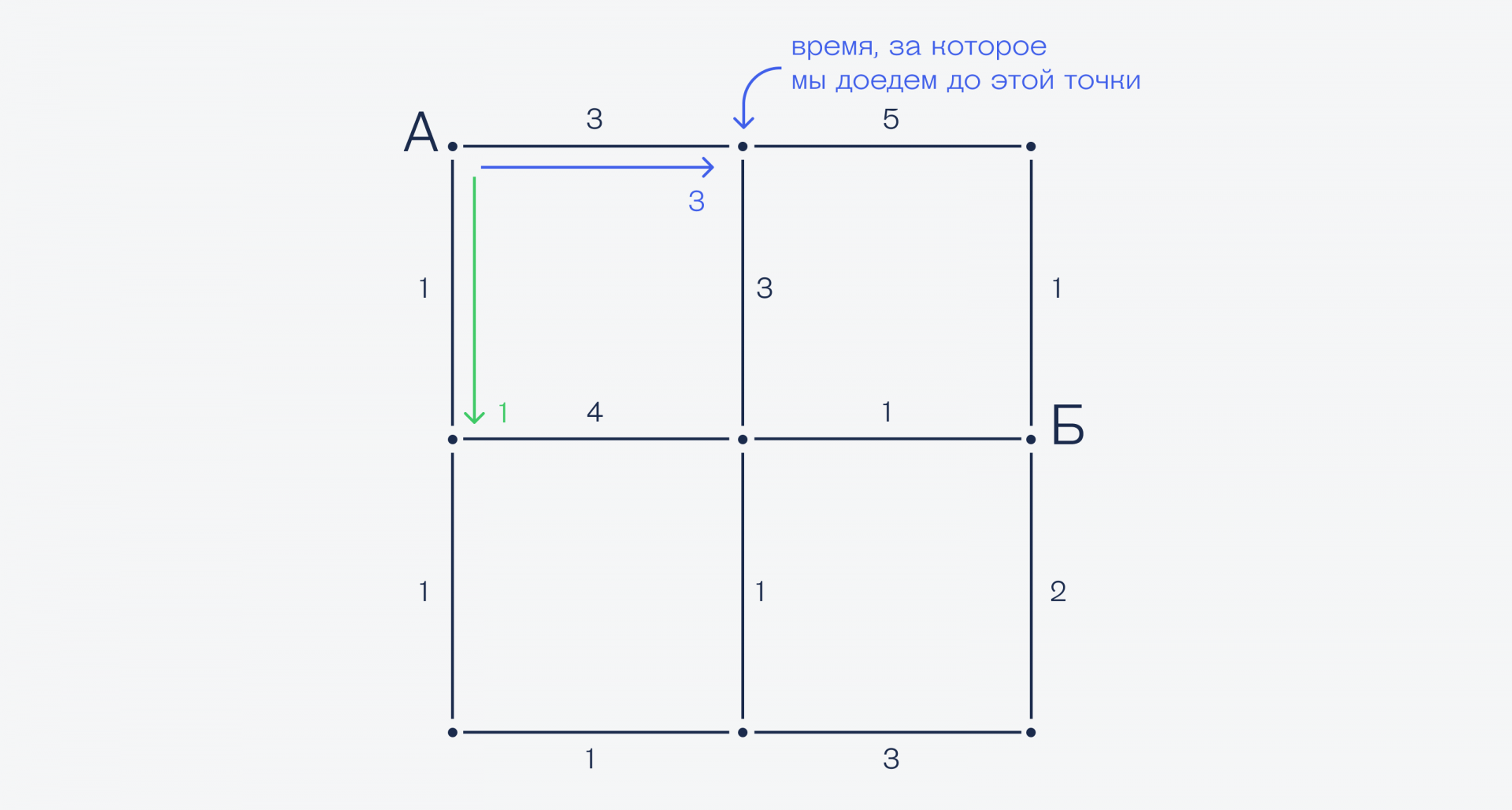
Значит, выбираем путь вниз. Теперь делаем то же самое для этой точки — смотрим, где быстрее: справа или внизу. Вниз быстрее (1 меньше, чем 4), поэтому едем по ней:

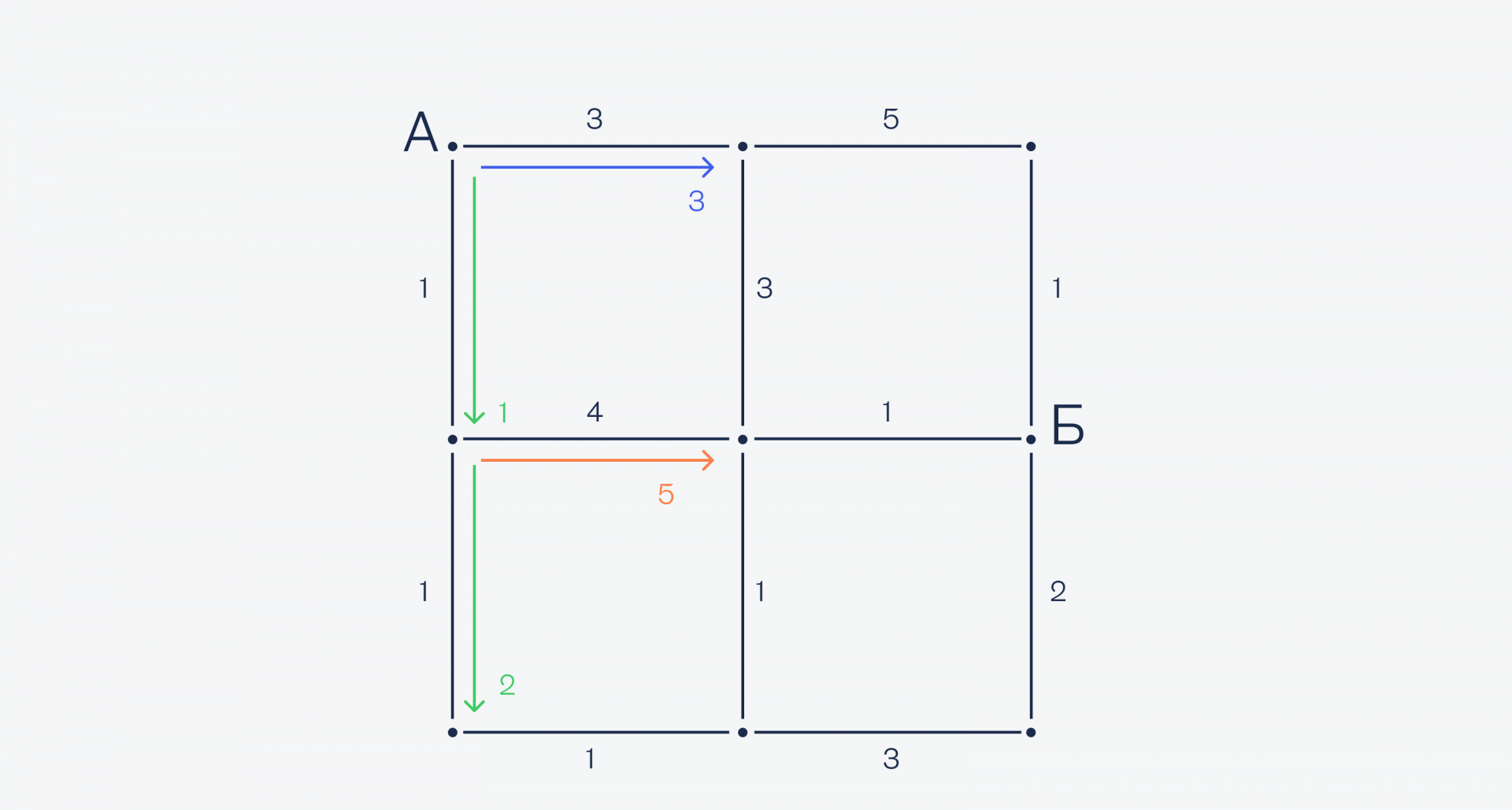
При этом мы не отбрасываем уже сделанные вычисления (всё равно уже посчитали), а запоминаем их на всякий случай. Из нижней точки есть только одна дорога — направо, поэтому едем по ней:

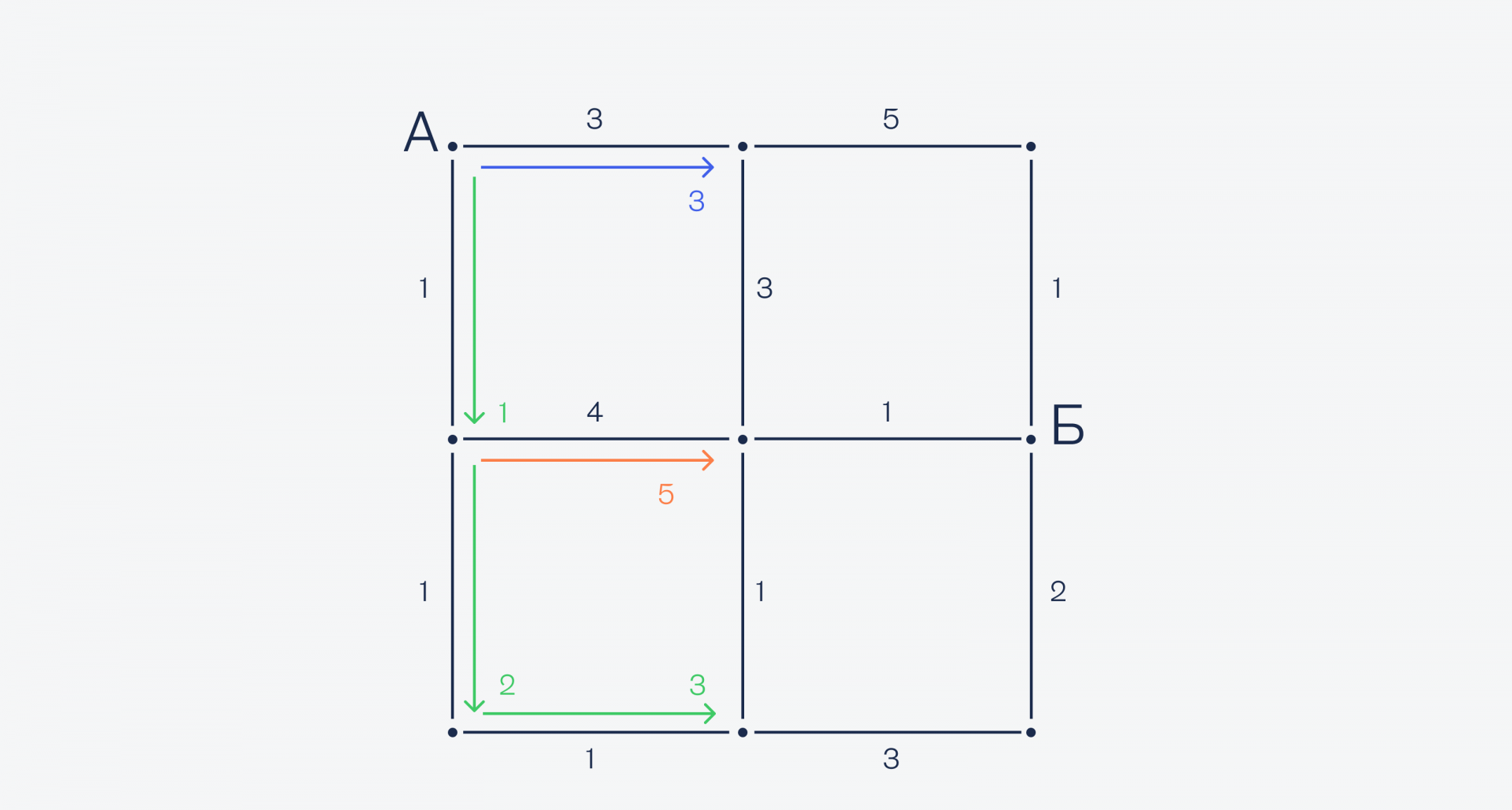
А теперь у нас получилась интересная ситуация: в центральную точку мы можем попасть как сверху, так и снизу, при этом и там, и там у нас одинаковое время — 3 минуты. Значит, посчитаем оба варианта — вдруг сверху будет быстрее и нам нужно будет перестроить маршрут заново:

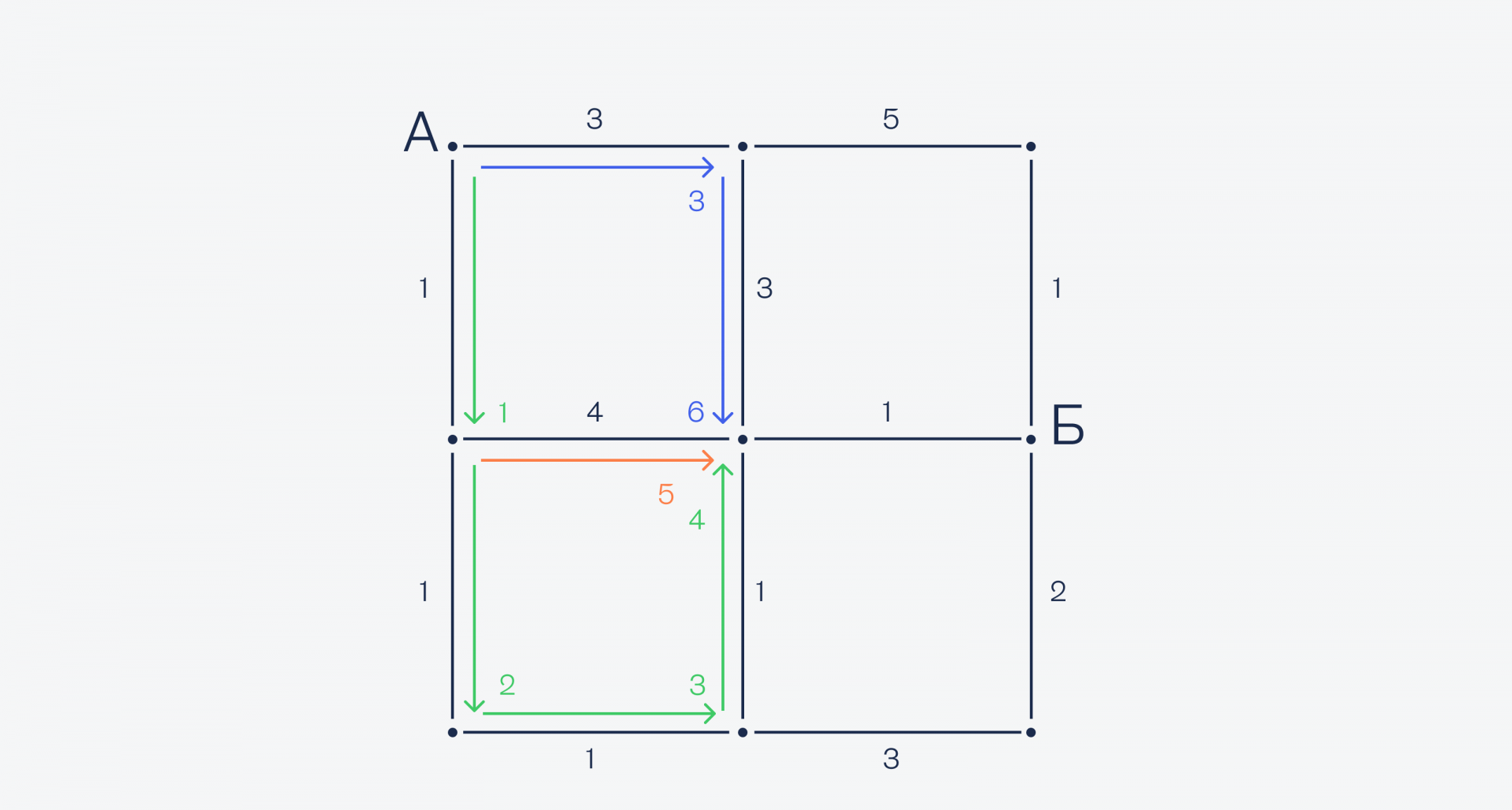
Оказывается, снизу ехать до центра быстрее, чем сверху — 4 минуты вместо 6, поэтому оставляем нижний маршрут. Наконец, из центральной точки до точки Б всего один путь — направо, поэтому выбираем его:

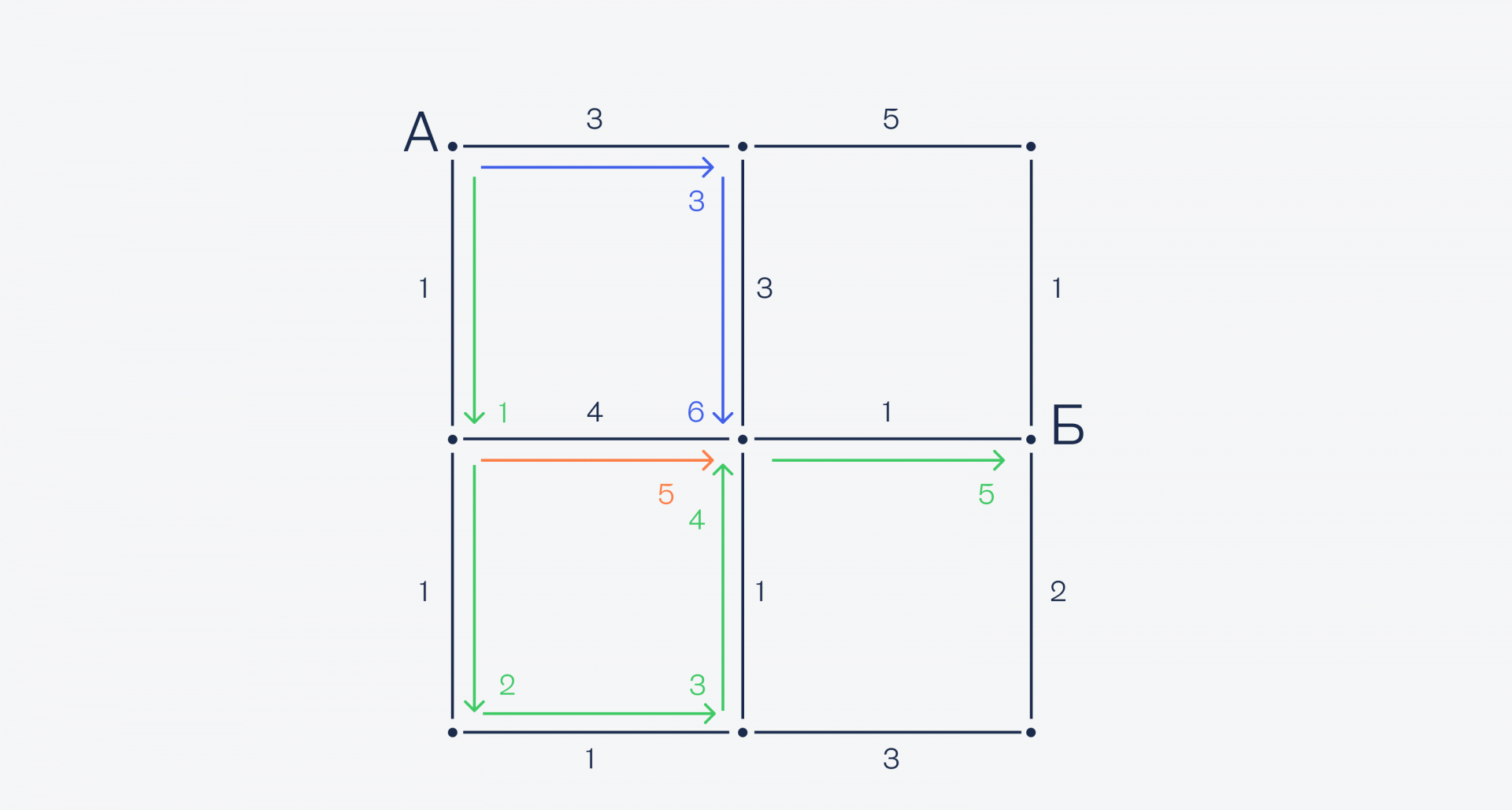
Как видите, нам не пришлось считать все варианты со всеми точками, а до некоторых мы просто не добрались. Это сильно сэкономило время и потребовало меньше ресурсов для вычисления.Такой алгоритм и лежит в основе автомобильных навигаторов — с вычислениями справится даже бюджетный смартфон.

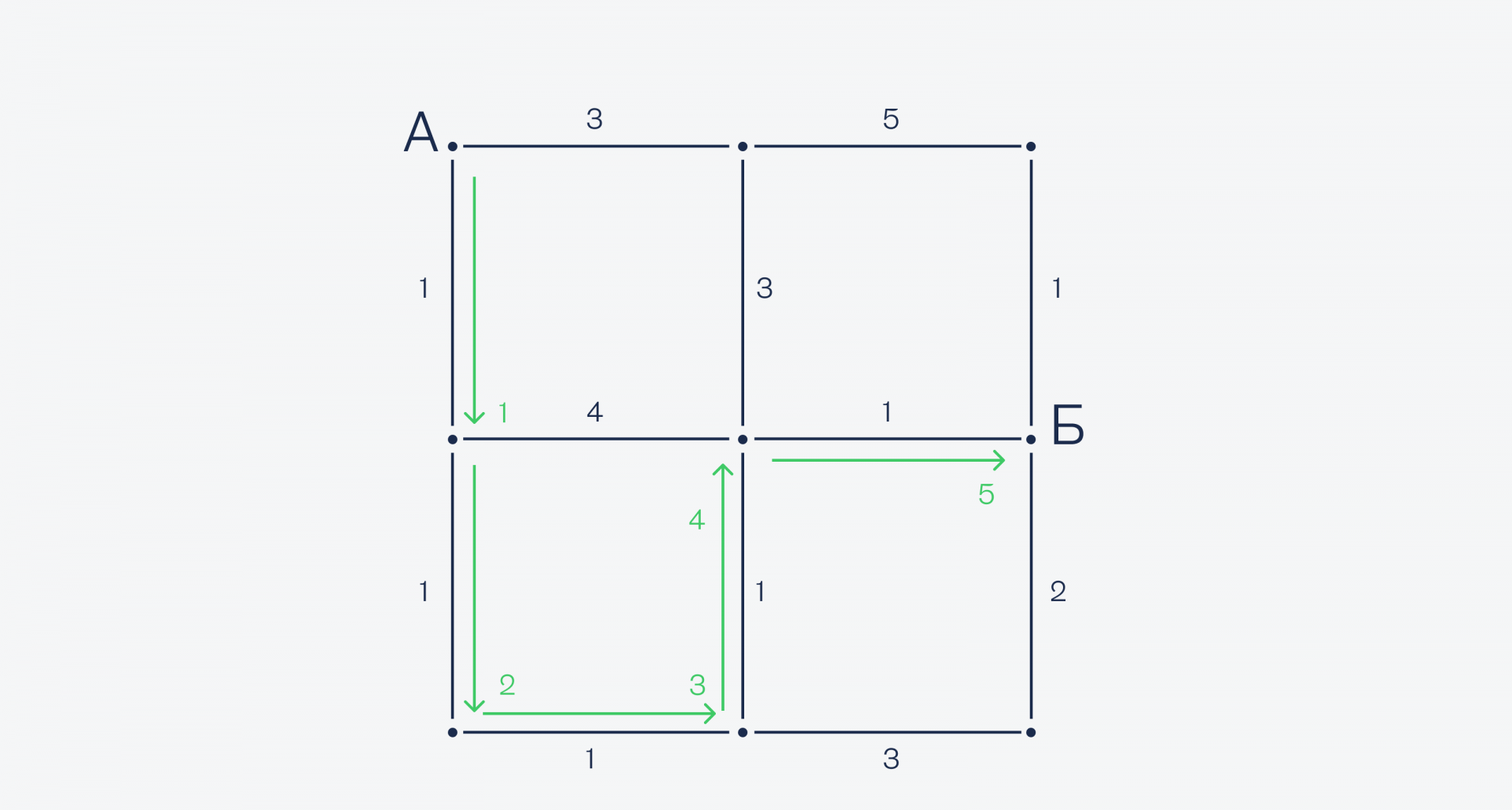
Что ещё учитывает навигатор

Чтобы алгоритм оставался простым и работал только со временем, все остальные параметры дорог тоже привязывают ко времени. Покажем, как это работает, на паре примеров.

Комфорт. Если нам нужно построить не самый быстрый, а самый комфортный маршрут, то мы можем отдать предпочтение автомагистралям и дорогам с несколькими полосами — на них обычно и асфальт получше, и резких поворотов поменьше. Чтобы навигатор выбирал именно такие дороги, им можно присвоить коэффициент 0,8 — это виртуально сократит время на дорогу по ним на 20%, а навигатор всегда выберет то, что быстрее. 

С просёлочными и грунтовыми дорогами ситуация обратная. Они редко бывают комфортными, а значит, им можно дать коэффициент 1,3, чтобы они казались алгоритму более долгими и он старался их избегать. А лесным дорогам можно поставить коэффициент 5 — навигатор их выберет, только если это единственная дорога то точки назначения.

Сложность маршрута и реальное время. Маршрут из А в Б почти никогда не бывает прямым — на нём всегда есть повороты, развороты и съезды, которые отнимают время. Чтобы навигатор это учитывал, в графы добавляют время прохождения поворота — либо коэффициентом, либо отдельным параметром. Из-за этого алгоритм будет искать действительно быстрый маршрут с учётом геометрии дорог.

Пробки. Если есть интернет, то всё просто: навигатор получает данные о состоянии дорог и добавляет разные коэффициенты в зависимости от загруженности. Иногда навигатор ведёт дворами, когда трасса свободна — это не ошибка навигатора, а его прогноз на время поездки: если через 10 минут в этом месте обычно собираются пробки, то там лучше не ехать, а заранее поехать в объезд.

Если интернета нет, то алгоритм просто использует усреднённую модель пробок на этом участке. Эта модель скачивается заранее и постоянно обновляется в фоновом режиме.

Как построить маршрут по всей России

Если нам нужно построить маршрут из Брянска в Тулу, то с точки зрения компьютера это безумно сложная задача: ему нужно перебрать десятки тысяч улиц и миллионы перекрёстков, чтобы понять, какой путь выбрать. С этим плохо справляется даже обычный компьютер, не говоря уже о телефоне.

Если мы в Яндекс Картах построим такой маршрут, то навигатор нам предложит сразу 4 варианта:

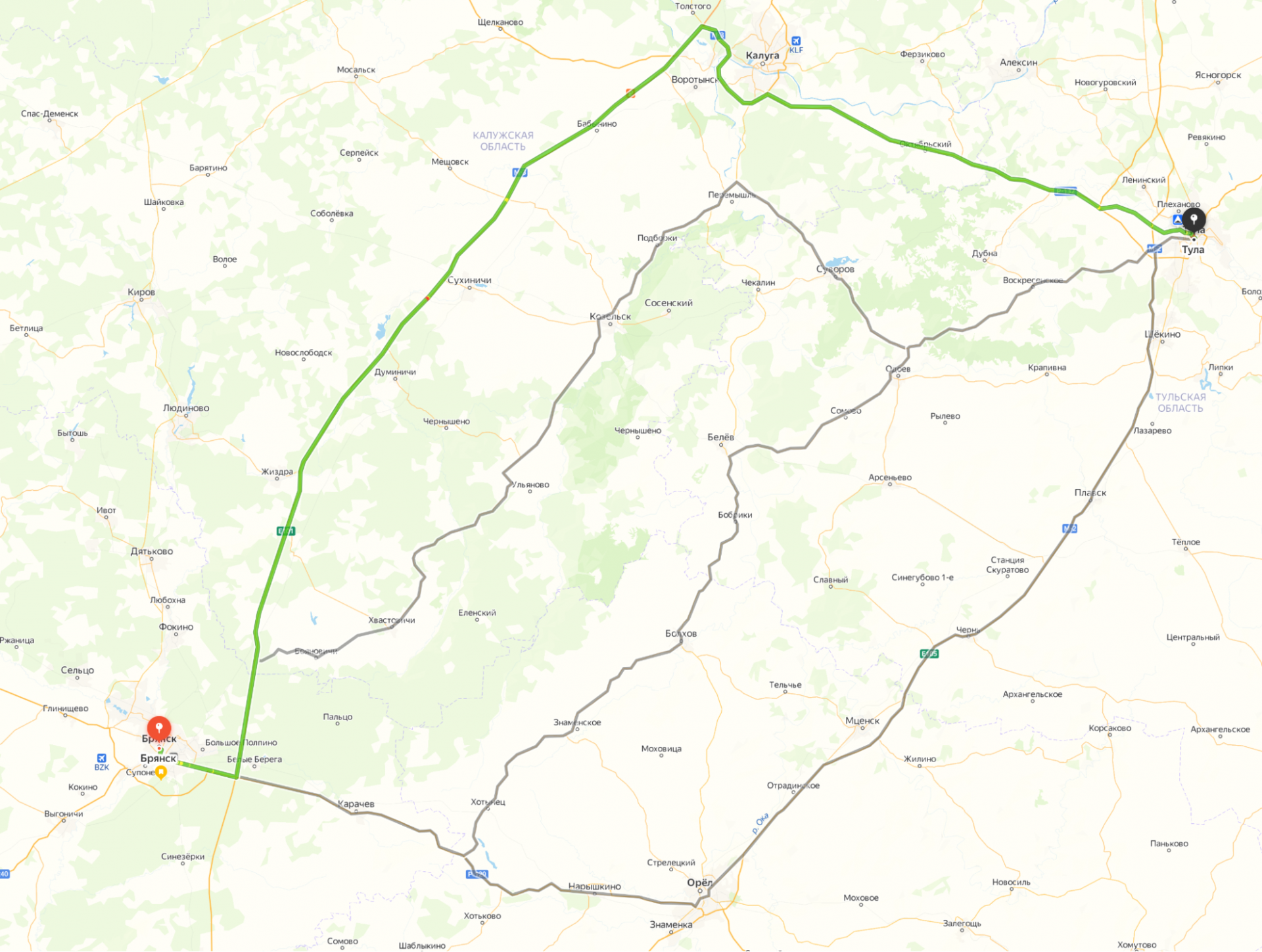
Но мы не ждали полчаса, пока сервер на той стороне посчитает все перекрёстки, а получили результат через пару секунд. Хитрость в том, что алгоритм использует уже заранее просчитанные варианты маршрутов и подставляет их для ускорения.

Например, если мы поедем в Тулу не из Брянска, а из Синезёрок, то поменяется только начальный маршрут по трассе М3, а всё остальное останется прежним:

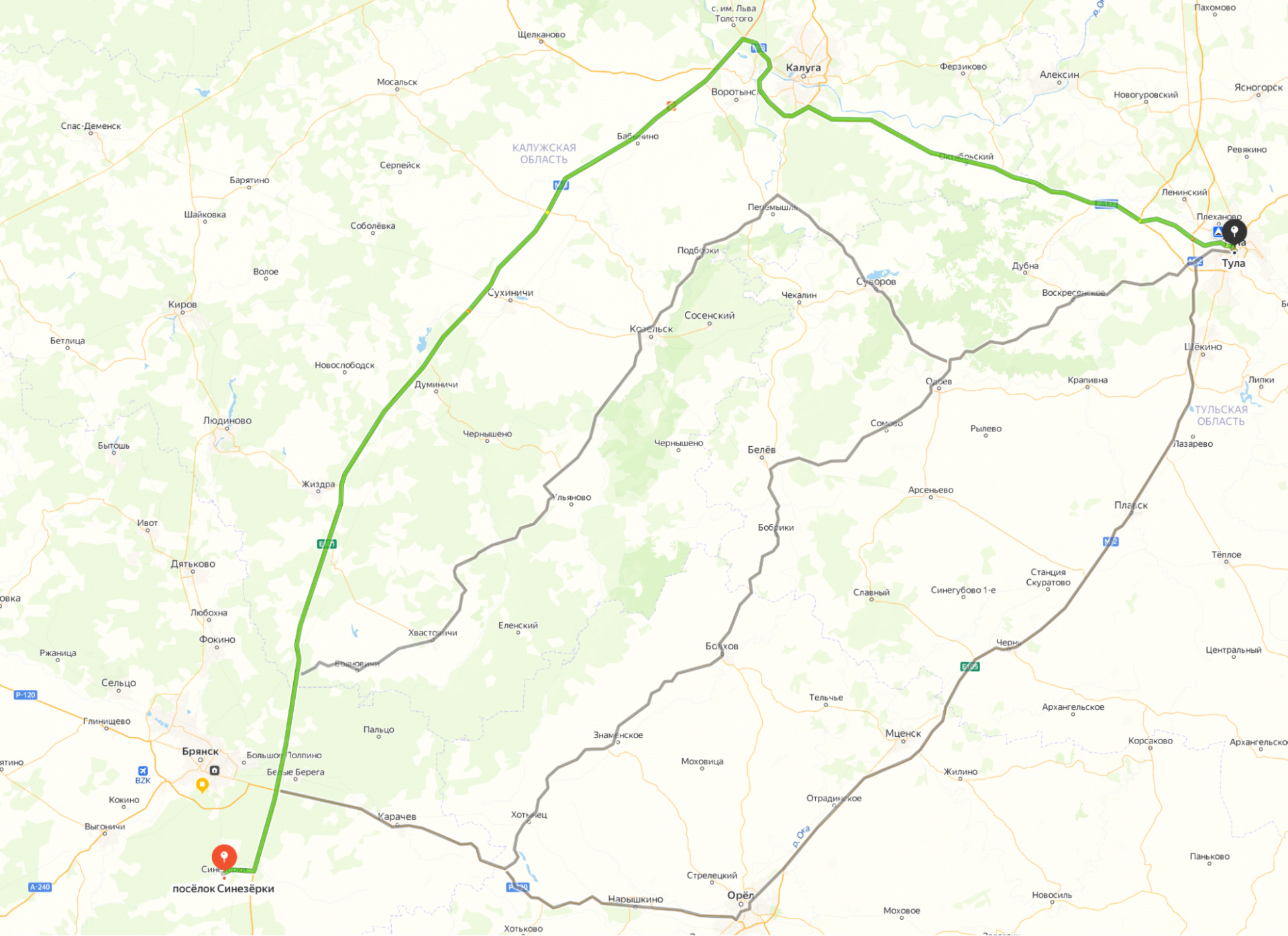
Получается, что навигатору не нужно всё пересчитывать — он находит только ключевые точки пути, а маршрут между ними уже просчитан до этого. Этот приём работает и при перестроении маршрута во время движения: навигатор смотрит, как нужно поменять путь, чтобы вернуть вас на уже известную дорогу.

Что дальше

Следующий этап — напишем алгоритм Дейкстры сами и посмотрим, как он работает по шагам.

From Wikipedia, the free encyclopedia

Pathfinding or pathing is the plotting, by a computer application, of the shortest route between two points. It is a more practical variant on solving mazes. This field of research is based heavily on Dijkstra’s algorithm for finding the shortest path on a weighted graph.

Pathfinding is closely related to the shortest path problem, within graph theory, which examines how to identify the path that best meets some criteria (shortest, cheapest, fastest, etc) between two points in a large network.

Algorithms[edit]

At its core, a pathfinding method searches a graph by starting at one vertex and exploring adjacent nodes until the destination node is reached, generally with the intent of finding the cheapest route. Although graph searching methods such as a breadth-first search would find a route if given enough time, other methods, which “explore” the graph, would tend to reach the destination sooner. An analogy would be a person walking across a room; rather than examining every possible route in advance, the person would generally walk in the direction of the destination and only deviate from the path to avoid an obstruction, and make deviations as minor as possible.

Two primary problems of pathfinding are (1) to find a path between two nodes in a graph; and (2) the shortest path problem—to find the optimal shortest path. Basic algorithms such as breadth-first and depth-first search address the first problem by exhausting all possibilities; starting from the given node, they iterate over all potential paths until they reach the destination node. These algorithms run in , or linear time, where V is the number of vertices, and E is the number of edges between vertices.

The more complicated problem is finding the optimal path. The exhaustive approach in this case is known as the Bellman–Ford algorithm, which yields a time complexity of , or quadratic time. However, it is not necessary to examine all possible paths to find the optimal one. Algorithms such as A* and Dijkstra’s algorithm strategically eliminate paths, either through heuristics or through dynamic programming. By eliminating impossible paths, these algorithms can achieve time complexities as low as .^[1]

The above algorithms are among the best general algorithms which operate on a graph without preprocessing. However, in practical travel-routing systems, even better time complexities can be attained by algorithms which can pre-process the graph to attain better performance.^[2] One such algorithm is contraction hierarchies.

Dijkstra’s algorithm[edit]

A common example of a graph-based pathfinding algorithm is Dijkstra’s algorithm. This algorithm begins with a start node and an “open set” of candidate nodes. At each step, the node in the open set with the lowest distance from the start is examined. The node is marked “closed”, and all nodes adjacent to it are added to the open set if they have not already been examined. This process repeats until a path to the destination has been found. Since the lowest distance nodes are examined first, the first time the destination is found, the path to it will be the shortest path.^[3]

Dijkstra’s algorithm fails if there is a negative edge weight. In the hypothetical situation where Nodes A, B, and C form a connected undirected graph with edges AB = 3, AC = 4, and BC = −2, the optimal path from A to C costs 1, and the optimal path from A to B costs 2. Dijkstra’s Algorithm starting from A will first examine B, as that is the closest. It will assign a cost of 3 to it, and mark it closed, meaning that its cost will never be reevaluated. Therefore, Dijkstra’s cannot evaluate negative edge weights. However, since for many practical purposes there will never be a negative edgeweight, Dijkstra’s algorithm is largely suitable for the purpose of pathfinding.

A* algorithm[edit]

A* is a variant of Dijkstra’s algorithm commonly used in games. A* assigns a weight to each open node equal to the weight of the edge to that node plus the approximate distance between that node and the finish. This approximate distance is found by the heuristic, and represents a minimum possible distance between that node and the end. This allows it to eliminate longer paths once an initial path is found. If there is a path of length x between the start and finish, and the minimum distance between a node and the finish is greater than x, that node need not be examined.^[4]

A* uses this heuristic to improve on the behavior relative to Dijkstra’s algorithm. When the heuristic evaluates to zero, A* is equivalent to Dijkstra’s algorithm. As the heuristic estimate increases and gets closer to the true distance, A* continues to find optimal paths, but runs faster (by virtue of examining fewer nodes). When the value of the heuristic is exactly the true distance, A* examines the fewest nodes. (However, it is generally impractical to write a heuristic function that always computes the true distance, as the same comparison result can often be reached using simpler calculations – for example, using Chebyshev distance over Euclidean distance in two-dimensional space.) As the value of the heuristic increases, A* examines fewer nodes but no longer guarantees an optimal path. In many applications (such as video games) this is acceptable and even desirable, in order to keep the algorithm running quickly.

RIPA algorithm[edit]

This is claimed to be the simplest and fastest of all pathfinding methods using nodes that branch out from central corridor ‘A’ to other connected Paths.
It can still calculate the optimal path without using any distance checks at all.

How it does this is by having pre-configured Paths from A to Z as it spreads out away from central corridor ‘A’.
If a final path cannot be reached mid way then will find its last connecting path at ‘A’.
At each step is checked from the start to the end as well as from the end to the start until a final connection can be made.

Its like driving from your street to a closer main road that gets to the highway until you exit the highway to the next main road and then the final street.
Paths can be from B to Z (after the central A) with 1,000 path nodes for each Path although can be expanded as necessary.

Each path node should be coded numerically in order for each path (ie B1, B2,B3 etc descending or ascending).
Written by Robert Codell in JavaScript but can be easily converted into other languages.

Open paths must be inserted into 2 arrays – one for fast check path points (ie AB or BD) and the other to record the actual node names to output later.
Runs very fast as very simply logic yet very functional.

Sample algorithm[edit]

This is a fairly simple and easy-to-understand pathfinding algorithm for tile-based maps. To start off, you have a map, a start coordinate and a destination coordinate. The map will look like this, X being walls, S being the start, O being the finish and _ being open spaces, the numbers along the top and right edges are the column and row numbers:

  1 2 3 4 5 6 7 8
X X X X X X X X X X
X _ _ _ X X _ X _ X 1
X _ X _ _ X _ _ _ X 2
X S X X _ _ _ X _ X 3
X _ X _ _ X _ _ _ X 4
X _ _ _ X X _ X _ X 5
X _ X _ _ X _ X _ X 6
X _ X X _ _ _ X _ X 7
X _ _ O _ X _ _ _ X 8
X X X X X X X X X X

First, create a list of coordinates, which we will use as a queue. The queue will be initialized with one coordinate, the end coordinate. Each coordinate will also have a counter variable attached (the purpose of this will soon become evident). Thus, the queue starts off as ((3,8,0)).

Then, go through every element in the queue, including new elements added to the end over the course of the algorithm, and for each element, do the following:

1. Create a list of the four adjacent cells, with a counter variable of the current element’s counter variable + 1 (in our example, the four cells are ((2,8,1),(3,7,1),(4,8,1),(3,9,1)))
2. Check all cells in each list for the following two conditions:
   1. If the cell is a wall, remove it from the list
   2. If there is an element in the main list with the same coordinate, remove it from the cells list
3. Add all remaining cells in the list to the end of the main list
4. Go to the next item in the list

Thus, after turn 1, the list of elements is this: ((3,8,0),(2,8,1),(4,8,1))

• After 2 turns: ((3,8,0),(2,8,1),(4,8,1),(1,8,2),(4,7,2))
• After 3 turns: (…(1,7,3),(4,6,3),(5,7,3))
• After 4 turns: (…(1,6,4),(3,6,4),(6,7,4))
• After 5 turns: (…(1,5,5),(3,5,5),(6,6,5),(6,8,5))
• After 6 turns: (…(1,4,6),(2,5,6),(3,4,6),(6,5,6),(7,8,6))
• After 7 turns: (…(1,3,7)) – problem solved, end this stage of the algorithm – note that if you have multiple units chasing the same target (as in many games – the finish to start approach of the algorithm is intended to make this easier), you can continue until the entire map is taken up, all units are reached or a set counter limit is reached

Now, map the counters onto the map, getting this:

  1 2 3 4 5 6 7 8
X X X X X X X X X X
X _ _ _ X X _ X _ X 1
X _ X _ _ X _ _ _ X 2
X S X X _ _ _ X _ X 3
X 6 X 6 _ X _ _ _ X 4
X 5 6 5 X X 6 X _ X 5
X 4 X 4 3 X 5 X _ X 6
X 3 X X 2 3 4 X _ X 7
X 2 1 0 1 X 5 6 _ X 8
X X X X X X X X X X

Now, start at S (7) and go to the nearby cell with the lowest number (unchecked cells cannot be moved to). The path traced is (1,3,7) -> (1,4,6) -> (1,5,5) -> (1,6,4) -> (1,7,3) -> (1,8,2) -> (2,8,1) -> (3,8,0). In the event that two numbers are equally low (for example, if S was at (2,5)), pick a random direction – the lengths are the same. The algorithm is now complete.

In video games[edit]

This section needs expansion. You can help by adding to it. (January 2017)

Chris Crawford in 1982 described how he “expended a great deal of time” trying to solve a problem with pathfinding in Tanktics, in which computer tanks became trapped on land within U-shaped lakes. “After much wasted effort I discovered a better solution: delete U-shaped lakes from the map”, he said.^[5]

Hierarchical path finding[edit]

The idea was first described by the video game industry, which had a need for planning in large maps with a low amount of CPU time. The concept of using abstraction and heuristics is older and was first mentioned under the name ABSTRIPS (Abstraction-Based STRIPS)^[6] which was used to efficiently search the state spaces of logic games.^[7] A similar technique are navigation meshes (navmesh), which are used for geometrical planning in games and multimodal transportation planning which is utilized in travelling salesman problems with more than one transport vehicle.

A map is separated into clusters. On the high-level layer, the path between the clusters is planned. After the plan was found, a second path is planned within a cluster on the lower level.^[8] That means, the planning is done in two steps which is a guided local search in the original space. The advantage is, that the number of nodes is smaller and the algorithm performs very well. The disadvantage is, that a hierarchical pathplanner is difficult to implement.^[9]

Example[edit]

A map has a size of 3000×2000 nodes. Planning a path on a node base would take very long. Even an efficient algorithm will need to compute many possible graphs. The reason is, that such a map would contain 6 million nodes overall and the possibilities to explore the geometrical space are exceedingly large. The first step for a hierarchical path planner is to divide the map into smaller sub-maps. Each cluster has a size of 300×200 nodes. The number of clusters overall is 10×10=100. In the newly created graph the amount of nodes is small, it is possible to navigate between the 100 clusters, but not within the detailed map. If a valid path was found in the high-level-graph the next step is to plan the path within each cluster. The submap has 300×200 nodes which can be handled by a normal A* pathplanner easily.

Algorithms used in pathfinding[edit]

• Dijkstra’s algorithm
• A* search algorithm, a special case of the Dijkstra’s algorithm
• D* a family of incremental heuristic search algorithms for problems in which constraints vary over time or are not completely known when the agent first plans its path
• Any-angle path planning algorithms, a family of algorithms for planning paths that are not restricted to move along the edges in the search graph, designed to be able to take on any angle and thus find shorter and straighter paths

Multi-agent pathfinding[edit]

Multi-agent pathfinding is to find the paths for multiple agents from their current locations to their target locations without colliding with each other, while at the same time optimizing a cost function, such as the sum of the path lengths of all agents. It is a generalization of pathfinding. Many multi-agent pathfinding algorithms are generalized from A*, or based on reduction to other well studied problems such as integer linear programming.^[10] However, such algorithms are typically incomplete; in other words, not proven to produce a solution within polynomial time. A different category of algorithms sacrifice optimality for performance by either making use of known navigation patterns (such as traffic flow) or the topology of the problem space.^[11]

See also[edit]

• Motion planning
• Any-angle path planning

References[edit]

External links[edit]

• https://melikpehlivanov.github.io/AlgorithmVisualizer
• http://sourceforge.net/projects/argorha
• StraightEdge Open Source Java 2D path finding (using A*) and lighting project. Includes applet demos.
• python-pathfinding Open Source Python 2D path finding (using Dijkstra’s Algorithm) and lighting project.
• Daedalus Lib Open Source. Daedalus Lib manages fully dynamic triangulated 2D environment modeling and pathfinding through A* and funnel algorithms.