Как составить алгоритм решения квадратного уравнения

Квадратное алгебраическое уравнение имеет вид:

ах^2 + bx + c = 0. (1)

Здесь а, b и с – коэффициенты. Сначала надо вычислить дискриминант квадратного уравнения

D = (b^2 – 4ac) (2)

Если D > 0, то квадратное уравнение имеет два корня х1 и х2. Обозначим С = корень(D). То есть надо вычислить квадратный корень из D. Имеем такие решения

х1 = (–b + C)/(2a) и x2 = (–b – C)/(2a). (3)

Если дискриминант D = 0, то C = 0 и оба корня одинаковы Х1 = Х2 (хотя в школе обычно говорят, что имеется только одно решение) и вычисляются по формуле

Х1 = Х2 = –b/(2a). (4). Эта формула следует из формулы (3) при С = D = 0.

Если дискриминант D меньше нуля, то корень из D вычислить нельзя, С будет мнимым числом. Вообще говоря, корни есть (2 штуки), но они будут мнимыми числами. Хотя в школе учат, что в этом случае корней НЕТ. Так и будем считать, что корней нет.

Алгоритм решения будет следующий

Но только здесь дискриминант D обозначен малой буквой d

Один из методов решения квадратных уравнений

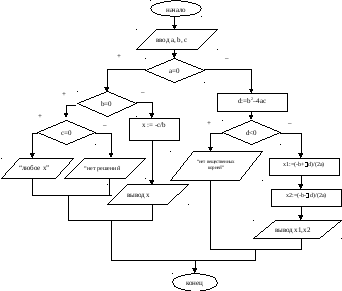
Алгоритм решения данной задачи сначала должен быть представлен в виде словесного описания или графически в виде блок-схемы. Алгоритм вычисления корней квадратного уравнения может быть представлен в виде блок-схем, изображенных на рисунках, отображающих основные элементы блок-схем и алгоритм вычисления корней квадратного уравнения:

Изображение алгоритма в виде блок-схемы позволяет наглядно представить последовательность действий, необходимых для решения поставленной задачи, убедиться самому программисту в правильности понимания поставленной задачи.

После разработки алгоритма решения задачи и представления его в виде блок-схемы можно перейти к написанию программы – последовательности инструкций на выбранном языке программирования, соответствующей разработанному алгоритму. Например, ниже приведен фрагмент программы решения квадратного уравнения, соответствующий приведенному выше алгоритму, составленному на языке Visual Basic.

procedure SqRoot(Editi,Edit2,Edit3:tEdit;Label2:tLabel);
var
a,b,c:real;
d:real;
xl,x2:real;
begin
<Ввод исходных данных>a:=StrToFloat(Editl.text);
b:=StrToFloat(Edit2.text);
с:=StrToFloat(Edj.t3.text);
< Вычисление дискриминанта >d:=Sqr(b)-4*a*c;
if d=0 then begin
Label2.color:=clRed;
Label2.font.color:=clRed;
Label2.caption:=’Дискриминант меньше нуля.’+#13+
‘Уравнение не имеет корней.’ end else
begin

х1:=(-b+Sqrt(d))/(2*a);
x2:=(-b-Sqrt(d))/(2*а);

Label2.font.color:=clBlack;
Label 2.caption=’Корни уравнения:’ +#13+’xl=1+FloatToStr(xl)
+#13+’x2=’+FloatToStr(x2);
end;
end.

Но программа, написанная на языке программирования, состоит из инструкций, понятных человеку, но не понятных процессору компьютера. Поэтому чтобы процессор смог выполнить работу в соответствии с инструкциями исходной программы, она должна быть переведена на язык команд процессора, то есть машинный язык. Задачу преобразования исходной программы в машинный код выполняет специальная программа – компилятор. Помимо преобразования исходной программы в машинную, компилятор выполняет проверку правильности записи инструкций исходной программы, т. е. осуществляет синтаксический анализ.

Компилятор создает исполняемую программу только в том случае, если в тексте исходной программы нет синтаксических ошибок. Однако генерация исполняемой программы машинного кода свидетельствует только об отсутствии в тексте программы синтаксических ошибок. Убедиться в правильности работы программы можно только во время ее тестирования – пробных запусках программы и при анализе полученных результатов. Например, если в программе нахождения корней квадратного уравнения допущена ошибка в записи выражения вычисления дискриминанта, то даже если это выражение будет синтаксически верно, программа выдаст неверные значения корней.

Решение квадратных уравнений средствами Visual Basic

Задача: Дано квадратное уравнение общего вида: ax 2 +bx+c=0. Ввести в память компьютера числовые коэффициенты: a, b, c, выполнить необходимый анализ введенной информации согласно известному из курса средней школы алгоритму решения квадратного уравнения: найти дискриминант d=b 2 -4ac и, проанализировав его знак, найти все действительные корни, если знак дискриминанта положительный, или сообщить о том, что действительных корней нет, если знак дискриминанта отрицательный.

Начать составление проекта решения данной задачи необходимо с ответа на вопрос: что нужно поместить на форму Form1?

Поместим на форму две кнопки: CommandButton1 и CommandButton2.

Для этого нужно воспользоваться Панелью элементов (объектов) управления General, которая расположена в левой части основного окна компилятора Visual Basic.

Первая кнопка CommandButton1 предназначается для начала работы программы согласно следующему алгоритму:

1. ввод коэффициентов исходного уравнения a, b, c;
2. расчет дискриминанта d=b 2 – 4ac;
3. анализ знака дискриминанта, вычисление корней уравнения и вывод их на форму, если знак дискриминанта d>0 (положительный);
4. вывод сообщения: «Решений нет», если знак дискриминанта d 2 -5x+6=0.

Далее рассмотрим процесс решения второго квадратного уравнения: 10x 2 +5x+200=0.

В окне InputBox вводим значение первого коэффициента уравнения a=10.

Ввод первого коэффициента a завершается нажатием кнопки Ok.

Аналогично в окне InputBox вводим значение второго коэффициента уравнения b=5.

Ввод второго коэффициента b так же завершается нажатием соответствующей кнопки Ok.

Наконец, в окне InputBox вводим значение третьего коэффициента нового уравнения c=200.

Ввод третьего коэффициента c так же завершается нажатием соответствующей кнопки Ok.

После этого программа, проанализировав полученную информацию, должна выдать в окне формы соответствующее сообщение о том, что данное уравнение не имеет решений.

И, наконец, рассмотрим процесс решения третьего квадратного уравнения: x 2 -8x+16=0.

Это уравнение имеет двукратный корень, так как его дискриминант d=0. Как и в двух предыдущих случаях, вводим коэффициенты квадратного уравнения. Первым вводим коэффициент a=1.

Далее вводим второй коэффициент уравнения b= –8.

Третий коэффициент уравнения c=16 вводим в последнюю очередь.

В итоге мы должны увидеть правильное решение третьего квадратного уравнения. Действительно последнее уравнение имеет два одинаковых корня.

Квадратные уравнения

Квадратное уравнение – уравнение вида a x 2 + b x + c = 0, где x – переменная, a , b и c – некоторые числа, причем a ≠ 0 .

Алгоритм решения квадратного уравнения:

1. Раскрыть скобки, перенести все слагаемые в левую часть, чтобы уравнение приобрело вид: a x 2 + b x + c = 0
2. Выписать, чему равны в числах коэффициенты: a = … b = … c = …
3. Вычислить дискриминант по формуле: D = b 2 − 4 a c
4. Если D > 0 , будет два различных корня, которые находятся по формуле: x 1,2 = − b ± D 2 a
5. Если D = 0, будет один корень, который находится по формуле: x = − b 2 a
6. Если D 0, решений нет: x ∈ ∅

Примеры решения квадратного уравнения:

1. − x 2 + 6 x + 7 = 0

a = − 1, b = 6, c = 7

D = b 2 − 4 a c = 6 2 − 4 ⋅ ( − 1 ) ⋅ 7 = 36 + 28 = 64

D > 0 – будет два различных корня:

x 1,2 = − b ± D 2 a = − 6 ± 64 2 ⋅ ( − 1 ) = − 6 ± 8 − 2 = [ − 6 + 8 − 2 = 2 − 2 = − 1 − 6 − 8 − 2 = − 14 − 2 = 7

Ответ: x 1 = − 1, x 2 = 7

a = − 1, b = 4, c = − 4

D = b 2 − 4 a c = 4 2 − 4 ⋅ ( − 1 ) ⋅ ( − 4 ) = 16 − 16 = 0

D = 0 – будет один корень:

x = − b 2 a = − 4 2 ⋅ ( − 1 ) = − 4 − 2 = 2

a = 2, b = − 7, c = 10

D = b 2 − 4 a c = ( − 7 ) 2 − 4 ⋅ 2 ⋅ 10 = 49 − 80 = − 31

D 0 – решений нет.

Также существуют неполные квадратные уравнения (это квадратные уравнения, у которых либо b = 0, либо c = 0, либо b = c = 0 ). Смотрите видео, как решать такие квадратные уравнения!

Программа для решения квадратных уравнений на C++

Довольно часто в пособиях по программированию встречаются задания по нахождению решений каких-нибудь математических уравнений. Задача нахождения корней квадратного уравнения — это довольно тривиальная задача, как и многие другие задачи. Решается она очень просто при помощи листа бумаги и ручки, но решение можно автоматизировать посредством написания прикладной программы и её использования. В этой статье мы напишем такую программу.

Алгоритм решения квадратного уравнения

Многие знают, что уравнение вида ax 2 + bx + c = 0 , где a не равно 0, называют квадратным уравнением.

Существуют различные способы решения квадратных уравнений, но мы рассмотрим решение через дискриминант.

Обозначается дискриминант буквой D . Из школьного курса знаем, что D = b 2 — 4ac .

Существует несколько условий:

• Если D > 0, то решение имеет 2 различных вещественных корня.
• Если D = 0, то оба вещественных корня равны.
• Если D для вводавывода в консоли, #include для работы с математическими функциями и область using namespace std;
  

Просим пользователя ввести значения переменных и сохраняем каждое значение

Проверяем условие, если дискриминант больше или равен 0, то находим корни и выводим

в противном случае выводим сообщение

На этом всё, осталось скомпилировать, запустить и проверить. Запускаем и вводим данные, чтобы D был меньше 0

В этом случае D = 3*3 — 4*2*3 = -15, а это меньше 0, значит ответ программа дала верный.

Ответы тоже верны. Программа работает правильно.

Ниже представлен весь листинг программы для нахождения корней квадратного уравнения на C++

Для вас это может быть интересно:

Программа для решения квадратных уравнений на C++ : 24 комментария

Программировать так сложно…

1. Nicknixer Автор записи 15.10.2016

Не так сложно, как Вам кажется! Немного литературы, немного практики и смотреть на код решения такой задачи Вы будете по-другому.

Доброго времени суток! Помогите пожалуйста написать программу, которая считает сколько символов в ряде двумерного массива. То есть , например массив 5 на 5, сколько символов в 1 ряде, сколько во 2 и т.д.

Ответил вам по электронной почте

Критику принимаете? 🙂
Программа дырявая как сито.

Если число очень маленькое, но положительное, например 10^(-20) — у вас будет переполнение или типо того. Оператор > проверяет знак числа (это отдельный бит), а оператор == для дробных чисел не имеет смысла, т.к. в младших разрядах числа обычно находится какой-нибудь мусор, который при таком сравнении дает false.

x = ( -1*b + sqrt(b*b – 4*a*c) ) / (2 * a);
x = ( -1*b – sqrt(b*b – 4*a*c) ) / (2 * a);

Тут есть три вопроса:
1) зачем два раза вычислять одно и тоже (я про корень)
2) что делать если мне корни надо как-то использовать, а не просто вывести (тут есть проблема, ведь у меня то один корень — то два). Чтобы лучше понять в чем проблема — попробуйте вынести вычисление корней в отдельную функцию. У вас то вообще, если корень один — то их выведется все равно два, одинаковых.
3) в переменной «a» может быть ноль (или близкое к нулю число) — при этом мы получим деление на ноль (а точнее, переполнение).

Но это ведь еще не все. Что будет если и «a» и «b» равны нулю? — тебе надо рассмотреть два варианта — если c = 0 (условно, близко к нулю), то корней бесконечно много. А если c != 0, то корней нет.

Вообще, эта задача — прекрасный пример для юнит-тестирования и демонстрации принципов разработки через тестирование. Именно его я рассматривал в своей статье по теме тестирования: Юнит-тестирование. Пример. Boost Unit Test. Дело в том, что тут куча вариантов сделать ошибку, при этом их понимание приходит не сразу, т.е. школьник решая задачу напишет по формуле которой учили (ну и вот как у вас). А потом надо разбираться и смотреть как программа может сломаться, при этом разрабатывать тесты.

1. Николай Сергейчук Автор записи 09.02.2017

Принимаем 🙂
Согласен с вами во всём! Программу можно реализовать намного лучше, используя различные проверки и валидацию входных данных.
Однако, статья рассчитана на аудиторию, которая только начинает познавать программирование или делает лабораторную. 🙂 Чтобы людям легче было понять, реализация данной программы упрощена до невозможности. И, возможно, несправедливо было с моей стороны не предупредить их о возможных ошибках в работе программы, которые могут вскрыться позже, если подать на вход определенные значения.
Кстати, у вас интересная статья по тестированию!

Николай, доброго времени суток! Можете помочь с написанием програмки в с++? 1-1/2!+1/3!-1/4!+1/5! и так до 1/100! ? Чтобы при заднии в строке номера члена последовательности выдавал сумму до него по такой вот формуле? Буду очень благодарен!

Пожалуйста подскажите как ввести экран правильный ответ дискриминанта

Помогите решить в Dev C++
Sqrt x^2+1+sqrt|x|,x0

Здравствуйте, можете помочь с решением биквадратного и триквадратного уравнения?

#include
using namespace std;
int main()
<
/*Решение квадратных уравнений*/
setlocale(0, «»);
cout a;
cout <> b;
cout <> c;
D = pow(b, 2) — 4 * a * c;
cout

ну и? если даже тупо скопировать код и вставить его в cpp.sh , ничего не работает. поебота какая то этот с++

Уважаемая, Лена! Я, надеюсь, вы знаете, что код программы, написанной на языке программирования C++ нельзя тупо вставить в блокнот и сохранить под названием «cpp.sh»? Если не знали, то я, видимо, открыл для вас Америку!

помогите решить. заданы 3 перемены a.b.c записать вы радение на С
< 7a/b+2a, если a=b,
Х= < -34, если a>b,
< 3a/(2b-100), если a>b и а не равно != с

iconcerts где забыл
#include

Я ради интереса написал программу нахождения корней квадратного уравнения на С++, с выводом корней как в десятичном виде, так и в виде простой дроби (причём уже сокращённой), потому что выводя корни в десятичном виде программа их одновременно сокращает и округляет и 1/3 превращается в 0.333333 хотя на самом деле 0.333333 (3), то есть для проверки правильно ли нашёл корни ваш ребёнок, вы с получите что-то типа: X1= 0.285714; X2=0.214286, а на самом деле это будет X1=2/7; X2=3/14, кроме того, если корень из дискриминанта не получается целым числом, вы уже получите двойную неточность: сначала при извлечении корня программа отсечёт значение до 4-6 цифр после запятой с округлением, а затем сделает то же самое при делении числителя на знаменатель. Я и здесь сделал вывод корней в двух значениях: в десятичном и в виде выражения X1= (-b + sqrt(D))/(2*a); X2= (-b — sqrt(D))/(2*a), то есть выводится примерно вот так X1=-5+sqrt(21)/2; X2=-5-sqrt(21)/2 с одновременным разложением дискриминанта под корнем на множители, вынесением этих множителей из-под корня, если они выносятся нацело, их перемножением и дальнейшим сокращением. Вот, например, имеем a=3, b=15, c=3, при решении получаем D=189 программа выдаёт десятичные корни X1= -0.208712 и X2= -4.79129, а в виде выражения имеем: X1= -5+sqrt(21)/2, то есть первоначально получаем: X1= -15+sqrt(189)/6, -> 189=21*9 -> -15+3sqrt(21)/6 далее идёт сокращение на 3 и итог -5+sqrt(21)/2

День добрый.
Недавно начал изучать C++. Решил попробовать написать решение квадратного уравнения именно через оператор вида «условие ? выполняется : не выполняется». Т.е. если условие выполняется, то имеем два решения (даже если d = 0, то тоже должно быть два решения x1 = x2), если d a;
std::cout <> b;
std::cout <> c;
d = pow(b, 2) — 4 * a*c;
d >= 0 ? xfst = ((-b + sqrt(d)) / double(2 * a)) , xscd = ((-b — sqrt(d)) / double(2 * a)) : std::cout

1. Николай Сергейчук Автор записи 12.02.2020

if (d >= 0) <
xfst = ((-b + sqrt(d)) / double(2 * a));
xscd = ((-b — sqrt(d)) / double(2 * a));
std::cout

Создать программу для решения квадратного уравнения.
У меня не получаеться, но и копифейсом я не хочу заниматься.
Прошу помогите. Заранее спасибо.

Здравствуйте! Как решить эту задачу? Приведенный пример сверху не подходит .

Давайте напишем действительно полезную программу! Вы наверняка уже устали считать дискриминант для квадратных уравнений? Давайте автоматизируем этот процесс.

На вход программы подаются три целых числа — коэффициенты уравнения ax^2 + bx + c = 0ax
2
+bx+c=0

Гарантируется, что a neq 0a

=0.

Выведите через пробел корни уравнения в порядке убывания и округленные «вниз». Если уравнение имеет корень кратности 2 — выведите одно число. Если у уравнения нет действительных корней — выведите «NO»

Для извлечения корней используйте функцию sqrt. Она содержится в библиотеке сmath ( она уже импортирована в коде ). Для округления воспользуйтесь функцией floor ( из той же библиотеки ).

1 0 -4
Sample Output 1:

2 -2
Sample Input 2:

1 2 2
Sample Output 2:

Пожалуйста подскажите как ввести экран ответ дискриминанта

Пожалуйста подскажите как ввести на екран ответь дискриминанта

Подскажите как правильно решить?
Обчислити z = (x1 + y1) / (x2 + y2), де х1, х2 — коренi рiвняння 2х^2 + x — 4 =0.
y1, y2 — коренi рiвняння ay^2 + 2y — 1 = 0. Усi коренi дiйснi.

using namespace std;

int main() <
double a = 2, b, c = -4;
int x1, x2;
double a1, b1 = 2, c1 = -1;
int y1, y2;
float z;

if((b*b — 4*a*c) >= 0 ) <
x1 = ( -1*b + sqrt(b*b — 4*a*c)) / (2 * a);
cout a1;

if((b1*b1 — 4*a1*c1) >= 0) <
y1 = ( -1*b1 + sqrt(b1*b1 — 4*a1*c1)) / (2 * a1);
cout = 0, y1 >= 0, y2 >= 0) <
z = (x1 + y1)/(x2 +y2);
cout

Добавить комментарий Отменить ответ

Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.

[spoiler title=”источники:”]

Квадратные уравнения

http://nicknixer.ru/programmirovanie/programma-dlya-resheniya-kvadratnyx-uravnenij-na-c/

[/spoiler]

Что такое квадратные уравнения?

А теперь подробно с примерами обсудим квадратные уравнения.

Любые уравнения, сводящиеся к виду (ax^2+bx+c=0), называются квадратными. Где буквы ( b,; с) – любые числа, (aneq0). Почему (aneq0) мы обсудим ниже.

Обратите внимание на порядок слагаемых в квадратном уравнении:
(a) – всегда стоит первая и обязательно умножается на (x^2), она называется старшим коэффициентом (или первым);
(b) – принадлежит второму слагаемому и всегда умножается просто на переменную (x), это у нас второй коэффициент;
(c) – называют свободным членом, она не умножается ни на какую переменную.

В дальнейшем старайтесь приводить квадратное уравнение к виду (ax^2+bx+c=0), чтобы слагаемые стояли именно в таком порядке. Это очень важно при решении уравнений, и поможет избежать множества ошибок.

Потренируемся определять значения коэффициентов ( a, ; b,; с), чтобы запомнить порядок:

Пример 1
$$2x^2+3x+4=0;$$
$$a=2 quad b=3 quad c=4.$$

Пример 2
$$5x^2-3x-0,7=0;$$
$$a=5 quad b=-3 quad c=-0,7.$$

Пример 3
$$-x^2+2x+10=0;$$
Минус перед (x^2) можно представить в виде (-x^2=-1*x^2). Единицу обычно не пишут, поэтому минус перед первым слагаемым означает, что (a=-1):
$$a=-1 quad b=2 quad c=10.$$

Пример 4
$$3+x^2-5x=0;$$
Слагаемые стоят в неправильном порядке. Так коэффициенты находить неудобно, поэтому переставим все слагаемые в нужном порядке. От перемены мест слагаемых сумма не меняется:
$$x^2-5x+3=0;$$
$$a=1 quad b=-5 quad c=3.$$

Пример 5
$$2x^2-3x=0;$$
В уравнении нет свободного члена (c), поэтому он будет равен (0):
$$a=2 quad b=-3 quad c=0.$$

Пример 6
$$-4x^2+1=0;$$
А здесь уже нет второго коэффициента (b):
$$a=-4 quad b=0 quad c=1.$$

Уравнения, приведенные в примерах №5 и 6, называются неполными квадратными уравнениями, так как в них коэффициенты (b) или (c) равны нулю.

А вот если в уравнении коэффициенты ( a, ; b,; с) не равны 0, то такое уравнение называется полным.

От того, полное ли квадратное уравнение или неполное, зависит, как мы будем его решать. Начнем с неполных уравнений, они немного легче, но почему-то как раз в них все часто ошибаются.

Неполные квадратные уравнения

Неполное квадратное уравнение – это уравнение, в котором один из коэффициентов (b) или (c) равен нулю, (aneq0).

Как решать квадратное уравнение (ax^2+bx=0)?

Рассмотрим уравнение, в котором (c=0), оно будет иметь вид:
$$ax^2+bx=0;$$
Чтобы его решить, нужно вынести общий множитель (x) за скобки:
$$x(ax+b)=0;$$
И вспомнить правило, что произведение равно нулю, когда хотя бы один из множителей равен нулю. Здесь два множителя: (x) и ((ax+b)). Приравниваем их к нулю и решаем каждое по-отдельности:
$$x=0;$$
Тут решать-то нечего, сразу дан корень.
Второе:
$$ax+b=0;$$
Обычное линейное уравнение:
$$ax=-b;$$
$$x=frac{-b}{a};$$

Получили, что уравнение имеет сразу два корня:(x=0) и (x=frac{-b}{a}).

Разберем на примере:

Пример 7
$$2x^2+8x=0;$$
Выносим общий множитель (x):
$$x(2x+8)=0;$$
$$quad x_1=0 quad и quad 2x+8=0;$$
$$2x+8=0;$$
$$2x=-8;$$
$$x_2=-4.$$
Ответ: (x_1=0 quad и quad x_2=-4.)

Как решать квадратное уравнение (ax^2+с=0)?

Вот с такими уравнениями надо быть очень внимательными. Важно помнить, что любое число (выражение), возведенное в квадрат, всегда больше или равно нуля, оно не может быть отрицательным.

Общая схема решения уравнений вида (ax^2+с=0):

• Выражаем (x^2) из уравнения:
  $$ax^2+c=0;$$
  $$ax^2=-c;$$
  $$x^2=frac{-c}{a};$$
• Если (-frac{c}{a} geq 0):
  $$x_1=sqrt{-frac{c}{a}};$$
  $$x_2=-sqrt{-frac{c}{a}};$$
• Если (-frac{c}{a} lt 0):
  РЕШЕНИЙ НЕТ.

Пример 8
$$2x^2-8=0;$$
$$2x^2=8;$$
$$x^2=frac{8}{2};$$
$$x^2=4;$$
$$x=pmsqrt{4};$$
$$x_1=2;$$
$$x_2=-2;$$
Ответ: (x_1=2 quad и quad x_2=-2.)

Пример 9
$$4x^2+36=0;$$
$$2x^2=-36;$$
$$x^2=frac{-36}{2}=-18;$$
Так как (-18 < 0), а (x^2) не может быть отрицательным, то это уравнение не имеет корней.
Ответ: Нет корней.

Пример 10
$$frac{1}{2}x^2-frac{1}{18}=0;$$
$$frac{1}{2}x^2=frac{1}{18};$$
Чтобы избавиться от (frac{1}{2}), умножим уравнение слева и справа на (2):
$$x^2=frac{2}{18};$$
$$x^2=frac{1}{9};$$
$$x=pmsqrt{frac{1}{9}};$$
$$x_1=frac{1}{3};$$
$$x_2=-frac{1}{3};$$
Ответ: (x_1=frac{1}{3} quad и quad x_2=-frac{1}{3}.)

Решение квадратных уравнений через дискриминант

Квадратные уравнения (ax^2+bx+c=0), у которых все коэффициенты ( a, ; b,; с) не равны 0, называются полными квадратными уравнениями.

Чтобы их решать, нужно уметь находить дискриминант квадратного уравнения. Ничего страшного в этом нет, несмотря на странное называние. Дискриминантом уравнения (ax^2+bx+c=0) называют выражение:
$$D=b^2-4ac;$$

1. Если дискриминант получился больше нуля ((D ge 0)), то квадратное уравнение имеет два корня, которые можно найти по формулам:
   $$x_1=frac{-b+sqrt{D}}{2a};$$
   $$x_2=frac{-b-sqrt{D}}{2a};$$
2. Если дискриминант равен нулю ((D=0)), то квадратное уравнение имеет один корень:
   $$x=frac{-b}{2a};$$
3. Если дискриминант меньше нуля ((D<0)), то квадратное уравнение не имеет корней.

Примеры квадратных уравнений

Пример 11
$$2x^2-9x+4=0;$$
Прежде чем решать уравнение, я рекомендую выписать все коэффициенты:
$$a=2 quad b=-9 quad c=4.$$
Используя значения коэффициентов, можем посчитать дискриминант:
$$D=b^2-4ac=(-9)^2-4*2*4=81-32=49;$$
Ура, дискриминант посчитан и он больше нуля! Значит корней будет два, найдем их по формулам:
$$x_1=frac{-b+sqrt{D}}{2a}=frac{-(-9)+sqrt{49}}{2*2}=frac{9+7}{4}=frac{16}{4}=4;$$
$$x_2=frac{-b-sqrt{D}}{2a}=frac{-(-9)—sqrt{49}}{2*2}=frac{9-7}{4}=frac{2}{4}=frac{1}{2};$$
Ответ: (x_1=4 quad и quad x_2=frac{1}{2}.)

Пример 12
$$10x^2+x-21=0;$$
$$a=10 quad b=1 quad c=-21.$$
$$D=b^2-4ac=1^2-4*10*(-21)=1+840=841;$$
$$x_1=frac{-b+sqrt{D}}{2a}=frac{-1+sqrt{841}}{2*10}=frac{-1+29}{20}=frac{28}{20}=frac{7}{5};$$
$$x_2=frac{-b-sqrt{D}}{2a}=frac{-1-sqrt{841}}{2*10}=frac{-1-29}{20}=frac{-30}{20}=frac{-3}{2};$$
Ответ: (x_1=frac{7}{5} quad и quad x_2=-frac{3}{2}.)

Пример 13
$$(x-7)^2=2x^2+11x+23;$$
Это уравнение еще нужно привести к стандартному виду, для этого раскроем скобки по формуле «квадрат разности» ((a-b)^2=a^2-2ab+b^2):
$$x^2-14x+49=2x^2+11x+23;$$
Перекинем все слагаемые в левую часть, не забывая при этом менять знак на противоположный:
$$x^2-14x+49-2x^2-11x-23=0;$$
Приводим подобные слагаемые:
$$-x^2-25x+26=0;$$
$$a=-1 quad b=-25 quad c=26.$$
$$D=b^2-4ac=(-25)^2-4*(-1)*26=625+104=729;$$
$$x_1=frac{-b+sqrt{D}}{2a}=frac{-(-25)+sqrt{729}}{2*(-1)}=frac{25+27}{-2}=frac{52}{-2}=-26;$$
$$x_2=frac{-b-sqrt{D}}{2a}=frac{-(-25)-sqrt{729}}{2*(-1)}=frac{25-27}{-2}=frac{-2}{-2}=1;$$
Ответ: (x_1=-26 quad и quad x_2=1.)

Пример 14
$$3x^2+7x+6=0;$$
$$a=3 quad b=7 quad c=6.$$
$$D=b^2-4ac=7^2-4*3*6=49-72=-23;$$
Стоп! Дискриминант получился отрицательный, это означает, что у этого квадратного уравнения не будет корней.
Ответ: Нет корней.

Пример 15
$$4x^2-4x+1=0;$$
$$a=4 quad b=-4 quad c=1.$$
$$D=b^2-4ac=(-4)^2-4*4*1=16-16=0;$$
Дискриминат получился равен нулю. В этом случае у квадратного уравнения будет всего один корень, который можно найти по формуле:
$$x=frac{-b}{2a}=frac{-(-4)}{2*4}=frac{4}{8}=frac{1}{2};$$
Ответ: (x=frac{1}{2}.)

Полезно знать! Если дискриминант получился равен нулю, то перед вами формула полного квадрата. Это значит, что квадратный многочлен можно разложить по формуле ((apm b)^2=a^2pm 2ab+b^2).
И пример №15 можно решить, используя эту формулу:
$$4x^2-4x+1=0;$$
$$(2x-1)^2=0;$$
Квадрат равен нулю только в том случае, если выражение под квадратом равно нулю:
$$2x-1=0;$$
$$2x=1;$$
$$x=frac{1}{2};$$
Ответ получили точно такой же, как и при решении через дискриминант.

Дискриминант деленный на 4

Квадратные уравнения иногда удобно решать по упрощенной формуле дискриминанта. Но применять ее можно не во всех случаях, а только, если коэффициент (b) в уравнении (ax^2+bx+c=0) четный (делится на 2).

Итак, представим, что коэффициент (b) четный, тогда дискриминант можно посчитать по формуле:
$$D_4=left(frac{b}{2}right)^2-ac;$$
А корни уравнения находятся по формулам:
$$x_1=frac{-frac{b}{2}+sqrt{D_4}}{a};$$
$$x_2=frac{-frac{b}{2}-sqrt{D_4}}{a};$$
Кстати, обычный дискриминант (D) отличается от (D_4) в 4 раза:
$$D_4=frac{D}{4}=frac{b^2-4ac}{4}=frac{b^2}{4}-frac{4ac}{4}=left(frac{b}{2}right)^2-ac;$$
Поэтому (D_4) называют «дискриминантом деленным на 4».

Эти формулы нужны, чтобы, когда это возможно, сократить вычисления. Разберем на примере:

Пример 16
$$7x^2-20x-1067=0;$$
$$a=7 quad b=-20 quad c=-1067.$$
(b=-20) – четный, поэтому воспользуемся дискриминантом деленным на 4:
$$D_4=left(frac{b}{2}right)^2-ac=left(frac{-20}{2}right)^2-7*(-1067)=(-10)^2+7469=100+7469=7569;$$
$$x_1=frac{-frac{b}{2}+sqrt{D_4}}{a}=frac{-frac{-20}{2}+sqrt{7569}}{7}=frac{10+87}{7}=frac{97}{7};$$
$$x_2=frac{-frac{b}{2}-sqrt{D_4}}{a}=frac{-frac{-20}{2}-sqrt{7569}}{7}=frac{10-87}{7}=frac{-77}{7}=-11;$$
Ответ: (x_1=frac{97}{7} quad и quad x_2=-11.)

Возникает вопрос, зачем вообще нужен этот (D_4), если все можно считать через обычный дискриминант? Если бы мы считали пример №16 как обычно, то наш дискриминант, который и так получился не маленьким – ((D_4=7659)), был бы в четыре раза больше. А чем больше числа, тем сложнее расчеты.

Теорема Виета для решения квадратных уравнений

Теорема Виета – это еще один способ упростить решение полных квадратных уравнений. Ее очень часто используют для решения несложных квадратных уравнений в уме и для анализа квадратного многочлена, особенно это актуально в сложных заданиях с параметром в ЕГЭ.

Прежде чем сформулировать теорему Виета, познакомимся с приведенными квадратными уравнениями.

Приведенное квадратное уравнение

Квадратные уравнения (ax^2+bx+c=0), у которых коэффициент (a) при (x^2) равен (1), называют приведенными.

Например:
$$x^2+4x-3=0;$$
$$x^2-140x-65=0;$$
Любое полное квадратное уравнение всегда можно свести к приведенному. Для этого надо поделить все уравнение на коэффициент (a):

Пример 17
Привести квадратное уравнение к приведенному.
$$3x^2-15x+9=0;$$
Разделим уравнение на (a=3). (Так можно делать: если левую и правую части уравнения поделить на одно и то же число, то корни уравнения от этого не изменятся.)
$$frac{3x^2-15x+9}{3}=frac{0}{3};$$
В результате каждое слагаемое поделится на (3):
$$frac{3x^2}{3}-frac{15x}{3}+frac{9}{3}=0;$$
$$x^2-5x+3=0;$$

Формулы Виета

Сумма корней приведенного квадратного уравнения (x^2+bx+c=0) равна второму коэффициенту (b) со знаком минус, а произведение корней равно свободному члену (c).

Пусть (x_1), и (x_2) – корни квадратного уравнения (x^2+bx+c=0), тогда справедливы формулы:
$$ begin{cases}
x_1+x_2=-b; \
x_1*x_2=c. \
end{cases}$$
На первый взгляд может показаться, что это очень запутанно, но на самом деле, теорема Виета часто помогает решить уравнение в уме. Попробуем на практике:

Пример 18
$$x^2+4x+3=0;$$
$$a=1 quad b=4 quad c=3.$$
Воспользуемся теоремой Виета и выпишем формулы:
$$ begin{cases}
x_1+x_2=-b; \
x_1*x_2=c. \
end{cases}$$
Подставим коэффициенты:
$$ begin{cases}
x_1+x_2=-4; \
x_1*x_2=3. \
end{cases}$$

Нужно найти такие (x_1) и (x_2), которые удовлетворяют и первому, и второму уравнениям в системе. Подобрать корни достаточно просто: рассмотрим второе уравнение, какие два числа дают при умножении (3ку)?

Либо: (3=1*3);
Либо: (3=(-1)*(-3)).

Осталось проверить, будут ли найденные множители удовлетворять первому уравнению в системе, просто подставим их:
$$1+3 neq -4;$$
$$-1+(-3) = -4;$$
Вот мы и нашли корни системы уравнений: (x_1=-1) и (x_2=-3). А самое главное, мы нашли корни исходного квадратного уравнения.
Ответ: (x_1=-1 quad и quad x_2=-3.)

Если потренироваться, то все эти вычисления можно легко проводить в уме, если коэффициенты небольшие. Главное запомнить, что произведение корней должно быть равно свободному члену (c), а сумма корней равна ((-b)).

Теорема Виета, если (aneq1)

По теореме Виета можно решать не только приведенные квадратные уравнения (у которых (a=1)). Но перед тем, как применять формулы Виета, надо привести уравнение к приведенному, поделив на первый коэффициент (a):
$$ax^2+bx+c=0; quad mid :a$$
$$frac{ax^2}{a}+frac{bx}{a}+frac{c}{a};$$
$$x^2+frac{b}{a}*x+frac{c}{a};$$
Получили приведенное квадратное уравнение, для которого можно записать формулы Виета, где вторым коэффициентом будет (frac{b}{a}), а свободным членом (frac{c}{a}):
$$ begin{cases}
x_1+x_2=-frac{b}{a}; \
x_1*x_2=frac{c}{a}. \
end{cases}$$

Пример 19
$$12x^2+x-1=0;$$
$$a=12 quad b=1 quad c=-1.$$
Коэффициент (a=12 neq 1), поэтому разделим все уравнение на (a=12):
$$12x^2+x-1=0; quad mid :12$$
$$x^2+frac{1}{12}x-frac{1}{12}=0;$$
$$a=1 quad b=frac{1}{12} quad c=-frac{1}{12}.$$

Теорема Виета:
$$ begin{cases}
x_1+x_2=-frac{1}{12}; \
x_1*x_2=-frac{1}{12}. \
end{cases}$$

Подбираем корни:
$$x_1=-frac{1}{3};$$
$$x_2=frac{1}{4};$$

Ответ: (x_1=-frac{1}{3} quad и quad x_2=frac{1}{4}.)

Теорема Виета удобна, когда у квадратного уравнения небольшие коэффициенты и можно легко подобрать корни. В остальных случаях лучше пользоваться дискриминантом.

ax²
+ bx
+ c
= 0.

Задача
хорошо знакома из математики. Исходными
данными здесь являются коэффициентыa,
b,
c.
Решением в общем случае являются два
корня x₁
и x₂,
которые вычисляются по формулам:

Все
величины, используемые в этой программе,
имеют вещественный тип.

алг
корни квадратного уравнения

вещ
a,
b,
c,
x1,
x2,
d

нач
ввод
a, b, c

d:=b²-4ac

x1:=(-b+d)/(2a)

x2:=(-b–d)/(2a)

вывод
x1, X2

кон

Слабость
такого алгоритма видна «невооруженным
глазом». Он не обладает важнейшим
свойством, предъявляемым к качественным
алгоритмам: универсальностью по отношению
к исходным данным. Какими
бы ни были значения исходных данных,
алгоритм должен приводить к определенному
результату и выходить на конец. Результатом
может быть числовой ответ, но может быть
и сообщение о том, что при таких данных
задача решения не имеет. Недопустимы
остановки в середине алгоритма из-за
невозможности выполнить какую-то
операцию. Это же свойство в литературе
по программированию называют
результативностью алгоритма (в любом
случае должен быть получен какой-то
результат).

Чтобы построить
универсальный алгоритм, сначала требуется
тщательно проанализировать математическое
содержание задачи.

Решение
уравнения зависит от значений коэффициентов
a,
b,
c.
Вот анализ этой задачи (ограничиваемся
только поиском вещественных корней):

если
a=0,
b=0,
c=0,
то любое х – решение уравнения;

если
a=0,
b=0,
c0,
то уравнение решений не имеет;

если
a=0,
b0,
то это линейное уравнение, которое
имеет одно решение: x=–c/b;

если
a0
и d=b²-4ac0,
то уравнение имеет два вещественных
корня (формулы приведены выше);

если
a0
и d<0,
то уравнение не имеет вещественных
корней.

Блок-схема алгоритма:

Этот
же алгоритм на алгоритмическом языке:

алг
корни
квадратного уравнения

вещ
a,
b,
c,
d,
x1,
x2

нач
ввод
a, b, c

если
a=0

то если
b=0

то если
c=0

то
вывод «любое х – решение»

иначе
вывод «нет решений»

кв

иначе
x:=
–c/b

вывод
х

кв

иначе
d:=b2–4ac

если
d<0

то
вывод «нет вещественных корней»

иначе
x1:=(-b+d)/(2a);
x2:=(-b–d)/(2a)

вывод
“x1=”,x1,
“x2=”,x2

кв

кв

кон

В этом алгоритме
многократно использована структурная
команда ветвления.
Общий вид команды ветвления в блок-схемах
и на алгоритмическом языке следующий:

если условие то серия 1 иначе серия 2 кв

Вначале проверяется
«условие» (вычисляется отношение,
логическое выражение). Если условие
истинно, то выполняется «серия 1» –
последовательность команд, на которую
указывает стрелка с надписью «да»
(положительная ветвь). В противном случае
выполняется «серия 2» (отрицательная
ветвь). В АЯ условие записывается после
служебного слова «если», положительная
ветвь – после слова «то», отрицательная
– после слова «иначе». Буквы «кв»
обозначают конец ветвления.

Если
на ветвях одного ветвления содержатся
другие ветвления, то такой алгоритм
имеет структуру вложенных
ветвлений.
Именно такую структуру имеет алгоритм
«корни квадратного уравнения». В нем
для краткости вместо слов «да» и «нет»
использованы соответственно «+» и «–».

Рассмотрим
следующую задачу: дано целое положительное
число n.
Требуется вычислить n!
(n-факториал).
Вспомним определение факториала.

Ниже
приведена блок-схема алгоритма. В нем
используются три переменные целого
типа: n
– аргумент; i
– промежуточная переменная; F
– результат. Для проверки правильности
алгоритма построена трассировочная
таблица. В такой таблице для конкретных
значений исходных данных по шагам
прослеживается изменение переменных,
входящих в алгоритм. Данная таблица
составлена для случая n=3.

	Шаг	n	F	i	Условие
1 2 3 4 5 6 7 8 9 10 11 12 13 14	3	1 1 2 6 вывод	1 2 3 4	13, да 23, да 33, да 43, нет

Трассировка
доказывает правильность алгоритма.
Теперь запишем этот алгоритм на
алгоритмическом языке.

алг
Факториал

цел
n,
i,
F

нач
ввод
n

F:=1;
i:=1

пока
in,
повторять

нц F:=Fi

i:=i+1

кц

вывод
F

кон

Этот
алгоритм имеет циклическую структуру.
В алгоритме использована структурная
команда «цикл-пока», или «цикл с
предусловием». Общий вид команды
«цикл-пока» в блок-схемах и в АЯ следующий:

пока условие, повторять нц серия кц

Повторяется
выполнение серии команд (тела цикла),
пока условие цикла истинно. Когда условие
становится ложным, цикл заканчивает
выполнение. Служебные слова «нц» и «кц»
обозначают соответственно начало цикла
и конец цикла.

Цикл
с предусловием – это основная, но не
единственная форма организации
циклических алгоритмов. Другим вариантом
является цикл
с постусловием.
Вернемся к алгоритму решения квадратного
уравнения. К нему можно подойти с такой
позиции: если a=0,
то это уже не квадратное уравнение и
его можно не рассматривать. В таком
случае будем считать, что пользователь
ошибся при вводе данных и следует
предложить ему повторить ввод. Иначе
говоря, в алгоритме будет предусмотрен
контроль достоверности исходных данных
с предоставлением пользователю
возможности исправить ошибку. Наличие
такого контроля – еще один признак
хорошего качества программы.

алг квадратное уравнение вещ a, b, c, d, x1, x2 нач повторять ввод a, b, c до a0 d:=b2–4ac если d0 то x1:=(–b+d)/(2a) x2:=(–b–d)/(2a) вывод x1, x2 иначе вывод “нет вещественных корней” кв кон

В общем виде
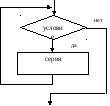
структурная команда «цикл с постусловием»
или «цикл-до» представляется так:

серия нет да

повторять серия до условие

Здесь
используется условие окончания цикла.
Когда оно становится истинным, цикл
заканчивает работу.

Составим
алгоритм решения следующей задачи: даны
два натуральных числа M
и N.
Требуется вычислить их наибольший общий
делитель – НОД(M,N).

Эта
задача решается с помощью метода,
известного под названием алгоритма
Евклида. Его
идея основана на том свойстве, что если
M>N,
то НОД(M<N)=НОД(M-N,N).
Попробуйте самостоятельно доказать
это свойство. Другой факт, лежащий в
основе алгоритма, тривиален: НОД(М,М)=М.
Для «ручного» выполнения этот алгоритм
можно описать в форме следующей
инструкции:

1. если
   числа равны, то взять их общее значение
   в качестве ответа; в противном случае
   продолжить выполнение алгоритма;

2. определить большее
   из чисел;

3. заменить большее
   число разностью большего и меньшего
   значений;

4. вернуться к
   выполнению пункта 1.

Блок-схема
и алгоритм на АЯ будут следующими:

алг Евклид цел M, N нач ввод M, N пока MN, повторять нц если M>N то M:=M–N иначе N:=N–M кв кц кон

Алгоритм
имеет структуру цикла с вложенным
ветвлением. Проделайте самостоятельно
трассировку этого алгоритма для случая
M=18,
N=12.
В результате получится НОД=6, что,
очевидно, верно.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #