Всегда хотелось найти универсальный способ
решения задач, но, наверное, его просто не
существует. Однако, можно составить рекомендации
для решения отдельных групп задач (что я и делал,
решая различные задачи), при этом я постоянно
изучал методическую литературу (задачники для
поступающих в ВУЗы, методические пособия для
учителей, учебные пособия для студентов и др.) и
понял, что не нужно “изобретать велосипед”, ведь
уже давно составлены такие схемы.
В предлагаемом вам материале собраны схемы
(алгоритмы, если точнее, то предписания
алгоритмического типа) предложенные разными
авторами. По возможности мной были сохранены
схемы в том виде, в каком они приводились в
первоисточнике. Те же, кто желает более детально
ознакомиться с приведенными в материале схемами,
может обратиться к первоисточникам, ссылки на
которые указаны возле каждой схемы.
Как искать решение? [2] стр. 212
- Понять предложенную задачу.
- Найти путь от неизвестного к данным, если нужно,
рассмотрев промежуточные задачи (“анализ”). - Реализовать найденную идею решения (“синтез”).
- Решение проверить и оценить критически.
Кинематика материальной точки. [1] стр.
18
- Понять предложенную задачу (увидеть физическую
модель). - Анализ (построить математическую модель
явления): - Выбрать систему отсчета (это предполагает выбор
тела отсчета, начала системы координат,
положительного направления осей, момента
времени, принимаемого за начальный). - Определить вид движения вдоль каждой из осей и
написать кинематические уравнения движения
вдоль каждой оси – уравнения для координат и для
скорости (если тел несколько, уравнения пишутся
для каждого тела). - Определить начальные условия (координаты и
проекции скоростей в начальный момент времени), а
также проекции ускорения на оси и подставить эти
величины в уравнения движения. - Определить дополнительные условия, т.е.
координаты или скорости для каких-либо моментов
времени (для каких-либо точек траектории), и
написать кинематические уравнения движения для
выбранных моментов времени (т.е. подставить эти
значения координат и скорости). - Полученную систему уравнений решить
относительно искомой величины. - Решение проверить и оценить критически.
Динамика материальной точки. [1] стр. 36
- Понять предложенную задачу (увидеть физическую
модель). - Анализ (построить математическую модель
явления): - Выбрать систему отсчета.
- Найти все силы, действующие на тело, и
изобразить их на чертеже. Определить (или
предположить) направление ускорения и
изобразить его на чертеже. - Записать уравнение второго закона Ньютона в
векторной форме и перейти к скалярной записи,
заменив все векторы их проекциями на оси
координат. - Исходя из физической природы сил, выразить силы
через величины, от которых они зависят. - Если в задаче требуется определить положение
или скорость точки, то к полученным уравнениям
динамики добавить кинетические уравнения. - Полученную систему уравнений решить
относительно искомой величины. - Решение проверить и оценить критически.
Статика. [1] стр. 53
- Понять предложенную задачу (увидеть физическую
модель). - Анализ (построить математическую модель
явления): - Выбрать систему отсчета.
- Найти все силы, приложенные к находящемуся в
равновесии телу. - Написать уравнение, выражающее первое условие
равновесия (Fi
= 0), в векторной форме и перейти к скалярной его
записи. - Выбрать ось, относительно которой
целесообразно определять момент сил. - Определить плечи сил и написать уравнение,
выражающее второе условие равновесия (Mi = 0).
- Исходя из природы сил, выразить силы через
величины, от которых они зависят. - Полученную систему уравнений решить
относительно искомой величины. - Решение проверить и оценить критически.
Закон сохранения импульса. [1] стр. 67
- Понять предложенную задачу (увидеть физическую
модель). - Анализ (построить математическую модель
явления): - Выбрать систему отсчета.
- Выделить систему взаимодействующих тел и
выяснить, какие силы для нее являются
внутренними, а какие – внешними. - Определить импульсы всех тел системы до и после
взаимодействия. - Если в целом система незамкнутая, сумма
проекций сил на одну из осей равна нулю, то
следует написать закон сохранения лишь в
проекциях на эту ось. - Если внешние силы пренебрежительно малы в
сравнении с внутренними (как в случае удара тел),
то следует написать закон сохранения суммарного
импульса (p = 0) в векторной форме и
перейти к скалярной. - Если на тела системы действуют внешние силы и
ими нельзя пренебречь, то следует написать закон
изменения импульса
(p
= Ft)
в векторной форме и перейти к скалярной. - Записать математически все вспомогательные
условия. - Полученную систему уравнений решить
относительно искомой величины. - Решение проверить и оценить критически.
Закон сохранения механической энергии.
[1] стр. 82
- Понять предложенную задачу (увидеть физическую
модель). - Анализ (построить математическую модель
явления): - Выбрать систему отсчета.
- Выделить два или более таких состояний тел
системы, чтобы в число их параметров входили как
известные, так и искомые величины. - Выбрать нулевой уровень отсчета потенциальной
энергии. - Определить, какие силы действуют на тела
системы – потенциальные или непотенциальные. - Если на тела системы действуют только
потенциальные силы, написать закон сохранения
механической энергии в виде: Е1 = Е2. - Раскрыть значение энергии в каждом состоянии и,
подставить их в уравнение закона сохранения
энергии. - Полученную систему уравнений решить
относительно искомой величины. - Решение проверить и оценить критически.
Теплота (первое начало термодинамики Q = U
+ A). [3] стр. 168
Задачи об изменении внутренней энергии тел
можно разделить на три группы.
В задачах первой группы рассматривают
такие явления, где в изолированной системе при
взаимодействии тел изменяется лишь их
внутренняя энергия без совершения работы над
внешней средой.
- Понять предложенную задачу (увидеть физическую
модель). - Анализ (построить математическую модель
явления): - Определить изолированную систему.
- Установить у каких тел внутренняя энергия
уменьшается, а у каких – возрастает. - Составить уравнение теплового баланса (
U = 0), при записи
которого в выражении cm(t2 – t1),
для изменения внутренней энергии, нужно вычитать
из конечной температуры тела начальную и
суммировать члены с учетом получающегося знака. - Полученное уравнение решить относительно
искомой величины. - Решение проверить и оценить критически.
В задачах второй группы рассматриваются
явления, связанные с превращением одного вида
энергии в другой при взаимодействии двух тел.
Результат такого взаимодействия – изменение
внутренней энергии одного тела в следствие
совершенной им или над ним работы.
- Понять предложенную задачу (увидеть физическую
модель). - Анализ (построить математическую модель
явления): - Следует убедиться, что в процессе
взаимодействия тел теплота извне к ним не
подводится, т.е. действительно ли Q = 0. - Установить у какого из двух взаимодействующих
тел изменяется внутренняя энергия и что является
причиной этого изменения – работа, совершенная
самим телом, или работа, совершенная над телом. - Записать уравнение 0 =
U + A для
тела, у которого изменяется внутренняя энергия,
учитывая знак перед А и к.п.д. рассматриваемого
процесса. - Если работа совершается за счет уменьшения
внутренней энергии одного из тел, то А=U, а если
внутренняя энергия тела увеличивается за счет
работы, совершенной над телом, тоА =
U.
- Найти выражения для
U и A.
- Подставляя в исходное уравнение вместо
U
и A их выражения, получим окончательное
соотношение для определения искомой величины. - Полученное уравнение решить относительно
искомой величины. - Решение проверить и оценить критически.
Задачи третьей группы объединяют в себе две
предыдущие.
Тепловое расширение твердых и жидких тел.
[3] стр. 184
- Понять предложенную задачу (увидеть физическую
модель). - Анализ (построить математическую модель
явления): - Для каждого теплового состояния каждого тела
записать соответствующую формулу теплового
расширения. - Если в задаче наряду с расширением тел
рассматриваются другие процессы, сопутствующие
расширению, – теплообмен, изменение
гидростатического давления жидкости или
выталкивающей силы, то к уравнениям теплового
расширения надо добавить формулы калориметрии и
гидростатики. - Синтез (получить результат).
- Решить полученную систему уравнений
относительно искомой величины. - Решение проверить и оценить критически.
Газы. [3] стр. 195
По условию задачи даны два или несколько
состояний газа и при переходе газа из одного
состояния в другое его масса не меняется.
- Понять предложенную задачу (увидеть физическую
модель). - Анализ (построить математическую модель
явления): - Представить какой газ участвует в том или ином
процессе. - Определить параметры p,V и T,
характеризующие каждое состояние газа. - Записать уравнение объединенного газового
закона Клапейрона для данных состояний. - Если один из трех параметров остается
неизменным, уравнение Клапейрона автоматически
переходит в одно из трех уравнений: закон Бойля –
Мариотта, Гей-Люссака или Шарля. - Записать математически все вспомогательные
условия. - Решить полученную систему уравнений
относительно неизвестной величины. - Решение проверить и оценить критически.
По условию задачи дано только одно
состояние газа, и требуется определить какой
либо параметр этого состояния или же даны два
состояния с разной массой газа.
- Понять предложенную задачу (увидеть физическую
модель). - Анализ (построить математическую модель
явления): - Установить, какие газы участвуют в
рассматриваемых процессах. - Определить параметры p,V и T,
характеризующие каждое состояние газа. - Для каждого состояния каждого газа (если их
несколько) составить уравнение Менделеева –
Клапейрона. Если дана смесь газов, то это
уравнение записывается для каждого компонента.
Связь между значениями давлений отдельных газов
и результирующим давлением смеси
устанавливается законом Дальтона. - Записать математически дополнительные условия
задачи - Решить полученную систему уравнений
относительно неизвестной величины. - Решение проверить и оценить критически.
Насыщающие и ненасыщающие пары. Влажность. [3]
стр. 219
- Понять предложенную задачу (увидеть физическую
модель). - Анализ (построить математическую модель
явления): - Установить число состояний газа,
рассматриваемых в условии задачи, обратить
особое внимание на то, дается ли чистый пар
жидкости или смесь пара с сухим воздухом. - Для каждого состояния пара записать уравнение
Менделеева – Клапейрона и формулу относительной
влажности, если о последней что-либо сказано в
условии. Составить уравнение Менделеева –
Клапейрона для каждого состояния сухого воздуха
(если дана смесь пара с воздухом). В тех случаях,
когда при переходах из одного состояния в другое
масса пара не меняется, вместо уравнения
Менделеева – Клапейрона можно использовать
сразу объединенный газовый закон. - Записать математически все вспомогательные
условия - Решить полученную систему уравнений
относительно неизвестной величины. - Решение проверить и оценить критически.
Электростатика. [3] стр. 234
Решение задачи о точечных зарядах и системах,
сводящихся к ним, основано на применении законов
механики с учетом закона Кулона и вытекающих из
него следствий.
- Понять предложенную задачу (увидеть физическую
модель). - Анализ (построить математическую модель
явления): - Расставить силы, действующие на точечный заряд,
помещенный в электрическое поле, и записать для
него уравнение равновесия или основное
уравнение динамики материальной точки. - Выразить силы электрического взаимодействия
через заряды и поля и подставить эти выражения в
исходное уравнение. - Если при взаимодействии заряженных тел между
ними происходит перераспределение зарядов, к
составленному уравнению добавляют уравнение
закона сохранения зарядов. - Записать математически все вспомогательные
условия - Решить полученную систему уравнений
относительно неизвестной величины. - Решение проверить и оценить критически.
Постоянный ток. [2] стр. 274
Задачи на определение силы тока, напряжения
или сопротивления на участке цепи.
- Понять предложенную задачу (увидеть физическую
модель). - Анализ (построить математическую модель
явления): - Начертить схему и указать на ней все элементы.
- Установить, какие элементы цепи включены
последовательно, какие – параллельно. - Расставить токи и напряжения на каждом участке
цепи и записать для каждой точки разветвления
(если они есть) уравнения токов и уравнения,
связывающие напряжения на участках цепи. - Используя закон Ома, установить связь между
токами, напряжениями и э.д.с. - Если в схеме делают какие-либо переключения
сопротивлений или источников, уравнения
составляют для каждого режима работы цепи. - Решить полученную систему уравнений
относительно неизвестной величины. - Решение проверить и оценить критически.
Электромагнетизм. [2] стр. 323
Задачи о силовом действии магнитного поля на
проводники с током.
- Понять предложенную задачу (увидеть физическую
модель). - Анализ (построить математическую модель
явления): - Сделать схематический чертеж, на котором
указать контур с током и направление силовых
линий поля. Отметить углы между направлением
поля и отдельными элементами контура. - Используя правило левой руки, определить
направление сил поля (сила Ампера), действующих
на каждый элемент контура, и проставить векторы
этих сил на чертеже. - Указать все остальные силы, действующие на
контур. - Исходя из физической природы сил, выразить силы
через величины, от которых они зависят. - Решить полученную систему уравнений
относительно неизвестной величины. - Решение проверить и оценить критически.
Задачи о силовом действии магнитного поля на
заряженные частицы.
- Понять предложенную задачу (увидеть физическую
модель). - Анализ (построить математическую модель
явления): - Нужно сделать чертеж, указать на нем силовые
линии магнитного и электрического полей,
проставить вектор начальной скорости частицы и
отметить знак ее заряда. - Изобразить силы, действующие на заряженную
частицу. - Определить вид траектории частицы.
- Разложить силы, действующие на заряженную
частицу, вдоль направления магнитного поля и по
направлению, ему перпендикулярному. - Составить основное уравнение динамики
материальной точки по каждому из направлений
разложения сил. - Исходя из физической природы сил, выразить силы
через величины, от которых они зависят. - Решить полученную систему уравнений
относительно неизвестной величины. - Решение проверить и оценить критически.
Задачи на закон электромагнитной индукции.
- Понять предложенную задачу (увидеть физическую
модель). - Анализ (построить математическую модель
явления): - Установить причины изменения магнитного
потока, связанного с контуром, и определить какая
из величин В, S или, входящих в выражение для Ф,
изменяется с течением времени. - Записать формулу закона электромагнитной
индукции. - Выражение для Ф представить в развернутом
виде (Ф) и
подставить в исходную формулу закона
электромагнитной индукции. - Записать математически все вспомогательные
условия. - Полученную систему уравнений решить
относительно искомой величины. - Решение проверить и оценить критически.
Преломление света. [3] стр. 366
Задачи о преломлении света на плоской границе
раздела двух сред.
- Понять предложенную задачу (увидеть физическую
модель). - Анализ (построить математическую модель
явления): - Установить переходит ли луч из оптически менее
плотной среды в более плотную или наоборот. - Сделать чертеж, где указать ход лучей, идущих из
одной среды в другую. - В точке падения луча на границу раздела сред
провести нормаль и отметить углы падения и
преломления. - Записать формулу закона преломления для
каждого перехода луча из одной среды в другую. - Составить вспомогательные уравнения,
связывающие углы и расстояния, используемые в
задаче. - Полученную систему уравнений решить
относительно искомой величины. - Решение проверить и оценить критически.
Разумеется, в статье приведены не все схемы, да
и это, наверное, невозможно, ведь “сколько
существует задач, столько же и алгоритмов” ([4]
стр. 11) их решения (все же найти универсальный
способ решения очень хочется!!!).
Литература.
- Гутман В.И., Мощанский В.Н. Алгоритмы
решения задач по механике в средней школе: Кн. Для
учителя. – М.: Просвещение, 1988. – 95 с. - Пойа Д. Как решать задачу. – Львов: журнал
“Квантор”, 1991. - Балаш В.А. Задачи по физике и методы их
решения. Изд. 3-е, переаб. и испр. Пособие для
учителей. М.: Просвещение, 1974. – 430 с. - Игруполо В.С., Вязников Н.В. Физика:
алгоритмы, задачи, решения: Пособие для всех, кто
изучает и преподает физику. – М.: Илекса,
Ставрополь: Сервисшкола, 2002. – 592 с.
Рекомендую так же изучить следующую
литературу:
- Каменский С.Е., Орехов В.П. Методика решения
задач по физике в средней школе. – М.:Просвещение,
1971. - Усова А.В., Тулькибаева Н.Н. Практикум по
решению физических задач. 2-е изд. – М.:
Просвещение, 2001. – 206 с. - Кобушкин В.К. Методика решения задач по
физике. – Издательство ленинградского
университета, 1970. - Савченко Н.Е. Решение задач по физике.
Пособие для поступающих в вузы. – Минск, “Вышэйш.
школа”, 1977. – 240 с.
Алгоритмы решения задач
Для
решения качественных задач алгоритм:
1
этап — внимательно ознакомиться с условием задачи;
2
этап — выяснить, какие тела взаимодействуют;
3
этап — выяснить, о каком физическом явлении или группе явлений идет речь;
4
этап — выяснить состояние тела при начальных условиях;
5
этап — выяснить, что происходит с физическими телами в результате
действия физического явления (например, изменение формы, объема или агрегатного
состояния, а также силы, возникающие при этом);
6
этап — выяснить, как это сказывается на взаимодействующих телах;
7
этап — ответить на вопрос задачи.
Количественные задачи
– задачи, в которых все физические величины заданы количественно какими-то
числами. При этом физические величины могут быть как скалярными, так и
векторными:
1
этап — записать кратко условие задачи в виде «Дано»;
2
этап — перенести размерность физических величин в систему «СИ»;
3
этап — выполнить анализ задачи (записать какое физическое явление
рассматривается в задаче, сделать рисунок, обозначить на рисунке все известные
и неизвестные величины, записать уравнения, которые описывают физическое
явление, вывести из этих уравнений искомую величину в виде расчетной формулы);
4
этап — сделать проверку размерности расчетной формулы;
5
этап — сделать вычисления по расчетной формуле;
6
этап — обдумать полученный результат (Может ли быть такое с точки зрения
здравого смысла?);
7
этап — записать ответ задачи.
Графические задачи.
К
задачам этого типа относятся такие, в которых все или часть данных заданы в
виде графических зависимостей между ними. В решении таких задач можно выделить
следующие этапы:
1
этап — прочитать внимательно условие задачи;
2
этап — выяснить из приведенного графика, между какими величинами представлена
связь; выяснить, какая физическая величина является независимой, т.е.
аргументом; какая величина является зависимой, т.е. функцией; определить
по виду графика, какая это зависимость; выяснить, что требуется — определить
функцию или аргумент; по возможности записать уравнение, которое описывает
приведенный график;
3
этап — отметить на оси абсцисс (или ординат) заданное значение и восстановить
перпендикуляр до пересечения с графиком. Опустить перпендикуляр из точки
пересечения на ось ординат (или абсцисс) и определить значение искомой
величины;
4
этап — оценить полученный результат; записать ответ.
Алгоритм решения задач по кинематике:
1
этап — внимательно прочитать задачу и проанализировать ее условие, т.е.
выяснить характер движения, вспомнить уравнения, описывающие это движение;
2
этап — выписать численные значения заданных величин; выразить все
величины в единицах «СИ»;
3
этап — сделать схематический чертеж (траекторию движения, векторы
скорости, ускорения, перемещения и т.д.);
4
этап — выбрать систему координат (при этом следует выбрать такую систему,
чтобы уравнения были несложными);
5
этап — составить для данного движения основные уравнения, которые
отражают математическую связь между изображенными на схеме физическими
величинами; число уравнений должно быть равно числу неизвестных величин;
6
этап — решить составленную систему уравнений в общем виде, в буквенных
обозначениях, т.е. получить расчетную формулу;
7
этап — выбрать систему единиц измерения («СИ»), подставить в расчетную
формулу вместо букв наименования единиц, произвести действия с наименованиями и
проверить, получается ли о результате единица измерения искомой величины;
8
этап — выразить все заданные величины в избранной системе единиц;
подставить в расчетные формулы и вычислить значения искомых величин;
9
этап — проанализировать решение и сформулировать ответ.
Алгоритм решения задач по динамике:
1
этап — внимательно прочитать условие задачи и выяснить характер движения;
2
этап — записать условие задачи, выразив все величины в единицах «СИ»;
3
этап — сделать чертеж с указанием все сил, действующих на тело, векторы
ускорений и системы координат;
4
этап — записать уравнение второго закона Ньютона в векторном виде;
5
этап — записать основное уравнение динамики (уравнение второго закона Ньютона)
в проекциях на оси координат с учетом направления осей координат и векторов;
6
этап — найти все величины, входящие в эти уравнения; подставить в уравнения;
7
этап — решить задачу в общем виде, т.е. решить уравнение или систему уравнений
относительно неизвестной величины;
8
этап — проверить размерность;
9
этап — получить численный результат и соотнести его с реальными значениями
величин.
Алгоритм решения задач на тепловые явления:
1
этап — внимательно прочитать условие задачи, выяснить, сколько тел участвует в
теплообмене и какие физические процессы происходят (например, нагревание или
охлаждение, плавление или кристаллизация, парообразование или конденсация);
2
этап — кратко записать условие задачи, дополняя необходимыми табличными
величинами; все величины выразить в системе «СИ»;
3
этап — записать уравнение теплового баланса с учетом знака количества теплоты
(если тело получает энергию, то ставят знак «+», если тело отдает — знак «-»);
4
этап — записать необходимые формулы для расчета количества теплоты;
5
этап — записать полученное уравнение в общем виде относительно искомых величин;
6
этап — произвести проверку размерности полученной величины;
7
этап — вычислить значения искомых величин.
Алгоритмы решения задач по физике
Всегда хотелось найти универсальный способ решения задач, но, наверное, его просто не существует. Однако, можно составить рекомендации для решения отдельных групп задач
Как искать решение?
- Понять предложенную задачу.
- Найти путь от неизвестного к данным, если нужно, рассмотрев промежуточные задачи (“анализ”).
- Реализовать найденную идею решения (“синтез”).
- Решение проверить и оценить критически.
Кинематика материальной точки.
Понять предложенную задачу (увидеть физическую модель).
- Анализ (построить математическую модель явления):
- Выбрать систему отсчета (это предполагает выбор тела отсчета, начала системы координат, положительного направления осей, момента времени, принимаемого за начальный).
- Определить вид движения вдоль каждой из осей и написать кинематические уравнения движения вдоль каждой оси – уравнения для координат и для скорости (если тел несколько, уравнения пишутся для каждого тела).
- Определить начальные условия (координаты и проекции скоростей в начальный момент времени), а также проекции ускорения на оси и подставить эти величины в уравнения движения.
- Определить дополнительные условия, т.е. координаты или скорости для каких-либо моментов времени (для каких-либо точек траектории), и написать кинематические уравнения движения для выбранных моментов времени (т.е. подставить эти значения координат и скорости).
- Полученную систему уравнений решить относительно искомой величины.
- Решение проверить и оценить критически.
Динамика материальной точки.
Понять предложенную задачу (увидеть физическую модель).
- Анализ (построить математическую модель явления):
- Выбрать систему отсчета.
- Найти все силы, действующие на тело, и изобразить их на чертеже. Определить (или предположить) направление ускорения и изобразить его на чертеже.
- Записать уравнение второго закона Ньютона в векторной форме и перейти к скалярной записи, заменив все векторы их проекциями на оси координат.
- Исходя из физической природы сил, выразить силы через величины, от которых они зависят.
- Если в задаче требуется определить положение или скорость точки, то к полученным уравнениям динамики добавить кинетические уравнения.
- Полученную систему уравнений решить относительно искомой величины.
- Решение проверить и оценить критически.
Статика.
Понять предложенную задачу (увидеть физическую модель).
- Анализ (построить математическую модель явления):
- Выбрать систему отсчета.
- Найти все силы, приложенные к находящемуся в равновесии телу.
- Написать уравнение, выражающее первое условие равновесия (
Fi = 0), в векторной форме и перейти к скалярной его записи.
- Выбрать ось, относительно которой целесообразно определять момент сил.
- Определить плечи сил и написать уравнение, выражающее второе условие равновесия (
Mi = 0).
- Исходя из природы сил, выразить силы через величины, от которых они зависят.
- Полученную систему уравнений решить относительно искомой величины.
- Решение проверить и оценить критически.
Закон сохранения импульса.
- Понять предложенную задачу (увидеть физическую модель).
- Анализ (построить математическую модель явления):
- Выбрать систему отсчета.
- Выделить систему взаимодействующих тел и выяснить, какие силы для нее являются внутренними, а какие – внешними.
- Определить импульсы всех тел системы до и после взаимодействия.
- Если в целом система незамкнутая, сумма проекций сил на одну из осей равна нулю, то следует написать закон сохранения лишь в проекциях на эту ось.
- Если внешние силы пренебрежительно малы в сравнении с внутренними (как в случае удара тел), то следует написать закон сохранения суммарного импульса (
p = 0) в векторной форме и перейти к скалярной.
- Если на тела системы действуют внешние силы и ими нельзя пренебречь, то следует написать закон изменения импульса
(p = F
t) в векторной форме и перейти к скалярной.
- Записать математически все вспомогательные условия.
- Полученную систему уравнений решить относительно искомой величины.
- Решение проверить и оценить критически.
Закон сохранения механической энергии.
- Понять предложенную задачу (увидеть физическую модель).
- Анализ (построить математическую модель явления):
- Выбрать систему отсчета.
- Выделить два или более таких состояний тел системы, чтобы в число их параметров входили как известные, так и искомые величины.
- Выбрать нулевой уровень отсчета потенциальной энергии.
- Определить, какие силы действуют на тела системы – потенциальные или непотенциальные.
- Если на тела системы действуют только потенциальные силы, написать закон сохранения механической энергии в виде: Е1 = Е2.
- Раскрыть значение энергии в каждом состоянии и, подставить их в уравнение закона сохранения энергии.
- Полученную систему уравнений решить относительно искомой величины.
- Решение проверить и оценить критически.
Теплота (первое начало термодинамики Q = U + A). [3] стр. 168
Задачи об изменении внутренней энергии тел можно разделить на три группы.
В задачах первой группы рассматривают такие явления, где в изолированной системе при взаимодействии тел изменяется лишь их внутренняя энергия без совершения работы над внешней средой.
- Понять предложенную задачу (увидеть физическую модель).
- Анализ (построить математическую модель явления):
- Определить изолированную систему.
- Установить у каких тел внутренняя энергия уменьшается, а у каких – возрастает.
- Составить уравнение теплового баланса (
U = 0), при записи которого в выражении cm(t2 – t1), для изменения внутренней энергии, нужно вычитать из конечной температуры тела начальную и суммировать члены с учетом получающегося знака.
- Полученное уравнение решить относительно искомой величины.
- Решение проверить и оценить критически.
В задачах второй группы рассматриваются явления, связанные с превращением одного вида энергии в другой при взаимодействии двух тел. Результат такого взаимодействия – изменение внутренней энергии одного тела в следствие совершенной им или над ним работы.
- Понять предложенную задачу (увидеть физическую модель).
- Анализ (построить математическую модель явления):
- Следует убедиться, что в процессе взаимодействия тел теплота извне к ним не подводится, т.е. действительно ли Q = 0.
- Установить у какого из двух взаимодействующих тел изменяется внутренняя энергия и что является причиной этого изменения – работа, совершенная самим телом, или работа, совершенная над телом.
- Записать уравнение 0 =
U + A для тела, у которого изменяется внутренняя энергия, учитывая знак перед А и к.п.д. рассматриваемого процесса.
- Если работа совершается за счет уменьшения внутренней энергии одного из тел, то А=
U, а если внутренняя энергия тела увеличивается за счет работы, совершенной над телом, то
А =
U.
- Найти выражения для
U и A.
- Подставляя в исходное уравнение вместо
U и A их выражения, получим окончательное соотношение для определения искомой величины.
- Полученное уравнение решить относительно искомой величины.
- Решение проверить и оценить критически.
Задачи третьей группы объединяют в себе две предыдущие.
Тепловое расширение твердых и жидких тел.
- Понять предложенную задачу (увидеть физическую модель).
- Анализ (построить математическую модель явления):
- Для каждого теплового состояния каждого тела записать соответствующую формулу теплового расширения.
- Если в задаче наряду с расширением тел рассматриваются другие процессы, сопутствующие расширению, – теплообмен, изменение гидростатического давления жидкости или выталкивающей силы, то к уравнениям теплового расширения надо добавить формулы калориметрии и гидростатики.
- Синтез (получить результат).
- Решить полученную систему уравнений относительно искомой величины.
- Решение проверить и оценить критически.
Газы.
По условию задачи даны два или несколько состояний газа и при переходе газа из одного состояния в другое его масса не меняется.
- Понять предложенную задачу (увидеть физическую модель).
- Анализ (построить математическую модель явления):
- Представить какой газ участвует в том или ином процессе.
- Определить параметры p,V и T, характеризующие каждое состояние газа.
- Записать уравнение объединенного газового закона Клапейрона для данных состояний.
- Если один из трех параметров остается неизменным, уравнение Клапейрона автоматически переходит в одно из трех уравнений: закон Бойля – Мариотта, Гей-Люссака или Шарля.
- Записать математически все вспомогательные условия.
- Решить полученную систему уравнений относительно неизвестной величины.
- Решение проверить и оценить критически.
По условию задачи дано только одно состояние газа, и требуется определить какой либо параметр этого состояния или же даны два состояния с разной массой газа.
- Понять предложенную задачу (увидеть физическую модель).
- Анализ (построить математическую модель явления):
- Установить, какие газы участвуют в рассматриваемых процессах.
- Определить параметры p,V и T, характеризующие каждое состояние газа.
- Для каждого состояния каждого газа (если их несколько) составить уравнение Менделеева – Клапейрона. Если дана смесь газов, то это уравнение записывается для каждого компонента. Связь между значениями давлений отдельных газов и результирующим давлением смеси устанавливается законом Дальтона.
- Записать математически дополнительные условия задачи
- Решить полученную систему уравнений относительно неизвестной величины.
- Решение проверить и оценить критически.
Насыщающие и ненасыщающие пары. Влажность.
- Понять предложенную задачу (увидеть физическую модель).
- Анализ (построить математическую модель явления):
- Установить число состояний газа, рассматриваемых в условии задачи, обратить особое внимание на то, дается ли чистый пар жидкости или смесь пара с сухим воздухом.
- Для каждого состояния пара записать уравнение Менделеева – Клапейрона и формулу относительной влажности, если о последней что-либо сказано в условии. Составить уравнение Менделеева – Клапейрона для каждого состояния сухого воздуха (если дана смесь пара с воздухом). В тех случаях, когда при переходах из одного состояния в другое масса пара не меняется, вместо уравнения Менделеева – Клапейрона можно использовать сразу объединенный газовый закон.
- Записать математически все вспомогательные условия
- Решить полученную систему уравнений относительно неизвестной величины.
- Решение проверить и оценить критически.
Электростатика.
Решение задачи о точечных зарядах и системах, сводящихся к ним, основано на применении законов механики с учетом закона Кулона и вытекающих из него следствий.
- Понять предложенную задачу (увидеть физическую модель).
- Анализ (построить математическую модель явления):
- Расставить силы, действующие на точечный заряд, помещенный в электрическое поле, и записать для него уравнение равновесия или основное уравнение динамики материальной точки.
- Выразить силы электрического взаимодействия через заряды и поля и подставить эти выражения в исходное уравнение.
- Если при взаимодействии заряженных тел между ними происходит перераспределение зарядов, к составленному уравнению добавляют уравнение закона сохранения зарядов.
- Записать математически все вспомогательные условия
- Решить полученную систему уравнений относительно неизвестной величины.
- Решение проверить и оценить критически.
Постоянный ток.
Задачи на определение силы тока, напряжения или сопротивления на участке цепи.
- Понять предложенную задачу (увидеть физическую модель).
- Анализ (построить математическую модель явления):
- Начертить схему и указать на ней все элементы.
- Установить, какие элементы цепи включены последовательно, какие – параллельно.
- Расставить токи и напряжения на каждом участке цепи и записать для каждой точки разветвления (если они есть) уравнения токов и уравнения, связывающие напряжения на участках цепи.
- Используя закон Ома, установить связь между токами, напряжениями и э.д.с.
- Если в схеме делают какие-либо переключения сопротивлений или источников, уравнения составляют для каждого режима работы цепи.
- Решить полученную систему уравнений относительно неизвестной величины.
- Решение проверить и оценить критически.
Электромагнетизм.
Задачи о силовом действии магнитного поля на проводники с током.
- Понять предложенную задачу (увидеть физическую модель).
- Анализ (построить математическую модель явления):
- Сделать схематический чертеж, на котором указать контур с током и направление силовых линий поля. Отметить углы между направлением поля и отдельными элементами контура.
- Используя правило левой руки, определить направление сил поля (сила Ампера), действующих на каждый элемент контура, и проставить векторы этих сил на чертеже.
- Указать все остальные силы, действующие на контур.
- Исходя из физической природы сил, выразить силы через величины, от которых они зависят.
- Решить полученную систему уравнений относительно неизвестной величины.
- Решение проверить и оценить критически.
Задачи о силовом действии магнитного поля на заряженные частицы.
- Понять предложенную задачу (увидеть физическую модель).
- Анализ (построить математическую модель явления):
- Нужно сделать чертеж, указать на нем силовые линии магнитного и электрического полей, проставить вектор начальной скорости частицы и отметить знак ее заряда.
- Изобразить силы, действующие на заряженную частицу.
- Определить вид траектории частицы.
- Разложить силы, действующие на заряженную частицу, вдоль направления магнитного поля и по направлению, ему перпендикулярному.
- Составить основное уравнение динамики материальной точки по каждому из направлений разложения сил.
- Исходя из физической природы сил, выразить силы через величины, от которых они зависят.
- Решить полученную систему уравнений относительно неизвестной величины.
- Решение проверить и оценить критически.
Задачи на закон электромагнитной индукции.
- Понять предложенную задачу (увидеть физическую модель).
- Анализ (построить математическую модель явления):
- Установить причины изменения магнитного потока, связанного с контуром, и определить какая из величин В, S или
, входящих в выражение для Ф, изменяется с течением времени.
- Записать формулу закона электромагнитной индукции.
- Выражение для Ф представить в развернутом виде (
Ф) и подставить в исходную формулу закона электромагнитной индукции.
- Записать математически все вспомогательные условия.
- Полученную систему уравнений решить относительно искомой величины.
- Решение проверить и оценить критически.
Преломление света.
Задачи о преломлении света на плоской границе раздела двух сред.
- Понять предложенную задачу (увидеть физическую модель).
- Анализ (построить математическую модель явления):
- Установить переходит ли луч из оптически менее плотной среды в более плотную или наоборот.
- Сделать чертеж, где указать ход лучей, идущих из одной среды в другую.
- В точке падения луча на границу раздела сред провести нормаль и отметить углы падения и преломления.
- Записать формулу закона преломления для каждого перехода луча из одной среды в другую.
- Составить вспомогательные уравнения, связывающие углы и расстояния, используемые в задаче.
- Полученную систему уравнений решить относительно искомой величины.
- Решение проверить и оценить критически.
Разумеется, в статье приведены не все схемы, да и это, наверное, невозможно, ведь “сколько существует задач, столько же и алгоритмов” ([4] стр. 11) их решения (все же найти универсальный способ решения очень хочется!!!).
Литература.
- Гутман В.И., Мощанский В.Н. Алгоритмы решения задач по механике в средней школе: Кн. Для учителя. – М.: Просвещение, 1988. – 95 с.
- Пойа Д. Как решать задачу. – Львов: журнал “Квантор”, 1991.
- Балаш В.А. Задачи по физике и методы их решения. Изд. 3-е, переаб. и испр. Пособие для учителей. М.: Просвещение, 1974. – 430 с.
- Игруполо В.С., Вязников Н.В. Физика: алгоритмы, задачи, решения: Пособие для всех, кто изучает и преподает физику. – М.: Илекса, Ставрополь: Сервисшкола, 2002. – 592 с.
Научиться решать задачи по физике можно,…
только решая задачи по физике.
Итак, вы горите желанием научиться решать задачи, вы не боитесь трудностей, вы готовы быть усердным и внимательным, тогда начнём.
Все физические задачи, независимо от раздела, который вы сейчас изучаете, можно решить, выполняя определённые шаги, которые назовём «Алгоритм решения задач по физике».
Ознакомьтесь с ним.
Алгоритм решения задач по физике онлайн
1. Внимательно прочитайте задачу.
2. Запишите в «Дано» все данные и правильно запишите искомую величину.
3. Сделайте перевод единиц в СИ, если это необходимо.
4. Сделайте чертёж или схему, если это необходимо.
5. Напишите формулу или закон, по которым находится искомая величина.
6. Запишите дополнительные формулы, если это необходимо. Сделайте математические преобразования.
7. Подставьте цифровые значения в окончательную формулу. Вычислите ответ. Проанализируйте его.
8. Запишите ответ.
9. Похвалите себя.
Все пункты надо выполнять именно в этом порядке. Пункты 4 и 5, в зависимости от раздела физики, из которого решаем задачу, будем дополнять (эти дополнения покажу ниже).
Итак, решим следующую задачу с применением «Алгоритма решения задач онлайн».
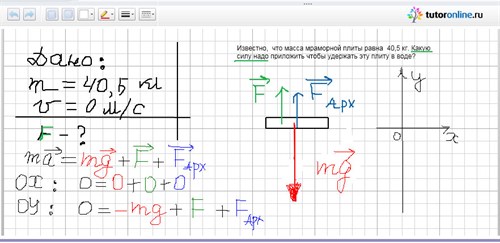
Задача 1. Известно, что масса мраморной плиты равна 40,5 кг. Какую силу надо приложить, чтобы удержать эту плиту в воде?
Выполняем п.1 и 2 нашего алгоритма:
1. Внимательно прочитайте задачу.
2. Запишите в «Дано» все данные и правильно запишите искомую величину.
Пункт 3 нашего алгоритма здесь делать не надо, так как все величины даны в СИ.
Выполняем следующий пункт.
4. Сделайте чертёж или схему, если это необходимо. На чертеже рисуем все силы, действующие на тело (это необходимо по условию задачи). А также рисуем координатные оси.
(Предполагаем, что мы удерживаем плиту от падения, т. е. искомая сила будет направлена вверх).
Выполняем следующий пункт.
5. Напишите формулу или закон, по которым находится искомая величина. (В данном случае это II закон Ньютона. Напоминаю, что исходная его запись должна быть в векторном виде).
Выполняем следующий пункт.
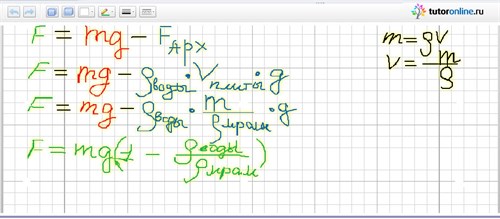
6. Запишите дополнительные формулы, если это необходимо. (В данном случае нам надо записать II закон Ньютона в проекциях на оси ОХ и ОУ). Сделайте математические преобразования.
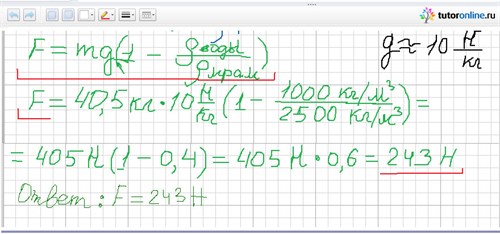
7. Подставьте цифровые значения в окончательную формулу. Вычислите ответ. Проанализируйте его. (В нашем случае, при решении мы получили положительное значение искомой величины. Это говорит о том, что направление искомой силы см п. 4 было выбрано верно).
8. Запишите ответ.
9. Похвалите себя. (Вы действительно сделали то, что удаётся немногим. Вы – молодец).
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.
Алгоритм решения задач по физике
Автор: Персиянов Максим Игоревич
Организация: МАОУ Зареченская СОШ
Населенный пункт: Московская область, Одинцовского г.о., р.п. Заречье
Главной проблемой в статье, является совершенствование системы образования, стимулируемое социальным заказом общества, что усложняет требования к развивающему характеру обучения учащихся средней школы. В настоящее время школьники должны не только знать, уметь и владеть определенными видами учебно-познавательной деятельности, они должны быть способны и готовы их применять на практике, т. е. быть компетентными.
Ученик, осознающий потребности и мотивы изучения конкретных вопросов курса физики, может ставить конкретные задачи (образовательные, развивающие и воспитательные), направленные на развитие способностей учащихся, интереса к изучению предмета.
Физика занимает особое, уникальное место среди школьных дисциплин, так как этот учебный предмет создаёт у учащихся представление о научной картине мира.
Но главная трудность в изучении физики является решение задач, таким образом, многие все еще не уверены в своих силах, и как только речь об контрольной или экзамене, и вовсе начинается самый настоящий страх, не справится с решением задач.
По моему мнению, решение задач по физике непростая задача для каждого ученика. Теория – это конечно хорошо, но, когда доходит дело до того, чтобы внедрить ее на практике, возникают определенные сложности. Вот тогда и нужно знать, какому конкретному алгоритму следовать, в решении задач, чтобы в итоге получить верный результат решаемой задачи. Здорово, когда люди сами могут составить алгоритм, по которому можно будет решить задачи, но для этого нужно обладать достаточным объемом знаний, так что как правило, все пользуются готовым алгоритмом решений задач по физике. Готовые алгоритмы передаются от преподавателя ученикам, другими словами это методика, с помощью которой решаются задачи.
Универсальных решений для всех задач не существует и, тем не менее, есть ряд определенных правил, которые подходят для всех задач и правила, которые подходят для решения отдельных групп задач. Таким образом, для каждого раздела физики есть свой комплекс правил, которые можно использовать в решение задач (алгоритм решения задач по кинетике, алгоритм решения задач по механике и т.д.)
Но самое главное, уже с начала обучения предмета «Физика», как правило это 7 класс, решать физические задачи нужно не по действиям, а в общем виде, и только в конце подставлять данные значения, а также использовать очень мощный инструмент проверки – производить действия с единицами измерения физических величин.
Алгоритм решения задач по физике:
1. Внимательно прочти условие задачи.
2. Произведи краткую запись условия задачи с помощью общепринятых буквенных обозначений (СИ).
3. Выполни рисунки или чертежи задачи.
4. Определи, каким методом будет решаться задача.
5. Запиши основные уравнения, описывающие процессы, предложенные задачной системой.
6. Найди решение в общем виде, выразив искомые величины, через заданные.
7. Проверь правильность решения задачи в общем виде, произведя действия с наименованием величин.
8. Произведи вычисления.
9. Произведи оценку реальности полученного решения.
10. Запиши ответ, отвечая на поставленный в задаче вопрос.
В заключении отмечу, что приемлемы любые методы преподавания, способствующие возбуждению у учащихся познавательного интереса.
Педагогу необходимо быть творческим, озарённым, непредсказуемым, всё время совершенствовать свой профессиональный уровень и идти в ногу со временем.
В приложении к статье прикладываю два примера задач, в формате презентации, где пошагово реализуется этот алгоритм.
Приложения:
- file1.pptx.zip.. 140,9 КБ
- file0.pptx.zip.. 83,9 КБ