Как составить алгоритм решения задачи проекта

Алгоритм – это точное предписание,
определяющее вычислительный процесс,
ведущий от варьируемых начальных данных
к искомому результату (ГОСТ 19.781-74).

Алгоритм содержит указание о том, какие
операции необходимо выполнить над
исходными данными и в какой последовательности
для решения задачи.

Поэтому при разработке алгоритма
необходимо четко представлять поставленную
задачу, чтобы предусмотреть все возможные
варианты действий.

К алгоритмам предъявляются следующие
требования.

Определенность (детерминированность)
означает однозначность толкования
отображаемого алгоритмом вычислительного
процесса.

Результативность алгоритма
заключается в возможности получения
результата решения задачи для допустимых
исходных данных за конечное число шагов.

Массовость означает, что решение
однотипных задач с различными исходными
данными может быть осуществлено по
одному алгоритму.

Дискретность означает, что определяемый
алгоритмом вычислительный процесс
может быть расчленен на отдельные этапы,
элементарные операции.

Понятность (доступность) –
алгоритм должен учитывать специфику
исполнителя и, при необходимости, ему
должны предоставляться дополнительные
сведения; На практике используются
следующие формы представления алгоритмов:

1. Словесная
   запись (не формализованная запись
   алгоритма на естественном языке,
   например, рецепт приготовления манной
   каши);

2. Блок-схема (наиболее наглядная
   графическая форма представления
   алгоритмов, используемая профессионалами
   особенно в тех случаях, когда алгоритм
   обладает изощренной логикой исполнения);

3. Псевдокоды
   (язык программирования для бедных,
   когда нет возможности преподавать
   основы алгоритмизации с использованием
   ЭВМ – полуформализованные описания
   алгоритмов, включающий в себя как
   элементы “птичьего” языка
   программирования);

4. Компьютерная программа (жестко
   формализованная запись алгоритма,
   ориентированная на исполнителя – ЭВМ).
   Для разработки компьютерных программ
   используются инструментальные средства,
   называемые языками программирования.

Рассмотрим запись алгоритма Евклида
нахождения наибольшего общего делителя
(НОД) для двух натуральных чисел во всех
четырех перечисленных выше формах.

начало,
конец алгоритма

простое
действие, вычисление

задание
исходных данных, вывод результата

проверка
условия

Это линейный
тип алгоритма
(следование)

к
содержанию

задание
исходных данных, вывод результата

Правила разработки, оформления и
обращения программ и программной
документации определяются ЕДИНОЙ
системой программной документации
(ЕСПД) – комплексов государственных
стандартов (ГОСТ 19.001-77).

Требования стандартов ЕСПД предъявляются
к оформлению программ и программной
документации в любой области, где
применяются вычислительные машины.

2.4Выбор языка программирования

Для составления программ используются
следующие языки: машинные,
машинно-ориентированные и машинно-независимые
(алгоритмические языки).

Машинный язык представляет собой
свод правил кодирования в цифровом виде
определенных операций (арифметических,
логических, посылочных и др.), которые
способен выполнять компьютер.

Программы для современных компьютеров,
как правило, составляют на языках
высокого уровня, однако для выполнения
программы на компьютере необходимо
переводить ее на машинный язык, так как
непосредственное выполнение программы
на компьютере осуществляется на машинном
языке. Данный перевод осуществляется
автоматически с помощью специальных
программ (трансляторов, компиляторов
или интерпретаторов).

Необходимо отметить, что в ряде случаев
(например, при ограниченных ресурсах
компьютера) программы составляются на
машинных языках (для микропроцессорных
систем, микрокалькуляторов, при
необходимости для мини- и микро-
компьютеров, для специализированных
компьютеров).

На языке машины программа представляется
в виде последовательности команд, каждая
из которых записывается в специальной
цифровой форме.

Команда представляет собой управляющую
информацию представленную в виде
машинного слова и предназначенную для
управления работой компьютера при
выполнении одной машинной операции.

В каждой команде указывается:

– код операции;

– адреса ячеек памяти, из которых
необходимо выбрать операнды для
выполнения операции, а также указывается
куда (в какую ячейку памяти) направить
результат операции или указывается
способ определения этих адресов.

Характерные особенности программирования
на машинном языке:

– детальное разбиение алгоритма на
элементарные шаги;

– предварительное распределение ячеек
памяти.

Достоинства: экономичность программ
(малый объем памяти, высокое быстродействие
и точность).

Недостатки: трудоемкость процесса
составления программ, громоздкость
текста (записи) программ (т.к. они состоят
из элементарных операций машины).

Машинно-ориентированный язык
отличается от машинного только тем, что
вместо числовых значений, выражающих
код операции команды и адреса операндов,
используются символические (буквенные
обозначения).

Машинная ориентированность означает,
что в основе этих языков лежит система
команд вычислительной машины.

Примером является язык АССЕМБЛЕР, каждый
оператор которого соответствует одной
команде компьютера.

Программа на АССЕМБЛЕРе также
детализирована, как и при использовании
машинного языка. Однако применение
АССЕМБЛЕРа имеет ряд преимуществ:

– с символическим языком удобнее работать,
чем с цифровыми кодами;

– текст программы, записанный на АССЕМБЛЕРе
перерабатывается в программу на машинном
языке с помощью транслятора, который
обеспечивает распределение ячеек
памяти, представление оператора языка
в машинном формате и др.

Программирование на машинно-ориентированных
языках требует знания не только сущности
задачи и алгоритма ее решения, но и
структуры, технических особенностей
компьютера, способов программирования
на ней.

Часто сознательно избирают АССЕМБЛЕР,
если стремятся наиболее эффективно
использовать возможности машины.

Машинно-независимые (алгоритмические)
языки высокого уровня ориентированы
на особенности задач и не зависят от
конкретных компьютеров.

В настоящее время широкое применение
находят языки программирования Си++,
Паскаль, Бейсик.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Исключительно важно использовать язык блок-схем при разработке алгоритма решения задачи. Решение одной и той же задачи может быть реализовано с помощью различных алгоритмов, отличающихся друг от друга как по времени счета и объему вычислений, так и по своей сложности. Запись этих алгоритмов с помощью блок-схем позволяет сравнивать их, выбирать наилучший алгоритм, упрощать, находить и устранять ошибки.

Отказ от языка блок-схем при разработке алгоритма и разработка алгоритма сразу на языке программирования приводит к значительным потерям времени, к выбору неоптимального алгоритма. Поэтому необходимо изначально разработать алгоритм решения задачи на языке блок-схем, после чего алгоритм перевести на язык программирования.

При разработке алгоритма сложной задачи используется метод пошаговой детализации. На первом шаге продумывается общая структура алгоритма без детальной проработки отдельных его частей. Блоки, требующие детализации, обводятся пунктирной линией и на последующих шагах разработки алгоритма продумываются и детализируются.

В процессе разработки алгоритма решения задачи можно выделить следующие этапы:

• Этап 1 . Математическое описание решения задачи.
• Этап 2 . Определение входных и выходных данных.
• Этап 3 . Разработка алгоритма решения задачи.

Базовые алгоритмические конструкции

В теории программирования доказано, что для записи любого, сколь угодно сложного алгоритма достаточно трех базовых структур:

• следование (линейный алгоритм);
• ветвление (разветвляющийся алгоритм);
• цикл-пока (циклический алгоритм).

Линейные алгоритмы

Линейный алгоритм образуется из последовательности действий, следующих одно за другим. Например, для определения площади прямоугольника необходимо сначала задать длину первой стороны, затем задать длину второй стороны, а уже затем по формуле вычислить его площадь.

Пример

ЗАДАЧА. Разработать алгоритм вычисления гипотенузы прямоугольного треугольника по известным значениям длин его катетов a и b.

На примере данной задачи рассмотрим все три этапа разработки алгоритма решения задачи:

Этап 1. Математическое описание решения задачи.

Математическим решением задачи является известная формула:

,

где с-длина гипотенузы, a, b – длины катетов.

Этап 2. Определение входных и выходных данных.

Входными данными являются значения катетов a и b. Выходными данными является длина гипотенузы – c.

Этап 3. Разработка алгоритма решения задачи.

Словесное описание алгоритма	Запись алгоритма на языке блок-схем
Начало алгоритма. Ввод значений длин катетов a и b. Вычисление длины гипотенузы с по формуле Вывод значения длины гипотенузы. Конец алгоритма	На данной схеме цифрами указаны номера элементов алгоритма, которые соответствуют номерам пунктов словесного описания алгоритма.

Разветвляющиеся алгоритмы

Алгоритм ветвления содержит условие, в зависимости от которого выполняется та или иная последовательность действий.

Пример

ЗАДАЧА. Разработать алгоритм вычисления наибольшего числа из двух чисел x и y.

Этап 1. Математическое описание решения задачи.

Из курса математики известно, если x > y, то наибольшее число x, если x < y, то наибольшее число y, если x = y, то число x равно числу y.

Этап 2. Определение входных и выходных данных.

Входными данными являются значения чисел x и y. Выходным данными являются:

• наибольшее число
• любое из чисел, если числа равны

Для решения задачи нам необходимо знать значения x и y.

Этап 3. Разработка алгоритма решения задачи.

Словесное описание алгоритма	Запись алгоритма на языке блок-схем
Начало алгоритма. Ввод значений x и y. Сравниваем x и y. Если x = y, то переход к шагу 4, иначе к шагу 5. Вывод информации: числа x и y равны. Переход к шагу 8. Сравниваем x и y. Если x > y, то переход к шагу 6, иначе к шагу 7. Вывод информации: число x больше y. Переход к шагу 8. Вывод информации: число y больше x. Переход к шагу 8. Конец алгоритма.

В схеме алгоритма решения задачи цифрами указаны номера элементов алгоритма, которые соответствуют номерам шагов словесного описания алгоритма

В рассматриваемом алгоритме (рис.3) имеются три ветви решения задачи:

• первая: это элементы 1, 2, 3, 4, 8.
• вторая: это элементы 1, 2, 3, 5, 6, 8
• третья: это элементы 1, 2, 3, 5, 7, 8.

Выбор ветви определяется значениями x и y в элементах 3 и 5, которые являются условиями, определяющими порядок выполнения элементов алгоритма. Если условие (равенство), записанное внутри символа «решение», выполняется при введенных значениях x и y, то следующими выполняется элементы 4 и 8. Это следует из того, что они соединены линией с надписью «да» и направление (последовательность) вычислений обозначена стрелочкой.

Если условие в элементе 3 не выполняется, то следующим выполняется элемент 5. Он соединен с элементом 3 линией с надписью «нет». Если условие, записанное в элементе 5, выполняется, то выполняется элементы 6 и 8, в противном случае выполняются элементы 7 и 8.

Циклические алгоритмы

Циклический алгоритм – определяет повторение некоторой части действий (операций), пока не будет нарушено условие, выполнение которого проверяется в начале цикла. Совокупность операций, выполняемых многократно, называется телом цикла.

Алгоритмы, отдельные действия в которых многократно повторяются, называются циклическими алгоритмами, Совокупность действий, связанную с повторениями, называют циклом.

При разработке алгоритма циклической структуры выделяют следующие понятия:

• параметр цикла – величина, с изменением значения которой связано многократное выполнение цикла;
• начальное и конечное значения параметров цикла;
• шаг цикла – значение, на которое изменяется параметр цикла при каждом повторении.

Цикл организован по определенным правилам. Циклический алгоритм состоит из подготовки цикла, тела цикла и условия продолжения цикла.

 

В подготовку цикла входят действия, связанные с заданием исходных значений для параметров цикла:

• начальные значения цикла;
• конечные значения цикла;
• шаг цикла.

В тело цикла входят:

• многократно повторяющиеся действия для вычисления искомых величин;
• подготовка следующего значения параметра цикла;
• подготовка других значений, необходимых для повторного выполнения действий в теле цикла.

В условии продолжения цикла определяется допустимость выполнения повторяющихся действий. Если параметр цикла равен или превысил конечное значение цикла, то выполнение цикла должно быть прекращено.

 Пример

ЗАДАЧА. Разработать алгоритм вычисления суммы натуральных чисел от 1 до 100.

Этап 1. Математическое описание решения задачи.

Обозначим сумму натуральных чисел через S. Тогда формула вычисления суммы натуральных чисел от 1 до 100 может быть записана так:

где Xi – натуральное число X c номером i, который изменяется от 1 до n, n=100 – количество натуральных чисел.

Этап 2. Определение входных и выходных данных.

Входными данными являются натуральные числа: 1, 2, 3, 4, 5, …, 98, 99, 100.

Выходные данные – значение суммы членов последовательности натуральных чисел.

Параметр цикла – величина, определяющая количество повторений цикла. В нашем случае i – номер натурального числа.

Подготовка цикла заключается в задании начального и конечного значений параметра цикла.

• начальное значение параметра цикла равно 1,
• конечное значение параметра цикла равно n,
• шаг цикла равен 1.

Для корректного суммирования необходимо предварительно задать начальное значение суммы, равное 0.

Тело цикла. В теле цикла будет выполняться накопление значения суммы чисел, а также вычисляться следующее значение параметра цикла по формулам:

S=S+i;              I=I+1;

Условие продолжения цикла: цикл должен повторяться до тех пор, пока не будет добавлен последний член последовательности натуральных чисел, т.е. пока параметр цикла будет меньше или равен конечному значению параметра цикла.

Этап 3. Разработка алгоритма решения задачи.

Введем обозначения: S – сумма последовательности, i – значение натурального числа.

Начальное значение цикла i=1, конечное значение цикла i =100, шаг цикла 1.

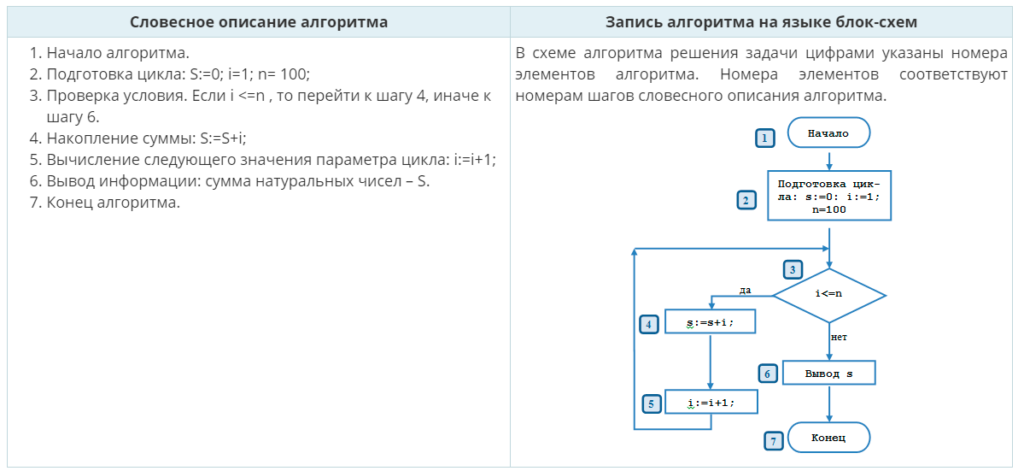
Словесное описание алгоритма	Запись алгоритма на языке блок-схем
Начало алгоритма. Подготовка цикла: S:=0; i=1; n= 100; Проверка условия. Если i <=n , то перейти к шагу 4, иначе к шагу 6. Накопление суммы: S:=S+i; Вычисление следующего значения параметра цикла: i:=i+1; Вывод информации: сумма натуральных чисел – S. Конец алгоритма.	В схеме алгоритма решения задачи цифрами указаны номера элементов алгоритма. Номера элементов соответствуют номерам шагов словесного описания алгоритма.

Мы уже рассказывали про алгоритмы, их виды и свойства. В этой статье поговорим о том, как составить алгоритм решения какой-нибудь задачи, что и в какой последовательности следует написать.

При решении задач на алгоритмы немаловажным является умение использовать язык блок-схем. Процесс решения одной и той же задачи можно реализовать посредством применения алгоритмов разных классов, поэтому результат может отличаться и по времени счета, и по объему вычислений, и по сложности. Записывая алгоритмическую последовательность с помощью составления блок-схем, вы сможете сравнить решения, выбрав самый лучший algorithm. Также появляется возможность упростить способ решения, найти и устранить ошибку.

Можно ли отказаться от языка блок-схем при описании алгоритма и сразу составить его на языке программирования? Можно, однако существует риск выбора неоптимального решения и существенных потерь времени. Именно поэтому при данной постановке вопроса рекомендуется сначала составлять способ решения задачи путем создания блок-схемы, а уже потом переводить алгоритм на нужный язык программирования.

Когда речь идет о задаче высокого класса сложности, не обойтись без пошаговой реализации. Сначала продумывают общую структуру алгоритмической последовательности, то есть детальная проработка отдельных частей здесь не требуется. Модули, которые далее потребуют более детального рассмотрения, обводят пунктиром, чтобы потом продумать и детализировать.

В решении задачи на алгоритмы выделяют ряд этапов:

1. Математическое описание.
2. Определение входных/выходных данных.
3. Разработка алгоритма по решению поставленной задачи.

Алгоритмические конструкции базовых классов

В теории программирования считают, что для того, чтобы составить запись любого, даже самого сложного алгори тма, хватит  3-х базовых структур. Речь идет о следующих алгоритмах:

• линейного класса;
• ветвления (речь идет о разветвляющихся алгоритмах);
• циклического класса.

Алгоритмы линейного класса

Образуются из последовательности действий, которые следуют одно за другим. К примеру, чтобы определить площадь прямоугольника, надо сначала задать длину 1-й стороны, потом — 2-й стороны, ну а в конце уже можно решать пример по формуле нахождения площади.

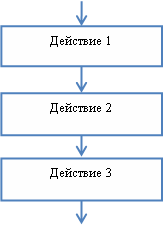
В качестве примера возьмем задание с разработкой алгоритма по вычислению гипотенузы прямоугольного треугольника, зная длины катетов a и b. Вспоминаем вышеописанные этапы разработки:

1. Математическое описание.

Математически задача решается по следующей формуле:

Здесь c является длиной гипотенузы, a, b – длинами катетов.

2. Определяем входные/выходные данные.

Входные данные — значения катетов a и b. Выходные — длина гипотенузы c.

3. Разработка алгоритма.

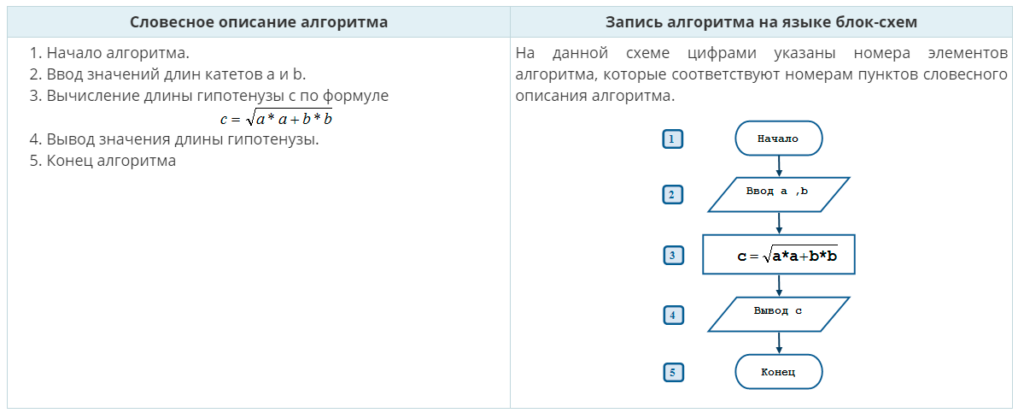
Алгоритмы ветвления

В таких алгоритмических последовательностях всегда существует какое-нибудь условие. В зависимости от того, соблюдается это условие либо нет, происходит выполнение той либо иной последовательности действий.

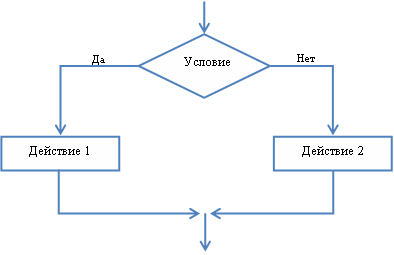
Для примера возьмем задание, постановка которого связана с разработкой алгоритма по вычислению наибольшего числа из 2-х чисел: x и y.

1. Математическое описание.

Из первых классов математики мы знаем, что когда x > y, то x больше y и наоборот, что является очевидными вещами. И если x = y, то числа равны.

2. Определяем входные/выходные данные.

Входные данные — это значения x и y. Выходными данными являются:

• самое большое число;
• любое из чисел в том случае, если они равны.

Таким образом, чтобы решить эту задачу на алгоритмы, надо знать значения переменных x и y.

3. Разработка.

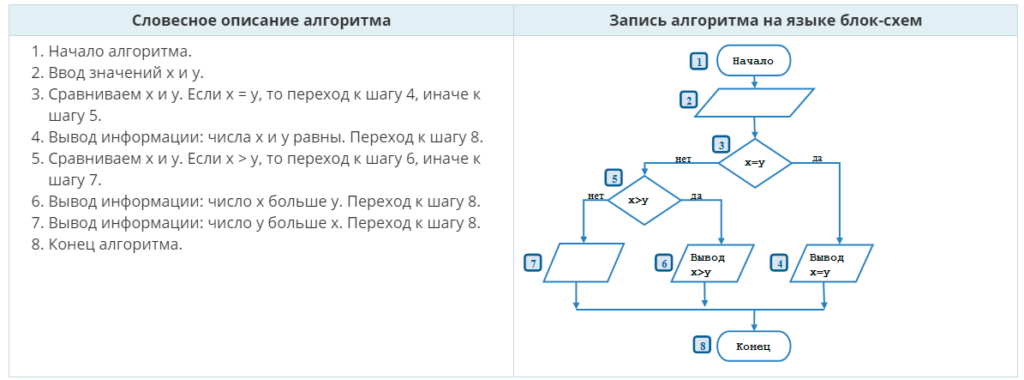
В вышеуказанной схеме цифрами отмечены номера алгоритмических элементов, соответствующие номерам шагов словесного описания. Здесь есть 3 ветви решения:

• 1, 2, 3, 4, 8;
• 1, 2, 3, 5, 6, 8;
• 1, 2, 3, 5, 7, 8.

Алгоритмы циклического класса

В алгоритмах циклического класса некоторая часть действий из задания повторяется до тех пор, пока не нарушится заранее определенное условие. Выполнение условия проверяется в начале. Совокупность операций, которые выполняются многократно, — это тело цикла.

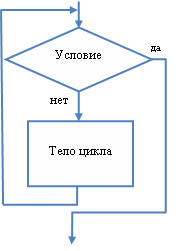
В алгоритмических последовательностях этого класса выделяют ряд понятий:

• параметр цикла (с изменением этой величины связано многократное выполнение цикла);
• начальное и конечное значения циклических параметров;
• шаг цикла (речь идет о значении, на которое меняется параметр при каждом повторе).

Работу циклов организуют по специальным правилам. Алгоритмическая последовательность циклического класса включает в себя и подготовку, и тело, и условия продолжения работы.

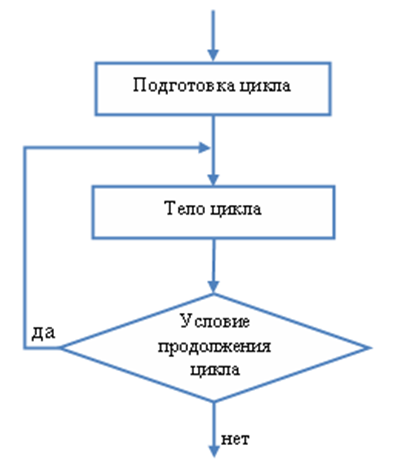
В подготовку входят действия, которые связаны с заданием исходных значений:

• начальные значения;
• конечные значения;
• шаг.

В тело цикла входят:

• многократно повторяющиеся операции по вычислению искомых величин;
• подготовка последующего значения параметра;
• подготовка иных значений, нужных для повторного выполнения действий непосредственно в теле.

В условии продолжения цикла определяют допустимость выполнения повторяемых операций. Когда циклический параметр равен либо превышает конечное значение, выполнение прекращается.

Рассмотрим задание, постановка которого связана с разработкой алгоритма вычисления суммы натуральных чисел в диапазоне от 1 до 100.

1. Математическое описание.

Сначала следует обозначить сумму натуральных чисел буквой S. В результате формулу вычисления суммы чисел от 1 до 100 можно записать следующим образом:

Здесь Xi является натуральным числом X c номером i. Этот номер меняется от 1 до n. А n=100 обозначает общее кол-во натуральных чисел.

2. Определяем входные/выходные данные.

Входные данные — это натуральные числа: 1, 2, 3, …, 99, 100.

Выходные данные представляют собой значение суммы членов последовательности натуральных чисел.

Относительно параметра цикла — речь идет о величине, определяющей число циклических повторений. В нашем задании i представляет собой номер натурального числа.

Подготовка цикла — задание начального и конечного значений циклического параметра. Тут надо пояснить следующее:

• начальное значение циклического параметра равняется единице,
• конечное значение — n,
• шаг равен 1.

Чтобы обеспечить корректность суммирования, надо, чтобы начальное значение суммы предварительно равнялось нулю.

Тело цикла. В теле станут выполняться как накопление значения суммы, так и вычисление последующего значения циклического параметра по формулам ниже:

• S=S+i;             
• I=I+1.

Циклическое повторение должно осуществляться до тех пор, пока не добавится последний член последовательности натуральных чисел, то есть до тех пор, пока циклический параметр будет меньше либо равен окончательному значению параметра.

3. Разработка.

Вводим следующие обозначения: S – это сумма последовательности, i – это значение натурального числа.

Начальное циклическое значение i=1, конечное — i =100, шаг равен 1.

По материалам: https://www.turbopro.ru/index.php/osnovy-programmirovaniya/6836-algoritmy-razrabotka-algoritma-resheniya-zadachi.

Интегрированный проект по математике и информатике
«Алгоритм решения задач»

Автор
проекта

Формулирование
проблемы

Тема
проекта

Цель
проекта

Количество
времени, необходимое для реализации проекта

Для
учащихся какого класса разработан проект

Основополагающий
вопрос проекта

Проблемные
вопросы проекта

Учебные
вопросы проекта

Список
формируемых УУД

Краткая
аннотация к проекту

Этапы
проекта

Продукт
проекта

Оценка
и контроль проекта

Список
дидактических материалов, необходимых для реализации проекта

Ресурсы проекта
(список литературы и веб-адресов, необходимых для проведения проекта)

Продукт проекта

Алгоритм решения задачи

1.      Прочитай
задачу. Представь, о чем говорится в задаче, что делают в задаче

2.      Определи
условие, данные задачи

3.      Прочитай
вопрос, искомое задачи.

4.      Найди
слова помощники.

5.      Выбери
действие (смотри таблицу).

6.      Сверь,
ответил ли ты на вопрос.

7.      1.Если
да, напиши ответ по вопросу         7.2.Если нет, вернись к п.4     

Выбор
действия

Структура задачи	Сложение +	Вычитание –	Умножение .	Деление :
Условие	На … больше Это на … меньше	На … меньше Это на … больше	Взяли по …несколько раз. В … раз больше. Это в …раз меньше.	Разложили… В …  раз меньше Это в … раз больше
Вопрос	Сколько всего?	Сколько осталось? На сколько больше (или меньше)?	Сколько всего?	Сколько у каждого? Сколько групп? Во сколько раз больше (или меньше)?

Карта самооценки  

ФИ_____________________________

№ задачи	Решил сам	Решил с подсказкой	Решил с помощью учителя
1.
2.
…

Практическая работа №1

Тема: «Разработка алгоритма работы над проектом»

1. Теоретические сведения (лекция)

Индивидуальный проект или исследование с точки зрения обучающегося – это возможность максимального раскрытия своего творческого потенциала. Это деятельность, позволит проявить себя индивидуально или в группе, попробовать свои силы, приложить свои знания, принести пользу, показать публично достигнутый результат. Это деятельность, направленная на решение интересной проблемы, сформулированной зачастую самими обучающимися в виде задачи, когда результат этой деятельности – найденный способ решения проблемы – носит практический характер, имеет важное прикладное значение и, что весьма важно, интересен и значим для самих открывателей.

Индивидуальный проект

Проблема проекта «Почему?» (это важно для меня лично)

Актуальность проблемы – мотивация

Цель проекта

Задачи проекта

Методы и способы

Результат

«Зачем?» (мы делаем проект)

«Что?» (для этого мы делаем)

«Как?» (мы это можем делать)

«Что получится?» (как решение проблемы)

Целеполагание

Постановка задач

Выбор способов и методов планирование

Ожидаемый результат

Этапы работы над проектом

Процедуру работы над проектом можно разбить на 6 этапов. Последовательность этапов работы над проектом соответствует этапам продуктивной познавательной деятельности: проблемная ситуация – проблема, заключенная в ней и осознанная человеком – поиск способов решения проблемы – решение.

Этапы работы над проектом можно представить в виде следующей схемы:

Подготовительный:

§ определение руководителей проектов;

§ поиск проблемного поля;

§ выбор темы и её конкретизация;

Поисковый:

§ уточнение тематического поля и темы проекта, её конкретизация;

§ определение и анализ проблемы;

§ постановка цели проекта.

Аналитический:

§ анализ имеющейся информации;

§ сбор и изучение информации;

§ поиск оптимального способа достижения цели проекта (анализ альтернативных решений), построение алгоритма деятельности;

§ составление плана реализации проекта: пошаговое планирование работ;

§ анализ ресурсов.

Практический:

§ выполнение запланированных технологических операций;

§ текущий контроль качества;

§ внесение (при необходимости) изменений в конструкцию и технологию.

Презентационный:

§ Подготовка презентационных материалов;

§ Презентация проекта;

§ Изучение возможностей использования результатов проекта (выставка, продажа, включение в банк проектов, публикация).

Контрольный

§ анализ результатов выполнения проекта;

§ оценка качества выполнения проекта.

2. Практическое задание

Обучающийся должен:

знать:

– состав компонентов методологического аппарата исследования;

– особенности каждого из структурных компонентов;

– место каждого из компонентов в структуре собственного исследования;

уметь:

– формулировать проблему, объект, предмет, цель, задачи и гипотезу исследования.

Состав компонентов методологического аппарата исследования: тема, объект, предмет, проблема, цель, задача, гипотеза.

Характеристика каждого из структурных компонентов. Содержательное разнообразие видов научных работ: работы теоретического, опытно-экспериментального, практического характера.

Выявление содержательных особенностей категориально-понятийного аппарата применительно к теме исследовательской работы.

Актуальность выбранной темы обосновывает необходимость проведения исследования.

Объект исследования – это область, в рамках которой ведётся исследование совокупности связей, отношений и свойств как источника необходимой для исследователя информации.

Предмет исследования более конкретен и включает только те связи и отношения, которые подлежат непосредственному изучению в данной работе, он устанавливает границы научного поиска в каждом объекте. Предмет всегда изучается в рамках какого-то объекта.

Цель формулируется кратко и предельно точно, в смысловом отношении выражая то основное, что намеревается сделать исследователь. Как правило, цель начинается с глаголов: «выяснить», «выявить», «сформировать», «обосновать», «провести», «разработать», «предложить пути» и т.д.

Цель конкретизируется и развивается в задачах исследования. В задачах обозначают комплекс проблем, которые необходимо решить в ходе эксперимента. Задачи могут отражать определённую пошаговость достижения цели, последовательность действий. Решение задачи позволяет пройти определенный этап исследования. Формулировка задач тесно связана со структурой исследования, причем отдельные задачи могут быть поставлены как для теоретической (обзор литературы по проблеме), так и для экспериментальной части исследования. Задачи определяют содержание исследования и структуру текста работы. Задача начинаются с глагола (изучить…, рассмотреть…, проанализировать…, описать…, установить…, оценить…, охарактеризовать…, проанализировать…, вывести формулу …, обосновать …, определить …, исследовать …, разработать методику… и т.п.). Формулировки этих задач необходимо делать как можно более тщательно, поскольку описание их решения должно составить содержание глав исследования.

Первая задача заключается в исследовании теоретических основ проблемы, заявленной в теме. Соответственно первая глава носит теоретический характер. Вторая глава по своему характеру практическая и связана с выработкой конкретных рекомендаций по решению проблем. В ней даются практические рекомендации и обосновывается эффективность их применения.

Гипотеза исследования – это развёрнутое предположение, подробно излагающее модель, методику, систему мер, то есть технологию того нововведения, в результате которого ожидается достижение цели исследования. Гипотез может быть несколько – какие-то из них подтвердятся, какие-то нет. Как правило, гипотеза формулируется в виде сложноподчинённого предложения («Если …, то …» или «Чем …, тем …»). Делая предположения, обычно используются слова: может быть, предположим, допустим, возможно, что, если, наверное. В ходе эксперимента гипотеза уточняется, дополняется, развивается или отвергается.

Гипотеза – это основание, предположение, суждение о закономерной связи явлений. Дети часто высказывают самые разные гипотезы по поводу того, что видят, слышат, чувствуют. Множество интересных гипотез рождается в результате попыток поиска ответов на собственные вопросы. Гипотеза – это предвидение событий. Изначально гипотеза не истинна и не ложна – она просто не определена. Стоит ее подтвердить, как она становится теорией, если ее опровергнуть, она также прекращает свое существование, превращаясь из гипотезы в ложное предположение. Первое, что заставляет появиться на свет гипотезу, это – проблема. Способы проверки гипотез обычно делятся на две большие группы: теоретические и эмпирические. Первые предполагают опору на логику и анализ других теорий (имеющихся знаний), в рамках которых данная гипотеза выдвинута. Эмпирические способы проверки гипотез предполагают наблюдения и эксперименты.

Построение гипотез – основа исследовательского, творческого мышления. Гипотезы позволяют открывать и затем в ходе теоретического анализа, мысленных или реальных экспериментов оценивать их вероятность. Таким образом, гипотезы дают возможность увидеть проблему в другом свете, посмотреть на ситуацию, с другой стороны.

Например:

Тема: «Анализ финансовых результатов предприятия и разработка мероприятий по их улучшению (на примере Муниципальное унитарное предприятие «Шахунское пассажирское автотранспортное предприятие»)».

Объект исследования: Муниципальное унитарное предприятие «Шахунское пассажирское автотранспортное предприятие».

Предмет исследования: финансовые результаты деятельности предприятия.

Цель исследования: разработать мероприятия по повышению эффективности деятельности предприятия и улучшению его финансовых результатов.

Задачи:

1. Рассмотреть теоретические основы анализа финансовых результатов деятельности предприятия.

2. Выявить основные факторы, оказывающие негативное влияние на финансовые показатели.

3. Дать организационно-экономическую характеристику предприятия.

4. Проанализировать финансовые результаты деятельности предприятия для выявления резервов их улучшения.

Задание: Сформулировать тему, объект, предмет, проблему, цель, задачи и гипотезу своего исследования.

В таблице ниже приведена общая форма структуры и этапов учебного проекта. Заполнив таблицу и получив практические навыки, спланируйте учебную деятельность по разрабатываемому Вами проекту, т.е. составьте собственный алгоритм работы над проектом. Время на выполнение 15 минут.

Структура и этапы учебного проекта	Вероятные варианты	Время, используемые методы
Определение темы проекта
Формулировка проблемы преподавателем
Формулировки возможных вариантов проблем учащимися
Выдвижение гипотез решения сформулированных проблем, распределение задач по группам, формирование групп
Определение названия проекта.
Формулировка дидактических целей проекта
Формулировка методических задач
Обсуждение алгоритма (плана) работы группы
Обсуждение возможных методов исследования каждой группой.
Обсуждение возможных источников информации, инструкция о заполнении папок директории «Источники», сообщение об авторском праве
Самостоятельная работа учащихся в группах, обсуждение задания каждого в группе.
Самостоятельная работа групп по выполнению заданий.
Подготовка презентации по отчету о проделанной работе (промежуточные результаты). Самостоятельная работа.
Промежуточное обсуждение полученных данных.
Продолжение выполнения заданий группами, самостоятельная работа.
Защита и оппонирование полученных результатов и выводов.
Внутренняя оценка работы каждого участника группы.
Внешняя оценка работы групп.

Пример заполнения таблицы.

Определение темы проекта «Влияние промышленных выбросов на кислотность осадков».

Формулировка проблемы «Влияние кислотных дождей на окружающую среду».

Формулировки возможных вариантов проблем «Кислотные дожди и огород моей бабушки», «Выживаемость помидоров на нашей даче под кислотными дождями», «Кислотные дожди и воздух района моего города».

Выдвижение гипотез решения сформулированных проблем «Если мы перестанем сжигать мусор на помойках, то кислотность осадков снизится на 50%. Задача: узнать, верно ли это».

Определение названия проекта «Кислотные дожди».

Формулировка дидактических целей проекта Формирование – компетентности в сфере самостоятельной познавательной деятельности, – компетентности в бытовой сфере, – навыков самостоятельной работы с большими объемами информации, – умения увидеть проблему и наметить пути ее решения; – формирование критического мышления, – навыков работы в команде и т.д. – и т.д.

Формулировка задач – Освоить представление об электролитической диссоциации веществ и окислительно-восстановительных процессах (химия), – освоить понятие «загрязненность среды» (экология) – научить проводить химический анализ жидкостей на кислотность (химия), – научить пользоваться Power Point для оформления результатов (информатика) – научиться кратко излагать свои мысли устно и письменно (русский яз, литература) – и т.д.

Рассмотрение возможных методов исследования

Методы: анализ источников, анкетирование, лабораторные опыты, наблюдения, интервью, эксперимент, тестирование, видео-аудио-запись

Рассмотрение возможных источников информации, инструкция Книги (какие?), интервью (с кем?), опросы (кого?), сайты (какие?), видеофрагменты (где взять и как соблюсти авторские права?) и т.д.

Подготовка презентации Подготовка презентационных материалов

Защита проекта

Публичная защита проекта

Внешняя оценка

Рекомендуемые параметры внешней оценки:

– значимость проблемы, адекватность изучаемой тематике;

– целесообразность используемых методов исследования;

– степень активности каждого участника; – коллективность в работе, взаимовыручка и поддержка;

– доказательность предлагаемых решений, четкость выводов;

– эстетика оформления результатов проекта;

– умение отвечать на вопросы оппонентов, и т.д.

Алгоритм работы над проектом можно составить в различных формах: таблица, график, рисунок, презентация и т.д., проявив при этом креативность, фантазию, творчество и нестандартное мышление.