Следование — алгоритмическая конструкция, в которой действия выполняются последовательно друг за другом.
Алгоритмы с конструкцией «следование» называются линейными алгоритмами.
Общий вид конструкции «следование».
Линейный алгоритм приготовления чая.
Такой алгоритм может потребовать детализации некоторых пунктов, потому что процесс заваривания чая может отличаться.
Пример линейного алгоритма, который может выполнять исполнитель Робот.
Он знает команды: вверх, вниз, вправо, влево, закрасить.
С помощью операции div вычисляется целое частное, с помощью операции mod — остаток.
Вопросы занятия:
·
Следование;
·
Линейные
алгоритмы;
·
Составление
линейных алгоритмов.
Алгоритмы
постоянно присутствуют в нашей жизни. Например, в учебной деятельности ученик
выполняет много разнообразных алгоритмов: при решении уравнений и текстовых
задач, применении правил русского и иностранного языков, проведении опытов и
так далее.
Например,
решая задачи на уроке математики, каждый ученик является исполнителем
следующего алгоритма:
1. Прочитать
условие задачи.
2. Выяснить,
значения каких величин известны и значения каких величин нужно найти.
3. Составить
план решения задачи.
4. Записать
решение задачи.
5. Записать
ответ.
На
уроках русского языка ученики часто выполняют алгоритм разбора слова по
составу:
1. Определить
окончание слова и обозначить его.
2. Определить
основу слова.
3. Подобрать
однокоренные слова.
4. Определить
корень слова и обозначить его.
5. Обозначить
приставку слова.
6. Обозначить
суффикс слова.
Выполняют
действия по алгоритму и на производстве. Например, в проектном бюро завода процесс
изготовления нового устройства всегда начинается с проектирования этого
изделия. Проектировщики выполняют следующий алгоритм:
1. Определить
назначение будущего изделия, основные требования к нему, условия использования.
2. Проанализировать
уже существующие аналогичные изделия.
3. Создать
эскизный проект.
4. Разработать
технический проект.
5. Разработать
техническую документацию.
Каждому
человеку ежедневно необходимо решать массу задач в повседневной жизни, в учёбе,
в исследовательской деятельности, во время путешествий и отдыха, на
производстве и так далее. Все эти задачи описываются своим алгоритмом. И этих
алгоритмов огромное множество.
Однако
для записи любого алгоритма хватает трёх основных алгоритмических
конструкций (структур) – это следование, ветвление и повторение.
Эту
идею предложил и доказал Э́дсгер Ви́бе Де́йкстра нидерландский
учёный, известный своими работами в области алгоритмики. Труды Де́йкстра
оказали влияние на развитие информатики и информационных технологий; он
является одним из разработчиков концепции структурного программирования.
Следование
–
это основная алгоритмическая конструкция, которая показывает естественный,
последовательный порядок действий.
А
алгоритмы в которых применяется только структура «следование», называются линейными
алгоритмами.
Графически
алгоритмическую конструкцию «следование» изображают следующим образом:
Выполняемое
действие или процесс изображается с помощью прямоугольника. Сюда записываются
действия, которые необходимо выполнить при переходе на этот блок.
В
блок Процесс входит одна линяя связи и выходит одна линяя связи.
Количество
блоков процесс определяется количеством команд в алгоритме.
Давайте
вместе выполним алгоритм, представленный на блок-схеме.
Итак,
начало. Далее следует блок данных, который изображается с помощью
параллелограмма, он содержит исходные данные или в нём выведены результаты.
Нам
необходимо загадать число в диапазоне от 1 до 5. Загадаем, например, число 3.
теперь переходим к блоку процесс. Здесь нам нужно прибавить к задуманному –
число 20. Получаем 23. Следующее действие – нужно прибавить к полученному
числу, первоначально задуманное число. Получим 26.
Следующее
действие, нужно разделить полученное число на 2 и отнять от частного наше
задуманное число. Получим 10. Конец. Алгоритм выполнен.
Обратите
внимание, мы с вами выполняли команды один раз последовательно друг за другом.
То
есть, линейный алгоритм – это алгоритм, в котором команды выполняются в
порядке их записи, то есть последовательно друг за другом один раз.
Перейдём
к практической части урока.
Первое
задание составим линейный алгоритм для исполнителя Робот. Итак, робот находится
в клетке А, нужно перевести робота в клетку В и все отмеченные клетки
закрасить.
Системой
команд исполнителя робот являются четыре команды перемещения – это вверх, вниз,
влево и вправо. При выполнении данных команд робот перемещается на одну клетку
в выбранном направлении. По команде Закрасить робот закрасит клетку в которой
находится.
Итак,
начинаем выполнение алгоритма с команды – «использовать робот». Далее
записываем имя алгоритма – «в клетку В».
Начало.
Выполним
наш алгоритм пошагово, с помощью пульта. На панели инструментов нажимаем кнопку
Робот пульт.
Итак,
смотрим на поле робота. Он находится в клетке А, которая отмечена, значит
первая команда будет закрасить.
Следующая
команда, вправо и снова клетка отмечена, значит необходимо выполнить команду
закрасить. И так далее, выполняем команды, пока не окажемся в клетке В.
Для
записи данного алгоритма мы использовали основную алгоритмическую конструкцию
Следование, так как все команды мы записали в естественном последовательном
порядке. А данный алгоритм будет линейным.
Рассмотрим
следующее задание.
Необходимо
записать команды для алгоритма, определяющего, сумму первой и последней цифры
заданного трёхзначного числа.
Для
решения задачи достаточно найти число сотен и число единиц в заданном числе и
сложить их.
Чтобы
вычислить количество единиц, необходимо исходное число разделить на 10 и взять
остаток. Чтобы вычислить количество сотен, необходимо разделить исходное число
на 100 и взять целую часть.
В
алгоритмическом языке есть специальные операции:
Операция
деления нацело div. Целочисленное
деление отличается от обычной операции деления тем, что делит число нацело с
отбрасыванием остатка.
Результат
целочисленного деления равен нулю, если делимое меньше делителя. Например,
значением выражения 5 div 7=0.
Или
другой пример: переменной x:=67div10.
Здесь переменная x получит значение 6, то
есть 6 – это целая часть от деления числа 67 на 10.
И
операция остаток от деления mod.
Деление по модулю вычисляет остаток, полученный при выполнении целочисленного
деления.
Например,
переменной y:=65 mod
10. Здесь переменная y
получит значение 5, то есть 5 – это остаток от деления числа 65 на 10.
Значит
для решения нашей задачи нам нужно
Исполним
команды алгоритма для числа 468.
Рассмотрим
задачу: Дядя Фёдор, отправляясь в путешествие, заправил автомобиль на n
рублей. Цена 1 литра бензина — 35 рублей. В руководстве по эксплуатации
автомобиля он прочитал следующее: «Чтобы преодолеть расстояние в 100
километров, нужно 7 литров бензина». Через сколько километров пути Дяде Фёдору
необходимо будет дозаправить автомобиль если учесть, что он потратил на бензин
пятьсот рублей?
Нам
необходимо представить решение данной задачи в виде блок-схемы.
Пришло
время подвести итоги урока.
Для
записи любого алгоритма хватает трёх основных алгоритмических конструкций
(структур) – это следование, ветвление и повторение.
В
алгоритмическом языке есть специальные операции:
Операция
деления нацело div, с помощью данной
операции вычисляется целое частное.
И
операция остаток от деления mod,
с помощью этой операции вычисляется остаток.
- Уроки Информатики
- Информатика в старших классах
- Основы программирования
- Алгоритмы

Основано на учебнике Босовой Людмилы Леонидовны, infolike.narod.ru
Человеку в жизни и практической деятельности приходится решать множество различных задач. Решение каждой из них описывается своим алгоритмом, и разнообразие этих алгоритмов очень велико. Вместе с тем для записи любого алгоритма достаточно трёх основных алгоритмических конструкций (структур):
- следования,
- ветвления,
- повторения.
Следование
Следование — алгоритмическая конструкция, отображающая естественный, последовательный порядок действий. Алгоритмы, в которых используется только структура «следование», называются линейными алгоритмами.
Линейный алгоритм представляет собой набор команд, выполняемых последовательно друг за другом. Еще раз повторю, что линейным называется алгоритм, в котором все этапы решения задачи выполняются строго последовательно. Структура линейного алгоритма и его Графическое представление приведено на рисунке:
Пример 1. Линейный алгоритм приготовления отвара шиповника.
Обратите внимание, что многие из предписание того алгоритма могут потребовать детализации — представления виде некоторой совокупности более мелких предписаний.
Линейная структура самая простая, она означает, что действия должны выполняться (следовать) одно за другим, независимо ни от чего. Алгоритм нахождения суммы двух чисел – пример линейного алгоритма.
Пример 2. Некоторый исполнитель может выполнять над целыми числами кроме операций сложения, вычитания, умножения и деления ещё две операции: с помощью операции div вычисляется целое частное, с помощью операции mod — остаток.
Например
Покажем, как с помощью этих операций можно реализовать алгоритм работы кассира, выдающего покупателю сдачу (s) наименьшим количеством банкнот по 500 (k500), 100 (k100), 50 (k50) и 10 (k10) рублей.
1 2 3 4 5 6 7 |
k500:=s div 500 s:=s mod 500 k100:= s div 100 s:=s mod 100 k50:= s div 50 s:=s mod 50 k10:=s div 10 |
В качестве практического занятия вы можете попробовать восстановить последовательность указанных команд на графическом языке программирования Blockly
Все статьи раздела
- Коменты VK
- Анонимные коменты, G+ или Facebook
Информатика, 11 класс. Урок № 2.
Тема — Базовые алгоритмические структуры
Перечень вопросов, рассматриваемых в теме: алгоритм, блок-схема, следование, линейный алгоритм, ветвление, полная форма ветвления, неполная форма ветвления, разветвляющийся алгоритм, повторение, циклический алгоритм, цикл с предусловием, цикл с постусловием, цикл с параметром, комбинации базовых алгоритмических структур
Глоссарий по теме: следование, ветвление, повторение, цикл с предусловием, цикл с постусловием, цикл с параметром.
Основная литература по теме урока:
Л. Л. Босова, А. Ю. Босова. Информатика. Базовый уровень: учебник для 11 класса
— М.: БИНОМ. Лаборатория знаний, 2017
Дополнительная литература по теме урока:
И. Г. Семакин, Т. Ю. Шеина, Л. В. Шестакова. Информатика и ИКТ. Профильный уровень: учебник для 11 класса — М.: БИНОМ. Лаборатория знаний, 2012
Теоретический материал для самостоятельного изучения
В 1969 году нидерландский ученый Эдсгер Дийкстра доказал важную теорему. Суть ее в том, что для решения любой логической задачи можно составить алгоритм, используя лишь три алгоритмических структуры: следование, ветвление и повторение. Эти структуры называют базовыми.
Самой простой структурой является «следование».
Алгоритм реализован через последовательную алгоритмическую структуру, если все команды этого алгоритма выполняются один раз, причем в том порядке, в котором они записаны.
Алгоритм, основанный на конструкции «следование» называется линейным алгоритмом. Примером такого алгоритма может служить алгоритм вычисления дискриминанта квадратного уравнения, блок-схема которого приведена на рисунке 1.
Рис. 1
Следующей конструкцией является «ветвление». Она встречается, если действия алгоритма зависят от некоторого условия.
Алгоритм реализован через алгоритмическую конструкцию «ветвление», если от входных данных зависит, какие команды будут выполняться. Условие, которое выражает эту зависимость, фактически является вопросом, на который можно ответить либо «да», либо «нет».
Существуют полная и неполная формы ветвления.
В полной форме если условие выполняется, то алгоритм переходит к выполнению первой серии команд, а если не выполняется — то ко второй.
В неполной форме алгоритм выполняет серию команд только если условие истинно. В противном случае ничего не происходит.
Алгоритм, основанный на конструкции «ветвление» называется разветвляющимся алгоритмом. Примером такого алгоритма может служить алгоритм нахождения корней квадратного уравнения, блок-схема которого приведена на рисунке 2.
Рис. 2
И, наконец, последняя алгоритмическая конструкция — «повторение».
Алгоритм реализован с использованием алгоритмической конструкции «повторение», если некая группа подряд идущих шагов алгоритма (она называется телом цикла) может выполняться многократно в зависимости от входных данных.
Алгоритм, содержащий конструкцию «повторение» называется циклическим алгоритмом.
Существует несколько разновидностей циклических алгоритмов.
Первый — цикл с заданным условием продолжения работы (цикл с предусловием или цикл-пока).
Второй — цикл с заданным условием окончания работы (цикл с постусловием или цикл-до).
И третий — цикл с заданным числом повторений (цикл с параметром).
Доказано, что при решении задач можно ограничиться только одним циклом — циклом с предусловием. Но в ряде случаев цикл с постусловием или цикл с параметром делают решение задачи легче.
Примером решения одной и той же задачи с помощью различных циклов может служить задача возведения некоторого числа a в натуральную степень n.
Для логических переменных в С++ определены логические операции !, &&, ||, соответствующие операциям НЕ, И, ИЛИ, выполняемым над высказываниями.
Логические выражения, в которых наряду с простыми условиями (сравнениями) используются логические операции, называют составными условиями.
Приведем таблицу истинности для логических операций.
|
Логическая переменная |
Результат операции |
|||
| A | B | !(A) | A && B | A || B |
| true | true | false | true | true |
| false | true | true | false | true |
| true | false | false | false | true |
| false | false | true | false | false |
В логических выражениях могут встречаться как арифметические, так и логические операции. Порядок выполнения операций определяется их приоритетом [1]:
1. !;
2. *, /, %;
3/ +, –;
4. <, >, <=, >=
5. ==, !=;
6. &&;
7. ||.
Операции с одинаковым приоритетом выполняются по порядку, слева направо. Для изменения порядка выполнения операций применяют скобки (примеры 3.3 и 3.4).
При составлении программ часто нужно строить отрицания сложным логическим выражениям. Для этого полезно использовать тождества, известные из алгебры логики (пример 3.5) и следующую таблицу:
|
Условие |
Противоположное условие (отрицание условия) |
|
a < b |
a >= b |
|
a > b |
a <= b |
|
a == b |
a != b |
Пример 3.6. Написать программу, которая выдаст на экран значение true или false в зависимости от того, находится ли число B между числами A и C.
Этапы выполнения задания
I. Исходные данные: переменные a, b, c (вводимые числа).
II. Результат: rez (true или false).
III. Алгоритм решения задачи.
1. Ввод исходных данных.
2. Вычисление значения логической переменной. Рассмотрим два случая:
2.1. Верно неравенство: а < b < c. Этому неравенству соответствует логическое выражение: а < b && b < с. Присвоим переменной r1 значение этого выражения.
2.2. Верно неравенство: а > b > c. Этому неравенству соответствует логическое выражение: а > b && b > с. Присвоим переменной r2 значение этого выражения.
2.3. Ответом на задачу будет значение логического выражения r1 or r2.
3. Вывод результата.
IV. Описание переменных: a, b, c – int, r1, r2, rez – bool.
[1] Обратите внимание, что приоритет операций отличается от того, который принят в Pascal (http://informatika8.adu.by/#fif2-2).
Пример 3.3. Определение порядка действий для выражения:
a || c < b && d
Первым выполняется сравнение c и b, затем логическая операция &&, потом — ||.
Пример 3.4. Рассмотрим выражение:
(a < b) && (c < d)
Здесь скобки определяют приоритет выполнения операций: т. е. сначала должны выполниться сравнения, а затем —логическая операция &&. Однако в С++ операции сравнения обладают более высоким приоритетом, чем логические операции (в отличие от Pascal), поэтому приведенная выше запись эквивалентна:
a < b && c < d
Пример 3.5. Построение отрицаний:
!!a Û a;
!(a && b) Û !a || !b;
!(a || b) Û !a && !b.
Рассмотрим выражение !a > b с переменными а и b типа int. Здесь операция ! относится к переменной a. Поскольку целые могут рассматриваться как логические, то отрицанием любого числа, кроме нуля, будет 0, отрицанием нуля будет 1. Затем полученный результат (0 или 1) сравнится с числом b. Для отрицания сравнения выражение нужно записать так: !(a > b).
В языке С++ используются значки «&» и «|». Этими значками обозначаются битовые операции над целыми числами. Значок «&» соответствует операции and (И), проводимой над двоичными разрядами числа, а значок «|» — операции or (ИЛИ). Кроме этих операций, над битами числа можно выполнять операции «~» not (инверсия) и «^» xor (исключающее ИЛИ, сложение по модулю 2).
Пример 3.6.
V. Программа:
#include <iostream>
using namespace std;
int main()
{
int a, b, c;
cout << “vvedi 3 chisla” << endl;
cin >> a >> b >> c;
bool r1 = a < b && b < c;
bool r2 = a > b && b > c;
bool rez = r1 || r2;
cout << boolalpha;
cout << “b mezdu a i c – “;
cout << rez << endl;
return 0;
}
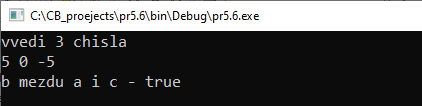
VI. Тестирование.
Запустить программу и ввести значения а = 5, b = 0, c = –5. Результат:
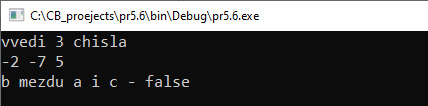
Запустить программу и ввести значения a = –2, b = –7, с = 5. Результат:
VII. Анализ результатов. Для полного тестирования программы нужно проверить все 6 возможных случаев взаимного расположения a, b, c.
В программировании на С++ могут использоваться диграфы (англ. digraphs) — последовательности из двух или более символов, которые компилятор воспринимает как один (или более символов). Они созданы и используются для ввода символов, отсутствующих на клавиатуре или в кодировке. К диграфам относят слова and и or, которые эквивалентны && и ||.