JavaScript, Node.JS
Рекомендация: подборка платных и бесплатных курсов таргетированной рекламе – https://katalog-kursov.ru/
Вы когда-нибудь задумывались, как работает Math.random()? Что такое случайное число и как оно получается? А представьте вопрос на собеседовании?—?напишите свой генератор случайных чисел в пару строк кода. И так, что же это такое, случайность и возможно ли ее предсказать?
Меня очень увлекают различные IT головоломки и задачки и генератор случайных чисел — одна из таких задачек. Обычно в своем телеграм канале я разбираю всякие головоломки и разные задачи с собеседований. Задача про генератор случайных чисел набрала большую популярность и мне захотелось увековечить ее в недрах одного из авторитетных источников информации — то бишь здесь, на Хабре.
Данный материал будет полезен всем тем фронтендерам и Node.js разработчикам, кто на острие технологий и хочет попасть в блокчейн проект/стартап, где вопросы про безопасность и криптографию, хотя бы на базовом уровне, спрашивают даже у фронтендеров.
Генератор псевдослучайных чисел и генератор случайных чисел
Для того, чтобы получить что-то случайное, нам нужен источник энтропии, источник некого хаоса из который мы будем использовать для генерации случайности.
Этот источник используется для накопления энтропии с последующим получением из неё начального значения (initial value, seed), которое необходимо генераторам случайных чисел (ГСЧ) для формирования случайных чисел.
Генератор ПсевдоСлучайных Чисел использует единственное начальное значение, откуда и следует его псевдослучайность, в то время как Генератор Случайных Чисел всегда формирует случайное число, имея в начале высококачественную случайную величину, которая берется из различных источников энтропии.
Энтропия?—?это мера беспорядка. Информационная энтропия?—?мера неопределённости или непредсказуемости информации.
Выходит, что чтобы создать псевдослучайную последовательность нам нужен алгоритм, который будет генерить некоторую последовательность на основании определенной формулы. Но такую последовательность можно будет предсказать. Тем не менее, давайте пофантазируем, как бы могли написать свой генератор случайных чисел, если бы у нас не было Math.random()
ГПСЧ имеет некоторый алгоритм, который можно воспроизвести.
ГСЧ?—?это получение чисел полностью из какого либо шума, возможность просчитать который стремится к нулю. При этом в ГСЧ есть определенные алгоритмы для выравнивания распределения.
Придумываем свой алгоритм ГПСЧ
Генератор псевдослучайных чисел (ГПСЧ, англ. pseudorandom number generator, PRNG)?—?алгоритм, порождающий последовательность чисел, элементы которой почти независимы друг от друга и подчиняются заданному распределению (обычно равномерному).
Мы можем взять последовательность каких-то чисел и брать от них модуль числа. Самый простой пример, который приходит в голову. Нам нужно подумать, какую последовательность взять и модуль от чего. Если просто в лоб от 0 до N и модуль 2, то получится генератор 1 и 0:
function* rand() {
const n = 100;
const mod = 2;
let i = 0;
while (true) {
yield i % mod;
if (i++ > n) i = 0;
}
}
let i = 0;
for (let x of rand()) {
if (i++ > 100) break;
console.log(x);
}
Эта функция генерит нам последовательность 01010101010101… и назвать ее даже псевдослучайной никак нельзя. Чтобы генератор был случайным, он должен проходить тест на следующий бит. Но у нас не стоит такой задачи. Тем не менее даже без всяких тестов мы можем предсказать следующую последовательность, значит такой алгоритм в лоб не подходит, но мы в нужном направлении.
А что если взять какую-то известную, но нелинейную последовательность, например число PI. А в качестве значения для модуля будем брать не 2, а что-то другое. Можно даже подумать на тему меняющегося значения модуля. Последовательность цифр в числе Pi считается случайной. Генератор может работать, используя числа Пи, начиная с какой-то неизвестной точки. Пример такого алгоритма, с последовательностью на базе PI и с изменяемым модулем:
const vector = [...Math.PI.toFixed(48).replace('.','')];
function* rand() {
for (let i=3; i<1000; i++) {
if (i > 99) i = 2;
for (let n=0; n<vector.length; n++) {
yield (vector[n] % i);
}
}
}
Но в JS число PI можно вывести только до 48 знака и не более. Поэтому предсказать такую последовательность все так же легко и каждый запуск такого генератора будет выдавать всегда одни и те же числа. Но наш генератор уже стал показывать числа от 0 до 9.
Мы получили генератор чисел от 0 до 9, но распределение очень неравномерное и каждый раз он будет генерировать одну и ту же последовательность.
Мы можем взять не число Pi, а время в числовом представлении и это число рассматривать как последовательность цифр, причем для того, чтобы каждый раз последовательность не повторялась, мы будем считывать ее с конца. Итого наш алгоритм нашего ГПСЧ будет выглядеть так:
function* rand() {
let newNumVector = () => [...(+new Date)+''].reverse();
let vector = newNumVector();
let i=2;
while (true) {
if (i++ > 99) i = 2;
let n=-1;
while (++n < vector.length) yield (vector[n] % i);
vector = newNumVector();
}
}
// TEST:
let i = 0;
for (let x of rand()) {
if (i++ > 100) break;
console.log(x)
}
Вот это уже похоже на генератор псевдослучайных чисел. И тот же Math.random()?—?это ГПСЧ, про него мы поговорим чуть позже. При этом у нас каждый раз первое число получается разным.
Собственно на этих простых примерах можно понять как работают более сложные генераторы случайных числе. И есть даже готовые алгоритмы. Для примера разберем один из них?—?это Линейный конгруэнтный ГПСЧ(LCPRNG).
Линейный конгруэнтный ГПСЧ
Линейный конгруэнтный ГПСЧ(LCPRNG)?—?это распространённый метод для генерации псевдослучайных чисел. Он не обладает криптографической стойкостью. Этот метод заключается в вычислении членов линейной рекуррентной последовательности по модулю некоторого натурального числа m, задаваемой формулой. Получаемая последовательность зависит от выбора стартового числа?—?т.е. seed. При разных значениях seed получаются различные последовательности случайных чисел. Пример реализации такого алгоритма на JavaScript:
const a = 45;
const c = 21;
const m = 67;
var seed = 2;
const rand = () => seed = (a * seed + c) % m;
for(let i=0; i<30; i++)
console.log( rand() )
Многие языки программирования используют LСPRNG (но не именно такой алгоритм(!)).
Как говорилось выше, такую последовательность можно предсказать. Так зачем нам ГПСЧ? Если говорить про безопасность, то ГПСЧ?—?это проблема. Если говорить про другие задачи, то эти свойства?—?могут сыграть в плюс. Например для различных спец эффектов и анимаций графики может понадобиться частый вызов random. И вот тут важны распределение значений и перформанс! Секурные алгоритмы не могут похвастать скоростью работы.
Еще одно свойство?—?воспроизводимость. Некоторые реализации позволяют задать seed, и это очень полезно, если последовательность должна повторяться. Воспроизведение нужно в тестах, например. И еще много других вещей существует, для которых не нужен безопасный ГСЧ.
Как устроен Math.random()
Метод Math.random() возвращает псевдослучайное число с плавающей запятой из диапазона [0, 1), то есть, от 0 (включительно) до 1 (но не включая 1), которое затем можно отмасштабировать до нужного диапазона. Реализация сама выбирает начальное зерно для алгоритма генерации случайных чисел; оно не может быть выбрано или сброшено пользователем.
Как устроен алгоритм Math.random()?—?интересный вопрос. До недавнего времени, а именно до 49 Chrome использовался алгоритм MWC1616:
uint32_t state0 = 1;
uint32_t state1 = 2;
uint32_t mwc1616() {
state0 = 18030 * (state0 & 0xffff) + (state0 >> 16);
state1 = 30903 * (state1 & 0xffff) + (state1 >> 16);
return (state0 << 16) + (state1 & 0xffff);
}Именно этот алгоритм генерит нам последовательность псевдослучайных чисел в промежутке между 0 и 1.
Предсказываем Math.random()
Чем это было чревато? Есть такой квест: alf.nu/ReturnTrue
В нем есть задача:
{
let rand = Math.random();
function random4(x) {
return rand === x;
}
}
random4(???)
Что нужно вписать вместо вопросов, чтобы функция вернула true? Кажется что это невозможно. Но, это возможно, если вы заглядывали в спеку и видели алгоритм ГПСЧ V8. Решение этой задачи в свое время мне показал Роман Дворнов:
random4(function(){var A=18030,B=36969,F=65535,Z=16,M=Math,I=M.imul,c=M.random,M=M.pow(2,32),k,d,g=c()*M,h=c()*M;for(k=0;F^k&&(c=I(A,g>>>Z)+k++)&F^h>>>Z;);for(k=0;F^k&&(d=I(B,g&F)+k++)&F^h&F;);for(k=2;k—;g=c<<Z|d&F)c=c/A|c%A<<Z,d=d/B|d%B<<Z;return(g<0?g+M:g)/M}())
Этот код работал в 70% случаев для Chrome < 49 и Node.js < 5. Рома Дворнов, как всегда, показал чудеса магии, которая не что иное, как глубокое понимание внутренних механизмов браузеров. Я все жду, когда Роман сделает доклад на основе этих событий или напишет более подробную статью.
Что здесь происходит? Все дело в том, что алгоритм можно предсказать. Чтобы это было нагляднее, можно сгенерировать картинку случайных пикселей. На сайте есть такой генератор. Вот что было, когда в браузере был алгоритм MWC1616:
Видите эти равномерности на левом слайде? Изображение показывает проблему с распределением значений. На картинке слева видно, что значения местами сильно группируются, а местами выпадают большие фрагменты. Как следствие?—?числа можно предсказать.
Выходит что мы можем отреверсить Math.random() и предсказать, какое было загадано число на основе того, что получили в данный момент времени. Для этого получаем два значения через Math.random(). Затем вычисляем внутреннее состояние по этим значениям. Имея внутреннее состояние можем предсказывать следующие значения Math.random() при этом не меняя внутреннее состояние. Меняем код так так, чтобы вместо следующего возвращалось предыдущее значение. Собственно все это и описано в коде-решении для задачи random4. Но потом алгоритм изменили (подробности читайте в спеке). Его можно будет сломать, как только у нас в JS появится нормальная работа с 64 битными числами. Но это уже будет другая история.
Новый алгоритм выглядит так:
uint64_t state0 = 1;
uint64_t state1 = 2;
uint64_t xorshift128plus() {
uint64_t s1 = state0;
uint64_t s0 = state1;
state0 = s0;
s1 ^= s1 << 23;
s1 ^= s1 >> 17;
s1 ^= s0;
s1 ^= s0 >> 26;
state1 = s1;
return state0 + state1;
}
Его все так же можно будет просчитать и предсказать. Но пока у нас нет “длинной математики” в JS. Можно попробовать через TypedArray сделать или использовать специальные библиотеки. Возможно кто-то однажды снова напишет предсказатель. Возможно это будешь ты, читатель. Кто знает 😉
Сrypto Random Values
Метод Math.random() не предоставляет криптографически стойкие случайные числа. Не используйте его ни для чего, связанного с безопасностью. Вместо него используйте Web Crypto API (API криптографии в вебе) и более точный метод window.crypto.getRandomValues().
Пример генерации случайного числа:
let [rvalue] = crypto.getRandomValues(new Uint8Array(1));
console.log( rvalue )
Но, в отличие от ГПСЧ Math.random(), этот метод очень ресурсоемкий. Дело в том, что данный генератор использует системные вызовы в ОС, чтобы получить доступ к источникам энтропии (мак адрес, цпу, температуре, etc…).
Алгоритмы рандома
Время на прочтение
5 мин
Количество просмотров 60K
В этой статье вы увидите самые разнообразные
велосипеды
алгоритмы для генерации случайных чисел.
Про что статья
Про алгоритмы генерирующие псевдослучайные числа, которые отличаются между собой качеством результата и скоростью исполнения. Статья будет полезна тем, кто хочет получить высокопроизводительную генерацию чисел в своих программах или разработчикам софта для микроконтроллеров и старых платформ по типу ZX Spectrum или MSX.
C++ rand
Первое что узнаёт начинающий программист С++ по теме получения рандома — функция rand, которая генерирует случайное число в пределах от 0 и RAND_MAX. Константа RAND_MAX описана в файле stdlib.h и равна 32’767, но этом может быть не так, например в Linux (см. коммент). Если же rand() в вашем компиляторе генерирует числа в пределах 32’767 (0x7FFF) и вы хотите получить случайное число большого размера, то код ниже можно рассматривать как вариант решения этой проблемы:
int64_t A = rand();
A <<= 15; // сдвиг на 15, так как 7FFF покрывает 15 бит
A |= rand();
A <<= 15;
A |= rand();
A <<= 15;
A |= rand();
A <<= 3;
A |= rand() & 0b111; // дополнительные 3 случайных бита
Реализация функции rand в старом C была проста и имела следующий вид:
static unsigned long int next = 1;
int rand()
{
next = next * 1103515245 + 12345;
return (unsigned int)(next / 65536) % 32768;
}
Данная реализация имела не очень хорошее распределение чисел и ныне в C++ улучшена. Так же стандартная библиотека C++ предлагает дополнительные способы получения случайного числа, о которых ниже.
С++11 STL random
Данный сорт рандома появился в C++11 и представляет из себя следующий набор классов: minstd_rand, mt19937, ranlux, knuth_b и разные их вариации.
Чтобы последовательность случайных чисел не повторялась при каждом запуске программы, задают «зерно» псевдослучайного генератора в виде текущего времени или, в случае с некоторыми ретро (и не только) играми — интервалы между нажатиями клавиш с клавиатуры/джойстика. Библиотека random же предлагает использовать std::random_device для получения зерна лучше чем от time(NULL), однако в случае с компилятором MinGW в Windows функция практически не работает так как надо. До сих пор…
// пример, как это использовать:
#include <random>
#include <ctime>
std::mt19937 engine; // mt19937 как один из вариантов
engine.seed(std::time(nullptr));
/*
на случай, если у вас UNIX-чё-то или компилятор не MinGW
std::random_device device;
engine.seed(device());
*/
int val = engine(); // так получать рандом
Некоторые из алгоритмов в STL random могут работать быстрее чем rand(), но давать менее качественную последовательность случайных чисел.
PRNG — Pseudo-random Numbers Generator
Можете считать это название — синонимом линейного конгруэнтного метода. PRNG алгоритмы похожи на реализацию rand в C и отличаются лишь константами.
unsigned PRNG()
{
static unsigned seed = 1; // зерно не должно быть 0
seed = (seed * 73129 + 95121) % 100000;
return seed;
}
PRNG алгоритмы быстро работают и легки в реализации на многих языках, но не обладают большим периодом.
XorShift
Алгоритм имеющий множество вариаций отличающихся друг от друга периодом и используемыми регистрами. Подробности и разновидности XorShift’а можете посмотреть на Википедии или Хабре. Приведу один из вариантов с последовательностью 2 в 128-й степени.
struct seed_t
{
unsigned x = 1; // начальные значения могут быть любыми
unsigned y = 123;
unsigned z = 456;
unsigned w = 768;
};
unsigned XorShift128()
{
static seed_t s;
unsigned t = s.x^(s.x<<11);
s.x = s.y;
s.y = s.z;
s.z = s.w;
s.w = (s.w^(s.w>>19)) ^ (t^(t>>8));
return s.w;
}
Данный генератор очень хорош тем, что в нём вообще нет операций деления и умножения — это может быть полезно на процессорах и микроконтроллерах в которых нету ассемблерных инструкций деления/умножения (PIC16, Z80, 6502).
8-bit рандом в эмуляторе z26
Z26 это эмулятор старенькой приставки Atari2600, в коде которого можно обнаружить рандом ориентированный на работу с 1-байтовыми регистрами.
// P2_sreg - static uint8_t
void P2_Read_Random()
{
P2_sreg =
(((((P2_sreg & 0x80) >> 7) ^
((P2_sreg & 0x20) >> 5)) ^
(((P2_sreg & 0x10) >> 4) ^
((P2_sreg & 0x08) >> 3))) ^ 1) |
(P2_sreg << 1);
DataBus = P2_sreg;
}
Однажды мне пришлось сделать реализацию этого алгоритма для z80:
Ассемблерный код
; рандом с эмулятора z26
; a - output
; rdseed - 1 байт зерно
randz26:
exx
ld a,(rdseed)
and 20h
sra a
sra a
sra a
sra a
sra a
ld h, a
ld a,(rdseed)
and 80h
sra a
sra a
sra a
sra a
sra a
sra a
sra a
xor h
ld l, h
ld a,(rdseed)
and 08h
sra a
sra a
sra a
ld h, a
ld a,(rdseed)
and 10h
sra a
sra a
sra a
sra a
xor h
ld h, a
ld a, l
xor h
xor 1
ld h, a
ld a,(rdseed)
sla a
or h
ld (rdseed),a
exx
ret
Компактный рандом для Z80 от Joe Wingbermuehle
Если вам интересно написание программ под машины с зилогом, то представляю вашему вниманию алгоритм от Joe Wingbermuehle (работает только на зилоге):
; By Joe Wingbermuehle
; a res 1 byte - out val
; rdseed res 1 byte - need for rand. != 0
rand8:
exx
ld hl,(rdseed)
ld a,r
ld d,a
ld e,(hl)
add hl,de
add a,l
xor h
ld (rdseed),hl
exx
ret
Генератор рандома в DOOM
В исходниках игры Дум есть такой интересный файл под названием m_random.c (см. код), в котором описана функция «табличного» рандома, то есть там вообще нет никаких формул и магии с битовыми сдвигами.
Приведу более компактный код наглядно показывающий работу этой функции.
const uint8_t random_map[] =
{
4, 1, 63, 3,
64, 22, 54, 2,
0, 52, 75, 34,
89, 100, 23, 84
};
uint8_t get_random()
{
static uint8_t index = 0;
index = (index + 1) & 0xF; // 0xF, потому что столько значений в random_map
return random_map[index];
}
Варик для z80
; табличный рандом (как в DOOM)
; rand_table - ссылка на начало массива. Желательно подключить
; бинарный файл размера 256 байт со случайными цифрами.
; a - output num
randtab:
exx
; index
ld a, (rdseed)
inc a
;and filter ; for crop array index
ld (rdseed), a
; calc array address
ld hl, rand_table
ld d, 0
ld e, a
add hl, de
ld a, (hl) ; get num from arr
exx
ret
Конечно же это ни какой не рандом и последовательность случайных чисел легко предугадать даже на уровне интуиции в процессе игры, но работает всё это крайне быстро. Если вам не особо важна криптографическая стойкость и вы хотите что-то быстро генерирующее «типа-рандом», то эта функция для вас. Кстати в Quake3 рандом выглядит просто — rand()&0x7FFF.
RDRAND
Некоторые современные процессоры способны генерировать случайные числа с помощью одной ассемблерной команды — RDRAND. Для использования этой функции в C++ вы можете вручную прописать нужные инструкции ассемблерными вставками или же в GCC подключить файл immintrin.h и выбрать любую из вариаций функции _rdrandXX_step, где XX означает число бит в регистре и может быть равно 16, 32 или 64.
#include <immintrin.h>
unsigned val;
_rdrand32_step(&val);
Если вы увидите ошибку компиляции, то это значит, что вы не включили флаг -mrdrnd или ваш компилятор/процессор не поддерживает эту инструцию. Возможно это самый быстрый генератор случайных чисел, но есть вопросы в его криптографической стойкости, так что думайте.
Концовка
Класс std::minstd_rand из библиотеки STL random работает быстрее обыкновенного rand() и может стать его альтернативной заменой, если вас не особо волнует длинна периода в minstd. Возможны различия в работе этих функций в Windows и Unix’ах.
Инфа по теме
- Статья рассказывающая о C++11 random и некоторых особенностях работы с ним: Генерация случайных чисел в Modern C++
- Какие вообще есть генераторы в STL random. ссыль
- Вики статья про XorShift с разными реализациями: тык
- Гит эмулятора z26. Код рандома в файле c_pitfall2.c: гит
- Генератор рандома в Думчике: гит
P.S. Моя первая статья. Напишите что лишнее, чего добавить/убавить
Теги: c++, генератор случайных чисел, генерация пвседослучайных чисел, гсч, гспч, srand(), rand()
Возможность генерации случайных чисел необходима для работы некоторых программ, например, игр или приложений научно-статистического моделирования. В игре без рандомных событий монстры будут атаковать вас одинаково, вы будете постоянно находить одни и те же артефакты и т. д. Именно поэтому уметь генерировать случайные числа — обязанность любого программиста.
Случайные и псевдослучайные числа. В чём разница?
В реальной жизни, чтобы получить случайный результат мы кидаем кости или тасуем колоду карт. Итог будет зависеть от множества физических переменных (силы тяжести, трения, сопротивления воздуха, мастерства игрока и т. п.). Во многих смыслах мы действительно получаем случайный результат, ведь спрогнозировать его почти невозможно.
У компьютеров всё иначе. Они находятся в строго контролируемом цифровом мире, где существуют лишь два значения: правда и ложь. Именно поэтому ПК изначально создан для получения прогнозируемого результата. Следовательно, он неспособен генерировать случайные числа в полном смысле этого слова. Однако компьютер может имитировать случайность, а достигается это путём использования генераторов псевдослучайных чисел.
Что такое генератор случайных чисел?
Генератор случайных (псевдослучайных) чисел, он же ГСЧ (ГСПЧ) — это программа, принимающая начальное значение и выполняющая с этим значением ряд математических операций, что приводит к конвертации числа в другую цифру, отличную от стартовой. После этого программа применяет новое сгенерированное значение для дальнейших математических операций с последующей генерацией очередного числа, не связанного ни с первым, ни со вторым. И так далее. Таким образом, алгоритм генерирует ряд новых чисел, которые будут нам казаться действительно случайными.
Простой алгоритм случайных чисел
Написать простейший генератор случайных чисел несложно. Вот как выглядит программа на C++, которая позволяет генерировать 100 рандомных чисел:
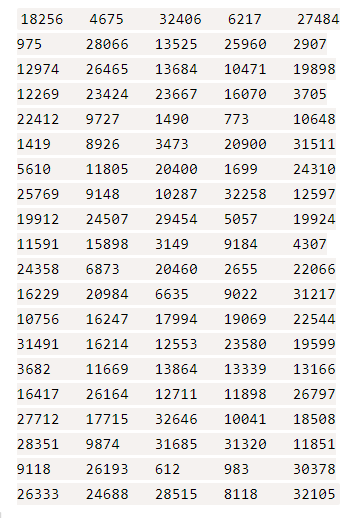
#include <iostream> unsigned int PRNG() { // Начальное число - 4 541 static unsigned int seed = 4541; // Берём начальное число и генерируем новое значение // Из-за применения очень больших чисел (и переполнения) угадать следующее число, исходя из предыдущего, довольно сложно seed = (8253729 * seed + 2396403); // Берём начальное число и возвращаем значение в диапазоне от 0 до 32 767 return seed % 32768; } int main() { // Выводим 100 случайных чисел for (int count=0; count < 100; ++count) { std::cout << PRNG() << "t"; // Если вывели 5 чисел, вставляем символ новой строки if ((count+1) % 5 == 0) std::cout << "n"; } }А вот результат:
Каждое число в этом ряду кажется нам случайным по отношению к предыдущему. Однако, говоря по правде, данный алгоритм достаточно примитивен.
Но зачем изобретать велосипед, когда для генерации у нас есть специальные функции?
Функции srand() и rand()
В языки программирования C и C++ встроены собственные генераторы случайных чисел. Реализованы они с помощью двух отдельных функций, которые находятся в заголовочном файле cstdlib:
1) srand(). Устанавливает значение, передаваемое пользователем, в качестве стартового. Вызывается лишь 1 раз: в начале программы (как правило, в верхней части функции main());2) rand(). Обеспечивает генерацию следующего случайного числа в имеющейся последовательности. Число будет находиться в промежутке от нуля до RAND_MAX (это константа в cstdlib, значение которой составляет 32 767).
Что такое случайность в компьютере? Как происходит генерация случайных чисел? В этой статье мы постарались дать простые ответы на эти вопросы.
В программном обеспечении, да и в технике в целом существует необходимость в воспроизводимой случайности: числа и картинки, которые кажутся случайными, на самом деле сгенерированы определённым алгоритмом. Это называется псевдослучайностью, и мы рассмотрим простые способы создания псевдослучайных чисел. В конце статьи мы сформулируем простую теорему для создания этих, казалось бы, случайных чисел.
Определение того, что именно является случайностью, может быть довольно сложной задачей. Существуют тесты (например, колмогоровская сложность), которые могут дать вам точное значение того, насколько случайна та или иная последовательность. Но мы не будем заморачиваться, а просто попробуем создать последовательность чисел, которые будут казаться несвязанными между собой.
Часто требуется не просто одно число, а несколько случайных чисел, генерируюемых непрерывно. Следовательно, учитывая начальное значение, нам нужно создать другие случайные числа. Это начальное значение называется семенем, и позже мы увидим, как его получить. А пока давайте сконцентрируемся на создании других случайных значений.
Создание случайных чисел из семени
Один из подходов может заключаться в том, чтобы применить какую-то безумную математическую формулу к семени, а затем исказить её настолько, что число на выходе будет казаться непредсказуемым, а после взять его как семя для следующей итерации. Вопрос только в том, как должна выглядеть эта функция искажения.
Давайте поэкспериментируем с этой идеей и посмотрим, куда она нас приведёт.
Функция искажения будет принимать одно значение, а возвращать другое. Назовём её R.
R(Input) -> Output
Начнём с того, что R – это простая функция, которая всего лишь прибавляет единицу.
R(x) = x + 1
Если значение нашего семени 1, то R создаст ряд 1, 2, 3, 4, … Выглядит совсем не случайно, но мы дойдём до этого. Пусть теперь R добавляет константу вместо 1.
R(x) = x + c
Если с равняется, например, 7, то мы получим ряд 1, 8, 15, 22, … Всё ещё не то. Очевидно, что мы упускаем то, что числа не должны только увеличиваться, они должны быть разбросаны по какому-то диапазону. Нам нужно, чтобы наша последовательность возвращалась в начало – круг из чисел!
Числовой круг
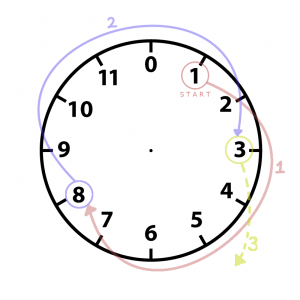
Посмотрим на циферблат часов: наш ряд начинается с 1 и идёт по кругу до 12. Но поскольку мы работаем с компьютером, пусть вместо 12 будет 0.
Теперь начиная с 1 снова будем прибавлять 7. Прогресс! Мы видим, что после 12 наш ряд начинает повторяться, независимо от того, с какого числа начать.
Здесь мы получаем очень важно свойство: если наш цикл состоит из n элементов, то максимальное число элементов, которые мы можем получить перед тем, как они начнут повторяться это n.
Теперь давайте переделаем функцию R так, чтобы она соответствовала нашей логике. Ограничить длину цикла можно с помощью оператора модуля или оператора остатка от деления.
R(x) = (x + c) % m
На этом этапе вы можете заметить, что некоторые числа не подходят для c. Если c = 4, и мы начали с 1, наша последовательность была бы 1, 5, 9, 1, 5, 9, 1, 5, 9, … что нам конечно же не подходит, потому что эта последовательность абсолютно не случайная. Становится понятно, что числа, которые мы выбираем для длины цикла и длины прыжка должны быть связаны особым образом.
Если вы попробуете несколько разных значений, то сможете увидеть одно свойство: m и с должны быть взаимно простыми.
До сих пор мы делали “прыжки” за счёт добавления, но что если использовать умножение? Умножим х на константу a.
R(x) = (ax + c) % m
Свойства, которым должно подчиняться а, чтобы образовался полный цикл, немного более специфичны. Чтобы создать верный цикл:
- (а – 1) должно делиться на все простые множители m
- (а – 1) должно делиться на 4, если m делится на 4
Эти свойства вместе с правилом, что m и с должны быть взаимно простыми составляют теорему Халла-Добелла. Мы не будем рассматривать её доказательство, но если бы вы взяли кучу разных значений для разных констант, то могли бы прийти к тому же выводу.
Выбор семени
Настало время поговорить о самом интересном: выборе первоначального семени. Мы могли бы сделать его константой. Это может пригодиться в тех случаях, когда вам нужны случайные числа, но при этом нужно, чтобы при каждом запуске программы они были одинаковые. Например, создание одинаковой карты для каждой игры.
Еще один способ – это получать семя из нового источника каждый раз при запуске программы, как в системных часах. Это пригодится в случае, когда нужно общее рандомное число, как в программе с бросанием кубика.
Конечный результат
Когда мы применяем функцию к её результату несколько раз, мы получаем рекуррентное соотношение. Давайте запишем нашу формулу с использованием рекурсии:
x(n) = (a * x(n - 1) + c) % m
Где начальное значение х – это семя, а – множитель, с – константа, m – оператор остатка от деления.
То, что мы сделали, называется линейным конгруэнтным методом. Он очень часто используется, потому что он прост в реализации и вычисления выполняются быстро.
В разных языках программирования реализация линейного конгруэнтного метода отличается, то есть меняются значения констант. Например, функция случайных чисел в libc (стандартная библиотека С для Linux) использует m = 2 ^ 32, a = 1664525 и c = 1013904223. Такие компиляторы, как gcc, обычно используют эти значения.
Заключительные замечания
Существуют и другие алгоритмы генерации случайных чисел, но линейный конгруэнтный метод считается классическим и лёгким для понимания. Если вы хотите глубже изучить данную тему, то обратите внимание на книгу Random Numbers Generators, в которой приведены элегантные доказательства линейного конгруэнтного метода.
Генерация случайных чисел имеет множество приложений в области информатики и особенно важна для криптографии.
На этом всё, спасибо что прочитали!
Оригинал статьи
В статье вы узнаете, как использовать std.random и чем он хорош
Содержание
В 2011 году новый стандарт C++11 добавил в язык заголовок <random>, в котором описаны средства для работы со случайными числами на профессиональном уровне. Эти средства заменяют функцию rand и дают гораздо больше гибкости.
Но чтобы этим воспользоваться, надо немного разбираться в теории.
Почему в IT все числа неслучайные
Казалось бы, что мешает использовать в программах случайные числа? К сожалению, процессор на это не способен: его поведение строго детерминировано и не допускает никаких случайностей.
- Для генерации по-настоящему случайных, ничем не связанных чисел операционной системе приходится использовать средства, недоступные обычным приложениям; такие случайные числа называются криптографически стойкими случайными числами
- Генерация системой таких случайных чисел работает медленно, и при нехватке скорости система просто отдаёт приложениями псевдослучайные числа либо заставляет их ожидать, пока появится возможность вернуть случайное число
Вы можете узнать об этом подробнее, прочитав о разнице между устройствами
/dev/randomи/dev/urandomв ОС Linux
Pseudo-random Numbers Generator (PRNG)
Генератор псевдослучайных чисел (PRNG) – это алгоритм генерации последовательности чисел, похожих на случайные числа. Псевдослучайные числа не являются по-настоящему случайные, т.е. между ними остаются связывающие их закономерности.
Общий принцип генерации легко показать в примере:
#include <iostream>
int main()
{
unsigned value = 18;
// Порождаем и выводим 20 чисел, используя число 18 как зерно
for (int i = 0; i < 20; ++i)
{
// Итеративно вычисляем новое значение value.
value = (value * 73129 + 95121) % 100000;
std::cout << value << std::endl;
}
}
Несложная итеративная формула, содержащая умножение, сложение и деление по остатку на разные константы, создаёт целую серию чисел, похожих на случайные:
11443
10268
83693
13222
6759
74032
13953
64058
25307
70724
3221
43630
13391
65560
65065
66210
98915
82860
96765
55510
Очевидно, что между числами есть взаимосвязь: они вычислены по одной и той же формуле. Но для пользователя видимой взаимосвязи нет.
Время как источник случайности
Если вы запустите предыдущую программу несколько раз, вы обнаружите проблему: числа будут те же самые. Причина проста – в начале последовательности мы используем всегда одно и то же число, 18. Для последовательности это число является зерном (англ. seed), и чтобы последовательность менялась с каждым запуском, зерно должно быть случайным.
Простейший, но не самый лучший способ получения зерна: взять текущее календарное время в секундах. Для этой цели мы воспользуемся функцией std::time_t time(std::time_t* arg).
Функция std::time возвращает число, представляющее время, прошедшее с полуночи 1 января 1970 года. Обычно это время в секундах, также известное как UNIX Timestamp. Параметр
argможно игнорировать и передавать нулевой указатель (вы можете в этом убедиться, прочитав документацию).
#include <iostream>
#include <ctime>
int main()
{
unsigned value = unsigned(std::time(nullptr));
// Порождаем и выводим 20 чисел, используя время UNIX как зерно.
for (int i = 0; i < 20; ++i)
{
value = (value * 73129 + 95121) % 100000;
std::cout << value << std::endl;
}
}
Теперь программа при каждом запуске будет выводить разные цепочки псевдослучайных чисел. При условии, что вы запускаете её не чаще одного раза в секунду.
Такие случайные числа далеко не идеальны: например, их нельзя использовать в криптографии, потому что злоумышленник может примерно оценить, в каком промежутке времени были созданы случайные числа, и сильно сократить затраты на дешифровку сообщения. В разработке простых учебных приложений такие числа вполне подходят
Ограничение числа по диапазону
Ограничить числа по диапазону можно путём деления по остатку (что сократит длину входного диапазона) и добавления нижней границы диапазона:
#include <iostream>
#include <ctime>
#include <cassert>
// Структура генератора псевдослучайных чисел хранит одно число,
// зерно следующего случайного числа.
struct PRNG
{
unsigned seed = 0;
};
void initGenerator(PRNG& generator)
{
// Получаем случайное зерно последовательности
generator.seed = unsigned(std::time(nullptr));
}
// Генерирует число на отрезке [minValue, maxValue].
unsigned random(PRNG& generator, unsigned minValue, unsigned maxValue)
{
// Проверяем корректность аргументов
assert(minValue < maxValue);
// Итеративно изменяем текущее число в генераторе
generator.seed = (generator.seed * 73129 + 95121);
// Приводим число к отрезку [minValue, maxValue]
return (generator.seed % (maxValue + 1 - minValue)) + minValue;
}
int main()
{
PRNG generator;
initGenerator(generator);
// Порождаем и выводим 10 чисел на отрезке [0, 7].
std::cout << "ten numbers in range [0, 7]:" << std::endl;
for (int i = 0; i < 10; ++i)
{
std::cout << random(generator, 0, 7) << std::endl;
}
// Порождаем и выводим 10 чисел на отрезке [10, 20].
std::cout << "ten numbers in range [10, 20]:" << std::endl;
for (int i = 0; i < 10; ++i)
{
std::cout << random(generator, 10, 20) << std::endl;
}
}
Всё то же, только лучше: заголовок <random>
Заголовок random разделяет генерацию псевдослучайных чисел на 3 части и предоставляет три инструмента:
- класс std::random_device, который запрашивает у операционной системы почти случайное целое число; этот класс более удачные зёрна, чем если брать текущее время
- класс std::mt19937 и другие классы псевдо-случайных генераторов, задача которых – размножить одно зерно в целую последовательность чисел
- класс std::uniform_int_distribution и другие классы распределений
Класс mt19937 реализует алгоритм размножения псевдослучайных чисел, известный как Вихрь Мерсенна. Этот алгоритм работает быстро и даёт хорошие результаты – гораздо более “случайные”, чем наш самописный метод, показанный ранее.
О распределениях скажем подробнее:
- линейное распределение вероятностей (uniform distribution) возникает, когда вероятность появления каждого из допустимых чисел одинакова, т.е. каждое число может появиться с равным шансом
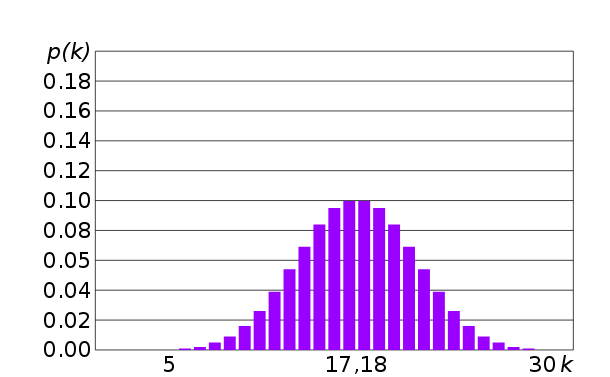
- в некоторых прикладных задачах нужны другие распределения, в которых одни числа появляются чаще других – например, часто используется нормальное распределение (normal distribution)
В большинстве случаев вам подойдёт линейное распределение. Изредка пригодится нормальное, в котором вероятность появления числе тем ниже, чем дальше оно от среднего значения:
Теперь мы можем переписать
#include <iostream>
#include <random>
#include <cassert>
struct PRNG
{
std::mt19937 engine;
};
void initGenerator(PRNG& generator)
{
// Создаём псевдо-устройство для получения случайного зерна.
std::random_device device;
// Получаем случайное зерно последовательности
generator.engine.seed(device());
}
// Генерирует целое число в диапазоне [minValue, maxValue)
unsigned random(PRNG& generator, unsigned minValue, unsigned maxValue)
{
// Проверяем корректность аргументов
assert(minValue < maxValue);
// Создаём распределение
std::uniform_int_distribution<unsigned> distribution(minValue, maxValue);
// Вычисляем псевдослучайное число: вызовем распределение как функцию,
// передав генератор произвольных целых чисел как аргумент.
return distribution(generator.engine);
}
// Генерирует число с плавающей точкой в диапазоне [minValue, maxValue)
float getRandomFloat(PRNG& generator, float minValue, float maxValue)
{
// Проверяем корректность аргументов
assert(minValue < maxValue);
// Создаём распределение
std::uniform_real_distribution<float> distribution(minValue, maxValue);
// Вычисляем псевдослучайное число: вызовем распределение как функцию,
// передав генератор произвольных целых чисел как аргумент.
return distribution(generator.engine);
}
int main()
{
PRNG generator;
initGenerator(generator);
// Порождаем и выводим 10 чисел на отрезке [0, 7]
std::cout << "ten integer numbers in range [0, 7]:" << std::endl;
for (int i = 0; i < 10; ++i)
{
std::cout << random(generator, 0, 7) << std::endl;
}
// Порождаем и выводим 10 чисел на отрезке [10, 20]
std::cout << "ten float numbers in range [10, 20]:" << std::endl;
for (int i = 0; i < 10; ++i)
{
std::cout << getRandomFloat(generator, 10.f, 20.f) << std::endl;
}
}
Особенность платформы: random_device в MinGW
Согласно стандарту C++, принцип работы std::random_device отдаётся на откуп разработчикам компилятора и стандартной библиотеки. В компиляторе G++ и его стандартной библиотеке libstdc++ класс random_device правильно работает на UNIX-платформах, но на Windows в некоторых дистрибутивах MinGW вместо случайных зёрен он возвращает одну и ту же константу!
В качестве обходного манёвра мы можем использовать текущее время в качестве зерна случайности. Для этого изменим функцию initGenerator:
#include <iostream>
#include <random>
#include <cassert>
#include <ctime>
struct PRNG
{
std::mt19937 engine;
};
void initGenerator(PRNG& generator)
{
// Используем время с 1 января 1970 года в секундах как случайное зерно
const unsigned seed = unsigned(std::time(nullptr));
generator.engine.seed(seed);
}
Приём №1: выбор случайного значения из предопределённого списка
Допусти, вы хотите случайно выбрать имя для кота. У вас есть список из 10 имён, которые подошли бы коту, но вы хотите реализовать случайный выбор. Достаточно случайно выбрать индекс в массиве имён! Такой же метод подошёл не только для генерации имени, но также для генерации цвета из заранее определённой палитры и для других задач.
Идея проиллюстрирована в коде
#include <iostream>
#include <vector>
#include <string>
#include <random>
#include <ctime>
struct PRNG
{
std::mt19937 engine;
};
void initGenerator(PRNG& generator)
{
// Используем время с 1 января 1970 года в секундах как случайное зерно
const unsigned seed = unsigned(std::time(nullptr));
generator.engine.seed(seed);
}
// Генерирует индекс в диапазоне [0, size)
size_t getRandomIndex(PRNG& generator, size_t size)
{
// Создаём распределение
std::uniform_int_distribution<size_t> distribution(0, size - 1);
// Вычисляем псевдослучайное число: вызовем распределение как функцию,
// передав генератор произвольных целых чисел как аргумент.
return distribution(generator.engine);
}
int main()
{
std::vector<std::string> names = {
"Barsik",
"Murzik",
"Pushok",
"Amor",
"Balu",
"Vert",
"Damar",
"Kamelot",
"Mavrik",
"Napoleon"
};
PRNG generator;
initGenerator(generator);
// Порождаем и выводим 3 случайных имёни из заданного списка
std::cout << "3 random cat names:" << std::endl;
for (int i = 0; i < 3; ++i)
{
const size_t nameIndex = getRandomIndex(generator, names.size());
std::cout << names[nameIndex] << std::endl;
}
}
Приём №2: отбрасываем неподходящее значение
Если предыдущую программу запустить несколько раз, то рано или поздно у вас возникнет ситуация, когда одно и то же имя было выведено дважды. Что, если вам нужно уникальное значение, не выпадавшее прежде за время запуска программы?
Тогда используйте цикл, чтобы запрашивать случайные значения до тех пор, пока очередное значение не попадёт под ваши требования. Будьте аккуратны: если требования нереалистичные, вы получите бесконечный цикл!
Доработаем программу, добавив цикл while в функцию main. Для сохранения уже использованных имён воспользуемся структурой данных std::set из заголовка <set>, представляющей динамическое множество.
#include <iostream>
#include <vector>
#include <string>
#include <set>
#include <random>
#include <ctime>
struct PRNG
{
std::mt19937 engine;
};
void initGenerator(PRNG& generator)
{
// Используем время с 1 января 1970 года в секундах как случайное зерно
const unsigned seed = unsigned(std::time(nullptr));
generator.engine.seed(seed);
}
// Генерирует индекс в диапазоне [0, size)
size_t getRandomIndex(PRNG& generator, size_t size)
{
// Создаём распределение
std::uniform_int_distribution<size_t> distribution(0, size - 1);
// Вычисляем псевдослучайное число: вызовем распределение как функцию,
// передав генератор произвольных целых чисел как аргумент.
return distribution(generator.engine);
}
int main()
{
std::vector<std::string> names = {
"Barsik",
"Murzik",
"Pushok",
"Amor",
"Balu",
"Vert",
"Damar",
"Kamelot",
"Mavrik",
"Napoleon"
};
PRNG generator;
initGenerator(generator);
// Множество, хранящее индексы использованных имён.
std::set<size_t> usedIndexes;
// Порождаем и выводим 3 случайных имёни из заданного списка
std::cout << "3 random cat names:" << std::endl;
for (int i = 0; i < 3; ++i)
{
size_t nameIndex = 0;
while (true)
{
// Запрашиваем случайный индекс
nameIndex = getRandomIndex(generator, names.size());
// Проверяем, что индекс ранее не встречался
if (usedIndexes.find(nameIndex) == usedIndexes.end())
{
// Если не встречался, добавляем в множество и выходим
// из цикла: уникальный индекс найден
usedIndexes.insert(nameIndex);
break;
}
else
{
// Отладочная печать отброшенного индекса
std::cout << "discard index " << nameIndex << std::endl;
}
}
std::cout << "index: " << nameIndex << std::endl;
std::cout << names[nameIndex] << std::endl;
}
}