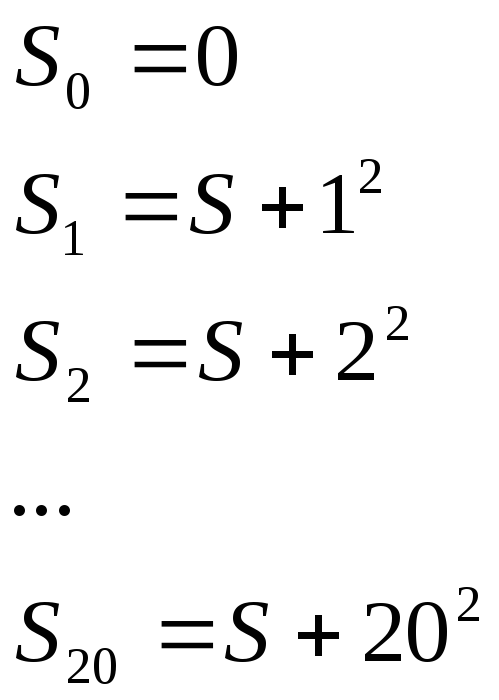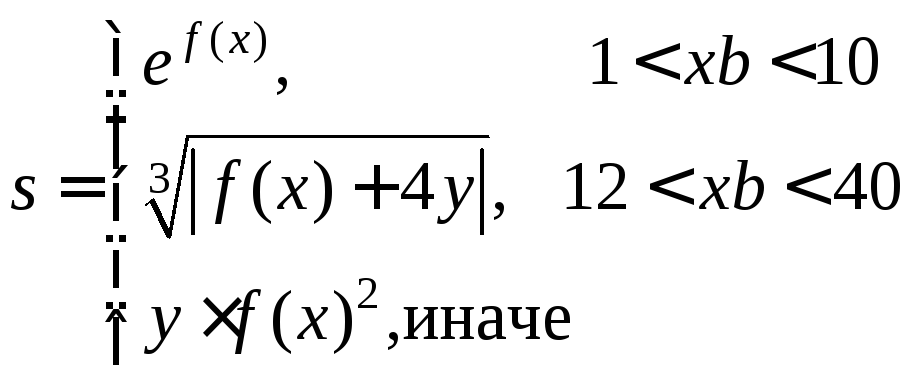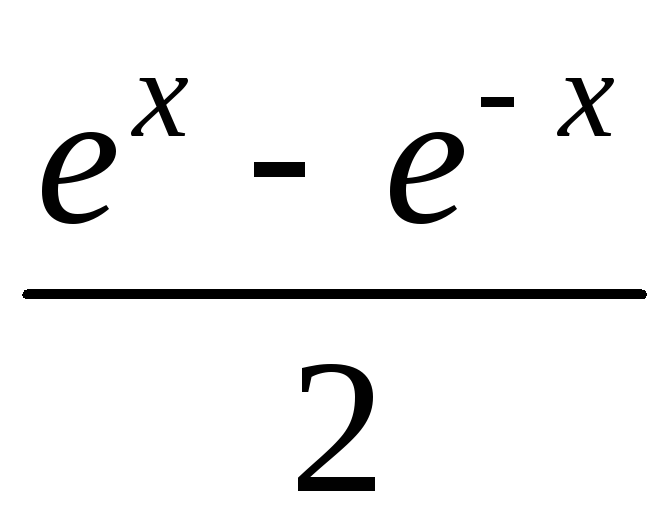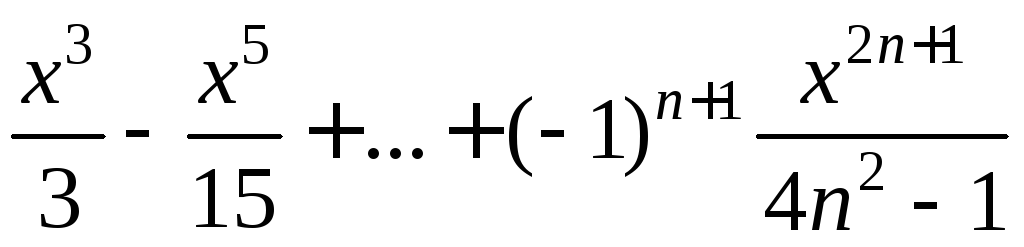Исключительно важно использовать язык блок-схем при разработке алгоритма решения задачи. Решение одной и той же задачи может быть реализовано с помощью различных алгоритмов, отличающихся друг от друга как по времени счета и объему вычислений, так и по своей сложности. Запись этих алгоритмов с помощью блок-схем позволяет сравнивать их, выбирать наилучший алгоритм, упрощать, находить и устранять ошибки.
Отказ от языка блок-схем при разработке алгоритма и разработка алгоритма сразу на языке программирования приводит к значительным потерям времени, к выбору неоптимального алгоритма. Поэтому необходимо изначально разработать алгоритм решения задачи на языке блок-схем, после чего алгоритм перевести на язык программирования.
При разработке алгоритма сложной задачи используется метод пошаговой детализации. На первом шаге продумывается общая структура алгоритма без детальной проработки отдельных его частей. Блоки, требующие детализации, обводятся пунктирной линией и на последующих шагах разработки алгоритма продумываются и детализируются.
В процессе разработки алгоритма решения задачи можно выделить следующие этапы:
- Этап 1 . Математическое описание решения задачи.
- Этап 2 . Определение входных и выходных данных.
- Этап 3 . Разработка алгоритма решения задачи.
Базовые алгоритмические конструкции
В теории программирования доказано, что для записи любого, сколь угодно сложного алгоритма достаточно трех базовых структур:
- следование (линейный алгоритм);
- ветвление (разветвляющийся алгоритм);
- цикл-пока (циклический алгоритм).
Линейные алгоритмы
Линейный алгоритм образуется из последовательности действий, следующих одно за другим. Например, для определения площади прямоугольника необходимо сначала задать длину первой стороны, затем задать длину второй стороны, а уже затем по формуле вычислить его площадь.
Пример
ЗАДАЧА. Разработать алгоритм вычисления гипотенузы прямоугольного треугольника по известным значениям длин его катетов a и b.
На примере данной задачи рассмотрим все три этапа разработки алгоритма решения задачи:
Этап 1. Математическое описание решения задачи.
Математическим решением задачи является известная формула:
,
где с-длина гипотенузы, a, b – длины катетов.
Этап 2. Определение входных и выходных данных.
Входными данными являются значения катетов a и b. Выходными данными является длина гипотенузы – c.
Этап 3. Разработка алгоритма решения задачи.
| Словесное описание алгоритма | Запись алгоритма на языке блок-схем |
|
На данной схеме цифрами указаны номера элементов алгоритма, которые соответствуют номерам пунктов словесного описания алгоритма. |
Разветвляющиеся алгоритмы
Алгоритм ветвления содержит условие, в зависимости от которого выполняется та или иная последовательность действий.
Пример
ЗАДАЧА. Разработать алгоритм вычисления наибольшего числа из двух чисел x и y.
Этап 1. Математическое описание решения задачи.
Из курса математики известно, если x > y, то наибольшее число x, если x < y, то наибольшее число y, если x = y, то число x равно числу y.
Этап 2. Определение входных и выходных данных.
Входными данными являются значения чисел x и y. Выходным данными являются:
- наибольшее число
- любое из чисел, если числа равны
Для решения задачи нам необходимо знать значения x и y.
Этап 3. Разработка алгоритма решения задачи.
| Словесное описание алгоритма | Запись алгоритма на языке блок-схем |
|
|
В схеме алгоритма решения задачи цифрами указаны номера элементов алгоритма, которые соответствуют номерам шагов словесного описания алгоритма
В рассматриваемом алгоритме (рис.3) имеются три ветви решения задачи:
- первая: это элементы 1, 2, 3, 4, 8.
- вторая: это элементы 1, 2, 3, 5, 6, 8
- третья: это элементы 1, 2, 3, 5, 7, 8.
Выбор ветви определяется значениями x и y в элементах 3 и 5, которые являются условиями, определяющими порядок выполнения элементов алгоритма. Если условие (равенство), записанное внутри символа «решение», выполняется при введенных значениях x и y, то следующими выполняется элементы 4 и 8. Это следует из того, что они соединены линией с надписью «да» и направление (последовательность) вычислений обозначена стрелочкой.
Если условие в элементе 3 не выполняется, то следующим выполняется элемент 5. Он соединен с элементом 3 линией с надписью «нет». Если условие, записанное в элементе 5, выполняется, то выполняется элементы 6 и 8, в противном случае выполняются элементы 7 и 8.
Циклические алгоритмы
Циклический алгоритм – определяет повторение некоторой части действий (операций), пока не будет нарушено условие, выполнение которого проверяется в начале цикла. Совокупность операций, выполняемых многократно, называется телом цикла.
Алгоритмы, отдельные действия в которых многократно повторяются, называются циклическими алгоритмами, Совокупность действий, связанную с повторениями, называют циклом.
При разработке алгоритма циклической структуры выделяют следующие понятия:
- параметр цикла – величина, с изменением значения которой связано многократное выполнение цикла;
- начальное и конечное значения параметров цикла;
- шаг цикла – значение, на которое изменяется параметр цикла при каждом повторении.
Цикл организован по определенным правилам. Циклический алгоритм состоит из подготовки цикла, тела цикла и условия продолжения цикла.
В подготовку цикла входят действия, связанные с заданием исходных значений для параметров цикла:
- начальные значения цикла;
- конечные значения цикла;
- шаг цикла.
В тело цикла входят:
- многократно повторяющиеся действия для вычисления искомых величин;
- подготовка следующего значения параметра цикла;
- подготовка других значений, необходимых для повторного выполнения действий в теле цикла.
В условии продолжения цикла определяется допустимость выполнения повторяющихся действий. Если параметр цикла равен или превысил конечное значение цикла, то выполнение цикла должно быть прекращено.
Пример
ЗАДАЧА. Разработать алгоритм вычисления суммы натуральных чисел от 1 до 100.
Этап 1. Математическое описание решения задачи.
Обозначим сумму натуральных чисел через S. Тогда формула вычисления суммы натуральных чисел от 1 до 100 может быть записана так:
где Xi – натуральное число X c номером i, который изменяется от 1 до n, n=100 – количество натуральных чисел.
Этап 2. Определение входных и выходных данных.
Входными данными являются натуральные числа: 1, 2, 3, 4, 5, …, 98, 99, 100.
Выходные данные – значение суммы членов последовательности натуральных чисел.
Параметр цикла – величина, определяющая количество повторений цикла. В нашем случае i – номер натурального числа.
Подготовка цикла заключается в задании начального и конечного значений параметра цикла.
- начальное значение параметра цикла равно 1,
- конечное значение параметра цикла равно n,
- шаг цикла равен 1.
Для корректного суммирования необходимо предварительно задать начальное значение суммы, равное 0.
Тело цикла. В теле цикла будет выполняться накопление значения суммы чисел, а также вычисляться следующее значение параметра цикла по формулам:
S=S+i; I=I+1;
Условие продолжения цикла: цикл должен повторяться до тех пор, пока не будет добавлен последний член последовательности натуральных чисел, т.е. пока параметр цикла будет меньше или равен конечному значению параметра цикла.
Этап 3. Разработка алгоритма решения задачи.
Введем обозначения: S – сумма последовательности, i – значение натурального числа.
Начальное значение цикла i=1, конечное значение цикла i =100, шаг цикла 1.
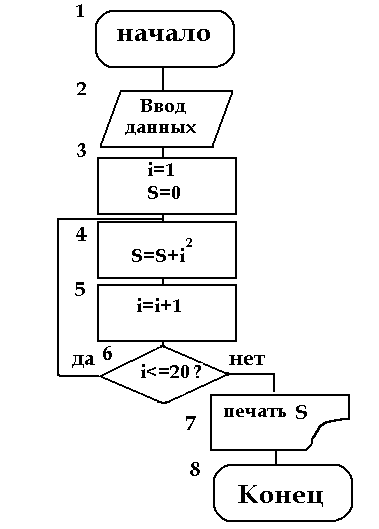
| Словесное описание алгоритма | Запись алгоритма на языке блок-схем |
|
В схеме алгоритма решения задачи цифрами указаны номера элементов алгоритма. Номера элементов соответствуют номерам шагов словесного описания алгоритма. |
Видеоурок 1: Разбор заданий ЕГЭ на алгоритмы
Видеоурок 2: Разбор задания ЕГЭ на циклы
Лекция: Построение алгоритмов и практические вычисления

Составим блок-схему алгоритма вычисления суммы знакопеременного ряда:
с заданной точностью ε.
Необходимо представить алгоритм в виде псевдокода.
Для решения данной задачи используем обозначения:
S – частичная сумма ряда (стартовое значение равно 0);
ε – точность вычисления;
i – номер очередного слагаемого;
m – значение очередного слагаемого;
p – числитель очередного слагаемого.
Требуемая точность вычисления будет достигнута в случае, когда очередное слагаемое станет по абсолютной величине меньше ε. Составим блок-схему алгоритма:
На псевдокоде запись алгоритма будет выглядеть следующим образом:
алг Сумма (арг вещ х, ε рез вещ S)
дано l 0<х<1
надо l S=x-x2/2+x3/3+x4/4+…
нач цел i, вещ m, p
вводх, ε
S := 0; i :=1
m :=1; p := -1
нц покаabc(m)>ε
Р := -p*x
m := p/i
S := S+m
i := i+1
кц
вывод S
кон

Массивы – это множество элементов, значение которых относится к одному типу.
Все значения массива являются упорядоченными и имеют свой индекс.
Индекс позволяет присвоить элементу массива свое место.
Именно поэтому найти некий элемент в массиве можно с помощью его имени и индекса.
Максимальное количество элементов данного массива – это его размерность.
Если массив состоит из некоторого ряда элементов, то он называется векторным или одномерным, если же он состоит из нескольких рядов, то он называется матричным или многомерным массивом.
. В массиве а каждый элемент равен 0 или 1. Заменить все нули единицами и наоборот.
Решение. Достаточно одного оператора присваивания в теле цикла:
a[i] := 1 – a[i]
. В массиве каждый элемент равен 0,1 или 2. Переставить элементы массива так, чтобы сначала располагались все 0, затем все 1 и, наконец, все 2. Дополнительный массив не использовать.
Решение. Можно не переставлять элементы массива, а подсчитать количество 0,1,2 и заново заполнить массив требуемым образом.
алг Сумма (арг цел n, рез арг вещ таб А[1:n] )
дано l массив А содержит нули, единицы и двойки
надо l упорядочить массив по возрастанию
нач цел i, k1, k2
k1 := 0; k2 :=0
нц дляi от 1 до n
если А[i] =0
то k1 := k1+1; всё
если А[i] =1
то k2 := k2+1; всё
кц
нц дляi от 1 до k1
А[i] =0
кц
нц для i от k1+1 до k2+2
А[i] =1
кц
нц для i от k1+k2 до n
А[i] =2
кц
кон
. Даны два n-элементных массива x и Y одного типа. Поменять местами все xi и Yi, (i=1…n) не используя промежуточные величины.
Решение. Обмен можно выполнить в цикле для всех i от 1 до n с помощью серии из трех операторов присваивания:
x[i] := x[i] + y[i]
y[i] := x[i] – y[i]
x[i] := x[i] – y[i]
. Найти сумму элементов одномерного массива А(n).
Решение. Для суммирования положительных элементов массива вместо оператора S := S+А[i] необходимо записать:
если А[i]>0
то S := S+А[i]
всё
На псевдокоде алгоритм расчета суммы выглядит следующим образом:
алг Сумма (арг цел n, арг вещ таб А[1:n], рез вещ S )
дано l массив А
надо l найти сумму элементов массива
нач
цел i
S := 0
нц для i от 1 до n
S := S+А[i]
кц
кон
Действия над массивом
Данные в массиве можно искать или же сортировать.
Основным действием, которое производится над массивом, называется поиск.
Именно он лежит в основе множества других возможных манипуляций с массивами. В зависимости от того упорядочен массив или нет, поиск выполняется различным образом.
Если массив не упорядочен, то для поиска определенного элемента необходимо просмотреть каждое значение, имеющееся в массиве. Такой вид поиска называется линейным. Если же массив упорядочен, то используют метод половинного деления или бинарный.
Сортировка – это действие, которое приводит к изменению положения элементов в заданном массиве, согласно поставленным условиям.
Сортировка производится перед поиском для более быстрого его завершения.
Существует большое разнообразие способов сортировки. Давайте рассмотрим некоторые из них:
1. Сортировка с помощью обмена
Данный способ сортировки предусматривает сравнение элемента с соседними и в случае необходимости смена их местами. Подобные перемещения элементов массива относительно друг друга производятся до тех пор, пока массив не будет упорядочен. В литературе данный метод можно так же встретить под названием «метод пузырьков» или «пузырьковая сортировка». Элементы в массиве передвигаются на свое место подобно пузырькам, которые поднимается на высоту, согласно собственному размеру.
Пример сортировки массива с помощью псевдокода:
алг Обменная_сортировка (арг цел n, арг рез вещ таб А[1:n] )
дано l А – массив размерности n
надо l упорядочить массив по возрастанию
нач
цел i, j
вещ Tmp
нц дляiот2доn
нц дляjотnдо1
еслиА[j]<А[j-1]
тоTmp :=А[j]; А[j] :=А[j-1];
А[j-1] :=Tmp
всё
кц
кц
кон
2. Метод сортировки прямым включением
В данном случае все элементы делятся на два массива – один уже отсортированный, а второй произвольный. Постепенно из неотсортированного массива берется элемент и вставляется на свое место в отсортированный массив. То есть программа ищет позицию необходимого элемента и вставляет его. Следует помнить, что это приводит к сдвигу всех остальных элементов.
Пример алгоритма методом сортировки прямым включением:
алг Сортировка_вставкой (арг цел n, арг рез вещ таб А[1:n] )
дано l А – массив размерности n
надо l упорядочить массив по возрастанию
нач
цел i, j
вещ Tmp
нц дляiот2доn
Tmp :=А[j]; j :=i-1;
нц покаj>= 1 и А[j]>Tmp
А[j+1] :=А[j]
j :=i-1
кц
А[j+1] :=Tmp
кц
кон
3. Метод сортировки прямым выбором
Данный способ заключается в поиске элемента, который будет самым большим (меньшим), после чего он ставится в начало массива. И так до тех пор, пока сортировка не будет выполнена полностью.
Пример алгоритма сортировки методом прямого выбора:
алг Сортировка_выбором (арг цел n, арг рез вещ таб А[1:n] )
дано l А – массив размерности n
надо l упорядочить массив по возрастанию
нач
цел i, k
вещ Min
нц дляiот1доn-1
Min :=А[j]; k :=i
нц дляj от i+1 до n
еслиMin > А[j]
тоMin :=А[j]; k :=j
всё
кц
А[k] :=А[i]; А[i] :=Min
кц
кон

Подпрограмма – это готовый алгоритм, который можно использовать многократно в различных программах.
Подпрограммы включают в основной алгоритм более сложной программы. Они делятся на функции и процедуры.
Функция – выражение, используемое для вычислений, которому присваивается идентификатор функции.
Процедура – это некое действие, которое не позволяет вернуть исходное значение переменных.
Подпрограммы делятся на стандартные и пользовательские.
Стандартные программы изначально встроены в язык программирования, который вы используете. Их еще называют встроенными.
Любой язык программирования имеет библиотеки, в которых изначально забиты стандартные программы, пользоваться которыми можно с помощью идентификатора.
Если же некая стандартная программа была написана вами, и вы сохраняете её в библиотеку, то она называется пользовательской.
Примеры составления блок-схемы алгоритма
Пример 1.
Составить схему алгоритма вычисления
значения :
Для
начала для построения блок –схемы
алгоритма опишем последовательность
действий, необходимых для решения данной
задачи:
-
начало
-
ввод
чисел a,b -
вычисление
х -
вычисление
z -
вывод
результата -
конец
Исходя из этого
составляем блок-схему алгоритма согласно
ГОСТ, используя соответствующие блоки.
Пример
2. Составить
схему алгоритма вычисления значения:
x=a+b
при a>b,
x=a*b,
при a<=b.
Пример 3. Составить схему алгоритма вычисления значения:
Для начала для
построения блок –схемы алгоритма опишем
последовательность действий, необходимых
для решения данной задачи:
Исходя из этого
составляем блок-схему алгоритма согласно
ГОСТ, используя соответствующие блоки.
Порядок выполнения работы
-
Изучить
теоретические сведения по теме
”Построение блок-схем алгоритмов”. -
Получить
у преподавателя индивидуальное задание
и нарисовать блок-схему алгоритма
согласно заданному варианту. -
Ответить
на контрольные вопросы. -
Сформулировать
выводы.
Контрольные вопросы
-
Основные
этапы решения задач на компьютере. -
Свойства алгоритма.
Типы вычислительных процессов. -
Блок схемы. Понятие
и правила построения. -
Примеры построения
блок-схем алгоритмов.
Задание
№1: Разработайте
алгоритм и представьте его в графическом
виде (блок-схемы) для следующих задач:
Задание 1.1
Вычислить значение выражения при
заданных исходных данных.
Указание.
Для упрощения выражений введите
промежуточные переменные.
Сравнить полученное
значение с указанным правильным
результатом.
1.
При
x = 14.26;
y = – 1.22;
z = 3.5ответs
= 0.749155.
2.
При
x = –4.5; y = 0.75;
z = –0.845ответs
= –3.23765.
3.
При
x = 3.74;
y=–0.825; z = 0.16ответs
= 1.05534.
4.
При
x = 0.4;
y = –0.875; z = –0.475ответ
s = 1.98727.
5.
При
x = –15.246; y = 4.642;
z = 21 ответ
s = –182.038.
6.
При
x = 16.55;
y = –2.75; z = 0.15
ответ s
= –40.6307.
7.
При
x = 0.1722; y = 6.33; z = 3.25ответ
s = –205.306.
8.
При
x = –2.235;
y = 2.23; z = 15.221
ответ s
= 39.3741.
9.
При
x = 1.825;
y = 18.225; z = –3.298ответ
s = 1.21308.
10.
При
x = 3.981;
y = –1.625;
z = 0.512
ответ s
= 1.26185.
11.
При
x = 6.251; y = 0.827; z = 25.001
ответ
s = 0.712122.
12.
При
x
= 3.251; y
= 0.325; z
= 0.466
ответ s
= 4.23655.
13.

При
x
= 17.421; y
= 10.365;
z
= 0.828
ответ s
= 0.330564.
14.

При
x
= 12.3;
y
= 15.4; z
= 0.252
ответ s
= 82.8256.
15.
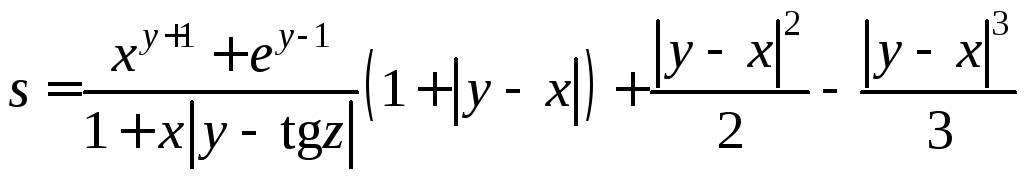
При
x
= 2.444; y
= 0.869;
z
= –0.13
ответ s
= –0.498707.
Задание
1.2 Вычислить
значение выражения при заданных исходных
данных. Предусмотреть вывод информации
о выбранной ветви вычислений.
|
1. |
|
2. |
|
|
3. |
|
4. |
|
|
5. |
|
6. |
|
|
7. |
|
8. |
|
|
9. |
|
10. |
|
|
11. |
|
12. |
|
|
13. |
|
14. |
|
|
15. |
|
Задание
1.3 Вывести
на экран таблицу значений функции Y(x)
и ее разложения в ряд S(x)
для x,
изменяющегося от a
до b
с шагом h
= (b –
a)/10,
табл. 1.
Таблица 1.
|
№ |
a |
b |
S(x) |
n |
Y(x) |
|
1 |
0.1 |
1 |
|
160 |
|
|
2 |
0.1 |
1 |
|
100 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
3 |
0.1 |
1 |
|
120 |
|
|
4 |
0.1 |
1 |
|
80 |
|
|
5 |
0.1 |
1 |
|
140 |
|
|
6 |
0.1 |
1 |
|
80 |
|
|
7 |
0.1 |
1 |
|
120 |
|
|
8 |
0.1 |
1 |
|
100 |
|
|
9 |
0.1 |
1 |
|
140 |
|
|
10 |
0.1 |
0.5 |
|
150 |
|
|
11 |
0.1 |
1 |
|
100 |
|
|
12 |
0.1 |
1 |
|
80 |
|
|
13 |
–2 |
–0.1 |
|
160 |
|
|
14 |
0.2 |
0.8 |
|
120 |
|
|
15 |
0.1 |
0.8 |
|
180 |
|
Задание
№2:
Решите представленные ниже задачи,
указав номер задачи и полученный ответ.
Задача
2.1
Определите
результаты работы блок-схемы алгоритма
при
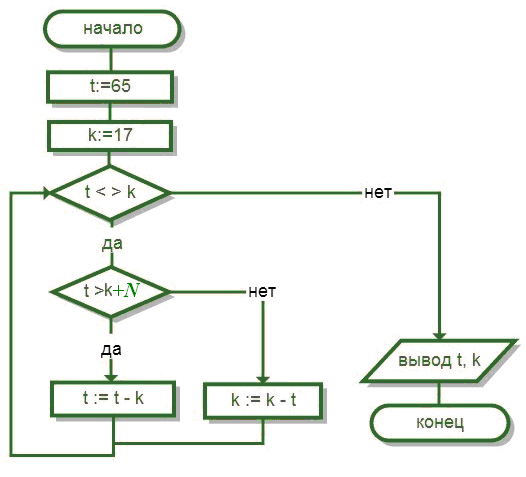
Задача
2.2
Какие
значения примут t и k в
результате работы фрагмента блок-схемы
алгоритма?
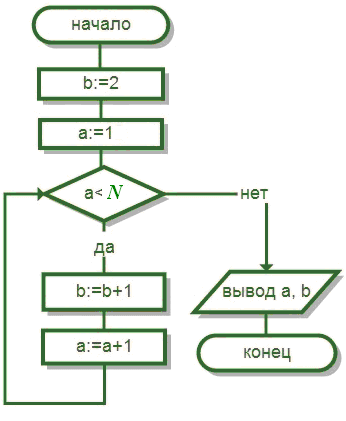
Задача
2.3.
Определите
значения
элементов
массива А2,
А4,
А6,
А8
при N=8
в результате работы фрагмента алгоритма
Итак, опустив долгие и нудные восхваления Паскаля, которые так любят публиковать в своих статьях редакторы многих сайтов, приступим непосредственно к самому основному – к программированию.
В школах, как правило, изучение Паскаля начинают с решения простейших задач путем составления различных алгоритмов или блок-схем, которое многие так часто игнорируют, считая никому не нужной ерундой. А зря. Я, как и любой другой человек, хоть немного соображающий в программировании (не важно где – в Паскале, Си, Дельфи), могу уверить Вас – умение правильно и быстро составлять схемы является фундаментом, основой программирования.
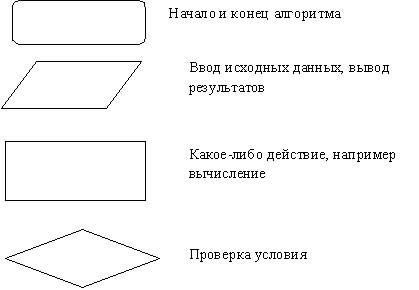
Блок-схема — графическое представление алгоритма. Она состоит из функциональных блоков, которые выполняют различные назначения (ввод/вывод, начало/конец, вызов функции и т.д.).
Существует несколько основных видов блоков, которые нетрудно запомнить:
Сегодняшний урок я решила посвятить не только изучению блок-схем, но также и изучению линейных алгоритмов. Как Вы помните, линейный алгоритм — наипростейший вид алгоритма. Его главная особенность в том, что он не содержит никаких особенностей. Как раз это и делает работу с ним простой и приятной.
Задача №1: «Рассчитать площадь и периметр прямоугольника по двум известным сторонам».
Данная задача не должна представлять особой трудности, так как построена она на хорошо известных всем нам формулах расчета площади и периметра прямоугольника, поэтому зацикливаться на выведении этих формул мы не будем.
Составим алгоритм решения подобных задач:
1) Прочитать задачу.
2) Выписать известные и неизвестные нам переменные в «дано». (В задаче №1 к известным переменным относятся стороны: a, b ;к неизвестным — площадь S и периметр P)
3) Вспомнить либо составить необходимые формулы. (У нас: S=a*b; P=2*(a+b))
4) Составить блок-схему.
5) Записать решение на языке программирования Pascal.
Запишем условие в более кратком виде.
Дано: a, b
Найти: S, P
Блок-схема:
Структура программы, решающей данную задачу, тоже проста:
- 1) Описание переменных;
- 2) Ввод значений сторон прямоугольника;
- 3) Расчет площади прямоугольника;
- 4) Расчет периметра прямоугольника;
- 5) Вывод значений площади и периметра;
- 6) Конец.
А вот и решение:
Program Rectangle;
Var a, b, S, P: integer;
Begin
write('Введите стороны прямоугольника!');
readln(a, b);
S:=a*b;
P:=2*(a+b);
writeln('Площадь прямоугольника: ', S);
write('Периметр прямоугольника: ', P);
End.
Задача №2: Скорость первого автомобиля — V1 км/ч, второго – V2 км/ч, расстояние между ними S км. Какое расстояние будет между ними через T часов, если автомобили движутся в разные стороны? Значения V1, V2, T и S задаются с клавиатуры.
Решение осуществляем, опять же, следуя алгоритму. Прочитав текст, мы переходим к следующему пункту. Как и во всех физических или математических задачах, это запись условий задачи:
Дано: V1, V2, S, Т
Найти: S1
Далее идет самая главная и в то же время самая интересная часть нашего решения – составление нужных нам формул. Как правило, на начальных стадиях обучения все необходимые формулы хорошо нам известны и взяты из других технических дисциплин (например, на нахождение площади различных фигур, на нахождение скорости, расстояния и т.п.).
Формула, используемая для решения нашей задачи, выглядит следующим образом:
S1=(V1+V2)*T+S
Следующий пункт алгоритма – блок-схема:
А также решение, записанное в Pascal :
Program Rasstoyanie;
Var V1, V2, S, T, S1: integer; {Ввод }
begin
write('Введите скорость первого автомобиля: ');
readln(V1);
write('Введите скорость второго автомобиля: ');
readln(V2);
write('Введите время: ');
readln(T);
write('Введите расстояние между автомобилями: ');
readln(S);
S1:=(V1+V2)*T+S;
writeln('Через ', t,'ч. расстояние ', S1,' км.');
End.
Вам может показаться, что две эти программы правильны, но это не так. Ведь сторона треугольника может быть 4.5, а не 4, а скорость машины не обязательно круглое число! А Integer — это только целые числа. Поэтому при попытке написать во второй программе другие числа выскакивает ошибка:
Чтобы решить эту проблему вам надо вспомнить какой тип в Pascal отвечает за нецелые числа. В этом уроке мы рассматривали основные типы. Итак, это вещественный тип — Real. Вот, как выглядит исправленная программа:
Как видите, эта статья полезна для прочтения как новичкам, так и уже более опытными пользователям Pascal, так как составление блок-схем не только очень простое и быстрое, но и весьма увлекательное занятие.