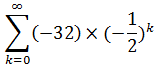Видеоурок 1: Разбор заданий ЕГЭ на алгоритмы
Видеоурок 2: Разбор задания ЕГЭ на циклы
Лекция: Построение алгоритмов и практические вычисления

Составим блок-схему алгоритма вычисления суммы знакопеременного ряда:
с заданной точностью ε.
Необходимо представить алгоритм в виде псевдокода.
Для решения данной задачи используем обозначения:
S – частичная сумма ряда (стартовое значение равно 0);
ε – точность вычисления;
i – номер очередного слагаемого;
m – значение очередного слагаемого;
p – числитель очередного слагаемого.
Требуемая точность вычисления будет достигнута в случае, когда очередное слагаемое станет по абсолютной величине меньше ε. Составим блок-схему алгоритма:
На псевдокоде запись алгоритма будет выглядеть следующим образом:
алг Сумма (арг вещ х, ε рез вещ S)
дано l 0<х<1
надо l S=x-x2/2+x3/3+x4/4+…
нач цел i, вещ m, p
вводх, ε
S := 0; i :=1
m :=1; p := -1
нц покаabc(m)>ε
Р := -p*x
m := p/i
S := S+m
i := i+1
кц
вывод S
кон

Массивы – это множество элементов, значение которых относится к одному типу.
Все значения массива являются упорядоченными и имеют свой индекс.
Индекс позволяет присвоить элементу массива свое место.
Именно поэтому найти некий элемент в массиве можно с помощью его имени и индекса.
Максимальное количество элементов данного массива – это его размерность.
Если массив состоит из некоторого ряда элементов, то он называется векторным или одномерным, если же он состоит из нескольких рядов, то он называется матричным или многомерным массивом.
. В массиве а каждый элемент равен 0 или 1. Заменить все нули единицами и наоборот.
Решение. Достаточно одного оператора присваивания в теле цикла:
a[i] := 1 – a[i]
. В массиве каждый элемент равен 0,1 или 2. Переставить элементы массива так, чтобы сначала располагались все 0, затем все 1 и, наконец, все 2. Дополнительный массив не использовать.
Решение. Можно не переставлять элементы массива, а подсчитать количество 0,1,2 и заново заполнить массив требуемым образом.
алг Сумма (арг цел n, рез арг вещ таб А[1:n] )
дано l массив А содержит нули, единицы и двойки
надо l упорядочить массив по возрастанию
нач цел i, k1, k2
k1 := 0; k2 :=0
нц дляi от 1 до n
если А[i] =0
то k1 := k1+1; всё
если А[i] =1
то k2 := k2+1; всё
кц
нц дляi от 1 до k1
А[i] =0
кц
нц для i от k1+1 до k2+2
А[i] =1
кц
нц для i от k1+k2 до n
А[i] =2
кц
кон
. Даны два n-элементных массива x и Y одного типа. Поменять местами все xi и Yi, (i=1…n) не используя промежуточные величины.
Решение. Обмен можно выполнить в цикле для всех i от 1 до n с помощью серии из трех операторов присваивания:
x[i] := x[i] + y[i]
y[i] := x[i] – y[i]
x[i] := x[i] – y[i]
. Найти сумму элементов одномерного массива А(n).
Решение. Для суммирования положительных элементов массива вместо оператора S := S+А[i] необходимо записать:
если А[i]>0
то S := S+А[i]
всё
На псевдокоде алгоритм расчета суммы выглядит следующим образом:
алг Сумма (арг цел n, арг вещ таб А[1:n], рез вещ S )
дано l массив А
надо l найти сумму элементов массива
нач
цел i
S := 0
нц для i от 1 до n
S := S+А[i]
кц
кон
Действия над массивом
Данные в массиве можно искать или же сортировать.
Основным действием, которое производится над массивом, называется поиск.
Именно он лежит в основе множества других возможных манипуляций с массивами. В зависимости от того упорядочен массив или нет, поиск выполняется различным образом.
Если массив не упорядочен, то для поиска определенного элемента необходимо просмотреть каждое значение, имеющееся в массиве. Такой вид поиска называется линейным. Если же массив упорядочен, то используют метод половинного деления или бинарный.
Сортировка – это действие, которое приводит к изменению положения элементов в заданном массиве, согласно поставленным условиям.
Сортировка производится перед поиском для более быстрого его завершения.
Существует большое разнообразие способов сортировки. Давайте рассмотрим некоторые из них:
1. Сортировка с помощью обмена
Данный способ сортировки предусматривает сравнение элемента с соседними и в случае необходимости смена их местами. Подобные перемещения элементов массива относительно друг друга производятся до тех пор, пока массив не будет упорядочен. В литературе данный метод можно так же встретить под названием «метод пузырьков» или «пузырьковая сортировка». Элементы в массиве передвигаются на свое место подобно пузырькам, которые поднимается на высоту, согласно собственному размеру.
Пример сортировки массива с помощью псевдокода:
алг Обменная_сортировка (арг цел n, арг рез вещ таб А[1:n] )
дано l А – массив размерности n
надо l упорядочить массив по возрастанию
нач
цел i, j
вещ Tmp
нц дляiот2доn
нц дляjотnдо1
еслиА[j]<А[j-1]
тоTmp :=А[j]; А[j] :=А[j-1];
А[j-1] :=Tmp
всё
кц
кц
кон
2. Метод сортировки прямым включением
В данном случае все элементы делятся на два массива – один уже отсортированный, а второй произвольный. Постепенно из неотсортированного массива берется элемент и вставляется на свое место в отсортированный массив. То есть программа ищет позицию необходимого элемента и вставляет его. Следует помнить, что это приводит к сдвигу всех остальных элементов.
Пример алгоритма методом сортировки прямым включением:
алг Сортировка_вставкой (арг цел n, арг рез вещ таб А[1:n] )
дано l А – массив размерности n
надо l упорядочить массив по возрастанию
нач
цел i, j
вещ Tmp
нц дляiот2доn
Tmp :=А[j]; j :=i-1;
нц покаj>= 1 и А[j]>Tmp
А[j+1] :=А[j]
j :=i-1
кц
А[j+1] :=Tmp
кц
кон
3. Метод сортировки прямым выбором
Данный способ заключается в поиске элемента, который будет самым большим (меньшим), после чего он ставится в начало массива. И так до тех пор, пока сортировка не будет выполнена полностью.
Пример алгоритма сортировки методом прямого выбора:
алг Сортировка_выбором (арг цел n, арг рез вещ таб А[1:n] )
дано l А – массив размерности n
надо l упорядочить массив по возрастанию
нач
цел i, k
вещ Min
нц дляiот1доn-1
Min :=А[j]; k :=i
нц дляj от i+1 до n
еслиMin > А[j]
тоMin :=А[j]; k :=j
всё
кц
А[k] :=А[i]; А[i] :=Min
кц
кон

Подпрограмма – это готовый алгоритм, который можно использовать многократно в различных программах.
Подпрограммы включают в основной алгоритм более сложной программы. Они делятся на функции и процедуры.
Функция – выражение, используемое для вычислений, которому присваивается идентификатор функции.
Процедура – это некое действие, которое не позволяет вернуть исходное значение переменных.
Подпрограммы делятся на стандартные и пользовательские.
Стандартные программы изначально встроены в язык программирования, который вы используете. Их еще называют встроенными.
Любой язык программирования имеет библиотеки, в которых изначально забиты стандартные программы, пользоваться которыми можно с помощью идентификатора.
Если же некая стандартная программа была написана вами, и вы сохраняете её в библиотеку, то она называется пользовательской.
написать алгоритм вычисления суммы ряда. Хотя бы примерно как делать. Хотя бы примерно как делать.
Ученик
(216),
на голосовании
11 лет назад
Голосование за лучший ответ
Настюха
Гуру
(3097)
11 лет назад
Составить алгоритм вычисления суммы ряда
с заданной точностью (для данного знакочередующегося степенного ряда требуемая точность будет достигнута, когда очередное слагаемое станет по абсолютной величине меньше) .
Вычисление сумм – типичная циклическая задача. Особенностью же нашей конкретной задачи является то, что число слагаемых (а, следовательно, и число повторений тела цикла) заранее неизвестно. Поэтому выполнение цикла должно завершиться в момент достижения требуемой точности.
При составлении алгоритма нужно учесть, что знаки слагаемых чередуются и степень числа х в числителях слагаемых возрастает.
Решая эту задачу “в лоб” путем вычисления на каждом i-ом шаге частичной суммы
S:=S+(-1)**(i-1)*x**i/i ,
мы получим очень неэффективный алгоритм, требующий выполнения большого числа операций. Гораздо лучше организовать вычисления следующим образом: если обозначить числитель какого-либо слагаемого буквой р, то у следующего слагаемого числитель будет равен -р*х (знак минус обеспечивает чередование знаков слагаемых) , а само слагаемое m
будет равно p/i, где i – номер слагаемого.
Алгоритм, в состав которого входит итерационный цикл, называется итерационным алгоритмом. Итерационные алгоритмы используются при реализации итерационных численных методов. В итерационных алгоритмах необходимо обеспечить обязательное достижение условия выхода из цикла (сходимость итерационного процесса) . В противном случае произойдет зацикливание алгоритма, т. е. не будет выполняться основное свойство алгоритма – результативность.
17
Рис.9. Алгоритм вычисления корней уравнения X2+B*X+C=0
Задания для самостоятельного выполнения
Составить визуальные разветвленные алгоритмы для следующих задач.
1.Для двух чисел Х,У определить, являются ли они корнями уравнения А*Р^4+D*P^2+C=0
2.Если среди трех чисел А,В,С имеется хотя бы одно четное вычислить максимальное, иначе – минимальное 3.Ввести положительное А>=1. Найти наибольшее из выражений вида 1А и SIN(A).
4.Ввести два числа . Меньшее заменить полусуммой, а большее – удвоенным произведением. 5.Ввести три числа А,В,С . Удвоить каждое из них , если А>=В>=С, иначе поменять значения А и В.
6.Определить является ли точка с координатами X,Y точкой пересечения диагоналей квадрата со стороной R ,одна вершина которого расположена в начале координат.
7.* Определить значения функции в зависимости от значения аргумента
|
а*х2 , |
если х > 10 |
|
|
у= |
1/х , |
если –10 ≤ х ≤ 10 |
|
Sin(х) , если х < 10 |
7.ЦИКЛИЧЕСКИЕ АЛГОРИТМЫ
Циклические алгоритмы являются наиболее распространенным видом алгоритмов, в них предусматривается повторное выполнение определенного набора действий при выполнении некоторого условия. Такое повторное выполнение часто называют циклом.
Существуют два основных видов циклических алгоритмов: циклические алгоритмы с предусловием, циклические алгоритмы с постусловием. Они отличаются друг от друга местоположением условия выхода их цикла.
Цикл с предусловием начинается с проверки условия выхода из цикла. Это логическое выражение, например I<=6. Если оно истинно, то выполняются те действия, которые должны повторяться. В противном случае, если логическое выражение I<=6 ложно, то этот цикл прекращает свои действия.
Цикл с постусловием функционирует иначе. Сначала выполняется один раз те действия, которые подлежат повторению, затем проверяется логическое выражение , определяющее условие выхода из цикла, например, I>6
.Проверка его осуществляется тоже по-другому. Если условие выхода истинно, то цикл с постусловием прекращает свою работу, в противном случае – происходит повторение действий, указанных в цикле. Повторяющиеся действия в цикле

18
называются “телом цикла”.Разновидности циклов приведены на рис. 10а),б).
|
i=1 |
|||||||||||||||||
|
i=1 |
|||||||||||||||||
|
K:=K+1 |
|||||||||||||||||
|
I<=6 |
|||||||||||||||||
|
K |
|||||||||||||||||
|
i:=i+0,1 |
+ |
||||||||||||||||
K:=K+S
+
i>6 K
i:=i+1
|
а) Цикл с постусловием |
б) Цикл с предусловием |
Рис. 10. Виды циклических алгоритмов
Классическим примером циклического алгоритма служит алгоритм для вычисления степени числа Y=Xⁿ . Этот алгоритм может быть реализован на основе операции умножения. Табличное представление такого алгоритма, отражающего зависимость У от Х при изменении показателя степени n от 1 до 3, представлено в табл.3. В этой таблице показанны также реккурентные соотношения между У и Х, определяющие как на каждом шаге зависит значение У от значения Х и от значения У, вычисленного на предыдущем шаге.
Таблица 3.Реккурентные соотношения при вычислении Y=Xⁿ
|
n |
Y |
Реккурентные соотно- |
|
шения |
||
|
1 |
Y[1]=X |
Y=X |
|
2 |
Y[2]=X*X или |
Y=X*X или Y=Y*X |
|
Y[2]=Y[1]*X |
||
|
3 |
Y[3]=X*X*X или |
Y=X*X*X или Y=Y*X |
|
Y[3]=Y[2]*X |
||

Текстовая форма алгоритма
___________________
Начало
Присвоить Х = -15
+
ПОКА Х <= 15
|
1.Вычислить |
K:=K+1 |
|
|
Y= SIN(X) |
||
|
Y:=Y*x |
||
|
2.Вывести |
||
|
Y,X |
S:=S+Y
3.Вычислить X=X+1,5
КОНЕЦ
|
19 |
|
|
НАЧАЛО |
|
|
Ввод x, N |
|
|
S:=0 |
НАЧАЛО |
|
Y:=x |
|
|
K:=1 |
X:= -15 |
|
K<N |
x<=15 |
|
КОНЕЦ |
|
|
Y =sin (X) |
|
|
Вывод S |
|
|
Y, X |
|
|
КОНЕЦ |
|
|
X: =X+1,5 |
Рис.12. Алгоритм вычисления суммы ряда S=x+x^2+x^3+…+x^n
Пример 5.Пусть требуется составить алгоритм вычисления суммы ряда
S=x+x^2+x^3+…+x^n.
Решение. Исходные данные для алгоритма это переменные x и n. На каждом шаге будем вычислять очередной член суммы Y и прибавлять его к предыдущему значению суммы S.Для этого используем реккурентную формулу вычисления степени Х (см. таблицу 3) Y=Y*Х, тогда сумма ряда на каждом шаге итерации будет вычисляться по формуле S=S+Y. Количество итераций K изменяется от 1 до n и равно количеству членов ряда. Начальное значение суммы ряда S равно 0. На рис. 12 представлен циклический алгоритм с предусловием для вычисления заданной суммы ряда.
Пример 6. Требуется составить алгоритм получения на отрезке
[-15,15] множества значений функции Y= SIN(X) в виде таблицы значений (X,Y) при изменении аргумента Х по формуле X[k]=X[k-1]+h, где h=1,5.
Решение. Такие задачи относят к задачам табулирования функций. Из условия задачи определяем, что начальное значение отрезка табулирования X= -15, конечное значение – X=15. Процесс получения множества пар Х,Y) является итерационным, значит проектируемый алгоритм будет циклическим. Условие выхода из цикла Х>15. На рис. 13 представлен циклический алгоритм с предусловием вычисления табличного значения функ-
20
ции Y= SIN(X) на отрезке -15<X<15 при изменении Х на каждом шаге итерации на величину 1,5. Результатом выполнения алгоритма является циклический вывод множеств пар
(Y,X) .
Рис. 13. Циклический алгоритм табулирования функции Y =sin (X)
Задания для самостоятельного выполнения
Составить визуальные циклические алгоритмы для следующих задач.
1.Вычислить число в факториале Y=X!
2.Вычислить сумму ряда , общий член которого задан формулой An=(x*n)/n!.
3.При табулировании функции y=cos(x+a) на отрезке [1,10] c шагом h=1 определить сумму значений y , больших p.
4.Подсчитать количество цифр в целом числе Х.
5.Вычислить сумму значений функции у=x^2 на отрезке [1,5] c шагом 1.
6.* Найти минимальное значение функции Y=Sin(X)*X , на отрезке [C,D] с шагом 0.001. Реализовать цикл с постусловием.
7.Протабулировать функцию y=sin(x) на отрезке [1,5] с шагом h=0,5. Вывести предпоследнее положительное значение функции.
8.Определить постановку задачи и составить визуальный алгоритм для этой задачи, если табличное представление ее решения изображено ниже:
|
Условие N>0 |
S |
N |
|
|
0 |
125 |
||
|
125>0 |
да |
0+5=5 |
12 |
|
12>0 |
да |
5+2=7 |
1 |
|
1>0 |
да |
7+1=8 |
0 |
|
0>0 |
нет |
9.Составить визуальную и табличную формы алгоритма по его текстовому представлению, а также определить конечное значение S .
|
А) I=0; S=0; |
В) I=1; S=0; |
|
ПОКА I<3 |
ПОКА I >1 |
|
I=I+3 |
S=S+1/I |
|
S=S+I*I |
I=I-1 |
|
ВЫВОД S |
ВЫВОД S |
10. Составить визуальную и текстовую форму представления алгоритма, заданного в табличной форме.

21
|
0 |
||
|
1 |
2 |
0+1+2=3 |
|
3 |
3+1+3=7 |
|
|
2 |
2 |
7+2+2=11 |
|
3 |
11+2+3=16 |
11.Определить является ли данный фрагмент алгоритма циклом, если да, то какого вида и какое действие является телом цикла?
|
A) |
I=1 |
В) |
I =1 |
||||
|
I<=6 |
+ + |
|
|
+ |
||
|
K |
||
|
+ |
||
|
K:=K+S |
I := I +1 |
|
22
12.* Протабулировать функцию Y=tg(X), при изменении X на отрезке [A,B] с шагом K и определить количество точек разрыва(M) этой функции.
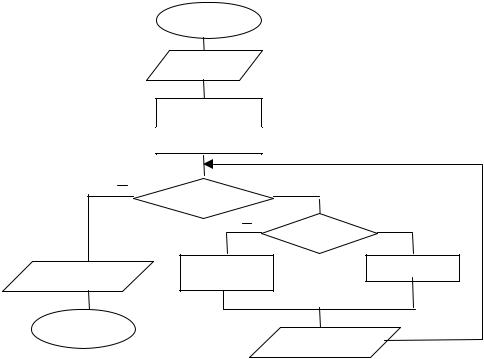
13.Определите местонахождение ошибок в алгоритмическом решении следующей задачи. Найти минимальное значение функции Y=A*X2+Sin(X)*X0,5 , для Х изменяющемся на отрезке [C,D] с шагом 0,01.
|
НАЧАЛО |
|
|
C, D |
|
|
X := C |
|
|
M := A*X2+SIN(X)*X 0. 5 |
|
|
Y := A*X2+SIN(X)*X 0. 5 |
|
|
Y <M |
Y=М |
|
C := Y |
|
|
Y, X |
|
|
X := X+0.001 |
|
|
X > D |
M |
|
КОНЕЦ |
23
8.АЛГОРИТМЫ ОБРАБОТКИ ПОСЛЕДОВАТЕЛЬНОСТЕЙ ЧИСЕЛ
Последовательность значений – это набор однотипных величин, которые вводятся и обрабатываются циклически. Примером последовательности целых чисел может быть следующий набор значений: (2,5,-4,10,1,0). Последовательности значений отличаются от массивов значений тем, что в памяти одновременно все значения последовательности не хранятся. Для обозначения значения последовательности используют одну переменную, в которую на каждом шаге итерации вводится очередное значение последовательности. Отличительной особенностью последовательности является также возможность содержания неопределенного или неизвестного заранее количества ее значений. В этом случае критерием окончания последовательности служит некоторое особое значение, например, ноль.
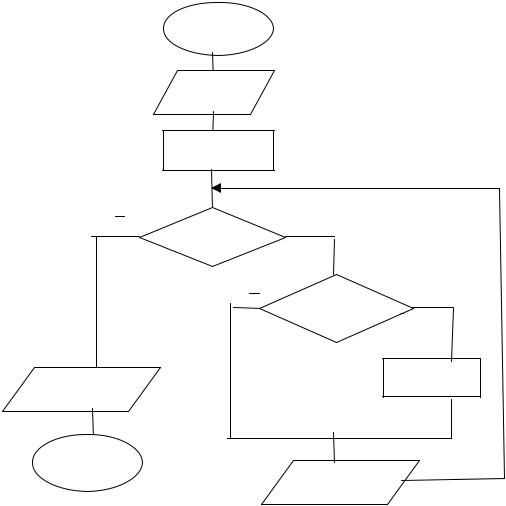
Пример 7. В числовой последовательности определить сумму положительных и произведение отрицательных чисел. Реализовать с помощью цикла с предусловием. Признак конца последовательности – значение 0. Решение. Обозначим за Х переменную, содержащую очередное значение последовательности, за S – сумму положительных значений , за Р – произведение отрицательных значений. Полученный алгоритм приведен на рис. 14. Условие
Рис.14. Алгоритм вычисления суммы положительных и произведения отрицательных значений числовой последовательности
для выбора вычислений Х>0. Для вычисления суммы значений воспользуемся реккурентной формулой S=S+X с начальным значением S=0, для вычисления произведения – реккурентной формулой P=P*X с начальным значением Р=1. Условие выхода из цикла неравенство Х<>0.
|
НАЧАЛО |
||
|
Ввод X |
||
|
P:=1 |
||
|
S:=0 |
||
|
X<>0 |
+ |
|
|
+ |
||
|
X>0 |
||
|
Вывод P, S |
P:=P*X |
S:=S+X |
КОНЕЦ
Ввод Х
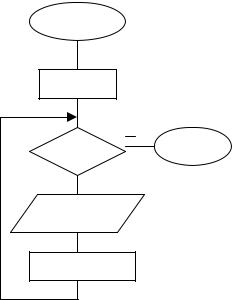
Пример 8.Составить циклический алгоритм для определения в последовательности целых чисел количества четных чисел.
Решение. Обозначим за Х переменную, содержащую очередное значение последовательности, за K – количество четных значений (рис. 15). Условие для выбора четных значений Х mod 2=0 (остаток приделении Х
24
на 2 равен 0). Для вычисления количества значений воспользуемся реккурентной формулой К=К+1 с начальным значением К=0.
Рис. 15. Алгоритм определения количества четных чисел в последовательности значений
Задания для самостоятельного выполнения
Составить визуальные циклические алгоритмы для следующих задач обра-
НАЧАЛО
Ввод X
K=0
+
X<>0
K:=K+1
Вывод K
КОНЕЦ
Ввод Х
ботки последовательности значений.
1.В последовательности вещественных чисел подсчитать произведение чисел, кратных
3.
2.В последовательности чисел сравнить ,что больше сумма положительных или произведение отрицательных.
3.В последовательности чисел определить предпоследнее отрицательное число.(При решении введите дополнительную переменную для хранения предпоследнего отрицательного числа).
4.В последовательности целых положительных чисел определить
максимальное число (Рекомендуем реализовать такой алгоритм :
|
25 |
||||||
|
Вводим Х |
mах=Х |
|||||
|
Начало |
Цикл с постусловием |
|||||
|
а. Если элемент Х > max |
||||||
|
то max:=Х (значение этого элемента); |
||||||
|
б. Вводим новый элемент последовательности Х. |
||||||
|
K=1 |
Условие выхода из цикла Х=0 ) |
|||||
|
5. |
В последовательности целых чисел определить |
|||||
|
третье положительное число и подсчитать ко- |
||||||
|
Конец |
личество цифр в нем. |
|||||
|
K<=9 |
||||||
|
Ввод А(к) |
9.АЛГОРИТМЫ ОБРАБОТКИ |
|||||
|
ОДНОМЕРНЫХ ЧИСЛОВЫХ |
||||||
|
МАССИВОВ |
||||||
|
К=К+1 |
||||||
|
Под структурой данных типа массив |
||||||
|
понимают |
однородную структуру |
одно- |
||||
|
Рис. 16.Алгоритм ввода элементов |
типных |
данных, одновременно хранящихся |
||||
|
в |
последовательных ячейках оперативной |
|||||
|
памяти. Эта структура должна иметь имя и |
||||||
|
определять заданное количество данных (элементов). Однотипность данных |
||||||
|
определяет возможность использования циклических алгоритмов для |
обра- |
|||||
|
ботки всех элементов массива. |
Количество итераций цикла определяется |
|||||
|
количеством элементов массива Одновременное хранение в памяти всех эле- |
||||||
|
ментов массива позволяет решать |
большой |
набор задач, таких как поиск |
||||
|
элементов, упорядочение и изменение порядка следования элементов. |
||||||
|
Доступ |
к любому элементу массива осуществляется по его номеру ( |
|||||
|
индексу ). Поэтому для обращения |
к |
элементу массива используют |
||||
|
имя_массива(номер элемента), например, А(5). |
||||||
|
Массив называется одномерным , если для получения доступа к его |
||||||
|
элементам достаточно одной индексной переменной. |
||||||
|
Рассмотрим простой алгоритм ввода элементов одномерного числового |
||||||
|
массива A из 9 элементов. В этом циклическом алгоритме условие выхода из |
||||||
|
цикла определяется значением специальной |
||||||
|
переменной К, которая называется |
счетчиком элементов массива А |
|||||
|
(рис.16), эта же переменная К определяет количество итераций циклического |
||||||
|
алгоритма ввода элементов массива. На каждом шаге итерации переменная |
||||||
|
К(значение номера элемента массива А) изменяется на 1, то есть происходит |
||||||
|
переход к новому элементу массива.В дальнейшем, при рассмотрении |
||||||
|
алгоритмов обработки одномерных массивов в целях устранения дублирова- |
||||||
|
ния алгоритм ввода элементов массива будем заменять одним блоком, |
под- |
|||||
|
разумевая, что он реализуется по схеме, циклического алгоритма, представ- |
||||||
|
ленного на ри- |
сунке 16. |
26
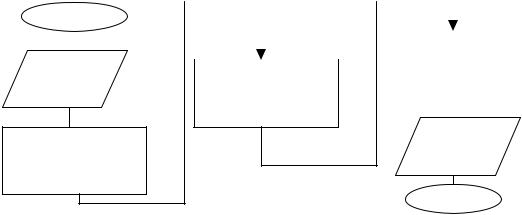
Пример 9. Составить алгоритм определения в одномерном числовом массиве А из N элементов суммы положительных элементов.
Решение. Алгоритм представлен на рисунке 17. В этом алгоритме переменная К – является счетчиком элементов массива, S – сумма элементов массива, она вычисляется по реккурентной формуле S=S+A(K). Ввод количества и значений элементов массива осуществляется вначале в отдельном блоке ввода, который реализуется по схеме алгоритма ввода элементов массива, изображенного на рис.16.
+
Часто для проверки правильности работы алгоритмов на конкретных наборах данных используют таблицу трассировки. Эта таблица содержит столько столбцов, сколько переменных и условий в алгоритме, в ней мы вы-
полняем действия шаг за шагом от начала до конца алгоритма для конкретных наборов входных данных.НАЧАЛО
|
Пример 10. Составить алгоритм поиска |
элемента |
с максимальным значением в |
||||||||||||||||||||||||
|
М |
||||||||||||||||||||||||||
|
одномерном массиве А(1..n) и его таблицу трассировки |
для значений (3, 7, 0, 9). |
|||||||||||||||||||||||||
|
Решение. |
Введем обозначения K- текущий номер элемента, A[K] – текущее значение элемента массива, |
|||||||||||||||||||||||||
|
Ввод N и А( 1.. N) |
||||||||||||||||||||||||||
|
N=4 количество элементов одномерного массива, M- номер максимального элемента массива, A[M] – зна- |
||||||||||||||||||||||||||
|
чение максимального элемента массива. Основной идеей |
алгоритма |
является выполнение сравнения теку- |
||||||||||||||||||||||||
|
+ |
A[М], |
|||||||||||||||||||||||||
|
щего элемента массива A[K] и элемента с максимальным значением |
||||||||||||||||||||||||||
|
определенным на предыдущем |
A [K]>A[M] |
|||||||||||||||||||||||||
|
шаге итерации. |
По алгоритму |
НАЧАЛО |
||||||||||||||||||||||||
|
изображенному |
на рис.18 |
по- |
||||||||||||||||||||||||
|
лучено |
максимальное значе- |
|||||||||||||||||||||||||
|
ние для массива |
(3, 7, 0, |
9), |
N, |
A(N) |
||||||||||||||||||||||
|
процесс |
и правильный резуль- |
|||||||||||||||||||||||||
|
тат поиска которого показаны в |
||||||||||||||||||||||||||
|
таблице 4. |
+ |
|||||||||||||||||||||||||
|
K<=N K := 1 |
||||||||||||||||||||||||||
|
Вывод А[M] |
||
|
K <= N |
Вывод S |
|
|
КОНЕЦ |
||
|
+ |
КОНЕЦ |
|
|
A(K) > 0 |
+ |
|
|
S := S+A(k) |
||
K := K + 1
Рис. 17. Алгоритм вычисления суммы положительных элементов
27
Рис.18. Алгоритм поиска максимального значения в массиве
Таблица 4. Таблица трассировки алгоритма примера 10.
|
Номер элемен- |
Значение эле- |
Номер |
макси- |
Значение |
мак- |
Проверка |
|
|
та массива К |
мента А (К) |
мального М |
симальнго А(М) |
А(К)>А(М) |
|||
|
1 |
3 |
1 |
3 |
Нет |
|||
|
2 |
7 |
1 |
2 |
3 |
7 |
да |
|
|
3 |
0 |
2 |
7 |
нет |
|||
|
4 |
9 |
2 |
4 |
7 |
9 |
да |
Рассмотрим несколько более сложных алгоритмов, в которых осуществляется изменение порядка следования элементов в одномерном массиве . К таким алгоритмам относят алгоритмы с перестановкой элементов местами, алгоритмы удаления некоторых элементов или циклического переноса некоторых элементов в начало или конец массива.
Основным требованием при составлении алгоритмов обработки массивов является неиспользование дополнительных массивов.
Чтобы точнее уяснить постановку задачи следует сначала рассмотреть частные решения для конкретных наборов входных данных (провести анализ) , затем обобщить полученное решение и определить набор решаемых задач. Составив визуальный алгоритм, его следует проверить на различных наборах исходных данных. Эти наборы исходных данных требуется подбирать таким образом, чтобы при заполнении таблиц трассировок проверить все пути вычислений данного алгоритма от начальной вершины до конечной.
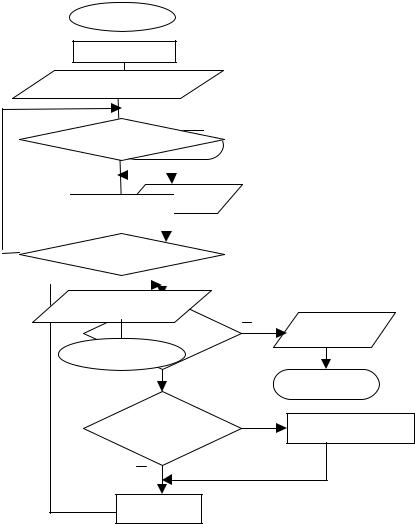
Пример 11.Составить алгоритм решения и таблицу трассировки следующей задачи. В одномерном массиве поменять местами 2-ой нулевой элемент и последний положительный элемент. Применить нисходящее проектирование алгоритма.
Решение. Пусть одномерный массив содержит 9 элементов: (5, 0, 4, -3, -7, 0, -2, -4, 0). Среди этих элементов имеются три нулевых значения, отрицательные и положительные значения. Второй нулевой элемент имеет порядковый номер 6, а последний положительный элемент – номер 3, его значение равно 4. Если поменять местами 2-ой нулевой элемент и последний положительный в исходном массиве (5, 0, 4, -3, -7, 0, -2, -4, 0)
то получим новый массив, в котором изменен порядок следования элементов 5, 0, 0, -3, -7, 4, -2, -4, 0 . Основными операциями алгоритма будут: поиск второго нулевого элемента массива, поиск по-
следнего положительного элемента массива и перестановка найденных элементов. Отметим, что для пере-
|
НАЧАЛО |
|||||||||
|
Перестановка эле- |
|||||||||
|
Ввод мас- |
ментов в массиве |
||||||||
|
Определение номера |
|||||||||
|
сива |
|||||||||
|
последнего |
|||||||||
|
элемента >0 |
|||||||||
Вывод Определение номера массива второго нулевого
элемента
КОНЕЦ
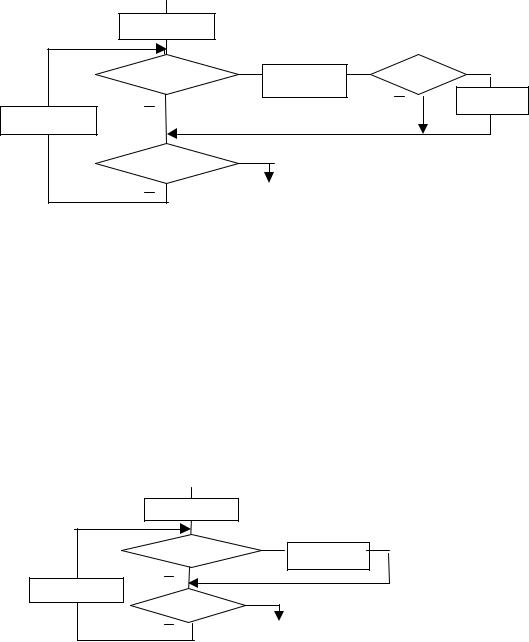
становки элементов необходимо знать номера переставляемых элементов. На рис. 19 изображен обобщенный алгоритм решения задачи, который в дальнейшем будет детализирован.
28
Рис. 19. Обобщенный алгоритм к примеру 11
Ввод количества и значений элементов массива осуществляется вначале в отдельном блоке ввода, который реализуется по схеме алгоритма ввода элементов массива, изображенного на рис.16.
Поиск второго нулевого элемента массива будем осуществлять в цикле, проверяя значение очередного элемента на 0. Если очередной элемент равен 0, то для подсчета количества таких элементов используем реккурентную формулу M=M+1. В тот момент времени, когда значение М=2, нам необходимо запомнить номер текущего элемента массива, так как это и есть искомый второй положительный элемент исходного массива. На рис.20 приведен фрагмент алгоритма, реализующего поиск второго нулевого элемента в некотором массиве А из N элементов.
Рис. 20. Фрагмент алгоритма поиска второго нулевого элемента в массиве А, состоящем из N элементов. Здесь К- номер очередного элемента, А(К) – значение
|
K:=1 , m=0 |
||
|
A [K]=0 |
+ |
m=2 |
|
m:=m+1 |
P:=K
K:=K+1
+
K=N
очередного элемента, m -количество нулевых элементов, Р- номер второго нулевого элемента в массиве
Поиск последнего положительного элемента массива будем осуществлять аналогично в цикле, запоминая номер очередного элемента, значение которого больше нуля, в дополнительной переменной S. Учитывая тот факт, что после того как будут просмотрены и проверены на положительность все элементы массива в переменной S будет храниться номер последнего положительного элемента массива. На рис. 21 представлен фрагмент алгоритма поиска последнего положительного элемента в массиве А.
Рис. 21. Фрагмент алгоритма поиска последнего положительного элемента
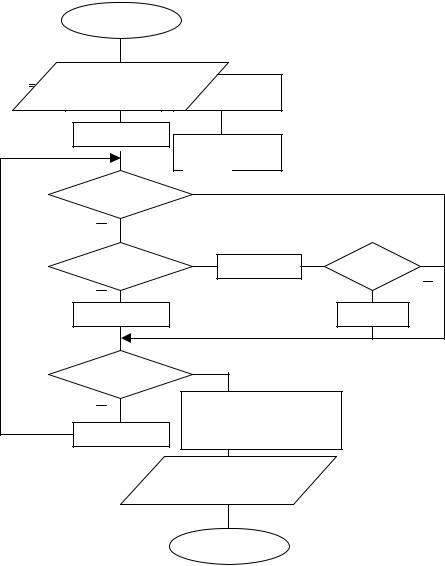
Рассмотрим фрагменты алгоритма, приведенные на рис. 20 и 21. Можно заметить, что оба этих фрагмента выполняют поиск под управлением цикла, с одинаковым числом повторений, равным количеству элементов исходного массива N. Поэтому в итоговом алгоритме решения задачи примера 11 вместо композиции этих двух фрагментов в виде двух последовательных циклов можно использовать параллельное выполнение операций поиска под управлением одного цикла, который приведен на рис. 22.
+
S=K
K:=K+1
+
29
Рис 22. Алгоритм поиска второго нулевого и последнего положительного элементов массива А.
|
НАЧАЛО |
||
|
Ввод N и элемен- |
||
|
Q: =A [P] |
A [P]: =A [S] |
|
|
тов А(1.. N) |
||
|
K:=1, m=0 |
A [S]: =Q |
|
|
+ |
||
|
A [K]<0 |
||
|
A [K]=0 |
+ |
m=2 |
|
m:=m+1 |
||
|
+ |
||
|
S:=K |
P:=K |
|
|
K=N |
+ |
|
|
Перестановка |
||
|
K:=K+1 |
элементов массива |
|
|
Вывод нового |
||
|
массива A[1..N] |
КОНЕЦ
Напомним, что исходный одномерный массив содержит 9 элементов: (5, 0, 4, -3, -7, 0, -2, -4, 0).По условию задачи необходимо поменять местами 2-ой нулевой элемент и последний положительный элемент.
Так как задачи поиска необходимых для перестановки элементов алгоритмически решены (рис. 22), то рассмотрим задачу перестановки элементовДля реализации перестановки найденных элементов достаточно воспользоваться управляющей структурой следования. Для того, чтобы во время перестановки не потерять переставляемые значения используем дополнительную переменную Q, временно хранящую одно из переставляемых значений элемента массива, в частности второе нулевое значение.На рис. 23 представлен универсальный алгоритм перестановки двух элементов одномерного массива, имеющих порядковые номера P и
S .
30
Рис. 23.Фрагмент перестановки двух элементов массива, с номерами S и P
Подводя итог для алгоритмического решения примера 11, приведем на рис. 24 алгоритм для вывода элементов преобразованного массива после перестановки найденных элементов.
Рис. 24. Алгоритм вывода элементов массива
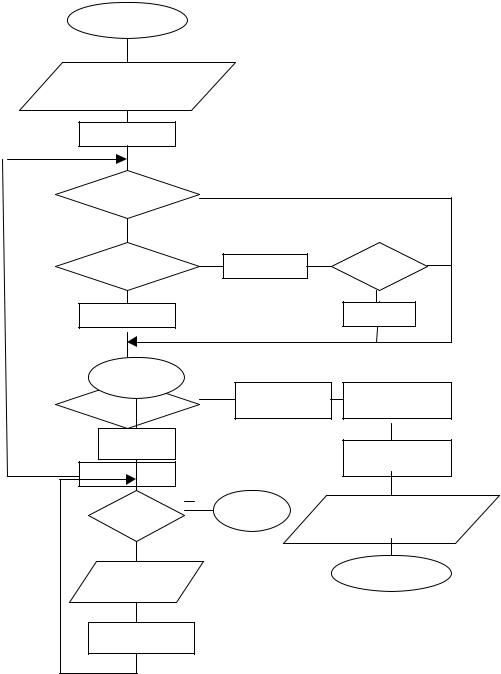
Таким образом, процесс проектирование первоначального алгоритма перестановки второго нулевого элемента и последнего положительного элемента в одномерном массиве завершен. Полученный алгоритм представлен на рис.25. Следует заметить, что целью решения примера 11 было показать процесс нисходящего проектирования алгоритма ” сверху-вниз ” с использованием декомпозиции и метода структурной алгоритмизации. Отметим, что с целью упрощения в полученном алгоритме не рассматриваются ситуации, когда в составе элементов массива отсутствуют положительные значения или нулевые значения в количестве большем одного.
|
НАЧАЛО |
||
|
Ввод N и элемен- |
||
|
тов А(1.. N) |
||
|
K=1, m=0 |
||
|
A [K]<0 |
||
|
A [K]=0 |
m:=m+1 |
m=2 |
|
S:=K |
P:=K |
|
|
Начало |
||
|
Q: =A [P] |
A [P]: =A [S] |
|
|
K=1 |
A [S]: =Q |
|
|
K:=K+1 |
||
|
K<=9 |
Конец |
Вывод нового |
|
массива A[1..N] |
||
|
+ |
||
|
Вывод |
КОНЕЦ |
|
|
А к |
||
|
К=К+1 |
Рис.25. Алгоритм перестановки второго нулевого и последнего положительного элемента в одномерном массиве
31
Для проверки правильности работы полученного алгоритма составим таблицу трассировки для одномерного массива из 9 элементов: (5, 0, 4, -3, -7, 0, -2, -4, 0), приведенных в примере 11. Напомним, что заполнение таблицы происходит по строкам. Считаем, что все начальные значения числовых переменных равны 0. В таблице 5 выполнена трассировка фрагмента поиска второго нулевого и последнего положительного элементов (их номеров), а в таблице 6 выполнена трассировка следующего фрагмента алгоритма по перестановке в массиве найденных элементов, где K- текущий номер элемента, A[K] – текущее значение элемента массива, М- количество нулей, обнаруженных в массиве при анализе очередного элемента, P- номер второго нулевого элемента массива, S- номер последнего положительного элемента массива, A[S] – значение последнего положительного элемента массива, A[P] – значение второго нулевого элемента массива.
|
Таблица 5.Таблица трассировки операций |
Таблица 6. Таблица трассировки |
|
поиска второго нулевого элемента и |
перестановки найденных элемен- |
|
последнего положительного |
тов массива |
|
К |
Входной мас- |
M |
М=2 |
Р |
S |
|
сив А(К) |
|||||
|
1 |
5 |
0 |
Нет |
1 |
|
|
2 |
0 |
1 |
Нет |
||
|
3 |
4 |
3 |
|||
|
4 |
-3 |
||||
|
5 |
-7 |
||||
|
6 |
0 |
2 |
Да |
6 |
|
|
7 |
-2 |
||||
|
8 |
-4 |
||||
|
9 |
0 |
3 |
Нет |
|
A(P) |
Q |
А(S) |
Выходной мас- |
||
|
А(6) |
А(3) |
сив А(К) |
|||
|
0 |
0 |
4 |
1 |
5 |
|
|
4 |
0 |
4 |
2 |
0 |
|
|
4 |
0 |
0 |
3 |
0 |
|
|
4 |
-3 |
||||
|
5 |
-7 |
||||
|
6 |
4 |
||||
|
7 |
-2 |
||||
|
8 |
-4 |
||||
|
9 |
0 |
Пример 12. Составить алгоритм удаления в одномерном массиве элемента с максимальным значением. Решение. Анализ постановки задачи позволяет выделить две последовательно решаемые задачи: поиск элемента с максимальным значением и удаление этого значения из массива. Алгоритм первой задачи был рассмотрен ранее в примере 10 (рис.18). В этом алгоритме был определен номер максимального значения М, а максимальное значение определялось как А(М). Удаление элемента из массива приводит к уменьшению количества элементов массива за счет их перемещения на позицию удаляемого. Например, требуется удалить максимальное значение в массиве (2,4,13,5,7). Максимальное значение в этом примере равно 13. После удаления количество элементов данного массива уменьшится на 1 и станет равным 4, а массив примет вид (2,4,5,7). Таким образом, можно сделать вывод , что для удаления элемента из массива необходимо знать его номер, например М, удаление производится путем сдвига на одну позицию влево всех следующих за удаляемым элементов А(М)=А(М+1), этот сдвиг должен осуществляться под управлением цикла. Цикл завершит свою работу, когда последний элемент массива сдвинется на место предпоследнего элемента .
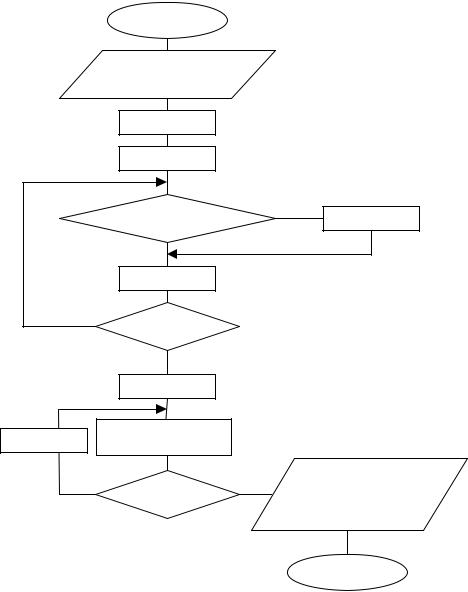
После приведенных рассуждений и используя алгоритмическое решение примера 10, изображенное на рис.18, составим алгоритм удаления элемента с максимальным значением из одномерного массива из N элементов (см. рис.26).
32
Рис. 26. Алгоритм удаления элемента с максимальным значением
К – номер очередного элемента, М- номер элемента с максимальным значением, N-1 – уменьшенное
|
НАЧАЛО |
|
|
Ввод N и элемен- |
|
|
тов А(1.. N) |
|
|
А |
|
|
K:=1 |
|
|
M:=1 |
|
|
A [K]>A [M] |
M:=K |
|
K:=K+1 |
|
|
K>N |
|
|
K=М |
|
|
A [K]: =A [K+1] |
|
|
K:=K+1 |
|
|
Вывод N-1 элемента |
|
|
K=N-1 |
массива A |
КОНЕЦ
в результате удаления одного элемента количество элементов массива А, A [K]: =A [K+1] – удаление путем сдвига влево следующих за удаляемым элементов на одну позицию.
Задания для самостоятельного выполнения
Составить визуальные циклические алгоритмы и таблицы трассировки для следующих задач обработки одномерных массивов.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В этом уроке мы расскажем как вычислить сумму бесконечного сходящегося ряда (последовательности) с определенной точностью. Будет рассмотрена соответствующая программа, написанная на языке программирования Си. В конце статьи можно скачать исходник этой программы для Visual Studio.
Сходящийся ряд — это числовая последовательность элементов множества X, имеющая предел в этом множестве.
Сходящийся ряд
Рассмотрим задачу вычисления суммы сходящегося ряда с определенной точностью на примере. Пусть дан ряд:
Вычисление суммы ряда с определенной точностью ε означает, что сумма ряда вычисляется до тех пор, пока модуль разности между текущим и предыдущим членом последовательности больше ε. В виде формулы это утверждение можно записать так: |an — an-1| > ε, то есть пока это выражение истинно, вычисления продолжаются.
Сначала напишем на языке Си функцию, которая будет вычислять и возвращать значение k-го члена ряда по переданному в нее значению k.
|
double f(int k) { double res; res = –32.0; res *= (double)powf(–0.5, k); return res; } |
res — это переменная вещественного типа повышенной точности double, в которую будет записан результат вычисления k-го члена ряда. Это же значение и будет возвращаться функцией.
Выражение res *= (double)powf(-0.5, k); эквивалентно выражению res = res * (double)powf(-0.5, k);
Оператор powf — это оператор возведения числа в степень. В нашем случае он вычисляет: -0.5k.
Функцию f можно записать короче:
|
double f(int k) { return –32.0 * powf(–0.5, k); } |
Теперь перейдем к функции main. Для начала считаем с консоли число e — это и будет заданная точность вычислений ε.
|
float e; printf(“e = “); scanf_s(“%f”, &e); |
Объявим переменные, в которых будут хранится: значение предыдущего, значение текущего члена ряда, сумма ряда и номер текущего члена ряда (число k) соответственно.
|
double previous, current; double sum = 0; int k = 0; |
Отдельно вычислим первый член ряда (потом он станет «предыдущим»), чтобы затем перейти к вычислениям в цикле.
|
current = f(k); sum += current; k++; |
Запись выражения sum += current; эквивалентна записи: sum = sum + current;
Теперь перейдем к вычислениям в цикле. Условием выхода из цикла будет ложность выражения: |an — an-1| > ε.
|
do { previous = current; current = f(k); sum += current; k++; } while (abs(current – previous) > e); |
Сумма посчитана. Осталось вывести результат вычислений в консоль.
|
printf(“sum = %fn”, sum); |
В итоге код программы с необходимыми подключенными библиотеками будет выглядеть следующим образом:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
#include <stdio.h> #include <math.h> #include <conio.h> double f(int k) { double res; res = –32.0; res *= (double)powf(–0.5, k); return res; } int main() { float e; printf(“e = “); scanf_s(“%f”, &e); double previous, current; double sum = 0; int k = 0; current = f(k); sum += current; k++; do { previous = current; current = f(k); sum += current; k++; } while (abs(current – previous) > e); printf(“sum = %fn”, sum); _getch(); return 0; } |
Оператор _getch(); в строке 34 нужен для того, чтобы консоль не закрывалась сразу по завершении исполнения программы.
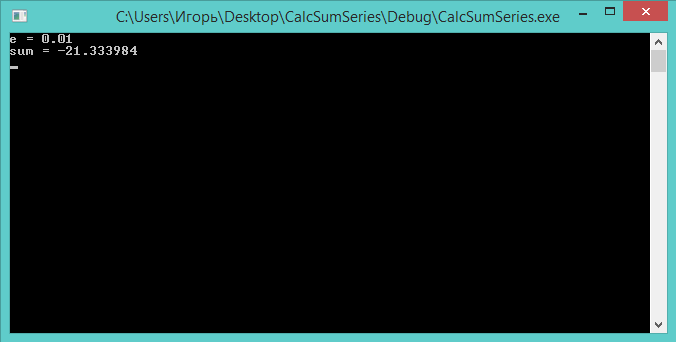
Демонстрация работы программы для нашего ряда представлена на скриншоте ниже. Точность вычислений составляет: ε = 0.01.
Скачать исходник
Суммирование
Начнем с простейшей задачи – вычисление суммы элементов массива:
 |
( 3.1) |
Классический алгоритм выглядит так:
S = 0; for(int i = 0; i < n; i++) S = S + x[i];
Листинг
3.1.
Последовательный алгоритм вычисления суммы элементов массива
Алгоритм последовательный и не допускает распараллеливания, поскольку на каждом шаге цикла используется значение S, вычисленное на предыдущем шаге. Заметьте, цикл не допускает распараллеливания, если в теле цикла есть оператор присваивания, у которого одна и та же скалярная переменная встречается как в левой, так и в правой части оператора (S в нашем примере).
Поскольку в алгоритме используется только один цикл типа for с шагом, равным единица, то алгоритм имеет линейную временную сложность:
 |
( 3.2) |
Когда суммирование должен выполнять только один процессор, то это оптимальный по времени алгоритм. Но суммирование можно вести самыми разными способами, если к вычислению суммы привлечь несколько процессоров. В
“Параллельные вычисления”
мы уже анализировали “пирамидальный” алгоритм суммирования, допускающий распараллеливание. Вот возможная запись такого алгоритма на С#:
int[] y = new int[n];
Array.Copy(x, y, n);
int m = n;
while (m != 1)
{
for (int i = 0, j = m - 1; i < j; i++, j--)
y[i] = y[i] + y[j];
m = (m + 1) / 2;
}
S = y[0];
Листинг
3.2.
Пирамидальный алгоритм вычисления суммы элементов массива
В этом более сложном варианте алгоритма появились два цикла. Внутренний цикл for может быть распараллелен. Нетрудно видеть, что множества переменных, используемых на каждой итерации этого цикла, взаимно не пересекаются. Выполнение этого условия достаточно для распараллеливания. Внешний цикл while распараллелить нельзя, поскольку итерации “склеиваются” общей переменной m.
Для компьютера с одним процессором этот алгоритм будет хуже классического алгоритма по ряду причин:
- Ему нужна дополнительная память, поскольку промежуточные результаты необходимо запоминать. Для этого введен массив y той же размерности, что и исходный массив x.
- Алгоритм усложнен, – вместо одного цикла классического алгоритма, вводятся два цикла. Алгоритм менее понятен и отладка его может вызывать затруднение. Несомненно, что программисту потребуется больше времени на разработку и отладку такого алгоритма.
- Алгоритм при последовательном выполнении хотя и имеет ту же временную сложность – O(n), но константа у него больше, чем у классического алгоритма, поскольку во внутреннем цикле используются три переменные с индексами, вместо одной, как в классическом алгоритме.
В чем же достоинство этого алгоритма? Одно несомненное достоинство у него есть – он допускает распараллеливание. Если запускать его на идеальном метакомпьютере с неограниченным числом процессоров, то тогда, используя n/2 процессоров, все вычисления внутреннего цикла можно выполнять параллельно.
Сложность внутреннего цикла при распараллеливании будет равна O(1), а общая сложность определяется внешним циклом и равна O(log n). В
“Параллельные вычисления”
, где этот алгоритм уже анализировался, помимо ускорения в рассмотрение вводилась и такая характеристика алгоритма как эффективность. У пирамидального алгоритма эффективность низкая, поскольку для достижения максимального ускорения требуется n/2 процессоров – число, пропорциональное размерности массива. Метакомпьютеры и даже суперкомпьютеры с большим числом процессоров не всегда под рукой, но и при их наличии приходится заботиться об эффективности.
Давайте рассмотрим алгоритмы суммирования, ориентированные на конечное число процессоров – на многоядерные компьютеры. Пусть в нашем распоряжении есть компьютер с фиксированным числом процессоров – р. Как выполнить суммирование, используя все возможности такого компьютера? Естественный алгоритм, допускающий распараллеливание, понятен, – нужно провести распараллеливание по данным, разбив исходный массив на р групп, примерно равной размерности. Тогда можно параллельно выполнить суммирование для каждой группы, после чего просуммировать полученные результаты. И в этом случае понадобится дополнительная память – массив размерности р, хранящий результаты промежуточных сумм.
Разбиение массива на группы можно выполнить разными способами. Разумными представляются две стратегии. Первая состоит в том, чтобы исходный массив нарезать на р отрезков и поручить каждому процессору суммирование элементов соответствующего отрезка. Вторая стратегия основана на том, чтобы каждый процессор суммировал элементы, отстоящие на расстоянии р. Если соответствующим образом выбрать начальный элемент для каждого процессора, то это позволит вести параллельное суммирование.
Вот вариант записи сегментного алгоритма, соответствующего первой стратегии:
int count_p = Environment.ProcessorCount;
int[] y = new int[count_p];
int m = n / count_p + 1;
int start = 0, finish = 0;
for(int k =0; k < count_p; k++)
{
start = k * m;
finish = (k+1)*m < n ? (k+1)*m : n;
for (int i = start; i < finish; i++)
y[k] += x[i];
}
S = y[0];
for (int i = 1; i < count_p; i++)
S += y[i];
Листинг
3.3.
Сегментный алгоритм вычисления суммы p процессорами
Чуть проще шаговый алгоритм, соответствующий второй стратегии:
int[] y = new int[count_p];
for (int k = 0; k < count_p; k++)
{
for (int i = k; i < n; i += count_p)
y[k] += x[i];
}
S = y[0];
for (int i = 1; i < count_p; i++)
S += y[i];
Листинг
3.4.
Шаговый алгоритм вычисления суммы p процессорами
Оба эти варианта допускают параллельное выполнение тела внешнего цикла. В этом случае сложность алгоритма определяется сложностью операторов, составляющих тело этого цикла, фактически, сложностью внутреннего цикла – O(n/count_p). Ускорение для обоих вариантов равно count_p – числу процессоров, а эффективность равна единице. Таковы теоретические оценки. В последующих главах посмотрим, что можно получить на практике.
Задача суммирования крайне важна, поскольку встречается в самых разных приложениях. Она легко обобщается на случай, когда суммируются не элементы массива, а функции, зависящие от параметра i:
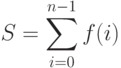 |
( 3.3) |
Все, что сказано о суммировании, касается и других подобных задач – нахождение произведения элементов массива, максимального или минимального элемента и других задач этого класса.
Суммирование рядов
Нахождение суммы конечного ряда принципиально не отличается от нахождения суммы элементов массива. Поговорим о том, как вычислять сумму бесконечного сходящегося ряда:
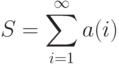 |
( 3.4) |
Необходимым условием сходимости ряда является стремление 
В программировании не ставится задача вычисления точного значения S в формуле (3.4), – достаточно вычислить это значение с некоторой точностью. В сравнении с конечными суммами дополнительная сложность в построении алгоритма состоит в том, что заранее неизвестно, сколь много членов ряда необходимо вычислить, чтобы найти сумму ряда с нужной точностью. Классический алгоритм основан на том, что суммирование прекращается, как только очередной член суммы 


Вот пример записи такого алгоритма:
double eps = 1E-15;
double i = 1;
double a = 1;
double S = 0;
while (Math.Abs(a) > eps)
{
//Вычисление общего члена ряда
a = 1.0 / ((4 * i + 1) * (4 * i - 1)); // пример
S += a;
i++;
}
Листинг
3.5.
Классический алгоритм вычисления суммы сходящегося ряда
С программистской точки зрения алгоритмы 3.1 и 3.5 во многом схожи. Разница в том, что в первом случае используется цикл for, во-втором – цикл while. Из-за этого различия труднее оценить временную сложность алгоритма, поскольку нет такого естественного параметра как n в алгоритме 3.1. Число суммирований зависит как от формулы, задающей общий член ряда, так и от выбранной точности вычислений – 
Другой подход к вычислению суммы сходящегося ряда состоит в том, чтобы вместо точности 

Вернемся к рассмотрению алгоритма 3.5. По уже указанным причинам он не допускает распараллеливания. Но, как и для вычисления конечных сумм, нетрудно построить допускающую распараллеливание версию, ориентированную на p процессоров. Для конечных сумм мы рассматривали два варианта – сегментный и шаговый алгоритм.
Сегментный алгоритм требует нарезки на сегменты примерно равной длины, для этого нужно знать N – число суммируемых элементов. Поэтому этот вариант алгоритма следует применять тогда, когда заранее выбирается N.
Модификацию шагового алгоритма, допускающего распараллеливание, выполнить несложно. Для каждого процессора нужно задать начальное значение, после чего процессор будет вести суммирование, пока общий член не станет меньше заданной точности 
double i = 1;
double a = 0;
double[] y = new double[count_p];
for (int k = 0; k < count_p; k++)
{
i = k+1;
a = 1.0 / ((4 * i + 1) * (4 * i - 1)); //начальное значение
while (Math.Abs(a) > eps)
{
y[k] += a;
i += count_p ;
a = 1.0 / ((4 * i + 1) * (4 * i - 1));
}
}
S = y[0];
for (int k = 1; k < count_p; k++)
S += y[k];
Листинг
3.6.
Шаговый алгоритм вычисления суммы сходящегося ряда p процессорами