По теме: методические разработки, презентации и конспекты

Методика работы над задачами по технологии УДЕ
В предлагаемом материале описана методика работы над задачами с применением технологии укрупненных дидактических единиц (УДЕ) (автор П.М. Эрдниев).Ключевым моментом технологии является решение прямой …

“Методика работы над задачами. Решение задач разного вида.”
Конспект урока математики…
Приемы решения задач и работы с задачей на уроках математике по системе Н.Б.Истоминой.
Статья. Можно использовать как доклад – выступление на МО….
Схемы-опоры к задачам. Алгоритм работы над задачей
Материал предназначен для индивидуальной работы, работы в группах или групповой работы…

Карточка-памятка: алгоритм выполнения деления с остатком и его проверка.
Карточка-памятка используется, как раздаточный материал в помощь детям при изучении темы “Деление с остатком” в 3 классе….

Презентация – Задача, ее составные части. Памятка: как работать с задачей.
Задача, ее составные части. Памятка: как работать с задачей….

Шаблон работы с задачами для групповой работы
Данный шаблон содержит все основные этапы работы с задачей….
Скачать материал
Выберите документ из архива для просмотра:
Пошаговый алгоритм решения задачи.pptx
Выбранный для просмотра документ Пошаговый алгоритм решения задачи.pptx

Скачать материал




- Сейчас обучается 82 человека из 37 регионов


- Сейчас обучается 35 человек из 26 регионов


Описание презентации по отдельным слайдам:
-

1 слайд
Пошаговый
алгоритм
решения
задачиОбщий подход к решению любых задач
Автор презентации:
О.В. Курочкина,
учитель математики
МАОУ «Школа № 17»,
г. Ачинск, 2018 г. -

2 слайд
1-й этап —
анализ задачиНа этом этапе, прежде всего, надо разобраться в том, каковы условия задачи, в чем состоит ее требование (вопрос).
-

3 слайд
2-й этап —
построение модели задачи
На этом этапе результаты анализа оформляются, то есть, строится модель задачи в виде схематической записи, таблицы, графика, рисунка, краткой записи. -

4 слайд
3-й этап — поиск
способа решения задачи
На данном этапе ищется известный способ решения, если его нет, то задача разбивается на подзадачи, решив которые будет либо полностью решена исходная задача, либо она существенно упростится, если разбить задачу на подзадачи не удается, то ее пытаются преобразовать в равносильную задачу, способ решения которой известен. Если задача плохо определенная, в ней имеются неопределенные неизвестные или неясна связь между данными и искомыми, то тогда вводится столько вспомогательных элементов, сколько необходимо, чтобы задача стала строго определенной, и для ее решения применяется какой – либо известный метод. -

5 слайд
4-й этап — осуществление решения задачи
На данном этапе оформляется решение задачи. -

6 слайд
5-й этап —
проверка решения задачи
После того как решение задачи осуществлено и изложено (письменно или устно), необходимо убедиться, что это решение правильное, что оно удовлетворяет всем условиям задачи. -

7 слайд
6-й этап —
исследование задачи
На данном этапе нужно установить, при каких условиях задача имеет решение и сколько различных решений она имеет в каждом отдельном случае; при каких условиях задача вообще не имеет решения. -

8 слайд
7-й этап
Формулирование ответа задачи. -

9 слайд
8-й этап
Познавательный анализ задачи
и ее решения. -

10 слайд
СПАСИБО
ЗА
ВНИМАНИЕ!
Краткое описание документа:
Необходимо обратить внимание на то, что алгоритмы решения задач, изучаемых в школе, даны в учебниках в свернутом виде. Между тем, человек может решать задачу по известному алгоритму лишь в развернутом виде алгоритма — в форме пошаговой программы. Учителю, хорошо владеющему математикой, не представляет никакого труда в уме, как бы автоматически развернуть свернутый алгоритм в пошаговую программу. Но ученику, особенно слабому, развернуть свернутый алгоритм в пошаговую программу в уме – трудно.
Свернутые алгоритмы в курсе математики могут быть даны в разных видах: в виде словесного правила, формулы, тождества, теоремы и т.д. Учеников нужно научить каждый такой свернутый алгоритм развернуть в пошаговую программу, сначала явно – с формулировкой каждого шага, а затем, по мере овладения этим действием – неявно, в уме.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 262 417 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 30.01.2018
- 521
- 2
- 30.01.2018
- 535
- 0
- 30.01.2018
- 316
- 0
- 30.01.2018
- 981
- 4
- 30.01.2018
- 290
- 0
Рейтинг:
1 из 5
- 30.01.2018
- 701
- 0
- 30.01.2018
- 736
- 0
- 30.01.2018
- 707
- 6
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»
-
Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
-
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
Современные формы обучения, инновации в преподавании, введение новых
технологий диктуют учителю необходимость постигать секреты мастерства, а значит,
и совершенствовать методы обучения и воспитания учащихся.
Исследования психологов и педагогов, опыт коллег показывают: чтобы научить
детей самостоятельно учиться и проявлять творчество необходимо применение
деятельностного подхода в обучении. Для этого учащихся нужно замотивировать и
обучить их приемам и способам учебной деятельности, которые помогут сформировать
необходимые знания, умения и навыки.
Курс школьной математики имеет достаточно широкие возможности для применения
различных приемов, методов и технологий. В последние годы в содержание школьного
курса естественным образом закладывается алгоритмическая линия. Так как
применение алгоритмов является приоритетным в моей работе, то нужно отметить
что, между понятиями “прием” и “алгоритм” существует много общего, ни и есть
принципиальные отличия, а именно:
– прием – это рациональный способ работы, который состоит из отдельных
действий, он может быть выражен в виде правил или инструкций, его можно
перестроить и на его основе создать новый прием. Приемы деятельности допускают
самостоятельный выбор учениками конкретных действий по решению учебных задач;
– алгоритм – это общепонятное и однозначное предписание, которое определяет
последовательность действий, позволяющее достичь искомый результат. Алгоритм
предполагает жесткое выполнение шагов, а прием дает общее направление
деятельности по решению учебных задач, не регламентируя каждый шаг. Поэтому я в
своей работе выделяю два подхода: 1) обучение алгоритмам; 2) формирование
приемов решения задач. Школьные задачи делятся на: алгоритмические,
полуалгоритмические, полуэвристические и эвристические. Каждый тип задачи
предполагает свои схемы решения, подходы, применение логики и изобретательности.
На начальном этапе обучения математике применение алгоритмов способствует
формированию и прочному усвоению навыков владения математическими методами.
Также осуществляется подготовка к формированию первоначальных представлений о
математическом моделировании. Уже в начальных классах прослеживается применение
простейших алгоритмов выполнения арифметических операций, дети овладевают
навыками выполнения последовательных действий. Решают задачи с составлением схем
и кратких записей. Это можно рассматривать как пропедевтику операционного стиля
мышления.
Следующий уровень алгоритмической культуры учащихся – введение понятия
алгоритма и формирование его основных свойств. Это происходит в среднем звене
школы. Именно в этот период необходимо сочетания алгоритма и образца ответа, что
дает возможность ученику, верно, ответить на поставленный вопрос, сопроводив его
правильной речью. У учителя появляется возможность предлагать задачи с
элементами творчества. А материал, предлагаемый в наших школьных учебниках,
является хорошей базой для обучения составлению простейших алгоритмов и
дальнейшей их записи в разных формах. Мы применяем табличную, графическую
(блок-схема), словесную и формульную форму записи алгоритмов.
В качестве примера, иллюстрирующего процесс алгоритмизации как средство
обучения, можно указать на решение задач методом уравнений. Примером
графического алгоритма является блок-схема для отыскания количества решений
системы двух линейных уравнений с двумя неизвестными (см. Рисунок 1).
Отыскания числа решений системы двух линейных уравнений (блок-схема)
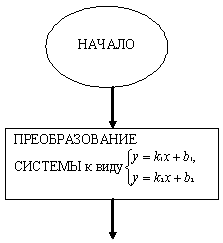
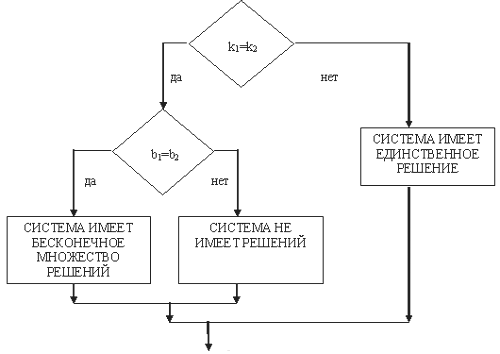

Рис. 1
Графические алгоритмы
Табличную форму алгоритма можно продемонстрировать на примере таблицы,
составляемой для исследования функций и дальнейшего построения графиков (см.
рис. 2).
Исследование функции и построение графика
Функция задана уравнением у = f(x). Исследовать
функцию и построить ее график.
1. Таблица исследования функции

2. Построение графика
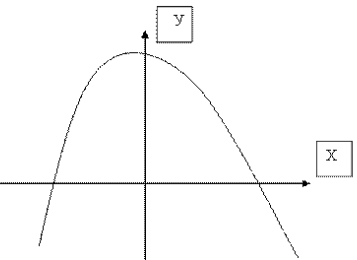
Рис. 2
Табличный алгоритм
Пример формульного способа – последовательность нахождения компонентов при
составлении уравнения касательной к графику той или иной функции (см. рис. 3).
Уравнение касательной к графику функции

Рис. 3
Формульный способ
Словесный алгоритм используется практически во всех правилах выполнения
действий, например, правило сложения чисел с разными знаками (см. рис. 4).
Алгоритм сложения чисел с разными знаками

Рис. 4
Словесный алгоритм
В старших классах работа становится разнообразней и содержательней,
появляется возможность включать упражнения разного типа и уровня сложности,
предполагающее, что приемы деятельности могут быть разной степени сложности и
обобщенности. Они состоят из большого числа действий, выполнение которых
приводит к применению алгоритмов на отдельных этапах работы.
Такой подход к преподаванию математики в основной школе определяет условия
для формирования у учащихся навыков, позволяющих в старших классах успешно
изучать базовый курс “Информатики и ИКТ”. Применение алгоритмов в старших
классах, по мнению некоторых учителей, отбивает творческий подход к решению
задач, но с другой стороны, твердое знание основных задач курса и умение их
решать, является твердым фундаментом для активизации самостоятельной и
творческой работы учащихся.
Список литературы
- Кухарев Н.В. На пути к профессиональному совершенству. – М.:
Просвещение, 1990. - Епишева О.Б. Крутич В.И. Учить школьников учиться математике. –
М.: Просвещение, 1990. - Сост. Глейзер Г.Д. Повышение эффективности обучения математике в
школе. – М.: Просвещение, 1991. - Груденов Я.И. Совершенствование методики работы учителя
математики. – М.: Просвещение, 1990. - Байдак В.А. и др. Формирование алгоритмической культуры у
учащихся. – М.: Просвещение, 1989.
СПОСОБЫ РЕШЕНИЙ ВСЕХ ВИДОВ ЗАДАЧ.
КРАТКИЕ ЗАПИСИ. ЧЕРТЕЖИ. ФОРМУЛЫ.
ЧАСТИ ЛЮБОЙ ЗАДАЧИ ДЛЯ ЛЮБОГО КЛАССА
Выучить и знать всегда:
Компоненты любой задачи:
УСЛОВИЕ – ВОПРОС – РЕШЕНИЕ – ОТВЕТ
Задание
Прочитай задачу и подчеркни УСЛОВИЕ – синей ручкой, ВОПРОС – зелёной ручкой. ОПОРНЫЕ СЛОВА – обведи в овал простым карандашом.
Объяснение
Например, в задаче:
В вазе 3 белых и 2 розовых гвоздики. Сколько всего гвоздик в вазе?
————————————————- ————————————–
ОПОРНЫЕ СЛОВА нужно уметь находить для нахождения главного в задаче.
Опорные слова – это основа краткой записи.
В указанной задаче опорные слова:
Первое опорное слово – БЕЛЫХ (выделено жирным), который сокращаем в первом классе Б., но, начиная со второго класса, БЕЛ.
Второе опорное слово – РОЗОВЫХ (выделено жирным),, которое в первом классе сокращаем Р., но, начиная со второго класса, РОЗ.
Третье опорное слово всегда содержится в вопросе. В данной задаче третье опорное слово – ВСЕГО, которое в краткой записи задачи заменяется ФИГУРНОЙ СКОБКОЙ С ВОПРОСОМ ПОСЕРЕДИНЕ.
Б . – 3 г.
. – 3 г.
Р. – 2 г. ? г.
Потренируйся
Прочитай задачи и подчеркни УСЛОВИЕ – синей ручкой, ВОПРОС – зелёной ручкой. ОПОРНЫЕ СЛОВА – обведи в овал простым карандашом.
-
В вазе лежало 5 карамелек и 3 шоколадных конфеты. Сколько всего конфет лежало в вазе?
-
За два дня Вера прочитала 8 страниц. В первый день она прочитала 2 страницы. Сколько страниц она прочитала во второй день?
-
У Оли было 3 куклы. На день рождения девочке подарили 4 куклы. Сколько кукол стало у Оли?
-
В автобусе ехало 9 человек. На остановке вышли 5 человек. Сколько человек осталось в автобусе?
-
У Юры 3 машинки, а у Максима 5 машинок. Сколько всего машинок у мальчиков?
-
Саша и Лёва поймали 8 карасей. Лёва поймал 3 карася. Сколько карасей поймал Саша?
-
У Васи 5 марок, а у Коли на 4 марки больше. Сколько марок у Коли?
-
Длина огорода 7 м, а его ширина на 2 м меньше. Какова ширина огорода?
-
У портнихи 5 катушек белых ниток, а чёрных катушек на 2 меньше. Сколько катушек чёрных ниток у портнихи?
-
На одном этаже 5 жильцов, а на другом этаже на 2 жильца меньше. Сколько жильцов на другом этаже?
-
За два дня турист прошёл 9 км. В первый день он прошёл 4 км. Сколько км он прошёл во второй день?
-
Длина синего отрезка 4 см, а красного на 2 см больше. Чему равна длина красного отрезка?
-
На столе стояли 4 тарелки. Мама поставила ещё 2 тарелки. Сколько тарелок стало на столе?
-
У Вани было 2 диска с мультфильмами. Ему купили ещё 3 диска. Сколько дисков стало у Вани?
-
В первой группе детского сада 5 детей, во второй на 3 ребёнка меньше. Сколько детей во второй группе?
-
На ветке сидело 3 воробья и 2 снегиря. Сколько всего птиц сидело на ветке?
-
Серёжа исписал за первую четверть 3 тетради, за вторую четверть – 4 тетради, а за третью четверть столько, сколько за первую и вторую вместе. Сколько тетрадей исписал Серёжа в третьей четверти?
-
В одном стручке 5 горошин и в другом столько же. Сколько горошин в двух стручках?
-
На стоянке было 2 машины. Вечером приехало ещё 2 машины. Сколько машин стало?
-
У кошки 4 белых и столько же черных котят. Сколько всего котят у кошки?
-
В букете 2 колокольчика, 5 ромашек, а васильков столько, сколько колокольчиков и ромашек вместе. Сколько васильков в букете?
-
На кусте было 3 распустившиеся розы. Скоро распустилось ещё 3 роз. Сколько роз стало на кусте?
-
В спортивном зале занималось 6 человек. Когда несколько человек пришло, то стало 10 человек. Сколько человек пришло в спортивный зал?
-
У подъезда росло 4 дерева. Дети посадили столько же деревьев. Сколько деревьев стало у подъезда?
-
У мамы было 4 гвоздики. Потом ей подарили ещё 3 гвоздики. Сколько гвоздик стало у мамы?
-
На даче росли 4 куста смородины. Посадили ещё 2 куста. Сколько кустов смородины стало на даче?
-
Бабушка испекла 10 пирожков. После обеда их осталось 9. Сколько пирожков съели за обедом?
-
На опушке играло 7 лисят. Когда несколько лисят убежало, осталось 3 лисёнка. Сколько лисят убежало?
-
В первый день Митя нарисовал 3 рисунка, во второй 6 рисунков. Сколько всего рисунков теперь у Мити?
-
В классе 9 дисков. Из них 7 с песнями, а остальные со сказками. Сколько дисков со сказками в классе?
ТИПЫ ПРОСТЫХ ЗАДАЧ
Задачи на нахождение суммы
В вазе 3 белых и 2 розовых гвоздики. Сколько всего гвоздик в вазе?
Б




 . – 3 г.
. – 3 г.
Р. – 2 г. ? г.
3 + 2 = 5 (г.)
Ответ: 5 гвоздик в вазе.
Во дворе было 3 мальчика. К ним пришли ещё 2 мальчика. Сколько мальчиков стало во дворе?
Б



 ыло – 3 м.
ыло – 3 м.
Пришли – 2 м.
Стало – ? м.
3 + 2 = 5 (м.)
Ответ: 5 мальчиков стало во дворе.
В пакете лежали 3 зелёных , 2 жёлтых яблока, а красных яблок столько сколько зелёных и жёлтых яблок вместе. Сколько красных яблок лежало в пакете?
З




 . – 3 яб.
. – 3 яб.
Ж. – 2 яб. К. – ? яб.
3 + 2 = 5 (яб.)
Ответ: 5 яблок в пакете.
Задачи на нахождение остатка
Н






 а тарелке было 5 персиков. 3 персика съели. Сколько персиков осталось на тарелке?
а тарелке было 5 персиков. 3 персика съели. Сколько персиков осталось на тарелке?
Было – 5 п.
Съели – 3 п.
Осталось – ? п.
5 – 3 = 2 (п.)
Ответ: 2 персика осталось на тарелке.
Задачи на увеличение и уменьшение числа на несколько единиц
Антон нашёл 5 больших подосиновиков, а маленьких на 2 больше. Сколько маленьких подосиновиков нашёл Антон?
Б




. – 5 п.
М






. –? п., на 2 п. больше
Рассуждай так: На 2 больше, это значит столько же сколько и больших подосиновиков и ещё 2.Значит надо к 5 прибавить ещё два.
5 + 2 = 7 (п.)
Ответ: 7 маленьких подосиновиков нашёл Антон.
У



 Иры 5 кукол, а у Ани на 2 куклы меньше. Сколько кукол у Ани?
Иры 5 кукол, а у Ани на 2 куклы меньше. Сколько кукол у Ани?
Ир. – 5 к.
Ан. –? к., на 2 к. меньше





Рассуждай так: На 2 меньше, это значит столько же сколько и кукол у Иры, но без 2. Значит надо от 5 отнять два.
5 – 2 = 3(к.)
Ответ: 3 куклы у Ани.
Задачи на разностное сравнение
У

 Вики 5 тетрадей, а у Марины 2 тетради. На сколько больше тетрадей у Вики, чем у Марины? (На сколько меньше тетрадей у Марины, чем у Вики?)
Вики 5 тетрадей, а у Марины 2 тетради. На сколько больше тетрадей у Вики, чем у Марины? (На сколько меньше тетрадей у Марины, чем у Вики?)
В
 . – 5 т.
. – 5 т.
М
 . – 2 т. на ? т.
. – 2 т. на ? т.
Рассуждай так: Чтобы узнать на сколько одно число больше или меньше другого, надо из большего вычесть меньшее.
5 – 2 = на 3(т.)
Ответ: на 3 тетради больше у Вики, чем у Марины
Задачи на нахождение неизвестного слагаемого
В



 саду было 6 роз. Из них 4 красные, а остальные розовые. Сколько розовых роз было в саду?
саду было 6 роз. Из них 4 красные, а остальные розовые. Сколько розовых роз было в саду?
К




 . – 4 р.
. – 4 р.
Р. – ? р. 6 р.
6 – 4 = 2 (р.)
Рассуждай так: чтобы найти неизвестное слагаемое надо из суммы вычесть известное слагаемое.
Ответ: 2 розовые розы цвели в саду.
У Саши 6 самолётиков. Когда мама купила ему ещё несколько самолётиков, у него их стало 10. Сколько самолётиков купили Саше?
Было – 6 с.
Купили – ? с.
Стало – 10 с.
10 – 6 = 4 (с.)
Рассуждай так: чтобы найти неизвестное слагаемое надо из суммы вычесть известное слагаемое.
Ответ: 4 самолётика купили Саше.
Задачи на нахождение неизвестного уменьшаемого
В саду были розы. 4 розы срезали, и осталось ещё 3 розы Сколько роз было в саду?
Было –? р.
Срезали – 4 р.
Осталось – 3 р.
3 + 4 = 7 (р.)
Рассуждай так: Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
Ответ: 7 роз цвели в саду.
Задачи на нахождение неизвестного вычитаемого
В саду цвели 7 роз. Несколько роз срезали, и осталось ещё 3 розы Сколько роз срезали в саду?
Цвели –7 р.
Срезали – ? р.
Осталось – 3 р.
7 – 3 = 4 (р.)
Рассуждай так: Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность
Ответ: 4 розы срезали в саду.
Задачи на умножение
В одном наборе 3 ручки. Сколько ручек в 7 наборах?
1н.- 3 р.
7н. – ? р.
Рассуждай так: 3 ручки повторяются 7 раз, значит,
3 • 7 = 21(р.)
Ответ: 21 ручка в 7 наборах.
Задачи на увеличение и уменьшение числа в несколько раз
Антон нашёл 6 больших подосиновиков, а маленьких в 2 раза больше. Сколько маленьких подосиновиков нашёл Антон?
Б. – 6 п.
М. –? п., в 2 раза. больше
6 • 2 = 12(п.)
Ответ: 12 маленьких подосиновиков нашёл Антон.
У Иры 6 кукол, а у Ани в 2 раза меньше. Сколько кукол у Ани?
Ир. – 6 к.
Ан. –? к., в 2 раза меньше
6 : 2 = 3(к.)
Ответ: 3 куклы у Ани.
Задачи на деление по содержанию и на равные части
18 апельсинов раздали детям по 3 штуки каждому. Сколько детей получили апельсины?
1 р.— Зап.
? д. —18 ап.
18:3 = 6 (д.)
Ответ: 6 детей получили апельсины.
18 апельсинов раздали 6 детям поровну. Сколько апельсинов получил каждый ребёнок?
6 д.—18 ап.
1 р. — ? ап.
18:6 = 3(ап.)
Ответ: 3 апельсина получил каждый ребёнок.
Задачи на кратное сравнение
В одной вазе 6 яблок, в другой вазе 3 яблока. Во сколько раз в первой вазе яблок больше, чем во второй? (Во сколько раз во второй вазе меньше яблок, чем в первой?)
I – 6 яб. Во ? раз
II – 3 яб
Рассуждай так: Чтобы узнать, во сколько раз одно число больше или меньше другого, надо большее число разделить на меньшее:
6:3 = в 2(р.)
Ответ: в 2 раза больше яблок в первой вазе, чем во второй (в 2 раза меньше яблок во второй вазе, первой).
Задачи с косвенными вопросами
В одной книжке 10 картинок. Это на 3 картинки меньше, чем во второй книжке. Сколько картинок во второй книжке?
I – 10 к., это на 3 к. меньше
II – ? к.
Рассуждай так: Если в первой книжке на 3 картинки меньше, то во второй книжке на 3 картинки больше:
10 + 3 = 13 (к.)
Проверяю: в одной книжке 10 картинок, а другой 13. В первой книжке на 3 картинки меньше. Верно.
Ответ: 13 картинок во второй книжке.
В одной книжке 10 картинок. Это на 3 картинки больше, чем во второй книжке. Сколько картинок во второй книжке?
I – 10 к., это на 3 к. больше
II – ? к.
Рассуждай так: Если в первой книжке на 3 картинки больше, то во второй книжке на 3 картинки меньше:
10 – 3 = 7 (к.)
Проверяю: в одной книжке 10 картинок, а другой 7. В первой книжке на 3 картинки больше. Верно.
Ответ: 7 картинок во второй книжке.
У Валеры 4 машинки. Это в 2 раза меньше, чем у Серёжи. Сколько машинок у Серёжи?
В. – 4 м., это в 2 раза меньше
С. – ? к.
Рассуждай так: Если у Валеры машинок в 2 раза меньше, то у Серёжи их в 2 раза больше.
4 • 2 = 8(м.)
Проверяю: у Валеры 4 машинки, у Серёжи 8 машинок. У Валеры машинок в 2 раза меньше. Верно.
Ответ: 8 машинок у Серёжи.
У Валеры 4 машинки. Это в 2 раза больше, чем у Серёжи. Сколько машинок у Серёжи?
В. – 4 м., это в 2 раза больше
С. – ? к.
Рассуждай так: Если у Валеры машинок в 2 раза больше, то у Серёжи их в 2 раза меньше.
4 : 2 = 2(м.)
Проверяю: у Валеры 4 машинки, у Серёжи 2 машинки. У Валеры машинок в 2 раза больше. Верно.
Ответ: 2 машинки у Серёжи.
Задачи на цену, количество и стоимость
Килограмм яблок стоит 30 рублей. Сколько стоят 3 кг яблок?
Цена Количество Стоимость
30 руб. 3 кг ? руб.
Ст = Ц • К
30 • 3 = 90 (руб.)
Ответ: 90 рублей заплатили за 3 кг яблок.
За 3 кг слив заплатили 60 рублей. По какой цене покупали сливы?
Цена Количество Стоимость
? руб. 3 кг 60 руб.
Ц = Ст : К
60 : 3 = 20 (руб.)
Ответ: 20 рублей стоит 1 кг слив.
Килограмм груш стоит 20 рублей. Сколько груш купили, если за покупку заплатили 60 рублей?
Цена Количество Стоимость
20 руб. ? кг 60 руб.
К = Ст : Ц
60 : 20 = 3 (кг)
Ответ: 3 кг груш купили.
Задачи нахождение числа по доле и доли по числу.
В книге 90 страниц. Дедушка прочитал 1/3 часть книги. Сколько страниц прочитал дедушка?
Вся кн. – 90 стр.
1/3 кн. – ? стр.
Рассуждай так: Чтобы найти долю числа, надо число разделить на знаменатель и умножить на числитель.
60 : 3 • 1 = 20 (стр.)
Ответ: 20 страниц прочитал дедушка.
Длина ¼ верёвки составляет 8 метров. Определи длину всей верёвки.
¼ в . – 8м
Вся в. – ? м
Рассуждай так: Чтобы найти число по доле, надо число разделить на числитель и умножить на знаменатель.
8: 1 • 4 = 32 (м)
Ответ: 32 метра длина всей верёвки.
Методика Узоровой-Нефёдовой
ПО РЕШЕНИЮ ВСЕХ ВИДОВ СОСТАВНЫХ ЗАДАЧ.
ЦЕПОЧКА РАССУЖДЕНИЙ
После нахождения опорных слов, составления краткой записи или чертежа, мы настоятельно рекомендуем ЛЮБУЮ задачу начинать решать С КОНЦА, то есть с ВОПРОСА. Эта СИСТЕМАТИЧЕСКАЯ ЦЕПОЧКА РАССУЖДЕНИЙ приведет ребёнка к правильному решению ЛЮБОЙ ЗАДАЧИ.
В приведённых ниже разборах задач, ЦЕПОЧКА РАССУЖДЕНИЙ ТОГО, ЧТО НАДО НАЙТИ сначала идёт после слов: Рассуждай так.
Потом ЦЕПОЧКА РАССУЖДЕНИЙ превращается в схему, типа:
Осталось Ушло
Как составлялась эта схема? Была задача:
Во дворе гуляли 16 ребят. Сначала домой ушли 6 девочек, а потом 3 мальчика. Сколько ребят осталось во дворе?
Пошаговый образец рассуждения вслух ребёнка:
Решаем с конца, с вопроса.
– Что спрашивается в задаче?
– сколько ребят осталось.
– значит, первое слово в цепочке пишем – осталось.
Осталось
– чтобы узнать, сколько осталось, надо знать, сколько БЫЛО и сколько УШЛО. Сколько БЫЛО мы знаем, сколько УШЛО – не знаем, значит в цепочке дописываем слово Ушло.
Осталось Ушло
– так как в цепочке ДВА СЛОВА, то, значит, в задаче ДВА ДЕЙСТВИЯ.
РЕШАЕМ ЗАДАЧУ, РАСРУЧИВАЕМ ЦЕПОЧКУ С КОНЦА.
– Первое слово с конца – УШЛО, значит, сначала узнаем, сколько ребят УШЛО:
6+3 = 9 (р)
– Второе слово в цепочке – Осталось. Значит, вторым действием мы отвечаем на главный вопрос задачи и узнаём, сколько ребят Осталось.
16 – 9 = 7 (р)
Почему так важна такая ЦЕПОЧКА РАССУЖДЕНИЙ,
которая пишется слева направо, а раскручивается с конца, справа налево?
Почему ЦЕПОЧКА РАССУЖДЕНИЙ НЕОБХОДИМА
при решении КАЖДОЙ ЗАДАЧИ?
-
Потому что ТОЛЬКО при ТАКОМ систематическом ПОДХОДЕ Ваш ребёнок сможет решать ЛЮБУЮ ЗАДАЧУ в начальной и средней школе, экономя Вам лично время, силы и нервы.
-
Потому что это развивает логику ребёнка
-
Потому что такая ЦЕПОЧКА РАССУЖДЕНИЙ развивает ВСЕГО ребёнка по ВСЕМ НАПРАВЛЕНИЯМ.
P.s. Я знаю, что эту задачу можно решить другими способами. Тогда будут другие цепочки.
ТИПЫ СОСТАВНЫХ ЗАДАЧ
Задачи на нахождение суммы
Антон нашёл 5 больших подосиновиков, а маленьких на 2 больше. Сколько всего подосиновиков нашёл Антон?
Б
. – 5 п.
М. –? п., на 2 п. больше ? п.
Рассуждай так: Чтобы узнать, сколько всего подосиновиков нашёл Антон, нужно знать, сколько больших и маленьких подосиновиков он нашёл. Сколько больших подосиновиков он нашёл мы знаем. Надо найти сколько маленьких.
1)5 + 2 = 7 (п.) – маленьких
2) 5 + 7 = 12 (п.)
5 + (5 + 2) = 12 (п.)
Ответ: 12 подосиновиков нашёл Антон.
У Иры 5 кукол, а у Ани на 2 куклы меньше, чем у Ани, а у Светы кукол столько, сколько их у Иры и Ани вместе Сколько кукол у Светы?
И
р. – 5 к.
Ан. –? к., на 2 к. меньше С. – ? к.
Рассуждай так: Чтобы узнать сколько кукол у Светы, нужно знать, сколько кукол у Иры и Ани вместе. Сколько кукол у Иры мы знаем. Нужно узнать, сколько кукол у Ани.
1)5 – 2 = 3(к.) – у Ани
2) 5 + 3 = 8 (к.)
5 + (5 – 2) = 8 (к.)
Ответ: 8 кукол у Светы.
Антон нашёл 6 больших подосиновиков, а маленьких в 2 раза больше. Сколько всего подосиновиков нашёл Антон?
Б . – 6 п.
. – 6 п.
М. –? п., в 2 раза больше ? г.
Рассуждай так: Чтобы узнать, сколько всего подосиновиков нашёл Антон, нужно знать, сколько больших и маленьких подосиновиков он нашёл. Сколько больших подосиновиков он нашёл мы знаем Надо найти сколько маленьких.
1) 6 • 2 = 12(п.)– маленьких
2) 6 + 12 = 18 (п.)
6 + 6 • 2 = 18 (п.)
Ответ: 18 подосиновиков нашёл Антон.
У Иры 6 кукол, а у Ани в 2 раза меньше. Сколько кукол у Иры и Ани вместе?
Ир. – 6 к.
Ан. –? к., в 2 раза меньше ? к.
Рассуждай так: Чтобы узнать сколько всего кукол Иры и Ани вместе, нужно знать, сколько кукол у Иры и сколько кукол у Ани. Сколько кукол у Иры мы знаем Надо найти сколько кукол у Ани.
1) 6 : 2 = 3(к.) у Ани
2) 6 + 3 = 9 (к.)
6 + 6 : 2 = 9 (к.)
Ответ: 9 кукол у Иры и Ани вместе.
У Валеры 4 машинки. Это в 2 раза меньше, чем у Серёжи. Сколько машинок у мальчиков?
В. – 4 м., это в 2 раза меньше ? м.
С. – ? к.
Рассуждай так: Чтобы определить, сколько машинок у мальчиков, надо выяснить, сколько машинок у каждого мальчика. Сколько машинок у Валеры, известно. Надо узнать, сколько машинок у Серёжи, а потом узнать, сколько машинок у мальчиков. Если у Валеры машинок в 2 раза меньше, то у Серёжи их в 2 раза больше.
1) 4 • 2 = 8(м.) у Серёжи
2) 4 + 8 = 12 (м.)
4 + 4 • 2 = 12 (м.)
Ответ: 12 машинок у мальчиков.
У Валеры 4 машинки. Это в 2 раза больше, чем у Серёжи. Сколько машинок у мальчиков?
В. – 4 м., это в 2 раза больше ? м.
С. – ? к.
Рассуждай так: Чтобы определить, сколько машинок у мальчиков, надо выяснить, сколько машинок у каждого мальчика. Сколько машинок у Валеры, известно. Надо узнать, сколько машинок у Серёжи, а потом узнать, сколько машинок у мальчиков. Если у Валеры машинок в 2 раза больше, то у Серёжи их в 2 раза меньше.
1) 4 : 2 = 2(м.) у Серёжи
2) 4 + 2 = 6 (м.)
4 + 4 : 2 = 6(м.)
Ответ: 6 машинок у мальчиков.
Задачи на нахождение остатка
Во дворе были 7 девочек и 9 мальчиков, 3 мальчика ушли. Сколько детей осталось во дворе?
Было Ушли Осталось
Д. – 7 ч. ? ч.
М. – 9 ч. 3 ч. ? ч.
1 способ
Осталось Было
1) Сколько детей было во дворе?
7 +9 = 16 (р.)
2) Сколько детей осталось во дворе?
16-3 = 13 (р.)
(7+ 9)-3 = 13 (р.)
2 способ
Осталось детей Осталось мальчиков
1) Сколько мальчиков осталось во дворе?
9-3 = 6(м.)
2) Сколько детей осталось во дворе?
6 + 7 = 13 (д.)
7+ (9-3) = 13 (д.)
Ответ: 13 детей остались во дворе
Во дворе гуляли 16 ребят. Сначала домой ушли 6 девочек, а потом 3 мальчика. Сколько ребят осталось во дворе?
Гуляли Ушли Осталось
16 чел. Д. – 6 чел. ? чел.
М. – 3 чел. ? чел.
1 способ
Осталось Ушло
1) Сколько ребят ушло домой?
6 + 3 = 9 (чел.)
2) Сколько ребят осталось во дворе?
16-9 = 7 (чел.)
16-(6 + 3) = 7 (чел.)
2 способ
Осталось детей Осталось после девочек
1) Сколько детей осталось во дворе, после того как ушли девочки?
16-6 = 10 (чел.)
2) Сколько детей осталось во дворе?
10- 3 = 7 (чел.)
16-6-3 = 7 (чел.)
Ответ: 7 ребят, остались во дворе
У Вали в одной коробке 8 ручек, во второй на 2 ручки больше. 10 ручек Валя подарила Сколько ручек осталось у Вали?
Было Подарила Осталось
I – 8 р.
II – ? р., на 2 р. больше ? р. 10 р. ? р.
Осталось Было II
Чтобы узнать, сколько ручек осталось у Вали, надо мать, сколько всего было ручек, и сколько ручек ‘она подарила. Сколько ручек подарила Валя, мы знаем. Чтобы узнать, Сколько ручек было, нужно знать, сколько ручек в каждой коробке. Сколько ручек в первой коробке, мы знаем. Узнаем, сколько ручек во второй коробке.
1) 8 + 2 = 10 (р.) — во второй коробке
2) 8 + 10 = 18 (р.) — было
3) 18 – 10 = 8 (р.)
(8 + (8+2)) – 10 = 8 (р.)
Ответ: 8 ручек осталось.
У Вали в двух коробках по 8 ручек, 10 ручек Валя подарила. Сколько ручек осталось у Вали?
Было — 2 к. по 8 р.
Подарила —10 р.
Осталось—? р.
Рассуждай так: Чтобы определить, сколько ручек осталось у Вали, надо знать, сколько ручек было, и сколько она их подарила. Сколько ручек Валя подарила, известно. Узнаем, сколько ручек было у Вали.
1) 8 • 2 =16 (р.) — было у Вали
2) 16 – 10 = 6 (р.)
8 • 2-10 = 6 (р.)
Ответ: 6 ручек осталось у Вали.
Задачи на нахождение третьего слагаемого
Три девочки собирали грибы. Первая нашла 5 грибов, вторая 3. Сколько грибов нашла третья девочка, если всего они собрали 10 грибов?
I – 5 г.
II – 3 г. 10 г.
III – ? г.
Рассуждай так: Чтобы узнать, сколько грибов нашла третья девочка, необходимо знать, сколько грибов нашли вместе первая и вторая девочка.
1) 5 + 3 = 8 (г.) — нашли I и II девочки вместе
2) 10 – 8 = 2 (г.)
10 – ( 5+3) = 2 (г.)
Ответ: 2 гриба нашла третья девочка
Задачи на нахождение вычитаемого
У хомяка было 6 земляных и 4 грецких орехов. Хомяк сгрыз несколько орехов, у него осталось 7 орехов. Сколько орехов сгрыз хомяк?
Было Сгрыз Осталось
З. – 6 ор.
Г. – 4 ор. ? ор. ? ор. 7 ор.
Сгрыз Было
Рассуждай так: Чтобы узнать, сколько орехов сгрыз хомяк, знать, сколько у него их было и сколько осталось. Сколько осталось орехов, мы знаем. Необходимо узнать, всего было орехов
1)6 + 4 = 10 (ор.) —было у хомяка
2)10-7 = 3(ор.)
(6+4)-7 = 3(ор.)
Ответ: 3 ореха сгрыз хомяк.
У причала стояло 8 катеров. Утром ушло в море 3 катера. Сколько катеров ушло в море днём, если вечером осталось 4 катера?
Стояло Ушло Осталось
8 к. Ут. – 3 к. ? к. 4 к.
Д. – ? к.
Ушло Днём Ушло Всего
Рассуждай так: Чтобы узнать, сколько катеров ушло в море днём, надо знать, сколько катеров было, ушло и осталось. Сколько было и осталось катеров, мы знаем. Чтобы знать, сколько катеров ушло в море днём, надо знать, сколько всего катеров ушло в море.
1)8 – 4 = 4(к.) — ушло в море
2)4 – 3 = 1 (к.)
(8 – 4) – 3 = 1 (к.)
Ответ: 1 катер ушёл в море днём
В вазе было 3 красных и 6 зелёных яблок, Когда мама жила в вазу ещё несколько яблок, в вазе стало 12 яблок. Сколько яблок мама положила в вазу?
Было Положила Осталось
К. – 3 яб. ? яб. ? яб. 12 яб.
З. – 6 яб.
Рассуждай так: Чтобы узнать, сколько яблок мама положила в вазу нужно знать, сколько яблок было и стало в вазе. Сколько стало яблок, мы знаем. Необходимо узнать, сколько яблок было в вазе
1) 3 + 6 =9 (яб.) — было в вазе,
2)12-9 = 3(яб.)
12 – (3 + 6) = 3 (яб.)
Ответ: 3 яблока мама положила в вазу
У хомяка было 4 стручка гороха по 6 горошин в каждом стручке. Когда несколько горошин хомяк съел, у него осталось 7 горошин. Сколько горошин съел хомяк?
Было– 4 с. по 6 г.
Съел —? г.
Осталось -7 г.
Рассуждай так: Чтобы определить, сколько горошин съел хомяк, надо знать, сколько у него было и осталось горошин. Сколько осталось горошин, известно. Надо узнать, сколько было горошин у хомяка.
1)6 • 4 = 24 (г.) – было
2) 24-7 =17(г.)
6 • 4-7= 17 (г.)
Ответ: 17 горошин съел хомяк.
Задачи на нахождение уменьшаемого
У хомяка были орехи. Когда хомяк сгрыз 6 земляных орехов и 4 грецких ореха, то у него осталось 7 орехов. Сколько орехов было у хомяка?
Было Сгрыз Осталось
? ор. З. – 6ор. ? ор. 7ор.
Г. – 4 ор.
Было Сгрыз
Рассуждай так: Чтобы узнать, сколько орехов было у. хомяка, необходимо знать, сколько он сгрыз и сколько у него осталось орехов. Сколько осталось орехов, мы знаем. Надо узнать, сколько всего орехов он сгрыз.
-
6 + 4 = 10 (ор.) — сгрыз
-
10 + 7 = 17 (ор.)
(6 + 4) +7 = 17 (ор.) Ответ: 17 орехов было у хомяка У причала стояли катера. Утром в море ушло 3 катера. Сколько катеров было в море у причала, если вечером осталось 8 больших и 4 маленьких катера? Было Ушло Осталось
? к. 3к. Б. – 8 к. ? к.
М. – 4 к.
Было Осталось Рассуждай так: Чтобы узнать, сколько катеров было у причала, надо знать, сколько катеров ушло и сколько осталось. Сколько в море ушло катеров, мы знаем. Необходимо узнать, сколько всего катеров осталось у причала.
1)8 + 4 = 12 (к.) осталось у причала
2)12 + 3 = 15 (к.)
(8+4) + 3 = 15 (к.)
Ответ: 15 катеров было у причала
В вазе были яблоки. Когда мама положила в вазу ещё 3 красных яблока и 6 зелёных яблок, в вазе стало 12 яблок. Сколько яблок было в вазе?
Было Положила Стало
? яб. К. – 3 яб. ? яб. 12 яб.
З. – 6 яб.
Было Положила Рассуждай так: Чтобы узнать, сколько яблок было в вазе, надо знать, сколько яблок положила мама и сколько их стало в вазе. Сколько стало яблок, мы знаем. Надо узнать, сколько всего яблок положила мама в вазу
1)3 + 6 = 9 (яб.) — положила мама
2)12-9=3(яб.)
12 – (3 + 6) = 3 (яб.)
Ответ: 3 яблока было в вазе
Бригаде строителей надо отремонтировать комнаты. После того как они отремонтировали 6 трёхкомнатных квартир, им осталось отремонтировать ещё 12 комнат. Сколько комнат надо отремонтировать строителям?
Надо отремонтировать—? ком.
Отремонтировали – 6 кв. по 3 ком.
Осталось-12 ком.
Надо отремонтировать Отремонтировали
Рассуждай так: Чтобы определить, сколько комнат надо отремонтировать строителям, надо знать, сколько они отремонтировали и сколько им осталось отремонтировать комнат. Сколько комнат осталось отремонтировать, известно. Требуется узнать, сколько они отремонтировали комнат.
1) 3 • 6 = 18 (к.) — отремонтировали
2) 18 + 12 = 30 (к.)
3 • 6+ 12 = 30 (к.)
Ответ: 30 комнат надо отремонтировать строителям.
Задачи на приведение к единице
В 7 одинаковых ящиках 28 кг киви. Сколько кг киви в 4 таких ящиках?
7 ящ. – 28 кг
4 ящ. – ? кг
4ящ. 1 ящ.
Рассуждай так: Чтобы узнать, сколько киви в 4 ящиках, надо сначала определить, сколько киви в 1 ящике.
1) 28 : 7 = 4 (кг) – в одном ящике
2) 4 • 4 = 16 (кг)
28 : 7 • 4 = 16 (кг)
Ответ: 16 кг киви в 4 ящиках.
В 7 одинаковых ящиках 28 кг киви. Сколько надо таких ящиков для 40 кг киви
7 ящ. – 28 кг
? ящ. – 40 кг
Ящ. для 40 кг 1 ящ.
Рассуждай так: Чтобы узнать, сколько потребуется ящиков для 40 кг киви, надо сначала определить, сколько киви в 1 ящике.
1) 28 : 7 = 4 (кг) – в одном ящике
2) 40 : 4 = 10 (ящ.)
40 : (28 : 7) = 10 (ящ.)
Ответ: 10 ящиков надо для 40 кг киви.
Задачи на разностное и кратное сравнение
В саду росло 10 деревьев. Из них 8 яблонь, а остальные груши. На сколько больше яблонь, чем груш?
Яб. – 8д.
Г. – ? д. на ? д. 10 д.
На ? д. Г.
Рассуждай так: Чтобы узнать, на сколько больше яблонь, чем груш, надо знать, сколько груш росло в саду.
-
– 8 = 2 (д.) – груши
2)8 – 2 = на 6 (д.)
8 – (10 – 8) = на 6 (д.)
Ответ: на 6 яблонь в саду больше, чем груш
Платье стоит 180 руб., а юбка в 3 раза дешевле. На сколько рублей платье дороже, чем юбка?
П.-180 руб.
Юб. – ? руб., в 3 раза дешевле на ? руб.
На ? руб. Юб.
Рассуждай так: Чтобы узнать, на сколько одно число больше или меньше другого, надо из большего числа вычесть меньшее.
Чтобы узнать, на сколько дороже платье, чем юбка, надо определить, сколько стоит юбка.
1) 180 : 3 = 60 (руб.) — стоит юбка
2)180-60 = на 120(руб.)
180-180 : 3 = на 120 (руб.)
Ответ: на 120 руб. платье дороже, чем юбка.
Платье стоит 180 руб., а юбка на 120 руб. дешевле. В о сколько раз платье дороже юбки?
П.-180 руб.
Юб. – ? руб., на 120 руб. дешевле во ? раз
Во? раз Юб.
Рассуждай так: Чтобы узнать, во сколько раз одно число больше или меньше другого, надо большее число разделить на меньшее
Чтобы узнать, во сколько раз дороже стоит платье, чем юбка, надо знать, сколько стоит юбка.
1) 180 – 120 == 60 (руб.) — стоит юбка
2) 180: 60=в 3 (раза)
180:(180-120) = в 3(раза)
Ответ: в 3 раза дороже стоит платье, чем юбка.
У Валеры 4 машинки. Это в 2 раза меньше, чем у Сережи. На сколько машинок меньше у Валеры, чем у Серёжи?
В. — 4м., в 2 раза меньше
С. – ? м. На ? м.
На ? м. С.
Рассуждай так: Чтобы узнать, на сколько одно число больше или меньше другого, надо из большего числа вычесть, меньшее.
Чтобы узнать, на сколько машинок меньше у Валеры, чем у Серёжи, надо знать, сколько машинок у каждого мальчика. Сколько машинок у Валеры, известно. Надо узнать, сколько машинок у Серёжи. Если у Валеры машинок в 2 раза меньше, то у Сережи — в 2 раза больше.
1)4 • 2 = 8 (м.) — у Серёжи
2)8 – 4= на 4 (м.)
4 • 2 – 4 = на4(м.)
Ответ: на 4 машинки меньше у Валеры, чем у Серёжи.
У Валеры 4 машинки. Это на 2 машинки больше, чем у Серёжи. Во сколько раз больше машинок у Валеры, чем у Серёжи?
В. — 4м., на 2 м. больше
С. – ? м. во ? раз.
Во ? раз С.
Рассуждай так: Чтобы узнать, во сколько раз одно число больше или меньше другого, надо большее число разделить на меньшее.
Чтобы узнать, сколько машинок у мальчиков, надо знать, сколько машинок у каждого мальчика. Сколько машинок у Валеры, известно. Надо узнать, сколько машинок у Серёжи, а потом узнать, сколько машинок у мальчиков. Если у Валеры машинок в 2 раза больше, то у Серёжи — в 2 раза меньше.
1)4 – 2 = 2 (м) — у Серёжи
2) 4: 2 = в 2 (раза)
4 : (4 – 2) = в 2 (раза)
Ответ: в 2 раза больше машинок у Валеры, чем у Серёжи.
В вазе стояло 10 белых гвоздик, розовых на 5 меньше, чем белых. А красных гвоздик столько, сколько белых и розовых вместе. Во сколько раз больше в вазе стояло красных гвоздик, чем розовых?
Б. – 10 г.
Р. – ? г., на 5 г. меньше во ? раз
К. – ? г.
Во ? раз К Р
Рассуждай так: Чтобы узнать, во сколько раз одно число больше или меньше другого, надо большее число разделить на меньшее.
Чтобы узнать, во сколько раз больше в вазе стояло красных гвоздик, чем розовых, надо знать, сколько красных, белых и розовых гвоздик в вазе. Известно, сколько белых гвоздик л вазе. Для того чтобы узнать, сколько красных гвоздик, надо знать, сколько розовых гвоздик в вазе.
1) 10 – 5 = 5 (г.) — розовых
2) 10 + 5 = 15 (г.) — красных
3)15:5 = в 3(раза)
Ответ: в 3 раза больше в вазе стояло красных гвоздик, чем розовых.
В саду росло 4 ряда яблонь по 8 деревьев в ряду и 2 груш по 5 деревьев в ряду. На сколько больше в саду яблонь, чем груш?
Яб. – 4 р. по 8 д.
Г. – 2 р. по 5 д. на ? д.
На ? д. Г. Яб.
Рассуждай так: Чтобы узнать, на сколько одно число больше или меньше другого, надо из большего числа вычесть меньшее. Чтобы узнать, на сколько больше яблонь, чем груш, надо знать, сколько яблонь и сколько груш росло в саду.
1)8 • 4 = 32 (д.) — яблони
2)5 • 2 = 10(д.) —груши
3) 32 – 10 = на 22 (д.)
8 • 4 – 5 • 2 = на 22 (д.)
Ответ: на 22 яблони в саду больше, чем груш.
В 5 букетах 40 ромашек и в 3 букетах 12 васильков. Во сколько раз больше в одном букете ромашек, чем васильков?
Цветов в 1 букете Кол-во букетов Всего цветов
Р. – ? ц. 5 б. 40 ц.
В. – ? ц. Во ? раз 3 б. 12 ц.
Во ? раз Вас. в 1 букете Роз в 1 букете
Рассуждай так: Чтобы узнать, во сколько раз одно число больше или меньше другого, надо большее число разделить на меньшее.
Чтобы узнать, во сколько раз в одном букете ромашек больше, чем васильков, надо знать, сколько васильков и сколько ромашек в одном букете.
1) 40 : 5 = 8 (р.) – в одном букете
2) 12: 3= 4 (в.) – в одном букете
3) 8 : 4 = в 2 (раза)
(40 : 5) : ( 12 : 3) = в 2 (раза)
Ответ: в 2 раза больше в одном букете ромашек, чем васильков
Задачи на нахождение суммы двух произведений
У продавца было 5 ящиков со сливами по 7 кг в каждом и 4 ящика с виноградом по 12 кг в каждом . Сколько всего кг фруктов было у продавца?
Масса 1 ящика Кол-во ящиков Масса всех ящиков
С. – 7 кг 5 ящ. ? кг ? кг
В. – 12 кг 4 ящ. ? кг
Всего В. С.
Рассуждай так: Чтобы узнать, сколько фруктов у продавца, надо знать, сколько винограда и сколько слив.
1) 7• 5 = 35 (кг) – сливы
2) 12 • 4 = 48 (кг) – винограда
3) 35 + 48 = 83 (кг)
7• 5 + 12 • 4 = 83 (кг)
Ответ: 83 кг фруктов было у продавца.
Задачи на нахождение неизвестного слагаемого
С трёх грядок собрали по 5 кг клубники и с нескольких грядок по 4 кг земляники. Всего собрали 23 кг ягод. Определите число грядок, с которых собрали землянику.
К. – 3 г. по 5 кг
3.— ? г по 4 кг 23 кг
Грядок Земляники Кг земляники Кг клубники
Рассуждай так: Чтобы узнать число грядок, с которых собрали землянику, нужно знать, сколько собрали всего килограммов клубники и сколько всего килограммов земляники.
1) 5 • 3 = 15 (кг) — клубники
2) 23 – 15 = 8 (кг) – земляники
3) 8: 4 = 2 (г.)
Ответ: с двух грядок собрали землянику.
В столовой за неделю израсходовали 60 кг крупы. 4 дня расходовали по 12 кг крупы в день, а остальную поровну в следующие 3 дня. Сколько крупы в день расходовали в последние дни?
4дня – по 12 кг
3 дня – по ? кг 60 кг
Кг в день Кг за 3 дня Кг за 4 дня
Рассуждай так: Чтобы определить, сколько крупы в день расходовали в последние дни, надо знать, сколько всего крупы за 4 дня и сколько крупы израсходовали за 3 дня.
1) 12 • 4 = 48 (кг) — израсходовано за 4 дня
2) 60 — 48 = 12 (кг) — израсходовано за 3 дня
3) 12 : 3 = 4 (кг)
(60 —12 • 4): 3=4 (кг)
Ответ: по 4 кг крупы расходовали в последние дни.
Задачи на деление суммы на число и числа на сумму
В магазин привезли 48 кг пряников и печенья. В двух коробках были пряники, а в четырёх коробках печенье. Сколько килограммов в каждой коробке?
магазин привезли 48 кг пряников и печенья. В двух коробках были пряники, а в четырёх коробках печенье. Сколько килограммов в каждой коробке?
Пр. – 2 к. по ? кг
П. – 4 к. по ? кг 48 кг
Масса 1 к. Всего к.
Рассуждай так: Чтобы определить массу каждой коробки, надо знать, сколько всего привезли коробок с пряниками и печенье.
1. 2 + 4 = 6 (к.) – привезли в магазин
2. 48 : 6 = 8 (кг)
48 : ( 2 + 4) = 8 (кг)
Ответ: масса каждой коробки 8 кг.
15 белых роз и 10 розовых поставили в вазы по 5 роз каждую. Сколько потребовалось ваз?
Б. – 15 р. ? в. по 5 роз
Р. – 10 р.
В. Всего роз
Рассуждай так: Чтобы определить, сколько нужно ваз, надо знать, сколько всего было белых и розовых роз.
-
10 = 25 (р.) – поставили в вазы
2)25 : 5 = 5 (в.)
(15 + 10) :5 = 5 (в.)
Ответ: 5 ваз потребовалось
Задачи на нахождение цены, количества, стоимости.
Мама купила 5 столовых ложек и 8 чайных ложек по одинаковой цене. За столовые ложки она заплатила 100 рублей. Сколько стоили чайные ложки?
Цена Количество Стоимость
С. одина 5 л. 100 руб.
Ч. ковая 8 л. ? руб.
Стоимость Ч. Цена С.
Рассуждай так: Чтобы найти цену, надо знать стоимость и количество. Количество столовых ложек и их стоимость известна.. Можно найти цену.
1) Ц = Ст: К
100 : 5 = 20 (руб.) – цена столовой ложки
2) Ст = Ц • К
20 • 8 = 160 (руб.)
100 :5 • 8 = 160 (руб.)
Ответ: 160 рублей мама заплатила за чайные ложки
Мама купила 5 столовых ложек и несколько чайных ложек . Цена столовой ложки 20 рублей, а чайной – 10 рублей. Стоимость столовых и чайных ложек одинаковая. Сколько мама купила чайных ложек?
Цена Количество Стоимость
С. 20 руб. 5 л. одина-
Ч. 10 руб. ? л. ковая
Кол-во Ч. Стоимость С.
Рассуждай так: Чтобы найти стоимость, надо знать цену и количество. Количество столовых ложек и их цена известна. Можно найти стоимость.
1) Ст = Ц • К
20 • 5 = 100 (руб.) – стоимость столовых ложек
2) К = Ст : Ц
100 : 10 = 10 (л.)
(20• 5 ) : 10 = 10 (л.)
Ответ: 10 чайных ложек купила мама.
Задачи на пропорциональное движение
В первых классах школы учится всего 75 детей. В каждом классе по 13 девочек и 12 мальчиков. Сколько всего девочек и сколько мальчиков в первых классах?
Детей в одном классе Кол-во классов Всего детей
Д. – 13 чел. ? кл. ? чел.
М. – 12 чел. ? чел. 75 чел.
М. или Д. Кол-во классов Всего детей в одном классе
Рассуждай так: Чтобы определить, сколько всего девочек и сколько всего мальчиков, мы должны знать количество классов, а для этого надо выяснить, сколько детей в одном классе.
1)13 + 12 = 25(чел.) – в одном классе
2) 75 : 25 = 3 (кл.) – в школе
3) 13 • 3 = 39 |чел.) – девочек
4) 12 • 3 – 36 (чел.) – мальчиков
Ответ: в первых классах 39 девочек и 36 мальчиков
В девяти клетках 20 серых и 25 белых кроликов. Сколько клеток с серыми кроликами и сколько клеток с белыми кроликами?
Кроликов в клетке Кол-во клеток Всего кроликов
С. – ? к. ? кл. 20кр.
Б. – ? к. ? кл. 9 кл. 25 кр.
Кол-во клеток С. или Б. Кроликов в 1 клетке Всего кроликов
Рассуждай так: Чтобы определить, сколько клеток с серыми и сколько клеток с белыми кроликами, мы должны знать, сколько серых и сколько белых кроликов в одной клетке, а для этого надо знать, сколько всего кроликов.
1) 20 + 25 = 45 (кр.) — в 9 клетках
2) 45 : 9 = 5 (кр.) – в 1 клетке
3) 20 : 5 = 4 (кл.)
4) 25 : 5 = 5 (кл.)
Ответ: 5 клеток с белыми кроликами, 4 клетки с серыми кроликами
Задачи на нахождение неизвестного по двум разностям
В одном куске 3 м шёлка, а во втором 7 м щёлка, Второй кусок стоит на 240 руб. дороже. Сколько стоит каждый кусок?
|
Цена |
Кол-во |
Стоимость |
|
Одинаковая |
Зм |
?руб. |
|
7м |
? руб., на 240 руб. дороже |
Рассуждай так: Чтобы найти стоимость, мы должны знать цену и количество. Чтобы определить цену, надо знать стоимость и количество. Известно, что стоимость второго куска на 240 руб. больше. Почему? Потому что второй кусок больше первого. Мы узнаем разность стоимостей, узнаем разность количеств и тогда можно найти цену.
1) 7 – 3 = 4 (м) — на столько метров второй кусок длиннее первого
2) Ц = Ст : К
240 : 4 = 60 (руб.) – цена шёлка
3) Ст = Ц • К
60 • 3 = 180 (руб.) – стоит 1 кусок
4) Ст = Ц • К
60 • 7 = 420 (руб.)
Ответ : 420 рублей стоит второй кусок ткани.
21
Алгоритмы и схемы для обучения
решению задач по математике.
«Алгоритм решения
задач с помощью уравнения»:
1)
Обозначить буквой х неизвестную величину,
записав ответ на вопрос задачи (Пусть…).
2)
Составить уравнение по условию задачи.
3)
Решить это уравнение.
4)
Записать краткий ответ на вопрос задачи.
В
дальнейшем при решении более сложных
задач, в которых несколько неизвестных
величин, содержание первого пункта
этого алгоритма становится таким:
1)Обозначить
переменной х одну из неизвестных величин,
если другие в несколько раз больше этой
величины или составляют какую-то ее
часть, выраженную дробью или процентами.
Дополняется
четвертый пункт алгоритма:
4) Проверив найденные
значения величин на соответствие условию
или смыслу задачи, записать краткий
ответ на вопрос задачи.
2.
В 6 классе при изучении темы «Обыкновенные
дроби» учащиеся испытывают затруднения
при приведении дробей к наименьшему
общему знаменателю (НОЗ).
Преодолеть
эти затруднения помогает памятка,
которую я назвала
«Секреты при нахождении
НОЗ дробей»:
-
Если
знаменатели – взаимно простые числа,
то НОЗ – произведение знаменателей. -
Если
один из знаменателей делится без остатка
на другие знаменатели, то этот знаменатель
– НОЗ. -
В
общем случае: умножьте больший знаменатель
на 2 и проверьте, делится ли полученное
число на другие знаменатели. Если
делится, то НОЗ найден, а если нет, то
больший знаменатель умножьте на 3 и
т.д.
3.
При решении геометрических задач часто
используются признаки равенства
треугольников, поэтому в 7 классе при
изучении этой темы вместе с учениками
была разработана и уже много лет
опробована «Опорно-логическая схема
решения задач на применение признаков
равенства треугольников». Ее можно
использовать при решении задач различных
уровней сложности в 7-11 классах, так как
она состоит из трех логически связанных
между собой частей (части закрашены
разными цветами).
Рассмотрим
треугольник____________
и треугольник____________ .
_________________
= _________________ (почему?);
_________________
= _________________ (почему?) ;
_________________
= _________________ (почему?) .

Треугольник______________
= треугольнику________________
(по__________
признаку)

Отрезок__________
= отрезку____________
Или
Угол____________
= углу___________ .

Отрезок____________
– медиана треугольника___________ .
Или
Отрезок_____
– биссектриса угла______ или треугольника_______
.
Или
Отрезок__________
– высота треугольника __________.
Или
Треугольник________
– равнобедренный (равносторонний,
прямоугольный).
4.
При решении других геометрических задач
необходимо умение применять признаки
подобия треугольников. Чаще всего
используется первый признак подобия
(по двум углам). Здесь может помочь
«Опорно-логическая схема решения задач
на применение первого признака подобия
треугольников»:
Рассмотрим
треугольник____________
и треугольник____________ .
Угол____________
= углу_____________ (почему?);
Угол_____________
= углу____________ (почему?).

Треугольник____________
подобен треугольнику____________
(по
1 признаку).

1)Составить
пропорцию, первым членом которой является
искомая величина.
2)Решить
эту пропорцию.
5. В 8
классе учащиеся изучают важнейшую
теорему геометрии – теорему Пифагора
и получают навыки решения задач на
применение этой теоремы. Очень важно
для учителя, чтобы приобретенные умения
и навыки ученики применяли и в старших
классах, так как большое количество
задач решается именно при помощи теоремы
Пифагора. У каждого ученика есть
«Алгоритм
решения задач на применение теоремы
Пифагора»:
1)Выделить
на чертеже прямоугольный треугольник,
стороной которого является искомый
отрезок.
2)Определить
катет это или гипотенуза.
3)Записать
для этого треугольника теорему Пифагора
(для гипотенузы) или следствие из нее
(для катета) в обозначениях данной
задачи.
4)Подставив в формулу
известные величины, найти неизвестную
величину
Алгоритм
решения задач на совместную работу.
Принимаем
всю работу, которую необходимо выполнить
за 1.
Находим
производительность труда каждого
рабочего в отдельности, т.е. , где t –
время, за которое этот рабочий может
выполнить всю работу, работая отдельно.
Находим
ту часть всей работы, которую выполняет
каждый рабочий отдельно за то время,
которое он работал.
Составляем
уравнение, приравнивая объем всей работы
к сумме слагаемых, каждое из которых
есть часть всей работы, выполненная
отдельно каждым из рабочих.
Задача
№1
Один
комбайнер может убрать урожай пшеницы
с участка на 24 ч быстрее, чем другой. При
совместной работе они закончат уборку
урожая за 35 часов. Сколько времени
потребуется каждому комбайнеру, чтобы
одному убрать урожай?
1.
Принимаем площадь участка, с которого
необходимо собрать урожай, за 1.
2.
Пусть х – время, необходимое первому
комбайнеру для уборки всего урожая, у
– время, необходимое второму
комбайнеру для уборки всего
урожая. Тогда– производительность
первого комбайнера, – производительность
второго комбайнера.
3.
35 – часть участка, с которого может
убрать урожай первый комбайнер за 35
часов работы, 35 – часть участка, с
которого может убрать урожай второй
комбайнер за 35 часов работы.
4.Составим
систему уравнений:
у
= 60, х = 84
Ответ:
для уборки всего урожая первому комбайнеру
потребуется 84 часа, второму – 60 часов.
Задача
№2
Две
бригады, работая совместно, могут
выполнить некоторое задание за 3 ч 36
мин. Сколько времени затратит на
выполнение этого задания каждая бригада,
работая в отдельности, если известно,
что первой бригаде требуется для этого
на 3 часа больше времени, чем второй.
Задача
№3
Мастер
и ученик должны были выполнить некоторое
задание. После четырех дней совместной
работы ученик был переведен в другой
цех, и, чтобы закончить выполнение
задания, мастеру пришлось еще 2 дня
работать одному. За сколько дней мог бы
выполнить каждый из них это задание,
если известно, что мастеру для этого
требуется на 3 дня меньше, чем ученику?
Алгоритм
решения задач, в которых используется
формула двузначного числа.
Вводится
обозначение:
х
– цифра десятков
у
– цифра единиц
Искомое
двузначное число 10х + у
Составить
систему уравнений
Задача
№1.
Двузначное
число в четыре раза больше суммы его
цифр. Если к этому числу прибавить
произведение его цифр, то получится 32.
Найдите это двузначное число.
Х
– цифра десятков. У – цифра единиц. 10х
+ у – искомое число.
2х2
+ 12х – 32 =0
х2
+6х – 16 =0
х1
=-8 (посторонний корень) х2 =2, тогда у =4.
Ответ:
24.
Задача
№2.Двузначное число в трое больше суммы
его цифр. Если из этого числа вычесть
произведение его цифр, то получится 13.
Найдите это двузначное число. (27).
Задача
№3.Двузначное число в шесть раз больше
суммы его цифр. Если это число сложить
с произведением его цифр, то получится
74. Найдите это число.(54).
Задача
№4.
Сумма
квадратов цифр двузначного числа равна
13. Если от этого числа отнять 9, то получим
число, записанное теми же цифрами, но в
обратном порядке. Найти число.(32).
Задача
№5.
Произведение
цифр двузначного числа в три раза меньше
самого числа. Если к искомому числу
прибавить 18, то получится число, написанное
теми же цифрами, но в обратном порядке.
Найти это число.
Алгоритм
решения задач на смеси.
х
– масса первого раствора, у – масса
второго раствора, (х + у ) – масса полученной
смеси.
Найти
содержание растворенного вещества в
растворах, т.е.
а
% от х, в % от у, с % от (х+у)
Составить
систему уравнений.
Задача
№1
Смешали
30% -ный раствор соляной кислоты с 10% -ным
и получили 600г 15% -ого раствора. Сколько
граммов каждого раствора было взято?
Введем
обозначение. Пусть взяли х г первого
раствора, у г – второго раствора, тогда
масса третьего раствора – (х+у).
Определим
количество растворенного вещества в
первом, втором, третьем растворах, т.е.
найдем 30% от х, 10% от у, 15% от 600.
Составим
систему уравнений:
0,3х
+ 60 – 0,1х = 90
0,2х
= 30
х
= 30:0,2
х
= 150, у = 600 – 150 = 450
Ответ:
взяли 150 г первого раствора и 450 г второго
раствора.
Задача
№2
Имеется
лом стали двух сортов с содержанием
никеля 5% и 40%. Сколько нужно взять металла
каждого их этих сортов, чтобы получить
140 т стали с содержанием 30% никеля?
Задача
№3Смешали 10% -ный и 25% -ный растворы соли
и получили 3 кг 20% -ного раствора. Какое
количество каждого раствора в килограммах
было использовано?
Алгоритм
решения показательных уравнений
1.Используя
определение степени, свойства степеней
привести показательное уравнение к
виду k f(x)= k q(x) или k f(x)= m, где m-постоянное
число
2.
В зависимости от вида уравнения
использовать один из вариантов:
а)
используя утверждение: если равны
степени и основания степеней, то равны
и показатели степеней,- перейти от
уравнения k f(x) = k q(x) к уравнению f(x) = q(x)
б)
Уравнение вида k f(x) = m следует
прологарифмировать по основанию 10:
Алгоритм
решения линейных уравнений
1.
Представить уравнение в стандартном
виде ( ах = в) для чего:
а)
раскрыть скобки (если есть)
б)
перенести слагаемые из правой части в
левую и привести подобные слагаемые.
2.
Найти корень по формуле: х = в/а
3.
Записать ответ
Неравенства
вида ах > с, ах < с, f(х)п(ч) > f(x)q(x) (*)
называются показательными неравенствами.
1.Привести
к стандартному виду (*)
2.Учитывая
область определения и свойства
логарифмической функции, получить
равносильные неравенства:
а)
, б) , или в)
3.Решив
полученные неравенства, записать ответ.
Логарифмические
неравенства
Неравенства
вида (*) называются простейшими
(стандартными) логарифмическими
неравенствами.
1.
Представить уравнение в стандартном
виде. (*)
2.
Учитывая область определения и свойства
логарифмической функции, получить
равносильные неравенства: а) б) в) 3.
Записать ответ
Решение
логарифмических уравнений
1.Используя
определение логарифма, его свойства,
привести уравнение к виду lоg f(x)=lоg q(x)
или lоg f(x)=k, где k – постоянное число,
причем f(x)>0, q(x) >0
2.Перейти
к системе на основании того, что если
логарифмы двух выражений равны, то равны
и сами выражения
3.Решить
получившуюся систему.
Алгоритм
решения простейших тригонометрических
неравенств с помощью единичной окружности
1.Замени
данное неравенство тригонометрическим
уравнением
2.Построй
углы, соответствующие в пределах одного
периода, данному значению тригонометрической
функции.
3.Отметь
на окружности интервал, для которого
выполняется данное неравенство
4.Запиши
решения в пределах промежутка,
охватывающего полный период функции
5.Прибавь
к найденному решению к периодов функции,
где к Î Z
6.Запиши
ответ.
Решение
показательных уравнений
1.Используя
определение степени, свойства степеней
привести показательное уравнение к
виду k f(x)= k q(x) или k f(x)= m, где m-постоянное
число
2.
В зависимости от вида уравнения
использовать один из вариантов:
а)
используя утверждение: если равны
степени и основания степеней, то равны
и показатели степеней,- перейти от
уравнения k f(x) = k q(x) к уравнению f(x) = q(x)
б)
Уравнение вида k f(x) = m следует
прологарифмировать по основанию 10
Метод
замены переменной
Данный
метод полезно применять, когда неизвестное
входит в уравнение всюду и в виде одной
и той же комбинации (особенно, если эта
комбинация содержит степени неизвестного
выше первой).
Суть
метода : Увидеть такую комбинацию
отдельных членов уравнения, которая
позволит вместо исходного уравнения
получить уравнение более простое
(относительно новой переменной), а потом
закончить решение уравнения.
Схема
метода:
1)в
уравнении вида f(x) = 0 выделить комбинацию
одного типа q(x), содержащие неизвестную.
2)Ввести
новую переменную у = q(x).
3)Выразив
f(x) через у получить новое уравнение
g(x) = 0
4)Решив
уравнение g(x) = 0, найти его корни у1, у2,
у3,…, ук
5)Составить
совокупность уравнений q(x)= у1, , q(x)= у2,,
…, q(x)= ук. (обратная замена)
6)Решить
данную совокупность. Ее решения и будут
решениями исходного уравнения
Общий
прием решения неравенства первой степени
с одним неизвестным.
1.Определить,
является ли данное неравенство
неравенством вида ах Ä b, где Ä – один из
знаков: >. <, ≥, ≤. Если «да», то п. 4,
если «нет», то п.2.
2.Установить,
какие из следующих тождественных и
равносильных преобразований нужно
выполнить, чтобы привести неравенство
к виду ах Ä b: раскрытие скобок, приведение
к общему знаменателю, перенесение членов
из одной части в другую, приведение
подобных.
3.Привести
с помощью выбранных преобразований
неравенство к виду ах Ä b.
4.Найти
решение неравенства по правилу: х Ä b :
а при а > 0 или х (- Ä) b : а, где (- Ä) – знак
неравенства, противоположный знаку Ä.
5.Записать
ответ. (см Таблицу)
Метод
интервалов
Пусть
необходимо решить неравенство вида
f(x) Ä 0, где Ä – один из знаков неравенства.
Если
его левая часть представима в виде
произведения линейных множителей, то
данное неравенство может быть решено
по следующей схеме:
1.
Разложим f(x) на линейные множители: f(x)
= (х –х1)(х – х2)…(х – хк).
2.
Найдем корни уравнения f(x) = 0: х1, х2. …хк.
3.
Рассмотрим промежутки, на которые
найденные корни разбивают числовую
прямую: (- ¥; х1), (х1; х2), … (хк; +¥). На каждом
из них каждый линейный множитель имеет
постоянный знак. Определим знак каждого
линейного множителя на каждом полученном
промежутке.
4.
Определим знак f(x) на каждом найденном
промежутке.
5В
решение включим те промежутки, на которых
f(x) имеет знак, соответствующий знаку
неравенства.
Замечание:
Данным методом решаются и дробные
неравенства
Метод
решения квадратного уравнения
1.
Преобразовать исходное уравнение к
виду ах2 + вх + с = 0, где а >0.
2
Проверить равенство нулю коэффициентов
b и с. если b = 0 или с = 0, то перейти к п.3.,
если b ≠ 0 и с ≠ 0, то перейти к п.4.
3.
Если b = с = 0, то найти неизвестное по
правилу, указанному в строке 1 таблицы
.
Если
b ≠ 0, с = 0, то найти неизвестное по правилу,
указанному в строке 2 таблицы
Если
b = 0, с ≠ 0, то найти неизвестное по правилу,
указанному в строке 3 таблицы.
4.
Найти дискриминант уравнения D = b2 –
4ас.
5.
Найти неизвестное по правилу, указанному
в строке 4 таблицы
6.
Записать ответ.
Свободные
члены b и с Решение уравнения
b
= с = 0 х1,2 = 0
b
≠ 0, с = 0 х1 = 0, х2 = b:а
b
= 0, с ≠ 0
а)
с < 0
б)
с > 0
х1,2
= + Ö- с: арешений нет
b
≠ 0 и с ≠ 0
а)
D = b2 – 4ас > 0
б)
D = b2 – 4ас = 0
в)
D = b2 – 4ас < 0
х1,2
=( – b+Ö D) : 2а
х1,2
= – b : 2а
решений
нет.
Алгоритм
решения неравенства вида ах< b, a>1,
b>0
1.Изобразить
схематически график функции у = ах
2.С
помощью графика укажите то значение х,
которому соответствует значение у,
равное b
3.С
помощью графика укажите множество
значений х, которым соответствуют
значения у, меньшие b.
Алгоритм
решения уравнений с переменной в
знаменателе
1.Представьте
уравнение в виде f(x) = 0
2.Представьте
выражение f(x) в виде дроби ;
3.Замените
уравнение = 0 равносильной ему системой
4.Решите
уравнение q(x) = 0
5.Для
каждого корня q(x) = 0 проверить выполнение
условия g(х) 0
Формулы
сокращенного умножения
Квадрат
суммы двух величин равен квадрату первой
плюс удвоенное произведение первой на
вторую плюс квадрат второй. (a+b)2=a2+2ab+b2
Квадрат
разности двух величин равен квадрату
первой минус удвоенное произведение
первой на вторую плюс квадрат второй.
(a–b)2=a2-2ab+b2
Произведение
суммы двух величин на их разность равно
разности их квадратов. (a+b)(a–b)=a2-b2
Куб
суммы двух величин равен кубу первой
плюс утроенное произведение квадрата
первой на вторую плюс утроенное
произведение первой на квадрат второй
плюс куб второй. (a+b)3=a3+3a2b+3ab2+b3
Куб
разности двух величин равен кубу первой
минус утроенное произведение квадрата
первой на вторую плюс утроенное
произведение первой на квадрат второй
минус куб второй. (a–b)3=a3-3a2b+3ab2-b3
Произведение
суммы двух величин на неполный квадрат
разности равно сумме их кубов. (
a+b)(a2-ab+b2)=a3+b3
Произведение разности двух
величин на неполный квадрат суммы равно
разности их кубов. (a-b)(a2+ab+b2)=a3-
b3

Формулы
и
свойства
степеней
a1 =
а, a0 = 1 (a ≠ 0), a-n = 1/an.
1°
aman = am+n;
2°
am/an = am-n;
3°
(ab)n = anbn;
4°
(am)n = amn;
5°
(a/b)n = an/bn.
