Аналитическое решение (англ. closed-form expression выражение в замкнутой форме)— математическое выражение с конечным числом стандартных операций.
Пример: корни многочленов[править | править код]
Решения любого квадратного уравнения с комплексными коэффициентами могут быть выражены аналитически через сложение, вычитание, умножение, деление и извлечение квадратного корня, каждое из которых является элементарной функцией. Например, квадратное уравнение
поддается обработке, поскольку ее решения могут быть выражены аналитически, то есть в терминах элементарных функций:
Точно так же решения уравнений кубической и четвертой степени (третьей и четвертой степени) могут быть выражены с помощью арифметики, квадратных корней и корней n -й степени. Однако существуют уравнения пятой степени без аналитических решений, например x5 − x + 1 = 0 ; это теорема Абеля-Руффини.
Изучение существования замкнутых форм у корней многочленов является исходной мотивацией и одним из главных достижений области математики, получившей название теории Галуа.
Альтернативные определения[править | править код]
Изменение определения «хорошо известного» для включения дополнительных функций может изменить набор уравнений с решениями в замкнутой форме. Многие кумулятивные функции распределения не могут быть выражены аналитически, если только не считать хорошо известными специальные функции, такие как функция ошибки или гамма-функция. Уравнение пятой степени можно решить, если включить общие гипергеометрические функции, хотя решение слишком сложно алгебраически, чтобы быть полезным. Для многих практических компьютерных приложений вполне разумно предположить, что гамма-функция и другие специальные функции хорошо известны, поскольку численные реализации широко доступны.
Аналитическое выражение[править | править код]
Аналитическое выражение (также известное как выражение в аналитической форме или аналитическая формула) — это математическое выражение, построенное с использованием хорошо известных операций, которые легко поддаются вычислению. Подобно выражениям в закрытой форме, набор хорошо известных разрешенных функций может варьироваться в зависимости от контекста, но всегда включает основные арифметические операции (сложение, вычитание, умножение и деление), возведение в степень до действительного показателя степени (включая извлечение n-го корня), логарифмы и тригонометрические функции.
Однако класс выражений, считающихся аналитическими, как правило, шире, чем класс выражений в закрытой форме. В частности, обычно допускаются специальные функции, такие как функции Бесселя и гамма-функция, а также часто допускаются бесконечные ряды и непрерывные дроби. С другой стороны, пределы вообще и интегралы в частности обычно исключаются.
Если аналитическое выражение включает только алгебраические операции (сложение, вычитание, умножение, деление и возведение в степень до рационального показателя) и рациональные константы, то оно более конкретно называется алгебраическим выражением.
Сравнение разных классов выражений[править | править код]
Выражения в закрытой форме являются важным подклассом аналитических выражений, которые содержат ограниченное или неограниченное количество приложений известных функций. В отличие от более широких аналитических выражений выражения в закрытой форме не включают бесконечные ряды или непрерывные дроби; не включает интегралов или пределов. Действительно, по теореме Стоуна — Вейерштрасса любая непрерывная функция на единичном интервале может быть выражена как предел многочленов, поэтому любой класс функций, содержащих многочлены и замкнутый относительно пределов, обязательно будет включать все непрерывные функции.
Точно так же говорят, что уравнение или система уравнений имеют решение в закрытой форме тогда и только тогда, когда по крайней мере одно решение может быть выражено в виде выражения в закрытой форме; и говорят, что оно имеет аналитическое решение тогда и только тогда, когда хотя бы одно решение может быть выражено в виде аналитического выражения. Существует тонкое различие между «функцией в закрытой форме» и «<i id=”mwaw”>числом</i> в закрытой форме» при обсуждении «решения в закрытой форме», обсуждаемом в (Chow 1999) и ниже. Закрытое или аналитическое решение иногда называют явным решением.Шаблон:Mathematical expressions
Работа с выражениями незамкнутой формы[править | править код]
Преобразование в выражения закрытой формы[править | править код]
Выражение:
не имеет закрытой формы, так как суммирование влечет за собой бесконечное число элементарных операций. Однако суммированием геометрического ряда это выражение можно представить в замкнутом виде: [1]
Дифференциальная теория Галуа[править | править код]
Интеграл выражения в закрытой форме сам по себе может выражаться или не выражаться в виде выражения в закрытой форме. Это исследование называется дифференциальной теорией Галуа по аналогии с алгебраической теорией Галуа.
Примечания[править | править код]
- ↑ Holton. Numerical Solution, Closed-Form Solution. Дата обращения: 31 декабря 2012. Архивировано из оригинала 4 февраля 2012 года.
|
|
Макеты страниц
чисел, то функцию называют числовой функцией числового аргумента. Аналогично функцию  областью определения которой является некоторое множество систем чисел
областью определения которой является некоторое множество систем чисел  и множеством значений которой является некоторое множество чисел, называют числовой функцией числовых аргументов.
и множеством значений которой является некоторое множество чисел, называют числовой функцией числовых аргументов.
Как известно, числовые функции числовых аргументов задаются различными способами: табличным, графическим, посредством формул и др. Чаще всего они задаются с помощью формул или, как принято говорить, с помощью аналитических выражений.
Под формулой или аналитическим выражением, задающим функцию  в современной математике подразумевают запись тех вычислительных операций, которые надо выполнить в определенной последовательности над постоянными числами и численными значениями аргументов
в современной математике подразумевают запись тех вычислительных операций, которые надо выполнить в определенной последовательности над постоянными числами и численными значениями аргументов  чтобы получить соответствующее численное значение функции
чтобы получить соответствующее численное значение функции  . К вычислительным (или аналитическим) операциям относят операции сложения, умножения, вычитания, деления и операцию перехода к пределу, т. е. нахождения по заданной последовательности чисел
. К вычислительным (или аналитическим) операциям относят операции сложения, умножения, вычитания, деления и операцию перехода к пределу, т. е. нахождения по заданной последовательности чисел  ее предела
ее предела  если он существует.
если он существует.
Примерами аналитических выражений являются: 

Функции, которые можно задать с помощью аналитических выражений, называются аналитически изобразимыми.
Не следует отождествлять понятия функции и аналитического выражения. Всякое аналитическое выражение задает некоторую функцию, но не всякая функция является аналитически изобразимой.
Так как всякое аналитическое выражение задает некоторую функцию, то для записи аналитических выражений употребляют те же символы, что и для записи функций. Если аргументам, входящим в аналитическое выражение  дать определенные численные
дать определенные численные
значения, например,  затем выполнить все указанные в этом выражении действия, то получится определенное число, которое обозначают символом
затем выполнить все указанные в этом выражении действия, то получится определенное число, которое обозначают символом  и называют значением этого выражения при значениях аргументов
и называют значением этого выражения при значениях аргументов  При рассмотрении аналитического выражения или функции, заданной с помощью аналитического выражения, указывается, какие именно системы числовых значений аргументов являются допустимыми.
При рассмотрении аналитического выражения или функции, заданной с помощью аналитического выражения, указывается, какие именно системы числовых значений аргументов являются допустимыми.
В некоторых случаях из смысла аналитического выражения бывает понятно, какие значения аргумента или системы значений аргументов следует считать допустимыми. Например, длина окружности С задается формулой  где
где  радиус окружности. В аналитическом выражении
радиус окружности. В аналитическом выражении  радиус
радиус  аргумент. Очевидно, что допустимыми значениями аргумента
аргумент. Очевидно, что допустимыми значениями аргумента  следует в этом случае считать положительные действительные числа.
следует в этом случае считать положительные действительные числа.
Если дано аналитическое выражение от нескольких аргументов  и не указано, какие системы значений аргументов являются допустимыми, то допустимой считается всякая система значений
и не указано, какие системы значений аргументов являются допустимыми, то допустимой считается всякая система значений  при которых выполнимы все математические действия, указанные в рассматриваемом выражении.
при которых выполнимы все математические действия, указанные в рассматриваемом выражении.
Например, для той же функции  если нет указаний на геометрический смысл аргумента
если нет указаний на геометрический смысл аргумента  допустимыми следует считать все значения
допустимыми следует считать все значения  из рассматриваемого числового поля, поскольку для них всегда выполнима операция умножения на число
из рассматриваемого числового поля, поскольку для них всегда выполнима операция умножения на число  . Для выражения
. Для выражения  допустимой будет всякая система значений
допустимой будет всякая система значений  удовлетворяющая условию
удовлетворяющая условию 
Два аналитических выражения от данных аргументов (а также функции, заданные этими выражениями) называются тождественно равными или тождественными, если их значения равны при любой допустимой системе значений аргументов.
Таким образом, если  тождественные выражения, то при всех допустимых системах значений аргументов имеет место равенство
тождественные выражения, то при всех допустимых системах значений аргументов имеет место равенство

Это равенство называется тождеством.
Для обозначения тождества иногда применяют символ  Примерами тождеств являются равенства
Примерами тождеств являются равенства

Заметим, что понятие тождественности двух выражений относительно; оно зависит от множества допустимых систем значений аргументов. Два выражения могут быть тождественны на одном множестве допустимых систем значений аргументов и не быть тождественными на другом, более широком множестве их.
Так, выражения  тождественны на множестве неотрицательных действительных чисел и не тождественны на множестве всех действительных чисел, так как
тождественны на множестве неотрицательных действительных чисел и не тождественны на множестве всех действительных чисел, так как

и

Замену аналитического выражения другим, тождественным ему выражением называют тождественным преобразованием данного выражения.
При решении задач часто приходится записывать ту или иную задачу с помощью определенных соотношений между некоторыми аналитическими выражениями. Такую запись задачи называют аналитической.
Оглавление
- Глава I. ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
- § 2. Понятия кольца и поля
- § 3. Упорядоченные поля
- § 4. Понятие функции и аналитического выражения
- § 5. Элементарные функции и их классификация
- § 6. Метод математической индукции
- Глава II. ОБЩИЕ СВЕДЕНИЯ ОБ УРАВНЕНИЯХ
- § 1. Понятие уравнения. Решения уравнения
- § 2. Классификация уравнений, изучаемых в элементарной математике
- § 3. Равносильность уравнений
- § 4. Преобразование уравнений при их решении
- Глава III. ЭЛЕМЕНТАРНЫЕ МЕТОДЫ РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ И ДРОБНО-РАЦИОНАЛЬНЫХ УРАВНЕНИЙ С ОДНИМ НЕИЗВЕСТНЫМ
- § 1. Алгебраические уравнения n-й степени с одним неизвестным
- § 2. Корни квадратного трехчлена
- § 3. Исследование квадратного трехчлена над полем действительных чисел
- § 4. Двучленные уравнения
- § 5. Трехчленные уравнения, приводящиеся к квадратным
- § 6. Симметрические уравнения
- § 7. Алгебраическое уравнение n-й степени с рациональными коэффициентами
- § 8. Частные приемы решения уравнений высших степеней
- § 9. Дробно-рациональные уравнения
- Глава IV. ТЕОРИЯ СОЕДИНЕНИЙ
- § 2. Перестановки
- § 3. Сочетания
- § 4. Размещения
- § 5. Перестановки с повторениями
- § 6. Сочетания с повторениями
- § 7. Размещения с повторениями
- Глава V. БИНОМ НЬЮТОНА И ПОЛИНОМИАЛЬНАЯ ТЕОРЕМА
- § 1. Бином Ньютона
- § 2. Биномиальные коэффициенты и их основные свойства
- § 3. Треугольник Паскаля
- § 4. Полиномиальная теорема
- § 5. Вычисление сумм степеней первых n чисел натурального ряда
- Глава VI. МНОГОЧЛЕНЫ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- § 1. Многочлен от нескольких переменных и его каноническая форма
- § 2. Однородный многочлен от n переменных и число его членов
- § 3. Число членов в каноническом представлении многочлена от n переменных
- § 4. Тождественность двух многочленов
- § 5. Тождественные преобразования многочленов. Тождество Лагранжа
- § 6. Применение метода неопределенных коэффициентов при выполнении алгебраических действий над многочленами
- Глава VII. СИСТЕМЫ УРАВНЕНИЙ С НЕСКОЛЬКИМИ НЕИЗВЕСТНЫМИ
- § 1. Понятие системы уравнений
- § 2. Равносильность систем уравнений
- § 3. Уравнения и системы уравнений, являющиеся следствием данной системы уравнений
- § 4. Основные элементарные методы решения систем уравнений
- § 5. Решение нелинейных систем алгебраических уравнений элементарными методами
- 1. Решение системы двух уравнений с двумя неизвестными, из которых одно—второй степени, а другое — первой.
- 2. Решение системы двух уравнений второй степени с двумя неизвестными, которые не имеют членов первой степени.
- 3. Решение системы двух уравнений второй степени с двумя неизвестными в общем виде.
- 4. Решение системы двух однородных уравнений с двумя неизвестными.
- 5. Решение системы двух уравнений с двумя неизвестными, одно из которых однородное, а второе не однородное.
- 7. Решение нелинейной системы алгебраических уравнений, в состав которой входят линейные уравнения.
- 8. Решение нелинейной системы алгебраических уравнений, левая часть одного из которых представляется в виде произведения.
- § 6. Графическое решение нелинейных систем алгебраических уравнений с двумя неизвестными
- Глава VIII. НЕРАВЕНСТВА
- § 1. Основные свойства неравенств
- § 2. Тождественные неравенства
- § 3. Применение неравенств для определения наибольших и наименьших значений
- § 4. Решение неравенств
- § 5. Решение алгебраических неравенств с одним неизвестным первой и второй степени
- § 6. Решение систем алгебраических неравенств первой степени с двумя неизвестными
- § 7. Применение неравенств для задания числовых и точечных множеств
- Глава IX. ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ НАД ПОЛЕМ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ
- § 1. Корни с натуральными показателями в поле действительных чисел
- § 2. Тождественные преобразования иррациональных выражений в поле действительных чисел
- § 3. Решение иррациональных уравнений и систем, в состав которых входят иррациональные уравнения, в поле действительных чисел
- Глава X. ПОКАЗАТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ В ПОЛЕ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ
- § 1. Теоретические основы решения показательных и логарифмических уравнений
- § 2. Решение показательных уравнений с одним неизвестным
- § 3. Решение логарифмических уравнений с одним неизвестным
- § 4. Решение трансцендентных уравнений, приводящихся к показательным и логарифмическим уравнениям
- § 5. Решение некоторых трансцендентных систем уравнений
- § 6. Графические способы решения трансцендентных уравнений и систем
- ЛИТЕРАТУРА
Если
функциональная зависимость
такова, что f
обозначает
аналитическое выражение, т.е. совокупность
математических операций,
которые производятся в определенной
последовательности над аргументом x,
то говорят,
что функция задана аналитически.
Например:
y = x2
–
2;
![]()
;
y =
3 –
ln
x2
и т.п.
Каждое
аналитическое выражение, содержащее
аргумент x,
имеет естественную
область применения.
Под этой областью понимают множество
всех тех значений x,
для которых выражение сохраняет смысл,
т.е. имеет вполне определенное конечное
действительное значение. Так, для
выражения x2
– 2
такой областью будет все множество R
действительных чисел, т.е. бесконечный
интервал (–∞
+∞
Для выражения
![]()
эта область сведется к замкнутому
промежутку
за пределами которого значение его
перестает быть действительным. Напротив,
выражению
![]()
придется в качестве естественной
области применения отнести открытый
промежуток (–1,1),
ибо на концах его знаменатель обращается
в нуль. Иногда область значений, для
которых выражение сохраняет смысл,
состоит из разрозненных промежутков:
для
![]()
это будут промежутки (–∞,–1]
и [1,+∞), для
![]()
– промежутки (–∞,–1],
(–1,
1) и (1, +∞)
и т.д.
Если
функция задана аналитически, то она
может быть изображена графически на
координатной плоскости хOу.
В
последующем изложении нам в большинстве
случаев придется рассматривать функции,
заданные аналитическим выражением для
которых область определения функции
распространяется на всю естественную
область применимости аналитического
выражения. Поэтому, если в дальнейшем
нет специальной оговорки, то под
областью определения функции,
заданной аналитически,
мы будем подразумевать естественную
область применимости аналитического
выражения.
Если же по каким-либо причинам область
определения функции, заданной аналитическим
выражением, ограничена множеством Р,
а выражение имеет смысл и вне множества
Р,
выходить за пределы области определения
Р
функции, разумеется, все же нельзя.
Такая
ситуация может возникнуть, если функция
задается не одной и той же формулой для
всех значений аргумента х,
но для одних – одной формулой, а для
других – другой. Примером такой функции,
в промежутке (–∞
+∞,
может служить функция, определяемая
следующими двумя формулами

Здесь
естественная область применения каждого
выражения выходит за пределы области
определения Р,
на котором данное выражение задает
функцию.
Другая
ситуация, которая типична для
рассматриваемого случая, –
это установление области определения
сложной функции
![]()
,
для которой и внешняя y = f(u),
и внутренняя u = (x)
функции
заданы аналитическими выражениями.
Областью определения такой сложной
функции является или вся область
определения функции u
= (x),
или та ее часть, в которой определяются
значения u,
не выходящие из области определения
внешней функции y
= f(u).
Например,
областью определения функции
![]()
(![]()
,
u = 1–
x2)
является
отрезок [–1,1],
так как u
< 0
при
|x|
> 1
и, следовательно, функция
не определена при этих значениях x
(хотя функция
u = 1 – x2
определена
при всех значениях x).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Чтобы задать функцию, нужно указать некоторый способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции, то есть способ описания закона f. Функция может задаваться аналитическим, графическим, табличным или словесным способом.
Аналитическое выражение – формула, указывающая, какие математические действия надо произвести над аргументом x, чтобы получить соответствующие значения y. Способ задания значений функции с помощью аналитического выражения называется аналитическим способом задания функции . Функция может быть задана и с помощью нескольких различных аналитических выражений с разными областями определения. В этом случае область определения функции – область определения каждого из этих аналитических выражений (при условии, что эти отдельные области нигде “не конфликтуют”). Аналитически функция задается, если область ее определения не является конечной, особенно, в теоретических проблемах.
Пример.Рассмотрим кусочно-аналитически заданную функцию
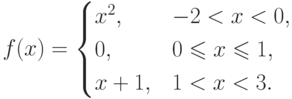
Область определения этой функции X={x : -2<x<3}.
При табличном задании функции ряд дискретных значений аргумента x1, x2,…, xn и соответствующих им значений функции y1, y2,…, yn задаются в виде таблицы.
Пример.Различные статистические и социологические данные записывают
в виде таблиц: уровня жизни, динамики безработицы, численности населения и т.п.
Третьим способом задания функции является графический способ.
Абсциссой x точки (x;y) на плоскости xOy называется длина отрезка [O;x], отсекаемого от точки отсчета O оси Ox плоскости. Ординатой этой точки называется длина отрезка [O;y] оси Oy плоскости xOy .
Графиком функции y=f(x) называется множество точек (x;y) на плоскости xOy (геометрическое место точек на плоскости), каждая из которых обладает тем свойством, что ее абсцисса есть значение аргумента функции, а ордината – соответствующее этому аргументу значение функции. Графически функция определяется обычно в экспериментальных науках, например, в разделах физики, химии.
Пример.График кусочно-заданной на интервале (-2;3) функции f(x), приведенной выше, будет иметь вид, изображенный рис. 4.1. Хотя этот график и состоит из трех “вроде бы” самостоятельных частей (часть параболы; часть оси Ox ; часть прямой, параллельной биссектрисе координатного угла), тем не менее, это один график (график одной кусочно-заданной функции). График функции может не быть непрерывной линией. При x=1 указанный на рис. 4.1. график теряет свойство быть непрерывным. Функция имеет при x=1 разрыв (о разрывах функции мы подробнее поговорим ниже).
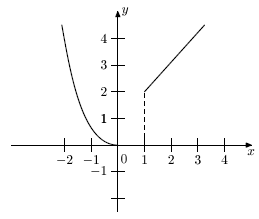
Рис.
4.1.
График кусочно-заданной функции
При словесном задании функции словесно указываются множества X, Y и закон f.
Пример.
Функция Дирихле, рассмотренная нами выше, была определена
словесно, так как значения из множеств X, Y
– “словесны, расплывчаты”.
Если задана некоторая однозначная функция 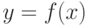 ,
,  ,
,  , то каждому значению
, то каждому значению  ставится в соответствие только одно значение
ставится в соответствие только одно значение  . Если при этом каждому значению
. Если при этом каждому значению  соответствует лишь одно значение
соответствует лишь одно значение  , то говорят, что отображение f есть взаимно однозначное отображение .
, то говорят, что отображение f есть взаимно однозначное отображение .
Так как каждому  в этом случае ставится в соответствие одно значение
в этом случае ставится в соответствие одно значение  , то можно говорить, что определена функция вида
, то можно говорить, что определена функция вида 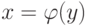 с областью определения
с областью определения  и областью значений
и областью значений  .
.
Функция 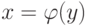 называется функцией, обратной к (прямой) функции y=f(x) . Обратную к f функцию g часто обозначают f-1 (g=f-1).
называется функцией, обратной к (прямой) функции y=f(x) . Обратную к f функцию g часто обозначают f-1 (g=f-1).
Если дана функция y=f(x) и для любого значения 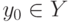 уравнение f(x)=y0 имеет единственный корень
уравнение f(x)=y0 имеет единственный корень 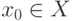 , то функция y=f(x) обратима. Если функция
, то функция y=f(x) обратима. Если функция  определена и возрастает (убывает) на промежутке X, то у нее существует обратная функция, причем обратная функция
определена и возрастает (убывает) на промежутке X, то у нее существует обратная функция, причем обратная функция  определена и возрастает (убывает) на Y. Таким образом, график обратной функции
определена и возрастает (убывает) на Y. Таким образом, график обратной функции 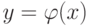 симметричен с графиком данной функции y=f(x) относительно биссектрисы первого и третьего координатных углов.
симметричен с графиком данной функции y=f(x) относительно биссектрисы первого и третьего координатных углов.
Пример.
Функция y=x2 с областью определения D(f)=R, областью изменения 
и функция  не является взаимно
не является взаимно
однозначной, а функция y=x3 с обратной
однозначной функцией ![x=sqrt[3]{y}](https://intuit.ru/sites/default/files/tex_cache/792d1c3ee23e28c1e0d0e3ec30bb379f.png) – взаимно однозначная.
– взаимно однозначная.
Пусть дано некоторое соотношение, связывающее две переменные x и y. Если все его члены перенести в левую часть, то оно запишется в виде: F(x,y)=0. Если существуют различные пары действительных чисел (x,y), удовлетворяющих данному соотношению, то соотношение F(x,y)=0 можно считать способом задания переменной y как функции от x. С помощью этого соотношения каждому значению  ставится в соответствие
ставится в соответствие  (фиксируем каждый раз x, решаем, при фиксированном x, уравнение и находим y ). Функция от x, определяемая соотношением F(x,y)=0, называется неявно заданной функцией .
(фиксируем каждый раз x, решаем, при фиксированном x, уравнение и находим y ). Функция от x, определяемая соотношением F(x,y)=0, называется неявно заданной функцией .
Пример.Соотношение 2x-y+1=0 неявно задает y
как функцию от x ; эту функцию можно выразить явно,
разрешив уравнение относительно y: y=1+2x.
Соотношение x2+y2-1=0 неявно задает двухзначную
функцию 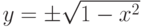 ; уравнение
; уравнение 
задает неявную функцию y (не выражаемую явно через x ).
Функция f(x) называется четной, если f(x)=f(-x) для всех  , где X – область определения функции y=f(x) . График четной функции симметричен относительно оси Oy. Функция называется нечетной, если f(x)=-f(-x), для любого
, где X – область определения функции y=f(x) . График четной функции симметричен относительно оси Oy. Функция называется нечетной, если f(x)=-f(-x), для любого  . График нечетной функции симметричен относительно начала координат. Области определения четной и нечетной функции симметричны относительно начала координат. Функция может быть ни нечетной, ни четной.
. График нечетной функции симметричен относительно начала координат. Области определения четной и нечетной функции симметричны относительно начала координат. Функция может быть ни нечетной, ни четной.
Пример.
Функция y=x2cos(x) – четная, так как y(-x)=(-x)2cos(-x)= x2cos(x)=y(x),
а функция y=x2sin(x) – нечетная, так как y(-x)=(-x)2sin(-x)=-x2sin(x)=-y(x).
Функция y=x+2 не является ни четной, ни
нечетной, так как y(-x)=-x+2.





Аналитический способ задания функции
Аналитический способ задания функции. Давайте дадим ряд объяснений относительно того, как определять функции с помощью аналитических или аналитических формул, которые играют очень важную роль в математическом анализе. 1°.Во-первых, какие аналитические операции или действия могут быть включены в эти выражения? В первую очередь, понимаются все операции, изучаемые в элементарной алгебре и тригонометрии: арифметические операции, возведение в степень (и извлечение корня), логарифмы, движение от углов к тригонометрическим значениям и наоборот(см.§ 2 ниже).Однако по мере развития информации об анализе важно подчеркнуть, что другие операции, прежде всего, присоединяются к переходу к тем пределам, которые содержатся в главе III.
Каждое аналитическое выражение, содержащее аргумент x, имеет, так сказать, естественную область применения.
Людмила Фирмаль
- Поэтому полное содержание терминов «аналитическое выражение» или «Формула» раскрывается лишь постепенно. 2°. Второй комментарий связан с областью определения функции аналитическим выражением или аналитическим выражением. Это набор всех значений x, которые имеют значение. То есть она имеет вполне определенное и конечное реальное значение. Объясним это на простейшем примере. В этом районе будет все Один G + L * Итак, для выражения Действительное число. Для Формулы y 1-x% эта область сводится к замкнутому интервалу[-1, 1], и если она превышена Его значение становится непрактичным.
Напротив, выражение■^—должно включать интервал открытия (-1, 1)как естественную область применения, так как знаменатель исчезнет в конце. Диапазон значений, в котором выражение имеет значение, может состоять из различных пробелов. для yx * 1 это будут интервалы (oo, −1) и[1,+°o); для x9 * _^ это будут интервалы (oo, −1), (-1, 1) и (1,+ oo) и т. д.). В следующем изложении необходимо рассмотреть как более сложные, так и общие аналитические формулы, а также не раз заняться изучением характеристик функции, то есть самого анализатора, который определяется такими формулами по всей области, имеющей значение. Однако можно рассмотреть и другую ситуацию. Мы считаем, что необходимо заранее привлечь внимание читателей.
- Представим себе, что частный вопрос, где переменная x существенно ограничена областью изменения, привел к рассмотрению функции/(q), допускающей аналитическое expression. It может случиться, что это выражение имеет смысл и пересекает границу за пределами региона, но, конечно, это все еще невозможно. Например, если вы хотите исследовать свободное падение тяжелой точки с высоты земли на вершину, вы прибегаете к формуле Но… ’Т’ [16,2)] смешно считать отрицательные значения / * 2 ^ Или значение больше, чем T = y. как легко видеть, так как в момент 1 = T точка уже падает на Землю.
И это несмотря на то, что само выражение сохраняет смысл всего материального. 3°.Функция не определяется одним и тем же выражением для всех значений ее аргументов, но в некоторых случаях она определяется другим выражением для одного выражения, а в других случаях она определяется другим выражением. Примеры таких функций * ) Конечно, такое выражение интереса не вызывает. значение X не имеет смысла. Интервал (oo,+ oo) может быть функцией, определяемой следующими 3 выражениями: f (x)= 1, если | * / > 1 (т. е. Если или x <^-1)、 f (x)= −1, если / lm / <M(то есть −1 <^ q; < ^ 1) И напоследок f (x)= 0 x = ±и.
Здесь аналитическая формула играет подчиненную вспомогательную роль.
Людмила Фирмаль
- Однако не следует предполагать, что существует фундаментальное различие между функцией, определенной в выражении 1 для всех значений xy, и функцией, которая использует несколько выражений в этом определении. Обычно функция, определяемая несколькими выражениями, может быть определена в 1 (хотя выражение несколько сложнее). в частности, это верно в отношении вышеуказанных функций[см. P°43.5)]. в будущем мы будем встречаться много раз с такими же примерами.
Смотрите также:
Решение задач по математическому анализу






