Категория: OLAP, SSAS
Опубликовал:
28.11.2012
К списку статей
Пожалуй, для компании любой отрасли актуальна тема анализа остатков (остатков по счетам ПБУ, 302-П, остатки товаров и готовой продукции на складах, резервные остатки и т.д.), причем важно знать остатки как на конкретную дату, так и какова динамика остатков за произвольный период времени. Даже в разговорной речи мы оперируем термином “в сухом остатке”.
Остаток – полуаддитивный показатель, в разрезе обычных измерений (договоры, центры финансового учета, менеджеры и т.д.) величины остатков суммируются, а в разрезе измерений времени (отчетные финансовые даты, календарные даты) значения сворачиваются: остаток на последнюю дату месяца = остаток на конец месяца, остаток на последнюю дату последнего месяца квартала = остаток на конец квартала и так далее вверх по иерархии.
Остатки могут:
- быть посчитаны и храниться в учетной системе;
- рассчитываться на каждую отчетную дату (или на начало каждой недели, или на начало каждого месяца) на этапе ETL и храниться в реляционном хранилище/витрине данных;
- вычисляться в OLAP-кубе на лету по формуле.
С точки зрения BI, если имеет место быть первый вариант и ему можно доверять, то воспринимаем это как данность и пользуемся готовыми данными. Между вторым и третьим вариантом у нас есть выбор:
| Вариант расчета остатков | Плюсы | Минусы |
|---|---|---|
| 2. Рассчитывать и хранить в DWH / Data Mart |
удобно и легко использовать готовые остатки;
хранимые готовые остатки используются как входные данные для OLAP, других прикладных систем, так и для Ad-hoc SQL-запросов |
усложнение ETL;
нагрузка на сервер баз данных, особенно, когда в учетных системах наблюдаются случаи правки операций задним числом, и требуется пересчитать остатки в DWH |
| 3. Вычислять в OLAP |
простая и быстрая реализация | снижение производительности OLAP на больших объемах данных, когда вычисляемые остатки используются в других вычисляемых мерах и/или сложный дизайн куба;
пользователи OLAP любят дриллиться до гранулярных данных – подневных остатков, но в данном случае будут лишены такой возможности; продвинутые аналитики вряд ли будут рады постоянно вычислять остатки в своих SQL-запросах к DWH / Data Mart, и начнут материализовывать рассчитываемые значения в своих песочницах со всеми вытекающими последствиями |
Остановимся на варианте №2 более подробно. Допустим, в витрине данных сформирована таблица Periodic Snapshot с остатками на каждый день по каждому кредитному договору в течение всего времени жизни отдельного договора. Поскольку в данном бизнес-кейсе имеем дело с небольшим конечным количеством видов счетов (ссудный счет, начисленные проценты и т.д.), то остатки по каждому из них храним в отдельном поле (получается транспонированная таблица, некоторые из полей будут сильно разреженными). Для удобства использования суммы остатков приведены к единой валюте эквивалента, например, национальной валюте.
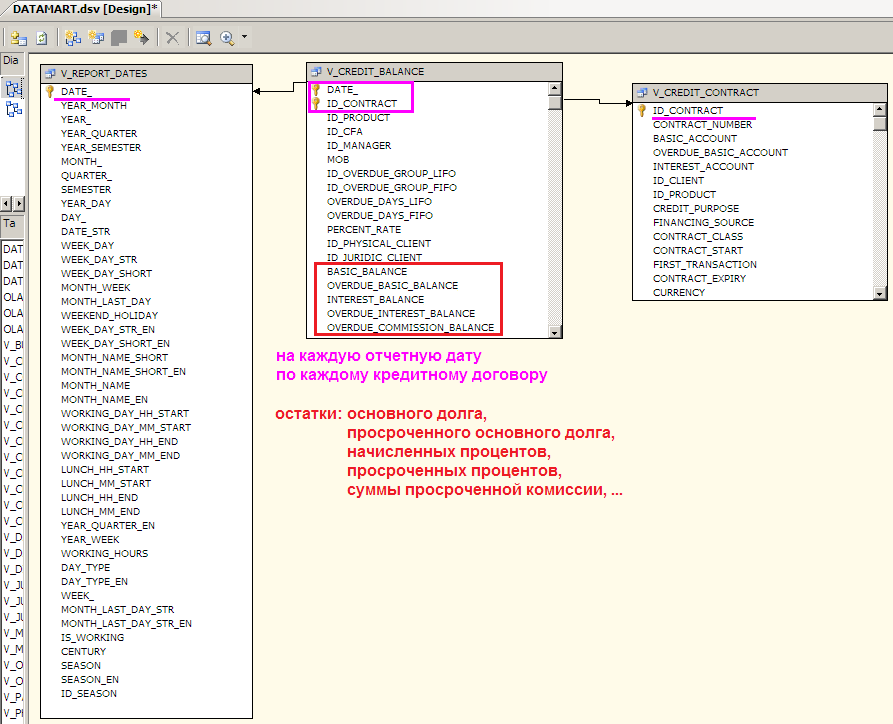
В другом бизнес-кейсе (например, для задачи план-фактного анализа) в подобной таблице могут храниться остатки только на 1-ое число каждого месяца.
Создадим простой куб, для физических мер – остатков назначим тип агрегирования LastChild и спрячем их:

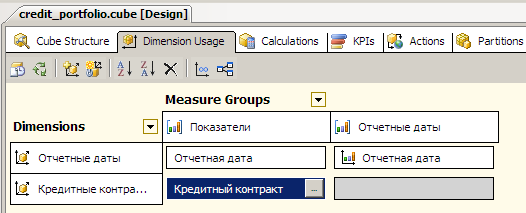
Затем в MDX-скрипте пропишем вычисляемые меры, попутно решая задачу конвертации сумм остатков в эквиваленты других валют:
--------------------------------------------------------------------------------------------------------------------------------------------------- CALCULATE; -- виртуальная мера-константа назначается по умолчанию для того, чтобы при интерактивном использовании куба -- при набрасывании измерений по осям строк/столбцов сводной таблицы НЕ включалась в работу -- физическая мера куба, что особенно полезно для ProClarity Desktop CREATE MEMBER CURRENTCUBE.[MEASURES].VirtualDefaultMember AS 1, VISIBLE = 0 ; ALTER CUBE CURRENTCUBE UPDATE DIMENSION [MEASURES], DEFAULT_MEMBER = [MEASURES].VirtualDefaultMember ; -- для измерения "Отчетные даты" устанавливается выбранной по умолчанию дата, -- равная дате наиболее поздней, на которую есть контракты ALTER CUBE CURRENTCUBE UPDATE DIMENSION [Отчетные даты], DEFAULT_MEMBER ='TAIL( FILTER([Отчетные даты].[Год-квартал-месяц-дата].MEMBERS, [MEASURES].[MEASURES].[Количество_записей]<> NULL), 1 ).ITEM(0)' ; CREATE MEMBER CURRENTCUBE.[MEASURES].[Остаток ОД] AS [MEASURES].[Остаток_ОД] -- в реальном проекте устанавливаем пересчет остатков по курсу на дату в эквивалент выбранной валюты -- [MEASURES].[Остаток_ОД] / [MEASURES].[Курс_валюты] ,FORMAT_STRING = "Currency" ,ASSOCIATED_MEASURE_GROUP = 'Показатели' -- способ сведения мер из различных размерных групп в единую ветку ,DISPLAY_FOLDER = 'ОстаткиБалансовые' -- пользователям нравится, когда все разложено по логическим папкам ,VISIBLE = 1; CREATE SET CURRENTCUBE.[Дата актуальности остатков] AS 'TAIL( FILTER([Отчетные даты].[Год-квартал-месяц-дата].MEMBERS, [MEASURES].[MEASURES].[Количество_записей]<> NULL), 1 ).ITEM(0)'; -- "Протягивание" полуаддитивной меры наверх по иерархии измерения "Отчетные даты" для незакрытого месяца: SCOPE ([MEASURES].[Остаток ОД]) ; TAIL( FILTER([Отчетные даты].[Год-квартал-месяц-дата].MEMBERS, [MEASURES].[MEASURES].[Количество_записей]<> NULL), 1 ).ITEM(0).Parent = TAIL( FILTER([Отчетные даты].[Год-квартал-месяц-дата].MEMBERS, [MEASURES].[MEASURES].[Количество_записей]<> NULL), 1 ).ITEM(0) ; TAIL( FILTER([Отчетные даты].[Год-квартал-месяц-дата].MEMBERS, [MEASURES].[MEASURES].[Количество_записей]<> NULL), 1 ).ITEM(0).Parent.Parent = TAIL( FILTER([Отчетные даты].[Год-квартал-месяц-дата].MEMBERS, [MEASURES].[MEASURES].[Количество_записей]<> NULL), 1 ).ITEM(0) ; TAIL( FILTER([Отчетные даты].[Год-квартал-месяц-дата].MEMBERS, [MEASURES].[MEASURES].[Количество_записей]<> NULL), 1 ).ITEM(0).Parent.Parent.Parent = TAIL( FILTER([Отчетные даты].[Год-квартал-месяц-дата].MEMBERS, [MEASURES].[MEASURES].[Количество_записей]<> NULL), 1 ).ITEM(0) ; TAIL( FILTER([Отчетные даты].[Год-квартал-месяц-дата].MEMBERS, [MEASURES].[MEASURES].[Количество_записей]<> NULL), 1 ).ITEM(0).Parent.Parent.Parent.Parent = TAIL( FILTER([Отчетные даты].[Год-квартал-месяц-дата].MEMBERS, [MEASURES].[MEASURES].[Количество_записей]<> NULL), 1 ).ITEM(0) ; FORMAT_STRING(This)= "Currency" ; END SCOPE ; -- впрочем, скрипт можно несколько упростить ---------------------------------------------------------------------------------------------------------------------------------------------------
Существенное замечание: если в таблице фактов нет значений на последнюю дату месяца (месяц не закрылся, события еще не наступили), то при навигации вдоль оси сводной таблицы по иерархии дат с раскрытием только до уровня месяц / квартал будут отсутствовать итоговые строки за последние месяц/квартал. Другими словами, если последняя дата, на которую есть остатки – 22.05.2011, то мы не увидим (как того, возможно, нам бы хотелось) итого за май 2011г., итого за 2 квартал 2011г. Поначалу это кажется странным, но поразмыслив, логика поведения полуадитивного типа агрегирования становится понятной. Если нужно видеть итог по незакрытому периоду, то следует применить SCOPE … END SCOPE вычисление: определяется самая поздняя дата, на которую есть данные, и значение остатка присваивается родительским элементам.
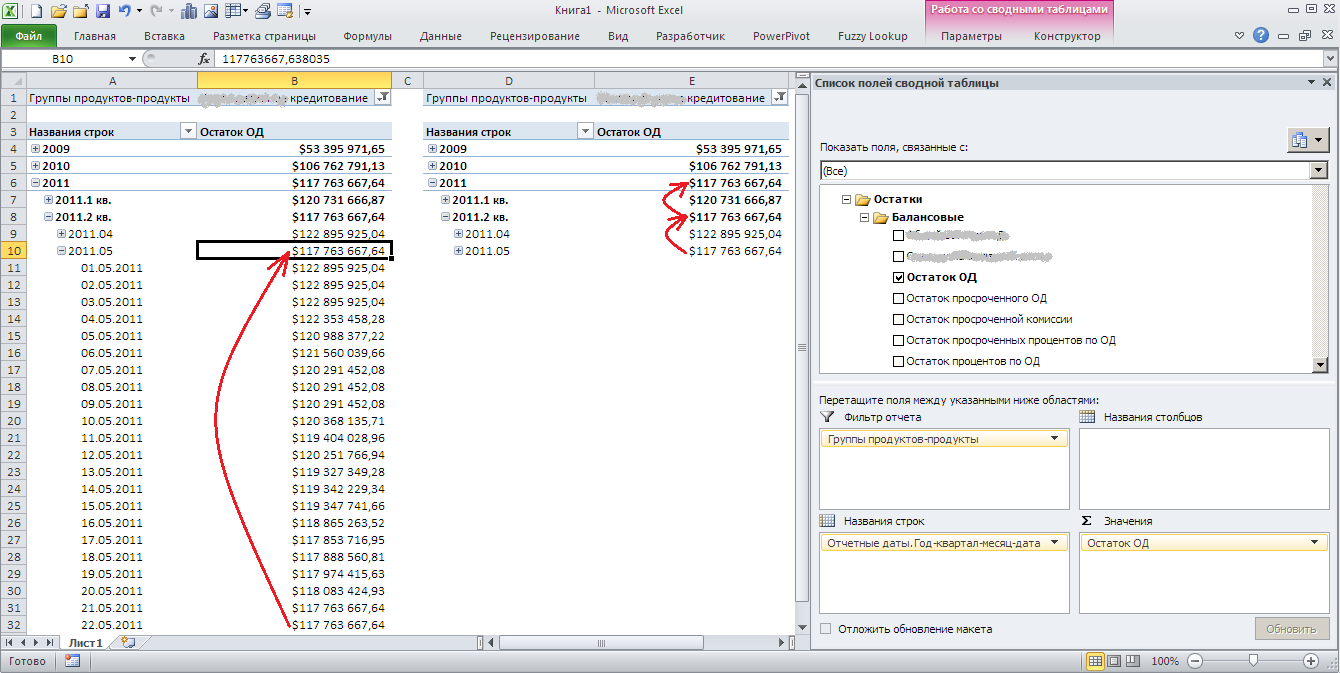
После партиционирования размерной группы, создания дизайна агрегатов, сборки куба и прогрева кэша в итоге подобные отчеты будут откликаться за считанные секунды.
dvbi.ru
2012-11-28 22:17:00Z
Последнее изменение: 2021-12-12 22:49:55Z
Возрастная аудитория: 14-70
Комментариев: 0
Теги: Примеры
Связанные статьи:
Пожалуйста, проголосуйте и ниже поставьте лайк:
Следующая статья:
SSAS – применение SCD2 для решения практических задач
Предыдущая статья:
Разграничение доступа к элементам измерений и мерам
К списку статей
07.06. 2022
Анализ остатков готовой продукции
Ранее мы рассмотрели кейс по аналитике остатков «#10 Анализ для производственных компаний: Анализ остатков по предприятиям» в этой статье мы рассмотрим анализ остатков готовой продукции производственной компании, которая продает свою продукцию через центры обслуживания клиентов, где можно купить товары оптом или в розницу, и соответственно в каждом из этих центров (их более 200 в России, а также большое количество за пределами России) есть какие-то остатки, мы хотим посмотреть:
1. Сколько денег находится в излишних остатках?
2. Сколько денег мы недополучаем из-за отсутствия товаров на складах?
Мы хотим анализировать данные:
1. В разрезе одного месяца и ежедневные остатки ( не только на начало и конец месяца)
2. С детализацией номенклатурной позиции и дня
3. Для каждой группы ABC (к какой категории относится та или иная позиция)
KPI и бизнес-логика дашборда по анализу остатков готовой продукции
KPI в рамках дашборда. Мы хотим анализировать следующие показатели:
1. Недопродажи = недополученная выручка
2. Перезапас (в рублях)
3. Обеспеченность (в процентах)
4. Нахождение в перезапасе (в процентах)
Бизнес-логика (для пользователей компании это может быть не совсем очевидно, поэтому основную логику и определения «что» есть «что», лучше отражать на дашборде (страничка где будет все описано), чтобы можно было обратить к показателям, логики расчетов и так далее): Статусы остатков рассчитываются относительно средних базовых продаж за последние три месяца, нормативный запас устанавливается для каждого склада исходя из времени на пополнение с РЦ, недопродажи рассчитываются исходя из средних базовых продаж за последние три месяца, перезапас рассчитывается для остатков, превышающих нормативный запас по производственной себестоимости.
Исходные данные
Таблица остатков
Таблица нормативов
Эти нормативы определяются из срока доставки, срока производства, то есть из срока пополнения остатков и расположения этого склада.
Таблица продаж
Фактические данные (таблицы факты). Структура может быть другой. Их может быть не три — а пять. Например отдельно нормативные остатки, отдельно таблица остатков, справочник, склады — привязка к городу в другом месте. Современный подход анализа данных дает прекрасные возможности соединять большое количество исходных данных, причем из разных источников, вы можете взять часть исходных данных, причем из разных источников, вы можете взять часть данных из учетной системы, а часть данных из Excel.
Дашборд «Перезапас товаров/ готовой продукции»
Было принято решение сделать три отдельных дашборда, чтобы не перегружать отчеты информацией: основные показатели, перезапас и дефицит.
Упрощенный дашборд перезапаса товаров на складе. Мы можем посмотреть излишки готовой продукции на складе в разрезе города, AВC группы товаров, серии товаров, по каждому городу. В целом по стране видим 76 млн излишних остатков готовой продукции на складе. Погружаемся в то, из чего эта цифра состоит и видим, что в группе А несколько позиций, по которым существенный перезапас, который длится все дни, также можем посмотреть перезапас в рублях. Исходя из анализа этого дашборда, можем строить планы, делать выводы, разбираться в причинах и принимать оперативные бизнес-решения на основе данных.
Дашборд «Обеспеченность товаров/ готовой продукции»
Упрощенный дашборд дефицита готовой продукции на складе. Имеем показатель «обеспеченность», который показывает нам сколько процентов времени (отношение количества дней к длительности выбранного месяца) товары были в доступности, а также недопродажи, в то время когда товары были недоступны. Мы можем посмотреть эти показатели по каждому товару и увидеть, отсутствовал ли товар всего лишь какой-то один день либо его не было в продаже какое-то значительное количество дней. Исходя из этого, можем строить планы, делать выводы, разбираться в причинах и принимать оперативные бизнес-решения на основе данных.
Дашборд «Остатки готовой продукции на складах. Основные показатели»
Данный дашборд построен на основе данных по остаткам центров обслуживания клиентов, отчета о продажах, отчета о себестоимости. Для расчета нормативов страхового запаса принимаются нормативы ДЛ в днях. Далее этот норматив умножается на средние продажи по каждой позиции за выбранный период продаж.
Пользователь имеет возможность задать следующие параметры:
1. Период расчета средних продаж. При расчете средних продаж не учитываются дни, когда остаток по товару был равен нулю.
2. Неснижаемый запас — количество дней, ниже которого запас не должен опускаться во избежание дефицита. Стандартное значение — 7 дней.
3. Страховой запас — запас, который не должен превышаться. Рассчитывается обеспеченность индивидуально для каждого центра обслуживания клиентов. Цифра содержится в таблице «Показатели по центрам обслуживания клиентов».
Себестоимость лишних остатков в данном отчете — это себестоимость разности между фактическим остатком и страховым запасом. Возможные виды взаимодействия с данными:
1. Фильтры в верхней части отчета применяются ко всем графикам отчета.
2. Выбор центра обслуживания клиентов можно осуществить нажатием на соответствующую строку в таблице «Показатели по центрам обслуживания клиентов» При этом все графики будут отфильтрованы по выбранному центру обслуживания клиентов.
Итак, общий дашборд с основными показателями показывает динамику внутри месяца, внутри нескольких месяцев по товарам с нулевым остатком по группам ABC, мы видим динамику внутри месяца по товарам с перезапасом и себестоимость остатков склада в рублях.
Заключение
С помощью этого дашборда руководитель предприятия (или отдельного процесса), а также менеджеры разного уровня могут анализировать остатки готовой продукции на складах, выявлять проблемные группы, номенклатурные позиции с большим остатком или большими излишками, анализировать ситуацию в конкретных предприятиях, сравнивать их — искать проблему и принимать оперативные управленческие решения, основываясь на данных.
Если есть исходные данные, то создание такого отчета занимает от нескольких часов до одного рабочего дня. Причем, созданный вами отчет не единоразовый, его легко обновлять (при появлении новых или обновленных данных) и легко использовать менеджерам разного уровня.
Данная статья подготовлена по проектам, созданным командой АНАЛИТИКА ПЛЮС.
О компании АНАЛИТИКА ПЛЮС
Получить консультацию по новому стеку наших технологий, архитектуре BI-решения, оптимизации источников данных, построению сложных дашбордов от экспертов компании АНАЛИТИКА ПЛЮС
АНАЛИТИКА ПЛЮС — ваш надежный партнер по аналитическим решениям с 2012 года. Мы работаем, чтобы вы достигали поставленных целей. Чтобы ваши данные работали, приносили пользу, помогали вам зарабатывать и принимать стратегически правильные решения. Для достижения этого мы предоставляем нашу экспертизу и лучший стек технологий, гарантирующий как работоспособность вашего решения, так и наилучший процесс сбора, обработки и анализа данных, в том числе больших данных.
Наши клиенты сегодня:
1) Производство:
— Строительство и производство строительных материалов — КНАУФ Инсулейшн, Самолет Девелопмент, Эталон
— Пищевая промышленность — Сибирский Гурман и Балтика
— Производство кормов для животных — TitBit
— Целлюлозно-бумажная промышленность — ИЛИМ
— Фарминдустрия — Материа Медика
— Металлургия — РусАл, НорНикель
— Нефтедобыча и нефтепереработка — ЛУКОйл
2) Оптовые и розничные поставщики —ЭТМ
3) Аптечные сети — Монастырёв, Апрель
4) Российские представительства —Lindt & Sprüngli
5) Рекламные агентства —Родная Речь, Медиа Инстинкт
6) Телеком — МегаФон, Yota, Ростелеком
7) Логистика и транспорт — НефтеТрансСервис, Smartavia
8) Е-commerce — Авито, Яндекс, Профи.Ру, Рамблер, gifts.ru
Нам доверяют:
Хотите научиться работать с данными?
Академия Аналитики — онлайн-образовательный проект, который создан командой АНАЛИТИКА ПЛЮС для того, чтобы компании быстро и успешно внедряли решения для анализа данных, а их сотрудники профессионально росли.
Подробнее про обучение в Академии Аналитики и доступ на платформу онлайн обучения: https://analytikaplus.ru/akademiya-analitiki-videokursy/
В
окне Multiple
Regression
выберем
вкладку
Residuals/assumptions/prediction,
позволяющую оценить остатки и нажмем
на кнопку Perform
Residual
analysis.
Далее кнопкой активизируем окно (рис.
2.6).
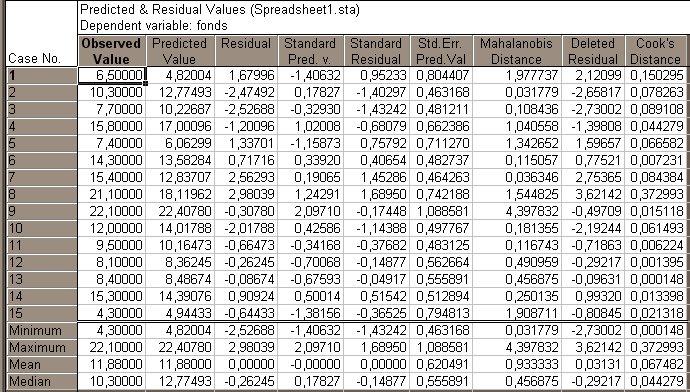
Рис.
2.6. Наблюдаемые и предсказанные значения
остатков
Первые
четыре столбца этой таблицы определяют:
номера наблюдений (названия областей),
фактические (Observed
Value)
и расчетные значения (Predicted
Value)
количества продукции, отклонения
фактических данных от расчетных
(Residual).
Четыре последних строки содержат
минимальное, максимальное, среднее и
медианное значения показателей. Равенство
нулю среднего значения остатков
свидетельствует о корректности расчетов.
Рис.
2.7. Доверительные интервалы для зависимой
переменной
Построим
регрессию выработки по фондам для более
однородной совокупности – для предприятий
федерального подчинения (при z
=
1). Можно ожидать, что качество подгонки
улучшится. Предварительно визуально
оценим данные процедурой Scatterplot.
При
отборе наблюдений будем использовать
кнопку Select
cases
во вкладке Advanced.
Зададим условие отбора в окне By
expression:
z
= 1.
Полученный график отображен на рис.
2.8.
Рис.
2.8. Диаграмма рассеяния по отобранным
данным
Возвращаемся
в
окно
Multiple
Regression.
Нажав
на кнопку
Select
cases,
убеждаемся, что там также автоматически
установлено условие отбора z
=
1 (если нет – устанавливаем это условие).
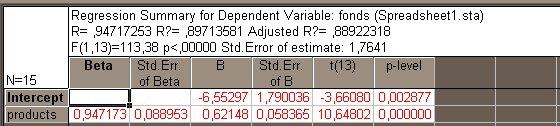
Рис.
2.9. Таблица результатов регрессионного
анализа по отобранным данным
Получаем
результаты анализа
Product
=
12.55 + 1.44 fonds,
R2
= RI
= 0.897,
S
= 2.68.
Коэффициент
детерминации увеличился с 0.597 до 0.897,
значение s
уменьшилось
с 5.01 до 2.68; действительно, подгонка
улучшилась.
2.3. Контрольное задание
По
заданной таблице зависимости признаков
X
и Y,
соответствующей номеру варианта,
провести регрессионный анализ:
1)
Найти выборочные уравнения прямых линий
регрессии
на
и
на
.
2)
Найти значение выборочного коэффициента
корреляции, провести анализ результатов.
3)
Провести анализ остатков.
Варианты
заданий находятся в практическом задании
№ 2.
Л а б о р а т о р н а я р а б о т а № 3 Дисперсионный анализ
Цель:
изучение
методики применения дисперсионного
анализа при проверке гипотезы о равенстве
математических ожиданий, либо при
установлении того, оказывает ли
качественный фактор
существенное влияние на исследуемую
величину.
3.1. Теоретическая часть
Задачей
дисперсионного анализа является изучение
влияния одного или нескольких факторов
на рассматриваемый признак.
Однофакторный
дисперсионный анализ используется в
тех случаях, когда есть в распоряжении
три или более независимые выборки,
полученные из одной генеральной
совокупности путем изменения какого-либо
независимого фактора, для которого по
каким-либо причинам нет количественных
измерений.
Для
этих выборок предполагают, что они имеют
разные выборочные средние и одинаковые
выборочные дисперсии. Поэтому необходимо
ответить на вопрос, оказал ли этот фактор
существенное влияние на разброс
выборочных средних или разброс является
следствием случайностей, вызванных
небольшими объемами выборок. Другими
словами если выборки принадлежат одной
и той же генеральной совокупности, то
разброс данных между выборками (между
группами) должен быть не больше, чем
разброс данных внутри этих выборок
(внутри групп).
Пусть
–
-й
элемент-выборки
,
где– число выборок,
– число данных в
-выборке.
Тогда– выборочное среднее
-выборки
определяется по формуле.
Общее среднее вычисляется по формуле,
где.
Основное
тождество дисперсионного анализа имеет
следующий вид:
,
где
– сумма квадратов отклонений выборочных
среднихот общего среднего
(сумма квадратов отклонений между
группами);
–сумма
квадратов отклонений наблюдаемых
значений
от выборочной средней
(сумма квадратов отклонений внутри
групп);
–общая
сумма квадратов отклонений наблюдаемых
значений
от общего среднего
.
Расчет
этих сумм квадратов отклонений
осуществляется по следующим формулам:
,
,
.
В
качестве критерия необходимо
воспользоваться критерием Фишера:
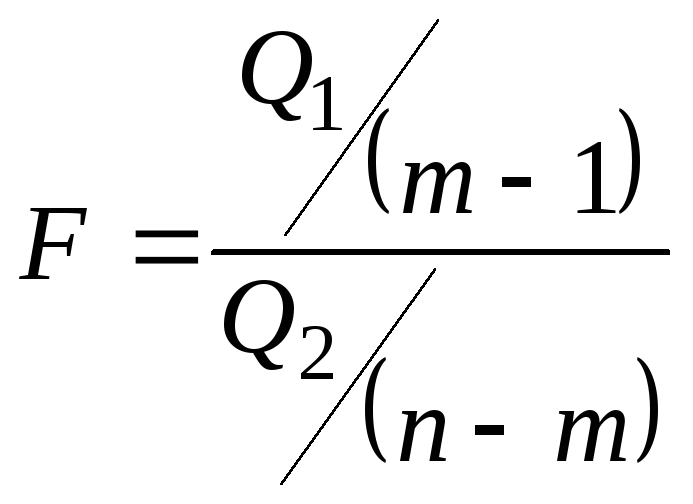
Если
расчетное значение критерия Фишера
будет меньше, чем табличное значение
– нет оснований считать, что независимый
фактор оказывает влияние на разброс
средних значений, в противном случае,
независимый фактор оказывает существенное
влияние на разброс средних значений (– уровень значимости, уровень риска,
обычно для экономических задач).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Три аналитических отчета в управленке, которые спасут деньги компании
Разбираемся, чем поможет анализ задолженности контрагентов, контроль товарных остатков и анализ движения денежных средств.

Отчет по контролю товарных остатков
Данные скажут об остатках материалов, товаров, готовой продукции в разрезе склада — как в количестве, так и в сумме.
Ценность отчета в том, что он показывает затоваривание склада — это в первую очередь «замороженные» деньги компании. Если объема товаров не хватает, это приводит к сбою производства или поставок.
Отчет собираете из конечного сальдо счетов:
- 10 (за исключением 10.07, 10.11);
- 21, 41 (за исключением 41.11, 41.12, 41.К).
Контроль товарных остатков дает руководству инструмент, который поможет планировать товарооборот и объемы производства.
Анализ задолженности контрагентов
Анализ поможет выявить и отследить «возраст» долга. Задолженности подразделяются на четыре типа:
- Вы должны поставщикам.
- Поставщики должны вам.
- Вы должны покупателям.
- Покупатели должны вам.
Чтобы корректно сформировать отчет, пропишите в договорах сроки поставок и оплат.
Ценность отчета в том, что он дает контроль за движением денег. Дебиторка — тоже «замороженные» деньги, кредиторка — риски для претензий.
Анализ движения денежных средств
Этот анализ показывает движение денег прямым методом, без учета аналитики по сферам деятельности.
Отчет формируется так:
Как полноценно внедрить управленку в компанию и давать руководству нужные решения
«Клерк» собрал экспертов, которые настроили управленку уже в сотнях компаний. Вместе с ними запустили курс повышения квалификации по управленке.
За один месяц вы пройдете 42 онлайн-урока, выполните 8 тестов, чтобы закрепить материал. Пообщаетесь с кураторами и другими участниками в закрытом Telegram-чате. Мы будем давать домашние задания.
В конце курса сдадите итоговую аттестацию и получите удостоверение на 140 ак. часов — данные внесем в ФИС ФРДО Рособрнадзора, оригинал отправим по почте.
Вас будут учить:

Пройдите онлайн-курс повышения квалификации и внедрите управленку в компанию
Научим настраивать аналитику и формировать отчеты
Получите удостоверение на 140 ак. часов (ФИС ФРДО)
Заполните форму ниже и нажмите «Начать учиться»
Материал из MachineLearning.
Перейти к: навигация, поиск
Содержание
- 1 Постановка задачи
- 2 Описание алгоритма
- 2.1 Анализ регрессионных остатков
- 2.2 Оценка значимости признаков
- 3 Гетероскедастичность
- 3.1 Визуальный анализ
- 3.2 Статистические методы детекции
- 3.2.1 Тест Уайта
- 3.2.2 Тест Голдфелда-Кванта
- 3.2.3 Тест Ансари-Брэдли
- 3.3 Эвристика
- 4 Вычислительный эксперимент на модельных данных
- 4.1 Три модели
- 4.1.1 Модель №1 (хорошая)
- 4.1.2 Модель №2 (плохая, одномерная)
- 4.1.3 Модель №3 (плохая,многомерная)
- 4.2 Выводы
- 4.1 Три модели
- 5 Исходный код
- 6 См. также
- 7 Литература
Для получения информации об адекватности построенной модели многомерной линейной регрессии используется анализ регрессионных остатков.
Постановка задачи
Задана выборка откликов и признаков. Рассматривается множество линейных регрессионных моделей вида:
. Требуется создать инструмент анализа адекватности модели используя анализ регрессионных остатков и исследовать значимость признаков и поведение остатков в случае гетероскедастичности.
Описание алгоритма
Анализ регрессионных остатков
Анализ регрессионных остатков заключается в проверке нескольких гипотез:
-
(1)
-
(2)
-
(3)
-
(4)
— независимы
где ,
, — регрессионные остатки конкретной модели.
– отклики посчитанные по модели, а
– эмпирические отклики.
Для проверки первой гипотезы воспользуемся критерием знаков.
Проверка второй гипотезы, по сути, является проверкой на гомоскедастичность, то есть на постоянство дисперсии, случай гетероскедастичности будет рассмотрен ниже. Для этого воспользуемся двумя статистическими тестами: тестом Ансари-Брэдли и критерием Голдфелда-Кванта.
Так как тест Ансари-Брэдли фактически осуществляет проверку гипотезы, что у двух предоставленных выборок дисперсии одинаковы, а мы фактически имеем только один вектор остатков, то произведем несколько тестов, сравнивая в каждом две случайные выборки из нашего вектора остатков.
Проверку нормальности распределения осуществим с помощью критерия согласия хи-квадрат, модифицированного для проверки на нормальность, то есть сравнивая данное нам распределение в остатках с нормальным распределением, имеющим моментные характеристики, вычисленные из вектора остатков. Наконец, проверку последнего условия реализуем с помощью статистики Дарбина-Уотсона.
Оценка значимости признаков
Задача состоит в проверке для каждого из признаков, дает ли нам учет этого признака в модели более хорошие результаты, нежели его отсутствие. Оценивать результаты будем с помощью коэффициента детерминации:
где — эмпирический отклик,
— отклик, посчитанный по модели, и
— математическое ожидание
.
Гетероскедастичность
Термин гетероскедастичность применяется в ситуации, когда ошибки в различных наблюдениях некоррелированы, но их дисперсии — разные. Соответственно термин гомоскедастичность применяется в случае постоянных дисперсий.
Визуальный анализ
Одним из основных методов предварительного исследования на гетероскедастичность является визуальный анализ графика остатков. Целью данного анализа является нахождение факторов влияющих на изменение дисперсии, номер измерения или значение одного из признаков. Для сравнения приведем несколько примеров.
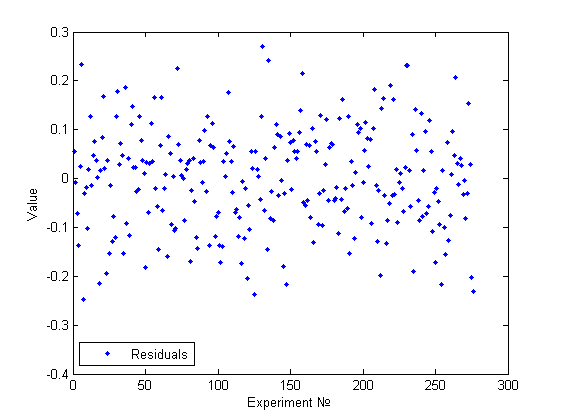
Выше представлена госмоскедастичная модель. Действительно, используя визуальный анализ, не получается найти какие-то признаки непостоянства дисперсии и тем более какие-то зависимости.
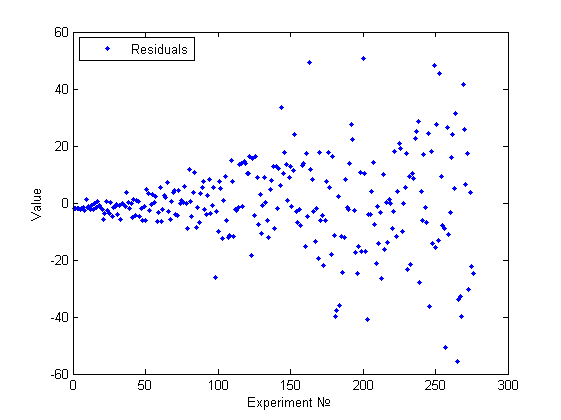
В данном случае визуально можно констатировать факт непостоянства дисперсии и даже связать это изменение с номером эксперимента (или возможно с одним из признаков, если он монотонно изменялся по номеру эксперимента).
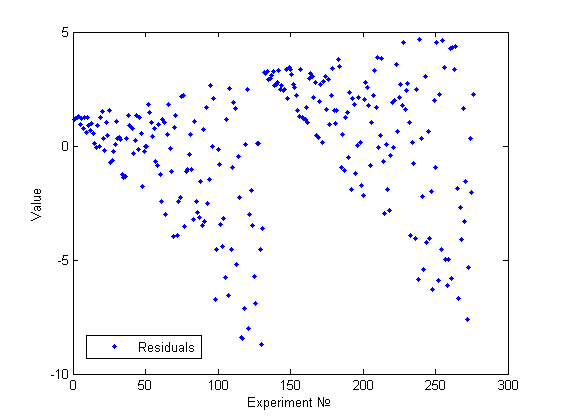
Еще один пример визуально определимой гетероскедастичности.
Статистические методы детекции
Опишем суть нескольких общеупотребительных статистических тестов на гетероскедастичность.
Во всех этих тестах основной гипотезой является равенство
против альтернативной гипотезы
: не
.
Тест Уайта
Содержательный смысл теста в том, что часто гетероскедастичность модели вызвана зависимостью (возможно довольно сложной) дисперсий ошибок от признаков. Реализуя эту идею, Уайт предложил метод тестирования гипотезы без каких-либо предположений о структуре гетероскедастичности. Сначала к исходной модели применяется обычный метод наименьших квадратов и находятся остатки регрессии
. Затем осуществляется регрессия квадратов этих остатков
на все признаки, их квадраты, попарные произведения и константу.
Тогда при гипотезе величина
асимптотически имеет распределение
, где
— коэффициент детерминации, а
— число регрессоров второй регрессии.
Плюс данного теста — его универсальность. Минусы : 1) если гипотеза отвергается, то никаких указаний на функциональную форму гетероскедастичности мы не получаем; 2) несомненным минусом является поиск вслепую вида регрессии(начинаем приближать простыми полиномами второй степени без какой бы то ни было причины на это)
Тест Голдфелда-Кванта
Этот тест применяется, когда есть предположение о прямой зависимости дисперсии ошибок от некоторого признака. Алгоритм метода:
- упорядочить данные по убыванию того признака, относительно которого сделано предположение;
- Делим наблюдения на три части, причём они должны быть равны или примерно равны, а также первая и третья должны быть одинаковы.
- Провести две независимые регрессии для первой части и для последней. Рассчитать выровненные значения и построить соответствующие остатки (
):
и
;
- Cоставить cтатистику Фишера
. Если
кр, следовательно есть гетероскедостичность.
Тест Ансари-Брэдли
Тест получает на вход две выборки размеров и
и проверяет на равенство дисперсий распределения, из которых они могли быть получены. Алгоритм метода пошагово:
- Расположим
по возрастанию;
- Расставим метки таким образом :
Эвристика
Суть данной эвристики состоит в ранжировании псевдодисперсий и в анализе полученной гистограммы. Под псевдодисперсией будем понимать величины
, где
. Простейший анализ гистограммы, состоящей из 10 интервалов, будем проводить сравнением количества элементов на первых двух интервалах. Это отношение будем сравнивать с некоторой, заранее заданной константой, на основе чего и будем принимать решение о гетероскедастичности. Вот пример гистограммы для гомоскедастичного случая (график его остатков был представлен ранее):
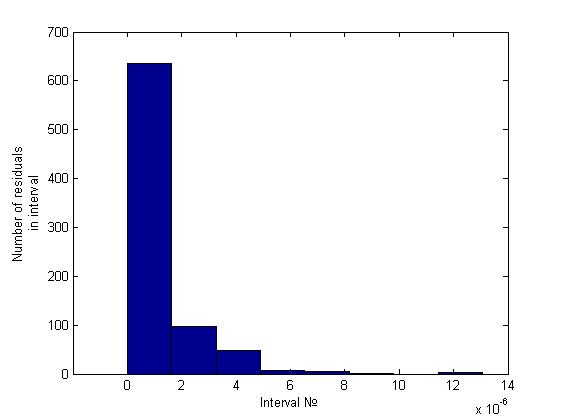
Легко заметить, что порядок отношения первых двух столбцов – около пяти-шести к одному, что же касается гетероскедастичного случая, это отношение будет больше семи (было замечено вплоть до 34) примеры можно посмотреть ниже, в вычислительном эксперименте.
Вычислительный эксперимент на модельных данных
В данном отчете представлены результаты применения созданного инструмента анализа представленной модели с помощью исследования ее регрессионных остатков. Отчет состоит из трех экспериментов, демонстрирующих плюсы и минусы созданного инструмента.
Три модели
Представленные модели были подобраны так, чтобы визуальный анализ регрессионных остатков не давал очевидных результатов. Будем проводить исследование в два этапа – вначале проверяя модель на выполнение основных гипотез, затем исследуя модель на гетероскедастичность с помощью теста Голдфелда-Кванта и несложной эвристики.
Модель №1 (хорошая)
Наша модель : , где
. Таким образом все гипотезы должны выполняться и гетероскедастичность должна отсутствовать.
[A,x,res] = GetGoodExample [meanst, distab, normchi2, normjb] = ResAnalysis(res) GoldfeldQuandt(A(:,1:end-1),A(:,end),1) GoldfeldQuandt(A(:,1:end-1),A(:,end),2) HistAnalys(res)
Получаем результат:
% Проверка основных гипотез meanst = 0 distab = 0.0500 normchi2 = 0 normjb = 0 %Проверка на гетероскедастичность% goldfeldquandt1 = 0 goldfeldquandt2 = 0 result = 0
График остатков этой модели уже был приведен выше и не представляет особого интереса.
Модель №2 (плохая, одномерная)
Наша модель : , где
. Таким образом, модель очевидным образом гетероскедастична, но визуальным анализом это сложно обнаружить(см.рисунок).
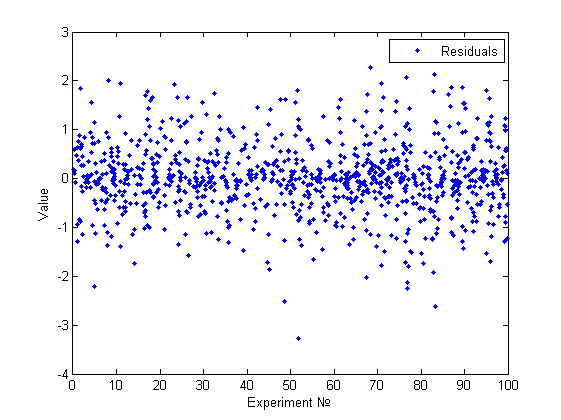
[A,x,res] = GetBadExample [meanst, distab, normchi2, normjb] = ResAnalysis(res) GoldfeldQuandt(A(:,1:end-1),A(:,end),1) HistAnalys(res)
Получаем результат:
% Проверка основных гипотез meanst = 0 distab = 0.0340 normchi2 = 1.0020 normjb = 1.0020 %Проверка на гетероскедастичность% goldfeldquandt1 = 0 result = 1
Нормальность отвергнута. Гетероскедастичность была обнаружена только эвристикой. Приведем гистограмму полученную эвристикой:
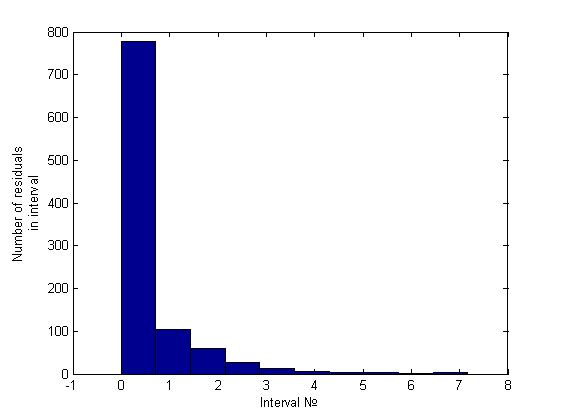
Модель №3 (плохая,многомерная)
Наша модель : , где
. Таким образом, модель очевидным образом гетероскедастична, но снова визуальным анализом это сложно обнаружить(см.рисунок).
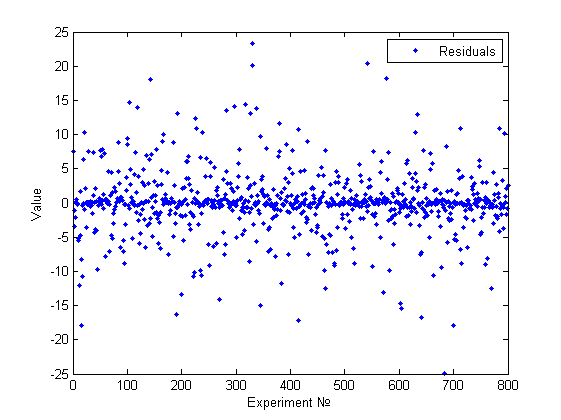
[A,x,res] = GetBadExample1 [meanst, distab, normchi2, normjb] = ResAnalysis(res) GoldfeldQuandt(A(:,1:end-1),A(:,end),1) GoldfeldQuandt(A(:,1:end-1),A(:,end),2) GoldfeldQuandt(A(:,1:end-1),A(:,end),5) HistAnalys(res)
Получаем результат:
% Проверка основных гипотез meanst = 0 distab = 0.0288 normchi2 = 1.0025 normjb = 1.0025 %Проверка на гетероскедастичность% goldfeldquandt1 = 1 goldfeldquandt2 = 1 goldfeldquandt5 = 0 result = 1
Нормальность отвергнута. Гетероскедастичность была обнаружена как эвристикой, так и тестом Голдфелда-Квандта (зависимость от первой и второй и независимость от пятой переменной). Приведем гистограмму полученную эвристикой:
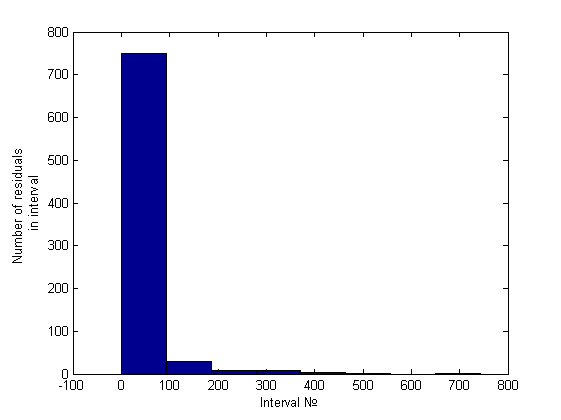
Выводы
Статистические проверки на нормальность показали себя с наилучшей стороны. Эвристика показала хорошие результаты в исследовании на гетероскедастичность. Тест Голдфелда-Квандта не сработал только в одном тесте. Тест Ансари-Брэдли (использовался для проверки на постоянство дисперсии) показал наихудшие результаты, так как с его помощью не удалось различить две существенно разные модели. Это вполне объяснимо: мы применяли этот тест для сравнения дисперсий двух случайных выборок взятых из нашего вектора остатков. Вполне очевидно что результат достаточно не предсказуем вследствие именно этой случайности выборок. В итоге мы получали одинаковые результаты для разных моделей. (причем увеличение числа экспериментов не решает данной проблемы).
Исходный код
Функции анализирующие остатки (реализовано в MATLAB)
См. также
Wikipedia о гетероскедастичности, англ.
Коэффициент детерминации
Анализ регрессионных остатков
Литература
- Н.Джонсон, Ф.Лион Статистика и планирование эксперимента в технике и науке, перевод с английского «Мир»,1980. — 610 c.
- Я. Р. Магнус, П. К. Катышев, А. А. Пересецкий Эконометрика. Начальный курс:Учеб. — 6 изд.,перераб.и доп. — М.:Дело,2004. — 576 с. ISBN 5-7749-0055-Х
- Applied Logistic Regression/ David W. Hosmer,Stanley Lemeshow.-2nd ed. -Wiley-Interscience Publication,2000. – 397 c. ISBN 0-471-35632-8
- Кобзарь А. И. Прикладная математическая статистика. — М.: Физматлит, 2006. — 816 с. ISBN 5-9221-0707-0
| |
Данная статья была создана в рамках учебного задания.
В настоящее время задание завершено и проверено. См. также методические указания по использованию Ресурса MachineLearning.ru в учебном процессе. |