В этой статье рассмотрим двоичное дерево, как оно строится и варианты обходов.
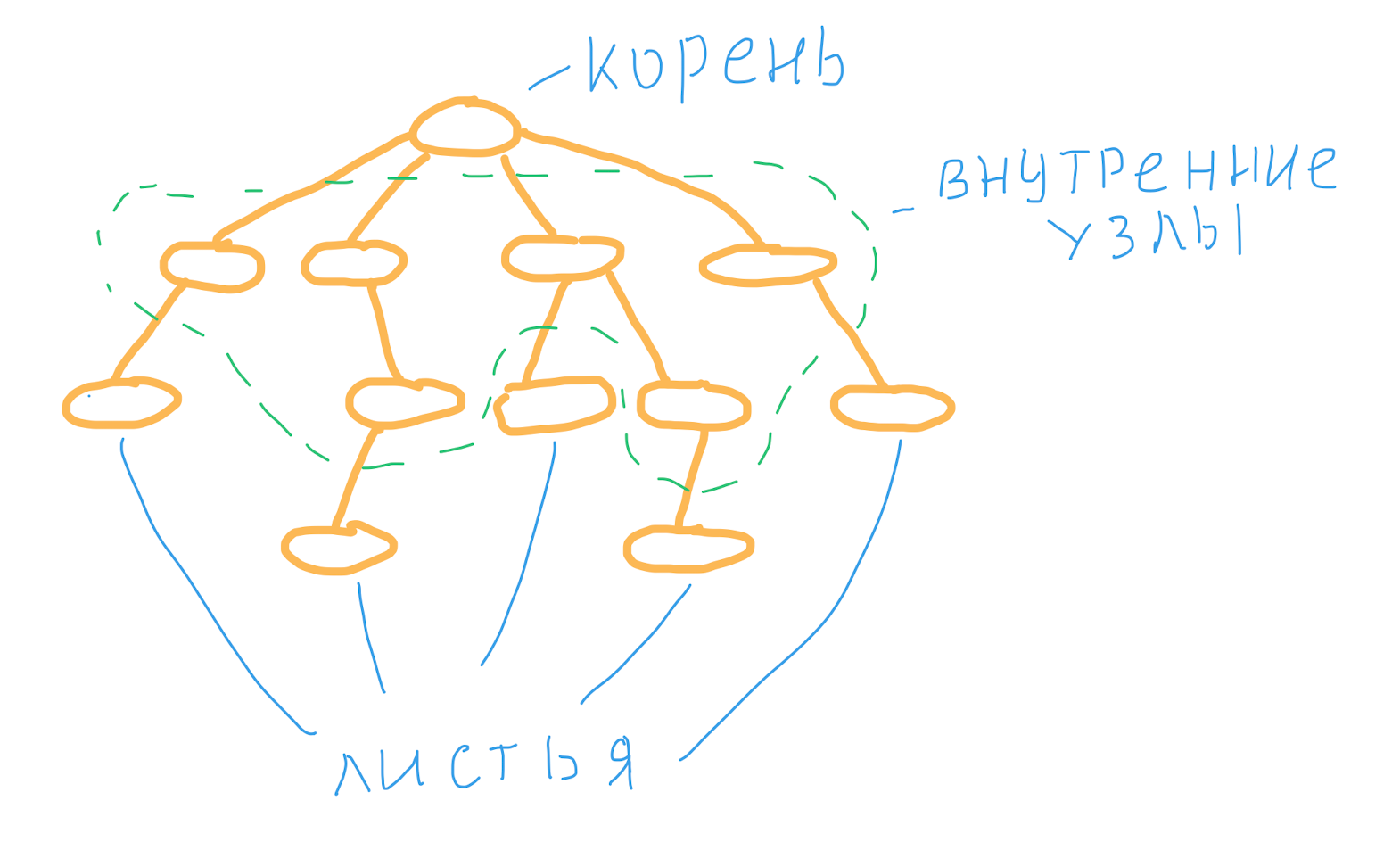
Двоичное дерево в первую очередь дерево. В программировании – структура данных, которая имеет корень и дочерние узлы, без циклических связей. Если рассмотреть отдельно любой узел с дочерними элементами, то получится тоже дерево. Узел называется внутренним, если имеет хотя бы одно поддерево. Cамые нижние элементы, которые не имеют дочерних элементов, называются листами или листовыми узлами.
Дерево обычно рисуется сверху вниз.
В узлах может храниться любая информация, от примитивных типов до объектов. В этой статье, мы рассмотрим реализацию, когда в узле также хранятся ссылки на дочерние элементы. Кроме такого подхода, возможен альтернативный подход для двоичного дерева — хранение в массиве.
Первая особенность двоичного дерева, что любой узел не может иметь более двух детей. Их называют просто — левый и правый потомок, или левое и правое поддерево.
Вторая особенность двоичного дерева, и основное правило его построения, заключается в том что левый потомок меньше текущего узла, а правый потомок больше. Отношение больше/меньше имеет смысл для сравниваемых объектов, например числа, строки, если в дереве содержатся сложные объекты, то для них берётся какая-нибудь процедура сравнения, и она будет отрабатывать при всех операциях работы с деревом.
Создание дерева, вставка
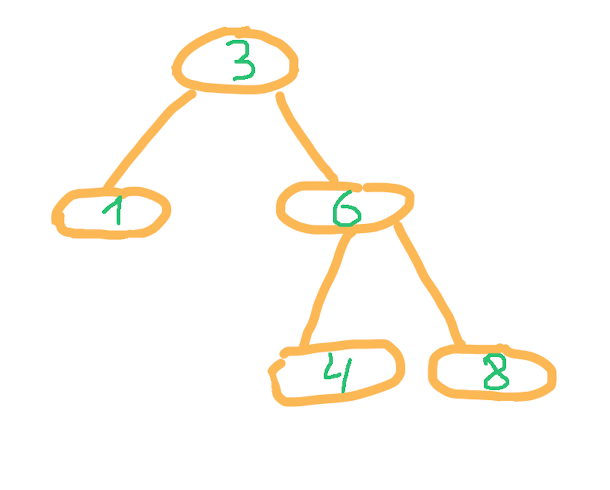
Рассмотрим существующее двоичное дерево. Корень содержит число 3, все узлы в левом поддереве меньше текущего, в правом — больше. Такие же правила действуют для любого рассматриваемого узла и его поддеревьев.
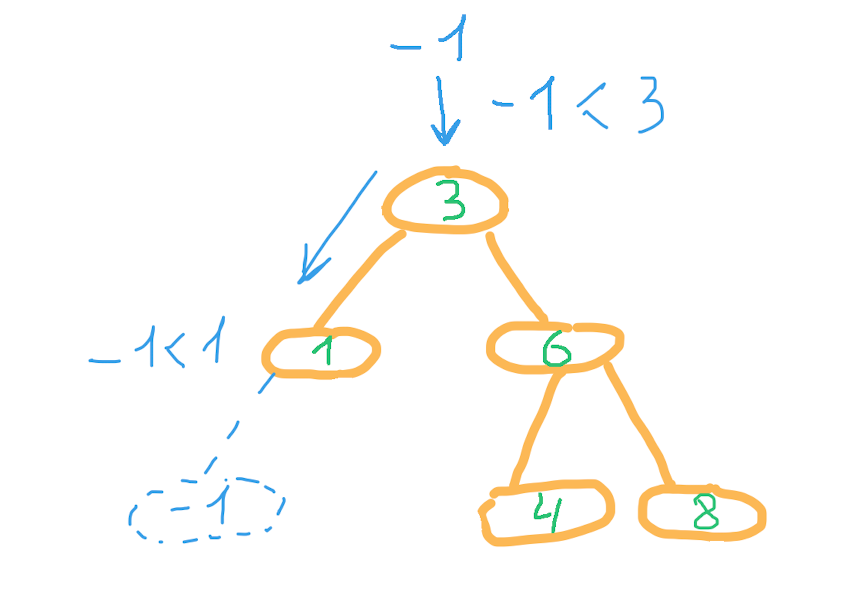
Попробуем вставить в это дерево элемент -1.
Из корня идем в левое поддерево, так как -1 меньше 3. Из узла со значением 1 также идём в левое поддерево. Но в этом узле левое поддерево отсутствует, вставляем в эту позицию элемент, создавая новый узел дерева.
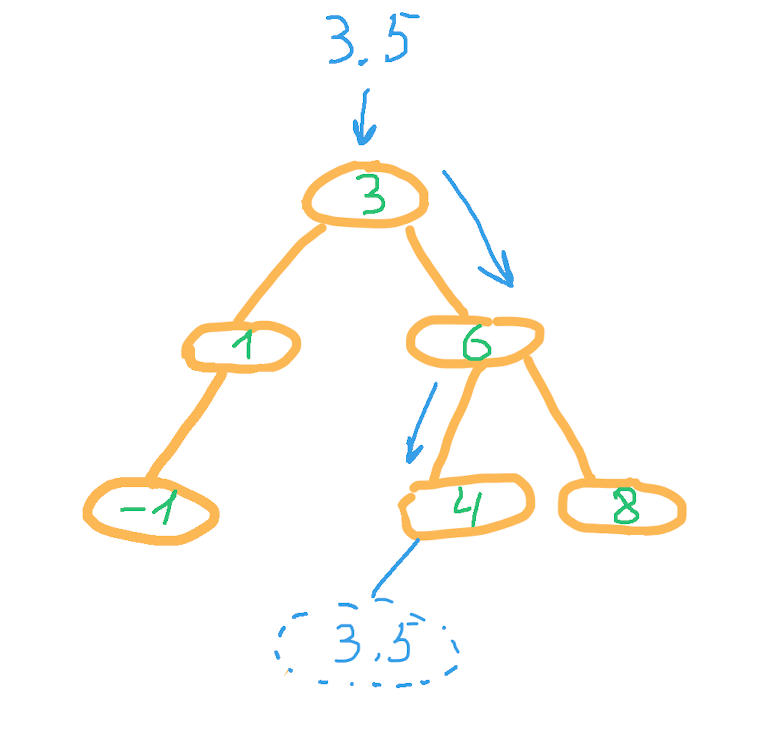
Вставим в получившееся дерево элемент 3.5.
Проходим по дереву, сравнивая на каждом из этапов вставляемое значение с элементом в узле, пока не дойдем до узла, в котором следующий узел для сравнения отсутствует, в эту позицию и вставляем новый узел.
Если дерево не существует, то есть root равен null, то элемент вставляется в корень, после этого проводится вставка по описанному выше алгоритму.
Напишем класс для создания двоичного дерева:
// дополнительный класс для хранения информации узла
class BinaryTreeItem {
constructor(itemValue) {
this.value = itemValue;
this.left = null;
this.right = null;
}
}
const elementExistMessage =
"The element has already in the tree";
class BinaryTree {
// в начале работы дерево пустое, root отсутствует
constructor() {
this.root = null;
}
insertItem(newItem) {
// создание нового узла дерева
const newNode = new BinaryTreeItem(newItem);
// проверка на пустой root, если пустой, то заполняем
// и завершаем работу
if (this.root === null) {
this.root = newNode;
return;
}
// вызов рекурсивного добавления узла
this._insertItem(this.root, newNode);
}
_insertItem(currentNode, newNode) {
// если значение в добавляемом узле
// меньше текущего рассматриваемого узла
if (newNode.value < currentNode.value) {
// если меньше и левое поддерево отсутствует
// то добавляем
if (currentNode.left === null) {
currentNode.left = newNode;
} else {
// если левое поддерево существует,
// то вызываем для этого поддерева
// процедуру добавления нового узла
this._insertItem(currentNode.left, newNode);
}
}
// для правого поддерева алгоритм аналогичен
// работе с левым поддеревом, кроме операции сравнения
if (newNode.value > currentNode.value) {
if (currentNode.right === null) {
currentNode.right = newNode;
} else {
this._insertItem(currentNode.right, newNode);
}
}
// если элемент равен текущему элементу,
// то можно реагировать по разному, например просто
// вывести предупреждение
// возможно стоит добавить проверку на NaN,
// зависит от потребностей пользователей класса
if (newNode.value === currentNode.value) {
console.warn(elementExistMessage);
}
}
}
const binaryTree = new BinaryTree();
binaryTree.insertItem(3);
binaryTree.insertItem(1);
binaryTree.insertItem(6);
binaryTree.insertItem(4);
binaryTree.insertItem(8);
binaryTree.insertItem(-1);
binaryTree.insertItem(3.5);
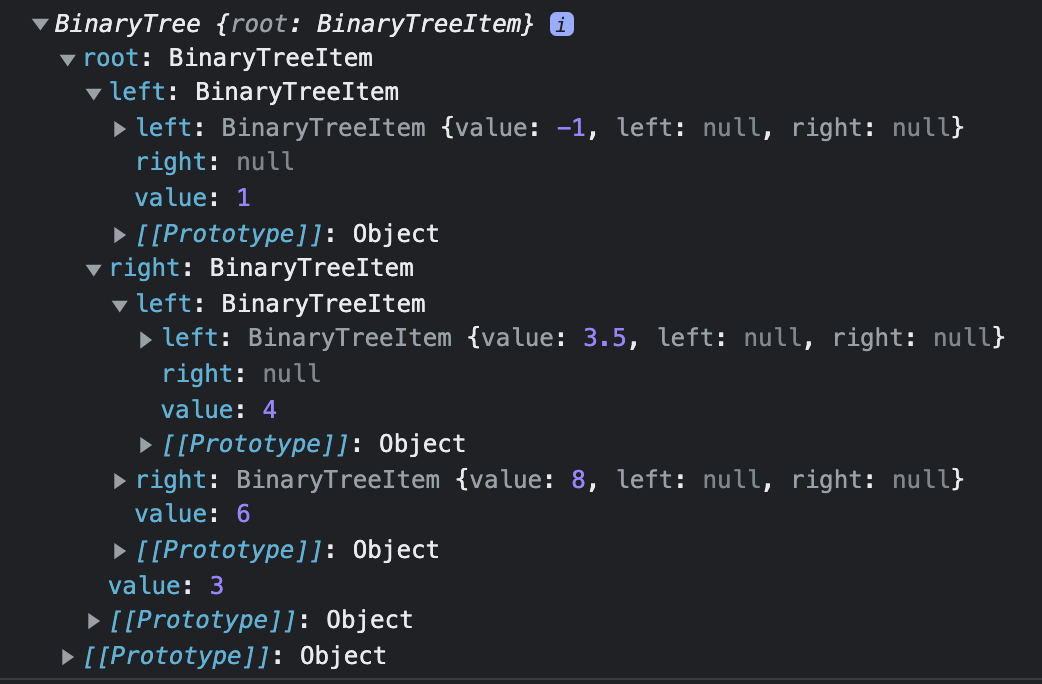
console.log(binaryTree);На скриншоте ниже то, какую информацию хранит в себе binaryTree:
Обход
Рассмотрим несколько алгоритмов обхода/поиска элементов в двоичном дереве.
Мы можем спускаться по дереву, в каждом из узлов есть выбор куда можем пойти в первую очередь и какой из элементов обработать сначала: левое поддерево, корень или право поддерево. Такие варианты обхода называются обходы в глубину (depth first).
Какие возможны варианты обхода (слово поддерево опустим):
- корень, левое, правое (preorder, прямой);
- корень, правое, левое;
- левое, корень, правое (inorder, симметричный, центрированный);
- левое, правое, корень (postorder, обратный);
- правое, корень, левое;
- правое, левое, корень.
Также используется вариант для обхода деревьев по уровням. Уровень в дереве — его удалённость от корня. Сначала обходится корень, после этого узлы первого уровня и так далее. Называется обход в ширину, по уровням, breadth first, BFS — breadth first search или level order traversal.
Выбирается один из этих вариантов, и делается обход, в каждом из узлов применяя выбранную стратегию.
Обычно для обходов в глубину применяется рекурсия. Реализуем один из вариантов, например симметричный: левое поддерево, корень, правое поддерево.
При этом мы обработаем первым самый левый узел, где левое поддерево окажется пустым, но правое может присутствовать. То есть в каждом из узлов будем спускаться ниже и ниже, пока левое поддерево не окажется пустым.
class BinaryTreeItem {
constructor(itemValue) {
this.value = itemValue;
this.left = null;
this.right = null;
}
}
const elementExistMessage =
"The element has already in the tree";
class BinaryTree {
constructor() {
this.root = null;
}
insertItem(newItem) {
// .....
}
inorder(handlerFunction) {
// просто вызываем функцию с другими параметрами,
// добавляя текущий обрабатываемый узел
// в рекурсивные вызов
this._inorderInternal(this.root, handlerFunction);
}
_insertItem(currentNode, newNode) {
// .....
}
_inorderInternal(currentNode, handlerFunction) {
// если узла нет, то его обрабатывать не нужно
if (currentNode === null) return;
// порядок обхода, для каждого из поддеревьев:
// 1. проваливаемся в левое поддерево
// 2. вызываем обрабатывающую функцию
// 3. проваливаемся в правое поддерево
this._inorderInternal(currentNode.left,
handlerFunction);
handlerFunction(currentNode.value);
this._inorderInternal(currentNode.right,
handlerFunction);
}
}
const binaryTree = new BinaryTree();
binaryTree.insertItem(3);
binaryTree.insertItem(1);
binaryTree.insertItem(6);
binaryTree.insertItem(4);
binaryTree.insertItem(8);
binaryTree.insertItem(-1);
binaryTree.insertItem(3.5);
binaryTree.inorder(console.log);
// вызов inorder(console.log) выведет
// -1
// 1
// 3
// 3.5
// 4
// 6
// 8
Для реализации других вариантов обхода просто меняем порядок вызова функций в функции _inorderInternal. И нужно не забыть переименовать функцию, чтобы название соответствовало содержимому.
Рассмотрим inorder алгоритм обхода на примере дерева, созданного в предыдущем блоке кода.
// 1
this._inorderInternal(currentNode.left, handlerFunction);
// 2
handlerFunction(currentNode.value);
// 3
this._inorderInternal(currentNode.right, handlerFunction);
Сначала мы спустимся в самое левое поддерево — узел -1. Зайдем в его левое поддерево, которого нет, первая конструкция выполнится, ничего не сделав внутри функции. Вызовется обработчик handlerFunction, на узле -1. После этого произойдёт попытка войти в правое поддерево, которого нет. Работа функции для узла -1 завершится.
В вызов для узла -1 мы пришли через вызов функции _inorderInternal для левого поддерева узла 1. Вызов для левого поддерева -1 завершился, вызовется обработчик для значения узла 1, после этого — для правого поддерева. Правого поддерева нет, функция для узла 1 заканчивает работу. Выходим в обработчик для корня дерева.
Для корня дерева левое поддерево полностью отработало, происходит переход ко второй строке процедуры обхода — вызов обработчика значения узла. После чего вызов функции для обработчика правого поддерева.
Аналогично продолжая рассуждения, и запоминая на какой строке для определенного узла мы вошли в рекурсивный вызов, можем пройти алгоритм «руками», лучше понимая его работу.
Для обходов в ширину используется дополнительный массив.
class BinaryTreeItem {
constructor(itemValue) {
this.value = itemValue;
this.left = null;
this.right = null;
}
}
const elementExistMessage =
"The element has already in the tree";
class BinaryTree {
constructor() {
this.root = null;
}
insertItem(newItem) {
// .....
}
breadthFirstHandler(handlerFunction) {
if (this.root === null) return;
// массив, в который будем добавлять элементы,
// по мере спускания по дереву
const queue = [this.root];
// используем позицию в массиве для текущего
// обрабатываемого элемента
let queuePosition = 0;
// можем убирать обработанные элементы из очереди
// например функцией shift
// для обработки всегда брать нулевой элемент
// и завершать работу, когда массив пуст
// но shift работает за линейное время, что увеличивает
// скорость работы алгоритма
// while (queue.length > 0) {
// const currentNode = queue.shift();
while (queuePosition < queue.length) {
// текущий обрабатываемый элемент в queuePosition
const currentNode = queue[queuePosition];
handlerFunction(currentNode.value);
// добавляем в список для обработки дочерние узлы
if (currentNode.left !== null) {
queue.push(currentNode.left);
}
if (currentNode.right !== null) {
queue.push(currentNode.right);
}
queuePosition++;
}
}
_insertItem(currentNode, newNode) {
// ......
}
}
const binaryTree = new BinaryTree();
binaryTree.insertItem(3);
binaryTree.insertItem(1);
binaryTree.insertItem(6);
binaryTree.insertItem(4);
binaryTree.insertItem(8);
binaryTree.insertItem(-1);
binaryTree.insertItem(3.5);
binaryTree.breadthFirstHandler(console.log);
// вызов breadthFirstHandler(console.log) выведет
// 3 корень
// 1 узлы первого уровня
// 6
// -1 узлы второго уровня
// 4
// 8
// 3.5 узел третьего уровня
Поиск
Операция поиска — вернуть true или false, в зависимости от того, содержится элемент в дереве или нет. Может быть реализована на основе поиска в глубину или ширину, посмотрим на реализацию на основе алгоритма обхода в глубину.
search(value) {
return this._search(this.root, value);
}
_search(currentNode, value) {
// дополнительные проверки,
// обрабатывающие завершение поиска
// либо проваливание в несуществующий узел
// либо найденной значение
if (currentNode === null) return false;
if (currentNode.value === value) return true;
// this._search проваливаются в дерево
// когда поиск завершен
// то по цепочке рекурсивных вызовов
// будет возвращен результат
if (value < currentNode.value) {
return this._search(currentNode.left, value);
}
if (value > currentNode.value) {
return this._search(currentNode.right, value);
}
}Функция сравнения или получение ключа
До этого мы рассматривали простые данные, для которых определена операция сравнения между ключами. Не всегда возможно реализовать сравнение таким простым образом.
Можно сделать функцию, которая будет получать ключ из данных, которые хранятся в узле.
class BinaryTreeItem {
constructor(itemValue) {
this.value = itemValue;
this.left = null;
this.right = null;
}
}
const elementExistMessage =
"The element has already in the tree";
class BinaryTree {
// параметр при создании дерева -
// функция получения ключа
// ключи должны быть сравнимы
constructor(getKey) {
this.root = null;
this.getKey = getKey;
}
insertItem(newItem) {
const newNode = new BinaryTreeItem(newItem);
if (this.root === null) {
this.root = newNode;
return;
}
this._insertItem(this.root, newNode);
}
breadthFirstHandler(handlerFunction) {
// .....
}
_insertItem(currentNode, newNode) {
// отличие во всех процедурах сравнения
// вместо просто сравнивания value
// перед этим применяем функцию получения ключа
if (this.getKey(newNode.value) <
this.getKey(currentNode.value)) {
if (currentNode.left === null) {
currentNode.left = newNode;
} else {
this._insertItem(currentNode.left, newNode);
}
}
if (this.getKey(newNode.value) >
this.getKey(currentNode.value)) {
if (currentNode.right === null) {
currentNode.right = newNode;
} else {
this._insertItem(currentNode.right, newNode);
}
}
if (this.getKey(newNode.value) ===
this.getKey(currentNode.value)) {
console.warn(elementExistMessage);
}
}
}
const getKey = (element) => element.key;
const binaryTree = new BinaryTree(getKey);
binaryTree.insertItem({ key: 3 });
binaryTree.insertItem({ key: 1 });
binaryTree.insertItem({ key: 6 });
binaryTree.insertItem({ key: 4 });
binaryTree.insertItem({ key: 8 });
binaryTree.insertItem({ key: -1 });
binaryTree.insertItem({ key: 3.5 });
binaryTree.breadthFirstHandler(console.log);Можно передать в конструктор специальную функцию сравнения. Эту функцию можно сделать как обычно делают функции сравнения в программировании, возвращать 0, если ключи равны. Значение больше нуля, если первый переданный объект больше второго, и меньше нуля если меньше. Важно не перепутать когда что возвращается и правильно передать параметры. Например, текущий узел, уже существующий в дереве, первым параметром, а тот, с которым производится текущая операция — вторым.
Для реализации такой возможности потребуется во всех местах сравнения использовать эту функцию
class BinaryTreeItem {
constructor(itemValue) {
this.value = itemValue;
this.left = null;
this.right = null;
}
}
const elementExistMessage =
"The element has already in the tree";
class BinaryTree {
// в конструкторе передаем функцию сравнения
constructor(compareFunction) {
this.root = null;
this.compareFunction = compareFunction;
}
insertItem(newItem) {
const newNode = new BinaryTreeItem(newItem);
if (this.root === null) {
this.root = newNode;
return;
}
this._insertItem(this.root, newNode);
}
breadthFirstHandler(handlerFunction) {
// .....
}
_insertItem(currentNode, newNode) {
// вместо сравнения value
// вызываем функцию сравнения
// и проверяем больше или меньше нуля
// получился результат сравнения
if (this.compareFunction(currentNode.value,
newNode.value) > 0) {
if (currentNode.left === null) {
currentNode.left = newNode;
} else {
this._insertItem(currentNode.left, newNode);
}
}
// текущий узел меньше нового,
// значит новый узел должен быть отправлен
// в правое поддерево
if (this.compareFunction(currentNode.value,
newNode.value) < 0) {
if (currentNode.right === null) {
currentNode.right = newNode;
} else {
this._insertItem(currentNode.right, newNode);
}
}
if (this.compareFunction(currentNode.value,
newNode.value) === 0) {
console.warn(elementExistMessage);
}
}
}
const compare = (object1, object2) => {
return object1.key - object2.key;
};
const binaryTree = new BinaryTree(compare);
binaryTree.insertItem({ key: 3 });
binaryTree.insertItem({ key: 1 });
binaryTree.insertItem({ key: 6 });
binaryTree.insertItem({ key: 4 });
binaryTree.insertItem({ key: 8 });
binaryTree.insertItem({ key: -1 });
binaryTree.insertItem({ key: 3.5 });
binaryTree.breadthFirstHandler(console.log);Заключение
Мы познакомились с концепцией двоичных деревьев и операциями для создания такого типа дерева. Эти операции интуитивно понятны, в следующей статье рассмотрим процедуру удаления и скорость работы двоичного дерева.
Бинарные деревья поиска и рекурсия – это просто
Время на прочтение
8 мин
Количество просмотров 521K
Существует множество книг и статей по данной теме. В этой статье я попробую понятно рассказать самое основное.
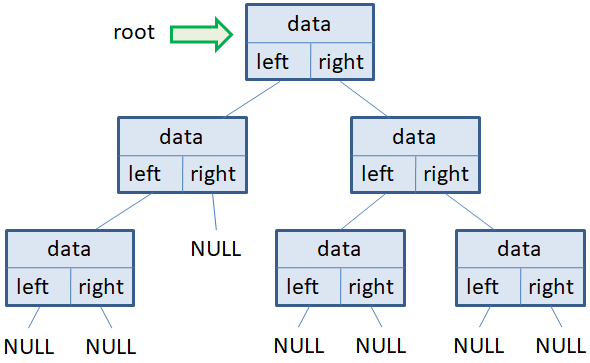
Бинарное дерево — это иерархическая структура данных, в которой каждый узел имеет значение (оно же является в данном случае и ключом) и ссылки на левого и правого потомка. Узел, находящийся на самом верхнем уровне (не являющийся чьим либо потомком) называется корнем. Узлы, не имеющие потомков (оба потомка которых равны NULL) называются листьями.
Рис. 1 Бинарное дерево
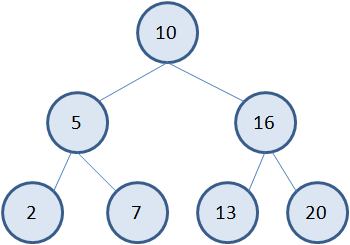
Бинарное дерево поиска — это бинарное дерево, обладающее дополнительными свойствами: значение левого потомка меньше значения родителя, а значение правого потомка больше значения родителя для каждого узла дерева. То есть, данные в бинарном дереве поиска хранятся в отсортированном виде. При каждой операции вставки нового или удаления существующего узла отсортированный порядок дерева сохраняется. При поиске элемента сравнивается искомое значение с корнем. Если искомое больше корня, то поиск продолжается в правом потомке корня, если меньше, то в левом, если равно, то значение найдено и поиск прекращается.
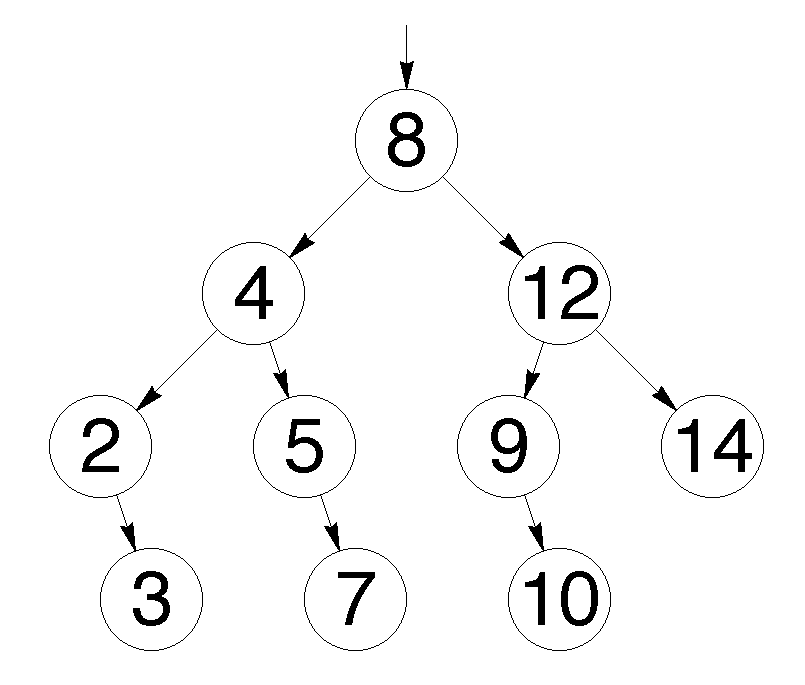
Рис. 2 Бинарное дерево поиска
Сбалансированное бинарное дерево поиска — это бинарное дерево поиска с логарифмической высотой. Данное определение скорее идейное, чем строгое. Строгое определение оперирует разницей глубины самого глубокого и самого неглубокого листа (в AVL-деревьях) или отношением глубины самого глубокого и самого неглубокого листа (в красно-черных деревьях). В сбалансированном бинарном дереве поиска операции поиска, вставки и удаления выполняются за логарифмическое время (так как путь к любому листу от корня не более логарифма). В вырожденном случае несбалансированного бинарного дерева поиска, например, когда в пустое дерево вставлялась отсортированная последовательность, дерево превратится в линейный список, и операции поиска, вставки и удаления будут выполняться за линейное время. Поэтому балансировка дерева крайне важна. Технически балансировка осуществляется поворотами частей дерева при вставке нового элемента, если вставка данного элемента нарушила условие сбалансированности.
Рис. 3 Сбалансированное бинарное дерево поиска
Сбалансированное бинарное дерево поиска применяется, когда необходимо осуществлять быстрый поиск элементов, чередующийся со вставками новых элементов и удалениями существующих. В случае, если набор элементов, хранящийся в структуре данных фиксирован и нет новых вставок и удалений, то массив предпочтительнее. Потому что поиск можно осуществлять алгоритмом бинарного поиска за то же логарифмическое время, но отсутствуют дополнительные издержки по хранению и использованию указателей. Например, в С++ ассоциативные контейнеры set и map представляют собой сбалансированное бинарное дерево поиска.
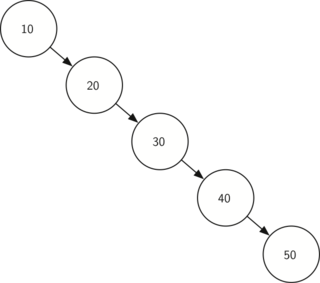
Рис. 4 Экстремально несбалансированное бинарное дерево поиска
Теперь кратко обсудим рекурсию. Рекурсия в программировании – это вызов функцией самой себя с другими аргументами. В принципе, рекурсивная функция может вызывать сама себя и с теми же самыми аргументами, но в этом случае будет бесконечный цикл рекурсии, который закончится переполнением стека. Внутри любой рекурсивной функции должен быть базовый случай, при котором происходит выход из функции, а также вызов или вызовы самой себя с другими аргументами. Аргументы не просто должны быть другими, а должны приближать вызов функции к базовому случаю. Например, вызов внутри рекурсивной функции расчета факториала должен идти с меньшим по значению аргументом, а вызовы внутри рекурсивной функции обхода дерева должны идти с узлами, находящимися дальше от корня, ближе к листьям. Рекурсия может быть не только прямой (вызов непосредственно себя), но и косвенной. Например А вызывает Б, а Б вызывает А. С помощью рекурсии можно эмулировать итеративный цикл, а также работу структуры данных стек (LIFO).
int factorial(int n)
{
if(n <= 1) // Базовый случай
{
return 1;
}
return n * factorial(n - 1); //рекурсивеый вызов с другим аргументом
}
// factorial(1): return 1
// factorial(2): return 2 * factorial(1) (return 2 * 1)
// factorial(3): return 3 * factorial(2) (return 3 * 2 * 1)
// factorial(4): return 4 * factorial(3) (return 4 * 3 * 2 * 1)
// Вычисляет факториал числа n (n должно быть небольшим из-за типа int
// возвращаемого значения. На практике можно сделать long long и вообще
// заменить рекурсию циклом. Если важна скорость рассчетов и не жалко память, то
// можно совсем избавиться от функции и использовать массив с предварительно
// посчитанными факториалами).
void reverseBinary(int n)
{
if (n == 0) // Базовый случай
{
return;
}
cout << n%2;
reverseBinary(n/2); //рекурсивеый вызов с другим аргументом
}
// Печатает бинарное представление числа в обратном порядке
void forvardBinary(int n)
{
if (n == 0) // Базовый случай
{
return;
}
forvardBinary(n/2); //рекурсивеый вызов с другим аргументом
cout << n%2;
}
// Поменяли местами две последние инструкции
// Печатает бинарное представление числа в прямом порядке
// Функция является примером эмуляции стека
void ReverseForvardBinary(int n)
{
if (n == 0) // Базовый случай
{
return;
}
cout << n%2; // печатает в обратном порядке
ReverseForvardBinary(n/2); //рекурсивеый вызов с другим аргументом
cout << n%2; // печатает в прямом порядке
}
// Функция печатает сначала бинарное представление в обратном порядке,
// а затем в прямом порядке
int product(int x, int y)
{
if (y == 0) // Базовый случай
{
return 0;
}
return (x + product(x, y-1)); //рекурсивеый вызов с другим аргументом
}
// Функция вычисляет произведение x * y ( складывает x y раз)
// Функция абсурдна с точки зрения практики,
// приведена для лучшего понимания рекурсии
Кратко обсудим деревья с точки зрения теории графов. Граф – это множество вершин и ребер. Ребро – это связь между двумя вершинами. Количество возможных ребер в графе квадратично зависит от количества вершин (для понимания можно представить турнирную таблицу сыгранных матчей). Дерево – это связный граф без циклов. Связность означает, что из любой вершины в любую другую существует путь по ребрам. Отсутствие циклов означает, что данный путь – единственный. Обход графа – это систематическое посещение всех его вершин по одному разу каждой. Существует два вида обхода графа: 1) поиск в глубину; 2) поиск в ширину.
Поиск в ширину (BFS) идет из начальной вершины, посещает сначала все вершины находящиеся на расстоянии одного ребра от начальной, потом посещает все вершины на расстоянии два ребра от начальной и так далее. Алгоритм поиска в ширину является по своей природе нерекурсивным (итеративным). Для его реализации применяется структура данных очередь (FIFO).
Поиск в глубину (DFS) идет из начальной вершины, посещая еще не посещенные вершины без оглядки на удаленность от начальной вершины. Алгоритм поиска в глубину по своей природе является рекурсивным. Для эмуляции рекурсии в итеративном варианте алгоритма применяется структура данных стек.
С формальной точки зрения можно сделать как рекурсивную, так и итеративную версию как поиска в ширину, так и поиска в глубину. Для обхода в ширину в обоих случаях необходима очередь. Рекурсия в рекурсивной реализации обхода в ширину всего лишь эмулирует цикл. Для обхода в глубину существует рекурсивная реализация без стека, рекурсивная реализация со стеком и итеративная реализация со стеком. Итеративная реализация обхода в глубину без стека невозможна.
Асимптотическая сложность обхода и в ширину и в глубину O(V + E), где V – количество вершин, E – количество ребер. То есть является линейной по количеству вершин и ребер. Записи O(V + E) с содержательной точки зрения эквивалентна запись O(max(V,E)), но последняя не принята. То есть, сложность будет определятся максимальным из двух значений. Несмотря на то, что количество ребер квадратично зависит от количества вершин, мы не можем записать сложность как O(E), так как если граф сильно разреженный, то это будет ошибкой.
DFS применяется в алгоритме нахождения компонентов сильной связности в ориентированном графе. BFS применяется для нахождения кратчайшего пути в графе, в алгоритмах рассылки сообщений по сети, в сборщиках мусора, в программе индексирования – пауке поискового движка. И DFS и BFS применяются в алгоритме поиска минимального покрывающего дерева, при проверке циклов в графе, для проверки двудольности.
Обходу в ширину в графе соответствует обход по уровням бинарного дерева. При данном обходе идет посещение узлов по принципу сверху вниз и слева направо. Обходу в глубину в графе соответствуют три вида обходов бинарного дерева: прямой (pre-order), симметричный (in-order) и обратный (post-order).
Прямой обход идет в следующем порядке: корень, левый потомок, правый потомок. Симметричный — левый потомок, корень, правый потомок. Обратный – левый потомок, правый потомок, корень. В коде рекурсивной функции соответствующего обхода сохраняется соответствующий порядок вызовов (порядок строк кода), где вместо корня идет вызов данной рекурсивной функции.
Если нам дано изображение дерева, и нужно найти его обходы, то может помочь следующая техника (см. рис. 5). Обводим дерево огибающей замкнутой кривой (начинаем идти слева вниз и замыкаем справа вверх). Прямому обходу будет соответствовать порядок, в котором огибающая, двигаясь от корня впервые проходит рядом с узлами слева. Для симметричного обхода порядок, в котором огибающая, двигаясь от корня впервые проходит рядом с узлами снизу. Для обратного обхода порядок, в котором огибающая, двигаясь от корня впервые проходит рядом с узлами справа. В коде рекурсивного вызова прямого обхода идет: вызов, левый, правый. Симметричного – левый, вызов, правый. Обратного – левый правый, вызов.
Рис. 5 Вспомогательный рисунок для обходов
Для бинарных деревьев поиска симметричный обход проходит все узлы в отсортированном порядке. Если мы хотим посетить узлы в обратно отсортированном порядке, то в коде рекурсивной функции симметричного обхода следует поменять местами правого и левого потомка.
struct TreeNode
{
double data; // ключ/данные
TreeNode *left; // указатель на левого потомка
TreeNode *right; // указатель на правого потомка
};
void levelOrderPrint(TreeNode *root) {
if (root == NULL)
{
return;
}
queue<TreeNode *> q; // Создаем очередь
q.push(root); // Вставляем корень в очередь
while (!q.empty() ) // пока очередь не пуста
{
TreeNode* temp = q.front(); // Берем первый элемент в очереди
q.pop(); // Удаляем первый элемент в очереди
cout << temp->data << " "; // Печатаем значение первого элемента в очереди
if ( temp->left != NULL )
q.push(temp->left); // Вставляем в очередь левого потомка
if ( temp->right != NULL )
q.push(temp->right); // Вставляем в очередь правого потомка
}
}
void preorderPrint(TreeNode *root)
{
if (root == NULL) // Базовый случай
{
return;
}
cout << root->data << " ";
preorderPrint(root->left); //рекурсивный вызов левого поддерева
preorderPrint(root->right); //рекурсивный вызов правого поддерева
}
// Функция печатает значения бинарного дерева поиска в прямом порядке.
// Вместо печати первой инструкцией функции может быть любое действие
// с данным узлом
void inorderPrint(TreeNode *root)
{
if (root == NULL) // Базовый случай
{
return;
}
preorderPrint(root->left); //рекурсивный вызов левого поддерева
cout << root->data << " ";
preorderPrint(root->right); //рекурсивный вызов правого поддерева
}
// Функция печатает значения бинарного дерева поиска в симметричном порядке.
// То есть в отсортированном порядке
void postorderPrint(TreeNode *root)
{
if (root == NULL) // Базовый случай
{
return;
}
preorderPrint(root->left); //рекурсивный вызов левого поддерева
preorderPrint(root->right); //рекурсивный вызов правого поддерева
cout << root->data << " ";
}
// Функция печатает значения бинарного дерева поиска в обратном порядке.
// Не путайте обратный и обратноотсортированный (обратный симметричный).
void reverseInorderPrint(TreeNode *root)
{
if (root == NULL) // Базовый случай
{
return;
}
preorderPrint(root->right); //рекурсивный вызов правого поддерева
cout << root->data << " ";
preorderPrint(root->left); //рекурсивный вызов левого поддерева
}
// Функция печатает значения бинарного дерева поиска в обратном симметричном порядке.
// То есть в обратном отсортированном порядке
void iterativePreorder(TreeNode *root)
{
if (root == NULL)
{
return;
}
stack<TreeNode *> s; // Создаем стек
s.push(root); // Вставляем корень в стек
/* Извлекаем из стека один за другим все элементы.
Для каждого извлеченного делаем следующее
1) печатаем его
2) вставляем в стек правого! потомка
(Внимание! стек поменяет порядок выполнения на противоположный!)
3) вставляем в стек левого! потомка */
while (s.empty() == false)
{
// Извлекаем вершину стека и печатаем
TreeNode *temp = s.top();
s.pop();
cout << temp->data << " ";
if (temp->right)
s.push(temp->right); // Вставляем в стек правого потомка
if (temp->left)
s.push(temp->left); // Вставляем в стек левого потомка
}
}
// В симметричном и обратном итеративном обходах просто меняем инструкции
// местами по аналогии с рекурсивными функциями.
Надеюсь Вы не уснули, и статья была полезна. Скоро надеюсь последует продолжение
банкета
статьи.
Курс по структурам данных: https://stepik.org/a/134212
На этом занятии мы затронем новую тему –
бинарные деревья. Что это такое? Давайте предположим, что нам в программе нужно
хранить и обрабатывать иерархические структуры данных, например,
генеалогическое древо семьи, или структура каталогов и файлов и т.п.
То есть, везде,
где есть некая начальная (корневая) вершина, от которой можно провести связи к
дочерним, а от них – к следующим дочерним, получается иерархическая древовидная
структура. Именно о таких структурах данных мы и будем вести речь на ближайших
занятиях.
Начальная
вершина дерева, от которого следуют все остальные, называется корнем дерева
(root). Сами элементы
дерева – узлами или вершинами (nodes). Причем, узел
слева, называется левым, а справа – правым. Если у вершины нет
левого или правого потомка, то обычно указывают значение NULL. Вершины, у
которых нет потомков, называются листьями. Само же дерево, у которого
каждая вершина может содержать не более двух дочерних узлов, называется бинарным
или двоичным. Всю эту терминологию и обозначения, мы в дальнейшем
будем активно использовать.
Структура бинарного дерева
Чаще всего в
практике программирования используют бинарные деревья. Даже когда у вершины
предполагается множество потомков, то зачастую задачу сводят все равно к
бинарным деревьям или какой-либо другой структуре данных. Поэтому мы в рамках
данного курса ограничимся именно бинарными деревьями.
Каждая вершина
такого дерева содержит, как минимум, три поля:
- data – данные,
хранимые в вершине дерева; - left – ссылка
(указатель) на потомка слева; - right – ссылка
(указатель) на потомка справа.
Иногда еще
добавляют ссылку на родительский узел. Но чаще всего ограничиваются этими тремя
полями.
На вершину
дерева, которая называется корнем, ведет указатель root. И через этот
указатель происходит вся работа с бинарным деревом: добавление/удаление
элементов; обход всех узлов дерева. То есть, из корневого узла можно пройти до
любого другого в данном дереве. При этом, количество вершин, через которые
нужно пройти, чтобы достичь некоторого узла, определяет уровень (level) дерева. Если
дерево не содержит ни одной вершины, то root = NULL. Также, если у
какой-либо вершины отсутствует левый или правый потомок, то соответствующий
указатель принимает значение NULL.
Добавление вершин в бинарное дерево
Давайте теперь
посмотрим, как можно формировать бинарное дерево, то есть, добавлять в него
новые вершины. Обычно, новые узлы добавляются к свободному указателю (то есть,
тот, который принимает значение NULL), начиная с корневого. То есть, первая
вершина всегда добавляется в корень, и других вариантов просто нет. А вот
далее, мы уже решаем добавить левый или правый узел. Строго говоря, ограничений
здесь никаких нет. Алгоритм добавления может быть самым разным, исходя из
поставленной задачи. Например, если нам нужно сформировать генеалогическое
древо, то, очевидно, в вершинах последовательно должны указываться потомки: на
нулевом уровне – некоторый человек; на первом – мама, папа; на втором –
бабушки, дедушки и т.д. Но есть отдельный класс задач, когда в вершинах
бинарного дерева хранятся данные, которые можно сравнивать на больше и меньше
(например, числа), и добавление нового узла происходит по правилам:
- если добавляемое
значение меньше значения в родительском узле, то новая вершина добавляет в
левую ветвь, иначе – в правую; - если добавляемое
значение уже присутствует в дереве, то оно игнорируется (то есть, дубли
отсутствуют).
Например,
предположим, мы собираемся хранить в вершинах бинарного дерева целые числа. И
будем последовательно добавлять узлы для значений:
10, 5, 7, 16,
13, 2, 20
Первое значение
10 просто добавляется в корневую вершину. Следующее значение 5. Смотрим от
корня. Пять меньше 10. Тогда, согласно нашим правилам, это значение нужно
записать в левую ветвь. Формируем новый узел со значением 5. Следующее значение
7. Снова идет от корня дерева. Семь меньше 10, переходим в левую ветвь. Здесь у
нас узел со значением 5. И пять больше 7. Следовательно, семь нужно добавить в
качестве правого узла дерева у вершины 5. Далее, идет число 16. Оно больше 10,
поэтому добавляем его в качестве правой вершины у корневой. Затем, число 13.
Оно также больше 10, но меньше 16. Следовательно, нужно добавить левый узел у
вершины 16. Следующее значение 2 меньше 10 и меньше 5. Добавляем новый узел
справа от узла 5. И последнее значение 20 – самое большое, поэтому оно станет
самой крайней правой вершиной дерева.
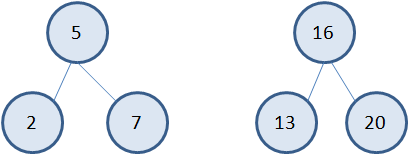
Благодаря такому
подходу в формировании бинарного дерева, у нас в левой ветви будут находиться
вершины со значениями меньше, чем у корневой, а в правой ветви – вершины со
значениями больше корневой. И этот вывод будет справедлив для любого
выделенного фрагмента поддерева, например:
Поиск значений в бинарном дереве
Хорошо, но что
нам это дает? Смотрите, здесь появляется несколько интересных эффектов. Первый
– это ускорение поиска заданного значения. Например, нам нужно определить,
находится ли число 2 в последовательности чисел 10, 5, 7, 16, 13, 2, 20. Если
бы мы хранили числа в обычном массиве:
то время поиска,
с точки зрения O большого, составило бы O(n), где n – число
элементов в массиве. Нам пришлось бы последовательно перебирать все элементы и
сравнивать значения с числом 2.
А вот в бинарном
дереве все несколько иначе и, в среднем, быстрее. Вначале число 2 сравнивается
с числом 10. Оно меньше, поэтому идем по левой ветви, где сосредоточены вершины
со значениями меньше 10. В результате, мы сразу отсекаем правую группу
элементов, значения которых заведомо не равны 2. За счет этого происходит
ускорение поиска. Затем, сравниваем 2 и 5. И, так как 2 меньше 5, то снова
переходим по левой ветви. Находим заданное значение. Как видите, нам
потребовалось всего три сравнения, чтобы найти число 2 в бинарном дереве. С
позиции О большого среднее число операций, необходимое для поиска нужного значения
составляет . И это
значительно быстрее, чем линейный поиск в массивах или связных списках.
Давайте теперь
посмотрим на работу алгоритма в случае, когда заданное значение для поиска в
бинарном дереве отсутствует. Например, это число 11. Очевидно, мы должны идти
сначала по правой ветви, в узле 16 – по левой, и доходим до листовой вершины
13. Далее, никаких узлов в дереве нет, но значение не было найдено,
следовательно, в дереве нет этого числа 11.
Или, такой
пример. Нам нужно найти число 5. Оно хранится в промежуточной вершине. Поэтому,
когда мы доходим до нее, то дальнейший процесс поиска прерывается, значение
найдено. Вот принцип, по которому выполняется поиск значений в вершинах
бинарного дерева.
Сбалансированные и несбалансированные деревья
Внимательный
зритель сейчас мог бы мне возразить и сказать, что у нас все так хорошо
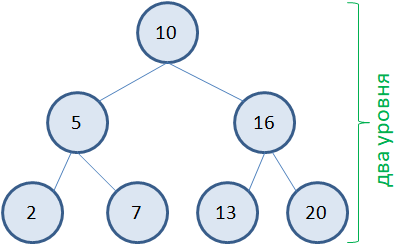
получается, потому что я привел пример «красивого» бинарного дерева с минимальным
числом уровней (всего два):
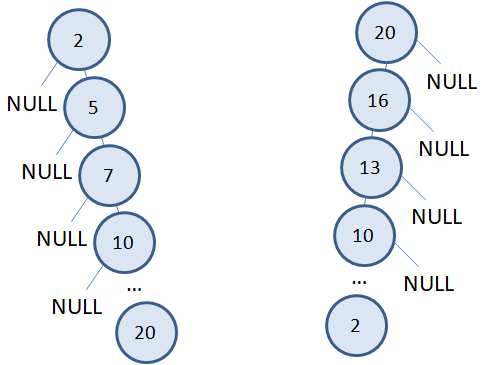
Но, если бы
числа при формировании дерева поступали в другом порядке, или по возрастанию:
2, 5, 7, 10, 13,
16, 20
или по убыванию:
20, 16, 13, 10,
7, 5, 2
то деревья
выглядели бы совсем иначе:
Фактически, они
вырождаются в односвязный список и объем вычислений для поиска заданного
значения в них составляет O(n). Так же, как и
в обычных массивах или связных списках. Выигрыша уже нет.
Такие
вырожденные деревья (и подобные им) называются несбалансированными. В
отличие от первого, которое относится к сбалансированным.
Вообще, дерево
называется сбалансированным, если в нем поддеревья от одной вершины отличаются
не более чем на один уровень. И именно в сбалансированных деревьях поиск
значений в вершинах выполняется за минимальное число шагов с объемом вычислений
O(log n). Поэтому, на
практике, стремятся строить деревья близкие к сбалансированным. Для этого
используют методы балансировки двоичных деревьев, среди которых, наиболее
известны следующие:
- АВЛ-дерево (AVL tree), разработан в
1968 году; - красно-черное
дерево (red-black tree), разработан в
1972 году; - расширяющееся
или косое дерево (splay tree), разработан в
1983 году.
Любой из этих
методов может быть реализован в бинарном дереве и вызываться при добавлении новых
вершин. В результате получаем более сбалансированное дерево при любых входных
последовательностях данных. В данном курсе мы не будем углубляться в эти темы.
Кому будет интересно, подробную информацию по этим методам легко найти на
просторах Интернета. Отмечу только, что если нам известно, что в решаемой
задаче данные (значения) поступают в случайном порядке, то в среднем, будет
формироваться бинарное дерево близкое к сбалансированному.
На этом мы
завершим наше первое знакомство с бинарными деревьями, а на следующем продолжим
и поговорим об алгоритмах обхода и удаления вершин бинарных деревьев.
Курс по структурам данных: https://stepik.org/a/134212
Видео по теме
Напомним свойства бинарных деревьев:
-
Должно быть не более двух дочерних узлов
-
Дочерние узлы тоже должны быть бинарными деревьями
-
Дочерние узлы называют левыми и правыми
В этом случае структура узла принимает следующий вид:
class BinaryTreeNode {
constructor(value, parent) {
this.left = null; //ссылка на левый дочерний узел
this.right = null; //ссылка на правый дочерний
this.parent = parent; //ссылка на родителя
this.value = value; //полезная нагрузка
}
}Java
class BinaryTreeNode {
public BinaryTreeNode left = null;
public BinaryTreeNode right = null;
public BinaryTreeNode parent;
public Object value;
BinaryTreeNode(Object value, BinaryTreeNode parent) {
this.parent = parent;
this.value = value;
}
}Python
class BinaryTreeNode:
def __init__(self, value, parent=None):
self.left = None # ссылка на левый дочерний узел
self.right = None # ссылка на правый дочерний узел
self.parent = parent # ссылка на родителя
self.value = value # полезная нагрузкаТеперь нам необходимо расширить наш класс и реализовать необходимые операции, чтобы взаимодействовать с проектируемым классом. Начнем с операции поиска узла.
С бинарными деревьями поиска можно выполнять следующие операции:
-
Искать узел
-
Вставлять узел
-
Удалять узел
-
Выполнять обход дерева
Разберем каждую операцию подробнее.
Поиск узла
Если искомое значение бинарного дерева поиска меньше значения узла, то оно может находиться только в левом поддереве. Искомое значение, которое больше значения узла, может быть только в правом поддереве. В таком случае мы можем применить рекурсивный подход и операция поиска будет выглядеть так:
function findNode(value){
let node = this;
while (node){
if (value == node.value) return node;
if (value < node.value) node = node.left;
if (value > node.value) node = node.right;
}
return null;
}Java
class BinaryTreeNode {
// ...
BinaryTreeNode findNode(int value) {
BinaryTreeNode node = this;
while (node != null) {
if (value == node.value) {
return node;
}
if (value < node.value) {
node = node.left;
}
if (value > node.value) {
node = node.right;
}
}
return null;
}
}Python
def find_node(self, value):
node = self
while node:
if value == node.value:
return node
if value < node.value:
node = node.left
if value > node.value:
node = node.right
return NoneВставка узла
Все значения меньше текущего значения узла надо размещать в левом поддереве, а большие — в правом. Чтобы вставить новый узел, нужно проверить, что текущий узел не пуст. Далее может быть два пути:
-
Если это так, сравниваем значение со вставляемым. По результату сравнения проводим проверку для правого или левого поддеревьев
-
Если узел пуст, создаем новый и заполняем ссылку на текущий узел в качестве родителя
Операция вставки использует рекурсивный подход аналогично операции поиска. Переведем данный алгоритм на язык JavaScript и получим следующий код метода вставки:
function insertNode(value){
return #insertNode(value, this)
}
function #insertNode(value, parentNode){
if (value < parentNode.value){
if (parentNode.left == null){
parentNode.left = new BinaryTreeNode(value, parentNode);
}
else {
#insertNode(value, parentNode.left);
}
}
if (value > parentNode.value){
if (parentNode.right == null){
parentNode.right = new BinaryTreeNode(value, parentNode);
}
else {
#insertNode(value, parentNode.right);
}
}
}Java
class BinaryTreeNode {
// ...
public void insertNode(int value) {
insertNode(value, this);
}
private void insertNode(int value, BinaryTreeNode parentNode) {
if (value < parentNode.value) {
if (parentNode.left == null) {
parentNode.left = new BinaryTreeNode(value, parentNode);
} else {
insertNode(value, parentNode.left);
}
}
if (value > parentNode.value){
if (parentNode.right == null){
parentNode.right = new BinaryTreeNode(value, parentNode);
} else {
insertNode(value, parentNode.right);
}
}
}
}Python
def insert_node(self, value):
return self._insert_node(value, self)
def _insert_node(self, value, parent_node):
if value < parent_node.value:
if parent_node.left is None:
parent_node.left = BinaryTreeNode(value, parent_node)
else:
self._insert_node(value, parent_node.left)
elif value > parent_node.value:
if parent_node.right is None:
parent_node.right = BinaryTreeNode(value, parent_node)
else:
self._insert_node(value, parent_node.right)Удаление узла
Чтобы удалить элемент в связном списке, нужно найти его и ссылку на следующий элемент перенести в поле ссылки на предыдущем элементе.
Если необходимо удалить корневой узел или промежуточные вершины и сохранить структуру бинарного дерева поиска, выбирают один из следующих двух способов:
-
Находим и удаляем максимальный элемент левого поддерева и используем его значение в качестве корневого или промежуточного узла
-
Находим и удаляем минимальный элемент правого поддерева и используем его значение в качестве корневого или промежуточного узла

Оба варианта приемлемы для нашего дерева. Реализуем в коде второй вариант:
function removeNode(value){
return #removeNode(value, this)
}
function #removeNode(value, node){
if (node == null) return null;
if (value < node.value) {
node.left = #removeNode(node.left, value);
}
else if (value > node.value){
node.right = #removeNode(node.right, value);
}
else{
if (node.left == null) return node.right;
if (node.right == null) return node.left;
}
let original = node;
node = node.right;
while (node.left){
node = node.left;
}
node.right = #removeMin(original.right);
node.left = original.left;
}Java
class BinaryTreeNode {
// ...
private BinaryTreeNode removeNode(int value, BinaryTreeNode node) {
if (node == null) {
return null;
}
if (value < node.value) {
node.left = removeNode(value, node.left);
}
else if (value > node.value) {
node.right = removeNode(value, node.right);
}
else{
if (node.left == null) {
return node.right;
}
if (node.right == null) {
return node.left;
}
}
BinaryTreeNode original = node;
node = node.right;
while (node.left != null){
node = node.left;
}
node.right = removeNode(original.right);
node.left = original.left;
return node.right;
}
}Python
def remove_node(self, value):
return self._remove_node(value, self)
def _remove_node(self, value, node):
if node is None:
return None
if value < node.value:
node.left = self._remove_node(value, node.left)
return node
elif value > node.value:
node.right = self._remove_node(value, node.right)
return node
else:
if node.left is None:
return node.right
elif node.right is None:
return node.left
else:
original = node
node = node.right
while node.left:
node = node.left
node.right = self._remove_min(original.right)
node.left = original.left
return nodeРеализация первого варианта будет выглядеть практически идентично. Только есть исключение: мы будем обходить правое поддерево и искать максимальное значение узла вместо минимального.
Для деревьев также существуют специфические операции, важнейшая из которых — обход дерева. Рассмотрим эту операцию подробнее.
Обход деревьев
Когда мы поработали с деревом и нам нужно его сохранить в файл или вывести в печать, нам больше не нужен древовидный формат. Здесь мы прибегаем к обходу дерева — последовательное единоразовое посещение всех вершин дерева.
Существуют такие три варианта обхода деревьев:
-
Прямой обход (КЛП): корень → левое поддерево → правое поддерево
-
Центрированный обход (ЛКП): левое поддерево → корень → правое поддерево
-
Обратный обход (ЛПК): левое поддерево → правое поддерево → корень
Такие обходы называются поиском в глубину. На каждом шаге итератор пытается продвинуться вертикально вниз по дереву перед тем, как перейти к родственному узлу — узлу на том же уровне. Еще есть поиск в ширину — обход узлов дерева по уровням: от корня и далее:

Реализация поиска в глубину может осуществляться или с использованием рекурсии, или с использованием стека. А поиск в ширину реализуется за счет использования очереди:
function traverseRecursive(node) {
if (node != null) {
console.log(`node = ${node.val}`);
traverseRecursive(node.left);
traverseRecursive(node.right);
}
}
function traverseWithStack() {
let stack = [];
stack.push(this);
while (stack.length > 0) {
let currentNode = stack.pop();
console.log(`node = ${currentNode.val}`);
if (currentNode.right != null) {
stack.push(currentNode.right);
}
if (currentNode.left != null) {
stack.push(currentNode.left);
}
}
}
function traverseWithQueue() {
let queue = [];
queue.push(this.root);
while (queue.length > 0) {
let currentNode = queue.shift();
console.log(`node = ${currentNode.val}`);
if (currentNode.left){
queue.push(currentNode.left);
}
if (currentNode.right) {
queue.push(currentNode.right);
}
}
}Java
class BinaryTreeNode {
// ...
public void traverseRecursive() {
traverseRecursive(this);
}
private void traverseRecursive(BinaryTreeNode node) {
if (node != null) {
System.out.println("node = " + node.value);
traverseRecursive(node.left);
traverseRecursive(node.right);
}
}
public void traverseWithStack() {
Deque<BinaryTreeNode> stack = new ArrayDeque<>();
stack.push(this);
while (stack.size() > 0) {
BinaryTreeNode currentNode = stack.pop();
System.out.println("node = " + currentNode.value);
if (currentNode.right != null) {
stack.push(currentNode.right);
}
if (currentNode.left != null) {
stack.push(currentNode.left);
}
}
}
public void traverseWithQueue() {
Deque<BinaryTreeNode> queue = new ArrayDeque<>();
queue.push(this);
while (queue.size() > 0) {
BinaryTreeNode currentNode = queue.removeFirst();
System.out.println("node" + currentNode.value);
if (currentNode.left != null ){
queue.push(currentNode.left);
}
if (currentNode.right != null) {
queue.push(currentNode.right);
}
}
}
}Python
def traverse_recursive(node):
if node is not None:
print(f"node = {node.value}")
traverse_recursive(node.left)
traverse_recursive(node.right)
def traverse_with_stack(root):
stack = []
stack.append(root)
while len(stack) > 0:
current_node = stack.pop()
print(f"node = {current_node.value}")
if current_node.right is not None:
stack.append(current_node.right)
if current_node.left is not None:
stack.append(current_node.left)
def traverse_with_queue(root):
queue = []
queue.append(root)
while len(queue) > 0:
current_node = queue.pop(0)
print(f"node = {current_node.value}")
if current_node.left:
queue.append(current_node.left)
if current_node.right:
queue.append(current_node.right)A binary tree is a tree data structure in which each node can have at most two children, which are referred to as the left child and the right child.
The topmost node in a binary tree is called the root, and the bottom-most nodes are called leaves. A binary tree can be visualized as a hierarchical structure with the root at the top and the leaves at the bottom.
Binary trees have many applications in computer science, including data storage and retrieval, expression evaluation, network routing, and game AI. They can also be used to implement various algorithms such as searching, sorting, and graph algorithms.
Representation of Binary Tree:
Each node in the tree contains the following:
- Data
- Pointer to the left child
- Pointer to the right child
In C, we can represent a tree node using structures. In other languages, we can use classes as part of their OOP feature. Below is an example of a tree node with integer data.
C
struct node {
int data;
struct node* left;
struct node* right;
};
C++
struct node {
int data;
struct node* left;
struct node* right;
};
class Node {
public:
int data;
Node* left;
Node* right;
};
Python
class Node:
def __init__(self, key):
self.left = None
self.right = None
self.val = key
Java
class Node {
int key;
Node left, right;
public Node(int item)
{
key = item;
left = right = null;
}
}
C#
class Node {
int key;
Node left, right;
public Node(int item)
{
key = item;
left = right = null;
}
}
Javascript
<script>
class Node
{
constructor(item)
{
this.key = item;
this.left = this.right = null;
}
}
</script>
Basic Operations On Binary Tree:
- Inserting an element.
- Removing an element.
- Searching for an element.
- Deletion for an element.
- Traversing an element. There are four (mainly three) types of traversals in a binary tree which will be discussed ahead.
Auxiliary Operations On Binary Tree:
- Finding the height of the tree
- Find the level of the tree
- Finding the size of the entire tree.
Applications of Binary Tree:
- In compilers, Expression Trees are used which is an application of binary trees.
- Huffman coding trees are used in data compression algorithms.
- Priority Queue is another application of binary tree that is used for searching maximum or minimum in O(1) time complexity.
- Represent hierarchical data.
- Used in editing software like Microsoft Excel and spreadsheets.
- Useful for indexing segmented at the database is useful in storing cache in the system,
- Syntax trees are used for most famous compilers for programming like GCC, and AOCL to perform arithmetic operations.
- For implementing priority queues.
- Used to find elements in less time (binary search tree)
- Used to enable fast memory allocation in computers.
- Used to perform encoding and decoding operations.
- Binary trees can be used to organize and retrieve information from large datasets, such as in inverted index and k-d trees.
- Binary trees can be used to represent the decision-making process of computer-controlled characters in games, such as in decision trees.
- Binary trees can be used to implement searching algorithms, such as in binary search trees which can be used to quickly find an element in a sorted list.
- Binary trees can be used to implement sorting algorithms, such as in heap sort which uses a binary heap to sort elements efficiently.
Binary Tree Traversals:
Tree Traversal algorithms can be classified broadly into two categories:
- Depth-First Search (DFS) Algorithms
- Breadth-First Search (BFS) Algorithms
Tree Traversal using Depth-First Search (DFS) algorithm can be further classified into three categories:
- Preorder Traversal (current-left-right): Visit the current node before visiting any nodes inside the left or right subtrees. Here, the traversal is root – left child – right child. It means that the root node is traversed first then its left child and finally the right child.
- Inorder Traversal (left-current-right): Visit the current node after visiting all nodes inside the left subtree but before visiting any node within the right subtree. Here, the traversal is left child – root – right child. It means that the left child is traversed first then its root node and finally the right child.
- Postorder Traversal (left-right-current): Visit the current node after visiting all the nodes of the left and right subtrees. Here, the traversal is left child – right child – root. It means that the left child has traversed first then the right child and finally its root node.
Tree Traversal using Breadth-First Search (BFS) algorithm can be further classified into one category:
- Level Order Traversal: Visit nodes level-by-level and left-to-right fashion at the same level. Here, the traversal is level-wise. It means that the most left child has traversed first and then the other children of the same level from left to right have traversed.
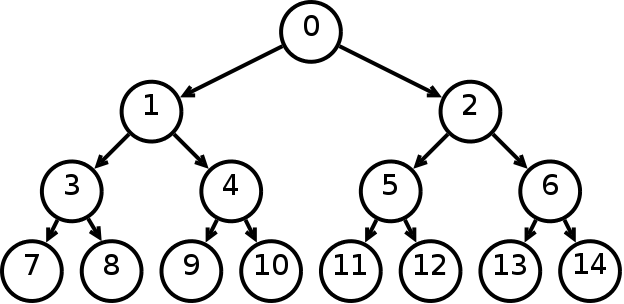
Let us traverse the following tree with all four traversal methods:
Pre-order Traversal of the above tree: 1-2-4-5-3-6-7
In-order Traversal of the above tree: 4-2-5-1-6-3-7
Post-order Traversal of the above tree: 4-5-2-6-7-3-1
Level-order Traversal of the above tree: 1-2-3-4-5-6-7
Implementation of Binary Tree:
Let us create a simple tree with 4 nodes. The created tree would be as follows.
Below is the Implementation of the binary tree:
C
#include <stdio.h>
#include <stdlib.h>
struct node {
int data;
struct node* left;
struct node* right;
};
struct node* newNode(int data)
{
struct node* node
= (struct node*)malloc(sizeof(struct node));
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
int main()
{
struct node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
getchar();
return 0;
}
C++
#include <bits/stdc++.h>
using namespace std;
class Node {
public:
int data;
Node* left;
Node* right;
Node(int val)
{
data = val;
left = NULL;
right = NULL;
}
};
int main()
{
Node* root = new Node(1);
root->left = new Node(2);
root->right = new Node(3);
root->left->left = new Node(4);
return 0;
}
Java
class Node {
int key;
Node left, right;
public Node(int item)
{
key = item;
left = right = null;
}
}
class BinaryTree {
Node root;
BinaryTree(int key) { root = new Node(key); }
BinaryTree() { root = null; }
public static void main(String[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
}
}
Python
class Node:
def __init__(self, key):
self.left = None
self.right = None
self.val = key
if __name__ == '__main__':
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
C#
using System;
public class Node {
public int key;
public Node left, right;
public Node(int item)
{
key = item;
left = right = null;
}
}
public class BinaryTree {
Node root;
BinaryTree(int key) { root = new Node(key); }
BinaryTree() { root = null; }
public static void Main(String[] args)
{
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
}
}
Javascript
<script>
class Node {
constructor(val) {
this.key = val;
this.left = null;
this.right = null;
}
}
var root = null;
root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
</script>
Conclusion:
Tree is a hierarchical data structure. Main uses of trees include maintaining hierarchical data, providing moderate access and insert/delete operations. Binary trees are special cases of tree where every node has at most two children.
What else can you read?
- Properties of Binary Tree
- Types of Binary Tree
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.