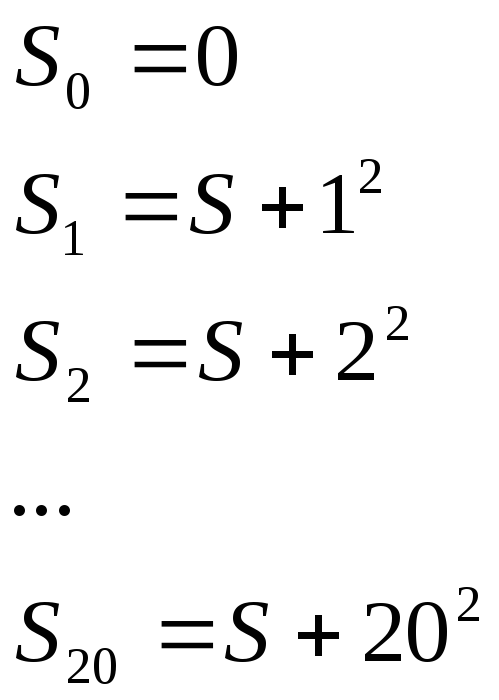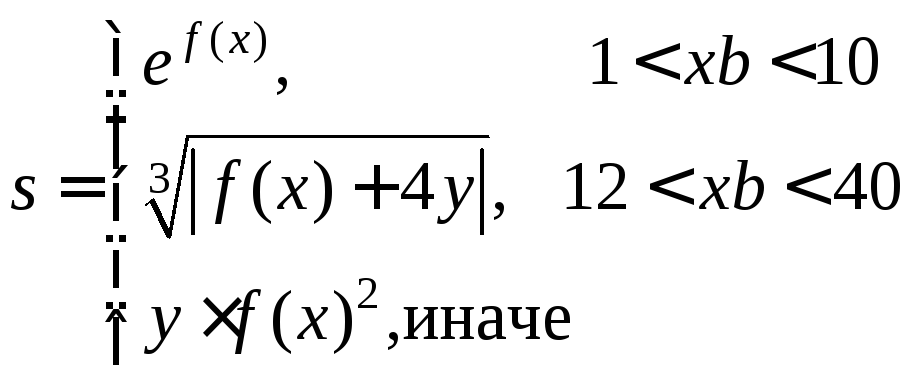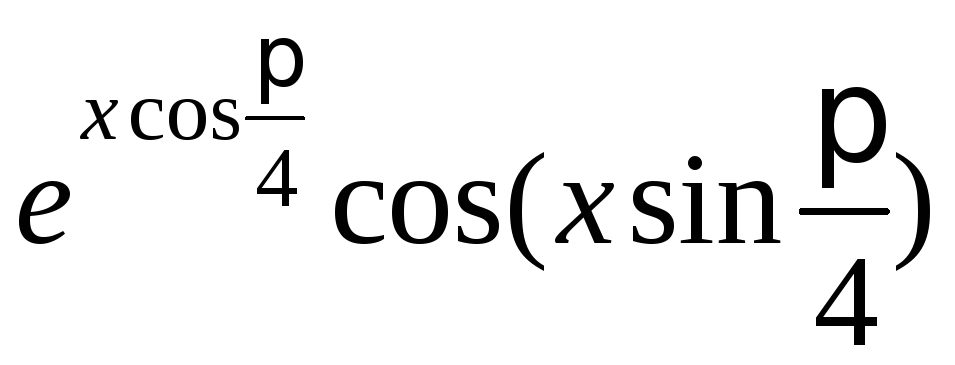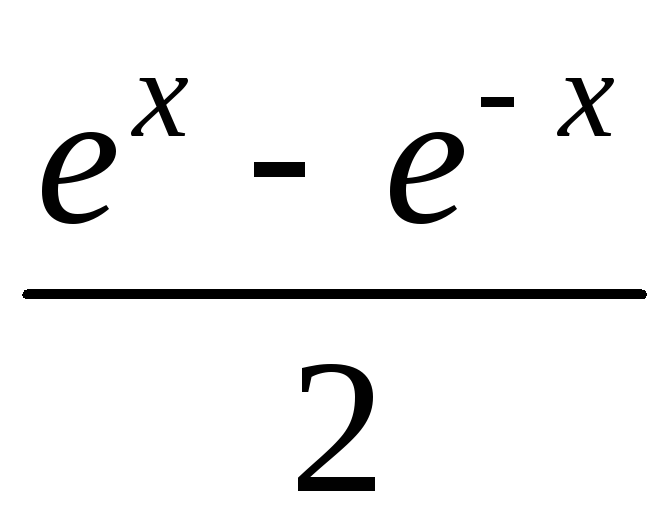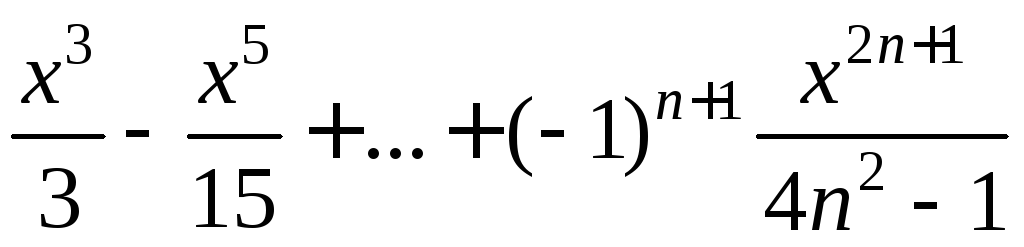Как составить блок схему алгоритма для решения задачи

Итак, опустив долгие и нудные восхваления Паскаля, которые так любят публиковать в своих статьях редакторы многих сайтов, приступим непосредственно к самому основному – к программированию.

В школах, как правило, изучение Паскаля начинают с решения простейших задач путем составления различных алгоритмов или блок-схем, которое многие так часто игнорируют, считая никому не нужной ерундой. А зря. Я, как и любой другой человек, хоть немного соображающий в программировании (не важно где – в Паскале, Си, Дельфи), могу уверить Вас – умение правильно и быстро составлять схемы является фундаментом, основой программирования.

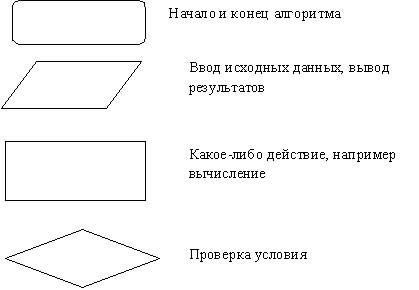
Блок-схема — графическое представление алгоритма. Она состоит из функциональных блоков, которые выполняют различные назначения (ввод/вывод, начало/конец, вызов функции и т.д.).

Существует несколько основных видов блоков, которые нетрудно запомнить:

Сегодняшний урок я решила посвятить не только изучению блок-схем, но также и изучению линейных алгоритмов. Как Вы помните, линейный алгоритм — наипростейший вид алгоритма. Его главная особенность в том, что он не содержит никаких особенностей. Как раз это и делает работу с ним простой и приятной.

Задача №1: «Рассчитать площадь и периметр прямоугольника по двум известным сторонам».

Данная задача не должна представлять особой трудности, так как построена она на хорошо известных всем нам формулах расчета площади и периметра прямоугольника, поэтому зацикливаться на выведении этих формул мы не будем.

Составим алгоритм решения подобных задач:

1) Прочитать задачу.
2) Выписать известные и неизвестные нам переменные в «дано». (В задаче №1 к известным переменным относятся стороны: a, b ;к неизвестным — площадь S и периметр P)
3) Вспомнить либо составить необходимые формулы. (У нас: S=a*b; P=2*(a+b))
4) Составить блок-схему.
5) Записать решение на языке программирования Pascal.

Запишем условие в более кратком виде.

Дано: a, b

Найти: S, P

Блок-схема:

Структура программы, решающей данную задачу, тоже проста:

• 1) Описание переменных;
• 2) Ввод значений сторон прямоугольника;
• 3) Расчет площади прямоугольника;
• 4) Расчет периметра прямоугольника;
• 5) Вывод значений площади и периметра;
• 6) Конец.

А вот и решение:

Program Rectangle;
Var a, b, S, P: integer;
Begin
write('Введите стороны прямоугольника!'); 
readln(a, b);
S:=a*b;
P:=2*(a+b);
writeln('Площадь прямоугольника: ', S);
write('Периметр прямоугольника: ', P);
End.

Задача №2: Скорость первого автомобиля — V1 км/ч, второго – V2 км/ч, расстояние между ними S км. Какое расстояние будет между ними через T часов, если автомобили движутся в разные стороны? Значения V1, V2, T  и S задаются с клавиатуры.

Решение осуществляем, опять же, следуя алгоритму. Прочитав текст, мы переходим к следующему пункту. Как и во всех физических или математических задачах, это запись условий задачи:

Дано: V1, V2, S, Т
Найти: S1

Далее идет самая главная и в то же время самая интересная часть нашего решения – составление нужных нам формул. Как правило, на начальных стадиях обучения все необходимые формулы хорошо нам известны и взяты из других технических дисциплин (например, на нахождение площади различных фигур, на нахождение скорости, расстояния и т.п.).

Формула, используемая для решения нашей задачи, выглядит следующим образом:

S1=(V1+V2)*T+S

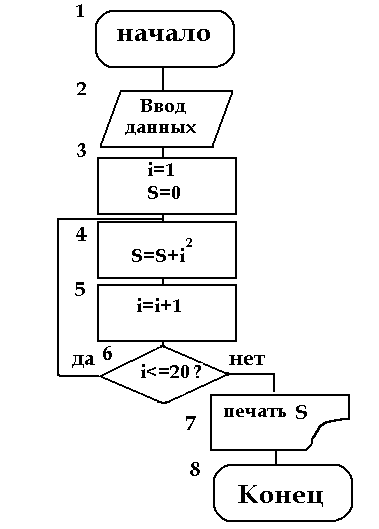
Следующий пункт алгоритма – блок-схема:

А также решение, записанное в Pascal :

Program Rasstoyanie;
Var V1, V2, S, T, S1: integer; {Ввод }
begin
write('Введите скорость первого автомобиля: '); 
readln(V1);
write('Введите скорость второго автомобиля: '); 
readln(V2);
write('Введите время: '); 
readln(T);
write('Введите расстояние между автомобилями: '); 
readln(S);
S1:=(V1+V2)*T+S;
writeln('Через ', t,'ч. расстояние ', S1,' км.');
End.

Вам может показаться, что две эти программы правильны, но это не так. Ведь сторона треугольника может быть 4.5, а не 4, а скорость машины не обязательно круглое число!  А Integer — это только целые числа. Поэтому при попытке написать во второй программе другие числа выскакивает ошибка:

Чтобы решить эту проблему вам надо вспомнить какой тип в Pascal отвечает за нецелые числа. В этом уроке мы рассматривали основные типы. Итак, это вещественный тип — Real.  Вот, как выглядит исправленная программа:

Как видите, эта статья полезна для прочтения как новичкам, так и уже более опытными пользователям Pascal, так как составление блок-схем не только очень простое и быстрое, но и весьма увлекательное занятие.

Примеры составления блок-схемы алгоритма

Пример 1.
Составить схему алгоритма вычисления
значения :

Для
начала для построения блок –схемы
алгоритма опишем последовательность
действий, необходимых для решения данной
задачи:

• начало

• ввод
  чисел a,b

• вычисление
  х

• вычисление
  z

• вывод
  результата

• конец

Исходя из этого
составляем блок-схему алгоритма согласно
ГОСТ, используя соответствующие блоки.

Пример
2. Составить
схему алгоритма вычисления значения:
x=a+b
при a>b,
x=a*b,
при a<=b.

Пример 3. Составить схему алгоритма вычисления значения:

Для начала для
построения блок –схемы алгоритма опишем
последовательность действий, необходимых
для решения данной задачи:

Исходя из этого
составляем блок-схему алгоритма согласно
ГОСТ, используя соответствующие блоки.

Порядок выполнения работы

1. Изучить
   теоретические сведения по теме
   ”Построение блок-схем алгоритмов”.

2. Получить
   у преподавателя индивидуальное задание
   и нарисовать блок-схему алгоритма
   согласно заданному варианту.

3. Ответить
   на контрольные вопросы.

4. Сформулировать
   выводы.

Контрольные вопросы

1. Основные
   этапы решения задач на компьютере.

2. Свойства алгоритма.
   Типы вычислительных процессов.

3. Блок схемы. Понятие
   и правила построения.

4. Примеры построения
   блок-схем алгоритмов.

Задание
№1: Разработайте
алгоритм и представьте его в графическом
виде (блок-схемы) для следующих задач:

Задание 1.1
Вычислить значение выражения при
заданных исходных данных.

Указание.
Для упрощения выражений введите
промежуточные переменные.

Сравнить полученное
значение с указанным правильным
результатом.

1.

При
x = 14.26;
y = – 1.22;
z = 3.5ответs
= 0.749155.

2.

При
x = –4.5; y = 0.75;
z = –0.845ответs
= –3.23765.

3.

При
x = 3.74;
y=–0.825; z = 0.16ответs
= 1.05534.

4.

При
x = 0.4;
y = –0.875; z = –0.475ответ
s = 1.98727.

5.

При
x = –15.246; y = 4.642;
z = 21 ответ
s = –182.038.

6.

При
x = 16.55;
y = –2.75; z = 0.15
ответ s
= –40.6307.

7.

При
x = 0.1722; y = 6.33; z = 3.25ответ
s = –205.306.

8.

При
x = –2.235;
y = 2.23; z = 15.221
ответ s
= 39.3741.

9.

При
x = 1.825;
y = 18.225; z = –3.298ответ
s = 1.21308.

10.

При
x = 3.981;
y = –1.625;
z = 0.512
ответ s
= 1.26185.

11.

При
x = 6.251; y = 0.827; z = 25.001
ответ
s = 0.712122.

12.

При
x
= 3.251; y
= 0.325; z
= 0.466
ответ s
= 4.23655.

13.

.

При
x
= 17.421; y
= 10.365;
z
= 0.828
ответ s
= 0.330564.

14.
.

При
x
= 12.3;
y
= 15.4; z
= 0.252
ответ s
= 82.8256.

15.

.

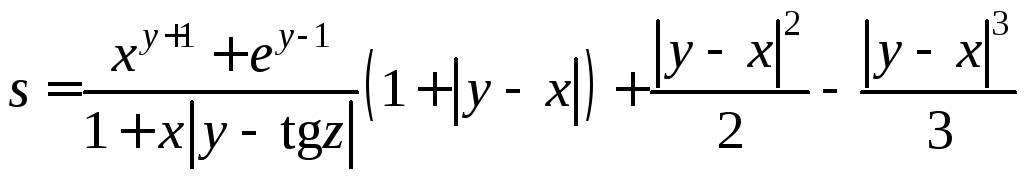
При
x
= 2.444; y
= 0.869;
z
= –0.13
ответ s
= –0.498707.

Задание
1.2 Вычислить
значение выражения при заданных исходных
данных. Предусмотреть вывод информации
о выбранной ветви вычислений.

1.		2.
3.		4.
5.		6.
7.		8.
9.		10.
11.		12.
13.		14.
15.

Задание
1.3 Вывести
на экран таблицу значений функции Y(x)
и ее разложения в ряд S(x)
для x,
изменяющегося от a
до b
с шагом h
= (b –
a)/10,
табл. 1.

Таблица 1.

№	a	b	S(x)	n	Y(x)
1	0.1	1		160
2	0.1	1		100
1	2	3	4	5	6
3	0.1	1		120
4	0.1	1		80
5	0.1	1		140
6	0.1	1		80
7	0.1	1		120
8	0.1	1		100
9	0.1	1		140
10	0.1	0.5		150
11	0.1	1		100
12	0.1	1		80
13	–2	–0.1		160
14	0.2	0.8		120
15	0.1	0.8		180

Задание
№2:
Решите представленные ниже задачи,
указав номер задачи и полученный ответ. 

Задача
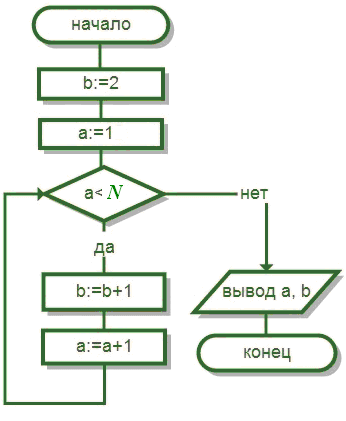
2.1
Определите
результаты работы блок-схемы алгоритма
при

Задача
2.2
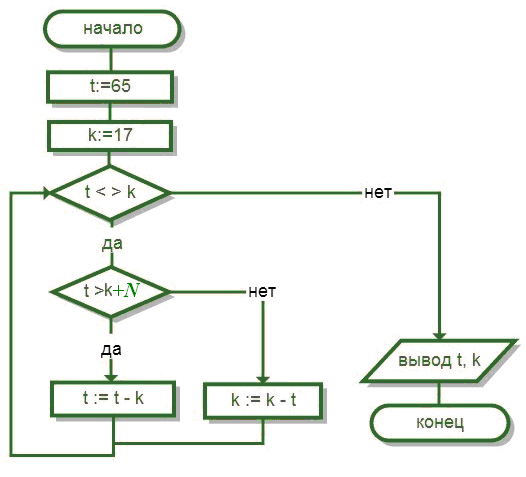
Какие
значения примут t и k в
результате работы фрагмента блок-схемы
алгоритма?

Задача
2.3.
Определите
значения
элементов
массива А₂,
А₄,
А₆,
А₈
при N=8
в результате работы фрагмента алгоритма

Если дать определение схеме, можно отметить основной момент: в первую очередь подразумевается абстракция какого-нибудь процесса (системы), при которой наиболее важные части отображаются наглядно (визуально). Схемы использовались на протяжении всей истории человечества: это и чертежи пирамид, и карты сухопутных и морских путей, и принципиальные электрические схемы.

Те же мореплаватели, создавая карты, делали это в соответствии с единой системой обозначений — это позволяло обмениваться информацией друг с другом. То же самое справедливо и для визуального отображения схем алгоритмов — существуют правила, единые обозначения и стандарты, регламентирующие их применение. В России это ГОСТ 19.701-90 «Схемы алгоритмов программ, данных и систем», который близок к международному стандарту ISO 5807:1985.

Главные элементы блок-схем алгоритмов

Прежде чем продолжить, стоит дать определение блок-схемы в соответствии со стандартом — речь идёт о совокупности символов, которые отвечают этапам работы алгоритма, причём эти символы имеют соединяющие линии:
— пунктирную — для соединения с комментарием;
— сплошную — отображает зависимости по управлению, допускается наличие на ней стрелки. В соответствии со стандартом составитель может не указывать стрелку, если дуга направляется сверху вниз или слева направо.

Также существуют и дополнительные виды линий, которые применяются, когда надо дать описание блок-схемам параллельных алгоритмов, однако в этой статье мы их рассматривать не будем, как и ряд других дополнительных спецсимволов.

В таблице ниже дан перечень основных символов, используемых при описании алгоритмов:

Задача и блок-схема алгоритма

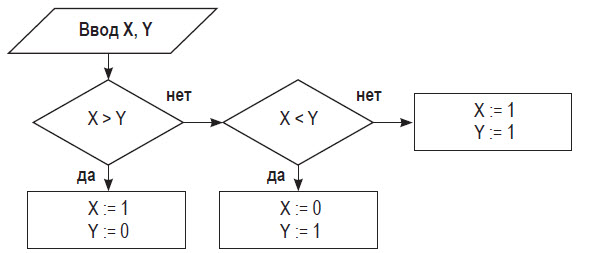
На картинке ниже дан алгоритм в виде схемы. В нем мы видим оператор присваивания :=, то есть X := 1 будет означать, что переменная Х примет значение 1. По результату алгоритмических действий надо определить итог работы представленного алгоритма, используя следующие входные данные: Х = 7, Y = 12.

Схема этого алгоритма и решение задачи будут выглядеть следующим образом:

Смотрим, как следует решать подобное задание:
1. Блок ввода данных определяет исходные значения Х и Y (в соответствии с условием это 7 и 12).
2. В первом блоке значения Х и Y сравниваются. Так как условие не является верным (7 < 12), осуществляется переход по линии с пометкой «нет».
3. Второй блок служит для второго сравнения — оно верное, в результате чего следующее действие — это переход по линии с отметкой «да».
4. Следующий этап является заключительным, то есть происходит вычисление результата работы алгоритма. По итогу всех вышеописанных действий мы получаем окончательный ответ, не требующий дополнительных вычислений: X := 0, Y := 1.

Решение алгоритма сортировки пузырьком

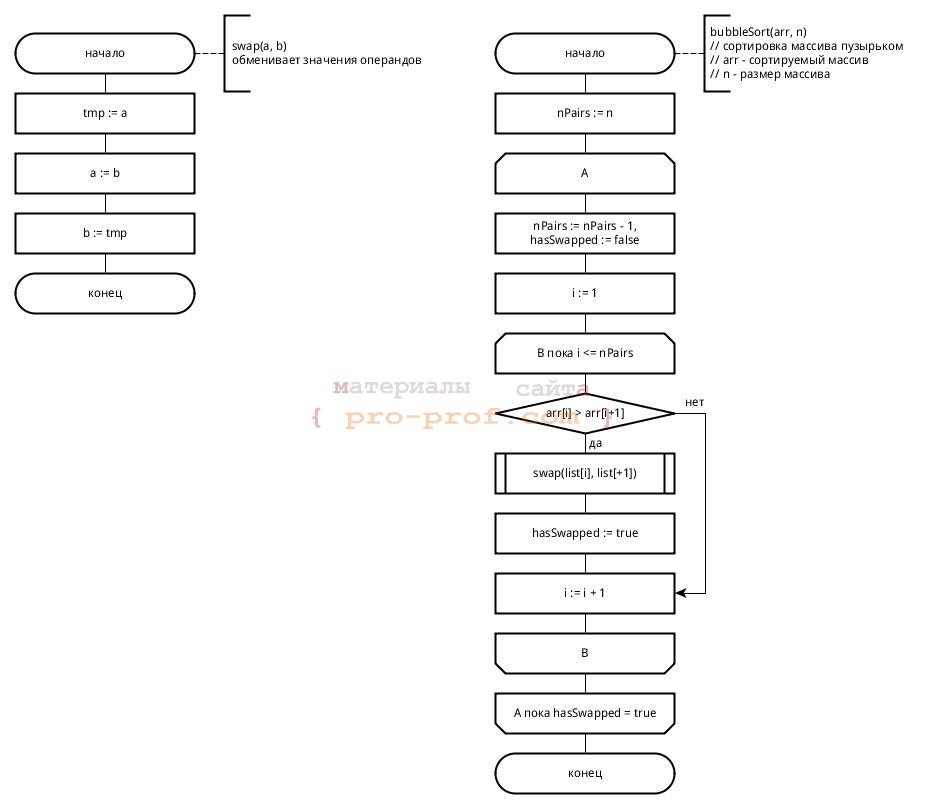
В этом примере давайте попробуем дать описание решению алгоритма сортировки по методу пузырьком (метод сортировки вставками). Здесь применяются 2 цикла. Во вложенном цикле осуществляется попарное сравнение элементов. Если нарушается порядок, происходит перестановка. По итогу выполнения одной итерации во внутреннем цикле, наибольший элемент будет смещён в самый конец массива. Внешний цикл будет выполняться, пока полностью весь массив не отсортируется.

На схеме отображено применение символов конца и начала цикла. Здесь условие внешнего цикла (А) проверяется в конце (с постусловием), а функционирует он до тех пор, пока переменная hasSwapped является true. Во внутреннем цикле используется предусловие для перебора пар элементов, которые сравниваются. Если они располагаются в неправильном порядке, они переставляются путём вызова внешней процедуры (swap). Для понимания назначения внешней процедуры, как и порядка следования аргументов этой процедуры, нужно оставлять комментарии. Если функция возвращает значение, то комментарий можно написать к символу-терминатору конца.

В этой статье мы постарались дать ответ, зачем нужны блок-схемы, каковы их основные элементы, как с их помощью решить алгоритмическую задачу. При подготовке материала использовались следующие источники:

• https://uchitel.pro/алгоритм-свойства-алгоритмов/;
• https://pro-prof.com/archives/1462.

Практическая
раборта № 1

Построение
блок-схем алгоритмов(теория)

Предпочтительнее
до записи на алгоритмическом языке представить алгоритм в виде блок-схемы. Для
построения алгоритма в виде блок-схемы необходимо знать назначении каждого из
блоков. В таблице 1. приводятся типы блоков и их назначение.

Таблица 1

№	Блок	Назначение блока
1		Начало или конец блок-схемы
2		Ввод или вывод данных
3		Процесс (в частности вычислительный)
4		условие
6		Цикл с параметром (for)

Основные
типы алгоритмов

Алгоритмизация выступает как набор
определенных практических приёмов, особых специфических навыков рационального
мышления в рамках заданных языковых средств. Алгоритмизация вычислений
предполагает решение задачи в виде последовательности действий, т.е. решение,
представленное в виде блок-схемы. Можно выделить типичные алгоритмы. К ним
относятся: линейные алгоритмы, разветвляющиеся алгоритмы, циклические
алгоритмы.

Линейные алгоритмы

Линейный алгоритм является наиболее
простым. В нём предполагается последовательное выполнение операций. В этом
алгоритме не предусмотрены проверки условий или повторений.

Пример: Вычислить функцию z=
(х-у)/x +y².

Составить блок-схему вычисления функции по
линейному алгоритму. Значения переменных х, у могут быть
любые, кроме нуля, вводить их с клавиатуры.

Решение: Линейный алгоритм вычисления
функции задан в виде блок-схемы на рис.1. При выполнении линейного алгоритма
значения переменных вводятся с клавиатуры, подставляются в заданную функцию,
вычисляется результат, а затем выводится результат.

Рис.1. Линейный алгоритм

Назначение блоков в схеме на
рис.1:

·       
Блок 1 в схеме служит в качестве
логического начала.

·       
Блок 2 соответствует вводу данных.

·       
Блок 3 представляет арифметическое
действие.

·       
Блок 4 выводит результат.

·       
Блок 5 в схеме служит в качестве
логического завершения схемы.

Алгоритмы ветвлений

Разветвляющийся алгоритм предполагает
проверку условий для выбора решения. Соответственно в алгоритме появятся две
ветви для каждого условия.

В
примере рассматривается разветвляющийся алгоритм, где в зависимости от условия
выбирается один из возможных вариантов решений. Алгоритм представляется в виде
блок-схемы.

Пример:
При выполнении условия x>0
вычисляется функция: z=
x+
y,
иначе, а именно, когда х=0 или x<0,
вычисляется функция: z=x²+y².

Составить
блок-схему вычисления функции по алгоритму ветвления. Значения переменных х,
у могут быть любые, вводить их с клавиатуры.

Решение:
На рис.2 представлен разветвляющийся алгоритм, где в зависимости от условия
выполнится одна из веток. В блок-схеме появился новый блок 3, который проверяет
условие задачи. Остальные блоки знакомы из линейного алгоритма.

Рис.2. Алгоритм ветвления

Пример: Найти максимальное значение
из трёх различных целых чисел, введенных с клавиатуры. Составить блок-схему
решения задачи.

Решение: Данный алгоритм
предполагает проверку условия. Для этого выбирается любая из трёх переменных и
сравнивается с другими двумя. Если она больше, то поиск максимального числа
окончен. Если условие не выполняется, то сравниваются две оставшиеся
переменные. Одна из них будет максимальной. Блок-схема к этой задаче
представлена на рис 3.

Рис. 3. Блок-схема поиска максимума

Циклические алгоритмы

Циклический алгоритм предусматривает
повторение одной операции или нескольких операций в зависимости от условия
задачи.

Из
циклических алгоритмов выделяют два типа:

1)                
с заданным количеством циклов или со
счётчиком циклов;

2)                
количество циклов неизвестно.

Пример:
В цикле вычислить значение функции z=x*y при условии, что одна из
переменных x
меняется в каждом цикле на единицу, а другая переменная у не
меняется и может быть любым целым числом. В результате выполнения цикла при
начальном значении переменной х=1 можно получить таблицу умножения.
Количество циклов может быть любым. Составить блок-схему решения задачи.

Решение:
В примере количество циклов задаётся. Соответственно выбирается алгоритм
циклов первого типа. Алгоритм этой задачи приводится на рис. 4.

Во
втором блоке вводятся количество циклов n и любые целые числа х,
y.

В
блок-схеме появился новый блок 3, в котором переменная i считает
количество циклов, после каждого цикла увеличиваясь на единицу, пока счётчик не
будет равен i=n. При i=n будет выполнен последний
цикл.

В
третьем блоке указывается диапазон изменения счётчика цикла (от i =1 до i=n).

В
четвёртом блоке изменяются значения переменных: z, x.

В
пятом блоке выводится результат. Четвёртый и пятый блоки повторяются в каждом
цикле.

Рис.4 . Циклический алгоритм со счётчиком
циклов

Этот
тип циклических алгоритмов предпочтителен, если дано количеством циклов.

Если количество циклов неизвестно, то
блок-схемы циклических алгоритмов могут быть представлены в виде рисунков 5, 6.

Пример:
Вычислить у=у-x
пока y>x,
если y=30,
x=4.
Подсчитать количество выполненных циклов, конечное значение переменной у.
В цикле вывести значение переменной у, количество выполненных
циклов. Составить блок-схему решения задачи.

Решение:
В примере количество циклов неизвестно. Соответственно выбирается алгоритм
циклов второго типа. Алгоритм этой задачи приводится на рис. 5.

Условие
проверяется на входе в цикл. В теле цикла выполняется два блока:

1)
у=у-х; i=i+1;

2)
вывод значений переменных i,
y.

Цикл
выполняется до тех пор, пока выполняется условие y>x. При условии
равенства этих переменных у=х или y<x цикл заканчивается.

Алгоритм,
представленный на рис.5, называется циклический алгоритм с предусловием,
так как условие проверяется в начале цикла или на входе в цикл.

Рис.5. Блок-схема
циклического алгоритма с предусловием

Во втором блоке вводятся y=30,
x=4.

В
третьем блоке проверяется условие y>x
на входе в цикл. Если условие выполняется, то переход к блоку 4, иначе на блок
6.

В
четвёртом блоке вычисляется значение переменной у, подсчитывается
количество выполненных циклов i=i+1.

В
пятом блоке выводится результат:

·       
значение переменной у,

·       
количество выполненных циклов i.

Пример:
Составить блок-схему примера (рисунок 5), проверяя условие выхода из цикла.
В этом примере условие задачи не меняется, и результат выведется тот же, но
блок-схема будет другой.

Решение:
В этом случае проверяется условие на выход из цикла: y<=x. При
этом условии цикл не выполняется. Условие в блок-схеме следует перенести в
конец цикла, после вывода на печать. Цикл выполняется до тех пор, пока
выполняется условие y>x.

Алгоритм,
если условие перенести в конец цикла, называется алгоритмом цикла с
постусловием. Алгоритм этой задачи приводится на рис. 6.

Во
втором блоке вводятся y=30,
x=4.

В
третьем блоке вычисляется значение переменной у, подсчитывается
количество выполненных циклов i=i+1.

В
четвёртом блоке выводится результат:

·       
значение переменной у,

·       
количество выполненных циклов i.

В
пятом блоке проверяется условие y<=x
на выход из цикла. Если условие выполняется, то переход к блоку 6, иначе на
блок 3 и цикл повторяется.

 

Рис.6 . Алгоритм цикла с
постусловием

Индивидуальные задания к работе:

1.
Найти
результат работы алгоритма:

Входные данные по вариантам

№	A	B	C	D
1	0	-1	-2	-3
2	1	0	-1	-2
3	2	1	0	-1
4	3	2	1	0
5	4	3	2	1
6	5	4	3	2
7	6	5	4	3
8	7	6	5	4
9	-3	7	6	5
10	-4	-3	7	6
11	-5	-4	-3	7
12	-6	-5	-4	-3
13	-7	-6	-5	-4
14	9	-7	-6	-5
15	8	7	-7	-6
16	5	5	8	-7
17	5	2	4	5

2.     При
заданном Х условие выполнется? Написать результат вычисления и ответ попадаем в
условие или нет.

Входные данные по вариантам

№	X1	X1
1	55	12
2	85	13
3	24	17
4	65	15
5	17	54
6	15	67
7	26	3
8	27	21
9	92	34
10	12	23
11	45	22
12	66	45
13	71	46
14	13	76
15	45	67
16	53	35
17	52	23

3.     Написать
результат выполнения алгоритма с указанными входными данными

Входные данные по вариантам

№	S
1	1,5
2	1,8
3	2,4
4	1,6
5	1,7
6	1,3
7	2,6
8	2,37
9	1,92
10	1,12
11	1,45
12	2,66
13	2,71
14	2,13
15	1,45
16	2,53
17	1,52

4.     Написать
результат выполнения алгоритма с указанными входными данными

Входные данные по вариантам

№	X
1	-1
2	0
3	1
4	2
5	3
6	4
7	5
8	6
9	7
10	-3
11	-4
12	-5
13	-6
14	-7
15	7
16	5
17	2

5.     Построить
блок схему к задаче(по вариантам). Указать тип алгоритма, что дано и что нужно
найти.

№	Задача
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

6.     Построить
блок схему к задаче(по вариантам). Указать тип алгоритма, что дано и что нужно
найти.

№	Задача
1	Дано двузначное число. Найти: число десятков в нем;
2	Дано двузначное число. Найти: число единиц в нем;
3	Дано двузначное число. Найти: сумму его цифр;
4	Дано двузначное число. Найти: произведение его цифр.
5	Дано двузначное число. Получить число, образованное при перестановке цифр заданного числа.
6	Дано трехзначное число. Найти: ачисло единиц в нем;
7	Дано трехзначное число. Найти: число десятков в нем;
8	Дано трехзначное число. Найти: сумму его цифр;
9	Дано трехзначное число. Найти: произведение его цифр.
10	Дано трехзначное число. Найти число, полученное при прочтении его цифр справа налево.
11	Дано трехзначное число. В нем зачеркнули первую слева цифру и приписали ее в конце. Найти полученное число.
12	Дано трехзначное число. В нем зачеркнули последнюю справа цифру и при- писали ее в начале. Найти полученное число.
13	Дано трехзначное число. Найти число, полученное при перестановке первой и второй цифр заданного числа
14	Дано трехзначное число. Найти число, полученное при перестановке второй и третьей цифр заданного числа.
15	Дано трехзначное число, в котором все цифры различны. Получить шесть чи- сел, образованных при перестановке цифр заданного числа.
16	Дано натуральное число n (n > 9). Найти: число единиц в нем;
17	Дано натуральное число n (n > 9). Найти: число десятков в нем.

7.     Построить
блок схему к задаче(по вариантам). Указать тип алгоритма, что дано и что нужно
найти.

№	Задача
1	Определить максимальное и минимальное значения из двух различных веще- ственных чисел.
2	Известны два расстояния: одно в километрах, другое — в футах ( 1 фут 0,305 м ). Какое из расстояний меньше?
3	Известны две скорости: одна в километрах в час, другая — в метрах в секун- ду. Какая из скоростей больше?
4	Даны радиус круга и сторона квадрата. У какой фигуры площадь больше?
5	Даны объемы и массы двух тел из разных материалов. Материал какого из тел имеет большую плотность?
6	Известны сопротивления двух несоединенных друг с другом участков элек- трической цепи и напряжение на каждом из них. По какому участку протекает меньший ток?
7	Даны вещественные числа a, b, c (a 0). Выяснить, имеет ли квадратное уравнение с данными параметрами решение
8	Известны площади круга и квадрата. Определить: уместится ли круг в квадрате?
9	Известны площади круга и квадрата. Определить:  уместится ли квадрат в круге?
10	Известны площади круга и равностороннего треугольника. Определить: уместится ли круг в треугольнике?
11	Известны площади круга и равностороннего треугольника. Определить: уместится ли треугольник в круге?
12	Дано двузначное число. Определить: какая из его цифр больше: первая или вторая;
13	Дано двузначное число. Определить: одинаковы ли его цифры
14	Дано двузначное число. Определить: кратна ли трем сумма его цифр;
15	Дано двузначное число. Определить: кратна ли сумма его цифр числу а.
16	Дано трехзначное число. Определить, какая из его цифр больше: первая или последняя;
17	Дано трехзначное число. Определить, какая из его цифр больше: вторая или последняя.

8.     Построить
блок схему к задаче(по вариантам). Указать тип алгоритма, что дано и что нужно
найти.

№	Задача
1	Одна штука некоторого товара стоит 20,4 руб. Напечатать таблицу стоимости 2, 3, …, 20 штук этого товара.
2	Напечатать таблицу соответствия между весом в фунтах и весом в килограм- мах для значений 1, 2, …, 10 фунтов (1 фунт = 453 г).
3	Напечатать таблицу перевода расстояний в дюймах в сантиметры для значе- ний 10, 11, …, 22 дюйма (1 дюйм = 25,4 мм).
4	Напечатать таблицу перевода 1, 2, … 20 долларов США в рубли по текущему курсу (значение курса вводится с клавиатуры).
5	Считая, что Земля — идеальная сфера с радиусом R 6350 км, определить расстояние до линии горизонта от точки с высотой над Землей, равной 1, 2, … 10 км.
6	. Напечатать таблицу умножения на 7:
7	Напечатать таблицу умножения на 9:
8	Напечатать “столбиком” значения sin 2 , sin 3 , …, sin 20 .
9	Напечатать таблицу стоимости 50, 100, 150, …, 1000 г сыра (стоимость 1 кг сыра вводится с клавиатуры).
10	Вывести “столбиком” следующие числа: 2,1, 2,2, 2,3, …, 2,8.
11	. Вывести “столбиком” следующие числа: 3,2, 3,2, 3,3, …, 3,9.
12	Вывести “столбиком” следующие числа: 2,2, 2,4, 2,6, …, 4,2.
13	Вывести “столбиком” следующие числа: 4,4, 4,6, 4,8, …, 6,4.
14	Напечатать таблицу стоимости 100, 200, 300, …, 2000 г конфет (стоимость 1 кг конфет вводится с клавиатуры).
15	Составить программу вывода любого числа любое заданное число раз в виде, аналогичном показанному в предыдущей задаче.
16	Напечатать таблицу умножения на 2:
17	Напечатать таблицу умножения на 5:

9.     Построить
блок схему к задаче(по вариантам). Указать тип алгоритма, что дано и что нужно
найти.

№	Задача
1	Даны числа а1, а2, а3…а10, . Определить их сумму
2	Известна масса каждого из 12 предметов. Определить общую массу всего на- бора предметов.
3	. Известны оценки абитуриента на четырех экзаменах. Определить сумму на- бранных им баллов.
4	В ведомости указана зарплата, выплаченная каждому из сотрудников фирмы за месяц. Определить общую сумму выплаченных по ведомости денег
5	Известна масса каждого предмета, загружаемого в автомобиль. Определить общую массу груза.
6	Известно сопротивление каждого из элементов электрической цепи. Все эле- менты соединены последовательно. Определить общее сопротивление цепи.
7	Известно сопротивление каждого из элементов электрической цепи. Все эле- менты соединены параллельно. Определить общее сопротивление цепи.
8	Известны оценки по физике каждого из 20 учеников класса. Определить сред- нюю оценку.
9	Известны оценки ученика по 10 предметам. Определить среднюю оценку
10	Известны оценки по алгебре каждого ученика класса. Определить среднюю оценку
11	Известна масса каждого предмета из некоторого набора предметов. Опреде- лить среднюю массу
12	Известны оценки двух учеников по четырем предметам. Определить сумму оценок каждого ученика.
13	Известны результаты двух спортсменов-пятиборцев в каждом из пяти видов спорта в баллах. Определить сумму баллов, полученных каждым спортсменом.
14	Известен возраст (в годах в виде 14,5 лет и т. п.) каждого ученика двух клас- сов. Определить средний возраст учеников каждого класса. В каждом классе учатся 20 человек.
15	Известно количество осадков, выпавших за каждый день января и марта. Оп- ределить среднедневное количество осадков за каждый месяц
16	Известен рост каждого ученика двух классов. Определить средний рост уче- ников каждого класса. Численность обоих классов одинаковая.
17	Известны оценки по физике каждого ученика двух классов. Определить среднюю оценку в каждом классе. Количество учащихся в каждом классе одинаковое.

10. Построить
блок схему к задаче(по вариантам). Указать тип алгоритма, что дано и что нужно
найти.

№	Задача
1	Дано натуральное число. а) Верно ли, что сумма его цифр больше 10?
2	Дано натуральное число. б) Верно ли, что произведение его цифр меньше 50?
3	Дано натуральное число. в) Верно ли, что количество его цифр есть четное число?
4	Дано натуральное число. г) Верно ли, что это число четырехзначное? Составное условие и вложенный условный оператор не использовать.
5	Дано натуральное число д) Верно ли, что его первая цифра не превышает 6?
6	Дано натуральное число. е) Верно ли, что оно начинается и заканчивается одной и той же цифрой?
7	Дано натуральное число. ж) Определить, какая из его цифр больше: первая или последняя.
8	Дано натуральное число. а) Верно ли, что сумма его цифр меньше a?
9	Дано натуральное число. б) Верно ли, что произведение его цифр больше b?
10	Дано натуральное число. в) Верно ли, что это число k-значное? Составное условие и вложенный услов- ный оператор не использовать.
11	Дано натуральное число. г) Верно ли, что его первая цифра превышает m?
12	Дано натуральное число. а) Верно ли, что сумма его цифр больше k, а само число четное?
13	Дано натуральное число. б) Верно ли, что количество его цифр есть четное число, а само число не пре- вышает b?
14	Дано натуральное число. в) Верно ли, что оно начинается цифрой x и заканчивается цифрой y?
15	Дано натуральное число.  г) Верно ли, что произведение его цифр меньше a, а само число делится на b?
16	Дано натуральное число. д) Верно ли, что сумма его цифр больше m, а само число делится на n?
17	Дано натуральное число. Определить: а) есть ли в нем цифра 3;

Схема — это абстракция какого-либо процесса или системы, наглядно отображающая наиболее значимые части. Схемы широко применяются с древних времен до настоящего времени — чертежи древних пирамид, карты земель, принципиальные электрические схемы. Очевидно, древние мореплаватели хотели обмениваться картами и поэтому выработали единую систему обозначений и правил их выполнения. Аналогичные соглашения выработаны для изображения схем-алгоритмов и закреплены ГОСТ и международными стандартами.

На территории Российской Федерации действует единая система программной документации (ЕСПД), частью которой является Государственный стандарт — ГОСТ 19.701-90 «Схемы алгоритмов программ, данных и систем» [1]. Не смотря на то, что описанные в стандарте обозначения могут использоваться для изображения схем ресурсов системы, схем взаимодействия программ и т.п., в настоящей статье описана лишь разработка схем алгоритмов программ.

Рассматриваемый ГОСТ практически полностью соответствует международному стандарту ISO 5807:1985.

Содержание:

1. Элементы блок-схем алгоритмов
2. Примеры блок-схем
3. Нужны ли блок-схемы? Альтернативы

Элементы блок-схем алгоритмов

Блок-схема представляет собой совокупность символов, соответствующих этапам работы алгоритма и соединяющих их линий. Пунктирная линия используется для соединения символа с комментарием. Сплошная линия отражает зависимости по управлению между символами и может снабжаться стрелкой. Стрелку можно не указывать при направлении дуги слева направо и сверху вниз. Согласно п. 4.2.4, линии должны подходить к символу слева, либо сверху, а исходить снизу, либо справа.

Есть и другие типы линий, используемые, например, для изображения блок-схем параллельных алгоритмов, но в текущей статье они, как и ряд специфических символов, не рассматриваются. Рассмотрены лишь основные символы, которых всегда достаточно студентам.

	Терминатором начинается и заканчивается любая функция. Тип возвращаемого значения и аргументов функции обычно указывается в комментариях к блоку терминатора.
	В ГОСТ определено множество символов ввода/вывода, например вывод на магнитные ленты, дисплеи и т.п. Если источник данных не принципиален, обычно используется символ параллелограмма. Подробности ввода/вывода могут быть указаны в комментариях.
	В блоке операций обычно размещают одно или несколько (ГОСТ не запрещает) операций присваивания, не требующих вызова внешних функций.
	Блок в виде ромба имеет один вход и несколько подписанных выходов. В случае, если блок имеет 2 выхода (соответствует оператору ветвления), на них подписывается результат сравнения — «да/нет». Если из блока выходит большее число линий (оператор выбора), внутри него записывается имя переменной, а на выходящих дугах — значения этой переменной.
	Вызов внешних процедур и функций помещается в прямоугольник с дополнительными вертикальными линиями.
	Символы начала и конца цикла содержат имя и условие. Условие может отсутствовать в одном из символов пары. Расположение условия, определяет тип оператора, соответствующего символам на языке высокого уровня — оператор с предусловием (while) или постусловием (do … while).
	Символ «подготовка данных» в произвольной форме (в ГОСТ нет ни пояснений, ни примеров), задает входные значения. Используется обычно для задания циклов со счетчиком.
	В случае, если блок-схема не умещается на лист, используется символ соединителя, отражающий переход потока управления между листами. Символ может использоваться и на одном листе, если по каким-либо причинам тянуть линию не удобно.
	Комментарий может быть соединен как с одним блоком, так и группой. Группа блоков выделяется на схеме пунктирной линией.

Примеры блок-схем

В качестве примеров, построены блок-схемы очень простых алгоритмов сортировки, при этом акцент сделан на различные реализации циклов, т.к. у студенты делают наибольшее число ошибок именно в этой части.

Сортировка вставками

Массив в алгоритме сортировки вставками разделяется на отсортированную и еще не обработанную части. Изначально отсортированная часть состоит из одного элемента, и постепенно увеличивается.

На каждом шаге алгоритма выбирается первый элемент необработанной части массива и вставляется в отсортированную так, чтобы в ней сохранялся требуемый порядок следования элементов. Вставка может выполняться как в конец массива, так и в середину. При вставке в середину необходимо сдвинуть все элементы, расположенные «правее» позиции вставки на один элемент вправо. В алгоритме используется два цикла — в первом выбираются элементы необработанной части, а во втором осуществляется вставка.

В приведенной блок-схеме для организации цикла используется символ ветвления. В главном цикле (i < n) перебираются элементы необработанной части массива. Если все элементы обработаны — алгоритм завершает работу, в противном случае выполняется поиск позиции для вставки i-того элемента. Искомая позиция будет сохранена в переменной j в результате выполнения внутреннего цикла, осуществляющем сдвиг элементов до тех пор, пока не будет найден элемент, значение которого меньше i-того.

На блок-схеме показано каким образом может использоваться символ перехода — его можно использовать не только для соединения частей схем, размещенных на разных листах, но и для сокращения количества линий. В ряде случаев это позволяет избежать пересечения линий и упрощает восприятие алгоритма.

Сортировка пузырьком

Сортировка пузырьком, как и сортировка вставками, использует два цикла. Во вложенном цикле выполняется попарное сравнение элементов и, в случае нарушения порядка их следования, перестановка. В результате выполнения одной итерации внутреннего цикла, максимальный элемент гарантированно будет смещен в конец массива. Внешний цикл выполняется до тех пор, пока весь массив не будет отсортирован.

На блок-схеме показано использование символов начала и конца цикла. Условие внешнего цикла (А) проверяется в конце (с постусловием), он работает до тех пор, пока переменная hasSwapped имеет значение true. Внутренний цикл использует предусловие для перебора пар сравниваемых элементов. В случае, если элементы расположены в неправильном порядке, выполняется их перестановка посредством вызова внешней процедуры (swap). Для того, чтобы было понятно назначение внешней процедуры и порядок следования ее аргументов, необходимо писать комментарии. В случае, если функция возвращает значение, комментарий может быть написан к символу терминатору конца.

Сортировка выбором

В сортировке выбором массив разделяется на отсортированную и необработанную части. Изначально отсортированная часть пустая, но постепенно она увеличивается. Алгоритм производит поиск минимального элемента необработанной части и меняет его местами с первым элементом той же части, после чего считается, что первый элемент обработан (отсортированная часть увеличивается).

На блок-схеме приведен пример использования блока «подготовка», а также показано, что в ряде случаев можно описывать алгоритм более «укрупнённо» (не вдаваясь в детали). К сортировке выбором не имеют отношения детали реализации поиска индекса минимального элемента массива, поэтому они могут быть описаны символом вызова внешней процедуры. Если блок-схема алгоритма внешней процедуры отсутствует, не помешает написать к символу вызова комментарий, исключением могут быть функции с говорящими названиями типа swap, sort, … .

На блоге можно найти другие примеры блок-схем:

• блок-схема проверки правильности расстановки скобок арифметического выражения [2];
• блок-схемы алгоритмов быстрой сортировки и сортировки слиянием [3].

Часть студентов традиционно пытается рисовать блок-схемы в Microsoft Word, но это оказывается сложно и не удобно. Например, в MS Word нет стандартного блока для терминатора начала и конца алгоритма (прямоугольник со скругленными краями, а не овал). Наиболее удобными, на мой взгляд, являются утилиты MS Visio и yEd [5], обе они позволяют гораздо больше, чем строить блок-схемы (например рисовать диаграммы UML), но первая является платной и работает только под Windows, вторая бесплатная и кроссплатфомренная. Все блок-схемы в этой статье выполнены с использованием yEd.

Частные конторы никакие блок-схемы не используют, в книжках по алгоритмам [6] вместо них применяют словесное описание (псевдокод) как более краткую форму. Возможно блок-схемы применяют на государственных предприятиях, которые должны оформлять документацию согласно требованиям ЕСПД, но есть сомнения — даже для регистрации программы в Государственном реестре программ для ЭВМ никаких блок-схем не требуется.

Тем не менее, рисовать блок-схемы заставляют школьников (примеры из учебников ГОСТ не соответствуют) — выносят вопросы на государственные экзамены (ГИА и ЕГЭ), студентов — перед защитой диплом сдается на нормоконтроль, где проверяется соответствие схем стандартам.

Разработка блок-схем выполняется на этапах проектирования и документирования, согласно каскадной модели разработки ПО, которая сейчас почти не применяется, т.к. сопровождается большими рисками, связанными с ошибками на этапах проектирования.

Появляются подозрения, что система образования прогнила и отстала лет на 20, однако аналогичная проблема наблюдается и за рубежом. Международный стандарт ISO 5807:1985 мало чем отличается от ГОСТ 19.701-90, более нового стандарта за рубежом нет. Там же производится множество программ для выполнения этих самых схем — Dia, MS Visio, yEd, …, а значит списывать их не собираются. Вместо блок-схем иногда применяют диаграммы деятельности UML [6], однако удобнее они оказываются, разве что при изображении параллельных алгоритмов.

Периодически поднимается вопрос о том, что ни блок-схемы, ни UML не нужны, да и документация тоже не нужна. Об этом твердят программисты, придерживающиеся методологии экстремального программирования (XP) [7], ходя даже в их кругу нет единого мнения.

В ряде случаев, программирование невозможно без рисования блок-схем, т.к. это один процесс — существуют визуальные языки программирования, такие как ДРАКОН [8], кроме того, блок-схемы используются для верификации алгоритмов (формального доказательства их корректности) методом индуктивных утверждений Флойда [9].

В общем, единого мнения нет. Очевидно, есть области, в которых без чего-то типа блок-схем обойтись нельзя, но более гибкой альтернативы нет. Для формальной верификации необходимо рисовать подробные блок-схемы, но для проектирования и документирования такие схемы не нужны — я считаю разумным утверждение экстремальных программистов о том, что нужно рисовать лишь те схемы, которые помогают в работе и не требуют больших усилий для поддержания в актуальном состоянии [10].

Список использованных источников:

1. ГОСТ 19.701–90 (ИСО 5807–85) «Единая система программной документа­ции».
2. Алгоритм. Свойства алгоритма https://pro-prof.com/archives/578
3. Алгоритмы сортировки слиянием и быстрой сортировки https://pro-prof.com/archives/813
4. yEd Graph Editor https://www.yworks.com/products/yed
5. Книги: алгоритмы https://pro-prof.com/books-algorithms
6. Рамбо Дж., Якобсон А., Буч Г. UML: специальный справочник. -СПб.: Питер, 2002. -656 с.
7. Кент Бек Экстремальное программирование: разработка через тестирование – СПб.: Питер – 2003
8. Визуальный язык ДРАКОН https://drakon.su/
9. Шилов Н.В. Верификация шаблонов алгоритмов для метода отката и метода ветвей и границ. Моделирование и анализ информационных систем, ISSN 1818 – 1015, т.18, №4, 2011
10. Брукс Ф., Мифический человеко — месяц или как создаются программные системы. СПб. Символ Плюс, 1999 — 304 с. ил.