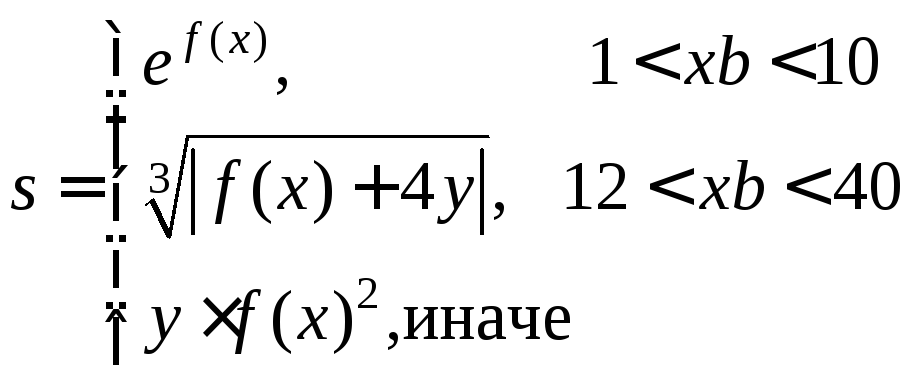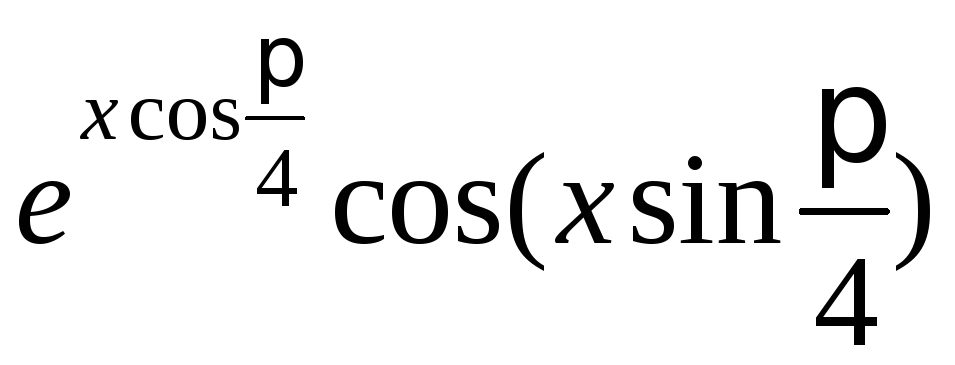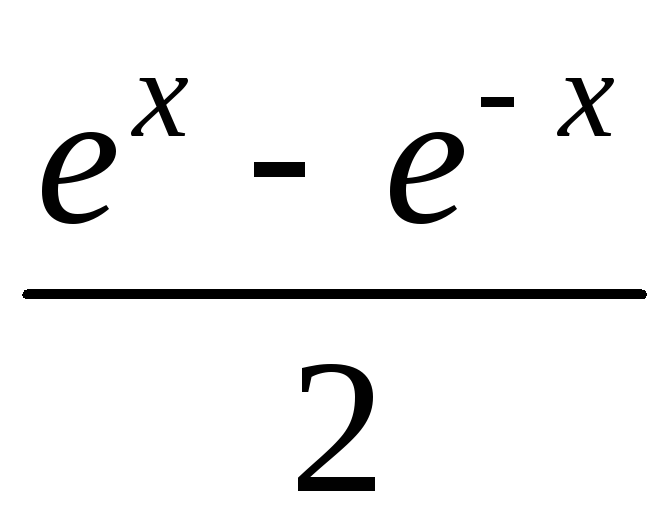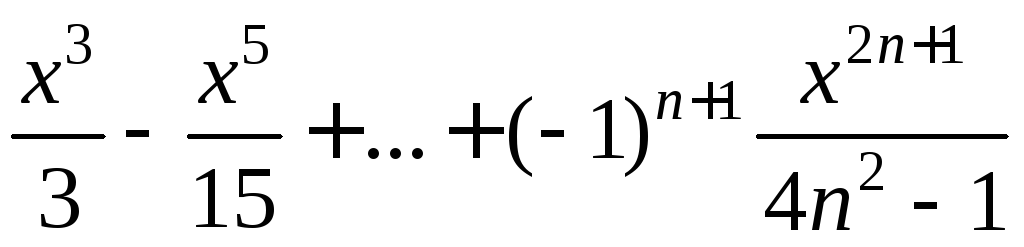Как составить блок схему алгоритма расчета функции

2.1 Разработка алгоритма.
2.2 Блок-схема.
2.3 Структуры алгоритмов.

2.1 Разработка алгоритма.

Алгоритм – это

a. описание последовательности действий для решения задачи или достижения поставленной цели;

b. правила выполнения основных операций обработки данных;

c. описание вычислений по математическим формулам.

Перед началом разработки алгоритма необходимо четко уяснить задачу: что требуется получить в качестве результата, какие исходные данные необходимы и какие имеются в наличии, какие существуют ограничения на эти данные. Далее требуется записать, какие действия необходимо предпринять для получения из исходных данных требуемого результата.

На практике наиболее распространены следующие формы представления алгоритмов:

 словесная (записи на естественном языке);

 графическая (изображения из графических символов);

 псевдокоды (полуформализованные описания алгоритмов на условном алгоритмическом языке, включающие в себя как элементы языка программирования, так и фразы естественного языка, общепринятые математические обозначения и др.);

 программная (тексты на языках программирования).

Словесный способ записи алгоритмов представляет собой описание последовательных этапов обработки данных. Алгоритм задается в произвольном изложении на естественном языке.

Пример. Записать алгоритм нахождения наибольшего общего делителя (НОД) двух натуральных чисел.

Алгоритм может быть следующим:

1. задать два числа;

2. если числа равны, то взять любое из них в качестве ответа и остановиться, в противном случае продолжить выполнение алгоритма;

3. определить большее из чисел;

4. заменить большее из чисел разностью большего и меньшего из чисел;

5. повторить алгоритм с шага 2.

Описанный алгоритм применим к любым натуральным числам и должен приводить к решению поставленной задачи. Убедитесь в этом самостоятельно, определив с помощью этого алгоритма наибольший общий делитель чисел 125 и 75.

Словесный способ не имеет широкого распространения по следующим причинам:

 такие описания строго не формализуемы;

 страдают многословностью записей;

 допускают неоднозначность толкования отдельных предписаний.

Графический способ представления алгоритмов является более компактным и наглядным по сравнению со словесным.

При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий.

Такое графическое представление называется схемой алгоритма или блок-схемой.

Псевдокод представляет собой систему обозначений и правил, предназначенную для единообразной записи алгоритмов.

Он занимает промежуточное место между естественным и формальным языками.

С одной стороны, он близок к обычному естественному языку, поэтому алгоритмы могут на нем записываться и читаться как обычный текст. С другой стороны, в псевдокоде используются некоторые формальные конструкции и математическая символика, что приближает запись алгоритма к общепринятой математической записи.

В псевдокоде не приняты строгие синтаксические правила для записи команд, присущие формальным языкам, что облегчает запись алгоритма на стадии его проектирования и дает возможность использовать более широкий набор команд, рассчитанный на абстрактного исполнителя. Однако в псевдокоде обычно имеются некоторые конструкции, присущие формальным языкам, что облегчает переход от записи на псевдокоде к записи алгоритма на формальном языке. В частности, в псевдокоде, так же, как и в формальных языках, есть служебные слова, смысл которых определен раз и навсегда. Единого или формального определения псевдокода не существует, поэтому возможны различные псевдокоды, отличающиеся набором служебных слов и основных (базовых) конструкций.

2.2 Блок-схема.

Блок-схемой называют графическое представление алгоритма, в котором он изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий.

В блок-схеме каждому типу действий (вводу исходных данных, вычислению значений выражений, проверке условий, управлению повторением действий, окончанию обработки и т.п.) соответствует геометрическая фигура, представленная в виде блочного символа. Блочные символы соединяются линиями переходов, определяющими очередность выполнения действий.

Приведем наиболее часто употребляемые символы.

Название символа	Обозначение и пример заполнения	Пояснение
Процесс		Вычислительное действие или последовательность действий
Решение		Проверка условий
Модификация		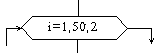Начало цикла
Предопределенный процесс		Вычисления по подпрограмме, стандартной подпрограмме
Ввод-вывод		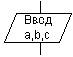Ввод-вывод в общем виде
Пуск-останов		Начало, конец алгоритма, вход и выход в подпрограмму
Документ		Вывод результатов на печать

Блок “процесс” применяется для обозначения действия или последовательности действий, изменяющих значение, форму представления или размещения данных. Для улучшения наглядности схемы несколько отдельных блоков обработки можно объединять в один блок. Представление отдельных операций достаточно свободно.

Блок “решение” используется для обозначения переходов управления по условию. В каждом блоке “решение” должны быть указаны вопрос, условие или сравнение, которые он определяет.

Блок “модификация” используется для организации циклических конструкций. (Слово модификация означает видоизменение, преобразование). Внутри блока записывается параметр цикла, для которого указываются его начальное значение, граничное условие и шаг изменения значения параметра для каждого повторения.

Блок “предопределенный процесс” используется для указания обращений к вспомогательным алгоритмам, существующим автономно в виде некоторых самостоятельных модулей, и для обращений к библиотечным подпрограммам.

Пример. Составить блок-схему алгоритма определения высот ha, hb, hc треугольника со сторонами a, b, c, если

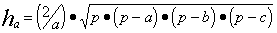
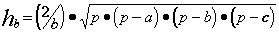
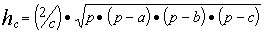
где p = (a + b + c) / 2. 
Решение. Введем обозначение 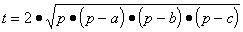 тогда h_a = t/a, h_b = t/b, h_c = t/c. Блок-схема должна содержать начало, ввод a, b, c, вычисление p, t, h_a, h_b, h_c, вывод результатов и останов.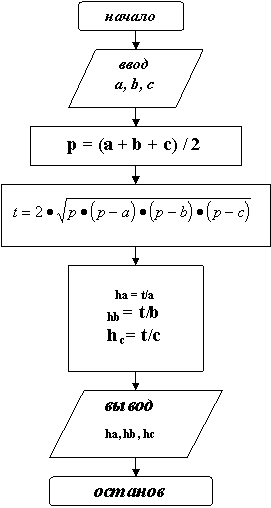 

2.3 Структуры алгоритмов.

Алгоритмы можно представлять как некоторые структуры, состоящие из отдельных базовых (т.е. основных) элементов. Естественно, что при таком подходе к алгоритмам изучение основных принципов их конструирования должно начинаться с изучения этих базовых элементов

Логическая структура любого алгоритма может быть представлена комбинацией трех базовых структур: следование, ветвление, цикл.

Характерной особенностью базовых структур является наличие в них одного входа и одного выхода.

1. Базовая структура следование. Образуется из последовательности действий, следующих одно за другим:

2. Базовая структура ветвление. Обеспечивает в зависимости от результата проверки условия (да или нет) выбор одного из альтернативных путей работы алгоритма. Каждый из путей ведет к общему выходу, так что работа алгоритма будет продолжаться независимо от того, какой путь будет выбран.

Структура ветвление существует в четырех основных вариантах:

 если-то;

 если-то-иначе;

 выбор;

 выбор-иначе.

1) если-то 
 если условие
   то действия 
 конец если

2) если-то-иначе 
 если условие
   то действия 1
   иначе действия 2
 конец если

3) выбор 
 выбор
   при условие 1: действия 1
   при условие 2: действия 2
   . . . . . . . . . . . .
   при условие N: действия N 
 конец выбора

4) выбор-иначе 
 выбор
   при условие 1: действия 1
   при условие 2: действия 2
   . . . . . . . . . . . .
   при условие N: действия N
   иначе действия N+1 
 конец выбора
 

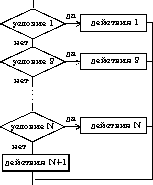
Пример. Составить блок-схему алгоритма вычисления функции

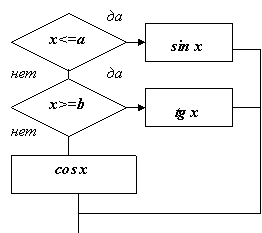
Базовая структура цикл. Обеспечивает многократное выполнение некоторой совокупности действий, которая называется телом цикла.

Структура цикл существует в трех основных вариантах:

Цикл типа для.

Предписывает выполнять тело цикла для всех значений некоторой переменной (параметра цикла) в заданном диапазоне.

Цикл типа пока.

Предписывает выполнять тело цикла до тех пор, пока выполняется условие, записанное после слова пока.

Цикл типа делать – пока.

Предписывает выполнять тело цикла до тех пор, пока выполняется условие, записанное после слова пока. Условие проверяется после выполнения тела цикла.

Заметим, что циклы для и пока называют также циклами с предпроверкой условия а циклы делать – пока – циклами с постпроверкой условия. Иными словами, тела циклов для и пока могут не выполниться ни разу, если условие окончания цикла изначально не верно. Тело цикла делать – пока выполнится как минимум один раз, даже если условие окончания цикла изначально не верно.

цикл для i от i1 до i2 шаг i3
   тело цикла (последовательность действий) 
 конец цикла

цикл пока условие
   тело цикла (последовательность действий)
 конец цикла

цикл делать
   тело цикла (последовательность действий) 
 пока условие
 конец цикла

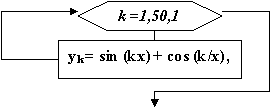
Пример. Составить блок-схему алгоритма вычисления функции

y_k = sin (kx) + cos (k/x), k = 1, 2, …, 50

Пример. Составить блок-схему вычисления функции

y = a³ / (a² + x²)

при x, изменяющимся от x = 0 до x = 3 с шагом Dx = 0,1

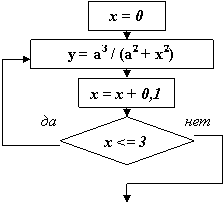
Итерационные циклы. Особенностью итерационного цикла является то, что число повторений операторов тела цикла заранее неизвестно. Для его организации используется цикл типа пока. Выход из итерационного цикла осуществляется в случае выполнения заданного условия.

На каждом шаге вычислений происходит последовательное приближение и проверка условия достижения искомого результата.

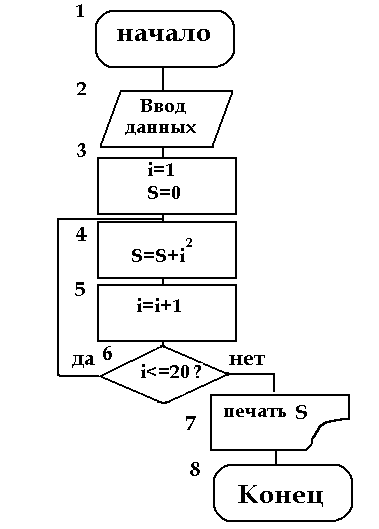
Пример. Составить алгоритм вычисления суммы ряда

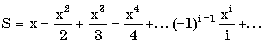
с заданной точностью (для данного знакочередующегося степенного ряда требуемая точность будет достигнута, когда очередное слагаемое станет по абсолютной величине меньше).

Вычисление сумм – типичная циклическая задача. Особенностью же нашей конкретной задачи является то, что число слагаемых (а, следовательно, и число повторений тела цикла) заранее неизвестно. Поэтому выполнение цикла должно завершиться в момент достижения требуемой точности.

При составлении алгоритма нужно учесть, что знаки слагаемых чередуются и степень числа х в числителях слагаемых возрастает.

Решая эту задачу “в лоб” путем вычисления на каждом i-ом шаге частичной суммы

S:=S+(-1)**(i-1)*x**i/i ,

мы получим очень неэффективный алгоритм, требующий выполнения большого числа операций. Гораздо лучше организовать вычисления следующим образом: если обозначить числитель какого-либо слагаемого буквой р, то у следующего слагаемого числитель будет равен -р*х (знак минус обеспечивает чередование знаков слагаемых), а само слагаемое m

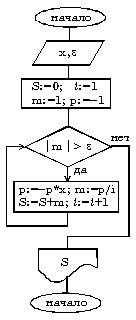
будет равно p/i, где i – номер слагаемого.

Алгоритм, в состав которого входит итерационный цикл, называется итерационным алгоритмом. Итерационные алгоритмы используются при реализации итерационных численных методов. В итерационных алгоритмах необходимо обеспечить обязательное достижение условия выхода из цикла (сходимость итерационного процесса). В противном случае произойдет зацикливание алгоритма, т.е. не будет выполняться основное свойство алгоритма – результативность.

Вложенные циклы.

Возможны случаи, когда внутри тела цикла необходимо повторять некоторую последовательность операторов, т. е. организовать внутренний цикл. Такая структура получила название цикла в цикле или вложенных циклов. Глубина вложения циклов (то есть количество вложенных друг в друга циклов) может быть различной.

При использовании такой структуры для экономии машинного времени необходимо выносить из внутреннего цикла во внешний все операторы, которые не зависят от параметра внутреннего цикла.

Пример вложенных циклов для. Вычислить сумму элементов заданной матрицы А(5,3).

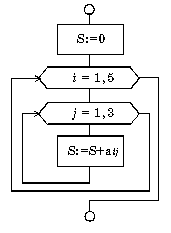
Пример вложенных циклов пока. Вычислить произведение тех элементов заданной матрицы A(10,10), которые расположены на пересечении четных строк и четных столбцов.

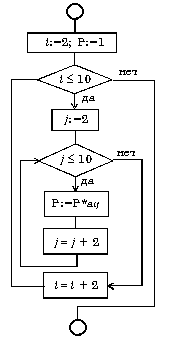
Примеры составления блок-схемы алгоритма

Пример 1.
Составить схему алгоритма вычисления
значения :

Для
начала для построения блок –схемы
алгоритма опишем последовательность
действий, необходимых для решения данной
задачи:

• начало

• ввод
  чисел a,b

• вычисление
  х

• вычисление
  z

• вывод
  результата

• конец

Исходя из этого
составляем блок-схему алгоритма согласно
ГОСТ, используя соответствующие блоки.

Пример
2. Составить
схему алгоритма вычисления значения:
x=a+b
при a>b,
x=a*b,
при a<=b.

Пример 3. Составить схему алгоритма вычисления значения:

Для начала для
построения блок –схемы алгоритма опишем
последовательность действий, необходимых
для решения данной задачи:

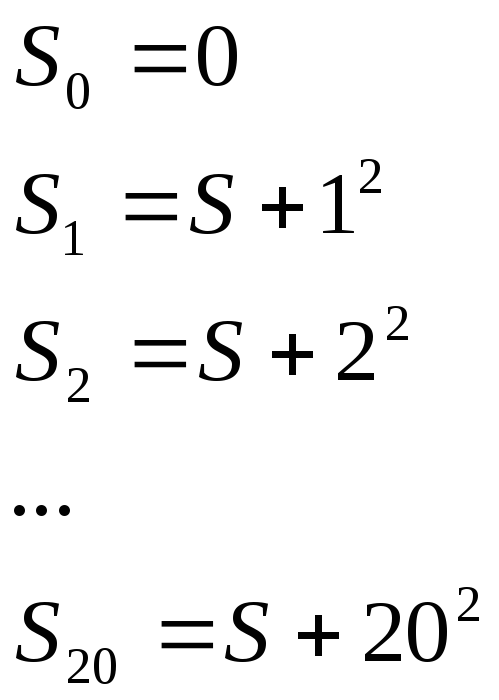
Исходя из этого
составляем блок-схему алгоритма согласно
ГОСТ, используя соответствующие блоки.

Порядок выполнения работы

1. Изучить
   теоретические сведения по теме
   ”Построение блок-схем алгоритмов”.

2. Получить
   у преподавателя индивидуальное задание
   и нарисовать блок-схему алгоритма
   согласно заданному варианту.

3. Ответить
   на контрольные вопросы.

4. Сформулировать
   выводы.

Контрольные вопросы

1. Основные
   этапы решения задач на компьютере.

2. Свойства алгоритма.
   Типы вычислительных процессов.

3. Блок схемы. Понятие
   и правила построения.

4. Примеры построения
   блок-схем алгоритмов.

Задание
№1: Разработайте
алгоритм и представьте его в графическом
виде (блок-схемы) для следующих задач:

Задание 1.1
Вычислить значение выражения при
заданных исходных данных.

Указание.
Для упрощения выражений введите
промежуточные переменные.

Сравнить полученное
значение с указанным правильным
результатом.

1.

При
x = 14.26;
y = – 1.22;
z = 3.5ответs
= 0.749155.

2.

При
x = –4.5; y = 0.75;
z = –0.845ответs
= –3.23765.

3.

При
x = 3.74;
y=–0.825; z = 0.16ответs
= 1.05534.

4.

При
x = 0.4;
y = –0.875; z = –0.475ответ
s = 1.98727.

5.

При
x = –15.246; y = 4.642;
z = 21 ответ
s = –182.038.

6.

При
x = 16.55;
y = –2.75; z = 0.15
ответ s
= –40.6307.

7.

При
x = 0.1722; y = 6.33; z = 3.25ответ
s = –205.306.

8.

При
x = –2.235;
y = 2.23; z = 15.221
ответ s
= 39.3741.

9.

При
x = 1.825;
y = 18.225; z = –3.298ответ
s = 1.21308.

10.

При
x = 3.981;
y = –1.625;
z = 0.512
ответ s
= 1.26185.

11.

При
x = 6.251; y = 0.827; z = 25.001
ответ
s = 0.712122.

12.

При
x
= 3.251; y
= 0.325; z
= 0.466
ответ s
= 4.23655.

13.

.

При
x
= 17.421; y
= 10.365;
z
= 0.828
ответ s
= 0.330564.

14.
.

При
x
= 12.3;
y
= 15.4; z
= 0.252
ответ s
= 82.8256.

15.

.

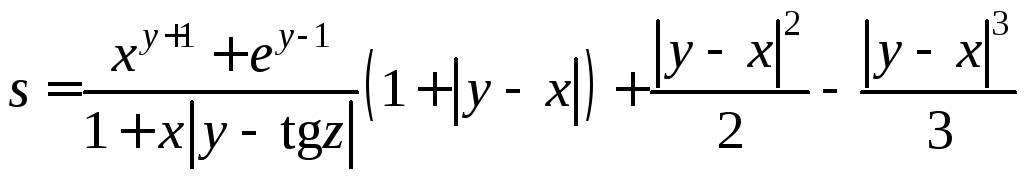При
x
= 2.444; y
= 0.869;
z
= –0.13
ответ s
= –0.498707.

Задание
1.2 Вычислить
значение выражения при заданных исходных
данных. Предусмотреть вывод информации
о выбранной ветви вычислений.

Задание
1.3 Вывести
на экран таблицу значений функции Y(x)
и ее разложения в ряд S(x)
для x,
изменяющегося от a
до b
с шагом h
= (b –
a)/10,
табл. 1.

Таблица 1.

Задание
№2:
Решите представленные ниже задачи,
указав номер задачи и полученный ответ. 

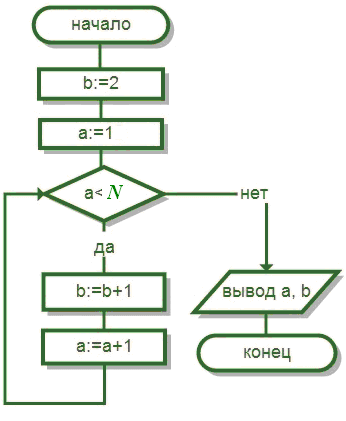
Задача
2.1
Определите
результаты работы блок-схемы алгоритма
при

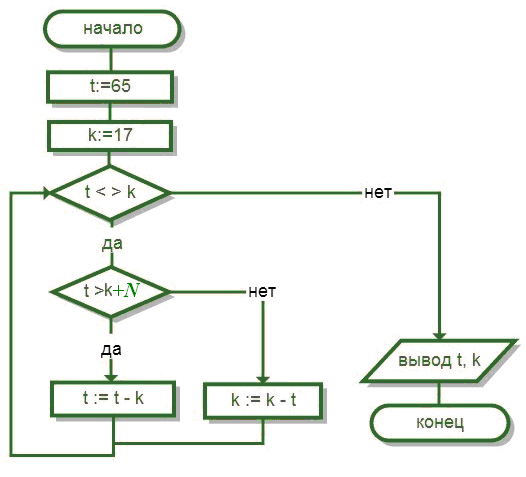
Задача
2.2
Какие
значения примут t и k в
результате работы фрагмента блок-схемы
алгоритма?

Задача
2.3.
Определите
значения
элементов
массива А₂,
А₄,
А₆,
А₈
при N=8
в результате работы фрагмента алгоритма

Сообщение было отмечено marina110374 как решение

Решение

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

Program Prak;
{Вариант N 00 Выполнил: студент 1 курса Петров С. М. }
Uses
  Crt;
Const
  w = 0.753;
  v = 1.23;
  z = 33;
Var
  x, A, B, S, f, g, p: Double;
Begin
  ClrScr;
  Write('x = ');
  ReadLn(x);
  Write('A = ');
  ReadLn(A);
  Write('B = ');
  ReadLn(B);
  WriteLn('Исходные данные');
  WriteLn('x = ', x:11:4, ',  A = ', A:11:4, ',  B = ', B:11:4);
  f := x * x * x * 2 * pi * b;
  if (sin(f) = 0) or (cos(f) = 0) then
    WriteLn('S не определено')
  else
    begin
      f := sin(f) / cos(f);
      if f > 0 then
        f := exp(ln(f) / 3)
      else
        if f < 0 then
          f := -exp(ln(-f) / 3);
      f := B * sqr(cos(x)) / f;
      g := ln(abs(exp(A + 2 * x) / exp(B * ln(w)))) / exp(sqrt(abs(2 * pi * x * x - B * B * B)));
      p := exp(z * ln(v));
      WriteLn('Промежуточные данные');
      WriteLn('f = ', f:11:4, ',  g = ', g:11:4, ',  p = ', p:11:4);
      S := f + g + p;
      WriteLn('Результат');
      WriteLn('S = ', S:12:5)
    end;
  ReadLn
End.

0

Схема — это абстракция какого-либо процесса или системы, наглядно отображающая наиболее значимые части. Схемы широко применяются с древних времен до настоящего времени — чертежи древних пирамид, карты земель, принципиальные электрические схемы. Очевидно, древние мореплаватели хотели обмениваться картами и поэтому выработали единую систему обозначений и правил их выполнения. Аналогичные соглашения выработаны для изображения схем-алгоритмов и закреплены ГОСТ и международными стандартами.

На территории Российской Федерации действует единая система программной документации (ЕСПД), частью которой является Государственный стандарт — ГОСТ 19.701-90 «Схемы алгоритмов программ, данных и систем» [1]. Не смотря на то, что описанные в стандарте обозначения могут использоваться для изображения схем ресурсов системы, схем взаимодействия программ и т.п., в настоящей статье описана лишь разработка схем алгоритмов программ.

Рассматриваемый ГОСТ практически полностью соответствует международному стандарту ISO 5807:1985.

Содержание:

1. Элементы блок-схем алгоритмов
2. Примеры блок-схем
3. Нужны ли блок-схемы? Альтернативы

Элементы блок-схем алгоритмов

Блок-схема представляет собой совокупность символов, соответствующих этапам работы алгоритма и соединяющих их линий. Пунктирная линия используется для соединения символа с комментарием. Сплошная линия отражает зависимости по управлению между символами и может снабжаться стрелкой. Стрелку можно не указывать при направлении дуги слева направо и сверху вниз. Согласно п. 4.2.4, линии должны подходить к символу слева, либо сверху, а исходить снизу, либо справа.

Есть и другие типы линий, используемые, например, для изображения блок-схем параллельных алгоритмов, но в текущей статье они, как и ряд специфических символов, не рассматриваются. Рассмотрены лишь основные символы, которых всегда достаточно студентам.

	Терминатором начинается и заканчивается любая функция. Тип возвращаемого значения и аргументов функции обычно указывается в комментариях к блоку терминатора.
	В ГОСТ определено множество символов ввода/вывода, например вывод на магнитные ленты, дисплеи и т.п. Если источник данных не принципиален, обычно используется символ параллелограмма. Подробности ввода/вывода могут быть указаны в комментариях.
	В блоке операций обычно размещают одно или несколько (ГОСТ не запрещает) операций присваивания, не требующих вызова внешних функций.
	Блок в виде ромба имеет один вход и несколько подписанных выходов. В случае, если блок имеет 2 выхода (соответствует оператору ветвления), на них подписывается результат сравнения — «да/нет». Если из блока выходит большее число линий (оператор выбора), внутри него записывается имя переменной, а на выходящих дугах — значения этой переменной.
	Вызов внешних процедур и функций помещается в прямоугольник с дополнительными вертикальными линиями.
	Символы начала и конца цикла содержат имя и условие. Условие может отсутствовать в одном из символов пары. Расположение условия, определяет тип оператора, соответствующего символам на языке высокого уровня — оператор с предусловием (while) или постусловием (do … while).
	Символ «подготовка данных» в произвольной форме (в ГОСТ нет ни пояснений, ни примеров), задает входные значения. Используется обычно для задания циклов со счетчиком.
	В случае, если блок-схема не умещается на лист, используется символ соединителя, отражающий переход потока управления между листами. Символ может использоваться и на одном листе, если по каким-либо причинам тянуть линию не удобно.
	Комментарий может быть соединен как с одним блоком, так и группой. Группа блоков выделяется на схеме пунктирной линией.

Примеры блок-схем

В качестве примеров, построены блок-схемы очень простых алгоритмов сортировки, при этом акцент сделан на различные реализации циклов, т.к. у студенты делают наибольшее число ошибок именно в этой части.

Сортировка вставками

Массив в алгоритме сортировки вставками разделяется на отсортированную и еще не обработанную части. Изначально отсортированная часть состоит из одного элемента, и постепенно увеличивается.

На каждом шаге алгоритма выбирается первый элемент необработанной части массива и вставляется в отсортированную так, чтобы в ней сохранялся требуемый порядок следования элементов. Вставка может выполняться как в конец массива, так и в середину. При вставке в середину необходимо сдвинуть все элементы, расположенные «правее» позиции вставки на один элемент вправо. В алгоритме используется два цикла — в первом выбираются элементы необработанной части, а во втором осуществляется вставка.

В приведенной блок-схеме для организации цикла используется символ ветвления. В главном цикле (i < n) перебираются элементы необработанной части массива. Если все элементы обработаны — алгоритм завершает работу, в противном случае выполняется поиск позиции для вставки i-того элемента. Искомая позиция будет сохранена в переменной j в результате выполнения внутреннего цикла, осуществляющем сдвиг элементов до тех пор, пока не будет найден элемент, значение которого меньше i-того.

На блок-схеме показано каким образом может использоваться символ перехода — его можно использовать не только для соединения частей схем, размещенных на разных листах, но и для сокращения количества линий. В ряде случаев это позволяет избежать пересечения линий и упрощает восприятие алгоритма.

Сортировка пузырьком

Сортировка пузырьком, как и сортировка вставками, использует два цикла. Во вложенном цикле выполняется попарное сравнение элементов и, в случае нарушения порядка их следования, перестановка. В результате выполнения одной итерации внутреннего цикла, максимальный элемент гарантированно будет смещен в конец массива. Внешний цикл выполняется до тех пор, пока весь массив не будет отсортирован.

На блок-схеме показано использование символов начала и конца цикла. Условие внешнего цикла (А) проверяется в конце (с постусловием), он работает до тех пор, пока переменная hasSwapped имеет значение true. Внутренний цикл использует предусловие для перебора пар сравниваемых элементов. В случае, если элементы расположены в неправильном порядке, выполняется их перестановка посредством вызова внешней процедуры (swap). Для того, чтобы было понятно назначение внешней процедуры и порядок следования ее аргументов, необходимо писать комментарии. В случае, если функция возвращает значение, комментарий может быть написан к символу терминатору конца.

Сортировка выбором

В сортировке выбором массив разделяется на отсортированную и необработанную части. Изначально отсортированная часть пустая, но постепенно она увеличивается. Алгоритм производит поиск минимального элемента необработанной части и меняет его местами с первым элементом той же части, после чего считается, что первый элемент обработан (отсортированная часть увеличивается).

На блок-схеме приведен пример использования блока «подготовка», а также показано, что в ряде случаев можно описывать алгоритм более «укрупнённо» (не вдаваясь в детали). К сортировке выбором не имеют отношения детали реализации поиска индекса минимального элемента массива, поэтому они могут быть описаны символом вызова внешней процедуры. Если блок-схема алгоритма внешней процедуры отсутствует, не помешает написать к символу вызова комментарий, исключением могут быть функции с говорящими названиями типа swap, sort, … .

На блоге можно найти другие примеры блок-схем:

• блок-схема проверки правильности расстановки скобок арифметического выражения [2];
• блок-схемы алгоритмов быстрой сортировки и сортировки слиянием [3].

Часть студентов традиционно пытается рисовать блок-схемы в Microsoft Word, но это оказывается сложно и не удобно. Например, в MS Word нет стандартного блока для терминатора начала и конца алгоритма (прямоугольник со скругленными краями, а не овал). Наиболее удобными, на мой взгляд, являются утилиты MS Visio и yEd [5], обе они позволяют гораздо больше, чем строить блок-схемы (например рисовать диаграммы UML), но первая является платной и работает только под Windows, вторая бесплатная и кроссплатфомренная. Все блок-схемы в этой статье выполнены с использованием yEd.

Частные конторы никакие блок-схемы не используют, в книжках по алгоритмам [6] вместо них применяют словесное описание (псевдокод) как более краткую форму. Возможно блок-схемы применяют на государственных предприятиях, которые должны оформлять документацию согласно требованиям ЕСПД, но есть сомнения — даже для регистрации программы в Государственном реестре программ для ЭВМ никаких блок-схем не требуется.

Тем не менее, рисовать блок-схемы заставляют школьников (примеры из учебников ГОСТ не соответствуют) — выносят вопросы на государственные экзамены (ГИА и ЕГЭ), студентов — перед защитой диплом сдается на нормоконтроль, где проверяется соответствие схем стандартам.

Разработка блок-схем выполняется на этапах проектирования и документирования, согласно каскадной модели разработки ПО, которая сейчас почти не применяется, т.к. сопровождается большими рисками, связанными с ошибками на этапах проектирования.

Появляются подозрения, что система образования прогнила и отстала лет на 20, однако аналогичная проблема наблюдается и за рубежом. Международный стандарт ISO 5807:1985 мало чем отличается от ГОСТ 19.701-90, более нового стандарта за рубежом нет. Там же производится множество программ для выполнения этих самых схем — Dia, MS Visio, yEd, …, а значит списывать их не собираются. Вместо блок-схем иногда применяют диаграммы деятельности UML [6], однако удобнее они оказываются, разве что при изображении параллельных алгоритмов.

Периодически поднимается вопрос о том, что ни блок-схемы, ни UML не нужны, да и документация тоже не нужна. Об этом твердят программисты, придерживающиеся методологии экстремального программирования (XP) [7], ходя даже в их кругу нет единого мнения.

В ряде случаев, программирование невозможно без рисования блок-схем, т.к. это один процесс — существуют визуальные языки программирования, такие как ДРАКОН [8], кроме того, блок-схемы используются для верификации алгоритмов (формального доказательства их корректности) методом индуктивных утверждений Флойда [9].

В общем, единого мнения нет. Очевидно, есть области, в которых без чего-то типа блок-схем обойтись нельзя, но более гибкой альтернативы нет. Для формальной верификации необходимо рисовать подробные блок-схемы, но для проектирования и документирования такие схемы не нужны — я считаю разумным утверждение экстремальных программистов о том, что нужно рисовать лишь те схемы, которые помогают в работе и не требуют больших усилий для поддержания в актуальном состоянии [10].

Список использованных источников:

1. ГОСТ 19.701–90 (ИСО 5807–85) «Единая система программной документа­ции».
2. Алгоритм. Свойства алгоритма https://pro-prof.com/archives/578
3. Алгоритмы сортировки слиянием и быстрой сортировки https://pro-prof.com/archives/813
4. yEd Graph Editor https://www.yworks.com/products/yed
5. Книги: алгоритмы https://pro-prof.com/books-algorithms
6. Рамбо Дж., Якобсон А., Буч Г. UML: специальный справочник. -СПб.: Питер, 2002. -656 с.
7. Кент Бек Экстремальное программирование: разработка через тестирование – СПб.: Питер – 2003
8. Визуальный язык ДРАКОН https://drakon.su/
9. Шилов Н.В. Верификация шаблонов алгоритмов для метода отката и метода ветвей и границ. Моделирование и анализ информационных систем, ISSN 1818 – 1015, т.18, №4, 2011
10. Брукс Ф., Мифический человеко — месяц или как создаются программные системы. СПб. Символ Плюс, 1999 — 304 с. ил.