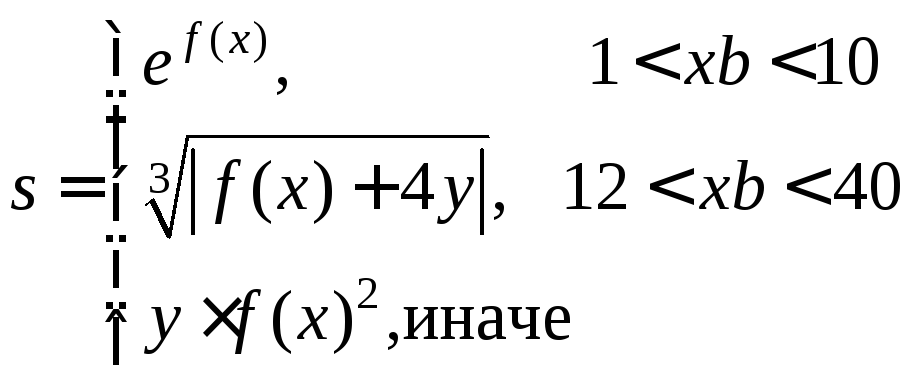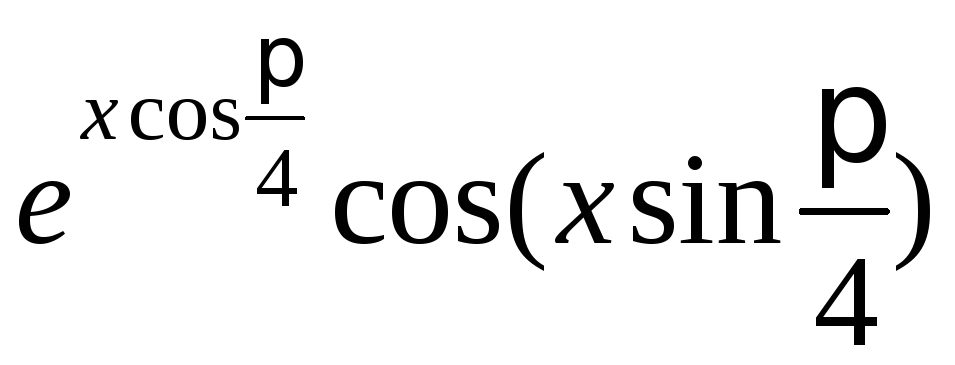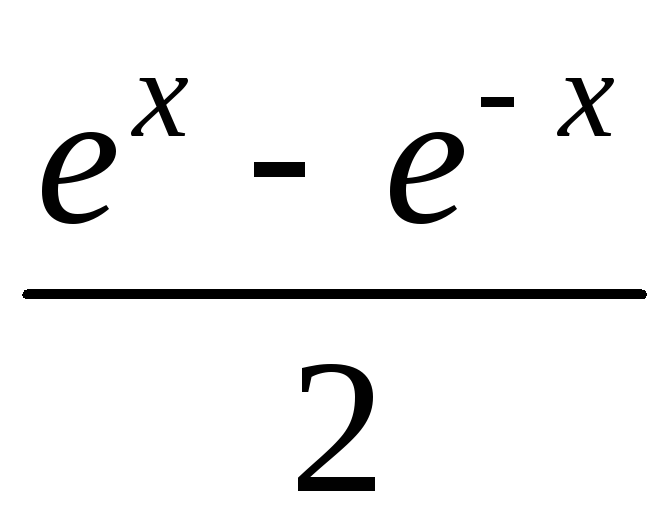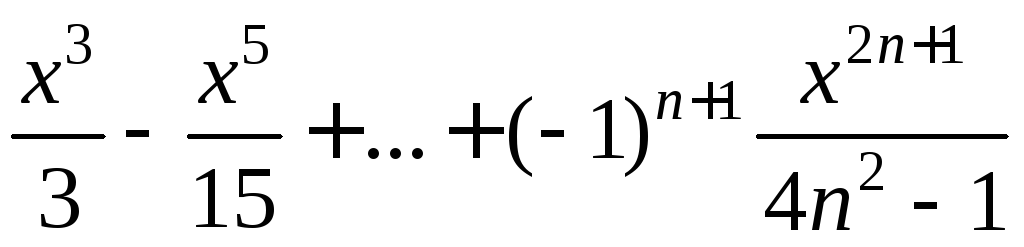На чтение 15 мин Просмотров 2 Опубликовано 11 апреля 2023 Обновлено 11 апреля 2023
Содержание
- Порядок выполнения работы. 1. Составление блок – схемы вычисления арифметического выражения.
- Урок 4. Блок-схема
- Как составить блок схему арифметического вычисления
- ОАиП | БФЭК
- Учебное пособие
- Составление блок-схем алгоритмов
Порядок выполнения работы. 1. Составление блок – схемы вычисления арифметического выражения.
1. Составление блок – схемы вычисления арифметического выражения.
В качестве примера рассмотрим следующее выражение:
Z= 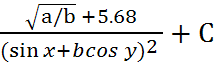
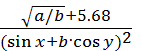
1.1. Входные данные: a=114.6; b=53.47.103; x=36o; y=0.87. Выходные данные: Z.
Для удобства вычислений введем вспомогательные переменные:
x1 — радианная мера аргумента х, заданного в градусах,
z1 — числитель дроби, z2 — знаменатель дроби.
1.2. Нарисуйте блок – схему с соответствующими пояснениями (рис. 1.1).
Дата добавления: 2014-12-09 ; просмотров: 754 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник
Урок 4. Блок-схема
Итак, опустив долгие и нудные восхваления Паскаля, которые так любят публиковать в своих статьях редакторы многих сайтов, приступим непосредственно к самому основному – к программированию.
В школах, как правило, изучение Паскаля начинают с решения простейших задач путем составления различных алгоритмов или блок-схем, которое многие так часто игнорируют, считая никому не нужной ерундой. А зря. Я, как и любой другой человек, хоть немного соображающий в программировании (не важно где – в Паскале, Си, Дельфи), могу уверить Вас – умение правильно и быстро составлять схемы является фундаментом, основой программирования.
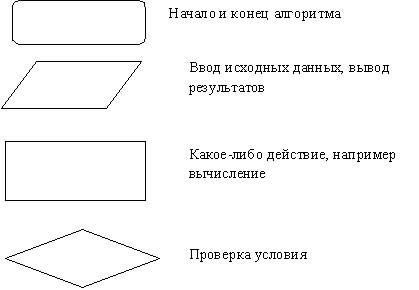
Блок-схема — графическое представление алгоритма. Она состоит из функциональных блоков, которые выполняют различные назначения (ввод/вывод, начало/конец, вызов функции и т.д.).
Существует несколько основных видов блоков, которые нетрудно запомнить:
Сегодняшний урок я решила посвятить не только изучению блок-схем, но также и изучению линейных алгоритмов. Как Вы помните, линейный алгоритм — наипростейший вид алгоритма. Его главная особенность в том, что он не содержит никаких особенностей. Как раз это и делает работу с ним простой и приятной.
Задача №1: «Рассчитать площадь и периметр прямоугольника по двум известным сторонам».
Данная задача не должна представлять особой трудности, так как построена она на хорошо известных всем нам формулах расчета площади и периметра прямоугольника, поэтому зацикливаться на выведении этих формул мы не будем.
Составим алгоритм решения подобных задач:
1) Прочитать задачу.
2) Выписать известные и неизвестные нам переменные в «дано». (В задаче №1 к известным переменным относятся стороны: a, b ;к неизвестным — площадь S и периметр P)
3) Вспомнить либо составить необходимые формулы. (У нас: S=a*b; P=2*(a+b))
4) Составить блок-схему.
5) Записать решение на языке программирования Pascal.
Запишем условие в более кратком виде.
Структура программы, решающей данную задачу, тоже проста:
- 1) Описание переменных;
- 2) Ввод значений сторон прямоугольника;
- 3) Расчет площади прямоугольника;
- 4) Расчет периметра прямоугольника;
- 5) Вывод значений площади и периметра;
- 6) Конец.
Задача №2: Скорость первого автомобиля — V1 км/ч, второго – V2 км/ч, расстояние между ними S км. Какое расстояние будет между ними через T часов, если автомобили движутся в разные стороны? Значения V1, V2, T и S задаются с клавиатуры.
Решение осуществляем, опять же, следуя алгоритму. Прочитав текст, мы переходим к следующему пункту. Как и во всех физических или математических задачах, это запись условий задачи:
Далее идет самая главная и в то же время самая интересная часть нашего решения – составление нужных нам формул. Как правило, на начальных стадиях обучения все необходимые формулы хорошо нам известны и взяты из других технических дисциплин (например, на нахождение площади различных фигур, на нахождение скорости, расстояния и т.п.).
Формула, используемая для решения нашей задачи, выглядит следующим образом:
Следующий пункт алгоритма – блок-схема:

А также решение, записанное в Pascal :
Вам может показаться, что две эти программы правильны, но это не так. Ведь сторона треугольника может быть 4.5, а не 4, а скорость машины не обязательно круглое число! А Integer — это только целые числа. Поэтому при попытке написать во второй программе другие числа выскакивает ошибка:

Чтобы решить эту проблему вам надо вспомнить какой тип в Pascal отвечает за нецелые числа. В этом уроке мы рассматривали основные типы. Итак, это вещественный тип — Real. Вот, как выглядит исправленная программа:
Как видите, эта статья полезна для прочтения как новичкам, так и уже более опытными пользователям Pascal, так как составление блок-схем не только очень простое и быстрое, но и весьма увлекательное занятие.
Здесь понятней чем в школе.
мля… прикиньте, я узнал про этот сайт только ПОСЛЕ того как сделал программу с условием, узнавая все в инструкции
Ребята , вопрос на засыпку, как заставить «,» (введенную пользователем в числе) заменить на «.» внутри программы, что бы не вылетало юхни с ошибкой.
Взять строку введенную пользователем, заменить «,» на «.».
Если совсем гуглить не умеете, то вам сюда — http://www.cyberforum.ru/pascal/thread190664.html
>> скорость машины не обязательно круглое число!
Нет такого понятия, как «круглое число».
Обе ваши блок-схемы не соответствуют ГОСТу (сдать такие на курсовой проект не получится). ГОСТ определяет блоки начала и конца, как «прямоугольник со скругленными краями», а не «скругленными углами».
>> умение правильно и быстро составлять схемы является фундаментом, основой программирования.
Большинство программистов так не считает. Кроме того, попробуйте поспрашивать у программистов «когда они последний раз составляли блок-схему?» — окажется что в ВУЗе (когда с них зачем-то сдирали знание ГОСТа).
>> так как составление блок-схем не только очень простое и быстрое, но и весьма увлекательное занятие.
Очень сложное, долгое и бесполезное занятие. Для хоть сколько-нибудь большой программы (в тысячу строк хотя бы, как курсак) блок-схемы будут огромные и их будут десятки. А что делать если они перестают соответствовать коду? — вот даже в вашей первой задаче надо будет добавить проверку, что юзер не ввел отрицательные значения сторон, что делать? — исправления кода займут 1 минуту, а исправление блок-схем 10 минут, и зачем тогда этим заниматься?
Программист не должен писать блок-схемы (он их должен читать и понимать и при необходимости исправлять). Блок-схемы это графический язык общения, который понимает как программист, так и не программист. Чтобы пользователь не общался с программистом своими «хотелками», типа я хочу, чтобы вот это правильно считалось, и это число складывалось с этим, а потом выводилось сюда (или вообще говорил — хочу что бы работало), а рисовал все в виде блок-схем с четким алгоритмом. Тогда по идее у программиста будет понимание того, что от него хотят (и он через пять минут не забудет все что ему сказали). Либо, когда общаются два программиста пишущих на разных языках программирования (LISP и Java) и одному нужно объяснить как работает его код, что бы другой переписал его на другом языке.
Как объяснить преподавателю как работает программа, если преподаватель не знает языка программирования на котором написана ваша программа? Или как преподавателю объяснить алгоритм задачи студентам пишущим и реализующим этот алгоритм или программу на разных языках программирования? Нужен какой-то универсальный язык общения и обычно это просто текст «что нужно сделать» на русском языке, а не намного облегчающая жизнь программиста блок-схема.
Вам могут сказать — сделай модуль авторизации (ты же знаешь как, ну как всегда и как везде), а могут нарисовать блок-схему модуля авторизации с учетом всех пожеланий, типа того, что пароль должен содержать не менее 6 символов и что нужно делать в противном случае т.д. То есть блок схему должен уметь рисовать тот кто ставит задачу, а не программист. Либо программист (архитектор либо менеджер проекта), который ставит задачу другим программистам.
Вы слишком придирчивы, серьезно (я говорю про последние два пункта). Понятно, что статья (как почти и весь сайт) написана почти только для школьников, которым об этом твердят в школе. Здесь же им просто объясняют те вещи, которые они на учебе недопоняли
Блок схемы всей программы могут не понадобиться. Это же тонны бумаги и много времени. И да, они устаревают и актуализировать их трудоёмко.
Но при обсуждении новых вариантов решения задачи с другими программистами удобно оперировать блоками с криво-косо нарисованными краями и линиями. Начертил на бумаге или доске и все понятно.
На практике я встречал фотографии доски с блок-схемами, прикреплённые к задачам в Jira.
Не по ГОСТу 🙂
Спасибо, теперь я напишу программу, которая делает код по блок схеме и наоборот
program Logarifm;
Var
X,y,z:real;
function Lgrfm(A,B:Real):Real;
var
Osn:Real;
begin
Osn:=ln(A)/ln(B);
Lgrfm:=Osn;
end;
begin
Write(‘Введите X = ‘);
ReadLn(X);
Write(‘Введите Y = ‘);
ReadLn(Y);
Z:=Lgrfm(X,2)+Lgrfm(Y,3);
WriteLn(‘Z = ‘,Z:10:3);
ReadLn;
end.
Отличный сайт, мне все нравится все понятно и четко, нашел нужные программы.
В блок-схемах начало и конец алгоритма обозначаются не прямоугольником со скруглёнными краями, а овалом!
Ребята, что сделали сайт молодцы)) Оч полезная инфа, что нужно поправить, чтобы сайт стал еще лучше:
1) мне не хватает структуры уроков порядковой (или хотябы под уроками чтобы была ссылка на следующий), поэтому приходится на другие уроки искать ссылки по сайту и в контексте уроков;
2)нет описания функций используемых в примерах (по крайней мере, возможно по причине отсутствия структуры, я их не нашел), поэтому беру на сторонних ресурсах описания таких функций как dec() inc() sqr() odd().
А вообще как я понял сайт составлялся школьниками «на коленках», поэтому я не придираюсь, а просто говорю им спасибо за их труд. Желаю успехов.
Источник
Как составить блок схему арифметического вычисления
1. Придумать имена переменным и заполнить таблицу
среднее арифметическое чисел
2. Определить формулы для решения
3. Определить тип переменных
В наших задачах все входные переменные — целые.
Тип выходных и промежуточных переменных зависят от выражения, по которому вычисляется выражение.
Тип переменной будет вещественной (дробной), если:
— в выражении используется деление или квадратный корень,
— в выражении участвует вещественная переменная.
В нашем случае переменная s будет вещественная, т.к. в выражении s = (x + y)/2 используется деление.
4. Составить блок-схему алгоритма
3) Дальше в условии задачи: » Вычислить среднее арифметическое чисел «. Для вычисления используем блок вычисления, в котором записываем формулу для вычисления среднего арифметического » s = (x + y)/2″ .
4) Далее, по условию задачи идет фраза: » Если первое число больше среднего арифметического «. Слово «если» означает, что надо использовать блок условия (ромб), а в нем написать с помощью математических знаков «Первое число (буква x) больше (знак >) среднего арифметического (буква s)», получим «x > s».
5) Условие может быть в двух вариантах: полная форма, когда присутствуют обе ветки: «да» и «нет», и краткая форма, когда действия производятся только по ветке «да», а ветка «нет» — пустая. В условии нашей задачи нет фразы «Иначе», значит надо использовать краткую форму разветвления.
6) В условии задачи фраза » то уменьшить его на 5 » означает, что по ветке «Да» надо использовать блок вычисления, в котором запишем формулу: первое число (буква x) уменьшить на 5 и присвоить этому же числу, т.е.»x=x-5″.
7) По условию задачи п осле разветвления требуется » Выдать на экран среднее арифметическое «. И спользуем блок вывода данных, в котором напишем букву s, в которой мы сохранили среднее арифметическое.
8) Аналогично оформим » Выдать числа » с помощью блоков вывода, впишем в блоке имена переменных x и y.
9) Окончание алгоритма оформим с помощью блока окончания.
5. Составить тестовую таблицу для проверки работы алгоритма
Сначала заполним первую колонку таблицы: выпишем все действия из блок-схемы, кроме вывода на экран.
Источник
ОАиП | БФЭК
Учебное пособие
Составление блок-схем алгоритмов
Блок-схемы используются для визуального представления алгоритмов.
Определение:
Алгоритм — это последовательность шагов, ведущая к решению задачи
Определение:
Блок-схема — это схематическое изображение, иллюстрирующее последовательность операторов, которые необходимо выполнить для достижения результата
Инструкции изображаются, используя специальные символы. Символы связываются между собой стрелками, для указания порядка выполнения.
Блок-схемы широко используются при написании программ, так как они:
- Гораздо проще для понимания, чем запись в виде команд.
- Упрощают процесс отладки.
- Позволяют составить эффективную программную документацию.
- Облегчают процесс демонстрации и обсуждения программы.
Блоки, из которых составляются блок-схемы, представлены на Рисунке 1.
Рассмотрим работу с блок-схемами на примере. Для этого нарисуем блок-схему программы нахождения суммы двух чисел:
Блок-схема, показанная на Рисунке 2, иллюстрирует линейную логику. Здесь нет повторений и ветвления.
Способность сравнивать значения и исполнять, в зависимости от полученного результата, различные участки программы превращает компьютер из большого калькулятора в мощное средство решения различных практических задач. Операторы выбора применяются для:
- Сравнения данных
- Выбора одного из альтернативных путей решения задачи.
Например, при снятии денег с банковского счета производится сравнение снимаемой суммы с суммой на счете. Если снимаемая сумма меньше, то заказ выполняется. В противном случае происходит отказ от обслуживания.
Определение:
Ветвление — это процесс выбора из двух, или более альтернативных путей вычисления. Рассмотрим ветвление на следующих примерах:
Пример 1. Посмотрим на то, как будет выглядеть блок-схема алгоритма проверки чисел на четность:
- Ветвление используется в том случае, когда необходимо разделить поток вычислений на два и более альтернативных варианта. Основанием для выбора маршрута является результат проверки истинности условия ветвления.
Пример 2. Рассмотрим блок-схему алгоритма, определяющего максимальное из 3-х чисел (см. рис. 4):
Как мы видим, ветвление производится, когда нам необходимо выбрать дальнейший маршрут в зависимости от истинности некоего условия, называемого также условием ветвления.
Основные типы блок-схем, использующих ветвление, представлены на Рисунке 5:
На Рисунке 5(а) представлена неполная конструкция условного ветвления. Здесь, в зависимости от выбранного маршрута движения, выполняется один или несколько вычислительных шагов, или происходит дальнейшее движение без вычислений, до момента слияния маршрутов.
На Рисунке 5(b) представлен полный вариант условного ветвления. Здесь, в зависимости от выбранного маршрута движения, выполняется одна или другая последовательность вычислений, после чего маршруты вновь сливаются.
Определение:
Цикл — это многократно выполняемый участок алгоритма.
Тело цикла-это последовательность выполняемых в цикле операторов.
Итерация — однократное выполнение тела цикла.
- С фиксированным числом итераций
- С переменным числом итераций
Рассмотрим различия между этими двумя типами на следующих примерах:
Пример 3. Пусть есть данные о расходах за каждый месяц года. Блок-схема алгоритма подсчитывающего расходы за год будет иметь вид:
Рисунок 6 иллюстрирует цикл с фиксированным числом итераций — число месяцев в году известно и последовательность вычислений не может быть повторена более 12 раз.
Мы читаем расходы за один месяц и добавляем их к общему результату. После этого номер месяца сравнивается с 12.
Если номер месяца равен 12, то цикл завершается, и выводятся данные о расходах за год. В противном случае цикл повторяется для следующего месяца.
Пример 4. Пусть есть информация о каждом жителе города (имя, возраст, пол и т.д.). Необходимо составить список жителей старше 50 лет. Блок-схема соответствующего алгоритма будет иметь вид:
Рисунок 7 иллюстрирует цикл с переменным числом итераций — нам заранее неизвестно число жителей города старше 50 лет. Этот цикл выполняется до тех пор, пока есть еще неучтенные люди. Цикл представляется в виде следующей элементарной блок-схемы:
- В цикле с фиксированным числом итераций количество итераций известно заранее. Вычисления, производящиеся внутри цикла, не оказывают никакого влияния на число итераций.
- Цикл с переменным числом итераций выполняется до тех пор, пока не будет выполнено некоторое условие. Количество итераций в таком цикле может варьироваться.
- Циклы обычно выполняются до тех пор, пока какое-либо условие не примет значение true или false.
РАЗДЕЛЕНИЕ БЛОК-СХЕМ НА ЧАСТИ
При работе с блок-схемами мы часто сталкиваемся со следующими проблемами:
- Блок-схема может не поместиться на одной странице.
- Может оказаться сложным связать все элементы блок-схемы друг с другом непосредственно.
Для решения этих проблем блок-схемы обычно разбивают на отдельные части, для состыковки которых используются элементы- соединители.
Соединительный элемент имеет свой собственный, уникальный номер и состоит из двух частей. Эти части изображаются в местах разрыва соединительных линий. Для определения принадлежности частей соединительному элементу, номер элемента записывается на каждой из частей.
Например, разбив на 2 части блок-схему, изображенную на Рисунке 2 мы получим:
- Соединители вставляются в местах разрыва блок-схемы. Расположение каждого объединения указывается с помощью уникального номера.
- В блок-схеме может быть только одна вершина Начало и только одна вершина Конец.
- Используйте машинно-независимые элементы.
- Не обязательно представлять в блок-схеме каждый шаг программы. Можно ограничиться наиболее важными блоками.
- Желательно использовать наглядные названия переменных и блоков.
- Помните, программа должна быть написана так, чтобы любой другой программист смог бы легко понять ее.
МЕТОД ПРОГОНКИ
Метод прогонки используется для проверки правильности работы программы без использования компьютера. Для этого составляется специальная таблица, в которую записываются значения переменных по шагам. Этот метод позволяет эффективно находить и устранять логические ошибки. Проиллюстрируем этот метод следующим примером:
ТАБЛИЦА ПОШАГОВОГО ПРОГОНА
| X | Y | М | |
| Начальные значения | 10 | 5 | 0 |
| после шага 5 | 10 | 5 | 65 |
| после шага 6 | 10 | 9 | 65 |
| после шага 7 | 10 | 9 | 74 |
Таким образом, на 8-м шаге на экран будет выведено: 10, 9 и 74.
Источник
Примеры составления блок-схемы алгоритма
Пример 1.
Составить схему алгоритма вычисления
значения :
Для
начала для построения блок –схемы
алгоритма опишем последовательность
действий, необходимых для решения данной
задачи:
-
начало
-
ввод
чисел a,b -
вычисление
х -
вычисление
z -
вывод
результата -
конец
Исходя из этого
составляем блок-схему алгоритма согласно
ГОСТ, используя соответствующие блоки.
Пример
2. Составить
схему алгоритма вычисления значения:
x=a+b
при a>b,
x=a*b,
при a<=b.
Пример 3. Составить схему алгоритма вычисления значения:
Для начала для
построения блок –схемы алгоритма опишем
последовательность действий, необходимых
для решения данной задачи:
Исходя из этого
составляем блок-схему алгоритма согласно
ГОСТ, используя соответствующие блоки.
Порядок выполнения работы
-
Изучить
теоретические сведения по теме
”Построение блок-схем алгоритмов”. -
Получить
у преподавателя индивидуальное задание
и нарисовать блок-схему алгоритма
согласно заданному варианту. -
Ответить
на контрольные вопросы. -
Сформулировать
выводы.
Контрольные вопросы
-
Основные
этапы решения задач на компьютере. -
Свойства алгоритма.
Типы вычислительных процессов. -
Блок схемы. Понятие
и правила построения. -
Примеры построения
блок-схем алгоритмов.
Задание
№1: Разработайте
алгоритм и представьте его в графическом
виде (блок-схемы) для следующих задач:
Задание 1.1
Вычислить значение выражения при
заданных исходных данных.
Указание.
Для упрощения выражений введите
промежуточные переменные.
Сравнить полученное
значение с указанным правильным
результатом.
1.
При
x = 14.26;
y = – 1.22;
z = 3.5ответs
= 0.749155.
2.
При
x = –4.5; y = 0.75;
z = –0.845ответs
= –3.23765.
3.
При
x = 3.74;
y=–0.825; z = 0.16ответs
= 1.05534.
4.
При
x = 0.4;
y = –0.875; z = –0.475ответ
s = 1.98727.
5.
При
x = –15.246; y = 4.642;
z = 21 ответ
s = –182.038.
6.
При
x = 16.55;
y = –2.75; z = 0.15
ответ s
= –40.6307.
7.
При
x = 0.1722; y = 6.33; z = 3.25ответ
s = –205.306.
8.
При
x = –2.235;
y = 2.23; z = 15.221
ответ s
= 39.3741.
9.
При
x = 1.825;
y = 18.225; z = –3.298ответ
s = 1.21308.
10.
При
x = 3.981;
y = –1.625;
z = 0.512
ответ s
= 1.26185.
11.
При
x = 6.251; y = 0.827; z = 25.001
ответ
s = 0.712122.
12.
При
x
= 3.251; y
= 0.325; z
= 0.466
ответ s
= 4.23655.
13.

При
x
= 17.421; y
= 10.365;
z
= 0.828
ответ s
= 0.330564.
14.

При
x
= 12.3;
y
= 15.4; z
= 0.252
ответ s
= 82.8256.
15.
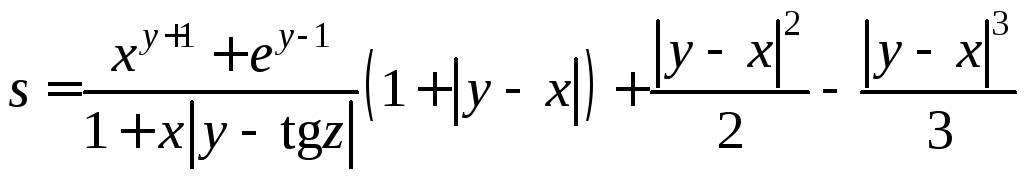
При
x
= 2.444; y
= 0.869;
z
= –0.13
ответ s
= –0.498707.
Задание
1.2 Вычислить
значение выражения при заданных исходных
данных. Предусмотреть вывод информации
о выбранной ветви вычислений.
|
1. |
|
2. |
|
|
3. |
|
4. |
|
|
5. |
|
6. |
|
|
7. |
|
8. |
|
|
9. |
|
10. |
|
|
11. |
|
12. |
|
|
13. |
|
14. |
|
|
15. |
|
Задание
1.3 Вывести
на экран таблицу значений функции Y(x)
и ее разложения в ряд S(x)
для x,
изменяющегося от a
до b
с шагом h
= (b –
a)/10,
табл. 1.
Таблица 1.
|
№ |
a |
b |
S(x) |
n |
Y(x) |
|
1 |
0.1 |
1 |
|
160 |
|
|
2 |
0.1 |
1 |
|
100 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
3 |
0.1 |
1 |
|
120 |
|
|
4 |
0.1 |
1 |
|
80 |
|
|
5 |
0.1 |
1 |
|
140 |
|
|
6 |
0.1 |
1 |
|
80 |
|
|
7 |
0.1 |
1 |
|
120 |
|
|
8 |
0.1 |
1 |
|
100 |
|
|
9 |
0.1 |
1 |
|
140 |
|
|
10 |
0.1 |
0.5 |
|
150 |
|
|
11 |
0.1 |
1 |
|
100 |
|
|
12 |
0.1 |
1 |
|
80 |
|
|
13 |
–2 |
–0.1 |
|
160 |
|
|
14 |
0.2 |
0.8 |
|
120 |
|
|
15 |
0.1 |
0.8 |
|
180 |
|
Задание
№2:
Решите представленные ниже задачи,
указав номер задачи и полученный ответ.
Задача
2.1
Определите
результаты работы блок-схемы алгоритма
при
Задача
2.2
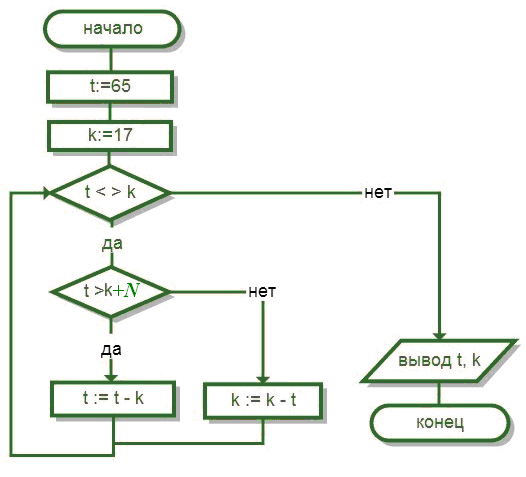
Какие
значения примут t и k в
результате работы фрагмента блок-схемы
алгоритма?
Задача
2.3.
Определите
значения
элементов
массива А2,
А4,
А6,
А8
при N=8
в результате работы фрагмента алгоритма
Схема — это абстракция какого-либо процесса или системы, наглядно отображающая наиболее значимые части. Схемы широко применяются с древних времен до настоящего времени — чертежи древних пирамид, карты земель, принципиальные электрические схемы. Очевидно, древние мореплаватели хотели обмениваться картами и поэтому выработали единую систему обозначений и правил их выполнения. Аналогичные соглашения выработаны для изображения схем-алгоритмов и закреплены ГОСТ и международными стандартами.
На территории Российской Федерации действует единая система программной документации (ЕСПД), частью которой является Государственный стандарт — ГОСТ 19.701-90 «Схемы алгоритмов программ, данных и систем» [1]. Не смотря на то, что описанные в стандарте обозначения могут использоваться для изображения схем ресурсов системы, схем взаимодействия программ и т.п., в настоящей статье описана лишь разработка схем алгоритмов программ.
Рассматриваемый ГОСТ практически полностью соответствует международному стандарту ISO 5807:1985.
Содержание:
- Элементы блок-схем алгоритмов
- Примеры блок-схем
- Нужны ли блок-схемы? Альтернативы
Элементы блок-схем алгоритмов
Блок-схема представляет собой совокупность символов, соответствующих этапам работы алгоритма и соединяющих их линий. Пунктирная линия используется для соединения символа с комментарием. Сплошная линия отражает зависимости по управлению между символами и может снабжаться стрелкой. Стрелку можно не указывать при направлении дуги слева направо и сверху вниз. Согласно п. 4.2.4, линии должны подходить к символу слева, либо сверху, а исходить снизу, либо справа.
Есть и другие типы линий, используемые, например, для изображения блок-схем параллельных алгоритмов, но в текущей статье они, как и ряд специфических символов, не рассматриваются. Рассмотрены лишь основные символы, которых всегда достаточно студентам.
 |
Терминатором начинается и заканчивается любая функция. Тип возвращаемого значения и аргументов функции обычно указывается в комментариях к блоку терминатора. |
 |
В ГОСТ определено множество символов ввода/вывода, например вывод на магнитные ленты, дисплеи и т.п. Если источник данных не принципиален, обычно используется символ параллелограмма. Подробности ввода/вывода могут быть указаны в комментариях. |
 |
В блоке операций обычно размещают одно или несколько (ГОСТ не запрещает) операций присваивания, не требующих вызова внешних функций. |
 |
Блок в виде ромба имеет один вход и несколько подписанных выходов. В случае, если блок имеет 2 выхода (соответствует оператору ветвления), на них подписывается результат сравнения — «да/нет». Если из блока выходит большее число линий (оператор выбора), внутри него записывается имя переменной, а на выходящих дугах — значения этой переменной. |
 |
Вызов внешних процедур и функций помещается в прямоугольник с дополнительными вертикальными линиями. |
 |
Символы начала и конца цикла содержат имя и условие. Условие может отсутствовать в одном из символов пары. Расположение условия, определяет тип оператора, соответствующего символам на языке высокого уровня — оператор с предусловием (while) или постусловием (do … while). |
 |
Символ «подготовка данных» в произвольной форме (в ГОСТ нет ни пояснений, ни примеров), задает входные значения. Используется обычно для задания циклов со счетчиком. |
 |
В случае, если блок-схема не умещается на лист, используется символ соединителя, отражающий переход потока управления между листами. Символ может использоваться и на одном листе, если по каким-либо причинам тянуть линию не удобно. |
 |
Комментарий может быть соединен как с одним блоком, так и группой. Группа блоков выделяется на схеме пунктирной линией. |
Примеры блок-схем
В качестве примеров, построены блок-схемы очень простых алгоритмов сортировки, при этом акцент сделан на различные реализации циклов, т.к. у студенты делают наибольшее число ошибок именно в этой части.
Сортировка вставками
Массив в алгоритме сортировки вставками разделяется на отсортированную и еще не обработанную части. Изначально отсортированная часть состоит из одного элемента, и постепенно увеличивается.
На каждом шаге алгоритма выбирается первый элемент необработанной части массива и вставляется в отсортированную так, чтобы в ней сохранялся требуемый порядок следования элементов. Вставка может выполняться как в конец массива, так и в середину. При вставке в середину необходимо сдвинуть все элементы, расположенные «правее» позиции вставки на один элемент вправо. В алгоритме используется два цикла — в первом выбираются элементы необработанной части, а во втором осуществляется вставка.
В приведенной блок-схеме для организации цикла используется символ ветвления. В главном цикле (i < n) перебираются элементы необработанной части массива. Если все элементы обработаны — алгоритм завершает работу, в противном случае выполняется поиск позиции для вставки i-того элемента. Искомая позиция будет сохранена в переменной j в результате выполнения внутреннего цикла, осуществляющем сдвиг элементов до тех пор, пока не будет найден элемент, значение которого меньше i-того.
На блок-схеме показано каким образом может использоваться символ перехода — его можно использовать не только для соединения частей схем, размещенных на разных листах, но и для сокращения количества линий. В ряде случаев это позволяет избежать пересечения линий и упрощает восприятие алгоритма.
Сортировка пузырьком
Сортировка пузырьком, как и сортировка вставками, использует два цикла. Во вложенном цикле выполняется попарное сравнение элементов и, в случае нарушения порядка их следования, перестановка. В результате выполнения одной итерации внутреннего цикла, максимальный элемент гарантированно будет смещен в конец массива. Внешний цикл выполняется до тех пор, пока весь массив не будет отсортирован.
На блок-схеме показано использование символов начала и конца цикла. Условие внешнего цикла (А) проверяется в конце (с постусловием), он работает до тех пор, пока переменная hasSwapped имеет значение true. Внутренний цикл использует предусловие для перебора пар сравниваемых элементов. В случае, если элементы расположены в неправильном порядке, выполняется их перестановка посредством вызова внешней процедуры (swap). Для того, чтобы было понятно назначение внешней процедуры и порядок следования ее аргументов, необходимо писать комментарии. В случае, если функция возвращает значение, комментарий может быть написан к символу терминатору конца.
Сортировка выбором
В сортировке выбором массив разделяется на отсортированную и необработанную части. Изначально отсортированная часть пустая, но постепенно она увеличивается. Алгоритм производит поиск минимального элемента необработанной части и меняет его местами с первым элементом той же части, после чего считается, что первый элемент обработан (отсортированная часть увеличивается).
На блок-схеме приведен пример использования блока «подготовка», а также показано, что в ряде случаев можно описывать алгоритм более «укрупнённо» (не вдаваясь в детали). К сортировке выбором не имеют отношения детали реализации поиска индекса минимального элемента массива, поэтому они могут быть описаны символом вызова внешней процедуры. Если блок-схема алгоритма внешней процедуры отсутствует, не помешает написать к символу вызова комментарий, исключением могут быть функции с говорящими названиями типа swap, sort, … .
На блоге можно найти другие примеры блок-схем:
- блок-схема проверки правильности расстановки скобок арифметического выражения [2];
- блок-схемы алгоритмов быстрой сортировки и сортировки слиянием [3].
Часть студентов традиционно пытается рисовать блок-схемы в Microsoft Word, но это оказывается сложно и не удобно. Например, в MS Word нет стандартного блока для терминатора начала и конца алгоритма (прямоугольник со скругленными краями, а не овал). Наиболее удобными, на мой взгляд, являются утилиты MS Visio и yEd [5], обе они позволяют гораздо больше, чем строить блок-схемы (например рисовать диаграммы UML), но первая является платной и работает только под Windows, вторая бесплатная и кроссплатфомренная. Все блок-схемы в этой статье выполнены с использованием yEd.
Частные конторы никакие блок-схемы не используют, в книжках по алгоритмам [6] вместо них применяют словесное описание (псевдокод) как более краткую форму. Возможно блок-схемы применяют на государственных предприятиях, которые должны оформлять документацию согласно требованиям ЕСПД, но есть сомнения — даже для регистрации программы в Государственном реестре программ для ЭВМ никаких блок-схем не требуется.
Тем не менее, рисовать блок-схемы заставляют школьников (примеры из учебников ГОСТ не соответствуют) — выносят вопросы на государственные экзамены (ГИА и ЕГЭ), студентов — перед защитой диплом сдается на нормоконтроль, где проверяется соответствие схем стандартам.
Разработка блок-схем выполняется на этапах проектирования и документирования, согласно каскадной модели разработки ПО, которая сейчас почти не применяется, т.к. сопровождается большими рисками, связанными с ошибками на этапах проектирования.
Появляются подозрения, что система образования прогнила и отстала лет на 20, однако аналогичная проблема наблюдается и за рубежом. Международный стандарт ISO 5807:1985 мало чем отличается от ГОСТ 19.701-90, более нового стандарта за рубежом нет. Там же производится множество программ для выполнения этих самых схем — Dia, MS Visio, yEd, …, а значит списывать их не собираются. Вместо блок-схем иногда применяют диаграммы деятельности UML [6], однако удобнее они оказываются, разве что при изображении параллельных алгоритмов.
Периодически поднимается вопрос о том, что ни блок-схемы, ни UML не нужны, да и документация тоже не нужна. Об этом твердят программисты, придерживающиеся методологии экстремального программирования (XP) [7], ходя даже в их кругу нет единого мнения.
В ряде случаев, программирование невозможно без рисования блок-схем, т.к. это один процесс — существуют визуальные языки программирования, такие как ДРАКОН [8], кроме того, блок-схемы используются для верификации алгоритмов (формального доказательства их корректности) методом индуктивных утверждений Флойда [9].
В общем, единого мнения нет. Очевидно, есть области, в которых без чего-то типа блок-схем обойтись нельзя, но более гибкой альтернативы нет. Для формальной верификации необходимо рисовать подробные блок-схемы, но для проектирования и документирования такие схемы не нужны — я считаю разумным утверждение экстремальных программистов о том, что нужно рисовать лишь те схемы, которые помогают в работе и не требуют больших усилий для поддержания в актуальном состоянии [10].
Список использованных источников:
- ГОСТ 19.701–90 (ИСО 5807–85) «Единая система программной документации».
- Алгоритм. Свойства алгоритма https://pro-prof.com/archives/578
- Алгоритмы сортировки слиянием и быстрой сортировки https://pro-prof.com/archives/813
- yEd Graph Editor https://www.yworks.com/products/yed
- Книги: алгоритмы https://pro-prof.com/books-algorithms
- Рамбо Дж., Якобсон А., Буч Г. UML: специальный справочник. -СПб.: Питер, 2002. -656 с.
- Кент Бек Экстремальное программирование: разработка через тестирование – СПб.: Питер – 2003
- Визуальный язык ДРАКОН https://drakon.su/
- Шилов Н.В. Верификация шаблонов алгоритмов для метода отката и метода ветвей и границ. Моделирование и анализ информационных систем, ISSN 1818 – 1015, т.18, №4, 2011
- Брукс Ф., Мифический человеко — месяц или как создаются программные системы. СПб. Символ Плюс, 1999 — 304 с. ил.
Каждый человек на протяжении своей жизни решает множество задач разной сложности. Но даже самые простые из задач выполняются последовательно, то есть за несколько шагов. Эту последовательность можно назвать алгоритмом. Последовательности бывают разные, но начинать их изучение лучше всего с линейных.
Прежде чем приступить к рассмотрению основной темы статьи, следует сделать краткое отступление и сказать несколько слов про алгоритмический язык.
Алгоритмический язык
Представьте, что человеку, работающему за компьютером, поставлена некая вычислительная задача. В языке программирования решение этой задачи выполняется с помощью алгоритмизации. Решение предполагает: — разбиение на этапы;
— разработку алгоритма;
— составление программы решения на алгоритмическом языке;
— ввод данных;
— отладку программы (возможны ошибки — их надо исправить);
— выполнение на ПК;
— анализ результатов.
Алгоритмический язык является средством описания алгоритмов, а уже алгоритм, в свою очередь, представляет собой чёткое описание определённой последовательности действий, направленных на решение необходимой задачи.
Свойства алгоритма
Их несколько:
— конечность. Любой алгоритм должен быть завершённым, а окончание наступает после выполнения определённого числа шагов;
— однозначность, понятность. Не допускается разных толкований, неопределённости и двусмысленности — всё должно быть чётко и ясно, а также понятно исполнителю — и правила выполнения действий линейного алгоритма, и сами действия;
— результативность. Итог работы — результат, полученный за конечное число шагов;
— универсальность, массовость. Качественный алгоритм способен решать не одну задачу, а целый класс задач, имеющих схожую постановку/структуру.
Линейная структура
Любой алгоритм составляется из ряда базовых структур. Простейшей базовой структурой является следование — структура с линейными характеристиками. Из этого можно сформулировать определение.
Линейный алгоритм — это алгоритм, образуемый командами, которые выполняются однократно и именно в той последовательности, в которой записаны. Линейная структура, по сути, проста. Записать её можно как в текстовой, так и в графической форме.
Представим, что у нас стоит задача пропылесосить ковёр в комнате. В текстовой форме алгоритм будет следующим:
— принести пылесос к месту уборки;
— включить;
— пропылесосить;
— выключить;
— унести пылесос.
И каждый раз, когда нам надо будет пылесосить, мы будем выполнять один и тот же алгоритм.
Теперь поговорим про графическую форму представления.
Блок-схема
Для изображения алгоритма графически используют блок-схемы. Они представляют собой геометрические фигуры (блоки), соединённые стрелками. Стрелки показывают связь между этапами и последовательность их выполнения. Каждый блок сопровождается надписью.
Рассмотрим фигуры, которые используются при визуализации типичной линейной последовательности.
Блок начала-конца:
Блок ввода-вывода данных (отображает список вводимых и выводимых переменных):
Арифметический блок (отображает арифметическую операцию/группу операций):
Условный блок (позволяет описать условие). Алгоритмы с таким блоком используются при графической визуализации алгоритмов с ветвлением:
Условного блока нет в классическом линейном алгоритме, так как в нём, как уже было сказано ранее, все операции выполняются последовательно, то есть одна за другой. В линейном алгоритме размещение блоков выглядит следующим образом:
А вот, как решается задача по нахождению площади треугольника по формуле Герона. Здесь a, b, c – это длины сторон, S – площадь треугольника, P – периметр.
Следует обратить внимание, что запись «=» — это не математическое равенство, а операция присваивания. В результате этой операции переменная, стоящая слева от оператора, получает значение, которое указано справа. Значение не обязательно должно быть сразу определено (a = 3) — оно может вычисляться посредством выражения (a = b + z), где b = 1, a z = 2.
Примеры линейных алгоритмов
Если рассмотреть примеры решения на языке Pascal (именно этот язык до сих пор используется для изучения основ алгоритмизации и программирования), то можно увидеть следующую картину:
И, соответственно, блок-схема программы линейной структуры будет выглядеть следующим образом:
Как составить программу линейной структуры?
Порядок следующий: — определите, что именно относится к исходным данными, а также каков типы/класс этих данных, выберите имена переменных; — определите, каков тип данных будет у искомого результата, выберите название переменных (переменной); — определите, какие математические формулы связывают результат и исходные данные; — если требуется наличие промежуточных данных, определите класс/типы этих данных и выберите имена; — опишите все используемые переменные; — запишите окончательный алгоритм. Он должен включать в себя ввод данных, вычисления, вывод результатов.
На этом всё, в следующий раз рассмотрим на примерах программу разветвлённой структуры. Если же вас интересует тема алгоритмизации в контексте разработки программного обеспечения, ждём вас на профессиональном курсе OTUS!
Источники:
• https://inep.sfedu.ru/wp-content/uploads/2018/05/25/lection_27.pdf;
• https://www.sites.google.com/site/415ict/textbooks/prog-9/02-linejnyj-algoritm.
Как работает пирамидальная сортировка выбором? Разберемся в этом 20 июля на открытом уроке в OTUS с Евгением Волосатовым, программистом с 20-летним опытом. Сортировка выбором — один из самых простых алгоритмов сортировки. Ее можно значительно ускорить, если использовать структуру данных «куча» для поиска максимального элемента за О(1) константное время. В результате получится алгоритм пирамидальной сортировки HeapSort. На этом открытом уроке мы расскажем идею алгоритма и наглядно продемонстрируем его работу на визуальных примерах с конкретными числами. Вебинар пройдет в рамках онлайн-курса «Алгоритмы и структуры данных» и позволит познакомиться с преподавателем.
Практическая
раборта № 1
Построение
блок-схем алгоритмов(теория)
Предпочтительнее
до записи на алгоритмическом языке представить алгоритм в виде блок-схемы. Для
построения алгоритма в виде блок-схемы необходимо знать назначении каждого из
блоков. В таблице 1. приводятся типы блоков и их назначение.
Таблица 1
|
№ |
Блок |
Назначение |
|
1 |
|
Начало блок-схемы |
|
2 |
|
Ввод |
|
3 |
|
Процесс |
|
4 |
|
условие |
|
6 |
|
Цикл |
Основные
типы алгоритмов
Алгоритмизация выступает как набор
определенных практических приёмов, особых специфических навыков рационального
мышления в рамках заданных языковых средств. Алгоритмизация вычислений
предполагает решение задачи в виде последовательности действий, т.е. решение,
представленное в виде блок-схемы. Можно выделить типичные алгоритмы. К ним
относятся: линейные алгоритмы, разветвляющиеся алгоритмы, циклические
алгоритмы.
Линейные алгоритмы
Линейный алгоритм является наиболее
простым. В нём предполагается последовательное выполнение операций. В этом
алгоритме не предусмотрены проверки условий или повторений.
Пример: Вычислить функцию z=
(х-у)/x +y2.
Составить блок-схему вычисления функции по
линейному алгоритму. Значения переменных х, у могут быть
любые, кроме нуля, вводить их с клавиатуры.
Решение: Линейный алгоритм вычисления
функции задан в виде блок-схемы на рис.1. При выполнении линейного алгоритма
значения переменных вводятся с клавиатуры, подставляются в заданную функцию,
вычисляется результат, а затем выводится результат.
Рис.1. Линейный алгоритм
Назначение блоков в схеме на
рис.1:
·
Блок 1 в схеме служит в качестве
логического начала.
·
Блок 2 соответствует вводу данных.
·
Блок 3 представляет арифметическое
действие.
·
Блок 4 выводит результат.
·
Блок 5 в схеме служит в качестве
логического завершения схемы.
Алгоритмы ветвлений
Разветвляющийся алгоритм предполагает
проверку условий для выбора решения. Соответственно в алгоритме появятся две
ветви для каждого условия.
В
примере рассматривается разветвляющийся алгоритм, где в зависимости от условия
выбирается один из возможных вариантов решений. Алгоритм представляется в виде
блок-схемы.
Пример:
При выполнении условия x>0
вычисляется функция: z=
x+
y,
иначе, а именно, когда х=0 или x<0,
вычисляется функция: z=x2+y2.
Составить
блок-схему вычисления функции по алгоритму ветвления. Значения переменных х,
у могут быть любые, вводить их с клавиатуры.
Решение:
На рис.2 представлен разветвляющийся алгоритм, где в зависимости от условия
выполнится одна из веток. В блок-схеме появился новый блок 3, который проверяет
условие задачи. Остальные блоки знакомы из линейного алгоритма.
Рис.2. Алгоритм ветвления
Пример: Найти максимальное значение
из трёх различных целых чисел, введенных с клавиатуры. Составить блок-схему
решения задачи.
Решение: Данный алгоритм
предполагает проверку условия. Для этого выбирается любая из трёх переменных и
сравнивается с другими двумя. Если она больше, то поиск максимального числа
окончен. Если условие не выполняется, то сравниваются две оставшиеся
переменные. Одна из них будет максимальной. Блок-схема к этой задаче
представлена на рис 3.
Рис. 3. Блок-схема поиска максимума
Циклические алгоритмы
Циклический алгоритм предусматривает
повторение одной операции или нескольких операций в зависимости от условия
задачи.
Из
циклических алгоритмов выделяют два типа:
1)
с заданным количеством циклов или со
счётчиком циклов;
2)
количество циклов неизвестно.
Пример:
В цикле вычислить значение функции z=x*y при условии, что одна из
переменных x
меняется в каждом цикле на единицу, а другая переменная у не
меняется и может быть любым целым числом. В результате выполнения цикла при
начальном значении переменной х=1 можно получить таблицу умножения.
Количество циклов может быть любым. Составить блок-схему решения задачи.
Решение:
В примере количество циклов задаётся. Соответственно выбирается алгоритм
циклов первого типа. Алгоритм этой задачи приводится на рис. 4.
Во
втором блоке вводятся количество циклов n и любые целые числа х,
y.
В
блок-схеме появился новый блок 3, в котором переменная i считает
количество циклов, после каждого цикла увеличиваясь на единицу, пока счётчик не
будет равен i=n. При i=n будет выполнен последний
цикл.
В
третьем блоке указывается диапазон изменения счётчика цикла (от i =1 до i=n).
В
четвёртом блоке изменяются значения переменных: z, x.
В
пятом блоке выводится результат. Четвёртый и пятый блоки повторяются в каждом
цикле.
Рис.4 . Циклический алгоритм со счётчиком
циклов
Этот
тип циклических алгоритмов предпочтителен, если дано количеством циклов.
Если количество циклов неизвестно, то
блок-схемы циклических алгоритмов могут быть представлены в виде рисунков 5, 6.
Пример:
Вычислить у=у-x
пока y>x,
если y=30,
x=4.
Подсчитать количество выполненных циклов, конечное значение переменной у.
В цикле вывести значение переменной у, количество выполненных
циклов. Составить блок-схему решения задачи.
Решение:
В примере количество циклов неизвестно. Соответственно выбирается алгоритм
циклов второго типа. Алгоритм этой задачи приводится на рис. 5.
Условие
проверяется на входе в цикл. В теле цикла выполняется два блока:
1)
у=у-х; i=i+1;
2)
вывод значений переменных i,
y.
Цикл
выполняется до тех пор, пока выполняется условие y>x. При условии
равенства этих переменных у=х или y<x цикл заканчивается.
Алгоритм,
представленный на рис.5, называется циклический алгоритм с предусловием,
так как условие проверяется в начале цикла или на входе в цикл.
Рис.5. Блок-схема
циклического алгоритма с предусловием
Во втором блоке вводятся y=30,
x=4.
В
третьем блоке проверяется условие y>x
на входе в цикл. Если условие выполняется, то переход к блоку 4, иначе на блок
6.
В
четвёртом блоке вычисляется значение переменной у, подсчитывается
количество выполненных циклов i=i+1.
В
пятом блоке выводится результат:
·
значение переменной у,
·
количество выполненных циклов i.
Пример:
Составить блок-схему примера (рисунок 5), проверяя условие выхода из цикла.
В этом примере условие задачи не меняется, и результат выведется тот же, но
блок-схема будет другой.
Решение:
В этом случае проверяется условие на выход из цикла: y<=x. При
этом условии цикл не выполняется. Условие в блок-схеме следует перенести в
конец цикла, после вывода на печать. Цикл выполняется до тех пор, пока
выполняется условие y>x.
Алгоритм,
если условие перенести в конец цикла, называется алгоритмом цикла с
постусловием. Алгоритм этой задачи приводится на рис. 6.
Во
втором блоке вводятся y=30,
x=4.
В
третьем блоке вычисляется значение переменной у, подсчитывается
количество выполненных циклов i=i+1.
В
четвёртом блоке выводится результат:
·
значение переменной у,
·
количество выполненных циклов i.
В
пятом блоке проверяется условие y<=x
на выход из цикла. Если условие выполняется, то переход к блоку 6, иначе на
блок 3 и цикл повторяется.
Рис.6 . Алгоритм цикла с
постусловием
Индивидуальные задания к работе:
1.
Найти
результат работы алгоритма:
Входные данные по вариантам
|
№ |
A |
B |
C |
D |
|
1 |
0 |
-1 |
-2 |
-3 |
|
2 |
1 |
0 |
-1 |
-2 |
|
3 |
2 |
1 |
0 |
-1 |
|
4 |
3 |
2 |
1 |
0 |
|
5 |
4 |
3 |
2 |
1 |
|
6 |
5 |
4 |
3 |
2 |
|
7 |
6 |
5 |
4 |
3 |
|
8 |
7 |
6 |
5 |
4 |
|
9 |
-3 |
7 |
6 |
5 |
|
10 |
-4 |
-3 |
7 |
6 |
|
11 |
-5 |
-4 |
-3 |
7 |
|
12 |
-6 |
-5 |
-4 |
-3 |
|
13 |
-7 |
-6 |
-5 |
-4 |
|
14 |
9 |
-7 |
-6 |
-5 |
|
15 |
8 |
7 |
-7 |
-6 |
|
16 |
5 |
5 |
8 |
-7 |
|
17 |
5 |
2 |
4 |
5 |
2. При
заданном Х условие выполнется? Написать результат вычисления и ответ попадаем в
условие или нет.
Входные данные по вариантам
|
№ |
X1 |
X1 |
|
1 |
55 |
12 |
|
2 |
85 |
13 |
|
3 |
24 |
17 |
|
4 |
65 |
15 |
|
5 |
17 |
54 |
|
6 |
15 |
67 |
|
7 |
26 |
3 |
|
8 |
27 |
21 |
|
9 |
92 |
34 |
|
10 |
12 |
23 |
|
11 |
45 |
22 |
|
12 |
66 |
45 |
|
13 |
71 |
46 |
|
14 |
13 |
76 |
|
15 |
45 |
67 |
|
16 |
53 |
35 |
|
17 |
52 |
23 |
3. Написать
результат выполнения алгоритма с указанными входными данными
Входные данные по вариантам
|
№ |
S |
|
1 |
1,5 |
|
2 |
1,8 |
|
3 |
2,4 |
|
4 |
1,6 |
|
5 |
1,7 |
|
6 |
1,3 |
|
7 |
2,6 |
|
8 |
2,37 |
|
9 |
1,92 |
|
10 |
1,12 |
|
11 |
1,45 |
|
12 |
2,66 |
|
13 |
2,71 |
|
14 |
2,13 |
|
15 |
1,45 |
|
16 |
2,53 |
|
17 |
1,52 |
4. Написать
результат выполнения алгоритма с указанными входными данными
Входные данные по вариантам
|
№ |
X |
|
1 |
-1 |
|
2 |
0 |
|
3 |
1 |
|
4 |
2 |
|
5 |
3 |
|
6 |
4 |
|
7 |
5 |
|
8 |
6 |
|
9 |
7 |
|
10 |
-3 |
|
11 |
-4 |
|
12 |
-5 |
|
13 |
-6 |
|
14 |
-7 |
|
15 |
7 |
|
16 |
5 |
|
17 |
2 |
5. Построить
блок схему к задаче(по вариантам). Указать тип алгоритма, что дано и что нужно
найти.
|
№ |
Задача |
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
|
|
14 |
|
|
15 |
|
|
16 |
|
|
17 |
|
6. Построить
блок схему к задаче(по вариантам). Указать тип алгоритма, что дано и что нужно
найти.
|
№ |
Задача |
|
1 |
Дано двузначное число. |
|
2 |
Дано двузначное число. |
|
3 |
Дано двузначное число. |
|
4 |
Дано двузначное число. |
|
5 |
Дано двузначное число. |
|
6 |
Дано трехзначное число. |
|
7 |
Дано трехзначное число. |
|
8 |
Дано трехзначное число. |
|
9 |
Дано трехзначное число. |
|
10 |
Дано трехзначное число. |
|
11 |
Дано трехзначное число. |
|
12 |
Дано трехзначное число. |
|
13 |
Дано трехзначное число. |
|
14 |
Дано трехзначное число. |
|
15 |
Дано трехзначное число, |
|
16 |
Дано натуральное число |
|
17 |
Дано натуральное число |
7. Построить
блок схему к задаче(по вариантам). Указать тип алгоритма, что дано и что нужно
найти.
|
№ |
Задача |
|
1 |
Определить максимальное |
|
2 |
Известны два |
|
3 |
Известны две скорости: |
|
4 |
Даны радиус круга и |
|
5 |
Даны объемы и массы |
|
6 |
Известны сопротивления |
|
7 |
Даны вещественные числа |
|
8 |
Известны площади круга |
|
9 |
Известны площади круга |
|
10 |
Известны площади круга |
|
11 |
Известны площади круга |
|
12 |
Дано двузначное число. |
|
13 |
Дано двузначное число. |
|
14 |
Дано двузначное число. |
|
15 |
Дано двузначное число. Определить: |
|
16 |
Дано трехзначное число. |
|
17 |
Дано трехзначное число. |
8. Построить
блок схему к задаче(по вариантам). Указать тип алгоритма, что дано и что нужно
найти.
|
№ |
Задача |
|
1 |
Одна штука некоторого |
|
2 |
Напечатать таблицу |
|
3 |
Напечатать таблицу |
|
4 |
Напечатать таблицу |
|
5 |
Считая, что Земля — |
|
6 |
. Напечатать таблицу |
|
7 |
Напечатать таблицу |
|
8 |
Напечатать |
|
9 |
Напечатать таблицу |
|
10 |
Вывести |
|
11 |
. Вывести |
|
12 |
Вывести |
|
13 |
Вывести “столбиком” |
|
14 |
Напечатать таблицу |
|
15 |
Составить программу |
|
16 |
Напечатать таблицу |
|
17 |
Напечатать таблицу |
9. Построить
блок схему к задаче(по вариантам). Указать тип алгоритма, что дано и что нужно
найти.
|
№ |
Задача |
|
1 |
Даны числа а1, а2, |
|
2 |
Известна масса каждого |
|
3 |
. Известны оценки |
|
4 |
В ведомости указана |
|
5 |
Известна масса каждого |
|
6 |
Известно сопротивление |
|
7 |
Известно сопротивление |
|
8 |
Известны оценки по |
|
9 |
Известны оценки ученика |
|
10 |
Известны оценки по |
|
11 |
Известна масса каждого |
|
12 |
Известны оценки двух |
|
13 |
Известны результаты |
|
14 |
Известен возраст (в |
|
15 |
Известно количество |
|
16 |
Известен рост каждого |
|
17 |
Известны оценки по |
10. Построить
блок схему к задаче(по вариантам). Указать тип алгоритма, что дано и что нужно
найти.
|
№ |
Задача |
|
1 |
Дано натуральное число. |
|
2 |
Дано натуральное число. |
|
3 |
Дано натуральное число. |
|
4 |
Дано натуральное число. |
|
5 |
Дано натуральное число |
|
6 |
Дано натуральное число. |
|
7 |
Дано натуральное число. |
|
8 |
Дано натуральное число. |
|
9 |
Дано натуральное число. |
|
10 |
Дано натуральное число. |
|
11 |
Дано натуральное число. |
|
12 |
Дано натуральное число. |
|
13 |
Дано натуральное число. |
|
14 |
Дано натуральное число. |
|
15 |
Дано натуральное |
|
16 |
Дано натуральное число. |
|
17 |
Дано натуральное число. |