Статья рассказывает про алгоритмы с разветвлённой структурой. Читатель узнает, чем их решение отличается от решения линейных алгоритмов, как выглядит программный способ записи таких алгоритмов, а также какова будет блок-схема.

В предыдущей статье шла речь об алгоритмах, их особенностях и свойствах. Особое внимание было уделено линейной структуре как самому простому способу реализации. Сегодня поговорим о более сложных алгоритмах, обладающих разветвлённой структурой. Но прежде чем продолжать, следует кое-что вспомнить.
Алгоритм – это ясный перечень действий, который направлен на решение какой-либо задачи. Одно из свойств алгоритма — дискретность. Дискретность связана с наличием в алгоритмической последовательности ряда операций (этапов, действий), выполняемых пошагово, то есть дискретно. Алгоритм обладает свойством дискретности, так как он представляет собой процесс решения задачи в виде последовательного выполнения простых шагов. И каждое действие исполняется лишь после окончания исполнения предыдущего. Также предполагается наличие определённых исходных данных и результата выполнения.
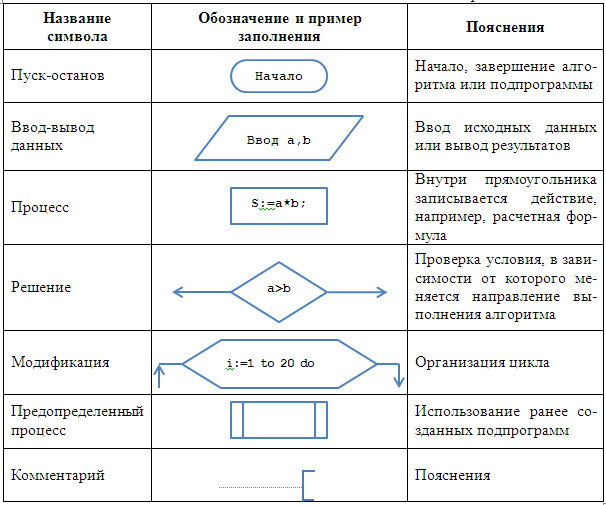
Блок-схема — графический способ описания алгоритмов. Графическое представление обеспечивает наглядность и упрощает запись, делая последовательность более понятной. При использовании схемы каждому действию соответствует определённая геометрическая фигура (эти фигуры называют блоками). Вот наиболее часто употребляемые:
Ещё раз о линейности
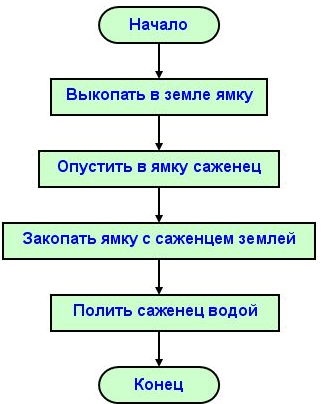
Линейная последовательность — самая простая из возможных структур. При наличии линейности команды выполняются в чёткой последовательности и в порядке их записи, то есть друг за другом. Вот линейная алгоритмическая последовательность посадки дерева:
1) выкапывание ямки в земле;
2) размещение в ямке саженца;
3) закапывание ямки;
4) поливание места посадки водой.
Такой линейный алгоритм имеет следующую блок-схему:
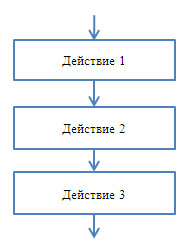
А вот и общая схема линейного алгоритма:
Ветвление в алгоритмических последовательностях
На практике очень редко встречается, чтобы последовательность всех требуемых действий была известна заранее. Если на минуту покинуть мир алгоритмизации и программирования, можно спроецировать ветвление на многие жизненные ситуации. Если на улице дождь, человек берёт зонт, если очень жарко, будет выбрана одежда полегче и т. д. Всё зависит от условия выбора. Как тут не вспомнить рыцаря на распутье из русских народных сказок?

«Направо пойдёшь — жену найдёшь, налево пойдешь — богатым будешь, прямо пойдёшь — смерть найдёшь».
Подобная ситуация заставляет принимать решения с учётом определённого условия. Если нужна жена, то витязь идёт направо, если богатство, то налево, если жизнь не мила, то прямо. Условия, которые влияют на решение, располагаются между словами «если» и «то».
От значения условий зависит дальнейшее поведение. Когда условие выполняется, оно принимает значение «истина», когда нет — «ложь». Иногда анализ ситуации и выбор не вызывают особых затруднений, а иногда принять решение очень трудно. А всё потому, что принимающий решение пытается продумать каждый из вариантов и предугадать последствия выбора. Нельзя не вспомнить гроссмейстера, который анализирует позицию на ходы вперёд, прежде чем передвинуть фигуру на шахматной доске.
Компьютерные программы и игры тоже построены на выборе действий. А блок-схема при наличии ветвления приобретает иной вид:
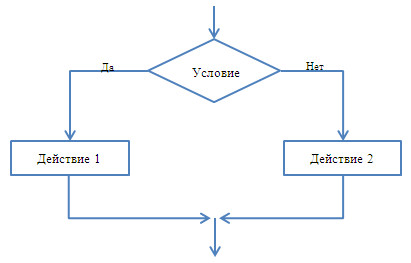
Логика разветвляющих алгоритмов
Логику можно описать следующим образом:
ЕСЛИ <условие истинно> ТО <действие 1> ИНАЧЕ <действие 2>Ветвление — метод и форма организации действий, когда в зависимости от выполнения определённого условия совершается та либо иная последовательность шагов.
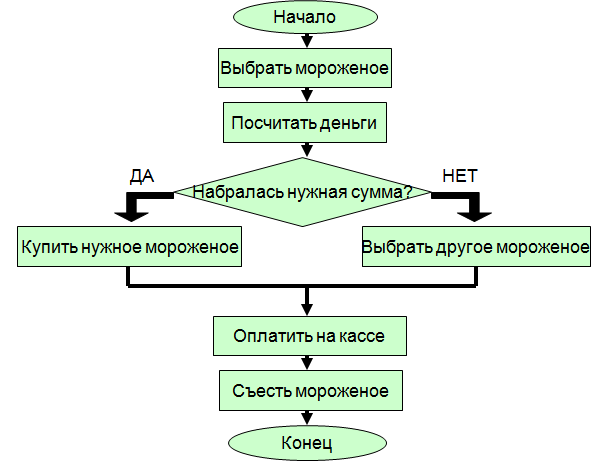
В результате совсем несложно составить алгоритм покупки мороженого с учётом наличия необходимой суммы денег. Описать эту алгоритмическую последовательность с помощью схемы и блоков тоже не составит труда:
Для закрепления можно решить задачу.
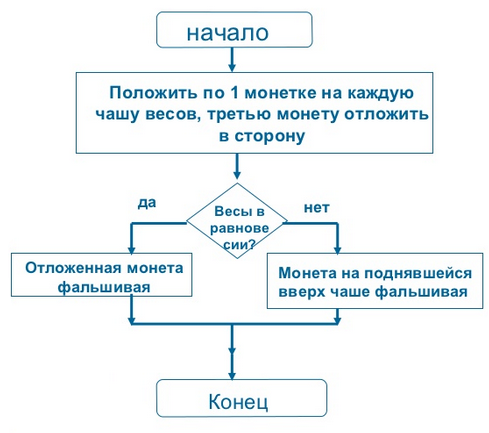
Есть 3 монеты одинакового достоинства. Одна из монет фальшивая (известно, что она имеет меньший вес). Найдите фальшивую монету на чашечных весах без гирь с помощью только одного взвешивания.
Решение легко описывается посредством схематических блоков:
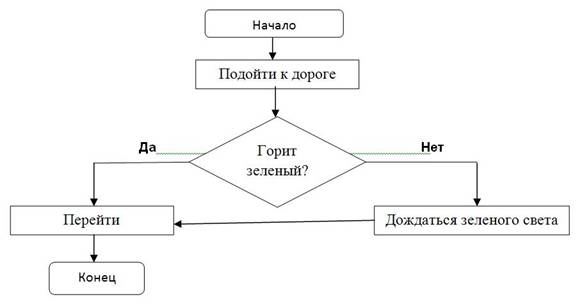
Следующий пример легко экстраполируется в жизнь. Речь идёт об алгоритме для перехода дороги при наличии светофора. Он имеет следующий вид:
1. Подходим к светофору.
2. Смотрим, какой горит свет.
3. Если зелёный, переходим дорогу.
4. Если красный, ждём, пока загорится зелёный, а потом переходим дорогу.Соответствующая блок-схема:
Программный способ записи
Чтобы алгоритм было понятен компьютеру, машине и любой другой цифровой системе, следует оформить его в таком виде, который эта система способна воспринимать. То есть надо написать программу, используя для этого команды из СКИ. СКИ — это список команд исполнителя — перечень команд, ему понятных. А любой исполнитель способен исполнить лишь те команды, которые включены в его СКИ, а если говорить человеческим языком — входят в набор его компетенций.
Для примера можно реализовать алгоритм на языке программирования Pascal. Исходя из вышесказанного, следует использовать команды, входящие в терминологию Pascal.
Простейший пример описания алгоритма с разветвляющейся структурой — условный оператор IF. Полная конструкция этого условного оператора имеет следующий вид:
if<логическое выражение>then<оператор 1>else<оператор 2>Здесь if — это «если», then — это «то», else — «иначе».
Условный оператор работает просто:
— вычисляется значение логического выражения, которое расположено после служебного слова IF;
— если результат — истина, выполняется оператор 1, который размещён после THEN, причём действие после ELSE пропускается;
— если результат — ложь, пропускается уже действие после THEN, а действие после ELSE выполняется с помощью оператора 2.Теперь можно вспомнить пресловутого витязя на распутье и написать простую программу, реализующую этот алгоритм с помощью соответствующих условных операторов.
program Algoritm_vetvlenia; Var x :string; Begin WriteLn ('Витязь, куда путь держишь?'); ReadLn (x); If x='Направо' then writeLn ('Направо пойдёшь — жену найдёшь'); If x='Налево' then writeLn ('Налево пойдешь — богатым будешь'); If x='Прямо' then writeLn ('Прямо пойдёшь — смерть найдёшь'); ReadLn; End.Попробовать этот алгоритм в работе можно на любом онлайн-компиляторе, поддерживающим Pascal. Но не стоит на этом останавливаться — лучше всего написать собственную программу, что позволит получить максимальную пользу от урока.
Источники:
• http://informatic.hop.ru/p33.htm;
• https://interneturok.ru/lesson/informatika/6-klass/algoritm-i-ispolniteli/prakticheskaya-rabota-2-sostavlenie-algoritmov;
• https://www.turbopro.ru/index.php/algoritmizatsiya-i-ispolniteli/5210-algoritmy-ponyatie-i-vidy-algoritma-blok-skhemy;
• https://www.yaklass.ru/p/informatika/6-klass/algoritmy-14002/tipy-algoritmov-13610/re-61ead1ff-bc77-453f-ac99-e46da267f3f3.
Занятие 3. Графическая реализация разветвляющегося алгоритма
В разветвляющемся алгоритме обязательным блоком является блок условия, который представлен на рис. 2.4.

Рис.
2.4.
Использование блока условия в общем виде
Внутри блока условия записывается условие. Если данное условие верно, то выполняются блоки, идущие по стрелке “да”, т.е. “Набор действий 1”. Если условие оказывается неверным, т.е. ложным, то выполняются блоки, идущие по стрелке “нет”, а именно “Набор действий 2”. Разветвление заканчивается, когда обе стрелки (“да” и “нет”) соединяются. На рис. 2.5 представлен еще один вариант использования блока условия. Бывают задачи, в которых, исходя из условия, необходимо либо выполнить действие, либо пропустить его. Если условие верно выполняется, то следуют блоки, соответствующие стрелке “да”, т.е. “Набор действий 1”. Если же условие оказывается ложным, то следует перейти по стрелке “нет”. Т.к. стрелке “нет” не соответствует ни одного блока с действием, то ни одного действия не будет выполнено. Т.е. получается, что мы пропустили и не выполнили “Набор действий 1”.

Рис.
2.5.
Вариант использования блока условия
В разветвляющемся алгоритме возможна запись сразу нескольких условий, которые могут объединяться союзом “ИЛИ” или пересекаться союзом “И”. Рассмотрим случай двух условий: “условие 1” и “условие 2”.
Если необходимо, чтобы оба условия были верными одновременно, то следует использовать логическое пересечение “И”:
Если достаточно, чтобы только одно условие выполнялось – либо первое, либо второе, то следует использовать логическое объединение “ИЛИ”:
"условие 1 ИЛИ условие 2".
Приведем простейшие примеры, соответствующие разветвляющемуся алгоритму.
Пример 4. Джон звонит Полу по городскому телефону, но трубку может взять не только Пол. Составить блок-схему, описывающую действия Джона в этом случае.
Решение. В отличие от примера 1, здесь присутствует условие – Пол ли взял трубку телефона. На данное условие можно однозначно ответить: “да”, Пол, или “нет”, кто-то другой. Если трубку взял Пол, то Джону нужно с ним поговорить, и цель будет достигнута. Если трубку взял кто-то другой, то необходимо позвать Пола к телефону, поговорить с ним, и цель также будет достигнута. Третьего варианта, например, “не туда попали” или “его нет дома” мы не рассматриваем. Результат блок-схемы представлен на рис. 2.6.

Рис.
2.6.
Блок-схема для примера 4
Пример 5. Ученику требуется купить учебник. В магазине в наличие оказался нужный учебник в жесткой и мягкой обложке. Составить блок-схему, описывающую действия ученика.
Решение. В данном примере присутствует условие: “Нужна жесткая обложка”.
Ученик может согласиться с этим высказыванием, тогда он выполнит действие, соответствующее стрелке “да” и купит учебник в жесткой обложке.
Если ученик не соглашается с данным условием, то будет выполняться действие, соответствующее стрелке “нет”, и в этом случае ученик купит учебник в мягкой обложке.
И в том, и в другом случае, цель будет достигнута и задача будет выполнена, т.к. ученик купит учебник.
Результат блок схемы представлен на рис. 2.7.

Рис.
2.7.
Блок-схема для примера 5
Пример 6. Даны числа 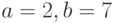 . Вычислить сумму
. Вычислить сумму  и разность
и разность  чисел
чисел  и
и  . Сравнить полученные значения
. Сравнить полученные значения  и
и  и указать большее из них.
и указать большее из них.
Решение. Как и в примере 3, сначала необходимо задать значения  и
и  . Затем рассчитать сумму и разность по формулам:
. Затем рассчитать сумму и разность по формулам: 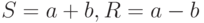 , и вывести полученные числа на экран (блок вывода данных). Когда значения
, и вывести полученные числа на экран (блок вывода данных). Когда значения  и
и  будут получены, следует сравнить их между собой. Условие запишется в виде:
будут получены, следует сравнить их между собой. Условие запишется в виде:  . Если полученная сумма
. Если полученная сумма  будет больше разности
будет больше разности  , то мы пойдем по стрелке “да” и выведем фразу “
, то мы пойдем по стрелке “да” и выведем фразу “ “. Если же условие окажется ложным (т.е.
“. Если же условие окажется ложным (т.е.  ), то пойдем по стрелке “нет” и выведем фразу “
), то пойдем по стрелке “нет” и выведем фразу “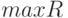 “. Результат блок схемы представлен на рис. 2.8.
“. Результат блок схемы представлен на рис. 2.8.
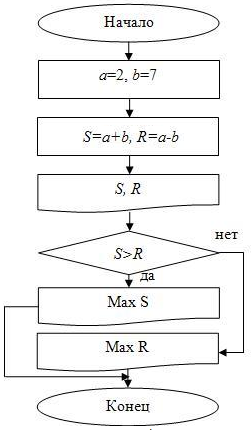
Рис.
2.8.
Блок-схема для примера 6

В предыдущих уроках мы рассмотрели наиболее простой, линейный тип алгоритмов. Напомню, что всего существует три типа: линейные, разветвляющиеся и циклические (алгоритмы с повторениями). В этом уроке я расскажу вам о втором типе алгоритмов — об алгоритмах с ветвлениями.
Ветвления
Ветвление – это команда алгоритма, в которой делается выбор, выполнять или не выполнять какую-нибудь группу команд в зависимости от условий.
Ветвление используется в двух случаях:
- Когда требуется пропустить определенную команду или группу команд.
- Когда нужно записать выбор тех или иных действий в зависимости от условия.
В блок-схеме условие ветвления изображается в ромбе, из которого обязательно выходят ДВЕ стрелки – первая (стрелка «Да») указывает на команды, которые будут выполняться в случае, если условие соблюдено; вторая (стрелка «Нет») – на команды, которые будут выполнены, если условие не соблюдено. Даже если команда, на которую указывает одна из стрелок (Чаще всего «Нет») отсутствует, стрелка все равно имеет место быть.

В словесной формулировке запись ветвления выглядит так:
ЕСЛИ <условие выбора > ТО <команды, выполняемые при соблюдении условия> ИНАЧЕ <команды, выполняемые при несоблюдении условия>
Реализация ветвления в Паскаль.
Как же реализовать ветвление в Паскаль? Проще, чем вы думаете:
if <условие выбора > then <команды, выполняемые при соблюдении условия> else <команды, выполняемые при несоблюдении условия>
Запомните! Перед else никогда не ставят точку с запятой!
Давайте поговорим об условии выбора. Понятно, что этологическое выражение. Если оно является правдой, то выполняется главная ветвь, если ложь, то боковая ветвь.
Рассмотрим несколько задач из сборника М.Э.Абрамяна «1000 задач по программированию».
If1. Дано целое число. Если оно является положительным, то прибавить к нему 1; в противном случае не изменять его. Вывести полученное число.
В данной программе даже не надо реализовывать боковую ветвь.

program if1; var a: integer; begin read(a); if a > 0 then Inc(a); write(a); end.
If2. Дано целое число. Если оно является положительным, то прибавить к нему 1; в противном случае вычесть из него 2. Вывести полученное число.
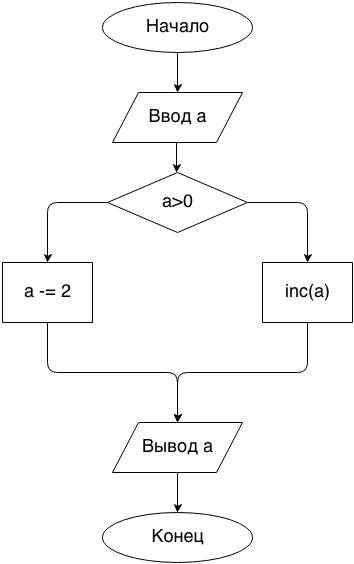
program if2; var a: integer; begin read(a); if a > 0 then Inc(a) else a -= 2; write(a); end.
If3. Дано целое число. Если оно является положительным, то прибавить к нему 1; если отрицательным, то вычесть из него 2; если нулевым, то заменить его на 10. Вывести полученное число.
Для того чтобы решить эту задачу мы должны использовать вложенный if.

program if3;
var
a: integer;
begin
read(a);
if a >= 0 then
if a = 0 then a := 10 else Inc(a) {перед else нет точки с запятой.}
else a -= 2;
write(a);
end.
If5. Даны три целых числа. Найти количество положительных и количество отрицательных чисел в исходном наборе.
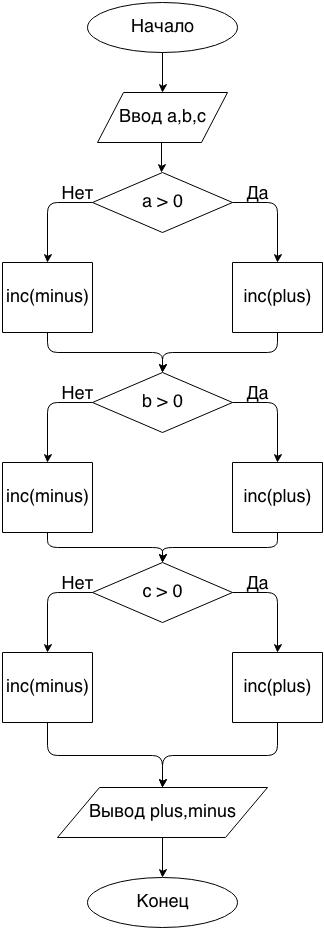
program if5;
var
a, b, c, plus, minus: integer;
begin
write('Введите три целых числа: ');
read(a, b, c);
plus := 0;
minus := 0;
if a > 0 then Inc(plus) else Inc(minus);
if b > 0 then Inc(plus) else Inc(minus);
if c > 0 then Inc(plus) else Inc(minus);
writeln('Количество положительных чисел - ', plus);
writeln('Количество отрицательных чисел - ', minus);
end.
If30. Дано целое число, лежащее в диапазоне 1–999. Вывести его строку-описание вида «четное двузначное число», «нечетное трехзначное число» и т. д.

program if30;
var
a: integer;
begin
write('Введите число: ');
read(a);
if Odd(a) then write('Нечетное ') else write('Четное ');
if a >= 100 then write('трехзначное число') else
if a < 10 then write('однозначное число') else write('двухзначное число');
end.
Вот и все! Не забывайте кликать по кнопочкам и добавлять наш сайт в закладки!
В этой статье будут рассмотрены примеры блок-схем, которые могут встретиться вам в учебниках по информатике и другой литературе. Блок-схема представляет собой алгоритм, по которому решается какая-либо задача, поставленная перед разработчиком. Сначала нужно ответить на вопрос, что такое алгоритм, как он представляется графически, а самое главное – как его решить, зная определенные параметры. Нужно сразу отметить, что алгоритмы бывают нескольких видов.
Что такое алгоритм?
Это слово ввел в обиход математик Мухаммед аль-Хорезми, который жил в период 763-850 года. Именно он является человеком, который создал правила выполнения арифметических действий (а их всего четыре). А вот ГОСТ от 1974 года, который гласит, что:
Алгоритм – это точное предписание, которое определяет вычислительный процесс. Причем имеется несколько переменных с заданными значениями, которые приводят расчеты к искомому результату.
Алгоритм позволяет четко указать исполнителю выполнять строгую последовательность действий, чтобы решить поставленную задачу и получить результат. Разработка алгоритма – это разбивание одной большой задачи на некую последовательность шагов. Причем разработчик алгоритма обязан знать все особенности и правила его составления.
Особенности алгоритма
Всего можно выделить восемь особенностей алгоритма (независимо от его вида):
- Присутствует функция ввода изначальных данных.
- Есть вывод некоего результата после завершения алгоритма. Нужно помнить, что алгоритм нужен для того, чтобы достичь определенной цели, а именно – получить результат, который имеет прямое отношение к исходным данным.
- У алгоритма должна быть структура дискретного типа. Он должен представляться последовательными шагами. Причем каждый следующий шаг может начаться только после завершения предыдущего.
- Алгоритм должен быть однозначным. Каждый шаг четко определяется и не допускает произвольной трактовки.
- Алгоритм должен быть конечным – необходимо, чтобы он выполнялся за строго определенное количество шагов.
- Алгоритм должен быть корректным – задавать исключительно верное решение поставленной задачи.
- Общность (или массовость) – он должен работать с различными исходными данными.
- Время, которое дается на решение алгоритма, должно быть минимальным. Это определяет эффективность решения поставленной задачи.
А теперь, зная, какие существуют блок-схемы алгоритмов, можно приступить к рассмотрению способов их записи. А их не очень много.
Словесная запись
Такая форма, как правило, применяется при описании порядка действий для человека: «Пойди туда, не знаю куда. Принеси то, не знаю что».
Конечно, это шуточная форма, но суть понятна. В качестве примера можно привести еще, например, привычную запись на стеклах автобусов:«При аварии выдернуть шнур, выдавить стекло».
Здесь четко ставится условие, при котором нужно выполнить два действия в строгой последовательности. Но это самые простые алгоритмы, существуют и более сложные. Иногда используются формулы, спецобозначения, но при обязательном условии – исполнитель должен все понимать.
Допускается изменять порядок действий, если необходимо вернуться, например, к предыдущей операции либо обойти какую-то команду при определенном условии. При этом команды желательно нумеровать и обязательно указывается команда, к которой происходит переход: «Закончив все манипуляции, повторяете пункты с 3 по 5».
Запись в графической форме
В этой записи участвуют элементы блок-схем. Все элементы стандартизированы, у каждой команды имеется определенная графическая запись. А конкретная команда должна записываться внутри каждого из блоков обычным языком или математическими формулами. Все блоки должны соединяться линиями – они показывают, какой именно порядок у выполняемых команд. Собственно, этот тип алгоритма более подходит для использования в программном коде, нежели словесный.
Запись на языках программирования
В том случае, если алгоритм необходим для того, чтобы задачу решала программа, установленная на ПК, то нужно его записывать специальным кодом. Для этого существует множество языков программирования. И алгоритм в этом случае называется программой.
Блок-схемы
Блок-схема – это представление алгоритма в графической форме. Все команды и действия представлены геометрическими фигурами (блоками). Внутри каждой фигуры вписывается вся информация о тех действиях, которые нужно выполнить. Связи изображены в виде обычных линий со стрелками (при необходимости).
Для оформления блок-схем алгоритмов имеется ГОСТ 19.701-90. Он описывает порядок и правила создания их в графической форме, а также основные методы решения. В этой статье приведены основные элементы блок-схем, которые используются при решении задач, например, по информатике. А теперь давайте рассмотрим правила построения.
Основные правила составления блок-схемы
Можно выделить такие особенности, которые должны быть у любой блок-схемы:
- Обязательно должно присутствовать два блока – «Начало» и «Конец». Причем в единичном экземпляре.
- От начального блока до конечного должны быть проведены линии связи.
- Из всех блоков, кроме конечного, должны выходить линии потока.
- Обязательно должна присутствовать нумерация всех блоков: сверху вниз, слева направо. Порядковый номер нужно проставлять в левом верхнем углу, делая разрыв начертания.
- Все блоки должны быть связаны друг с другом линиями. Именно они должны определять последовательность, с которой выполняются действия. Если поток движется снизу вверх или справа налево (другими словами, в обратном порядке), то обязательно рисуются стрелки.
- Линии делятся на выходящие и входящие. При этом нужно отметить, что одна линия является для одного блока выходящей, а для другого входящей.
- От начального блока в схеме линия потока только выходит, так как он является самым первым.
- А вот у конечного блока имеется только вход. Это наглядно показано на примерах блок-схем, которые имеются в статье.
- Чтобы проще было читать блок-схемы, входящие линии изображаются сверху, а исходящие снизу.
- Допускается наличие разрывов в линиях потока. Обязательно они помечаются специальными соединителями.
- Для облегчения блок-схемы разрешается всю информацию прописывать в комментариях.
Графические элементы блок-схем для решения алгоритмов представлены в таблице:
Линейный тип алгоритмов
Это самый простой вид, который состоит из определенной последовательности действий, они не зависят от того, какие данные вписаны изначально. Есть несколько команд, которые выполняются однократно и только после того, как будет сделана предшествующая. Линейная блок-схема выглядит таким образом:
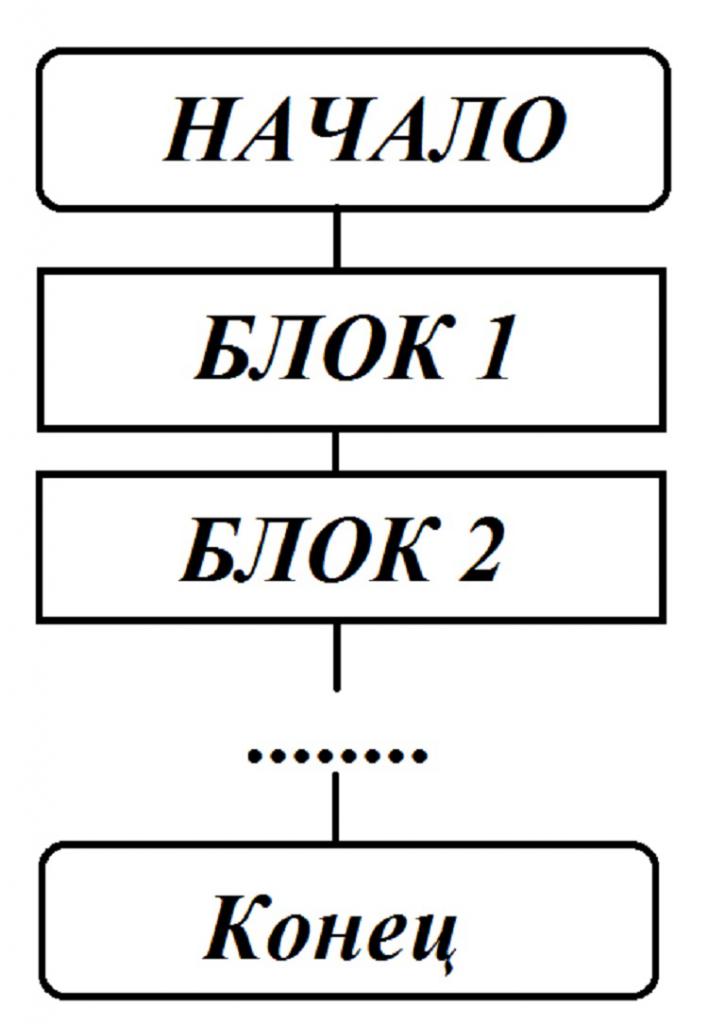
Причем связи могут идти как сверху вниз, так и слева направо. Используется такая блок-схема для записи алгоритмов вычислений по простым формулам, у которых не имеется ограничений на значения переменных, входящих в формулы для расчета. Линейный алгоритм – это составная часть сложных процессов вычисления.
Разветвляющиеся алгоритмы
Блок-схемы, построенные по таким алгоритмам, являются более сложными, нежели линейные. Но суть не меняется. Разветвляющийся алгоритм – это процесс, в котором дальнейшее действие зависит от того, как выполняется условие и какое получается решение. Каждое направление действия – это ветвь.
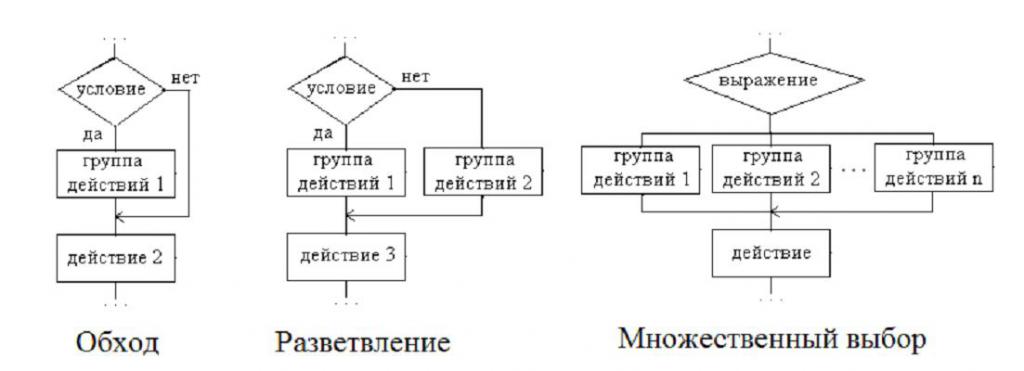
На схемах изображаются блоки, которые называются «Решение». У него имеется два выхода, а внутри прописывается логическое условие. Именно от того, как оно будет выполнено, зависит дальнейшее движение по схеме алгоритма. Можно разделить разветвляющиеся алгоритмы на три группы:
- «Обход» – при этом одна из веток не имеет операторов. Другими словами, происходит обход нескольких действий другой ветки.
- «Разветвление» – каждая ветка имеет определенный набор выполняемых действий.
- «Множественный выбор» – это разветвление, в котором есть несколько веток и каждая содержит в себе определенный набор выполняемых действий. Причем есть одна особенность – выбор направления напрямую зависит от того, какие заданы значения выражений, входящих в алгоритм.
Это простые алгоритмы, которые решаются очень просто. Теперь давайте перейдем к более сложным.
Циклический алгоритм
Здесь все предельно понятно – циклическая блок-схема представляет алгоритм, в котором многократно повторяются однотипные вычисления. По определению, цикл – это определенная последовательность каких-либо действий, выполняемая многократно (более, чем один раз). И можно выделить несколько типов циклов:
- У которых известно число повторений действий (их еще называют циклами со счетчиком).
- У которых число повторений неизвестно – с постусловием и предусловием.
Независимо от того, какой тип цикла используется для решения алгоритма, у него обязательно должна присутствовать переменная, при помощи которой происходит выход. Именно она определяет количество повторений цикла. Рабочая часть (тело) цикла – это определенная последовательность действий, которая выполняется на каждом шаге. А теперь более детально рассмотрим все типы циклов, которые могут встретиться при составлении алгоритмов и решении задач по информатике.
Циклы со счетчиками
На рисунке изображена простая блок-схема, в которой имеется цикл со счетчиком. Такой тип алгоритмов показывает, что заранее известно количество повторений данного цикла. И это число фиксировано. При этом переменная, считающая число шагов (повторений), так и называется – счетчик. Иногда в учебниках можно встретить иные определения – параметр цикла, управляющая переменная.
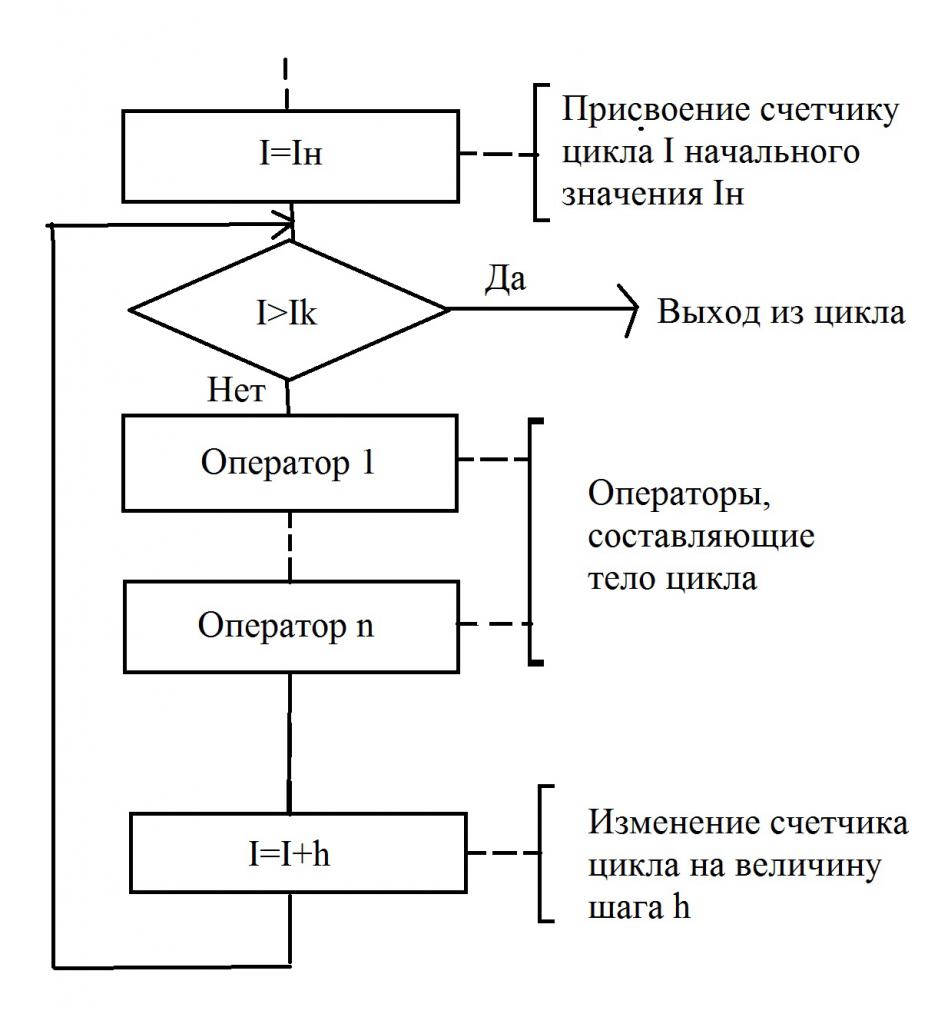
Блок-схема очень наглядно иллюстрирует, как работает цикл со счетчиком. Прежде чем приступить к выполнению первого шага, нужно присвоить начальное значение счетчику – это может быть любое число, оно зависит от конкретного алгоритма. В том случае, когда конечное значение меньше величины счетчика, начнет выполняться определенная группа команд, которые составляют тело цикла.
После того, как тело будет выполнено, счетчик меняется на величину шага счетчика, обозначенную буквой h. В том случае, если значение, которое получится, будет меньше конечного, цикл будет продолжаться. И закончится он лишь в тогда, когда конечное значение будет меньше, чем счетчик цикла. Только в этом случае произойдет выполнение того действия, которое следует за циклом.
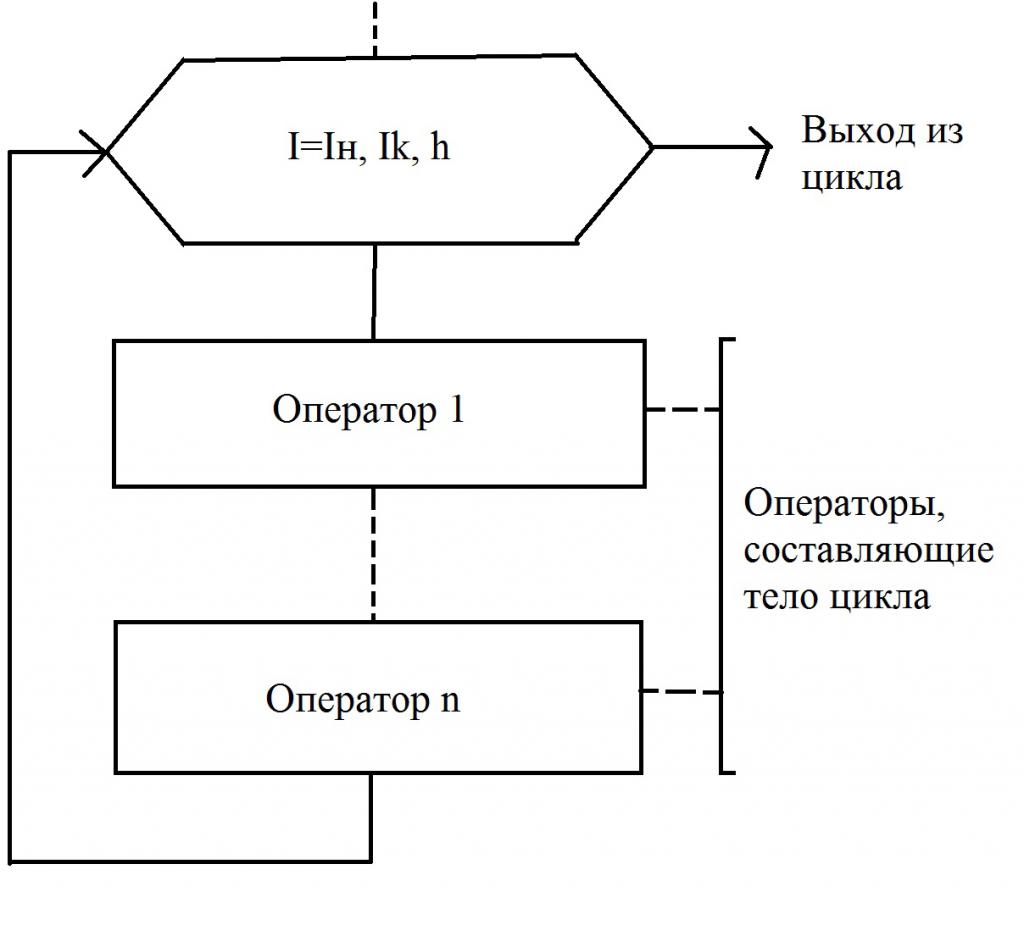
Обычно в обозначениях блок-схем используется блок, который называется «Подготовка». В нем прописывается счетчик, а затем указываются такие данные: начальное и конечное значения, шаг изменения. На блок-схеме это параметры I н, Ik и h, соответственно. В том случае, когда h=1, величину шага не записывают. В остальных случаях делать это обязательно. Необходимо придерживаться простого правила – линия потока должна входить сверху. А линия потока, которая выходит снизу (или справа, в зависимости от конкретного алгоритма), должна показывать переход к последующему оператору.
Теперь вы полностью изучили описание блок-схемы, изображенной на рисунке. Можно перейти к дальнейшему изучению. Когда используется цикл со счетчиком, требуется соблюдать определенные условия:
- В теле не разрешается изменять (принудительно) значение счетчика.
- Запрещено передавать управление извне оператору тела. Другими словами, войти в цикл можно только из его начала.
Циклы с предусловием
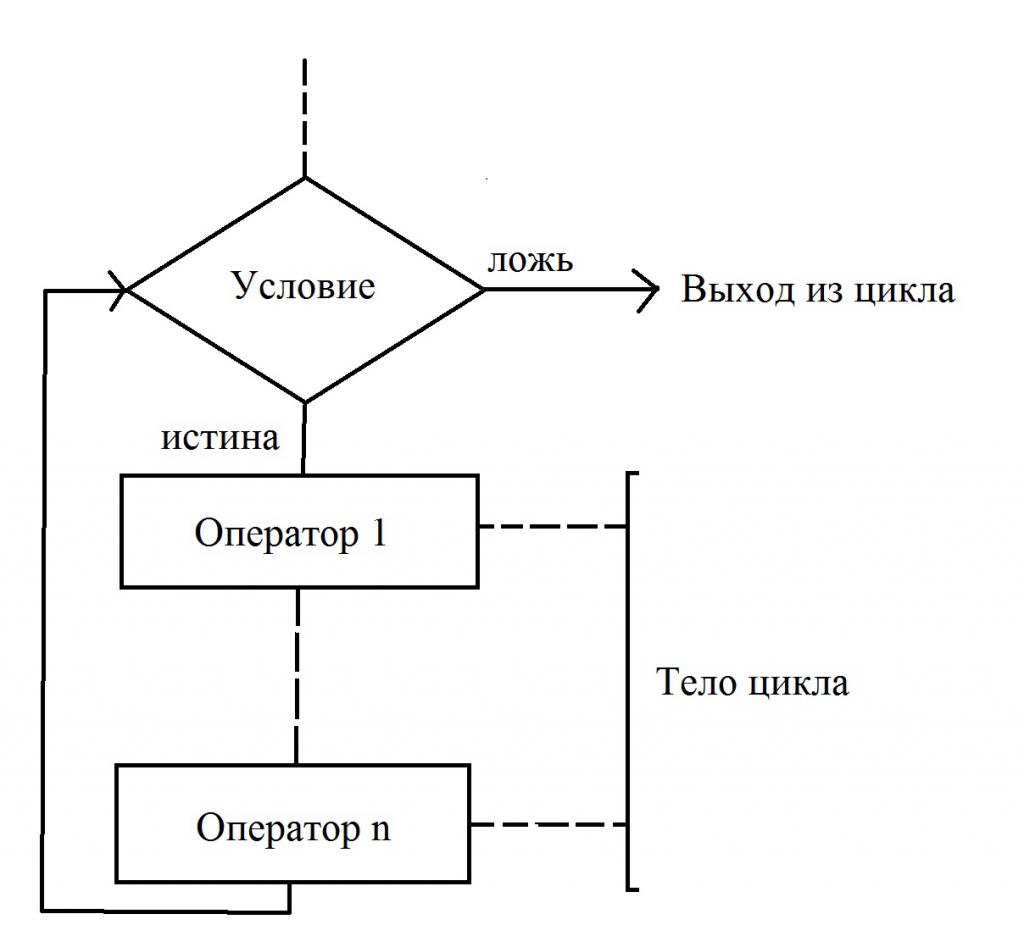
Этот тип циклов применяется в тех случаях, когда количество повторений заранее неизвестно. Цикл с предусловием – это тип алгоритма, в котором непосредственно перед началом выполнения тела осуществляется проверка условия, при котором допускается переход к следующему действию. Обратите внимание на то, как изображаются элементы блок-схемы.
В том случае, когда условие выполняется (утверждение истинно), происходит переход к началу тела цикла. Непосредственно в нем изменяется значение хотя бы одной переменной, влияющей на значение поставленного условия. Если не придерживаться этого правила, получим «зацикливание». В том случае, если после следующей проверки условия выполнения тела цикла оказывается, что оно ложное, то происходит выход.
В блок-схемах алгоритмов допускается осуществлять проверку не истинности, а ложности начального условия. При этом из цикла произойдет выход только в том случае, если значение условия окажется истинным. Оба варианта правильные, их использование зависит от того, какой конкретно удобнее использовать для решения той или иной задачи. Такой тип цикла имеет одну особенность – тело может не выполниться в случае, когда условие ложно или истинно (в зависимости от варианта, который применяется для решения алгоритма).
Ниже приведена блок-схема, которая описывает все эти действия:
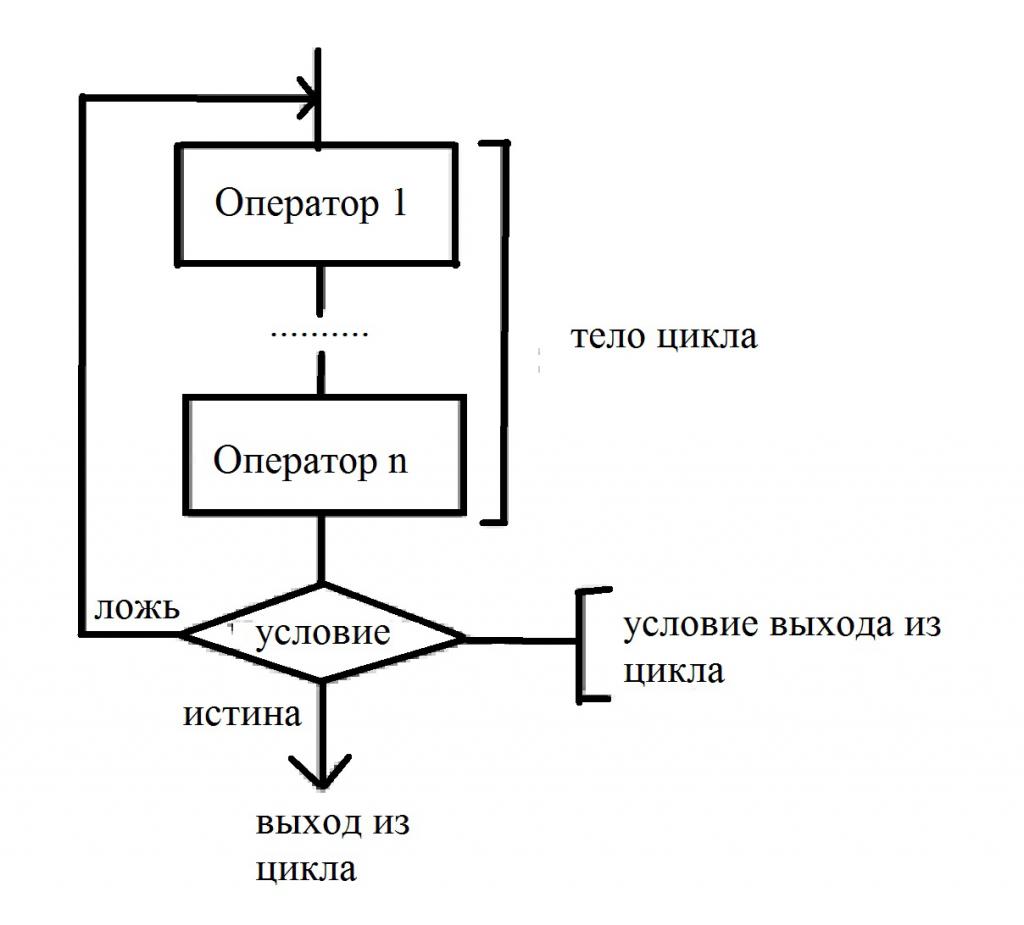
Что такое цикл с постусловием?
Если внимательно присмотреться, то этот вид циклов чем-то похож на предыдущий. Самостоятельно построить блок-схему, описывающую этот цикл, мы сейчас и попробуем. Особенность заключается в том, что неизвестно заранее число повторений. А условие задается уже после того, как произошел выход из тела. Отсюда видно, что тело, независимо от решения, будет выполняться как минимум один раз. Для наглядности взгляните на блок-схему, описывающую выполнение условия и операторов:
Ничего сложного в построении алгоритмов с циклами нет, достаточно в них только один раз разобраться. А теперь перейдем к более сложным конструкциям.
Сложные циклы
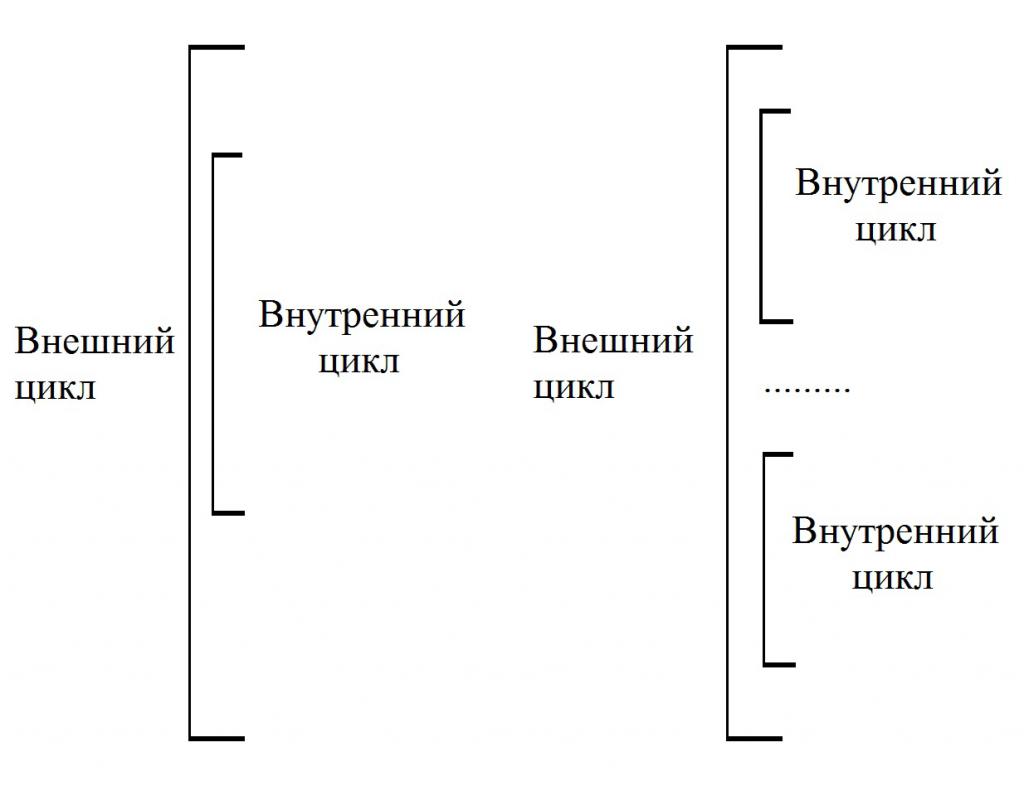
Сложные – это такие конструкции, внутри которых есть один или больше простых циклов. Иногда их называют вложенными. При этом те конструкции, которые охватывают иные циклы, называют «внешними». А те, которые входят в конструкцию внешних – внутренними. При выполнении каждого шага внешнего цикла происходит полная прокрутка внутреннего, как представлено на рисунке:
Вот и все, вы рассмотрели основные особенности построения блок-схем для решения алгоритмов, знаете принципы и правила. Теперь можно рассмотреть конкретные примеры блок-схем из жизни. Например, в психологии такие конструкции используются для того, чтобы человек решил какой-то вопрос:
Или пример из биологии для решения поставленной задачи:
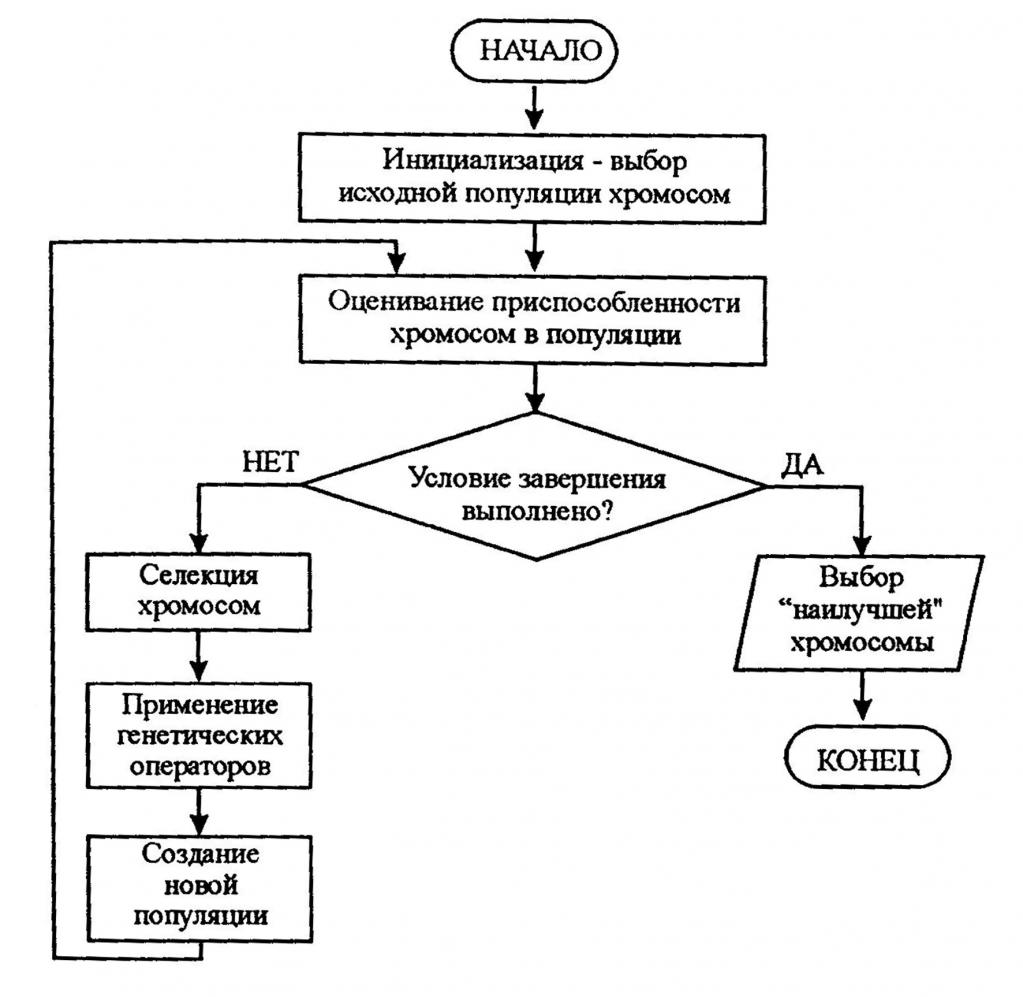
Решение задач с блок-схемами
А теперь рассмотрим примеры задач с блок-схемами, которые могут попасться в учебниках информатики. Например, задана блок-схема, по которой решается какой-то алгоритм:
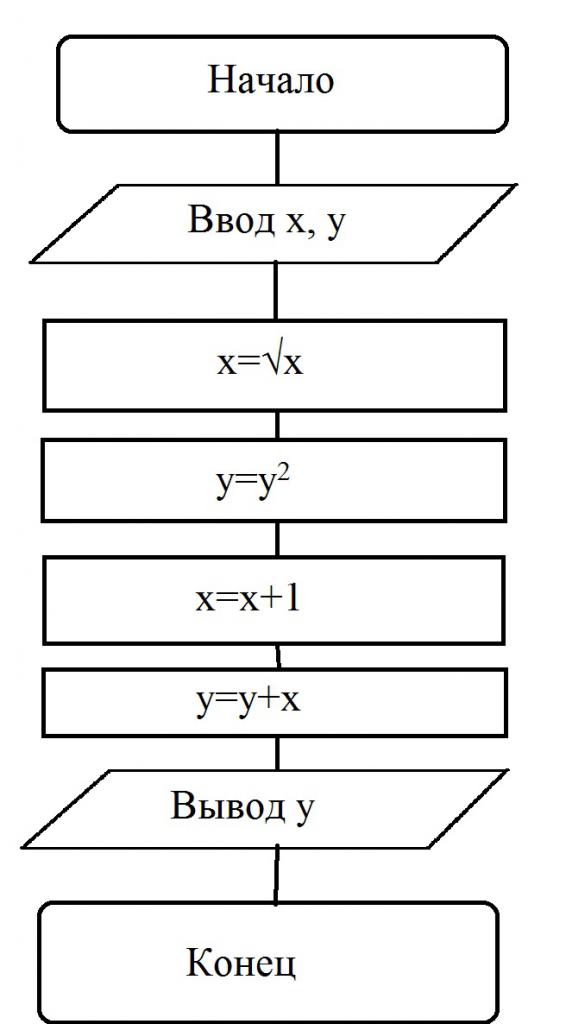
При этом пользователь самостоятельно вводит значения переменных. Допустим, х=16, а у=2. Процесс выполнения такой:
- Производится ввод значений х и у.
- Выполняется операция преобразования: х=√16=4.
- Выполняется условие: у=у2=4.
- Производится вычисление: х=(х+1)=(4+1)=5.
- Дальше вычисляется следующая переменная: у=(у+х)=(5+4)=9.
- Выводится решение: у=9.
На этом примере блок-схемы по информатике хорошо видно, как происходит решение алгоритма. Нужно обратить внимание на то, что значения х и у задаются на начальном этапе и они могут быть любыми.
Алгоритм разветвленной структуры
Алгоритм разветвленной структуры
Как мы уже говорили, любой алгоритм можно составить из нескольких базовых структур. Простейшей из них является линейная (следование). В ней команды выполняются однократно в той последовательности, как они записаны. Однако далеко не всегда для решения задачи последовательность действий одна и та же при любых исходных данных. Если на каком-то этапе исполнитель должен выбирать один вариант из нескольких, в алгоритме используют ветвление.
В алгоритме разветвленной структуры (ветвлении) в зависимости от истинности или ложности некоторого условия выбирается одна из двух серий команд.
Пример программы разветвленной структуры
Пример программы разветвленной структуры
Программа на языке Pascal
program choice;
var a, b, c, d: real;
begin
readln(a, b, c);
d := b * b – 4 * a * c;
if d < 0
then writeln(‘корней нет’)
else writeln(‘корни есть’);
end.
Обратите внимание, что перед словами then и else точка с запятой не ставится — они считаются частями одного условного оператора if…then…else.
В том случае, если при ложности условия никаких действий не выполняется, на блок-схеме на стрелке «НЕТ» не чертят никаких блоков, а в записи условного оператора пропускают «else».
Если серия состоит более чем из одной команды, ее необходимо заключить в операторные скобки begin…end.
Например:
if x > 0
then begin
y := sqrt(x);
z := z + y;
end
else z := z + x;
Если в программе есть ветвление, нужно…
Если в программе есть ветвление, нужно…
- Определить, какие существуют варианты действий и сколько их всего. Количество условных операторов будет на один меньше, чем число вариантов.
- Выяснить, при каких условиях должен выполняться каждый из вариантов.
- Если вариантов больше двух, выбрать последовательность проверки условий. При необходимости построить блок-схему.
- Записать алгоритм на языке программирования.
- Подобрать данные для тестирования программы (предусмотреть наборы данных, позволяющие проверить каждый вариант действий).
При записи условий в языке Pascal можно использовать следующие операции сравнения:
Результатом операции сравнения всегда будет логическое значение — либо false (ложь), либо true (истина).
Нередко условие, требующее проверки, нельзя выразить с помощью единственного сравнения. Тогда используют составные условия, образующиеся с помощью логических операций. В языке программирования Pascal их три (в некоторых реализациях — четыре):