На чтение 12 мин Просмотров 3 Опубликовано 11 апреля 2023 Обновлено 11 апреля 2023
Содержание
- От блок-схем к программированию
- Урок 4. Блок-схема
- Блок-схема линейного алгоритма
От блок-схем к программированию
Данная задача не должна представлять особой трудности, так как построена она на хорошо известных всем нам формулах расчета площади и периметра прямоугольника, поэтому зацикливаться на выведении этих формул мы не будем.
Составим алгоритм решения подобных задач:
1) Прочитать задачу.
2) Выписать известные и неизвестные нам переменные в «дано». (В задаче №1 к известным переменным относятся стороны: a,b ;к неизвестным — площадь S и периметр P)
3) Вспомнить либо составить необходимые формулы. (У нас: S=a*b; P=2*(a+b))
4) Составить блок-схему.
5) Записать решение на языке программирования Pascal.
Запишем условие в более кратком виде.
Структура программы, решающей данную задачу, тоже проста:
- 1) Описание переменных;
- 2) Ввод значений сторон прямоугольника;
- 3) Расчет площади прямоугольника;
- 4) Расчет периметра прямоугольника;
- 5) Вывод значений площади и периметра;
- 6) Конец.
Задача №2: Скорость первого автомобиля — V1 км/ч, второго — V2 км/ч, расстояние между ними S км. Какое расстояние будет между ними через T часов, если автомобили движутся в разные стороны? Значения V1, V2, T и S задаются с клавиатуры.
Решение осуществляем, опять же, следуя алгоритму. Прочитав текст, мы переходим к следующему пункту. Как и во всех физических или математических задачах, это запись условий задачи:
Далее идет самая главная и в то же время самая интересная часть нашего решения — составление нужных нам формул. Как правило, на начальных стадиях обучения все необходимые формулы хорошо нам известны и взяты из других технических дисциплин (например, на нахождение площади различных фигур, на нахождение скорости, расстояния и т.п.).
Формула, используемая для решения нашей задачи, выглядит следующим образом:
Следующий пункт алгоритма — блок-схема:
Источник
Урок 4. Блок-схема

Итак, опустив долгие и нудные восхваления Паскаля, которые так любят публиковать в своих статьях редакторы многих сайтов, приступим непосредственно к самому основному – к программированию.
В школах, как правило, изучение Паскаля начинают с решения простейших задач путем составления различных алгоритмов или блок-схем, которое многие так часто игнорируют, считая никому не нужной ерундой. А зря. Я, как и любой другой человек, хоть немного соображающий в программировании (не важно где – в Паскале, Си, Дельфи), могу уверить Вас – умение правильно и быстро составлять схемы является фундаментом, основой программирования.
Блок-схема — графическое представление алгоритма. Она состоит из функциональных блоков, которые выполняют различные назначения (ввод/вывод, начало/конец, вызов функции и т.д.).
Существует несколько основных видов блоков, которые нетрудно запомнить:
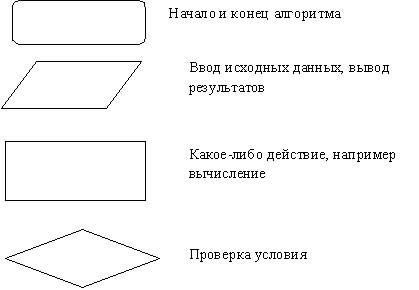
Сегодняшний урок я решила посвятить не только изучению блок-схем, но также и изучению линейных алгоритмов. Как Вы помните, линейный алгоритм — наипростейший вид алгоритма. Его главная особенность в том, что он не содержит никаких особенностей. Как раз это и делает работу с ним простой и приятной.
Задача №1: «Рассчитать площадь и периметр прямоугольника по двум известным сторонам».
Данная задача не должна представлять особой трудности, так как построена она на хорошо известных всем нам формулах расчета площади и периметра прямоугольника, поэтому зацикливаться на выведении этих формул мы не будем.
Составим алгоритм решения подобных задач:
1) Прочитать задачу.
2) Выписать известные и неизвестные нам переменные в «дано». (В задаче №1 к известным переменным относятся стороны: a, b ;к неизвестным — площадь S и периметр P)
3) Вспомнить либо составить необходимые формулы. (У нас: S=a*b; P=2*(a+b))
4) Составить блок-схему.
5) Записать решение на языке программирования Pascal.
Запишем условие в более кратком виде.
Структура программы, решающей данную задачу, тоже проста:
- 1) Описание переменных;
- 2) Ввод значений сторон прямоугольника;
- 3) Расчет площади прямоугольника;
- 4) Расчет периметра прямоугольника;
- 5) Вывод значений площади и периметра;
- 6) Конец.
Задача №2: Скорость первого автомобиля — V1 км/ч, второго – V2 км/ч, расстояние между ними S км. Какое расстояние будет между ними через T часов, если автомобили движутся в разные стороны? Значения V1, V2, T и S задаются с клавиатуры.
Решение осуществляем, опять же, следуя алгоритму. Прочитав текст, мы переходим к следующему пункту. Как и во всех физических или математических задачах, это запись условий задачи:
Далее идет самая главная и в то же время самая интересная часть нашего решения – составление нужных нам формул. Как правило, на начальных стадиях обучения все необходимые формулы хорошо нам известны и взяты из других технических дисциплин (например, на нахождение площади различных фигур, на нахождение скорости, расстояния и т.п.).
Формула, используемая для решения нашей задачи, выглядит следующим образом:
Следующий пункт алгоритма – блок-схема:
 Решение задачи №2.
Решение задачи №2.
А также решение, записанное в Pascal :
Вам может показаться, что две эти программы правильны, но это не так. Ведь сторона треугольника может быть 4.5, а не 4, а скорость машины не обязательно круглое число! А Integer — это только целые числа. Поэтому при попытке написать во второй программе другие числа выскакивает ошибка:
 Обратите внимание в Паскале, как и в любом другом языке программирования десятичная дробь вводится с точкой, а не с запятой!
Обратите внимание в Паскале, как и в любом другом языке программирования десятичная дробь вводится с точкой, а не с запятой!
Чтобы решить эту проблему вам надо вспомнить какой тип в Pascal отвечает за нецелые числа. В этом уроке мы рассматривали основные типы. Итак, это вещественный тип — Real. Вот, как выглядит исправленная программа:

Как видите, эта статья полезна для прочтения как новичкам, так и уже более опытными пользователям Pascal, так как составление блок-схем не только очень простое и быстрое, но и весьма увлекательное занятие.
Здесь понятней чем в школе.
мля… прикиньте, я узнал про этот сайт только ПОСЛЕ того как сделал программу с условием, узнавая все в инструкции
Ребята , вопрос на засыпку, как заставить «,» (введенную пользователем в числе) заменить на «.» внутри программы, что бы не вылетало юхни с ошибкой.
Взять строку введенную пользователем, заменить «,» на «.».
Если совсем гуглить не умеете, то вам сюда — http://www.cyberforum.ru/pascal/thread190664.html
>> скорость машины не обязательно круглое число!
Нет такого понятия, как «круглое число».
Обе ваши блок-схемы не соответствуют ГОСТу (сдать такие на курсовой проект не получится). ГОСТ определяет блоки начала и конца, как «прямоугольник со скругленными краями», а не «скругленными углами».
>> умение правильно и быстро составлять схемы является фундаментом, основой программирования.
Большинство программистов так не считает. Кроме того, попробуйте поспрашивать у программистов «когда они последний раз составляли блок-схему?» — окажется что в ВУЗе (когда с них зачем-то сдирали знание ГОСТа).
>> так как составление блок-схем не только очень простое и быстрое, но и весьма увлекательное занятие.
Очень сложное, долгое и бесполезное занятие. Для хоть сколько-нибудь большой программы (в тысячу строк хотя бы, как курсак) блок-схемы будут огромные и их будут десятки. А что делать если они перестают соответствовать коду? — вот даже в вашей первой задаче надо будет добавить проверку, что юзер не ввел отрицательные значения сторон, что делать? — исправления кода займут 1 минуту, а исправление блок-схем 10 минут, и зачем тогда этим заниматься?
Программист не должен писать блок-схемы (он их должен читать и понимать и при необходимости исправлять). Блок-схемы это графический язык общения, который понимает как программист, так и не программист. Чтобы пользователь не общался с программистом своими «хотелками», типа я хочу, чтобы вот это правильно считалось, и это число складывалось с этим, а потом выводилось сюда (или вообще говорил — хочу что бы работало), а рисовал все в виде блок-схем с четким алгоритмом. Тогда по идее у программиста будет понимание того, что от него хотят (и он через пять минут не забудет все что ему сказали). Либо, когда общаются два программиста пишущих на разных языках программирования (LISP и Java) и одному нужно объяснить как работает его код, что бы другой переписал его на другом языке.
Как объяснить преподавателю как работает программа, если преподаватель не знает языка программирования на котором написана ваша программа? Или как преподавателю объяснить алгоритм задачи студентам пишущим и реализующим этот алгоритм или программу на разных языках программирования? Нужен какой-то универсальный язык общения и обычно это просто текст «что нужно сделать» на русском языке, а не намного облегчающая жизнь программиста блок-схема.
Вам могут сказать — сделай модуль авторизации (ты же знаешь как, ну как всегда и как везде), а могут нарисовать блок-схему модуля авторизации с учетом всех пожеланий, типа того, что пароль должен содержать не менее 6 символов и что нужно делать в противном случае т.д. То есть блок схему должен уметь рисовать тот кто ставит задачу, а не программист. Либо программист (архитектор либо менеджер проекта), который ставит задачу другим программистам.
Вы слишком придирчивы, серьезно (я говорю про последние два пункта). Понятно, что статья (как почти и весь сайт) написана почти только для школьников, которым об этом твердят в школе. Здесь же им просто объясняют те вещи, которые они на учебе недопоняли
Блок схемы всей программы могут не понадобиться. Это же тонны бумаги и много времени. И да, они устаревают и актуализировать их трудоёмко.
Но при обсуждении новых вариантов решения задачи с другими программистами удобно оперировать блоками с криво-косо нарисованными краями и линиями. Начертил на бумаге или доске и все понятно.
На практике я встречал фотографии доски с блок-схемами, прикреплённые к задачам в Jira.
Не по ГОСТу 🙂
Спасибо, теперь я напишу программу, которая делает код по блок схеме и наоборот
program Logarifm;
Var
X,y,z:real;
function Lgrfm(A,B:Real):Real;
var
Osn:Real;
begin
Osn:=ln(A)/ln(B);
Lgrfm:=Osn;
end;
begin
Write(‘Введите X = ‘);
ReadLn(X);
Write(‘Введите Y = ‘);
ReadLn(Y);
Z:=Lgrfm(X,2)+Lgrfm(Y,3);
WriteLn(‘Z = ‘,Z:10:3);
ReadLn;
end.
Отличный сайт, мне все нравится все понятно и четко, нашел нужные программы.
В блок-схемах начало и конец алгоритма обозначаются не прямоугольником со скруглёнными краями, а овалом!
Ребята, что сделали сайт молодцы)) Оч полезная инфа, что нужно поправить, чтобы сайт стал еще лучше:
1) мне не хватает структуры уроков порядковой (или хотябы под уроками чтобы была ссылка на следующий), поэтому приходится на другие уроки искать ссылки по сайту и в контексте уроков;
2)нет описания функций используемых в примерах (по крайней мере, возможно по причине отсутствия структуры, я их не нашел), поэтому беру на сторонних ресурсах описания таких функций как dec() inc() sqr() odd().
А вообще как я понял сайт составлялся школьниками «на коленках», поэтому я не придираюсь, а просто говорю им спасибо за их труд. Желаю успехов.
Источник
Блок-схема линейного алгоритма
Линейный алгоритм – это алгоритм, в котором блоки выполняются последовательно сверху вниз от начала до конца.
На рисунке 1 приведен пример блок-схемы алгоритма вычисления периметра Р и площади S квадрата со стороной длины A.
Блок-схема алгоритма состоит из шести блоков. Выполнение алгоритма начинается с блока 1 «Начало». Этот блок символизирует включение автомата, настройку его на выполнение алгоритма и выделение памяти под все переменные, которые задействованы в алгоритме. В алгоритме рисунка 1 таких переменных три: A, Р, S. Следовательно, под каждую из них алгоритмом будет выделено по одной ячейке памяти. На этом блок 1 будет отработан.
Как видно из рисунка, блок 1 связан вертикальной линией потока с блоком 2. Эта линия не имеет стрелки, указывавшей направление потока. Следовательно, этот поток направлен вниз. Таким образом, после выполнения блока 1 управление будет передано на блок 2. Блок 2 «Перфокарта» ( см. табл. 1) показывает, что переменной A следует присвоить значение. Это означает, что в ячейку, отведенную автоматом под эту переменную, нужно поместить константу. На реальной компьютере эта константа может быть введена самыми разными способами. Способ зависит от того, как запрограммирован данный фрагмент. Можно, например, потребовать ввод константы с клавиатура или получить его из заранее подготовленного файла. Возможно эта константа будет получена через внешние источники данных, например, от физической установки, подключенной к компьютеру.
Для данного примера способ передачи константы не имеет значения, важно лишь то, что при выполнении блока 2 в ячейку с адресом А будет занесена конкретная константа. Пусть такой константой является число 5.
Далее управление по линии потока передается к блоку 3 «Процесс». В этом блоке при выполнении размещенной в ней команды число 4 умножается на константу, помещенную в ячейку А (т. е. 5), и результат (т. е. 20) присваивается переменной Р (т. е. константа 20 записывается в ячейку по адресу Р). После выполнения этих операций управление передается к блоку 4.
В блоке 4 аналогичным образом производится умножение значений переменной А и результат (константа 25) присваивается переменной S (в ячейку по адресу S будет занесена константа 25). После этого выполняется переход к блоку 5.
При выполнении команд блока 5 выводятся (например, на экран, бумагу, во внешний файл и т. д.) значения переменных А, Р, S, которые сохранились в соответствующих ячейках к этому моменту. Понятно, что для конкретного примера А = 5 будут выведена константы 5, 20, 25, т. е. длина сторона квадрата, его периметр и площадь. Далее управление передается последнему блоку 6.
В блоке б “Конец” производится освобождение ячеек памяти, которые были зарезервированы под переменные А, P, S, и алгоритм заканчивает работу.
Понятно, что при новом запуске этого же алгоритма можно получить совсем другие числа. Так, если в блоке 2 переменной А присвоить значение 20, то алгоритм выдаст в блоке 5 константы 20, 80, 400.
Детальное описание алгоритма рисунка 1 приведено для того, чтобы показать, в какой последовательности автомат выполняет предписанные операции и как при этом меняется состояние памяти автомата, т. е. для того, чтобы объяснить суть происходящих в автомате процессов. Из сказанного нужно уяснить, что автомат выполняет предписанную ему работу шаг за шагом. Всякий шаг обрабатывается процессором. Помимо вычислений процессор при необходимости отдает команды считывавшей/записывавшей головке, что и куда записывать, откуда читать. Конечный результат следует искать в ячейках памяти, каждая из которых до окончания алгоритма имеет известный адрес и хранит записанную в нее константу.
При выполнении проектов нет нужды давать столь подробное описание алгоритма. Тем не менее, описание должно быть выполнено с той степенью полноты, которая позволяет дать ясное представление о всех сторонах и особенностях алгоритмического процесса.
Источник
Линейный алгоритм – это алгоритм, в котором блоки выполняются последовательно сверху вниз от начала до конца.
На рисунке 1 приведен пример блок-схемы алгоритма вычисления периметра Р и площади S квадрата со стороной длины A.
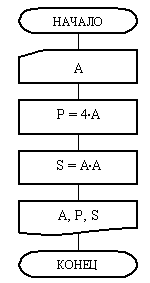
Блок-схема алгоритма состоит из шести блоков. Выполнение алгоритма начинается с блока 1 «Начало». Этот блок символизирует включение автомата, настройку его на выполнение алгоритма и выделение памяти под все переменные, которые задействованы в алгоритме. В алгоритме рисунка 1 таких переменных три: A, Р, S. Следовательно, под каждую из них алгоритмом будет выделено по одной ячейке памяти. На этом блок 1 будет отработан.
Как видно из рисунка, блок 1 связан вертикальной линией потока с блоком 2. Эта линия не имеет стрелки, указывавшей направление потока. Следовательно, этот поток направлен вниз. Таким образом, после выполнения блока 1 управление будет передано на блок 2. Блок 2 «Перфокарта» ( см. табл. 1) показывает, что переменной A следует присвоить значение. Это означает, что в ячейку, отведенную автоматом под эту переменную, нужно поместить константу. На реальной компьютере эта константа может быть введена самыми разными способами. Способ зависит от того, как запрограммирован данный фрагмент. Можно, например, потребовать ввод константы с клавиатура или получить его из заранее подготовленного файла. Возможно эта константа будет получена через внешние источники данных, например, от физической установки, подключенной к компьютеру.
Для данного примера способ передачи константы не имеет значения, важно лишь то, что при выполнении блока 2 в ячейку с адресом А будет занесена конкретная константа. Пусть такой константой является число 5.
Далее управление по линии потока передается к блоку 3 «Процесс». В этом блоке при выполнении размещенной в ней команды число 4 умножается на константу, помещенную в ячейку А (т. е. 5), и результат (т. е. 20) присваивается переменной Р (т. е. константа 20 записывается в ячейку по адресу Р). После выполнения этих операций управление передается к блоку 4.
В блоке 4 аналогичным образом производится умножение значений переменной А и результат (константа 25) присваивается переменной S (в ячейку по адресу S будет занесена константа 25). После этого выполняется переход к блоку 5.
При выполнении команд блока 5 выводятся (например, на экран, бумагу, во внешний файл и т. д.) значения переменных А, Р, S, которые сохранились в соответствующих ячейках к этому моменту. Понятно, что для конкретного примера А = 5 будут выведена константы 5, 20, 25, т. е. длина сторона квадрата, его периметр и площадь. Далее управление передается последнему блоку 6.
В блоке б “Конец” производится освобождение ячеек памяти, которые были зарезервированы под переменные А, P, S, и алгоритм заканчивает работу.
Понятно, что при новом запуске этого же алгоритма можно получить совсем другие числа. Так, если в блоке 2 переменной А присвоить значение 20, то алгоритм выдаст в блоке 5 константы 20, 80, 400.
Детальное описание алгоритма рисунка 1 приведено для того, чтобы показать, в какой последовательности автомат выполняет предписанные операции и как при этом меняется состояние памяти автомата, т. е. для того, чтобы объяснить суть происходящих в автомате процессов. Из сказанного нужно уяснить, что автомат выполняет предписанную ему работу шаг за шагом. Всякий шаг обрабатывается процессором. Помимо вычислений процессор при необходимости отдает команды считывавшей/записывавшей головке, что и куда записывать, откуда читать. Конечный результат следует искать в ячейках памяти, каждая из которых до окончания алгоритма имеет известный адрес и хранит записанную в нее константу.
При выполнении проектов нет нужды давать столь подробное описание алгоритма. Тем не менее, описание должно быть выполнено с той степенью полноты, которая позволяет дать ясное представление о всех сторонах и особенностях алгоритмического процесса.
Задача №1:
“Рассчитать площадь и периметр прямоугольника по двум известным сторонам”.
Данная задача не должна представлять особой трудности,
так как построена она на хорошо известных всем нам формулах расчета площади
и периметра прямоугольника, поэтому зацикливаться на выведении этих формул
мы не будем.
Составим алгоритм решения подобных задач:
1) Прочитать задачу.
2) Выписать известные и неизвестные нам переменные в “дано”.
(В задаче №1 к известным переменным относятся стороны: a,b ;к неизвестным – площадь S и периметр P)
3) Вспомнить либо составить необходимые формулы. (У нас: S=a*b; P=2*(a+b))
4) Составить блок-схему.
5) Записать решение на языке программирования Pascal.
Запишем условие в более кратком виде.
Дано: a,b
Найти: S,P
Блок-схема:

Структура программы, решающей данную задачу, тоже проста:
- 1) Описание переменных;
- 2) Ввод значений сторон прямоугольника;
- 3) Расчет площади прямоугольника;
- 4) Расчет периметра прямоугольника;
- 5) Вывод значений площади и периметра;
- 6) Конец.
А вот и решение:
- Program Rectangle;
- Var a,b,S,P: integer;
- Begin
- write('Введите стороны прямоугольника!');
- readln(a,b);
- S:=a*b;
- P:=2*(a+b);
- writeln('Площадь прямоугольника: ',S);
- write('Периметр прямоугольника: ',P);
- End.
Задача №2: Скорость первого автомобиля – V1 км/ч, второго – V2 км/ч, расстояние между ними S км. Какое расстояние будет между ними через T часов, если автомобили движутся в разные стороны? Значения V1, V2, T и S задаются с клавиатуры.
Решение осуществляем, опять же, следуя алгоритму. Прочитав текст, мы переходим к следующему пункту. Как и во всех физических или математических задачах, это запись условий задачи:
Дано: V1, V2, S, Т
Найти: S1
Далее идет самая главная и в то же время самая интересная часть нашего решения – составление нужных нам формул. Как правило, на начальных стадиях обучения все необходимые формулы хорошо нам известны и взяты из других технических дисциплин (например, на нахождение площади различных фигур, на нахождение скорости, расстояния и т.п.).
Формула, используемая для решения нашей задачи, выглядит следующим образом:
S1=(V1+V2)*T+S
Следующий пункт алгоритма – блок-схема:

А также решение, записанное в Pascal :
- Program Rasstoyanie;
- Var V1,V2,S,T,S1: integer; {Ввод }
- begin
- write('Введите скорость первого автомобиля: ');
- readln(V1);
- write('Введите скорость второго автомобиля: ');
- readln(V2);
- write('Введите время: ');
- readln(T);
- write('Введите расстояние между автомобилями: ');
- readln(S);
- S1:=(V1+V2)*T+S;
- writeln('Через ',t,'ч. расстояние ',S1,' км.');
Составить алгоритм и блок схему для решения следующей задачи: Найти площадь и периметр прямоугольника.
Наташа)
Ученик
(140),
на голосовании
6 лет назад
ИНФОРМАТИКА 9 КЛАСС
(помогите плеас)
Голосование за лучший ответ
Sumbra
Профи
(714)
6 лет назад
1)Получаем длины сторон ‘a’ и ‘b’
2)Вычисляем периметр (P) по формуле P=2(a+b) и площадь (S) по формуле S=a*b
3)Выводим P и S
Александр Иванов Ученик (83)
2 года назад
А можно площять и периметр написать в разных кводратах?
Похожие вопросы
Периметр треугольника блок схема
1. Даны длины сторон треугольника A , B , C . Найти площадь треугольника S . Составьте блок-схему алгоритма решения поставленной задачи.
2. Даны координаты вершин треугольника АВС. Найти его периметр. Составьте блок-схему алгоритма решения поставленной задачи.
3. Дана величина A , выражающая объем информации в байтах. Перевести А в более крупные единицы измерения информации. Составьте блок-схему алгоритма решения поставленной задачи
Вычисление периметра и площади треугольника
Задание на разработку проекта
Сформулируем содержательную постановку задачи: Создать приложение на VB которое должно вычислять периметр и площадь треугольника по заданным значениям трех его сторон:
Задано: А, В, С – значения сторон треугольника.
Требуется определить: Р – периметр треугольника, S – площадь треугольника.
Ограничения на значения исходных данных и их соотношения: А>0, В>0, C>0, А+В>С, А+C>В, В+C>А одновременно.
Проект должен иметь простой интерфейс пользователя:
- две кнопки управления;
- три поля, отображающие входные данные;
- два поля, отображающие выходные данные.
Формализация и уточнение задания:
Для решения задачи существуют известные формулы:
Р = А + В + С;
S = (формула Герона),
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
Структурное программирование
§ 9. Структурное программирование
Информатика. 11 класса. Босова Л.Л. Оглавление
На всех этапах подготовки к алгоритмизации задачи широко используется структурное представление алгоритма.
Cтруктурное программирование воплощает принципы системного подхода в процессе создания и эксплуатации программного обеспечения ЭВМ. В основу структурного программирования положены следующие достаточно простые положения:
- алгоритм и программа должны составляться поэтапно (по шагам).
- сложная задача должна разбиваться на достаточно простые части, каждая из которых имеет один вход и один выход.
- логика алгоритма и программы должна опираться на минимальное число достаточно простых базовых управляющих структур.
Структурное программирование иногда называют еще «программированием без GO TO». Рекомендуется избегать употребления оператора перехода всюду, где это возможно, но чтобы это не приводило к слишком громоздким структурированным программам.
К полезным случаям использования оператора перехода можно отнести выход из цикла или процедуры по особому условию, «досрочно» прекращающего работу данного цикла или данной процедуры, т.е. завершающего работу некоторой структурной единицы (обобщенного оператора) и тем самым лишь локально нарушающего структурированность программы.
Фундаментом структурного программирования является теорема о структурировании.
Эта теорема устанавливает, что, как бы сложна ни была задача, схема соответствующей программы всегда может быть представлена с использованием ограниченного числа элементарных управляющих структур.
Базовыми элементарными структурами являются структуры: следование, ветвление и повторение (цикл), любой алгоритм может быть реализован в виде композиции этих трех конструкций.

Первая (а) структура — тип последовательность (или просто последовательность), вторая (б) – структура выбора (ветвление), третья (в) – структура цикла с предусловием.
9.1. Общее представление о структурном программировании
Программирование как род занятий и сфера деятельности интенсивно развивается со второй половины прошлого века. За это время сложились определённые технологии, способствующие повышению производительности труда программистов, в том числе сокращению числа ошибок, упрощению отладки, модификации и сопровождения программного обеспечения. Особенно это важно при разработке больших и сложных программных комплексов, осуществляемой усилиями целых коллективов программистов.
Одна из таких технологий — структурное программирование — была разработана ещё в начале 70-х годов прошлого века и связана с именем выдающегося нидерландского ученого Эдсгера Дейкстры (1930-2002).
Структурное программирование — технология разработки программного обеспечения, в основе которой лежит представление программы в виде иерархической структуры логически целостных фрагментов (блоков).
Перечислим некоторые принципы структурного программирования.
1. Любая программа строится из трёх базовых управляющих конструкций: последовательность, ветвление, цикл.
2. В программе базовые управляющие конструкции могут быть вложены друг в друга произвольным образом.
3. Повторяющиеся фрагменты программы можно оформить в виде подпрограмм (процедур и функций). В виде подпрограмм можно оформить логически целостные фрагменты программы, даже если они не повторяются.
4. Все перечисленные конструкции должны иметь один вход и один выход.
5. Разработка программы ведётся пошагово, методом «сверху вниз».
О методе разработки алгоритма «сверху вниз» вы получили представление в курсе информатики основной школы. Напомним его ключевые моменты на примере разработки некоторой программы.
Сначала пишется короткий текст основной программы. В ней вместо каждого логически целостного фрагмента вставляется вызов подпрограммы, которая будет выполнять этот фрагмент. Вместо настоящих, работающих, подпрограмм в программу вставляются так называемые заглушки. Как правило, они удовлетворяют требованиям интерфейса заменяемого фрагмента, но не выполняют его функций.
На следующем шаге следует убедиться, что подпрограммы вызываются в правильной последовательности, т. е. верна общая структура программы.
После этого подпрограммы-заглушки последовательно заменяются на полнофункциональные, причём разработка каждой подпрограммы ведётся тем же методом, что и основной программы. На каждом этапе проверяется, что уже созданная программа правильно работает по отношению к подпрограммам более низкого уровня.
Разработка заканчивается тогда, когда ни на одном уровне не останется ни одной заглушки. Полученная программа проверяется и отлаживается.
Такая последовательность гарантирует, что на каждом этапе разработки программист будет иметь дело с обозримым и понятным ему множеством фрагментов, осознавая, что общая структура всех более высоких уровней программы верна.
Действия по вычислению длины отрезка представляют собой логически целостный фрагмент, который целесообразно оформить в виде вспомогательного алгоритма.
9.2. Вспомогательный алгоритм
Пример 1. Применим метод «сверху вниз» для разработки алгоритма нахождения периметра треугольника, заданного координатами своих вершин.
Пусть ХА, ХВ, YA, YB, ХС, YC — координаты вершин треугольника ABC. Его периметр — сумма длин отрезков АВ, ВС и АС.
Из курса геометрии вам известна формула для вычисления длины отрезка АВ по координатам его концов (рис. 2.11):

Действия по вычислению длины отрезка представляют собой логически целостный фрагмент, который целесообразно оформить в виде вспомогательного алгоритма.

Рис. 2.11. Отрезок АВ
Вспомогательный алгоритм — это алгоритм, целиком используемый в составе другого алгоритма.
На рисунке 2.12 представлены:
1) блок-схема алгоритма вычисления периметра треугольника, предполагающая вызов вспомогательного алгоритма Отрезок;
2) блок-схема вспомогательного алгоритма Отрезок.
При вызове вспомогательного алгоритма указываются его параметры (входные данные и результаты). Параметрами вспомогательного алгоритма Отрезок являются величины XI, Y1, Х2, Y2, D. Это формальные параметры, они используются при описании алгоритма. При конкретном обращении к вспомогательному алгоритму формальные параметры заменяются фактическими параметрами, т. е. именно теми величинами, для которых будет исполнен вспомогательный алгоритм. Типы, количество и порядок следования формальных и фактических параметров должны совпадать.

Рис. 2.12. Алгоритм вычисления периметра треугольника и вспомогательный алгоритм Отрезок
Команда вызова вспомогательного алгоритма исполняется следующим образом:
1) формальные входные данные вспомогательного алгоритма заменяются значениями фактических входных данных, указанных в команде вызова вспомогательного алгоритма;
2) для заданных входных данных исполняются команды вспомогательного алгоритма;
3) полученные результаты присваиваются переменным с именами фактических результатов;
4) осуществляется переход к следующей команде основного алгоритма.
Каким будет результат работы алгоритма при следующих исходных данных: ХА = 1, ХВ = 2, ХС = 3, YA = 1, YВ = 3, YC = 1.
9.3. Рекурсивные алгоритмы
Алгоритм называется рекурсивным, если на каком-либо шаге он прямо или косвенно обращается сам к себе.
Пример 2. Как известно, факториал натурального числа n определяется следующим образом: n! = 1 • 2 • 3 • … • n; 0! считается равным единице (0! = 1).
Иначе это можно записать так:

В определении факториала через рекурсию имеется условие n ? 1, при достижении которого вызов рекурсии прекращается.
В рекурсивном определении должно присутствовать ограничение (граничное условие), при выходе на которое дальнейшая инициация рекурсивных обращений прекращается.
Пример 3. Определим функцию S(n), вычисляющую сумму цифр в заданном натуральном числе n:

Самостоятельно определите функцию К(n), которая возвращает количество цифр заданного натурального числа n.
Пример 4. Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:

Требуется выяснить, чему равно значение функции F(7). По условию, F(1) = F(2) = 1.

Подобные вычисления можно проводить в уме, а их результаты фиксировать в таблице:

Пример 5. Исполнитель Плюс имеет следующую систему команд:
1) прибавь 1;
2) прибавь 2;
3) прибавь 4.

С помощью первой из них исполнитель увеличивает число на экране на 1, с помощью второй — на 2, с помощью третьей — на 4. Программа для исполнителя Плюс — это последовательность команд. Выясним, сколько разных программ, преобразующих число 20 в число 30, можно составить для этого исполнителя.
Количество программ, с помощью которых можно получить некоторое число n, будем рассматривать как функцию К(n).
Число, меньшее 20, при заданных начальных условиях и системе команд исполнителя Плюс получить невозможно. Следовательно, при n 20 может быть получено из чисел n — 1, n — 2 и n — 4 одной из трёх команд, входящих в систему команд исполнителя — «прибавь 1», «прибавь 2» и «прибавь 4» соответственно. При этом каждая программа получения из исходного числа чисел n-1, n-2 и n-4 удлинится на одну команду и будет приводить к числу n. Следовательно, К(n) = К(n — 1) + + К(n — 2) + К(n — 4).
Запишем все соотношения, определяющие функцию К(n):
Заполним по этой формуле таблицу для всех значений n от 20 до 30:

Итак, существует 169 различных программ, с помощью которых исполнитель Плюс может преобразовать число 20 в 30.
Любой объект, который частично определяется через самого себя, называется рекурсивным. Нас окружает множество рекурсивных объектов. Приведём примеры только некоторых из них.
1. Матрёшка — русская деревянная игрушка в виде расписной куклы, внутри которой находятся подобные ей куклы меньшего размера.

2. Два зеркала, поставленные друг напротив друга, — в них образуются два коридора из затухающих отражений. Это, например, можно наблюдать в спальном железнодорожном вагоне.

3. Примером рекурсивной структуры является замечательное стихотворение Р. Бернса «Дом, который построил Джек» в переводе С. Маршака.
4. Рекурсивную природу имеют геометрические фракталы. На рисунке представлено построение одного из геометрических фракталов — треугольника Серпинского. Чтобы его получить, нужно взять равносторонний треугольник с внутренней областью, провести в нём средние линии и «выкинуть» центральный из четырёх образовавшихся маленьких треугольников. Дальше эти же действия нужно повторить с каждым из оставшихся трёх треугольников, и т. д.

9.4. Запись вспомогательных алгоритмов на языке Pascal
Запись вспомогательных алгоритмов в языках программирования осуществляется с помощью подпрограмм. В языке Pascal различают два вида подпрограмм: процедуры и функции.
Процедура — подпрограмма, имеющая произвольное количество входных и выходных данных.
Описание процедуры имеет вид:
procedure ( ; var: );
begin
end;
В заголовке процедуры после её имени приводится перечень формальных параметров и их типов. Для вызова процедуры достаточно указать её имя со списком фактических параметров. При этом между фактическими и формальными параметрами должно быть полное соответствие по количеству, порядку следования и типу.
Пример 6. Запишем на языке Pascal программу нахождения периметра треугольника, заданного координатами его вершин. Вспомогательный алгоритм оформим с помощью процедуры.

Выполните программу на компьютере.
Подумайте, каким образом можно модифицировать программу, чтобы вычислять с её помощью периметр n-угольника. Каким образом при решении этой задачи можно использовать массивы?
Функция — подпрограмма, имеющая единственный результат, записываемый в ячейку памяти, имя которой совпадает с именем функции.
Описание функции имеет вид:

В заголовке функции после её имени приводится описание входных данных — указывается перечень формальных параметров и их типов. Там же указывается тип самой функции, т. е. тип результата. В блоке функции обязательно должен присутствовать оператор
Для вызова функции достаточно указать её имя со списком фактических параметров в любом выражении, в условиях (после слов if, while, until) или в операторе write главной программы.
Пример 7. Запишем на языке Pascal программу нахождения периметра треугольника, заданного координатами его вершин. Вспомогательный алгоритм оформим с помощью функции.

Выполните программу на компьютере.
На основе этой программы напишите функцию, вычисляющую площадь треугольника по целочисленным координатам его вершин. Используйте эту функцию для вычисления площади n-угольника.
САМОЕ ГЛАВНОЕ
Структурное программирование — технология разработки программного обеспечения, в основе которой лежит представление программы в виде иерархической структуры логически целостных фрагментов (блоков).
Основные принципы структурного программирования заключаются в том, что:
1) любая программа строится из трёх базовых управляющих конструкций: последовательность, ветвление, цикл;
2) в программе базовые управляющие конструкции могут быть вложены друг в друга произвольным образом;
3) повторяющиеся фрагменты программы можно оформить в виде подпрограмм (процедур и функций). В виде подпрограмм можно оформить логически целостные фрагменты программы, даже если они не повторяются;
4) все перечисленные конструкции должны иметь один вход и один выход;
5) разработка программы ведётся пошагово, методом «сверху вниз».
Вспомогательный алгоритм — это алгоритм, целиком используемый в составе другого алгоритма.
Алгоритм называется рекурсивным, если на каком-либо шаге он прямо или косвенно обращается сам к себе.
Запись вспомогательных алгоритмов в языках программирования осуществляется с помощью подпрограмм. В языке Pascal различают два вида подпрограмм: процедуры и функции.
Вопросы и задания
1. В чём заключается сущность структурного программирования? Какие преимущества обеспечивает эта технология?
2. Какой алгоритм называется вспомогательным?
3. Вспомните, в чём состоит суть метода последовательного построения (уточнения) алгоритма. Как он называется иначе?
4. Опишите основные шаги разработки программы методом «сверху вниз».
5. Дан прямоугольный параллелепипед, длины рёбер которого равны а, b и с.

Требуется определить периметр треугольника, образованного диагоналями его граней. Какой алгоритм целесообразно использовать при решении этой задачи в качестве вспомогательного?
6. Какой вспомогательный алгоритм называется рекурсивным? Что такое граничное условие и каково его назначение в рекурсивном алгоритме?
7. Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:

Требуется выяснить, чему равно значение функции F(10).
8. Исполнитель Калькулятор имеет следующую систему команд:
1) прибавь 1;
2) умножь на 2.
С помощью первой из них исполнитель увеличивает число на экране на 2, с помощью второй — в 2 раза.
1) Выясните, сколько разных программ, преобразующих число 1 в число 20, можно составить для этого исполнителя.
2) Сколько среди них таких программ, у которых в качестве промежуточного результата обязательно получается число 15?
3) Сколько среди них таких программ, у которых в качестве промежуточного результата никогда не получается число 12?
9. Попробуйте найти рекурсивные синтаксические структуры:
1) в поэме А. Блока «Двенадцать»;
2) в стихотворении М. Лермонтова «Сон»;
3) в романе М. Булгакова «Мастер и Маргарита»;
4) в фольклоре.
10. Найдите информацию о таких геометрических фракталах, как Снежинка Коха, Т-квадрат, Н-фрактал, кривая Леви, Драконова ломаная.
11. Напишите программу вычисления значения функции F(n), рассмотренной в примере 4 этого параграфа. Вычислите с её помощью значение функции F(7).
12. Напишите программу вычисления

13. Дана программа:

Не выполняя программу на компьютере, выясните, что получится в результате работы этой программы.
Проверьте свой результат, выполнив программу на компьютере.
Дополнительные материалы к главе смотрите в авторской мастерской.
[spoiler title=”источники:”]
http://reshimvse.com/article.php?id=26
http://murnik.ru/strukturnoe-programmirovanie
[/spoiler]
