Аннотация:
Существует ряд задач, в которых одни и те же действия нужно совершить над набором данных, массивом. Массивы применяются в разных задачах, начиная от математики (вектора, матрицы), заканчивая оконными приложениями (набор строк, параметры приложения и т.д.).
Цель данной лекции – ознакомить студентов с понятием массива, его видами; показать основные принципы работы с массивами.
Массив – это пронумерованный набор однотипных элементов.
Массивы бывают статическими и динамическими. У статического массива количество элементов известно заранее и не может быть изменено. У динамического массива количество элементов заранее неизвестно и определяется в процессе выполнения программы.
Также массивы различаются по размерности: одномерные, двумерные, трехмерные и т.д. Примером одномерного массива может послужить вектор 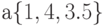 . Примером двухмерного массива может послужить матрица. Примером трехмерного массива может послужить набор высот местности.
. Примером двухмерного массива может послужить матрица. Примером трехмерного массива может послужить набор высот местности.
Массивы различают по типу элементов. Бывают целочисленные, вещественные (состоящие из дробных чисел), символьные массивы.
Примеры массивов:
- вектор
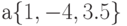 – одномерный вещественный массив из трех элементов;
– одномерный вещественный массив из трех элементов; - матрица
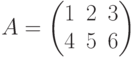 – двумерный целочисленный массив из шести элементов;
– двумерный целочисленный массив из шести элементов; -
 – одномерный символьный массив;
– одномерный символьный массив; -
 – не является массивом, т.к. часть элементов символы, часть элементов числа.
– не является массивом, т.к. часть элементов символы, часть элементов числа.
Мы будем рассматривать только статические одномерные и двумерные численные массивы.
Занятие 1. Одномерные массивы
Индекс – это номер элемента в массиве.
У одномерного массива один индекс, обычно он обозначается  .
.
Чтобы использовать одномерный массив в программе, необходимо:
- объявить массив в функции main():
тип_данных имя_массива[количество элементов]; double a[3]; //статический массив а из трех дробных чисел int b[7]; //статический массив b из семи целых чисел
- проинициализировать массив, т.е. задать каждому элементу конкретное числовое значение;
- провести вычисления, исследования.
Примечание. Индексация в массиве начинается с 0, т.е. индекс у самого первого элемента в массиве  . Индексация в массиве
. Индексация в массиве  указана на рис. 6.1.
указана на рис. 6.1.

Рис.
6.1.
Индексация одномерного массива
Способы инициализации одномерного массива представлены в табл. 6.1. Обратим внимание на то, что число  известно заранее и в программе фигурировать не будет.
известно заранее и в программе фигурировать не будет.
| Часть блок-схемы | Часть программы |
|---|---|
| 1. инициализация числами
|
double a[4]={0.5, -2,856, 1};
|
| 2. с клавиатуры:
|
double a[n];
int i;
for(i=0; i<n; i=i+1){
cout<<"a["<<i<<"]=";
cin>>a[i];
}
|
| 3. из файла:
|
double a[n];
int i;
fstream file;
file.open("1.txt", ios::in);
for(i=0; i<n; i=i+1){
file>>a[i];
}
file.close();
|
| 4. по заданной формуле a[i]=f(i):
|
double a[n];
int i;
for(i=0; i<n; i=i+1){
a[i]=f(i);
}
|
Примечание. Более подробно работа с файлами будет рассмотрена позже.
Вывод одномерного массива на экран представлен в табл. 6.2.
| Часть блок-схемы | Часть программы |
|---|---|
|
|
for(i=0; i<n; i=i+1){
cout<<"a["<<i<<"]="<<a[i]<<endl;
}
|
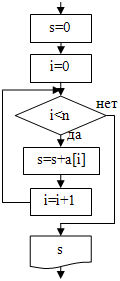
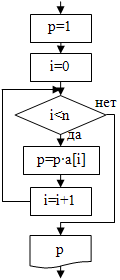
Принципы нахождения таких величин, как сумма, произведение, минимальное, максимальное значение, представлены в табл. 6.3.
| Часть блок-схемы | Часть программы |
|---|---|
| 1. нахождение суммы:
|
s=0;
for(i=0; i<n; i=i+1){
s=s+a[i];
}
cout<<"s="<<s<<endl;
|
| 2. нахождение произведения:
|
p=1;
for(i=0; i<n; i=i+1){
p=p*a[i];
}
cout<<"p="<<p<<endl;
|
| 3. нахождение среднего арифметического и количества элементов:
|
s=0, k=0;
for(i=0; i<n; i=i+1){
s=s+a[i];
k=k+1;
}
s=s/k;
cout<<"s="<<s<<endl;
cout<<"k="<<k<<endl;
|
| 4. нахождение максимального элемента:
|
max=-10E10;
imax=0;
for(i=0; i<n; i=i+1){
if(a[i]>max){
max=a[i];
imax=i;
}
}
cout<<"max="<<max<<" imax="<<imax<<endl;
|
| 5. нахождение минимального элемента:
|
min=10E10;
imin=0;
for(i=0; i<n; i=i+1){
if(a[i]<min){
min=a[i];
imin=i;
}
}
cout<<"min="<<min<<" imin="<<imin<<endl;
|
| 6. поменять местами элементы с индексами i1 и i2:
|
tmp=a[i1]; a[i1]=a[i2]; a[i2]=tmp; |
7. вычисление формулы ![S=sum^{n=1}_{i=0}f(a[i],i)](https://intuit.ru/sites/default/files/tex_cache/31789b72c1e4a1ccda1676153fedc730.png) : :
|
s=0;
for(i=0; i<n; i=i+1){
s=s+f(a[i],i);
}
cout<<"s="<<s<<endl;
|
Пример 1. Даны четыре одномерных массива: 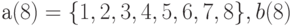 вводится с клавиатуры,
вводится с клавиатуры, 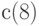 вычисляется по формуле
вычисляется по формуле 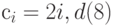 вычисляется по формуле
вычисляется по формуле 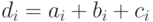 . Построить таблицу значений массивов.
. Построить таблицу значений массивов.
Решение. Сначала необходимо проинициализировать массивы согласно условию задачи.
Массив  задан числами (первый способ инициализации), поэтому он будет проинициализирован при объявлении.
задан числами (первый способ инициализации), поэтому он будет проинициализирован при объявлении.
В цикле по переменной  введем
введем  с клавиатуры (второй способ инициализации), массивы
с клавиатуры (второй способ инициализации), массивы  и
и  рассчитаем по формулам (четвертый способ инициализации).
рассчитаем по формулам (четвертый способ инициализации).
Далее организуем еще один цикл по переменной  , в котором выведем все проинициализированные массивы на экран.
, в котором выведем все проинициализированные массивы на экран.
Вывод таблицы на экран нельзя делать в первом цикле, т.к. в каждой итерации будет идти запрос очередного элемента  , тогда таблица со значениями массивов будет смешана с запросом элемента
, тогда таблица со значениями массивов будет смешана с запросом элемента  .
.
Блок-схема представлена на рис. 6.2.
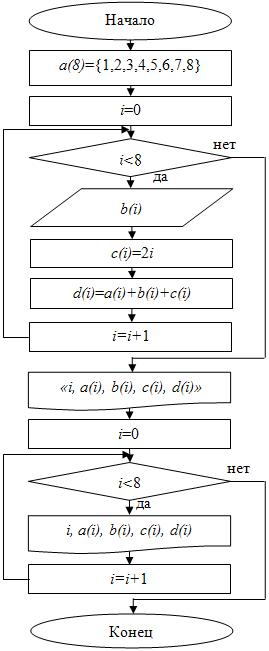
Рис.
6.2.
Блок-схема для примера 1
Код программы (Visual Studio) с оператором for:
// proga27.cpp: определяет точку входа для консольного приложения.
//
#include "stdafx.h"
#include <iostream>
#include <iomanip>
using namespace std;
int main()
{
double a[8]={1,2,3,4,5,6,7,8};
double b[8], c[8], d[8];
int i;
for(i=0; i<8; i=i+1){
cout<<"b["<<i<<"]=";
cin>>b[i];
c[i]=2.0*i;
d[i]=a[i]+b[i]+c[i];
}
cout<<setw(2)<<"i"<<setw(5)<<"a"<<setw(5)<<"b"<<setw(5)<<"c"<<setw(5)<<"d"<<endl;
for(i=0; i<8; i=i+1){
cout<<setw(2)<<i<<setw(5)<<a[i]<<setw(5)<<b[i]<<setw(5)<<c[i]<< setw(5)<<d[i]<<endl;
}
return 0;
}
Результат выполнения программы:

Пример 2. Массив 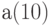 задан формулой
задан формулой 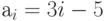 . Вычислить сумму положительных элементов массива и поменять местами первый и последний элементы.
. Вычислить сумму положительных элементов массива и поменять местами первый и последний элементы.
Решение.
Обозначим за  сумму положительных элементов массива. При расчете
сумму положительных элементов массива. При расчете  требуется дополнительное условие: “
требуется дополнительное условие: “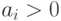 “. Первый элемент массива имеет индекс 0, последний элемент имеет индекс 9, поэтому будем менять местами
“. Первый элемент массива имеет индекс 0, последний элемент имеет индекс 9, поэтому будем менять местами  и
и  . Из-за перемены мест элементов массив изменится, поэтому выведем его еще раз.
. Из-за перемены мест элементов массив изменится, поэтому выведем его еще раз.
Блок-схема представлена на рис. 6.3.
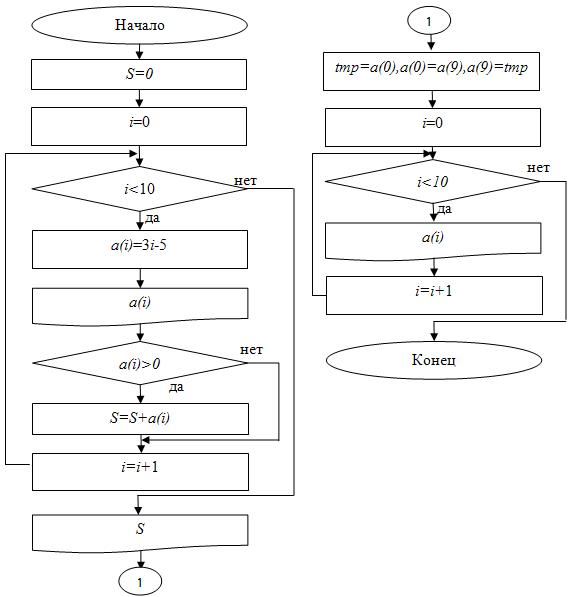
Рис.
6.3.
Блок-схема для примера 2
Код программы (Visual Studio) с оператором for:
// proga28.cpp: определяет точку входа для консольного приложения.
//
#include "stdafx.h"
#include <iostream>
#include <iomanip>
using namespace std;
int main(){
double S, tmp, a[10];
int i;
S=0;
for(i=0; i<10; i=i+1){
a[i]=3.0*i-5.0;
cout<<setw(3)<<a[i];
if(a[i]>0){
S=S+a[i];
}
}
cout<<endl;
cout<<"S="<<S<<endl;
tmp=a[0];
a[0]=a[9];
a[9]=tmp;
for(i=0; i<10; i=i+1){ cout<<setw(3)<<a[i]; }
cout<<endl;
return 0;}
Результат выполнения программы:

Ручной счет:
при i=0 a(0)=3i-5=3·0-5=-5; при i=1 a(1)=3i-5=3·1-5=-2; при i=2 a(2)=3i-5=3·2-5=1; при i=3 a(3)=3i-5=3·3-5=4; при i=4 a(4)=3i-5=3·4-5=7; при i=5 a(5)=3i-5=3·5-5=10; при i=6 a(6)=3i-5=3·6-5=13; при i=7 a(7)=3i-5=3·7-5=16; при i=8 a(8)=3i-5=3·8-5=19; при i=9 a(9)=3i-5=3·9-5=22; сумма положительных элементов S=1+4+7+10+13+16+19+22=92.·
Используя
команды повторения можно коротким
алгоритмом описать большой объем
действий, необходимых для решения
поставленной задачи. Массивы играют
аналогичную роль по отношению к данным
и позволяют коротким алгоритмом описать
действия с огромным объемом информации.
Применение массивов
при описании алгоритмов решения
практических задач позволяет:
-
записать коротким
алгоритмом работу с большим объемом
информации; -
расширить область
применимости алгоритма.
Необходимость в
применении массивов для описания
алгоритмов решения задач возникает,
когда при решении задач приходится
иметь дело с большим, конечным количеством
однотипных упорядоченных по индексам
объектов.
Массив
– это
упорядоченная по индексам, конечная
совокупность однотипных объектов,
образованных по одному и тому же правилу.
Отношение порядка в массиве задается
с помощью индексирования элементов
массива. Если для индексирования массива
используется один индекс, то массив
называется одномерным, если два или
больше, то многомерным. Для индексации
элементов двумерного массива указываются
два индекса, первый индекс, как правило,
номер строки, второй – номер столбца.
Одномерный массив часто называют
вектором, двумерный – матрицей.
При работе с
массивами, каждому массиву дается имя.
Работа с массивом – это работа с
элементами массива. Элементу массива
дается имя, соответствующее имени
массива, и указывается в квадратных или
круглых скобках порядковый номер этого
элемента в массиве.
Очевидно, чтобы
задать массив (таблицу), необходимо:
-
указать, что
однотипные объекты объединены в массив
(таблицу); -
указать имя
массива (таблицы), начальный и конечный
порядковые номера индексов его (её)
элементов; -
указать тип
значений элементов массива (таблицы).
При описании
массива после имени массива будем в
круглых (квадратных) скобках указывать
начальный и конечный номера каждого
индекса элементов массива через
двоеточие. Если массив многомерный, то
описание начального и конечного номеров
каждого индекса элементов массива
разделим запятой. Например, А(1:50) –
массив, элементы которого: А(1), А(2), … ,
А(50); В(1:2,1:3) – массив, элементы которого:
![]()
.
Пример 1.
Одномерный массив Осадки (1:365) –
количество осадков в течение года.
|
Дни года |
1 |
2 |
3 |
… |
364 |
365 |
|
Осадки в мм |
50 |
34 |
120 |
… |
23 |
5 |
Пример 2.
Двумерный массив Расписание (1:4,1:2) –
расписание уроков на 2 дня в 4 классе
общеобразовательной школы.
|
Дни Номер |
Понедельник |
Вторник |
|
1 |
Математика |
Русский язык |
|
2 |
Русский язык |
Математика |
|
3 |
Природоведение |
История |
|
4 |
Физкультура |
Рисование |
Массивы
имеют размер и размерность. Размер
массива –
это количество
элементов
в данном массиве, размерность
– количество
индексов,
необходимых для однозначного определения
места фиксированного элемента массива.
Массив примера 1 имеет размерность,
равную 1 (одномерный), размер – 365. Массив
примера 2 имеет размерность равную 2
(двумерный), размер 2∙4=8. Элемент массива
называется переменной с индексом,
переменная без индекса – простой
переменной. Над элементами массива
можно производить те операции, которые
допустимы для базового типа.
В
качестве типов индексов элементов
массива можно использовать целый тип.
Индексы могут задаваться константами,
переменными и выражениями. Значения
переменных и выражений задают номер
элемента массива, поэтому их значения
должны быть определены при обращении
к этому элементу. Элементами массива
могут быть значения любого типа данной
реализации языка.
Пример 3.
Пусть массив A
– одномерный массив, имеющий 4 элемента
целого типа – integer:
-12, 0, 41, -131.
направление изменения
индекса

1
2 3 4
|
– |
0 |
41 |
-131 |
A[1]=-12;
если
i=2,
то
A[i]=0;
если
i=1,
j=3,
то
A[i+j]=-131
Пример 4.
Массив Q
– двумерный массив, имеющий 3 строки и
4 столбца – 12 элементов вещественного
типа – real:
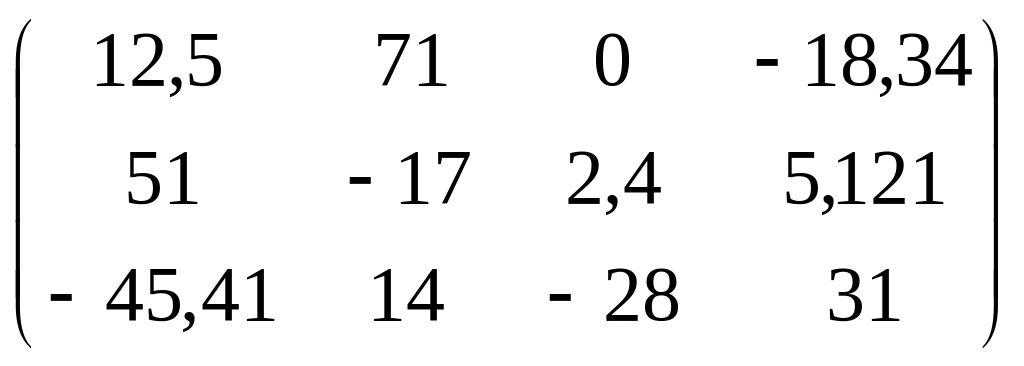
.
направление изменения второго индекса

1 2 3 4
|
1 |
12,5 |
71 |
0 |
-18,34 |
|
2 |
51 |
-17 |
2,4 |
5 |
|
3 |
-45,41 |
14 |
-28 |
31 |
н
аправление
изменения
первого
и
ндекса
Q[3,3]=-28;
если
i=1,
j=2,
s=2,
то
Q[i∙s,j+2]=Q[2,4]=5,121
З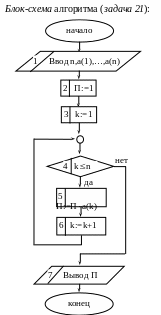
адача
21. Произведение
элементов массива. Составьте блок-схему
алгоритма нахождения произведения
вещественных чисел
П =
a(1)a(2)…a(n).
Решение.
Смотри
блок-схему алгоритма (задача 21),
использована циклическая структура
«while
P
do
S».
Произведение можно
находить так:
П:=а(1); П:=Па(2);
… ; П:=Па(n).
В блок-схеме вместо
этой цепочки операторов запишем оператор
П:=Па(k),
где k
изменяется от 1 до n;
k
– параметр цикла. Чтобы значение первого
произведения было равно a1,
следует положить начальное значение П
равным 1. Операторы 5-6 составляют тело
цикла.
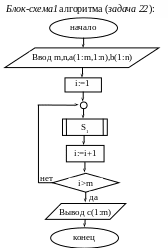
Задача 22.
Произведение матриц. Составьте блок-схему
нахождения произведения матрицы А
на матрицу В:
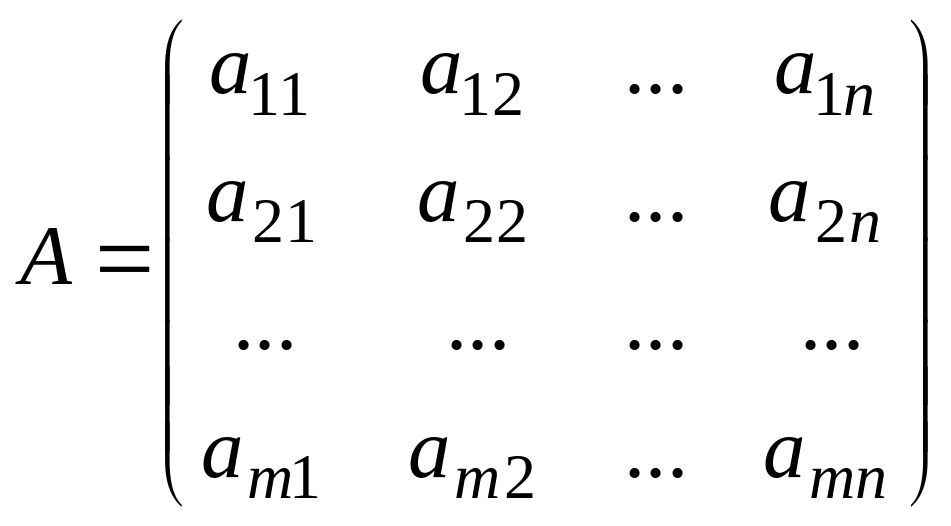
,
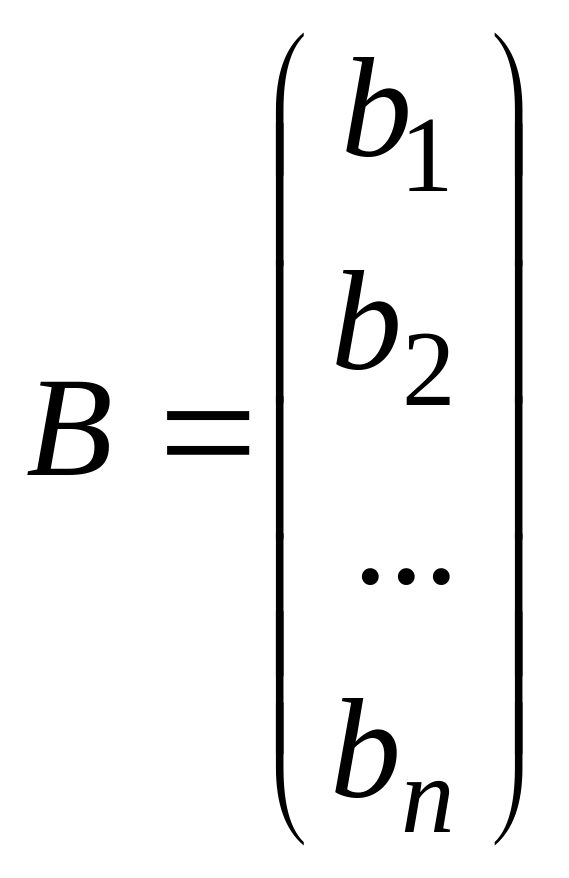
.
Решение.
Смотри блок-схемы 1-3 алгоритма (задача
22).
Смотри блок-схему
1 (задача 22). Произведение матрицы А
на матрицу
В
есть матрица-столбец; обозначим ее С.
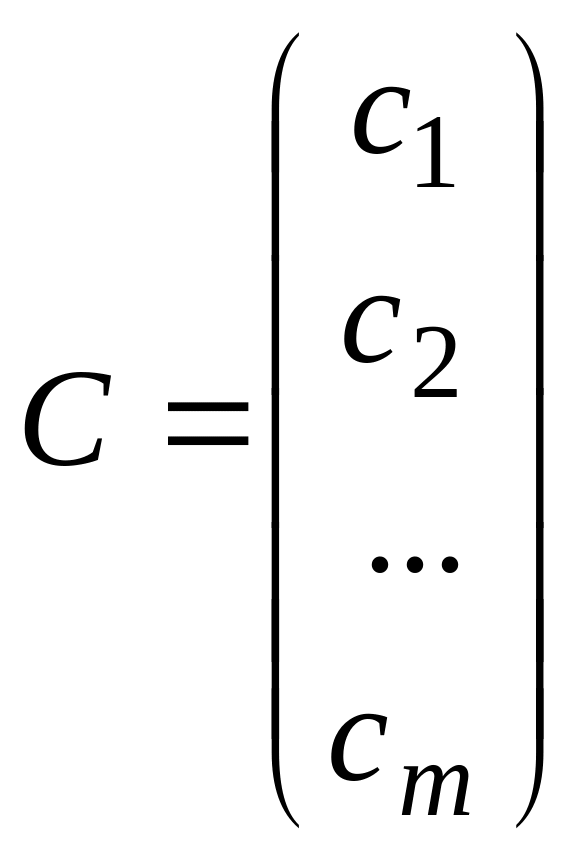
,
где
![]()
,
i=1,2,…,m.
Функциональный
блок, вычисляющий величину c(i),
обозначим S1.
Смотри блок-схему 2 (задача 22).
П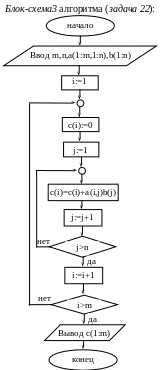
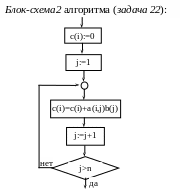
олучать
элементы c(i)
при фиксированном i
можно так: c(i) = c(i)+a(i,j)∙b(j),
где 1jn,
а начальное значение c(i)
равно 0.
Очевидно, что
функциональный блок S1
будет содержать циклическую структуру,
например, структуру «repeat
S
until
P».
Подставив
детализацию блока S1
(блок-схема 2 (задача 22)) в блок-схему 1
(задача 22), получим одну циклическую
структуру внутри другой, вложенные
циклы – блок-схема 3(задача 22).
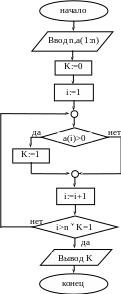
Задача
23.
Положительные числа. Дана числовая
последовательность a1,
a2,
… , an.
Определите, есть ли среди ai,
1in
положительные числа, если да, то
переменной K
присвойте значение 1, в противном случае
– значение 0. Составьте блок-схему
алгоритма решения поставленной задачи.
Решение.
Смотри блок-схему алгоритма (задача
23).
Б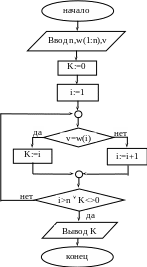
лок-схема
алгоритма
(задача
23):
Блок-схема
алгоритма (задача
24):
Поскольку
положительный элемент может оказаться
на i-ом
месте, где i<n,
то нужно иметь возможность выйти из
цикла при i<n.
С этой целью перед началом цикла
переменной K
присвоено значение 0, а если ai>0
– истинно, K
получит значение 1. Проверка окончания
организована так, что выход из цикла
произойдёт или при i>n
(положительного элемента нет), K
= 0, или при
i>n
и K = 1
(этот элемент – последний в массиве),
или при i<n
и K
= 1 (положительный
элемент – ai,
где 1in–1).
Задача 24.
Поиск
буквы. Пусть w
– слово, состоящее из n
букв русского алфавита: w(1),
w(2),
… , w(n);
v
– буква, относительно которой требуется
установить, входит ли она в слово. Если
входит, то укажите номер позиции первого
вхождения буквы в слово. Составьте
блок-схему алгоритма решения поставленной
задачи.
Решение.
Смотри блок-схему алгоритма (задача
24).
Будем просматривать
последовательно все буквы данного
слова. Для реализации этого используем
цикл с постусловием. Если буква v
не входит в слово, то выход из цикла
осуществляется при i>n,
где i
– номер рассматриваемой буквы. Значение
переменной K
в этом случае равно 0. Если буква v
входит в слово, выход из цикла может
быть осуществлен раньше, чем i
станет больше n,
при K<>
0, где K
– номер позиции первого вхождения
буквы v
в слово w.
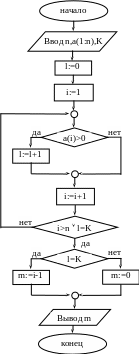
Задача 25.
Количество
положительных элементов. Дана
последовательность чисел a1,
a2,
… , an.
Присвойте переменной m
номер K-го
положительного элемента этой
последовательности. Если в последовательности
положительных элементов меньше K,
то переменной m
присвойте значение 0. Составьте блок-схему
алгоритма решения поставленной задачи.
Решение.
Смотри блок-схему алгоритма (задача
25).
Подсчет
количества положительных элементов
массива организуем с помощью цикла с
постусловием. Если положительных
элементов нет или их меньше, чем K,
выход из
цикла осуществим при i>n,
m
присвоим значение 0. При l
= K,
где l
– число положительных элементов, также
реализуем выход из цикла. При этом i
получит уже следующее значение. Значит,
номер K-го
положительного элемента на единицу
меньше i.
Задача 26.
Сдвиг в
массиве.
Переставьте вещественные элементы
массива A(1:n)
таким образом, чтобы они шли в следующем
порядке: А(n),
А(1), А(2), … , A(n-2),
A(n-1),
т.е. в массиве произведите сдвиг элементов
на одну позицию вправо. Составьте
блок-схему алгоритма решения поставленной
задачи.
Решение.
Смотри блок-схему алгоритма (задача
26).
Б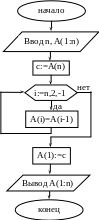
лок-схема
алгоритма (задача
25):
Блок-схема
алгоритма (задача
26):
Задача 27.
Максимальные
элементы массива. Дана последовательность
чисел a1,
a2,
… , an.
Найдите количество максимальных
элементов последовательности и их
номера. Составьте блок-схему решения
поставленной задачи.
Решение.
Смотри блок-схемы 1-2 алгоритма (задача
27).
В
блок-схеме1 алгоритма (задача 27) первый
цикл организуем для определения
максимального элемента, значение
которого присваивается переменной b.
Начальное значение b
положим равным a1.
Второй
цикл считает K
– количество одинаковых максимальных
элементов. Переменная M(K)
принимает значение индекса встретившегося
максимального элемента. M(K)
– числовая последовательность, членами
которой являются эти индексы.
Б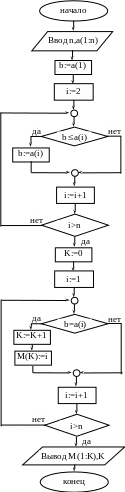
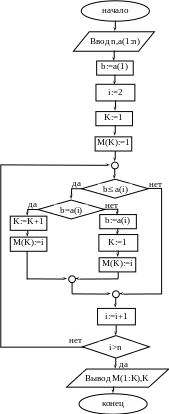
лок-схема1
алгоритма (задача
27):
Блок-схема2
алгоритма (задача
27):

Блок-схема2
алгоритма (задача 27) предполагает в
одном цикле на i-ом
шаге определение максимального элемента
из i
рассмотренных, подсчет количества
таких элементов и фиксирование их
номеров. Если на (i+1)-ом
шаге встречается больший элемент, то
операторы b:=ai,
K:=1,
mK:=i
зададут новые начальные значения
переменных b,
K,
mK,
и все вычисления будут проведены
относительно нового большего элемента.
Задача 28.
Дружественные числа.
Дружественными
числами называются два натуральных
числа, таких, что каждое из них равно
сумме всех натуральных делителей
другого, исключая само это другое число.
Числа 220 и 284 являются дружественными
числами, так как сумма делителей числа
220 – это 1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 =
284, а сумма делителей числа 284 – это 1 +
2 + 4 + 71 + 142 = 220. Составьте блок-схему
алгоритма нахождения дружественных
чисел на отрезке [2;n].
Решение.
Смотри блок-схему алгоритма (задача
28).
Блок-схема
алгоритма (задача
28):
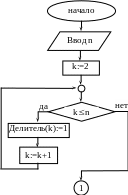
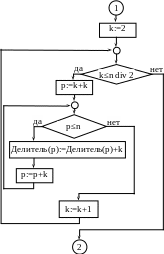
С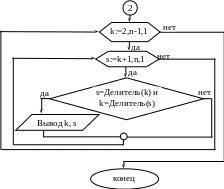
уммы
делителей чисел от 2 до n
организуем в виде массива Делитель(2:n),
где Делитель(k)
– текущая сумма делителей числа k.
Вычислим суммы делителей всех чисел
от 2 до n,
затем попарно сравним эти суммы, если
суммы делителей чисел k
и s,
принадлежащих [2;n],
равны, то числа k
и s
– дружественные, их необходимо вывести.
Н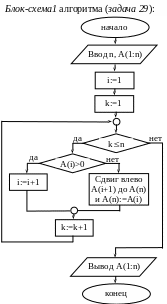
екоторые
пары дружественных чисел:
220 и 284,
1184 и 1210, 2620 и 2924, 5020 и 5564, 6232 и 6368 и т.д.
Задача 29.
Группировка.
Дан массив A(1:n),
элементы которого отличны от нуля.
Расположите их в таком порядке, чтобы
первыми были все положительные элементы,
а затем – все отрицательные, причем
порядок следования как положительных,
так и отрицательных элементов должен
сохраняться. При решении задачи нельзя
заводить новую таблицу. Составьте
блок-схему алгоритма решения поставленной
задачи.
Решение.
Смотри блок-схемы 1-2 алгоритма (задача
29).
Для решения
поставленной задачи будем перебирать
элементы массива с первого по n-ый.
Если A(i)>0,
никаких изменений в массиве не производим,
увеличиваем i
на единицу и переходим к исследованию
следующего элемента. Если же A(i)<0,
поставим его на n-ое
место (в конец таблицы), предварительно
освободив это n-ое
место, произведя сдвиг элементов массива
от A(i+1)
до A(n)
на один номер влево. Количество
просмотренных элементов массива будем
запоминать в переменной k.
Д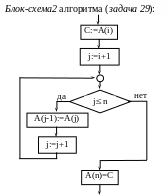
етализируем
блок «сдвиг влево на одну позицию и
перестановку A(i)
на n-ое
место»: скопируем A(i)
в переменную C,
произведем сдвиг и A(n)
присвоим значение C.
Смотри блок-схему2 алгоритма (задача
29).
Теперь детализированный
блок можно подставить в блок-схему1
алгоритма (задача 29).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
“Универсальная” блок-схема и 3 типовых алгоритма 🙂
Дважды за день заходила речь об одном и том же, да и жаль выкидывать пару картинок, могут ещё понадобиться. Речь шла об изображении базовых типовых алгоритмов, связанных с расчётом какой-либо элементарной характеристики последовательности (массива) – суммы, количества, произведения, максимума, минимума и т.п.
В картинках не показаны “начало” и “конец”, только содержательная часть.
ГОСТовские “перевёртыши” на практике крайне неудобны, классическое изображение с помощью “ромбика” часто сбивает начинающих с толку похожестью на обычное ветвление (плюс они забывают делать шаг в конце тела цикла),
а вот значок “цикла с параметром”, если отказаться от паскалевского шага, непременно равного единице, удобен и нормально воспринимается.
I Алгоритм табулирования (составление списка или таблицы)

Алгоритм табулирования (составление списка или таблицы)
Что писать в фигурках вместо цифр?
1. Примем, что управляющая переменная цикла называется x, а здесь зададим её начальное (x1) и конечное (x2) значения, а также шаг изменения dx. Это можно записать присваиванием x1=0,x2=1,dx=0.1 или поставить вместо прямоугольника параллелограмм (оператор ввода) с подписью “ввод x1,x2,dx“;
2. Обычно внутри значка “цикл с параметром” (цикл, пределы изменения и шаг управляющей переменной которого известны) пишут что-то вроде псевдокода: “для x от x1 до x2 шаг dx” или то же самое в форме x=x1,x1+dx..x2 или просто x=x1,x2,dx ;
3. Для очередного x вычислить y=f(x). Этот шаг может включать несколько действий и предполагать вставку дополнительных блоков “расчёт” или условных операторов;
4. Вывести строку таблицы: вывод x, f(x)
II. Алгоритм вычисления суммы, количества или произведения нужных элементов последовательности

Алгоритм вычисления суммы, количества или произведения нужных элементов последовательности
Вместо цифр в элементах блок-схему указываем:
1. Для каждой искомой величины задать по переменной и присвоить ей начальные значения: сумме s=0, количеству k=0, произведению p=1 (на самом деле, это не совсем корректно, но для обсуждаемого уровня сойдёт);
2. Выполняется как в задаче I;
3. Считаем очередной элемент последовательности y=f(x), с тем же замечанием, что к задаче I;
4-5. Если y отвечает условию задачи (проверка на шаге 4), сумма на шаге 5 ищется в виде s=s+f(x), количество в виде k=k+1, произведение в виде p=p*f(x). При нескольких искомых величинах блок вида 4-5 может повторяться несколько раз;
6. По выходе из цикла выводим найденную величину или величины.
III. Алгоритм поиска максимума или минимума
Блок схема задачи II годится и для этого случая.
1. Для каждого максимума или минимума задать по переменной (примем, что минимум обозначен min, а максимум – max) и присвоить каждой переменной начальные значения: максимуму – заведомо малое значение (например, -1030, оператор будет иметь вид Max=-1030) или первый элемент последовательности (массива); минимуму присвоить заведомо большое значение (например, 1030) или первый элемент последовательности;
2-3. Выполняются как в задачах I-II, с теми же замечаниями.
4-5. Для поиска максимума проверяется условие 4 f(x)>max, выполняется действие 5 вида max=f(x), дли минимума проверяется условие 4 f(x)<min и выполняется действие 5 вида min=f(x). С чем сравнивали max или min, то им и присваиваем.Могут понадобиться дополнительные условия, связанные логической операцией “И” либо “ИЛИ” с основным, например, поиск максимального из отрицательных элементов предполагает проверку y<0 and y>max;
6. По выходе из цикла выводим найденную величину или величины.
Несмотря на обилие средств для рисования блок-схем, удобнее простого Paint из Win7 и выше для этой цели ничего пока не придумали 🙂
IV. Схема ввода и обработки элементов одномерного массива
Как правило, ввод, обработка или вывод одномерного массива (вектора, списка) выполняется поэлементно с помощью цикла с параметром (цикла “for”). Счётчиком цикла служит номер элемента в массиве (обычно применяется нумерация с единицы). Ниже показаны ввод и обработка массива x из 6 элементов.

Схема ввода и обработки элементов одномерного массива
V. Реализация алгоритма в кратных (вложенных) циклах
Основное отличие – все действия над матрицей (таблицей) выполняются поэлементно в двойном цикле следующего вида:

Блок-схема двойного цикла с параметром
Здесь показан ввод матрицы A из 6 строк и 4 столбцов, а счётчиками внешнего и внутреннего цикла с параметром служат номера строки (i) и столбца (j) в матрице. Обработка и вывод элементов матрицы могут быть реализованы аналогичными конструкциями, часто, если элементы обрабатываются последовательно и независимо друг от друга, ввод и обработку или обработку и вывод можно объединить.
31.10.2016, 21:46 [10877 просмотров]
Блок-схема представляет собой графическое отображение какого-либо процесса, четко показывающего систематическую последовательность всех этапов выполнения поставленной задачи, а также все группы, которые вовлечены в данный процесс. Такая схема является системой графических символов (блоков) и линий переходов (стрелок) между ними. Каждый из таких блоков соответствует определенному шагу алгоритма. Внутри такого символа дается описание данного действия.
Для чего применяют блок-схемы?
Упомянутые системы призваны выполнять следующие функции:
– разрабатывать новый процесс;
– описывать и документировать текущий алгоритм;
– разрабатывать модификации к данному процессу либо исследовать звенья с вероятным возникновением ошибок и сбоев;
– определять, когда, где и как можно менять текущий алгоритм, с целью проверки устойчивости всей системы.
Разработка последовательности операций
Любая блок-схема строится на основе алгоритма действий, описывающего работу устройства или программы. Поэтому сначала строится сама система. “Алгоритмом” называют описание последовательности операций для решения поставленной задачи. По сути, это правила выполнения необходимых процессов обработки информации. Прежде чем приступить к построению алгоритма, требуется четко определить задачу: что необходимо получить в результате, какая исходная информация нужна, а какая уже имеется, есть ли ограничения для ее получения. После этого составляется список действий, которые необходимо осуществить для получения требуемого результата.
Типы алгоритмов
На практике чаще всего применяют следующие виды блок-схем:
– графическая, то есть в основе находятся геометрические символы;
– словесная: составляется с помощью обычных слов того или иного языка;
– псевдокоды: представляют собой полуформализованное описание на условно-алгоритмическом языке, которое включает в себя элементы языка программирования и фразы литературного, а также общепринятые математические символы;
– программная: для записи используются исключительно языки программирования.
Блок-схема устройства: описание
Графическое представление последовательности действий включает в себя изображение алгоритма, описывающего связи функциональных блоков данной схемы, которые соответствуют выполнению одного либо нескольких действий. Блок-схема массива состоит из отдельных элементов, размеры и правила построения которых определены государственным стандартом. Для каждого типа действия (ввода данных, вычисления значений выражений, проверки условий, управления повторением действий, окончания обработки и др.) предусмотрена отдельная геометрическая фигура, представленная в виде блока. Эти символы соединяются линиями, определяющими очередность действий.
Основные элементы, употребляемые при составлении блок-схем
Полный список графических символов, используемых для описания алгоритма, состоит из 42 элементов. Его весь мы приводить не будем, а рассмотрим только основное.
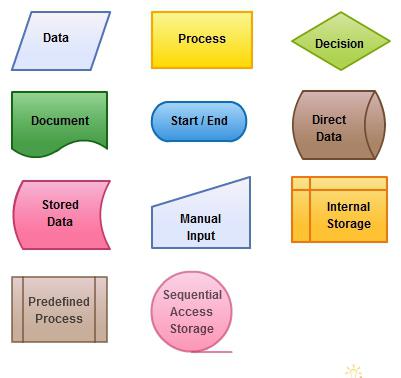
Элементы блок-схемы:
1. Процесс означает вычислительное действие либо последовательность таких действий, изменяющих значения, размещения данных или форму представления. Для наглядности схемы такие элементы можно объединить в один блок. Данный символ имеет вид прямоугольника, внутри которого записываются комментарии, сопровождающие выполнение операции (либо группы операций).
2. Решение. Данный блок применяется для обозначения перехода управления по определенному условию. В каждом таком элементе указывается вопрос, сравнение или условие, которые его определяет. Другими словами, решение – это выбор направления для выполнения программы или алгоритма в зависимости от некоего переменного условия. Графический вид данного элемента – это ромб. Упомянутый символ может использоваться в качестве изображения следующих унифицированных структур: выбор, развилка полная и неполная, цикл «до» и «пока».
3. Модификация. Этот блок означает начало цикла. Он применяется для организации циклической конструкции. Внутри такого элемента записывают параметр круга действий, указывают его начальные значения, граничное условие, а также шаг изменения параметра для последующего повторения. Другими словами, модификация – это выполнение меняющихся команд или их групп, операций, изменяющих программу. Графическое изображение этого символа представляет собой шестиугольник.
4. Предопределенный процесс означает вычисление по заданной или стандартной программе. Его используют для указания обращения к вспомогательному алгоритму, который существует автономно в виде отдельных самостоятельных модулей, а также для обращения к библиотечным подпрограммам. Графически вид этого символа представлен прямоугольником с двумя вертикальными полями по краям. Этот элемент служит для указаний обращений к функциям, процедурам, программным модулям.
5. Ввод-вывод данных в общем виде.
6. Пуск и остановка. Этот элемент означает начало и конец алгоритма, а также вход в программу и выход из неё. Графически данный символ напоминает прямоугольник, у которого вместо боковых прямых – дуги.
7. Документ означает вывод результатов работы на печать. Графически такой элемент напоминает прямоугольник, только вместо нижней прямой начертана полуволна.
8. Ручной ввод означает пуск данных в процесс обработки оператором с помощью устройства, которое сопряжено с компьютером (клавиатура). Графический символ ручного ввода представляет собой четырехугольник, у которого боковые линии параллельны, нижняя перпендикулярна им, а верхняя косая.
9. Дисплей означает ввод или вывод информации в случае, когда устройство непосредственно подключено к процессору. В тот момент, когда начинают воспроизводиться данные, оператор может вносить изменения во время их обработки. Графически данный элемент представляет фигуру, у которой нижняя и верхняя линии параллельны, правая – это дуга, а левая состоит из двух прямых в виде стрелки.
10. Линии потока – это стрелки, которые указывают последовательность связей. Ни одна блок-схема структуры не может обходиться без данного элемента. Существуют определенные правила начертания этих символов. Перечислим их:
– данные элементы должны быть параллельными линиям внешнего периметра или границам страницы, на которой изображена эта блок-схема;
– направление линии сверху вниз или слева направо считается основным, стрелками оно не обозначается, остальные случаи указания направлений обозначены ими;
– изменение направления данного элемента производится только под углом 90о.
11. Соединитель. Данный элемент предназначен для указания связи на прерванных линиях потока. Эти символы используются в том случае, если блок-схема программы строится из нескольких частей. Тогда линия потока от одной части должна закончиться «соединителем», а новой части – начаться с данного символа. Внутри такого элемента ставится один и тот же порядковый номер. Графическое изображение «соединителя» – это круг.
12. Межстраничный соединитель. Назначение этого элемента аналогично предыдущему, только используется он для соединения блок-схем, размещенных на разных страницах. Изображение такого элемента представлено пятиугольником в виде домика.
13. Комментарий – это связь между различными элементами блок-схемы с пояснениями. Упомянутый элемент позволяет включать в себя формулы и прочую информацию.
Построение блок-схем
Графическое построение алгоритма – это часть документации к устройству или программе, которая всегда имеется в избытке. Однако в большинстве случаев программное обеспечение вообще не нуждается в блок-схеме. Лишь единицам требуется построение алгоритма, занимающего несколько листов, остальным же достаточно символичной схемы. Простая блок-схема показывает структуру ветвления программ только в одном аспекте. Однако даже такая структура четко видна только при условии, что алгоритм помещается на одном листе. В обратном случае, когда блок-схема расположена на нескольких страницах, связанных межстраничными переходами, весьма сложно получить о ней верное представление. Если она размещается на одном листе, то для большой программы данное изображение алгоритма превращается в ее общий план с перечнем главных блоков и этапов. Конечно же, такой график не следует стандартам построения схем, но он и не нуждается в них, так как этот процесс полностью индивидуален. Правила, касающиеся типа символов, стрелок и порядка нумерации, необходимы только для разбора подробных блок-схем.
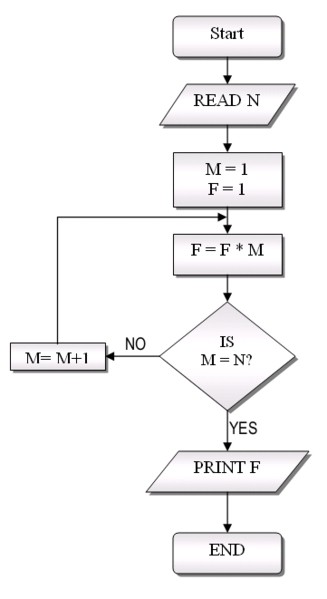
Массивы и построение алгоритмов
Массив представляет собой совокупность однотипной информации, которая хранится в последовательных кластерах памяти и имеет общее имя. Такие ячейки называются “элементами системы”. Все кластеры нумеруются по порядку. Такой номер называется “индексом элемента массива”. Как составить блок-схему для подобной системы? Рассмотрим пример создания алгоритма для элементарного массива одномерного типа. Простейшая система имеет условно вид строки. Зададим имя для данного массива – «А». Будем считать, что наша система состоит из восьми ячеек (от 1 до 8). Каждый из упомянутых кластеров содержит случайное число, которое называется “элементом массива”. Для обращения в конкретной ячейке необходимо указывать имя в квадратных скобках ([3]). Рассмотрим пример, в котором блок-схема массива предназначена для заполнения системы случайными числами с последующим выводом информации на экран. Что представляет собой такой алгоритм? Это элементарная система. По сути, она не имеет практического применения, однако удобна для учебного процесса. Рассматриваемая блок-схема (пример построения описан ниже) содержит всего семь основных элементов, соединенных линиями переходов.
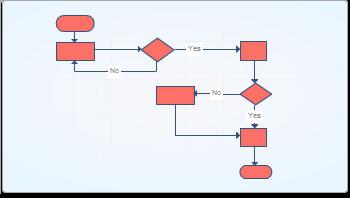
Описание последовательности выполнения задачи
1. Первым элементом схемы будет символ «Начало».
2. Вторым блоком – «Процесс», внутри которого вписываем «инициализация random».
3. Следующий элемент – «Модификация», в блоке вписываем значение ячеек массива.
4. Далее, согласно заданной функции, происходит переадресация на следующий блок «процесса», в котором задается обращение к конкретным кластерам системы с указанием ограничения случайных чисел в диапазоне от нуля до ста. После проведения данной операции происходит возврат к третьему блоку, а через него – далее на пятый.
5. В этом блоке «Модификации», согласно вписанной функции, происходит переадресация на следующий элемент.
6. «Вывод» производит отображение информации о новом содержимом массива на мониторе с последующим направлением на предыдущий блок. Далее – на последний элемент.
7. «Конец» работы алгоритма.
На базе такой блок-схемы составляется программа, которая обеспечит работу представленного алгоритма.
«Редактор блок-схем»
Если вы задаетесь вопросом о том, как составить блок-схему, то знайте, что существуют специальные программы, которые предназначены для создания, а также редактирования таких систем. Удобством графического отображения алгоритма является то, что пользователь не привязан к синтаксису конкретного языка программирования. Построенная блок-схема одинаково подходит для всех языков (например, С, Паскаль, Бейсик и другие). Кроме того, редактор может использоваться для построения диаграмм и проверки работоспособности схем. Такая программа является специализированным софтом. Она предоставляет разнообразный набор инструментов, необходимых для построения блок-схем, что делает ее более удобной, по сравнению с обычными графическими редакторами. Дополнительные опции позволяют оптимизировать процесс составления системы с дальнейшим ее преобразованием в функции и процедуры языка программирования. Кроме того, редактор блок-схем предлагает набор шаблонов, способных существенно ускорить работу начинающего пользователя. Ведь известно, что при построении алгоритма часто применяются повторяющиеся структуры, например разнообразные варианты циклов, альтернативы (полные и неполные), множественные ветвления и прочее. Редактор позволяет выделять часто используемые в блок-схемах элементы и добавлять их в создаваемую схему. Это избавляет от прорисовки их каждый раз заново. Кроме того, с помощью редактора можно импортировать функции и процедуры, реализованные на любом известном языке программирования. Данная опция полезна для разбора структуры алгоритма, который написан на малознакомом языке. Системные требования рассматриваемой программы довольно скромные, что позволяет использовать ее на любом персональном компьютере.
Заключение
Подводя итог, следу отметить, что подробные схемы построения алгоритмов уже устарели. В качестве описания процесса они никому не интересны. В лучшем случае блок-схемы пригодны для проведения обучения новичков, которые не умеют алгоритмически мыслить. Предложенные в свое время элементы со своим содержанием являлись языком высокого уровня, они объединяли операторов языка машины в отдельные группы. На данный момент каждый графический элемент соответствует конкретному оператору. Значит, сам символ превратился в случайное, а главное – бесполезное занятие по рисованию, от которого легко можно отказаться. Сегодня стали лишними даже линии переходов, так как каждый оператор уже определен. В действительности графическое построение алгоритмов больше превозносится, чем применяется на практике. Программист с большим опытом работы, прежде чем написать программу, редко чертит блок-схему. Когда стандарт организации требует графический алгоритм, то рисуют его уже после окончания работ.