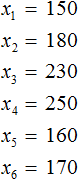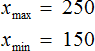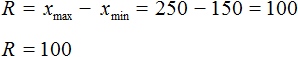Продолжаем изучать элементарные задачи по математике. Сегодня мы поговорим о статистике.
Статистика — это раздел математики в котором изучаются вопросы сбора, измерения и анализа информации, представленной в числовой форме. Происходит слово статистика от латинского слова status (состояние или положение дел).
Так, с помощью статистики мы можем узнать свое положение дел, касающихся финансов. С начала месяца можно вести дневник расходов и по окончании месяца, воспользовавшись статистикой, узнать сколько денег в среднем мы тратили каждый день или какая потраченная сумма была наибольшей в этом месяце либо узнать какую сумму мы тратили наиболее часто.
На основе этой информации можно провести анализ и сделать определенные выводы: следует ли в следующем месяце немного сбавить аппетит, чтобы тратить меньше денег, либо наоборот позволить себе не только хлеб с водой, но и колбасу.
Выборка. Объем. Размах
Что такое выборка? Если говорить простым языком, то это отобранная нами информация для исследования. Например, мы можем сформировать следующую выборку — суммы денег, потраченных в каждый из шести дней. Давайте нарисуем таблицу в которую занесем расходы за шесть дней
Выборка состоит из n-элементов. Вместо переменной n может стоять любое число. У нас имеется шесть элементов, поэтому переменная n равна 6
n = 6
Элементы выборки обозначаются с помощью переменных с индексами . Последний
элемент является шестым элементом выборки, поэтому вместо n будет стоять число 6.
Обозначим элементы нашей выборки через переменные
Количество элементов выборки называют объемом выборки. В нашем случае объем равен шести.
Размахом выборки называют разницу между самым большим и маленьким элементом выборки.
В нашем случае, самым большим элементом выборки является элемент 250, а самым маленьким — элемент 150. Разница между ними равна 100
Среднее арифметическое
Понятие среднего значения часто используется в повседневной жизни.
Примеры:
- средняя зарплата жителей страны;
- средний балл учащихся;
- средняя скорость движения;
- средняя производительность труда.
Речь идет о среднем арифметическом — результате деления суммы элементов выборки на их количество.
Среднее арифметическое — это результат деления суммы элементов выборки на их количество.
Вернемся к нашему примеру
Узнаем сколько в среднем мы тратили в каждом из шести дней:
Средняя скорость движения
При изучении задач на движение мы определяли скорость движения следующим образом: делили пройденное расстояние на время. Но тогда подразумевалось, что тело движется с постоянной скоростью, которая не менялась на протяжении всего пути.
В реальности, это происходит довольно редко или не происходит совсем. Тело, как правило, движется с различной скоростью.
Когда мы ездим на автомобиле или велосипеде, наша скорость часто меняется. Когда впереди нас помехи, нам приходиться сбавлять скорость. Когда же трасса свободна, мы ускоряемся. При этом за время нашего ускорения скорость изменяется несколько раз.
Речь идет о средней скорости движения. Чтобы её определить нужно сложить скорости движения, которые были в каждом часе/минуте/секунде и результат разделить на время движения.
Задача 1. Автомобиль первые 3 часа двигался со скоростью 66,2 км/ч, а следующие 2 часа — со скоростью 78,4 км/ч. С какой средней скоростью он ехал?
Сложим скорости, которые были у автомобиля в каждом часе и разделим на время движения (5ч)
Значит автомобиль ехал со средней скоростью 71,08 км/ч.
Определять среднюю скорость можно и по другому — сначала найти расстояния, пройденные с одной скоростью, затем сложить эти расстояния и результат разделить на время. На рисунке видно, что первые три часа скорость у автомобиля не менялась. Тогда можно найти расстояние, пройденное за три часа:
66,2 × 3 = 198,6 км.
Аналогично можно определить расстояние, которое было пройдено со скоростью 78,4 км/ч. В задаче сказано, что с такой скоростью автомобиль двигался 2 часа:
78,4 × 2 = 156,8 км.
Сложим эти расстояния и результат разделим на 5
Задача 2. Велосипедист за первый час проехал 12,6 км, а в следующие 2 часа он ехал со скоростью 13,5 км/ч. Определить среднюю скорость велосипедиста.
Скорость велосипедиста в первый час составляла 12,6 км/ч. Во второй и третий час он ехал со скоростью 13,5. Определим среднюю скорость движения велосипедиста:
Мода и медиана
Модой называют элемент, который встречается в выборке чаще других.
Рассмотрим следующую выборку: шестеро спортсменов, а также время в секундах за которое они пробегают 100 метров
Элемент 14 встречается в выборке чаще других, поэтому элемент 14 назовем модой.
Рассмотрим еще одну выборку. Тех же спортсменов, а также смартфоны, которые им принадлежат
Элемент iphone встречается в выборке чаще других, значит элемент iphone является модой. Говоря простым языком, носить iphone модно.
Конечно элементы выборки в этот раз выражены не числами, а другими объектами (смартфонами), но для общего представления о моде этот пример вполне приемлем.
Рассмотрим следующую выборку: семеро спортсменов, а также их рост в сантиметрах:
Упорядочим данные в таблице так, чтобы рост спортсменов шел по возрастанию. Другими словами, построим спортсменов по росту:
Выпишем рост спортсменов отдельно:
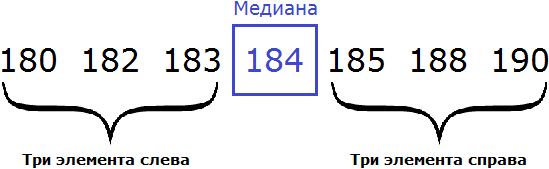
180, 182, 183, 184, 185, 188, 190
В получившейся выборке 7 элементов. Посередине этой выборки располагается элемент 184. Слева и справа от него по три элемента. Такой элемент как 184 называют медианой упорядоченной выборки.
Медианой упорядоченной выборки называют элемент, располагающийся посередине.
Отметим, что данное определение справедливо в случае, если количество элементов упорядоченной выборки является нечётным.
В рассмотренном выше примере, количество элементов упорядоченной выборки было нечётным. Это позволило нам быстро указать медиану
Но возможны случаи, когда количество элементов выборки чётно.
К примеру, рассмотрим выборку в которой не семеро спортсменов, а шестеро:
Построим этих шестерых спортсменов по росту:
Выпишем рост спортсменов отдельно:
180, 182, 184, 186, 188, 190
В данной выборке не получается указать элемент, который находился бы посередине. Если указать элемент 184 как медиану, то слева от этого элемента будут располагаться два элемента, а справа — три. Если как медиану указать элемент 186, то слева от этого элемента будут располагаться три элемента, а справа — два.
В таких случаях для определения медианы выборки, нужно взять два элемента выборки, находящихся посередине и найти их среднее арифметическое. Полученный результат будет являться медианой.
Вернемся к нашим спортсменам. В упорядоченной выборке 180, 182, 184, 186, 188, 190 посередине располагаются элементы 184 и 186
Найдем среднее арифметическое элементов 184 и 186
Элемент 185 является медианой выборки, несмотря на то, что этот элемент не является членом исходной и упорядоченной выборки. Спортсмена с ростом 185 нет среди остальных спортсменов. Рост в 185 см используется в данном случае для статистики, чтобы можно было сказать о том, что срединный рост спортсменов составляет 185 см.
Поэтому более точное определение медианы зависит от количества элементов в выборке.
Если количество элементов упорядоченной выборки нечётно, то медианой выборки называют элемент, располагающийся посередине.
Если количество элементов упорядоченной выборки чётно, то медианой выборки называют среднее арифметическое двух чисел, располагающихся посередине этой выборки.
Медиана и среднее арифметическое по сути являются «близкими родственниками», поскольку и то и другое используют для определения среднего значения. Например, для предыдущей упорядоченной выборки 180, 182, 184, 186, 188, 190 мы определили медиану, равную 185. Этот же результат можно получить путем определения среднего арифметического элементов 180, 182, 184, 186, 188, 190
Но медиана в некоторых случаях отражает более реальную ситуацию. Например, рассмотрим следующий пример:
Было подсчитано количество имеющихся очков у каждого спортсмена. В результате получилась следующая выборка:
0, 1, 1, 1, 2, 1, 2, 3, 5, 4, 5, 0, 1, 6, 1
Определим среднее арифметическое для данной выборки — получим значение 2,2
По данному значению можно сказать, что в среднем у спортсменов 2,2 очка
Теперь определим медиану для этой же выборки. Упорядочим элементы выборки и укажем элемент, находящийся посередине:
0, 0, 1, 1, 1, 1, 1, 1, 2, 2, 3, 4, 5, 5, 6
В данном примере медиана лучше отражает реальную ситуацию, поскольку половина спортсменов имеет не более одного очка.
Частота
Частота это число, которое показывает сколько раз в выборке встречается тот или иной элемент.
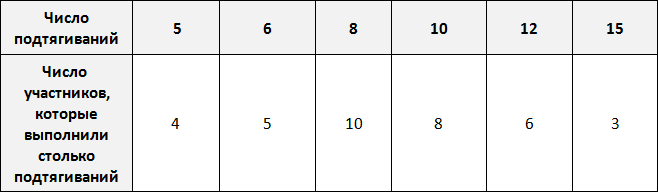
Предположим, что в школе проходят соревнования по подтягиваниям. В соревнованиях участвует 36 школьников. Составим таблицу в которую будем заносить число подтягиваний, а также число участников, которые выполнили столько подтягиваний.
По таблице можно узнать сколько человек выполнило 5, 10 или 15 подтягиваний. Так, 5 подтягиваний выполнили четыре человека, 10 подтягиваний выполнили восемь человек, 15 подтягиваний выполнили три человека.
Количество человек, повторяющих одно и то же число подтягиваний в данном случае являются частотой. Поэтому вторую строку таблицы переименуем в название «частота»:
Такие таблицы называют таблицами частот.
Частота обладает следующим свойством: сумма частот равна общему числу данных в выборке.
Это означает, что сумма частот равна общему числу школьников, участвующих в соревнованиях, то есть тридцати шести. Проверим так ли это. Сложим частоты, приведенные в таблице:
4 + 5 + 10 + 8 + 6 + 3 = 36
Относительная частота
Относительная частота это в принципе та же самая частота, которая была рассмотрена ранее, но только выраженная в процентах.
Относительная частота равна отношению частоты на общее число элементов выборки.
Вернемся к нашей таблице:
Пять подтягиваний выполнили 4 человека из 36. Шесть подтягиваний выполнили 5 человек из 36. Восемь подтягиваний выполнили 10 человек из 36 и так далее. Давайте заполним таблицу с помощью таких отношений:
Выполним деление в этих дробях:
Выразим эти частоты в процентах. Для этого умножим их на 100. Умножение на 100 удобно выполнить передвижением запятой на две цифры вправо:
Теперь можно сказать, что пять подтягиваний выполнили 11% участников, 6 подтягиваний выполнили 14% участников, 8 подтягиваний выполнили 28% участников и так далее.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

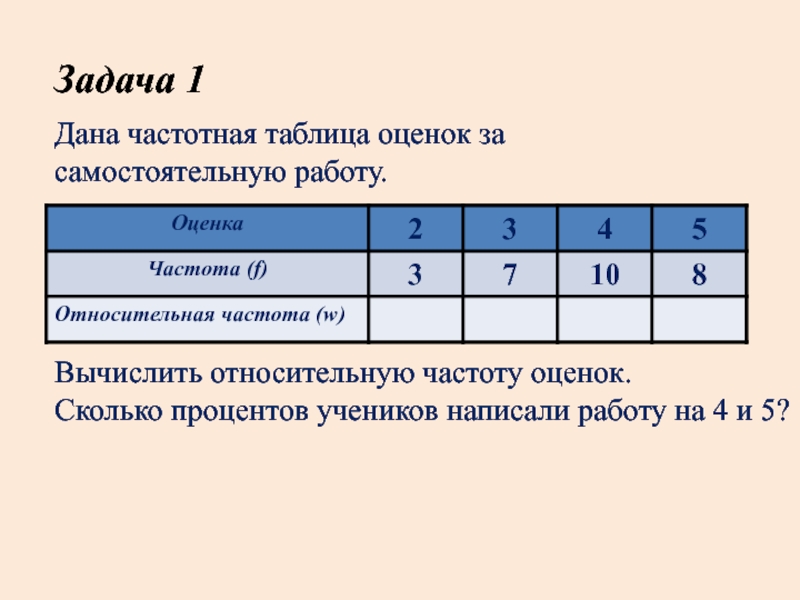
Слайд 2Задача 1
Дана частотная таблица оценок за
самостоятельную
работу.
Вычислить относительную частоту оценок.
Сколько процентов учеников
написали работу на 4 и 5?
Слайд 3Задача 2
Среди учеников начальных классов был проведен
выборочный опрос.
Вопрос. Сколько детей в вашей
семье?
В результате такого опроса получена следующая выборка:
2,2,3,3,3,3,4,2,3,3,2,3,2,3,2,3,2,4,3,2,2,3,2,4,5,2,3,3,2,4,3,2,3,4,3,2,3,5,3.
Составить частотную таблицу .
Какое наибольшее количества детей в семье?
Сколько процентов семей имеет 4 и 5 детей?

Слайд 4Вес учеников в килограммах следующий:
36, 39, 40, 36, 42, 39, 45, 36, 42, 36, 39, 45, 39, 38,39, 45, 40, 39, 45.
Составить таблицу относительных
частот.
Задача 3

Слайд 5Задача 4
В 7 классе города М провели
опрос на тему «Любимое занятие в свободное
время». Каждый из учащихся должен был выбрать из десяти предложенных вариантов только один. В таблице распределение ответов учащихся.
1.Вычислить относительную частоту для каждого увлечения в классе.
2.Чем увлекается большинство учеников класса?
3.Сколько процентов девочек класса увлекаются спортом?
4.Сколько процентов учеников класса увлекаются музыкой?

Слайд 6Пирог с ревенем
Задача 5
Рецепт пирога
1. Вычислить относительную
частоту каждого ингредиента в пироге.
2. Сколько процентов
сахара в пироге?

Загрузить PDF
Загрузить PDF
С абсолютной частотой все довольно просто: она определяет, сколько раз конкретное число содержится в имеющемся наборе данных (объектов или значений). А вот относительная частота характеризует отношение количества конкретного числа в наборе данных. Другими словами, относительная частота – это отношение количества определенного числа к общему количеству чисел в наборе данных. Имейте в виду, что вычислить относительную частоту достаточно легко.
-
1
Соберите данные. Если вы решаете математическую задачу, в ее условии должен быть дан набор данных (чисел). В противном случае проведите эксперимент или исследование и соберите необходимые данные. Подумайте, в какой форме записать исходные данные.
- Например, нужно собрать данные о возрасте людей, которые посмотрели определенный фильм. Конечно, можно записать точный возраст каждого человека, но в этом случае вы получите довольно большой набор данных с 60-70 числами в пределах от 10 до 70 или 80. Поэтому лучше сгруппировать данные по категориям, таким как «Моложе 20», «20-29», «30-39» «40-49», «50-59» и «Старше 60». Получится упорядоченный набор данных с шестью группами чисел.
- Другой пример: врач собирает данные о температуре пациентов в определенный день. Если записать округленные числа, например, 37, 38, 39, то результат будет не слишком точным, поэтому здесь данные нужно представить в виде десятичных дробей.
-
2
Упорядочьте данные. Когда вы соберете данные, у вас, скорее всего, получится хаотичный набор чисел, например, такой: 1, 2, 5, 4, 6, 4, 3, 7, 1, 5, 6, 5, 3, 4, 5, 1. Такая запись кажется практически бессмысленной и с ней сложно работать. Поэтому упорядочьте числа по возрастанию (от меньшего к большему), например, так: 1,1,1,2,3,3,4,4,4,5,5,5,5,6,6,7.[1]
- Упорядочивая данные, будьте внимательны, чтобы не пропустить ни одного числа. Посчитайте общее количество чисел в наборе данных, чтобы убедиться, что вы записали все числа.
-
3
Создайте таблицу с данными. Собранные данные можно организовать в виде таблицы. Такая таблица будет включать три столбца и использоваться для вычисления относительной частоты. Столбцы обозначьте следующим образом:[2]
Реклама
-
1
Найдите количество чисел в наборе данных. Относительная частота характеризует, сколько раз конкретное число содержится в имеющемся наборе данных по отношению к общему количеству чисел. Чтобы найти относительную частоту, нужно посчитать общее количество чисел в наборе данных. Общее количество чисел станет знаменателем дроби, с помощью которой будет вычислена относительная частота.[3]
- В нашем примере набор данных содержит 16 чисел.
-
2
Найдите количество определенного числа. То есть посчитайте, сколько раз конкретное число встречается в наборе данных. Это можно сделать как для одного числа, так и для всех чисел из набора данных.[4]
- Например, в нашем примере число
встречается в наборе данных три раза.
- Например, в нашем примере число
-
3
Разделите количество конкретного числа на общее количество чисел. Так вы найдете относительную частоту для определенного числа. Вычисление можно представить в виде дроби или воспользоваться калькулятором или электронной таблицей, чтобы разделить два числа.[5]
Реклама
-
1
Результаты вычислений запишите в созданную ранее таблицу. Она позволит представить результаты в наглядной форме. По мере вычисления относительной частоты результаты записывайте в таблицу напротив соответствующего числа. Как правило, значение относительной частоты можно округлить до второго знака после десятичной запятой, но это на ваше усмотрение (в зависимости от требований задачи или исследования). Помните, что округленный результат не равен точному ответу.[6]
- В нашем примере таблица относительных частот будет выглядеть следующим образом:
- x : n(x) : P(x)
- 1 : 3 : 0,19
- 2 : 1 : 0,06
- 3 : 2 : 0,13
- 4 : 3 : 0,19
- 5 : 4 : 0,25
- 6 : 2 : 0,13
- 7 : 1 : 0,06
- Итого : 16 : 1,01
-
2
Представьте числа (элементы), которых нет в наборе данных. Иногда представление чисел с нулевой частотой так же важно, как и представление чисел с ненулевой частотой. Обратите внимание на собранные данные; если между данными имеются пробелы, их нужно заполнить нулями.
- В нашем примере набор данных включает все числа от 1 до 7. Но предположим, что числа 3 нет в наборе. Возможно, это немаловажный факт, поэтому нужно записать, что относительная частота числа 3 равна 0.
-
3
Выразите результаты в процентах. Иногда результаты вычислений нужно преобразовать из десятичных дробей в проценты. Это общепринятая практика, потому что относительная частота характеризует процент случаев появления определенного числа в наборе данных. Чтобы преобразовать десятичную дробь в проценты, нужно десятичную запятую передвинуть на две позиции вправо и приписать символ процента.
- Например, десятичная дробь 0,13 равна 13%.
- Десятичная дробь 0,06 равна 6% (обратите внимание, что перед 6 стоит 0).
Реклама
Советы
- Относительная частота характеризует наличие или возникновение определенного события в наборе событий.
- Если сложить относительные частоты всех чисел из набора данных, вы получите единицу. Помните, что при сложении округленных результатов сумма не будет равна 1,0.
- Если набор данных слишком большой, чтобы обработать его вручную, воспользуйтесь программой MS Excel или MATLAB; это позволит избежать ошибок в процессе вычисления.
Реклама
Источники
Об этой статье
Эту страницу просматривали 145 557 раз.
Была ли эта статья полезной?
Слайд 2
Задача 1
Дана частотная таблица оценок за
самостоятельную работу.
Вычислить
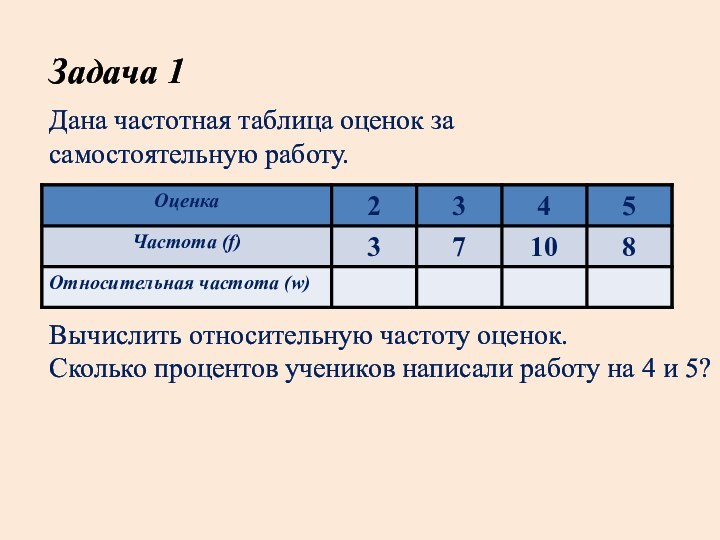
относительную частоту оценок.
Сколько процентов учеников написали работу на
4 и 5?
Слайд 3
Задача 2
Среди учеников начальных классов был проведен выборочный

опрос.
Вопрос. Сколько детей в вашей семье?
В результате такого
опроса получена следующая выборка:
2,2,3,3,3,3,4,2,3,3,2,3,2,3,2,3,2,4,3,2,2,3,2,4,5,2,3,3,2,4,3,2,3,4,3,2,3,5,3.
Составить частотную таблицу .
Какое наибольшее количества детей в семье?
Сколько процентов семей имеет 4 и 5 детей?
Слайд 4
Вес учеников в килограммах следующий:
36, 39, 40, 36, 42, 39, 45, 36, 42, 36, 39, 45, 39, 38,39, 45, 40, 39, 45.
Составить таблицу относительных частот.
Задача

Слайд 5
Задача 4
В 7 классе города М провели опрос

на тему «Любимое занятие в свободное время». Каждый из
учащихся должен был выбрать из десяти предложенных вариантов только один. В таблице распределение ответов учащихся.
1.Вычислить относительную частоту для каждого увлечения в классе.
2.Чем увлекается большинство учеников класса?
3.Сколько процентов девочек класса увлекаются спортом?
4.Сколько процентов учеников класса увлекаются музыкой?
Слайд 6
Пирог с ревенем
Задача 5
Рецепт пирога
1. Вычислить относительную частоту

каждого ингредиента в пироге.
2. Сколько процентов сахара в пироге?
Содержание
- Типы частот
- Шаги по составлению таблицы распределения частот
- Шаг 1
- Шаг 2
- Шаг 3
- Шаг 4
- Шаг 5
- Шаг 6
- Шаг 7
- Шаг 8
- Шаг 9
- Шаг 10
- Пример построения стола
- Упражнение решено
- Ссылки
А Распределение частоты В статистике это относится к тенденции, за которой следуют данные, организованные в группы, категории или классы, когда каждому присваивается номер, называемый частотой, который указывает, сколько данных находится в каждой группе.
Как правило, наблюдается, что эти частоты распределяются вокруг центральной группы: группы с наибольшим количеством данных.
Группы, которые находятся выше или ниже этой центральной категории, постепенно уменьшают свою частоту, становясь очень маленькими или незначительными для категорий, наиболее удаленных от категории с более высокой частотой.
Чтобы узнать частотное распределение набора данных, сначала создайте категории, а затем составьте таблицу частот. Визуальное представление частотной таблицы называется гистограммой.
Типы частот
Есть несколько типов частот:
1.- Абсолютная частота: он самый простой, и из него строятся остальные. Он просто состоит из общего количества данных, соответствующих категории.
2.- Относительная частота: абсолютная частота каждой категории, деленная на общее количество данных.
3.- Частота в процентах: это та же относительная частота, но умноженная на сто, указывающая процент появления значений в каждой категории.
4.- Накопленная частота: это сумма абсолютных частот категорий ниже или равных рассматриваемой категории.
5.- Кумулятивная частота в процентах: это сумма процентных частот категорий ниже или равных наблюдаемой категории.
Шаги по составлению таблицы распределения частот
Чтобы построить таблицу частотного распределения, необходимо выполнить несколько шагов.
Прежде всего, должны быть доступны данные, которые могут быть разного типа: возраст детей в школе, количество правильных ответов в тесте, рост сотрудников компании, длина листов. дерева и др.
Шаг 1
Определите минимальное значение xmin и максимальное значение xmax в наборе данных Икс.
Шаг 2
Рассчитайте диапазон R, который определяется как разница между максимальным значением минус минимальное значение: R = xmax – xmin.
Шаг 3
Определить количество k интервалов или классов, которые можно задать заранее. Номер k определит количество строк в частотной таблице.
Шаг 4
Если количество интервалов k ранее не указывалось, то оно должно быть установлено в соответствии со следующими руководящими принципами: наименьшее количество рекомендуемых категорий – 5, но оно может быть больше, и в этом случае предпочтительнее выбрать нечетное число.
Шаг 5
Есть формула, которая называется правило осетров что дает нам количество интервалов k рекомендуется для набора, состоящего из N данные:
k = [1 + 3,322⋅Log N]
Поскольку результат внутри скобки обязательно будет действительным числом, скобка говорит нам, что его необходимо округлить до ближайшего нечетного целого числа, чтобы получить целое значение k.
Шаг 6
Амплитуда рассчитывается К каждого интервала (классов или категорий), беря частное между диапазоном р и количество интервалов k: А = R / k. Если исходные данные являются целыми числами, то A округляется до ближайшего целого числа, в противном случае его реальное значение остается.
Шаг 7
Определите нижние пределы Li и верхние пределы Ls для каждого интервала или класса. Первый интервал или самый низкий класс имеет нижний предел Li наименьшего из исходных данных, то есть Li = xmin, а верхний предел – минимальное значение плюс ширина интервала, то есть Ls = xmin + A.
Шаг 8
Последовательные интервалы:
[xmin, xmin + A), [ xmin + A, xmin + 2⋅A), …, [ xmin + (k-1) A, xmin + k⋅A).
Шаг 9
Оценка класса Xc определяется для каждого интервала по следующей формуле: Xc = (Ls – Li) / 2 + Li.
Шаг 10
Размещается заголовок таблицы частот, который состоит из строки со следующими метками: классы, метка класса Xc, частота f, относительная частота fr (или процентная частота f%) и накопленная частота F (или накопленная частота в процентах). F%).
У нас будет следующее:
Первый столбец частотной таблицы– Содержит интервалы или классы, на которые были разделены данные.
Второй столбец: содержит метку класса (или среднюю точку) каждого подынтервала.
Третий столбец: содержит абсолютную частоту f каждого класса или категории.
Четвертая и пятая колонки: помещаются значения, соответствующие относительной частоте (или проценту) и накопленной частоте F (или накопленному проценту).
Пример построения стола
Следующие данные соответствуют правильным ответам анкеты из 100 вопросов, примененной к группе из 52 студентов:
65, 70, 70, 74, 61, 77, 85, 36, 70, 62, 62, 77, 80, 89, 39, 43, 70, 77, 79, 77, 88, 52, 85, 1, 55, 47, 73, 63, 59, 51, 56, 65, 85, 79, 53, 79, 3, 71, 7, 54, 8, 61, 61, 77, 67, 58, 61, 45, 48, 64, 15, 50.
Мы будем следовать шагам, чтобы построить таблицу частот:
1.- Минимальное и максимальное значения Xmin = 1, Xmax = 89.
2.- Диапазон: R = 89 – 1 = 88
3.- Определение количества интервалов по правило осетров: k = [1 + 3,322⋅Журнал 52] = [6,70] = 7.
4.- Расчет ширины интервалов: A = R / k = 88/7 = 12,57 ≈ 13.
5.- Интервалы: [1,14), [14, 27), [27, 40), [40, 53), [53, 66), [66, 79), [79, 92 ».
6.- Определяются оценки классов каждого интервала: 8, 21, 34, 47, 60, 73 и 86.
7.- Таблица сделана:
График частот для различных интервалов или категорий показан на рисунке 1.
Упражнение решено
Учитель записывает процент достижений целей по курсу физики для каждого студента. Однако оценка для каждого студента, хотя и зависит от процента достигнутых целей, ограничена определенными категориями, ранее установленными в правилах обучения университета.
Давайте рассмотрим конкретный случай: в разделе физики у нас есть процент достижений целей для каждого из 52 студентов:
15, 50, 62, 58, 51, 61, 62, 74, 65, 79, 59, 56, 77, 8, 55, 70, 7, 36, 79, 61, 77, 52, 35, 43, 61, 65, 70, 89, 64, 54, 85, 61, 39, 63, 70, 85, 70, 79, 48, 77, 73, 67, 45, 77, 71, 53, 88, 85, 47, 73, 77, 80.
В этом примере категории или классы соответствуют итоговой оценке, которая выставляется в соответствии с процентной долей x достигнутых целей:
1.- Очень плохо: 1 ≤ x <30
2.- Недостаточно: 30 ≤ x <50
3.- Достаточно: 50 ≤ x <70
4.- Хорошо: 70 ≤ x <85
5.- Отлично: 85 ≤ x ≤ 100
Чтобы составить частотную таблицу, данные упорядочиваются от наименьшего к наибольшему, и подсчитывается количество данных, соответствующих каждой категории, что и будет оценкой, которую студент получит за курс физики:
1.- Очень плохо: 4 ученика.
2.- Плохо: 6 учеников.
3.- Достаточно: 20 учеников.
4.- Хорошо: 17 учеников.
5.- Отлично: 5 учеников.
Ниже представлена гистограмма оценок, построенная на основе приведенной выше таблицы:
Ссылки
- Беренсон, М. 1985. Статистика для управления и экономики. Interamericana S.A.
- Канавос, Г. 1988. Вероятность и статистика: приложения и методы. Макгроу Хилл.
- Деворе, Дж. 2012. Вероятность и статистика для техники и науки. 8-е. Издание. Cengage.
- Левин, Р. 1988. Статистика для администраторов. 2-й. Издание. Прентис Холл.
- Шпигель, М. 2009. Статистика. Серия Шаум. 4-й Издание. Макгроу Хилл.
- Уолпол, Р. 2007. Вероятность и статистика для инженерии и науки. Пирсон.