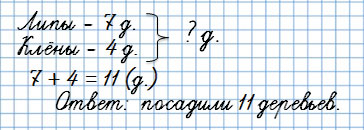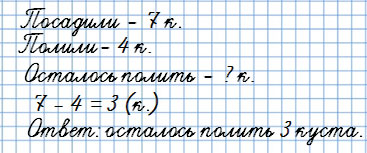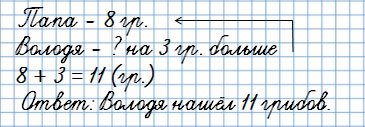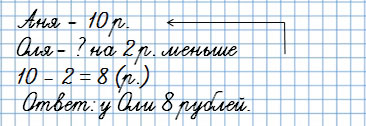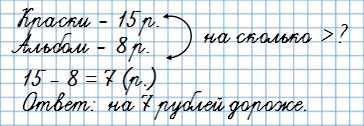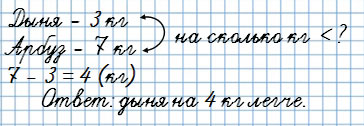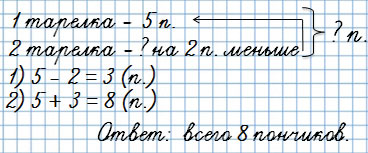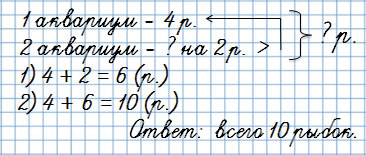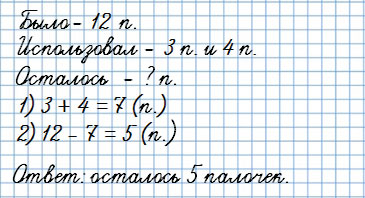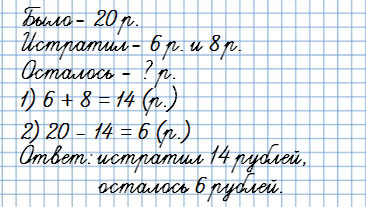Все, кто учился в школе, помнят, что к задачам составлялась краткая запись. Сейчас вместо краткой записи учителя могут использовать схемы и схематический чертёж к задачам. Это зависит от программы. О том, какие схематические чертежи к задачам бывают и как научить ребенка их составлять, эта статья. Сегодня поговорим о простых задачах, которые решаются сложением и вычитанием.
Пример 1
У Кати 7 шариков, а у Зины 2 шарика. Сколько всего шариков у девочек?
При составлении чертежа вводятся понятия “целое” и “части”. При сложении целое – это результат (сумма), а при вычитании – уменьшаемое.
В данной задаче целое – это то, сколько всего шариков. А части- количество шариков у каждой девочки.
Пример 2
На стоянке было 9 машин. Несколько машин уехали. Осталось 7 машин. Сколько машин уехали со стоянки?
Пример 3
У Кати 7 шариков, а у Зины на 2 шарика больше. Сколько шариков у Зины?
При составлении чертежа к этой задаче количество шаров у каждой девочки обозначаем своим отрезком. Показываем, что у Зины столько же шаров, сколько и у Кати, да еще 2.
Пример 4
У Зины 9 шаров, а у Кати на 2 шара меньше. Сколько шаров у Кати?
В чертеже к этой задаче важно показать, что количество шаров у Кати – это количество шаров у Зины, но без двух шаров.
Пример 5
У Кати 9 шаров, а у Зины 7 шаров. На сколько шаров у Кати больше, чем у Зины?
Делитесь своим мнением в комментариях, подписывайтесь на мой канал
Давайте подумаем, а для чего к задаче нужен чертеж. Разумеется, не ради самого чертежа. Предполагается, что чертеж должен должен сделать решение более понятным и простым. На деле выходит наоборот.
Могу сказать, исходя из своего собственного опыта и наблюдений за другими учениками, что составление схемы к задаче чаще вызывает больше затруднений, чем решение самой задачи. Многие прекрасно решают задачи, но вот чертеж к ним становится камнем преткновения.
Универсального ответа здесь не дашь. Составление чертежей напрямую зависит от условий конкретных задач.
Единственное, что можно отметить, на чертеже должны быть видны все данные из условия задачи, а также указано, что в ней спращивается.
Рассмотрим на примере задачи для четвертого класса на движение.
Задача:
Из деревни в разные стороны вышли 2 жителя, первый шел со скоростью 3 км/ч, второй – 4 км/ч. Через какое время расстояние между ними станет 35 километров?
Рисунок/чертеж к задаче:
Задачу можно решить как в два действия, так и в одно.
1) 1. 3+4=7 ( км/ч ) – скорость удаления жителей.
- 35:7=5 ( ч ) – время, за которое они удалятся друг от друга на 35 километров.
2) 35:(3+4)=5 ( ч ).
На чтение 3 мин. Просмотров 37.1k.
Обновлено 31.08.2021
Схемы задач на движение очень просто нарисовать. Они помогают представить наглядно условие задачи и найти верное решение. В дополнение к схеме в сложных случаях или когда ученик затрудняется с решением рекомендуется рисовать таблицу, где в шапке параметры скорости, времени и расстояния. Об этом подробнее ниже.
Узнайте также, как составить схемы к задачам по математике для 2 класса
Содержание
- Простые задачи на движение
- Решение
- Обратные задачи на движение
- Как найти скорость, если известно время и расстояние
- Как найти время, когда известны скорость и расстояние
- Схемы задач на встречное движение
- Решение
- Задачи на движение в одном направлении
- Шпаргалка по решению задач на скорость, время и расстояние
Простые задачи на движение
Простые задачи про путников, лыжников, мотоциклистов и другие движущиеся объекты (встречаются даже задачки про черепах) начинают решать еще в начальных классах. Именно на этих примерах удобно разбирать составление схем.
Задача 1. Пешеход вышел из пункта А в пункт Б со скоростью 5 км/ч. Через 3 часа он добрался до пункта Б. Какое расстояние между этими двумя пунктами?
Рисуем схему к задаче: прямая линия, соединяющая точки А и Б — это весь путь. Стрелкой обозначаем направление движения путника. Над стрелкой отмечаем скорость, если известна. Время или расстояние отмечаем под (или над) отрезком:
Если со схемой вы не смогли решить задачу, то предлагаю вам воспользоваться таблицей:
| скорость | время | расстояние |
| 5 км/ч | 3 ч | ? км |
Чтобы решать с помощью таблицы, запомните правила:
- Чтобы найти расстояние, нужно скорость умножить на время: S = V x t
- Чтобы найти скорость, нужно расстояние разделить на время, (это производное из первой формулы:
V = S : t ) - чтобы найти время, необходимо расстояние разделить на скорость. (также просто вывести из первой формулы:
t = S : t
Решение
5 х 3 = 15 км — расстояние между пунктами А и Б
Обратные задачи на движение
Как найти скорость, если известно время и расстояние
Чтобы не путать вас разными условиями задачи состав задачу, обратную первому примеру:
Задача 2. Расстояние между пунктами А и Б равно 15 км. Путник преодолел это расстояние за 3 часа. С какой скоростью шел пешеход?
| скорость | время | расстояние |
| ? км/ч | 3 ч | 15 км |
Решение
15 : 3 = 5 км/ч
Как найти время, когда известны скорость и расстояние
Задача 3. Расстояние между пунктами 15 км. Пешеход шел со скоростью 5 км/ч. За какое время пешеход преодолеет весь путь?
| Скорость | время | расстояние |
| 5 км/ч | ? ч | 15 км |
Решение
15 : 5 = 3 часа
Схемы задач на встречное движение
Чтобы начертить встречное движение, мы рисуем стрелочки из двух пунктов навстречу. Флажком обозначаем место встречи
Когда задачи со встречным или удаляющимся движением — это задачи на общую скорость. Скоро будет подробный урок о них на моем сайте.
Задача 4. Два пешехода вышли одновременно из пунктов А и Б навстречу друг другу. Скорость одного — 5 км/ч, другого — 3 км/ч. Через какое время они встретятся, если известно, что расстояние между пунктами 24 км?
Решение
1 способ:
5 + 3 =8 км/ч — общая скорость
24 : 8 = 3 часа
Задачи на движение в одном направлении
Задача 5. Два пешехода вышли из пунктов А и Б одновременно в одном направлении. Пешеход, который шел впереди, двигался со скоростью 3 км/ч, а второй — со скоростью 5 км/ч. Через какое время второй пешеход догонит первого, если расстояние между пунктами 2 км?
Здесь нужно выяснить скорость сближения. Так как один пешеход шел быстрее второго, то расстояние между ними сокращалось на 2 км/ч (мы посчитали так: 5 — 3 = 2 км/ч). Так как первоначальное расстояние между пунктами 2 км, то найдем время:
2км : 2 км/ч = 1 час.
Через 1 час пешеходы встретятся.
Шпаргалка по решению задач на скорость, время и расстояние
Вы можете воспользоваться данной памяткой при решении этого типа задач. Кликните для просмотра в полном размере и распечатайте, нажав на клавиатуре клавиши CTRL + P.
- Главная
- Справочники
- Справочник по математике для начальной школы
- Задачи
- Образцы оформления задачи
В разделе “Задачи” мы рассмотрели несколько видов задач. Теперь поучимся оформлять решения к ним.
1. Задачи на нахождение суммы
В вопросе задач такого типа всегда есть “Сколько всего?”
На школьном участке ребята посадили 7 лип и 4 клёна.
Сколько всего деревьев посадили ребята?
2. Задачи на нахождение остатка
В вопросе “Сколько … осталось?”
Мама с Юлей посадили 7 кустов смородины. Затем они полили 4 куста.
Сколько кустов смородины осталось полить?
3. Задачи на увеличение или уменьшение числа на несколько единиц
В условии “на … больше”
Папа с Володей собирали грибы. Папа нашёл 8 грибов, а Володя на 3 гриба больше.
Сколько грибов нашёл Володя?
В условии “на … меньше”
У Ани было 10 рублей, а у Оли на 2 рубля меньше.
Сколько денег было у Оли?
4. Задачи на разностное сравнение
В вопросе “На сколько больше…?”
Краски стоят 15 рублей, а альбом 8 рублей.
На сколько рублей краски дороже альбома?
“На сколько меньше…?”
Дыня весит 3 кг, а арбуз 7 кг.
На сколько кг дыня легче арбуза?
5. Задачи на нахождение неизвестного слагаемого
В условии “Было…Стало…”
В вопросе “Сколько добавили?”
У Саши было 4 карандаша. Когда ему купили еще несколько карандашей, у него их стало 9.
Сколько карандашей купили Саше?
6. Задачи на нахождение неизвестного вычитаемого
В условии “Было… Осталось…”
В вопросе “Сколько уехало?”
“Сколько человек вышло?”
В гараже было 9 машин. Когда несколько машин уехало, в гараже осталось 5 машин.
Сколько машин уехало?
7. Задачи на нахождение неизвестного уменьшаемого
В условии “Убрали… Осталось…”
В вопросе “Сколько было сначала?”
После того, как Дима отдал 2 свои машинки младшему брату, у него осталось 6 машинок.
Сколько машинок было у Димы сначала?
Задачи в 2 и 3 действия
Первый вид
Бабушка испекла пончики и разложила их по тарелкам. На первую тарелку она положила 5 пончиков, а на вторую на вторую на 2 пончика меньше.
Сколько всего пончиков испекла бабушка?
Второй вид
В классе два маленьких аквариума. В первом аквариуме 4 рыбки, а во втором – на 2 рыбки больше.
Сколько рыбок в двух аквариумах?
Третий вид
У Тани было 10 тетрадей. Она использовала 4 тетради.
На сколько больше тетрадей осталось, чем Таня использовала?
Четвёртый вид
У Юры было 12 счетных палочек. Для решения примеров он использовал сначала 3, а потом еще 4 палочки.
Сколько палочек у него осталось?
или
У Вани было 20 рублей. На покупку карандаша и ручки он истратил 6 и 8 рублей.
Сколько рублей осталось у Вани?
Задачи с составлением таблиц по из условию:
I тип:
На 3 одинаковые шторы израсходовали 18 м ткани. Сколько таких штор можно сшить из 30 м такой же ткани?
II тип:
В двух одинаковых пакетах 4 кг муки. Сколько килограммов муки в пяти таких пакетах?
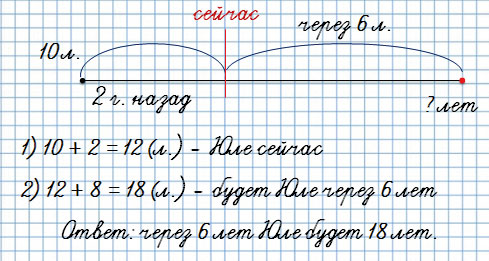
Задачи с составлением рисунка по условию:
Два года назад Юле было 10 лет. Сколько лет будет Юле через 6 лет?
Советуем посмотреть:
Обратные задачи
Цена. Количество. Стоимость
Скорость, время, расстояние
Задачи
Правило встречается в следующих упражнениях:
1 класс
Страница 15,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 19,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 23,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 25,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 30,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 31,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 32,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 33,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 5,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 6,
Моро, Волкова, Рабочая тетрадь, часть 2
2 класс
Страница 5,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 17,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 24,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 42,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 44,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 76,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 84,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 34,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 52,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 64,
Моро, Волкова, Рабочая тетрадь, часть 2
3 класс
Страница 42,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 72,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 65,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 69,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 37. ПР 4. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 13,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 32,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 22,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 43,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 54,
Моро, Волкова, Рабочая тетрадь, часть 2
4 класс
Страница 5,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 9,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 35,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 54,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 29,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 48,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 45,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 49,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 71,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 72,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
5 класс
Задание 348,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 399,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 402,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Номер 106,
Мерзляк, Полонский, Якир, Учебник
Номер 107,
Мерзляк, Полонский, Якир, Учебник
Номер 108,
Мерзляк, Полонский, Якир, Учебник
Номер 293,
Мерзляк, Полонский, Якир, Учебник
Номер 483,
Мерзляк, Полонский, Якир, Учебник
Номер 4,
Мерзляк, Полонский, Якир, Учебник
Номер 6,
Мерзляк, Полонский, Якир, Учебник
6 класс
Задание 361,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 384,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 405,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 419,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 424,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 432,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 434,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 436,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 447,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 2,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Слайд 1
Решение задач частями с помощью схемы
Слайд 2
Серёжа младше папы в 3 раза, а дедушки в 5 раз. Вместе всем троим 99 лет. Сколько лет каждому?
Слайд 3
С . П. Д. 99 лет ? ? ?
Слайд 4
Решение. Пусть 1 часть – возраст Серёжи. 1) 1 +3 +5 = 9 (ч.) составляют 99 лет. 2) 99 : 9 = 11 (л.) – возраст Серёжи. 3) 11 · 3 = 33 (г.) – возраст папы. 4) 11· 5 = 55 (л.) – возраст дедушки.
Слайд 5
Дима в субботу потратил на уроки в 4 раза меньше времени, чем на прогулку. Сколько времени Дима гулял, если он делал уроки на 180 минут меньше, чем прогуливался?
Слайд 6
Уроки Прогулка 180 минут ? ?
Слайд 7
Решение. Пусть 1 часть – время, потраченное Димой на уроки. 180 минут = 3 часа 1) 4 – 1 = 3 ( части) составляют 3 часа. 2) 3 : 3= 1 (час) Дима потратил на уроки. 3) 1 + 3 = 4 (часа) Дима гулял.
Слайд 8
За два дня Марина прочитала 126 страниц книги. Сколько страниц Марина прочитала за каждый день, если в первый день ею было прочитано на 14 страниц меньше, чем во второй?
Слайд 9
I день II день 14 стр. ? ? 126 страниц
Слайд 10
Решение. 1) 126 – 14 = 112 (стр.)- удвоенное количество страниц, прочитанных Мариной в первый день. 2) 112 : 2 = 56(стр.) прочитала Марина в первый день. 3) 56 + 14 = 70(стр.) прочитала Марина во второй день.