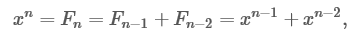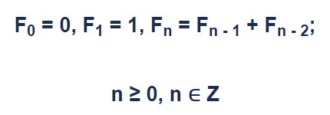Как составить числа фибоначчи - Сайт, где вы сможете решить свои вопросы

На чтение 3 мин Просмотров 192к. Опубликовано 27.05.2022

Содержание

Введение
Числа Фибоначчи циклом while
Числа Фибоначчи циклом for
Числа Фибоначчи рекурсией
Заключение

Введение

В статье разберём 3 способа получения ряда Фибоначчи на Python. Первые два способа будут с использованием циклов, а третий – рекурсивный.

Числа Фибоначчи – бесконечная последовательность чисел, каждое из которых является суммой двух предыдущих и так до бесконечности.

Формула:

Ряд Фибоначчи

Числа Фибоначчи циклом while

Для начала создадим переменную, в которую будет вводиться длина ряда:

n = int(input('Введите длину ряда: '))

Далее создадим две переменные (f1 и f2), которые будут равняться начальным единицам и выведем их:

f1 = f2 = 1
print(f1, f2, end=' ')

Создадим переменную i, которая будет равняться двум:

Добавим цикл, который не закончится, пока переменная i будет меньше переменной n:

while i < n:
	f1, f2 = f2, f1 + f2 # f1 приравнивается к f2, f2 приравнивается к f1 + f2
	print(f2, end=' ') # Выводится f2
	i += 1
print()

Числа Фибоначчи на Python:

n = int(input('Введите длину ряда: '))
f1 = f2 = 1
print(f1, f2, end=' ')

i = 2
while i < n:
	f1, f2 = f2, f1 + f2 # f1 приравнивается к f2, f2 приравнивается к f1 + f2
	print(f2, end=' ') # Выводится f2
	i += 1
print()

Числа Фибоначчи циклом for

Создадим переменную, в которую будет вводиться длина ряда:

n = int(input('Введите длину ряда: '))

Далее создадим две переменные (f1 и f2), которые будут равняться начальным единицам и выведем их:

f1 = f2 = 1
print(f1, f2, end=' ')

Добавим цикл, который начинается с 2, и заканчивается на n:

for i in range(2, n):
    f1, f2 = f2, f1 + f2 # f1 приравнивается к f2, f2 приравнивается к f1 + f2
    print(f2, end=' ') # Выводится f2

Числа Фибоначчи на Python:

n = int(input('Введите длину ряда: '))
f1 = f2 = 1
print(f1, f2, end=' ')
 
for i in range(2, n):
    f1, f2 = f2, f1 + f2
    print(f2, end=' ')

Числа Фибоначчи рекурсией

Для начала создадим рекурсивную функцию, назовём её fibonacci и добавим ей параметр n:

Добавим условие, что если n = 1, или n = 2, то возвращается единица, так как первый и второй элементы ряда Фибоначчи равны единице. Если же условие не срабатывает, то элементы складываются:

def fibonacci(n):
    if n == 1 or n == 2: # Если n = 1, или n = 2, вернуть в вызывающую ветку единицу, так как первый и второй элементы ряда Фибоначчи равны единице.
        return 1
    return fibonacci(n - 1) + fibonacci(n - 2)

Числа Фибоначчи на Python:

def fibonacci(n):
    if n == 1 or n == 2:
        return 1
    return fibonacci(n - 1) + fibonacci(n - 2)


n = int(input())
print(fibonacci(n))

Заключение

В данной статье мы научились вычислять n-ное число ряда Фибоначчи на Python. Надеюсь Вам понравилась статья, удачи! 🙂

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 21 декабря 2022 года; проверки требуют 33 правки.

Черепица с квадратами, длина сторон которых является последовательными числами Фибоначчи: 1, 1, 2, 3, 5, 8, 13 и 21

Спираль Фибоначчи: приближение золотой спирали, созданной путём рисования круговых дуг, соединяющих противоположные углы квадратов в мозаике Фибоначчи;^[1] (см. предыдущее изображение)

Чи́сла Фибона́ччи (вариант написания — Фибона́чи^[2]) — элементы числовой последовательности

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, … (последовательность A000045 в OEIS),

в которой первые два числа равны 0 и 1, а каждое последующее число равно сумме двух предыдущих чисел^[3]. Названы в честь средневекового математика Леонардо Пизанского (известного как Фибоначчи)^[4].

Правда, в некоторых книгах, особенно в старых^{[каких?]}, член $F_{0}$ , равный нулю, опускается — тогда последовательность Фибоначчи начинается с ${displaystyle F_{1}=F_{2}=1}$ ^[5]^[6].

Говоря более формально, последовательность чисел Фибоначчи ${displaystyle {F_{n}}}$ задаётся линейным рекуррентным соотношением:

${displaystyle F_{0}=0,quad F_{1}=1,quad F_{n}=F_{n-1}+F_{n-2}}$

где

{displaystyle ngeqslant 2, nin mathbb {Z} }

Иногда числа Фибоначчи рассматривают и для отрицательных значений как двусторонне бесконечную последовательность, удовлетворяющую тому же рекуррентному соотношению. Соответственно, члены с отрицательными индексами легко получить с помощью эквивалентной формулы «назад»: ${displaystyle F_{n}=F_{n+2}-F_{n+1}}$ :

n	…	−10	−9	−8	−7	−6	−5	−4	−3	−2	−1	0	1	2	3	4	5	6	7	8	9	10	…
$F_{n}$	…	−55	34	−21	13	−8	5	−3	2	−1	1	0	1	1	2	3	5	8	13	21	34	55	…

Легко заметить, что ${displaystyle F_{-n}=(-1)^{n+1}F_{n}}$ .

Происхождение

Количество пар кроликов образуют последовательность Фибоначчи

Последовательность Фибоначчи была хорошо известна в древней Индии^[7]^[8]^[9], где она применялась в метрических науках (просодии, другими словами — стихосложении) намного раньше, чем стала известна в Европе^[8]^[10]^[11].

Образец длиной n может быть построен путём добавления S к образцу длиной n − 1, либо L к образцу длиной n − 2 — и просодицисты показали, что число образцов длиною n является суммой двух предыдущих чисел в последовательности^[9]. Дональд Кнут рассматривает этот эффект в книге «Искусство программирования».

На Западе эта последовательность была исследована Леонардо Пизанским, известным как Фибоначчи, в его труде «Книга абака» (1202)^[12]^[13]. Он рассматривает развитие идеализированной (биологически нереальной) популяции кроликов, где условия таковы: изначально дана новорождённая пара кроликов (самец и самка); со второго месяца после своего рождения кролики начинают спариваться и производить новую пару кроликов, причём уже каждый месяц; кролики никогда не умирают^[14]^[15], — а в качестве искомого выдвигает количество пар кроликов через год.

В начале первого месяца есть только одна новорождённая пара (1).
В конце первого месяца по-прежнему только одна пара кроликов, но уже спарившаяся (1).
В конце второго месяца первая пара рождает новую пару и опять спаривается (2).
В конце третьего месяца первая пара рождает ещё одну новую пару и спаривается, вторая пара только спаривается (3).
В конце четвёртого месяца первая пара рождает ещё одну новую пару и спаривается, вторая пара рождает новую пару и спаривается, третья пара только спаривается (5).

В конце -го месяца количество пар кроликов будет равно количеству пар в предыдущем месяце плюс количеству новорождённых пар, которых будет столько же, сколько пар было два месяца назад, то есть ${displaystyle F_{n}=F_{n-2}+F_{n-1}}$ ^[16].
Возможно, эта задача также оказалась первой, моделирующей экспоненциальный рост популяции.

Название «последовательность Фибоначчи» впервые было использовано теоретиком XIX века Эдуардом Люка^[17].

Формула Бине

Формула Бине выражает в явном виде значение $F_{n}$ как функцию от n:

$F_{n}={frac {left({frac {1+{sqrt {5}}}{2}}right)^{n}-left({frac {1-{sqrt {5}}}{2}}right)^{n}}{sqrt {5}}}={frac {varphi ^{n}-(-varphi )^{-n}}{varphi -(-varphi )^{-1}}}={frac {varphi ^{n}-(-varphi )^{-n}}{2varphi -1}},$

где $varphi ={frac {1+{sqrt {5}}}{2}}$ — золотое сечение и varphi и ${displaystyle (-varphi )^{-1}=1-varphi }$ являются корнями характеристического уравнения $x^{2}-x-1=0.$
Вообще, аналогичная формула существует для любой линейной рекуррентной последовательности, какой служит и последовательность Фибоначчи.

Обоснование

^[18]

Преобразуем характеристическое уравнение ${displaystyle x^{2}-x-1=0}$ к виду ${displaystyle x^{2}=x+1,}$ умножим обе части на : ${displaystyle x^{3}=x^{2}+x}$ — и заменим в этой сумме $x^{2}$ на x+1 , что мы можем сделать в силу характеристического уравнения. Получим ${displaystyle x^{3}=x^{2}+x=(x+1)+x=2x+1.}$ Затем продолжим так же умножать на и преобразовывать $x^{2}$ , следуя первоначальному уравнению:

${displaystyle {begin{aligned}x^{4}&=2x^{2}+x=2(x+1)+x=\&=3x+2,\x^{5}&=3x^{2}+2x=3(x+1)+2x=\&=5x+3,\x^{6}&=5x^{2}+3x=5(x+1)+3x=\&=8x+5,\x^{7}&=8x^{2}+5x=8(x+1)+5x=\&=13x+8,\&cdots end{aligned}}}$

Таким образом образуется общее уравнение: ${displaystyle x^{n}=F_{n}x+F_{n-1}.}$ Чтобы это уравнение обратить в верное равенство и отсюда выразить сами числа Фибоначчи, нужно подставить корни varphi и ${displaystyle -varphi ^{-1}colon }$

${displaystyle {begin{cases}varphi ^{n}=F_{n}varphi +F_{n-1},\(-varphi )^{-n}=-F_{n}varphi ^{-1}+F_{n-1},end{cases}}}$

${displaystyle varphi ^{n}-(-varphi )^{-n}=F_{n}[varphi -(-varphi )^{-1}],qquad varphi ^{n}+(-varphi )^{-n}cdot varphi ^{2}=F_{n-1}(1+varphi ^{2}),}$

${displaystyle color {Black}{tfrac {1}{sqrt {5}}}left(({tfrac {1+{sqrt {5}}}{2}})^{n}-({tfrac {1-{sqrt {5}}}{2}})^{n}right)=F_{n},qquad {tfrac {1}{sqrt {5}}}left(({tfrac {1+{sqrt {5}}}{2}})^{n-1}-({tfrac {1-{sqrt {5}}}{2}})^{n-1}right)=F_{n-1}.}$

Следствие и обобщение

Из формулы Бине следует, что для всех число $F_{n}$ есть округление ${displaystyle {frac {varphi ^{n}}{sqrt {5}}},}$ то есть ${displaystyle F_{n}=leftlfloor {frac {varphi ^{n}}{sqrt {5}}}rightrceil .}$
В частности, при справедлива асимптотика ${displaystyle F_{n}sim {frac {varphi ^{n}}{sqrt {5}}}.}$

Формула Бине может быть аналитически продолжена следующим образом:

$F_{z}={frac {1}{sqrt {5}}}left(varphi ^{z}-{frac {cos {pi z}}{varphi ^{z}}}right).$

При этом соотношение $F_{z+2}=F_{z+1}+F_{z}$ выполняется для любого комплексного числа z.

Тождества

Иллюстрация формулы для суммы квадратов первых n чисел Фибоначчи^[19]

${displaystyle F_{1}+F_{2}+F_{3}+dots +F_{n}=F_{n+2}-1.}$ ^[20]

Доказательство

Докажем формулу индукцией по n:

База индукции:

${displaystyle F_{0}=F_{2}-1=0.}$

Шаг индукции: пусть утверждение для верно:

${displaystyle F_{1}+F_{2}+F_{3}+...+F_{n}=F_{n+2}-1.}$

Тогда надо доказать утверждение для

${displaystyle F_{1}+F_{2}+F_{3}+...+F_{n}+F_{n+1}=F_{n+3}-1.}$

Раскладываем ${displaystyle F_{n+3}}$

на ${displaystyle F_{n+2}}$

и ${displaystyle F_{n+1}colon }$

${displaystyle F_{1}+F_{2}+F_{3}+...+F_{n}+F_{n+1}=F_{n+2}+F_{n+1}-1}$

Сокращаем обе части на ${displaystyle F_{n+1}colon }$

${displaystyle F_{1}+F_{2}+F_{3}+...+F_{n}=F_{n+2}-1,}$

что и требовалось доказать. ∎

${displaystyle F_{1}+F_{3}+F_{5}+dots +F_{2n-1}=F_{2n}.}$ ^[20]^[21]

Доказательство

Докажем формулу индукцией по n:

База индукции:

${displaystyle F_{1}=F_{2}=1.}$

Шаг индукции: Пусть утверждение для верно:

${displaystyle F_{1}+F_{3}+F_{5}+dots +F_{2n-1}=F_{2n}.}$

Тогда надо доказать утверждение для

${displaystyle F_{1}+F_{3}+F_{5}+dots +F_{2n-1}+F_{2n+1}=F_{2n+2}.}$

Раскладываем ${displaystyle F_{2n+2}}$

на ${displaystyle F_{2n+1}}$

и ${displaystyle F_{2n}colon }$

${displaystyle F_{1}+F_{3}+F_{5}+dots +F_{2n-1}+F_{2n+1}=F_{2n+1}+F_{2n}.}$

Сокращаем обе части на ${displaystyle F_{2n+1}colon }$

${displaystyle F_{1}+F_{3}+F_{5}+dots +F_{2n-1}=F_{2n}.}$

что и требовалось доказать. ∎

${displaystyle F_{2}+F_{4}+F_{6}+dots +F_{2n}=F_{2n+1}-1.}$ ^[20]^[22]

Это тождество можно доказать вычитанием первого из второго: ${displaystyle {begin{alignedat}{2}(F_{1}+F_{2}+dots +F_{{color {Red}2}n})-(F_{1}+F_{3}+dots +F_{2n-1})&=F_{{color {Red}2}n+2}-1-F_{2n},\F_{2}+F_{4}+dots +F_{2n}&=F_{2n+1}-1.\end{alignedat}}}$

И более общие формулы:

где матрицы имеют размер

и где i — мнимая единица.

$(-1)^{n}=F_{n+1}F_{n-1}-F_{n}^{2}.$

С равенством Кассини сопряжено более общее утверждение, названное в честь Эжена Каталана: ${displaystyle F_{n}^{2}-F_{n-r}F_{n+r}=(-1)^{n-r}F_{r}^{2}.}$

Свойства

Тринадцать ( ${displaystyle F_{7}}$ ) способов расположения длинных (красные) и коротких слогов (серые) в каденции^[en] длины шесть: пять ( $F_{5}$ ) заканчивается длинным слогом и восемь ( ${displaystyle F_{6}}$ ) — коротким

Последовательные наклоны плоскости и график приближений к золотому сечению, рассчитанному путём деления каждого числа Фибоначчи на предыдущее

на множестве неотрицательных целых чисел x и y^[30].

Произведение и частное двух любых различных чисел Фибоначчи, отличных от единицы, никогда не является числом Фибоначчи.
Период чисел Фибоначчи по модулю натурального числа называется периодом Пизано и обозначается . Периоды Пизано образуют последовательность:

1, 3, 8, 6, 20, 24, 16, 12, 24, 60, 10, 24, 28, 48, 40, 24, 36, … (последовательность A001175 в OEIS).
Натуральное число является числом Фибоначчи тогда и только тогда, когда $5N^{2}+4$ или $5N^{2}-4$ является квадратом^[31].
Не существует арифметической прогрессии длиной больше 3, состоящей из чисел Фибоначчи^[32].
Число Фибоначчи $F_{n+2}=F_{n+1}+F_{n}$ равно количеству кортежей длины n из нулей и единиц, в которых нет двух соседних единиц. При этом $F_{{n+1}}$ равно количеству таких кортежей, начинающихся с нуля, а $F_{n}$ — начинающихся с единицы.
Произведение любых подряд идущих чисел Фибоначчи делится на произведение первых чисел Фибоначчи.
Бесконечная сумма чисел, обратных числам Фибоначчи, сходится, его сумма («обратная постоянная Фибоначчи») равна 3,359884…

Вариации и обобщения

В других областях

Жёлтая ромашковая головка, показывающая расположение в 21 (синяя) и 13 (аква) спиралей. Такие схемы, включающие последовательные числа Фибоначчи, встречаются у самых разных растений

Число возможных предков на линии наследования Х-хромосомы в данном поколении предков следует последовательности Фибоначчи (Хатчисон Л. Растущее семейное древо: сила ДНК в восстановлении семейных отношений)^[33]

Иллюстрация модели Фогеля для n = 1 … 500

Существует мнение, что почти все утверждения, находящие числа Фибоначчи в природных и исторических явлениях, неверны — это распространённый миф, который часто оказывается неточной подгонкой под желаемый результат^[34]^[35].

В природе

Филлотаксис (листорасположение) у растений описывается последовательностью Фибоначчи, если листья (почки) на однолетнем приросте (побеге, стебле) имеют так называемое спиральное листорасположение. При этом число последовательно расположенных листьев (почек) по спирали плюс один, а также число совершенных при этом полных оборотов спирали вокруг оси однолетнего прироста (побега, стебля) выражаются обычно первыми числами Фибоначчи.
Семена подсолнуха, сосновые шишки, лепестки цветков, ячейки ананаса также располагаются согласно последовательности Фибоначчи^[36]^[37]^[38]^[39].

В искусстве

В поэзии чаще находят отношение «золотого сечения» (золотую пропорцию), связанное через формулу Бине с числами Фибоначчи. Например, в поэме Ш. Руставели «Витязь в тигровой шкуре» и на картинах художников^[40].

Однако числа Фибоначчи встречаются и непосредственно в поэзии и в музыке^[41]

В кодировании

В теории кодирования предложены устойчивые так называемые «коды Фибоначчи»^[42], причём основание этих кодов — иррациональное число.

См. также

Дерево Фибоначчи
Метод Фибоначчи с запаздываниями
Метод Фибоначчи поиска экстремума
Фибоначчи
Фибоначчиева система счисления
Числа Бине
Числа Леонардо
Таблица Витхоффа
Последовательность коров Нараяны
Золотое сечение
Пропорционирование

Примечания

↑ John Hudson Tiner. Изучение мира математики: от древних записей до новейших достижений в области компьютеров. — New Leaf Publishing Group, 200. — ISBN 978-1-61458-155-0.
↑ См., например, Т. В. Кропотова, В. Г. Подольский, П. Е. Кашаргин. Введение в высшую математику. — Казанский федеральный университет институт физики.
↑ Lucas, 1891, p. 3.
↑ Числа Фибоначчи // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
↑ Beck & Geoghegan (2010).
↑ Bóna, 2011, p. 180.
↑ Goonatilake, Susantha (1998), Toward a Global Science, Indiana University Press, с. 126, ISBN 978-0-253-33388-9, <https://books.google.com/books?id=SI5ip95BbgEC&pg=PA126>
↑ ¹ ² Singh, Parmanand (1985), The So-called Fibonacci numbers in ancient and medieval India, Historia Mathematica Т. 12 (3): 229—244, DOI 10.1016/0315-0860(85)90021-7
↑ ¹ ² Knuth, Donald (2006), The Art of Computer Programming, vol. 4. Generating All Trees – History of Combinatorial Generation, Addison–Wesley, с. 50, ISBN 978-0-321-33570-8, <https://books.google.com/books?id=56LNfE2QGtYC&pg=PA50&dq=rhythms>
↑ Knuth, Donald (1968), The Art of Computer Programming, vol. 1, Addison Wesley, с. 100, ISBN 978-81-7758-754-8, <https://books.google.com/books?id=MooMkK6ERuYC&pg=PA100>
↑ Livio, 2003, p. 197.
↑ Pisano, 2002, pp. 404—405.
↑ Fibonacci’s Liber Abaci (Book of Calculation). The University of Utah (13 декабря 2009). Дата обращения: 28 ноября 2018.
↑ Hemenway, Priya. Divine Proportion: Phi In Art, Nature, and Science (англ.). — New York: Sterling, 2005. — P. 20—21. — ISBN 1-4027-3522-7.
↑ Knott, Dr. Ron The Fibonacci Numbers and Golden section in Nature – 1. University of Surrey (25 сентября 2016). Дата обращения: 27 ноября 2018.
↑ Knott, Ron Fibonacci’s Rabbits. University of Surrey Faculty of Engineering and Physical Sciences.
↑ Gardner, Martin (1996), Mathematical Circus, The Mathematical Association of America, с. 153, ISBN 978-0-88385-506-5
↑ Art of Problem Solving. artofproblemsolving.com. Дата обращения: 9 мая 2021.
↑ Фибоначчи числа // Энциклопедический словарь юного математика / Сост. Савин А. П.. — 2-е изд. — М.: Педагогика, 1989. — С. 312—314. — 352 с. — ISBN 5715502187.
↑ ¹ ² ³ ⁴ ⁵ Теорема изложена в данном файле.
↑ Пункт 23.
↑ Пункт 24.
↑ Следствие из пункта 36.
↑ Пункт 30.
↑ 64.
↑ Пункт 55.
↑ proof of Cassini’s identity. planetmath.org. Дата обращения: 30 мая 2021.
↑ Тождество Кассини.
↑ J H E Cohn. Square Fibonacci Numbers Etc, С. 109—113. Архивировано 11 июля 2010 года. Дата обращения: 1 июля 2010.
↑ P. Ribenboim. The New Book of Prime Number Records. — Springer, 1996. — С. 193.
↑ Ira Gessel. Problem H-187 // Fibonacci Quarterly. — 1972. — Т. 10. — С. 417—419.
↑ В. Серпинский. Задача 66 // 250 задач по элементарной теории чисел. — М.: Просвещение, 1968. — 168 с.
↑ Hutchison, Luke. Growing the Family Tree: The Power of DNA in Reconstructing Family Relationships (англ.) // Proceedings of the First Symposium on Bioinformatics and Biotechnology (BIOT-04) : journal. — 2004. — September.
↑ Fibonacci Flim-Flam. Архивная копия от 23 апреля 2012 на Wayback Machine (англ.).
↑ The Myth That Will Not Go Away (англ.).
↑ Золотое сечение в природе.
↑ Числа Фибоначчи.
↑ Числа Фибоначчи.
↑ Акимов О. Е. Конец науки.
↑ Волошинов А. В. Математика и искусство. Москва: Просвещение, 2000. 400 с. ISBN 5-09-008033-X
↑ Математика в стихах и музыке
↑ Стахов А., Слученкова А., Щербаков И. Код да Винчи и ряды Фибоначчи. СПБ. Издательство: Питер, 2006. 320 с. ISBN 5-469-01369-3

Литература

Н. Н. Воробьёв. Числа Фибоначчи. — Наука, 1978. — Т. 39. — (Популярные лекции по математике).
А. И. Маркушевич. Возвратные последовательности. — Гос. Издательство Технико-Теоретической Литературы, 1950. — Т. 1. — (Популярные лекции по математике).
А. Н. Рудаков. Числа Фибоначчи и простота числа 2¹²⁷ − 1 // Математическое Просвещение, третья серия. — 2000. — Т. 4.
Дональд Кнут. Искусство программирования, том 1. Основные алгоритмы = The Art of Computer Programming, vol. 1. Fundamental Algorithms. — 3-е изд. — М.: «Вильямс», 2006. — С. 720. — ISBN 0-201-89683-4.
Дональд Кнут, Роналд Грэхем, Орен Паташник. Конкретная математика. Основание информатики = Concrete Mathematics. A Foundation for Computer Science. — М.: Мир; Бином. Лаборатория знаний, 2006. — С. 703. — ISBN 5-94774-560-7.
Грант Аракелян. Математика и история золотого сечения. — М.: Логос, 2014. — 404 с. — ISBN 978-5-98704-663-0.
Ball, Keith M (2003), 8: Fibonacci’s Rabbits Revisited, Strange Curves, Counting Rabbits, and Other Mathematical Explorations, Princeton, NJ: Princeton University Press, ISBN 978-0-691-11321-0.
Beck, Matthias & Geoghegan, Ross (2010), The Art of Proof: Basic Training for Deeper Mathematics, New York: Springer, ISBN 978-1-4419-7022-0.
Bóna, Miklós (2011), A Walk Through Combinatorics (3rd ed.), New Jersey: World Scientific, ISBN 978-981-4335-23-2.
- Bóna, Miklós (2016), A Walk Through Combinatorics (4th Revised ed.), New Jersey: World Scientific, ISBN 978-981-3148-84-0.
Lemmermeyer, Franz (2000), Reciprocity Laws: From Euler to Eisenstein, Springer Monographs in Mathematics, New York: Springer, ISBN 978-3-540-66957-9.
Livio, Mario. The Golden Ratio: The Story of Phi, the World’s Most Astonishing Number (англ.). — First trade paperback. — New York City: Broadway Books (англ.) (рус., 2003. — ISBN 0-7679-0816-3.
Lucas, Édouard (1891), Théorie des nombres, vol. 1, Paris: Gauthier-Villars, Théorie des nombres в «Книгах Google», <https://archive.org/details/thoriedesnombr01lucauoft>.
Pisano, Leonardo (2002), Fibonacci’s Liber Abaci: A Translation into Modern English of the Book of Calculation, Sources and Studies in the History of Mathematics and Physical Sciences, Springer, ISBN 978-0-387-95419-6

Ссылки

Первые 300 чисел Фибоначчи (англ.).
Числа Фибоначчи в природе (англ.).

Источник

Время на прочтение
5 мин

Количество просмотров 306K

Введение

Программистам числа Фибоначчи должны уже поднадоесть. Примеры их вычисления используются везде. Всё от того, что эти числа предоставляют простейший пример рекурсии. А ещё они являются хорошим примером динамического программирования. Но надо ли вычислять их так в реальном проекте? Не надо. Ни рекурсия, ни динамическое программирование не являются идеальными вариантами. И не замкнутая формула, использующая числа с плавающей запятой. Сейчас я расскажу, как правильно. Но сначала пройдёмся по всем известным вариантам решения.

Код предназначен для Python 3, хотя должен идти и на Python 2.

Для начала – напомню определение:

F_n= F_n-1+ F_n-2

и F₁= F₂=1.

Замкнутая формула

Пропустим детали, но желающие могут ознакомиться с выводом формулы. Идея в том, чтобы предположить, что есть некий x, для которого F_n = xⁿ, а затем найти x.

что означает

сокращаем x^n-2

Решаем квадратное уравнение:

Откуда и растёт «золотое сечение» ϕ=(1+√5)/2. Подставив исходные значения и проделав ещё вычисления, мы получаем:

что и используем для вычисления F_n.

from __future__ import division
import math

def fib(n):
    SQRT5 = math.sqrt(5)
    PHI = (SQRT5 + 1) / 2
    return int(PHI ** n / SQRT5 + 0.5)

Хорошее:
Быстро и просто для малых n
Плохое:
Требуются операции с плавающей запятой. Для больших n потребуется большая точность.
Злое:
Использование комплексных чисел для вычисления F_n красиво с математической точки зрения, но уродливо — с компьютерной.

Рекурсия

Самое очевидное решение, которое вы уже много раз видели – скорее всего, в качестве примера того, что такое рекурсия. Повторю его ещё раз, для полноты. В Python её можно записать в одну строку:

fib = lambda n: fib(n - 1) + fib(n - 2) if n > 2 else 1

Хорошее:
Очень простая реализация, повторяющая математическое определение
Плохое:
Экспоненциальное время выполнения. Для больших n очень медленно
Злое:
Переполнение стека

Запоминание

У решения с рекурсией есть большая проблема: пересекающиеся вычисления. Когда вызывается fib(n), то подсчитываются fib(n-1) и fib(n-2). Но когда считается fib(n-1), она снова независимо подсчитает fib(n-2) – то есть, fib(n-2) подсчитается дважды. Если продолжить рассуждения, будет видно, что fib(n-3) будет подсчитана трижды, и т.д. Слишком много пересечений.

Поэтому надо просто запоминать результаты, чтобы не подсчитывать их снова. Время и память у этого решения расходуются линейным образом. В решении я использую словарь, но можно было бы использовать и простой массив.

M = {0: 0, 1: 1}

def fib(n):
    if n in M:
        return M[n]
    M[n] = fib(n - 1) + fib(n - 2)
    return M[n]

(В Python это можно также сделать при помощи декоратора, functools.lru_cache.)

Хорошее:
Просто превратить рекурсию в решение с запоминанием. Превращает экспоненциальное время выполнение в линейное, для чего тратит больше памяти.
Плохое:
Тратит много памяти
Злое:
Возможно переполнение стека, как и у рекурсии

Динамическое программирование

После решения с запоминанием становится понятно, что нам нужны не все предыдущие результаты, а только два последних. Кроме этого, вместо того, чтобы начинать с fib(n) и идти назад, можно начать с fib(0) и идти вперёд. У следующего кода линейное время выполнение, а использование памяти – фиксированное. На практике скорость решения будет ещё выше, поскольку тут отсутствуют рекурсивные вызовы функций и связанная с этим работа. И код выглядит проще.

Это решение часто приводится в качестве примера динамического программирования.

def fib(n):
    a = 0
    b = 1
    for __ in range(n):
        a, b = b, a + b
    return a

Хорошее:
Быстро работает для малых n, простой код
Плохое:
Всё ещё линейное время выполнения
Злое:
Да особо ничего.

Матричная алгебра

И, наконец, наименее освещаемое, но наиболее правильное решение, грамотно использующее как время, так и память. Его также можно расширить на любую гомогенную линейную последовательность. Идея в использовании матриц. Достаточно просто видеть, что

А обобщение этого говорит о том, что

Два значения для x, полученных нами ранее, из которых одно представляло собою золотое сечение, являются собственными значениями матрицы. Поэтому, ещё одним способом вывода замкнутой формулы является использование матричного уравнения и линейной алгебры.

Так чем же полезна такая формулировка? Тем, что возведение в степень можно произвести за логарифмическое время. Это делается через возведения в квадрат. Суть в том, что

где первое выражение используется для чётных A, второе для нечётных. Осталось только организовать перемножения матриц, и всё готово. Получается следующий код. Я организовал рекурсивную реализацию pow, поскольку её проще понять. Итеративную версию смотрите тут.

def pow(x, n, I, mult):
    """
    Возвращает x в степени n. Предполагает, что I – это единичная матрица, которая 
    перемножается с mult, а n – положительное целое
    """
    if n == 0:
        return I
    elif n == 1:
        return x
    else:
        y = pow(x, n // 2, I, mult)
        y = mult(y, y)
        if n % 2:
            y = mult(x, y)
        return y


def identity_matrix(n):
    """Возвращает единичную матрицу n на n"""
    r = list(range(n))
    return [[1 if i == j else 0 for i in r] for j in r]


def matrix_multiply(A, B):
    BT = list(zip(*B))
    return [[sum(a * b
                 for a, b in zip(row_a, col_b))
            for col_b in BT]
            for row_a in A]


def fib(n):
    F = pow([[1, 1], [1, 0]], n, identity_matrix(2), matrix_multiply)
    return F[0][1]

Хорошее:
Фиксированный объём памяти, логарифмическое время
Плохое:
Код посложнее
Злое:
Приходится работать с матрицами, хотя они не так уж и плохи

Сравнение быстродействия

Сравнивать стоит только вариант динамического программирования и матрицы. Если сравнивать их по количеству знаков в числе n, то получится, что матричное решение линейно, а решение с динамическим программированием – экспоненциально. Практический пример – вычисление fib(10 ** 6), числа, у которого будет больше двухсот тысяч знаков.

n = 10 ** 6
Вычисляем fib_matrix: у fib(n) всего 208988 цифр, расчёт занял 0.24993 секунд.
Вычисляем fib_dynamic: у fib(n) всего 208988 цифр, расчёт занял 11.83377 секунд.

Теоретические замечания

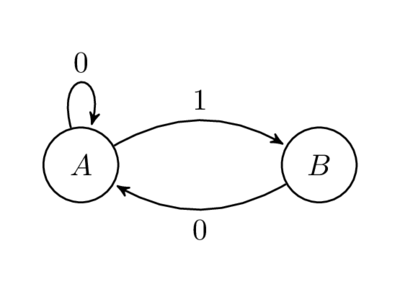
Не напрямую касаясь приведённого выше кода, данное замечание всё-таки имеет определённый интерес. Рассмотрим следующий граф:

Подсчитаем количество путей длины n от A до B. Например, для n = 1 у нас есть один путь, 1. Для n = 2 у нас опять есть один путь, 01. Для n = 3 у нас есть два пути, 001 и 101. Довольно просто можно показать, что количество путей длины n от А до В равно в точности F_n. Записав матрицу смежности для графа, мы получим такую же матрицу, которая была описана выше. Это известный результат из теории графов, что при заданной матрице смежности А, вхождения в Аⁿ — это количество путей длины n в графе (одна из задач, упоминавшихся в фильме «Умница Уилл Хантинг»).

Почему на рёбрах стоят такие обозначения? Оказывается, что при рассмотрении бесконечной последовательности символов на бесконечной в обе стороны последовательности путей на графе, вы получите нечто под названием “подсдвиги конечного типа”, представляющее собой тип системы символической динамики. Конкретно этот подсдвиг конечного типа известен, как «сдвиг золотого сечения», и задаётся набором «запрещённых слов» {11}. Иными словами, мы получим бесконечные в обе стороны двоичные последовательности и никакие пары из них не будут смежными. Топологическая энтропия этой динамической системы равна золотому сечению ϕ. Интересно, как это число периодически появляется в разных областях математики.

Источник

Числа Фибоначчи — это числа такой последовательности, в которой первые два элемента — 0 и 1, а каждый последующий элемент равен сумме двух предшествующих. Выглядит это так:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, …

Примечание Иногда 0 опускается, и в этом случае ряд начинается с 1, но мы будем использовать последовательность с 0 на первой позиции.

Формула записывается следующим образом:

Вычисление ряда Фибоначчи — стандартная задача, которую задают на собеседованиях, чтобы проверить кандидата на понимание алгоритмов. Не так популярна, как сортировка, но всё же.

Давайте вычислим ряд и его отдельные элементы, использовав для этого язык Java.

Цикл
Рекурсия
Stream
Тест

Вычислить ряд Фибоначчи циклом

Предположим, что нам нужно вывести на экран первые десять чисел последовательности Фибоначчи. Мы помним, что:

первый элемент ряда — 0, второй — 1;
каждый последующий — сумма двух предыдущих.

Тогда наша последовательность будет иметь такой вид:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34

Но нам нужно вывести результат с использованием программы. Держите код с объяснениями в комментариях:

public class Main{
	public static void main(String[] args) {
	    
	        //Объявляем переменные при известных первых двух:
		int num0 = 0;
		int num1 = 1;
		int num2;
		
		//Первые две переменные выводим вне цикла:
		System.out.print(num0 + " " + num1 + " ");
		for(int i = 3; i <= 10; i++){
			num2 = num0 + num1;
			
			//Каждый следующий элемент выводим в цикле:
			System.out.print(num2 + " ");
			
			//Предыдущим двум переменным присваиваем новые значения:
			num0 = num1;
			num1 = num2;
		}
	}
}

Выполнение завершится на десятом элементе. Количество элементов при этом можно менять, изменив значение в условиях цикла.

Найти число Фибоначчи через рекурсию

Рекурсивная функция — это такая функция, которая вызывает саму себя. Она также неплохо отрабатывает в алгоритмических задачах вроде чисел Фибоначчи, но ей требуется больше времени.

Почему так происходит? Всё дело в том, что рекурсивная функция приводит к многоразовому вызову одних и тех же операций. Именно из-за этого её не рекомендуется использовать, но если уж на собеседовании прозвучит такая задача, вы будете готовы.

Рассмотрим пример, в котором нам нужно получить n-ое число в ряде Фибоначчи:

public int fibonacciValue(num) {
  if (num <= 1) {
     return 0;
  } else if (num == 2) {
     return 1;
  } else {
     return fibonacciValue(num - 1) + fibonacciValue(num - 2);
  }
}

Если в качестве num задать большое значение, программа зависнет.

Тип int в Java может хранить значения до 2147483647, так что вычислить получится лишь первые 46 чисел Фибоначчи. Тип long хранит до 9223372036854775807, а это 91 число Фибоначчи. Класс BigInteger призван работать с действительно большими значениями, вот только само выполнение программы это никак не ускорит.

Использовать для вычисления Stream

Stream в Java — это компонент для самостоятельной внутренней итерации своих же элементов. Подробнее о нём вы можете почитать в нашей статье о Java Stream API.

И, разумеется, Stream подходит для вычисления элементов последовательности Фибоначчи:

Stream.iterate(new int[]{0, 1}, arr -> new int[]{arr[1], arr[0]+ arr[1]})
    
   //Задаём лимит значений:
   .limit(num)
   
   //Отбираем по первому элементу каждого массива:
   .map(y -> y[0])
   
   //Выводим в консоль:
   .forEach(x -> System.out.println(x));

В данном примере метод iterate() будет возвращать упорядоченный поток, ограниченный лимитом в num значений и созданный с применением функции к начальному массиву arr. В консоль будет выведено следующее:

{0,1}
{1,1}
{1, 2}
{2, 3}
{3, 5}
{5, 8}
{8, 13}
{13, 21}
…

А так мы получим сумму чисел последовательности по элемент num включительно:

int fibonacciValuesSum = Stream.iterate(new int[]{0, 1}, arr -> new int[]{arr[1], arr[0]+ arr[1]})
     .limit(num)
     .map(y -> y[0])
     .mapToInt(Integer::intValue)
     .sum();
System.out.println(fibonacciValuesSum);

Математический тест

Любите математику? Попробуйте решить наш математический тест:

Источник

В этой статье вы узнаете, как определить пользовательский тип последовательности в Python и как реализовать последовательность Фибоначчи с помощью кастомного типа Sequence.

Иногда полезно реализовать собственный тип последовательности, у которого есть функции, аналогичные встроенным функциям для кортежей или списков.

Как вы уже знаете, последовательность может быть изменяемой или неизменяемой. В этой статье мы сосредоточимся на создании пользовательского неизменяемого типа последовательности.

У неизменяемой последовательность должно быть две основные возможности:

Возвращать количество элементов последовательности.
Возвращать элемент по заданному индексу или вызывать ошибку IndexError, если индекс выходит за границы последовательности.

Если объект удовлетворяет вышеуказанным требованиям, получится производить следующие действия:

Использовать синтаксис квадратных скобок [] для получения элемента по индексу.
Перебирать элементы последовательности: например, с помощью цикла for.

Чтобы реализовать перечисленные выше возможности, нужно создать следующие методы:

__getitem__ — возвращает элемент по заданному индексу.
__len__ — возвращает длину последовательности.

1) Метод getitem

У метода __getitem__ должен быть аргумент index, который является целым числом. Метод __getitem__ должен вернуть элемент из последовательности на основе указанного индекса.

Диапазон значений index: от нуля до length - 1. Если индекс выходит за границы, метод __getitem__ должен выдать исключение IndexError.

Метод __getitem__ может принимать объект среза для слайсинга.

2) The len method

Если у пользовательской последовательности есть метод __len__, вы можете использовать встроенную функцию len(), чтобы получить количество элементов последовательности.

Последовательность Фибоначчи

Последовательность Фибоначчи примерно в 1170 году открыл Леонардо Фибоначчи, итальянский математик.

В последовательности Фибоначчи каждое число является суммой двух предшествующих ему чисел. Например:

1, 1, 2, 3, 5, 8 , 13, 21, …

Последовательность Фибоначии можно задать следующей формулой:

f(1) = 1
f(2) = 1
f(n) = f(n-1) + f(n-2) если n > 2

В некоторые источниках сказано, что последовательность Фибоначчи начинается с нуля, а не с 1, как сейчас. То есть вот так:

0, 1, 1, 2, 3, 5, 8 , 13, 21, ...

Но мы будем придерживаться исходной последовательности Фибоначчи, которая начинается с единицы.

Чтобы вычислить число Фибоначчи в Python, нужно создать такую рекурсивную функцию:

def fib(n):
    if n < 2:
        return 1
    return fib(n-2) + fib(n-1)

В этой рекурсивной функции fib(1) и fib(2) всегда возвращают 1. А когда n больше 2, fib(n) = fib(n-2) – fib(n-1).

Добавим print() в начало функции, чтобы посмотреть, как она работает, и вызовем функцию fib() с аргументом 6.

def fib(n):
    print(f'Считаю {n} число Фибоначчи')
    if n < 2:
        return 1
    return fib(n-2) + fib(n-1)


fin(6)

Вывод

Считаю 6 число Фибоначчи
Считаю 4 число Фибоначчи
Считаю 2 число Фибоначчи
Считаю 0 число Фибоначчи
Считаю 1 число Фибоначчи
Считаю 3 число Фибоначчи
Считаю 1 число Фибоначчи
Считаю 2 число Фибоначчи
Считаю 0 число Фибоначчи
Считаю 1 число Фибоначчи
Считаю 5 число Фибоначчи
Считаю 3 число Фибоначчи
Считаю 1 число Фибоначчи
Считаю 2 число Фибоначчи
Считаю 0 число Фибоначчи
Считаю 1 число Фибоначчи
Считаю 4 число Фибоначчи
Считаю 2 число Фибоначчи
Считаю 0 число Фибоначчи
Считаю 1 число Фибоначчи
Считаю 3 число Фибоначчи
Считаю 1 число Фибоначчи
Считаю 2 число Фибоначчи
Считаю 0 число Фибоначчи
Считаю 1 число Фибоначчи

Как вы видите, функция fib() часто повторяется.

Например, ей приходится трижды вычислять 3 число Фибоначчи. Это неэффективно.

Чтобы решить эту проблему, в Python есть декоратор под названием lru_cache из модуля functools.

lru_cache позволяет кэшировать результат работы функции. Когда вы передаете тот же аргумент функции, функция просто получает результат из кэша вместо того, чтобы пересчитывать его.

Ниже показано, как использовать декоратор lru_cache для ускорения работы функции fib():

from functools import lru_cache


@lru_cache
def fib(n):
    print(f'Считаю {n} число Фибоначчи')
    if n < 2:
        return 1
    return fib(n-2) + fib(n-1)


fib(6)

Вывод

Считаю 6 число Фибоначчи
Считаю 4 число Фибоначчи
Считаю 2 число Фибоначчи
Считаю 0 число Фибоначчи
Считаю 1 число Фибоначчи
Считаю 3 число Фибоначчи
Считаю 5 число Фибоначчи

Как вы видите, количество вычислений значительно уменьшилось.

Создаем последовательность Фибоначии

1. Сначала определим класс, реализующий последовательность Фибоначчи:

class Fibonacci:
    def __init__(self, n):
        self.n = n

Метод __init__ принимает целое число n, которое задает длину последовательности.

2. Теперь определим статический метод, который вычисляет значение определенного числа Фибоначчи:

@staticmethod
@lru_cache(2**16)
def fib(n):
    if n < 2:
        return 1
    return Fibonacci.fib(n-2) + Fibonacci.fib(n-1)

3. Реализуем метод __len__, чтобы мы могли использовать встроенную функцию len() для получения количества элементов из последовательности Фибоначчи:

def __len__(self):
    return self.n

4. Реализуем метод __getitem__ для поддержки индексации с помощью синтаксиса квадратных скобок []:

def __getitem__(self, index):
    if isinstance(index, int):
        if index < 0 or index > self.n - 1:
            raise IndexError

        return Fibonacci.fib(index)

Метод __getitem__ принимает целое число index. Метод __getitem__ проверяет, является ли индекс целым числом, используя функцию isinstance().

Если index выходит за границы последовательности, __getitem__ вызовет исключение IndexError. В противном случае он вернет число Фибоначчи индекса.

Соединим все вместе:

from functools import lru_cache


class Fibonacci:
    def __init__(self, n):
        self.n = n

    def __len__(self):
        return self.n

    def __getitem__(self, index):
        if isinstance(index, int):
            if index < 0 or index > self.n - 1:
                raise IndexError

            return Fibonacci.fib(index)

    @staticmethod
    @lru_cache(2**16)
    def fib(n):
        if n < 2:
            return 1
        return Fibonacci.fib(n-2) + Fibonacci.fib(n-1)

Кастомная последовательность Фибоначчи в виде Python-класса готова. Однако вы не сможете просто сохранить этот код в модуле fibonacci.py и использовать его в другом скрипте.

Давайте разберемся, как использовать созданную последовательность.

Используем последовательность Фибоначии

Ниже показано, как использовать последовательность Фибоначчи из модуля fibonacci.py:

from fibonacci import Fibonacci

fibonacci = Fibonacci(10)

# используем []
print('Используем последовательность Фибоначчи с помощью []:')
print(fibonacci[0])
print(fibonacci[1])
print(fibonacci[2])

print('Используем последовательность Фибоначчи с помощью цикла for:')
# используем for
for f in fibonacci:
    print(f)

Вывод

Используем последовательность Фибоначии с помощью []:
1
1
2
Используем последовательность Фибоначчи с помощью цикла for:
1
1
2
3
5
8
13
21
34
55

Как это работает

Создаем новый экземпляр последовательности Фибоначчи, в котором содержится 10 элементов.
Получаем доступ к элементам последовательности Фибначчи с помощью квадратных скобок [].
Используем последовательность Фибоначии в цикле for.

Добавляем поддержку срезов

Чтобы можно было делать срезы нашей последовательности, как показано ниже,

fibonacci[1:5]

… нужно добавить соответсвующую логику, которая будет обрабатывать объект среза.

В fibonacci[1:5] аргументом index метода __getitem__ является объект среза, начало которого равно 1, а конец — 5.

Вы можете использовать метод indices() объекта среза, чтобы получить индексы элементов для возврата из последовательности:

indices = index.indices(self.n)

self.n — это длина последовательности, которая будет «нарезана». В данном случае это количество элементов в последовательности Фибоначчи.

Чтобы вернуть список Фибоначчи из среза, вы можете передать индексы в функцию range() и сделать вот так:

[Fibonacci.fib(k) for k in range(*indices)]

Соберем все вместе:

from functools import lru_cache


class Fibonacci:
    def __init__(self, n):
        self.n = n

    def __len__(self):
        return self.n

    def __getitem__(self, index):
        if isinstance(index, int):
            if index < 0 or index > self.n - 1:
                raise IndexError

            return Fibonacci.fib(index)
        else:
            indices = index.indices(self.n)
            return [Fibonacci.fib(k) for k in range(*indices)]

    @staticmethod
    @lru_cache
    def fib(n):
        if n < 2:
            return 1
        return Fibonacci.fib(n-2) + Fibonacci.fib(n-1)

Теперь можно сделать срез последовательности следующим образом:

from fibonacci import Fibonacci

fibonacci = Fibonacci(10)
print(fibonacci[1:5])

Вывод

[1, 2, 3, 5]

Что нужно запомнить

Для создания кастомной последовательно нужно реализовать методы __len__ и __getitem__.
Метод __getitem__ должен возвращать элемент по заданному индексу или вызывать ошибку IndexError, если индекс выходит за границы последовательности.

Источник

Введение

Числа Фибоначчи циклом while

Числа Фибоначчи циклом for

Числа Фибоначчи рекурсией

Заключение

Происхождение

Формула Бине

Обоснование

Следствие и обобщение

Тождества

Свойства

Вариации и обобщения

В других областях

В природе

В искусстве

В кодировании

См. также

Примечания

Литература

Ссылки

Введение

Замкнутая формула

Рекурсия

Запоминание

Динамическое программирование

Матричная алгебра

Сравнение быстродействия

Теоретические замечания

Вычислить ряд Фибоначчи циклом

Найти число Фибоначчи через рекурсию

Использовать для вычисления Stream

Математический тест

1) Метод __getitem__

2) The __len__ method

Последовательность Фибоначчи

Создаем последовательность Фибоначии

Используем последовательность Фибоначии

Как это работает

Добавляем поддержку срезов

Что нужно запомнить

Вам также может понравиться

Как найти работа такси на своем авто

Нет армопояса как исправить

Как найти по штрих коду лекарства

Добавить комментарий Отменить ответ

1) Метод getitem

2) The len method