Сегодня попробуем вникнуть в изречение Кронекера: “Натуральные числа создал Господь, а остальное — дело человека”.
С натуральными числами мы знакомимся с раннего детства. Это числа, выражающие количества: один, два, три, сорок два. Если строго, то они строятся на базе пустого множества: пустое множество это нуль, множество, содержащее только пустое — единица, ну и далее: множество, изображающее число n+1, содержит все множества, от нуля до n.
В некоторых теориях натуральные числа строятся с единицы и нуль не включают. Я примыкаю к тем, кто считает нуль натуральным числом: это вполне себе количество!
На натуральных числах задают операции: пресловутые четыре действия. Сложение и умножение выполнимы всегда, а обратные к ним вычитание и деление — отнюдь.
Чтобы вычитание всегда выполнялось, вводят отрицательные числа. Формально -n — это такое число, что -n + n = 0. На них распространяются операции (единственным образом! Тут нет никакого произвола.) и целые числа доступны для работы. Решение уравнения по смыслу может быть положительным, а по факту — отрицательным: ну, значит что-то пошло не так.
Часто отрицательных чисел избегают: бухгалтеры пишут приход и расход в разные колонки, историки вводят года “до нашей эры”, физики оговаривают положительность коэффициентов. И это правильно, потому что инструмент для человека, а не наоборот.
Реальность отрицательных чисел обсуждать нет никакого смысла. Они есть как математическая абстракция, так же, как и натуральные числа. Одна селедка и один слон имеют общее в характеристике количества, но и только.
Кстати, в иврите “один” — это прилагательное, и как таковое идет после существительного, а прочие числительные ставятся до. Потому что “один” — это признак предмета.
Осязаемость отрицательным числам дают интерпретации, наполняющие их физическим смыслом. Например, долг удобно записывать как отрицательное число, или температуру ниже нуля, или заряд, противоположный положительному. Или уже упомянутые годы до НЭ. А работает это потому, что действия с этими величинами согласуются с правилами действий над числами. Взять в долг сто рублей, имея десять и отдать дважды по пятьдесят — будет опять десять. То же с температурой, и с зарядом, и с датами.
Порой числа могут подумать за автора задачи. Например, отцу 60 лет, сыну 35. Когда отец станет вдвое старше сына? Обозначив число лет до этого славного момента за x, составим уравнение и получим x=-10. Десять лет назад это было.
Идем дальше. Деление тоже осуществимо не всегда, но можно ввести рациональные числа и тогда можно делить всё на всё (кроме нуля). Нуль обсудим позже. Рациональные числа вводятся аналогично отрицательным: 1/n — это результат деления единицы на n, и главное — согласовать операции. Это делается, все мы знаем как со школы.
Рациональные числа тоже имеют смысловую интерпретацию: дольки апельсина, разрезание тортика, размен денег.
Уравнение может решаться в дробях, но дробный ответ не имеет смысла: классические полтора землекопа.
Следующий шаг связан со степенями. Возводить натуральное число в натуральную же степень — проблем нет, но вот обратные к степеням корни извлекаются не всегда. Вторая обратная к степени операция — логарифм — тоже. Даже в рациональных числах это невозможно. Приходится вводить идею непрерывности. О ней в другой раз, а пока рассмотрим еще одну проблему: корни четной степени из отрицательных чисел вообще невозможно извлечь. И логарифмы отрицательных чисел не существуют.
В самом деле, нет такого числа, которое в квадрате дало бы минус единицу. И степени, в которую надо возвести число два, например, чтобы получилась минус единица — тоже нет.
По привычной уже схеме вводим число i, так что i^2=-1. И распространяем операции на комплексные числа вида a+bi. Это делается, и тоже единственным образом. Складываются комплексные числа по частям:
(a+bi) + (c+di) = (a+c) + (b+d)i.
Умножать тоже можно простым раскрытием скобок, но есть способ лучше. Обычные числа расположены на числовой оси — прямой, на которой отмечены нуль и единица. Комплексные — на плоскости: на ней две перпендикулярные оси, в точке пересечения нуль, на осях отмечены единица и i, а число a+bi — это точка (a;b).
Числа вида bi называются мнимыми.
Можно записать число в полярных координатах, через расстояние до нуля (модуль) и угол между направление из нуля в точку, изображающую число, и положительным направлением вещественной оси. Этот угол называется аргумент числа и он — аналог знака. У положительных чисел аргумент нуль, у отрицательных равен п, а у комплесных — любой от 0 до 2п.
Функция arg(z) — это аргумент от 0 до 2п, а Arg(z) — многозначный аргумент, с учетом периодичности. Число z можно записать через его модуль |z| и аргумент arg(z) так:
z = |z|(cos arg(z) + i sin arg(z)).
Это тригонометрическая форма записи.
Ещё есть экспоненциальная форма, которая является определением возведения в мнимую степень: e^{ix} = cos(x) + i sin(x), или
z = |z|e^{i arg(z)}.
В этой форме удобно умножать числа и возводить в степень, а также вычислять логарифмы по любому основанию:
log(z) = log(|z|) + i arg(z).
Например, log(-1) = log(1) + iп = iп, а log(i) = log(|i|) + iп/2 = iп/2.
Через логарифм можно возвести в любую степень любое число:
i^i = e^{i ln(i)} = e^{-п/2}.
Когда-то меня удивляло, что мнимое число в мнимой степени — вещественно. Потом привык.
Косинус определяется формулой cos(z) = (e^{iz}+e^{-iz})/2, имеет смысл для всех комплексных значений и принимает любые значения. синус тоже.
А вы думали, “в военное время значение синуса может превышать четыре” — это такая шутка была?
Может возникнуть впечатление, что это лишь очередная ступенька, а для корнец четвертой, шестой, сорок второй степени понадобятся новые числа, а уж для логарифмов и других функций — и подавно.
Но нет. Комплексная плоскость — это естественное расширение числового поля. Всё. Там всё решается. Многочлен степени n, например, имеет всегда ровно n комплексных корней, которые могут повторяться.
У комплексных чисел нет простой физической интерпретации, и поэтому они выглядят какими-то нереальными, мнимыми. Но это иллюзия. Они так же реальны, как единица. Это неизбежный конец пути расширения числового поля, чтобы все операции были возможны и все уравнения решались.
Теперь поговорим о нуле и бесконечности. Некоторые операции делать все-таки нельзя: делить ненуль на нуль, делить нуль на нуль, брать логарифм от нуля и кое-что еще в том же духе. Некоторые уравнения не решаются, например 0x=1 или x+1=x.
Проблему можно частично решить, добавив число “бесконечность”. Частично — потому что нет хорошего способа это сделать. Что-то будет упущено. В частности, деление нуля на нуль никак не определить без противоречий. О разных способах введения бесконечности будет отдельная заметка.
Резюмируя, комплексная плоскость — реальна так же, как и натуральные числа. Это конечное расширение числового поля, в котором осуществимы все операции, кроме тех что дают бесконечный или неопределенный результат. Оно единственно, и не является чьей-то выдумкой.
Основы систем счисления
Время на прочтение
11 мин
Количество просмотров 502K
Изучая кодировки, я понял, что недостаточно хорошо понимаю системы счислений. Тем не менее, часто использовал 2-, 8-, 10-, 16-ю системы, переводил одну в другую, но делалось все на “автомате”. Прочитав множество публикаций, я был удивлен отсутствием единой, написанной простым языком, статьи по столь базовому материалу. Именно поэтому решил написать свою, в которой постарался доступно и по порядку изложить основы систем счисления.
Введение
Система счисления — это способ записи (представления) чисел.
Что под этим подразумевается? Например, вы видите перед собой несколько деревьев. Ваша задача — их посчитать. Для этого можно — загибать пальцы, делать зарубки на камне (одно дерево — один палецзарубка) или сопоставить 10 деревьям какой-нибудь предмет, например, камень, а единичному экземпляру — палочку и выкладывать их на землю по мере подсчета. В первом случае число представляется, как строка из загнутых пальцев или зарубок, во втором — композиция камней и палочек, где слева — камни, а справа — палочки
Системы счисления подразделяются на позиционные и непозиционные, а позиционные, в свою очередь, — на однородные и смешанные.
Непозиционная — самая древняя, в ней каждая цифра числа имеет величину, не зависящую от её позиции (разряда). То есть, если у вас 5 черточек — то число тоже равно 5, поскольку каждой черточке, независимо от её места в строке, соответствует всего 1 один предмет.
Позиционная система — значение каждой цифры зависит от её позиции (разряда) в числе. Например, привычная для нас 10-я система счисления — позиционная. Рассмотрим число 453. Цифра 4 обозначает количество сотен и соответствует числу 400, 5 — кол-во десяток и аналогично значению 50, а 3 — единиц и значению 3. Как видим — чем больше разряд — тем значение выше. Итоговое число можно представить, как сумму 400+50+3=453.
Однородная система — для всех разрядов (позиций) числа набор допустимых символов (цифр) одинаков. В качестве примера возьмем упоминавшуюся ранее 10-ю систему. При записи числа в однородной 10-й системе вы можете использовать в каждом разряде исключительно одну цифру от 0 до 9, таким образом, допускается число 450 (1-й разряд — 0, 2-й — 5, 3-й — 4), а 4F5 — нет, поскольку символ F не входит в набор цифр от 0 до 9.
Смешанная система — в каждом разряде (позиции) числа набор допустимых символов (цифр) может отличаться от наборов других разрядов. Яркий пример — система измерения времени. В разряде секунд и минут возможно 60 различных символов (от «00» до «59»), в разряде часов – 24 разных символа (от «00» до «23»), в разряде суток – 365 и т. д.
Непозиционные системы
Как только люди научились считать — возникла потребность записи чисел. В начале все было просто — зарубка или черточка на какой-нибудь поверхности соответствовала одному предмету, например, одному фрукту. Так появилась первая система счисления — единичная.
Единичная система счисления
Число в этой системе счисления представляет собой строку из черточек (палочек), количество которых равно значению данного числа. Таким образом, урожай из 100 фиников будет равен числу, состоящему из 100 черточек.
Но эта система обладает явными неудобствами — чем больше число — тем длиннее строка из палочек. Помимо этого, можно легко ошибиться при записи числа, добавив случайно лишнюю палочку или, наоборот, не дописав.
Для удобства, люди стали группировать палочки по 3, 5, 10 штук. При этом, каждой группе соответствовал определенный знак или предмет. Изначально для подсчета использовались пальцы рук, поэтому первые знаки появились для групп из 5 и 10 штук (единиц). Все это позволило создать более удобные системы записи чисел.
Древнеегипетская десятичная система
В Древнем Египте использовались специальные символы (цифры) для обозначения чисел 1, 10, 102, 103, 104, 105, 106, 107. Вот некоторые из них:
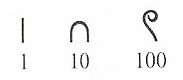
Почему она называется десятичной? Как писалось выше — люди стали группировать символы. В Египте — выбрали группировку по 10, оставив без изменений цифру “1”. В данном случае, число 10 называется основанием десятичной системы счисления, а каждый символ — представление числа 10 в какой-то степени.
Числа в древнеегипетской системе счисления записывались, как комбинация этих
символов, каждый из которых повторялся не более девяти раз. Итоговое значение равнялось сумме элементов числа. Стоит отметить, что такой способ получения значения свойственен каждой непозиционной системе счисления. Примером может служить число 345:

Вавилонская шестидесятеричная система
В отличии от египетской, в вавилонской системе использовалось всего 2 символа: “прямой” клин — для обозначения единиц и “лежачий” — для десятков. Чтобы определить значение числа необходимо изображение числа разбить на разряды справа налево. Новый разряд начинается с появления прямого клина после лежачего. В качестве примера возьмем число 32:

Число 60 и все его степени так же обозначаются прямым клином, что и “1”. Поэтому вавилонская система счисления получила название шестидесятеричной.
Все числа от 1 до 59 вавилоняне записывали в десятичной непозиционной системе, а большие значения — в позиционной с основанием 60. Число 92:

Запись числа была неоднозначной, поскольку не существовало цифры обозначающей ноль. Представление числа 92 могло обозначать не только 92=60+32, но и, например, 3632=3600+32. Для определения абсолютного значения числа был введен специальный символ для обозначения пропущенного шестидесятеричного разряда, что соответствует появлению цифры 0 в записи десятичного числа:
Теперь число 3632 следует записывать, как:

Шестидесятеричная вавилонская система — первая система счисления, частично основанная на позиционном принципе. Данная система счисления используется и сегодня, например, при определении времени — час состоит из 60 минут, а минута из 60 секунд.
Римская система
Римская система не сильно отличается от египетской. В ней для обозначения чисел 1, 5, 10, 50, 100, 500 и 1000 используются заглавные латинские буквы I, V, X, L, C, D и M соответственно. Число в римской системе счисления — это набор стоящих подряд цифр.
Методы определения значения числа:
- Значение числа равно сумме значений его цифр. Например, число 32 в римской системе счисления имеет вид XXXII=(X+X+X)+(I+I)=30+2=32
- Если слева от большей цифры стоит меньшая, то значение равно разности между большей и меньшей цифрами. При этом, левая цифра может быть меньше правой максимум на один порядок: так, перед L(50) и С(100) из «младших» может стоять только X(10), перед D(500) и M(1000) — только C(100), перед V(5) — только I(1); число 444 в рассматриваемой системе счисления будет записано в виде CDXLIV = (D-C)+(L-X)+(V-I) = 400+40+4=444.
- Значение равно сумме значений групп и цифр, не подходящих под 1 и 2 пункты.
Помимо цифирных, существуют и буквенные (алфавитные) системы счисления, вот некоторые из них:
1) Славянская
2) Греческая (ионийская)
Позиционные системы счисления
Как упоминалось выше — первые предпосылки к появлению позиционной системы возникли в древнем Вавилоне. В Индии система приняла форму позиционной десятичной нумерации с применением нуля, а у индусов эту систему чисел заимствовали арабы, от которых её переняли европейцы. По каким-то причинам, в Европе за этой системой закрепилось название “арабская”.
Десятичная система счисления
Это одна из самых распространенных систем счисления. Именно её мы используем, когда называем цену товара и произносим номер автобуса. В каждом разряде (позиции) может использоваться только одна цифра из диапазона от 0 до 9. Основанием системы является число 10.
Для примера возьмем число 503. Если бы это число было записано в непозиционной системе, то его значение равнялось 5+0+3 = 8. Но у нас — позиционная система и значит каждую цифру числа необходимо умножить на основание системы, в данном случае число “10”, возведенное в степень, равную номеру разряда. Получается, значение равно 5*102 + 0*101 + 3*100 = 500+0+3 = 503. Чтобы избежать путаницы при одновременной работе с несколькими системами счисления основание указывается в качестве нижнего индекса. Таким образом, 503 = 50310.
Помимо десятичной системы, отдельного внимания заслуживают 2-, 8-, 16-ая системы.
Двоичная система счисления
Эта система, в основном, используется в вычислительной технике. Почему не стали использовать привычную нам 10-ю? Первую вычислительную машину создал Блез Паскаль, использовавший в ней десятичную систему, которая оказалась неудобной в современных электронных машинах, поскольку требовалось производство устройств, способных работать в 10 состояниях, что увеличивало их цену и итоговые размеры машины. Этих недостатков лишены элементы, работающие в 2-ой системе. Тем не менее, рассматриваемая система была создана за долго до изобретения вычислительных машин и уходит “корнями” в цивилизацию Инков, где использовались кипу — сложные верёвочные сплетения и узелки.
Двоичная позиционная система счисления имеет основание 2 и использует для записи числа 2 символа (цифры): 0 и 1. В каждом разряде допустима только одна цифра — либо 0, либо 1.
Примером может служить число 101. Оно аналогично числу 5 в десятичной системе счисления. Для того, чтобы перевести из 2-й в 10-ю необходимо умножить каждую цифру двоичного числа на основание “2”, возведенное в степень, равную разряду. Таким образом, число 1012 = 1*22 + 0*21 + 1*20 = 4+0+1 = 510.
Хорошо, для машин 2-я система счисления удобнее, но мы ведь часто видим, используем на компьютере числа в 10-й системе. Как же тогда машина определяет какую цифру вводит пользователь? Как переводит число из одной системы в другую, ведь в её распоряжении всего 2 символа — 0 и 1?
Чтобы компьютер мог работать с двоичными числами (кодами), необходимо чтобы они где-то хранились. Для хранения каждой отдельной цифры применяется триггер, представляющий собой электронную схему. Он может находится в 2-х состояниях, одно из которых соответствует нулю, другое — единице. Для запоминания отдельного числа используется регистр — группа триггеров, число которых соответствует количеству разрядов в двоичном числе. А совокупность регистров — это оперативная память. Число, содержащееся в регистре — машинное слово. Арифметические и логические операции со словами осуществляет арифметико-логическое устройство (АЛУ). Для упрощения доступа к регистрам их нумеруют. Номер называется адресом регистра. Например, если необходимо сложить 2 числа — достаточно указать номера ячеек (регистров), в которых они находятся, а не сами числа. Адреса записываются в 8- и 16-ричной системах (о них будет рассказано ниже), поскольку переход от них к двоичной системе и обратно осуществляется достаточно просто. Для перевода из 2-й в 8-ю число необходимо разбить на группы по 3 разряда справа налево, а для перехода к 16-ой — по 4. Если в крайней левой группе цифр не достает разрядов, то они заполняются слева нулями, которые называются ведущими. В качестве примера возьмем число 1011002. В восьмеричной — это 101 100 = 548, а в шестнадцатеричной — 0010 1100 = 2С16. Отлично, но почему на экране мы видим десятичные числа и буквы? При нажатии на клавишу в компьютер передаётся определённая последовательность электрических импульсов, причём каждому символу соответствует своя последовательность электрических импульсов (нулей и единиц). Программа драйвер клавиатуры и экрана обращается к кодовой таблице символов (например, Unicode, позволяющая закодировать 65536 символов), определяет какому символу соответствует полученный код и отображает его на экране. Таким образом, тексты и числа хранятся в памяти компьютера в двоичном коде, а программным способом преобразуются в изображения на экране.
Восьмеричная система счисления
8-я система счисления, как и двоичная, часто применяется в цифровой технике. Имеет основание 8 и использует для записи числа цифры от 0 до 7.
Пример восьмеричного числа: 254. Для перевода в 10-ю систему необходимо каждый разряд исходного числа умножить на 8n, где n — это номер разряда. Получается, что 2548 = 2*82 + 5*81 + 4*80 = 128+40+4 = 17210.
Шестнадцатеричная система счисления
Шестнадцатеричная система широко используется в современных компьютерах, например при помощи неё указывается цвет: #FFFFFF — белый цвет. Рассматриваемая система имеет основание 16 и использует для записи числа: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B. C, D, E, F, где буквы равны 10, 11, 12, 13, 14, 15 соответственно.
В качестве примера возьмем число 4F516. Для перевода в восьмеричную систему — сначала преобразуем шестнадцатеричное число в двоичное, а затем, разбив на группы по 3 разряда, в восьмеричное. Чтобы преобразовать число в 2-е необходимо каждую цифру представить в виде 4-х разрядного двоичного числа. 4F516 = (100 1111 101)2. Но в 1 и 3 группах не достает разряда, поэтому заполним каждый ведущими нулями: 0100 1111 0101. Теперь необходимо разделить полученное число на группы по 3 цифры справа налево: 0100 1111 0101 = 010 011 110 101. Переведем каждую двоичную группу в восьмеричную систему, умножив каждый разряд на 2n, где n — номер разряда: (0*22+1*21+0*20) (0*22+1*21+1*20) (1*22+1*21+0*20) (1*22+0*21+1*20) = 23658.
Помимо рассмотренных позиционных систем счисления, существуют и другие, например:
1) Троичная
2) Четверичная
3) Двенадцатеричная
Позиционные системы подразделяются на однородные и смешанные.
Однородные позиционные системы счисления
Определение, данное в начале статьи, достаточно полно описывает однородные системы, поэтому уточнение — излишне.
Смешанные системы счисления
К уже приведенному определению можно добавить теорему: “если P=Qn (P,Q,n – целые положительные числа, при этом P и Q — основания), то запись любого числа в смешанной (P-Q)-ой системе счисления тождественно совпадает с записью этого же числа в системе счисления с основанием Q.”
Опираясь на теорему, можно сформулировать правила перевода из P-й в Q-ю системы и наоборот:
- Для перевода из Q-й в P-ю, необходимо число в Q-й системе, разбить на группы по n цифр, начиная с правой цифры, и каждую группу заменить одной цифрой в P-й системе.
- Для перевода из P-й в Q-ю, необходимо каждую цифру числа в P-й системе перевести в Q-ю и заполнить недостающие разряды ведущими нулями, за исключением левого, так, чтобы каждое число в системе с основанием Q состояло из n цифр.
Яркий пример — перевод из двоичной системы счисления в восьмеричную. Возьмем двоичное число 100111102, для перевода в восьмеричное — разобьем его справа налево на группы по 3 цифры: 010 011 110, теперь умножим каждый разряд на 2n, где n — номер разряда, 010 011 110 = (0*22+1*21+0*20) (0*22+1*21+1*20) (1*22+1*21+0*20) = 2368. Получается, что 100111102 = 2368. Для однозначности изображения двоично-восьмеричного числа его разбивают на тройки: 2368 = (10 011 110)2-8.
Смешанными системами счисления также являются, например:
1) Факториальная
2) Фибоначчиева
Перевод из одной системы счисления в другую
Иногда требуется преобразовать число из одной системы счисления в другую, поэтому рассмотрим способы перевода между различными системами.
Преобразование в десятичную систему счисления
Имеется число a1a2a3 в системе счисления с основанием b. Для перевода в 10-ю систему необходимо каждый разряд числа умножить на bn, где n — номер разряда. Таким образом, (a1a2a3)b = (a1*b2 + a2*b1 + a3*b0)10.
Пример: 1012 = 1*22 + 0*21 + 1*20 = 4+0+1 = 510
Преобразование из десятичной системы счисления в другие
Целая часть:
- Последовательно делим целую часть десятичного числа на основание системы, в которую переводим, пока десятичное число не станет равно нулю.
- Полученные при делении остатки являются цифрами искомого числа. Число в новой системе записывают, начиная с последнего остатка.
Дробная часть:
- Дробную часть десятичного числа умножаем на основание системы, в которую требуется перевести. Отделяем целую часть. Продолжаем умножать дробную часть на основание новой системы, пока она не станет равной 0.
- Число в новой системе составляют целые части результатов умножения в порядке, соответствующем их получению.
Пример: переведем 1510 в восьмеричную:
158 = 1, остаток 7
18 = 0, остаток 1
Записав все остатки снизу вверх, получаем итоговое число 17. Следовательно, 1510 = 178.
Преобразование из двоичной в восьмеричную и шестнадцатеричную системы
Для перевода в восьмеричную — разбиваем двоичное число на группы по 3 цифры справа налево, а недостающие крайние разряды заполняем ведущими нулями. Далее преобразуем каждую группу, умножая последовательно разряды на 2n, где n — номер разряда.
В качестве примера возьмем число 10012: 10012 = 001 001 = (0*22 + 0*21 + 1*20) (0*22 + 0*21 + 1*20) = (0+0+1) (0+0+1) = 118
Для перевода в шестнадцатеричную — разбиваем двоичное число на группы по 4 цифры справа налево, затем — аналогично преобразованию из 2-й в 8-ю.
Преобразование из восьмеричной и шестнадцатеричной систем в двоичную
Перевод из восьмеричной в двоичную — преобразуем каждый разряд восьмеричного числа в двоичное 3-х разрядное число делением на 2 (более подробно о делении см. выше пункт “Преобразование из десятичной системы счисления в другие”), недостающие крайние разряды заполним ведущими нулями.
Для примера рассмотрим число 458: 45 = (100) (101) = 1001012
Перевод из 16-ой в 2-ю — преобразуем каждый разряд шестнадцатеричного числа в двоичное 4-х разрядное число делением на 2, недостающие крайние разряды заполняем ведущими нулями.
Преобразование дробной части любой системы счисления в десятичную
Преобразование осуществляется также, как и для целых частей, за исключением того, что цифры числа умножаются на основание в степени “-n”, где n начинается от 1.
Пример: 101,0112 = (1*22 + 0*21 + 1*20), (0*2-1 + 1*2-2 + 1*2-3) = (5), (0 + 0,25 + 0,125) = 5,37510
Преобразование дробной части двоичной системы в 8- и 16-ую
Перевод дробной части осуществляется также, как и для целых частей числа, за тем лишь исключением, что разбивка на группы по 3 и 4 цифры идёт вправо от десятичной запятой, недостающие разряды дополняются нулями справа.
Пример: 1001,012 = 001 001, 010 = (0*22 + 0*21 + 1*20) (0*22 + 0*21 + 1*20), (0*22 + 1*21 + 0*20) = (0+0+1) (0+0+1), (0+2+0) = 11,28
Преобразование дробной части десятичной системы в любую другую
Для перевода дробной части числа в другие системы счисления нужно обратить целую часть в ноль и начать умножение получившегося числа на основание системы, в которую нужно перевести. Если в результате умножения будут снова появляться целые части, их нужно повторно обращать в ноль, предварительно запомнив (записав) значение получившейся целой части. Операция заканчивается, когда дробная часть полностью обратится в нуль.
Для примера переведем 10,62510 в двоичную систему:
0,625*2 = 1,25
0,250*2 = 0,5
0,5*2 = 1,0
Записав все остатки сверху вниз, получаем 10,62510 = (1010), (101) = 1010,1012
Нечаев В. И. Числовые системы. Пособие для студентов пед. ин-тов. М., 1975. – 199 с. с ил.
В этой книге глубокие математические идеи, с которыми студенты знакомятся в курсах математического анализа, алгебры и теории чисел, применяются для последовательного построения основных числовых систем — натуральных, целых, рациональных, действительных, комплексных, а также р-адических чисел и кватернионов.
СОДЕРЖАНИЕ
Предисловие …………………………………………3
§ 1. Введение……………………………………….4
§ 2. Системы с отношениями и алгебраическими операциями
2.1. Прямое произведение…………… . 9
2.2. n-членные отношения и n-арные алгебраические операции 10
2.3. Отображения ………………………………….16
2.4. Системы с отношениями и операциями………………21
2.5. Полугруппы и группы …………………………..22
2.6. Полукольца, кольца, тела и поля…………25
2.7. Векторные пространства и линейные алгебры…….31
2.8. Гомоморфизм и изоморфизм алгебраических систем … 35
2.9. Отношение эквивалентности……………………….37
2.10. Расширения алгебраических систем ……………41
§ 3. Аксиоматические теории
3.1. Аксиоматическая теория…………………………..43
3.2. Схема построения неформальной аксиоматической теории 44
3.3. Интерпретация и модель аксиоматической теории …. 44
3.4. Формулировка аксиоматической теории . ……………46
3.5. Свойства аксиоматических теорий……………………47
3.6. Формальные аксиоматические теории ………………..49
§ 4. Содержательная аксиоматическая теория натуральных чисел
4.1. Первичные термины …….. ……………..52
4.2. Аксиомы …………………..53
4.3. Свойства сложения………………………………53
4.4. Свойства умножения …… ………. 55
4.5. Порядок во множестве натуральных чисел…………..56
4.6. Свойства неравенств ………………….58
4.7. Конечные множества …………………..60
4.8. Сумма и произведение нескольких элементов полугруппы 63
4.9. Независимость аксиомы индукции и роль аксиомы индукции в обосновании теории неравенств, теории делимости и свойств арифметических действий….. 68
4.10. Категоричность аксиоматической теории натуральных чисел 72
4.11. Аксиома минимальности ………….. 74
4.12. Непротиворечивость арифметики и другие вопросы … 76
§ 5. Упорядоченные множества и алгебраические системы
5.1. Упорядоченные множества ……………………….78
5.2. Упорядоченные полугруппы …………………….85
5.3. Упорядоченные полукольца ……………………….88
5.4. Линейно упорядоченные кольца и тела . ……………90
§ 6. Системы целых и рациональных чисел
6.1. Первичные термины и аксиомы аксиоматической теории целых чисел ………………………..95
6.2. Свойства целых чисел ……………………………96
6.3. Категоричность системы целых чисел ………………..98
6.4. Непротиворечивость аксиоматической теории целых чисел 100
6.5. Первичные термины и аксиомы аксиоматической теории рациональных чисел ……………. , . 102
6.6. Свойства рациональных чисел ………….104
6.7. Категоричность аксиоматической теории рациональных чисел 106
6.8. Непротиворечивость аксиоматической теории рациональных чисел …………………………..107
§ 7. Последовательности в нормированных полях
7.1. Нормированные поля ……………. 110
7.2. Последовательности в нормированных полях ……112
7.3. Свойства последовательностей в нормированных полях … 115
7.4. Последовательности элементов линейно упорядоченного поля …………………….121
7.5. Последовательности элементов архимедовски линейно упорядоченного поля ………………..122
§ 8. Система действительных чисел
8.1. Первичные термины и аксиомы теории действительных чисел 126
8.2. Свойства действительных чисел …………127
8.3. Систематические дроби как аппарат для представления действительных чисел ………. ……..133
8.4. Категоричность аксиоматической теории действительных чисел ……………………135
8.5. Непротиворечивость аксиоматической теории действительных чисел ……………………136
8.6. Система р-адических чисел …………..139
8.7. Конечные и бесконечные цепные дроби………143
§ 9. Система комплексных чисел, кватернионы и теорема Фробениуса
9.1. Первичные термины и аксиомы теории комплексных чисел 164
9.2. Свойства комплексных чисел 165
9.3. Категоричность аксиоматической теории комплексных чисел 166
9.4. Непротиворечивость аксиоматической теории комплексных
чисел ……………………167

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ МОСКОВСКОЙ
ОБЛАСТИ
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ОБЛАСТНОЙ
ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ
Н.Г. Воробьева
Числовые системы
Курс лекций
Орехово-Зуево
2008
ПРЕДИСЛОВИЕ
Обучение
математическим дисциплинам в педагогическом
вузе направлено, в первую очередь, на
повышение математической культуры
будущего учителя математики. Математическая
культура – это умение взглянуть на
частные вопросы с позиции общих, знание
истоков данного вопроса, его связь с
другими, понимание значения данного
вопроса для дальнейшего изучения
дисциплины, определение места данного
материала в структуре изучаемого
предмета. Кроме хорошего знания своего
предмета, учитель должен владеть
методикой и технологией обучения. Этими
умениями студенты овладевают не только
на специальных предметах
психолого-педагогического цикла, но и
на занятиях по специальным дисциплинам.
И еще одним важным направлением в
подготовке будущего учителя является
развитие его познавательной активности
и творческих способностей. Курс «Числовые
системы» как нельзя лучше подходит для
реализации всех этих задач обучения.
Числовая линия
проходит через весь школьный курс
математики, начиная с первого класса.
Учащиеся и студенты настолько привыкают
к действиям с различными числами, что
не задумываются о том, как построена
каждая из числовых систем, существуют
ли другие числовые системы, что определяет
свойства чисел и т.п. Курс «Числовые
системы» призван решить задачи подготовки
учителя к изучению числовой линии в
школе с учетом теоретических и
методологических подходов к построению
различных числовых множеств. В связи с
этим важно проследить связь курса
«Числовые системы» курсом «Теория и
методика обучения математике», который
изучается студентами после первого.
Эта взаимосвязь позволит реализовать
один из основных дидактических принципов
обучения – принцип научности.
При изучении
школьной математики теоретическая
основа построения числовой линии
практически скрыта от учащихся, не
всегда выдержан достаточный уровень
строгости при введении новых числовых
множеств, что методически оправдано в
связи с возрастными особенностями
учащихся, так как необходимо найти
оптимальное сочетание уровня научности
и доступности. Кроме того, растянутое
по времени изучение числовых множеств
на протяжении всех лет обучения математике
в школе не позволяет полностью
систематизировать и структурировать
полученные знания, выявить пробелы в
осознании числовых систем как
математических объектов со своей
структурой и свойствами. В школьном
курсе математики числовые системы
играют практическую роль для решения
прикладных задач на вычисление и
измерение. В курсе «Числовые системы»
студенты встречаются с целенаправленным
и последовательным изучением числовых
множеств, их аксиоматическим построением,
знакомятся с новыми числовыми множествами
(двойные и дуальные числа, кватернионы,
гиперкомплексные числа), впервые
сталкиваются с вопросом конечности
расширения числовых множеств (теорема
Фробениуса). Числовые системы становятся
объектом изучения с точки зрения
алгебраических структур. В результате
становятся понятными многие вопросы,
связанные с выполнением арифметических
действий, выводимостью их свойств,
возможностью переноса свойств, полученных
в одном множестве на другое.
Курс «Числовые
системы» обобщает не только школьные
знания студентов, но и знания, полученных
ими при изучении других математических
дисциплин на первых курсах вуза, таких
как математический анализ (действительные
числа), алгебра (комплексные числа,
алгебраические системы). Важно отметить,
что данный курс позволяет показать
различные подходы к построению одной
и той же числовой системы (например,
действительный числа), а также построить
несколько моделей для элементов числового
множества (комплексные числа). Для
данного курса характерным является
широкое практическое использование
такого понятия как изоморфизм множеств,
изучение которого в курсе алгебры носит
абстрактный характер. Кроме этого,
большое значение при построении новых
числовых множеств имеет отношение
эквивалентности, которое определяет
разбиение множеств на классы попарно
эквивалентных элементов. Таким образом,
в данном курсе, как в капле воды, отражены
всевозможные абстрактные понятия,
математические методы в их практическом
применении.
На курс «Числовые
системы» отводится всего 18 часов лекций,
поэтому в рамки этих 9 лекций невозможно
вместить все теоретические вопросы.
Поэтому часть теоретических вопросов
выносятся на практические занятия (на
математическом отделении на них отводится
27 часов, а на физическом – всего 7), а
также на самостоятельную работу.
Особенностью данного курса является
концентрический подход к построению
каждой новой числовой системы, что
позволяет студентам самостоятельно
развернуть содержание новой темы на
основе ее краткой схемы. Например, схема
построения рациональных чисел практически
совпадает со схемой построения целых
чисел, поэтому тему «Рациональные числа»
студенты изучают самостоятельно, с
последующим обсуждением итогов работы
на практических занятиях. Как было
отмечено, при изучении данного курса
используются понятия, с которыми студенты
встречались при изучении других
математических дисциплин, это также
позволяет организовать самостоятельную
работу студентов. Так для построения
поля действительных чисел в качестве
элементов используются фундаментальные
последовательности рациональных чисел,
с этим понятием студенты встречались
в курсе математического анализа, поэтому
многие свойства фундаментальных
последовательностей они могут доказать
самостоятельно. Целью этой самостоятельной
работы является перенос ранее полученных
знаний в новую ситуацию, а также обобщение,
повторение и закрепление ранее изученного
материала. Для самостоятельной работы
студентам можно предложить выполнить
небольшие исследования по новым для
них числовым системам и сделать сообщения
для остальных студентов, найти практическое
применение новым числам и т.п. Таким
образом, курс «Числовые системы» играет
значительную роль в подготовке будущего
специалиста.
Курс «Числовые
системы» начинается с изучения темы
«Натуральные числа», хотя желательно
было бы начать с введения в данный курс,
т. е. с основных понятий. В данном случае
это такие понятия как алгебра,
алгебраическая структура, основные
алгебраические структуры: группа,
кольцо, поле, тело. В связи с недостатком
времени на лекции и исходя из того, что
этот материал известен студентам, можно
рассмотреть его на практическом занятии
и предложить задания для самостоятельной
работы. Любое повторение ранее изученного
материала должно осуществляться на
новом уровне и с учетом конкретных
задач. Например, можно дать несколько
эквивалентных определений одного и
того же понятия, студенты должны понимать
это и уметь устанавливать их взаимосвязь
и выводить одно из другого. В первую
очередь, по отношению к рассматриваемому
курсу, речь идет об определениях понятий
группы, кольца, поля.
Еще раз вернемся
к вопросу о всестороннем изучении
числовых систем в педагогическом вузе
на физико-математическом факультете.
Если проанализировать образовательные
стандарты, то с числовыми системами
студенты встречаются сначала в курсе
алгебры – этот этап изучения можно
рассматривать как пропедевтический,
затем в курсе «Числовые системы»
(систематическое изучение), а также в
курсах «Методика обучения математике»
(практическое применение) и «История
математики». Такой подход к изучению
числовых систем позволяет говорить о
возможности повышения качества подготовки
будущего учителя, если свести эти
элементы – составные части обучения –
в единую систему. К сожалению, практически
каждая часть изучается изолированно
друг от друга, за исключением ссылок,
которые делает преподаватель при
изучении своего предмета на ранее
изученный материал. Поэтому для повышения
эффективности обучения необходим
комплексный подход к изучению каждого
раздела математики, в том числе и числовых
систем. Как уже было сказано, одним из
средств реализации системного подхода
в обучении являются учебные задания
межпредметного характера, учебная
самостоятельная работа и исследовательская
работа студентов.
Лекция 1.
Рассмотрим аксиоматическое построение
множества натуральных чисел. Основным
объектом рассматриваемой теории будут
единица и натуральные числа,
основным отношением между натуральными
числами будет отношение «следует за».
Натуральные числа будем обозначать a,
b, c,
d…, а единицу
-1. отношение a=b
называется равенством, которое
означает, что одно и тоже натуральное
число обозначено различными буквами.
Отношение a≠b
называется неравенством, которое
означает, что a и b
обозначены различными натуральными
числами. Число, следующее за числом a,
обозначается через a′.
Аксиомы Пеано и
следствия из них.
Определение. Натуральными числами
называются элементы всякого непустого
множества N, в котором
для некоторых элементов a
и b установлено
отношение «b следует
за a», удовлетворяющее
следующим аксиомам:
А1: Существует натуральное
число 1(единица), которое не следует ни
за каким натуральным числом.
![]()
А2: Для любого натурального
числа a во множестве
N существует
одно, и только одно, следующее за ним
натуральное число a’
![]()
А3: Любое натуральное
число следует не более чем за одним
натуральным числом.
![]()
А4: (аксиома индукции)
Каждое множество натуральных чисел M,
которое содержит число 1 и которое
вместе с каждым числом a
содержит и его последующее число a’,
совпадает с множеством всех натуральных
чисел N.
![]()
Аксиома А4 есть принцип
математической индукции, который
позволяет доказывать теоремы о натуральных
числах
![]()
Аксиоматическая теория с формулировкой
<{N,1,′},{А1-А4}>
называется содержательной аксиоматической
теорией натуральногоряда.
Определение. Если натуральное число
b следует за натуральным
числом a (a’=b),
то число a называется
предшествующим числу b.
По аксиоме А1 единица не имеет
предшествующего числа.
Т1. Любое натуральное
число
![]() имеет
имеет
предшествующее число, и притом
единственное.
![]()
Доказательство.
Пусть M-множество
натуральных чисел содержит 1 и все те,
и только те, натуральные числа a,
каждое из которых имеет хотя бы одно
предшествующее ему натуральное число.
Множество M содержит
1 и вместе с каждым содержащимся в нем
числом a содержит и его
последующее число a′,
т.к. a′ имеет
предшествующее число a.
По А4 M=N.
Единственность предшествующего числа
следует из А3.
![]()

Единственность следует из А3.
Т2. Если последующие
числа не равны, то не равны и предшествующие
им числа.
![]()
Доказательство (от противного).
Предположим, что a=b,
то, по А2, имели бы a′=b′,
что противоречит условию теоремы.
Т3. Если данные числа
не равны, то не равны и их последующие
числа.
![]()
Доказательство.
Предположим, что a′=b′,
то по А3, имели бы a=b,
что противоречит условию теоремы.
Т4. Никакое натуральное
число не равно своему предшествующему.
![]()
Доказательство (на основе А4).
Пусть M– множество
всех тех, и только тех, натуральных
чисел, для которых теорема верна. M
содержит 1, т.к. по А1 1′≠1. Если
число
![]() ,
,
то a′≠a,
но тогда по Т3 будет выполняться
неравенство (a′)′≠a′,
т.е.
![]()
По А4 , M=N.

Если обозначить 1′ = 2, 2′ = 3, 3′
= 4,…, то получим обычное обозначение
натуральных чисел 1, 2, 3, 4, … .
Сложение
натуральных чисел.
Определение. Сложением натуральных
чисел называется бинарная алгебраическая
операция, определенная во множестве
натуральных чисел N,
которая обладает свойствами:
1°
![]()
2°
![]()
Число a + b
называется суммой, а число a
и b – слагаемыми.
Т5. Сложение натуральных
чисел существует, и притом только одно.
I Доказательство
единственности.
Предположим, что во множестве N
существует еще одна алгебраическая
операция
![]() ,
,
обладающая свойствами 1°, 2°
1°)
![]()
2° )
![]()
Выберем некоторое число a(пусть
a фиксировано) и докажем,
что при этом a и
![]()
выполняется равенство
![]()
(1)
Пусть M-множество всех
тех, и только тех, чисел b,
для которых при выбранном числе a
выполняется равенство (1). Если b
= 1, то из равенств a
+ 1 = a′ и a′
= a![]() 1
1
следует равенство a
+ b = a
![]() b,
b,
т.е. 1![]()
Если b![]() ,
,
то равенство (1) верно по свойствам
элементов множества M
![]()
При данном a
1.
![]()
2.
![]()
3.![]()
1-3 => M=N
Тогда из равенств a
+ b′ = (a
+ b)′ и (a![]() b)′
b)′
= a![]() b′
b′
имеем a + b′
= a![]() b′,
b′,
т.е.
![]() .
.
По А4 M = N.
Т.к. при доказательстве a
выбрано произвольно, то равенство (1)
верно при любых a и b,
т.е. обе операции во множестве N
могут отличаться друг от друга только
обозначениями самих операций, по существу
же они совпадают.
I I
Доказательство существования
Пусть
 для
для
которых существует операция
![]()
1.
![]()
2. Если a = 1, то
сложение можно производить по правилу
a + b
= b′ (2).
Однозначность этой операции следует
по А2
![]() .
.
Эта операция обладает свойствами 1 и 2.
1) a + 1 = 1′
(по правилу 2), но по условию a
= 1 (1′ = a′)
a + 1 = a′
2) По правилу (2) a +
b′ = (b′)′
и b′ = a
+ b, из которых
получаем a + b′
= (a + b)′.
Следовательно, 1![]() .
.
3. Если a![]() ,
,
то по свойству элементов множества M,
для a существует
однозначная операция, обладающая
свойствами 1° и 2°. Для числа a’ и
любого числа b сложение
можно производить по правилу a′
+ b = (a
+ b)′
(3).
По теореме 1(Т1) число a′
однозначно определяет a,
а т.к. a![]() ,
,
то сумма a + b
для любого (фиксированного) b
определяется однозначно, по А2
однозначно определяется для b
и число (a + b)′.
Этим доказана однозначность операции
(3).
-
a′ + 1
= (a + 1)′
= (a′)′ -
a′ + b′ = (a + b′)′ = ((a + b)
′)′ = (a′ + b)′
![]() a′
a′
операция сложения существует
![]()
1 – 3 => M = N
Таким образом, существует правило,
которое позволяет для любых натуральных
чисел a и b
однозначно найти натуральное число c
= a + b,
удовлетворяет свойствам 1° и 2° определения
сложения.
Следствие.
Для любых чисел a и b
справедливы равенства
![]()
![]()
Примеры.
1+1=1′ =2, 1+2=2+1=2′ =3
4+2=4+1′ =(4+1)′ =5′ =6
Т6.(закон коммутативности
сложения натуральных чисел)
![]()
Доказательство.
Пусть b фиксировано.
M-множество всех тех,
и только тех a, для
которых теорема верна
![]()
1.
![]()
2. a = 1; b+1=
1+b (верно для всех
b по следствию)
![]() .
.
3.![]()
1 – 3 => M=N.
Так как число b выбрано
произвольно, то теорема верна.
Т7.(закон ассоциативности
сложения натуральных чисел)
![]()
Доказательство.
Пусть a и b
фиксированные произвольно выбранные
числа.
![]()
1.
![]()
2. c = 1,
(a + b) + 1
= (a + b)′ = a + b′ = a + (b + 1)
![]() .
.
3.
![]()
1 – 3
![]()
M=N.
Так как числа a и
b выбраны произвольно,
то теорема верна для любых a,b
и c.
Умножение
натуральных чисел
Определение. Умножением натуральных
чисел называется алгебраическая
операция, определенная во множестве
натуральных чисел N
и обладающая свойствами:
1’
![]()
![]()
2’
![]()
Числа a и b
называются сомножителями, а число
![]() –
–
произведением. Вместо
![]()
можно писать ab.
Т8. Во множестве
натуральных чисел существует умножение,
и при том только одно.
I Доказательство
единственности.
Пусть существует еще одна операция
![]() ,
,
обладающая свойствами:
1’)
![]()
2’)
![]()
Докажем, что
![]()
Зафиксируем a
произвольно
![]()
1.
![]()
2.
![]()
3.![]()
1 – 3
![]()
M=N.
Так как число a
выбрано произвольно, то единственность
умножения доказана для любых натуральных
чисел a и b.
I I
Доказательство существования
Пусть b – фиксировано,
M – множество всех
тех и только тех a, для
которых существует операция умножения,
удовлетворяющая условиям 1′ и 2′.
1.
![]()
2. a = 1, умножение
можно производить по правилу
![]()
(4)
![]()
Эта операция однозначна, т.к. всякой
паре a, b
натуральных чисел ставится в соответствие
единственное число b.
Покажем, что условия 1′ и 2′
выполняется.
1)
![]()
2) ab′ = b′
= b + 1 = ab
+ a, следовательно
для a = 1 операция
умножения существует. 1![]() .
.
3. Если a![]() ,
,
то для a существует
однозначная операция, обладающая
свойствами 1′ и 2′. Для a′
и любого числа b
умножение можно производить по правилу
![]()
(5).
Эта операция однозначна, т.к. произведение
ab однозначно
определяется по предположению, а сумма
ab + b
– по однозначности сложения.
Проверим выполнение свойств 1′ и
2′:
1)
![]() ,
,
т.е.
![]()
2)
![]()
![]() a’
a’
при любом b операция
умножения существует
![]()
1 – 3
![]()
M=N.
Этим доказано, что существует правило,
которое позволяет для любых натуральных
чисел a и b
однозначно найти натуральное число c
= ab. При этом выполняются
свойства1′ и 2′. И эта операция
единственная.
Следствие.
1)
![]()
2)
![]()
Пример:
![]()
Т9.(закон коммутативности
умножения натуральных чисел)
![]()
Доказательство.
Пусть b выбрано
![]()
1.
![]()
2. a = 1;
![]()
(верно для всех b
по следствию)
![]() .
.
3.![]()
(ab = ba
верно при любом b)
1 – 3 => M=N.
Так как число b выбрано
произвольно, то теорема верна для любых
натуральных чисел a
и b.
Т10.(закон дистрибутивности)
![]()
Доказательство.
Теорема докажем индукцией по c.
Числа a и b
фиксированы.
![]()
1.
![]()
2. c = 1,
a (b + 1)
=a b′ = ab +a =![]()
![]() .
.
3.
![]()
![]() a(b
a(b
+ c′) = a(b + c)′ = a(b + c) + a = ab + ac + a =
= ab + (ac + a) = ab + ac′
![]()
![]()
1 – 3
![]()
M=N.
Так как a и b
выбраны произвольно, то теорема верна
для любых a,b
и c.
Следствие.
По Т9 и Т10
![]()
Т10 – левый закон
дистрибутивности
Следствие – правый закон
дистрибутивности
Во множестве натуральных чисел оба этих
закона совпадают, поэтому говорят просто
о законе дистрибутивности.
Т11 (закон ассоциативности
умножения натуральных чисел)
![]()
Доказательство.
Числа a и b
фиксированные произвольно
![]()
1.
![]()
2. c = 1,
![]() .
.
3.
![]()
1 – 3
![]()
M=N.
Так как a и b
выбраны произвольно, то теорема верна
для любых a,b
и c.
Пример: Таблица умножения.
2 ∙ 1 = 2
2 ∙ 2 = 2 ∙ 1′ = 2 ∙ 1 + 2 = 4
2 ∙ 3 = 2 ∙ 2′ = 2 ∙ 2 + 2 = 6
2 ∙ 4 = 2 ∙ 3′ = 2 ∙ 3 + 2 = 8
Лекция 2.
Порядок во
множестве натуральных чисел.
Основное отношение «следует за», которое
введено при аксиоматическом построении
системы натуральных чисел, связано с
понятием порядка. Но оно связывает
каждый элемент лишь с двумя соседними.
Можно ввести отношение порядка для
любых натуральных чисел. Это новое
отношение будет описываться словом
«больше».
Определение. Натуральное число a
больше натурального числа b
(пишут a > b),
если существует натуральное число k,
что выполняется равенство a
= b + k.
![]()
Если a больше b,
то b меньше a
(пишут b < a)
b < a
a
> b
Если
![]() ,
,
то пишут
![]() ,
,
a не меньше b.
Если
![]() ,
,
то пишут
![]() ,
,
a не больше b.
Т1.
![]()
Доказательство.
![]()
1.
![]()
2.
![]()
3.![]()
1 – 3
![]()
M=N.
Т2. Для любых натуральных
чисел a и b
имеет место один и только, из следующих
трех случаев.
1° a = b
2° a > b
3o a <
b
Доказательство. Нужно доказать, что
любых натуральных чисел a
и b имеет место один и
только, из случаев:
1° a = b
2° a = b + k
3o
b = a + m
I. Доказательство
единственности.
Покажем, что два из трех случаев
одновременно иметь место не могут.
Из Т1 следует, что не могут
одновременно выполняться первое и
второе условия
![]() ,
,
первое и третье условия
![]() .
.
По той же теореме, случай второй
несовместим с третьим:
![]() .
.
Таким образом, может выполняться не
более чем одно условие.
I I.
Доказательство существования.
Теперь докажем существование для любых
a и b
хотя бы одного из этих случаев.
Пусть a фиксировано.
M-множество всех
тех b, для которых
имеет место один из случаев 1°, 2°, 3o
1) b = 1 а) a
= 1 => a = b
1 случай
б)
![]() ,
,
то a имеет предшествующее
c, c′
= a => a
= c′ = c
+ 1 = 1 + c, т.е. имеет место
второй случай a = b
+ c. 1![]() .
.
2) b![]() ,
,
т.е. для выбранного a и
указанного b имеет место
один из случаев 1°, 2°, 3o
Для b’
имеем
-
a = b,
то b′ = b
+ 1, т.е. для b′
имеем третий случай b′
= a + 1 (b′
> a) -
a = b + k
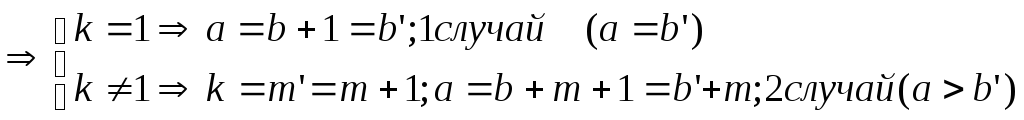
-
b = a
+ m, то b′
= (a + m)′
= a + m′,
т.е. для b′ имеем
третий случай. b′ ,
,
M = N
(b′ > a)
Так как число a выбрано
произвольно, то теорема верна для любых
натуральных чисел a
и b.
Т3.(транзитивность
неравенств)
![]()
![]()
Доказательство.
1)
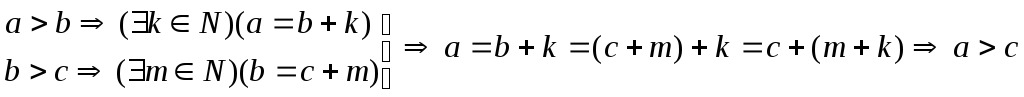
2) аналогично
Т4.(законы монотонности
сложения и умножения)
1)
![]()
2)
![]()
3)
![]()
Доказательство.
-
Утверждения первого пункта следуют из
однозначности сложения и умножения. -
a > b => a
= b + k => a
+ c = (b + k) + c = b + (k + c) = b + (c + k) = (b + c) + k
=>
=> a + c > b +
c
-
a < b => b
> a => b
+ c > a + c и
bc > ac
=> a + c < b + c
и ac< bc
Т4′.(обратная)
1)
![]()
2)
![]()
3)
![]()
Доказательство.
Докажем например ac
> bc => a
> b
Предположим противное a
= b => ac
= bc
a < b
=> ac < bc,
что противоречит условию
Следовательно ac >
bc => a
> b
Остальные утверждения доказываются
аналогично.
Определение. Неравенства a
> b и c
> d или a
< b и c
< d называются
неравенствами одинакового смысла.
Т5.
-
любые равенства можно почленно складывать
и умножать.
![]()
-
Любые неравенства можно почленно
складывать и перемножать с любым
равенством.
![]()
-
Любые неравенства одинакового смысла
можно почленно складывать и перемножать.
![]()
Доказательство.
Утверждения 1) и 2) получаются непосредственно
из Т4 заменой в одной части
c на d
или k на m.
3)По Т4
![]()
Для a < b
и c < d
аналогично.
Т6. Из всех натуральных
чисел единица является наименьшим
числом.
![]()
Доказательство.

Т7. (Аксиома Архимеда)
![]()
Доказательство.![]()
![]()
n = a
+ 1 (достаточно взять). Перемножим
неравенства n > a
и b![]() ,
,
получим bn > a.
Т8. Натуральные числа
n и n+1
являются соседними числами, т.е.
![]() ,
,
значит, если
![]()
Доказательство.
1)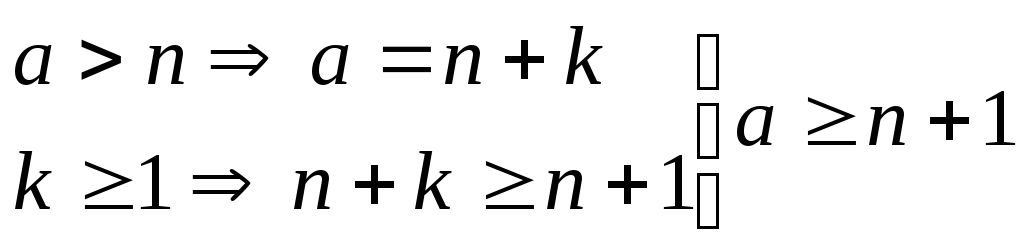
2)
![]()
a > n
не может быть по Т2
Метод полной
математической индукции.
Т. Если некоторое утверждение A
верно для числа 1 и из того, что оно
верно для числа n,
следует, что оно верно и для следующего
числа n′, то
утверждение A верно
и для любого натурального a.
Доказательство.
Пусть M-множество всех
тех натуральных чисел, для которых
утверждение A верно.
1![]() ,
,
т.к. по условию теоремы утверждение A
для 1 верно. Если n![]() ,
,
т.е. для n утверждение
A верно, то и n′![]() ,
,
т.к. из справедливости утверждения A
для n следует
справедливость его для n′.
По А4 M=N,
т.е. утверждение A
верно для любого натурального числа a.
Различные виды
доказательств по индукции
-
Принцип полной математической индукции.
Предложение Т(п) с переменной
![]()
верно для любого натурального числа п,
если выполнены следующие условия:
-
это предложение верно для п =1, т.е.
Т(1) =и; -
каково бы ни было натуральное число п,
из предположения о том, что это
предложение верно для всех п,
следует, что оно верно для следующего
числа п′, т.е. Т(п) =и

Т(п′) =и.
-
Усиленный принцип полной математической
индукции.
Предложение Т(п) с переменной
![]()
верно для любого натурального числа п,
если выполнены следующие условия:
1) это предложение верно для п =1,
т.е. Т(1) =и;
2) каково бы ни было натуральное число
т, из предположения о том, что это
предложение верно для всех п<m,
следует, что оно верно для m
, т.е. Т(m) =и.
-
Обобщенный принцип полной математической
индукции.
Пусть
![]() .
.
Предложение Т(п) с переменной
![]()
верно для любого натурального числа
п≥а , если выполнены следующие
условия:
1) это предложение верно для п =а,
т.е. Т(а) =и;
2) каково бы ни было натуральное число
п≥а, из предположения о том, что это
предложение верно для всех п, следует,
что оно верно для следующего числа п′,
т.е. Т(п) =и
![]()
Т(п′) =и.
-
Обобщенный усиленный принцип полной
математической индукции.
Пусть
![]() .
.
Предложение Т(п) с переменной
![]()
верно для любого натурального числа
п≥а , если выполнены следующие
условия:
1) это предложение верно для п =а,
т.е. Т(а) =и;
2) каково бы ни было натуральное число
т≥а, из предположения о том, что это
предложение верно для всех а≤п<m,
следует, что оно верно для m
, т.е. Т(m)
=и.
Пример. Доказать, что среднее геометрическое
нескольких положительных чисел не
больше их среднего арифметического.
Лекция 3.
Индуктивное
определение последовательности.
Определение1. Множество всех
натуральных чисел m, не
превосходящих некоторое натуральное
число n
![]() ,
,
называется начальным отрезком натурального
ряда и обозначается через [1,n].
Определение2. Если по какому-нибудь
правилу (закону) каждому натуральному
числу n поставим в
соответствие некоторый вполне определенный
элемент an,
принадлежащий данному множеству A,
то получим последовательность
a1, a2,
a3,…, an,…
элементов множества A.
Элементы, входящие в последовательность
называются ее членами, а элемент an
называется общим членом этой
последовательности.
Обозначение последовательности: {an}
Если последовательность задана только
на множестве натуральных чисел,
принадлежащих отрезку [1,п], то она
называется конечной. Конечная
последовательность {an}
может быть задана выписыванием всех ее
членов, чего нельзя сделать для
последовательности бесконечной,
т.е. последовательности заданной на
множестве всех натуральных чисел.
Существуют различные способы задания
последовательностей. Рассмотрим один
из них, называемый индуктивным
определением последовательности.
Пусть заданы члены последовательности
a1, a2,
a3,…, an.
Определение3. Соотношение между
всеми или некоторыми из указанных выше
членов последовательности, которые
позволяют вычислить следующий член
an+1
этой последовательности, называются
рекуррентными определяющими
соотношениями.
Примеры. Арифметические и
геометрические прогрессии определяются
заданием первого члена a,
разности d (знаменателя
q) и рекуррентным
определяющим соотношением.
-
арифметическая прогрессия a,
d: an
= a1 + d(n
– 1) или an
= an-1
+ d. -
Геометрическая прогрессия a,
q: an
= an-1q
или an = a1qn-1. -
Последовательность чисел Фибоначчи.
a1 = a2
= 1 и рекуррентные соотношения an+2
= an+1+an
1, 1, 2, 3, 5, 8, 13, 21,…
T. При заданных
рекуррентных определяющих соотношениях,
которые однозначно определяют член
последовательности an,
как только все члены am
при m < n
заданы и сами удовлетворяют заданным
соотношениям, существует одна, и только
одна, такая последовательность {an},
члены которой удовлетворяют заданным
рекуррентным соотношениям.
По другому, коротко: индуктивно
последовательность задается однозначно.
Доказательство.
Докажем методом математической индукции.
Докажем, что на каждом отрезке [1,n]
существует одна и только одна такая
последовательность.
-
Для отрезка [1,1] утверждение верно, т.к.
последовательность в этом случае
состоит из одного члена a1,
который, как не имеющий предшествующих
членов должен быть задан непосредственно. -
Пусть утверждение верно для всех
отрезков [1,m] (m
< n), тогда оно
будет верно и для отрезка [1,n],
т.к. последовательность a1,
a2, a3,…,
an-1,
an
получается из последовательности a1,
a2, a3,…,
an-1
присоединением члена an,
который, по условию теоремы, определяется
однозначно через предшествующие члены.
Этим доказано, что для каждого отрезка
[1,n] существует одна,
и только одна последовательность, члены
которой удовлетворяют данным рекуррентным
соотношениям.
Последовательность, определенная на
[1,n], определена и на
[1,m] (m
< n), все ее члены
удовлетворяют заданным соотношениям
и потому совпадают с соответствующими
членами последовательности, заданной
на отрезке [1,m].
Бесконечная последовательность {an},
удовлетворяющая условиям теоремы,
содержит в себе каждую последовательность,
заданную на отрезке [1,n].
Любой член ak
бесконечной последовательности {an}
определяется однозначно как общий член
всех конечных последовательностей, для
которых он определен.
Сумма и произведение
нескольких натуральных чисел.
Определение. Если дан начальный
отрезок натурального ряда [1,n],
то число n называется
числом элементов отрезка и числом
элементов любого множества, эквивалентного
отрезку [1,n]. В этом
смысле число n называется
количественным натуральным числом.
Натуральные числа, построенные на
аксиомах Пеано, называются порядковыми
натуральными числами.
Указанное определение устанавливает
взаимнооднозначное соответствие между
множеством всех порядковых натуральных
чисел и множеством всех количественных
натуральных чисел.
Определение. Установление
взаимнооднозначного соответствия между
элементами какого-либо конечного
множества и элементами некоторого
начального отрезка натурального ряда
[1,n] называется счетом
элементов данного конечного множества.
Пусть даны натуральные числа a1,
a2, a3,…,
an,
которые занумерованы натуральными
числами от 1 до n, т.е.
установлено взаимнооднозначное
соответствие между множеством данных
чисел и множеством чисел отрезка [1,n].
В таком случае говорят, что даны n
натуральных чисел.
Определение. Суммой n
натуральных чисел a1,
a2, a3,…,
an
называется n-ый член
последовательности {Sn},
который обозначается через Sn
= a1+ a2
+ a3 +…+ an
=
![]() ai,
ai,
сама же последовательность {Sn}
определяется рекуррентными соотношениями:
-
S1 =
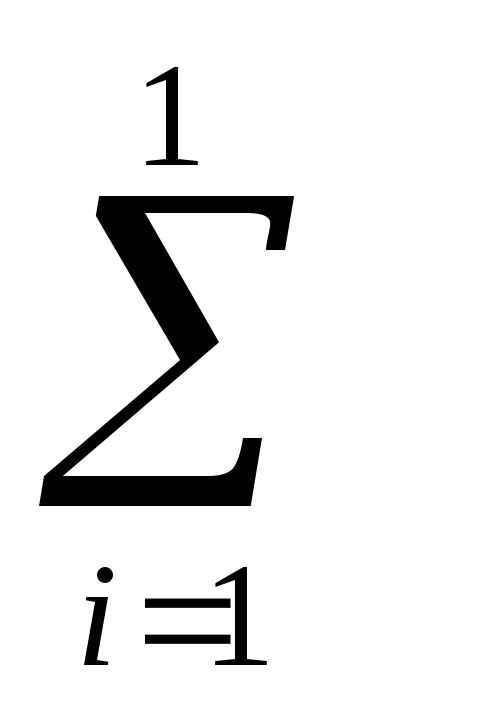 ai
ai
= a1 -
Sk+1
=
 ai
ai
=
 ai
ai
+ ak+1
= Sk
+ ak+1
( для всех k < n)
Определение. Произведением n
натуральных чисел a1,
a2, a3,…,
an
называется n-ый член
последовательности {Pn},
который обозначается через Pn
= a1 a2
a3 … an
=
![]() ai,
ai,
сама же последовательность {Pn}
определяется рекуррентными соотношениями:
-
P1 =
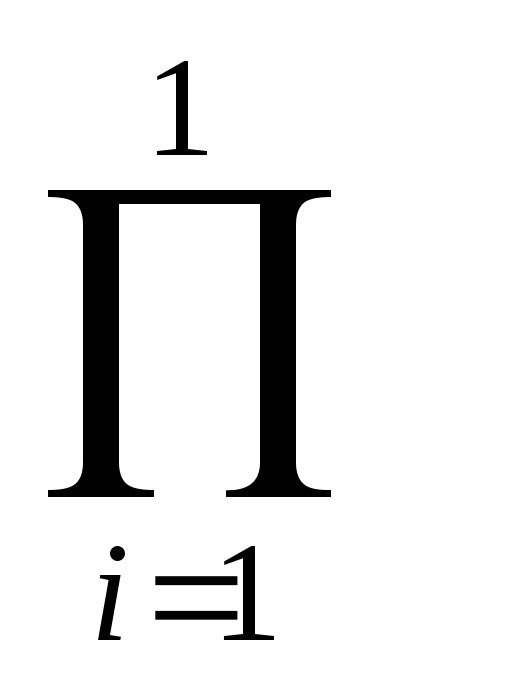 ai
ai
= a1
-
Pk+1
=
 ai
ai
= ( ai
ai
) ak+1
= Pk
ak+1
(для всех k <
n)
По теореме об индуктивном задании
последовательности при заданных числах
a1, a2,
a3,…, an
существуют единственные последовательности
S1, S2,
S3,…, Sn
и P1, P2,
P3,…, Pn-1,
заданные на отрезке [1,n].
Из единственности этих последовательностей
следует единственность суммы Sn
и произведения Pn
чисел a1, a2,
a3,…, an.
Т1. Законы ассоциативности
сложения и умножения справедливы для
любого числа натуральных чисел
1.
![]() ai
ai
+
![]() am+i
am+i
=
![]() ai
ai
2. (
![]() ai
ai
)(
![]() am+i
am+i
) =
![]() ai
ai
Доказательство.
Докажем методом полной математической
индукции по числу n.
-
n = 1,
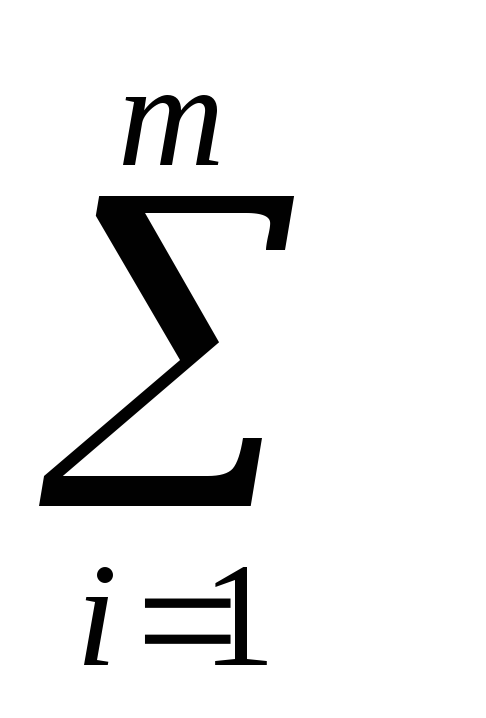 ai
ai
+ am+1
=
 ai
ai
(по рекуррентному соотношению)
(
![]() ai
ai
) am+i
=
![]() ai
ai
Для n = 1 теорема верна
-
Пусть теорема верна для n,
проверим для n′ = n
+ 1
![]() ai
ai
+
![]() am+i
am+i
=
![]() ai
ai
+ (![]() am+i
am+i
+ am+n+1
) = (![]() ai
ai
+
![]() am+i
am+i
) + am+n+1
=
=
![]() ai
ai
+ am+n+1
=
![]() ai
ai
Для произведения аналогично.
Таким образом, теорема верна для n
= 1, и из того, что она верна для числа n,
следует, что она верна и для числа n
+ 1. По теореме индукции теорема справедливы
для любого n.
Т2. Законы коммутативности
сложения и умножения справедливы для
любого числа натуральных чисел, т.е.
сумма n слагаемых и
произведение n
сомножителей не зависят от порядка
следования компонентов.
Доказательство.
Докажем эту теорему для произведения,
т.к. для суммы доказательство аналогично.
Пусть имеется произведение n
натуральных чисел, взятых в произвольном
порядке
aj1
aj2
aj3
… ajn
=
![]() ajl
ajl
в отличие от первоначального
a1
a2
a3 …
an
=
![]() ai
ai
.
Покажем, что
![]() ajl
ajl
=
![]() ai
ai
Доказательство будем проводить индукцией
по n.
1) n = 1,
![]() ajl
ajl
= a1 =
![]() ai
ai
теорема верна.
2) Предполагаем, что утверждение теоремы
верно для всех чисел, меньших n,
т.е. для любого числа сомножителей
меньших числа n. Положим
n = k
+ 1.
а) Пусть aj1
= an
=> j1 = n
![]()
= aj1
∙![]()
= an
∙![]()
= (![]() )∙ak+1=
)∙ak+1=
![]()
=
![]()
б) Пусть ajm+1
= an
=> jm+1
= n, где m
< k, k
= m + q,
n = m
+ q + 1
![]() ajl
ajl
= (![]() ajl
ajl
)∙ ajm+1
∙(![]() ajm+1+l
ajm+1+l
)= (![]() ajl
ajl
![]() ajm+1+l)
ajm+1+l)
ajm+1
= (![]() ai
ai![]() am+i
am+i
) an
= =(![]() ai
ai
) an
=
![]() ai
ai
в) Пусть ajn
= an
=> jn
= n
![]() ajl
ajl
=
![]() ajl
ajl
ajn
=
![]() ajl
ajl
an
=
![]() ai
ai
ak+1
=
![]() ai
ai
=
![]() ai
ai
Из 1-2 следует, что теорема справедлива
для всех натуральных чисел.
Т3. Для натуральных
чисел справедливы равенства:
![]() (
(
ai
+ bi
) =
![]() ai
ai
+
![]() bi
bi
![]() (ai
(ai
+ bi
) = (![]() ai
ai
) (![]() bi
bi
)
Доказательство.
Докажем только для суммы, т.к. доказательство
для произведения аналогично.
1) n
= 1,
![]() (
(
ai
+ bi
) = a1
+ b1
=
![]() ai
ai
+
![]() bi
bi
2) Пусть предложение верно для n,
покажем, что оно верно и для n′
= n + 1.
![]() (
(
ai
+ bi
) =
![]() (
(
ai
+ bi
) + an+1
+ bn+1=
![]() ai
ai
+
![]() bi
bi
+ an+1
+ bn+1
= (![]() ai
ai
+ an+1
) + + (![]() bi
bi
+ bn+1
) =
![]() ai
ai
+
![]() bi
bi
Из 1-2 следует, что теорема справедлива
для всех натуральных чисел.
Определение. Если все n
сомножителей равны между собой,
т.е. a1 = a2
= a3 = …= an
= a, то полагаем an
=
![]() a
a
Число an
называется n-й степенью
числа a.
Следствие1. При n
= 1 имеем : a1 =
![]() a
a
= a
Следствие 2. am
an
= am+n
(![]() a
a
) (![]() a
a
) =
![]() a
a
(закон ассоциативности)
Следствие3. (ab)n
= an
bn
![]() (ab)
(ab)
= (![]() a
a
) (![]() b
b
) (Т3)
Следствие4. (am)n
= amn
Доказательство.
Докажем индукцией по m.
1) m =1 (a1)n
= an
= a1n
2) Пусть при m = n
равенство (ak)n
= akn
справедливо, тогда при m
= k + 1 получаем:
(ak+1)n=(
ak
a1)n
= (ak)n
an
= akn
an
= akn
an
= akn+n
= a(k+1)n
Т4. Для любых натуральных
чисел n и a
справедливо равенство na
=
![]() a
a
.
![]()
(na =
![]() a)
a)
Докажем методом полной математической
индукции по n.
-
n = 1, 1a
= a =
 a
a -
Покажем, что если n
= k равенство
ka =
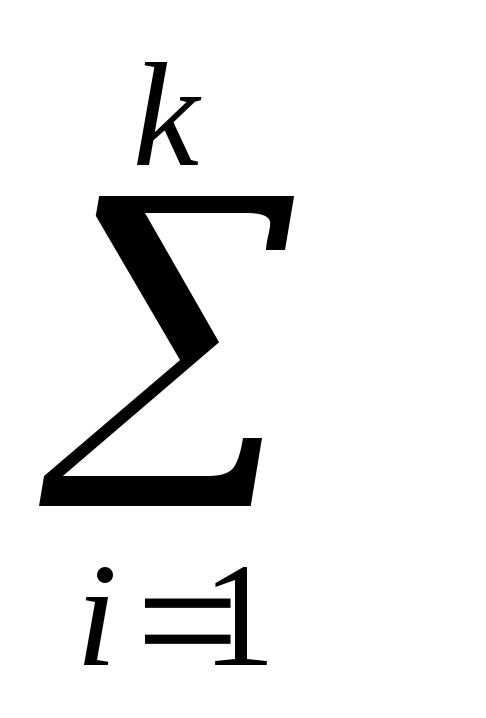 a
a
справедливо, то оно справедливо и при
n = k
+ 1.
na = ( k+1
) a = ka
+ a =
![]() a+
a+
a=
![]() a
a
=
![]() a
a
Эта теорема позволяет рассматривать
выражение na как
произведение натуральных чисел n
и a и как сумму n
слагаемых, каждое из которых равно a.
В частности натуральное число n
можно рассматривать как сумму n
слагаемых, каждое из которых равно
единице.
Т5. (закон дистрибутивности)
Для любого числа слагаемых имеет место
равенство:
b(![]() ai
ai
) = b(a1+
a2
+ a3 +…+
an
) = ba1+
ba2
+ ba3 +…+
ban
=
![]() (bai)
(bai)
Докажем методом полной математической
индукции по числу n.
-
n = 2, b(
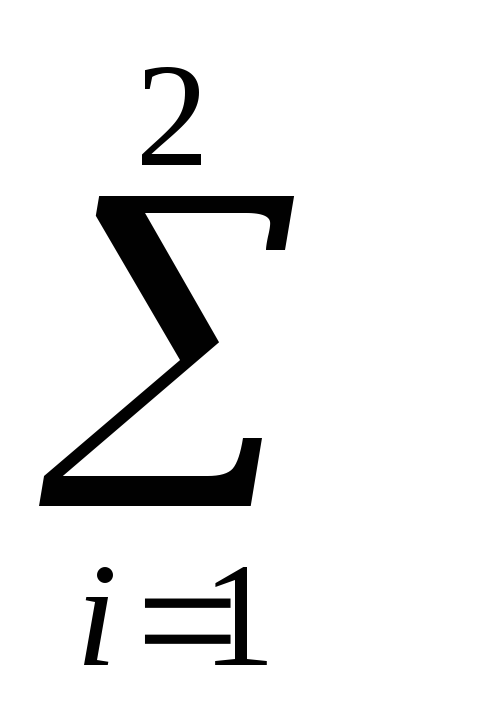 ai
ai
) = b(a1+
a2
) = ba1+
ba2
=
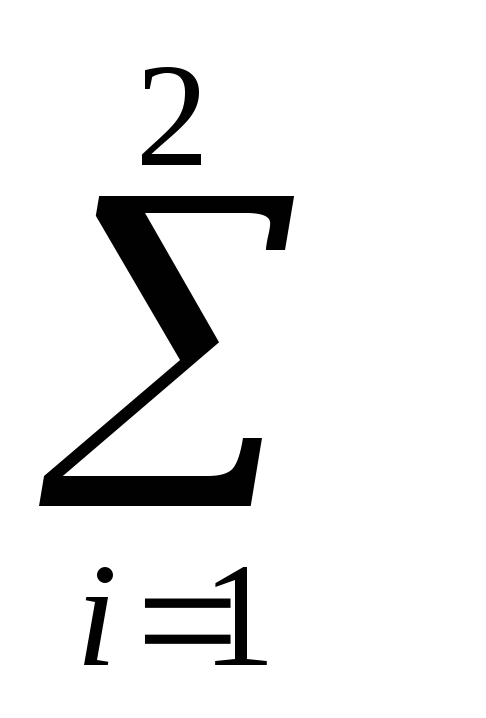 bai
bai -
Пусть теорема верна при n
= k, докажем для
n = k+
1
b(![]() ai
ai
) = b(![]() ai
ai
+ ak+1
) = b![]() ai
ai
+ bak+1
=
![]() (bai)
(bai)
+ bak+1
=
![]() (
(
bai )
Теорема доказана для любого натурального
числа n.
Следствие.
(
![]() ai
ai
)∙ (![]() bj
bj
) =
![]()
![]() ai
ai
bj
=![]()
![]() ai
ai
bj
Вычитание и
деление натуральных чисел
Определение. Разностью двух
чисел a и b
называется натуральное число x
= a – b,
удовлетворяющее уравнению b
+ x = a.
Действие, с помощью которого находится
разность чисел a и
b, называется вычитанием.
Число a называют
уменьшаемым, а число b–вычитаемым.
Вычитание есть действие, обратное
сложению.
Т. Разность двух чисел a–b
существует тогда и только тогда, когда
a > b.
Если a–b
существует, то она единственна.
Доказательство.
I Существование.
1) (a–b)
существует, т.е. a–b
= k, k
![]()
2)
![]()
существование разности a–b
= k
I I
Единственность

Определение. Частным двух чисел
a и b
называется натуральное число
![]() ,
,
удовлетворяющее равенству bx
= a.
Число a называют
делимым, а число b–делителем.
Действие, с помощью которого находится
частное чисел a и b,
называется делением.
Деление есть действие обратное умножению.
Т. Для того чтобы существовало
частное двух чисел, необходимо (но
недостаточно), чтобы
![]() .
.
Если частное существует, то оно
единственно.
Доказательство.
Пусть
![]() ,
,
если
![]()
Пусть уравнение bx
= a имеет два
решения x1 и x2

Вычитание и деление во множестве всех
натуральных чисел не являются бинарными
алгебраическими операциями, т.к. эти
действия не всегда выполнимы.
Лекция 4.
Непротиворечивость,
полнота и независимость аксиоматической
теории натуральных чисел.
Основными требованиями, предъявляемыми
к аксиомам данной теории, являются
непротиворечивость, полнота и
независимость.
Определение. Интерпретацией
данной аксиоматической теории называется
любое непустое множество M,
для элементов которого установлены
отношения(в частности, алгебраические
операции), удовлетворяющие тем требованиям,
которые высказаны в аксиомах этой
теории.
Интерпретация данной аксиоматической
теории позволяет прилагать эту теорию
к изучению конкретных множеств. Делая
логические выводы из систем аксиом,
получим утверждения, справедливые для
любого множества, являющегося
интерпретацией этой теории. В этом
состоит общность теории и границы ее
применений.
I Непротиворечивость.
Определение. Система аксиом называется
непротиворечивой, если на ее основании
нельзя получить как следствие два
противоречащих друг другу утверждения.
Непротиворечивость аксиоматической
теории доказывается построением
какой-нибудь интерпретации этой системы,
непротиворечивость которой уже доказана,
т.е. вопрос непротиворечивости данной
теории не может быть решен в рамках
данной теории. (Например, вопрос о
непротиворечивости геометрии Лобачевского
может быть решен так: если непротиворечива
теория арифметики, то непротиворечива
геометрия Евклида, а из непротиворечивости
геометрии Евклида следует непротиворечивость
геометрии Лобачевского).
При доказательстве непротиворечивости
содержательной арифметической теории
не на что опираться. Обычно ссылаются
на весь исторический опыт развития
математики и ее приложений в практике.
Никогда никто не встречал в своей
практике фактов, которые бы противоречили
выводам, полученным в арифметике.
II Независимость.
Определение. Система аксиом называется
независимой, если никакая из аксиом не
является следствием остальных аксиом
системы.
Для доказательства независимости
какой-либо аксиомы от остальных аксиом
системы достаточно найти интерпретацию,
в которой выполняются все аксиомы
системы, кроме исследуемой, причем
исследуемая аксиома в найденной
интерпретации не должна выполняться.
Для доказательства независимости всей
системы аксиом надо доказать независимость
каждой аксиомы от остальных аксиом,
следовательно, придется отыскивать
столько интерпретаций, сколько аксиом
содержится в данной системе.
Рассмотрим одно из возможных доказательств
независимости системы аксиом Пеано.
Для доказательства независимости первой
аксиомы от остальных аксиом первые три
аксиомы сохраним в прежней формулировке,
а аксиому индукции сформулируем в
следующем виде:
А4*: Каждое
непустое множество натуральных чисел
M совпадает с множеством
натуральных чисел N,
если оно обладает следующими двумя
свойствами:
1°. Если существует число 1, не следующее
ни за каким другим числом, то 1![]()
2°. Если число n![]() ,
,
то и следующее число n’![]() .
.
А1:
![]()
Постоим модель (интерпретацию), где
выполняются аксиомы
![]() .
.
Рассмотрим N = {a,
b, c},
a, b,
c – назовем
“натуральными числами”. Основное
отношение “следует за” определим
стрелками на чертеже
![]()
(b следует за a).![]()
В этой интерпретации первая аксиома
Пеано не выполняется, т.к. нет “числа”,
которое не следовало бы ни за каким
другим “числом”. Аксиомы 2, 3 и 4*
выполняются. Например, проверим выполнение
аксиомы 4*.
По условию, M –
непустое множество “натуральных чисел”
значит, оно содержит хотя бы одно “число”
из N, но тогда, по
свойству 2°, M содержит
и все остальные “числа” из N.
Пусть a![]() ,
,
по 2°
![]()
M = n
Утверждение доказано.
А2:![]()
Строим интерпретацию системы аксиом
![]() .
.
Рассмотрим N = {1,
a, b},
элементы 1, a, b
– назовем “натуральными числами”.
Расположим эти “числа” в порядке их
следования
![]() .
.
Тогда A1 выполняется
A2 нет,
т.к. для элемента b нет
следующего элемента
A3 имеет
место (не более одного предшествующего)
A4

А3:![]()
Строим интерпретацию
![]()
N = {1, a,
b, c,
d}
A1 выполняется
A2 выполняется
A3 нет,
т.к. элемент b следует
за двумя элементами a
и d
A4 выполняется
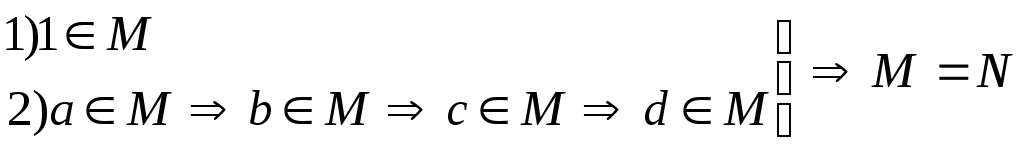
А4:![]()
Строим интерпретацию системы аксиом
![]()
Пусть множество “натуральных чисел”
N состоит из двух
непересекающихся подмножеств P
и Q.
![]()
В этой интерпретации выполняются аксиомы
1, 2, 3, но не выполняется А4,
т.к. M содержит1
вместе с каждым содержащимся в нем
“числом” n содержит
следующее “число” n’
, но не содержит элементов из множества
P, т.е.
![]()
Независимость систем аксиом Пеано
доказана.
I I
I Полнота системы
аксиом Пеано
Определение 1. Система аксиом
называется полной, если любые две ее
интерпретации изоморфны.
Полнота в этом смысле называется ее
категоричностью.
Определение 2. Система аксиом
называется полной, если всякое предложение
этой теории можно доказать или опровергнуть
(т.е. из любых двух высказываний
![]() и
и
![]()
не менее одного является теоремой).
Для доказательства полноты по второму
определению необходимо, чтобы логические
средства были включены в данную теорию,
т.е. теория должна быть формализована
в отличии от содержательной.
Поскольку мы рассматриваем содержательную
аксиоматическую теорию натуральных
чисел, то докажем полноту системы аксиом
Пеано первому определению (категоричность).
Определение. Две интерпретации M
и
![]()
данной системы аксиом называются
изоморфными, если они изоморфны
относительно всех соотношений,
указанных в этой системе аксиом.
Теорема. Система аксиом Пеано
является полной.
Доказательство.
Пусть даны две интерпретации аксиом
Пеано N и
![]() .
.
Каждая из них содержит “единицу”,
которая не следует ни за каким элементом
того же множества (А1). Эти
единицы обозначим e
и
![]() .
.
Установим соответствие между элементами
множеств N и
![]()
по следующему правилу:
1)
![]()
2) Если
![]() ,
,
то полагаем, по определению,
![]() .
.
При таком соответствии каждый элемент
из N будет иметь один,
и только один, образ в
![]() ,
,
т.к. e имеет один, и
только один, образ
![]() ,
,
если a имеет один, и
только один, образ
![]() ,
,
то и a’ имеет один,
и только один, образ
![]()
по принципу математической индукции
утверждение справедливо для любого a![]() .
.
Обратно, если
![]() ,
,
то (любое число
![]()
имеет единственное предшествующее
число b a
= b’) b
имеет в N предшествующее
число, т.е. b = a’.
Тогда
![]()
, т.е. элемент
![]()
имеет в N один, и только
один прообраз e .
Пусть
![]()
имеет в N один, и
только один, прообраз c,
тогда
![]() ,
,
т.е.
![]()
имеет в N не менее
один прообраз c′.
Если n-любой прообраз
элемента
![]() ,
,
то
![]() ,
,
т.е. n = m′.
Тогда
![]() .
.
Т.к. c-единственный
элемент, отображающийся в
![]() ,
,
то c = m,
а по А2 получаем c′
= m′ = n,
т.е. c′ – единственный
прообраз элемента
![]() .
.
По математической индукции любой элемент
![]()
имеет один, и только один, прообраз в N
.
Этим доказано, что установленное
соответствие между элементами множеств
N и
![]()
является взаимнооднозначным. Остается
еще показать, что при этом соответствие
сохраняется отношение “следует за”.
Если b следует за a,
т.е. b = a′,
то это же верно и для их образов, т.к. из
b = a′
следует
![]() .
.
Обратно, из
![]()
следует b = a′.
Теорема доказана.
Следствие. При установленном
взаимнооднозначном соответствии
сохраняется сложение, умножение и
порядок, т.е. из a + b
= c, ab
= d, a>b
всегда следуют верные соотношения
![]() ,
,
и обратно.
Изоморфизм.
Расширение колец,
полей и других алгебр.
Разбиение
множества на классы.
Пусть M и
![]()
– две алгебры с двумя бинарными
алгебраическими операциями сложения
и умножения.
M и
![]()
будут изоморфными, если между их
элементами установлено взаимнооднозначное
соответствие, такое, что сохраняет обе
указанные операции.
Если M
![]() ,
,
то справедливы следующие свойства:
-
a + b
= b
+ a
-
(a +
b) + c
= a + (b
+ c)

-
ab =
ba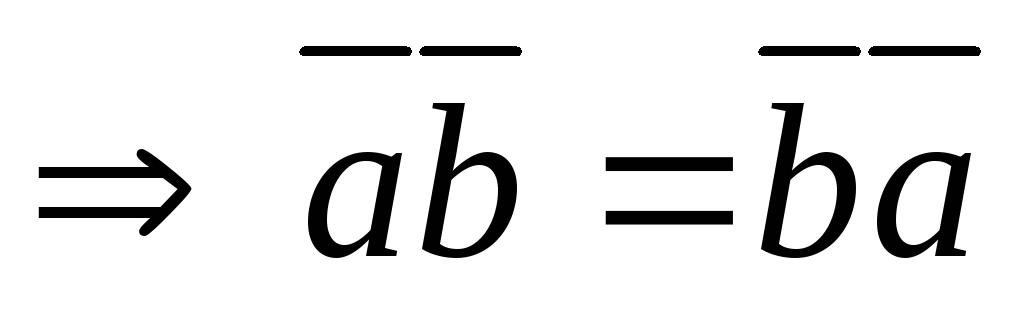
-
(ab)c
= a(bc)
-
(a
+ b)c
= ac +
bc
-
если множество M
содержит 0, то и множество

содержит
 ,
,
причем a + 0 = a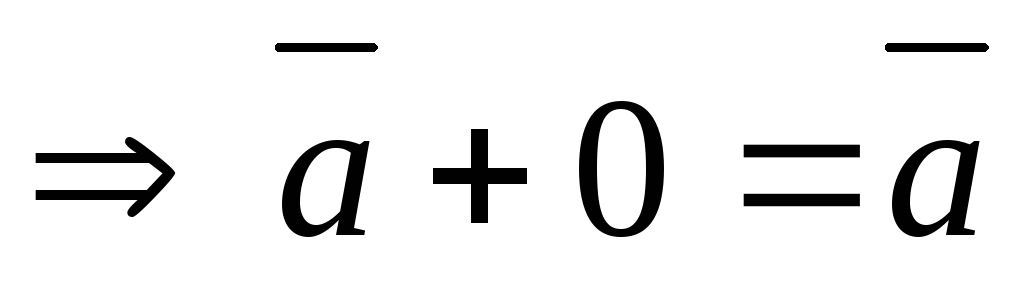 ,
,
т.е.

-
Если множество M
содержит вместе с элементом a
и элемент –a, то
a + (–a)
= 0
 ,
,
т.е. и в

для элемента

существует противоположный ему элемент ,
,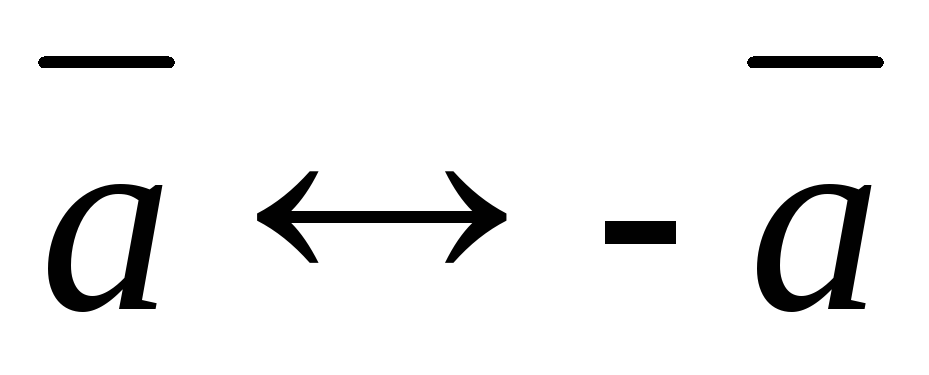
-
Если множество M
содержит единичный элемент e,
то и в множестве

содержится единичный элемент
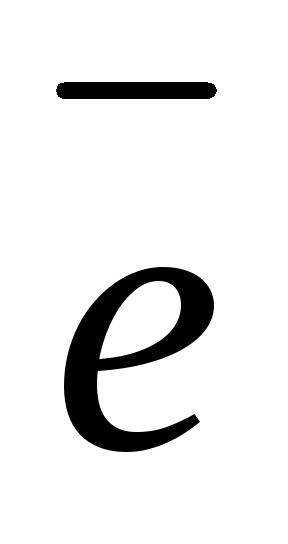 ,
,
т.к.
 ,
,
причем

-
Если множество M
содержит вместе с элементом
 и
и
элемент, ему обратный a-1,
то и множество

вместе с элементом

содержит
 ,
,
причем
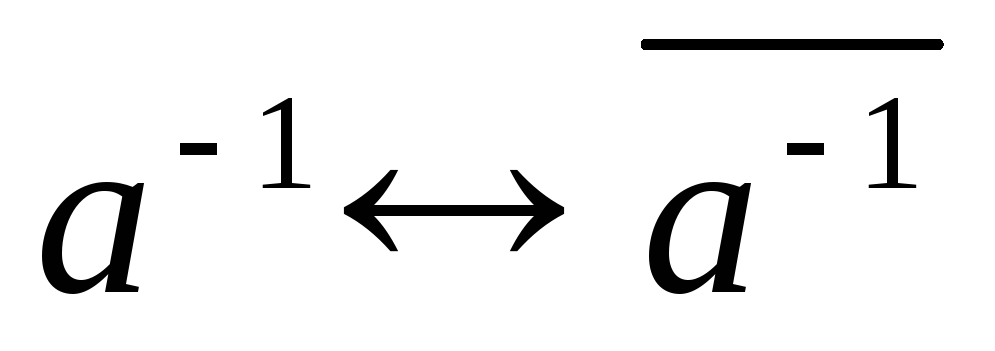 ,
,
т.к.

Если M относительно
сложения – группа, то и
![]()
относительно сложения будет группой,
если M относительно
обеих алгебраических операций,
определенных в нем, является кольцом
(телом, полем), то и множество![]()
относительно своих операций будет
кольцом (телом, полем). Все выводы,
полученные для одного из изоморфных
между собой алгебр, автоматически
переносятся и на другую алгебру, если
эти выводы опирались только на общие
свойства алгебраических операций.
Определение. Если множество M
с двумя алгебраическими операциями
(сложением и умножением) содержится в
кольце K относительно
этих же операций, то кольцо K
называется расширением множества
M. Если при этом
множество M само
является кольцом по отношению к тем же
операциям, то M
называется подкольцом кольца K.
Т. Пусть даны кольцо![]()
и M с двумя алгебраическими
операциями – сложением и умножением,
причем
![]()
и M не пересекающиеся.
Если кольцо
![]()
содержит
![]() ,
,
изоморфное M относительно
операций, определенных в кольце
![]()
и M, то существует
кольцо K, изоморфное
![]()
и являющееся расширением M.
![]()
Доказательство.
Произведем замену всех элементов
подмножества
![]()
в кольце
![]()
соответствующими им при изоморфизме
![]()
элементами из M. Затем
определим суммы и произведения
незамещенных и замещенных элементов
так, чтобы результаты совпадали с
результатами операций кольца
![]() .
.
Например, если до замены было
![]()
и
![]() ,
,
и если
![]()
и
![]()
заменяются соответственно на a
и c, а
![]()
и
![]()
остаются на месте, то по определению
полагаем
![]()
и
![]()
Этим способом из кольца
![]()
получаем кольцо K,
действительно являющееся расширением
M, причем
![]()
Если
![]()
является телом (полем), то и K
так же будет телом (полем).
Определение. Кольцо K,
являющееся расширением M
с двумя алгебраическими операциями –
сложением и умножением, называется
минимальным кольцом, содержащим M,
если K не имеет отличного
от себя подкольца, содержащего M.
Разбиение множества на классы
Рассмотрим вопрос о разбиении множества
M на классы и, связанное
с этим, отношение эквивалентности.
Если множество M
разбито на попарно непересекающиеся
непустые подмножества, исчерпывающие
все множество, то говорят, что множество
M разбито на классы.
Определение. Если множество M
разбито на классы, то два элемента a
и b данного множества
называются эквивалентными по
отношению данному разбиению тогда, и
только тогда, когда они принадлежат
одному и тому же классу.
a ~ b
Отношение эквивалентности рефлексивно,
симметрично и транзитивно.
Теорема![]() .
.
Если по какому-нибудь признаку между
элементами множества M
установлено отношение эквивалентности,
то оно полностью определяет разбиение
множества M на классы
попарно эквивалентных элементов. При
этом для каждой пары элементов a
и b из M
имеет место одно, и только одно, из
отношений: либо a ~
b, либо элемент a
не эквивалентен элементу b.
Доказательство.
Обозначим класс элементов эквивалентных
элементу a через K(a).
Тогда элементы одного и того же класса
будут попарно эквивалентны.
![]()

b ~ a
![]()
c ~ a
![]()
b ~ c
Если некоторый элемент
![]() эквивалентен
эквивалентен
некоторому элементу![]() ,
,
то он принадлежит этому классу.
![]() d
d
~ b
![]()
b ~ a
![]()
d ~ b
![]()
d ~ a
Пусть
![]() ,
,
то
![]()
покажем это.
Предположим, что есть элемент
![]()
и
![]() d
d
~ a и d
~ c![]() c
c
~ a![]()
![]() ,
,
что противоречит выбору c.
Построенные классы исчерпывают все
множество M, т.к. каждый
элемент a из M
принадлежит некоторому классу K(a).
Любые два класса K(a)
и K(b)
либо не пересекаются, либо совпадают.
Следствие.
K(a)
= K(b)
![]() a
a
~ b
Если множество M, в
котором определены алгебраические
операции, разбито на классы попарно
эквивалентных элементов, то эти же
операции можно определить и во множестве
K этих классов.
Если a
+ b = c
и ab
= d, то
K(a)
+ K(b)
= K(c)
K(a)
K(b)
= K(d)
Метод разбиения множества M
на классы используем в дальнейшем для
построения различных числовых систем.
Для построения же исходного множества
M каждый раз будем
использовать элементы ранее построенных
множеств, начиная с множества натуральных
чисел N, которое считаем
уже построенным.
Лекция 5
Схема изучения любых числовых систем:
- Введение. Запись и чтение числа.
- Сравнение чисел.
- Действия.
- Законы действий.
I. На этапе введения новых чисел рассматриваем:
а) мотивацию изучения новых чисел.
Мотивация может быть:
- арифметической (натуральные числа появились при счете предметов);
- геометрическая (дробные числа возникают при разбиении геометрической фигуры или предмета на равные части);
- измерительной (десятичные дроби требуются, когда мерка не укладывается целое число раз, поэтому ее разбивают на 10 равных частей);
- алгебраической (отрицательные числа возникают при решении уравнения , );
б) чтение и запись новых чисел. Здесь наибольшая трудность возникает при изучении обыкновенных и десятичных дробей. В первом случае нужно разъяснительная работа, объясняющая смысл числителя и знаменателя. Продумать и организовать работу по правильному прочтению числителя. Для облегчения чтения десятичных дробей удобно использовать разрядную таблицу;
в) изображение новых чисел на числовом прямой. Впервые с таким изображением ученики сталкиваются при изучении натуральных чисел, а затем повторяем умение изображать числа в течение всего курса изучения новых числовых систем;
г) при введении новых чисел следует выделять как общие (существенные), так и частные (несущественные) признаки этих чисел. Так наличие « , » дробление каждой разрядной единицы на десять равных частей — это существенные признаки десятичных дробей, а количество знаков после запятой или отсутствие целой части это не существенные.
д) для лучшего понимания и усвоения новых чисел нужна работа по представлению этих чисел на разных языках: словесном (определение), символическом (запись), образном (по геометрической картине или разрядной таблице суметь записать число), предметом (отрежьте 0.5 пластинки);
е) показать связь новых чисел со старыми.
II. При изучении сравнения, рассматриваются как общие способы сравнения, так и частные. К общим способам сравнения относятся:
1) способ сравнения чисел с помощью числовой прямой;
2) сравнение чисел через их разность.
К частным случаям сравнения относятся те специальные правила, которые сформулированы в школьных учебниках.
При изучении сравнения нельзя забывать вопрос о равенстве чисел.
III. Особое внимание при введении операций уделяем «сложению» и «умножению», так как смысл этих операций раскрывается не через определение. «Вычитание» и «деление» при изучении любых числовых систем, рассматриваются как операции, обратные к «сложению» и «умножению».
При изучении операций надо придерживаться следующей последовательности шагов:
1) мотивация;
2) составление алгоритма;
3) обоснование алгоритма;
4) отработка отдельных шагов;
5) рассмотрение всех частных случаев и частных ситуаций;
6) специальная работа по предотвращения ошибок;
7) обучение контролю при вычислении той или иной операции;
8) закрепление.
На этапе мотивации предлагается задача, которая не только показывает необходимость изучения операции, но и разъясняет ее смысл. Так при изучении умножения десятичных дробей показываем, что старое определение умножения через сложение, как это было при изучении умножения натуральных чисел, уже не годится. Смысл умножения 0,3 на 0,4 можно показать через нахождение площади прямоугольника, со сторонами 0,3 дм и 0,4 дм.
На этапе введения алгоритма решают поставленную на 1-ом этапе задачу, переведя новые числа в старые, так задача про прямоугольник может быть решена не в дм, а в см, т.е. мы свели задачу к натуральным числам. Полученный результат переводят в новые числа и стараются подметить закономерность перехода от условия к заключению без обращения к старым числам. В рассмотренном примере ставится проблема, как получить 0,12, используя 0,3 и 0,4. Заканчивается эта работа формулировкой алгоритма выполнения нужного действия. Все алгоритмы начинаются со слова «чтобы».
На этапе обоснования определяют те математические утверждения, которые лежат в основе рассматриваемого алгоритма.
Этап отработки отдельных шагов алгоритма определяется методикой формирования умений. Задача учителя – выделить те шаги, которые стоит только повторить, так как они были сформированы ранее, и те шаги, которые следует специально отработать. Так при изучении умножения десятичных дробей предлагаются упражнения, где известны множители, а произведение записано без « , ». Ученикам следует определить, где поставить « , » и почему. Удобно предлагать и обратные задания, когда « , » потерялась в множителях.
На этапе рассмотрения частных случаев основная цель состоит в усвоении последовательности шагов алгоритма, демонстрации всего поля применения алгоритма. Например, стоит продемонстрировать усовершенствованные алгоритмы: правило умножения на 10,100,1000, на 0,1; 0,01; 0,01…
На этапе специальной работы по предотвращения ошибок учитель на специальных упражнениях учит находить ошибки в выполнении той или иной операции, объясняет причину их возникновения. Очень полезно каждому учителю иметь справочник типичных ошибок.
На этапе обучения контролю учитель предлагает задания, обучающие ученика различным способам контроля, обобщает полученные результаты, выделяя эти способы контроля. Так при выполнении операции для проверки пользуются обратными операциями, прикидкой результатов, проверкой результатов по смыслу.
На этапе закрепления используют упражнения для тренажа (дидактические игры); упражнения дифференцированного характера (по сложности); обязательно решаются текстовые задачи с использованием изученной операции.
IV. К законам действий относятся сочетательный, переместительный и распределительный законы. К свойствам действий относятся специальные правила, например, как вычесть из числа сумму 2-х чисел.
