Как составить цепь по графу

Пути. Циклы. Цепи в графах

Пусть
G = (V, E)
некоторый граф. Путем
(маршрутом)
в графе G, соединяющим
вершины v₁
и v_n, называется
любая чередующаяся последовательность
вершин и ребер вида v₀,e
₀,v₁,e₁,v₂,e
₂…v_n-1,e
_n-1,v_n,
в которой каждое ребро e_i
инцидентно вершинам v_i
и v_i+1.

Путь
называется замкнутым,
если его начальная и
конечная вершины совпадают.

Путь
называется цепью,
если все его ребра
различны.

Цепь
называется простой,
если все ее вершины
различны.

Замкнутая
цепь называется циклом.

Цикл
называется простым,
если его вершины не
повторяются.

Вот
схематическое изображение простого
цикла:

А
вот схематическое изображение цикла,
не являющегося простым:

Для
пути v₀,
e ₀ ,v₁,
e₁ ,
….v_n число
ребер n называется
длиной пути.

Две
вершины графа могут быть связаны
некоторым путем: их называют связанными.
Например, в графе

a₁

a₂
a₃
.
a₄

a₅

вершины
a₃
и a₅
связаны (путем
),
а вершины a₄
и a₁
нет.

Простой
граф – это граф, не содержащий петель
и кратных ребер.

Граф называется
связным,
если для любой пары его вершин существует
соединяющая их простая цепь. Т.о. граф
связен, если из любой его вершины можно
прийти к любой другой. Таким образом,
выше приведен пример графа несвязного.
Связной
компонентой
графа называется такой его подграф,
который является сам по себе графом
связным и при этом совпадающим с любым
другим содержащим его связным подграфом.
Таким образом, связный граф обладает
единственной связной компонентой – это
он сам. А вот пример графа с тремя связными
компонентами (имена вершин не имеют
значения):

Компонентой
связности графа называется максимальный
(по числу вершин и ребер) связный подграф
этого граф.

Каждый
граф или сам является компонентой
связности или распадается на компоненты.
Граф, содержащий хотя бы две компоненты
связности, называется несвязным.
Связный граф состоит из одной компоненты
связности.

Граф
называется эйлеровым,
если он содержит цикл, проходящий через
все ребра этого графа по одному разу.
Такой цикл называется эйлеровым
циклом.

Вот
пример эйлерова графа:

А
вот пример графа, не являющегося
эйлеровым:

Обходы
графа

Во
многих задачах, решаемых с использованием
графов, требуется проложить маршрут от
одной вершины графа к другой или обойти
все его вершины, учитывая те или иные
ограничения.

Смысл
такой задачи на интуитивном уровне
ясен, но требуется уточнить понятия,
используемы при решении подобного рода
задач.

Прежде
всего, уточним термины “маршрут”,
“цепь”, “цикл” и “путь”.
Эти четыре понятия находятся в следующем
соотношении: пути и циклы – это особые
виды цепей, цепь – особый вид маршрута.

Маршрут
– это последовательность вершин и ребер
графа, следуя по которым, можно попасть
из одной его вершины в другую.

Цепь
– это маршрут без повторяющихся
ребер.

Путь
– это цепь, все вершины которой (за
исключением, быть может, начальной и
конечной) различны.

Цикл
– это цепь, у которой совпадают начальная
и конечная вершины, а все остальные
различны.

Пример.

Можно
составить следующие маршруты
из А в С в графе G:

М1:
А – е1 – В – е3 – С (путь);

М2:
А – е2 – Е – е6 – Д – е7 – Д – е6 – Е – е5
– С (не цепь);

М3:
А – е1 – B – е3 – C
– е5 – Е – е4 – С (цепь, но не путь).

Циклы:

А
– е1 – В – е3 – С – е4 – Е – е2 – А;

Е
– е4 – С – е5 – Е;

Д
– е7 – Д.

Граф
называют связным,
если из каждой его вершины существует
путь в любую другую его вершину. Граф,
рассмотренный в примере, является,
связным. Если удалить из него ребро , то
он потеряет связность и распадется на
компоненты: одна из компонент будет
содержать вершину Д и петлю , вторая
компонента – вершины А,В,С,Е, связанные
между собой всеми оставшимися ребрами.

Для
представления данных в алгоритмах на
дискретных структурах часто используются
графы, которые называются деревьями.

Деревом
называют связный неорграф, не содержащий
циклов.

На
рис. 6.8 показано, так называемое, корневое
дерево. Одна из вершин
корневого дерева (вершина 1) выделена,
ее называют корнем
дерева. Оставшиеся
вершины разбиты на поддеревья
(поддерево с вершинами 2,5,6 и поддерево
4,7,8,9). Вершины 5,6,3,7,8,9 называют листьями
дерева. Несвязный
неорграф, компонентами которого являются
деревья, называют лесом.

Если
граф связный, но не является деревом, в
нем всегда можно выделить часть,
включающую все вершины и образующую
дерево. Такую часть графа называют
остовом графа.
Если граф несвязен, то можно превратить
в дерево каждую его компоненту. Полученная
совокупность деревьев носит название
остовного леса.

Вообще
говоря, в графе можно выделить несколько
различных остовов. Каждый из них будет
являться деревом, включающим все вершины
графа, а следовательно, число ребер
любом из остовов будет на единицу меньше
числа вершин графа. Если выделен
какой-либо остов, то все ребра графа, не
вошедшие в этот остов, образуют коостов,
соответствующий данному остову.

Остовным
деревом связного графа G
называется любой его подграф, содержащий
все вершины графа G и являющийся деревом.

Пусть
G связный
граф. Тогда остовное дерево графа G
(если оно существует) должно содержать
n(G) – 1 ребер.
Таким образом, любое остовное дерево
графа G есть
результат удаления из G
ровно m(G)-(n(G)-1)=m(G)-n(G)+1
ребер.

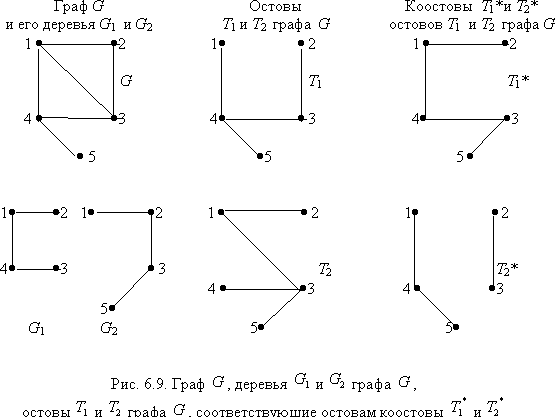
На
рис. 6.9 показан пример выделения деревьев,
остовов и коостовов из графа .

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Урок 7. Основы составления электрических схем

Здравствуйте, друзья! Сегодня мы рассмотрим один из этапов проектирования электрических устройств – составление электрических схем. Однако рассматривать их мы будем очень поверхностно, поскольку многое из того, что необходимо для проектирования, нам еще неизвестно, а минимальные знания уже необходимы. Тем не менее, эти начальные знания помогут нам в дальнейшем при чтении и составлении электрических схем. Тема довольно скучная, но правила есть правила и их необходимо соблюдать. Итак…

Что же такое электрическая схема? Какие они бывают? Зачем нужны? Как их составлять и как их читать? Начнем с того, какие же вообще схемы существуют. Для того, чтобы унифицировать составление технической документации (а схемы есть ни что иное, как часть этой документации) в нашей стране, Постановлением Государственного комитета СССР по стандартам от 29 августа 1984 г. № 3038 был введен Государственный Стандарт (ГОСТ) «Единая система конструкторской документации. Схемы. Виды и типы. Общие требования к выполнению», иначе именуемый ГОСТ 2.701-84, которому должны подчиняться любые схемы, выполненные вручную или автоматизированным способом, изделий всех отраслей промышленности, а также электрические схемы энергетических сооружений (электрических станций, электрооборудования промышленных предприятий и т. п.). Этим документом определены следующие виды схем:

• электрические;
• гидравлические;
• пневматические;
• газовые (кроме пневматических);
• кинематические;
• вакуумные;
• оптические;
• энергетические;
• деления;
• комбинированные.

Нас в первую очередь будет интересовать самый первый пункт – электрические схемы, которые составляются для электрических устройств. Однако ГОСТ определено так же несколько типов схем в зависимости от основного назначения:

• структурные;
• функциональные;
• принципиальные (полные);
• соединений (монтажные);
• подключения;
• общие;
• расположения;
• объединенные.

Сегодня мы рассмотрим электрические принципиальные схемы и основные правила их составления. Остальные виды схем имеет смысл рассматривать после того, как будут изучены электрические компоненты, и обучение подойдет к этапу проектирования сложных устройств и систем, тогда другие виды схем будут иметь смысл. Что же такое электрическая принципиальная схема и зачем она нужна? Согласно ГОСТ 2.701-84 схема принципиальная – схема, определяющая полный состав элементов и связей между ними и, как правило, дающая детальное представление о принципах работы изделия (установки). Такие схемы, например, поставлялись в документации к старым советским телевизорам. Это были огромные листы бумаги формата А2 или даже А1, на которых указывались абсолютно все составляющие телевизора. Наличие такой схемы существенно облегчало процесс ремонта. Сейчас такие схемы практически не поставляются с электронными приборами, потому как продавец надеется, что пользователю проще будет выкинуть прибор, чем его ремонтировать. Такой вот маркетинговый ход! Но это уже тема для отдельного разговора. Итак, принципиальная схема устройства необходима, во-первых, для того, чтобы иметь представление о том, какие элементы входят в состав устройства, во-вторых, как эти элементы соединены между собой и, в-третьих, какие характеристики имеют эти элементы. Так же, согласно ГОСТ 2.701-84 принципиальная схема должна давать понимание принципов работы устройства. Приведем пример такой схемы:

Рисунок 7.1 – Усилительный каскад на биполярном транзисторе, включенном по схеме с общим эмиттером, с термостабилизацией рабочей точки. Схема электрическая принципиальная

Однако перед нами встаёт небольшая проблема: а никаких, собственно, электронных элементов мы и не знаем… Что, например, за прямоугольники или параллельные черточки нарисованы на рисунке 7.1? Что обозначают надписи C2, R4, +Eпит? Рассмотрение электронных компонентов мы начнём через урок и постепенно узнаем основные характеристики каждого из них. И обязательно изучим принцип работы этого устройства с таким страшным названием по его принципиальной схеме. Сейчас же мы изучим основные правила рисования принципиальных электрических схем. Вообще правил много, но в основном они направлены на увеличение наглядности и понятности схемы, поэтому со временем запомнятся. Знакомиться с ними будем по мере необходимости, чтобы сразу не забивать голову лишней, пока не нужной информацией. Начнём с того, что каждый электрический компонент на электрической схеме обозначается соответствующим условным графическим обозначением (УГО). УГО элементов мы будем рассматривать параллельно с самими элементами, либо вы можете сразу посмотреть их в ГОСТ 2.721 – 2.768.

Правило 1. Порядковые номера элементам (устройствам) следует присваивать, начиная с единицы, в пределах группы элементов (устройств), которым на схеме присвоено одинаковое буквенное позиционное обозначение, например, R1, R2, R3 и т.д., C1, C2, С3 и т.д. Не допускается пропуск одного или нескольких порядковых номеров на схеме.

Правило 2. Порядковые номера должны быть присвоены в соответствии с последовательностью расположения элементов или устройств на схеме сверху вниз в направлении слева направо. При необходимости допускается изменять последовательность присвоения порядковых номеров в зависимости от размещения элементов в изделии, направления прохождения сигналов или функциональной последовательности процесса.

Правило 3. Позиционные обозначения проставляют на схеме рядом с условными графическими обозначениями элементов и (или) устройств с правой стороны или над ними. Кроме того, не допускается пересечение позиционного обозначения линиями связи, УГО элемента или любыми другими надписями и линиями.

Правило 4. Линии связи должны состоять из горизонтальных и вертикальных отрезков и иметь наименьшее количество изломов и взаимных пересечений. В отдельных случаях допускается применять наклонные отрезки линий связи, длину которых следует по возможности ограничивать. Пересечение линий связи, которого не удаётся избежать, выполняется под углом 90°.

Правило 5. Толщина линий связи зависит от формата схемы и размеров графических обозначений и выбирается из диапазона 0.2 – 1.0мм. Рекомендуемая толщина линий связи – 0.3 – 0.4мм. В пределах схемы все линии связи должны быть изображены одинаковой толщины. Допускается использование нескольких (не более трех) различных по толщине линий связи для выделения функциональных групп в пределах изделия.

Правило 6. Условные графические обозначения элементов изображают на схеме в положении, в котором они приведены в соответствующих стандартах, или повернутыми на угол, кратный 90°, если в соответствующих стандартах отсутствуют специальные указания. Допускается условные графические обозначения поворачивать на угол, кратный 45°, или изображать зеркально повернутыми.

Правило 7. При указании около условных графических обозначений номиналов элементов (резисторов, конденсаторов) допускается применять упрощенный способ обозначения единиц измерения:

Правило 8. Расстояние между линиями связи, между линей связи и УГО элемента, а так же краем листа должно быть не менее 5мм.

Для начала этих восьми правил вполне достаточно, чтобы научиться правильно составлять простые электрические принципиальные схемы. В уроке 5 мы рассматривали источники питания электрических схем, в частности, «сухие» элементы и аккумуляторные батареи, а в уроке 6 была рассмотрена лампа накаливания в качестве потребителя электрической энергии. Давайте исходя из описанных выше правил попробуем составить простейшую принципиальную схему, состоящую из трех элементов: источника (аккумуляторная батарея), приемника (лампа накаливания) и выключателя. Но сначала приведем УГО этих элементов:

А теперь последовательно включим эти элементы, собрав электрическую цепь:

Рисунок 7.4 – Первая принципиальная электрическая схема

Контакт SA1 называется нормально разомкнутым контактом, потому что в изначальном положении он разомкнут и ток через него не течет. При замыкании SA1 (например, это может быть выключатель, которым мы все зажигаем дома свет) лампа HL1 загорится, подпитываясь энергией батареи GB1, и гореть она будет до тех пор, пока не разомкнется ключ SA1, либо не кончится заряд аккумулятора.
Данная схема абсолютно точно и наглядно показывает последовательность соединения элементов и тип этих элементов, что исключает ошибки при сборке устройства на практике.
На сегодня пожалуй всё, еще один ужасно скучный урок на этом закончен. До скорых встреч!

Комментарии:

А оно тебе это надо все запоминать главное не теория, а практика.

Soglasen s Evgeniem. Praktika — samoe glavnoe! Odnako bez znaniya hot’ maleyshey bazi teorii praktika — bessmislenna.

Источник

Метод сигнальных графов в электротехнике (ТОЭ) — формулы и определения с примерами

Метод сигнальных графов

Общие представления о сигнальных графах:

Решение уравнения электрического равновесия сложных цепей даже в численной форме весьма трудоемко. Задача анализа цепи становится особенно сложной тогда, когда неизвестные токи и напряжения или комплексные частотные характеристики должны быть найдены в виде аналитических соотношений. В этих случаях весьма полезным может оказаться применение метода сигнальных графов, который позволяет упростить решение уравнений электрического равновесия линейных электрических цепей в аналитическом виде (символьной форме).

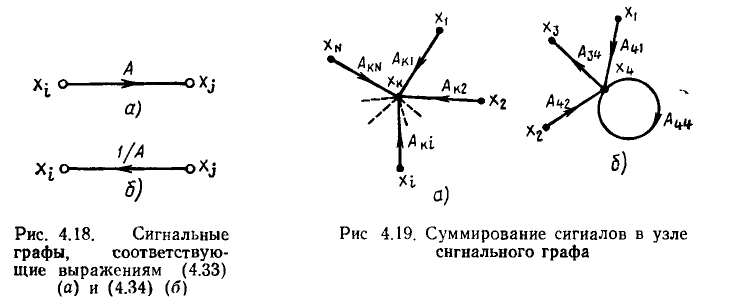
Как известно, сигнальный граф, или направленный граф прохождения сигналов, представляет собой наглядное графическое изображение системы уравнений, описывающей процессы в электрической цепи. Узлы (вершины) такого графа соответствуют входящим в эту систему неизвестным величинам (токам и напряжениям ветвей, контурным токам, узловым напряжениям) и величинам, характеризующим внешние воздействия на цепь (токам независимых источников тока, э. д. с. независимых источников напряжения, контурным э. д. с., узловым токам). Ветви сигнального графа отображают причинно-следственные связи между величинами, соответствующими отдельным узлам. В рамках метода сигнальных графов эти величины называются сигналами. Каждой ветви сигнального графа приписывается определенное направление и присваивается весовой коэффициент, который называется передачей ветви. Узлы сигнального графа обозначают теми же буквами, что и соответствующие узлам величины; направления ветвей показывают стрелками, около которых указывают передачу ветви.

Если ветвь с передачей А направлена от узла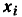

следовательно, при прохождении через ветвь сигнал умножается на передачу ветви. Разрешим уравнение (4.33) относительно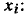

Сигнальный граф, соответствующий этому уравнению (рис. 4.18,6), будет отличаться от сигнального графа, соответствующего уравнению (4.33), направлением и передачей ветви. Таким образом, вид сигнального графа зависит от того,

относительно какой из величин разрешено заданное уравнение, т. е. от того, какая из величин рассматривается как причина, а какая — как следствие.

Если в узле 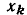сходится несколько ветвей (рис. 4.19, а), то значение сигнала в этом узле будет равно сумме сигналов всех входящих в него ветвей:

где N — число ветвей, направленных к узлу — передача ветви, направленной от узла к узлу 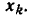Ветви, направленные от узла 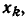на сигнал в этом узле не влияют и при подсчете 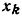не учитываются. В число ветвей, направленных к рассматриваемому узлу, могут входить и ветви, начинающиеся в данном узле (рис. 4.19, б). Такие ветви называются петлями. Значение переменной в узле, к которому подключена одна или несколько петель, находится по общему правилу (4.35), например (на рис. 4.19,6)

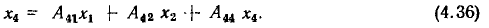
Из выражения (4.36) видно, что при наличии петель, подключенных к какому-либо узлу, переменная, соответствующая этому узлу, входит и в левую, и в правую часть уравнения (4.35).

Рассмотрим некоторые понятия, относящиеся к сигнальным графам.

Истоком называется узел сигнального графа, от которого направлены все примыкающие к нему ветви. Узел сигнального графа, к которому направлены все примыкающие к нему ветви, называется стоком. Узлы, которые имеют как входящие, гак н исходящие ветви, называются смешанными. Например, в графе (рис. 4.18, а) узел 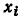— исток, узел 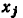— сток; в графе (рис. 4.19, 6) узлы 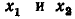— истоки, узел 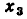— сток, узел 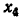— смешанный.

Если сигнал, соответствующий некоторому узлу сигнального графа, не выражается через сигналы других узлов, то такой узел является независимым. Если сигнал, соответствующий какому-либо узлу, выражается через сигналы других узлов, то такой узел является зависимым. К независимым узлам относятся истоки, к зависимым—стоки и смешанные узлы Очевидно, что уравнения вида (4.35) могут быть составлены только для зависимых узлов.

В сигнальном графе (рис. 4.20) узлы 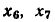— истоки, узел 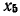— сток, узлы 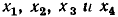относятся к смешанным. Для зависимых узлов 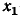— 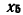можно составить систему уравнений

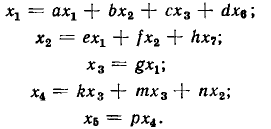
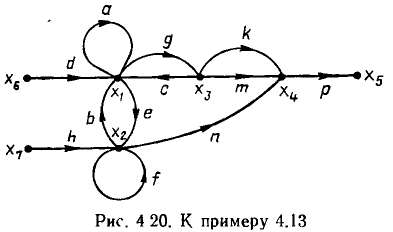
Путь между узлами 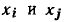сигнального графа — это непрерывная последовательность однонаправленных ветвей, связывающая узел 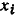с узлом 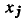и проходящая через каждый узел графа не более одного раза. Произведение передач ветвей, образующих путь между узлами 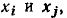называется передачей пути 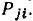Так, между узлами 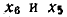сигнального графа (рис. 4.20) можно указать три пути с передачами 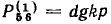(ветви d, g, k и р), 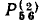=dgmp и 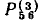= denp. Последовательность ветвей d, с, m и р не образует пути от вершины 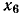к вершине 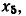так как направление ветви с не совпадает с направлением пути.

Замкнутый путь, который начинается н заканчивается в одном узле, называется контуром. Очевидно, что петля есть частный вид контура, в который входит одна ветвь. Произведение передач всех ветвей, входящих в j-й контур, называется передачей контура 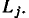На рис. 4.20 можно выделить четыре контура с передачами = be (ветви b и е), = gc (ветви g и с), = а (петля а) и = f (петля f). Ветви k и m не образуют контура, так как они не представляют собой замкнутой последовательности однонаправленных ветвей. Такие ветви называются параллельными.

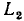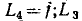Два контура или контур и путь называются соприкасающимися, если они имеют общие узлы. Если два контура или контур и путь не имеют общих узлов, то они являются несоприкасающимися. На рисунке контуры с передачами =gc и = a и 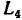=f являются иесоприкасающимися, а контуры с передачами 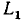= be и 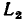= gc, 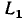= be и 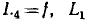= be и 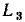= а — соприкасающимися. Контур с передачей 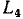= f не соприкасается с путями 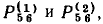но соприкасается с путем 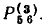Как видно из примера 4.13, каждому сигнальному графу можно однозначным образом поставить в соответствие систему линейных алгебраических уравнений, составленных относительно сигналов зависимых узлов.

Для решения обратной задачи — построения сигнального графа, соответствующего заданной системе уравнений, эта система уравнений должна быть приведена к причинно-следственной форме, т. е. каждое из входящих в систему уравнений должно быть разрешено относительно одной из переменных (различных для каждого из уравнений). Далее, определяется общее число узлов графа N, которое равно сумме числа неизвестных переменных и числа ненулевых свободиых членов уравнений. Построение сигнального графа начинается с нанесения точек, соответствующих его узлам. Затем узлы графа, в соответствии с системой уравнений, приведенной к причинно-следственной форме, соединяются между собой ветвями так, чтобы сумма сигналов всех ветвей, сходящихся в каждом узле, равнялась бы значению сигнала этого узла.

Хотя свойства сигнального графа не зависят от формы и длины ветвей, а также от взаимного расположения узлов графа на плоскости чертежа, с целью повышения наглядности рекомендуется истоки располагать в левой части чертежа, стоки — в правой, а остальные узлы — между ними.

В связи с тем что одну н ту же систему уравнений можно различными способами привести к причинно-следственной форме, каждой системе уравнений можно поставить в соответствие некоторое множество графов. Различные графы, соответствующие одной и той же исходной системе уравнений, называются равносильными. Рассмотрим несколько примеров построения графов, соответствующих заданной системе уравнений.

Построим сигнальный граф, соответствующий системе уравнений

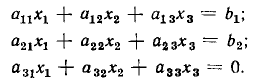
Приведем данную систему уравнений к причинно-следственной форме, для чего разрешим первое уравнение относительно 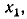второе — относительно 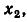а третье — относительно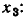

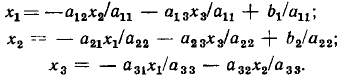
Число независимых переменных в этой системе уравнений равно трем, число ненулевых свободных членов — двум, следовательно, общее число узлов сигнального графа равно пяти. Располагая в левой части чертежа независимые узлы, соответствующие свободным членам 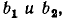а в правой части узлы, соответствующие неизвестным величинам 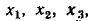и соединяя их ветвями в соответствии с системой уравнений, преобразованной к причинно-следственной форме, получим сигнальный граф, изображенный на рис. 4.21, а.

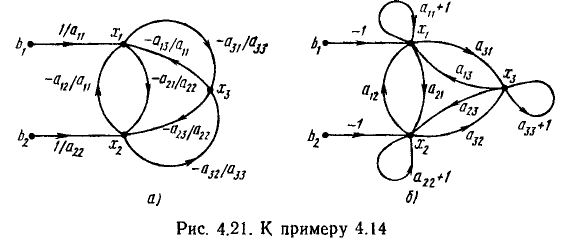
Исходная система уравнений может быть приведена к причинно-следственной форме и другим способом. Прибавляя к правой и левой частям первого уравнения второго 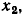третьего 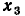и выполняя преобразования, получим

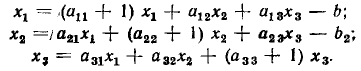
Этой системе уравнений соответствует сигнальный граф, изображенный на рис. 4.21, б.

Графы (рис. 4.21, а, б) имеют различную структуру и передачи ветвей, однако они соответствуют одной и той же исходной системе уравнений и поэтому являются равносильными. Очевидно, что если первое уравнение, входящее в исходную систему, разрешить не относительно 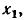а относительно 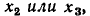то получатся другие варианты представления исходной системы уравнений в причинно-следственной форме, каждому из которых можно поставить в соответствие сигнальные графы, равносильные графам, изображенным на рис. 4.21.

Составим сигнальный граф, соответствующий узловым уравнениям цепи, схема которой приведена на рис. 4.2, а.

Узловые уравнения данной цепи были получены при рассмотрении примера 4.4.

Разрешая первое из уравнений относительно 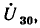а второе — относительно 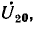получаем

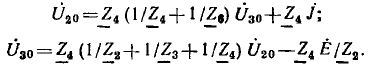
Этой системе уравнений соответствует сигнальный граф, приведенный на рис. 4.22.

Используя метод контурных токов, составим систему уравнений для определения тока 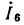цепи, схема которой приведена на рис. 4.2, а. Построим также сигнальный граф, соответствующий этой системе уравнений.

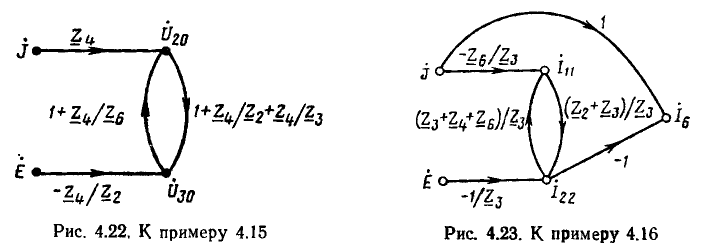
Контурные уравнения рассматриваемой цепи были сформированы при рассмотрении примера 4.3. Дополняя эти уравнения соотношением, связывающим ток с контурными токами получаем

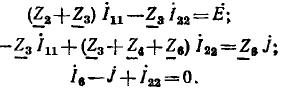
Разрешим каждое из этих уравнений относительно одной из неизвестных величин:

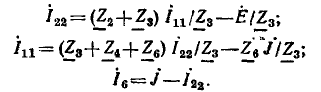
Этой системе уравнений соответствует сигнальный граф, изображенный на рис. 4.23.

Преобразования сигнальных графов

Используя правила построения сигнальных графов, соответствующих заданной системе уравнений, можно убедиться, что каждому равносильному преобразованию исходной системы уравнений соответствует некоторое преобразование сигнального графа и, наоборот, каждому преобразованию сигнального графа соответствует определенное преобразование исходной системы уравнений. На практике оказывается, что преобразования сигнальных графов выполняются проще и в более наглядной форме, чем преобразование соответствующих им уравнений. Поэтому при анализе цепей во многих случаях преобразование уравнений электрического равновесия заменяется преобразованием соответствующих сигнальных графов

Рассмотрим основные преобразования сигнальных графов.

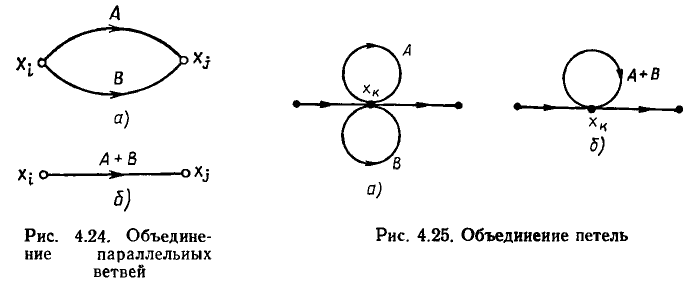
Объединение параллельных ветвей. Две параллельные ветви с передачами А и В могут быть заменены одной ветвью с передачей А + В. Действительно в соответствии с рис. 4.24, а сигнал в узле, к которому сходятся ветви с передачами А и В, исходящие из узла будет равен

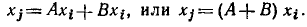
Последнему уравнению соответствует сигнальный граф, имеющий одну ветвь с передачей А + В, направленную от узла 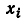к узлу 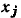(рис. 4.24, б). Правило объединения параллельных ветвей обобщается на любое число параллельно включенных ветвей, его можно применять для объединения петель, подключенных к одному узлу (рис. 4.25).

Объединение последовательности однонаправленных ветвей. Две последовательно включенные однонаправленные ветви с передачами А и В могут быть заменены одной ветвью с передачей АВ.

Действительно, графу, приведенному на рис. 4.26, а может быть поставлена в соответствие система уравнений

Исключая из (4.37) переменную 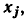получаем

Уравнению (4.38) соответствует сигнальный граф, содержащий одну ветвь с передачей АВ (рис. 4.26, б). Рассмотренное преобразование представляет собой частный случай устранения смешанного узла сигнального графа.

Устранение промежуточного узла. Смешанный узел, к которому подключено несколько не образующих контуров ветвей, причем только одна из ветвей направлена к узлу (рис. 4.27, а) или только одна из ветвей направлена от узла (рис. 4.27, в), называется промежуточным.

Для устранения промежуточного узла первого типа, в которой входит только одна ветвь, составим систему уравнений

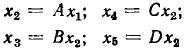
и исключим из нее переменную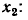

Системе уравнений (4.39) соответствует граф, не содержащий промежуточного узла 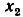(рис. 4.27, б). Аналогичным образом устраняется промежуточный узел, в который входит несколько ветвей, а выходит только одна (рис. 4.27, г).

Устранение контура. Сигнальному графу, изображенному на рис. 4.28, а, может быть поставлена в соответствие система уравнений

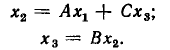
Подставляя первое из этих уравнений во второе, получаем

Уравнению (4.40) соответствует преобразованный граф, приведенный на рис. 4.28, б.

Исключение петли. Исключение петли с передачей А, подключенной к какому-либо узлу сигнального графа, сопровождается умножением передач ветвей, входящих в этот узел, на 1/(1 — А).

Действительно, для сигнального графа, приведенного на рис. 4.29, а, можно составить систему уравнений

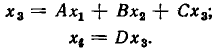
Приводя в первом из этих уравнений подобные члены н разрешая его относительно 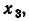получаем

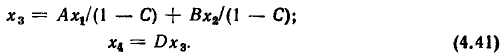
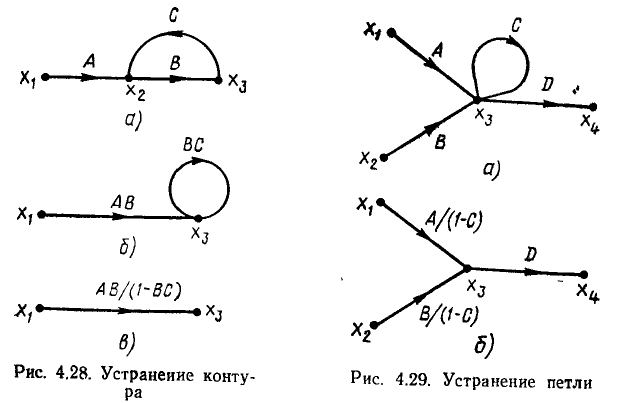
Как видно из соответствующего системе уравнений (4.41) сигнального графа (рис. 4.29, б), после устранения петли передачи ветвей, входящий в узел 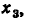оказались умноженными на 1/(1-С), а передача ветви, выходящей из узла осталась без изменения.

Применяя операцию устранения петли, преобразовавшей граф (см. рис. 4.28, б) можно заменить одной ветвью (см. рис. 4.28, в).

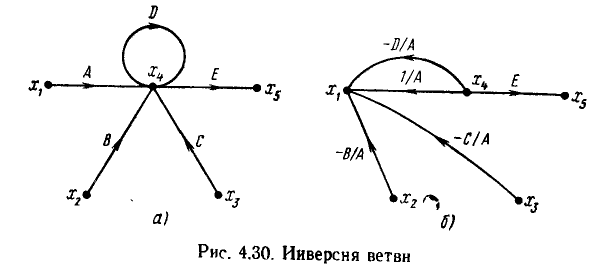
Инверсия (изменение направления) ветви. Рассмотрим некоторый граф (рис. 4.30, а), которому соответствует система уравнений

Пусть необходимо изменить направление какой-либо ветви, например, направленной из вершины в вершину С этой целью разрешим первое из уравнений (4.42) относительно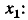

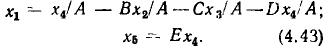
Системе уравнений (4.43) соответствует сигнальный граф, изображенный на рис. 4.30, б. Как видно из сравнения рис. 4.30, а и б, инвертирование ветви, направленной от узла 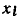к узлу 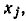сопровождается изменением передач и точек подключения всех ветвей, ранее направленных к узлу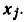

Ветвь с передачей А, направленная от узла 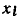к узлу 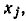заменяется направленной от узла 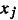к узлу 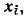с передачей l/А. Все ветви, ранее направленные к узлу 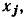заменяются ветвями, направленными к узлу 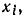передачи этих ветвей умножаются на —1/А. Ветви, не направленные ранее к узлу 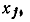при инвертировании ветви, направленной к 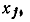остаются без изменений.

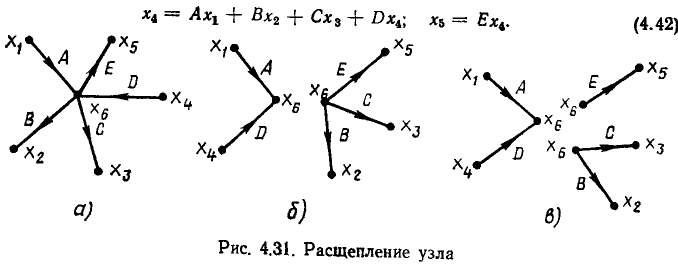
Расщепление узла. В связи с тем что сигнал в каждом узле сигнального графа определяется только сигналами входящих в него ветвей, любой узел сигнального графа может быть расщеплен на два узла: один — содержащий все ветви, направленные к узлу, другой — направленные от узла. Так, узел 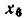графа, изображенного на рис. 4.31, а, может быть расщеплен на два узла (рис. 4.31, б). Узел, который содержит только исходящие из него ветви (исток), может быть расщеплен на произвольное количество узлов, не превышающее числа исходящих из него ветвей (рис. 4.31, в).

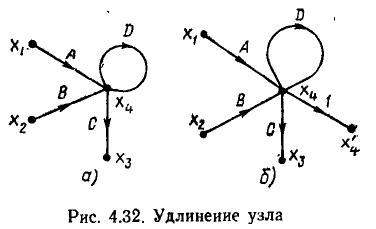
Удлинение узла. В ряде случае возникает необходимость во введении в сигнальный граф дополнительного узла, сигнал в котором совпадает с сигналом в одном из узлов 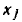сигнального графа. Такая операция называется удлинением узла 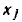. Для удлинения узла 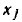этот узел должен быть соединен с вновь вводимым узлом 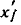ветвью, передача которой равна единице. Например,

для удлинения узла (рис. 4.32, а) введем новый узел 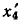и соединим его с узлом 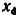ветвью, передача которой равна единице (рис. 4.32, б).

Совместное проведение описанных преобразований позволяет, как правило, существенно упростить структуру сигнального графа. Конечной целью преобразований обычно является получение наиболее простого графа, не допускающего дальнейших упрощений. Такой граф называется конечным. Конечный граф не содержит смешанных узлов, а включает в себя только стоки и истоки.

Упростим сигнальный граф, изображенный на рис. 4.23. Для этого последовательно исключим контур (рис. 4.33, а), петлю (рис. 4.33, б), промежуточный узел (рис. 4.33, в) и объединим параллельные ветви (рис. 4.33,г). Преобразованный граф, (рис. 4.33, г) не содержит смешанных узлов и не подлежит дальнейшему упрощению. Этот граф является конечным.

Применение сигнальных графов к анализу цепей

Применение метода сигнальных графов при анализе цепей оказывается весьма эффективным в тех случаях, когда требуется определить ток или напряжение только одной из ветвей цепи, а также найти ее комплексные частотные характеристики.

Как отмечалось, используя различные преобразования, исходный сигнальный граф можно привести к конечному. Если истоками графа являются узлы, сигналы которых 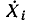есть комплексные изображения величин, характеризующих внешние воздействия на зажимах i—i’, а стоками — узлы, сигналы которых 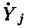представляют собой комплексные изображения искомых токов или напряжений ветвей, подключенных к зажимам j—j’, то, используя конечный граф, можно записать соотношения, в явной форме выражающие зависимость искомых неизвестных токов и напряжений от величин, характеризующих внешние воздействия. Передача ветви 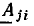конечного графа, связывающей исток 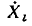со стоком 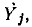будет равна комплексной частотной характеристике цепи 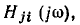измеренной в режиме, когда все источники внешнего воздействия, за исключением 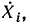выключены.

Трудоемкость преобразования сигнального графа к конечному во многом определяется выбором исходной системы уравнений электрического равновесия и тем, каким образом осуществлен переход от исходной системы уравнений к сигнальному графу. Для уменьшения числа узлов сигнального графа в качестве исходной системы уравнений рекомендуется применять систему уравнений электрического равновесия цепи, составленную по методу узловых напряжений или контурных токов, дополнив ее уравнениями, связывающими искомые токи и напряжения с контурными токами или узловыми напряжениями.

Определим ток 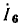цепи, комплексная схема замещения которой приведена на рис. 4.2, а, преобразуя сигнальный граф этой цепи (см. рис. 4.23) в конечный.

Граф, приведенный на рис. 4.23, соответствует контурным уравнениям рассматриваемой цепи, дополненным уравнением, выражающим связь искомого тока с контурными токами 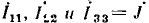(см. пример 4.16). Преобразование этого графа в конечный было проведено в примере 4.17. Непосредственно по виду конечного графа записываем выражение для искомого тока

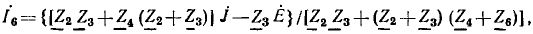
которое совпадает с выражениями для этого тока, полученными с использованием метода наложения (см. пример 4.8) и теоремы об эквивалентном источнике (см. пример 4.12).

Передача ветви, связывающей исток J и сток 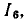равна комплексному коэффициенту передачи цепи по току 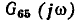от зажимов 5—5′ к зажимам 6—6′ (номера зажимов совпадают с номерами ветвей) в режиме, когда источник 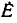закорочен:

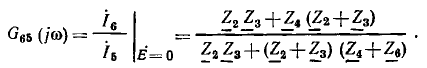
Передача ветви, направленной от истока 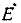к стоку 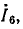равна передаточной проводимости цепи 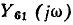в режиме, когда ветвь с источником тока 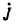разомкнута:

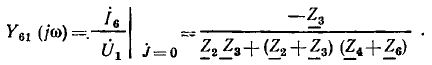
Следует отметить, что сведение исходного сигнального графа к конечному, особенно для сложных цепей, может оказаться трудоемким. Кроме того, если необходимо определить несколько неизвестных величин, эту процедуру приходится выполнять несколько раз. Поэтому в таких случаях для нахождения комплексных частотных характеристик цепи и неизвестных токов и напряжений целесообразно воспользоваться формулой Мейсона, которая позволяет вычислять передачи ветвей конечного графа непосредственно по исходному сигнальному графу, не прибегая к его преобразованиям.

Формула Мейсона имеет вид

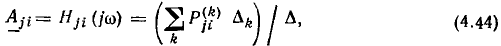
где 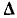— определитель сигнального графа, численно равный определителю исходной системы уравнений; 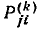— передача k-гo пути от истока 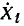к стоку 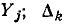— алгебраическое дополнение k-гo пути. Суммирование производится по всем возможным путям из узла 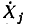в узел 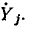Определитель сигнального графа

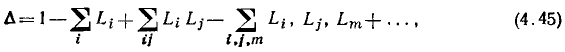
где 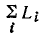—сумма передач всех контуров сигнального графа; 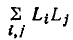— сумма произведений передач всех возможных пар несоприкасающихся контуров; 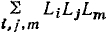—сумма произведений передач всех несоприкасающихся троек контуров и т. д. Алгебраическое дополнение k-гo пути также вычисляется по формуле (4.45), но при этом учитываются только контуры, не касающиеся пути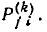

Используя формулу Мейсона, определим передаточную проводимость 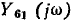цепи, схема которой приведена на рис. 4.2, а).

Сигнальный граф, составленный с использованием контурных уравнений цепи, был приведен на рис. 4.23 (см. пример 4.16). Этот граф содержит единственный контур, передача которого

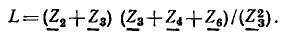
Используя выражение (4.45), найдем определитель сигнального графа

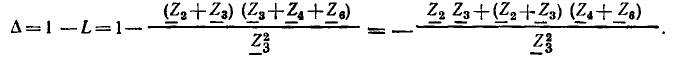
Между узлами существует единственный путь, проходящий по ветвям с передачами — 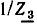и —1. Передача этого пути 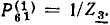Единственный контур сигнального графа имеет общую вершину 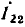с данным путем, поэтому 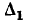= 1.

Подставляя полученные значения 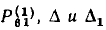в формулу Мейсона, получаем

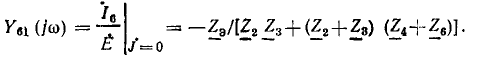
Как и следовало ожидать, это выражение совпадает с выражениями для 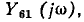полученными другими методами (см. примеры 4.8, 4.12, 4.18).

Используя формулу Мейсона, определим комплексный коэффициент передачи по току 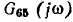цепи, схема которой приведена на рис. 4.2, а.

Сигнальный граф рассматриваемой цепи изображен на рис. 4.23. Выражение для определителя этого графа было получено в примере 4.19. Между узлами 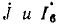существуют два пути с передачами

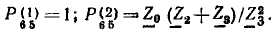
Алгебраическое дополнение первого пути

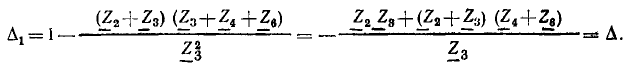
Алгебраическое дополнение второго пути равно единице. Используя формулу Мейсона, находим

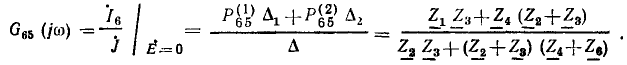
Нетрудно убедиться, что полученное выражение совпадает с выражениями для 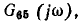найденными другими методами.

Рекомендую подробно изучить предметы:

Электротехника Основы теории цепей

Ещё лекции с примерами решения и объяснением:

• Электрическая ёмкость и ее расчет
• Линейные н нелинейные диэлектрики и конденсаторы
• Сопротивление и его расчет
• Линейные и нелинейные резисторы
• Нелинейные резистивные цепи
• Преобразование схем электрических цепей
• Установившиеся процессы в линейных электрических цепях
• Методы расчета простых электрических цепей

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Содержание:

Топология цепей:

Электрическая схема — это условное графическое изображение электрической цепи. В связи с тем что в теории цепей рассматривают исключительно эквивалентные схемы, в дальнейшем под термином «электрическая схема» или просто «схема» будем понимать именно эквивалентную схему электрической цепи. Схема электрической цепи определяет, таким образом, состав идеализированных активных и пассивных элементов моделирующей цепи, замещающей исследуемую цепь в рамках рассматриваемой задачи, параметры этих элементов и способ их соединения между собой.

Помимо идеализированных активных и пассивных элементов на схемах электрических цепей изображаются также идеализированные вспомогательные элементы: выводы цепи или ее частей, соединительные проводники и элементы коммутации. К элементам коммутации относят элементы, позволяющие изменять количество идеализированных пассивных и активных элементов, их параметры или способ соединения (переключатели, ключи и т. д.). При построении моделирующих цепей и изображении их схем предполагается, что идеализированные вспомогательные элементы не способны запасать электрическую энергию или преобразовывать ее в другие виды энергии, т. е. они не обладают сопротивлением, емкостью или индуктивностью. Поэтому, если реальные вспомогательные элементы электрической цепи характеризуются паразитными параметрами (сопротивлением, емкостью или индуктивностью), значения которых существенны в рамках решаемой задачи, то эти элементы

следует представить их моделирующими цепями, составленными из идеализированных вспомогательных элементов и соответствующих идеализированных пассивных элементов.

Способ изображения .идеализированных активных, пассивных и вспомогательных элементов и их взаимное расположение на схеме не оказывают влияния на характер электрических процессов в исследуемой цепи.

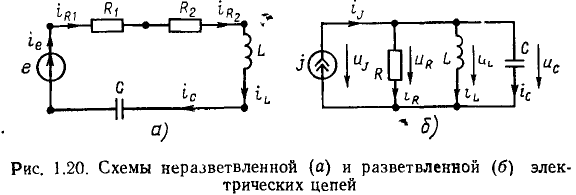
При необходимости на схеме указывают положительные направления токов и напряжений: для токов через внешние выводы цепи или через ее элементы — стрелками непосредственно на соединительных проводниках или выводах (рис. 1.20); для напряжений на отдельных элементах или участках цепи — стрелками между выводами соответствующих элементов или участков цепи (рис. 1.20, б). Положительные направления напряжений на пассивных элементах, а также на идеализированных активных элементах на схемах, как правило, не указывают.

Рядом со стрелками, указывающими положительные направления токов или напряжений, проставляют их условные буквенные обозначения, например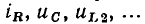

Внешние выводы отдельных участков моделирующей цепи, по аналогии с внешними выводами реальных элементов электрической цепи, называют полюсами. В зависимости от числа полюсов участки Цепей делят на двухполюсники и многополюсники (трехполюсники, четырехполюсники,            N-полюсники). Двухполюсник может состоять из одного или .нескольких идеализированных двух полюсных элементов (см., например, рис. 1.9—1.11) или может вообще не содержать идеализированных активных и пассивных элементов (например, короткозамыкающий двухполюсник или перемычка). Важное значение в теории цепей имеют многополюсники с четырьмя выводами — четырехполюсники (см. далее гл. 8). Отметим, что цепи, моделирующие реальные двухполюсные элементы, всегда являются двухполюсниками, в то время как цепи, моделирующие N-полюсные элементы, могут содержать менее чем N внешних выводов. Например, пятиэлектродным электронным лампам — пентодам, имеющим в зависимости от конструкции 5—7 внешних выводов, соответствуют схемы замещения по переменному току с 3—4 выводами.

В зависимости от характера соединения идеализированных двухполюсных элементов различают неразветвленные и разветвленные цепи. В неразветвленной цепи (рис. 1.20, а) через все элементы протекает один и тот же ток. В разветвленных цепях (рис. 1.20, б и рис. 1.21, а) токи через различные элементы могут быть неодинаковы.

Соединение группы идеализированных двухполюсных элементов, при котором через них протекает один и тот же ток, называется последовательным. Например, в неразветвленной цепи, схема которой представлена на рис. 1.20, а, все элементы включены последовательно 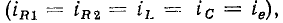а в разветвленной цепи (рис. 1.21, а) имеется две группы последовательно включенных элементов [источник напряжения е, сопротивление 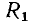и индуктивность 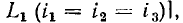а также сопротивление 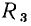и емкость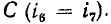

Соединение группы двухполюсных элементов, при котором все элементы находятся под одним и тем же напряжением, называется параллельным. Так, в разветвленной цепи, схема которой приведена на рис. 1.20, б, все элементы включены параллельно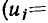

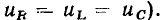
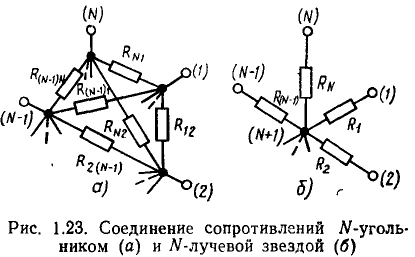
Комбинация последовательного и параллельного соединений элементов называется смешанным соединением (рис. 1.21, а). В ряде случаев соединение между входящими в цепь элементами не может быть отнесено ни к последовательному, ни к параллельному, ни к смешанному. К числу таких соединений относятся соединения треугольником (рис. 1.22, а) и звездой (рис. 1.22, б), которые являются частными случаями соединения N-угольником (рис. 1.23, а) и N-лучевой звездой (рис. 1.23, б). Характер соединения между идеализированными элементами цепи определяет ее топологические (структурные) свойства, для описания которых используют понятия ветви, узла и контура.

Ветвь представляет собой участок электрической цепи, вдоль которого протекает один и тот же ток. Она может состоять из одного или нескольких последовательно полюсных элементов. Например, в электрической цепи, схема которой приведена на рис. 1.21, б, можно выделить ветви, составленные из одного (ветви, содержащие сопротивление  или индуктивность двух (ветвь, содержащая сопротивление 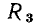и емкость С) и трех элементов (ветвь с источником напряжения е, сопротивлением 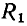и индуктивностью 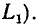Так как каждую ветвь можно рассматривать как двухполюсник, то соединения ветвей можно характеризовать теми же терминами, что и соединения идеализированных двухполюсных элементов (параллельное, последовательное и т. д.). Например, электрическую цепь, схема которой изображена на рис. 1.21, б, можно рассматривать как параллельное соединение четырех ветвей: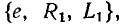

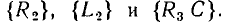
Место соединения ветвей называется у злом, причем место соединения двух ветвей называют устранимым узлом (при соединении двух ветвей текущие через них токи имеют одинаковые значения, поэтому две такие ветви могут быть заменены одной).

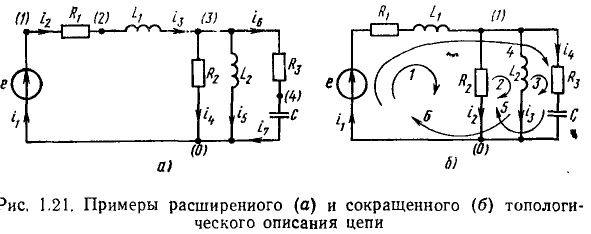
Иногда, в частности при автоматизированном составлении уравнений, описывающих процессы в электрических цепях, бывает удобно рассматривать каждый из идеализированных двухполюсных элементов, входящих в моделирующую цепь, в качестве отдельной ветви, при этом необходимо принимать во внимание все узлы, в том числе и устранимые. Будем называть такое топологическое описание цепи расширенным (см. рис. 1.21, а). При сокращенном топологическом описании цепи (см. рис. 1.21,5) группы последовательно включенных элементов рассматриваются в качестве отдельных ветвей и устранимые узлы во внимание не принимаются; таким образом, количество ветвей и, следовательно, количество рассматриваемых токов уменьшается (в нашем случае с 7 до 4).

Ветви электрической цепи нумеруют арабскими цифрами, начиная с единицы. Номера ветвей удобно выбирать совпадающими с номерами соответствующих токов, в этом случае номера ветвей на схеме можно не указывать. Узлы электрической цепи нумеруют, начиная с нуля. Порядок нумерации узлов значения не имеет, однако номер «0» удобно присваивать заземленному узлу или узлу, к которому сходится наибольшее число ветвей. Номера узлов условимся обозначать арабскими цифрами в круглых скобках, проставленными около соответствующего узла.

Любой замкнутый путь, проходящий по нескольким ветвям цепи, называется контуром. Например, в электрической цепи, схема которой приведена на рис. 1.21, б можно выделить шесть контуров, образованных ветвями {1,2}, {2,3}, {3,4}, {1,4}, {2,4} и {1,3}. Неразветвленная цепь (см. рис. 1.20, а) содержит только один контур.

Контур характеризуют направлением обхода (порядком перечисленных ветвей), причем каждая ветвь и каждый узел, входящие в контур, проходятся только один раз. Направление обхода контура выбирают произвольно и указывают изогнутой стрелкой (см. рис. 1.21, б).

В отличие от электрических элементов моделирующих цепей ветви, узлы и контуры называются топологическими элементами. Степень сложности исследования процессов в электрических цепях во многом определяется числом топологических элементов. В зависимости от их числа различают простейшие и сложные цепи. К простейшим цепям относятся одноконтурная (например, см. рис. 1.20, а) и двухузловая (например, см. рис. 1.20, б) цепи, к сложным— цепи с числом узлов более двух и числом контуров более одного.

Понятие о компонентных и топологических уравнениях. Законы Кирхгофа

Математическое описание процессов в электрических цепях базируется на уравнениях двух типов: компонентных и топологических.

Компонентные уравнения (уравнения ветвей) устанавливают связь между током и напряжением каждой ветви. Количество таких уравнений равно числу ветвей, а вид каждого из них зависит только от состава ветви, т. е. от входящих в ее состав идеализированных двухполюсных элементов. При расширенном топологическом описании число ветвей и, следовательно, количество компонентных уравнений равны числу идеализированных двухполюсных элементов, а компонентные уравнения имеют наиболее простой вид — они вырождаются в рассмотренные ранее уравнения, связывающие между собой ток и напряжение на зажимах идеализированных активных и пассивных элементов. Таким образом, уравнения, составленные на основании закона Ома (1.9), (1.10), представляют собой компонентные уравнения для ветви, содержащей один идеализированный пассивный элемент — сопротивление. При сокращенном топологическом описании количество компонентных уравнений уменьшается в соответствии с уменьшением числа ветвей, но сами уравнения имеют более сложный вид.

Топологические уравнения отражают свойства цепи, которые определяются только ее топологией и не зависят от того, какие электрические элементы входят в состав ветвей. К топологическим уравнениям относятся, в частности, уравнения, составленные на основании первого и второго законов Кирхгофа.

Первый закон Кирхгофа устанавливает связь между токами ветвей в каждом из узлов цепи: алгебраическая сумма мгновенных значений токов всех ветвей, подключенных к каждому из узлов моделирующей цепи, в любой момент времени равна нулю.

В соответствии с первым законом Кирхгофа для каждого из узлов идеализированной цепи (как при расширенном, так и при сокращенном топологическом описании) может быть составлено уравнение баланса токов в узле

где k — номер ветви, подключенной к рассматриваемому узлу. Суммирование токов производится с учетом выбранных положительных направлений: всем токам, одинаково ориентированным относительно узла, приписывается одинаковый знак. Условимся токи, направленные от узла, брать со знаком плюс, а токи, направленные к узлу, — со знаком минус. Такой выбор не носит принципиального характера, а сделан только для удобства последующего изложения, поскольку изменение знаков, приписанных токам, соответствовало бы умножению правой и левой частей (1.37) на —1. Токи ветвей, в которых содержатся управляемые или неуправляемые источники тока и напряжения, учитываются в уравнении (1.37) наравне с токами других ветвей.

Пример 1.1. 

Составим уравнения баланса токов для всх узлов цепи, схема которой изображена на рис. 1.24,а:

Если сгруппировать токи, направленные к узлу и перенести их в правую часть уравнения (1.37), а в левой части оставить токи, направленные от узла, то первый закон Кирхгофа можно сформулировать таким образом: сумма мгновенных значений токов, направленных к любому узлу цепи, в любой момент времени равна сумме токов, вытекающих из этого узла. Первый закон Кирхгофа является следствием закона сохранения заряда (уравнения непрерывности) и отражает тот факт, что в узлах идеализированной электрической цепи заряды не накапливаются и не расходуются.

На основании первого закона Кирхгофа можно составить уравнение баланса токов и для так называемого обобщенного узла, который представляет собой часть моделирующей цепи, охваченную произвольной замкнутой поверхностью. В этом случае в уравнении {1.37) алгебраически суммируются токи всех ветвей, входящих в

обобщенный узел, т. е. токи всех ветвей, пересекаемых указанной замкнутой поверхностью. Так, для обобщенного узла, выделенного пунктирной линией на рис. 1.24, а, уравнение баланса токов

Нетрудно убедиться, что уравнение (1.39) вытекает из уравнения (1.38).

Второй закон Кирхгофа устанавливает связь между напряжениями ветвей, входящих в произвольный контур: алгебраическая сумма мгновенных значений напряжений всех ветвей, входящих в любой контур-моделирующей цепи, в каждый момент времени равна нулю.

В соответствии со вторым законом Кирхгофа для каждого контура можно составить уравнения баланса напряжений ветвей

где k—номера ветвей, входящих в рассматриваемый контур. Суммирование напряжений производится с учетом их положительных направлений и выбранного направления обхода контура. Если положительное направление напряжения ветви совпадает с направлением обхода контура, то оно входит в (1.40) со знаком плюс, в противном случае— со знаком минус. Изменение направления обхода контура, очевидно, соответствует умножению левой и правой частей (1.40) на —1.

Пример 1.2.

Составим уравнения баланса напряжений ветвей для всех контуров цепи, схема которой приведена на рис. 1.24, б (номера напряжений ветвей совпадают с номерами соответствующих токов):

Уравнения по второму закону Кирхгофа можно составить не только для напряжений ветвей, но и для напряжений элементов, входящих в ветви каждого контура. Представляя напряжение каждой ветви в виде суммы напряжений элементов этой ветви и принимая во внимание, что положительное направление напряжения источника э. д. с. противоположно направлению э. д. с., систему уравнений (1.40) можно преобразовать к следующему виду:

Здесь — напряжения каждого из элементов рассматриваемого контура, за исключением напряжений источников э. д. с.; 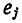— э. д. с. источников напряжения, действующих в контуре.

Используя (1.42), можно несколько видоизменить формулировку второго закона Кирхгофа: алгебраическая сумма мгновенных значений напряжений на элементах любого контура моделирующей цепи в каждый момент времени равна алгебраической сумме мгновенных значений э. д. с. источников напряжения, действующих в этом контуре. Напряжения на элементах контура и э. д. с. источников напряжения входят в (1.42) со знаком плюс, если положительные направления напряжений на элементах и направления э. д. с. источников напряжения совпадают с направлением обхода контура. В противном случае соответствующие слагаемые в (1.42) берутся со знаком минус.

Пример 1.3.

Запишем уравнения баланса напряжений на элементах всех контуров цепи (рис. 1.24. б):

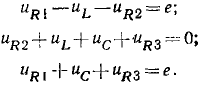
Второй закон Кирхгофа является следствием закона сохранения энергии и отражает тот факт, что энергия, затраченная сторонними силами на перенос произвольного заряда внутри источников, входящих в контур, равна энергии, затрачиваемой источниками на перенос этого заряда через пассивные элементы контура.

Следует подчеркнуть, что закон сохранения энергии выполняется при переносе заряда по любому замкнутому пути (не обязательно полностью проходящему через ветви цепи). Поэтому уравнения по второму закону Кирхгофа можно составить для любой совокупности элементов, образующих путь для электрического тока от произвольно выбранного узла (а) электрической цепи к узлу (б) с учетом напряжения между конечными точками этого пути 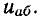Например, для ветвей 3 и 2 (рис. 1.24, а), образующих путь для электрического тока между узлами (2) и (0) электрической цепи, уравнение по второму закону Кирхгофа с учетом напряжения 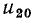между этими узлами запишется в виде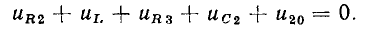

Для контуров, в которых есть источники тока, уравнения баланса напряжений составляют по общему правилу, причем напряжение на источнике тока учитывается в левой части уравнения (1.42). Так, для контура, образованного ветвями с сопротивлениями 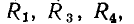емкостью 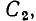источником напряжения е и источником тока j (рис. 1.24, а), уравнение баланса напряжений

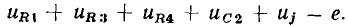
Так как вид и число уравнений, составленных на основании законов Кирхгофа, не зависят от того, какие элементы входят в состав цепи, а определяются только ее топологическими особенностями, то уравнения баланса токов и напряжений можно применять для математического описания процессов в моделирующих цепях, составленных из двухполюсных элементов любого типа (как линейных, так и нелинейных) при любой форме токов и напряжений независимых источников.

Очевидно, что количество уравнений баланса токов и напряжений равно сумме числа узлов и числа контуров исследуемой цепи. Можно убедиться, что не все из составленных уравнений будут линейно независимыми. Например, любое из четырех уравнений (1.38) может быть получено как линейная комбинация из трех других уравнений: так, уравнение для узла (0) можно получить суммируя уравнения, составленные для узлов (1), (2), (3), и умножая правую и левую части полученного уравнения на —1. Аналогично уравнения (1.41) не являются линейно независимыми.

В то же время на основании законов Кирхгофа для каждой цепи можно составить несколько различных систем линейно независимых топологических уравнений. Например, любые три уравнения из (1.38) и любые два уравнения из (1.41) образуют систему линейно независимых у равнений.

Будем называть системой независимых узлов и системой независимых контуров любые совокупности узлов и контуров цепи, для которых можно составить системы линейно независимых уравнений по законам Кирхгофа. Определение числа независимых узлов и контуров, а также выделение систем соответствующих узлов и контуров являются основными задачами топологии цепей.

Топологические графы электрических цепей

В общем случае граф есть совокупность отрезков произвольной длины и формы, называемых ветвями (ребрами), и точек их соединения, называемых узлами (вершинами). В теории электрических цепей в основном находят применение направленные, или ориентированные, графы, у которых каждому ребру приписывается определенное направление, указываемое стрелкой. Различают направленные топологические графы и направленные графы прохождения сигналов. Направленный топологический граф является упрощенной моделью электрической цепи, отражающей только ее топологические (структурные) свойства. Направленный граф прохождения сигналов представляет собой наглядное графическое изображение системы уравнений, описывающей процессы в электрической цепи. В дальнейшем будем называть направленный граф прохождения сигналов сигнальным графом, а направленный топологический граф просто графом цепи. 

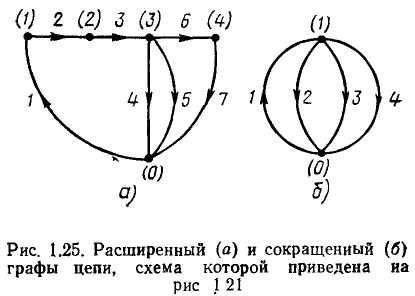
Граф электрической цепи строят по ее эквивалентной схеме. Каждую ветвь цепи заменяют при этом отрезком произвольной длины и формы — ветвью графа, а каждый узел цепи преобразуют в узел графа. На ветвях графа стрелками указывают их направления, которые совпадают с положительным направлением токов, протекающих по соответствующим ветвям цепи. Нумерация ветвей и узлов графа таже, что и нумерация ветвей и узлов схемы. Расширенному топологическому описанию цепи (см. рис. 1.21, а) соответствует расширенный граф цепи (рис. 1.25, а), сокращенному топологическому описанию (см. рис. 1.21,6) — сокращенный (рис. 1.25,6).

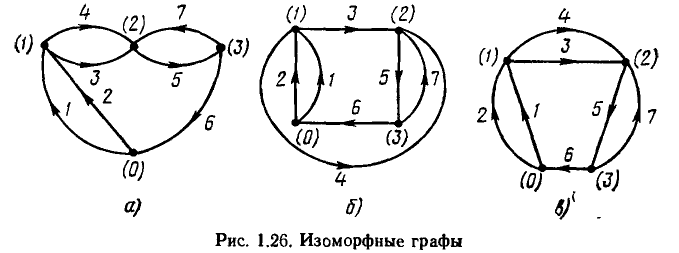
Свойства графа не зависят от формы и длины ветвей, а также от взаимного расположения узлов графа на плоскости и определяются только числом ветвей р, числом узлов q и способом соединения ветвей между собой. Графы, имеющие одинаковые количества узлов и ветвей, соединенных между собой одинаковым образом, называются изоморфными (рис. 1.26). Изменяя длину и форму ветвей, а также взаимное расположение узлов графа на плоскости, можно получить бесчисленное множество графов, изоморфных исходному. Такие преобразования графа называются изоморфными преобразованиями. Каждый из вариантов изображения графа, полученный путем таких преобразований, называется его геометрической реализацией.

Если узел i является концом ветви j, то говорят, что они инцидентны (от англ, incidence — сфера действия, охват). Каждая ветвь графа инцидентна двум узлам. Часть графа, которая наряду с некоторым подмножеством ветвей графа содержит и все инцидентные им узлы, называется подграфом.

Степенью узла называется число ветвей графа, инцидентных данному узлу. На рис. 1.25, а узлы (1) и (4) имеют вторую степень, узлы (0) и (3) — четвертую.

 Графы, изоморфные с точностью до узлов второй степени, называются гомеоморфными. После удаления из гомеоморфных графов узлов второй степени и объединения инцидентных этим вершинам ветвей гомеоморфные графы становятся изоморфными. Таким образом,

графы соответствующий расширенному и сокращенному топологическому описанию цепи, являются гомеоморфными. Примером гомеоморфных графов являются графы, изображенные на рис. 1.25.

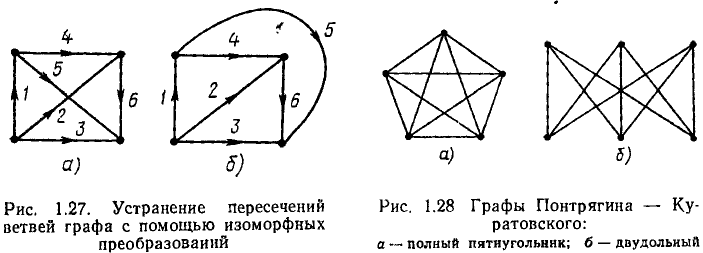
Планарным (плоским) называется такой граф, который в результате изоморфных преобразований может быть изображен на плоскости без пересечения ветвей. Так, граф, изображенный на рис. 1.27, а, содержит две пересекающиеся ветви, однако он является планарным, так как существует изоморфный ему граф, не имеющий пересечения ветвей (рис. 1.27, б). Можно убедиться, что все графы, содержащие не более четырех узлов, являются планарными.

Непланарный (объемный) граф не может быть изображен на плоскости без пересечения ветвей (рис. 1.28). При удалении из представленных на рисунке графов любой ветви они  становятся планарными. Полный пятиугольник и двудольный граф (рис. 1.28) называют также графами Понтрягина—Куратовского. Доказано, что произвольный граф является планарным тогда и только тогда, когда он не содержит подграфов, гомеоморфных одному из графов Понтрягина—Куратовского. Электрическая схема, которой соответствует планарный граф, также называется планарной. Непланарной схеме соответствует непланарный граф. Таким же образом вводятся понятия планарной и непланарной идеализированных электрических цепей.

Планарный граф делит плоскость, на которой он изображен, на внешнюю и внутренние области. Внутренние области, ограниченные ветвями графа, называются ячейками или окнами графа. Внешняя по отношению к графу часть плоскости называется базисной ячейкой.

Путь — это подграф, являющийся последовательностью соединенных между собой ветвей, выбранных таким образом, что каждому узлу (за исключением двух узлов, называемых граничными) инцидентны две ветви, а граничным узлам инцидентно по одной ветви (рис. 1.29). Каждая ветвь и каждый узел встречаются в пути только один раз.

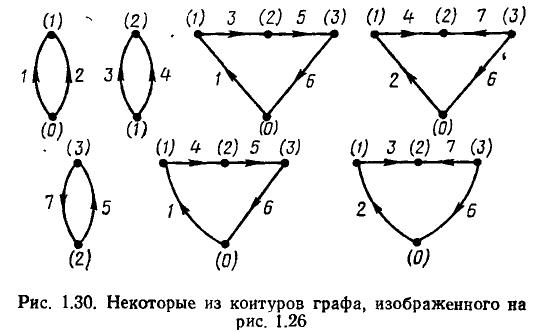
Замкнутый путь, т. е. путь, у которого начальные и конечные узлы совпадают, называется контуром (рис. 1.30). Каждому из узлов контура инцидентны две ветви. Очевидно, что между контурами графа и контурами исходной цепи существует взаимно однозначное соответствие.

Связный граф — это граф, между любыми двумя узлами которого существует, по крайней мере, один путь (см. рис. 1.25—1.28).

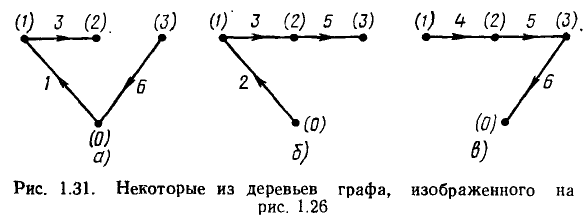
Деревом связного графа называется связный подграф, включающий все узлы графа, но не содержащий ни одного контура. Ветви графа, вошедшие в дерево, называются ветвями дерева; ветви, не вошедшие в дерево, называются связями (главными ветвями, хордами). Каждому графу может быть поставлено в соответствие несколько деревьев, отличающихся друг от друга составом ветвей дерева (рис. 1.31). Каждое из деревьев графа, содержащего р ветвей и q узлов, имеет 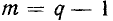ветвей дерева и

главных ветвей. При построении деревьев графов электрических це~ пей в число ветвей дерева обязательно вносят ветви, соответствующие идеализированным источникам напряжения. Ветви графа, соответствующие ветвям цепи, содержащим идеализированные источники тока, в число ветвей дерева не включают.

Добавление к дереву графа любой главной ветви образует контур. Контуры, образованные поочередным добавлением к дереву графа его главных ветвей, называются главными контурами (рис. 1.32). Таким образом, главный контур состоит из ветвей дерева и одной главной ветви.

Каждому дереву соответствует своя система из главных контуров, причем главные контуры, соответствующие определенному дереву, отличаются один от другого, по крайней мере, одной ветвью, а именно главной ветвью, входящей в каждый из главных контуров.

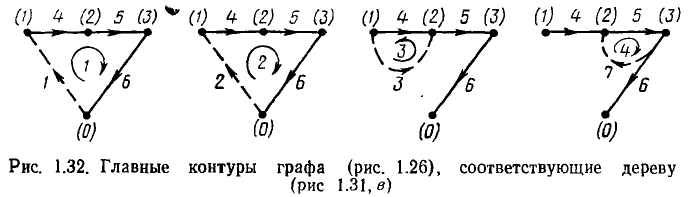
Каждому главному контуру обычно присваивают номер и приписывают ориентацию (направление обхода), совпадающие с номером и ориентацией соответствующей главной ветви.

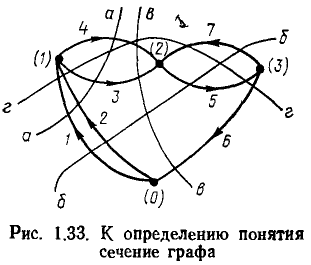
Сечением графа называется совокупность ветвей связного графа, пересекаемых замкнутой линией (линией сечения) или замкнутой поверхностью (поверхностью сечения), разделяющей граф на две части, причем ни одна из ветвей графа не пересекается дважды. Если удалить из связного графа ветви, образующие сечения, он распадается на две части, одна из которых может быть изолированным узлом.

Каждую из частей графа, лежащую по одну из сторон линии (поверхности) сечения можно рассматривать как обобщенный узел. Так, совокупности ветвей {1, 2, 3, 4}, {1, 2, 5, 7}, {3, 4, 6}, пересекаемых линиями а, б, в соответственно (рис. 1.33), образуют сечения, потому что при удалении каждой из этих совокупностей ветвей граф распадается на две части. Ветви, пересекаемые линией г, не образуют сечения, так как при удалении этих граф распадается более чем на две части.

Главным сечение графа называется такое сечение, в которое входит только одна ветвь выбранного дерева. Остальные ветви, входящие в главное сечение, являются связями (рис. 1.34). Количество главных сечений равно количеству ветвей дерева, т. е. m = q— 1. Каждому дереву может быть поставлена в соответствие своя система главных сечений, причем главные сечения, соответствующие выбранному дереву, отличаются друг от друга, по крайней мере, одной ветвью — ветвью дерева, входящей в каждое из сечений. Главным сечениям графа присваивают номера и приписывают ориентацию, совпадающие с номером ориентацией относительно соответствующей ветви дерева и ее сечения. 

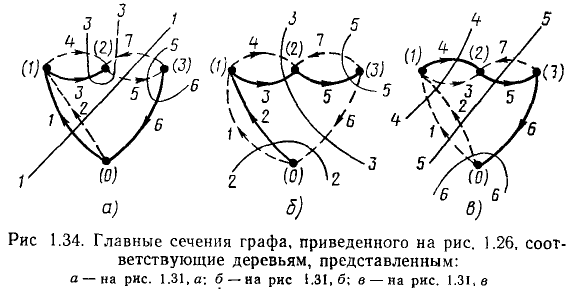
Если одна из частей, на которые граф делится линией сечения, представляет собой изолированный узел, то соответствующее сечение называется каноническим (сечения 3 и 6 на первом из графов, изображенных на рис. 1.34).

Топологические матрицы

Топологические матрицы служат для аналитического описания графов. Такое описание можно представить в виде списка (перечня) ветвей графа с указанием, каким узлам они инцидентны и с какой ориентацией, или с помощью полной матрицы узлов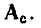

Полная матрица узлов (полная матрица инциденций, матрица соединений, структурная матрица) — это таблица, в которой число столбцов равно числу ветвей графа р, а число строк равно числу узлов q. Номера строк совпадают с номерами узлов (строка с нулевым номером обычно располагается последней), номера столбцов совпадают с номерами ветвей. Элемент матрицы 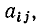расположенный на пересечении i-й строки и j-го столбца, может принимать значения +1, —1 и 0: 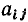= +1, если ветвь j инцидентна узлу i и направлена от этого узла; 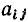= —1, если ветвь j инцидентна узлу i и направлена к этому узлу; 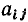= 0, если ветвь j не инцидентна узлу i. Так, графу, изображенному на рис. 1.26, а соответствует полная матрица инциденций

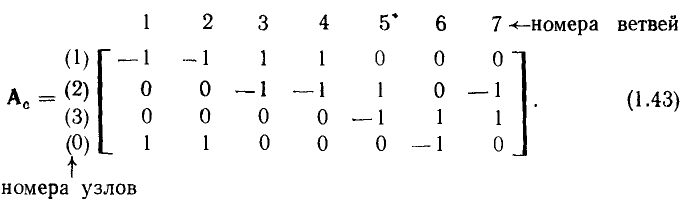
Нетрудно убедиться, что эта же полная матрица узлов (1.43) соответствует и всем графам, изоморфным графу, изображенному на рис. 1.26, а, в частности графам, приведенным на рис. 1.26, б, в. Таким образом, все изоморфные графы описываются одной и той же полной матрицей узлов. Имея полную матрицу узлов, всегда можно восстановить исходный граф с точностью до изоморфизма.

Число ненулевых элементов в каждой строке матрицы 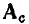равно числу ветвей, инцидентных соответствующему узлу, т. е. степени узла. В каждом столбце имеется только два ненулевых элемента: +1 и —1, так как каждая ветвь инцидентна двум узлам и направлена от одного из них к другому. Сумма всех элементов каждого столбца, а следовательно, и сумма всех строк полной матрицы узлов 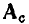равна нулю, т. е. строки полной матрицы узлов являются линейно зависимыми.

На практике обычно используют сокращенную (редуцированную) матрицу узлов А, которая получается из полней матрицы узлов путем отбрасывания любой из ее строк. Обычно отбрасывают строку, соответствующую узлу с номером 0, который будем называть базисным узлом. Так, отбрасывая строку с номером 0 у полной матрицы узлов (1.43), получаем сокращенную матрицу узлов А цепи, граф которой изображен на рис. 1.26:

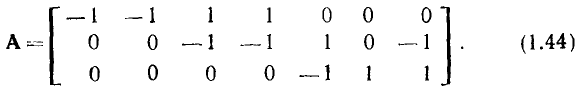
В теории графов доказывается, что все строки сокращенной матрицы узлов линейно независимы. Зная сокращенную матрицу узлов, соответствующую некоторому графу, всегда можно найти его полную матрицу узлов, для чего необходимо дополнить А одной строкой так, чтобы сумма всех строк матрицы 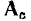равнялась нулю,

В связи с тем что каждая строка матриц 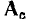и А несет информацию о том, какие ветви и с какой ориентацией подключены к определенному узду цепи, эти матрицы можно использовать для записи уравнений по первому закону Кирхгофа. Действительно, умножая полную матрицу узлов 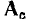на матрицу-столбец токов ветвей i, получаем

Каждая строка этого выражения есть алгебраическая сумма токов ветвей, подключенных к соответствующему узлу цепи, причем если ветвь направлена от узла, то соответствующий ток имеет знак плюс 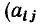=+1), если ветвь направлена к узлу, то знак минус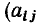= —1), Если же ветвь не инцидентна рассматриваемому узлу, то соответствующее слагаемое равно нулю 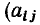= 0).

Тогда в соответствии с первым законом Кирхгофа окончательно имеем

В связи с тем что строки полной матрицы узлов являются линейно зависимыми, система уравнений (1.45) также будет линейно зависимой.

Для получения системы линейно независимых уравнений, составленных по первому закону Кирхгофа, можно воспользоваться сокращенной матрицей инциденций, строки которой являются линейно независимыми:

Таким образом, для любой цепи можно составить 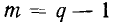 линейно независимых уравнений баланса токов, и, следовательно, любые m узлов графа представляют собой систему независимых узлов.

 Пример 1.4.

Составим систему линейно независимых уравнений баланса токов для цепи, граф которой изображен на рис. 1.26. Подставляя в (1.46) сокращенную матрицу узлов этой цепи (1.44), находим

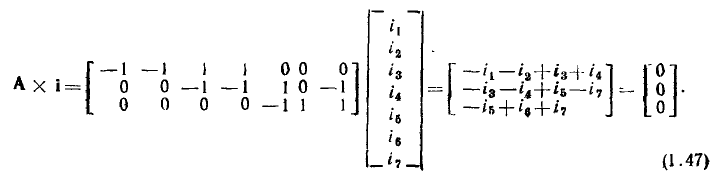
Как и следовало ожидать, система уравнений (1.47) совпадаете системой | уравнений (1.38), составленной на основании первого закона Кирхгофа для 1,2 и 3-го узлов рассматриваемой цепи.

Для матричной записи уравнений баланса токов в обобщенных узлах цепи и уравнений баланса напряжений используют матрицу главных сечений и матрицу главных контуров.

Матрица главных сечений Q (матрица сечении) представляет собой таблицу, число столбцов которой равно числу ветвей графа р, а число строк — числу главных сечений

m = q — 1

(номера столбцов совпадают с номерами ветвей, а номера строк с нотами главных сечений, т. е. с номерами соответствующих ветвей дерева).

Каждая строка матрицы главных сечений характеризует состав ветвей графа, входящих в данное сечение. Элементы i-й строки 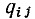принимают значение +1, если j-я ветвь графа входит в состав i-гo сечения причем ее ориентация совпадает с ориентацией сечения, т.е. с ориентацией соответствующей ветви дерева относительно линии сечения; 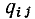=-1, если j-я ветвь входит в i-е сечение а ее ориентация противоположна ориентации сечения; = 0, если j-я ветвь не входит в i-e сечение.

Матрица главных сечений, соответствующая графу, приведенному на рис. 1.34, а, имеет следующий вид: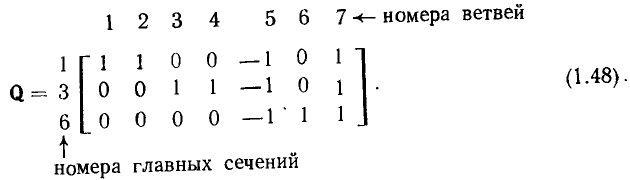

Используя матрицу главных сечений, можно в компактной форме записать систему из m=q-1 уравнений, составленных на основании первого закона Кирхгофа для главных сечений графа, соответствующих выбранному дереву:

где i — вектор токов ветвей.

Уравнения (1 49) являются линейно независимыми, так как каждое из них отличается от остальных, по крайней мере, одним током – током ветви дерева, входящей в данное главное сечение.

Подставляя (1.48) в (1.49), получим систему линейно независимых уравнений баланса токов для главных сечений графа (рис. 1.34, а).

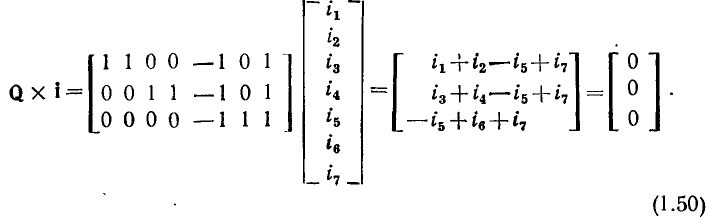
Если какое-либо из главных сечений графа является каноническим, то уравнение баланса токов для этого сечения с точностью до знака совпадает с уравнением баланса токов для соответствующего изолированного узла. Так, в системе уравнений (1.50) второе и третье уравнения, составленные для канонических сечений 3 и 6, совпадают со вторым и третьим уравнениями в системе уравнений (147), составленными соответственно для узлов 2 и 3 той же цепи. Если все главные сечения графа являются каноническими, то матрицы узлов А и сечений Q совпадают с точностью до знака элемента строки.

Матрица главных контуров В представляет собой таблицу, в которой число столбцов равно числу ветвей графа р, а число строк — числу главных контуров, т. е. числу главных ветвей графа 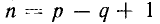(номера столбцов совпадают с номерами ветвей, а номера строк—с номерами главных контуров). Элементы i-й строки 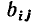могут принимать значения +1, —1 и 0; 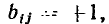если j-я ветвь входит в состав i-гo контура, причем ее ориентация совпадает с ориентацией контура; 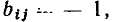если ориентация j-й ветви, входящей в i-й контур, не совпадает с ориентацией контура; 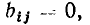если j-я ветвь не входит в i-й контур. Например, матрица главных контуров В графа (см. рис. 1.26), соответствующая дереву графа, приведенному на рис. 1.31, в, имеет следующий вид;

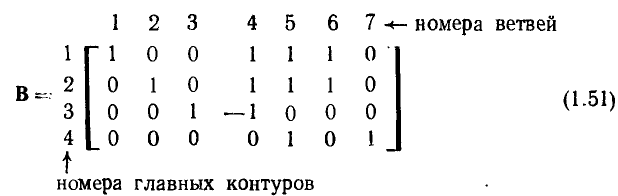
Матрицу главных контуров можно использовать для записи уравнений, составленных на основании второго закона Кирхгофа. Пусть исследуемая цепь содержит р ветвей, q узлов и 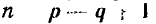главных контуров. Умножая матрицу главных контуров В на матрицу столбец напряжений ветвей u, получаем

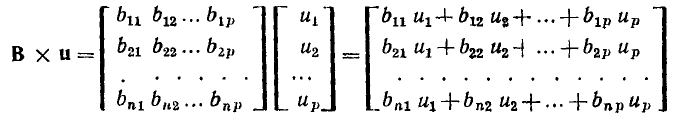
Каждая строка этого выражения представляет собой алгебраическую сумму напряжений ветвей, входящих в i-й главный контур, причем правило суммирования напряжений ветвей совпадает с соответствующим правилом, установленным для записи уравнений баланса напряжений в контуре (1.40). Так как в соответствии со вторым законом Кирхгофа сумма напряжений ветвей, входящих в каждый контур, в любой момент времени равна нулю, то окончательно имеем

Выражение (1.52) является матричной формой записи уравнений баланса напряжений для главных контуров цепи. Уравнения, входящие в (1.52), являются линейно независимыми, так как каждое из них отличается от остальных, по крайней мере, одним напряжением — напряжением главной ветви, замыкающей данный контур.

Таким образом, система из  главных контуров, соответствующих выбранному дереву, является системой независимых контуров. Следовательно, для каждой цепи можно составить п независимых уравнений по второму закону Кирхгофа.

Пример 1.5.

Рассмотрим применение матрицы контуров для формирования системы линейно независимых уравнений баланса напряжений для цепи, граф которой приведен на рис. 1.26. Умножая матрицу главных контуров этой цепи (1.51) на матрицу-столбец напряжений ветвей u, получаем

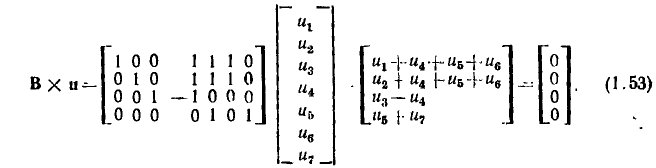
Следует отметить, что при выборе системы независимых контуров было использовано достаточное условие независимости уравнений, заключающееся в том, что для линейной независимости системы уравнений достаточно, чтобы каждое из уравнений содержало, по крайней мере, одну независимую переменную величину, отсутствующую в других уравнениях. Так как это условие не является необходимым, то для каждой цепи можно найти и другие системы независимых контуров, которые в ряде случаев могут не совпадать ни с одной из систем: главных контуров. В частности, ячейки плоского графа, число которых оказывается равным представляют собой систему независимых контуров. Их состав может быть описан матрицей основных контуров которая строится аналогично матрице главных контуров (контуры, соответствующие каждой из ячеек, нумеруют от 1 до n, каждому из них приписывают произвольную ориентацию). Например, для графа электрической цепи, изображенного на рис. 1.35:

В этом случае матрица основных контуров не совпадает ни с одной из возможных для данного графа матриц главных контуров.

Матрицу 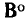можно, как и матрицу В, использовать для записи системы линейно независимых уравнений баланса напряжений:

Так, используя (1.54), можно составить систему уравнений баланса напряжений для ячеек графа, изображенного на рис. 1.35:

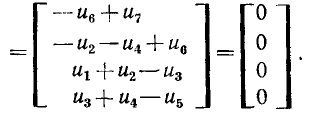
Следует подчеркнуть, что понятие ячейки (окна) было введено ранее только для плоских графов и что только для них возможен выбор ячеек в качестве независимых контуров.

Дуальные графы и дуальные цепи

Два плоских графа называются дуальными, если матрица узлов одного из них А равна матрице основных контуров В° другого и наоборот:

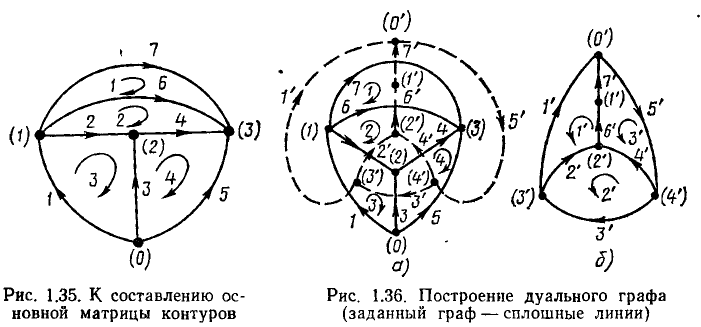
Очевидно, что дуальные графы должны иметь одинаковое число ветвей 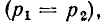причем число ветвей дерева одного из них m должно быть равно числу главных ветвей n другого:

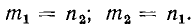
Для построения графа, дуального заданному (рис. 1.36, а), необходимо внутри каждой ячейки исходного графа разместить узел дуального графа [(1′), (2′) и т. д.], кроме того, один узел дуального графа располагается во внешней по отношению к исходному графу части плоскости, т. е. в базисной ячейке. Узлы дуального графа соединяются между собой ветвями так, чтобы каждая ветвь исходного графа пересекала одну ветвь дуального графа (пунктир на рис. 1.36, а). Номера узлов дуального графа совпадают с номерами контуров исходного графа, внутри которых они размещены. Узлу дуального графа, расположенному в базисной ячейке, присваивается номер 0′. Пересекающимся между собой ветвями исходного и дуального графов присваиваются одинаковые номера. Ориентация ветвей и контуров дуального графа (рис. 1.36, б) выбирается таким образом, чтобы обеспечить выполнение равенств (1.56).

Нетрудно убедиться, что матрицы узлов и основных контуров дуального графа (рис. 1.36,6) равны соответственно матрицам основных контуров 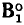и узлов 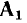исходного графа:

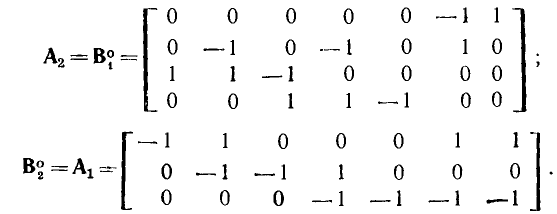
Как видно из рис. 1.36, ячейки дуального графа соответствуют узлам исходного графа, а узлы дуального графа — ячейкам исходного. Последовательному соединению ветвей исходного графа соответствует параллельное соединение ветвей дуального графа и наоборот. Если сформулированное правило нахождения дуального графа применить для построения графа, дуального изображенному на рис. 1.36, б, то получится граф, изоморфный исходному графу (рис. 1.36, а сплошные линии).

Используя понятие дуального графа, легко обобщить введенное ранее понятие дуальных цепей. Две цепи называются дуальными, если они имеют дуальные графы и каждому элементу одной цепи соответствует дуальный элемент другой.

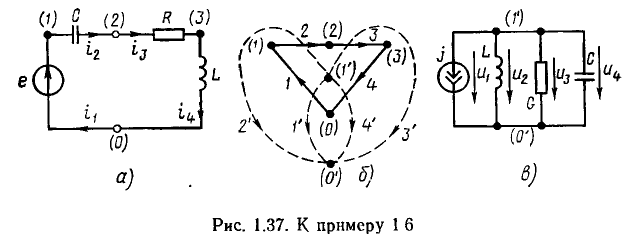
Для построения дуальной цепи сначала находят граф, дуальный расширенному топологическому графу исходной цепи, а затем каждую ветвь дуального графа заменяют элементом, дуальным элементу, расположенному в соответствующей ветви исходной цепи.

 Пример 1.6.

Построим цепь, дуальную приведенной на рис. 1.37, а. На рис. 1.37, б сплошными линиями показан граф исходной цепи, а пунктирными — дуальный ему граф (направление ветвей исходного графа соответствует направлению токов ветвей исходной цепи, а направление ветвей дуального графа—направлению напряжения ветвей дуальной цепи). Цепь, дуальная исходной, изображена на рис. 1.37, в.

Из определения дуальной цепи и равенств (1.56) следует, что уравнения баланса токов для одной из дуальных цепей будут совпадать с Уравнениями баланса напряжений для другой при условии, что в соответствующих уравнениях токи ветвей одной цепи будут заменены на напряжения ветвей другой цепи и наоборот. Это свойство дуальных Цепей иногда используют в качестве определения дуальных цепей.

В заключение заметим, что непланарные графы не имеют дуальных графов, в связи с чем идеализированной электрической цепи, схема которой не является планарной, не может быть поставлена в соответствие дуальная цепь.

Электрическая цепь характеризуется совокупностью элементов, из которых она
состоит, и способом их соединения. Соединение элементов электрической цепи наглядно
отображается ее схемой. Рассмотрим для примера две электрические схемы (рис.
1, 2), введя понятие ветви и узла.

Ветвью называется участок цепи, обтекаемый одним и тем же током.

Узел – место соединения трех и более ветвей.

Представленные схемы различны и по форме, и по назначению, но каждая из указанных
цепей содержит по 6 ветвей и 4 узла, одинаково соединенных. Таким образом, в
смысле геометрии (топологии) соединений ветвей данные схемы идентичны.

Топологические (геометрические) свойства электрической цепи не зависят от типа
и свойств элементов, из которых состоит ветвь. Поэтому целесообразно каждую
ветвь схемы электрической цепи изобразить отрезком линии. Если каждую ветвь
схем на рис. 1 и 2 заменить отрезком линии, получается геометрическая фигура,
показанная на рис. 3.

Условное изображение схемы, в котором каждая ветвь заменяется отрезком линии,
называется графом электрической цепи. При этом следует помнить, что ветви
могут состоять из каких-либо элементов, в свою очередь соединенных различным
образом.

Отрезок линии, соответствующий ветви схемы, называется ветвью графа.
Граничные точки ветви графа называют узлами графа. Ветвям графа может
быть дана определенная ориентация, указанная стрелкой. Граф, у которого все
ветви ориентированы, называется ориентированным.

Подграфом графа называется часть графа, т.е. это может быть одна ветвь
или один изолированный узел графа, а также любое множество ветвей и узлов, содержащихся
в графе.

В теории электрических цепей важное значение имеют следующие подграфы:

1. Путь – это упорядоченная последовательность ветвей, в которой каждые
две соседние ветви имеют общий узел, причем любая ветвь и любой узел встречаются
на этом пути только один раз. Например, в схеме на рис. 3 ветви 2-6-5;
4-5; 3-6-4; 1 образуют пути между одной и той же парой узлов 1
и 3. Таким образом, путь – это совокупность ветвей, проходимых непрерывно.

2. Контур – замкнутый путь, в котором один из узлов является начальным
и конечным узлом пути. Например, для графа по рис. 3 можно определить контуры,
образованные ветвями 2-4-6; 3-5-6; 2-3-5-4. Если между любой парой
узлов графа существует связь, то граф называют связным.

3. Дерево – это связный подграф, содержащий все узлы графа, но ни одного
контура. Примерами деревьев для графа на рис. 3 могут служить фигуры на рис.
4.

Рис.4

4. Ветви связи (дополнения дерева) – это ветви графа, дополняющие дерево
до исходного графа.

Если граф содержит m узлов и n
ветвей, то число ветвей любого дерева ,
а числа ветвей связи графа .

5. Сечение графа – множество ветвей, удаление которых делит граф на
два изолированных подграфа, один из которых, в частности, может быть отдельным
узлом.

Сечение можно наглядно изобразить в виде следа некоторой замкнутой поверхности,
рассекающей соответствующие ветви. Примерами таких поверхностей являются для
нашего графа на рис. 3 S₁ иS₂ . При этом
получаем соответственно сечения, образованные ветвями 6-4-5 и
6-2-1-5.

С понятием дерева связаны понятия главных контуров и сечений:

• главный контур – контур, состоящий из ветвей дерева и только одной
  ветви связи;
• главное сечение – сечение, состоящее из ветвей связи и только одной
  ветви дерева.

Топологические матрицы

Задать вычислительной машине топологию цепи рисунком затруднительно, так как
не существует эффективных программ распознавания образа. Поэтому топологию цепи
вводят в ЭВМ в виде матриц, которые называют топологическими матрицами.
Выделяют три таких матрицы: узловую матрицу, контурную матрицу и матрицу сечений.

1. Узловая матрица (матрица соединений) – это таблица коэффициентов
уравнений, составленных по первому закону Кирхгофа. Строки этой матрицы соответствуют
узлам, а столбцы – ветвям схемы.

Для графа на рис. 3 имеем число узлов m=4 и число
ветвей n=6. Тогда запишем матрицу А_Н
, принимая, что элемент матрицы
(i –номер строки; j –номер
столбца) равен 1, если ветвь j
соединена с узлом i и ориентирована от него, -1,
если ориентирована к нему, и 0, если ветвь
j не соединена с узломi . Сориентировав
ветви графа на рис. 3, получим

Данная матрица А_Н записана для всех четырех узлов и называется
неопределенной. Следует указать, что сумма элементов столбцов матрицы А_Н
всегда равна нулю, так как каждый столбец содержит один элемент +1 и
один элемент -1, остальные нули.

Обычно при расчетах один (любой) заземляют. Тогда приходим к узловой матрице
А (редуцированной матрице),
которая может быть получена из матрицы А_Н
путем вычеркивания любой ее строки. Например, при вычеркивании строки “4” получим

Число строк матрицы А
равно числу независимых уравнений для узлов ,
т.е. числу уравнений, записываемых для электрической схемы по первому закону
Кирхгофа. Итак, введя понятие узловой матрицы А,
перейдем к первому закону Кирхгофа.

Первый закон Кирхгофа

Обычно первый закон Кирхгофа записывается для узлов схемы, но, строго говоря,
он справедлив не только для узлов, но и для любой замкнутой поверхности, т.е.
справедливо соотношение

(1)

где
– вектор плотности тока;
– нормаль к участку dS замкнутой поверхности S.

Первый закон Кирхгофа справедлив и для любого сечения. В частности, для сечения
S₂ графа на рис. 3, считая, что нумерация и направления токов
в ветвях соответствуют нумерации и выбранной ориентации ветвей графа, можно
записать

.

Поскольку в частном случае ветви сечения сходятся в узле, то первый закон Кирхгофа
справедлив и для него. Пока будем применять первый закон Кирхгофа для узлов,
что математически можно записать, как:

(2)

т.е. алгебраическая сумма токов ветвей, соединенных в узел, равна нулю.

При этом при расчетах уравнения по первому закону Кирхгофа записываются для
(m-1) узлов, так как при записи уравнений для всех m узлов одно
(любое) из них будет линейно зависимым от других, т.е. не дает дополнительной
информации.

Введем столбцовую матрицу токов ветвей

I=

Тогда первый закон Кирхгофа в матричной форме записи имеет вид:

– где O – нулевая матрица-столбец. Как видим, в качестве узловой
взята матрица А, а не А_Н, т.к. с учетом
вышесказанного уравнения по первому закону Кирхгофа записываются для (m-1)
узлов.

В качестве примера запишем для схемы на рис. 3

Отсюда для первого узла получаем

,

что и должно иметь место.

2. Контурная матрица (матрица контуров) – это таблица коэффициентов
уравнений, составленных по второму закону Кирхгофа. Строки контурной матрицы
Всоответствуют контурам, а столбцы – ветвям схемы.

Элемент b_ij матрицы В равен 1, если
ветвь j входит в контур i и ее ориентация совпадает с направлением
обхода контура, -1, если не совпадает с направлением обхода контура,
и 0, если ветвьj не входит в контурi.

Матрицу В, записанную для главных контуров, называют матрицей
главных контуров. При этом за направление обхода контура принимают направление
ветви связи этого контура. Выделив в нашем примере (см. рис. 5) дерево, образуемое
ветвями 2-1-4, запишем коэффициенты для матрицы В.

Перейдем теперь ко второму закону Кирхгофа.

Под напряжением на некотором участке электрической цепи понимается разность
потенциалов между крайними точками этого участка, т.е.

(4)

Просуммируем напряжения на ветвях некоторого контура:

Поскольку при обходе контура потенциал каждой i-ой точки встречается
два раза, причем один раз с “+”, а второй – с “-”, то в целом сумма равна нулю.

Таким образом, второй закон Кирхгофа математически записывается, как:

(5)

– и имеет место следующую формулировку: алгебраическая сумма напряжений на
зажимах ветвей (элементов) контура равна нулю. При этом при расчете цепей с
использованием законов Кирхгофа записывается
независимых уравнений по второму закону Кирхгофа, т.е. уравнений, записываемых
для контуров, каждый из которых отличается от других хотя бы одной ветвью. Значение
топологического понятия “дерева”: дерево позволяет образовать независимые контуры
и сечения и, следовательно, формировать независимые уравнения по законам Кирхгофа.
Таким образом, с учетом (m-1) уравнений, составленных по первому закону
Кирхгофа, получаем систему из
уравнений, что равно числу ветвей схемы и, следовательно, токи в них находятся
однозначно.

Введем столбцовую матрицу напряжений ветвей

U=

Тогда второй закон Кирхгофа в матричной форме записи имеет вид

В качестве примера для схемы рис. 5 имеем

,

откуда, например, для первого контура получаем

,

что и должно иметь место.

Если ввести столбцовую матрицу узловых потенциалов

причем потенциал последнего узла ,
то матрица напряжений ветвей и узловых потенциалов связаны соотношением

U=AТ

(7)

где A^Т – транспонированная узловая матрица.

Для определения матрицы В по известной матрице А=А_ДА_С
, где А_Д – подматрица, соответствующая ветвям некоторого
дерева, А_С– подматрица, соответствующая ветвям связи, может
быть использовано соотношение В= (-А^Т_С А^-1Т_Д1).

3. Матрица сечений – это таблица коэффициентов уравнений, составленных
по первому закону Кирхгофа для сечений. Ее строки соответствуют сечениям, а
столбцы – ветвям графа.

Матрица Q , составленная для главных сечений, называется матрицей
главных сечений. Число строк матрицы Q равно числу независимых
сечений.

Элемент q_ij матрицы Q равен 1,
если ветвьвходит в i-е сечение и ориентирована согласно направлению сечения
(за положительное направление сечения принимают направление ветви дерева, входящей
в него), -1, если ориентирована противоположно направлению сечения, и
0, если ветвьj не входит в i-е сечение.

В качестве примера составим матрицу Q главных сечений для графа
на рис. 5. При указанной на рис. 5 ориентации ветвей имеем

В заключение отметим, что для топологических матриц А, В
и Q, составленных для одного и того же графа, выполняются соотношения

которые, в частности, можно использовать для проверки правильности составления
этих матриц. Здесь 0 – нулевая матрица порядка .

Приведенные уравнения позволяют сделать важное заключение: зная одну из топологических
матриц, по ее структуре можно восстановить остальные.

Литература

1. Теоретические основы электротехники. Т.1. Основы теории линейных
цепей./Под ред. П.А.Ионкина. Учебник для электротехн. вузов. Изд.2-е , перераб.
и доп. –М.: Высш. шк., 1976.-544с.

2. Матханов Х.Н. Основы анализа электрических цепей. Линейные цепи.:
Учеб. для электротехн. и радиотехн. спец. 3-е изд. переработ. и доп. –М.: Высш.
шк., 1990. –400с.

3. Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил,
С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.

Контрольные вопросы и задачи

1. Сформулируйте основные топологические понятия для электрических цепей.
2. Что такое узловая матрица?
3. Что такое контурная матрица?
4. Что такое матрица сечений?
5. Токи ветвей некоторой планарной цепи удовлетворяют следующей полной системе
   независимых уравнений:

.

Восстановив граф цепи, составить матрицы главных контуров и сечений, приняв,
что ветвям дерева присвоены первые номера.

Ответ:

6. Составить матрицу главных контуров для графа на рис. 3, приняв, что дерево
   образовано ветвями 2, 1 и 5

Ответ:

B=

7. Решить задачу 5, используя соотношения (8) и (9).

Чтобы доказать эйлерову цепь, сперва сформулируем и докажем такую теорему:

Возьмем самый длинный путь

в

и рассмотрим одну из его конечных точек

. Эта вершина примыкает к предпоследней вершине пути. Так как у

степень не меньше двух, то должно существовать еще одно ребро, инцидентное ей.

Если другая конечная точка этого ребра не находится на пути, то мы могли бы использовать, чтобы построить более длинный путь, чем

. Это невозможно, поэтому другая конечная точка ребра должна быть вершиной

пути. Это создает цикл от

к

и обратно к

.

У этой теоремы много применений. Здесь мы используем ее для доказательства теоремы об эйлеровых схемах. В доказательстве мы будем использовать термин четный граф для обозначения графа, в котором степень каждой вершины четная.

Докажем еще следующую теорему:

Если в

есть эйлерова цепь, то эта цепь должна входить и выходить из каждой вершины. Такое возможно несколько раз, если добавлять

к своей степени при каждом проходе. Поскольку эта цепь учитывает все ребра графа, каждая вершина должна иметь четную степень.

Докажем третью теорему — обратную импликацию индукцией по числу ребер. Базовый случай

ребер тривиально верен — это значит, что в графе есть только одна вершина и нет ребра.

Предположим, что утверждение справедливо для всех связных четных графов с e ребрами или меньше, и рассмотрим связный четный граф

с

ребром. Поскольку

связный и четный, у каждой вершины степень не менее двух, поэтому по Теореме у

есть цикл. Удалим ребра цикла из

.

Степень каждой вершины в уменьшенном графе будет по-прежнему четной, поскольку мы удаляем ровно два ребра из каждой вершины цикла. По гипотезе индукции, каждая из компонент редуцированного графа имеет эйлерову схему.

Эти схемы можно объединить с циклом, чтобы создать эйлеровы схемы в исходном графе путем обхода цикла. Когда мы достигаем вершины, которая является частью компоненты редуцированного графа, мы обходим ее по эйлеровой схеме этой компоненты и возвращаемся к вершине на цикле:

Чтобы получить эйлерову схему всего графа, начнем прослеживать цикл от

до

. Далее проследим эйлерову схему, которая существует в правой компоненте графа, начинается и заканчивается в

.

После этого проследим цикл от

до

, от

до

. В точке

мы следуем эйлеровой схеме, которая существует на левой компоненте графа, начинается и заканчивается в точке

. В конце мы возвращаемся по циклу от

до

, и завершаем эйлерову схему всего графа. Значит, теорема доказана.

Мы предполагаем, что можем работать с небольшими случаями и использовать, чтобы строить более крупные случаи. Большая часть работы заключается в описании того, как использовать малые случаи для получения больших.