Как составить дано к задаче на проценты

Задачи с процентами часто попадаются в экзаменационных заданиях. Многих они сбивают с толку – как разобраться с условием и как это решить? И совершенно зря, потому что с задачами на проценты каждый часто встречается в обычной жизни.

Пока такие задачки остаются оторванными от реальности строчками в учебнике, их бывает сложно понять и тем более решить. Чтобы стало понятнее, мы вам сейчас покажем примеры из обычной жизни, где вам могут встретиться проценты. А еще просто и доступно объясним, как решать задачи на проценты. И все у вас станет на свои места.

Задачи про проценты вокруг нас

Давайте оглядимся по сторонам: значения в процентах указаны на упаковках с любыми продуктами. Значок процента «%» смотрит на нас с рекламных плакатов скидок и распродаж. В новостях проценты сразу бросаются в глаза, когда речь идет о повышении цен на товары или коммунальные услуги. Разве вы сможете расшифровать все эти послания, если не научитесь решать задачи с процентами? Но вы, конечно, научитесь – мы в вас верим.

А вот такая ситуация: вы купили что-нибудь через интернет и получили извещение от ближайшего почтового отделения. Или сами собираетесь послать подарок другу в другой город. Вам обязательно надо уметь разбираться с процентами, чтобы узнать, сколько денег почта захочет получить за свои услуги по пересылке.

Или возьмем банковские кредиты и ипотеку. Банки в договорах всегда пишут мелкими буквами всякие вещи, которые полезно понимать. Например, какой процент по кредиту придется заплатить банку кроме тех денег, которые вы у него «одолжили» и обязаны вернуть.

А самый близкий школьникам пример связан с ЕГЭ. Каждый год после экзаменов публикуют официальную статистику. В которой немало задействованы и проценты. И эти проценты имеют прямое отношение к будущим выпускникам. Например, процент ребят, сдавших экзамен по математике на «хорошо» и «отлично» косвенно говорит о том, сколько абитуриентов с высокими баллами могли подать документы в вузы на технические специальности. А еще на программирование, прикладную математику и т.п. Чем их больше, тем выше конкурс. Если сравнивать их результаты со своими оценками, можно прикинуть собственные шансы на поступление.

Что такое процент?

Самое очевидное определение: процент – это десятичная дробь. В жизни редко что-то можно сравнивать целиком, чаще приходится сравнивать разные части чего-то целого. Поэтому мы используем такие понятия, как половина (1/2), треть (1/3), четверть (1/4). Ну да, все так привыкли к слову «четверть» в школе, что забывают о его формальном значении – «четвертая часть учебного года». Сравнивать сотые доли удобнее всего – так появился процент (1/100): pro centum – «за сто» на латыни.

Все задачи по математике на проценты вертятся вокруг сравнения частей одного целого, определения, какую долю составляет часть от целого, нахождения целого исходя из величины его части и т.п.

Проценты можно записать со знакомым всем значком процента: 1%. Можно представить в виде десятичной дроби (или натурального числа). Для этого нужно разделить на 100: 0,01. Можно наоборот: выразить число в процентах. Тогда его следует умножить на 100%.

Типы задач на проценты

Раз мы уже договорились, что задачи на проценты – это задачи на дроби, такой тактики будем придерживаться и дальше.

Тип 1: Находим процент (дробь) от числа.

• Задача. За месяц на предприятии изготовили 500 приборов. 20% изготовленных приборов не смогли пройти контроль качества. Сколько приборов не прошло контроль качества?
• Решение. Нужно найти 20% от общего количества изготовленных приборов (500). 20% = 0,2. 500 * 0,2 = 100. 100 из общего количества изготовленных приборов контроль не прошло.

Тип 2: Находим число по его проценту (дроби).

• Задача. Готовясь к экзамену, школьник решил 38 задач из пособия для самоподготовки. Что составляет 23% числа всех задач в пособии. Сколько всего задач собрано в этом пособии для самоподготовки?
• Решение. Мы не знаем, сколько всего задача в пособии. Но зато нам известно, что 38 задач составляют 25% от общего их количества. Запишем 23% в виде дроби: 0,23. Далее нам следует известную нам часть целого разделить на ту долю, которую она составляет от всего целого: 38/0,25 = 38 * 100/25 = 152. Именно 152 задачи включили в этот сборник.

Тип 3: Находим процентное отношение двух чисел (часть от целого числа).

• Задача. В классе 30 учеников. 14 из них – девочки. Сколько процентов девочек в классе?
• Решение. Чтобы узнать, какой процент составляет одно число от другого, нужно то число, которое требуется найти, разделить на общее количество и умножить на 100%. Значит, 14/30*100% = 7/15*100% = 7*100%/15 = 47%.

Тип 4: Увеличиваем число на процент.

• Задача. На прошлогоднем экзамене по математике 140 старшеклассников получили пятерки. В этом году число отличников выросло на 15%. Сколько человек получили пятерки за экзамен по математике в этом году?
• Решение. Если некое число а увеличено на х%, то оно увеличилось в (1 + х /100) раз. Откуда а * (1 + х /100). Подставим в эту формулу данные нам по условию задачи цифры и получим ответ: 140 * (1 + 15/100) = 161.

Тип 5: Уменьшаем число на процент.

• Задача. Год назад школу закончили 100 ребят. А в это году выпускников на 25 меньше. Сколько выпускников в этом году?
• Решение. Если число а уменьшено на х% и при этом 0 ≤ х ≤ 100, то число уменьшено в (1 – х/100) раз. И нужное нам число находим по формуле а * (1 – х/100). Подставляем цифры из условия задачи и получаем ответ: 100 * (1 – 25/100) = 75.

Тип 6: Задачи на простые проценты.

• Задача. Родители взяли в банке кредит 5000 рублей сроком на год под 15% ежемесячно. Сколько денег они заплатят банку через год?
• Решение. Простые проценты называются так, потому что они начисляются многократно, но всякий раз к исходной сумме. Если обозначить исходную сумму как а, сумму, которая наращивается, как S, процентную ставку как х% и количество периодов начисления процента как у, то формулу можно записать так: S = а * (1 + у * х/100). Теперь подставим сюда цифры из условия задачи и узнаем, сколько денег родители заплатят банку: S = 5000 * (1 + 12 * 15/100) = 14000.

Тип 7: Задачи на сложные проценты.

• Задача. На этот раз сумма кредита 25000 рублей, взятых под те же 15% сроком на 3 месяца. Снова надо узнать, сколько денег придется заплатить банку по истечении срока кредита.
• Решение. Сложные проценты отличаются от простых тем, что процент много раз начисляется не к исходной сумме, а к сумме с уже начисленными раньше процентами. Пускай снова S – наращиваемая сумма, а – исходная, х% – процентная ставка, у – количество периодов начисления процента. В этом случае формула принимает вид: S = а * (1 + х/100)^у. Подставляем цифры из условия: S = 25000 * (1 + 15/100)³ = 38021,875 – искомая сумма.

Кстати, простые задачи на проценты можно очень легко решать с помощью пропорции. Этот метод наглядный и дает такой же результат, так что выбирать можно каждому тот способ решения, который кажется проще. Давайте решим задачу №3 про класс и процент девочек в нем, составив пропорцию.

• Решение. Обозначим искомый процент девочек в классе как х, общее количество учеников примем за 100%. Пропорция выглядит так:

30 – 100%
14 – х%

Перемножим крест накрест левую и правую части пропорции и получим, что 30* х = 14 * 100 («30 относится к х также, как 14 относится к 100»). Откуда найти х уже совсем несложно: х = 14 * 100/30 = 47%.

Задачи на проценты с решением

Давайте решим несколько задач для подготовки к ЕГЭ. Как вы сами видите, решать их совсем несложно. Сейчас просто закрепим материал.

Задача 1. После открытия торгов на бирже в понедельник акции некой компании выросли в цене на неизвестное количество процентов. А во вторник на то же самое количество процентов упали в цене. В итоге они подешевели на 4% по отношению к своей первоначальной стоимости в понедельник. На какой процент акции этой компании поднимались в цене в понедельник?

Решение. Пускай первоначальная стоимость акций это 1. В понедельник акции дорожают на х * 100%. Их стоимость в это время: 1 + х * 1. Во вторник акции дешевеют на х * 100%. Их стоимость после этого: 1 + х – х * (1 + х). После чего они стали дешевле на 4%, т.е. стали стоить 0,96.

Отсюда 1 + х – х * (1 + х) = 0,96 ↔1 – х² = 0,96 ↔ х² = 0,04 ↔ х = 0,2. Т.е. в понедельник акции компании дорожали на 20%.

Задача 2. Четыре пары брюк дешевле одного пальто на 8%. Подсчитайте, на сколько процентов пять пар брюк стоят дороже, чем одно пальто.

Решение. Исходя из условия задачи, стоимость четырех пар брюк – это 92% от стоимости пальто. Легко подсчитать, что стоимость одной пары брюк – это 23% стоимости пальто (92/4 = 23). Теперь умножим стоимость одной пары брюк на пять и узнаем, что пять пар брюк обойдутся в 115% стоимости пальто (23 * 5 = 115). Т.е. пять пар брюк на 15% дороже, чем одно пальто.

Задача 3. Семья состоит из трех человек: муж, жена и дочь-студентка. Если зарплата мужа вырастет в два раза, общий доход семьи возрастет на 67%. Если дочери в три раза урежут стипендию, общий доход этой семьи уменьшится на 4%. Надо вычислить, какой процент в общий доход семьи приносит заработок жены.

Решение. Из условия следует, что общий доход семьи находится в прямой зависимости от доходов мужа. Не так важно, насколько ему поднимут зарплату. В любом случае общий доход семьи вырастет на 67%. Значит, зарплата мужа составляет как раз эти 67% от общего дохода. Если стипендия дочери уменьшится в три раза (т.е. на 1/3), останется 2/3 – это и есть 4%, на которые уменьшился бы семейных доход. Можно составить простую пропорцию и выяснить, что раз 2/3 стипендии – это 4% дохода, то вся стипендия – это 6%. А теперь отнимем от всего дохода вклад мужа и дочери и узнаем, какой процент составляет заработок жены в общем доходе семьи: 100% – 67%  – 6% = 27%.

Задача 4. В емкости находится 5 литров водного раствора с концентраций вещества, равной 12%. В емкость добавили еще 7 литров воды. Раствор какой концентрации (с каким процентным содержанием вещества) получился после этого?

Решение. Опишем концентрацию вещества в растворе такой формулой: С = Vвещества/ Vраствора * 100%. Изначально в растворе содержится 0,12 * 5 = 0,6 литра вещества. Когда были добавлены 7 литров воды, объем раствора в емкости увеличился. Но концентрация вещества понизилась (его объем остался неизменным). Подставим все известные нам цифры в формулу и получим ответ: 0,6/5 + 7 *100% = 0,6 /12 * 100% = 5%.

Задача 5. В свежих абрикосах 90% влаги, а в кураге, которая из них получается, только 5%. Сколько килограммов абрикосов нужно, чтобы получить 20 килограммов кураги?

Решение. Исходя из условия, в абрикосах 10% питательного вещества, а в кураге оно содержится в концентрированном виде – 95%. Поэтому в 20 килограммах кураги 20 * 0,95 = 19 кг питательного вещества. На вопрос задачи мы ответим, если разделим одинаковое количество питательного вещества, которое содержится в разных объемах свежих абрикосов и кураги, на его процентное содержание в абрикосах. Чтобы получить 20 килограммов кураги, нужно взять 19/0,1 = 190 килограммов свежих абрикосов.

Заключение

Сами видите, решать задачи на проценты не так уж сложно. Если усвоить основные правила и подключить воображение, вы сможете щелкать такие задачки как орешки.

Вы даже можете составить задачу на проценты сами по нашим образцам. Кстати, будет очень хорошо, если вы так и поступите. Можете оставить нам свои задачи в комментариях – пускай другие наши читатели решат ваши задачи. А вы сможете решить те, что придумают они. Чтобы задач для подготовки к экзаменам получилось больше, расскажите про эту статью своим друзьям в социальных сетях.

Вот увидите, задачи на проценты вам придется решать еще много раз даже после того, как вы закончите школу. Они встречаются в физике, химии, биологии. Да и в повседневной жизни умение решать их может не раз пригодится. Не бойтесь сложных задач – мы всегда поможем вам найти к ним ключ.

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Метод решения задач с процентами

Все соотношения и формулы, полученные для решения задач с процентами выводятся из пропорции

Данные задачи на проценты можно записать в виде следующих соотношений:

все – 100% часть – часть в %

которые можно записать в виде пропорции

все	=	100%
часть	часть в %

Используя эту пропорцию можно получить формулы для решения основных типов задач на проценты.

Примеры решения задач на проценты

30 соответствует 100% x соответствует 15%

решим полученное уравнение

Ответ: 15% от 30 равно 4.5.

20 соответствует 100% 35 соответствует x

решим полученное уравнение

Ответ: 35 составляет 175% от 20.

x соответствует 100% 20 соответствует 5%

решим полученное уравнение

Ответ: 400.

При изучении процентов вам также будут полезны:

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Как решать задачи с процентами

О чем эта статья:

Основные определения

Когда мы сравниваем разные части целого, мы используем такие понятия, как половина (1/2), треть (1/3), четверть (1/4). Это удобно: отрезать половину пирога, пройти треть пути, закончить первую четверть в школе.

Чтобы сравнивать сотые доли, придумали процент (1/100): с латинского языка — «за сто».

Процент — это одна сотая часть от любого числа. Обозначается вот так: %.

Как перевести проценты в десятичную дробь? Нужно убрать знак % и разделить число на 100. Например, 18% — это 18 : 100 = 0,18.

А если нужно перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Например:

Выразить дробь в процентах просто. Для перевода сначала превратим ее в десятичную дробь, а потом используем предыдущее правило и переведем десятичную дробь в проценты:

Типы задач на проценты

В 5, 6, 7, 8, 9 классах в задачках по математике на проценты сравнивают части одного целого, определяют долю части от целого, ищут целое по части. Давайте рассмотрим все виды задач на проценты.

Тип 1. Нахождение процента от числа

Чтобы найти процент от числа, нужно число умножить на процент.

Задача. За месяц на заводе изготовили 500 стульев. 20% изготовленных стульев не прошли контроль качества. Сколько стульев не прошло контроль качества?

Как решаем: нужно найти 20% от общего количества изготовленных стульев (500).

Ответ: из общего количества изготовленных стульев контроль не прошли 100 штук.

Тип 2. Нахождение числа по его проценту

Чтобы найти число по его проценту, нужно его известную часть разделить на то, сколько процентов она составляет от числа.

Задачи по поиску процента по числу и числа по его проценту очень похожи. Чтобы не перепутать — внимательно читаем условия, иначе зайдем в тупик или решим неправильно. Если в задании есть слова «который», «что составляет» и «который составляет» — перед нами задача по нахождению числа по его проценту.

Задача. Школьник решил 40 задач из учебника. Что составляет 16% числа всех задач в книге. Сколько всего задач собрано в этом учебнике?

Как решаем: мы не знаем, сколько всего задач в учебнике. Но нам известно, что 40 задач составляют 16% от общего количества. Запишем 16% в виде дроби: 0,16. Далее известную нам часть целого разделим на ту долю, которую она составляет от всего целого.

40 : 0,16 = 40 · 100 : 16 = 250

Ответ: 250 задач собрано в этом учебнике.

Тип 3. Нахождение процентного отношения двух чисел

Чтобы найти, сколько процентов одно число составляет от другого, нужно ту часть, о которой спрашивается, разделить на общее количество и умножить на 100%.

Задача. В классе учится 25 человек. 10 из них — девочки. Сколько процентов девочек в классе?

Как решаем: поделим 10 на 25, полученную дробь переведем в проценты.

10/25 * 100% = 2/5 * 100% = 2 * 100/5 = 40%

Ответ: в классе 40% девочек.

Тип 4. Увеличение числа на процент

Чтобы увеличить число на некоторое количество процентов, можно найти число, которое выражает нужное количество процентов от данного числа, и сложить его с данным числом.

А можно воспользоваться формулой:

a = b · (1 + с : 100),

где a — число, которое нужно найти,

b — первоначальное значение,

c — проценты.

Задача. В прошлом месяце стикерпак стоил 110 рублей. А в этом месяце на 12% больше. Сколько стоит стикерпак?

Как решаем: можно найти 12% от 110:

Прибавить к исходному числу:

110 + 13,2 = 123,2 рубля.

Или можно воспользоваться формулой, тогда:

110 · (1 + 12 : 100) = 110 · 1,12 = 123,2.

Ответ: стоимость стикерпака в этом месяце — 123 рубля 20 копеек.

Тип 5. Уменьшение числа на процент

Чтобы уменьшить число на несколько процентов, можно найти число, которое выражает нужное количество процентов данного числа, и вычесть его от данного числа.

А можно воспользоваться формулой:

a = b · (1 − с : 100),

где a — число, которое нужно найти,

b — первоначальное значение,

c — проценты.

Задача. В прошлом году школу закончили 100 ребят. А в этом году выпускников на 25% меньше. Сколько выпускников в этом году?

Как решаем: можно найти 25% от 100:

Вычесть из исходного числа 100 − 25 = 75 человек.

Или можно воспользоваться формулой, тогда:

100 · (1 − 25 : 100) = 75/p>

Ответ: 75 выпускников в этом году.

Тип 6. Задачи на простые проценты

Простые проценты — метод расчета процентов, при котором начисления происходят на первоначальную сумму вклада или долга.

Формула расчета выглядит так:

S = а · (1 + у · х : 100),

где a — исходная сумма,

S — сумма, которая наращивается,

x — процентная ставка,

y — количество периодов начисления процента.

Задача. Марии срочно понадобились деньги и она взяла на один год в долг 70 000 рублей под 8% ежемесячно. Сколько денег она вернет через год?

Как решаем: подставим в формулу данные из условий задачи.

70 000 · (1 + 12 · 8 : 100) = 137 200

Ответ: 137 200 рублей вернет Мария через год.

Тип 7. Задачи на сложные проценты

Сложные проценты — это метод расчета процентов, когда проценты прибыли прибавляют к сумме на остатке каждый месяц. В следующий раз проценты начисляют на эту новую сумму.

Формула расчета выглядит так:

S = а · (1 + х : 100) y ,

где S — наращиваемая сумма,

a — исходная,

x — процентная ставка,

y — количество периодов начисления процента.

Задача. Антон хочет оформить вклад 10 000 рублей на 5 лет в банке, который дает 10% годовых. Какую сумму снимет Антон через 5 лет хранения денег в этом банке?

Как решаем: просто подставим в формулу данные из условий задачи:

10000 · (1 + 10 : 100)3 = 13 310

Ответ: 13 310 рублей снимет Антон через год.

Курсы по математике для учеников с 1 по 11 классы. Вводный урок — бесплатно!

Есть случаи, когда найти процент от числа проще, если представить проценты в виде простых дробей. В таком случае будем искать часть числа.

• 10% — десятая часть целого. Чтобы найти десять %, понадобится известное разделить на 10.
• 20% — пятая часть целого. Чтобы вычислить двадцать % от известного, его нужно разделить на 5.
• 25% — четверть целого. Чтобы вычислить двадцать пять %, понадобится известное разделить на 4.
• 50% — половина целого. Чтобы вычислить половину, нужно известное разделить на 2.
• 75% — три четверти целого. Чтобы вычислить семьдесят пять %, нужно известное значение разделить на 4 и умножить на 3.

Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?

Ответ: средств хватит, так как пиджак стоит 6375 рублей.

Задачи на проценты с решением

Как мы уже убедились, решать задачи на проценты совсем несложно. Для закрепления материала рассмотрим реальные примеры на проценты из учебников и несколько заданий для подготовки к ЕГЭ.

Задача 1. Организм взрослого человека на 70% состоит из воды. Какова масса воды в теле человека, который весит 76 кг?

Ответ: масса воды 53,2 кг

Задача 2. Цена товара понизилась на 40%, затем еще на 25%. На сколько процентов понизилась цена товара по сравнению с первоначальной ценой?

Обозначим первоначальную цену товара через х. После первого понижения цена станет равной.

Второе понижение цены составляет 25% от новой цены 0,6х, поэтому после второго понижения получим:

0,6х – 0,25 * 0,6x = 0,45x

После двух понижений изменение цены составит:

Так как величина 0,55x составляет 55% от величины x, то цена товара понизилась на 55%.

Задача 3. Четыре пары брюк дешевле одного пальто на 8%. На сколько процентов пять пар брюк стоят дороже, чем одно пальто?

По условиям задачи стоимость четырех пар брюк — это 92% от стоимости пальто

Получается, что стоимость одной пары брюк — это 23% стоимости пальто.

Теперь умножим стоимость одной пары брюк на пять и узнаем, что пять пар брюк обойдутся в 115% стоимости пальто.

Ответ: пять пар брюк на 15% дороже, чем одно пальто.

Задача 4. Семья состоит из трех человек: муж, жена и дочь-студентка. Если зарплата мужа вырастет в два раза, общий доход семьи возрастет на 67%. Если дочери в три раза урежут стипендию, общий доход этой семьи уменьшится на 4%. Вычислить, какой процент в общий доход семьи приносит заработок жены.

По условиям задачи общий доход семьи напрямую зависит от доходов мужа. Благодаря увеличению зарплаты общий доход семьи вырастет на 67%. Значит, зарплата мужа составляет как раз 67% от общего дохода.

Если стипендия дочери уменьшится в три раза (т.е. на 1/3), останется 2/3 — это и есть 4%, на которые уменьшился бы семейных доход.

Можно составить простую пропорцию и выяснить, что раз 2/3 стипендии — это 4% дохода, то вся стипендия — это 6%.

А теперь отнимем от всего дохода вклад мужа и дочери и узнаем, какой процент составляет заработок жены в общем доходе семьи: 100 – 67 – 6 = 27.

Ответ: заработок жены составляет 27%.

Задача 5. В свежих абрикосах 90% влаги, а в сухофрукте кураге только 5%. Сколько килограммов абрикосов нужно, чтобы получить 20 килограммов кураги?

Исходя из условия, в абрикосах 10% питательного вещества, а в кураге в концентрированном виде — 95%.

Поэтому в 20 килограммах кураги 20 * 0,95 = 19 кг питательного вещества.

Значит, 19 килограммов питательного вещества в абрикосах — это 10% веса свежих абрикосов. Найдем число по проценту.

Ответ: 190 кг свежих абрикосов потребуется для изготовления 20 кг кураги.

Задачи на проценты: 3 способа решения с примерами

Как решать задачи на проценты? Есть 3 способа, выбирай тот, который для тебя проще и понятнее.

Умение быстро и правильно решать задачи на проценты важно, как для успешной сдачи ЕГЭ, так и для повседневной жизни. И если в ЕГЭ вы можете встретить такую задачу в задании 11, то в повседневной жизни такие задачи повсюду.

Зарплату повысили на 15%, а потом оштрафовали на 10%, после этого из зарплаты удержали налог 13% — сколько же мы получим в конце месяца? Коммунальные услуги повысили на 15%, сколько они теперь будут стоить? При возврате ж/д билета вернут только 20% стоимости, какую сумму мы получим? Все это задачи на проценты, которые нам приходится решать каждый день.

Поэтому умение быстро и правильно решать задачи на проценты – это полезно.

Задачи на проценты: вся суть

Задачи на проценты, как правило, описывают жизненную ситуацию. В ней присутствует какая-то величина, которая увеличивается или уменьшается на сколько-то процентов. Таким образом, в задаче на проценты упоминается такие данные, как первоначальная величина, конечная величина и процент, на который эта величина изменилась. Чаще всего в задаче требуется найти либо первоначальную величину, либо конечную величину, реже – процент, на который эта величина изменилась.

Решение задач на проценты с помощью формулы простого процента

Формула, которой мы пользуемся при решении задач на проценты, называется формула простого процента:

Х_{конечное} – конечная величина

Х_{первоначальное} – первоначальная величина

k – процент, на который первоначальная величина изменилась

Из этой формулы всегда можно найти первоначальную величину или процент, на который происходит изменение.

Знак стоящий перед k зависит от того, увеличивается первоначальная величина или уменьшается. Так, если величина увеличивается на сколько-то процентов, то ставим знак плюс. Если уменьшается – минус.

Для наглядности приведем несколько простых примеров.

Задача 1

В городе проживало 30 000 человек. В результате строительства нового микрорайона количество жителей увеличилось на 6%. Сколько человек стало проживать в городе?

Решение: Очевидно, что в этой задаче нам известна первоначальная величина – 30 000 человек и процент, на который она увеличилась +6% Нужно найти конечную величину.

30 000 * ((100 + 6)/100) = х

х = 31 800 человек

Ответ: 31 800 человек

Задача 2

Сколько килограмм яблок нужно собрать, чтобы получить из них 5 килограмм сушеных яблок, если известно, что в свежих яблоках содержится 90% воды?

Решение: В этой задаче нам известна конечная величина – 5 килограмм и процент, на который происходит изменение -90%. Нужно найти первоначальную величину:

5 = х * ((100 – 90) / 100)

Задача 3

Холодильник стоимостью 20 000 рублей был продан спустя месяц за 22 000 рублей. На сколько процентов увеличилась стоимость холодильника?

Решение: В данной задаче нам известна первоначальная (20 000 рублей) и конечная величина (22 000 рублей), а найти нужно процент, на который данная величина изменилась.

22 000 = 20 000 * ((100 + х) / 100)

22 000 / 20 000 = 1 + х/100

Решение задач на проценты: метод пропорции

Еще один способ решения задач на проценты – это метод пропорции. Это наиболее простой способ решения таких задач.

Напомним, что пропорция – это равенство двух отношений:

Для нас важно основное свойство пропорции, которое заключается в том, что произведение крайних членов пропорции равно произведению средних членов. Проще запомнить, что мы можем перемножить члены пропорции крест-накрест:

При решении задач на проценты с помощью метода пропорции необходимо руководствоваться следующим правилом:

Далее записываем пропорцию:

Давайте решим приведенные выше примеры задач на проценты с помощью метода пропорции.

Задача 4

В городе проживало 30 000 человек. В результате строительства нового микрорайона количество жителей увеличилось на 6%. Сколько человек стало проживать в городе?

Решение: Итак, в городе проживало 30 000 человек и это всё его население, т.е. 100%. Так и запишем:

Далее население выросло на 6%, т.е. всё его население стало составлять 100% + 6% = 106% и нам неизвестно, сколько это человек, т.е. Х человек. Запишем:

Таким образом, получаем:

Составим пропорцию: Правую дробь пропорции можно сократить на 2, получим: Теперь воспользуемся основным свойством пропорции и перемножим ее члены крест-накрест:

30 000 * 53 = 50х

Далее обе части полученного уравнения мы можем разделить на 50, получим:

Ответ: 31 800 человек

Задача 5

Сколько килограмм яблок нужно собрать, чтобы получить из них 5 килограмм сушеных яблок, если известно, что в свежих яблоках содержится 90% воды?

Решение: Нам неизвестно первоначальное количество всех яблок (всё количество), т.е. это Х, которое составляет 100%. Количество сушеных яблок (часть от первоначального количества яблок) составляет 5 кг. Причем известно, что количество сушеных яблок на 90% меньше от первоначального количества яблок (т.к. 90% — это вода, которая из них испарилась). Следовательно, количество сушеных яблок составит 100% — 90% = 10%. Запишем наши рассуждения:

Запишем наши рассуждения: Сократим правую дробь на 10, получим:Воспользуемся основным свойством пропорции и перемножим ее члены крест-накрест:

Задача 6

Холодильник стоимостью 20 000 рублей был продан спустя месяц за 22 000 рублей. На сколько процентов увеличилась стоимость холодильника?

Решение: Нам известно, что исходная цена – 20 000 рублей, следовательно, 20 000 рублей – это 100%. Тогда конечная цена 22 000 рублей – это неизвестное количество процентов, т.е. Х%. Так и запишем:

Теперь запишем пропорцию: Сократим левую дробь на 2 000, получим: Воспользуемся основным свойством пропорции, то есть перемножим ее члены крест-накрест:

В результате решения мы получили результат 110%, но он не является ответом! Ведь нам нужно найти, на сколько процентов изменилась стоимость холодильника. Чтобы это узнать, нужно из полученного числа процентов отнять 100%:

Решение задач на проценты методом коэффициентов

Можно назвать еще один метод решения задач на проценты, который является следствием из формулы простого процента. Так, формулу простого процента можно переписать следующим образом:

Таким образом, мы получили формулу для решения задач на проценты методом коэффициентов. Полученная формула удобна тем, что при достаточной практике простые задачи на проценты можно решать в уме, даже не задумываясь.

Например, яблоки стоили 150 рублей, затем они подорожали на 20%. Найдите новую стоимость яблок.

Применим полученную формулу и получим:

150 * 1,2 = 180 рублей

То есть мы интуитивно 20% превращаем в 0,2 прибавляем единицу, так как происходит увеличение на данное количество процентов, и умножаем на первоначальную стоимость.

Или другой пример. Зарплата работника составляла 25 000 рублей в месяц, в результате применения штрафа за опоздания зарплата сократилась на 10%. Найти сумму зарплаты, которую получит оштрафованный работник.

25 000 * 0,9 = 22 500 рублей

Опять же мы сразу понимаем, что 10% — это 0,1. Т.к. происходит уменьшение первоначальной величины на это количество процентов, то мы вычитаем из единицы этот процент и получаем 0,9. Затем умножаем полученное значение на первоначальную величину. Готово!

Давайте решим этим методом задачу про зарплату и налоги.

Задача 7

В России налог на доходы физических лиц составляет 13%. Зарплата Марии Ивановны после удержания налога на доходы составила 60 900 рублей. Найти сумму зарплаты Марии Ивановны до удержания налога.

Решение: Итак, 13% — это 0,13. Первоначальная зарплата уменьшилась на этот процент, значит, вычитаем из единицы и получаем 1 – 0,13 = 0,87. Подставляем в формулу:

Ответ: 70 000 рублей

Задача 8

В школе 1000 учеников, из них 20% — ученики начальной школы. Среди учеников средней и старшей школы 30% изучают французский язык. Сколько учеников в школе изучают французский язык, если в начальной школе французский язык не изучают?

Решение: Для начала из общего количества учеников исключим тех, кто французский язык точно не изучает, т.е. учеников начальной школы. Ученики начальной школы – это 20%, т.е. 0,2, мы уменьшаем на этот процент, следовательно, вычитаем из единицы и получаем 1 – 0,2 = 0,8.

Из 800 полученных учеников французский язык изучают только 30%.

Обратите внимание, что здесь идет речь о проценте от числа. Т.е. мы не уменьшаем на 30% (в этом случае мы вычитаем значение процента в долях из единицы) и не увеличиваем на 30% (в этом случае мы прибавляем к значению процента в долях к единице), а берем 30% от заданного числа (в этом случае мы умножаем заданное число на значение процента в долях). Всегда внимательно читайте условия задачи!

В нашем случае нам нужно найти 30% от 800:

Это и есть ответ. 240 учеников изучают французский язык в школе.

Ответ: 240 учеников.

Задача 9

Разберем еще одну задачу на проценты, которая часто встречается на ЕГЭ и в которой легко можно допустить ошибку.

Задача: Зарплата рабочего составляла 30 000 рублей, затем зарплату повысили на 30%, а потом понизили на 30%. Какую зарплату стал получать рабочий?

Решение: быстро прочитав условие задачи, сходу хочется дать ответ – зарплата останется прежней, ее размер не изменился. Но это не так! Давайте разбираться.

Будем решать по формуле простого процента.

Первое событие – зарплату повысили на 30%. Следовательно, первоначальную сумму мы увеличиваем на 30%:Второе событие – зарплату понизили на 30%. Следовательно, нашу увеличенную зарплату мы теперь уменьшаем на 30%:Таким образом, рабочий теперь будет получать зарплату 27 300 рублей.

Данную задачу мы могли бы решить в одно действие, применяя формулу для вычисления сложного процента. Напомним ее:

S = P (1 + i) n , где

S – это конечная сумма;

P – это первоначальная сумма;

i – это процент/100;

n – количество периодов.

Т.к. 30% — это 0,3, то, применяя формулу для вычисления сложного процента к нашей задаче, мы получим:

30 000 * (1 + 0,3) 1 (1 – 0,3) 1 = 27 300 рублей

Результат получился тот же.

Ответ: 27 300 рублей

В этой статье были разобраны достаточно простые примеры задач на проценты, чтобы максимально доступно продемонстрировать методы решения задач на проценты. В профильном ЕГЭ с процентами вы можете столкнуться в задаче с экономическим содержанием по вкладам и кредитам. Такие задачи гораздо сложнее и подробное их решение вы можете посмотреть на нашем сайте.

Итак, надеюсь, что данная статья помогла вам понять, как решать задачи на проценты. Мы увидели, что задачи на проценты можно решать тремя способами – с помощью формулы простого процента, методом пропорции и методом коэффициентов. Выбирайте тот, который вам наиболее понятен, и которым вам решать такие задачи проще.

[spoiler title=”источники:”]

http://skysmart.ru/articles/mathematic/kak-reshat-zadachi-s-procentami

http://yourrepetitor.ru/kak-reshat-zadachi-na-procenty/

[/spoiler]

Комитет образования и науки
Волгоградской области Государственное автономное  учреждение дополнительного
профессионального образования «Волгоградская государственная академия
последипломного образования»

КАФЕДРА
ТЕОРИИ И МЕТОДИКИ ОБУЧЕНИЯ МАТЕМАТИКЕ

Дипломный
проект

МЕТОДИКА
ОБУЧЕНИЯ УЧАЩИХСЯ ОСНОВНОЙ ШКОЛЫ РЕШЕНИЮ ЗАДАЧ НА ПРОЦЕНТЫ

Волгоград  
2017

Содержание

Введение___________________________________________________3

Глава I. Теоретические аспекты методики обучения учащихся основной
школы решению задач на проценты_________________________________7

1.1.  Для чего нужны проценты? _______________________________7

1.2. Из истории возникновения
процентов и их проникновения в школьный курс математики________________________________________9

1.3 .  Анализ изложения темы
«Проценты» в учебниках математики 5-6 классов_________________________________________________________10

1.4 Анализ изложения различных тем,
связанных с процентами в учебниках  алгебры 7-9 классов____________________________________13

Выводы по первой главе_____________________________________16

Глава II. Методические аспекты обучения учащихся основной школы
решению задач на проценты_______________________________________17

2.1 Методика формирования приёмов
решения задач на проценты__17

2.2 Методические рекомендации по
решению задач на проценты___19

Выводы по второй главе_____________________________________24

Заключение________________________________________________25

Приложение 1______________________________________________27

Литература_________________________________________________33

Введение

В настоящее время
появляется все больше специальностей, требующих высокого уровня образования,
связанного с непосредственным применением математики (экономика, бизнес,
финансы, физика, химия и многие другие). Другими словами, расширяется круг
школьников, для которых математика становиться профессионально значимым
предметом. Поэтому одна из важнейших задач школьного образования – обеспечить
учащимся глубокие и прочные знания, а также умение рационально применять их в
учебной и практической деятельности. Большое практическое значение имеет умение
решать задачи на проценты, поскольку понятие процента широко используется как в
реальной жизни, так и в различных областях науки.

Тема «Проценты»
является универсальной в том смысле, что она связывает между собой многие
точные и естественные науки, бытовые и производственные сферы жизни. Учащиеся
встречаются с процентами на уроках экономики, химии, экологии, при чтении
газет, просмотре телепередач. Умением грамотно и экономно проводить
элементарные процентные вычисления обладают далеко не все учащиеся, хотя многие
из них ориентированы на поступление в высшие учебные заведения. Практика
показывает, что очень многие выпускники не только не имеют прочных навыков
обращения с процентами в повседневной жизни, но даже не понимают смысла
процентов. Тому есть несколько причин.

Во-первых,
проценты изучаются на первом этапе основной школы, в 5–6 классах. К этому времени учащиеся умеют в
задачах практического характера находить дробь числа (величины), число
(величину) по его (ее) дроби и определять, какую часть одна величина составляет
от другой. Указанные умения если и обобщаются учителем в виде правил, то сами
правила никак не помогают перенести уже освоенное умение в новую ситуацию, так
как при решении конкретных задач на проценты речь идет не о числителе и
знаменателе дроби, а о количестве процентов, содержащихся в целом и его части.

Во-вторых, в
решении задач на проценты довольно скоро начинают применять пропорции. Это
требует предварительного определения характера пропорциональности величин
(прямая или обратная). Тем самым процесс решения задач «механизируется», что
мешает учащимся понять смысл своих действий.

В-третьих,
учащиеся 5-6 классов еще не имеют опыта практического применения процентов.
Следовательно, не имеют потребности в решении предлагаемых им задач на проценты.

Основные понятия,
изучаемые в теме «Проценты», являются важными понятиями для всего курса
математики: «раствор», «сплав», «смесь», «концентрация», «простой и сложный
процентный рост» и т.д., поэтому необходимо уже на начальном этапе обучения
добиться высокого уровня знаний, умений и навыков учащихся. В школьном курсе
тема «Проценты» изучается в V – VI классе, но в силу возрастных особенностей
школьников, их оторванности от практического применения процентов не может быть
усвоена осознанно. Именно начальный этап изучения этого материала определяет
дальнейшее успешное обучение учащихся, формирует умение переносить полученные
знания в новую ситуацию на протяжении изучения всего курса математики.

В курсе алгебры
основной школы этому вопросу не уделяется значительного внимания. Задачи на
проценты становятся прерогативой химии, которая внедряет свой взгляд на
проценты, а в математике их место остается только в рамках задач на повторение
и задач повышенной трудности. Таким образом, ученик постепенно забывают
проблемы универсальности процентов и разнообразие сфер их применения.

Важно отметить,
что в материалы Единого Государственного Экзамена входит задача на проценты. В
связи с этим вопрос о том, чтобы задачи на проценты заняли достойное место в
VII – IX классах является актуальным. В этот период школьники изучают различные
виды уравнений и их систем, широко применяемых при решении текстовых задач.
Использование процентов в содержании текстовых задач дает возможность связать
абстрактные математические понятия с реальной жизнью.

Проблема
исследования состоит в том, как построить процесс изучения данной темы, чтобы наиболее
эффективно реализовать основную образовательную задачу всего курса математики:
научить учащихся оперировать понятиями «процент», «процентное отношение двух
чисел», переносить полученные знания, умения и навыки в новую ситуацию,
выработать умения выполнять действия и преобразования, используя данные понятия?
Этот вопрос определил цель данного исследования:

Разработка
методических рекомендаций по изучению процентов в 5-9 классах.

Объектом исследования является процесс
обучения математике в 5-9 классах.

Предмет исследования – обучение
решению задач на проценты в основной школе.

Задачи данного исследования:

1. Проанализировать
 учебную, методическую литературу, связанную с проблемой изучения темы
«Проценты» в основной школе;

2.  Выявить
особенности содержания темы «Проценты» в учебниках Математика для основной
школы;

          3. Разработать методические рекомендации по изучению
данной темы и   систему задач на проценты (приложение 1).

Практическая
ценность результатов исследования: Результаты исследования  можно
применять как на основных уроках, так и на элективных курсах, на
индивидуально-групповых занятиях, а так же при подготовке учащихся к экзаменам
ОГЭ, ГВЭ и ЕГЭ.  

Структура работы: данная работа состоит из
введения, двух глав, заключения, приложения и списка используемых источников.

     Во введении обоснована
актуальность исследования, даны его основные характеристики.

  Глава 1 посвящена истории
возникновения понятия «процент», а так же проводится анализ содержания темы
«Проценты» в учебниках для 5-6 класса  Н.Я.Виленкина и 7-9 классы учебник  Ю.Н.Макарычева.

  В главе 2 рассматриваются
методические аспекты обучения учащихся основной школы решению задач на
проценты, методические рекомендации по решению задач на проценты, разработана
система задач на проценты.

В заключении приведены основные
выводы исследования.

В приложении – задачи на проценты .

Глава I. Теоретические аспекты методики
обучения учащихся основной школы решению задач на проценты

1.1.  Для чего нужны
проценты?

Роль и место
задач в обучении математике.

В
процессе обучения математике задачи выполняют разнообразные функции. Учебные
математические задачи являются очень эффективным и часто незаменимым средством
усвоения учащимися понятий и методов школьного курса математики, вообще
математических теорий. Велика роль задач в развитии мышления и в математическом
воспитании учащихся, в формировании у них умений и навыков в практических
применениях математики. Решение задач служит достижению всех тех целей, которые
ставятся перед обучением математике. Правильная методика обучения решению
математических задач играет существенную роль в формировании высокого уровня
математических знаний, умений и навыков учащихся. При обучении математике
задачи имеют большое и многостороннее значение.

Образовательное
значение математических задач.

Решая
математическую задачу, человек познает много нового: знакомится с новой
ситуацией, описанной в задаче, с применением математической теории к ее
решению, познает новый метод решения или новые теоретические разделы
математики, необходимые для решения задачи, и т. д. Иными словами, при решении
математических задач человек приобретает математические знания, повышает свое
математическое образование. При овладении методом решения некоторого класса
задач у человека формируется умение решать такие задачи, а при достаточной
тренировке – и навык.

Практическое
значение математических задач.

В процессе
решения математических задач школьник обучается, в частности, применять
математические знания для решения прикладных задач, готовится к практической
деятельности в будущем, к решению задач, выдвигаемых практикой, повседневной
жизнью. Почти во всех конструкторских расчетах приходится решать математические
задачи, исходя из запросов практики. Математические задачи решаются в физике,
химии, биологии, электро- и радиотехнике, особенно в их теоретических основах,
и др. Это означает, что при обучении математике в 5–6 классах учащимся следует
предлагать задачи, связанные с такими предметами, как физика, химия, география
и др. Например, задачи на «смеси и сплавы» (подобные задачи потом будут широко
применяться в курсе химии в старших классах), а также задачи с практическим,
жизненным содержанием.

Проценты в
повседневной жизни.

Современная жизнь
делает задачи на проценты актуальными, так как сфера практического приложения
процентных расчетов расширяется. Вопросы инфляции, повышение цен, рост
стоимости акций, снижение покупательской способности касаются каждого человека
в нашем обществе. Планирование семейного бюджета, выгодного вложения денег в
банки невозможны без умения производить несложные процентные вычисления. Сами
проценты не дают экономического развития, но их знание помогает в развитии
практических способностей, а также в развитии умения решать экономические
задачи. Осознанное изучение процентов может способствовать развитию таких
навыков как экономичность, расчетливость.

«Брать ссуду в
банке или купить в кредит? Может быть выгоднее накопить денег для покупки
дорогостоящей вещи?» Современный человек должен свободно решать задачи,
предлагаемые самой жизнью, уметь просчитать различные предложения магазинов,
кредитных отделов и различных банков и выбрать наиболее выгодные. Практические
задачи повседневной жизни человека в современном обществе, требуют для своего
решения не только первичных знаний о процентах, но и более глубоких знаний
(простые и сложные проценты, арифметическая и геометрическая прогрессия).

Математика, давно
став языком науки и техники, в настоящее время все шире проникает в
повседневную жизнь и обиходный язык, все более внедряется в традиционно далекие
от нее области. Интенсивная математизация различных областей человеческой
деятельности особенно усилилась с внедрением современных информационных
технологий, требующих математической грамотности человека буквально на каждом
рабочем месте. Понимание
процентов и умение производить процентные расчеты в настоящее время необходимо
каждому человеку, это способствует «вхождению» в современную
информационно-экономическую среду и, в конечном счете, облегчает социализацию.

1.2.  Из истории возникновения
процентов и их проникновения в школьный курс математики

Слово «процент»
от латинского слова «pro centum», что буквально означает «за сотню» или «со
ста». Идея выражения частей целого постоянно в одних и тех же долях, вызванная
практическими соображениями, родилась еще в древности у вавилонян. Ряд задач
клинописных табличек посвящен исчислению процентов. Проценты были особенно
распространены в Древнем Риме. Римляне называли процентами деньги, которые
платил должник заимодавцу за каждую сотню. В древнем Риме были широко
распространены денежные расчеты с процентами. Даже римский сенат вынужден был
устанавливать максимально допустимый процент, взимаемый с должника, т.к.
некоторые заимодавцы чрезмерно усердствовали в получении процентных денег.

От римлян проценты
перешли к другим народам Европы.

Знак %
происходит, как полагают, от итальянского слова cento (сто), которое в
процентных расчетах часто писалось сокращенно cto. Отсюда путем дальнейшего
упрощения в скорописи буква t превратилась в наклонную черту (/), возник
современный символ для обозначения процента. Запись отношений стала удобнее,
исчезли ноль и запятая, а символ % сразу указывает, что перед нами не граммы,
рубли или метры. Введение процентов оказалось удобным не только для оценки
содержания одного вещества в другом. В процентах стали измерять изменение
производства товаров, денежный доход и т.д.

Вообще,
изобретение математических знаков и символов значительно облегчило изучение
математики и способствовало дальнейшему ее развитию.

Современная жизнь
 делает задачи на проценты актуальными, так как сфера практического приложения
процентных расчетов расширяется. Везде — в газетах, по радио и телевидению, в
транспорте и на работе обсуждаются повышение цен, зарплат, рост стоимости
акций, снижение покупательной способности населения и т. п. Добавим сюда
объявления коммерческих банков, привлекающих деньги населения на различных
условиях, сведения о доходах по акциям различных предприятий и фондов, об
изменении процента банковского кредита и пр. Все это требует умения производить
хотя бы несложные процентные расчеты для сравнения и выбора более выгодных
условий. Формирование соответствующих умений в настоящее время оставляет желать
лучшего. Довольно часто даже взрослые люди считают, что повышение цены в 3 раза
соответствует повышению ее на 300%, а повышение зарплаты на 50% не могут
сравнить с увеличением ее в 1,5 раза.

1.3.  Анализ изложения темы
«Проценты» в учебниках математики 5-6 классов

Подходы к
рассмотрению решений типовых задач «на проценты», предлагаемых в современных
учебниках.

Первый подход. Первое знакомство с задачами
«на проценты» ведется без опоры на дроби. Способы решения типовых задач
опираются на содержательный смысл понятия «процент».

Нахождение
нескольких процентов от числа осуществляется в два действия: находится, чему
равен 1% от числа (величины), а затем умножается это число (величина) на
заданное число процентов. Нахождение числа, если известны несколько его
процентов, также осуществляется в два действия: находится, чему равен 1%
искомого числа (величины), а затем результат умножается на 100%. Если требуется
найти, сколько процентов составляет число (величина) а от числа (величины) b,
если нам известны два числа(обе величины), мы находим чему равен 1% числа
(величины) a, затем делим b на 1% числа (величины) a.

Изучение задач на
дроби осуществляется позже задач на проценты. Таким образом, по логике
восприятия информации используется индуктивный метод, т.е. обучение идет от
частного к общему. При таком построении материала учащиеся усваивают
содержательный смысл понятия и отрабатывают данный способ решения задач «на
проценты».

После
ознакомления с типовыми задачами на дроби (обыкновенные или десятичные),
школьники овладевают другим способом решения задач на проценты – как частного
случая задач «на части», перенося все приемы решения задач на дроби на задачи,
связанные с процентами, тем самым реализуется метод аналогии. Этот факт
значительно упрощает поиск решения «новых» задач.

Важно отметить,
что методически целесообразно сначала рассматривать нахождение 1% от данного
числа, затем – нахождение произвольного числа процентов; также в первую очередь
обсуждать, как найти число, 1% которого известен, далее эта задача
рассматривается для любого произвольного числа процентов. Именно при таком
подходе формируется понимание понятия «процент».

Действия с
обыкновенными и десятичными дробями, проценты рассматриваются в 5-6 классах,
поэтому к концу 6 класса школьники овладевают двумя способами решения задач на
проценты.

Второй подход. Задачи на проценты
изначально осваиваются как частный случай задач на дроби, то есть при изучении
материала используется дедуктивный метод – от общего случая, задач на дроби, к
частному.

Для нахождения
нескольких процентов числа (величины) необходимо найти, какую долю от числа
(величины) составляет данный процент (т.е. перевести проценты в обыкновенную
или десятичную дробь путем деления на 100%), а затем умножить исходное число
(величину) на эту долю. Для нахождения числа, если известны несколько его
процентов, выражаем процент дробью (обыкновенной или десятичной), затем делим
заданную часть числа (величины) на эту дробь. Если требуется найти, сколько
процентов составляет число (величина) а от числа (величины) b, если нам
известны два числа (обе величины), мы находим, какую долю числа (величины) b
составляет число (величина) a, а затем получившееся число умножить на 100%.

При таком подходе
учащимися не осваивается способы решения типовых задач «на проценты»,
опирающиеся на содержательный смысл понятия «процент», что влечет за собой
трудности в освоении понятия «Процент».

В учебнике Н.Я.
Виленкина и др. определение «процента» вводится в 5 классе, решаются типовые
задачи, опираясь на содержательный смысл понятия «процент». Так же, одной из
последующих тем является тема «Диаграммы». В 6 классе каждая из трех типовых
задач рассматривается вместе с соответствующей задачей на дроби: «нахождение
процентов от числа» одновременно рассматривается с «нахождением дроби от
числа», «нахождение числа, если известно его p%» – с «нахождением числа по его
дроби», и выражение в процентах отношения двух чисел или величин. Таким
образом, типовые задачи сводятся к задачам «на части» и рассматриваются на
разных уроках.

Важно также
отметить, что рассмотрение трех типовых задач на проценты целесообразнее
проводить на одном уроке, а не на разных.

После введения
понятия «процент» необходимо показать учащимся сферу его практического
применения. Наиболее удачной последующей темой являются диаграммы, используемые
для наглядного представления соотношения между частями целого.

Важно отметить,
что решение трех типовых задач «на проценты» необходимо рассматривать на одном
уроке, повторив предварительно соответствующие задачи на дроби, что позволит в
дальнейшем подчеркнуть взаимосвязь способов решения задач на дроби и на
проценты.

Знакомство с
процентами практически во всех учебниках начинается традиционным образом, а
именно рассказом учителя. Авторы, показывая удобство обозначения словом часто
используемых дробей (например: «треть», «четверть»), подводит учеников к
введению понятия «процент» как одной сотой части числа или величины.

 1.4.  Анализ изложения различных
тем, связанных с процентами в учебниках  алгебры 7-9 классов

В учебных
комплектах тему «Проценты» изучают в несколько подходов с 5 по 9 класс
включительно. При каждом подходе учащиеся возвращаются к процентам на новом
уровне, их знания пополняются, добавляются новые типы задач и приемы решения.
Такое многократное обращение к понятию приводит к тому, что постепенно оно
усваивается прочно и осознано.

Рассмотрим
учебник  Ю.Н.Макарычева, Н.Г.Миндюк, К..И.Нешкова, С.Б.Суворовой, под ред.
С.А.Теляковского.

В начале года при
изучении первых параграфов учащимся предлагаются задачи на нахождение 1 и
нескольких процентов от числа; задачи, при решении которых требуется найти
несколько процентов от величины; на нахождение числа и величины, если известны
несколько его (ее) процентов; задач типа «на сколько процентов одна величина
больше другой». Например.

18. За несколько
книг уплатили 320 р. Стоимость одной из книг составила 30%, а другой 45%
израсходованных денег. На сколько рублей первая книга дешевле второй?

45.  После того
как из бидона отлили 30% молока, в нем осталось 14 л. Сколько литров молока
было в бидоне первоначально?

119. Техническое
перевооружение цеха позволило выпускать в сутки 180 станков вместо 160. На
сколько процентов повысился выпуск станков в сутки?

В дополнительных
упражнениях предлагается задача, решая которую, учащиеся установят зависимость
между количеством процентов, на которое перевыполнили план, и числом
изготовленных бригадой деталей.

359.  Бригада по
плану должна изготовить 150 деталей за смену. Однако она перевыполнила план на
х%. Составьте формулу, выражающую зависимость у (число изготовленных бригадой
деталей) от х. Найдите по формуле:

а) значение у,
если х = 10; 30;

б) значение х,
если у = 150; 180.

Далее
рассматривается понятие «относительная погрешность» и способы ее нахождения.
Затем представлены задачи для самостоятельного решения. Например.

536.  Округлите
число 2,525 до десятых. Найдите относительную погрешность приближения,
полученного при округлении.

В последнем этапе
«Системы линейных уравнений» представлены 2 задачи, при решении которых
необходимо составить систему линейных уравнений с двумя переменными.

1186. Две бригады
должны были по плану изготовить за месяц 680 деталей. Первая бригада
перевыполнила месячное задание на 20%, а вторая на 15%, и поэтому обеими
бригадами было изготовлено сверх плана 118 деталей. Сколько деталей должна была
изготовить по плану каждая бригада за месяц?

Для решения
такого плана задач необходимо хорошо владеть техникой представления процентов в
виде десятичных дробей.

В дополнительных
упражнениях предлагаются учащимся 3 задачи на составление систем линейных
уравнений и 6 задач повышенной трудности (например, № 1245).

1245.  В двух
бочках было воды поровну. Количество воды в первой бочке сначала уменьшилось на
10%, а затем увеличилось на 10%. Количество воды во второй бочке сначала
увеличилось на 10%, а затем уменьшилось на 10%. В какой бочке стало больше
воды?

В задачах для
самостоятельного решения по теме «Стандартный вид многочлена» представлены
задачи, в которых сперва требуется записать буквенное выражение по условию, а
далее воспользоваться аппаратом алгебры. Например.

295. Длина
прямоугольника равна а м, а ширина b м. На сколько квадратных метров увеличится
его площадь, если длину увеличить на 10%, а ширину увеличить на 15%?

В параграфе
«Уравнения» в объяснительном тексте пункта «Решение задач с помощью уравнений»
дается общий алгоритм:

1) обозначить
неизвестное число буквой и составить уравнение, используя условие задачи;

2) решить
уравнение;

3) истолковать
результат в соответствии со смыслом задачи.

В задачах,
предлагаемых для самостоятельного решения, 8 задач на проценты. В том числе,
задача на смеси, задача на раствор, банковские расчеты.

В последней главе
«Системы линейных уравнений» представлены 6 задач, при решении которых
необходимо составить систему линейных уравнений с двумя переменными. Например.

1145. В двух
табунах было 120 лошадей. Когда число лошадей в первом табуне увеличилось на
40%, а во втором уменьшилось на 10%, в первом табуне стало на 30 лошадей
больше, чем во втором. Сколько лошадей было в каждом табуне?

Выводы по первой главе

1. Понятие
«Процент» появилось более чем 500 лет назад. Первоначально проценты применялись
только в торговых и денежных сделках. Затем область применения процентов
расширилась, они встречаются в хозяйственных и финансовых расчётах, статистике,
науке и технике, в повседневной жизни.

2.    Понятие
процента вводится как одна сотая часть числа (величины).

3. В школьных
учебниках по математике для 5-6 классов рассматриваются задачи трёх типов:

– нахождение
процентов от данного числа;

– нахождение
числа по его процентам;

– нахождение
процентного отношения двух чисел.

4.  В 7-9 классах
рассматривают задачи на проценты, решаемые алгебраическим способом: составляя
уравнение или систему уравнений. Это связано с тем, что в 7 классах
рассматриваются задачи, алгебраическая модель которых является линейным
уравнением или системой двух линейных уравнений с двумя неизвестными, в 8
классах – квадратные уравнения.

          5. Первые уроки отводятся
повторению, систематизации сведений об обыкновенных дробях. Продолжается
решение трех основных типов задач на проценты. При решении учащиеся могут
пользоваться двумя приемами – содержательным, на основе смысла дроби, или
формальным, на основе соответствующего правила.

Глава II. Методические аспекты обучения
учащихся основной школы решению задач на проценты

2.1 Методика формирования приёмов
решения задач на проценты.

1.Методика нахождения нескольких процентов от числа.

В данном разделе покажем методику нахождения нескольких процентов
от числа, так как эта тема является одной из трех важнейших, которые должны
понять студенты в теме «проценты». А главное они должны понять алгоритм
нахождения  одного или нескольких процентов от числа, и применять эти
способности на практике, при решении различных задач на проценты.

Важно, чтобы студенты поняли,  для того чтобы находить
проценты от числа нужно понять, что один процент является одной сотой от
данного числа. Из этого следует  необходимость определения одного процента
(а это главное, так как чтобы найти несколько процентов от числа нужно найти
сначала один процент) можно записать равенством:

1 % = 0,01 · а  
                                                                                              

Отсюда, любой студент быстро поймет, что 5% = 0,05;  23% =
0,23; 130%=1,3  и т. д.

Как найти 1% от числа? Раз 1% –  это одна сотая часть, надо
число разделить на 100. Мы уже сделали вывод, что деление на 100 можно заменить
умножением на 0,01. Поэтому, чтобы найти 1% от данного числа, нужно умножить
его на 0,01.

 А если нужно найти 5% от числа, то умножаем данное число на
0,05 и т.д.

Так что отсюда можно вывести алгоритм нахождения одного или
нескольких процентов от числа:

Чтобы найти данное число процентов от числа, нужно проценты
записать десятичной дробью, а затем число умножить на эту десятичную дробь.

2.Методика нахождения числа по его процентам.

Покажем общую методику нахождения числа от одного или нескольких
процентов. Это также является важной частью в изучение процентов, так как
встречаются не только задачи на нахождение процентов от числа, но числа по
процентам. Это особенно хорошо видно в задачах связанных с экономикой
(например, когда в банк кладется сумма под проценты, а через какое-то время
забирается с «набежавшими» процентами и нужно найти данную сумму).  Так
что студентам необходимо раскрыть алгоритм нахождения числа от нескольких
процентов.

Студенты знают, что один процент можно записать десятичной дробью:

1 % = 0,01 · а

Так вот возникает вопрос, как найти искомое  число, если
известно лишь, сколько процентов составляет другое число от искомого? Для этого
нужно сначала проценты записать десятичной дробью, после чего надо данное нам
число разделить на эту десятичную дробь, в результате мы получим число от
нескольких процентов.

Если дано, сколько процентов от искомого числа составляет данное
число, то чтобы найти искомое число, нужно заменить проценты десятичной дробью
и разделить на эту дробь данное число.

3.Методика нахождения процентного отношения.

Рассмотрим  последнее, но не менее важное для нахождения
процентов при решении задач – это нахождение процентного отношения. В этом
разделе изучим алгоритм нахождения процентного отношения.

Встречаются задачи, в которых даны два числа, и нужно найти их
процентное отношение. Для этого нужно взять первое число, назовем его «а», и
разделить его на второе число, назовем его число «в», а затем результат умножим
на сто процентов. Мы получим процентное отношение первого числа на второе

( а / в) · 100 %  
                                                                                             
 

Чтобы найти процентное отношение двух чисел «а» и «в», надо
отношение этих чисел умножить на 100 процентов, то есть получить данную
формулу.

Надо сразу отметить, что такие задачи очень важны в курсе изучения
не только процентов, но и всей математике. В них содержится и проценты числа, и
процентное содержание, а это, как правило, вносит растерянность и путаницу у
студентов при их решении, так как их приучили работать  с чем-то одним при
решении задач.

4.Методика изучения процентов концентрации, смеси и сплавы

Задачи на проценты, концентрации, смеси и сплавы встречаются не
только в математике, но и в химии, где рассматриваются различные соединения.
Они вызывают затруднения у студентов. Причина такой ситуации, на мой взгляд,
заключается в том, что тема “Проценты” изучается в классах, когда собственно
математики еще нет, изучается непродолжительно и, наконец, к задачам на
проценты не возвращаются в старших классах. Неумение решать текстовые задачи
показывает недостаточное знание математики.

Решение этих задач основывается на использовании различных
математических моделей: уравнений, неравенств, их систем с привлечением
процентов, арифметической и геометрической прогрессий, производной и др.

При решении задач на проценты необходимо уметь находить процент от
числа, число по его проценту, процентное отношение. Основная трудность лежит
при решении задач на сложные проценты – проценты, начисляемые на процентные
деньги.

2.2 Методические рекомендации по
решению задач на проценты.

1. Понятие
процента. Нахождение процента от числа, числа по его проценту, составление
процентного отношения.

Начать нужно с
повторения основных соотношений, с нахождения процента от числа, числа по его
проценту, составления процентного отношения и т. д.

Задачи на части и проценты часто вызывают затруднения у учащихся. Так
как проценты изучаются только в 5-6 классах, а потом мы к ним практически не
возвращаемся, многие выпускники испытывают страх перед задачами на проценты.
Чтобы этого не произошло, необходимо напомнить учащимся, что им уже известно и
показать более сложные задачи на проценты.

Теоретическая часть

Итак, что такое процент? Процент-  это сотая часть величины или
числа.

           
1%=1100=0,01. Значит, сама величина  составляет  100%.

Верна
запись      35%=35100=0,35.

Чтобы 
перевести проценты в дробь, надо  число % разделить на 100. И, наоборот,
десятичные дроби в проценты переводятся умножением на 100%.

Например:      
0,15=0,15*100%=15%

.                       
0,51 =0,51*100%=51%

                     
   0,2   =0,2  *100%=20%

                        
0,123=0,123*100%=12,3%

Чтобы
перевести обыкновенные дроби  в  %, дробь умножаем  на 100%:

                        
34=34*100%=75%; ;         23=23*100%=2003%=66 23%.

Практическая
часть

Решение простейших задач на проценты

Задача 
1. Найти 15%  от  числа  200.

Решение:
переводим 15%  в десятичную дробь и умножим на данное число 200.

                           
0.15*200=30.

Задача 
2.Найти 20% от 34.

Решение:
переводим 20%  в десятичную дробь и умножим на  число 34.

                            
0,2*34=0,15.

Задача 
3.Найти число, если 25% его составляют 80.

Решение:
переводим  25% в десятичную дробь и  данное число делим на
полученную                                

дробь.

                            
80:0,25 =320

Задача 
4.После снижения цены на 20% прибор стал стоить 160 рублей. Найти
первоначальную стоимость прибора.

Решение: 
после снижения стоимость прибора в процентах составляет                        

                           
100%-20%=80%

  Надо
найти число, 80% которого составляет 160.         60:0,8=200.

Задача 
5. Сколько процентов числа 50 составляет число 40?

Решение:
разделим число 40 на 50 и полученную дробь переводим в проценты.

                            
40:50=0,8=80%

Задача 
6.Сколько процентов  от числа 40 составляет  число 50?

Решение:
разделим число 50 на число 40 и полученную дробь переводим в проценты.

                         
     50:40=1,25=125%.

Задача 7.
На сколько процентов число 50  больше 40?

Решение:
число  40 составляет 100%.Чтобы найти, сколько % составляет число 50 от40

разделим 
50 на число 40 и умножим на 100:

                
50:40*100%=125%       125%-100%=25%

Задача 8.
На сколько % 40 меньше 50?

Решение:
Число 50 составляет 100%.Чтобы найти, сколько % составляет число 40 от 50,

разделим 
40 на число 50 и умножим  на  100.

                
40:50*100%=80%          100%-80%=20%

Задача 9.
Изделие  стоило 500 рублей. Цену уменьшили  на 10%. Сколько теперь
стоит         изделие?

Решение:
найдем  стоимость изделия в процентах:                 100%-10%=90%

найдем 
90% от 500:       500*0,9=450(руб.)

Контроль знаний

Тренировочный
тест№1  по теме «Проценты».

1.     
Запишите 1% в
виде десятичной дроби

а)
0,1375       б) 137,5       в)1,375       г)0,01375

2.  Сколько
процентов сахара содержит сироп, приготовленный из 750
г сахара и 1250г

 воды?

а)
40%             б) 37,5%         в) 60%                  г) 62,5%

3.  Мотоциклист
ехал из города А в город В. Проехав 42% пути, он оказался в 20,3
км от города В. Каково расстояние между А и В?

а)
483 км     б) другой ответ         в) 35
км       г)48,3 км

4.  Из 200 квартир
нового дома 65,5% -двухкомнатные, а остальные –трехкомнатные. Сколько
трехкомнатных квартир в этом доме?

а)
69                б) 131             в) 34               г) 19

5.  Сумма двух
чисел составляет 180% первого слагаемого. На сколько % первое слагаемое больше
второго?

а)
на 25%        б) на 20%       в) на 33%   г)
другой ответ

6.  Найдите число,
12% которого равны 240

а)28,8              б)
2000           в) 320             г) другой ответ

7. Первое число 40,
а второе 30. Какой % составляет первое число от разности этих чисел?

а) 40%            б)
400%          в) 133%      г) другой ответ

2.Решение типовых задач на проценты. Алгоритм решения
задач методом составления уравнений.

Теоретическая часть

Урок можно начать с постановки проблемы: что произойдет с
ценой товара, если сначала ее повысить на 25%, а потом понизить на 25%.
Ответить на вопрос, не производя вычислений. Чаще всего ученики дают неверный
ответ: «Не изменится.»

Необходимо обратить внимание учащихся на момент, когда приходится
определять, от какого числа следует искать процент. Подвести учащихся к
правильной и естественной схеме решения этой задачи нужно на примерах, а потом
сформулировать правило:

за 100% следует принимать то число, с которым происходит сравнение,
причем слова «больше на р %» или «меньше на р%» не имеют значения

Практическая часть

Задача10

На сколько процентов a  больше b , если b меньше, чем a на
20%?

Решение:
по условию b меньше, чем а на 20%. Значит, приняв а за
100%, для b получаем:

b=a–. Пусть теперь а
больше на х %, тогда, приняв за 100% число b, найдем

 а = b+ . Из этих двух равенств
следует такое: а = (а-) + ·( а – ). Решая это уравнение относительно х,
получим: х = 25%.                Ответ: 25%

Задача 11. Стоимость набора из 25 основных продуктов питания по
сравнению с ноябрем увеличилась на 24,7% и составила 3913 руб. Сколько стоила «
продовольственная корзина» в ноябре?

Решение.
Обозначив искомую цену за х, составим уравнение по условию задачи:

                                               Ответ:
3138 руб.

Задача 12. Магазин купил книгу со скидкой 10% от номинала, а продал с
наценкой10% от  закупочной цены. Продажная цена будет больше или меньше
номинала? На сколько? Какой % продажная цена составит от номинала?

Задача 13. Книгу купили со скидкой 10% от номинала. Больше или меньше
10% должна быть наценка на закупочную цену, чтобы книга продавалась по
номинальной цене?

Задачи для самостоятельного решения

Задача 14. Себестоимость продукции повысилась сначала на 10%, а затем
понизилась на 20%. На сколько % понизилась себестоимость продукции.

Задача 15. на сколько % увеличится произведение двух чисел, если одно
из них увеличилось на 20%, а другое – на 40%?

Задача 16. в течение года завод трижды уменьшал выпуск продукции на
одно и то же число %. Найдите это число, если известно, что общий % снижения
после трех изменений составил 65,7%.

3. Решение более сложных задач на проценты

Задача 17. Зонт стоил 360 р. В ноябре цена зонта была снижена на 15%, а
в декабре – еще на 10%. Какой стала стоимость зонта в декабре?

Решение:

 стоимость
зонта в ноябре составляла 85% от 360 р., то есть 360·0,85=306(р.). второе
снижение цены происходило по отношению к новой цене зонта; теперь следует
искать 90% от 306 р., то есть 306·0,9 = 275,4 (р.).

                                                                                   Ответ:
275 р. 40 к.

Задача 18. На осенней ярмарке фермер планирует продать не менее одной
тонны лука. Ему известно, что при хранении урожая теряется до 15% его массы, а
при транспортировке – до 10%.сколько лука должен собрать фермер, чтобы
осуществить свой план?

Решение:

 просчитаем
худший вариант. Пусть нужно собрать х т лука. Тогда после хранения может
остаться 0,85х т , и на ярмарку будет доставлено 0,9·0,85х т. Составим
уравнение: 0,9·0,85х = 1, откуда х ≈ 1,3 т.

                                                                                   Ответ:
не менее 1,3 т.

Задача 19. Букинистический  магазин при продаже книги по номиналу
запланировал определенный процент прибыли. Продал же со скидкой 10% от
номинальной цены и получил при этом 8% прибыли. Сколько % прибыли первоначально
предполагал получить магазин?

 4.
Правило начисления «сложных процентов»

Теоретическая часть

Для
выхода на формулу начисления «сложных процентов» полезно решить несколько
задач, аналогичных следующим:

Задача 20. В сбербанк  положили 1000 рублей. Подсчитайте,  какую сумму
должны получить через 2 года, если по истечению каждого года банк начисляет 3%
дохода?

Решение:
3%=0,03.      1000*0,03=30(руб.)

                                     
1000+30=1030(руб.) – за  1 год.

                                     
1030*0,03=30.9(руб.)

                                     
1030+30.9=1060,9(руб.)-за 2 год.             Ответ: 1060, 9 руб.

Задача 21. В банк положен вклад из расчета 3% годовых .Какой доход в %
принесет вклад через 4 года?

Решение:
обозначим сумму первоначального вклада за х, тогда через 1 год  сумма вклада
составит  х +0,03х=1,03х, через 2 года 1,03х+1,03х*0,03=1,03 х, через  3 года
-.(1,03)  х и

Через 4
года (1,03) х=1,12550881х

                     
1б12550881х-х=0,12550881х.

Через 4
года вклад принесет доход 12,550881%.                         Ответ: 12,
550881%

Задача 22. В сберкассу положили 200р., на которые начисляют 3% годовых.
Сколько денег будет в конце первого  года хранения?

Решение
полезно провести на конкретных числах и в общем виде.

Начальный капитал, р.	200	а
Процент прибыли, %	3	р
Прибыль, р.	200∙0,03
Конечный капитал	200+200∙0,03= =200·(1+0,03)│	к = а∙( 1+)

В итоге получилась формула зависимости

к =
а∙( 1+),  дающая
возможность решить три типа задач на денежные расчеты: на нахождение одного из
параметров, зная два других.

Вопрос.
Сколько денег будет в конце второго года хранения?

Отвечая
на него, получим:  к = а∙( 1+)(1) .  А третьего? А п-го?
В итоге получается формула  к = а∙( 1+), где а- начальный капитал,
р – процент прибыли за один промежуток времени;  п – число
промежутков. Эта формула называется формулой «сложных процентов».

Полученная формула
показывает, что значение величины к растет как геометрическая прогрессия,
первый член которой равен а, а знаменатель прогрессии 1+. Формула (1 ) является исходной
формулой при решении многих задач на проценты. Кроме формулы сложного
процентного роста, учащиеся должны знать и применять простого процентного
роста: к = а∙( 1+),            (2)             где
а ,р и п имеют тот же смысл, что и в формуле сложного процентного роста (отличие
состоит в том, что в этом  случае процент каждый раз берется от одного и того
же числа а). 

Следует уделять много внимания решению таких задач.

Выводы по второй главе

1. При разработке системы задач на проценты было
учтено то, что начать нужно с повторения основных соотношений, с нахождения
процента от числа, числа по его проценту, составления процентного отношения и
т. д.

Задачи на части и проценты
часто вызывают затруднения у учащихся. Так как проценты изучаются только в 5-6
классах, а потом мы к ним практически не возвращаемся, многие выпускники
испытывают страх перед задачами на проценты. Чтобы этого не произошло,
необходимо напомнить учащимся, что им уже известно и потом показать более сложные
задачи на проценты.

 2. Мною представлены методические рекомендации по
изучению темы «Проценты» в основной школе и разработана система задач на
проценты (приложение 1).

Заключение

Целью дипломной
работы являлось выявление методических особенностей изучения процентов в 5-9
классах, а также разработка соответствующих методических рекомендаций по
изучению темы «Проценты». Для достижения целей работы были решены следующие
задачи, заявленные во введении:

–                  
в главе I
проанализирована психолого-педагогическая, учебная, методическая литература,
связанная с проблемой изучения темы «Проценты» в основной школе; определены
роль и место темы в школьном курсе математики, а также выявлены  возможные
причины затруднения учащихся в освоении задач на проценты.

–                  
 проведен
сравнительный анализ изложения темы «Проценты» в учебниках математики 5-6
классов, проанализировано изложение различных тем, связанных с процентами, в
учебниках алгебры 7-9 классов; а также изучен педагогический опыт по теме Проценты.
В результате были систематизированы методические приемы, методы, средства,
формы работы для создания цельного представления о методах обучения решению
задач на проценты.

–                  
в главе
II представлены методические рекомендации по изучению темы «Проценты» в
основной школе.

Одной из главных
причин затруднения учащихся в освоении решений задач на проценты является
отсутствие у школьников опыта практического применения процентов, поэтому
ученики не имеют потребности в решении предлагаемых им задач. Мною разработаны
методические рекомендации к проведению факультативного курса «Проценты в
повседневной жизни», направленного на то, чтобы показать учащимся практическую
направленность математических знаний. Содержание задач приближены к современной
жизни и жизненному опыту учащихся, что служит сильным мотивом для решения
предлагаемых задач.

Задачи на
проценты рассматриваются преимущественно в 5-6 классах, в то время как в 7-9
классах навыки решения таких задач утрачиваются. Поскольку в заданиях ЕГЭ
встречаются задачи на проценты, именно в 7-9 классах необходимо проводить
работу, направленную на поддержание этих навыков и умений. Предложенные мною
задачи  можно использовать как на основных уроках, так и на элективных курсах,
на индивидуально-групповых занятиях.  

Таким образом,
ознакомившись с проблемой изучения темы «Проценты» в основной школе, важно
отметить, что задачи на проценты, широко используемые как в различных областях
науки, так и в реальной жизни, имеют большое практическое значение. Поэтому
необходимо построить процесс изучения данной темы таким образом, чтобы добиться
высокого уровня знаний, умений и навыков учащихся, столь необходимых для
дальнейшего успешного обучения учащихся не только по математике, но и по другим
школьным предметам. Навыки решения задач на проценты необходимо поддерживать и
развивать в старших классах средней школы.

Приложение 1

1.Задачи
«целое содержит 100 % самого себя»

1) Одновременно
проводились соревнования по прыжкам в высоту и в длину. 25% учащихся класса
соревновались в прыжках в высоту, 75% – в прыжках в длину. Все ли учащиеся
класса участвовали в соревнованиях?

2) Туристы
проехали 80 % намеченного маршрута на поезде и 15 % – на автобусе. Весь ли
маршрут они уже проехали?

3) Маша потратила
70 % имевшихся у нее денег на книги и 30 % – на тетради. Все ли деньги
потратила Маша?

4) Учитель
сказал: «С этой контрольной работой справились 100 % учащихся нашего класса».
Как это понимать?

5) Потратили 80 %
суммы. Сколько процентов этой суммы осталось?

6) Мужчины
составляют 75 % всех работников завода. Сколько процентов работников завода
составляют женщины?

7) Девочки
составляют 40 % класса. Сколько процентов класса составляют мальчики?

2. Нахождение
p% от числа или величины. Текстовые задачи.

1) Найдите 5 %;
17 %; 23 % от: а) 1 рубля; 6)1 метра; в) 1 центнера.

2) Увеличьте
число: 1) 60 на 10%; 2) 80 на 25%;3) 40 на 50%;4) 425 на 4%.

3)Уменьшите
число: 1) 60 на 10%; 2) 80 на 25%; 3) 90 на 50%; 4) 125 на 20%.

4) Что больше:

а) 30% от 40 или
40 % от 30?

б) 80 % от 60 или
60 % от 70?

5) Определите без
вычислений, что больше: а) 12% от 34 или 13% от 34; б) 12% от 49 или 12% от 50.

Для заданий 6 –
14 учащимся можно предложить составить только выражение для нахождения ответа,
не решая задачи до конца.

6) В магазин
привезли 2500 кг помидоров. В первый день продали 30 % всех помидоров. Сколько
килограммов помидоров осталось продать?

7) В школе 400
учащихся, 52% этого числа составляют девочки. Сколько мальчиков в школе?

8) В городе
100000 жителей и из них 80% составляют коренное население. Определите
количество коренных жителей в этом городе.

9) На субботник
вышли 160 человек. В ремонте дороги участвовали 25% всех людей, а остальные
сажали деревья. Сколько человек сажали деревья?

10) Надоили 150 л
молока. После того как отправили молоко в детский сад, осталось 80% имевшегося
молока. Сколько литров молока отправили в детский сад?

11) В ящике 120
кг пшена. После того как из ящика наполнили мешок пшеном, в ящике осталось 65%
всего пшена. Сколько килограммов пшена вошло в мешок?

12) Служащий
вложил 500 р. в акции своего предприятия и получил 20% дохода. Сколько рублей
дохода он получил?

13) В городе 64
тыс. избирателей, 85% всех избирателей приняли участие в выборах. Сколько
избирателей приняли участие в выборах?

14) В понедельник
рабочий перевыполнил дневное задание на 10%, а во вторник – на 8%. На сколько
процентов он перевыполнил задание двух дней?

Для заданий 15 –
31 также учащимся можно предложить составить только выражение для нахождения
ответа, не решая задачи до конца. Но ниже представленные задачи сложнее
предыдущих в силу того, что они решаются не в одно действие, и, поэтому,
труднее воспринимаются на слух. Целесообразнее в слабых классах тексты задач
представить на доске, презентации, и т.п.

15) В автобусном
парке 50% составляют городские автобусы, 75% остальных – автобусы
междугородного класса. Каких автобусов больше: городских или междугородного
класса?

16) У Алеши 80
марок, у Бори – на 20 % больше, чем у Алеши. У Вовы на 25% меньше, чем у Алеши.
Сколько марок у Бори и Вовы в отдельности?

17) В библиотеке
98000 книг. Книги на русском языке составляют 78% всех книг, из них 5% –
учебники. Сколько учебников на русском языке в библиотеке?

18) На столе
лежала пачка тетрадей. Сначала взяли 30% этих тетрадей, а потом 75% оставшихся
тетрадей. После этого на столе осталось 14 тетрадей. Сколько тетрадей было в
пачке первоначально?

19) В пакете
лежали сливы. Сначала из него взяли 50% слив, а затем 50% остатка. После этого
в пакете осталось 9 слив. Сколько слив было в пакете первоначально?

20) Сложили три
числа. Первое составило 25 % суммы, а второе – 40 %. Найдите третье число, если
оно на 45 меньше второго.

21) класса пошли
в кино, 15 % класса – на выставку, а остальные 8 человек готовились к школьному
вечеру. Сколько человек в классе?

22) В магазин
привезли овощи. В первый день продали 35 % и еще 240 кг, после чего в магазине
осталось 540 кг овощей. Сколько килограммов овощей привезли в магазин?

23) Женя за весну
похудел на 20%, потом поправился за лето на 30%, за осень опять похудел на 20%
и за зиму прибавил в весе 10%. Остался ли за этот год его вес прежним?

24) Две
противоположные стороны прямоугольника увеличили на 20%, две другие уменьшили
на 20%. Как изменилась площадь прямоугольника?

25) Мальчики
составляют 45% всех учащихся школы. Известно, что 30% мальчиков и 40% девочек
учатся без троек. Сколько процентов всех учащихся школы учится без троек?

26) На некотором
участке пути машинист уменьшил скорость поезда на 25%. На сколько процентов
увеличится время движения на этом участке?

27) В некотором
царстве, в некотором государстве правительство вынесло на всенародное
голосование проект закона о запрете рекламы спиртных напитков. Этот проект
поддержали 69% всего взрослого населения, принявшего участие в голосовании,
причем среди женщин 94%, а среди мужчин 41 %. Кого среди голосовавших было
больше: мужчин или женщин?

29) Магазин
продал на прошлой неделе некоторый товар. На этой неделе запланировано продать
того же товара на 10% меньше, но по цене на 10% больше. Большую или меньшую
сумму выручит магазин от продажи товара на этой неделе (по сравнению с прошлой)
и на сколько процентов?

30) Купили
конфеты и печенье. За 1 кг конфет заплатили на 50% больше, чем за 1 кг печенья,
но их купили на 50% меньше, чем печенья. За что заплатили больше и на сколько
процентов?

31) Как изменятся
расходы на оплату электроэнергии, если:

а) потребление
возрастет на 15%, а стоимость одного кВт·ч увеличится на 20%;

б) потребление
снизится на 15%, а стоимость одного кВт·ч увеличится на 20%;

в) потребление
возрастет на 15%, а стоимость одного кВт·ч уменьшится на 20%;

г) потребление
возрастет на 15%, а стоимость одного кВт·ч уменьшится на 20%.

3. Нахождение
величины, если известны ее p%.

1) В
соревнованиях было 9 победителей, что составило 18% числа всех участников
соревнований. Сколько было участников соревнований?

2) В школе 15
учеников учатся на «5». Это составляет 5% учащихся школы. Сколько всего
учащихся в школе?

3) В магазин
привезли партию лампочек. Среди них оказалось 16 разбитых лампочек, что составило
2% от общего числа. Сколько лампочек привезли в магазин?

4) Токарь до
обеденного перерыва обточил 24 детали, что составляет 60% сменной нормы.
Сколько деталей должен обточить токарь за смену?

5) Посадили
семена гороха, 270 из них взошли. Это составило 90% всех посаженных семян.
Сколько семян посадили?

6) Туристы прошли
75% маршрута, и им осталось пройти еще 5 км. Какова длина маршрута?

4.Нахождение
процентного отношения двух чисел и изменения величины в процентах.

1) Сколько
процентов числа 50 составляет число 40? Сколько процентов числа 40 составляет
число 50?

2) Посадили 50
семян, 47 из них взошли. Определите процент всхожести семян.

3) В школе 400
учащихся, 12 из них учатся на «5». Сколько процентов учащихся школы учится на
«5»?

4) Маша прочитала
120 страниц и ей осталось прочитать 130 страниц книги. Сколько процентов всех
страниц она прочитала? Сколько процентов всех страниц ей осталось прочитать?

5) В месяце было
12 солнечных и 18 пасмурных дней. Сколько процентов месяца составляют: а) солнечные
дни? б) пасмурные дни?

6) В поселке
построили 16 одноэтажных и 4 двухэтажных дома. Сколько процентов всех
построенных домов составляют одноэтажные дома?

7) В роще 700
берез и 300 сосен. Сколько процентов всех деревьев составляют сосны?

8) Зарплата
повысилась с 500 р. до 600 р. На сколько процентов повысилась зарплата?

5.Проценты и
банковские расчеты

1) Несколько лет
назад сберегательные кассы выплачивали доход из расчета 2 % вложенной суммы в
год. Сколько рублей оказывалось на счете через год, если на него положили:

 1)100р.;
2)200р.; 3)1000р.; 4)12000р?

2) При продаже
товара за 393 р. получено 10% прибыли. Определите себестоимость товара.

3) Товар стоил
500 р. Его цена повысилась на 20 %. На сколько рублей повысилась цена? Какова
новая цена товара?

4) Папа вложил
500 р. в акции своего предприятия и получил 20 % дохода. Какой доход в рублях
получил папа?

5) Стоимость
акций компании росла 5 месяцев на 15% ежемесячно. Верно ли, что за это время
стоимость акций удвоилась?

Литература

1.                
Алгебра:
Учеб. для 7 кл. общеобразоват. учреждений / Ю.Н.Макарычев, Н.Г.Миндюк,
К..И.Нешков и др.; Под ред. С.А.Теляковского. – 12-е изд. – М.: Просвещение,
2003.-223 с.: ил.

2.                
Барабанов
О.О. Задачи на проценты как проблема нормы словоупотребления // Математика в
школе. – 2003. – № 5.

3.                
Демидова
Т.Е. Тонких А.П. // Теория и практика решения текстовых задач: Учеб. Пособие
для студ. высш. пед. учеб. заведений. – М.: Издательский центр «Академия»,
2002. – 288 с.

4.                
Захарова
А.Е. Учимся решать задачи на проценты // Математика для школьников.— 2002.— №
37..

5.                
Математика:
Учеб. для 5 кл. сред. шк./Н.Я. Виленкин, А.С. Чесноков, С.И. Шварцбурд. и др..
– М.: Мнемозина, 2009.

6.                
Математика:
Учеб. для 6 кл. общеобразоват. учреждений/ Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков
и др. – М.: Мнемозина, 2009.

7.                
Программы
для общеобразоват. школ, гимназий, лицеев: Математика. 5-11 кл. / Сост. Г.М.
Кузнецова Н.Г. Миндюк. – 4-е издание, стереотип. – М.:Дрофа, 2004. – 320 с.

8.                
Проценты:
Методическая разработка для учащихся заочного отделения ММФ / А.В. Деревянкин.
– М.: Изд-во центра прикладных исследований при механико-математическом
факультете МГУ, 2007.-12с.

9.                
Самойлик
Г. История математики на уроках. Проценты// Математика. – 2002 – № 36.

10.           
Саранцев,
Г. И./ Методика обучения математике в средней шк: Учеб. пособие для студ.
математических спец. пед вузов и ун-тов. – М.: Просвещение, 2002. – 224 с.: ил.

11.           
http://www.1september.ru/

12.           
http://www.edu.ru/

13.           
http://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%BE%D1%86%D0%B5%D0%BD%D1%82

Актуальность данной темы.

Готовясь к  государственной итоговой аттестации, мы столкнулись с необходимостью уметь решать задачи на проценты. При повторении этой темы вспомнили, как решаются задачи разного типа на проценты, и рассмотрели некоторые методы их решения.  На элективном курсе «Решение задач с экономическим содержанием» мы узнали о широком применении процентов в жизни человека и общества в целом. А также узнали некоторые новые методы решения задач на проценты, среди них геометрический метод, а также понятие «сложного процента».  Появилась идея обобщить известные нам данные о решении таких задач, классифицировать типичные задачи на проценты и методы их  решения, чтобы в дальнейшем использовать собранный  материал для подготовки к ГИА и  ЕГЭ.

Цель работы:

1. Классифицировать типичные задачи на проценты.
2. Рассмотреть  различные методы решения задач на проценты.
3. Рассмотреть применение процентов в повседневной и деловой жизни человека.

Задачи работы:

1. Познакомиться с историей возникновения понятия «процент» и его последующем развитием.
2. Классифицировать типы задач на проценты:

а) нахождение нескольких процентов от числа,

б) нахождение числа по значению его процентов,

в) нахождение процентного отношения чисел, на сколько процентов одна величина больше другой..

3.  Разобрать различные методы решения типичных задач:

а)  используя определение понятия процента,

б)  правило нахождения дроби от числа,

в) правило нахождения числа по значению его дроби,

г)  пропорциональность величин,

4.  Применение алгебраического и геометрического метода.

5.  Рассмотреть применение процентов в повседневной и деловой жизни человека:

1)  в химии при решении задач на концентрацию веществ, смеси и сплавы, рассмотреть  разные методы их решения:

а) алгебраический,

б) арифметический.

2)  в статистике при обработке статистических данных:

а) круговые диаграммы,

3)  при покупке и продаже товаров,

4)  в банковском деле:

а) применение «сложных процентов».

1. История возникновения процентов.

Слово «процент» происходит от латинского  «procentum», что буквально означает «на сотню». В популярной литературе возникновение этого термина связывается с внедрением в Европе десятичной системы счисления в XV в. Однако, уже в «Дигестах Юстиниана», датируемых V в., мы находим вполне современное употребление процентов. «Фиск (императорская казна) не уплачивает проценты по заключенным им договорам, но сам получает проценты: например со съемщиков публичных поборов, если эти съемщики слишком поздно вносят деньги; также при просрочке уплаты налогов. Когда же фиск является приемником частного лица, то обычно он уплачивает проценты.

Несли должники, платившие проценты в размере меньше, чем 6 процентов в год, стали должниками фиска, то они обязаны уплачивать 6 процентов годовых с того времени, как требование против них перешло к фиску».

По-видимому, процент возник в Европе вместе с ростовщичеством как предтеча десятичной системы счисления.

Употребление термина «процент» в качестве нормы русского языка начинается, вероятно, с конца XVIII в. Об этом свидетельствует сравнительный анализ текстов двух фундаментальных учебников по математике Ефима Войтяховского (первое издание 1795г.) и Т.Ф. Осиповского (первое издание 1802 г.). В обоих учебниках имеется по нескольку задач «на проценты по вкладу», но Е. Войтяховский оперирует исключительно сотыми долями, тогда как Т.Ф. Осиповский уже употребляет термин «процент».

Привычка к употреблению процентов в сфере денежных отношений благоприятствовала быстрому их внедрению в развивающиеся технологии XIX в. Так, в словаре Брокгауза и Эфрона читаем следующее:

«По предварительным данным переписи 1897 г., население Петербурга оказалось возросшим за 6 лет на 178 тысяч, из которых 150 тысяч  приходится на прилив извне; из всего прироста 85% падает на крестьян, составляющих теперь до 59% всего петербургского населения»

Как видно из отрывка, уже на рубеже IX и XX вв. русскоязычное контекстное понимание процентов максимально локонизируется. В одном предложении фигурируют две различные стопроцентные базы. В последующем это становится нормой деловой речи и литературы.

Для удовлетворения возрастающих требований к точности исчисления малых долей вместо 1% вводится квант 1/1000 – так называемое промилле. Промилле можно часто встретить на страницах книг по медицине и фармакологии, обозначают 0/00.

В операциях с ценными металлами используется другое название кванта 1/1000 – проба. Так, золото 750-й пробы – это сплав с 75 – процентным содержанием золота.

Знак % произошел, как предполагается, благодаря опечатке. В рукописях pro centum часто заменяли словом «cento» (сто) и писали сокращенно – cto. В 1685 году в Париже была напечатана книга – руководство по коммерческой арифметике, где по ошибке наборщик вместо cto набрал %.

2. Понятие процента.

С этим понятием мы познакомились в 5 классе, изучая математику по учебнику «Математика, 5», В.Я Виленкин.

Процентом называют одну сотую часть.

Так как 1% равен сотой части величины, то вся величина равна 100%.

1% = 1/100. Соответственно, р% = р/100.

Процент некоторых величин имеет название:

 1кг – один процент центнера, 1см – один процент метра, 1а – один процент гектара и т.д.

Чтобы перевести проценты в десятичную дробь, надо разделить число процентов на 100.

Чтобы обратить десятичную дробь в проценты, надо её умножить на 100.

Например,

1% = 1/100 = 0,01; 2% = 2/100 = 0,02;  20% = 1/10 = 0,1; 100% = 1; 120% = 1,2.

0,03 = 3%;  0,25 = 25%;  0,5 = 50%;  1,2 = 120%.

3. Типичные задачи на проценты и методы их решения.

Различают основные типы задач на проценты.

• Нахождение нескольких процентов числа.

• Нахождение числа по значению его процентов.

• Нахождение сколько процентов одно число составляет от другого.

Решение типичных задач на проценты связано с применением различных методов:

• 1 метод: по определению процента.
• 2 метод: правила  нахождения дроби от числа или нахождения числа по значению дроби.
• 3 метод: пропорциональность величин.

1) 1 тип задач: нахождение нескольких процентов числа

Первый тип задач относится к той ситуации, когда даны количество А и некоторый процент р, а требуется найти количество, которое этот процент выражает.

Эта задача сводится к ответу на вопрос К1: каково количество, составляющее р% от А? Здесь ключевое слово от. То, что стоит за ним принимается за 100%. Этот вопрос может задаваться и в несколько иной форме, например, так: найти р%  от А.

 Аналогичен вопросу  К1 вопрос по нахождению дроби от числа.

При ответе на вопрос К1 можно использовать 1 метод.

а) 1 метод: по определению процента.

Для нахождения  дроби  от А  используют смысл знаменателя дроби, который показывает на сколько долей делят А, и смысл числителя, показывающий сколько долей надо взять. Для  ответа на поставленный вопрос используют  формулу: .

По аналогии отвечаем на вопрос К1.  

Зная, что р% = р/100, находим р% от А, используя формулу

  А : 100 * р.  

Если на количество А приходится 100%, то А : 100 показывает сколько приходится  на 1%, тогда на р% приходится    А :100 * р.

Рассмотрим это на примере решения задачи 1:

В классе 20 учеников. За контрольную работу по математике отметку «5» получили 20% всех учеников. Сколько учеников в классе получили отметку «5»?

     Решение.

1. 20 : 100 = 0,2 (уч.) – 1%
2. 0,2 *  20 = 4 (уч.) – получили отметку «5».

Ответ: 4 ученика.

б) 2 метод: правило  нахождения дроби от числа.

При ответе на вопрос К1 можно использовать изученное нами в 6 классе правило нахождения дроби от числа, в котором также встречается ключевое слова от.

Чтобы найти дробь от числа, надо число умножить на эту дробь.

Найдем  от А по формуле: А * .

Так как р% = р/100, то  р% от А найдем по формуле:  

А * р/100. 

Формула р/100 переводит % в десятичную дробь, поэтому при решении задачи этим методом % переводят в десятичную дробь.

Решение  задачи 1 методом 2.

Решение.

20% = 0,2

20 * 0,2 = 4 (уч.) – имеют отметку «5».

Ответ: 4 ученика.

в) 3 метод: пропорциональность величин.

При решении задач на проценты можно использовать изученные в 6 классе понятия прямо пропорциональных и обратно пропорциональных величин, пропорции и ее основное свойство.

• Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз, другая увеличивается (уменьшается) во столько же раз.
• Две величины называют обратно пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз, другая уменьшается (увеличивается) во столько же раз.
• Пропорцией называется равенство двух отношений.
• Основное свойство пропорции: в верной пропорции произведение крайних членов пропорции равно произведению крайних членов пропорции.

При ответе на вопрос К1 используют прямо пропорциональную зависимость между количественным выражением величины и ее процентным выражением.

Решение  задачи 1 методом 3.

	Количество учащихся	%
В классе	20уч.	100%
Получили «5»	х   ?уч	20%

Ответ: 4 ученика получили отметку «5».

1. 2 тип задач на проценты: нахождение числа по значению его процентов.

Этот тип задач относится к ситуации, когда известны р% некоторого количества, а необходимо найти это количество. Эта задача сводится к ответу на вопрос К2: каково количество, р% от которого есть А? Этот вопрос может звучать и так: каково количество, если А составляет р% этого количества? В этом вопросе ключевое слово составляет. За 100% принимается искомое количество.

Задачи этого типа решаются теми же методами, что и задачи 1 типа.

а) 1 метод: по определению процента 

При использовании 1метода при ответе на вопрос К2 используют аналогию с ответом на вопрос: А составляет  от какого числа? Для ответа на этот вопрос используют смысл знаменателя дроби, который показывает на сколько долей делят искомое количество, и смысл числителя, показывающий сколько взяли долей, соответствующие А. Для  ответа на поставленный вопрос используется формула:

По аналогии, так как р% = р/100, то для ответа на вопрос: А составляет р% от какой величины? используем формулу:

А : р * 100.

Формула А : р показывает сколько приходится  на 1%, тогда на 100% приходится  А : р * 100.

Рассмотрим это на примере решения задачи 2:

За контрольную работу по математике отметку «5» получили 4 ученика, что составляет 20% всех учеников. Сколько учеников в классе?

Решение.

1. 4 : 20 = 0,2 (уч.) – 1%
2. 0,2 * 100 = 20 (уч.) – в классе.

Ответ: 20 учеников.

б) 2 метод: правило  нахождения числа по значению его дроби.

 При ответе на вопрос К2 можно использовать изученное нами в 6 классе правило нахождения  числа по значению его дроби.

Чтобы найти число по значению его дроби, надо значение дроби разделить на эту дробь.

В этом случае для ответа на вопрос: А составляет  от какого числа? используют формулу:               .

Так как р% = р/100, то  при ответе на вопрос: А составляет р% от какой величины? используют формулу:

Формула р/100 переводит % в десятичную дробь, поэтому при решении задачи этим методом % переводят в десятичную дробь.

Решение  задачи 2 методом 2:

Решение.

1. 20% = 0,2
2. 4 : 0,2 = 20 (уч.) – в классе

Ответ: 20 учеников.

1. 3 тип задач на проценты: нахождение процентного отношения чисел.

Этот тип задач относится к вопросу К3: сколько процентов составляет А от В?  Аналогичный  вопрос:  какую часть составляет А от В? находится по формуле: А/В.  

В вопросе: сколько процентов составляет А от В? ключевым словом является от, то, что стоит за ним записывают в знаменатель дроби и принимают за 100%. При ответе на этот вопрос применяют формулу

А : В * 100%.

Задачи этого типа также можно решать, применяя пропорциональность величин.

Рассмотрим задачу 3.

Из 1800га поля 558га засажено картофелем. Какой процент поля засажен картофелем?

Решение.

засажено картофелем.

Ответ: 31%.

С вопросом К3 связан вопрос: на сколько процентов  А больше, чем В? Здесь ключевым словом является чем, а то, что стоит за ним пишется в знаменателе дроби и принимают за 100%.

Формула ответа на вопрос: (А – В)/В * 100%.

Аналогичен вопрос: на сколько процентов А меньше, чем В?

Формула ответа на вопрос: (В – А)/В * 100%.

Рассмотрим задачу 4.

Стоимость товара с 200 р. увеличилась в 2 раза. На сколько процентов увеличилась стоимость товара? На сколько процентов прежняя стоимость была меньше по сравнению с настоящей?

Решение.

    1) 200 * 2 = 400(р.) – стала стоимость

    2) 400 – 200 =200(р.) – изменилась стоимость,

    3) 200: 200 = 1 = 100% – увеличилась стоимость,

    4) 200 : 400 = 0,5 = 50% – прежняя стоимость меньше настоящей.

Ответ: увеличилась на 100%; меньше на 50%.

В этой задаче дважды применяется ответ на вопрос К3, но за 100% принимается разная величина.

4. Применение алгебраического и геометрического методов.

Рассмотрим задачу 5.

В одном городе Канады 70% жителей знают французский язык и 80% английский язык. Сколько процентов жителей этого города знают оба языка?

Алгебраический  метод:

Пусть х –жителей знают только английский, у – жителей только французский, z – оба языка. Тогда можно дважды увидеть вопрос К3 и, применив соответствующую формулу получить  2 уравнения:

(x + y)/( x + y + z) = 0,8, (y + z)/(x + y + z) = 0,7.

Сложив оба эти равенства, получим 1 + z/(x + y + z) = 1 + 0,5;

z/(x + y +z) * 100% = 50%.

Ответ: 50%.

Геометрический метод.

Разместим всех жителей  города на отрезке 100% так, что знающие английский стоят на отрезке сплошняком слева, а знающие французский  – сплошняком справа. Тогда общая часть этих множеств есть отрезок

 [30%; 80%], «протяженностью» в 50%.

1. Применение процентов в повседневной и деловой жизни человека.

С процентами мы сталкиваемся в своей повседневной жизни: при покупке товара в магазине со скидкой или при распродаже; при оформлении покупки товара в кредит.

Проценты широко используются в деловой жизни человека: при обработке статистических данных, взятии кредита в банке.

А также в некоторых профессиях, таких как медицина, требуются уметь определять концентрацию веществ.

1) в химии при решении задач на концентрацию веществ, смеси и сплавы.

Концентрация вещества в смеси – это часть, которую составляет масса вещества в смеси от массы смеси. Концентрация вещества может быть указана и числом и %.

Например:

1. Концентрация раствора 3 %;

(В 100 г раствора содержится 3 г вещества).

2. К одной части сахара прибавили 4 части воды. Какова концентрация полученного раствора?

(1: 5 ·100 = 20 %)

Следующую задачу нельзя решить устно.

1. В каких пропорциях нужно смешать раствор 50 % и 70 % кислоты, чтобы получить раствор 65 % кислоты?

а) алгебраический метод

Предположим, что первого раствора нужно взять х г, а второго у г. Считаем, что при смешении нет потерь массы, то есть масса смеси равна сумме масс смешиваемых растворов – (х + у) г. Найдем количество чистой кислоты в 1-ом растворе. Это 0,5х г, во втором растворе 0,7у г, а в смеси будет 0,65(х + у) г кислоты.

     По условию задачи составим и решим уравнение.  

   0,65 (х + у) = 0,5 х + 0,7 у,

   65 х – 50 х = 70 у – 65 у,

  15 х = 5 у,

   3 х = 1 у,

   х : у = 1 : 3.  Нужно взять: 1 часть раствора 50% кислоты и 3 части раствора 70% кислоты

б) арифметический метод.

Запишем концентрацию каждого раствора кислоты и концентрацию смеси.

Вычислим, на сколько концентрация первого раствора кислоты меньше, чем концентрация смеси и на сколько концентрация второго раствора кислоты больше, чем концентрация смеси и запишем результат по линиям.

65

Таким образом, 5 частей нужно взять 50% раствора кислоты и 15 частей 70% раствора кислоты, то есть отношение взятых частей            

Окончательно получаем: 50% раствора кислоты-1 часть, 70% раствора кислоты-3 части.

Докажем справедливость этого способа.

В каких пропорциях нужно смешать растворы а % и b % кислот, чтобы получить раствор с % кислоты? 

Предположим, что первого раствора нужно взять х г, а второго у г. Считаем, что при смешении нет потерь массы, то есть масса смеси равна сумме масс смешиваемых растворов.
Тогда масса смеси будет (х + у) г.

Теперь заполним 3-й столбик. Найдем количество чистой кислоты в 1-м растворе. Это 0,01·ах г, во втором растворе 0,01·bу г, а в смеси будет 0,01·c(х + у) г кислоты.

Составим и решим уравнение

0,01·c(х + у) = 0,01·ах + 0,01·bу,

cx +cy = ax + by

х(с – а) = у(b – c),

Заполним схему, учитывая, что а < c < b.

с

1. Морская вода содержит 5 % соли по массе. Сколько пресной воды нужно добавить к 30 кг морской воды, чтобы концентрация соли составляла 1,5 %?

Решение

1,5

   

Нужно взять 7 частей пресной воды и 3 части морской воды. По условию нам известно, что морской воды 30 кг и это 3 части нового раствора. Значит на одну часть раствора приходится 10 кг. Следовательно, 7 частей пресной воды – это 70 кг.

Ответ: нужно добавить 70 кг пресной воды.

2)  В статистике при обработке статистических данных.

 В статистике часто данные исследований представляются в процентах. Достаточно распространённым способом графического изображения структуры статистических совокупностей является секторная ( круговая) диаграмма, так как идея целого очень наглядно выражается кругом, который представляет всю совокупность, которой соответствуют 100%..

а) круговые диаграммы

Пример: статистика продаж обеденных блюд в кафе в течение полугода.

1. при покупке и продаже товаров.

С ценами на товары  и услуги люди встречаются каждый день, очень важно, чтобы эти встречи не оборачивались для людей финансовыми потерями.

1. Красивая тетрадка летом стоила 40 рублей. Перед началом учебного года, продавец поднял цену на 25%. Однако, тетрадки стали покупать так плохо, что он снизил цену на 10%. Всё равно не берут! Пришлось ему снизить цену ещё на 15%. Вот тут торговля пошла! Какова была окончательная цена?

Решение.

Продавец взвинтил цену на 25% от 40 рублей – это 10 рублей. То есть, подорожавшая тетрадка стала стоить 50 рублей.

А затем сбросил цену на 10% от 50 рублей. 10% от 50 рублей – это 5 рублей. Следовательно, после первого удешевления тетрадь стала стоить 45 рублей.

Считаем второе удешевление. 15% от 45 рублей – это 6,75 рубля. Стало быть, окончательная цена тетрадки:

 45 – 6,75 = 38,25 рубля.

Ответ: 38,25 рубля.

Мы в своей жизни часто оказываемся в роли покупателя, и имеем закономерное желание купить качественный товар по более низкой цене.

1. На весенней распродаже в одном магазине шарф стоимостью 350р. уценили на 40%, а через неделю еще на 5%. В другом магазине шарф, той же стоимости, уценили сразу на 40%. В каком магазине выгоднее купить этот шарф? Ответ: во втором магазине.

Рассмотрим наиболее типичные ситуации повышения – понижения цен.

Если первоначальная цена некоторого товара составляла А0 денежных единиц, то после ее повышения на х% она составила

А0 + А0 * х * 0,01 = А0(1 + х * 0,01).

Аналогично, если первоначальная цена А0 понизилась на х%, то новая составит А0(1 – х * 0,01).

В результате повышения первоначальной цены А0 на х% и последующего понижения на у% окончательная цена равна А0(1 + х * 0,01)(1- у * о,01).

Часто мы сталкиваемся с процентным изменением стоимости товара при покупке его в кредит.

В автосалон “SECOND LIFE AUTO”, вы можете приобрести подержанную автотехнику в отличном состоянии и по доступной цене

• 1. Задача о кредите.

      Договор о кредитовании на 3 месяца: в декабре-60% всей стоимости, в январе – 75% остатка, в феврале – всю оставшуюся сумму.

      Определите, пожалуйста, сколько рублей в каждом месяце вы заплатите и заполните “Договор о кредитовании”.

• 2. Задача о квитанции.

      За оформление права собственности нотариус возьмет с вас 1,5% от стоимости автомобиля в виде нотариальной пошлины. Во сколько рублей вам обойдется ваша покупка вместе с нотариальной пошлиной?

• 3. Задача о страховке.

      Автосалон предлагает заключить договор о страховании автомобиля от угона на 100000 рублей. Определите, какой процент от стоимости вашего автомобиля будет вам выплачен в случае угона. Заполните страховой полис. Страховой взнос-10 % от стоимости покупки.

1. в банковском деле.

Люди часто кладут деньги в банк с целью увеличения своего вклада.

Задача

       Банк начисляет по вкладам ежегодно 4% вклада. Вкладчик внес в этот банк 15000 р. Сколько денег он может снять со своего счета через два года?

       Решение

1. 15000*0,04 = 600(р.)- увеличение за первый год,
2. 15000 + 600 = 15600(р) – станет к концу первого года,
3. 15600*0,04 = 624 (р.) – увеличение за второй год,
4. 15600 + 624 = 16224(р.) – снимет со счета через 2 года.

Ответ: 16224 рубля.

        Формула сложных процентов:

N = a(1 + 0,01p)n, где а – первоначальный вклад, n – срок вклада,N – величина вклада через указанный срок вклада, р – число %.

        Решение

N = 15000*(1 + 0,01*4)2 = 16224(р.)

Вывод:

Умение решать  задачи на проценты очень важно для успешно сдачи ГИА, а также для применения процентов в различных жизненных ситуациях.

При решении задач на проценты  нужно следовать некоторым практическим советам:

1. В задачах на проценты – переходим от процентов к конкретным величинам. Или, если надо – от конкретных величин к процентам. Определяем тип задачи на проценты. Внимательно читаем задачу!

2. Очень тщательно изучаем, от чего нужно считать проценты. Если об этом не сказано прямым текстом, то обязательно подразумевается. При последовательном изменении величины, проценты подразумеваются от последнего значения. Внимательно читаем задачу!

3. Закончив решать задачу, читаем её ещё раз. Вполне возможно, вы нашли промежуточный ответ, а не окончательный. Внимательно читаем задачу!

Использованные источники.

• «Математика,5, 6». Н.Я.Виленкин.
• «Арифметический способ решения задач на смеси и сплавы». Т.В.Каюкова.
• «Справочное пособие по методам решения задач по математике». А.Г. Цыпкин.
• Элективный курс «Решение задач с экономическим содержанием» Т.А. Цаплина.
• История математики в школе (7- 9 кл), Глейзер Г.И
• Проценты в математике. Задачи на проценты.  http://www.egesdam.ru/page230.html
• Википедия – процент http://ru.wikipedia.org/wiki/%CF%F0%EE%F6%E5%ED%F2

Различные типы задач на проценты  и методы их решения.

Подготовила: Савинова  Анастасия,

ученица 9б класса МБОУ СОШ №18

(учитель математики Пастухова Н.А.)

г. Энгельс 2012

Рассмотрим три основных типа задач на проценты.

Нахождение процента от числа

Разбор примера

Предприятие изготовило за квартал 500 насосов, из которых
60% имели высшую категорию качества. Сколько насосов высшей категории качества
изготовило предприятие?

Решение:

Ответ: 300 насосов высшей категории качества.

Нахождение числа по его проценту

Так как задачи «процент по числу» и «число по его проценту» очень похожи и часто
не сразу понятно какой тип задачи перед нами, старайтесь внимательно читать
текст. Если вам встречаются слова «который», «что составляет» и «который составляет»,
скорее всего перед вами задача «число по его проценту».

Разбор примера

Ученик прочитал 138 страниц, что составляет 23%
числа всех страниц в книге. Сколько страниц в книге?

Решение:

Итак, нам неизвестно сколько всего страниц в книге. Но мы знаем, что часть, которую
прочитал ученик (138 страниц) составляет 23% от общего количества
страниц в книге.

Так как 138 стр. — это всего лишь часть, само количество
страниц, естественно, будет больше 138. Это поможет нам при проверке.

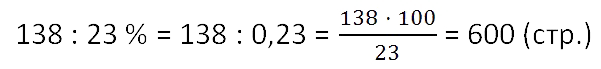
Проверка: 600 > 138 (это означает, что 138 является частью 600).

Ответ: 600 (стр.) — общее количество страниц в книге.

Сколько процентов одно число составляет от другого

Разбор примера

Из 200 арбузов 16 оказались незрелыми.
Сколько процентов всех арбузов составили незрелый арбузы?

Решение:

О чем спрашивают? О незрелых арбузах. Значит, 16
делим на общее количество арбузов и умножаем на 100%.

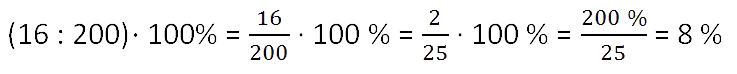
Ответ: 8% — составляют незрелые арбузы от всех арбузов.

---

Ваши комментарии

Оставить комментарий:

---