Скачать материал
без ожидания

Скачать материал
без ожидания


- Сейчас обучается 28 человек из 15 регионов


- Сейчас обучается 138 человек из 42 регионов


- Сейчас обучается 1151 человек из 83 регионов


Описание презентации по отдельным слайдам:
-

1 слайд
Комбинаторные задачи:
дерево возможных вариантов -

2 слайд
Имя урока: Комбинаторика
Девиз урока: «Услышал – забыл,
Увидел – запомнил,
Сделал – понял»
Китайская поговорка -

3 слайд
В странных русских сказаниях повествуется, как богатырь или другой добрый молодец, доехав до распутья, читает на камне:
Вперёд поедешь – голову сложишь.
Налево поедешь – меча лишишься.
А дальше говорится, как он выходит из того положения, в которое попал в результате выбора.
Направо поедешь – коня потеряешь.Но выбирать разные пути или варианты приходится и современному человеку. Эти пути и варианты складываются в самые разнообразные комбинации.
-

4 слайд
Что такое КОМБИНАТОРИКА?
Задачи, в которых требуется осуществить перебор всех возможных вариантов, или, как обычно говорят в таких случаях, всех возможных комбинаций, называют комбинаторными.
Область математики, изучающая комбинаторные задачи, называется комбинаторикой.
Комбинаторика – раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить. -

5 слайд
Задача №1
Запишите все трёхзначные числа, для записи которых употребляются только цифры 1 и 2.
1 2
1
1
2
2
1
1
1
1
2
2
2
2
Ответ: 111, 112, 121, 122, 211, 212, 221, 222 – восемь чисел.
Такой метод решения комбинаторных задач называется деревом выбора(дерево возможных вариантов) -

6 слайд
Задача №2
Запишите все трёхзначные числа, для записи которых употребляются только цифры 0,7. -

7 слайд
Задача 3
В 5 «А» классе в среду 4 урока: математика, информатика, русский язык, английский язык. Сколько можно составить вариантов расписания на среду?
Решение: построим картину-схему.
Для удобства закодируем названия предметов:
математика – м,
информатика – и,
русский язык – р,
английский язык – а. -

8 слайд
Решение задачи 3
Расписание1 урок м и р а
2 урок и р а м р а м и а м и р
3 урок р а и а и р р а м а м р и а м а м и и р м р м и
4 урок а р а и р и а р а м р м а и а м и м р и р м и м
Ответ: 24 варианта: мира, миар, мриа, мраи, маир, мари, имра, имар, ирма, ирам, иамр, иарм, рмиа, рмаи, рима, риам, рами, раим, амир, амри, аимр, аирм, арми, арим.
-

9 слайд
Построенная схема напоминает перевернутое дерево: от ствола («расписание») отходят ветки, сначала четыре (м, и, р, а), от каждой из четырех веток – еще по три, затем еще по две и еще по одной. Видимо поэтому такую схему называют деревом возможных вариантов.
Дерево возможных вариантов можно считать геометрической моделью рассматриваемой ситуации. -

10 слайд
Задача №4
В правление фирмы входят 5 человек. Из своего состава правления должно выбрать президента и вице-президента. Сколькими способами это можно сделать?
Президент
1Вице – президент
2 3 4 5
2
1 3 4 5
3
1 2 4 54
1 2 3 4
5
1 2 3 5
Такой метод решения комбинаторных задач называется правилом умножения.
Выбрать президента можно пятью способами, а для каждого выбранного президента четырьмя способами можно выбрать вице-президента . Следовательно, общее число способов выбрать президента и вице-президента фирмы равно: 5*4=20. -

11 слайд
Можно решить Задачу 3 короче, если применить правило умножения. Существует 4 варианта выбора первого урока. Для выбора второго урока есть только три варианта, так как один из четырех уроков мы уже выбрали. Тогда для третьего урока существует два варианта, а для четвертого только один. Применив правило умножения, получим
4 ∙ 3 ∙ 2 ∙1= 24
Ответ: 24 варианта. -

12 слайд
Задача №5
В классе 15 мальчиков и 10 девочек. Сколькими способами можно выбрать двух дежурных(одну девочку и одного мальчика)? -

13 слайд
Задача 2.
В 6 классе в четверг 5 уроков: математика, информатика, русский язык, английский язык, физкультура.
а) Сколько имеется вариантов расписания при условии, что физкультура – последний урок?
б) Сколько имеется вариантов расписания при условии, что физкультура – последний урок, а математика – первый?
-

14 слайд
Задача 2 (продолжение).
В 6 классе в четверг 5 уроков: математика, информатика, русский язык, английский язык, физкультура.в) Сколько всего можно составить вариантов расписания на четверг?
г) Сколько времени потратит завуч на запись всех вариантов, если известно, что на запись одного варианта у него уходит 30 секунд?
-

-

-

17 слайд
Задача №1
Запишите все трёхзначные числа, для записи которых употребляются только цифры 0,7.
Задача №2
Сколько двузначных чисел можно составить, используя цифры 1, 4 и 7? Нарисуйте дерево выбора на альбомном листе.
Задача №3
Составьте комбинаторную задачу, которая решается с помощью правила умножения. Сделайте к ней рисунок.
Задача № 4
Тренер попросил Филю составить трехзначное число из цифр 1, 2, 3, 4, причем цифры в числе
могут повторяться. Сколько чисел может составить Филя?
Задача № 5
Тренер попросил Филю составить трехзначное число из цифр 1, 2, 3, 4 так, чтобы цифры в числе
не повторялись. Сколько чисел может составить Филя?
Домашнее задание
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 255 877 материалов в базе
-
Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 24.04.2017
- 1052
- 0
- 24.04.2017
- 625
- 0
- 24.04.2017
- 1127
- 0
Рейтинг:
4 из 5
- 24.04.2017
- 32507
- 271
- 24.04.2017
- 2572
- 2
- 24.04.2017
- 7009
- 11
- 24.04.2017
- 846
- 3
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»
-
Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
Понятие графа
Кроме таблиц, удобным инструментом для перебора и подсчёта различных комбинаций является граф.
Граф – это абстрактный математический объект, представляющий собой множество вершин графа и набор рёбер, то есть соединений между парами вершин.

Граф из 6 вершин и 7 ребёр.
Например:
Сколько различных трёхзначных чисел можно написать с помощью цифр 0 и 1?

Получаем 4 числа: 100,101,110 и 111
Полный граф в комбинаторике
Полный граф– это граф со всеми возможными ребрами.

С помощью полного графа удобно решать задачи полного перебора про «всех со всеми».
Например:
5 школьных команд по волейболу сыграли серию игр. Каждая команда провела с другими командами по одному матчу. Сколько всего матчей было сыграно?
Изобразим полный граф с 5-ю вершинами и посчитаем количество ребёр.

N = 10. Значит, было сыграно 10 матчей.
Граф-дерево
Дерево – это граф без циклов, у которого между парами вершин имеется только одно ребро.

Граф-дерево с 9 узлами и 8 ребрами.
Из каждого узла выходит не более 2 ребер.
Такое дерево называют бинарным.
С помощью дерева удобно составлять упорядоченные комбинации элементов.
Например:
На столе стоит три стакана сока – апельсиновый, виноградный и яблочный. Можно взять только два стакана. Сколько есть возможных вариантов и каких?
По правилу произведения число возможных вариантов: $3 cdot 2 = 6$. Поскольку, порядок выбора неважен, остаётся $frac{6}{2} = 3$ варианта. Построим граф:

3 варианта: 1) апельсиновый + яблочный, 2)апельсиновый + виноградный, 3) виноградный + яблочный.
Примеры
Пример 1. Вася, Петя, Коля и Толя хотят быть дежурными в столовой. Но можно выбрать только троих. Сколько вариантов выбора есть?
Построим полный граф.

Каждая тройка ребят соответствует треугольнику в этом графе.
Например, Вася образует три треугольника с оставшимися тремя ребятами:
$ frac{3cdot 2}{2} = 3$ – ВПК, ВТК и ВТП
Без Васи есть только один треугольник – ПКТ
Общее количество треугольников 3+1=4
Ответ: 4 варианта
Пример 2. Под рукой есть 6 видов овощей (капуста, морковь, лук, помидоры, огурцы и перец). Для салата нужно 3 вида овощей. Сколько всего различных салатов можно приготовить?
Построим полный граф.

Каждые три овоща на полном графе образуют треугольник.
Например, капуста образует треугольники с оставшимися 5 овощами. Таких треугольников $ frac{5cdot 4}{2} = 10$, где деление на 2 учитывает повторение ребра в каждой паре («лук-огурец» = «огурец-лук» и т.д.).
Количество треугольников, в которые не входит капуста: $ frac{4cdot 3}{2} = 6$
Количество треугольников, в которые не входят капуста и морковь: $ frac{3cdot 2}{2} = 3$
Количество треугольников, в которые не входят капуста, морковь и перец: $ frac{2cdot 1}{2} = 1$
Итого 10+6+3+1 = 20 различных треугольников.
Ответ: 20 салатов
Примечание: по расчетной формуле $C_6^3 = frac{6cdot 5 cdot 4}{1cdot 2 cdot 3} = 20$ – ответ правильный.
Пример 3*. Сколько существует способов занять 1,2 и 3 места на чемпионате, в котором участвуют 11 команд? Решите задачу с помощью полного графа.
Если построить полный граф с 11-ю вершинами, каждая тройка команд в нём образует треугольник.

По аналогии с примерами 1 и 2, общее количество треугольников:
$$N = left(frac{10cdot 9}{2} + frac{9cdot 8}{2}right) + left(frac{8cdot 7}{2} + frac{7cdot 6}{2}right) + left(frac{6cdot 5}{2} + frac{5cdot 4}{2}right) + left(frac{4cdot 3}{2} + frac{3cdot 2}{2}right) + frac{2cdot 1}{2} = $$
$$ = 9 frac{(10+8)}{2} + 7 frac{(8+6)}{2} + 5 frac{(6+4)}{2} + 3 frac{(4+2)}{2} +1 = $$
$$ = 9^2+7^2+5^2+3^2+1 = 165 $$
Так, как порядок мест важен, в каждом треугольнике $– 3cdot2 = 6$ вариантов распределения медалей.
По правилу произведения: $6cdot165 = 990$ – общее количество способов.
Ответ: 990 вариантов
Примечание: по расчетной формуле $A_3^{11} = 11cdot10cdot9 = 990 $ – ответ правильный.
Пример 4. В столовой есть на выбор
- два первых блюда: щи (Щ) и борщ (Б)
- три вторых блюда: мясо (М), рыба (Р), блинчики с творогом (Т)
- два напитка: компот (К) и сок (С)
Сколько вариантов обедов можно составить из этих блюд и каких?
По правилу произведения общее количество вариантов обедов: $2cdot3cdot2 = 12$
Построим дерево для перечисления вариантов:

Ответ: 12 вариантов
1) Немного истории.
В математике и ее приложениях часто
приходится иметь дело с различного рода
множествами и подмножествами: устанавливать их
связь между элементами каждого, определять число
множеств или их подмножеств, обладающих заданным
свойством. Такие задачи приходится
рассматривать при определении наиболее выгодных
коммуникаций внутри города, при организации
автоматической телефонной связи, работы морских
портов, при выявлении связей внутри сложных
молекул, генетического кода, а также в
лингвистике, в автоматической системе
управления, значит и в теории вероятностей, и в
математической статистике со всеми их
многочисленными приложениями.
Поговорим об одном из разделов теории
вероятности – комбинаторике.
Комбинаторика – ветвь математики,
изучающая комбинации и перестановки предметов.
Еще комбинаторику можно понимать как перебор
возможных вариантов. Комбинаторика возникла в 17
веке. Долгое время она лежала вне основного русла
развития математики.
С задачами, в которых приходилось выбирать те или
иные предметы, располагать их в определенном
порядке и отыскивать среди разных расположений
наилучшие, люди столкнулись еще в доисторическую
эпоху, выбирая наилучшее положение охотников во
время охоты, воинов – во время битвы,
инструментов – во время работы.
Комбинаторные навыки оказались полезными и в
часы досуга. Нельзя точно сказать, когда наряду с
состязаниями в беге, метании диска, прыжках
появились игры, требовавшие, в первую очередь,
умения рассчитывать, составлять планы и
опровергать планы противника.
Со временем появились различные игры (нарды,
карты, шашки, шахматы и т.д.). В каждой из этих игр
приходилось рассматривать различные сочетания
фигур, и выигрывал тот, кто их лучше изучил, знал
выигрышные комбинации и умел избегать
проигрышных. Не только азартные игры давали пищу
для комбинаторных размышлений математиков. Еще с
давних пор дипломаты, стремясь к тайне переписки,
изобретали сложные шифры, а секретные службы
других государств пытались эти шифры разгадать.
Стали применять шифры, основанные на
комбинаторных принципах, например, на различных
перестановках букв, заменах букв с
использованием ключевых слов и т.д.
Комбинаторика как наука стала развиваться в 18
веке параллельно с возникновением теории
вероятностей, так как для решения вероятностных
задач необходимо было подсчитать число
различных комбинаций элементов. Первые научные
исследования по комбинаторике принадлежат
итальянским ученым Дж.Кардано, Н.Тарталье (1499-1557),
Г.Галилею (1564-1642) и французс- ким ученым Б.Паскалю
(1623-1662) и П.Ферма.
Комбинаторику как самостоятельный раздел
математики первым стал рассматривать немецкий
ученый Г.Лейбниц в своей работе “ Об искусстве
комбинаторики ”, опубликованной в 1666 году. Он
также впервые ввел термин “комбинаторика”.
Значительный вклад в развитие комбинаторики
внес Л.Эйлер. В современном обществе с развитием
вычислительной техники комбинаторика
“добилась” новых успехов. В настоящее время в
образовательный стандарт по математике включены
основы комбинаторики, решение комбинаторных
задач методом перебора, составлением дерева
вариантов (еще его называют “дерево
возможностей”) с применением правила умножения.
Так, например, “дерево возможностей” помогает
решать разнообразные задачи, касающиеся
перебора вариантов происходящих событий. Каждый
путь по этому “дереву” соответствует одному из
способов выбора, число способов выбора равно
числу точек в нижнем ряду “дерева”. Правило
умножения заключается в том, что для того, чтобы
найти число всех возможных исходов независимого
проведения двух испытаний А и В, следует
перемножить число всех исходов испытания А и
число всех исходов испытания В. В задачах по
комбинаторике часто применяется такое понятие
как факториал (в переводе с английского “factor” –
“множитель”).
Итак, произведение всех натуральных чисел от 1 до
n включительно называют n-факториалом и пишут: n!=1 2
3 … (n-1) n
В комбинаторике решаются задачи, связанные с
рассмотрением множеств и составлением различных
комбинаций из элементов этих множеств. В
зависимости от правил составления можно
выделить три типа комбинаций: перестановки,
размещения, сочетания.
2) ЗАДАЧИ
1. В школьной столовой на первое можно
заказать борщ, солянку, грибной суп, на второе –
мясо с макаронами, рыбу с картошкой, курицу с
рисом, а на третье – чай и компот. Сколько
различных обедов можно составить из указанных
блюд?
1 способ. Перечислим возможные
варианты
|
Чай(Ч) |
Мясо с макаронами(М) |
Рыба с картошкой(Р) |
Курица с рисом(Кр) |
|
Борщ (Б) |
БМЧ/ БМК |
БРЧ/БРК |
БКрЧ/БКрК |
|
Солянка(С) |
СМЧ/ СМК |
СРЧ/СРК |
СКрЧ/СКрК |
|
Грибной суп(Г) |
ГМЧ/ГМК |
ГРЧ/ГРК |
ГКрЧ/ГКрК |
18 вариантов.
2 способ. Дерево возможностей.
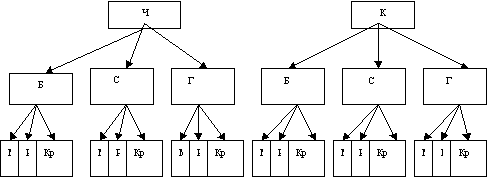
3 способ. Используя правило
умножения, получаем: 3х3х2=1
2. Свете на день рождения подарили 4
плюшевых игрушки, 2 мяча и 5 кукол. Мама положила
все игрушки в большую коробку. Сколькими
способами Света сможет достать из коробки 1
плюшевую игрушку, 1 мяч и 1 куклу?
1 способ. Обозначим мячи – М1, М2,
игрушки- И1,И2,И3, И4, куклы- К1,К2, К3, К4, К5.
Перечислим возможные варианты:
М1-И1-К1, М1-И1-К2, М1-И1-К3, М1-И1-К4, М1-И1-К5,
М1-И2-К1, М1-И2-К2, М1-И2-К3, М1-И2-К4, М1-И2-К5,
М1-И3-К1, М1-И3-К2, М1-И3-К3, М1-И3-К4, М1-И3-К5,
М1-И4-К1, М1-И4-К2, М1-И4-К3, М1-И4-К4, М1-И4-К5
М2-И1-К1, М2-И1-К2, М2-И1-К3, М2-И1-К4, М2-И1-К5,
М2-И2-К1, М2-И2-К2, М2-И2-К3, М2-И2-К4, М2-И2-К5,
М2-И3-К1, М2-И3-К2, М2-И3-К3, М2-И3-К4, М2-И3-К5,
М2-И4-К1, М2-И4-К2, М2-И4-К3, М2-И4-К4, М2-И4-К5
Ответ: 40 вариантов.
2 способ. Используя правило умножения,
получаем: 2х4х5= 40
3. Сколько четных двузначных чисел
можно составить из цифр 0, 2, 3, 6, 7, 9?
1 способ.
Перечислим возможные варианты.
|
0 |
2 |
6 |
|
|
2 |
20 |
22 |
26 |
|
3 |
30 |
32 |
36 |
|
6 |
60 |
62 |
66 |
|
7 |
70 |
72 |
76 |
|
9 |
90 |
92 |
96 |
2 способ. Дерево возможностей.
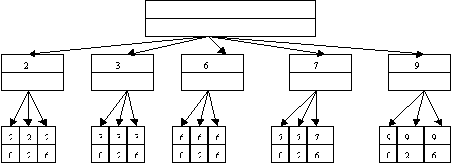
3 способ. Используя правило
умножения, получаем: 5х3=15 .
4. Мисс Марпл, расследуя убийство,
заметила отъезжающее от дома мистера Дэвидсона
такси. Она запомнила первую цифру “2”. В городке
номера машин были трехзначные и состояли из цифр
1,2,3,4 и 5. Скольких водителей, в худшем случае, ей
придется опросить, чтобы найти настоящего
убийцу?
1 способ. Перечислим возможные
варианты номеров такси:
|
1 |
2 |
3 |
4 |
5 |
|
|
1 |
211 |
212 |
213 |
214 |
215 |
|
2 |
221 |
222 |
223 |
224 |
225 |
|
3 |
231 |
232 |
233 |
234 |
235 |
|
4 |
241 |
242 |
243 |
244 |
245 |
|
5 |
251 |
252 |
253 |
254 |
255 |
Ответ: 25 человек.
2 способ. Используя правило
умножения, получаем: 5х5=25
5. Саша, Петя, Денис, Оля, Настя часто
ходят в кафе. Каждый раз, обедая там, они
рассаживаются по-разному. Сколько дней друзья
смогут это сделать без повторения?
1 способ. Пронумеруем стулья, на
которых должен сесть каждый, и будем считать, что
они рассаживаются поочередно:
№1 – Саша – есть возможность выбрать из 5
вариантов (стульев)
№2 – Петя – 4 варианта
№3- Денис – 3 варианта
№4- Оля – 2 варианта
№5 – Настя- 1 вариант
Используя правило умножения, получаем:
5х4х3х2х1=120
2 способ. Решаем, используя понятие
факториала: 5!=120
6. Из учащихся пяти 11 классов нужно
выбрать двоих дежурных. Сколько пар дежурных
можно составить (ученики в паре не должны быть из
одного класса)?
1 способ. Перечислим возможные
варианты состава пары:
11А-11Б, 11А-11В, 11А-11Г, 11А-11Д,
11Б-11В, 11Б-11Г, 11Б-11Д, 11В-11Г, 11В-11Д, 11Г-11Д
Ответ: 10 пар.
2 способ. Из пяти классов нужно
выбрать 2 дежурных.
Число элементарных событий = ![]() = 10
= 10
7. В 8 “а” классе лучше всех
математику знают 5 учеников: Вася, Дима, Олег, Катя
и Аня. На олимпиаду по математике нужно отправить
пару, состоящую из 1 мальчика и 1 девочки.
Сколькими способами учительница может эту пару
выбрать?
1 способ. Обозначим имена детей
первыми заглавными буквами.
Получаем следующие пары:
В-К, В-А, Д-К, Д-А, О-К, О-А.
Ответ: 6 пар.
2 способ. Мальчиков 3, из них 1 можно
выбрать ![]() ,
,
девочек 2, из них можно 1 выбрать ![]() , используя
, используя
правило умножения, получаем:
![]() х
х ![]() = 6
= 6
8. В соревнованиях по фигурному
катанию принимали участие россияне, итальянцы,
украинцы, немцы, китайцы и французы.
Сколькими способами могут
распределится места по окончании соревнований?
Обозначим участников по первой заглавной букве
страны и пронумеруем: Р1, И2, У3, Н4,К5, Ф6
Р1 – имеют возможность занять с1-6 места, т.е. 6
вариантов
И2 – 5 вариантов
У3- 4 варианта
Н4- 3 варианта
К5- 2 варианта
Ф6- 1 вариант
Используя правило умножения, получаем: 6х5х4х3х2х1=
720
2 способ. Используя понятие
факториала, получаем: 6!=720
9. В 9 “б” классе 6 человек (Галя,
Света, Катя, Оля, Максим, Витя) учатся на все
пятерки. Департамент образования премировал
лучших учащихся путевками в Анапу. Но, к
сожалению, путевок всего четыре. Сколько
возможно вариантов выбора учеников на отдых?
Обозначим первыми заглавными буквами
имен учащихся.
Возможны следующие тройки:
Г-С-К-О, Г-С-К-М, Г-С-К-В,
Г-С-О-М, Г-С-О-В, Г-С-М-В
С-К-О-М, С-К-О-В, С-К-М-В,
К-О-М-В, С-О-М-В, Г-К-О-В,
Г-К-О-В, Г-О-М-В, Г-К-М-В
2 способ. Из 6 человек нужно выбрать
4, число элементарных событий равно ![]() = 15
= 15
10. Пете на день рождения подарили 7
новых дисков с играми, а Вале папа привез 9 дисков
из командировки. Сколькими способами они могут
обменять 4 любых диска одного на 4 диска другого?
Вычислим, сколько четверок из 7 дисков
можно составить у Пети:
![]() =35, число
=35, число
четверок у Вали из 9 дисков –![]() = 126
= 126
По правилу умножения находим число обменов 35х126=4410
11. Войсковое подразделение состоит
из 5 офицеров, 8 сержантов и 70 рядовых. Сколькими
способами можно выделить отряд из 2 офицеров, 4
сержантов и 15 рядовых?
Из 5 офицеров выбрать 2 можно с помощью
числа сочетаний ![]() =10 способами, из 8 сержантов 4 –
=10 способами, из 8 сержантов 4 – ![]() =70, из 70 рядовых 15 –
=70, из 70 рядовых 15 –![]() . По правилу
. По правилу
умножения находим число выбора отряда:
10х70х![]() = 700х
= 700х![]()
12. В ювелирную мастерскую привезли 6
изумрудов, 9 алмазов и 7 сапфиров. Ювелиру
заказали браслет, в котором 3 изумруда, 5 алмазов и
2 сапфиров. Сколькими способами он может выбрать
камни на браслет?
Из 6 изумрудов 3 он может выбрать ![]() =20 способами, из 9
=20 способами, из 9
алмазов 5 –![]() =126,
=126,
из 7 сапфиров 2 – ![]() =21.
=21.
По правилу умножения находим число вариантов
20х126х21=52920
13. На выборах победили 9 человек –
Сафонов, Николаев, Петров, Кулаков, Мишин, Гусев,
Володин, Афонин, Титов. Из них нужно выбрать
председателя, заместителя и профорга. Сколькими
способами это можно сделать?
Здесь речь идет о размещениях ![]()
Можно было решать по-другому. На должность
председателя выбираем из 9 человек, на
заместителя – из 8, на профорга – из 7
По правилу умножения получаем 9х8х7=504
14. В районе построили новую школу. Из
пришедших 25 человек нужно выбрать директора
школы, завуча начальной школы, завуча среднего
звена и завуча по воспитательной работе.
Сколькими способами это можно сделать?
На должность директора выбираем из 25
человек, на завуча начальной – из 24, завуча
среднего звена – из 23, завуча по воспитательной
работе – 22. По правилу умножения получаем:
25х24х23х22 = 303600
Или, зная формулу размещения, получаем ![]()
15. В студенческом общежитии в одной
комнате живут трое студентов Петя, Вася и Коля. У
них есть 6 чашек, 8 блюдец и 10 чайных ложек (все
принадлежности отличаются друг от друга).
Сколькими способами ребята могут накрыть стол
для чаепития (так, что каждый получит чашку,
блюдце и ложку)?
Для Пети набор можно набрать 6х8х10=480
способами, для Васи – 5х7х9=315, для Коли – 4х6х8=192. По
правилу умножения получаем
480х315х192=29030400 способами.
16. В кабинете заведующего ювелирного
магазина имеется код, состоящий из двух
различных гласных букв русского алфавита, за
которой следуют 3 различные цифры. Сколько
вариантов придется перебрать мошеннику, чтобы
раздобыть драгоценности, которые там хранятся?
В русском языке 9 гласных букв – а, е, е,
и, о, у, э, ю, я. Выбрать из них 2 можно ![]() =36 способами. Из 10
=36 способами. Из 10
цифр выбрать 3 можно![]() =120 способами. Применяя правило умножения,
=120 способами. Применяя правило умножения,
получаем:
36х120=4320
17. Сколькими способами можно составить
трехцветный флаг из полос разной ширины, если
имеются материи из 8 тканей?
Эта задача на размещение ![]()
Другой способ решения.
1цвет выбирается из 8 тканей 8 способами
2цвет выбирается 7 способами
3 цвет – 6способами
Используя правило умножения, получаем 8х7х6=336
способов.
18. В 9 классе 15 предметов. Завучу школы
нужно составить расписание на субботу, если в
этот день 5 уроков. Сколько различных вариантов
расписания можно составить, если все уроки
различные?
Из 15 предметов 5 любых можно выбрать 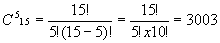
19. В огороде у бабушки растут 3 белые, 2
алые и 4 чайных розы. Сколькими различными
способами можно составить букет из трех роз
разного цвета?
1 способ. Обозначим белые – Б1, Б2, Б3,
алые – А1,А2, чайные – Ч1, Ч2, Ч3,Ч4
Перечислим возможные варианты
Б1-А1-Ч1, Б1-А1-Ч2, Б1-А1-Ч3, Б1-А1-Ч4, Б1-А2-Ч1,Б1-А2-Ч2, Б1-А2-Ч3,
Б1-А2-Ч4
Б2- А1-Ч1, Б2-А1-Ч2, Б2-А1-Ч3, Б2-А1-Ч4, Б2-А2-Ч1,Б2-А2-Ч2, Б2-А2-Ч3,
Б2-А2-Ч4
Б3- А1-Ч1, Б3-А1-Ч2, Б3-А1-Ч3, Б3-А1-Ч4, Б3-А2-Ч1,Б3-А2-Ч2, Б3-А2-Ч3,
Б3-А2-Ч4
Ответ: 24 варианта.
2способ. Дерево возможностей
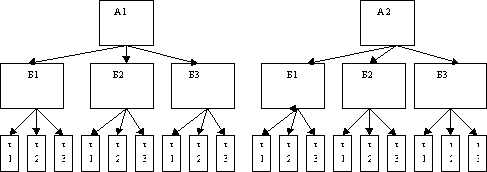
3 способ. Используя правило
умножения, получаем: 2х3х4=24
20. К 60-летию Победы группа школьников
отправилась по местам боевых действий в
Смоленской области. Они планировали осуществить
поход по маршруту деревни Сосновка-Быковка-
Масловка- Видово. Из С в Б можно проплыть по реке
или пройти пешком, из Б в М- пешком или на
автобусе, из М в В – по реке, пешком или автобусе.
Сколько вариантов похода есть у щкольников?
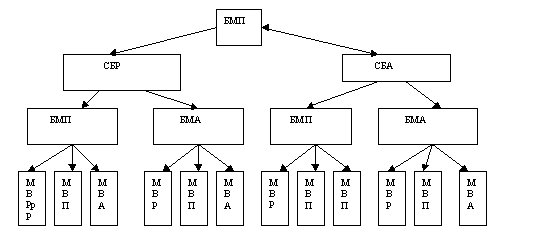
1 способ. Обозначим СБ – путь из
Сосновки в Бытовку, ВГ – путь из Быковки в
Масловку, МВ – путь из Масловки в Видово.
По реке -Р, пешком – П, на автобусе – А
Перечислим возможные варианты:
СБР- БМП-МВР, СБР- БМП-МВП, СБР- БМП-МВА
СБР-БМА-МВР, СБР-БМА-МВП, СБР-БМА-МВА
СБА- БМП-МВР, СБА- БМП-МВП, СБА- БМП-МВА
СБА-БМА-МВР, СБА-БМА-МВП, СБА-БМА-МВА
Ответ: 12 вариантов.
2 способ. Дерево возможностей
ЛИТЕРАТУРА
1) Еженедельное учебно-методическое
приложение “Математика” Изд. Пресса. Москва.1999 г
2) Ю.Н.Макарычев и др. Алгебра 9. Учебник
для класса с углубленным изучением математики.
Изд. Мнемозина, Москва.2005 год.
3) Л.Г. Петерсон. Математика 4 класс. Изд.
Баласс. Москва.1999 г.
4) Ю.Н. Тюрин и др. Теория вероятностей и
статистика. МЦНМО. Москва. 2004 год.
Слайд 1Комбинаторные задачи:
дерево возможных вариантов

Слайд 2ИМЯ УРОКА: КОМБИНАТОРИКА
ДЕВИЗ УРОКА: «УСЛЫШАЛ – ЗАБЫЛ,
УВИДЕЛ – ЗАПОМНИЛ,
СДЕЛАЛ – ПОНЯЛ»
КИТАЙСКАЯ ПОГОВОРКА

Слайд 3В странных русских сказаниях повествуется, как богатырь или другой добрый молодец,
доехав до распутья, читает на камне:
Вперёд поедешь – голову сложишь.
Налево поедешь – меча лишишься.
А дальше говорится, как он выходит из того положения, в которое попал в результате выбора.
Направо поедешь – коня потеряешь.
Но выбирать разные пути или варианты приходится и современному человеку. Эти пути и варианты складываются в самые разнообразные комбинации.
Слайд 4
Что такое КОМБИНАТОРИКА?
Задачи, в которых требуется осуществить перебор всех возможных вариантов,
или, как обычно говорят в таких случаях, всех возможных комбинаций, называют комбинаторными.
Область математики, изучающая комбинаторные задачи, называется комбинаторикой.
Комбинаторика – раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить.

Слайд 5Задача №1
Запишите все трёхзначные числа, для записи которых употребляются только
цифры 1 и 2.
1 2
1
1
2
2
1
1
1
1
2
2
2
2
Ответ: 111, 112, 121, 122, 211, 212, 221, 222 – восемь чисел.
Такой метод решения комбинаторных задач называется деревом выбора(дерево возможных вариантов)

Слайд 6Задача №2
Запишите все трёхзначные числа, для записи которых употребляются только
цифры 0,7.

Слайд 7ЗАДАЧА 3
В 5 «А» классе в среду
4 урока: математика, информатика, русский язык, английский язык. Сколько можно составить вариантов расписания на среду?
Решение: построим картину-схему.
Для удобства закодируем названия предметов:
математика – м,
информатика – и,
русский язык – р,
английский язык – а.

Слайд 8РЕШЕНИЕ ЗАДАЧИ 3
Расписание
1 урок м и р а
2 урок и р а м р а м и а м и р
3 урок р а и а и р р а м а м р и а м а м и и р м р м и
4 урок а р а и р и а р а м р м а и а м и м р и р м и м
Ответ: 24 варианта: мира, миар, мриа, мраи, маир, мари, имра, имар, ирма, ирам, иамр, иарм, рмиа, рмаи, рима, риам, рами, раим, амир, амри, аимр, аирм, арми, арим.
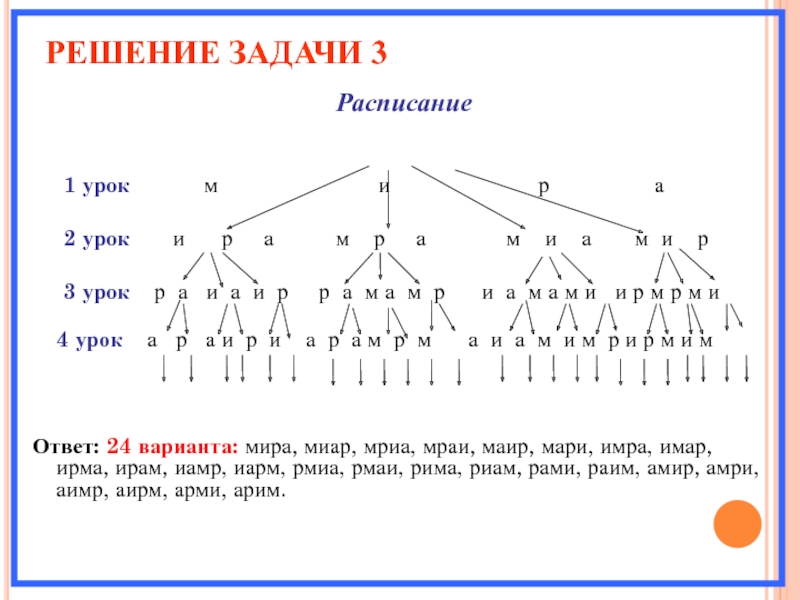
Слайд 9Построенная схема напоминает перевернутое дерево: от ствола («расписание») отходят ветки, сначала
четыре (м, и, р, а), от каждой из четырех веток – еще по три, затем еще по две и еще по одной. Видимо поэтому такую схему называют деревом возможных вариантов.
Дерево возможных вариантов можно считать геометрической моделью рассматриваемой ситуации.

Слайд 10Задача №4
В правление фирмы входят 5 человек. Из своего состава правления
должно выбрать президента и вице-президента. Сколькими способами это можно сделать?
Президент
Вице – президент
2 3 4 5
2
1 3 4 5
3
4
1 2 3 4
5
1 2 3 5
Такой метод решения комбинаторных задач называется правилом умножения.
Выбрать президента можно пятью способами, а для каждого выбранного президента четырьмя способами можно выбрать вице-президента . Следовательно, общее число способов выбрать президента и вице-президента фирмы равно: 5*4=20.

Слайд 11
Можно решить Задачу 3 короче, если применить правило умножения. Существует 4
варианта выбора первого урока. Для выбора второго урока есть только три варианта, так как один из четырех уроков мы уже выбрали. Тогда для третьего урока существует два варианта, а для четвертого только один. Применив правило умножения, получим
4 ∙ 3 ∙ 2 ∙1= 24
Ответ: 24 варианта.

Слайд 12
Задача №5
В классе 15 мальчиков и 10 девочек. Сколькими способами можно
выбрать двух дежурных(одну девочку и одного мальчика)?

Слайд 13ЗАДАЧА 2.
В 6 классе в четверг 5 уроков: математика, информатика, русский
язык, английский язык, физкультура.
а) Сколько имеется вариантов расписания при условии, что физкультура – последний урок?
б) Сколько имеется вариантов расписания при условии, что физкультура – последний урок, а математика – первый?

Слайд 14ЗАДАЧА 2 (ПРОДОЛЖЕНИЕ).
В 6 классе в четверг 5 уроков: математика, информатика,
русский язык, английский язык, физкультура.
в) Сколько всего можно составить вариантов расписания на четверг?
г) Сколько времени потратит завуч на запись всех вариантов, если известно, что на запись одного варианта у него уходит 30 секунд?

Слайд 17Задача №1
Запишите все трёхзначные числа, для записи которых употребляются только
цифры 0,7.
Задача №2
Сколько двузначных чисел можно составить, используя цифры 1, 4 и 7? Нарисуйте дерево выбора на альбомном листе.
Задача №3
Составьте комбинаторную задачу, которая решается с помощью правила умножения. Сделайте к ней рисунок.
Задача № 4
Тренер попросил Филю составить трехзначное число из цифр 1, 2, 3, 4, причем цифры в числе
могут повторяться. Сколько чисел может составить Филя?
Задача № 5
Тренер попросил Филю составить трехзначное число из цифр 1, 2, 3, 4 так, чтобы цифры в числе
не повторялись. Сколько чисел может составить Филя?
Домашнее задание

- Главная
- Справочники
- Справочник по математике 5-9 класс
- Комбинаторика
- Комбинаторные задачи
Комбинаторика (от латинского слова combinare, означающего №соединять”, “сочетать”) – это область математики, которая изучает способы выбора, расположения, сочетания различных объектов. Решение задач в данном разделе математики требует рассмотрения и подсчёта всех возможных комбинаций (отсюда название комбинаторные задачи). Решая эти задачи, обычно надо отвечать на вопрос “Сколькими способами…?” или “Сколько вариантов..?“
Задача: Нам даны фигуры: треугольник, овал и прямоугольник . Необходимо построить пирамидку, состоящую из трех разных фигур. Сколькими способами это можно сделать?
Метод перебора
Данный метод удобен при небольшом числе вариантов. Решение в данном случае происходит путём перебора всех возможных вариантов. При этом очень важно выбрать правильный вариант перебора – логику перебора.
Воспользуемся методом перебора: Пусть в основании пирамидки находится прямоугольник, тогда возможны варианты построения: прямоугольник – овал – треугольник и прямоугольник – треугольник – овал.

Теперь в основании положим овал, тогда возможны варианты построения: овал – прямоугольник – треугольник и овал – треугольник – прямоугольник.
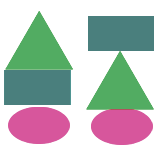
Теперь в основании положим треугольник, тогда возможны варианты построения: треугольник – прямоугольник – овал и треугольник – овал – прямоугольник.
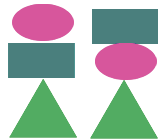
Итак, мы получили шесть возможных вариантов:
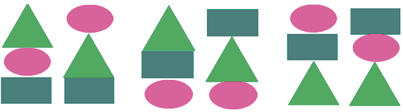
Ответ: 6 способов.
При решении данной задачи мы изображали фигуры, но для упрощения решения можно использовать кодирование. Данный прием позволяет заметить фигуры, например, первыми буквами их названия, то есть овал обозначаем буквой О, треугольник – Т, прямоугольник – П. Тогда решение будет выглядеть так:
Т О Т П О П
О Т П Т П О
П П О О Т Т
Дерево возможных вариантов
Данный метод заключается в построении схемы, которая и называется деревом возможных вариантов. Данная схема действительно похожа на перевернутое дерево, “корень” которого обозначается “*”. Построим данную схему для нашей задачи: Для этого от “корня” проведем три “ветки” – отрезки, на концах которых подпишем варианты фигур, которые мы можем взять за основание. Далее от каждой фигуры проводим такое количество “веток”, которое будет соответствовать числу вариантов фигур на втором месте, в нашем случае по две “ветки” от каждой фигуры. Затем от каждой фигуры, стоящей на втором месте, проводим такое число “веток”, которое будет соответствовать числу вариантов фигур на третьем месте, в нашем случае по одной “ветке” от каждой фигуры. Тогда имеем следующее дерево возможных вариантов:
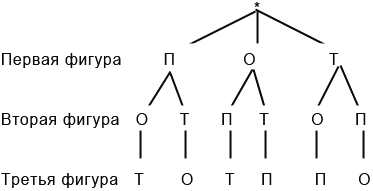
Метод отрезков
Данный метод используется только для составления всевозможных пар. Например, рассмотрим прямую, на которой обозначены точки A, B, C, D, F:
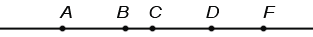
Необходимо ответить на вопрос: ” Сколько отрезков изображено на рисунке?”. Мы знаем, что отрезок обозначается двумя буквами, значит, для ответа на вопрос необходимо перебрать всевозможные пары букв. Это можно сделать при помощи следующей схемы: Отметим точки так, чтобы никакие 3 не лежали на одной прямой:
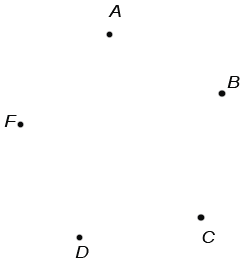
Соединим данные точки отрезками между собой. Число отрезков будет числом вариантов, то есть числом отрезков, изображенных на рисунке:
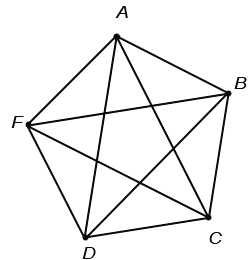
Итак, мы получили 10 отрезков, соединяющих точки.
Ответ: На рисунке 10 отрезков.
Советуем посмотреть:
Случайные события. Вероятность случайного события
Комбинаторика
Правило встречается в следующих упражнениях:
5 класс
Задание 283,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 598,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 694,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 733,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 835,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1035,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 871,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 872,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Номер 841,
Мерзляк, Полонский, Якир, Учебник
Номер 842,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 990,
Мерзляк, Полонский, Якир, Учебник
Номер 1023,
Мерзляк, Полонский, Якир, Учебник
Номер 1212,
Мерзляк, Полонский, Якир, Учебник
Номер 1239,
Мерзляк, Полонский, Якир, Учебник
Задание 53,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 232,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 355,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 410,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 462,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 24,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
7 класс
Номер 78,
Мерзляк, Полонский, Якир, Учебник
Номер 301,
Мерзляк, Полонский, Якир, Учебник
