Привет! Сегодня узнаем, как решать 4 задание из ЕГЭ по информатике нового формата 2021.
Четвёртое задание из ЕГЭ по информатике раскрывает тему кодирование информации. Одним из центральных приёмов при решении задач подобного типа является построение дерева Фано. Рассмотрим на примерах этот метод.
Задача (стандартная)
По каналу связи передаются сообщения, содержащие только шесть букв: А, B, C, D, E, F. Для передачи используется неравномерный двоичный код, удовлетворяющий условию Фано. Для букв A, B, C используются такие кодовые слова: А — 11, B — 101, C — 0. Укажите кодовое слово наименьшей возможной длины, которое можно использовать для буквы F. Если таких слов несколько, укажите то из них, которое соответствует наименьшему возможному двоичному числу.
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова. Коды, удовлетворяющие условию Фано, допускают однозначное декодирование
Решение:
Т.к. код букв должен удовлетворять условию Фано (т.е. однозначно декодироваться), то
расположим буквы, которые уже имеют код (A, B, C), на Дереве Фано.
Дерево Фано для двоичного кодирования начинается с двух направлений, которые означают 0(ноль) и 1(единицу) (цифры двоичного кодирования).
От каждого направления можно также рисовать только два направления: 0(ноль) и 1(единицу) и т.д. Для удобства будем рисовать 1(единицу) только вправо, а 0(ноль) только влево.
Получается структура похожая на дерево!
В конце каждой ветки можно располагать букву, которую мы хотим закодировать, но если мы расположили букву, от этой ветки больше нельзя делать новых ответвлений.
Такой подход позволяет однозначно декодировать сообщение, состоящее из этих букв.
Буква C заблокировала левую ветку, поэтому будем работать с правой частью нашего дерева.
Если мы расположим какую-нибудь букву на оставшуюся ветку (100), то эта ветка заблокируется, и нам некуда будет писать остальные 2 буквы. Поэтому продолжаем ветку (100) дальше.
Теперь свободно уже две ветки, а нам нужно закодировать ещё три буквы. Поэтому должны ещё раз продолжить дерево от какой-нибудь ветки.
Но уже видно, что букве F будет правильно присвоить код 1000, т.к. нам в условии сказано, что код буквы F должен соответствовать наименьшему возможному двоичному числу. Как расположить буквы D и E в данной задаче не принципиально.
Ответ: 1000.
Ещё один важный тип задания 4 из ЕГЭ по информатике нового формата 2021.
Задача (стандартная)
По каналу связи передаются сообщения, содержащие только семь букв: А, Б, И, К, Л, С, Ц. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: Б — 00, К — 010, Л — 111. Какое наименьшее количество двоичных знаков потребуется для кодирования слова АБСЦИССА?
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
Решение:
Коды букв должны удовлетворять условию Фано. Некоторые буквы уже имеют заданные коды (Б, К, Л). Нам нужно, чтобы слово АБСЦИССА имело как можно меньше двоичных знаков. Заметим, что буква C встречается три раза, а буква A два раза, значит, этим буквам стараемся присвоить как можно меньшую длину!
Отметим на дереве Фано уже известные буквы (Б, К, Л).
У нас осталось 4 (четыре) буквы, а свободных веток 3(три), поэтому мы должны продолжить дерево. но какую ветку продолжить ?
1 вариант
Если продолжить линию 1-0, то получится такая картина :
Теперь получились 4(четыре) свободные ветки равной длины (3(трём) двоичным символам). Т.к. ветки равной длины, то не важно на какую ветку какую букву расположим.
Посчитаем общую длину слова АБСЦИССА.
3 + 2 + 3 + 3 + 3 + 3 + 3 + 3 = 23.
2 вариант
Продлим линию 1-1-0 (можно и 0-1-1, не принципиально, т.к. эти ветки имеют одинаковую длину.), то получится:
С мы присваиваем 1-0, т.к. это буква повторяется в сообщении самое большое количество раз, значит, ей присваиваем самый маленький код, чтобы всё сообщение имело наименьшую длину.
Из этих же соображений букве А присваиваем код из трёх двоичных символов 0-1-1.
Подсчитаем общее количество символов в сообщении.
3 + 2 + 2 + 4 + 4 + 2 + 2 + 3 = 22
Длина получилась меньше, чем в первом варианте. Других вариантов нет, поэтому ответ будет 22.
Ответ: 22.
Задача (не сложная)
Для передачи по каналу связи сообщения, состоящего только из символов А, Б, В и Г, используется неравномерный (по длине) код: А-10, Б-11, В-110, Г-0. Через канал связи передаётся сообщение: ВАГБААГВ. Закодируйте сообщение данным кодом. Полученное двоичное число переведите в восьмеричный вид.
Решение:
В этой задаче ничего не сказано про условие Фано. Здесь уже все буквы закодированы, осталось написать сам код.
Задача сводится к переводу из двоичной системы в восьмеричную систему. На эту тему был урок на моём сайте.
Ответ: 151646.
На этом всё! Увидимся на следующих занятиях по подготовке к ЕГЭ по информатике.
Этого не знаю. Это просто примерные задачи, которые наиболее часто попадаются в книжках и на сайтах по подготовке к ЕГЭ по информатике.
Здравствуйте, а вот такое задание ПО КАНАЛУ СВЯЗИ ПЕРЕДАЮТСЯ СООБЩЕНИЯ, СОДЕРЖАЩИЕ ТОЛЬКО 4 БУКВЫ : А, Б, В, Г; ДЛЯ ПЕРЕДАЧИ ИСП. ДВОИЧНЫЙ КОД, ДОПУСКАЮЩИЙ ОДНОЗНАЧНОЕ ДЕКОДИРОВАНИЕ. ДЛЯ БУКВ А, Б, В ИСПОЛЬЗУЮТСЯ ТАКИЕ КОДОВЫЕ СЛОВА: А:00011, Б:1001, В: 01100.
УКАЖИТЕ КРАТЧАЙШЕЕ КОДОВОЕ СЛОВО ДЛЯ БУКВЫ Г, ПРИ КОТОРОМ КОД БУДЕТ ДОПУСКАТЬ ОДНОЗНАЧНОЕ ДЕКОДИРОВАНИЕ. ЕСЛИ ТАКИХ КОДОВ НЕСКОЛЬКО, УКАЖИТЕ КОД С НАИМЕНЬШИМ ЧИСЛОВЫМ ЗНАЧЕНИЕМ. В ответе указано число 10. Не могу понять почему. У меня 11.
Здравствуйте, а вот такое задание ПО КАНАЛУ СВЯЗИ ПЕРЕДАЮТСЯ СООБЩЕНИЯ, СОДЕРЖАЩИЕ ТОЛЬКО 4 БУКВЫ : А, Б, В, Г; ДЛЯ ПЕРЕДАЧИ ИСП. ДВОИЧНЫЙ КОД, ДОПУСКАЮЩИЙ ОДНОЗНАЧНОЕ ДЕКОДИРОВАНИЕ. ДЛЯ БУКВ А, Б, В ИСПОЛЬЗУЮТСЯ ТАКИЕ КОДОВЫЕ СЛОВА: А:00011, Б:1001, В: 01100.
УКАЖИТЕ КРАТЧАЙШЕЕ КОДОВОЕ СЛОВО ДЛЯ БУКВЫ Г, ПРИ КОТОРОМ КОД БУДЕТ ДОПУСКАТЬ ОДНОЗНАЧНОЕ ДЕКОДИРОВАНИЕ. ЕСЛИ ТАКИХ КОДОВ НЕСКОЛЬКО, УКАЖИТЕ КОД С НАИМЕНЬШИМ ЧИСЛОВЫМ ЗНАЧЕНИЕМ. В ответе указано число 10. Не могу понять почему. У меня 11.
Ольга Владимировна Сорокина, как я понимаю, суть задания в том, что здесь действует либо прямое, либо обратное условие Фано. (Примечание. Условие Фано означает, что соблюдается одно из двух условий.
Либо никакое кодовое слово не является началом другого кодового слова,
либо никакое кодовое слово не является окончанием другого кодового слова.
Это обеспечивает возможность однозначной расшифровки закодированных
сообщений.)
Поэтому 10 является ответом, так как ни один код для букв не оканчивается на 10 (срабатывает обратное условие Фано)
Кодирование – это перевод информации с одного языка, в последовательность кодов. Для удобства ее хранения, передачи и обработки.
При вводе в компьютер информации, происходит ее двоичное кодирование. Информация может быть текстовая, графическая, звуковая. Код символа хранится в оперативной памяти компьютера. В процессе вывода символа на экран производится обратная операция — декодирование, т. е. преобразование кода символа в его изображение, символ или звук.
Декодирование – процесс обратный кодированию, т.е. расшифровка кодов.
Кодирование информации может быть равномерным и неравномерным.
При равномерном кодировании каждому символу соответствует код одинаковой длины.
При неравномерном кодировании различным символам могут соответствовать коды различной длины.
Условие Фано
Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова.
Например пара кодовых слов 10 и 101 не выполняют условие Фано, потому что 101 является началом 10. А вот 100 и 101 уже выполняют условие Фано.
В конце статьи мы разберем задание в котором нужно найти кодовое слово для буквы удовлетворяющее условию Фано. На примере часто бывает проще разобраться!
Код который удовлетворяет условию Фано, называется префиксным. Префиксный код однозначно декодируется с начала.
Вы можете встретить еще постфиксный код – это код, в котором никакое кодовое слово не является концом другого кодового слова. Такое закодированное сообщение декодируется однозначно и только с конца. Постфиксный код удовлетворяет обратному условию Фано.
Бинарное дерево на рисунке построено до значений из таблицы триад, можно продолжить строить дерево, но принцип я думаю понятен.
Для кодирования некоторой последовательности, состоящей из букв У, К, Е, Н, Г решили использовать неравномерный двоичный код удовлетворяющий условию Фано. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Для букв У, К, Е использовали соответственно кодовые слова 00, 010, 11. Для двух оставшихся букв – Н и Г – кодовые слова не известны.
Укажите кратчайшее возможное кодовое слово для буквы Н, при котором код будет удовлетворять указанному условию. Если таких кодов несколько, то укажите код с наименьшим числовым значением.
В тех местах где мы находим кодовые слова букв которые нам уже известны, ветка дерева обрывается. Если мы продолжим ее строить, то коды которые будем получать дальше не будут удовлетворять условию Фано.
Если вы уже знакомились с Разбором демоверсии 2021 и делали это внимательно, то вы заметите, что данная задача очень похожа на №4. Я вам предлагаю решить четвертый номер из демоверсии, будьте внимательны, там есть подвох!
Задание №4 по информатике. Демоверсия ЕГЭ. Разбор.
А свои ответы и разборы можете писать в комментариях. И не забывайте подписываться, чтобы не пропустить новые статьи!
Содержание
- Алгоритм вычисления кодов Шеннона-Фано
- Пример кодового дерева
- ЕГЭ по информатике 2021 — Задание 4 (Условие Фано)
- Алгоритм Шеннона-Фано
Алгоритм вычисления кодов Шеннона-Фано



Код Шеннона-Фано строится с помощью дерева. Построение этого дерева начинается от корня. Всё множество кодируемых элементов соответствует корню дерева (вершине первого уровня). Оно разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Эти подмножества соответствуют двум вершинам второго уровня, которые соединяются с корнем.
Далее каждое из этих подмножеств разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Им соответствуют вершины третьего уровня. Если подмножество содержит единственный элемент, то ему соответствует концевая вершина кодового дерева; такое подмножество разбиению не подлежит. Подобным образом поступаем до тех пор, пока не получим все концевые вершины. Ветви кодового дерева размечаем символами 1 и 0, как в случае кода Хаффмана.
При построении кода Шеннона-Фано разбиение множества элементов может быть произведено, вообще говоря, несколькими способами. Выбор разбиения на уровне n может ухудшить варианты разбиения на следующем уровне (n + 1) и привести к неоптимальности кода в целом. Другими словами, оптимальное поведение на каждом шаге пути ещё не гарантирует оптимальности всей совокупности действий.
Поэтому код Шеннона-Фано не является оптимальным в общем смысле, хотя и дает оптимальные результаты при некоторых распределениях вероятностей. Для одного и того же распределения вероятностей можно построить, вообще говоря, несколько кодов Шеннона-Фано, и все они могут дать различные результаты. Если построить все возможные коды Шеннона-Фано для данного распределения вероятностей, то среди них будут находиться и все коды Хаффмана, то есть оптимальные коды.
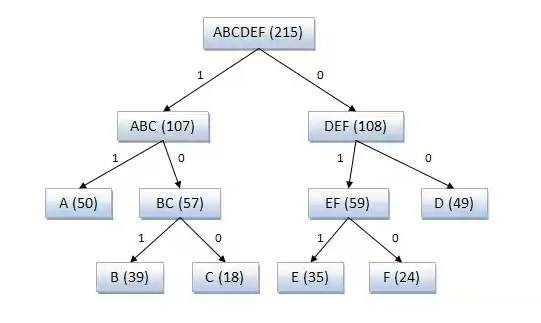
Пример кодового дерева
Исходные символы:
A (частота встречаемости 50)
B (частота встречаемости 39)
C (частота встречаемости 18)
D (частота встречаемости 49)
E (частота встречаемости 35)
F (частота встречаемости 24)
Полученный код: A — 11, B — 101, C — 100, D — 00, E — 011, F — 010.
Кодирование Шеннона-Фано является достаточно старым методом сжатия, и на сегодняшний день оно не представляет особого практического интереса. В большинстве случаев, длина последовательности, сжатой по данному методу, равна длине сжатой последовательности с использованием кодирования Хаффмана. Но на некоторых последовательностях могут сформироваться неоптимальные коды Шеннона-Фано, поэтому более эффективным считается сжатие методом Хаффмана.
Пример 1. Закодируем буквы алфавита в коде Шеннона-Фано.
Пусть имеется случайная величина X (x1, x2, x3, x4, x5, x6, x7, x8), имеющая восемь состояний с распределением вероятностей
Для кодирования алфавита из восьми букв без учета вероятностей равномерным двоичным кодом нам понадобятся три символа:
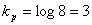
Чтобы ответить, хорош этот код или нет, необходимо сравнить его с оптимальным значением, то есть определить энтропию
Определив избыточность L по формуле L=1-H/H0=1-2,75/3=0,084, видим, что возможно сокращение длины кода на 8,4%.
Все буквы записываются в порядке убывания их вероятностей, затем делятся на равновероятные группы, которые обозначаются 0 и 1, затем вновь делятся на равновероятные группы и т.д. (см.табл.4.1)
| X | P | Коды | |
| x1 | 1/4 | ——- | ——- |
| x2 | 1/4 | ——- | ——- |
| x3, | 1/8 | ——- | |
| x4 | 1/8 | ——- | |
| x5 | 1/16 | ||
| x6 | 1/16 | ||
| x7 | 1/16 | ||
| x8 | 1/16 |
Средняя длина полученного кода будет равна
Итак, мы получили оптимальный код. Длина этого кода совпала с энтропией. Данный код оказался удачным, так как величины вероятностей точно делились на равновероятные группы.
Возьмем 32 две буквы русского алфавита. Частоты этих букв известны. В алфавит включен и пробел, частота которого составляет 0,145. Метод кодирования представлен в таблице
| Буква | Рi | Код | ||
| ? | 0.145 | — | ||
| о | 0.095 | — | ||
| е | 0.074 | |||
| а | 0.064 | |||
| и | 0.064 | |||
| н | 0.056 | |||
| т | 0.056 | … | … | — |
| с | 0.047 | … | … | |
| . | … | |||
| ф | 0.03 |
Средняя длина данного кода будет равна, 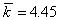
Энтропия H=4.42 бит/буква. Эффективность полученного кода можно определить как отношение энтропии к средней длине кода. Она равна 0,994. При значении равном единице код является оптимальным. Если бы мы кодировали кодом равномерной длины 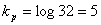
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями: 


Источник
ЕГЭ по информатике 2021 — Задание 4 (Условие Фано)
Привет! Сегодня узнаем, как решать 4 задание из ЕГЭ по информатике нового формата 2021.
Четвёртое задание из ЕГЭ по информатике раскрывает тему кодирование информации. Одним из центральных приёмов при решении задач подобного типа является построение дерева Фано. Рассмотрим на примерах этот метод.
По каналу связи передаются сообщения, содержащие только шесть букв: А, B, C, D, E, F. Для передачи используется неравномерный двоичный код, удовлетворяющий условию Фано. Для букв A, B, C используются такие кодовые слова: А — 11, B — 101, C — 0. Укажите кодовое слово наименьшей возможной длины, которое можно использовать для буквы F. Если таких слов несколько, укажите то из них, которое соответствует наименьшему возможному двоичному числу.
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова. Коды, удовлетворяющие условию Фано, допускают однозначное декодирование
Т.к. код букв должен удовлетворять условию Фано (т.е. однозначно декодироваться), то расположим буквы, которые уже имеют код (A, B, C), на Дереве Фано.
Дерево Фано для двоичного кодирования начинается с двух направлений, которые означают 0(ноль) и 1(единицу) (цифры двоичного кодирования).
От каждого направления можно также рисовать только два направления: 0(ноль) и 1(единицу) и т.д. Для удобства будем рисовать 1(единицу) только вправо, а 0(ноль) только влево.
Получается структура похожая на дерево!
В конце каждой ветки можно располагать букву, которую мы хотим закодировать, но если мы расположили букву, от этой ветки больше нельзя делать новых ответвлений.
Такой подход позволяет однозначно декодировать сообщение, состоящее из этих букв.
.jpg)
Буква C заблокировала левую ветку, поэтому будем работать с правой частью нашего дерева.
Если мы расположим какую-нибудь букву на оставшуюся ветку (100), то эта ветка заблокируется, и нам некуда будет писать остальные 2 буквы. Поэтому продолжаем ветку (100) дальше.
.jpg)
Теперь свободно уже две ветки, а нам нужно закодировать ещё три буквы. Поэтому должны ещё раз продолжить дерево от какой-нибудь ветки.
Но уже видно, что букве F будет правильно присвоить код 1000, т.к. нам в условии сказано, что код буквы F должен соответствовать наименьшему возможному двоичному числу. Как расположить буквы D и E в данной задаче не принципиально.
Ещё один важный тип задания 4 из ЕГЭ по информатике нового формата 2021.
По каналу связи передаются сообщения, содержащие только семь букв: А, Б, И, К, Л, С, Ц. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: Б — 00, К — 010, Л — 111. Какое наименьшее количество двоичных знаков потребуется для кодирования слова АБСЦИССА?
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
Коды букв должны удовлетворять условию Фано. Некоторые буквы уже имеют заданные коды (Б, К, Л). Нам нужно, чтобы слово АБСЦИССА имело как можно меньше двоичных знаков. Заметим, что буква C встречается три раза, а буква A два раза, значит, этим буквам стараемся присвоить как можно меньшую длину!
Отметим на дереве Фано уже известные буквы (Б, К, Л).
У нас осталось 4 (четыре) буквы, а свободных веток 3(три), поэтому мы должны продолжить дерево. но какую ветку продолжить ?
Если продолжить линию 1-0, то получится такая картина :
.jpg)
Теперь получились 4(четыре) свободные ветки равной длины (3(трём) двоичным символам). Т.к. ветки равной длины, то не важно на какую ветку какую букву расположим.
Посчитаем общую длину слова АБСЦИССА.
.jpg)
3 + 2 + 3 + 3 + 3 + 3 + 3 + 3 = 23.
Продлим линию 1-1-0 (можно и 0-1-1, не принципиально, т.к. эти ветки имеют одинаковую длину.), то получится:
С мы присваиваем 1-0, т.к. это буква повторяется в сообщении самое большое количество раз, значит, ей присваиваем самый маленький код, чтобы всё сообщение имело наименьшую длину.
Из этих же соображений букве А присваиваем код из трёх двоичных символов 0-1-1.
Подсчитаем общее количество символов в сообщении.
.jpg)
3 + 2 + 2 + 4 + 4 + 2 + 2 + 3 = 22
Длина получилась меньше, чем в первом варианте. Других вариантов нет, поэтому ответ будет 22.
Для передачи по каналу связи сообщения, состоящего только из символов А, Б, В и Г, используется неравномерный (по длине) код: А-10, Б-11, В-110, Г-0. Через канал связи передаётся сообщение: ВАГБААГВ. Закодируйте сообщение данным кодом. Полученное двоичное число переведите в восьмеричный вид.
В этой задаче ничего не сказано про условие Фано. Здесь уже все буквы закодированы, осталось написать сам код.
Задача сводится к переводу из двоичной системы в восьмеричную систему. На эту тему был урок на моём сайте.
На этом всё! Увидимся на следующих занятиях по подготовке к ЕГЭ по информатике.
Источник
Алгоритм Шеннона-Фано
Алгоритм метода Шеннона-Фано — один из первых алгоритмов сжатия, который впервые сформулировали американские учёные Шеннон и Фано, и он имеет большое сходство с алгоритмом Хаффмана. Алгоритм основан на частоте повторения. Так, часто встречающийся символ кодируется кодом меньшей длины, а редко встречающийся — кодом большей длины.
В свою очередь, коды, полученные при кодировании, префиксные. Это и позволяет однозначно декодировать любую последовательность кодовых слов. Но все это вступление.
Для работы оба алгоритма должны иметь таблицу частот элементов алфавита.
Итак, алгоритм Хаффмана работает следующим образом:
- На вход приходят упорядоченные по невозрастанию частот данные.
- Выбираются две наименьших по частоте буквы алфавита, и создается родитель (сумма двух частот этих «листков»).
- Потомки удаляются и вместо них записывается родитель, «ветви» родителя нумеруются: левой ветви ставится в соответствие «1», правой «0».
- Шаг два повторяется до тех пор, пока не будет найден главный родитель — «корень».
Алгоритм Шеннона-Фано работает следующим образом:
- На вход приходят упорядоченные по невозрастанию частот данные.
- Находится середина, которая делит алфавит примерно на две части. Эти части (суммы частот алфавита) примерно равны. Для левой части присваивается «1», для правой «0», таким образом мы получим листья дерева
- Шаг 2 повторяется до тех пор, пока мы не получим единственный элемент последовательности, т.е. листок
Таким образом, видно, что алгоритм Хаффмана как бы движется от листьев к корню, а алгоритм Шеннона-Фано, используя деление, движется от корня к листям.
Ну вот, быстро осмыслив информацию, можно написать код алгоритма Шеннона-Фано на паскале. Попросили именно на нем написать. Поэтому приведу листинг вместе с комментариями.
Ну вот собственно и все, о чем я хотел рассказать. Всю информацию можно взять из википедии. На рисунках приведены частоты сверху.
Источник
На этой странице вы узнаете
- Как закодировать сообщение “КУРЛЫК” правильно?
- Что такое равномерное кодирование?
- Так как кодировать сообщения максимально эффективно?
Понятие однозначного декодирования
Вы любите шпионов? А готовы почувствовать себя в их шкуре?
Нам нужно передать секретное сообщение на базу, а раз оно секретное, никто не должен понять, что мы передаем. Для этого надо представить наше сообщение в каком-то новом виде, который на первый взгляд будет бессмысленным, но мы будем знать, как его расшифровать.

Главное — чтобы расшифровать было возможно.
Мы уже знаем, что для компьютера информацию надо представить в двоичномкоде — подробнее об этом рассказано в статье «Основные понятия об информации». Но сам процесс кодирования информации — не такая простая вещь. Есть несколько факторов, которые нужно соблюсти, чтобы кодирование прошло хорошо.
Но чтобы научиться делать что-то правильно, сначала надо разобраться, как сделать неправильно. Давайте попробуем произвольным образом закодировать буквы К, У, Р, Л, Ы, чтобы составлять из них сообщения.
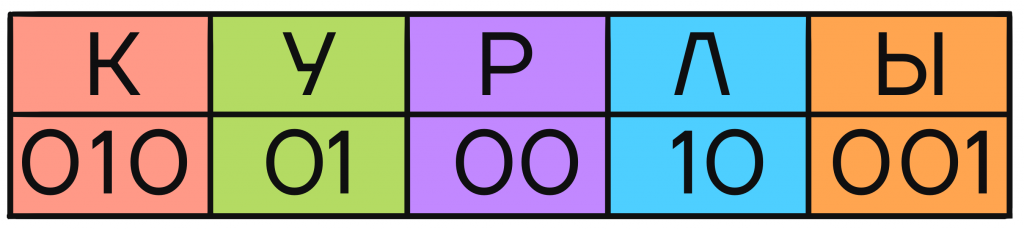
Каждой букве в табличке сопоставлено несколько символов, в нашем случае цифр. Эти символы — кодовое слово буквы, позволяющее отличить ее от других букв в закодированном сообщении.
С помощью кодовых слов каждой отдельной буквы закодируем сообщение КУРЛЫК, для этого на место каждой буквы будем подставлять соответствующее ей кодовое слово:

С проблемой мы столкнемся при попытке расшифровать сообщение. Чтобы это сделать, надо выделить в коде сообщения отдельные кодовые слова и подставить на их место соответствующие буквы. Но при расшифровке этого кода можно получить другой вариант:
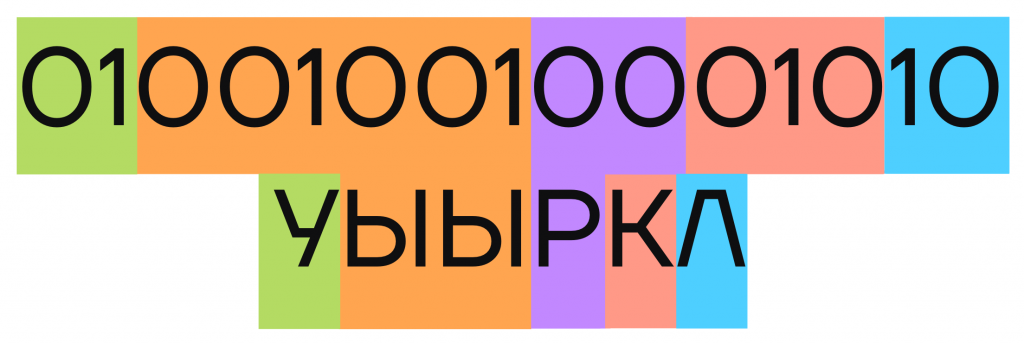
Чтобы кодирование считалось качественным и надежным, код должен удовлетворять условию однозначного декодирования — после кодирования сообщений у них должен быть единственный вариант расшифровки.
Равномерное кодирование
Но как можно соблюдать это условие? Или еще круче — как строить кодовые слова, которые заранее будут этому условию удовлетворять?
Это первый вариант подхода к однозначному декодированию.Он подразумевает кодирование отдельных элементов кодами, имеющими одинаковую длину.
И такой подход действительно спасает ситуацию. Если каждое кодовое слово будет иметь одинаковую длину, и при этом все они будут различны, выделять в зашифрованном сообщении отдельные кодовые слова не составит труда, как и сопоставлять их с соответствующими им буквами.
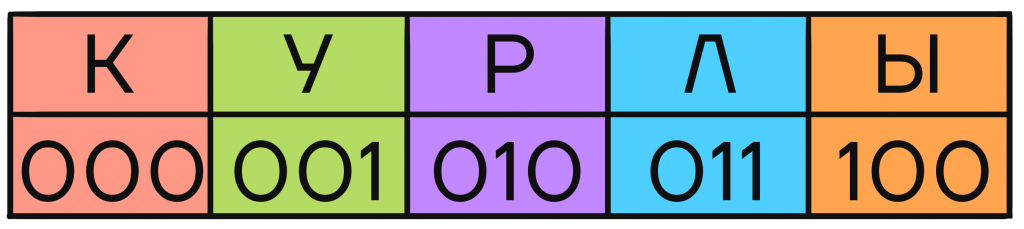
Кодируем сообщение КУРЛЫК:

И при попытке декодирования, поочередно выделяя кодовые слова одинаковой длины, мы не имеем никаких проблем с сопоставлением и получаем исходное сообщение без альтернативных вариантов.

Такой метод действительно прост и в освоении, и при составлении кодовых слов, и при расшифровке. Но есть один минус — он не всегда эффективен.
Выбирая длину одного кодового слова, мы можем заранее определить количество возможных кодов: так как на каждой позиции может быть либо 0, либо 1, количество возможных кодов N длины i будет равно
(N = 2^i).
Выбрав длину 3 для наших кодовых слов, мы имеем 8 различных кодов, хотя кодируем всего 5 букв.
В других ситуациях потери могут быть плачевнее: для кодирования, например, 33 букв русского алфавита длина кодового слова должна быть не меньше 6 (если выберем 5, получим максимум 25 = 32 кодового слова, но тогда 1 буква останется незакодированной).
Но имея 26 = 64 кодовых слова для 33-х букв алфавита, мы явно взяли кодов больше, чем нужно.
Почему это плохо? Рассмотрим следующую ситуацию.
Вася собирает вещи для переезда и ему надо упаковать какой-то набор вещей в коробку. Если в ней много свободного места — это плохо, потому что Вася может взять коробку поменьше и ему будет легче нести маленькую коробку. Также и здесь, если в нашей кодировке много неиспользованных кодов — это плохо, потому что можно оптимальнее перекодировать необходимый набор символов, и зашифрованные сообщения станут занимать меньше места на компьютере или быстрее передаваться по интернету.
Естественно, равномерное кодирование — все еще возможный вариант, при котором код будет однозначно декодируемым, но нет ли более рационального подхода?
Условие Фано и дерево вариантов
Хороший вариант — составление кодовых слов, которые удовлетворяют условию Фано.
Условие Фано гласит: «ни одно кодовое слово не должно быть началом другого кодового слова».
В составленных нами в самом начале статьи кодовых словах это условие нарушалось — код буквы К (010) начинался с кода буквы У (01), а код Ы (001) — с кода Р (00). Из-за этого мы не могли быть точно уверены, где закончилось кодовое слово, а где оно продолжается.
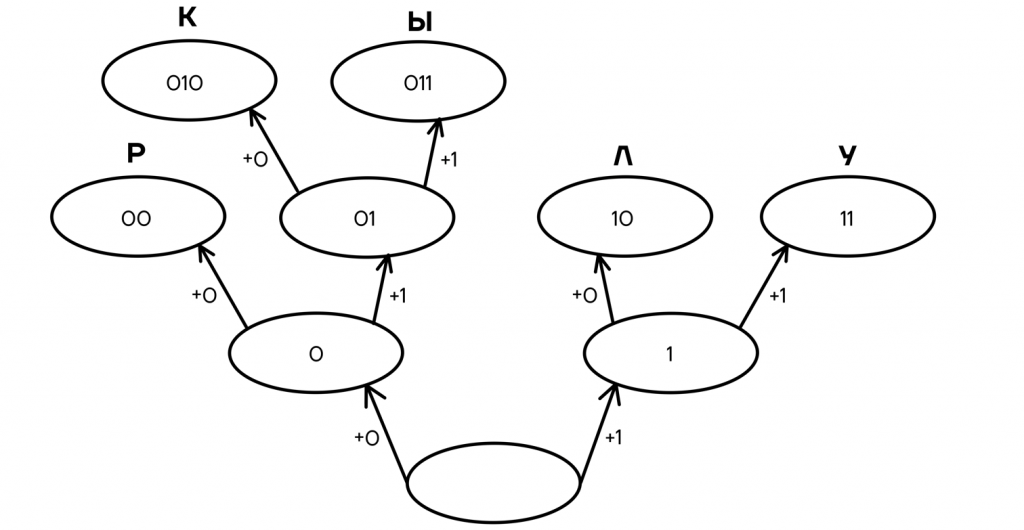
Очень просто строить код, который будет удовлетворять условию Фано, с помощью дерева вариантов — структуры, в нашем случае помогающей получить кодовые слова максимально просто и понятно. Принцип работы дерева состоит в том, что в его узлах будут находиться кодовые слова, а из узла могут выходить два ребра, соответствующие добавлению в конец кодового слова 0 и 1, таким образом заменяя одно кодовое слово на два новых, которые длиннее на один символ.
1. Начальный узел — пустой.
2. К любому узлу могут быть добавлены ребра, создающие два новых узла, в каждом из которых находится новое кодовое слово на 1 символ длиннее предыдущего (с добавленным в конец символом 0 и 1, соответственно).
3. Шаг 2 выполняется до тех пор, пока не будет получено необходимое количество конечных узлов (самых последних, из которых не выходит ни одного ребра).
Давайте попробуем таким образом получить ровно 5 кодовых слов, чтобы закодировать наши буквы К, У, Р, Л, Ы.
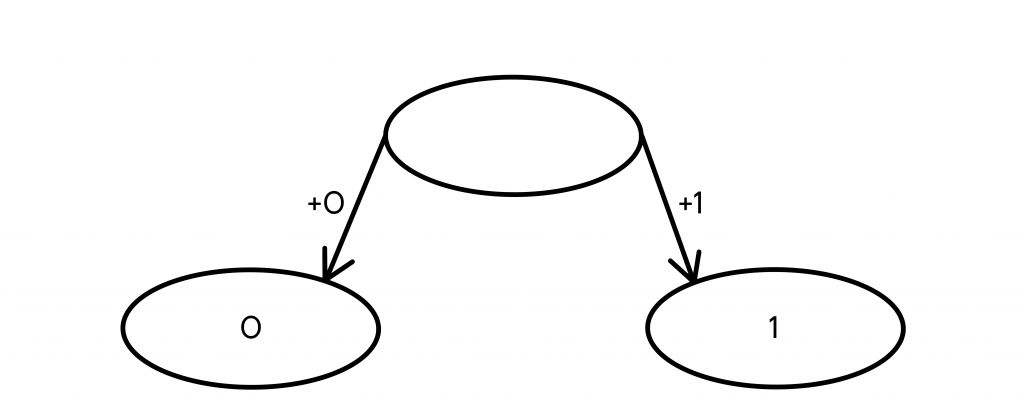
- Первые два кодовых слова, которые мы можем получить из ничего — 0 и 1.
Чтобы продолжить построение дерева, выбираем любой из конечных узлов и также добавляем ему 0 и 1 в конец.
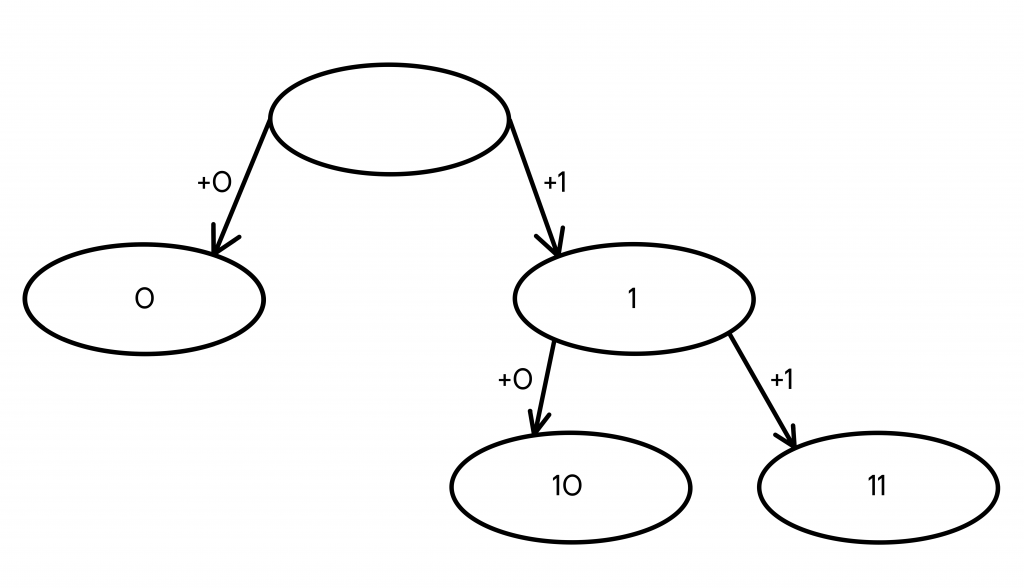
- Допустим, мы добавим 0 и 1 к кодовому слову 1, и вместо него теперь получим два новых — 10 и 11. Теперь кодовых слов у нас уже три — 0, 10 и 11.
Все еще мало, продолжаем построение дерева.
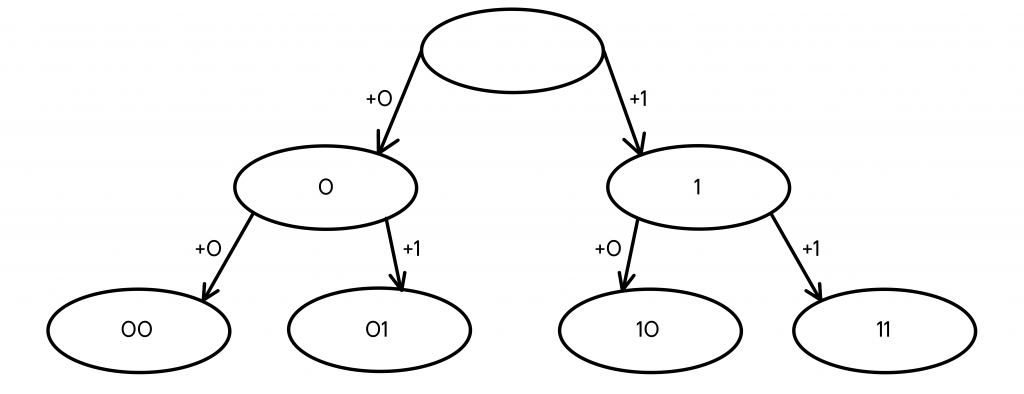
- Мы проделали ту же операцию с кодовым словом 0, заменив его на 2 новых — 00 и 01.
Кодовых слов стало 4, этого все еще мало, нужно продолжить построение дерева.
- Из конечных узлов можно выбрать любой для продолжения построения, например — 01, продолжив это кодовое слово, получаем два новых — 010 и 011.
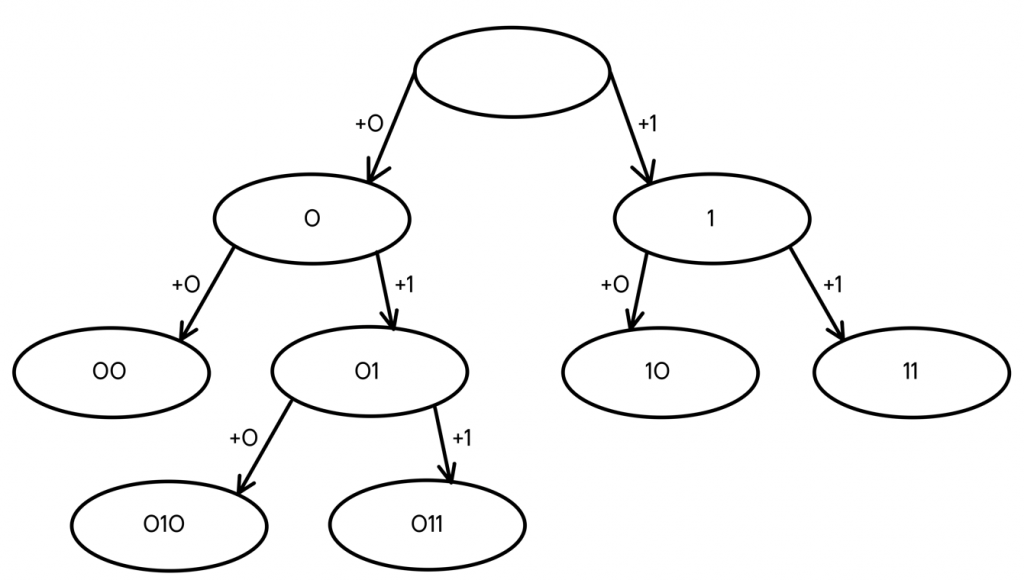
В итоге мы имеем 5 конечных узлов В них находятся кодовые слова, которые можно распределить любым удобным или необходимым способом между кодируемыми буквами. Например, так:
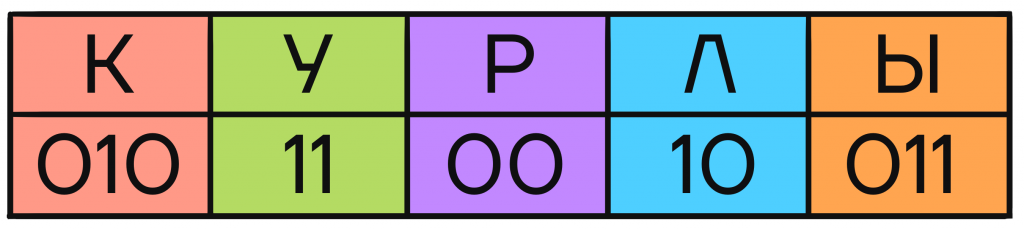
Такой код будет однозначно декодируемым, так как ни одно слово не заканчивается посередине другого, и мы всегда можем быть уверены, что одно кодовое слово закончилось и началось новое.
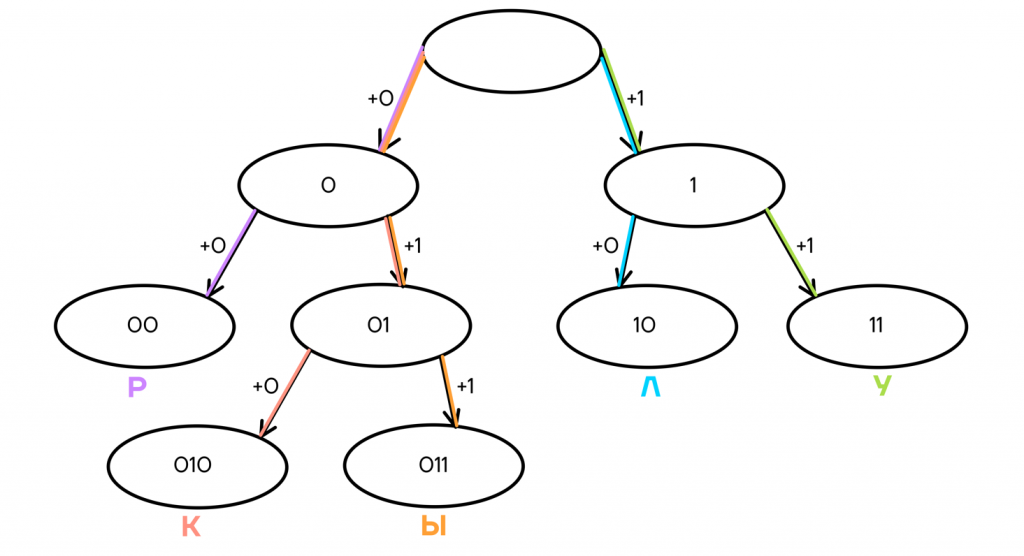
Так, код 010110010011010 мы можем однозначно декодировать, читая его слева направо:
Его формулировка немного отличается: «ни одно кодовое слово не должно быть окончанием другого». Такая формулировка уже допустит сосуществование кодовых слов 011 и 01, но не допустит 110 и 10, так как второе совпадает с окончанием первого.
Здесь построение дерева вариантов и чтение кодов происходит в точности до наоборот — при построении мы добавляем символы не в конец, а в начало предыдущего кодового слова и читаем код справа налево.
И код 010110001110010 будет читаться уже в другую сторону – из конца в начало:
Практика
В жизни чаще всего используются равномерные кодировки в силу многих причин, таких как:
- Большая устойчивость.
Представим, что мы передаем слово КУРЛЫК разными вариантами, но при передаче допускаем ошибку в четвертом бите (в четвертом символе нашего кода). Посмотрим, что получится в итоге.

Выводы:
- В первом случае из-за одного неправильного бита сломалась половина символов текста, и даже поменялось количество этих символов.
- Во втором случае текст отличается от первоначального только тем символом, на который влиял сломанный бит.
Таким образом, мы видим большую устойчивость равномерного кодирования.
2. Простота расширения.
Мы обсуждали, что проблема равномерного кодирования — в большом количестве «пустых мест». Но эти пустые места могут быть полезны. Например, захочет разработчик добавить в код несколько новых эмодзи. У него как раз есть незанятые коды для этих символов. Согласитесь, это удобнее, чем переписывать всю кодировку целиком.
Неравномерные же кодировки часто применялись еще до появления компьютеров. Например, одной из самых известных неравномерных кодировок являлась азбука Морзе, применявшаяся в работе телеграфов, передаче радиосигналов и других способах передачи информации.
Также применение неравномерной кодировки есть в 4 задаче ЕГЭ и во 2 задаче ОГЭ.
Разберем задачу №4 ЕГЭ:
По каналу связи передаются закодированные сообщения о состоянии системы, состоящие из пяти символов: A, B, C, D, E. При передаче сообщений используется двоичный код, при этом он допускает однозначное декодирование. Для символов A, B, C используются эти кодовые слова: 1, 010 и 001 (соответственно).
В ответе нужно указать наименьшее по длине кодовое слово для буквы D. Если таких кодов несколько, то в ответе укажите наименьший по значению.
Решение.
Шаг 1. Построим дерево вариантов кодовых слов и отметим на нем уже известные коды букв:
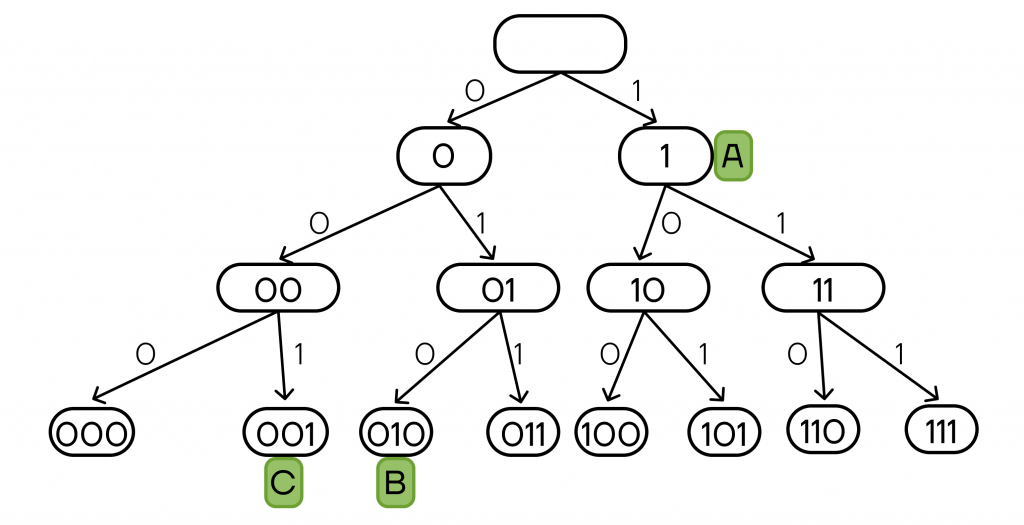
Шаг 2. Заметим, что раз для символа A кодовое слово 1, то в дальнейшем нам не подойдут любые коды, начинающиеся с 1, так как для них и символа A не будет выполняться условие однозначного декодирования.
Шаг 3. Начнем разбирать по возрастанию кодовые слова, начинающиеся с 0:
- 0 — не подойдет, будет началом для кодовых слов 001 и 010.
- 00 — не подойдет, будет началом слова 001.
- 01 — не подойдет, будет началом слова 010.
- 000 — подойдет.
- 001 — не подойдет, буква C.
- 010 — не подойдет, буква B.
- 011 — подойдет.
Шаг 4. Получаем два недостающих кодовых слова равной длины: 000 и 011. Значит, можем использовать их для букв Е и D, при этом сохранив однозначное декодирование. Для D нужно слово, меньшее по значению, тогда верным ответом будет 000.
Ответ: 000
В этой статье мы познакомились с условием Фано и научились правильно кодировать и декодировать сообщения. Но различные виды информации требуют собственных уникальных подходов. Приглашаем вас продолжить изучение темы в статьях «Кодирование изображения» и «Кодирование звука».
Фактчек
- Условие однозначного декодирования необходимо для того, чтобы у закодированного сообщения был ровно один вариант расшифровки — исходный.
- Однозначное декодирование может давать равномерное кодирование, при котором все кодовые слова имеют одинаковую длину, или кодовые слова, составленные по условию Фано, которое гласит: «ни одно кодовое слово не должно совпадать с началом другого кодового слова».
- Существует другая вариация этого условия — обратное условие Фано, оно гласит: «ни одно кодовое слово не должно совпадать с окончанием другого кодового слова».
- Для составления кодовых слов, удовлетворяющих условию Фано, используется дерево вариантов.
Проверь себя
Задание 1.
Для чего необходимо условие однозначного декодирования?
- Для более удобной шифровки сообщений.
- Для построения минимально возможных кодовых слов.
- Для сохранения возможности абсолютно точно получить исходное сообщение из закодированного.
- Для красоты.
Задание 2.
Выберите верные утверждения:
- При равномерном кодировании все кодовые слова имеют одну длину.
- При равномерном кодировании кодовые слова не могут начинаться на один и тот же символ.
- Для соблюдения условия Фано необходимо, чтобы ни одно кодовое слово не совпадало с окончанием другого кодового слова.
- Обратное условие Фано не гарантирует однозначное декодирование.
- Для составления кодовых слов, удовлетворяющих обратному условию Фано, используется дерево вариантов.
Задание 3.
Выберите наборы кодовых слов, которые удовлетворяют условию однозначного декодирования по любому из критериев, описанных в статье:
- 1, 11, 111, 1111, 11111, 0.
- 01, 001, 0001, 00001, 1
- 000, 111, 100, 001
- 10, 11, 00, 1001
- 10, 100, 1000, 10000
Задание 4.
Для передачи сообщений используются буквы А, Б, В, Г, Д. Известны некоторые кодовые слова: А = 01, Б = 111, В = 00, Г = 110. Какое кодовое слово может соответствовать кодовому слову для буквы Д, чтобы весь код удовлетворял условию Фано?
- 0
- 11
- 101
- 1100
Ответы: 1. — 3; 2. — 1, 5; 3. — 2, 3, 4, 5; 4. — 3.
Урок посвящен тому, как решать 4 задание ЕГЭ по информатике
Содержание:
- Кодирование информации
- Кодирование и расшифровка сообщений
- Решение 4 заданий ЕГЭ
Кодирование информации
4-е задание: «Кодирование и декодирование информации»
Уровень сложности
— базовый,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 2 минуты.
Проверяемые элементы содержания: Умение кодировать и декодировать информацию
До ЕГЭ 2021 года — это было задание № 5 ЕГЭ
Типичные ошибки и рекомендации по их предотвращению:
“Из-за невнимательного чтения условия задания экзаменуемые иногда не замечают, что требуется найти кодовое слово минимальной длины с максимальным (минимальным) числовым значением.
Кроме того, если в задании указано, что несколько букв остались без кодовых слов (как, например, в задании демоварианта), то кодовое слово для указанной буквы должно быть подобрано таким образом, чтобы осталась возможность найти кодовые слова, удовлетворяющие условию Фано, и для других букв. Так, например, если мы букву А закодируем нулём, а букву Б единицей, то букву В мы уже никак не сможем закодировать с соблюдением условия Фано, поэтому длину кодового слова для А или Б следует увеличить”
ФГБНУ “Федеральный институт педагогических измерений”
- Кодирование — это представление информации в форме, удобной для её хранения, передачи и обработки. Правило преобразования информации к такому представлению называется кодом.
- Кодирование бывает равномерным и неравномерным:
- при равномерном кодировании всем символам соответствуют коды одинаковой длины;
- при неравномерном кодировании разным символам соответствуют коды разной длины, это затрудняет декодирование.
Пример: Зашифруем буквы А, Б, В, Г при помощи двоичного кодирования равномерным кодом и посчитаем количество возможных сообщений:
Таким образом, мы получили равномерный код, т.к. длина каждого кодового слова одинакова для всех кодов (2).
Кодирование и расшифровка сообщений
Декодирование (расшифровка) — это восстановление сообщения из последовательности кодов.
Для решения задач с декодированием, необходимо знать условие Фано:
Условие Фано: ни одно кодовое слово не должно являться началом другого кодового слова (что обеспечивает однозначное декодирование сообщений с начала)
Префиксный код — это код, в котором ни одно кодовое слово не совпадает с началом другого кодового слова. Сообщения при использовании такого кода декодируются однозначно.
- если сообщение декодируется с конца, то его можно однозначно декодировать, если выполняется обратное условие Фано:
- условие Фано – это достаточное, но не необходимое условие однозначного декодирования.
Обратное условие Фано: никакое кодовое слово не является окончанием другого кодового слова
Постфиксный код — это код, в котором ни одно кодовое слово не совпадает с концом другого кодового слова. Сообщения при использовании такого кода декодируются однозначно и только с конца.
Однозначное декодирование обеспечивается:
Однозначное декодирование
Декодирование
Егифка ©:
Задание демонстрационного варианта 2022 года ФИПИ
Плейлист видеоразборов задания на YouTube:
ЕГЭ 4.1: Для кодирования букв О, В, Д, П, А решили использовать двоичное представление чисел 0, 1, 2, 3 и 4 соответственно (с сохранением одного незначащего нуля в случае одноразрядного представления).
Закодируйте последовательность букв ВОДОПАД таким способом и результат запишите восьмеричным кодом.
✍ Решение:
- Переведем числа в двоичные коды и поставим их в соответствие нашим буквам:
О -> 0 -> 00 В -> 1 -> 01 Д -> 2 -> 10 П -> 3 -> 11 А -> 4 -> 100
ВОДОПАД:010010001110010
010 010 001 110 010 ↓ ↓ ↓ ↓ ↓ 2 2 1 6 2
Результат: 22162
Теоретическое решение ЕГЭ данного задания по информатике, видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Рассмотрим еще разбор 4 задания ЕГЭ:
ЕГЭ 4.2: Для 5 букв латинского алфавита заданы их двоичные коды (для некоторых букв — из двух бит, для некоторых — из трех). Эти коды представлены в таблице:
| a | b | c | d | e |
|---|---|---|---|---|
| 000 | 110 | 01 | 001 | 10 |
Какой набор букв закодирован двоичной строкой 1100000100110?
✍ Решение:
- Во-первых, проверяем условие Фано: никакое кодовое слово не является началом другого кодового слова. Условие верно.
- Код разбиваем слева направо согласно данным, представленным в таблице. Затем переведём его в буквы:
✎ 1 вариант решения:
110 000 01 001 10 ↓ ↓ ↓ ↓ ↓ b a c d e
Результат: b a c d e.
✎ 2 вариант решения:
-
Этот вариант решения 4 задания ЕГЭ более сложен, но тоже верен.
- Сделаем дерево, согласно кодам в таблице:
- Сопоставим закодированное сообщение с кодами в дереве:
110 000 01 001 10
Результат: b a c d e.
Кроме того, вы можете посмотреть видеорешение этого задания ЕГЭ по информатике (теоретическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Решим следующее 4 задание:
ЕГЭ 4.3:
Для передачи чисел по каналу с помехами используется код проверки четности. Каждая его цифра записывается в двоичном представлении, с добавлением ведущих нулей до длины 4, и к получившейся последовательности дописывается сумма её элементов по модулю 2 (например, если передаём 23, то получим последовательность 0010100110).
Определите, какое число передавалось по каналу в виде 01100010100100100110.
✍ Решение:
- Рассмотрим пример из условия задачи:
Было2310 Стало00101001102
0010100110 (0010 - 2, 0011 - 3)
01100 01010 01001 00110
0110 0101 0100 0011
0110 0101 0100 0011 ↓ ↓ ↓ ↓ 6 5 4 3
Ответ: 6 5 4 3
Вы можете посмотреть видеорешение этого задания ЕГЭ по информатике, теоретическое решение:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
ЕГЭ 4.4:
Для кодирования некоторой последовательности, состоящей из букв К, Л, М, Н решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы Н использовали кодовое слово 0, для буквы К — кодовое слово 10.
Какова наименьшая возможная суммарная длина всех четырёх кодовых слов?
Подобные задания для тренировки
✍ Решение:
✎
1 вариант решения
основан на логических умозаключениях:
- Найдём самые короткие возможные кодовые слова для всех букв.
- Кодовые слова 01 и 00 использовать нельзя, так как тогда нарушается условие Фано (начинаются с 0, а 0 — это Н).
- Начнем с двухразрядных кодовых слов. Возьмем для буквы Л кодовое слово 11. Тогда для четвёртой буквы нельзя подобрать кодовое слово, не нарушая условие Фано (если потом взять 110 или 111, то они начинаются с 11).
- Значит, надо использовать трёхзначные кодовые слова. Закодируем буквы Л и М кодовыми словами 110 и 111. Условие Фано соблюдается.
- Суммарная длина всех четырёх кодовых слов равна:
(Н)1 + (К)2 + (Л)3 + (М)3 = 9
✎ 2 вариант решения:
- Будем использовать дерево. Влево откладываем 0, вправо — 1:
- Теперь выпишем соответствие каждой буквы ее кодового слова согласно дереву:
(Н) -> 0 -> 1 символ (К) -> 10 -> 2 символа (Л) -> 110 -> 3 символа (М) -> 111 -> 3 символа
(Н)1 + (К)2 + (Л)3 + (М)3 = 9
Ответ: 9
4.5:
По каналу связи передаются сообщения, содержащие только 4 буквы: А, Б, В, Г; для передачи используется двоичный код, допускающий однозначное декодирование. Для букв А, Б, В используются такие кодовые слова:
А: 101010, Б: 011011, В: 01000
Укажите кратчайшее кодовое слово для буквы Г, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Подобные задания для тренировки
✍ Решение:
- Наименьшие коды могли бы выглядеть, как 0 и 1 (одноразрядные). Но это не удовлетворяло бы условию Фано (А начинается с единицы — 101010, Б начинается с нуля — 011011).
- Следующим наименьшим кодом было бы двухбуквенное слово 00. Так как оно не является префиксом ни одного из представленных кодовых слов, то Г = 00.
Результат: 00
4.6:
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, решили использовать неравномерный двоичный код, позволяющий однозначно декодировать двоичную последовательность, появляющуюся на приемной стороне канала связи. Использовали код:
А - 01 Б - 00 В - 11 Г - 100
Укажите, каким кодовым словом должна быть закодирована буква Д. Длина этого кодового слова должна быть наименьшей из всех возможных. Код должен удовлетворять свойству однозначного декодирования. Если таких кодов несколько, укажите код с наименьшим числовым значением.
✍ Решение:
- Так как необходимо найти кодовое слово наименьшей длины, воспользуемся деревом. Влево будем откладывать нули, а вправо — единицы:
- Поскольку у нас все ветви завершены листьями, т.е. буквами, кроме одной ветви, то остается единственный вариант, куда можно поставить букву Д:
- Перепишем сверху вниз получившееся кодовое слово для Д: 101
Результат: 101
Подробней разбор урока можно посмотреть на видео ЕГЭ по информатике 2017:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
4.7: Демоверсия ЕГЭ 2018 информатика (ФИПИ):
По каналу связи передаются шифрованные сообщения, содержащие только десять букв: А, Б, Е, И, К, Л, Р, С, Т, У. Для передачи используется неравномерный двоичный код. Для девяти букв используются кодовые слова.
Укажите кратчайшее кодовое слово для буквы Б, при котором код будет удовлетворять условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Подобные задания для тренировки
✍ Решение:
- Для решения будем использовать дерево. Ветви, соответствующие нулю, будем откладывать влево, единице — вправо.
- При рассмотрении дерева видим, что все ветви «закрыты» листьями, кроме одной ветви — 1100:

Результат: 1100
Подробное теоретическое решение данного 4 (раньше №5) задания из демоверсии ЕГЭ 2018 года смотрите на видео:
📹 Видеорешение на RuTube здесь
4.8:
По каналу связи передаются шифрованные сообщения, содержащие только четыре букв: А, Б, В, Г; для передачи используется двоичный код, допускающий однозначное декодирование. Для букв А, Б, В используются кодовые слова:
А: 00011 Б: 111 В: 1010
Укажите кратчайшее кодовое слово для буквы Г, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
✍ Решение:
- Для решения будем использовать дерево. Ветви, соответствующие нулю, будем откладывать влево, единице — вправо.
- Поскольку в задании явно не указано о том, что код должен удовлетворять условию Фано, то дерево нужно построить как с начала (по условию Фано), так и с конца (обратное условие Фано).
- Получившееся числовое значение кодового слова для буквы Г — 01.
- Получившееся числовое значение кодового слова для буквы Г — 00.
- После сравнения двух кодовых слов (01 и 00), код с наименьшим числовым значением — это 00.
Дерево по условию Фано (однозначно декодируется с начала):
Дерево по обратному условию Фано (однозначно декодируется с конца):
Результат: 00
4.9:
По каналу связи передаются сообщения, содержащие только буквы: А, Е, Д, К, М, Р; для передачи используется двоичный код, удовлетворяющий условию Фано. Известно, что используются следующие коды:
Е – 000 Д – 10 К – 111
Укажите наименьшую возможную длину закодированного сообщения ДЕДМАКАР.
В ответе напишите число – количество бит.
Подобные задания для тренировки
✍ Решение:
- С помощью дерева отобразим известные коды для букв:
- В результирующем слове — ДЕДМАКАР — вде буквы А. Значит, для получения наименьшей длины необходимо для буквы А выбрать наименьший код в дереве. Учтем это и достроим дерево для остальных трех букв А, М и Р:
- Расположим буквы в порядке их следования в слове и подставим их кодовые слова:
Д Е Д М А К А Р 10 000 10 001 01 111 01 110
Результат: 20
Смотрите виде решения задания:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
.jpg?7)
.jpg?6)
.jpg?4)
.jpg?4)
.jpg?4)
.jpg?4)
.jpg?4)
.jpg?4)
.jpg?4)



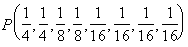
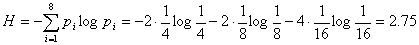
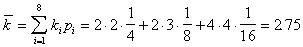
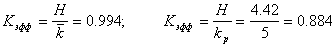

.jpg)
.jpg)
.jpg)
.jpg)


















