-
Главная
-
ГДЗ
- 5 класс
- Математика
-
Виленкин учебник
- 27
Новая редакция 2018-2023 г.
Смотрите также:
-
Задание 27 в старой редакции (2011 – 2017 г.)
- Учебник старой редакции (2011 – 2017 г.)
Вернуться к содержанию учебника
Страница 12
22
23
24
25
26
27
28
29
30
31
32
Вопрос
Составьте дерево возможных вариантов и запишите все двузначные числа, в запись которых входят лишь цифры 2 и 3. Найдите сумму этих чисел.
Подсказка
Вспомните:
- Какие числа называют двузначными.
- Сложение чисел.
Ответ
22
23
24
25
26
27
28
29
30
31
32

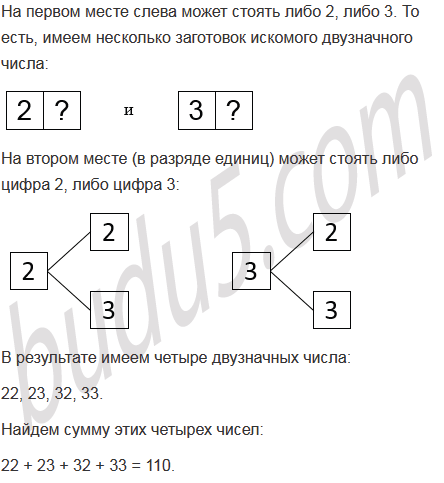
22
23
24
25
26
27
28
29
30
31
32
Вернуться к содержанию учебника
Смотрите также:
-
Задание 27 в старой редакции (2011 – 2017 г.)
- Учебник старой редакции (2011 – 2017 г.)
Скачать материал
без ожидания

Скачать материал
без ожидания


- Сейчас обучается 42 человека из 30 регионов


- Сейчас обучается 961 человек из 80 регионов


- Сейчас обучается 83 человека из 35 регионов


Описание презентации по отдельным слайдам:
-

1 слайд
Комбинаторные задачи:
дерево возможных вариантов -

2 слайд
Имя урока: Комбинаторика
Девиз урока: «Услышал – забыл,
Увидел – запомнил,
Сделал – понял»
Китайская поговорка -

3 слайд
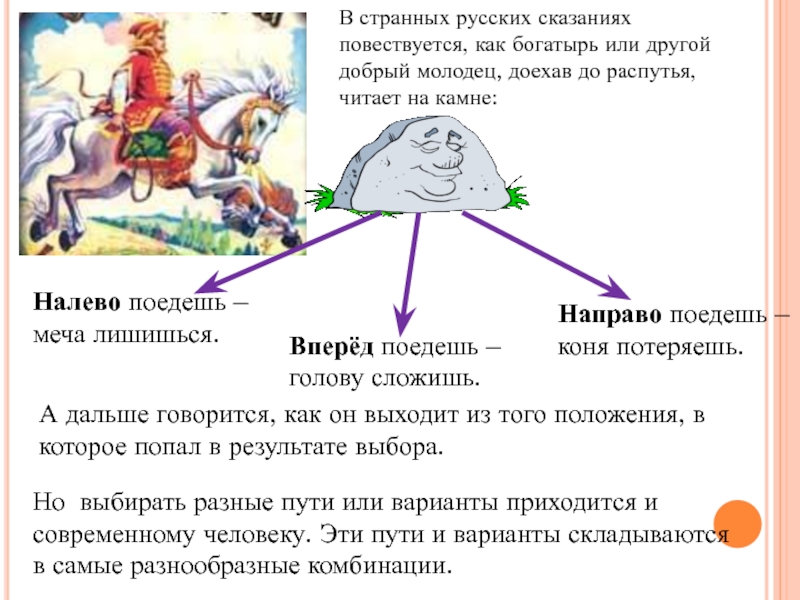
В странных русских сказаниях повествуется, как богатырь или другой добрый молодец, доехав до распутья, читает на камне:
Вперёд поедешь – голову сложишь.
Налево поедешь – меча лишишься.
А дальше говорится, как он выходит из того положения, в которое попал в результате выбора.
Направо поедешь – коня потеряешь.Но выбирать разные пути или варианты приходится и современному человеку. Эти пути и варианты складываются в самые разнообразные комбинации.
-

4 слайд
Что такое КОМБИНАТОРИКА?
Задачи, в которых требуется осуществить перебор всех возможных вариантов, или, как обычно говорят в таких случаях, всех возможных комбинаций, называют комбинаторными.
Область математики, изучающая комбинаторные задачи, называется комбинаторикой.
Комбинаторика – раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить. -

5 слайд
Задача №1
Запишите все трёхзначные числа, для записи которых употребляются только цифры 1 и 2.
1 2
1
1
2
2
1
1
1
1
2
2
2
2
Ответ: 111, 112, 121, 122, 211, 212, 221, 222 – восемь чисел.
Такой метод решения комбинаторных задач называется деревом выбора(дерево возможных вариантов) -

6 слайд
Задача №2
Запишите все трёхзначные числа, для записи которых употребляются только цифры 0,7. -

7 слайд
Задача 3
В 5 «А» классе в среду 4 урока: математика, информатика, русский язык, английский язык. Сколько можно составить вариантов расписания на среду?
Решение: построим картину-схему.
Для удобства закодируем названия предметов:
математика – м,
информатика – и,
русский язык – р,
английский язык – а. -

8 слайд
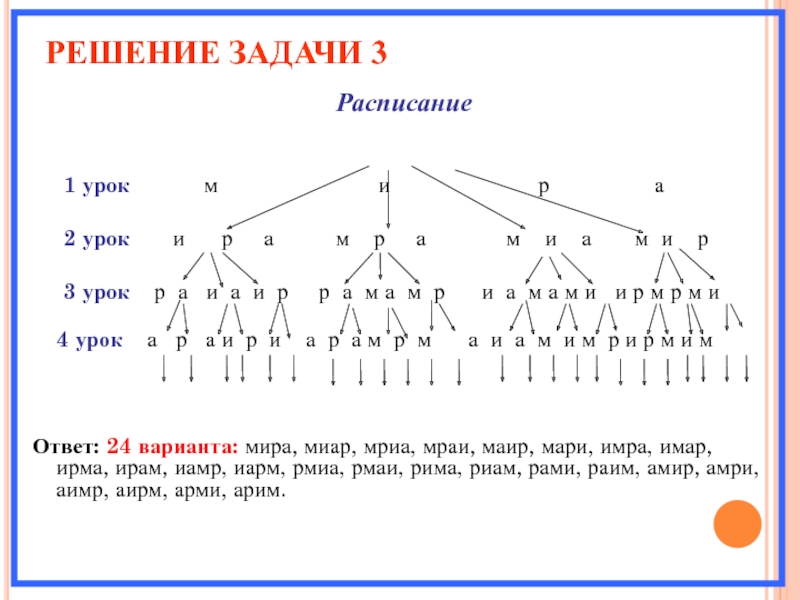
Решение задачи 3
Расписание1 урок м и р а
2 урок и р а м р а м и а м и р
3 урок р а и а и р р а м а м р и а м а м и и р м р м и
4 урок а р а и р и а р а м р м а и а м и м р и р м и м
Ответ: 24 варианта: мира, миар, мриа, мраи, маир, мари, имра, имар, ирма, ирам, иамр, иарм, рмиа, рмаи, рима, риам, рами, раим, амир, амри, аимр, аирм, арми, арим.
-

9 слайд
Построенная схема напоминает перевернутое дерево: от ствола («расписание») отходят ветки, сначала четыре (м, и, р, а), от каждой из четырех веток – еще по три, затем еще по две и еще по одной. Видимо поэтому такую схему называют деревом возможных вариантов.
Дерево возможных вариантов можно считать геометрической моделью рассматриваемой ситуации. -

10 слайд
Задача №4
В правление фирмы входят 5 человек. Из своего состава правления должно выбрать президента и вице-президента. Сколькими способами это можно сделать?
Президент
1Вице – президент
2 3 4 5
2
1 3 4 5
3
1 2 4 54
1 2 3 4
5
1 2 3 5
Такой метод решения комбинаторных задач называется правилом умножения.
Выбрать президента можно пятью способами, а для каждого выбранного президента четырьмя способами можно выбрать вице-президента . Следовательно, общее число способов выбрать президента и вице-президента фирмы равно: 5*4=20. -

11 слайд
Можно решить Задачу 3 короче, если применить правило умножения. Существует 4 варианта выбора первого урока. Для выбора второго урока есть только три варианта, так как один из четырех уроков мы уже выбрали. Тогда для третьего урока существует два варианта, а для четвертого только один. Применив правило умножения, получим
4 ∙ 3 ∙ 2 ∙1= 24
Ответ: 24 варианта. -

12 слайд
Задача №5
В классе 15 мальчиков и 10 девочек. Сколькими способами можно выбрать двух дежурных(одну девочку и одного мальчика)? -

13 слайд
Задача 2.
В 6 классе в четверг 5 уроков: математика, информатика, русский язык, английский язык, физкультура.
а) Сколько имеется вариантов расписания при условии, что физкультура – последний урок?
б) Сколько имеется вариантов расписания при условии, что физкультура – последний урок, а математика – первый?
-

14 слайд
Задача 2 (продолжение).
В 6 классе в четверг 5 уроков: математика, информатика, русский язык, английский язык, физкультура.в) Сколько всего можно составить вариантов расписания на четверг?
г) Сколько времени потратит завуч на запись всех вариантов, если известно, что на запись одного варианта у него уходит 30 секунд?
-

-

-

17 слайд
Задача №1
Запишите все трёхзначные числа, для записи которых употребляются только цифры 0,7.
Задача №2
Сколько двузначных чисел можно составить, используя цифры 1, 4 и 7? Нарисуйте дерево выбора на альбомном листе.
Задача №3
Составьте комбинаторную задачу, которая решается с помощью правила умножения. Сделайте к ней рисунок.
Задача № 4
Тренер попросил Филю составить трехзначное число из цифр 1, 2, 3, 4, причем цифры в числе
могут повторяться. Сколько чисел может составить Филя?
Задача № 5
Тренер попросил Филю составить трехзначное число из цифр 1, 2, 3, 4 так, чтобы цифры в числе
не повторялись. Сколько чисел может составить Филя?
Домашнее задание
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 257 302 материала в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 24.04.2017
- 1055
- 0
- 24.04.2017
- 625
- 0
- 24.04.2017
- 1129
- 0
Рейтинг:
4 из 5
- 24.04.2017
- 32546
- 272
- 24.04.2017
- 2572
- 2
- 24.04.2017
- 7009
- 11
- 24.04.2017
- 846
- 3
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»
-
Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
Тема урока: Решение комбинаторных задач
Методы решения комбинаторных задач:
-
метод перебора (подбираются задачи на развитие мышления);
-
табличный метод (все условия вносятся в таблицу, в ней же выполняется решение);
-
построение дерева возможных вариантов решений;
-
правило умножения.
Табличный метод
Решить комбинаторные задачи можно с помощью таблиц. Они, как и дерево возможных вариантов, наглядно представляют решение таких задач.
Задача 1. Сколько нечетных двузначных чисел можно составить из цифр 1, 3, 4, 6, 7, 8, 9?
Решение. Составим таблицу: слева первый столбец – первые цифры искомых чисел, вверху первая строка – вторые цифры.
|
1 |
3 |
7 |
9 |
|
|
1 |
11 |
13 |
17 |
19 |
|
3 |
31 |
33 |
37 |
39 |
|
4 |
41 |
43 |
47 |
49 |
|
6 |
61 |
63 |
67 |
69 |
|
7 |
71 |
73 |
77 |
79 |
|
8 |
81 |
83 |
87 |
89 |
|
9 |
91 |
93 |
97 |
99 |
Ответ: 28.
Задача 2. Маша, Оля, Вера, Ира, Андрей, Миша и Игорь готовились стать ведущими на Новогоднем празднике. Назовите возможные варианты, если ведущими могут быть только одна девочка и один мальчик.
Решение. Составим таблицу: слева первый столбец – имена девочек, вверху первая строка – имена мальчиков.
|
Андрей |
Миша |
Игорь |
|
|
Маша |
Маша – Андрей |
Маша – Миша |
Маша – Игорь |
|
Оля |
Оля – Андрей |
Оля – Миша |
Оля – Игорь |
|
Вера |
Вера – Андрей |
Вера – Миша |
Вера – Игорь |
|
Ира |
Ира – Андрей |
Ира – Миша |
Ира – Игорь |
Ответ: Все возможные варианты перечисляются в строках и столбцах таблицы. Всего 12 вариантов.
Задача 3. В школьной столовой приготовили на завтрак плов (П), кашу (К), блины (Б), а из напитков – сок (С), чай (Ч) и молоко (М). сколько различных вариантов завтрака можно составить?
|
П |
К |
Б |
|
|
С |
СП |
СК |
СБ |
|
Ч |
ЧП |
ЧК |
ЧБ |
|
М |
МП |
МК |
МБ |
Ответ: 9 вариантов.
Метод построения дерева возможных вариантов решений
Подбирая различные комбинации, можно запутаться. В этом случае приходит на помощь метод построения дерева возможных вариантов решений. Внешне такая схема напоминает дерево, отсюда и название.
Если его правильно построить, ты не упустишь ни один из возможных вариантов решения.
Рассмотрим задачу 1. Учитель попросил Олега разложить на полке 3 шара – желтый, красный, синий. Сколькими способами Олег может это сделать?
Начать можно и с желтого, и с красного, и с синего шара. Дерево вариантов будет выглядеть так:
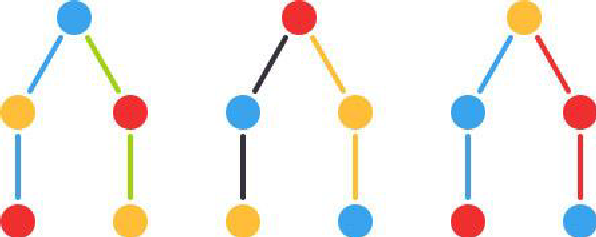
Эта схема действительно похожа на дерево, правда, «вверх ногами» и без ствола. Каждый первый шар – это «корень» дерева, а ветви дерева – это различные варианты расположения шаров. По этой схеме несложно посчитать, что возможных комбинаций всего 6.
Ответ: 6 способов.
Схему-дерево возможных рассуждений можно располагать по-разному (корень вверху или внизу).
Правило умножения
Применяется для нахождения числа всех возможных исходов независимого проведения двух испытаний А и В, перемножив число всех исходов испытания А и число всех исходов испытания В.
Задача.
Сколько трехзначных чисел можно составить из цифр: 1, 2, 5, 8 используя в записи числа каждую из них не более одного раза?
Решение.
Первую цифру выбираем четырьмя способами (1, 2, 5, 8), вторую цифру можно выбрать тремя способами, и на выбор третьей цифры остается два способа. Количество искомых трехзначных чисел равно произведению 4 · 3 · 2 = 24.
Ответ: 24.
Решить самостоятельно:
-
В финальном забеге на 100 м участвуют Смирнов, Петров и Орлов. Назовите возможные варианты распределения призовых мест. (Решить, используя табличный метод)
-
В столовой предлагают два первых блюда: щи и борщ; три вторых блюда: рыба, гуляш и плов; два третьих: компот и чай. Перечислите все возможные варианты обедов из трех блюд. Проиллюстрируйте ответ, построив дерево возможных вариантов.
-
Сколько трехзначных чисел можно составить из цифр: 1, 2, 5, 8 используя в записи числа каждую из них не более одного раза?
(Решить по правилу умножения)
ВИДЕО УРОК
Комбинаторикой называется область математики, в
которой изучаются вопросы о том, сколько различных комбинаций, подчинённых тем
или иным условиям, можно составить из элементов заданного множества.
Составляя комбинации, мы фактически выбираем из этого
множества различные элементы и объединяем их в группы по нашим потребностям,
поэтому вместо слова “комбинаторика”, часто используют слово “выборки”
элементов.
Комбинаторная
задача – задача, требующая осуществления перебора всех возможных
вариантов или подсчёта их числа.
Перебор возможных вариантов.
Простые задачи
решают обыкновенным полным перебором возможных вариантов.
ЗАДАЧА:
У Маши имеются юбка с брюками и кофта, свитер, рубашка.
Сколько комплектов можно составить из этой одежды ?

РЕШЕНИЕ:

ЗАДАЧА:
Какие двузначные числа можно составить из цифр
1, 3,
4, 5 ?
РЕШЕНИЕ:
11, 13,
14, 15, 33,
31, 34, 35,
41, 43,
44, 45, 51,
53, 54, 55.
Табличный метод (все условия вносятся в таблицу, в ней же
выполняется решение).
Решить
комбинаторные задачи можно с помощью таблиц. Они наглядно представляют решение
таких задач.
ЗАДАЧА:
Сколько нечётных двузначных чисел можно составить из цифр:
1, 2, 3, 5,
6, 7, 8, 9 ?
РЕШЕНИЕ:
Составим таблицу: слева первый
столбец – первые цифры искомых чисел, вверху первая строка вторые цифры.

ОТВЕТ: 40.
ЗАДАЧА:
Сколько нечётных двузначных чисел можно составить из цифр:
1, 3, 4, 6,
7, 8, 9 ?
РЕШЕНИЕ:
Составим таблицу: слева первый
столбец – первые цифры искомых чисел, вверху первая строка вторые цифры.

ОТВЕТ: 28.
ЗАДАЧА:
Маша, Оля, Вера, Ира, Андрей, Миша и Игорь готовились
стать ведущими на Новогоднем празднике. Назовите возможные варианты, если ведущими
могут быть только одна девочка и один мальчик.
РЕШЕНИЕ:
Составим таблицу: слева первый
столбец – имена девочек, вверху первая строка – имена мальчиков.

ОТВЕТ:
Все возможные варианты перечисляются в строках и столбцах
таблицы.
Построение граф – схемы.
Граф – совокупность объектов со связями между ними.
Объекты
представляются как вершины,
или узлы графа,
а связи – как дуги,
или рёбра.

ЗАДАЧА:
Встретились пятеро друзей, как положено,
поздоровались друг с другом. Сколько рукопожатий было сделано ?
РЕШЕНИЕ:

ОТВЕТ: 10.
ЗАДАЧА:
Постройте отрезок АВ, и отметьте на нём 4
точки М,
С. К, Д. Определите с помощью грф – схемы количество отрезков.
РЕШЕНИЕ:

ОТВЕТ: 15.
При построении граф-схем кроме дуг и вершин используется петля. она используется в случаях, когда требуется показать, что число делится само на себя.
ЗАДАЧА:
Выберите граф, на котором показано, что одно число делится на другое и на само себя.

ОТВЕТ: Первый граф.
Дерево
возможных вариантов решений.
Самые
разные комбинаторные задачи решаются с помощью составления специальных схем.
Внешне такая схема напоминает дерево, отсюда и название – дерево возможных вариантов.
Дерево
возможных вариантов – граф, схема, отражающая структуру задачи, упорядочения
многошагового процесса принятия решений.
Ветви дерева отображают различные события, которые могут иметь место,
а корень дерева
– состояние, в котором возникает необходимость выбора.

ЗАДАЧА:
Запишите все трёхзначные числа, которые
можно составить из цифр 1,
2, 3, так, чтобы числа не повторялись.
РЕШЕНИЕ: ЗАДАЧА:
ЗАДАЧА:
Катя, Лена и Соня сегодня дежурные. Им
нужно расставить книги (К),
вымыть пол (П),
полить цветы (Ц). Сколькими
способами они могут распределить между собой обязанности ?
РЕШЕНИЕ:

ЗАДАЧА:
Какие трёхзначные числа можно составить из
цифр
0, 3, 5 ?
РЕШЕНИЕ:
Построим дерево
возможных вариантов, учитывая, что 0 не может быть первой
цифрой в числе.

ОТВЕТ:
300, 303,
305, 330, 333,
335, 350, 353,
355,
500, 503, 505, 530, 533, 535, 550, 553, 555,
ЗАДАЧА:
Имеются три слова “ДРУЖБА”, “ДЕЛО”,
“ЛЮБИТ”. Сколькими способами из этих слов
можно составить фразу ?
РЕШЕНИЕ:
Обозначим предложенные слова заглавными буквами:
ДРУЖБА – Д
ЛЮБИТ – Л
ДЕЛО – Е (возьмём вторую букву этого слова).
Построим дерево
возможных вариантов:

ОТВЕТ: 6 способов.
Задания к уроку 1
- Задание 1
- Задание 2
- Задание 3
Слайд 1Комбинаторные задачи:
дерево возможных вариантов

Слайд 2ИМЯ УРОКА: КОМБИНАТОРИКА
ДЕВИЗ УРОКА: «УСЛЫШАЛ – ЗАБЫЛ,
УВИДЕЛ – ЗАПОМНИЛ,
СДЕЛАЛ – ПОНЯЛ»
КИТАЙСКАЯ ПОГОВОРКА

Слайд 3В странных русских сказаниях повествуется, как богатырь или другой добрый молодец,
доехав до распутья, читает на камне:
Вперёд поедешь – голову сложишь.
Налево поедешь – меча лишишься.
А дальше говорится, как он выходит из того положения, в которое попал в результате выбора.
Направо поедешь – коня потеряешь.
Но выбирать разные пути или варианты приходится и современному человеку. Эти пути и варианты складываются в самые разнообразные комбинации.
Слайд 4
Что такое КОМБИНАТОРИКА?
Задачи, в которых требуется осуществить перебор всех возможных вариантов,
или, как обычно говорят в таких случаях, всех возможных комбинаций, называют комбинаторными.
Область математики, изучающая комбинаторные задачи, называется комбинаторикой.
Комбинаторика – раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить.

Слайд 5Задача №1
Запишите все трёхзначные числа, для записи которых употребляются только
цифры 1 и 2.
1 2
1
1
2
2
1
1
1
1
2
2
2
2
Ответ: 111, 112, 121, 122, 211, 212, 221, 222 – восемь чисел.
Такой метод решения комбинаторных задач называется деревом выбора(дерево возможных вариантов)

Слайд 6Задача №2
Запишите все трёхзначные числа, для записи которых употребляются только
цифры 0,7.

Слайд 7ЗАДАЧА 3
В 5 «А» классе в среду
4 урока: математика, информатика, русский язык, английский язык. Сколько можно составить вариантов расписания на среду?
Решение: построим картину-схему.
Для удобства закодируем названия предметов:
математика – м,
информатика – и,
русский язык – р,
английский язык – а.

Слайд 8РЕШЕНИЕ ЗАДАЧИ 3
Расписание
1 урок м и р а
2 урок и р а м р а м и а м и р
3 урок р а и а и р р а м а м р и а м а м и и р м р м и
4 урок а р а и р и а р а м р м а и а м и м р и р м и м
Ответ: 24 варианта: мира, миар, мриа, мраи, маир, мари, имра, имар, ирма, ирам, иамр, иарм, рмиа, рмаи, рима, риам, рами, раим, амир, амри, аимр, аирм, арми, арим.
Слайд 9Построенная схема напоминает перевернутое дерево: от ствола («расписание») отходят ветки, сначала
четыре (м, и, р, а), от каждой из четырех веток – еще по три, затем еще по две и еще по одной. Видимо поэтому такую схему называют деревом возможных вариантов.
Дерево возможных вариантов можно считать геометрической моделью рассматриваемой ситуации.

Слайд 10Задача №4
В правление фирмы входят 5 человек. Из своего состава правления
должно выбрать президента и вице-президента. Сколькими способами это можно сделать?
Президент
Вице – президент
2 3 4 5
2
1 3 4 5
3
4
1 2 3 4
5
1 2 3 5
Такой метод решения комбинаторных задач называется правилом умножения.
Выбрать президента можно пятью способами, а для каждого выбранного президента четырьмя способами можно выбрать вице-президента . Следовательно, общее число способов выбрать президента и вице-президента фирмы равно: 5*4=20.

Слайд 11
Можно решить Задачу 3 короче, если применить правило умножения. Существует 4
варианта выбора первого урока. Для выбора второго урока есть только три варианта, так как один из четырех уроков мы уже выбрали. Тогда для третьего урока существует два варианта, а для четвертого только один. Применив правило умножения, получим
4 ∙ 3 ∙ 2 ∙1= 24
Ответ: 24 варианта.

Слайд 12
Задача №5
В классе 15 мальчиков и 10 девочек. Сколькими способами можно
выбрать двух дежурных(одну девочку и одного мальчика)?

Слайд 13ЗАДАЧА 2.
В 6 классе в четверг 5 уроков: математика, информатика, русский
язык, английский язык, физкультура.
а) Сколько имеется вариантов расписания при условии, что физкультура – последний урок?
б) Сколько имеется вариантов расписания при условии, что физкультура – последний урок, а математика – первый?

Слайд 14ЗАДАЧА 2 (ПРОДОЛЖЕНИЕ).
В 6 классе в четверг 5 уроков: математика, информатика,
русский язык, английский язык, физкультура.
в) Сколько всего можно составить вариантов расписания на четверг?
г) Сколько времени потратит завуч на запись всех вариантов, если известно, что на запись одного варианта у него уходит 30 секунд?

Слайд 17Задача №1
Запишите все трёхзначные числа, для записи которых употребляются только
цифры 0,7.
Задача №2
Сколько двузначных чисел можно составить, используя цифры 1, 4 и 7? Нарисуйте дерево выбора на альбомном листе.
Задача №3
Составьте комбинаторную задачу, которая решается с помощью правила умножения. Сделайте к ней рисунок.
Задача № 4
Тренер попросил Филю составить трехзначное число из цифр 1, 2, 3, 4, причем цифры в числе
могут повторяться. Сколько чисел может составить Филя?
Задача № 5
Тренер попросил Филю составить трехзначное число из цифр 1, 2, 3, 4 так, чтобы цифры в числе
не повторялись. Сколько чисел может составить Филя?
Домашнее задание

