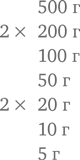Как составить диаграмму кэрролла

Диаграммы Кэрролла

Этот вид диаграмм назван в честь автора «Алисы в Стране чудес», который занимался не только писательством, но и преподавал математику в Оксфорде. Чарльз Доджсон (настоящее имя Кэрролла) особенно интересовался логикой и в 1896 г. опубликовал книгу «Символическая логика» (Symbolic Logic), где представил диаграмму, названную им «двухбуквенной». Позже этой диаграмме дали имя ее автора, и сегодня каждый учащийся начальной школы изучает диаграмму Кэрролла как метод категоризации объектов.

Особенно удобна диаграмма Кэрролла для группировки математических объектов. К примеру, карточки с числами можно рассортировать по самым разным признакам: четные/нечетные, больше/меньше 20, кратные/некратные пяти…

Проверьте себя

41. Диаграмма Кэрролла

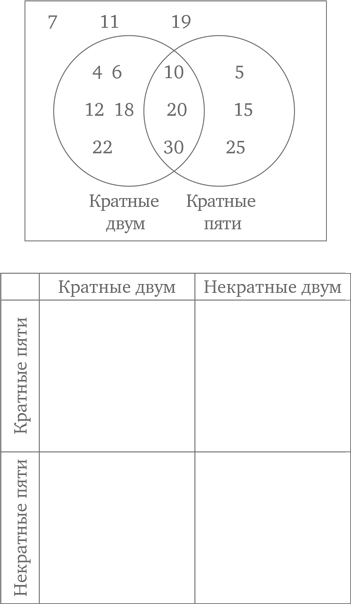
Где на диаграмме Кэрролла оказались бы числа с приведенной ниже диаграммы Венна?

Предмет:
математика

Раздел 4B:
Изучение группировок и множеств элементов

Тема: Показ
информации на диаграмме Кэрролла

Школа: Назарбаев
Интеллектуальная школа

Дата:  

Имя учителя:

Класс: 1

Количество
присутствующих:

Количество
отсутствующих:

Цели обучения

ММ1.11 
Иметь представление о диаграмме Кэрролла

Цели урока

Все учащиеся
будут:

распределять числа по группам;

Многие учащиеся
будут:

составлять признаки и
распределять числа по группам;

Некоторые
учащиеся будут:

самостоятельно искать идеи для
составления диаграммы Кэрролла.

Языковые цели

Учащиеся могут:

Предметная
лексика и терминология:

диаграмма,
вертикаль, горизонталь, признаки.

Серия полезных фраз
для диалога/письма

·      ДИscussthЭ chartthat ИscrЭatЭД. КhИchИsthЭ most ПoПularфruИtchoИcЭ? HoКДo
КЭ knoК?

·      Has
ЭvЭrylЭarnЭr’schoИcЭbЭЭnrЭcorДЭД? HoК can КЭ chЭck?

·      Ask
lЭarnЭrsИфthЭy can thИnkoфothЭrquЭstИons that КЭ mИГhthavЭИnvЭstИГatЭД.
ИфИДЭasarЭ not фorthcomИnГ, ‘lЭaД’ thЭДИscussИon by suГГЭstИnГ– КhatЭlsЭcoulД
КЭ havЭПutИnthЭbaskЭt? КhatothЭrthИnГscoulД КЭ try, to
sЭЭИфПЭoПlЭhavЭфavourИtЭs?КhatothЭrquЭstИonscoulД КЭ havЭaskЭД about our
фruИtbaskЭt?

·      TakЭИДЭasanД
ask – КhatДo you thИnkthЭrЭsultmИГhtbЭ? КhatКoulДthЭПИctoГram look lИkЭ?

Обсуждение:

• В честь
  кого названа диаграмма?
• Кем был
  Кэрролл Льюис?
• Зачем нужна
  нам диаграмма Кэрролла?

Можешь ли ты
сказать почему…?

Предшествующие
знания

Сложение и вычитание чисел

План

Планируемое
время

Запланированная
деятельность (впишите свои задания вместо указанных ниже)

    Ресурсы

Начало урока

Оргмомент

Число, классная работа

Продолжи ряд на 3 числа

1, 9, 17, _____,_____,_______ .

Самопроверка

1, 9, 17, 25, 33, 41.

– Просигнальте мне с помощью трёх пальцев (обратная
связь).

– Сейчас ребята, вам предстоит выполнить математический
диктант. Какие критерии успеха предлагаете?

Предполагаемые
критерии успеха

Задание: выполнить математический диктант
Цель: решить математические задания на слух
Учащийся:
достиг	стремится
верно, решает 4 задачи из 5.	решает 3 и менее заданий.
допускает 1-2 исправления.	допускает более 2 – ух исправлений.

Математический диктант

1.В
1 классе спортивной школы 13 девочек, из них 5-ро занимаются
спортивно-бальными танцами, а остальные художественной гимнастикой. Сколько
девочек  занимается художественной гимнастикой?

2.В
1 «С» классе 16 учащихся занимаются спортом, а в 1 «А» – 9. Насколько больше
учащихся из 1 «С» занимаются спортом, чем учащиеся из 1 «А»?

3.У
мамы было 100 тенге, после того как она купила банан своему сыну, у неё
осталось 30 тенге. Сколько денег она израсходовала  на банан?

4.
В первом классе учитель провёл исследование на тему «Какой из трёх фруктов учащиеся
любят больше всего?» Результаты исследования были показаны с помощью столбчатой
диаграммы.  5-ро учащихся выбрали яблоки, 6 –ро учащихся выбрали груши, а
остальные учащиеся выбрали бананы. Сколько учащихся предпочитают бананы, если
известно, что в классе 20 учеников?

5.
9 девочек ежедневно соблюдают режим дня, 4 девочки – соблюдают режим дня
только на каникулах. Сколько всего соблюдающих и не соблюдающих режим дня девочек?

–
Кто помнит, о чём была последняя задача в математическом диктанте? (о режиме
дня)

–
Предлагаю всем встать и потанцевать под песенку о режиме дня.

Песня
о режиме дня

Взаимооценивание
в парах

(достиг/стремится
учащиеся ставят друг другу, в парах на полях тетрадей)

Ответы:

1.      8
девочек

2.      На 7
учащихся больше

3.      70 тенге
израсходовано

4.      9
учащихся предпочитают бананы

5.      13
девочек

–
А сейчас, я приглашаю сюда всех, для того чтобы разбиться на мальчиков и не
мальчиков, на тех кто достиг и тех кто не достиг. То есть сгруппироваться.

–
Скажите, а что мы с вами создали? (диаграмму Кэрролла)

–
Как вы думаете, зачем я предложила вам её построить?

–
Как думаете, какова тема урока?

Показ
информации на диаграмме Кэрролла

–
Какова будет цель урока?

Презентация

Слайд 1

Слайд 2

Слайд 3

Слайд 4

http://academy4baby.ru/wp-content/uploads/2014/03/Rasporyadok-dnya—Lesha-Abromovich.mp3

Слайд 5

Ленты,
чтобы создать огромную диаграмму в классе.

Середина
урока

Вопрос-ответ

–
На прошлых занятиях вы получили небольшую информацию по данной диаграмме.
Сейчас, прошу вас устно составить вопросы? Сколько успеете…

–
А теперь прошу группы пройти на ковер и разместиться на нем группами.

Группы
задают вопросы друг другу и отвечают на них. Учащиеся сигнализируют с
помощью жестов.

О диаграмме
Кэрролла Льюиса

Диаграмма
Кэрролла названа в честь Кэрролла Льюиса.

Настоящее
имя  Кэрролла Льюиса – Доджсон Чарлз Лутвидж.

Годы
жизни Кэрролла Льюиса1832 – 1898.

Кэрролл
Льюис был преподавателем оксфордского колледжа Крайст-черч.

Кэрролл
Льюис приобрёл всемирную известность своими сказками «Алиса в Стране Чудес» и
«Алиса в Зазеркалье».

–
Давайте вспомним такие понятия как признаки, вертикаль и
горизонталь, что они обозначают (показать на готовой диаграмме Кэрролла).

Работа по теме
урока

Группа
№2 Творческое задание

Группа №2
Задание: составить диаграмму Кэрролла на тему «В здоровом теле – здоровый дух!»
Цель: придумать и составить диаграмму Кэрролла.
Учащиеся:
Достигли, если	стремятся, если
Признаки соответствуют теме «В здоровом теле – здоровый дух!»	Признаки не соответствуют теме «В здоровом теле – здоровый дух!»
Верно, составили признаки по вертикали и по горизонтали.	Верно, составили признаки, но неправильно распределили рисунки по группам.
Верно, распределили рисунки по группам.	Неверно, составили признаки и неправильно распределили рисунки по группам.

Группа
№3 Творческое задание

Группа №3
Задание: составить диаграмму Кэрролла на тему «Еда и напитки»
Цель: составить диаграмму Кэрролла.
Учащиеся:
Достигли, если	стремятся, если
Признаки соответствуют теме «Еда и напитки».	Признаки не соответствуют теме «Еда и напитки».
Верно, составили признаки по вертикали и по горизонтали.	Верно, составили признаки, но неправильно распределила рисунки по группам.
Верно, распределили рисунки по группам.	Неверно, составили признаки и неправильно распределили рисунки по группам.

Группа
№4. В диаграмме расчерчены только графы.

Группа №4
Задание: покажите чётные и нечётные числа до 10, а также чётные и нечётные числа после 10, с помощью диаграммы Кэрролла. Используйте числа, находящиеся в конверте.
Цель: составить признаки по вертикали и горизонтали, распределить числа по группам.
Учащиеся:
Достигли, если	стремятся, если
Верно, составили признаки по вертикали и по горизонтали	Верно, составили признаки, но неправильно распределили числа по группам.
Верно, распределили числа по группам	Неверно, составили признаки и неправильно распределили числа по группам.

Группа
№5. В диаграмме расчерчены графы, а также написаны признаки по вертикали: «до
20», «после 20».

Группа №5
Задание: показать чётные и нечётные числа до 20, а также чётные и нечётные числа после 20, с помощью диаграммы Кэрролла Льюиса. Используй числа от 1 до 57.
Цель: составить признаки по горизонтали и сгруппировать числа соответственно им.
Учащийся:
достиг	стремится
Верно, составила признаки по горизонтали	Верно, составила признаки по горизонтали, но неправильно распределила числа по группам.
Верно, распределила числа по группам	Неверно, составила признаки и неправильно распределила числа по группам.

Группа
№1. В диаграмме расчерчены графы, а также написаны признаки по вертикали- «до
20», «после 20», по горизонтали – «чётные», «нечётные», а также даны числа от
1до 57.

Группа №1
Задание: показать чётные и нечётные числа до 20, а также чётные и нечётные числа после 20, с помощью диаграммы Кэрролла Льюиса. Используй числа от 1 до 57.
Цель: сгруппировать числа соответственно их признакам
Учащийся:
достиг	стремится
Верно, распределила числа по группам	Неверно, составила признаки и неправильно распределила числа по группам.

Измерение
температуры (техника ФО)

Деятельность
учащихся останавливается,

и
учитель задает вопрос: «Что мы делаем?» Ответив на этот вопрос,
учащиеся предоставляют информацию об уровне понимания сути задания или
процесса его выполнения.

Взаимооценивание

Учащиеся
помещают свои работы на доске.

Группа
№2 и группа №3 взаимооценивают друг друга, то есть переходят к работе другой
группы и рассуждают по критериям…достигли или не достигли…

Самооценивание

Учитель
показывает учащимся правильно составленную и верно заполненную диаграмму
Кэрролла на слайде. Учащиеся по ней оценивают свою работу.

	числа до 10	числа после 10
Чётные	2, 4, 6, 8.	12,14,16,18, 20.
Нечётные	1, 3, 5, 7, 9.	11,13,15,17, 19.

Песочные
часы

Слайд
6

Слайд
7

Группы
№2,3

А-3

Приложения

Слайд
8

Группы

 №
4,5,2

Карточки
Д, а с обратной стороны С.

Слайд
9

Карточки
Д, а с обратной стороны С.

Конец

урока

Рефлексия

Упражнение
на проверку усвоения нового материала

На
стенах класса висят листы А-4 с надписями:

Могу
сам составить диаграмму Кэрролла!

Могу
составить признаки по заданной теме и правильно распределить числа по
группам.

Могу
правильно распределить числа по группам.

Мне
нужна помощь в распределении чисел по группам.

Дополнительная
информация

Дифференциация –
Как вы планируете помогать учащимся? Какие задания вы планируете давать более
способным ученикам?

Оценивание – как
вы планируете отслеживать прогресс/знания учащихся?

Межпредметные 
связи
«Самопознание»
«ИКТ»
Ценности

·        
Для
учащихся с низким уровнем мотивации учитель организовывает поддержку и помощь

Наблюдать за учащимися во время
их работы фронтально, в парах, в группах и фиксировать свои наблюдения в журнале.

Развитие толерантного отношения
друг другу в процессе построения диаграммы Кэрролла.

Рефлексия

Были ли цели обучения/урока
достижимыми?

Чему сегодня научились учащиеся?

Какой была атмосфера обучения?

Успешными ли были действия по
дифференциации между учащимися?

Придерживался ли я временного
графика? Какие отступления от плана я сделал и почему?

Итоговое
оценивание

Назовите два
наиболее успешных момента (как преподавания, так и обучения)?

1:

2:

Назовите два
момента, которые бы способствовали улучшению урока (как преподавания, так и
обучения)?

1:

2:

Что нового я
узнал о классе и его отдельных учащихся и как это отразится на проведении
моего следующего урока?

Площади более сложных фигур

Метод счета квадратиков работает также для фигур любой другой формы, хотя не везде и не всегда вам встретятся удобные для счета целые квадратики. К примеру:

В этом треугольнике два целых квадратика и четыре половинки, что дает суммарно четыре полных квадратика.

Учащимся начальной школы редко предлагают считать что-то менее удобное, чем половинки квадратиков, но на самом деле эту идею можно развить. Существует правило, позволяющее довольно точно определить площадь: все неполные квадратики, в которых больше половины квадрата, считаются целыми, а все те, в которых меньше, – не считаются вообще. Таким образом, в треугольнике ниже присутствует шесть целых квадратиков и три с «более-чем-половиной», что дает нам площадь, равную девяти квадратикам.

Проверьте себя

40. Загадочный квадратик

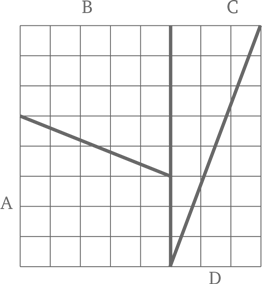
Перед вами жуткая головоломка, в которой один квадратик площади возникает совершенно ниоткуда! Исходным материалом для нее служит обычная решетка размером 8 × 8 клеток и площадью соответственно 64 клетки.

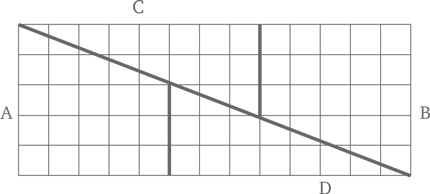
Вы видите, что решетка на рисунке разрезана на четыре части – A, B, C и D. Эти же самые части можно сложить иначе и получить следующий прямоугольник:

Убедитесь, что все части имеют в точности ту же форму, что и на первом рисунке. А теперь сосчитайте квадратики. Длина нашего прямоугольника составляет 13 клеток, ширина – 5. 13 раз по 5 будет 65… но это на единицу больше, чем в первоначальном квадрате. Откуда взялся лишний квадратик?

Объем

От учащихся начальной школы не требуется знание того, как вычисляется объем твердого тела. Тем не менее дети знакомятся с измерением объема жидкости в литрах; считается также, что они должны чувствовать и разумно оценивать, больше или меньше литра жидкости входит в конкретную емкость.

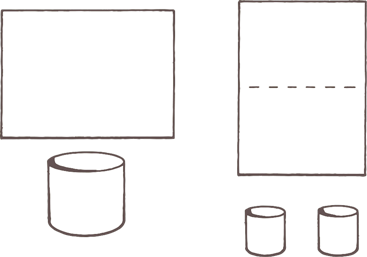
Несмотря на то что объем тела не будет рассматриваться в этом курсе сколько-нибудь подробно, полезно познакомить ребенка с некоторыми идеями, имеющими отношение к объему. Взяв два листа А4, можно провести интересный эксперимент.

Скатайте один лист вдоль длинной стороны, чтобы получилась длинная тонкая трубочка, а второй – вдоль короткой стороны, чтобы трубка получилась потолще и покороче.

Эти две трубки имеют разную форму, но сделаны из одного и того же листа бумаги. В какую из них войдет больше гречневой крупы?

Если инстинкт говорит вам, что в каждый цилиндр должно поместиться одинаковое количество гречки, то он ошибается. В короткую широкую трубку входит больше – приблизительно на 40 %.

Теперь разрежьте лист A4 пополам и сверните два одинаковых широких цилиндра меньшего размера. Где объем больше – в крупном цилиндре или в двух его маленьких копиях? Возможно, первое, что подсказывает инстинкт, – это то, что между этими вариантами нет никакой разницы; однако после того, как вы сделаете цилиндры, верный ответ станет очевидным.

Просто взглянув на получившиеся цилиндры, можно увидеть, что две меньшие трубки в сумме вместят явно меньше, чем одна большая. Объем большой трубки, опять же, превосходит суммарный объем двух маленьких приблизительно на 40 %.

Вес

С граммами и килограммами ваших детей познакомят в школе. Кроме того, их научат производить взвешивание – измерять вес при помощи весов. Не в каждой школе сегодня найдутся старомодные весы с чашками, что очень плохо, поскольку они великолепно помогают не только разобраться в том, что такое вес, но и получить представление о дробях – и даже об «уравнениях» (уравнение – это как равновесие чашек на весах, где количество чего-то на одной стороне точно соответствует количеству на другой).

В весах используются метрические гири, обычно такие:

Это позволяет вам измерить любой вес от 5 г до 1105 г с точностью до ближайших пяти граммов.

Опорные точки для взвешивания

Занимаясь измерениями, полезно создать вместе с ребенком набор «эталонов», или опорных точек, – обычных повседневных вещей, которые могут при необходимости послужить единицами измерения и помочь в определении того или иного параметра, если рядом не окажется соответствующих измерительных инструментов. Приведем для начала небольшой список – и поговорите с ребенком о том, какие еще предметы можно в него включить.

Статистика и вероятность

Когда многие из нынешних родителей учились в школе, ни статистика, ни теория вероятности практически не были включены в курс математики. Однако в настоящее время они составляют заметную часть учебного плана. Статистика, как правило, представляется как «обработка данных»; тема же, посвященная вероятности, – если в школе, где учится ваш ребенок, решили ее ввести (а она уже не входит в национальную программу обучения) – будет, вероятно, называться «Шанс».

«Обработка данных» – сухое формальное название для процесса, который может быть очень увлекательным: поставить вопрос; решить, какая информация необходима, чтобы на него ответить; собрать, разделить на категории и представить полученные сведения в виде таблиц; интерпретировать эти таблицы; использовать информацию для лучшего понимания окружающего мира. В то же время любой ребенок, хоть раз игравший в карты или в кости, знаком с идеей шанса (или вероятности), хотя в раннем возрасте дети, как правило, думают об этих вещах не слишком научно и называют их «удачей».

Проблемы, которые часто возникают у детей в связи с обработкой информации и вероятностями

1. Дети полагают, что «отрицательная» информация менее полезна, чем положительная. К примеру, в игре «Угадай число» – варианте игры с 20 вопросами, когда один играющий должен задумать число, а другой – установить, что тот загадал, задавая вопросы, на которые нужно отвечать «да» или «нет». Вопрос «Это число четное?» и ответ «Нет» дает ровно столько же информации, что и вопрос «Это число нечетное?» и ответ «Да», но дети склонны оценивать ответ «Нет» как менее полезный.

2. Уверены, что диаграмма представляет собой «картину» события, и потому неверно ее интерпретируют.

3. Не осознают, что круговые диаграммы отражают соотношение частей в группе, а не размер группы в целом.

Подсчет и частоты

Если вам приходилось когда-нибудь что-нибудь подсчитывать, зачеркивая четыре палочки пятой (||||), для того, чтобы, скажем, знать, сколько очков набирается в игре или сколько людей входит в школьный зал, то вы, как и многие другие, продолжаете давнюю традицию. Ту, которой уже около 40 000 лет! Мы знаем об этом благодаря так называемой кости из Лебомбо – старейшему известному на данный момент математическому памятнику. Это кость павиана, на которой какой-то пещерный человек проводил подсчет и оставлял отметки. Этой кости примерно 37 000 лет, и, вероятно, она не была первым подобным предметом. Разумеется, мы понятия не имеем, что считали с ее помощью – прошедшие дни, добытых животных или членов племени, – кто знает? Но, как бы то ни было, ясно, что желание учитывать количество появилось у нашего биологического вида довольно давно.

На ранних экземплярах таких «счетных дощечек» отметки стоят простым частоколом, хаотично, но на более поздних костях уже отмечается какая-то система, а со временем нормой становится группировка по пять штук.

Такой счет – простейший способ сбора и представления данных. Подсчет одновременно двух вещей – к примеру, очков, набранных каждой командой в игре мальчиков против девочек, – производится точно так же и позволяет с одного взгляда определить и количество, и соотношение этих двух вещей.

Иногда эта система счета используется просто для регистрации каких-то одинаковых вещей или событий – числа людей, пришедших на представление, или машин, заезжающих на парковку. Но составив табличку, можно одновременно отслеживать и несколько параметров: сгруппировать машины по маркам; выяснить, чипсы с какими ароматами пользуются наибольшим спросом; подсчитать число леденцов каждого цвета в разноцветной упаковке. Такие таблички известны как частотные таблицы; полученные с их помощью данные часто представляют в виде графиков и диаграмм, преобразовывая информацию в визуальную форму.

Сравнение, сортировка, систематизация

Это – три слона, на которых держится любая обработка информации. Взгляните на множество перечисленных в предыдущих главах способов, при помощи которых мы группировали и называли числа – целые числа, дроби, четные/нечетные, квадраты чисел, кратные, делители и т. п. Или припомните разнообразные типы и названия геометрических фигур: симметричные, двумерные или трехмерные, правильные и т. п.

В основе обработки информации лежит умение замечать общие свойства объектов и их различия, а затем распределять эти объекты по категориям.

Что лишнее в группе?

Которая из этих четырех фигур является здесь лишней?

Большинство людей сразу выберет треугольник, поскольку на данной картинке он единственная фигура с тремя сторонами. Но это лишь одна из возможных причин, по которым треугольник в этом наборе оказывается лишним. Как по-вашему, существуют ли другие объяснения? Прежде чем читать дальше, попробуйте назвать еще по крайней мере пять причин.

Вот некоторые:

• Его углы в сумме дают 180° (у каждой из остальных фигур сумма углов равна 360°).

• Он имеет три оси симметрии.

• У него самая маленькая площадь.

• У него самый маленький периметр.

• В нем три угла.

• Все его углы острые.

• Из шести таких треугольников можно сложить шестиугольник.

Треугольник не единственный возможный вариант ответа на вопрос «Какая фигура здесь лишняя?». В каждой из остальных фигур есть что-то, что ее выделяет: все, кроме одной, имеют равные стороны; все, кроме одной, имеют горизонтальное основание; у всех, кроме одной, все углы одинаковы… Это наглядно показывает, что классификация объектов редко бывает очевидной и однозначной. А поскольку при обработке информации постоянно требуется распределять информацию по категориям, то чем чаще ребенок будет придумывать и обдумывать всевозможные категории, тем лучше.

Игра: «Что здесь лишнее?»

Эта игра может стать увлекательным и творческим занятием для ребенка любого возраста. С маленькими детьми можно взять обычные бытовые предметы. Положите перед ним, к примеру, ложку, чашку, бутылку и вилку. Сможете ли вы вместе с сыном или дочкой найти критерии, по которым лишним в этой коллекции может быть назван каждый предмет по очереди? А если взять карандаш, пластмассовую линейку, фломастер и ластик? Кто из вас сможет найти самую необычную или глупую причину, по которой какой-то из этих предметов можно счесть лишним? Для начала приведем несколько примеров:

• Карандаш лишний, потому что только у него нет ни одной гибкой части.

• Линейка лишняя, потому что только она производит странный звук, если положить ее на край стола и щелкнуть по кончику

• Только у ластика есть другое название (стирательная резинка).

Дети постарше могут исследовать числовые множества. Сколько различных ответов можно дать на вопрос: «Какое число здесь лишнее: 20, 15, 24, 25?»?

Вариантом игры «Что здесь лишнее?» может стать игра «О чем я думаю?». Договоритесь, какого рода можно выбирать предметы. Скажем, обычные вещи, которые ребенок видит каждый день, – одежда на полке или посуда на столе. Можно вообразить и что-то из математики: целые числа меньше 100, трехмерные геометрические фигуры. Сможет ли ребенок определить, о чем вы думаете, задавая вопросы, предполагающие ответы «Да» или «Нет»? К примеру, на столе перед вами находятся чашка, стакан, сэндвич и яблоко:

– Это съедобно?

– Нет.

– Это прозрачно?

– Нет.

– Это чашка?

– Да.

Игра: «найди число»

Вы с ребенком по очереди задумываете число от 1 до 100, а затем, чтобы его найти, задаете вопросы, на которые можно ответить только либо «Да», либо «Нет»:

– Я задумал число от 1 до 100.

– Оно четное?

– Да.

– Оно больше 50?

– Нет.

– Оно кратно 3?

– Да.

– Оно больше 25?

– Да.

И так далее.

Наилучшая стратегия в подобных играх (то есть та, которая быстрее всего позволит отгадать задуманное число) состоит в том, чтобы задавать такие вопросы, которые предполагали бы, что все оставшиеся возможные ответы разделяются на две равные группы, одна из которых имеет ответ «Да», а другая – «Нет». Поэтому «Это число четное?» отлично подходит на роль первого вопроса: половина возможных ответов является четной, а вторая половина – нет. С другой стороны, вопрос «Кончается ли это число на нуль?» не очень хорош, поскольку 90 из 100 чисел не заканчиваются на нуль и вероятность отрицательного ответа на этот вопрос весьма велика.

Сортировка и диаграммы Венна

В определенный момент в начальной школе ваш ребенок познакомится с двумя способами сортировки – при помощи диаграмм Венна (о которых вы, вероятно, слышали) и Кэрролла (с которыми вы, скорее всего, не сталкивались). Хотя оба способа позволяют сделать, в сущности, одно и то же, данные в них представляются немного по-разному и потому акцент делается на разных вещах.

Чтобы помочь ребенку освоить диаграммы Венна, можно организовать игру с двумя связанными петлей веревочками и набором различных предметов. Можно разложить на столе яблоко, апельсин, оранжевый восковой мелок и простой карандаш и исследовать возможные способы разбиения этого множества предметов на две группы. Это может быть группа съедобных вещей и группа оранжевых предметов. Ребенок быстро поймет, что некоторые вещи следует отнести к обеим группам: так, апельсин оранжевый и к тому же съедобен. Значит, две веревочных петли должны будут пересечься.

Кроме того, хотя это не очевидно на первый взгляд, существует и четвертое место, где могут находиться предметы, – пространство вокруг петель. В нашем примере то, что не оранжевое и невозможно съесть, должно будет остаться за пределами обоих групп.

В начальной школе диаграмма Венна часто представляется только как пересечение двух контуров, но в некоторых ситуациях один из контуров может полностью находиться внутри другого. Так, если одна из петель представляет группу «животные, которые дают молоко», а вторая – группу «коровы», то, поскольку все коровы дают молоко, коровы полностью включены в группу молочных животных. Диаграмма Венна для этого случая становится похожей на яичницу-глазунью.

Кроме того, не существует правила, согласно которому петель (групп) должно быть обязательно две. Вы можете создать их столько, сколько нужно, чтобы представить все нужные вам категории, хотя в случае, когда групп больше трех, пересечения между ними сильно усложняются.

Диаграммы Кэрролла

Этот вид диаграмм назван в честь автора «Алисы в Стране чудес», который занимался не только писательством, но и преподавал математику в Оксфорде. Чарльз Доджсон (настоящее имя Кэрролла) особенно интересовался логикой и в 1896 г. опубликовал книгу «Символическая логика» (Symbolic Logic), где представил диаграмму, названную им «двухбуквенной». Позже этой диаграмме дали имя ее автора, и сегодня каждый учащийся начальной школы изучает диаграмму Кэрролла как метод категоризации объектов.

Особенно удобна диаграмма Кэрролла для группировки математических объектов. К примеру, карточки с числами можно рассортировать по самым разным признакам: четные/нечетные, больше/меньше 20, кратные/некратные пяти…

Проверьте себя

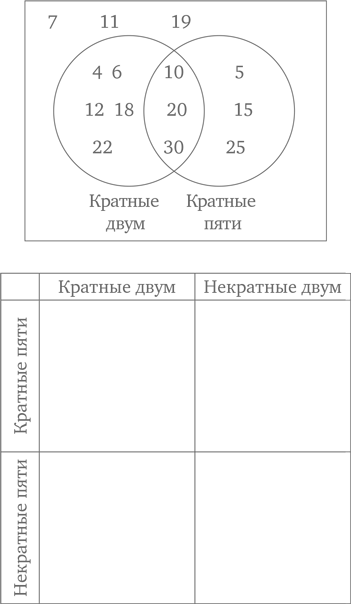
41. Диаграмма Кэрролла

Где на диаграмме Кэрролла оказались бы числа с приведенной ниже диаграммы Венна?

Проекты по обработке данных

Не так давно почти весь школьный опыт обработки данных сводился у учащихся начальной школы к рисованию столбчатых диаграмм по готовым наборам данных. Дети тратили много времени на раскрашивание диаграмм, но мало что реально узнавали об обработке данных. Теперь построение всевозможных диаграмм и графиков лучше поручить технике – любая электронная таблица может быстро представить ваши данные в виде таблицы или диаграммы, – поэтому учитель может больше внимания уделить полномасштабным проектам обработки данных.

Работа над проектом начинается с выбора темы исследования. Это может быть что-нибудь очень простое: «Каких машин больше на дороге перед школой – зеленых или желтых?» Здесь достаточно просто пересчитать те и другие автомобили, а затем представить данные для сравнения. Но дети вполне способны провести в классе и более тонкое исследование, скажем, такое: «Помогает ли повторение выучить таблицу умножения?»

Далее в классе дети обсудят, как можно это исследовать. К примеру, они могли бы договориться и в течение, скажем, недели каждый день повторять таблицу умножения (к примеру, таблицу умножения на три). Тогда они собрали бы данные о том, как класс знает эту таблицу в начале недели, для чего провели бы общий контрольную работу. Затем, после нескольких дней практики, повторили бы тест и вновь собрали данные.

Представление результатов

Существует немало различных способов представления результатов. К таким способам относятся не только привычные столбчатые и круговые диаграммы и графики, но и множество других, более сложных форм, таких как точечная диаграмма. Одно из решений, которые необходимо принять в ходе работы над проектом по обработке данных, – о том, какой тип диаграммы использовать для представления результатов; это важно, поскольку диаграммы разных типов позволяют сделать разные выводы.

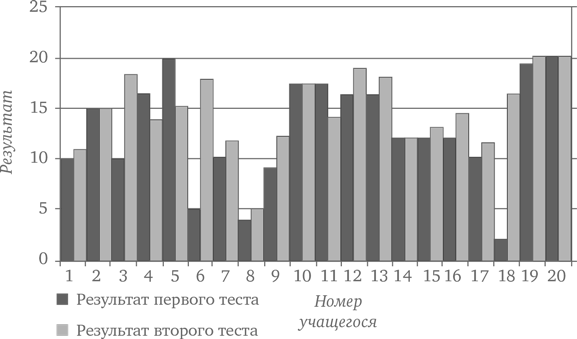
Отвечая на вопрос «Помогает ли повторение выучить таблицу умножения?», младшие дети могли бы изобразить рядом показатели каждого учащегося на блоке столбчатых диаграмм.

Затем они попытались бы интерпретировать полученные результаты, задавая себе примерно такие вопросы:

• На сколько максимально улучшился результат?

• Показал ли кто-нибудь ухудшение результата?

• У всех ли результат улучшился? У скольких улучшился?

• В целом показал ли класс улучшение?

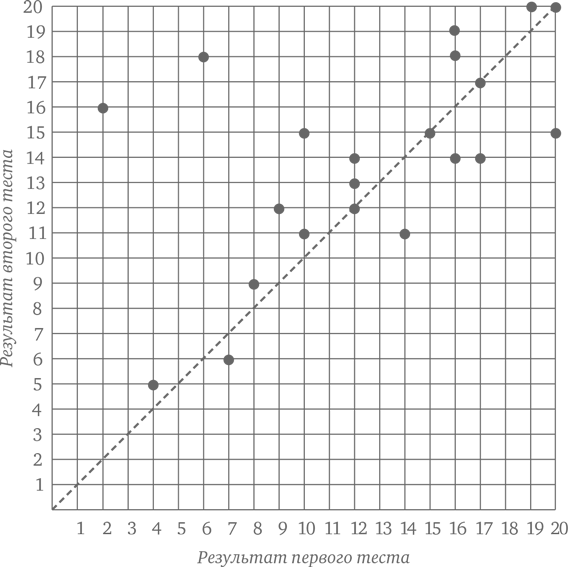
Дети постарше, возможно, предпочли бы использовать точечную диаграмму, которая иногда бывает более информативной. На ней координатами точки служат результаты каждого ребенка в первом и втором тесте (по одной оси – в первом, по другой – во втором). Диагональная линия показывает, где находились бы все точки, если бы результаты обоих тестов были одинаковыми. У детей, получивших за второй тест более высокую оценку, точки ложатся выше этой линии, у тех, у кого оценка снизилась, – ниже. В таком представлении проще с одного взгляда понять, сколько детей показали лучший результат, и сколько – худший. (Похоже также, что те дети, кто плохо написали первый тест, как правило, повысили свои показатели, а те, кто в первый раз добились успеха, либо не улучшили прежний результат, либо улучшили его, но незначительно.)

В голове ребенка

У младших школьников случаются проблемы с интерпретацией графиков и диаграмм, поскольку дети склонны рассматривать их как буквальные изображения происходящих процессов.

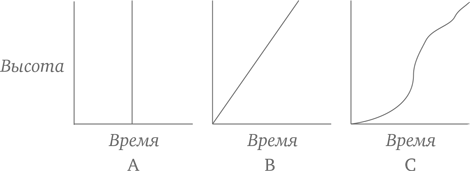
Представьте, что какой-нибудь школьник поднимает флаг на утренней линейке. Который из этих графиков лучше всего представляет движение флага вверх по шесту? По горизонтальной оси откладывается время в секундах, по вертикальной – высота над землей флага в метрах.

Многие дети (и некоторые взрослые) выберут график A, потому что он зрительно напоминает флагшток и, как и сам флаг, поднимается «прямо вверх».

На самом же деле, поскольку горизонтальная ось описывает движение времени, график A означает, что флаг взлетает на полную высоту мгновенно, что невозможно. Какой же график правильный – B или С? На B флаг поднимается равномерно и свое движение по шесту начинает с той же скоростью, с какой и заканчивает. График C предполагает, что вначале флаг движется медленно (кривая близка к горизонтальной шкале, что означает, что флаг первые несколько секунд поднимается еле-еле), затем ускоряется, а в конце замедляется вновь. Поэтому вполне возможно, что B – график подъема флага механическим устройством, а C достаточно точно отражает происходящее, когда флаг поднимает человек. Чтобы научиться разбираться в подобных графиках, нужно немало поработать.

Проверьте себя

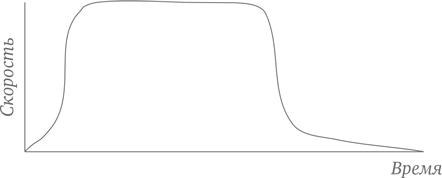
42. Какой вид спорта?

Как вы считаете, какой вид спорта представлен на этом графике: гольф, бег на 100 м или рыбная ловля?

График сказки

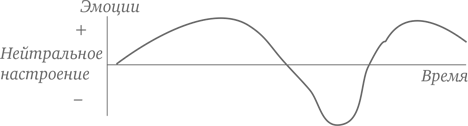
Есть один забавный способ разобраться вместе с ребенком в том, что график – это вовсе не буквальное изображение происходящего. Для этого нужно построить график эмоционального состояния какого-нибудь действующего лица по ходу сюжета известной сказки. На оси Х размечаем ход времени, а по оси Y откладываем эмоции от самых негативных внизу до самых позитивных вверху. Каждый может выбрать сказку по своему вкусу, а затем попытаться сопоставить график с развитием действия. Представьте, к примеру, как приведенный график соотносится с чувствами Красной Шапочки и событиями сказки.

Простая диаграмма Кэрролла.

A диаграмма Кэрролла, квадрат Льюиса Кэрролла, двухбуквенная диаграмма или двусторонняя таблица – это диаграмма используется для группировки вещей по принципу да / нет. Числа или объекты классифицируются как «x» (с атрибутом x) или «не x» (без атрибута «x»). Они названы в честь Льюиса Кэрролла, псевдонима из Чарльз Латвидж Доджсон.

Содержание

• 1 Использование
• 2 См. Также
• 3 Ссылки
• 4 Дополнительная литература
• 5 Внешние ссылки

Использование

Более сложная диаграмма Кэрролла.

Хотя диаграммы Кэрролла могут быть такими же простыми, как и первая из приведенных выше, наиболее известными типами являются диаграммы, похожие на вторую. один, где показаны два атрибута. «Вселенная» диаграммы Кэрролла содержится в прямоугольниках на диаграмме, так как любой номер или объект должен либо иметь атрибут, либо не иметь его.

Диаграммы Кэрролла часто изучают школьники, но их также можно использовать за пределами области образования, поскольку они представляют собой удобный способ категоризации и отображения информации.

См. Также

Викискладе есть материалы, связанные с диаграммами Кэрролла .

• Диаграмма
• Карта Карно
• Теория множеств
• Диаграмма Венна
• Игра Логика

Ссылки

Дополнительная литература

• Mac Queen, Gailand (октябрь 1967 г.). Логическая диаграмма (PDF) (Диссертация). Университет Макмастера. Архивировано из оригинала (PDF) 14 апреля 2017 года. Проверено 14 апреля 2017 г.
• Эдвардс, Энтони Уильям Фэрбэнк (2004). Шестеренки разума: история диаграмм Венна. Балтимор, Мэриленд, США: Johns Hopkins University Press. ISBN 0-8018-7434-3 .

Внешние ссылки

• Богомольный, Александр (2017) [1996]. «Логическая игра Льюиса Кэрролла». Разрежьте узел. Архивировано из оригинала 03.05.2017. Проверено 3 мая 2017 г.

• «Интерактивный демонстратор диаграммы Кэрролла (и игры логики) на lewiscarrollresources.net».

Carroll диаграмма , квадрат Льюиса Кэрролл , Двухбуквенная диаграмма или двухсторонняя таблица является диаграмма используется для группировки вещей в да / нет моды. Числа или объекты классифицируются как «x» (с атрибутом x) или «не x» (без атрибута «x»). Они названы в честь Льюиса Кэрролла , на псевдоним из Чарльза Доджсона Lutwidge .

использование

Хотя диаграммы Кэрролла могут быть такими же простыми, как и первая из приведенных выше, наиболее известны типы, подобные второму, где показаны два атрибута. «Вселенная» диаграммы Кэрролла содержится в прямоугольниках на диаграмме, поскольку любое число или объект должны либо иметь атрибут, либо не иметь его.

Диаграммы Кэрролла часто изучают школьники , но их также можно использовать за пределами области образования , поскольку они представляют собой удобный способ категоризации и отображения информации.

Смотрите также

• Диаграмма
• Карта Карно
• Теория множеств
• Диаграмма Венна
• Игра логики

использованная литература

дальнейшее чтение

• Мак Куин, Гейланд (октябрь 1967 г.). Логическая диаграмма (PDF) (Диссертация). Университет Макмастера . Архивировано из оригинального (PDF) 14 апреля 2017 года . Проверено 14 апреля 2017 .
• Эдвардс, Энтони Уильям Фэрбэнк (2004). Шестеренки разума: история диаграмм Венна . Балтимор, Мэриленд, США: Издательство Университета Джона Хопкинса . ISBN 0-8018-7434-3.

внешние ссылки

• Богомольный, Александр (2017) [1996]. «Логическая игра Льюиса Кэрролла» . Разрежьте узел . Архивировано 03 мая 2017 года . Проверено 3 мая 2017 .
• «Интерактивный демонстратор диаграммы Кэрролла (и игры логики) на lewiscarrollresources.net» .