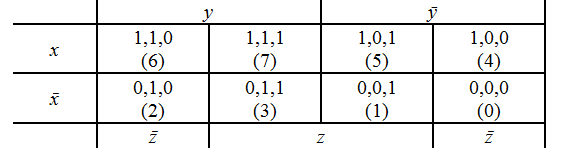Метод диаграмм Вейча
Диаграмма
Вейча – это специального вида таблица,
используемая для задания логических
функций и позволяющая упростить процесс
поиска минимальных форм.
Для логических
функций, зависящих от n
переменных, диаграмма Вейча представляет
собой прямоугольник, разделенный на 2n
клеток. Каждой клетке диаграммы ставится
в соответствие двоичный n-мерный
набор. Взаимно однозначное соответствие
между двоичными наборами и клетками
диаграммы устанавливается разметкой
последней.
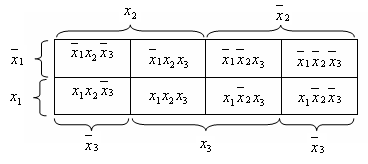
Для функций,
зависящих от трех переменных, один из
возможных вариантов разметки диаграммы
Вейча имеет вид, показанный на рис.1.
Четыре верхних
клетки диаграммы соответствуют двоичным
наборам, в которых переменная х1
принимает значение 0; четыре нижних
клетки соответствуют наборам, в которых
переменная х1
принимает значение 1.
Клетки, составляющие
левую половину диаграммы, соответствуют
наборам, в которых переменная х2
принимает значения 1, а в правой половине
находятся клетки, в которых переменная
х2
принимает значение 0.
Рис. 1.
Четыре центральные
клетки соответствуют наборам, в которых
переменная х3
принимает значения 1, а в левом и правом
крайних столбцах находятся клетки, в
которых переменная х3
принимает значение 0.
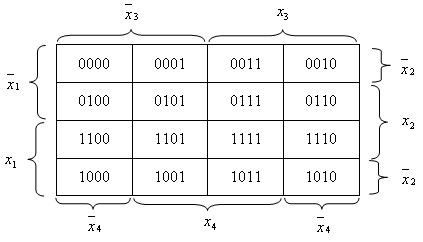
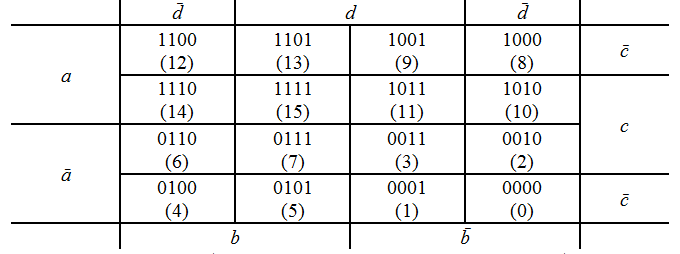
На рис. 2 приведены
пример разметки диаграммы для логических
функций четырех переменных.
Рис. 2.
Диаграммы Вейча
для большего числа переменных могут
быть составлены из диаграмм меньшего
числа переменных. Например, диаграмму
Вейча для пяти переменных можно составить,
соединив две диаграммы для четырех
переменных. При этом удобно подсоединять
их друг к другу одноименными столбцами
(рис. 3). Тогда соседними клетками будут
также клетки столбцов, симметрично
расположенных относительно линии
присоединения диаграмм Вейча четырех
переменных для одноименных строк.
Рис. 3.
В клетки,
соответствующие конституентам единицы
минимизируемой булевой функции,
записываются единицы, а в остальные —
нули. Поэтому исходная минимизируемая
функция первоначально должна быть
представлена в СДНФ. Если функция задана
аналитически, то она приводится к СДНФ
с помощью операции развертывания,
заключающейся в умножении некоторых
членов на выражение вида
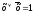
Минимизация булевых
функций с использованием диаграмм Вейча
основывается на отыскании склеивающихся
конституент единицы. Для диаграммы
Вейча склеивающиеся конституенты
единицы располагаются в соседних,
вертикально или горизонтально
расположенных клетках. Для диаграммы
трех переменных (рис. 1) соседними клетками
являются также клетки левого и правого
столбцов для одноименных строк. Наглядно
это можно представить, если наклеить
диаграмму на цилиндр так, чтобы левая
ее граница совпала с правой.
Для диаграммы
Вейча четырех переменных (рис. 2) соседними
клетками будут также клетки, расположенные
в верхних и нижних строках для одноименных
столбцов.
Процесс отыскания
минимальной ДНФ заключается в том, чтобы
всю совокупность единиц диаграммы Вейча
накрыть наименьшим числом наиболее
коротких произведений. Для этого соседние
клетки диаграммы, содержащие единицы,
объединяют в группы (склеиваются).
Каждой такой группе
будет соответствовать группа склеивающихся
конституент единицы. Причем количество
клеток, входящих в одну группу, равно
2k
(где k
= 1, 2, 3, …), а каждая клетка, входящая в
группу, должна иметь k
соседних клеток.
Для получения
минимальной ДНФ достаточно выполнить
следующие условия:
каждая единичная
клетка должна входить хотя бы в одну
группу (при этом одна и та же клетка
может входить в несколько групп);
в каждую группу
должно входить максимальное количество
клеток, т.е. ни одна группа, удовлетворяющая
обоим вышеприведенным правилам, не
должна быть частью другой группы,
удовлетворяющей этим же правилам;
количество групп
должно быть минимальным.
Рекомендации по
минимизации булевых функций с
использованием диаграмм Вейча:
1. Рассматриваются
поочередно клетки, содержащие единицы,
и анализируются всевозможные варианты
склеивания. При этом сначала склеивание
выполняется только для тех клеток
(единиц), для которых вариант склеивания
единственный. В результате будут выделены
обязательные (или существенные) простые
импликанты.
2. Оставшиеся
несклеенные клетки (единицы) необходимо
склеивать таким образом, чтобы образовать
минимальное число групп с максимальным
числом клеток в каждой группе.
3. Каждой группе
объединенных клеток в минимальной ДНФ
будет соответствовать простая импликанта,
определяемая как конъюнкция только тех
переменных, значения которых постоянны
для всех наборов, задающих клетки данной
группы.
Группе, состоящей
из 2k
клеток, соответствует конъюнкция из n
– k
букв, где n
— число переменных в исходной булевой
функции.
Пример 1.
Найти минимальную ДНФ для булевой
функции трех переменных, заданных
следующей таблицей истинности(табл.1):
Таблица 1
|
№ на |
х1 |
х2 |
х3 |
z |
|
0 |
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
|
2 |
0 |
1 |
0 |
0 |
|
3 |
0 |
1 |
1 |
1 |
|
4 |
1 |
0 |
0 |
1 |
|
5 |
1 |
0 |
1 |
0 |
|
6 |
1 |
1 |
0 |
1 |
|
7 |
1 |
1 |
1 |
1 |
СДНФ для этой
функции
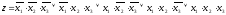
Составим диаграмму
Вейча (рис. 4)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Метод минимизирующих карт (карты Карно, диаграммыВейча)
Карты Карно (их разновидностью являются диаграммы Вейча) являются графическим представлением таблиц истинности. Поэтому они строятся или по таблице истинности анализируемой функции, или же по ее СДНФ.
Диаграммы Вейча представляет собой прямоугольник, разбитый на ячейки, число которых равно общему числу наборов для данной функции n переменных, то есть оно равно 2n. Так, для функции 3-х переменных ячеек будет 8, для 4-х переменных – 16 и т.д.
Каждая ячейка соответствует определенному набору, или терму, причем наборы располагаются так, чтобы соседние наборы, или термы как по горизонтали, так и по вертикали, отличались бы только значением одной переменной: в одной ячейке она была бы в прямом виде, а в соседней – с инверсией. Причем надо учесть, что ячейки, расположенные на противоположных концах каждой строки или столбца, также являются соседними.
Функцию в СДНФ наносят на карту, отмечая, например, знаком “1” ячейки, соответствующие тем наборам, на которых ФАЛ равна единице, т.е. в СДНФ функции эта ячейка соответствует одному изееминтермов. Остальные ячейки отмечаются знаком “0”.
Диаграмма Вейча для функции 3-х переменных
Диаграмма Вейча для функции 4-х переменных
Если данную таблицу рассматривать как цилиндр, образованный соединением первой и последней колонок, то тогда склеивающиеся между собой конституэнты единицы или нуля в диаграммах Вейча будут расположены в соседних клетках. При этом прямоугольники, покрывающие 2kсоседних клеток, описывают имликанту (имплиценту), имеющую ранг (n-k), где n – число переменных, от которых зависит функция.
Клетки, содержащие в диаграмме Вейча единицы, будем называть 1-клетками, а клетки, содержащие нули – 0-клетками.
Основное свойство диаграмм Вейча заключается в том, что любая первичная импликанта ранга (n-m) образует на ней прямоугольник и только прямоугольник 1-клеток площадью 2m, где n – количество переменных, от которых зависит функция. Такие прямоугольники называют m-кубами (m=0,1,…,n.; 0-кубу соответствует минтерм, а n-кубу – константа “единица”). Так любая пара единиц в соседних клетках диаграммы Вейча для логической функции трех переменных представляется импликантой второго ранга. Четыре единицы, образующие прямоугольник, выражаются одной переменной (с отрицанием или без него).
Чтобы записать первичную импликанту, представляющую собой некий m-куб на диаграмме Вейча, необходимо просто составить конъюнкцию тех переменных, которые в пределах данного m-куба сохраняют постоянные значения (только прямые или только инверсные).
Получение минимальной ДНФ с помощью диаграмм Вейча сводится к отысканию минимального числа m-кубов максимально-го размера, состоящих из 1-клеток, и составлению дизъюнкции импликант, соответствующих этим m-кубам (каждая 1-клетка должна войти хотя бы в один m-куб, любая 1-клетка может входить одновременно в несколько различных m-кубов).
При получении МДНФ с помощью диаграммы Вейча необходимо обратить внимание на следующее:
- m-кубу, покрывающему2m 1-клеток, соответствует первичная импликанта, не зависящая от m переменных, причем исключаются те m переменных, которые в прямоугольной области на диаграмме Вейча, состоящей из 1-клеток, имеют различное значение (прямое и инверсное);
- прямоугольные области на диаграмме Вейча, используемые при минимизации, могут состоять только из 2m соседних клеток, где m = 0,1,…,n;
- каждая клетка на диаграмме Вейча, вне зависимости от способа разметки этой диаграммы, имеет ровно n соседних клеток; в связи с этим диаграмма Вейча представляется нанесенной на поверхность соответствующего тела (цилиндра – для случая трех переменных, тора – для случая четырех переменных);
- поиск минимального покрытия 1-клеток следует начинать с выбора тех 1-клеток, которые могут войти в один и только один m-куб; если после этого на диаграмме остаются 1 клетки, не вошедшие ни в один из m-кубов, то следует рассмотреть несколько вариантов покрытий этих клеток; с целью минимизации результата оставшиеся 1-клетки покрываются, по возможности, m-кубами максимального размера.
Получение минимальной КНФ проводится аналогичным образом по отношению к 0 клеткам.
|
|
Макеты страниц
Из-за сложности использования аналитического метода минимизации, связанной с трудоемкой работой по отысканию соседних минтермов, наибольшее распространение получил графический метод минимизации с помощью диаграмм Вейча, несомненным достоинством которого является наглядность и простота использования при небольшом числе переменных 
Диаграммы Вейча (ДВ) представляют собой один из табличных способов задания функций и состоят из клеток, каждая из которых соответствует определенной точке 









Рис. 1.1
Для минимизации функций двух переменных использовать диаграммы Вейча нет смысла, так как эти функции легко упрощаются аналитическим методом или непосредственно по таблице истинности. Рассмотрим диаграммы Вейча для функций трех переменных 





номер данной клетки будет Определяться числом 
Любой минтерм 










Две клетки диаграммы Вейча называются соседними, если им соответствуют соседние минтермы. Для удобства отыскания контермов, покрывающих 





Рассмотрим пример. Пусть требуется составить ДВ-3 для функции 




т.е. в ДВ-3 (см. рис. 1.1,в) единицами заполняются клетки, соответствующие этим минтермам. Таким образом, имеется жесткая связь между таблицей истинности (см. табл. 1.5), аналитическим выражением для функции и диаграммой Вейча (см. рис. 1.1,в).
Некоторые особенности взаимосвязи таблицы истинности и диаграммы Вейча требуют пояснений. В таблице истинности (табл. 1.5) значения аргументов указаны в явном виде в трех столбцах, обозначенных через 



х (это соответствие указано в табл. 1.5). Легко заметить, что половине клеток ДВ-3, обозначенной через 









Указание в явном виде одних величин вместо других в таблицах истинности и диаграммах Вейча связано с различием в их назначении-, таблицы истинности наиболее удобны для первоначального описания переключательных функций, а диаграммы Вейча — для их минимизации.
Клетки, содержащие в диаграмме Вейча единицы, будем называть 1-клетками, а клетки, содержащие йули, — 







Основное свойство диаграммы Вейча заключается в том, что 1-клетки любого контерма 














Таким образом, в соответствии с общим правилом минимизации, получение МДНФ с помощью диаграмм Вейча сводится к отысканию минимального числа m-кубов максимального размера, состоящих из 1-клеток, т.е. к отысканию минимального покрытия m-кубами 1-клеток и составлению дизъюнкции контермов 
должна войти хотя бы в один m-куб). Согласно идемпотентным законам любая 1-клетка может входить в несколько различных 
На рис. 1.1,в пунктиром обозначены два 1-куба, образованные 1-клетками с номерами 5 и 7, 1 и 5, которым соответствуют контермы 


Минимальная нормальная форма в базисе И-НЕ этой функции получается из МДНФ в соответствии с (1.80):

Для получения МКНФ функции 



а МКНФ получается на основании закона двойственности:

Минимальная нормальная форма в базисе ИЛИ-НЕ данной функции получается из МКНФ в соответствии с (1.76):

Из рис. 1.1, г следует, что минимальное покрытие 1-клеток функции 




Диаграммы Вейча для четырех переменных (ДВ-4) показаны на рис. 1.2. Так как 






Диаграмма Вейча, показанная на рис. 


Рис. 1.2
3-куба и двух 2-кубов, которым соответствуют контермы 

Минимальное же покрытие 0-клеток состоит из двух 1-кубов, которым соответствуют контермы 

Из МДНФ и МКНФ не составляет труда получить МНФ в базисах И-НЕ и ИЛИ-НЕ.
Выбор m-кубов, покрывающих 1-клетки диаграммы Вейча, не всегда столь очевиден, как это было в предыдущих примерах. На рис. 1.2.6 часть 1-клеток можно было бы покрыть 



Таким образом, не всегда следует начинать покрытие 1-клеток с отыскания m-кубов максимального размера.
Сформулируем общие правила минимизации функций с помощью диаграмм Вейча, справедливые для любого числа переменных 
для получения МДНФ необходимо найти минимальное покрытие 1-клеток, которое состоит из минимального числа 
m-кубу, покрывающему 



прямоугольные области на диаграммах Вейча, используемые при покрытии функции 


покрытие следует начинать с выбора тех 1-клеток, которые могут войти в один и только один m-куб, а затем выбранные таким образом 1-клетки покрываются m-кубами максимального размера (это правило позволяет исключить возможность появления лишних m-кубов, как это могло иметь место в примере на рис. 1.2,в);
если 1-клеток, входящих только в один m-куб, нет, то следует рассмотреть несколько вариантов минимизации.

Рис. 1.3
Диаграммы Вейча для числа переменных 



48, 5 и 53, 16 и 32 и т. п. (см. рис. 1.3,в) не являются соседними, так как они расположены не в соседних ДВ-4.
Легко убедиться в том, что 




В ДВ-6 ш-кубы, расположенные в одинаковых местах всех четырех ДВ-4, образуют 

Основываясь на сформулированных выше правилах минимизации с помощью диаграмм Вейча, достаточно просто также отыскивать МДНФ функций семи и восьми переменных. Для этого нужно только подходящим образом выбрать способ расположения 



Модификация диаграмм (карт) Вейча, введенных в 1952 г., известна под названием карт Карно (1953 г.) [7, 9]. Известны также методы минимизации Квайна — Мак-Класки, Блейка и др. [7].
Оглавление
- Предисловие
- Глава 1. Основы теории переключательных функций
- 1.2. Позиционные системы счисления
- 1.3. Переключательные функции
- 1.4. Принцип и закон двойственности
- 1.5. Теоремы разложения
- 1.6. Решение систем логических уравнений
- 1.7. Первичные термы, минтермы и макстермы
- 1.8. Совершенные нормальные формы представления функций
- 1.9. Конъюнктивные и дизъюнктивные термы
- 1.10. Минимизация переключательных функций
- 1.11. Диаграммы Вейча
- 1.12. Минимизация неполностью определенных функций, совместная минимизация нескольких функций
- 1.13. Скобочные формы функций
- 1.14. Закон двойственности для логических схем
- 1.15. Линейные функции
- Глава 2. Анализ и синтез логических схем
- 2.2. Модели логических элементов
- 2.3. Модели логических схем
- 2.4. Анализ логических схем
- 2.5. Синтез комбинационных схем, свободных от состязаний
- Глава 3. Синтез асинхронных потенциальных автоматов
- 3.2. Асинхронные потенциальные автоматы
- 3.3. Асинхронные потенциальные триггеры и элементы памяти
- Триггеры типа R-S
- Триггеры типа D-L
- Триггеры типа D-L-R с приоритетом входа R.
- Триггеры типа D-L-R с приоритетом входа L.
- Триггеры типа R-S-L.
- Триггеры типа DN-LN
- Аналитический метод синтеза и анализа триггеров.
- 3.4. Задание асинхронных потенциальных автоматов таблицами и графами переходов
- 3.5. Синтез асинхронных потенциальных счетчиков
- 3.6. Синтез асинхронных импульсных триггеров
- Триггеры типа dJ-dK.
- Классификация триггеров.
- 3.7. Синтез синхронных триггеров
- Триггеры типа J-K
- Синхронно-асинхронные триггеры.
- 3.8. Примеры синтеза асинхронных потенциальных автоматов
- Цифровые фазочастотные детекторы.
- Квантизатор временных интервалов.
- 3.9. Генераторы сигналов
- Автогенераторы.
- Управляемые автогенераторы.
- Глава 4. Синтез синхронных автоматов
- 4.2. Синхронные триггеры
- Триггеры типов D и R-S с импульсным тактовым сигналом.
- Синхронные триггеры типов R-S и D-L
- Синхронно-асинхронные триггеры.
- Синхронные триггеры типа J-K
- Триггеры типа Т.
- Классификация синхронных триггеров.
- Преобразования типов синхронных триггеров.
- Триггеры типов D-T-L и D-T-L/R
- Функции переходов синхронно-асинхронных триггеров.
- 4.3. Примеры синтеза синхронных автоматов
- 4.4. Сдвигающие регистры
- Синтез счетчиков на сдвигающих регистрах.
- Сдвигающие регистры с загрузкой данных.
- Реверсивные сдвигающие регистры.
- 4.5. Синхронные счетчики
- Синхронные двоичные счетчики.
- Синхронные двоично-десятичные счетчики.
- Каскадирование двоичных и двоично-десятичных счетчиков.
- Синхронные двоичные реверсивные счетчики.
- Реверсивные двоично-десятичные счетчики.
- Каскадирование реверсивных счетчиков.
- Счетчики на сдвигающих регистрах.
- Кольцевые счетчики.
- Линейные счетчики.
- Программируемые счетчики.
- 4.6. Асинхронные счетчики
- Асинхронные счетчики с умножением частоты счетного сигнала.
- Асинхронные импульсно-потенциальные счетчики.
- Асинхронное программирование модуля пересчета счетчиков.
- Глава 5. Логические элементы и триггеры
- Логические элементы.
- Классификация ИС по степени интеграции.
- 5.2. Интегральные схемы КМОП серий
- 5.3. Триггеры Шмитта
- 5.4. Логические элементы с открытым коллекторным выходом
- Логические элементы с открытым коллекторным выходом.
- Применения ЛЭ с открытым коллекторным выходом.
- Интерфейсные ЛЭ с открытым коллекторным выходом.
- Логические элементы с открытым стоковым выходом.
- Типовые цоколевки ИС.
- 5.5. Логические элементы с тремя состояниями выхода
- Шинные драйверы с Z-состоянием выхода.
- Основные правила графического изображения ИС.
- 5.6. Преобразователи уровней напряжения и тока
- 5.7. Асинхронные потенциальные триггеры и регистры памяти
- 5.8. Синхронные триггеры и регистры памяти
- 5.9. Шинные приемопередатчики
- Шинные приемопередатчики с Z-состоянием выхода.
- Шинные приемопередатчики с открытым коллекторным выходом.
- Шинные приемопередатчики с регистрами памяти.
- Шинные приемопередатчики со сдвигающим регистром.
- Шинные трехнаправленные приемопередатчики.
- 5.10. Мультивибраторы
- 5.11. Генераторы
- Схемы устранения “дребезга” механических контактов.
- Автогенераторы периодических сигналов.
- 5.12. Рекомендации по выбору серий ИС
- Глава 6. Коммутаторы и арифметические устройства
- 6.1. Дешифраторы
- 6.2. Демультиплексоры
- 6.3. Мультиплексоры
- Мультиплексоры без стробирования.
- Мультиплексоры со стробированием.
- Мультиплексоры с Z-состоянием выхода.
- Каскадирование мультиплексоров.
- Функциональные мультиплексоры.
- Регистры памяти с мультиплексными входами данных.
- Мультиплексоры с регистрами памяти данных и адреса.
- Сдвигающие мультиплексоры.
- 6.4. Синтез комбинационных схем и цифровых автоматов на мультиплексорах
- Синтез схем на 8-канальных мультиплексорах.
- Синтез на двухразрядных 4-канальных мультиплексорах.
- Синтез генератора синусоидальной функции на мультиплексорах.
- Синтез триггеров на мультиплексорах.
- Синтез счетчиков на мультиплексорах.
- 6.5. Аналоговые ключи и мультиплексоры-демультиплексоры
- 6.6. Шифраторы
- 6.7. Цифровые компараторы
- Программируемые цифровые компараторы.
- Адресные компараторы.
- Применения адресных компараторов.
- 6.8. Схемы сравнения двоичных чисел
- 8-разрядные схемы сравнения двоичных чисел.
- 6.9. Прямой, обратный и дополнительный коды
- Дополнительный код.
- Сложение чисел в обратном коде.
- Код с избытком 3.
- 6.10. Сумматоры
- Двоичные параллельные сумматоры с последовательным переносом.
- Двоичные сумматоры с параллельным переносом.
- Применения сумматоров.
- Десятичные сумматоры.
- Последовательные двоичные сумматоры.
- 6.11. Арифметическо-логические устройства
- 6.12. Пороговые схемы и мажоритарные элементы
- 6.13. Умножители двоичных чисел
- Быстрые умножители.
- БИС умножителя 12×12 разрядов 1802ВР4.
- Последовательные умножители.
- 6.14. Конвейерные устройства
- Конвейерный быстрый умножитель.
- Конвейерные АЦП.
- 6.15. Синтез линейных комбинационных схем
- Сумматор по модулю q.
- Умножитель по модулю q.
- Глава 7. Сдвигающие регистры и счетчики
- 7.1. Сдвигающие регистры без параллельной записи данных
- Сдвигающие устройства с выходными регистрами памяти.
- 7.2. Сдвигающие регистры с параллельной записью данных
- Сдвигающие регистры с расширением знака.
- Сдвигающие регистры с входным регистром памяти.
- 7.3. Реверсивные сдвигающие регистры
- Реверсивные сдвигающие регистры типов PI/SO и PI/PO.
- Многофункциональные устройства на основе реверсивных сдвигающих регистров.
- 7.4. Асинхронные счетчики
- Двоично-десятичные асинхронные счетчики.
- 7.5. Синхронные двоичные счетчики
- Программирование модуля пересчета двоичных счетчиков.
- Переключение модулей пересчета двоичных счетчиков.
- Функциональные устройства на основе двоичных счетчиков.
- 7.6. Синхронные двоично-десятичные счетчики
- 7.7. Синхронные реверсивные счетчики
- 7.8. Счетчики с расщепленным тактовым сигналом
- 7.9. Счетчики на сдвигающих регистрах
- 7.10. Кольцевые счетчики
- 7.11. Делители частоты
- Нормированные умножители частоты.
- 7.12. Линейные генераторы
- Приложение 1. Перечень отечественных и зарубежных ИС
- Приложение 2. Параметры интегральных схем