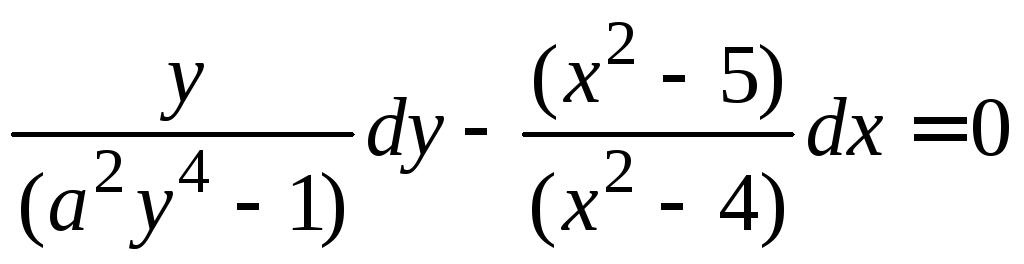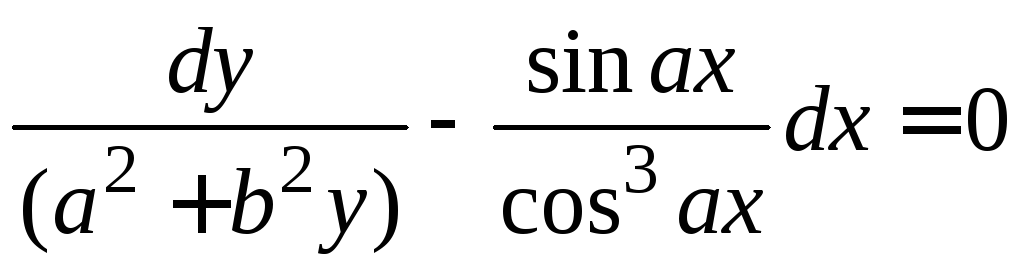Как составить дифференциальное уравнение данных семейств линий

Как составить дифференциальное уравнение данных семейств линий

Составление дифференциальных уравнений семейств линий

Пусть дано уравнение однопараметрического семейства плоских кривых

y=varphi(x,a) quad (a-text{parametr}).

(1)

Дифференцируя (1) по x, найдем

y'=varphi'_x(x,a).

(2)

Исключая параметр a из (1) и (2), получаем дифференциальное уравнение

F(x,y,y')=0,

(3)

выражающее свойство, общее всем кривым семейства (1). Уравнение (3) будет искомым дифференциальным уравнением семейства (1).

Если однопараметрическое семейство кривых определяется уравнением

Phi(x,y,a)=0,

то дифференциальное уравнение этого семейства получим, исключая параметр a из уравнений begin{cases}Phi(x,y,a)=0,\[3pt] dfrac{partialPhi}{partial x}+dfrac{partialPhi}{partial y},y'=0.end{cases}

Пусть теперь имеем соотношение

Phi(x,y,a_1,a_2,ldots,a_n)=0.

(4)

где a_1,a_2,ldots,a_n — параметры. Дифференцируя (4) n раз по x и исключая параметры a_1,a_2,ldots,a_n из (4) и полученных уравнений, приходим к соотношению вида

F(x,y,y',y'',ldots,y^{(n)})=0.

(5)

Это дифференциальное уравнение заданного n-параметрического семейства линий (4) в том смысле, что (4) есть общий интеграл уравнения (5).

Пример 1. Найти дифференциальное уравнение семейства гипербол frac{x^2}{a^2}-frac{y^2}{1}=1.

Решение. Дифференцируя это уравнение по x, получаем

frac{2x}{a^2}-2yy'=0, или frac{x}{a^2}=yy'.

Умножим обе части на x, тогда frac{x^2}{a^2}=xyy'. Подставляя в уравнение семейства найдем xyy'-y^2=1.

Пример 2. Найти дифференциальное уравнение семейства линий y=a(1-e^{-x/a}), где a — параметр.

Решение. Дифференцируем обе части уравнения по x:

y'=e^{-x/a}

Из выражения для y' находим a=-frac{x}{ln{y'}}
и, подставляя это выражение для a в уравнение семейства линий, получим

y=-frac{x}{ln{y'}}(1-y'), или yln{y'}+x(1-y')=0.

Пример 3. Составить дифференциальное уравнение семейства прямых, отстоящих от начала координат на расстояние, равное единице.

Решение. Будем исходить из нормального уравнения прямой

xcosalpha+ysinalpha-1=0,

(6)

где alpha — параметр.

Дифференцируя (6) по x, найдем cosalpha+y'sinalpha=0, откуда y'=-operatorname{ctg}alpha, следовательно,

sinalpha=frac{1}{sqrt{1+(y')^2}}, quad cosalpha=-frac{1}{sqrt{1+(y')^2}}.

Подставив sinalpha и cosalpha в (6), получим

-frac{xy'}{sqrt{1+(y')^2}}+frac{y}{sqrt{1+(y')^2}}-1=0, или y=xy'+sqrt{1+(y')^2},.

2°. Задачи на траектории

Пусть дано семейство плоских кривых, зависящее от одного параметра alpha,

Phi(x,y,a)=0,

(7)

Кривая, образующая в каждой своей точке постоянный угол alpha с проходящей через эту точку кривой семейства (7), называется изогональной траекторией этого семейства; если, в частности, alphapislash2, то — ортогональной траекторией.

Считая семейство (7) заданным, будем разыскивать его изогональные траектории.

А. Ортогональные траектории. Составляем дифференциальное уравнение данного семейства кривых (см. п. 1). Пусть оно имеет вид

F(x,y,y')=0.

Дифференциальное уравнение ортогональных траекторий имеет вид

F!left(x,y,-frac{1}{y'}right)=0.

Общий интеграл этого уравнения Phi_1(x,y,C)=0 дает семейство ортогональных траекторий.

Пусть семейство плоских кривых задано уравнением в полярных координатах

Phi(rho,varphi,a)=0,

(8)

где a — параметр. Исключая параметр a из (8) и frac{partialPhi}{partialvarphi}=0, получаем дифференциальное уравнение семейства (8): F(rho,varphi,rho')=0. Заменяя в нем rho' на -frac{rho^2}{rho'},

получаем дифференциальное уравнение семейства ортогональных траекторий

F!left(rho,varphi,-frac{rho^2}{rho'}right)=0.

Б. Изогональные траектории. Пусть траектории пересекают кривые данного семейства под углом alpha, причем operatorname{tg}alpha=k. Можно показать, что дифференциальное уравнение изогональных траекторий имеет вид

F!left(x,y,frac{y'-k}{1+ky'}right)=0.

Пример 4. Найти ортогональные траектории семейства линий y=kx.

Решение. Семейство линий y=kx состоит из прямых, проходящих через начало координат. Для нахождения дифференциального уравнения данного семейства дифференцируем по x обе части уравнения y=kx. Имеем y'=k. Исключая параметр k из системы уравнений begin{cases}y=kx,\y'=k,end{cases} будем иметь дифференциальное уравнение семейства xy'=y. Заменяя в нем y' на -frac{1}{y'}, получаем дифференциальное уравнение ортогональных траекторий -frac{x}{y'}=y, или yy'+x=0. Полученное уравнение является уравнением с разделяющимися переменными; интегрируя его, найдем уравнение ортогональных траекторий x^2+y^2=C (Cgeqslant0). Ортогональными траекториями являются окружности с центром в начале координат (рис. 15).

Ортогональные траектории семейства прямыхОртогональные траектории семейства окружностей

Пример 5. Найти уравнение семейства линий, ортогональных к семейству x^2+y^2=2ax.

Решение. Данное семейство линий представляет собой семейство окружностей, центры которых находятся на оси Ox и которые касаются оси Oy.

Дифференцируя по x обе части уравнения данного семейства, найдем x+yy'=a. Исключая параметр a из уравнений x^2+y^2=2ax, x+yy'=a, получаем дифференциальное уравнение данного семейства x^2-y^2+2xyy'=0. Дифференциальное уравнение ортогональных траекторий есть

x^2-y^2+2xy!left(-frac{1}{y'}right)=0, или y'=frac{2xy}{x^2-y^2},.

Это уравнение является однородным. Интегрируя его, найдем x^2+y^2=Cy. Интегральные кривые являются окружностями, центры которых расположены на оси Oy и которые касаются оси Ox (рис. 16).

Ортогональные траектории семейства парабол

Пример 6. Найти ортогональные траектории семейства парабол y=ax^2.

Решение. Составляем дифференциальное уравнение семейства парабол. Для этого дифференцируем обе части данного уравнения по xcolon y'=2ax. Исключая параметр a, найдем frac{y'}{y}=frac{2}{x}, или y'=frac{2y}{x} дифференциальное уравнение данного семейства. Заменяя в уравнении y' на -frac{1}{y'}, получим дифференциальное уравнение ортогональных траекторий

-frac{1}{y'}=frac{2y}{x}, или frac{dx}{dy}=-frac{x}{2y},.

Интегрируя, найдем y^2=-frac{x^2}{2}+C или frac{x^2}{2}+y^2=C>0. Ортогональным семейством является семейство эллипсов (рис. 17).

Пример 7. Найти ортогональные траектории семейства лемнискат rho^2=acos2varphi.

Решение. Имеем rho^2=acos2varphi~Rightarrow~rhorho'=-asin2varphi. Исключая параметр a, получим дифференциальное уравнение данного семейства кривых rho'=-rhooperatorname{tg}2varphi,. Заменяя rho' на -frac{rho^2}{rho'}, найдем дифференциальное уравнение семейства ортогональных траекторий -frac{rho^2}{rho'}=-rhooperatorname{tg}2varphi,, откуда frac{drho}{rho}=operatorname{ctg}2varphi,dvarphi. Интегрируя, находим уравнение ортогональных траекторий

rho^2=Csin2varphi,.

Ортогональными траекториями семейства лемнискат являются лемнискаты, ось симметрии которых образуют с полярной осью угол pm45^{circ} (рис. 18).

Ортогональные траектории семейства лемнискат

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Составление дифференциального уравнения семейства кривых

Составление уравнений семейства кривых

Чтобы построить дифференциальное уравнение, которому удовлетворяют кривые семейства:

φ (1)

необходимо продифференцировать равенство (1) n раз, считая y функцией от x, а затем из полученных уравнений и уравнения (1) исключить произвольные постоянные C1 … Cn.

Линии, пересекающие все кривые данного семейства под одним и тем же углом ϕ, называются изогональными траекториями . Углы β и α наклона траектории и кривой к оси Ox связаны соотношением β = α ± φ.

— дифференциальное уравнение данного семейства кривых, а

— уравнение семейства изогональных траекторий.

Тогда tg α = f (x,y), tg β = f1 (x,y).

Отсюда следует, что если дифференциальное уравнение семейства кривых написано и угол φ известен, то найти tg β не составит труда, а после также легко можно будет написать уравнение траекторий.

Частный случай:

Если уравнение семейства кривых записано в виде:

,

то при составлении уравнения траекторий можно обойтись без решения уравнения относительно y’, в этом случае будет достаточно y’ заменить на tg α = tg (β ± φ), где tg β = y’ — угловой коэффициент касательной к траектории.

Пример №1

Составить дифференциальное уравнение семейства кривых:

  • Так как уравнение содержит два параметра (С1 и С2), то и дифференцировать будем два раза:

Первая производная:

Вторая производная:

  • Дальше, чтобы составить дифференциальное уравнение семейства кривых необходимо избавиться от С1 , а для этого выведем его из уравнения первой производной С1 = -2(y — С2)y’ и подставим в наше уравнение:

(2)

  • Теперь также нужно избавиться от параметра C2, а для этого выведем ее из второй производной: y — C2 = -y’ 2 / y» и подставим это в (2):

  • Ну и наконец упростим полученное уравнение и получим:

Пример №2

Для закрепления составим еще одно уравнение:

Решение абсолютно идентично предыдущему, за исключением того, что вместо параметров С1 и С2 здесь представлены параметры a, b и с. Ну и, конечно, раз параметров три, то нам понадобятся производные первого, второго и третьего порядка.

Делать описание каждого шага я уже не буду, думаю вы уже сами разберетесь:

Первая производная:

Вторая производная:

Третья производная:

Ответ:

Ну, думаю, если вы разобрались в первыми двумя примерами, то все остальные вы решите без труда, а чтобы это проверить дам вам парочку заданий «на дом».

Пример №3

Выразим коэффициенты a и b через 1-ую и 2-ую производные:

Первая производная: , где

Вторая производная: , где

Подставим значение b второй производной в значение a первой производной:

А теперь подставим полученные значения a и b в исходное уравнение и упростим:

⇒

Ответ:

Пример №4

Ну а здесь все еще проще:

Возведем обе части уравнения в квадрат:

Чтобы воспользоваться основным тригонометрическим тождеством, вычтем из единицы обе части уравнения:

Ну и теперь как мы видим во второй части получилось исходное уравнение, только в квадрате, а значит оно будет равно:

Приведем к общему виду и запишем ответ:

Ответ:

Ну и на этой ноте мы с вами закончим данный урок, всем спасибо!

Если вам что-то непонятно (или нашли неточности в уроке) пишите в комментариях и мы вам обязательно ответим в ближайшее время.

Составление дифференциальных уравнений семейств линий

Пусть дано уравнение однопараметрического семейства плоских кривых

Дифференцируя (1) по , найдем

Исключая параметр из (1) и (2), получаем дифференциальное уравнение

выражающее свойство, общее всем кривым семейства (1). Уравнение (3) будет искомым дифференциальным уравнением семейства (1).

Если однопараметрическое семейство кривых определяется уравнением

то дифференциальное уравнение этого семейства получим, исключая параметр из уравнений

Пусть теперь имеем соотношение

где — параметры. Дифференцируя (4) раз по и исключая параметры из (4) и полученных уравнений, приходим к соотношению вида

Это дифференциальное уравнение заданного n-параметрического семейства линий (4) в том смысле, что (4) есть общий интеграл уравнения (5).

Пример 1. Найти дифференциальное уравнение семейства гипербол .

Решение. Дифференцируя это уравнение по , получаем

Умножим обе части на , тогда . Подставляя в уравнение семейства найдем .

Пример 2. Найти дифференциальное уравнение семейства линий , где — параметр.

Решение. Дифференцируем обе части уравнения по :

Из выражения для находим
и, подставляя это выражение для в уравнение семейства линий, получим

Пример 3. Составить дифференциальное уравнение семейства прямых, отстоящих от начала координат на расстояние, равное единице.

Решение. Будем исходить из нормального уравнения прямой

Дифференцируя (6) по , найдем , откуда , следовательно,

Подставив и в (6), получим

2°. Задачи на траектории

Пусть дано семейство плоских кривых, зависящее от одного параметра ,

Кривая, образующая в каждой своей точке постоянный угол с проходящей через эту точку кривой семейства (7), называется изогональной траекторией этого семейства; если, в частности, , то — ортогональной траекторией .

Считая семейство (7) заданным, будем разыскивать его изогональные траектории.

А. Ортогональные траектории . Составляем дифференциальное уравнение данного семейства кривых (см. п. 1). Пусть оно имеет вид

Дифференциальное уравнение ортогональных траекторий имеет вид

Общий интеграл этого уравнения дает семейство ортогональных траекторий.

Пусть семейство плоских кривых задано уравнением в полярных координатах

получаем дифференциальное уравнение семейства ортогональных траекторий

Б. Изогональные траектории . Пусть траектории пересекают кривые данного семейства под углом , причем . Можно показать, что дифференциальное уравнение изогональных траекторий имеет вид

Пример 4. Найти ортогональные траектории семейства линий .

Решение. Семейство линий состоит из прямых, проходящих через начало координат. Для нахождения дифференциального уравнения данного семейства дифференцируем по обе части уравнения . Имеем . Исключая параметр из системы уравнений будем иметь дифференциальное уравнение семейства . Заменяя в нем на , получаем дифференциальное уравнение ортогональных траекторий , или . Полученное уравнение является уравнением с разделяющимися переменными; интегрируя его, найдем уравнение ортогональных траекторий . Ортогональными траекториями являются окружности с центром в начале координат (рис. 15).

Пример 5. Найти уравнение семейства линий, ортогональных к семейству .

Решение. Данное семейство линий представляет собой семейство окружностей, центры которых находятся на оси и которые касаются оси .

Дифференцируя по обе части уравнения данного семейства, найдем . Исключая параметр из уравнений получаем дифференциальное уравнение данного семейства . Дифференциальное уравнение ортогональных траекторий есть

Это уравнение является однородным. Интегрируя его, найдем . Интегральные кривые являются окружностями, центры которых расположены на оси и которые касаются оси (рис. 16).

Пример 6. Найти ортогональные траектории семейства парабол .

Решение. Составляем дифференциальное уравнение семейства парабол. Для этого дифференцируем обе части данного уравнения по . Исключая параметр , найдем , или дифференциальное уравнение данного семейства. Заменяя в уравнении на , получим дифференциальное уравнение ортогональных траекторий

Интегрируя, найдем или 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAJUAAAAuBAMAAADTgUbKAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAD3RSTlMAmsOBAetBIBAxYUJRcbGvhmSvAAACYklEQVRIx2NgGOTgoNIEahnFrsEYQC2z2L6xfaOaHxN4vlMvwJgEqGfWReoZxSXQQZU4nMAxgWEygyUVjOJQVFz3kD3+/wcqmOU3IV8l3iMtLYEKZiUy5K/Qolq42xdQzSgWVQfcgWlMkte5OT4ylOGS7KsJJsUs+TN/GaxxSV4tsCfFLKEiZV+c+Wdew3osgeKC0xuSjfiiUQgzDBfFa3MtQBXzTiEmNMMxhI7qODTJo5acPIGi2OOIC5lT1IAuzfgXmO2+okZ96QGucOylD5I6DglmdMPuGwBDTA/I4BSHB6A8A8tHgmY1CZuie/oriNQFEUlww4IccCRSqFnsjyYwnFmkpIgm6/QLREJM2acNUcryyYFFH59ZfUUKLIGwYikNDEABPv8HktJCiGGcILMa8Jh1y/UB51+oEKcxGBwABZcCklKXwiiQYrZPDAz6GxgYFgrCAcjhXMbGpkBdQEtWnF/A+xNLQQBK1xxwbrEOKAwJmcUg38AUgsUsA5DT4SVLM8gsDkLhxRDE4P8Aix9B7poIDzAtkGIWQvHI8pkh/wIs7HeDASjs64H1O4c6zCgd4tIXMBLfY2lj8H50YJgEFd8ITRMM+xNwVPswPy4VCsXm7qWBRlBnJUnDs13s1QXw0tMci1ke2wOxFsN7j0MDURwhWLUcxpq0Vn8BRt4uVWAmp4kRydCKmZLyDfYvIKPi/t/A/BlDlFHpGTk1d2gD8ydMYReyajUXBsbP1GvmtEZQzyxRqrV8GbgiqeesqRM4qWUUpwYi51PsrGNpwlQyikP///8/1PKikpKSJuXGAACuZpWkdXHGfwAAAABJRU5ErkJggg==” style=”vertical-align: middle;” />. Ортогональным семейством является семейство эллипсов (рис. 17).

Пример 7. Найти ортогональные траектории семейства лемнискат .

Решение. Имеем . Исключая параметр , получим дифференциальное уравнение данного семейства кривых Заменяя на , найдем дифференциальное уравнение семейства ортогональных траекторий откуда . Интегрируя, находим уравнение ортогональных траекторий

Ортогональными траекториями семейства лемнискат являются лемнискаты, ось симметрии которых образуют с полярной осью угол (рис. 18).

Примеры решений задач по дифференциальным уравнениям

Теперь, когда вы научились находить производные и интегралы, самое время перейти к более сложной теме: решению дифференциальных уравнений (они же дифуры, диффуры и диф.уры :)), то есть уравнений, которые вместе с самой функцией (и/или аргументом), содержат и производную или даже несколько.

Как же решать дифференциальные уравнения? Главное, что понадобится, это а) умение правильно определить тип дифференциального уравнения и б) умение хорошо интегрировать – это существенная часть работы. А дальше следовать алгоримам для каждого из типов уравнений, которые подробно описаны в учебниках и ниже в примерах.

В этом разделе вы найдете решенные задачи на составление и решение дифференциальных уравнений. Примеры решений дифуров выложены бесплатно для вашего удобства и отсортированы по темам – изучайте, ищите похожие, решайте свои. Есть трудности в выполнении заданий? Мы готовы оказать помощь по дифференциальным уравнениям

Как решить дифференциальное уравнение онлайн?

Да ладно, неужели только вручную? Мучиться, определять тип, переносить, интегрировать, заменять, снова интегрировать, подставлять, выводить? Наверняка ведь есть онлайн-калькуляторы, которые позволяют решать дифференциальные уравнения?

У меня две новости, хорошая и плохая. Хорошая в том, что действительно самые распространенные типы дифференциальных уравнений математические программы умеют решать. Плохая в том, что обычно они выводят ответ (для научных расчетов этого достаточно), а не полное решение.

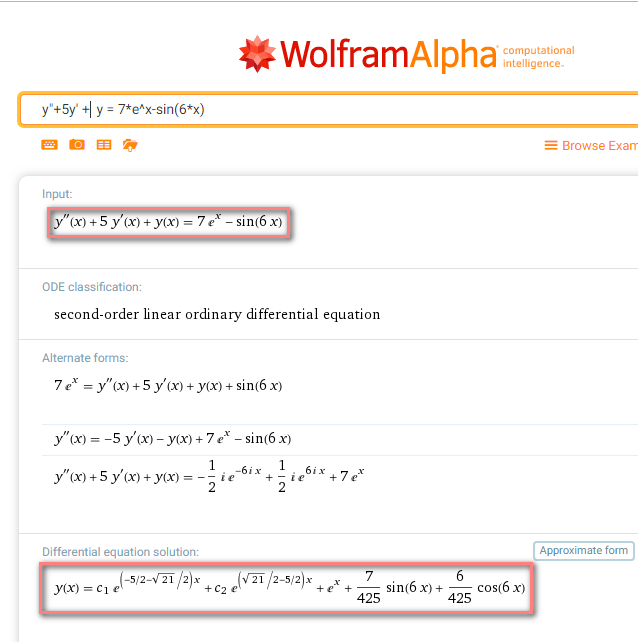
Есть известный математический сервис www.wolframalpha.com, которые представляет полные решения множества математических задач, в том числе диффуров онлайн (на английском языке) за 7 долларов в месяц. Ответы же доступны всем и могут помочь проверять правильность своего решения (см. ниже на скриншоте обведено само уравнение и его решение). Подробнее об этом сайте и типичных задачах, решаемых на нем, вы можете узнать тут.

Если вы забьете в поисковик что-то вроде “решить дифференциальное уравнение онлайн”, то получите десятки ссылок на сайты, обещающие именно это.

Я проверила все сайты с первых страниц Яндекса и Гугла. Большая часть сайтов использует результаты расчетов www.wolframalpha.com (см. выше) и показывает вам ответ (и рекламу :)). Некоторые при этом не показывают даже ответа или говорят, что уравнение введено некорректно (хотя это вполне стандартное решаемое вручную линейное уравнение с постоянными коэффициентами). Полное решение не выдал ни один сайт.

Выводы? Бесплатно и полно и онлайн – не бывает. Хотите получать полные решения – используйте платную подписку на ВольфрамАльфа (или проконсультируйтесь у нас). Хотите ответы – там же бесплатно. Хотите научиться решать? Придется засучить рукава. Примеры на этой странице и ссылки внизу помогут вам. Удачи!

Общий интеграл, семейство кривых

Задача 1. Показать, что функция $y^2-x^2-Cy=0$ является общим интегралом дифференциального уравнения $y'(x^2+y^2)-2xy=0.$

Задача 2. Составить дифференциальное уравнение семейства кривых $C_1 x+(y-C_2)^2=0.$

Решения дифференциальных уравнений 1 порядка

Задача 3. Найти общее решение линейного дифференциального уравнения первого порядка $ xy’+x^2+xy-y=0.$

Задача 4. Решить однородное дифференциальное уравнение $y’=-y/x quad (x ne 0).$

Задача 5. Решить дифференциальное уравнение $(y^4-2x^3y)dx+(x^4-2xy^3)dy=0.$

Задача 6. Решить однородное дифференциальное уравнение $(2x+y+1)dx+(x+2y-1)dy=0.$

Задача 7. Решить линейное дифференциальное уравнение первого порядка $y’-2xy=3x^2-2x^4.$

Задача 8. Решить дифференциальное уравнение $(x+y^2)y’=y-1.$

Решение задачи Коши для ДУ

Задача 9. Решить дифференциальное уравнение с разделяющимися переменными $(1+x^2)dy-2xydx=0.$ Найти частное решение, удовлетворяющее начальному условию $y(0)=1$.

Задача 10. Решить задачу Коши для дифференциального уравнения второго порядка $2y y” +1 =(y’)^2, , y(1/3)=1, , y'(1/3)=2$.

Задача 11. Найти решение задачи Коши для дифференциального уравнения $$ y’= frac<2y-x><2x+y>, y(1)=1. $$

Задача 12. Решить задачу Коши для дифференциального уравнения третьего порядка $$ y”’=x+cos x, quad y(0)=0, y'(0)=0, y”(0)=0. $$

Решения дифференциальных уравнений 2 порядка

Задача 13. Решить дифференциальное уравнение второго порядка с постоянными коэффициентами $y”+4y’+4y=xe^<2x>.$

Задача 14. Решить задачу Коши для дифференциального уравнения второго порядка с постоянными коэффициентами методом вариации: $$ y”-3y’=frac<9e^<-3x>><3+e^<-3x>>, quad y(0)=4ln 4, y'(0)=3(3ln 4-1). $$

Cоставление дифференциальных уравнений

Задача 15. Скорость остывания нагретого тела пропорциональна разности температур тела и окружающей среды. За 10 минут тело охладилось от 100 до 60 градусов. Температура среды постоянна и равна 20 градусам. Когда тело остынет до 25 градусов?

Задача 16. Моторная лодка движется в спокойной воде со скоростью 5 м/сек. На полном ходу ее мотор выключается и через 40 сек после этого скорость лодки уменьшается до 2 м/сек. Определить скорость лодки через 2 минуты после остановки мотора, считая, что сопротивление воды пропорционально скорости движения лодки.

Решения нелинейных дифференциальных уравнений

Задача 17. Решить дифференциальное уравнение $y^2 ^2 -2xyy’+2y^2-x^2=0.$

Задача 18. Решить дифференциальное уравнение $^2-4xyy’+8y^2=0.$

[spoiler title=”источники:”]

http://mathhelpplanet.com/static.php?p=sostavlenie-differentsialnyh-uravnenii-semyeistv-linii-i-zadachi-na-traektorii

http://www.matburo.ru/ex_ma.php?p1=madiff

[/spoiler]

Источник

Составление уравнений семейства кривых

Чтобы построить дифференциальное уравнение, которому удовлетворяют кривые семейства:

φ          (1)

необходимо продифференцировать равенство (1) n раз, считая y функцией от x, а затем из полученных уравнений и уравнения (1) исключить произвольные постоянные C1 … Cn.

Изогональные траектории

Линии, пересекающие все кривые данного семейства под одним и тем же углом ϕ, называются изогональными траекториями. Углы β и α наклона траектории и кривой к оси Ox связаны соотношением β = α ± φ.

Пусть

— дифференциальное уравнение данного семейства кривых, а

— уравнение семейства изогональных траекторий.

Тогда tg α = f (x,y), tg β = f1 (x,y).

Отсюда следует, что если дифференциальное уравнение семейства кривых написано и угол φ известен, то найти tg β не составит труда, а после также легко можно будет написать уравнение траекторий.

Частный случай:

Если уравнение семейства кривых записано в виде:

,

то при составлении уравнения траекторий можно обойтись без решения уравнения относительно y’, в этом случае будет достаточно y’ заменить на tg α = tg (β ± φ), где tg β = y’ — угловой коэффициент касательной к траектории.

Пример №1

Составить дифференциальное уравнение семейства кривых:

  • Так как уравнение содержит два параметра (С1 и С2), то и дифференцировать будем два раза:

Первая производная:

Вторая производная:

  • Дальше, чтобы составить дифференциальное уравнение семейства кривых необходимо избавиться от С1 , а для этого выведем его из уравнения первой производной С1 = -2(y — С2)y’ и подставим в наше уравнение:

      (2)

  • Теперь также нужно избавиться от параметра C2, а для этого выведем ее из второй производной: y — C2 = -y’2 / y» и подставим это в (2):

  • Ну и наконец упростим полученное уравнение и получим:

Пример №2

Для закрепления составим еще одно уравнение:

Решение абсолютно идентично предыдущему, за исключением того, что вместо параметров С1 и С2 здесь представлены параметры a, b и с. Ну и, конечно, раз параметров три, то нам понадобятся производные первого, второго и третьего порядка.

Делать описание каждого шага я уже не буду,  думаю вы уже сами разберетесь:

Первая производная:

Вторая производная:

Третья производная:

Ответ:

Ну, думаю, если вы разобрались в первыми двумя примерами, то все остальные вы решите без труда, а чтобы это проверить дам вам парочку заданий «на дом».

Пример №3 

Выразим коэффициенты a и b через 1-ую и 2-ую производные:

Первая производная: , где

Вторая производная: , где

Подставим значение b второй производной в значение a первой производной:

А теперь подставим полученные значения a и b в исходное уравнение и упростим:

⇒ 

Ответ: 

Пример №4

Ну а здесь все еще проще:

Найдем производную:

Возведем обе части уравнения в квадрат:

Чтобы воспользоваться основным тригонометрическим тождеством, вычтем из единицы обе части уравнения:

Ну и теперь как мы видим во второй части получилось исходное уравнение, только в квадрате, а значит оно будет равно:

И, следовательно,

Приведем к общему виду и запишем ответ:

Ответ: 

Ну и на этой ноте мы с вами закончим данный урок, всем спасибо!

Если вам что-то непонятно (или нашли неточности в уроке) пишите в комментариях и мы вам обязательно ответим в ближайшее время.

Уроки по теории вероятности

Первая тема, которую я бы хотел рассмотреть на уроках элементарной алгебры — это выражения. Числовые выражения Числовые выражения — это выражения, состоящие только из цифр и знаков арифметических действий. Число, которое получается в результате выполнения действий в числовом выражении, называют значением выражения. Пример №1 Найти значение выражения: 12 * 6 — 16 : 4 Значение

Курс данного предмета мы начнем непосредственно с матриц, потому что именно они составляют основу данной дисциплины. Определение матрицы Матрицей  размерности называется прямоугольная таблица чисел, содержащая — строк и — столбцов, число расположенное в -ой строке и -столбце обозначается и называется элементом матрицы , т. е. Операции над матрицами Рассмотрим основные операции, проводимые над матрицами: сумма матриц;

Данная статья занесена в архив так как написана новая, возможно более понятная статья, переходите по ссылке на нее http://mathcentr.ru/matritsa-i-operatsii-nad-nej/ Как вы, наверное, уже поняли матрицы ничем не отличаются от обычных чисел, по правде говоря — это просто много цифр в одном числе))) И разумеется, существуют такие же операции над матрицами, как и над числами, но не все и

Продолжаем изучать матрицы и сегодня на уроке мы научимся находить и вычислять обратную матрицу. Обратная матрица Матрица называется транспонированной к матрице , если выполняется условие: , для всех , где и — элементы матриц и соответственно. Проще говоря, транспонированная матрица — это перевернутая матрица, т.е. столбцы записаны строками, а строки столбцами. Пример №1 Транспонировать матрицу

Мы рассмотрели самые основные тригонометрические функции (не обольщайтесь помимо синуса, косинуса, тангенса и котангенса существует еще целое множество других функций, но о них позже), а пока рассмотрим некоторые основные свойства уже изученных функций. Тригонометрические функции числового аргумента Какое бы действительное число ни взять, ему можно поставить в соответствие однозначно определенное число . Правда, правило соответствия

Источник

1.1. Дифференциальные уравнения семейства кривых

Пусть задано
семейство кривых:
,
где– параметр. Необходимо составить
дифференциальное уравнение, решением
которого является это семейство.

Общая схема решения
этой задачи:

1) Равенство
определяет неявную функцию.
Тогда на некотором промежутке справедливо
тождество:.
Дифференцируя это тождество по переменной,
получим:===0.

2) Запишем систему
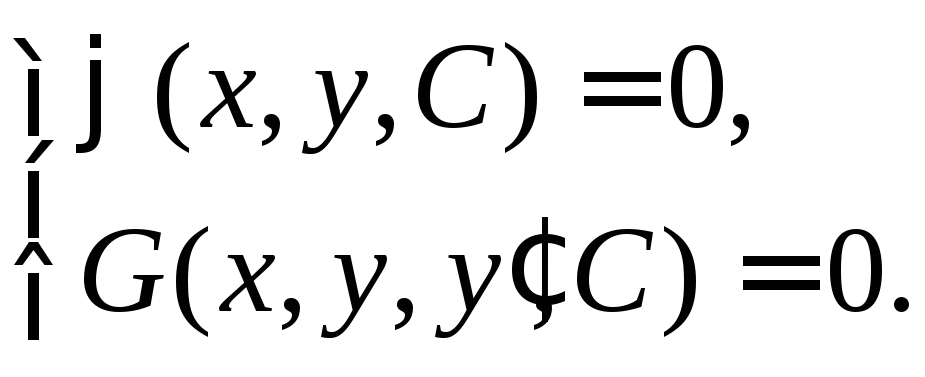
Исключив параметриз этой системы, получим дифференциальное
уравнение, решением которого является
семейство кривых:.

Пример 1.1.Имеем
семейство кривых:.
Необходимо построить дифференциальное
уравнение, для которого данное семейство
кривых является решением.

Решение: 1)
Считая, что выражение
определяет неявную функцию,продифференцируем это выражение по
независимой переменной.
Имеем.

2) Запишем систему
Для исключения из системы параметраумножим первое уравнение наи
приравняем левые части первого и второго
равенств. Получим дифференциальное
уравнение,
или,
решением которого является заданное
семейство кривых.

Ответ..

Задание 1.1.
Составить дифференциальное уравнение
для семейства кривых.

Вар.

Семейство:

Вар.

Семейство:

1.1.1.

.

1.1.16.

.

1.1.2.

.

1.1.17.

.

1.1.3.

.

1.1.18.

.

1.1.4.

.

1.1.19.

.

1.1.5.

.

1.1.20.

.

1.1.6.

.

1.1.21.

.

1.1.7.

.

1.1.22.

.

1.1.8.

.

1.1.23.

.

1.1.9.

.

1.1.24.

.

1.1.10.

.

1.1.25.

.

1.1.11.

=.

1.1.26.

.

1.1.12.

.

1.1.27.

.

1.1.13.

.

1.1.28.

.

1.1.14.

.

1.1.29.

.

1.1.15.

.

1.1.30.

.

1.2. Дифференциальные уравнения с разделяющимися переменными

Известно, что в
общем случае дифференциальное уравнение
с разделяющимися переменными может
быть представлено в виде:

.
(1.1)

Для интегрирования
уравнения переменные
идолжны быть разделены. Для этого требуется
разделить равенство (1.1) на произведение.
В результате получим:

. (1.2)

Интегрируя (1.2),
находим общее решение исходного уравнения
(1.1) в виде выражения: .

Для перехода к
записи (1.2) выполнялось деление на
функции:
и.
Если возможны равенстваи,
необходимо функциииучесть как решения исходного уравнения.

Пример 1.2.Решить дифференциальное уравнение.

Решение.1)
Заданное уравнение есть уравнение с
разделяющимися переменными, гдеи.
Так каки,
то функцииинеобходимо учесть как решения исходного
уравнения.

2)
Теперь считаем, что
.
Разделив заданное уравнение на
,
получим уравнение
с разделенными переменными.

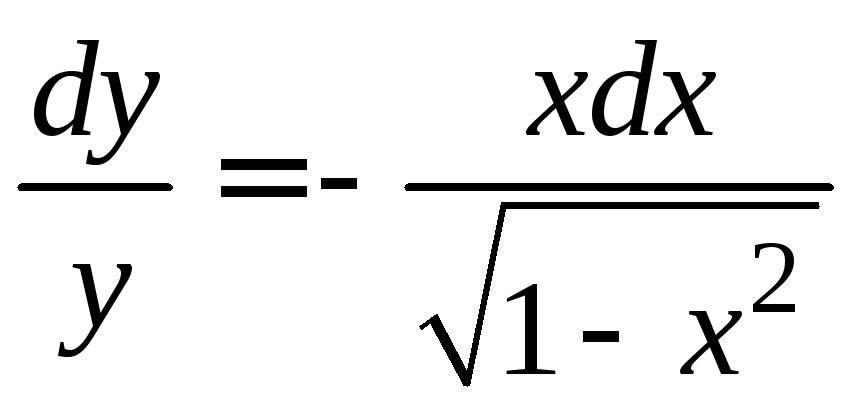
3) В
результате
интегрирования находим общее решение
уравнения в виде

или
.
Учитывая, что

− произвольная постоянная величина,
запишем общее решение в виде
.
При
=0
из общего решения получаем также решение

.

Ответ.;.

Задание 1.2. Решить
уравнение с разделяющимися переменными.

Вар.

Уравнение:

Вар.

Уравнение:

1.2.1.

1.2.16.

1.2.2.

1.2.17.

1.2.3.

1.2.18.

1.2.4.

1.2.19.

1.2.5.

1.2.20.

1.2.6.

1.2.21.

1.2.7.

1.2.22.

1.2.8.

1.2.23.

1.2.9.

1.2.24.

1.2.10.

1.2.25.

1.2.11.

1.2.26.

1.2.12.

1.2.27.

1.2.13.

1.2.28.

1.2.14.

1.2.29.

1.2.15.

1.2.30.

Соседние файлы в папке БДЗ по ДУ

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Составить дифференциальное уравнение семейства линий (ln y=ax+by).

Решение
Уравнение имеет два параметра, продифференцируем его дважды:
[frac{1}{y}y’=a+by’]
[-frac{1}{y^2}y’^2+frac{y”}{y}=by”]
Выразим (b) из второго уравнения:
[b=frac{y”y-y’^2}{y^2y”}]
Подставим (b) в первое уравнение и выразим (a):
[frac{1}{y}y’=a+by’]
[frac{1}{y}y’=a+frac{y”y-y’^2}{y^2y”}y’]
[a=frac{y’}{y}-frac{y”y-y’^2}{y^2y”}y’]
[a=frac{y’y”y-y”yy’+y’^3}{y^2y”}=frac{y’^3}{y^2y”}]
Подставим (a) и (b) в исходное уравнение (ln y=ax+by):
[ln y=frac{y’^3}{y^2y”}x+frac{y”y-y’^2}{y^2y”}y]
[y^2y”ln y =xy’^3+(y”y-y’^2)y]
[y^2y”ln y =xy’^3+y”y^2-y’^2y]
[y^2y”(ln y-1) =y’^2(xy’-y)]
Таким образом, дифференциальное уравнение семейства линий имеет вид:
[y^2y”(ln y-1) =y’^2(xy’-y).]

Источник

Добавить комментарий