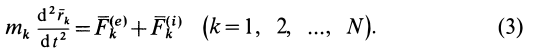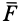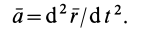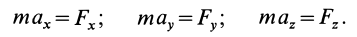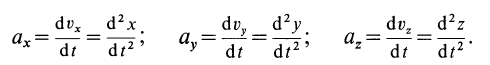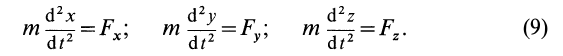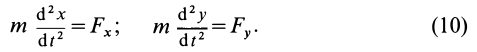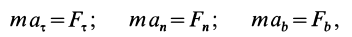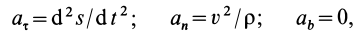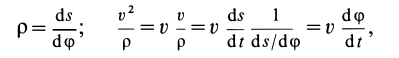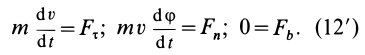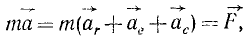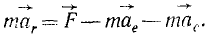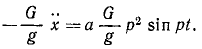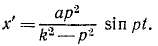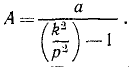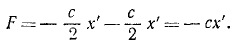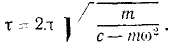Механической
системой называется совокупность
материальных точек или тел, положение
и движение которых зависят от положения
и движения всех остальных точек.
Механическая
система может быть образована из
свободных точек, движение которых не
ограничено какими-либо геометрическими
связями. Примером механической системы
из точек с геометрическими связями
служит любой механизм.
силы, действующие
на точки несвободной механической
системы, можно подразделить на активные
силы
и реакции связей
.
с другой стороны, действующие на точки
системы силы можно подразделить на
внешниеи на внутренние
.
Внутренними силами взаимодействуют
между собой точки данной системы.
Внешними силами действуют на точки
системы точки или тела, не входящие в
данную систему. Главный вектори главный момент
всех внутренних сил системы относительно
любого центра равны нулю:
;
(7.1)
.
(7.2)
Для n
точек механической системы можно
записать n
дифференциальных уравнений движения
в векторной форме типа
(7.3) или 3n
дифференциальных уравнения движения
в проекциях на координатные оси вида:
;
;
.
(7.4)
Чтобы найти
уравнение движения механической системы
под действием заданных сил, необходимо
проинтегрировать при известных начальных
условиях систему дифференциальных
уравнений второго порядка, что сопряжено
с большими трудностями.
Дифференциальные
уравнения движения механической системы
можно использовать для вывода общих
теорем динамики, с помощью которых можно
решать задачи о движении материальной
точки или механической системы, установить
зависимость между основными динамическими
характеристиками механического движения
материальных тел.
8. Теорема о движении центра масс.
Центром масс или
центром инерции системы является
геометрическая точка, положение которой
определяется в каждый момент времени:
,
,
,
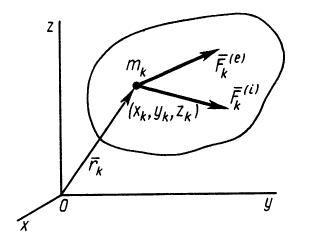
(8.1) где М – масса системы,
равная сумме масс всех точек системы;
mk—
масса произвольной точки Mk;
xk,
yk,
zk
– координаты
произвольной точки Mk
системы.
В однородном поле
земного тяготения центр масс совпадает
с центром тяжести.
Центр масс существует
для любой механической системы независимо
от действующих сил.
Центр масс системы
движется как материальная точка, масса
которой равна массе всей системы и к
которой приложен все внешние силы,
действующие на систему (теорема о
движении центра масс).
,
(8.2) где М—масса
системы;
ac—ускорение
центра масс;
—
главный вектор всех внешних сил системы.
Теорема о движении
центра масс имеет два следствия, которые
определяют закон сохранения движения
центра масс.
Рисунок 18
1. Если главный вектор всех
внешних сил, действующих на систему,
равен нулю, то центр масс системы будет
находиться в покое или двигаться
равномерно и прямолинейно.
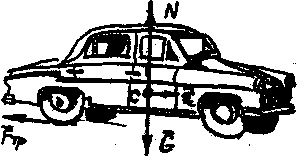
В автомобиле (рис.
18) действие газов на поршень двигателя
является внутренней силой. Внешние силы
– это сила тяжести автомобиля
,
нормальна реакция дороги,
сила трениямежду колесами автомобиля и дороги. При
отсутствии сцепления колес с дорогой
(=0)
действие внутренних сил не может изменить
закона движения центра масс. Если,
,
то поэтому.
При начальной скорости центра масс,
центр масс будет оставаться в покое.
2. Если сумма
проекций всех внешних сил, действующих
на систему, на какую-либо ось равна нулю,
то проекция скорости центра масс на
данную ось будет оставаться постоянной.
Если
,
то,
поэтому.
Если в начальный момент времени,
то учитывая, что,
координата центра масс остается
постоянной (xc=const).
Для человека, стоящего на абсолютно
гладкой горизонтальной поверхности
(рис. 19), внешними силами является его
вес
и нормальная реакция
.
Сила трения на гладкой поверхности
отсутствует, т.е.,xc=const.На
гладкой поверхности человек может
подпрыгнуть в вертикальном направлении,
так как в проекции на ось у теорема о
движении масс
п
>0, т.е. центр масс может переместиться
по вертикали. Перемещение по горизонтали
будет возможно при действии силы трения
скольжения (рис. 19,б). Применяя теорему
о движении центра масс, можно решать
прямую и обратную задачи динамики
поступательного движения в следующей
последовательности:
имеет вид
.
При отталкивании от земли за счет
деформации мышцR>P,
1. выбрать систему
координат;
2. изобразить все
внешние силы;
3. записать теорему
о движении центра масс в проекции на
ось координат;
4. определить
искомые величины в соответствии с
условиями задачи.
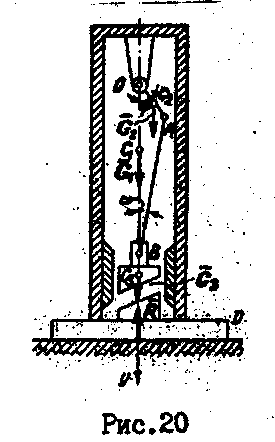
ПРИМЕР 10.
Определить действие
фундамента кривошипного пресса при
холостом ходе, если кривошип ОА=r
вращается с постоянной угловой скоростью
,
длина кривошипа АВ=,
вес фундамента и корпусаG1,
вес кривошипа
G2,
вес штампа В
G3.
В начальный момент кривошип занимал
вертикальное нижнее положение (рис.
20).
РЕШЕНИЕ.
1. На пресс действуют
внешние силы: сила тяжести корпуса с
фундаментом
,
кривошипа,
штампаи нормальная реакция грунта
.
Запишем теорему о движении центра масс
системы в проекции на ось у:
,
(1) где.
(2)
3. Выразим ординату
ус
центра масс
,
(3) гдеG=G1+G2+G3.
Угол поворота
кривошипа
.
y1=OC1=const;
y2=OC2cos=0,5rcos
;
y3=OAcos+ABcos
+BC3=2cos
+
cos
+BC3;
где
ВС3=const.
Из
ОАВ:
;
;
.
Если разложить
в ряд, отбросив члены ряда, содержащие
в степени выше второй, получим
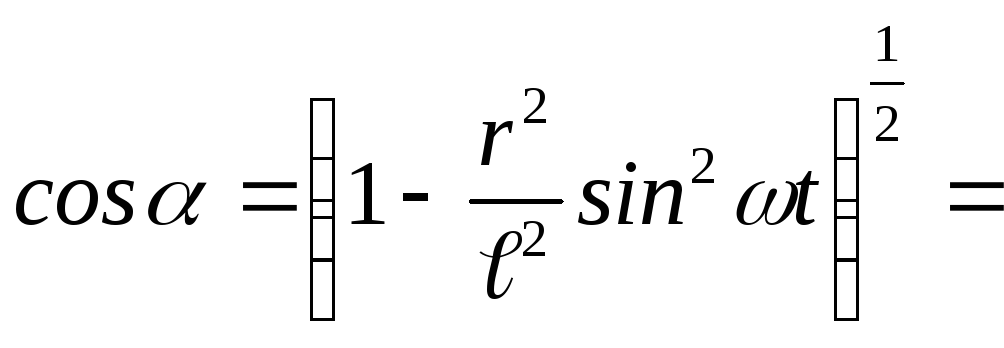
;
тогда;

(4)
Продифференцируем
(4) дважды по времени и подставим в (1)
;
(5)
;
отсюда находим нормальную реакцию
грунта, а следовательно, величину
давления на фундамент в зависимости от
угла поворота кривошипа
.
ПРИМЕР 11.
Механическая
система состоит из прямоугольной
вертикальной плиты 1 массой m1=18кг,
движущейся вдоль горизонтальных
направляющих, и груза D
массой m2=6кг.
В момент времени t0=0,
когда плита двигалась со скоростью
u0=2м/с,
груз начал двигаться вдоль желоба в
соответствии с уравнением S=AD=0,4sin(t2)
(S—в
метрах, t—в
секундах (рис. 21)). Определить скорость
плиты в момент времени t1=1с.
Р
1. Внешними силами,
действующими на систему, являются вес
пластины
,
вес грузаи нормальная реакция поверхности
.
2. Применим теорему
о движении центра масс в проекции на
ось х:
.
(1) Так как,
,
то.
(2)
3. Выразим произведение
,
где х1,
х2
– абсциссы плиты и груза.
.
Тогда.
(3) Продифференцируем (3) по времени,
(4) где— искомая скорость плиты.
При t=0
u1=u0;
.
Следовательно,
С1=(m1+m2)u0.
(5) С учетом (2), (4) и (5) получим
,
откуда находим скорость плиты.
При t1=1c
м/с.
Соседние файлы в предмете Теоретическая механика
- #
- #
- #
- #
Дифференциальное уравнение движения системы в теоретической механике
Дифференциальное уравнение движения системы:
Пусть даны внешние и внутренние силы, действующие на систему, состоящую из
Систему 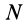
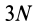
Задача интегрирования дифференциальных уравнений механической системы еще сложнее, если на механическую систему наложены связи, силы реакций которых заранее не известны и должны быть дополнительно определены по заданным силам и связям аналогично случаю движения несвободной материальной точки по поверхности и кривой линии.
В некоторых случаях из дифференциальных уравнений движения системы можно получить первые интегралы, т. е. соотношения, в которые не входят производные второго порядка от координат по времени.
Если известны первые интегралы, то задача интегрирования системы дифференциальных уравнений облегчается. Хотя отдельные первые интегралы и не могут полностью описать движения всех точек системы, однако они иногда характеризуют важные стороны движения системы в целом.
Первые интегралы системы дифференциальных уравнений удобно получать из так называемых общих теорем динамики, когда выполняются некоторые дополнительные условия для действующих сил. Кроме того, общие теоремы динамики, даже когда по ним нельзя определить первые интегралы, дают ценную информацию о движении точки или системы. В некоторых задачах, где не требуется полного знания движения системы, эти сведения могут оказаться достаточными.
Общие теоремы динамики являются следствиями системы дифференциальных уравнений движения точки или соответственно системы точек.
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Теоремы об изменении количества движения и о движении центра масс
- Теорема об изменении кинетического момента
- Теорема об изменении кинетической энергии
- Потенциальное силовое поле
- Движение несвободной материальной точки
- Относительное движение материальной точки
- Геометрия масс
- Свойства внутренних сил системы
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Составление дифференциального уравнения движения механической системы
Содержание
1. Составление дифференциального уравнения движения механической системы
2. Определение реакций внешних и внутренних связей
3. Определение закона движения системы
4. Результаты расчетов
5. Анализ результатов вычислений
6. Результаты анализа
Цели и задачи
Наличие упругих связей в механической системе в сочетании с внешним периодическим воздействием может привести к дополнительным колебательным движениям ее элементов. Поэтому теория колебаний и, в частности, раздел, посвященный малым линейным колебаниям, имеет много важных приложений в различных областях науки и техники.
Выделение линейных моделей в особый класс вызывается рядом причин:
• с помощью линейных моделей исследуется широкий круг явлений, происходящих в различных механических системах;
• интегрирование линейных дифференциальных уравнений с постоянными коэффициентами является, с математической точки зрения, элементарной задачей.
Поэтому инженер–исследователь стремится по возможности описать поведение системы с помощью линейной модели для облегчения процедуры анализа ее движения.
При проектировании механических систем обычно используют критические режимы внешних воздействий на них. В этом случае внешние факторы: – коэффициент демпфирования, – амплитуда и частота возмущающей силы, изменяются незначительно. Конструктивные параметры механических систем (их геометрические размеры) определяются условиями их функционирования и, следовательно, могут изменяться в очень узком диапазоне. Актуальной становится такая задача исследования механической системы, при которой могут изменяться массовые параметры системы и жесткость упругого элемента.
Поэтому целью курсовой работы является исследование и анализ динамического поведения механической системы с упругими связями с помощью основных теорем и принципов теоретической механики.
Для достижения этой цели, необходимо решить поставленные задачи:
1. составить дифференциальное уравнение движения системы;
2. сформировать систему уравнений для определения динамических реакций внешних и внутренних связей;
3. Найти закон движения системы, т. е. проинтегрировать дифференциальное уравнение движения при заданных начальных условиях;
4. провести численный анализ полученного решения с использованием ЭВМ.
Груз 1 один подвешен на нити к центру невесомого блока 2. Меньшая ступень блока 2 прикреплена нитью к горизонтальной поверхности, а нить, намотанная на большую ступень – навита на закрепленный в центре блок 3. Далее нить с блока 3 наматывается на меньшую ступень катка 4, который катится по шероховатой горизонтальной поверхности, касаясь ее большей ступенью. Центр катка связан с пружиной, другой конец которой закреплен неподвижно. Нити и пружина, которые являются невесомыми, параллельны соответствующим плоскостям. Нити являются нерастяжимыми и абсолютно гибкими. Сопротивление, возникающее в подшипниках блока, пропорционально первой степени угловой скорости блока: . Качение катка происходит без скольжения, сопротивление качению отсутствует. Центр масс блока расположен на оси его вращения. К грузу приложена возмущающая сила . При движении системы нити всегда натянуты. Схема механической системы представлена ниже:
Исследовать движение механической системы. Определить реакции внешних и внутренних связей, если
– массы груза, блока и катка,
c – коэффициент жесткости пружины,
– коэффициент демпфирования,
– радиусы ступеней невесомого блока 2,
– радиус блока 3,
– радиусы ступеней катка 4 и радиус инерции относительно оси, проходящей через центр масс,
– предельное значение коэффициента сцепления катка 4 и опорной плоскости,
– предельное значение удлинения пружины;
— начальная координата и начальная скорость груза.
Составление дифференциального уравнения движения механической системы
Рассматриваемая механическая система имеет одну степень свободы: это обеспечивается условиями, принятыми при формулировке задания, — тела являются абсолютно твердыми, нити — нерастяжимыми и всегда натянутыми, проскальзывание при движении катка отсутствует. Следовательно, для задания положения системы нужен один параметр. Будем определять положение системы с помощью координаты S, задающей положение центра масс груза (рис.2). Начало отсчета координаты Sсовместим с положением центра масс груза при равновесии системы. Углы поворота блока и катка отсчитываем по ходу часовой стрелки. Положение центра масс катка определяем координатой
, отсчитываемой от положения центра масс катка при равновесии системы:
если , то , , и и наоборот, причем нулевому значению координаты Sсоответствуют нулевые значения координат , , и .
Для составления дифференциального уравнения движения системы используем теорему об изменении кинетической энергии механической системы в дифференциальной форме:
(1)
где: T— кинетическая энергия системы, — сумма мощностей внешних
сил, — сумма мощностей внутренних сил.
Пусть в произвольный момент система занимает положение, в котором
S>0, а скорость груза направлена вдоль опорной плоскости в положительном направлении координаты S.
Вычислим кинетическую энергию системы как сумму кинетических энергий тел, образующих механическую систему.
Груз 1 совершает поступательное движение. Его кинетическая энергия:
Блок 2 невесом и его кинетическая энергия равна 0.
Блок 3 совершает вращательное движение вокруг неподвижной оси. Его кинетическая энергия:
где — момент инерции блока 3 относительно оси вращения, —
модуль угловой скорости.
Каток 4 совершает плоскопараллельное движение, поэтому его кинетическая энергия равна:
Тогда кинетическая энергия всего механизма имеет вид:
(2)
Так как механическая система (мс) имеет 1 степень свободы, то величины легко выражаются через . Связи между этими величинами будут иметь вид:
(3)
Блок 3 – сплошной однородный цилиндр, для катка 4 известен радиус инерции, поэтому моменты инерции этих тел относительно осей, проходящих через их центры масс и перпендикулярных плоскости чертежа, будут вычисляться:
Подставляя моменты инерции и выражения (3) в формулу (2), получим полную кинетическую энергию системы:
(4)
где величина называется приведенной массой. кг
Теперь вычислим правую часть уравнения (1) – сумму мощностей внешних и внутренних сил, при этом учтем, что мощность силы равна скалярному произведению вектора силы на скорость точки приложения силы, а мощность пары сил – скалярному произведению вектора пары на угловую скорость твердого тела, к которому приложена пара:
Рассматриваемая нами механическая система является неизменяемой, так как входящие в систему тела абсолютно твердые, а нити — абсолютно гибкие и нерастяжимые. Следовательно, скорости их точек относительно друг друга равны нулю и сумма мощностей внутренних сил также будет равна нулю
(6)
С учетом кинематических соотношений (3) сумму мощностей внешних
сил преобразуем к виду:
(7)
– приведенная сила.
Упругую силу считаем пропорциональной удлинению пружины. Полное удлинение пружины равно сумме статического и динамического удлинений
Приведенная сила в развернутом виде примет вид:
(8)
Где – приведенная жесткость,
– приведенный коэффициент сопротивления.
Подставляя выражения (4), (6) и (7) в (1), получаем после сокращения на дифференциальное уравнение движения системы:
(9)
Учтем, что при равновесии системы (возмущающая сила отсутствует) скорость и ускорение груза равны нулю по определению , а координата груза равна нулю в силу постановки задачи (начало отсчета совпадает с положением равновесия груза 1 S=0). В этом случае уравнение (9) приводится к виду , и условием равновесия системы будет служить уравнение
(10)
Подставляя (10) в уравнение (9) и учитывая формулу (8) для приведенной силы, получаем дифференциальное уравнение движения системы
Представим данное уравнение в виде:
(11)
где введены коэффициенты, имеющие определенный физический смысл:
– частота собственных колебаний,
– показатель степени затухания колебаний.
– относительная амплитуда возмущающей силы.
(12)
Уравнения (11), (12) представляют математическую модель для решения второй задачи динамики.
Как составить дифференциальное уравнение механической системы
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО ДИНАМИКЕ
Исследование колебаний механической системы с одной степенью свободы
Эти задачи следующие:
2. Построение расчетной схемы .
Ф ормулировка задачи – это условие ( текст) з адачи. Она осу ществляется руководител ем работ сов местно с испол нителе м.
Рас четная схема – эт о рисунок , на ко тор ом изображены :
а) ра циональ но выбранная система координат;
Математическая моде ль – э то система д иф фере нциальных уравн ений, алгебраических уравнений и на чальн ых условий, описывающих динамическое поведение механической системы.
Дано: m1, m2, m3 – массы тел механической системы, с – жесткость упру гого элемента, r 1 – радиус одн ородн ого катка 1, r2, R2 – радиусы ст упеней блока 2, i2 – рад иус инерции блока 2 , – коэффициент с опротив ления среды, – угол наклона плос кост и, по которой катится каток 1.
Определить: применяя основные теоремы динамики системы и аналитические методы теоретической механики, определить закон движения первого тела и реакции внешних и внутренних связей. Провести численный анализ полученного решения с использованием ЭВМ.
Порядок выполнения работы:
3) Сформулировать начальные услови я движения.
4) Найти решение дифференциального уравнения движения.
6) По дставив на йденные постоянны е интегрирования в решение дифференциального уравнения, записать закон движ ен ия объ ект а .
8) Построить алгоритм вычис лени й для реализации н а ЭВМ.
9) Произ вес ти вычисления в дисплейном классе.
10) Произв ес ти графическую обработк у результатов вычис лений.
1. Применение основных теорем динамики механической системы
1.1. Постановка второй основной задачи динамики механической системы
Расчетная схема представлена на рис.2
– силы тяжести,
– нормальная реакция опорной плоск ости,
– си ла сцепления ,
– упругая реакция пружины,
– реакции подшипника блока 2,
– сила вязкого сопротивления,
– возмущающая си ла.
Рассматриваемая механическая система имеет одну степень свободы (нити нерастяжимые, качение катка 1 происходит без скольжения). Будем определять ее положение с помощью координаты S. Начало отсчета координаты совместим с положением статического равновесия центра масс груза 3.
Для пост роения дифферен циального уравнения движен ия с истемы используем теорему об изменении к инетической энергии механической системы в форме:
, (1.1)
где Т – кинетическая энергия системы,
– сумма мощностей внеш ни х сил,
– сумма мощнос тей внутренних сил.
Теорема (1.1) формулируется так: “Производная по времени от кинетической энергии механической системы равн а алгебраической сумме мощностей внеш них и внутренних сил, д ейс твующих на точки механической системы”.
Вычислим ки нетическую энергию сис темы как сумму кинетических эн ергий тел 1-3:
. (1.2)
Каток 1 совершает плоскопараллельное движение, поэто му его кинетическая энергия опре деляется по теореме Кенига:
где VC1 – скорость центра масс катка;
JC1 – момент инерции относительно центральной оси катка;
– угловая скорость катка.
Блок 2 совершает вращ ательное движение около неподвижной оси. Его кинетическая энергия
, (1.4)
где JC2 – момент инерции относительно центральной оси блока;
– угловая скорость блока.
Груз 3 совершает поступательное движение. Его кинетическая энергия равна:
. (1.5)
Кинетическая энергия всего механизма будет равна:
. (1.6)
Выразим VC1, и через скорость груза 3. Положив V3 = V, получим
(1.7)
Подставляя (1.3), (1.4), (1.5) в (1.6) с учетом (1.7), получаем:
(1.8)
, (1.9)
. (1.10)
Величину будем называть приведенной массой.
Найдем производную от кинетической энергии по времени
. (1.11)
Теперь вычислим правую часть уравнения (1.1) – сумму мощностей внешних и внутренних сил.
. (1.12)
Рассматриваемая нами механическая система является неизменяемой, т.е. тела, входящие в систему, недеформируемы и скорости их точек относительно друг друга равны нулю. Поэтому сумма мощностей всех внутренних сил будет равняться нулю:
. (1.13)
Будут равняться нулю и мощности некоторых внешних сил, приложенных в точках, скорости которых равны нулю. Как видно из расчетной схемы, таковыми являются силы
.
; (1.14)
или, раскрывая скалярные произведения,
. (1.15)
С учетом кинематических соотношений (1.7) сумму мощностей внешних сил преобразуем к виду:
(1.16)
, (1.17)
. (1.18)
Величину F пр будем называть приведенной силой.
Преобразуем выражение (1.18). Упругую силу считаем пропорциональной удлинению пружины. Полное удлинение пружины f равно сумме статического f ст и динамического SC1 удлинений
,
причем из выражения (1.7) для VС1 следует, что .
Тогда упругая сила будет равна:
. (1.19)
Сила вязкого сопротивления . Приведенную силу с учетом последних формул для F уп и R запишем в виде:
. (1.20)
В состоянии покоя приведенная сила равна нулю. Полагая в (1.20) и , получаем условие равновесия системы
. (1.21)
Из уравнения (1.21) определяется статическое удлинение пружины
. (1.22)
Учитывая (1.22) в (1.20), получаем окончательное выражение для приведенной силы:
. (1.23)
Подставим выражения для производной от кинетической энергии (1.11) и сумму мощностей всех сил (1.17) с учетом (1.23) в уравнение (1.1). Тогда, получаем дифференциальное уравнение движения системы:
. (1.24)
Запишем последнее уравнение в виде:
, (1.25)
где введены коэффициенты, имеющие определенный физический смысл:
– циклическая частота свободных колебаний,
– показатель степени затухания колебаний.
Запишем начальные условия движения:
. (1.26)
В ыражения (1.25) и (1.26) совместно представляют математическую модель для решения второй задачи динамики.
1.2. Определение закона движения системы.
Проинтегрируем дифференциальное уравнение (1.25). Пусть возмущающая сила изменяется по гармоническому закону:
где – амплитуда возмущающей силы,
р – циклическая частота возмущения.
Общее решение S неоднородного дифференциального уравнения (1.25) складывается из общего решения однородного уравнения и частного решения неоднородного: . Однородное дифференциальное уравнение, соответствующее данному неоднородному (1.25), имеет вид:
. (2.2)
Решение этого уравнения ищем в виде функции
, (2.3)
где А и – неопределенные постоянные величины.
Подставляя (2.3) в (2.2), получаем:
Так как мы ищем нетривиальное решение, то . Следовательно, должно выполняться условие
. (2.4)
Уравнение (2.4) называется характеристическим уравнением дифференциального уравнения (2.2). Это уравнение имеет два корня:
. (2.5)
В зависимости от знака подкоренного выражения, корни характеристического уравнения могут быть комплексно-сопряженными или действительными. Возможны три случая:
– подкоренное выражение отрицательное, следовательно корни комплексно-сопряженные,
– подкоренное выражение равно нулю, корни действительные, кратные.
– подкоренное выражение больше нуля, корни действительные, разные.
В первом случае ( ) общее решение уравнения (2.2) имеет вид:
, (2.6)
где А 1 , А2 – постоянные интегрирования,
,
,
нетрудно представить в виде:
где a , – постоянные интегрирования.
Во втором случае ( ) общее решение имеет вид:
В третьем случае ( ) общее решение имеет вид:
.
Далее предполагается, что в рассматриваемом примере имеет место случай .
. (2.11)
Частное решение ищем в виде правой части
. (2.12)
Сравнивая коэффициенты при соответствующих тригонометрических функциях справа и слева, получаем систему алгебраических уравнений для определения постоянных А и В:
,
.
Решая эту систему, получаем следующие выражения для коэффициентов А и В:
;
. (2.13)
Таким образом, решение (2.12) определено. Складывая (2.8) и (2.12), получаем общее решение неоднородного уравнения (2.11)
Константы а и определяются из начальных условий (1.26). Для этого найдем производную по времени от (2.14)
Подчинив (2.14) и (2.15) начальным условиям, получим систему уравнений относительно искомых констант
,
.
Решая эту систему, получаем:
,
. (2.16)
Подставляя (2.16) в (2.14), получаем закон движения механизма.
1.3. Определение реакций внешних и внутренних связей.
Для решения этой задачи расчленяем механизм на отдельные части и изображаем расчетные схемы отдельно для каждого тела (рис.3).
Определение реакций связей проведем с помощью теоремы об изменении количества движения
, (3.1)
и теоремы об изменении кинетического момента относительно центра масс
. (3.2)
В соответствии с расчетными схемами (рис. 3) записываем уравнения (3.1) и (З.2) в проекциях на оси координат
, (3.3)
, (3.4)
; (3.5)
, (3.6)
, (3.7)
; (3.8)
. (3.9)
С учетом кинематических соотношений (1.7) систему уравнений (3.3) -(3.9) преобразуем к виду:
,
,
, (3.10)
,
,
,
.
Уравнения (3.10) составляют систему алгебраических уравнений относительно функций
, N 1, F сц , T 12, T 23, X 2, Y 2.
Решая эту систему, получаем и дифференциальное уравнение движения системы, и выражения для определения реакций.
2.1. Составлени е дифференциального уравнения движения механизма с помощью принципа Даламбера-Лагранжа.
. (4.1)
Здесь – сумма элементарных работ всех активных сил на возможном перемещении системы;
– сумма элементарных работ всех сил инерции на возможном перемещении системы.
Изобразим на рисунке активные силы и силы инерции (рис.4). Реакции идеальных связей не учитывают и не отображают на расчетной схеме, поскольку по определению работа их реакций на любом возможном перемещении системы равна нулю. Пружина является неидеальной связью. Введем реакцию этой связи в число активных сил.
Сообщим системе возможное перемещение. Возможная работа активных сил определяется как сумма следующих элементарных работ:
. (4.2)
Вычисляя последовательно элементарные работы активных сил и суммируя их, получаем после несложных преобразований
. (4.3)
Аналогичное выражение для приведенной силы F пр получено ранее [см. (1.23)].
Найдем возможную работу сил инерции:
. (4.4)
Для величин главных векторов и главных моментов сил инерции имеем следующие выражения:
; ;
; . (4.5)
Используя кинематические соотношения (1.7), можно записать
; ;
; ; (4.6)
; .
Тогда возможную работу сил инерции можно преобразовать к виду
(4.7)
, (4.8)
. (4.9)
Аналогичное выражение для приведенной массы системы было получено ранее [см.(1.10)]. Подставляя выражения (4.3) и (4.8) в общее уравнение динамики (4.1), получаем
. (4.10)
Поделив (4.10) на , получим дифференциальное уравнение вынужденных колебаний системы:
, (4.11)
;
. (4.12)
Дифференциальное уравнение (4.11) полностью совпадает с полученным ранее уравнением (1.25).
2.2. Составление дифференциального уравнения движения механизма с помощью уравнений Лагранжа 2- го рода.
Составим теперь уравнения Лагранжа 2-го рода. Для механической системы с одной степенью свободы дифференциальное уравнение движения в обобщенных координатах имеет вид:
, (4.13)
– обобщенная скорость.
Выражение для кинетической энергии системы было найдено ранее (1.8):
,
.
Учитывая, что , получаем
. (4.14)
Производные от кинетической энергии
; ; . (4.15)
Для определения обобщенной силы Q сообщим системе возможное перемещение (рис. 4) и вычислим сумму элементарных работ всех активных сил на возможных перемещениях точек их приложения [см. (4.3)]:
.
С другой стороны для системы с одной степенью свободы
. (4.16)
Сравнивая два последних соотношения, получаем
Подставляя производные от кинетической энергии (4.15) и обобщенную силу (4.16) в уравнение Лагранжа, получаем
. (4.18)
Полученное уравнение (4.18) совпадает с уравнениями (1.25) и (4.11).
3. Анализ колебаний механической системы с одной степенью свободы
3.1. Колебания механической системы при отсутствии сил сопротивления среды
В дифференциальном уравнении движения системы, полученном ранее (1.25), полагаем , тогда уравнение движения примет вид:
(5.1)
Начальные условия: при заданы и .
3.1.1. Свободные колебания
Если внешнее возмущение отсутствует (т.е. ), то дифференциальное уравнение движения становится однородным:
(5.2)
и называется дифференциальным уравнением свободных колебаний, т.е. таких движений системы, которые происходят под действием так называемых восстанавливающих сил. Восстанавливающие силы – это такие силы, каждая из которых стремится вернуть систему в состояние статического равновесия (силы тяжести, упругие силы).
Решение уравнения (5.2) с учетом начальных условий имеет вид:
(5.3)
где ; ; . (5.4)
Анализируя решение (5.3) можно сделать следующие выводы:
1. Свободные колебания (рис.5.1) системы с одной степенью свободы представляют собой гармонические колебания.
2. Амплитуда (максимальное отклонение системы от состояния равновесия) и начальная фаза зависят от начальных условий.
3. Циклическая частота и соответственно период колебаний от начальных условий не зависят, а зависят только от жесткой и инерционной характеристик системы.
4. Отношения амплитуд колебаний различных точек системы не зависят от начальных условий, так как начальные условия влияют на амплитуды только через множитель , общий для всех точек.
5. Все точки системы всегда находятся в одной фазе, т.е. они одновременно проходят через свои равновесные положения; координаты всех точек одновременно достигают своих максимальных значений.
3.1.2. Вынужденные колебания
При воздействии возмущающей силы решение неоднородного дифференциального уравнения (5.1) с учетом начальных условий представим в виде:
(5.5)
где .
Первые два слагаемых правой части уравнения (5.5):
(5.6)
соответствуют свободным колебаниям с частотой (рис.5.1), т.е. колебаниям, которые совершал бы осциллятор при отсутствии возмущений. При нулевых начальных условиях, т.е. когда , такие колебания во все время действия возмущающей силы не возникают.
Третье слагаемое в (5.5)
(5.7)
– гармоническое колебание, происходящее с собственной частотой системы, но с амплитудой, зависящей от амплитуды возмущающей силы
(5.8)
Эти колебания также относятся к свободным колебаниям. Они всегда сопровождают вынужденные колебания при любых начальных условиях, от которых они вообще не зависят.
Их называют сопровождающими колебаниями (рис. 5.2).
Четвертое слагаемое в выражении (4.5):
(5.9)
представляет собой вынужденные колебания системы (рис. 5.3).
Таким образом, колебания линейного осциллятора в рассмотренном случае представляют собой линейное наложение трех гармонических колебаний: свободных, сопровождающих и вынужденных (рис. 5.4).
Отметим следующие свойства вынужденных колебаний:
1. Вынужденные колебания происходят с частотой возмущающей силы.
2. Вынужденные колебания не зависят от начальных условий, поэтому для изменения, например, амплитуды (при заданной возмущающей силе) вынужденных колебаний необходимы существенные изменения параметров конструкции: ее жесткости, распределения масс, тогда как в свободных колебаниях для этого достаточно изменить начальные условия.
3. Если , то знак отклонения будет совпадать со знаком возмущающей силы , т.е. сила и вызванн ые ею вынужденные колебания будут находиться в одной фазе.
Если , то знак отклонения будет противоположен знаку силы.
Переписав для этого случая выражение (5.9) в виде:
, (5.10)
убеждаемся, что при возмущающая сила и вызванные ею колебания находятся в противоположенных фазах.
4. Если , то выражения (5.7) и (5.9) теряют смысл. Для анализа колебаний в этой ситуации эти выражения рассматриваются совместно
(5.11)
т.е. получим неопределенность, которую можно раскрыть по правилу Лопиталя , заменив дробь в (5.11) пределом
.
Таким образом, в этом случае общий интеграл (5.5) будет иметь вид:
. (5.12)
И здесь, как в (5.5) движение осциллятора представляет собой линейное наложение трех колебательных движений, но с одним существенным отличием от (5.5): вынужденные колебания представлены непериодическим слагаемым:
, (5.13)
в коэффициенты которого входит время t .
С течением времени он растет по абсолютной величине безгранично, причем вынужденные колебания происходят с возрастающей по линейному закону амплитудой.
Такая ситуация при колебаниях называется резонансом.
5. Если частота вынужденных колебаний не равна частоте свободных колебаний, но близка к ней, то, записав выражение (5.11) в виде:
, (5.14)
полагаем , но , , и преобразовываем (5.14) к виду:
. (5.15)
Используя тригонометрическое выражение:
,
, (5.16)
т.е. ,
где – есть амплитуда колебаний, являющаяся периодичной функцией времени и меняется весьма медленно с большим периодом , чем период самих колебаний , т.е. , и малой частотой .
Подобная рассмотренному случаю ситуация представляет собой биение (рис. 5.5).
Таким образом, когда частота вынужденных колебаний весьма близка к частоте свободных (или собственных) колебаний системы, но не равна ей, в колебательной системе возникает биение.
3.2. Колебания механической системы в вязкой среде
Дифференциальное уравнение движения имеет вид (1.25):
. (5.17)
Начальные условия: . (5.18)
3.2.1. Свободные колебания
Полагая в (5.17) , т.е. возмущения отсутствуют, получим
(5.19)
Ограничимся случаем малых сопротивлений и примем .
Тогда общее решение однородного уравнения (5.19) с учетом начальных условий можно представить в виде (рис. 5.6):
, (5.20)
где . (5.21)
. (5.22)
Из закона движения системы (5.20) видно, что в сопротивляющейся среде:
1) свободные колебания являются затухающими;
2) частота затухающих колебаний меньше частоты незатухающих колебаний ;
3) амплитуда затухающих колебаний убывает по экспоненциальному закону;
4) период затухающих колебаний больше периода незатухающих колебаний ;
5) отношение любых двух соседних амплитуд: и есть величина постоянная
. (5.23)
Это отношение называется декрементом затухания. Логарифм этого коэффициента
(5.24)
называется логарифмическим декрементом.
Декремент или логарифмический декремент используются для оценки быстроты убывания амплитуды затухающих колебаний.
3.2.2. Вынужденные колебания в сопротивляющейся среде
Дифференциальное уравнение движения в этом случае является неоднородным:
, (5.25)
его общее решение имеет вид:
. (5.26)
При начальных условиях постоянные интегрирования будут такими
(5.27)
После подстановки постоянных интегрирования (5.27) в общее решение (5.26) получим закон движения механической системы:
(5.28)
; (5.29)
;
(5.30)
– коэффициент динамичности. (5.31)
В выражении (5.28) первое слагаемое представляет собой собственные затухающие колебания (рис. 5.6):
.
Второе и третье слагаемые в совокупности представляют собой сопровождающие колебания (рис. 5.7):
. (5.32)
(5.33)
– вынужденные колебания с частотой возмущающей силы (рис. 5.8).
Таким образом, амплитуда вынужденных колебаний при резонансе достигает значительной величины при малых сопротивлениях.
. (5.34)
Если , но близка к ней, то, положив , выражение (5.32) для сопровождающих колебаний представится в виде:
. (5.35)
Рассматривая (5.33) и (5.35) совместно и, добавив выражение
,
равное нулю, получим закон движения механической системы в виде:
(5.36)
Но выражение в квадратных скобках можно представить так (5.15):
. (5.37)
Тогда получим, положив ,
(5.38)
Последнее слагаемое в (5.38) представляет собой колебания биений с затухающей амплитудой
,
т.е. . (5.39)
Второе слагаемое в (5.38) – это незатухающие вынужденные колебания
. (5.40)
Первое слагаемое в (5.38) – это затухающие сопровождающие колебания
. (5.41)
Таким образом, в реальных условиях колебания биений, вызываемые возмущенной силой с частотой, близкой к частоте затухающих колебаний, могут иметь практическое значение только в начале движения, в так называемый переходный период, и при малом значении коэффициента затухания n . При установившемся движении, которое наступает тем быстрее, чем больше сопротивление, движение системы определяется уравнением :
.
3.3. Коэффициент динамичности
Как было отмечено выше (5.31), коэффициентом динамичности называется отношение максимального динамического отклонения механической системы от положения устойчивого равновесия к статическому отклонению под воздействием силы, равной амплитуде возмущающей силы (рис. 5.10).
, (5.42)
где ,
т.е. согласно выражению (5.31):
. (5.43)
Максимальное значение , следовательно, и амплитуды вынужденных колебаний D , достигается при минимальном значении подкоренного выражения (5.43):
. (5.44)
Найдем, при каком значении р функция (5.44) минимальная.
. (5.45)
Из (5.45) следует, что
. (5.46)
Это возможно, если
(5.47)
Подставляя (5.46) в (5.43), получаем
. (5.48)
При малом значении сопротивления :
. (5.49)
При резонансе :
,
т.е. максимальное значение амплитуды и ее значение при резонансе весьма близки друг к другу (практически одинаковы).
В области, достаточно удаленной от резонанса, при установившемся движении и малом коэффициенте затухания, силами сопротивления можно пренебрегать.
Графические иллюстрации видов колебаний
Рис. 5.1. Собственные колебания
Рис.5.2 Сопровождающие колебания
Рис.5.3 Вынужденные колебания
Рис. 5.4 Результирующие колебания
Рис. 5.5 Биения – результирующие колебания
Колебания в вязкой среде
Рис.5.6. Собственные колебания в вязкой среде
Рис.5.7 Сопровождающие колебания в вязкой среде
Рис. 5.8. Вынужденные колебания
Рис. 5.9 Результирующие колебания в вязкой среде
Рис. 5.10 Коэффициент динамичности
Рис. 5.11. Резонанс ( ) при нулевых значениях начальных перемещения и скорости
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
[spoiler title=”источники:”]
http://poisk-ru.ru/s35599t18.html
http://www.teoretmeh.ru/primerdinamika2.htm
[/spoiler]
Преподаватель который помогает студентам и школьникам в учёбе.
Дифференциальное уравнение движения системы в теоретической механике
Дифференциальное уравнение движения системы:
Пусть даны внешние и внутренние силы, действующие на систему, состоящую из
Рис. 39
Систему 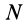
Задача интегрирования дифференциальных уравнений механической системы еще сложнее, если на механическую систему наложены связи, силы реакций которых заранее не известны и должны быть дополнительно определены по заданным силам и связям аналогично случаю движения несвободной материальной точки по поверхности и кривой линии.
В некоторых случаях из дифференциальных уравнений движения системы можно получить первые интегралы, т. е. соотношения, в которые не входят производные второго порядка от координат по времени.
Если известны первые интегралы, то задача интегрирования системы дифференциальных уравнений облегчается. Хотя отдельные первые интегралы и не могут полностью описать движения всех точек системы, однако они иногда характеризуют важные стороны движения системы в целом.
- Заказать решение задач по теоретической механике
Первые интегралы системы дифференциальных уравнений удобно получать из так называемых общих теорем динамики, когда выполняются некоторые дополнительные условия для действующих сил. Кроме того, общие теоремы динамики, даже когда по ним нельзя определить первые интегралы, дают ценную информацию о движении точки или системы. В некоторых задачах, где не требуется полного знания движения системы, эти сведения могут оказаться достаточными.
Общие теоремы динамики являются следствиями системы дифференциальных уравнений движения точки или соответственно системы точек.
- Теоремы об изменении количества движения и о движении центра масс
- Теорема об изменении кинетического момента
- Теорема об изменении кинетической энергии
- Потенциальное силовое поле
- Движение несвободной материальной точки
- Относительное движение материальной точки
- Геометрия масс
- Свойства внутренних сил системы
Глава XXII. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС СИСТЕМЫ
§ 106. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ
Рассмотрим систему, состоящую из 




Аналогичный результат получим для любой точки. Следовательно, для всей системы будет

Уравнения (13) представляют собой дифференциальные уравнения движения системы в векторной форме (в них 
Проектируя равенства (13) на какие-нибудь координатные оси, получим дифференциальные уравнения движения системы в проекциях на эти оси.
Полное решение основной задачи динамики для системы будет состоять в том, чтобы, зная заданные силы и наложенные связи, проинтегрировать соответствующие дифференциальные уравнения и определить в результате закон движения каждой из точек системы и реакции связей. Сделать это аналитически удается лишь в отдельных случаях, когда число точек системы невелико, или же интегрируя уравнения численно с помощью ЭВМ.
Однако при решении многих конкретных задач необходимость находить закон движения каждой из точек системы не возникает, а бывает достаточно найти какие-то характеристики, определяющие движение всей системы в целом.
Например, чтобы установить, как движется под действием приложенных сил кривошипно-ползунный механизм (см. рис. 158 в § 57), достаточно определить закон вращения кривошипа, т. е. найти зависимость угла его поворота 
Но предварительно решим одну задачу, показывающую, что искомый результат можно иногда эффективно находить и непосредственно, используя дифференциальные уравнения движения системы.
Задача 122. Динамический гаситель колебаний. Укрепленный на пружине груз 1 совершает вынужденные колебания под действием возмущающей силы Q, проекция которой 

Рис. 283
Определить, при каких условиях можно погасить эти колебания, прикрепив к грузу 1 на пружине с коэффициентом жесткости 









Чтобы колебания груза 1 гасились, должно быть 

Из первого уравнения 

Это и будет искомым условием гашения, в котором одной из величин 






Дифференциальные уравнения движения материальной точки в теоретической механике
Содержание:
Дифференциальные уравнения движения материальной точки:
Используя основной закон динамики, можно вывести дифференциальные уравнения движения материальной точки в различных системах координат. По аксиоме о связях и силах реакций связей можно получить дифференциальные уравнения движения и несвободной точки так же, как и для свободной, только ко всем приложенным к точке силам надо добавить силы реакций связей.
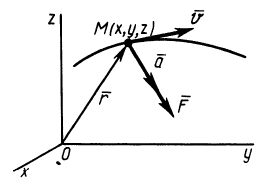
Силы реакций связей при движении точки могут зависеть в общем случае не только от вида наложенных на точку связей и приложенных к ней сил, но и от характера ее движения, например от ее скорости при движении в воздухе или в какой-либо другой сопротивляющейся среде. В дальнейшем не будем делать различия между свободной и несвободной материальными точками. Обозначая равнодействующую всех заданных сил и сил реакций связей
Из кинематики точки известно, что ускорение 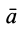
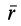
Дифференциальное уравнение движения материальной точки в векторной форме имеет вид
Если спроецировать обе части уравнений (7) или (8) на координатные оси, то можно получить дифференциальные уравнения движения точки в проекциях на эти оси.
В декартовой системе координат в общем случае
Проекции ускорения на координатные оси можно выразить через вторые производные по времени от координат движущейся точки:
Рис. 3
Дифференциальные уравнения движения материальной точки в прямоугольной декартовой системе координат имеют вид
Частные случаи дифференциального уравнения движения материальной точки
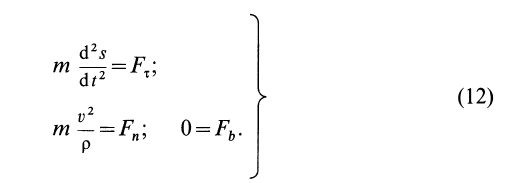
Если известно, что материальная точка движется в одной и той же плоскости, то, принимая ее за координатную плоскость 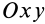
Так как 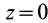
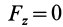
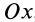
Так как при движении 
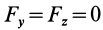
где 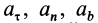
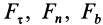
где 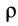
Второе уравнение из (12) можно преобразовать:
где 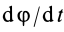
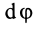
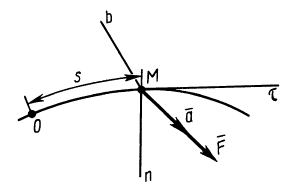
Дифференциальные уравнения (12) можно представить в виде
Рис. 4
Эта форма дифференциальных уравнений движения точки удобна при исследовании некоторых случаев полета снарядов и ракет, особенно по траектории, лежащей в плоскости. Тогда 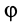
Дифференциальные уравнения движения точки можно представить в любой другой системе координат. Для этого надо знать выражения проекций ускорения на эти оси координат.
Дифференциальные уравнения относительного движения точки
Кориолисовыми силами инерции называют две векторные величины, имеющие размерность силы и добавляемые к силам, приложенным к материальной частице, для определения ее относительного ускорения
Все дифференциальные уравнения движения, с которыми мы ознакомились в этой главе, относятся к абсолютному движению, т. е. к движению по отношению к инерциальной системе отсчета. Для написания дифференциальных уравнений движения точки (или частицы) относительно подвижных осей подставим в основное уравнение динамики (123) вместо абсолютного ускорения точки его выражение (110):
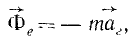
имеющую размерность силы, равную произведению массы материальной частицы на ее переносное ускорение и направленную противоположно этому ускорению, называют переносной силой инерции Кориолиса.
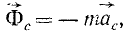
равную произведению массы материальной частицы на ее кориолисово ускорение и направленную противоположно этому ускорению, называют поворотной силой инерции Кориолиса.
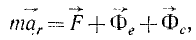
или в проекциях на оси координат:
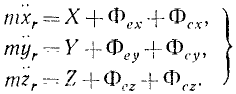
Таким образом, относительное движение материальной точки можно описать такими же (по форме) дифференциальными уравнениями, как и абсолютное, но к действующим на точку силам нужно прибавить две кориолисовы силы инерции: переносную и поворотную.
Эти величины следует отличать от даламберовых сил инерции (см. гл. XX), введение которых позволяет решать задачи динамики методом статики.
Пример решения задачи №1
Определить амплитуду вынужденных колебаний в относительном движении вибрографа для записи вертикальных колебаний фундамента (рис. 171), совершающего вместе с фундаментом колебания по закону χ = a sin pt, если вес груза равен G и жесткость пружины с.
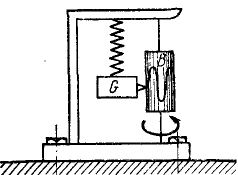
Рис. 171
Решение. Рама жестко соединена с фундаментом и участвует в его колебаниях, как и вращающийся барабан В, на котором груз G, перемещаясь вверх и вниз, записывает колебания фундамента. Вертикальные перемещения х’ груза G по отношению к раме являются относительными и по отношению к барабану, если пренебречь его вращением. Уравнение этих относительных перемещений можно составить как уравнение абсолютного движения, если к заданным силам добавить переносную кориолисову силу, равную и противоположную произведению вектора переносного ускорения на массу груза. Переносная сила инерции груза равна
Напишем дифференциальное уравнение относительных колебаний груза, сократив на m:
x’ + k 2 χ’ = ар 2 sin pt.
где 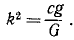
Амплитуда этих колебаний тем менее отличается от амплитуды колебаний фундамента, чем меньше собственная частота k прибора сравнительно с частотой р, т. е. чем меньше жесткость пружины и чем больше масса груза.
Ответ.
Пример решения задачи №2
Ползун G (рис. 172) может скользить по хорде AB равномерно вращающегося горизонтального диска, к точкам А и В которой он прикреплен двумя одинаковыми пружинами жесткостью 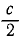
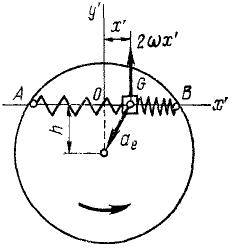
Рис. 172
Решение. Построим оси подвижной системы координат с началом в точке О (в положении относительного равновесия ползуна), направив Ox’ но хорде.
Определим силы, действующие на ползун. Если ползун отклонится от равновесного положения О на величину х’, то одна из пружин сожмется, а другая растянется. Согласно закону Гука сила каждой из пружин пропорциональна деформации х’ и направлена к точке О. Следовательно, на ползун действует активная сила
Кроме активной силы, надо учесть действие кориолисовых сил: Φe—переносной и Φc-поворотной.
Переносная сила инерции равна произведению массы т ползуна на его переносное ускорение: 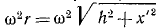
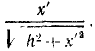
Поворотная сила Кориолиса равна произведению массы ползуна иа кориолисово ускорение 2ωx’ и направлена против этого ускорения. Таким образом, чтобы определить направление поворотной силы Кориолиса, надо вектор относительной скорости повернуть на 90° против переносного вращения. Находим, что поворотная сила инерции действует перпендикулярно AB и проекция ее на Ox’ равна нулю.
При найденных значениях активных сил и кориолисовых сил дифференциальное уравнение относительного движения ползуна по хорде имеет вид:
mх’ = — cx’ + mω 2 x’= — (с—mω 2 )x’.
Это уравнение выражает гармоническое колебание с периодом
Ответ. 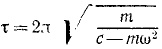
Пример решения задачи №3
Составить дифференциальное уравнение относительного движения ползуна, описанного в предыдущей задаче, считая, что при его движении вдоль хорды AB возникает трение, пропорциональное нормальному давлению на хорду.
Решение. Нормальное давление обусловлено поворотной силой инерции и нормальной составляющей переносной силы инерции.
Поворотная сила ползуна Φс=2mωx’ переменна по величине и направлению. Она направлена перпендикулярно к хорде AB, но в сторону положительных значений у’, если точка G движется в сторону отрицательных значений х’, т. е, если х’ 2 h. Эта составляющая в рассматриваемом механизме всегда направлена в сторону положительных у’, а потому в суммарном давлении обе кориолисовы силы складываются при х’ 0, и дифференциальное уравнение относительного движения точки имеет вид
mх’ =— (с—mω 2 ) x’ — fm (2ωx’ ± ω2h),
причем знак второго слагаемого в скобках надо брать положительным при х’ 0. Решение такого уравнения при движении точки G влево и вправо получается, конечно, различным. Если Л — 0 и хорда является диаметром, то вместо кулонова трения получается вязкое демпфирование, зависящее от скорости.
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Две основные задачи динамики точки
- Прямолинейное движение точки
- Криволинейное движение материальной точки
- Движение несвободной материальной точки
- Сложное движение точки
- Сложение движение твердого тела
- Кинематика сплошной среды
- Аксиомы классической механики
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Дифференциальные уравнения движения системы


Дифференциальные уравнения движения системы
- Приложите внешнюю силу и внутреннюю силу, действующую на систему, состоящую из N точек (рис. 39). Если внешняя сила M » ‘и вся внутренняя сила F’1 приложены к каждой точке в системе, вы можете построить дифференциальное уравнение движения, например, для любой точки Арт в системе. w »0 = Ae, + FL ° (* = 1, 2, …, N). (3) Система дифференциальных уравнений (3) называется дифференциальным уравнением движения механической системы в векторном виде.
Кинетическая энергия машины, начиная с определенного момента, увеличивается или уменьшается в зависимости от того, превышает ли основная работа движущей силы основную работу сопротивления. Людмила Фирмаль
Проецирование векторного дифференциального уравнения (3) на декартовы декартовы оси дает систему дифференциальных уравнений 3 Вт, которые описывают движение точек в механической системе. Поэтому, чтобы найти движение механической системы в соответствии с условиями силы, заданными для каждой точки в системе, необходимо интегрировать систему дифференциальных уравнений 3N. Эта проблема не может быть решена точно, даже если это общая точка в общем случае.
- В случае двух материальных точек, которые движутся только под действием силы взаимодействия по универсальному закону притяжения (задача двух тел), это очень сложно, и случай трех точек взаимодействия (задача трех тел) не может быть полностью решен. Задача интегрирования дифференциального уравнения в механическую систему является более сложной, если механическая система ограничена и ее сила реакции заранее не известна, для перемещения несвободных материальных точек вдоль поверхностей и кривых. Как и в случае, он должен быть дополнительно определен с учетом приведенных сил и ограничений.
В некоторых случаях интегралы первого порядка могут быть получены из дифференциальных уравнений движения системы, то есть отношений, которые не включают производные второго порядка по временным координатам. Если вы знаете первый интеграл, задача интеграции системы дифференциальных уравнений становится проще. Отдельные начальные интегралы не могут полностью учитывать движение всех точек в системе, но могут характеризовать важные аспекты общего движения системы.
Если начальное отклонение и скорость груза также находятся в плоскости l, то маятник должен всегда находиться в плоскости l и быть закреплен на центральной рамке отсчета. Людмила Фирмаль
Первый интеграл системы дифференциальных уравнений может быть удобно получен из так называемой общей теоремы. Намики — это когда выполняются некоторые дополнительные требования действующего подразделения. Кроме того, общая теорема динамики дает ценную информацию о движении точек или систем, даже если исходные интегралы не могут быть определены из них. Эта информация может быть достаточной для некоторых задач, которые не требуют полного знания поведения системы. Общая теорема динамики является результатом дифференциальной системы уравнений движения точки или системы точек.




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
iSopromat.ru
Составление систем дифференциальных уравнений движения материальной точки, на которую действует некоторая система сил для определения движения точки под действием этих сил.
Пусть на материальную точку действует некоторая система сил и требуется определить движение точки под действием этих сил.
Уравнение второго закона динамики для материальной точки массой m запишется в виде
Спроецировав уравнение (1) на декартовы оси координат, получим систему из трех уравнений
В зависимости от того, что известно о движении точки, дифференциальные уравнения записывают или в декартовых или в естественных координатах.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
источники:
http://lfirmal.com/differencialnye-uravneniya-dvizheniya-sistemy/
http://isopromat.ru/teormeh/kratkaja-teoria/differencialnye-uravnenia-dvizhenia-tochki