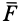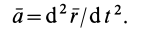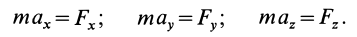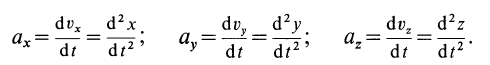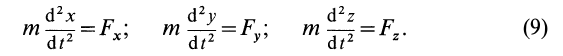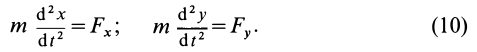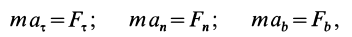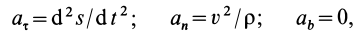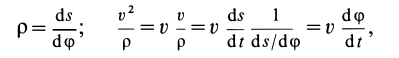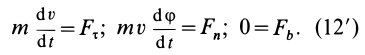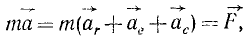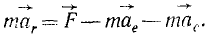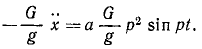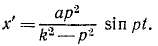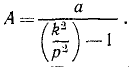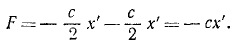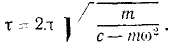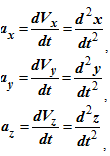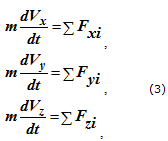Содержание:
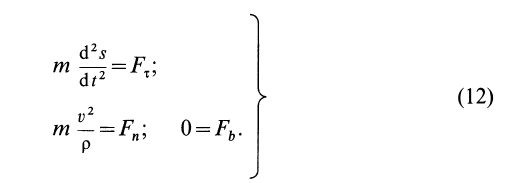
Дифференциальные уравнения движения материальной точки:
Используя основной закон динамики, можно вывести дифференциальные уравнения движения материальной точки в различных системах координат. По аксиоме о связях и силах реакций связей можно получить дифференциальные уравнения движения и несвободной точки так же, как и для свободной, только ко всем приложенным к точке силам надо добавить силы реакций связей.
Силы реакций связей при движении точки могут зависеть в общем случае не только от вида наложенных на точку связей и приложенных к ней сил, но и от характера ее движения, например от ее скорости при движении в воздухе или в какой-либо другой сопротивляющейся среде. В дальнейшем не будем делать различия между свободной и несвободной материальными точками. Обозначая равнодействующую всех заданных сил и сил реакций связей
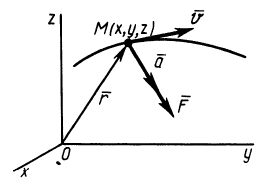
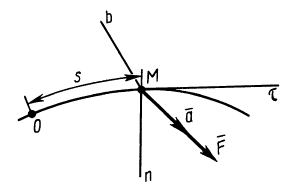
Из кинематики точки известно, что ускорение 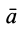
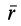
Дифференциальное уравнение движения материальной точки в векторной форме имеет вид
Если спроецировать обе части уравнений (7) или (8) на координатные оси, то можно получить дифференциальные уравнения движения точки в проекциях на эти оси.
В декартовой системе координат в общем случае
Проекции ускорения на координатные оси можно выразить через вторые производные по времени от координат движущейся точки:
Рис. 3
Дифференциальные уравнения движения материальной точки в прямоугольной декартовой системе координат имеют вид
Частные случаи дифференциального уравнения движения материальной точки
Если известно, что материальная точка движется в одной и той же плоскости, то, принимая ее за координатную плоскость 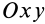
Так как 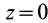
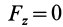
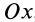
Так как при движении 
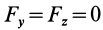
где 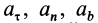
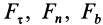
где 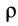
Второе уравнение из (12) можно преобразовать:
где 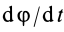
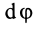
Дифференциальные уравнения (12) можно представить в виде
Рис. 4
Эта форма дифференциальных уравнений движения точки удобна при исследовании некоторых случаев полета снарядов и ракет, особенно по траектории, лежащей в плоскости. Тогда 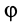
Дифференциальные уравнения движения точки можно представить в любой другой системе координат. Для этого надо знать выражения проекций ускорения на эти оси координат.
Дифференциальные уравнения относительного движения точки
Кориолисовыми силами инерции называют две векторные величины, имеющие размерность силы и добавляемые к силам, приложенным к материальной частице, для определения ее относительного ускорения
Все дифференциальные уравнения движения, с которыми мы ознакомились в этой главе, относятся к абсолютному движению, т. е. к движению по отношению к инерциальной системе отсчета. Для написания дифференциальных уравнений движения точки (или частицы) относительно подвижных осей подставим в основное уравнение динамики (123) вместо абсолютного ускорения точки его выражение (110):
откуда
Векторную величину
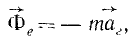
имеющую размерность силы, равную произведению массы материальной частицы на ее переносное ускорение и направленную противоположно этому ускорению, называют переносной силой инерции Кориолиса.
Векторную величину
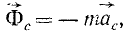
равную произведению массы материальной частицы на ее кориолисово ускорение и направленную противоположно этому ускорению, называют поворотной силой инерции Кориолиса.
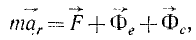
или в проекциях на оси координат:
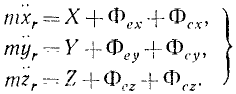
Таким образом, относительное движение материальной точки можно описать такими же (по форме) дифференциальными уравнениями, как и абсолютное, но к действующим на точку силам нужно прибавить две кориолисовы силы инерции: переносную и поворотную.
Эти величины следует отличать от даламберовых сил инерции (см. гл. XX), введение которых позволяет решать задачи динамики методом статики.
Пример решения задачи №1
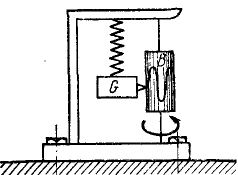
Определить амплитуду вынужденных колебаний в относительном движении вибрографа для записи вертикальных колебаний фундамента (рис. 171), совершающего вместе с фундаментом колебания по закону χ = a sin pt, если вес груза равен G и жесткость пружины с.
Рис. 171
Решение. Рама жестко соединена с фундаментом и участвует в его колебаниях, как и вращающийся барабан В, на котором груз G, перемещаясь вверх и вниз, записывает колебания фундамента. Вертикальные перемещения х’ груза G по отношению к раме являются относительными и по отношению к барабану, если пренебречь его вращением. Уравнение этих относительных перемещений можно составить как уравнение абсолютного движения, если к заданным силам добавить переносную кориолисову силу, равную и противоположную произведению вектора переносного ускорения на массу груза. Переносная сила инерции груза равна
Напишем дифференциальное уравнение относительных колебаний груза, сократив на m:
x’ + k2χ’ = ар2 sin pt.
где 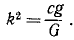
Амплитуда этих колебаний тем менее отличается от амплитуды колебаний фундамента, чем меньше собственная частота k прибора сравнительно с частотой р, т. е. чем меньше жесткость пружины и чем больше масса груза.
Ответ.
- Заказать решение задач по теоретической механике
Пример решения задачи №2
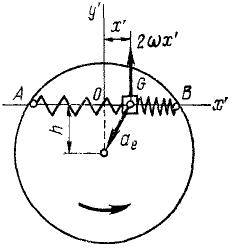
Ползун G (рис. 172) может скользить по хорде AB равномерно вращающегося горизонтального диска, к точкам А и В которой он прикреплен двумя одинаковыми пружинами жесткостью 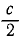
Рис. 172
Решение. Построим оси подвижной системы координат с началом в точке О (в положении относительного равновесия ползуна), направив Ox’ но хорде.
Определим силы, действующие на ползун. Если ползун отклонится от равновесного положения О на величину х’, то одна из пружин сожмется, а другая растянется. Согласно закону Гука сила каждой из пружин пропорциональна деформации х’ и направлена к точке О. Следовательно, на ползун действует активная сила
Кроме активной силы, надо учесть действие кориолисовых сил: Φe—переносной и Φc-поворотной.
Переносная сила инерции равна произведению массы т ползуна на его переносное ускорение: 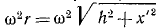
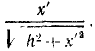
Поворотная сила Кориолиса равна произведению массы ползуна иа кориолисово ускорение 2ωx’ и направлена против этого ускорения. Таким образом, чтобы определить направление поворотной силы Кориолиса, надо вектор относительной скорости повернуть на 90° против переносного вращения. Находим, что поворотная сила инерции действует перпендикулярно AB и проекция ее на Ox’ равна нулю.
При найденных значениях активных сил и кориолисовых сил дифференциальное уравнение относительного движения ползуна по хорде имеет вид:
mх’ = — cx’ + mω2x’= — (с—mω2)x’.
Это уравнение выражает гармоническое колебание с периодом
Ответ. 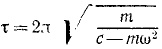
Пример решения задачи №3
Составить дифференциальное уравнение относительного движения ползуна, описанного в предыдущей задаче, считая, что при его движении вдоль хорды AB возникает трение, пропорциональное нормальному давлению на хорду.
Решение. Нормальное давление обусловлено поворотной силой инерции и нормальной составляющей переносной силы инерции.
Поворотная сила ползуна Φс=2mωx’ переменна по величине и направлению. Она направлена перпендикулярно к хорде AB, но в сторону положительных значений у’, если точка G движется в сторону отрицательных значений х’, т. е, если х’ < 0, и, наоборот, в сторону отрицательных у’, если х’ положительно. А так как сила трения направлена всегда против относительной скорости, то силу трения, обусловленную давлением Φс, мы вполне определим по величине и по знаку выражением
— f2mωx’.
Нормальная составляющая переносной силы инерции ползуна постоянна по величине и всегда направлена в сторону положительных у’. Чтобы ее определить, надо 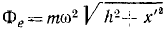
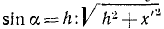
mх’ =— (с—mω2) x’ — fm (2ωx’ ± ω2h),
причем знак второго слагаемого в скобках надо брать положительным при х’ < 0 и отрицательным при х’ > 0. Решение такого уравнения при движении точки G влево и вправо получается, конечно, различным. Если Л — 0 и хорда является диаметром, то вместо кулонова трения получается вязкое демпфирование, зависящее от скорости.
- Две основные задачи динамики точки
- Прямолинейное движение точки
- Криволинейное движение материальной точки
- Движение несвободной материальной точки
- Сложное движение точки
- Сложение движение твердого тела
- Кинематика сплошной среды
- Аксиомы классической механики
Составление систем дифференциальных уравнений движения материальной точки, на которую действует некоторая система сил для определения движения точки под действием этих сил.
Пусть на материальную точку действует некоторая система сил и требуется определить движение точки под действием этих сил.
Уравнение второго закона динамики для материальной точки массой m запишется в виде
m∙ a = ΣFi (1)
где a — ускорение точки;
Fi — силы, действующие на точку, включая реакции связей.
Спроецировав уравнение (1) на декартовы оси координат, получим систему из трех уравнений
m∙ ax = ΣFxi
m∙ ay = ΣFyi (2)
m∙ az = ΣFzi
где ax , ay , az — проекции ускорения точки на декартовы оси координат;
Fxi , Fyi , Fzi — проекция i<-той силы на соответствующую ось.
Учитывая, что
получаем систему дифференциальных уравнений первого порядка относительно проекций скорости точки
или второго порядка относительно координат точки
Спроецировав уравнение (1) на естественные оси координат, получим следующую систему уравнений
где aτ и an — касательное и нормальное ускорение точки;
Fτi , Fni , Fbi — проекции i-той силы на касательную, нормаль и бинормаль соответственно.
Учитывая, что
aτ = dV/dt,
an = V2/ρ,
ab = 0
получим:
mdV/dt = ΣFτi
mV2/ρ = ΣFni (5)
0 = ΣFbi
В зависимости от того, что известно о движении точки, дифференциальные уравнения записывают или в декартовых или в естественных координатах.
- Пример решения задачи по теме
- Интегрирование дифференциальных уравнений движения
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
Динамика
1. Предмет и основные задачи динамики.
Д
изучает механическое движение материальных
тел под действием приложенных сил.
Простейшим материальным объектом
является материальная точка. Абсолютно
твердое тело можно рассматривать как
неизменяемую систему материальных
точек. Расстояние между точками остаются
постоянными.
Силы, действующие
на материальные тела, могут быть
постоянными или переменными. Постоянной
можно считать силу тяжести. Переменные
силы могут зависеть от времени, от
положения тела или от его скорости. В
частности, сила
упругости
зависит от положения груза, сила
сопротивлениязависит от скорости (рис. 1). От времени
зависит сила тяги электровоза при
постепенном включении реостата. На тело
одновременно может действовать несколько
разных сил. Так, при возвращении на землю
космического аппарата на него действуют:
постоянная сила тяжести, сила сопротивления,
зависящая от скорости, сила тяготения,
зависящая от положения тела. Законы
сложения или приведения переменных сил
такие же, как и постоянных сил.
Движение материальных
объектов рассматривается по отношению
к определенной системе отсчета. Систему
отсчета, связанную с землей, называют
инерциальной. В такой системе соблюдается
основной закон динамики:
,
(1.1)
где m-масса
точки,
–
ускорение точки.
Масса – это мера
инертности. Она не зависит от природы
силы, приложенной к точке. Чем больше
масса, тем большую силу необходимо
приложить к точке, чтобы изменить ее
скорость.
Материальная точка
является свободной, если на нее не
наложены связи. Движение такой точки
зависит от действующих на нее активных
(заданных) сил и начальных условий. Если
на точку наложены какие-либо связи, то
ее движение зависит от активных сил и
реакций связей.
Множество частных
задач динамики можно свести к двум
основным задачам:
-
по заданному
движению материальной точки или системы
определить силы, действующие на точку
или систему – прямая задача динамики; -
по заданным силам,
действующим на точку или систему,
определить закон движения этой системы
– обратная задача.
2. Дифференциальные уравнения движения материальной точки.
Для решения
соответствующей задачи динамики
необходимо составить уравнения,
устанавливающие зависимость между
массой движущей точки, ее ускорением и
действующими на нее ускорениями.
Дифференциальное уравнение движения
точки в векторной форме и имеет вид:
(2.1)
Уравнение (2.1) можно
спроецировать на оси декартовой системы
координат:
,
,
(2.2)
Если точка по
криволинейной траектории, то для решения
соответствующей задачи динамики
используют дифференциальные уравнения
движения точки в естественной форме (в
проекциях на естественные оси координат):
,
.
(2.3)
-
Решение первой задачи динамики.
При решении первой
задачи динамики можно использовать
дифференциальные уравнения движения
точки в векторной, координатной и
естественной форме. Решение задачи
необходимо осуществлять в следующем
порядке:
1. изобразить точку
в текущий момент времени;
2. показать активные
(заданные) силы, действующие на точку;
3. освободить точку
от связей, заменяя действие связей
реакциями;
4. выбрать систему
координат, если она не указана в задаче;
5. составить
дифференциальные уравнения движения
точки в выбранной системе координат;
6. по заданным
уравнениям движения определить проекции
ускорения на оси координат;
7. из дифференциальных
уравнений движения определить проекции
силы, действующей на точку.
РЕШЕНИЕ ПЕРВОЙ
ЗАДАЧИ ДИНАМИКИ ДЛЯ СВОБОДНОЙ МАТЕРИАЛЬНОЙ
ТОЧКИ
ПРИМЕР 1.
Материальная точка
массой m
движется по окружности радиуса R
согласно уравнению OM=S=Re2t
(рис. 2). Определить величину равнодействующей
сил, приложенных к точке, как функцию
времени.
РЕШЕНИЕ.
1. Так как точка
движется по криволинейной траектории,
используем дифференциальные уравнения
движения точки в проекциях на естественные
оси: касательную
и нормаль
:
,
.
(1)
2. Выразим из закона
движения точки проекции ускорения на
естественные оси
;
;
(2)
Рисунок
1
.
(3)
Подставим (2) и
(3) в (1), выразим проекции силы
на
естественные оси:
;
.
Силу,
действующую на точку, выразим через ее
проекции
на естественные оси
.
РЕШЕНИЕ ПЕРВОЙ
ЗАДАЧИ ДЛЯ НЕСВОБОДНОЙ МАТЕРИАЛЬНОЙ
ТОЧКИ
ПРИМЕР 2.
Определить давление
автомобиля весом Р=10000Н, движущегося с
постоянной скоростью
36км/ч
по мосту с радиусом кривизны20м,
если автомобиль находится в центре
вогнутого (рис. 3,а) и выпуклого (рис. 3,б)
моста.
Рисунок
2
РЕШЕНИЕ
.
1. Применим
дифференциальное уравнение движения
точки в проекции на нормаль n:
,
(1)
где
— сумма проекций на нормаль заданных
сил и реакций связей;
для схемы а):
;
Н;
для схемы б):
;
Н.
Соседние файлы в предмете Теоретическая механика
- #
- #
- #
- #
Дифференциальные уравнения движения точки
С помощью дифференциальных уравнений движения решается вторая задача динамики. Правила составления таких уравнений зависят от того, каким способом хотим определить движение точки.
1) Определение движения точки координатным способом.
Рассмотрим свободную материальную точку, движущуюся под действием сил ,
,..,
. Проведем неподвижные координатные оси Oxyz (рис.4). Проектируя обе части равенства
на эти оси и учитывая,что
и т.д., получим дифференциальные уравнения криволинейного движения точки в проекциях на оси прямоугольной декартовой системы координат:
,
,
.
Рис.4
Так как действующие на точку силы могут зависеть от времени, от положения точки и от ее скорости, то правые части уравнений могут содержать время t, координаты точки х, у, z и проекции ее скорости . При этом в правую часть каждого из уравнений могут входить все эти переменные.
Рекомендуемые материалы
Чтобы с помощью этих уравнений решить основную задачу динамики, надо, кроме действующих сил, знать еще начальные условия, т.е. положение и скорость точки в начальный момент. В координатных осях Oxyz начальные условия задаются в виде: при
.
Зная действующие силы, после интегрирования уравнений найдем координаты х, y, z движущейся точки, как функции времени t, т.е. найдем закон движения точки.
Пример 3. Изучим движение тела, брошенного с начальной скоростью под углом
к горизонту, рассматривая его как материальную точку массы т. При этом сопротивлением воздуха пренебрежём, а поле тяжести будем считать однородным (Р=const), полагая, что дальность полёта и высота траектории малы по сравнению с радиусом Земли.
Поместим начало координат О в начальном положении точки. Направим ось вертикально вверх; горизонтальную ось Ox расположим в плоскости, проходящей через Оy и вектор
, а ось Oz проведём перпендикулярно первым двум осям (рис.5). Тогда угол между вектором
и осью Ox будет равен
.
Рис.5
Изобразим движущуюся точку М где-нибудь на траектории. На точку действует одна только сила тяжести , проекции которой на оси координат равны:
,
,
.
Подставляя эти величины в дифференциальные уравнения и замечая, что и т.д. мы после сокращения на m получим:
,
,
.
Умножая обе части этих уравнений на dt и интегрируя, находим:
,
,
Начальные условия в нашей задаче имеют вид:
при t=0:
,
,
,
.
Удовлетворяя начальным условиям, будем иметь:
,
,
.
Подставляя эти значения С1, С2 и С3 в найденное выше решение и заменяя ,
,
на
придём к уравнениям:
.
Интегрируя эти уравнения, получим:
.
Подстановка начальных данных даёт С4=С5=С6=0, и мы окончательно находим уравнения движения точки М в виде:
(1)
Из последнего уравнения следует, что движение происходит в плоскости Оxy.
Имея уравнение движения точки, можно методами кинематики определить все характеристики данного движения.
1. Траектория точки. Исключая из первых двух уравнений (1) время t, получим уравнение траектории точки:
(2)
Это – уравнение параболы с осью, параллельной оси Оy. Таким образом, брошенная под углом к горизонту тяжёлая точка движется в безвоздушном пространстве по параболе (Галилей).
2. Горизонтальная дальность. Определим горизонтальную дальность, т.е. измеренное вдоль оси Оx расстояние ОС=Х. Полагая в равенстве (2) y=0, найдём точки пересечения траектории с осью Ох. Из уравнения:
получаем
Первое решение дает точку О, второе точку С. Следовательно, Х=Х2 и окончательно
. (3)
Из формулы (3) видно, что такая же горизонтальная дальность Xбудет получена при угле , для которого
, т.е. если угол
. Следовательно, при данной начальной скорости
в одну и ту же точку С можно попасть двумя траекториями: настильной (
) и навесной (
).
При заданной начальной скорости наибольшая горизонтальная дальность в безвоздушном пространстве получается, когда
, т.е. при угле
.
3. Высота траектории. Если положить в уравнении (2)
, то найдется высота траектории Н:
. (4)
4. Время полета. Из первого уравнения системы (1) следует, что полное время полета Т определяется равенством . Заменяя здесь Х его значением, получим
.
При угле наибольшей дальности все найденные величины равны:
Полученные результаты практически вполне приложимы для ориентировочного определения характеристик полета снарядов (ракет), имеющих дальности порядка 200…600 км, так как при этих дальностях (и при ) снаряд основную часть своего пути проходит в стратосфере, где сопротивлением воздуха можно пренебречь. При меньших дальностях на результат будет сильно влиять сопротивление воздуха, а при дальностях свыше 600 км силу тяжести уже нельзя считать постоянной.
Пример 4. Из пушки, установленной на высоте h, произвели выстрел под углом к горизонту (рис. 6). Ядро вылетело из ствола орудия со скоростью u. Определим уравнения движения ядра.
Рис.6
Чтобы правильно составить дифференциальные уравнения движения, надо решать подобные задачи по определённой схеме.
а) Назначить систему координат (количество осей, их направление и начало координат). Удачно выбранные оси упрощают решение.
б) Показать точку в промежуточном положении. При этом надо проследить за тем, чтобы координаты такого положения обязательно были положительными (рис.6).
в) Показать силы, действующие на точку в этом промежуточном положении (силы инерции не показывать!).
В этом примере – это только сила , вес ядра. Сопротивление воздуха учитывать не будем.
г) Составить дифференциальные уравнения по формулам: . Отсюда получим два уравнения:
и
.
д) Решить дифференциальные уравнения.
Полученные здесь уравнения – линейные уравнения второго порядка, в правой части – постоянные. Решение этих уравнений элементарно.
и
Осталось найти постоянные интегрирования. Подставляем начальные условия (при t = 0 x = 0, y = h,,
) в эти четыре уравнения:
,
, 0 = С2, h = D2.
Подставляем в уравнения значения постоянных и записываем уравнения движения точки в окончательном виде
Имея эти уравнения, как известно из раздела кинематики, можно определить и траекторию движения ядра, и скорость, и ускорение, и положение ядра в любой момент времени.
Как видно из этого примера, схема решения задач довольно проста. Сложности могут возникнуть только при решении дифференциальных уравнений, которые могут оказаться непростыми.
2) Определение движения точки естественным способом.
Координатным способом обычно определяют движение точки, не ограниченные какими-либо условиями, связями. Если на движение точки наложены ограничения, на скорость или координаты, то определить такое движение координатным способом совсем не просто. Удобнее использовать естественный способ задания движения.
Определим, например, движение точки по заданной неподвижной линии, по заданной траектории (рис. 7).
Рис.7
На точку М кроме заданных активных сил , действует реакция линии. Показываем составляющие реакции
по естественным осям
Составим основное уравнение динамики и спроектируем его на естественные оси
Так как то получим дифференциальные уравнения движения, такие
(5)
Здесь сила – сила трения. Если линия, по которой движется точка, гладкая, то Т = 0 и тогда второе уравнение будет содержать только одну неизвестную – координату s:
.
Решив это уравнение, получим закон движения точки , а значит, при необходимости, и скорость и ускорение. Первое и третье уравнения (5) позволят найти реакции
и
.
Пример 5. Лыжник спускается по цилиндрической поверхности радиуса r. Определим его движение, пренебрегая сопротивлениями движению (рис. 8).
Рис.8
Схема решения задачи та же, что и при координатном способе (пример 4). Отличие лишь в выборе осей. Здесь оси N и Т движутся вместе с лыжником. Так как траектория – плоская линия, то ось В, направленную по бинормали, показывать не нужно (проекции на ось В действующих на лыжника сил будут равны нулю).
Дифференциальные уравнения по (5) получим такие
(6)
Первое уравнение получилось нелинейным: . Так как
, то его можно переписать так:
. Такое уравнение можно один раз проинтегрировать. Запишем
Тогда в дифференциальном уравнении переменные разделятся:
. Интегрирование дает решение
Так как при t = 0:
и
, то С1= 0 и
а
К сожалению, в элементарных функциях второй интеграл найти невозможно. Но и полученное решение позволяет сделать некоторые выводы. Можно найти скорость лыжника в любом положении как функцию угла . Так в нижнем положении, при
,
. А из второго уравнения (6) при
можно определить давление:
. То есть давление на лыжника в нижнем положении равно его трехкратному весу.
Пример 6: Точка, имеющая массу m, движется из состояния покоя по окружности радиуса R с постоянным касательным ускорением . Определить действующую на точку силу в момент, когда она пройдет по траектории расстояние
.
Рис.9
Решение: Применяя дифференциальные уравнения движения точки в проекциях на естественные оси, имеем:
;
;
;
Так как , то
,
2.1. Основные принципы инженерной защиты населения – лекция, которая пользуется популярностью у тех, кто читал эту лекцию.
;
;
; следовательно
;
; следовательно
Дифференциальное векторное уравнение движения точки
Основной закон механики, как указывалось, устанавливает для материальной точки связь между кинематическими (w — ускорение) и кинетическими (

Он справедлив для инерциальных систем, которые выбираются в качестве основных систем, поэтому фигурирующее в нем ускорение 
Как указывалось, сила, действующая на точку, в общем случае зависит от времени 



В последней записи основной закон механики представляет собой дифференциальное уравнение второго порядка, служащее для определения уравнения движения точки в конечной форме. Уравнение, приведенное выше, называется уравнением движения точки в дифференциальной форме и векторном виде.
Дифференциальные уравнение движения точки в проекциях на декартовы координаты
Интегрирование дифференциального уравнения (см. выше) в общем случае представляет собой сложную задачу и обычно для решения ее от векторного уравнения переходят к скалярным уравнениям. Так как сила, действующая на точку, зависит от времени 




Естественная форма дифференциальных уравнений движения точки
В тех случаях, когда заранее известна траектория точки, например, когда на точку наложена связь, определяющая ее траекторию, удобно пользоваться проекцией векторного уравнения движения на естественные оси, направленные по касательной, главной нормали и бинормали траектории. Проекции силы, которые назовем соответственно 



то уравнения движения в проекции на естественные оси имеют вид:

Последние уравнения называются естественными уравнениями движения. Из этих уравнений следует, что проекция действующей на точку силы на бинормаль 






Дифференциальные уравнения движения точки в криволинейных координатах
Если положение точки задано ее криволинейными координатами 

Или, так как 

то последние уравнения перепишем в виде:

где скалярные произведения