Как решать дифференциальные уравнения
СОДЕРЖАНИЕ ТЕКУЩЕЙ СТАТЬИ
- Основные понятия и определения
-
- Определения
- Типы уравнений
- Алгоритм решения
- Дифференциальные уравнения первого порядка
-
- ДУ с разделяющимися переменными
- Однородные ДУ
- Линейные неоднородные ДУ
- ДУ Бернулли
- ДУ в полных дифференциалах
- Дифференциальные уравнения второго порядка
-
- ДУ допускающие понижение порядка
- Линейные однородные ДУ с постоянными коэффицентами
- Линейные неоднородные ДУ с постоянными коэффициентами
- Метод Лагранжа
Введите уравнение
Условия к задаче (необязательно)
Пример 1 Пример 2 Правила ввода
Дифференциальные уравнения бывают обыкновенными и в частных производных. В этой статье мы будем говорить об обыкновенных уравнениях и о том, как их решать.
Основные понятия и определения
Определения
Обыкновенные дифференциальные уравнения – это уравнения, содержащие функцию $y(x)$ только от одной неизвестной переменной (например, $x$).
Рассмотрим это на следующих практических примерах. $$ y’ = xy $$ $$ y” = 1 $$
Итак, в первом диффуре присутствует независимая переменная $x$, неизвестная функция $y(x)$ и производная этой функции $y'(x)$. А во втором случае нет $x, y(x),y'(x)$, а есть только вторая производная функции $y”(x)$. Значит, для того, чтобы уравнение называлось дифференциальным необязательно иметь $y(x)$ и $x$, а должно быть производная $y(x)$ любого порядка.
Порядок дифференциального уравнения – это порядок старшей производной неизвестной функции $y(x)$ в уравнении.
В первом случае максимальная производная первого порядка, значит, и само ДУ первого порядка. А во втором случае уравнение имеет вторую производную $y”(x)$, поэтому это ДУ второго порядка.
Общее решение дифференциального уравнения – это семейство функций $y = f(x,C)$, при подстановке которых в заданное исходное уравнение мы получаем равенство левой и правой части. Здесь $C$ произвольная константа. Процесс нахождения таких решений называется интегрированием дифференциального уравнения.
Частное решение дифференциального уравнения – это решение, полученное из общего решения, путем нахождения константы $C$ из дополнительных условий в задаче.
Типы уравнений
- ДУ первого порядка
– с разделяющимися переменными
– однородные
– линейные неоднородные
– уравнение Бернулли - ДУ второго порядка
– уравнения допускающие понижение порядка
– однородные с постоянными коэффициентами
– неоднородные с постоянными коэффициентами
Алгоритм решения
- По старшей производной функции $y(x)$ определить порядок ДУ
- Зная порядок, определить тип уравнения
- Узнав тип, подобрать подходящий метод решения
- Используя метод, найти общее решение
- Получить частное решение из общего путем вычисления неизвестной $C$
В некоторых случаях для решения дифференциальных уравнений удобно переписать производные в таком виде (например, это нужно для ДУ с разделяющимися переменными). $$y’ = frac{dy}{dx}$$
ОБЯЗАТЕЛЬНО! Чтобы успешно решать дифференциальные уравнения необходимо уметь находить интегралы. Поэтому, если вы забыли данную тему, то её нужно вспомнить!
| Пример 1 |
| Дана функция $y = Ce^{frac{x^2}{2}} $. Проверить является ли функция решением дифференциального уравнения $y’ = xy$ |
| Решение |
|
Для того, чтобы проверить является ли функция решением нужно подставить её в исходное ДУ. Найдем производную функции. $$y’ = (Ce^{frac{x^2}{2}})’ = Ce^{frac{x^2}{2}} cdot (frac{x^2}{2})’ = Ce^{frac{x^2}{2}} cdot x = Cxe^{frac{x^2}{2}}$$ Теперь подставим $y’$ и $y$ в исходное уравнение. $$ Cxe^{frac{x^2}{2}} = x Ce^{frac{x^2}{2}} $$ Получили равенство левой и правой части, значит, функция $y = Ce^{frac{x^2}{2}} $ является общим решением ДУ. |
| Ответ |
| $$y = Ce^{frac{x^2}{2}} $$ |
Дифференциальные уравнения первого порядка
ДУ с разделяющимися переменными
Уравнения такого типа имеют следующий вид: $$ f_1(x)g_1(y)dy = f_2(x)g_2(y)dx$$ Общее решение такого ДУ нужно находить путем разделения переменных с иксами и с игреками: $$int frac{g_1(y)}{g_2(y)}dy = int frac{f_2(x)}{f_1(x)}dx$$
СОВЕТ: Если не удается определить тип диффура первого порядка, то рекомендуем мысленно попытаться разделить переменные иксы от игреков. Возможно перед вами хитрое дифференциальное уравнение с разделяющимися переменными.
Алгоритм нахождения общего решения:
- Переписываем производные через $y’ = frac{dy}{dx}$
- Разделяем все $y$ в левую часть уравнения, а все $x$ в правую
- Интегрируем обе части уравнения
| Пример 2 |
| Найти общее решение дифференциального уравнения первого порядка с разделяющимися переменными $y’ = xy$ |
| Решение |
|
Видим, что в условии задачи присутствует производная от неизвестной функции $y(x)$ первого порядка. Значит, перед нами диффур 1-го порядка. Забегая вперед скажем, что данный диффур из задачи является дифференциальным уравнением с разделяющимися переменными. Что это означает? Это означает, что можно в уравнении перенести всё что содержит $y$ в левую часть равенства, а то, что содержит $x$ перенести в правую часть. То есть разделить “игрики” от “иксов” по разные стороны. Но прежде, чем это делать стоит переписать производную таким образом: $$y’ = frac{dy}{dx}$$ После замены производной игрека исходное уравнение приобретает такой формат: $$frac{dy}{dx} = xy$$ Теперь, как сказали ранее, начинаем отделять игрики от иксов по разные стороны. Для этого обе части уравнения необходимо умножить на $dx$, а ещё разделить на $y$. $$ frac{dy}{y} = xdx $$ Теперь необходимо проинтегрировать обе части уравнения, чтобы получить функцию $y$. Для этого навешиваем значок интеграла на обе части уравнения. $$ int frac{dy}{y} = int xdx $$ Вспоминаем, что левый интеграл равен натуральному логарифму, а правый интеграл $frac{x^2}{2}$. А так как интеграл неопределенный, то необходимо прибавить константу $C$. $$ ln|y| = frac{x^2}{2} + C $$ Теперь необходимо вытащить $y$ для того, чтобы записать окончательный ответ в виде общего решения. Для этого вспоминаем, что игрик в $ln|y| = x$ равен $y = e^x$. Поэтому продолжая решать наше уравнение получаем. $$ y = e^{frac{x^2}{2} + C} $$ Далее вспоминаем свойство степеней $a^{x+y} = a^x cdot a^y$. Таким образом делаем преобразования нашего уравнения. Так как $e^C$ это константа, то её можно переписать следующим видом $e^C = C$. И после этого получаем окончательный ответ исходного уравнения, называемый общим решением. $$ y = Ce^{frac{x^2}{2}} $$ |
| Ответ |
| $$ y = Ce^{frac{x^2}{2}} $$ |
| Пример 3 |
| Найти частное решение дифференциального уравнения первого порядка с разделяющимися переменными $y’ = frac{2x}{1+x^2}$, если $y(0) = 0$. |
| Решение |
|
Начнем решать с того, что представим производную в исходном уравнении в виде $y’ = frac{dy}{dx}$: $$ frac{dy}{dx} = frac{2x}{1+x^2} $$ Теперь разделяем переменные иксы от игреков по разные стороны равенства путем умножения обеих частей уравнения на $dx$: $$ dy = frac{2x}{1+x^2} dx $$ Навешиваем знак интеграла на левую и правую часть, а затем решаем интегралы: $$ int dy = int frac{2x}{1+x^2} dx $$ $$ y = int frac{2x}{1+x^2} dx $$ Замечаем, что $(1+x^2)’ = 2x$. Поэтому $2x$ можно занести под знак дифференциала, чтобы решить интеграл: $$ y = int frac{d(1+x^2)}{1+x^2} = ln (1+x^2) + C $$ Получили общее решение $y = ln (1+x^2) + C$. В условии задачи просят найти частное решение при условии $y(0) = 0$. Это означает, что нужно из последного условия найти константу $C$. Из $y(0) = 0$ видно, что $x = 0$, а $y = 0$. Подставляем их в общее решение дифференциального уравнения и вычисляем $C$: $$ln(1+0^2)+C = 0$$ $$ln 1+C = 0$$ $$0 + C = 0$$ $$C=0$$ Теперь заменив в общем решении $C$ на ноль, получаем частное решение: $$y = ln(1+x^2)$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$y = ln(1+x^2)$$ |
Однородные ДУ
Чтобы проверить является ли предложенное уравнение однородным нужно заменить $x$ и $y$ на $lambda x$ и $lambda y$. Производную $y’$ заменять не нужно. Если все $lambda$ после элементарных преобразований удастся уничтожить, то перед вами однородное дифференциальное уравнение первого порядка.
Решается по следующему алгоритму:
- Проверить уравнение на однородность с помощью $lambda$
- Привести уравнение к виду $y’ = f(frac{y}{x})$
- Выполнить замену $frac{y}{x} = t$ и $y’ = t’x+t$
- Решить уравнение методом разделяющихся переменных
| Пример 4 |
| Найти общее решение дифференциального уравнения первого порядка $$y’ = frac{y}{x} – 1$$ |
| Решение |
|
Так как разделить переменные не получается, то проверим уравнение на однородность. Для этого вместо $x$ и $y$ выполним подстановку $lambda x$ и $lambda y$: $$y’ = frac{lambda y}{lambda x} – 1$$ Выполняем сокращение $lambda$ в числителе и знаменателе: $$y’ = frac{y}{x} – 1$$ После сокращения все $lambda$ уничтожились, значит перед нами однородное дифференциальное уравнение первого порядка. Решим его с помощью замены $frac{y}{x} = t$ и $y’ = t’x + t$: $$ t’x + t = t – 1$$ Переносим $t$ в одну сторону и тем самым уничтожаем его: $$ t’x = -1 $$ Теперь это ДУ с разделяющимися переменными. Запишем его в привычном для него виде: $$ frac{dt}{dx} x = -1 $$ Разделим переменные домножением на $dx$ и делением на $x$ обеих частей равенства: $$dt = -frac{dx}{x}$$ Интегрируем обе части: $$int dt = – int frac{dx}{x}$$ $$t = -ln|x|+C$$ Выполняем назад замену $t = frac{y}{x}$: $$frac{y}{x} = -ln|x|+C$$ Умножаем обе части на $x$, чтобы получить окончательный ответ общего решения: $$y = -xln|x| +Cx$$ |
| Ответ |
| $$y = -xln|x| +Cx$$ |
| Пример 5 |
| Решить дифференциальное уравнение первого порядка $xy+y^2=(2x^2+xy)y’$ |
| Решение |
|
Сперва проверим уравнение на однородность. Подставляем $lambda$ вместо $x$ и $y$. $$lambda x cdot lambda y + (lambda y)^2 = (2 (lambda x)^2 + lambda xcdot lambda y)y’$$ После вынесения $lambda$ слева и справа за скобки получаем $$ lambda^2(xy+y^2) = lambda^2(2x^2+xy)y’,$$ где все $lambda$ сокращаются. А это подтвержает однородность уравнения. Перед тем, как выполнить замену $t = frac{y}{x}$ нужно привести исходное уравнение к виду $y = f(frac{y}{x})$. Для этого разделим левую и правую часть равенства на $x^2$: $$frac{y}{x}+frac{y^2}{x^2} = (2+frac{y}{x})y’.$$ Теперь производим замену $t = frac{y}{x}$ и $y’ = t’x+t$ в преобразованном уравнении: $$t+t^2=(2+t)(t’x+t).$$ Раскрываем скобки и сокращаем одинаковые слагаемые $$t+t^2 = 2t’x+2t+t’xt+t^2$$ $$2t’x+t’xt=-t.$$ Далее в полученном уравнении разделяем переменные $t$ и $x$ по разные стороны знака равенства. Для этого выносим за скобку $t’x$ $$t’x(2+t)=-t.$$ Делим на $t$ обе части уравнения $$t’xfrac{2+t}{t}=-1.$$ Представляем производную $t’ = frac{dt}{dx}$ и переносим $dx$ и $x$ в правую часть равенства $$frac{2+t}{t}dt = -frac{dx}{x}.$$ Интегрируем обе части уравнения $$int frac{2+t}{t}dt = – int frac{dx}{x}$$ $$int frac{2}{t}dt+int dt = -int frac{dx}{x}$$ $$2ln|t|+t = -ln|x|+C.$$ Выполняем обратную замену $t = frac{y}{x}$: $$2ln|frac{y}{x}|+frac{y}{x}=-ln|x|+C.$$ Упрощаем полученное равенство с помощью элементарных преобразований и свойств натурального логарифма $$2ln|y|-2ln|x|+frac{y}{x} = -ln|x|+C$$ $$2ln|y|+frac{y}{x}=ln|x|+C$$ $$2ln|y|+frac{y}{x}=ln|x|+ln|C|$$ $$2ln|y|+frac{y}{x}=ln|Cx|$$ $$ln y^2+frac{y}{x}=ln|Cx|$$ $$ln y^2 = ln|Cx|-frac{y}{x}$$ $$y^2 = Cxe^frac{-y}{x}.$$ Привели решение к такому виду через $y^2$. Это называется общим интегралом дифференциального уравнения. Ответ в таком виде остается в таком формате. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$y^2 = Cxe^frac{-y}{x}$$ |
Линейные неоднородные ДУ
Линейное неоднородное дифференциальное уравнение 1-го порядка имеет следующий вид $$y’+p(x)y=q(x).$$
Для его решения существует два способа: метод Бернулли и вариация произвольной постоянной. В первом методе нужно сделать замену на произведение двух функций $y = uv$, а во втором способе необходимо найти неизвестную функцию $C(x)$.
Алгоритм метода Бернулли:
- Выполняем замену $y=uv$ и $y’ = u’v+uv’$
- Находим функции $u(x)$ и $v(x)$ с помощью решения системы двух уравнений
- Подставляем найденные $u(x)$ и $v(x)$ в уравнение $y=uv$, чтобы получить ответ
Алгоритм метода вариации произвольной постоянной:
- Решаем исходное уравнение в качестве однородного методом разделяющихся переменных
- В полученном общем решении заменяем константу $C$ на функцию $C(x)$
- Подставляем общее решение и его производную в исходное уравнение, чтобы найти $C(x)$
- Полученное $C(x)$ подставляем в общее решение однородного уравнения и записываем ответ
| Пример 6 |
| Найти частное решение дифференциального уравнения первого порядка методом Бернулли $xy’-2y=2x^4$, если $y(1)=0$. |
| Решение |
|
Приводим уравнение к виду $y’+p(x)y=q(x)$ путем деления на $x$ обеих частей равенства $$y’-2frac{y}{x}=2x^3.$$ Делаем замену в полученном уравнении на $y=uv$ и $y’=u’v+uv’$ $$u’v+uv’-2frac{uv}{x}=2x^3.$$Выносим за скобку $u$, чтобы в дальнейшем составить систему уравнений: $$u’v+u(v’-2frac{v}{x})=2x^3.$$ Теперь приравниваем к нулю выражение в скобках и составляем систему уравнений $$begin{cases} v’ – 2frac{v}{x} = 0 \ u’v = 2x^3 end{cases},$$ в которой начнем сначала решать первое уравнение для нахождения функции $v(x)$. Разделяем в нём переменные $$begin{cases} frac{dv}{dx} = 2frac{v}{x} \ u’v = 2x^3 end{cases} Leftrightarrow begin{cases} frac{dv}{v} = 2frac{dx}{x} \ u’v = 2x^3 end{cases}.$$ Интегрируем первое уравнение в системе, чтобы получить функцию $v(x)$ $$begin{cases} ln|v| = 2ln|x| \ u’v = 2x^3 end{cases} Leftrightarrow begin{cases} v = x^2 \ u’v = 2x^3 end{cases}.$$ Теперь, зная, чему равно $v$ подставляем его во второе уравнение $$begin{cases} v=x^2 \ u’x^2 = 2x^3 end{cases} Leftrightarrow begin{cases} v=x^2 \ u = x^2+C end{cases}.$$ Записываем общее решение дифференциального уравнения $$y = uv Rightarrow y = x^4+Cx^2.$$ В условии задачи требуется найти частное решение из условия $y(1)=0$. Подставим в найденное общее решение $x=1$ и $y=0$, чтобы вычислить $C$ $$1^4+Ccdot 1^2 = 0 Rightarrow C = -1. $$ С учётом, что $C=-1$ записываем частное решение дифференциального уравнения $$y = x^4 – x^2.$$ |
| Ответ |
| $$y = x^4 – x^2$$ |
| Пример 7 |
| Найти общее решение дифференциального уравнения первого порядка $y’sin x-ycos x = 1$ методом вариации произвольной постоянной $C$. |
| Решение |
|
Перепишем уравнение в виде $$ y’ – y frac{cos x}{sin x} = frac{1}{sin x} .$$ Теперь записываем однородное дифференциальное уравнение $$y’ – y frac{cos x}{sin x} = 0,$$ решим его методом разделяющихся переменных: $$frac{dy}{dx} = y frac{cos x}{sin x}$$ $$int frac{dy}{y} = int frac{cos x}{sin x} dx.$$ Слева получается натуральный логарифм, а справа заносим косинус под знак дифференциала, чтобы получить логарифм синуса: $$ln|y| = ln|sin x| + C$$ $$y = Csin x.$$ Теперь заменяем константу $C$ на функцию $C(x)$ в полученном решении и находим производную $$y = C(x)sin x Rightarrow y’ = C'(x)sin x+ C(x)cos x.$$ Подставляем $y$ и $y’$ в неоднородное уравнение и решаем его относительно $C(x)$: $$C'(x)sin x+ C(x)cos x – C(x)sin x frac{cos x}{sin x} = frac{1}{sin x}$$ $$C'(x)sin x = frac{1}{sin x}$$ $$C'(x) = frac{1}{sin^2 x}.$$ В последнем уравнении можно разделить переменные, что и делаем, а затем интегрируем: $$ d(C(x)) = int frac{dx}{sin^2 x}$$ $$C(x) = -ctg x + C.$$ Берем решение $y = C(x)sin x$ и подставляем в него найденное $C(x) = -ctg x + C$ $$y = (-ctg x + C) sin x = Csin x – cos x.$$ Таким образом получили общее решение дифференциального уравнения $y = Csin x – cos x$. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$y = Csin x – cos x$$ |
ДУ Бернулли
Дифференциальное уравнение Бернулли имеет следующий вид $$y’ + g(x)y = f(x)y^alpha qquad (alpha neq 0), (alpha neq 1).$$
Алгоритм решения:
- Выполняем подстановку $y = z^frac{1}{1-alpha}$
- После подстановки получаем линейное уравнение $z’+p(x)z=q(x)$
- Решив линейное уравнение делаем обратную замену $z = y^{1-alpha}$
| Пример 8 |
| Найти общее решение дифференциального уравнения первого порядка $y’+y=xy^2$. |
| Решение |
|
Это уравнение Бернулли. Видим, что $alpha = 2$. Значит делаем замену на $y = z^frac{1}{1-alpha} = z^{-1}$. Отсюда $y’ = -frac{1}{z^2} cdot z’$. После подстановки в исходное уравнение имеем $$ -frac{z’}{z^2}+frac{1}{z}=frac{x}{z^2}.$$ Умножаем обе части равенства на $(-z^2)$, чтобы привести уравнение к линейному ДУ $$z’-z=-x, $$ которое можно решить методом Бернулли, либо вариацией произвольной постоянной. Выберем первый способ. Применяем подстановку $y=uv$ и $y’=u’v+uv’$ для последнего уравнения $$u’v+uv’-uv=-x.$$ Выносим за скобку $u$, чтобы затем построить систему уравнений для нахождения функций $u(x)$ и $v(x)$ $$u’v+u(v’-v) = -x.$$ Приравниваем к нулю скобку и получаем систему $$begin{cases} v’-v = 0 \ u’v = -x end{cases}.$$ Начинаем решать её с первого уравнения. Разделяем в нем переменные и затем интегрируем $$begin{cases} int frac{dv}{v} = int dx \ u’v = -x end{cases} Leftrightarrow begin{cases} ln|v| = x \ u’v = -x end{cases} Leftrightarrow begin{cases} v = e^x \ u’v = -x end{cases}. $$ Зная, что $v = e^x$ подставляем его во второе уравнение системы и решаем $$begin{cases} v = e^x \ u’ = -frac{x}{e^x} end{cases} Leftrightarrow begin{cases} v = e^x \ u = int (-x)e^{-x} dx end{cases}.$$ Для взятия интеграла воспользуемся методом интегрирования по частям $$u = int (-x)e^{-x} dx = begin{vmatrix} u = -x & du = -dx \ dv = e^{-x}dx & v = -e^{-x} end{vmatrix} = xe^{-x} – int e^{-x} dx = xe^{-x} +e^{-x} + C$$ Итак, получаем, что $$z = uv Rightarrow z = (xe^{-x} + e^{-x}+C) e^x = Ce^x +x + 1. $$ Вспоминаем, что была ещё одна замена в самом начале решения задачи $y = z^{-1}$, поэтому общее решение выглядит следующим образом $$y = frac{1}{Ce^x + x + 1}.$$ |
| Ответ |
| $$y = frac{1}{Ce^x + x + 1}$$ |
ДУ в полных дифференциалах
Дифференциальные уравнения в полных дифференциалах имеют следующий вид $$P(x,y) dx + Q(x,y) dy = 0, $$ при выполнении условия $frac{partial P}{partial y} = frac{partial Q}{partial x} $.
Алгоритм решения заключается в том, чтобы найти функцию $U(x,y)=C$, полный дифференциал которой, есть исходное ДУ:
- Проверяем условие, подтверждающее, что перед нами ДУ в полных дифференциалах
- Получаем $U(x,y)$ интегрируя функцию $P(x,y)$ по переменной $x$. В результате этого появится неизвестная функция $varphi(y)$
- Дифференцируем $U(x,y)$ по $y$ и приравниваем к $Q(x,y)$, чтобы найти $varphi(y)$
| Пример 9 |
| Найти общий интеграл $U(x,y)=C$ дифференциального уравнения $$(2x+5y)dx+(5x+3y^2)dy=0.$$ |
| Решение |
|
Убедимся, что данное уравнение в полных дифференциалах. Для этого проверим условие $frac{partial P}{partial y} = frac{partial Q}{partial x} $. Находим производные $$ P’_y = (2x+5y)’_y = 5, Q’_x = (5x+3y^2)’_x = 5, $$ и видим, что условие выполняется $P’_y=P’_x=5$. Находим функцию $U(x,y)$ беря интеграл по $x$ от функции $P(x,y)$ $$U(x,y) = int (2x+5y) dx = x^2 + 5yx + varphi(y).$$ Далее необходимо продифференцировать найденную $U(x,y)$ по $y$ $$U’_y = 5x + varphi'(y).$$ Осталось найти неизвестную функцию $varphi(y)$ приравняв $U’_y$ к $Q(x,y)$: $$5x + varphi'(y) = 5x+3y^2$$ $$varphi'(y) = 3y^2$$ $$varphi(y) = int 3y^2 dy = y^3 + C.$$ Теперь зная чему равна $varphi(y)$ подставляем её в $U(x,y)$ $$U(x,y)=x^2+5xy+y^3+C.$$ Записываем ответ в таком виде $$x^2+5xy+y^3 = C.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$x^2+5xy+y^3 = C.$$ |
Дифференциальные уравнения второго порядка
ДУ допускающие понижение порядка
Дифференциальные уравнения, допускающие понижение порядка бывают двух видов:
- Без функции $y$: $F(x,y’,y”)=0$
- Без переменной $x$: $F(y,y’,y”)=0$
Для решения таких диффуров в первом случае делаем замену $y’ = p(x)$, а во втором $y’ = p(y)$.
| Пример 10 |
| Найти частное решение дифференциального уравнения второго порядка $xy”+y’=0$ при условиях $y(1) = 0$ и $y'(1)=1$. |
| Решение |
|
Видим, что данный дифур попадает под первый случай, когда отсутствует в уравнении $y$, а есть только его производные. Значит, делаем замену $y’ = p(x)$ $$xp’+p=0.$$ Данное уравнение имеет разделяющиеся переменные. Начнем с того, что перепишем уравнение через $p’ = frac{dp}{dx}$ $$xfrac{dp}{dx} = -p.$$ Разделяем переменные налево и направо от знака равенства и затем интегрируем: $$ frac{dp}{p} = -frac{dx}{x}$$ $$ int frac{dp}{p} = -int frac{dx}{x}$$ $$ln|p| = -ln|x|+C_1.$$ Теперь избавимся от логарифмов, чтобы получить $p$: $$p = e^{-ln|x| + C_1}$$ $$p = frac{C_1}{x}.$$ Вспоминаем про ранее выполненную замену $$y’ = p(x) = frac{C_1}{x}.$$ Интегрируем для того, чтобы найти $y$ $$y = int frac{C_1}{x} dx = C_1 ln|x| + C_2.$$ Таким образом, общее решение дифференциального уравнения $$y = C_1 ln|x| + C_2.$$ Займемся поиском частного решения. Для этого используем два дополнительных равенства из условия задачи: $$y(1) = 0 Rightarrow C_1 ln|1| + C_2 = 0 Rightarrow C_2 = 0$$ $$y'(1)=1 Rightarrow frac{C_1}{1} = 1 Rightarrow C_1 = 1.$$ Записываем частное решение дифференциального уравнения $$y = ln|x|.$$ |
| Ответ |
| $$y = ln|x|$$ |
| Пример 11 |
| Найти частное решение дифференциального уравнения второго порядка $$yy”+y’^2 = 1, qquad y(0) = 1, y'(0) = 1.$$ |
| Решение |
|
Видим, что в диффуре отсутствует в явном виде переменная $x$, поэтому необходимо сделать замену $y’ = p(y)$ и отсюда $y” = p'(y)cdot y’ = p'(y)p$. Делаем замену и получаем уравнение $$yp'(y)p + p^2 = 1,$$ которое решим методом разделения переменных: $$ypfrac{dp}{dy} = 1-p^2$$ $$frac{p}{1-p^2}dp = frac{1}{y}dy.$$ Далее по плану необходимо проинтегрировать обе части уравнения, чтобы получить $p$ $$int frac{p}{1-p^2}dp = int frac{1}{y}dy.$$ В первом интеграле заносим под знак дифференциала $1-p^2$, чтобы получился натуральный логарифм, а во втором, используя таблицу интегрирования можно сразу записать ответ: $$-frac{1}{2} int frac{d(1-p^2)}{1-p^2} = ln|y| + C $$ $$-frac{1}{2} ln|1-p^2| = ln|y| + C.$$ Необходимо избавиться от логарифмов. Умножим обе части равенства на $(-2)$, а затем занесем эту двойку над икреком: $$ln|1-p^2| = -2ln|y|+C$$ $$ln|1-p^2| = ln frac{1}{y^2} + C.$$ Итак, теперь убирая логарифмы получаем: $$1-p^2 = C frac{1}{y^2}$$ $$p^2 = 1 – Cfrac{1}{y^2}$$ $$(y’)^2 = 1 – Cfrac{1}{y^2}.$$ Теперь найдем значение константы $C$ благодаря дополнительным условиям задачи $y = 1$ и $y’ = 1$. Подставляем их в последнее уравнение $$1^2 = 1 – Cfrac{1}{1^2} Rightarrow C = 0.$$ Зная теперь, что $C=0$ подставляем его в уравнение $(y’)^2 = 1 – Cfrac{1}{y^2}$: $$(y’)^2 = 1$$ $$y’ = pm 1.$$ Из условия помним, что $y’ = 1 > 0$, значит, берем только решение $y’ = 1$ и продолжаем его решать интегрированием $$y = int 1 dx = x + C.$$ Осталось найти снова постоянную $C$ теперь уже из условия $y(0) = 1$ $$y(0) = 0 + C = 1 Rightarrow C = 1.$$ Вот теперь можно записать ответ в виде частного решения, которое требовалось найти по условию данной задачи $$y = x + 1.$$ |
| Ответ |
| $$y = x + 1$$ |
Линейные однородные ДУ с постоянными коэффицентами
Линейность дифференциального уравнения заключается в том, что в уравнение входит неизвестная функция $y(x)$ и её производные только в первой степени, между собой не перемножаясь. Однородность определяется тем, что уравнение не содержит свободного члена. То есть он равен нулю.
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами выглядит следующим образом $$y”+py’+qy = 0.$$ Чтобы его решить необходимо составить характиристический многочлен и найти его корни. Для этого нужно заменить $y$ на $lambda$, степень которых будет соответствовать порядку производной $$y” Rightarrow lambda^2, qquad y’ Rightarrow lambda, qquad y Rightarrow 1.$$
В зависимости от получившихся корней имеем общее решение в различных видах:
- Действительные корни $lambda_1 neq lambda_2$, тогда $y = C_1e^{lambda_1 x}+C_2e^{lambda_2 x}$
- Действительные корни $lambda_1 = lambda_2$, тогда $y = C_1e^{lambda_1 x}+C_2xe^{lambda_1 x}$
- Комплексные корни $lambda_{1,2} = alphapmbeta i$, тогда $y = C_1e^{alpha x}cos beta x + C_2e^{alpha x}sin beta x$.
| Пример 12 |
| Найти общее решение дифференциального уравнения второго порядка $y”+y’-2y = 0$. |
| Решение |
|
Первым делом составляем характеристический многочлен. Заменяем $y$ на $lambda$ со степенями соответствующими порядку производной $y$ $$lambda^2 + lambda -2 = 0.$$ Обратите внимание, что $y$ имеет производную нулевого порядка, поэтому он заменяется на $lambda^0 = 1$. Итак, перед нами квадратное уравнение, начинаем решать: $$lambda_{1,2} = frac{-1pm sqrt{1^2-4cdot 1 cdot (-2)}}{2cdot 1} = frac{-1pm 3}{2}$$ $$lambda_1 = -2, qquad lambda_2 = 1.$$ Так как получили отличающиеся действительные корни, то общее решение записывается следующим образом $$y = C_1 e^{-2x} + C_2 e^{x}.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$y = C_1 e^{-2x} + C_2 e^{x}$$ |
Линейные неоднородные ДУ с постоянными коэффициентами
Линейное неоднородное ДУ с постоянными коэффициентами отличается от предыдущего типа уравнений наличием правой части от знака равенства $$y”+py’+q = f(x).$$
Общее решение такого диффура складывается из двух частей: общего решения однородного уравнения и частного решения неоднородного уравнения $$y_text{о.н.} = y_text{о.о.} + y_text{ч.н.}.$$
Частное решение неоднородного уравнения $y_text{ч.н.}$ подбирается исходя из вида правой части дифференциального уравнения. Затем в нём неизвестные постоянные находятся методом неопределенных коэффициентов.
| № | Правая часть | Корни характеристического многочлена | Вид частного решения |
| 1 | $$P_n (x)$$ | Число 0 не является корнем характеристического уравнения. | $$tilde{P_n}(x)$$ |
| Число 0 – корень характеристического уравнения кратности $S$. | $$x^s tilde{P_n}(x)$$ | ||
| 2 | $$P_n (x) e^{alpha x}$$ | Число $alpha$ не является корнем характеристического уравнения. | $$tilde{P_n} (x) e^{alpha x}$$ |
| Число $alpha$ является корнем характеристического уравнения кратности $S$. | $$x^s tilde{P_n} (x) e^{alpha x}$$ | ||
| 3 | $$P_n (x) cos beta x + Q_m (x) sin beta x$$ | Число $pm ibeta$ не является корнем характеристического уравнения. | $$tilde {P_n} cos beta x + tilde{Q_m} sin beta x$$ |
| Число $pm ibeta$ является корнем характеристического уравнения кратности $S$. | $$x^s (tilde {P_n} cos beta x + tilde{Q_m} sin beta x)$$ | ||
| 4 | $$e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$ | Число $alpha pm ibeta$ не является корнем характеристического уравнения. | $$e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$ |
| Число $alpha pm ibeta$ является корнем характеристического уравнения. | $$x^s e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$ |
| Пример 13 |
| Найти общее решение дифференциального уравнения второго порядка $y”+y = 4xcos x$. |
| Решение |
|
Сначала находим общее решение однородного уравнения $$y” + y = 0.$$ Строим характеристический многочлен $$lambda^2 + 1 = 0,$$ и находим его корни $$lambda_{1,2}=pm i.$$ Записываем получившееся общее решение однородного уравнения $$y_text{о.о.} = C_1 cos x + C_2 sin x.$$ Теперь необходимо подобрать частное решение неоднородного уравнения. Для этого смотрим на правую часть исходного уравнения и видим, что здесь многочлен первой степени умножается на косинус. Значит, необходимо выбрать из таблицы 3й случай. Причем корень характеристического уравнения совпадает с аргументом косинуса. Это значит, что требуется домножение на $x$ $$y_text{ч.н.} = x[(Ax+B)cos x + (Cx+D)sin x].$$Упростим последнее равенство и найдем от него вторую производную: $$y_text{ч.н.} = (Ax^2+Bx)cos x + (Cx^2 + Dx) sin x$$ $$y’_text{ч.н.} = (2Ax+B)cos x-(Ax^2+Bx)sin x + (2Cx+D)sin x + (Cx^2 + Dx) cos x.$$ Упростим $y’_text{ч.н}$ для удобства нахождения второй производной $$y’_text{ч.н.} = (2Ax+B+Cx^2+Dx)cos x + (2Cx+D-Ax^2-Bx)sin x.$$ Теперь можно найти вторую производную $$y”_text{ч.н.} = (2A+2Cx+D)cos x-(2Ax+B+Cx^2+Dx)sin x + (2C-2Ax-B)sin x + (2Cx+D-Ax^2-Bx)cos x.$$ Упрощаем последнее выражение $$y”_text{ч.н.} = (2A+4Cx+2D-Ax^2-Bx)cos x + (2C-4Ax-2B-Cx^2-Dx)sin x.$$ Подставляем найденные $y_text{ч.н.}$ и $y”_text{ч.н.}$ в исходный диффур из “дано” задачи $$(2A+4Cx+2D-Ax^2-Bx)cos x + (2C-4Ax-2B-Cx^2-Dx)sin x + (Ax^2+Bx)cos x + (Cx^2 + Dx) sin x = 4xcos x.$$ Упрощаем его $$(2A+4Cx+2D)cos x + (2C-4Ax-2B)sin x = 4xcos x.$$ Теперь подгоняем левую часть под правую, так чтобы можно было применить метод неопределенных коэффициентов и найти неизвестные $A,B,C,D$ $$(2A+2D)cos x+4Cxcos x + (2C-2B)sin x+(-4Ax)sin x = 4xcos x.$$ Смотрим на левую и правую часть и составляем систему $$begin{cases} 2A+2D = 0 \ 4C=4 \ 2C-2B=0 \ -4A = 0 end{cases} Leftrightarrow begin{cases} D=0 \ C= 1 \ B=1 \ A = 0end{cases}.$$ Подставляем полученные коэффициенты в частное решение неоднородного уравнения $$y_text{ч.н.} = xcos x + x^2sin x.$$ Теперь вспоминая, что $y_text{о.н.} = y_text{о.о.} + y_text{ч.н.}$ можем записать окончательный ответ $$y_text{о.н.} = C_1 cos x + C_2 sin x + xcos x + x^2sin x.$$ |
| Ответ |
| $$y = C_1 cos x + C_2 sin x + xcos x + x^2sin x$$ |
| Пример 14 |
| Найти общее решение дифференциального уравнения второго порядка $y”+y’=5x+2e^x$. |
| Решение |
|
Сначала найдем общее решение однородного дифференциального уравнения $$y”+y’=5x+2e^x.$$ Составляем характеристический многочлен однородного уравнения и находим его корни: $$lambda^2 + lambda = 0$$ $$lambda(lambda + 1) = 0$$ $$lambda_1 = 0, qquad lambda_2=-1.$$ Теперь можно записать общее решение $$y_text{о.о.} = C_1 + C_2e^{-x}.$$ Далее необходимо по правой части исходного неоднородного уравнения найти его частное решение путем подбора, используя данные таблицы. Первое слагаемое есть многочлен первой степени. И так как один из корней характеристического уравнения является нулем кратности 1, то решение ищем в виде $y = (Ax+B)x$. Второе слагаемое представляет собой произведение многочлена нулевой степени на экспоненту. Так как аргумент экспоненты не совпадает с одним из корней характеристического многочлена, то подбор будем делать в виде $y = Ce^x$. В итоге правую часть будем искать в виде суммы $$y_text{ч.н.} = (Ax+B)x+Ce^x.$$ Находим первую и вторую производную последней функции: $$y’ = 2Ax+B+Ce^x$$ $$y”=2A+Ce^x.$$ Подставляем полученные производные $y’$ и $y”$ в исходное дифференциальное уравнение: $$2A+Ce^x+2Ax+B+Ce^x = 5x+2e^x$$ $$2Ax+B+2A+2Ce^x=5x+2e^x.$$ Далее необходимо, используя метод неопределенных коэффициентов, найти значения $A,B,C$ составив систему уравнений $$begin{cases} 2A=5 \ 2C=2 \ B+2A = 0 end{cases} Leftrightarrow begin{cases} A=frac{5}{2} \ C=1 \ B=-5 end{cases}.$$ Подставляем найденные коэффициенты и получаем частное решение неоднородного уравнения $$y_text{ч.н.} = (frac{5}{2}x-5)x + e^x = frac{5}{2}x^2 – 5x + e^x.$$ Таким образом теперь можно записать общее решение неоднородного диффура $$y_text{о.н.} = y_text{о.о.} + y_text{ч.н.}=C_1 + C_2e^{-x} + frac{5}{2}x^2 – 5x + e^x.$$ |
| Ответ |
| $$y = C_1 + C_2e^{-x} + frac{5}{2}x^2 – 5x + e^x$$ |
Метод Лагранжа
Данный метод позволяет решать линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами даже в тех, случаях, когда правая часть уравнения не подходит под табличный вид. В этом случае целесообразно применить данный метод решения.
- Находим общее решение однородного уравнения $y = C_1 y_1(x) + C_2 y_2(x)$
- Варьируем постоянные $C_1$ и $C_2$ на функции $C_1(x)$ и $C_2(x)$
- Решаем систему методом Крамера $begin{cases} C_1 ‘(x) y_1 (x) + C_2 ‘(x) y_2 (x) = 0 \ C_1 ‘(x) y_1 ‘(x) + C_2 ‘(x) y_2 ‘(x) = f(x) end{cases} $
- Получаем $C_1(x)$ и $C_2(x).$
| Пример 15 |
| Найти частное решение дифференциального уравнения $$y”-2y’+y=frac{e^x}{x}, text{ при } y(1)=e, y'(1)=3e.$$ |
| Решение |
|
Так как правая часть диффура не подходит под табличный формат, то не получится подбирать частное решение по правой части как делали это в предыдущем примере. Воспользуется методом Лагранжа или как его еще называют вариация произвольной постоянной. Для начала найдем общее решение однородного уравнения $$y”-2y’+y=0.$$ Составляем характеристический многочлен и находим его корни: $$lambda^2-2lambda+1=0$$ $$(lambda-1)^2 = 0 Rightarrow lambda = 1 text{ с кратностью 2}.$$ Так как корень кратный, то общее решение однородного уравнения записывается следующим образом $$y = C_1 e^x + C_2 xe^x.$$ Теперь необходимо варьировать постоянные $C_1$ и $C_2$ на соответствующие функции $C_1 (x)$ и $C_2 (x)$. Теперь получившееся решение следует записать в виде $y = C_1 (x) e^x + C_2 (x) xe^x$. Здесь заметим, что $y_1 = e^x$ и $y_2 = xe^x$. Это нужно для дальнейшего хода решения, а именно построения системы уравнений. Составляем систему уравнений и решаем её методом Крамера $$begin{cases} C_1 ‘(x) e^x+C_2 ‘(x) xe^x = 0 \C_1 ‘(x) e^x + C_2 ‘(x) (e^x+xe^x) = frac{e^x}{x} end{cases}.$$ Находим главный определитель системы $$Delta = begin{vmatrix} e^x & xe^x \ e^x & e^x+xe^x end{vmatrix} = e^x(e^x+xe^x)-xe^{2x} = e^{2x}.$$ Вычисляем дополнительные определители: $$Delta_1 = begin{vmatrix} 0 & xe^x \ frac{e^x}{x} & e^x + xe^x end{vmatrix} = -xe^x frac{e^x}{x} = e^{2x}$$ $$Delta_2 = begin{vmatrix} e^x & 0 \ e^x & frac{e^x}{x} end{vmatrix} = e^x frac{e^x}{x} = frac{e^{2x}}{x}.$$ Итак, получаем решение системы уравнений $$C_1 ‘(x) = frac{Delta_1}{Delta} = frac{e^{2x}}{e^{2x}} = 1, qquad C_2 ‘(x) = frac{Delta_2}{Delta} = frac{e^{2x}}{x} frac{1}{e^{2x}} = frac{1}{x}.$$ Далее интегрируем полученные решения, чтобы избавиться от производной: $$C_1(x) = int 1 dx = x+tilde{C_1}$$ $$C_2(x)=int frac{dx}{x}=ln|x|+tilde{C_2}.$$ Подставляем полученные $C_1(x)$ и $C_2(x)$ в общее решение однородного уравнения и записываем общее решение неоднородного дифференциального уравнения $$y = (x+tilde{C_1}) e^x + (ln|x|+tilde{C_2}) xe^x.$$ По условию нам требуется найти частное решение при условиях $y(1)=e$ и $y'(1)=3e$. Поэтому находим сначала производную $$y’=e^x+(x+tilde{C_1})e^x+e^x+(ln|x|+tilde{C_2})(e^x+xe^x), $$ раскрываем скобки $$y’ = 2e^x+xe^x+tilde{C_1}e^x+e^xln|x|+xe^xln|x|+tilde{C_2}e^x+tilde{C_2}xe^x,$$ а затем составляем систему уравнений $$begin{cases} y'(1)=3e+tilde{C_1}e+2tilde{C_2}e = 3e \ y(1) = e+tilde{C_1}e + tilde{C_2}e = e end{cases} Rightarrow begin{cases} tilde{C_1}+2tilde{C_2}=0 \ tilde{C_1}+tilde{C_2}=0 end{cases} Rightarrow begin{cases} tilde{C_2} = 0 \ tilde{C_1}=0 end{cases}.$$ Теперь можно записать частное решение к задаче $$y = xe^x + xln|x|e^x = xe^x(1+ln|x|).$$ |
| Ответ |
| $$y = xe^x(1+ln|x|)$$ |
Пусть известен общий интеграл некоторого дифференциального уравнения первого порядка
![]() . (3.5)
. (3.5)
Покажем, как найти это уравнение. Для этого продифференцируем равенство (1.14) по переменной ![]()
 . (3.6)
. (3.6)
Составить дифференциальное уравнение первого порядка – значит найти соотношение между ![]() ,
, ![]() и
и ![]() . Но для этого достаточно исключить произвольную постоянную
. Но для этого достаточно исключить произвольную постоянную ![]() из системы уравнений (3.5) и (3.6):
из системы уравнений (3.5) и (3.6):

В результате получим новое уравнение, связывающее ![]() ,
, ![]() и
и ![]() вида
вида
![]() .
.
Это и есть искомое дифференциальное уравнение. С геометрической точки зрения его называют дифференциальным уравнением семейства кривых (3.5).
Пример 3.8. Найти дифференциальное уравнение семейства окружностей
![]() .
.
Решение. Имеем систему уравнений

Отсюда
![]() ,
, ![]() .
.
Итак, искомое уравнение
![]() ,
,
То есть
![]() .
.
Окончательно
![]() .
.
| < Предыдущая | Следующая > |
|---|

Часто одно лишь упоминание дифференциальных уравнений вызывает у студентов неприятное чувство. Почему так происходит? Чаще всего потому, что при изучении основ материала возникает пробел в знаниях, из-за которого дальнейшее изучение диффуров становиться просто пыткой. Ничего не понятно, что делать, как решать, с чего начать?
Однако мы постараемся вам показать, что диффуры – это не так сложно, как кажется.
Основные понятия теории дифференциальных уравнений
Со школы нам известны простейшие уравнения, в которых нужно найти неизвестную x. По сути дифференциальные уравнения лишь чуточку отличаются от них – вместо переменной х в них нужно найти функцию y(х), которая обратит уравнение в тождество.
Дифференциальные уравнения имеют огромное прикладное значение. Это не абстрактная математика, которая не имеет отношения к окружающему нас миру. С помощью дифференциальных уравнений описываются многие реальные природные процессы. Например, колебания струны, движение гармонического осциллятора, посредством дифференциальных уравнений в задачах механики находят скорость и ускорение тела. Также ДУ находят широкое применение в биологии, химии, экономике и многих других науках.
Дифференциальное уравнение (ДУ) – это уравнение, содержащее производные функции y(х), саму функцию, независимые переменные и иные параметры в различных комбинациях.
Существует множество видов дифференциальных уравнений: обыкновенные дифференциальные уравнения, линейные и нелинейные, однородные и неоднородные, дифференциальные уравнения первого и высших порядков, дифуры в частных производных и так далее.
Решением дифференциального уравнения является функция, которая обращает его в тождество. Существуют общие и частные решения ДУ.
Общим решением ДУ является общее множество решений, обращающих уравнение в тождество. Частным решением дифференциального уравнения называется решение, удовлетворяющее дополнительным условиям, заданным изначально.
Порядок дифференциального уравнения определяется наивысшим порядком производных, входящих в него.

Обыкновенные дифференциальные уравнения
Обыкновенные дифференциальные уравнения – это уравнения, содержащие одну независимую переменную.
Рассмотрим простейшее обыкновенное дифференциальное уравнение первого порядка. Оно имеет вид:
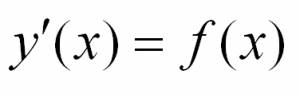
Решить такое уравнение можно, просто проинтегрировав его правую часть.
Примеры таких уравнений:
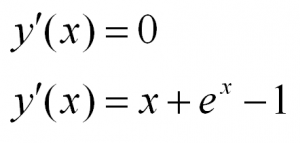
Уравнения с разделяющимися переменными
В общем виде этот тип уравнений выглядит так:
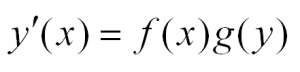
Приведем пример:
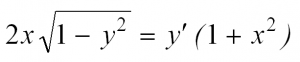
Решая такое уравнение, нужно разделить переменные, приведя его к виду:
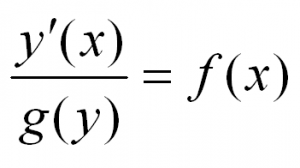
После этого останется проинтегрировать обе части и получить решение.

Линейные дифференциальные уравнения первого порядка
Такие уравнения имеют вид:
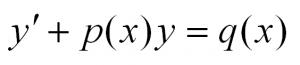
Здесь p(x) и q(x) – некоторые функции независимой переменной, а y=y(x) – искомая функция. Приведем пример такого уравнения:
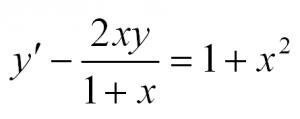
Решая такое уравнение, чаще всего используют метод вариации произвольной постоянной либо представляют искомую функцию в виде произведения двух других функций y(x)=u(x)v(x).
Для решения таких уравнений необходима определенная подготовка и взять их “с наскока” будет довольно сложно.
Пример решения ДУ с разделяющимися переменными
Вот мы и рассмотрели простейшие типы ДУ. Теперь разберем решение одного из них. Пусть это будет уравнение с разделяющимися переменными.
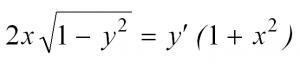
Сначала перепишем производную в более привычном виде:
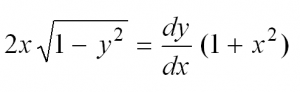
Затем разделим переменные, то есть в одной части уравнения соберем все “игреки”, а в другой – “иксы”:
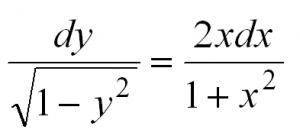
Теперь осталось проинтегрировать обе части:
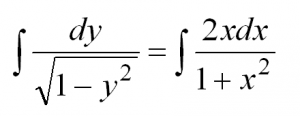
Интегрируем и получаем общее решение данного уравнения:
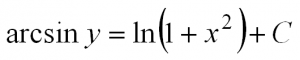
Конечно, решение дифференциальных уравнений – своего рода искусство. Нужно уметь понимать, к какому типу относится уравнение, а также научиться видеть, какие преобразования нужно с ним совершить, чтобы привести к тому или иному виду, не говоря уже просто об умении дифференцировать и интегрировать. И чтобы преуспеть в решении ДУ, нужна практика (как и во всем). А если у Вас в данный момент нет времени разбираться с тем, как решаются дифференциальные уравнения или задача Коши встала как кость в горле или вы не знаете, как правильно оформить презентацию, обратитесь к нашим авторам. В сжатые сроки мы предоставим Вам готовое и подробное решение, разобраться в подробностях которого Вы сможете в любое удобное для Вас время. А пока предлагаем посмотреть видео на тему “Как решать дифференциальные уравнения”:
I. Обыкновенные дифференциальные
уравнения
1.1. Основные понятия и определения
Дифференциальным уравнением называется
уравнение, связывающее между собой
независимую переменную x, искомую
функцию y и её производные или
дифференциалы.
Символически дифференциальное уравнение
записывается так:
F(x,y,y’)=0, F(x,y,y”)=0, F(x,y,y’,y”,.., y(n))=0
Дифференциальное уравнение называется
обыкновенным, если искомая функция зависит
от одного независимого переменного.
Решением дифференциального уравнения
называется такая функция ![]() ,
,
которая обращает это уравнение в тождество.
Порядком дифференциального уравнения
называется порядок старшей производной,
входящей в это уравнение
Примеры.
1. Рассмотрим дифференциальное уравнение
первого порядка
![]()
Решением этого уравнения является
функция y = 5 ln x. Действительно, ![]() ,
,
подставляя y’ в уравнение, получим ![]()
– тождество.
А это и значит, что функция y = 5 ln x– есть
решение этого дифференциального уравнения.
2. Рассмотрим дифференциальное уравнение
второго порядка y” – 5y’ +6y = 0. Функция ![]()
– решение этого уравнения.
Действительно, ![]() .
.
Подставляя эти выражения в уравнение,
получим: ![]() ,
,
![]()
– тождество.
А это и значит, что функция ![]()
– есть решение этого дифференциального
уравнения.
Интегрированием дифференциальных
уравнений называется процесс нахождения
решений дифференциальных уравнений.
Общим решением дифференциального
уравнения называется функция вида ![]() ,в
,в
которую входит столько независимых
произвольных постоянных, каков порядок
уравнения.
Частным решением дифференциального
уравнения называется решение, полученное
из общего решения при различных числовых
значениях произвольных постоянных.
Значения произвольных постоянных
находится при определённых начальных
значениях аргумента и функции.
График частного решения
дифференциального уравнения называется интегральной
кривой.
Примеры
1.Найти частное решение дифференциального
уравнения первого порядка
xdx + ydy = 0, если y = 4 при x = 3.
Решение. Интегрируя обе части уравнения,
получим ![]()
Замечание. Произвольную постоянную С,
полученную в результате интегрирования,
можно представлять в любой форме, удобной
для дальнейших преобразований. В данном
случае, с учётом канонического уравнения
окружности произвольную постоянную С
удобно представить в виде ![]() .
.
![]()
– общее решение дифференциального
уравнения.
Частное решение уравнения,
удовлетворяющее начальным условиям y =
4 при x = 3 находится из общего
подстановкой начальных условий в общее
решение: 32 + 42= C2; C=5.
Подставляя С=5 в общее решение, получим x2
+y2 = 52.
Это есть частное решение
дифференциального уравнения, полученное из
общего решения при заданных начальных
условиях.
2. Найти общее решение дифференциального
уравнения ![]()
Решением этого уравнения является всякая
функция вида ![]() ,
,
где С – произвольная постоянная.
Действительно, подставляя в уравнения ![]() ,
,
получим: 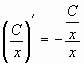 ,
,
![]() .
.
Следовательно, данное дифференциальное
уравнение имеет бесконечное множество
решений, так как при различных значениях
постоянной С равенство ![]()
определяет различные решения уравнения ![]() .
.
Например, непосредственной подстановкой
можно убедиться, что функции ![]()
являются решениями уравнения ![]() .
.
Задача, в которой требуется найти частное
решение уравнения y’ = f(x,y)
удовлетворяющее начальному условию y(x0)
= y0, называется задачей Коши.
Решение уравнения y’ = f(x,y),
удовлетворяющее начальному условию, y(x0)
= y0, называется решением задачи Коши.
Решение задачи Коши имеет простой
геометрический смысл. Действительно,
согласно данным определениям, решить
задачу Коши y’ = f(x,y) при условии y(x0)
= y0,, означает найти интегральную
кривую уравнения y’ = f(x,y) которая
проходит через заданную точку M0(x0,y0).
II. Дифференциальные уравнения первого
порядка
2.1. Основные понятия
Дифференциальным уравнением первого
порядка называется уравнение вида F(x,y,y’) =
0.
В дифференциальное уравнение первого
порядка входит первая производная и не
входят производные более высокого порядка.
Уравнение y’ = f(x,y) называется
уравнением первого порядка, разрешённым
относительно производной.
Общим решением дифференциального
уравнения первого порядка называется
функция вида ![]() ,
,
которая содержит одну произвольную
постоянную.
Пример. Рассмотрим дифференциальное
уравнение первого порядка ![]() .
.
Решением этого уравнения является
функция ![]() .
.
Действительно, заменив в данном уравнении,
![]()
его значением, получим
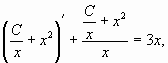
![]()
то есть 3x=3x
Следовательно, функция ![]()
является общим решением уравнения![]()
при любом постоянном С.
Найти частное решение данного уравнения,
удовлетворяющее начальному условию y(1)=1
Подставляя начальные условия x = 1, y =1
в общее решение уравнения ![]() ,
,
получим ![]()
откуда C = 0.
Таким образом, частное решение получим из
общего ![]()
подставив в это уравнение, полученное
значение C = 0 ![]()
![]()
– частное решение.
2.2. Дифференциальные уравнения с
разделяющимися переменными
Дифференциальным уравнением с
разделяющимися переменными называется
уравнение вида: y’=f(x)g(y) или через
дифференциалы ![]() ,
,
где f(x) и g(y)– заданные функции.
Для тех y, для которых ![]() ,
,
уравнение y’=f(x)g(y) равносильно уравнению,
![]()
в котором переменная y присутствует
лишь в левой части, а переменная x- лишь в
правой части. Говорят, «в уравнении y’=f(x)g(y
разделим переменные».
Уравнение вида ![]()
называется уравнением с разделёнными
переменными.
Проинтегрировав обе части уравнения ![]()
по x, получим G(y) = F(x) + C– общее
решение уравнения, где G(y) и F(x) –
некоторые первообразные соответственно
функций ![]()
и f(x), C произвольная постоянная.
Алгоритм решения дифференциального
уравнения первого порядка с разделяющимися
переменными
- Производную функции переписать через её
дифференциалы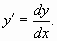
- Разделить переменные.
- Проинтегрировать обе части равенства,
найти общее решение. - Если заданы начальные условия, найти
частное решение.
Пример 1
Решить уравнение y’ = xy
Решение. Производную функции y’
заменим на ![]()
![]()
разделим переменные ![]()
![]()
проинтегрируем обе части равенства:
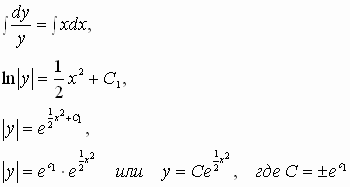
Ответ: ![]()
Пример 2
Найти частное решение уравнения
2yy’ = 1- 3x2,
если y0 = 3 при x0 = 1
Это—уравнение с разделенными
переменными. Представим его в
дифференциалах. Для этого перепишем данное
уравнение в виде ![]()
Отсюда ![]()
Интегрируя обе части последнего
равенства, найдем ![]()
Подставив начальные значения x0 = 1,
y0 = 3 найдем С 9=1-1+C, т.е. С = 9.
Следовательно, искомый частный интеграл
будет ![]()
или ![]()
Пример 3
Составить уравнение кривой, проходящей
через точку M(2;-3) и имеющей касательную с угловым
коэффициентом ![]()
Решение. Согласно условию ![]()
Это уравнение с разделяющимися
переменными. Разделив переменные, получим: ![]()
Проинтегрировав обе части уравнения,
получим: 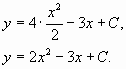
Используя начальные условия, x = 2 и y
= – 3 найдем C:
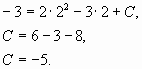
Следовательно, искомое уравнение имеет
вид ![]()
2.3. Линейные дифференциальные уравнения
первого порядка
Линейным дифференциальным уравнением
первого порядка называется уравнение вида y’
= f(x)y + g(x)
где f(x) и g(x) – некоторые заданные функции.
Если g(x)=0 то
линейное дифференциальное уравнение
называется однородным и имеет вид: y’ = f(x)y
Если ![]()
то уравнение y’ = f(x)y + g(x) называется неоднородным.
Общее решение линейного однородного
дифференциального уравнения y’ = f(x)y задается формулой: ![]()
где С – произвольная постоянная.
В частности, если С =0, то решением
является y = 0 Если линейное однородное уравнение имеет
вид y’ = ky где k – некоторая постоянная, то его общее решение
имеет вид: ![]() .
.
Общее решение линейного неоднородного
дифференциального уравнения y’ = f(x)y + g(x) задается формулой ![]() ,
,
т.е. равно сумме общего решения
соответствующего линейного однородного
уравнения и частного решения ![]()
данного уравнения.
Для линейного неоднородного уравнения
вида ![]() y’
y’
= kx + b,
где k и b–
некоторые числа и ![]() частным
частным
решением будет являться постоянная функция
![]() .
.
Поэтому общее решение имеет вид ![]() .
.
Пример. Решить уравнение y’ + 2y +3 = 0
Решение. Представим уравнение в виде y’
= -2y – 3 где k = -2, b= -3 Общее решение задается формулой ![]()
![]() .
.
Следовательно, ![]()
где С – произвольная постоянная.
Ответ: ![]()
2.4. Решение линейных дифференциальных
уравнений первого порядка методом Бернулли
Нахождение общего решения линейного
дифференциального уравнения первого
порядка y’ = f(x)y + g(x) сводится к решению двух дифференциальных
уравнений с разделенными переменными с
помощью подстановки y=uv,
где u и v – неизвестные функции от x.
Этот метод решения называется методом
Бернулли.
Алгоритм решения линейного дифференциального
уравнения первого порядка
y’ = f(x)y + g(x)
1. Ввести подстановку y=uv.
2. Продифференцировать это равенство y’ =
u’v + uv’
3. Подставить y и y’ в данное уравнение:
u’v + uv’ = f(x)uv + g(x) или u’v + uv’ + f(x)uv = g(x).
4. Сгруппировать члены уравнения так, чтобы
u вынести
за скобки: ![]()
![]()
5. Из скобки, приравняв ее к нулю, найти
функцию ![]()
![]()
Это уравнение с разделяющимися
переменными: ![]()
Разделим переменные и получим: ![]()
Откуда ![]() .
.
![]() .
.
6. Подставить полученное значение v в уравнение ![]()
(из п.4):
![]()
и найти функцию ![]()
Это уравнение с разделяющимися переменными:
![]()
![]()
7. Записать общее решение в виде: ![]()
![]() ,
,
т.е. ![]() .
.
Пример 1
Найти частное решение уравнения y’ = -2y
+3 = 0 если y =1 при x = 0
Решение. Решим его с помощью
подстановки y=uv, .y’ = u’v + uv’
Подставляя y и y’
в данное уравнение, получим ![]()
Сгруппировав второе и третье слагаемое
левой части уравнения, вынесем общий
множитель u за
скобки![]()
Выражение в скобках приравниваем к нулю и,
решив полученное уравнение, найдем функцию v
= v(x)![]()
Получили уравнение с разделенными
переменными. Проинтегрируем обе части
этого уравнения: ![]()
Найдем функцию v:
![]()
Подставим полученное значение v в уравнение ![]()
Получим: ![]()
Это уравнение с разделенными переменными.
Проинтегрируем обе части уравнения:![]()
Найдем функцию u = u(x,c) ![]()
Найдем общее решение: ![]()
Найдем частное решение уравнения,
удовлетворяющее начальным условиям y = 1 при
x = 0:
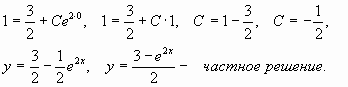
Ответ: ![]()
III. Дифференциальные уравнения высших
порядков
3.1. Основные понятия и определения
Дифференциальным уравнением второго
порядка называется уравнение, содержащее
производные не выше второго порядка. В
общем случае дифференциальное уравнение
второго порядка записывается в виде: F(x,y,y’,y”)
= 0
Общим решением дифференциального
уравнения второго порядка называется
функция вида ![]()
![]() ,
,
в которую входят две произвольные
постоянные C1 и C2.
Частным решением дифференциального
уравнения второго порядка называется
решение, полученное из общего ![]()
при некоторых значениях произвольных
постоянных C1 и C2.
3.2. Линейные однородные дифференциальные
уравнения второго порядка с
постоянными коэффициентами.
Линейным однородным дифференциальным
уравнением второго порядка с постоянными
коэффициентами называется уравнение вида
y” + py’ +qy = 0, где pи q–
постоянные величины.
Алгоритм решения однородных дифференциальных
уравнений второго порядка с постоянными
коэффициентами
1. Записать дифференциальное уравнение в
виде: y” + py’ +qy = 0.
2. Составить его характеристическое
уравнение, обозначив y” через r2,
y’ через r, yчерез
1:![]()
r2 + pr +q = 0
3.Вычислить дискриминант D = p2 -4q
и найти корни характеристического
уравнения; при этом если:
а) D > 0; следовательно,
характеристическое уравнение имеет два
различных действительных корня ![]() .
.
Общее решение дифференциального уравнения
выражается в виде ![]() ,
,
где C1 и C2 – произвольные постоянные.
б) D = 0; следовательно,
характеристическое уравнение имеет равные
действительные корни ![]() .
.
Общее решение дифференциального уравнения
выражается в виде ![]()
в) D < 0; следовательно,
характеристическое уравнение имеет
комплексные корни, ![]()
Общее решение дифференциального уравнения
выражается, в виде
![]()
Примеры.
1. Найти частное решение дифференциального
уравнения
![]()
Решение. Составим характеристическое
уравнение ![]()
![]()
D>0,
![]()
Общее решение ![]()
Дифференцируя общее решение, получим ![]()
Составим систему из двух уравнений 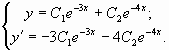
Подставим вместо ![]() ,
,![]() и
и
![]()
заданные начальные условия:
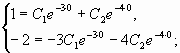
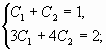
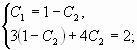
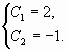
![]()
Таким образом, искомым частным решением
является функция
![]() .
.
2. Найти частное решение уравнения
![]()
Решение
![]() <0,
<0,
![]()
Общее решение ![]()
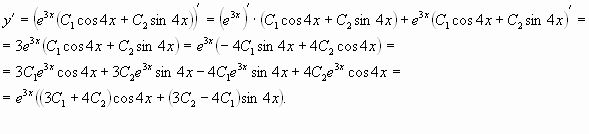
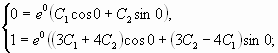
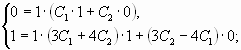
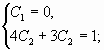
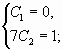
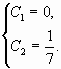
![]() –
–
частное решение.
IV. Практическая работа
Вариант 1
1. Составить уравнение кривой, проходящей
через точку M(1;2) и имеющей угловой коэффициент ![]() .
.
2. Найти частные решения дифференциальных
уравнений:
а)![]()
б) ![]()
в) ![]()
г) ![]()
Вариант 2
1. Составить уравнение кривой, проходящей
через точку M(2;1) и имеющей угловой коэффициент ![]()
2. Найти частные решения дифференциальных
уравнений:
а)![]()
б) ![]()
в) ![]()
г) ![]()
V. Ответы
|
Вариант 1 |
Вариант 2 |
|
1. |
1. |
|
2. а) |
2. а) |
|
б) |
б) |
|
в) |
в) |
|
г) |
г) |
Имея результаты
Теоремы (8.5), можем заняться обоснованием
свойства
![]() фундаментальной системы решений. Именно,
фундаментальной системы решений. Именно,
доказать, что запись решения в виде
линейной комбинации совокупности
независимых функций-решений:![]() ,
,![]() ,…,
,…,![]() линейного однородного уравнения
линейного однородного уравнения![]() –
–
го порядка (14), есть общее решение. Это
значит, что мы решение задачи Коши для
заданных начальных условий выделяет
единственную интегральную кривую.
Следующая теорема
полностью определяет важные для
практического применения свойства
совокупности функций-решений:
![]() ,
,![]() ,…,
,…,![]() линейного однородного уравнения
линейного однородного уравнения![]() –
–
го порядка.
|
Теорема: (8.6) |
Если
с
где |
►Доказательство
теоремы:
1). Пусть
в точке ![]()
![]()
заданы условия: ![]() ,
,
![]() =
=![]() ,…,
,…,
![]() =
=![]() .
.
2). Найдём
производные функции (17):
![]() ,
,
и запишем уравнения для заданной
начальной точки ![]() :
:
![]() =
=![]() ,
,
![]() =
=![]() ,
,
. . .
. . . . . . . . . . . . . . . . . . , (18)
![]() =
=![]() .
.
3). Система
(18)
есть система линейных однородных
уравнений. По предположению (так как
функции
![]() ,
,![]() ,…,
,…,![]()
образуют ФСР) определитель этой системы
![]() ,
,
следовательно, для точки
![]() =
=![]()
система (18) имеет единственное
ненулевое решение:
![]() .
.
Это значит, что для функции:
![]() =
=![]()
задача Коши решается однозначно, то
есть эта функция есть общее
решение.
Итак, свойство
![]()
фундаментальной системы решений
доказано! ◄
☺☺
Пример
8–07: Известно
общее решение уравнения:
![]() =
=![]() .
.
Найти частное решение уравнения, если
заданы начальные условия: ![]() ,
,![]() ,
,![]() .
.
Решение:
1).
Вычислим производные общего решения:
![]() =
=![]() ,
,![]() =
=![]() .
.
2).
Составим систему уравнений для значения
![]() :
:

Решив систему, получим значения
произвольных постоянных величин:
![]() =–1,
=–1,
![]() =1,
=1,
![]() =2.
=2.
3).
Запишем частное решение:
![]() =
=![]() .
.
Ответ:
частное решение:
![]() =
=![]() .
.
☻
§ 4. Линейные однородные уравнения с постоянными коэффициентами.
Начнем с уравнений
2-го порядка. С одной стороны, эти уравнения
не требуют сразу большого объёма
вычислений. В то же время получаемые
алгоритмы решений будут обобщаться
индуктивным переходом от порядка
![]() к порядку
к порядку![]() достаточно просто.
достаточно просто.
4.1. Линейные однородные уравнения 2-го порядка.
Пусть линейное
однородное уравнение 2-го порядка с
постоянными коэффициентами записано
в виде: ![]() .(19)
.(19)
Учитывая опыт
дифференцирования функции
![]() =
=![]() ,
,
нетрудно догадаться, что такая функция
могла бы быть решением уравнения (19)…
Действительно, подставив в уравнение
(19) функцию![]() =
=![]() и её производные:
и её производные:![]() =
=![]() ,
,![]() =
=![]() ,
,
получим алгебраическое уравнение:
![]() ,
,
или
![]() . (20)
. (20)
Для уравнения:
![]() уравнение
уравнение![]() называютхарактеристическим
называютхарактеристическим
уравнением. Корни этого уравнения
называютхарактеристическими
корнямидифференциального
равнения (19). Общая формула для вычисления
корней:
![]() =
=
![]() . (21)
. (21)
Замечание:
Следует обратить внимание на взаимно
однозначное соответствие между записью
дифференциального уравнения и записью
его характеристического уравнения!
В общем случае
корни многочлена с действительными
коэффициентами могут быть: 1) действительные
и различные, 2) действительные равнее,
3) комплексные сопряжённые. Рассмотрим
каждый из этих случаев отдельно.
Случай-1.
Корни![]() и
и![]() – действительные и различные:
– действительные и различные:![]()
![]()
![]() .
.
В этом случае
решения уравнения (19) записываем в виде:
![]() =
=![]() и
и![]() =
=![]() .
.
Так как![]()
![]()
![]() ,
,
то![]()
![]()
![]() .
.
Это значит, что отношение функций-решений![]() =
=![]()
![]()
![]() и решения
и решения![]() и
и![]() независимы и могут быть приняты в
независимы и могут быть приняты в
качестве ФСР. В соответствии с доказанной
Теоремой, запишем общее решение уравнения
(19) в виде:![]() =
=![]() . (22)
. (22)
Случай-2.
Корни![]() и
и![]() – действительные и равные:
– действительные и равные:![]() =
=![]() =
=![]() .
.
Это значит:![]() .
.
В этом случае
решения уравнения (19) записываем в виде:
![]() =
=![]() и
и![]() =
=![]() ,
,![]() =
=![]() .
.
Это значит, что функции-решения не могут
быть приняты в качестве ФСР. Догадались
искать выражение для решения![]() в виде произведения:
в виде произведения:![]() =
=![]() ,
,
где множитель![]() пока неизвестная функция. Так как функция
пока неизвестная функция. Так как функция![]() =
=![]() должна быть решением уравнения (19),
должна быть решением уравнения (19),
вычислим её производные![]() =
=![]() ;
;![]() =
=![]() .
.
Подставим![]() ,
,![]() и
и![]() в уравнение (19). После сокращения на
в уравнение (19). После сокращения на
общий множитель![]() ,
,
получим равенство:
![]() . (23)
. (23)
Так как в выражении
(23) обе скобки равны нулю, то необходимо
![]() =0.
=0.
Это дифференциальное уравнение имеет
общее решение:![]() =
=![]() .
.
Нам подойдёт любое частное решение
уравнения![]() =0.
=0.
Выберем простейшее:![]() =
=![]() .
.
Независимость
решений
![]() =
=![]() и
и![]() =
=![]() =
=![]() очевидна, выберем их в качестве ФСР
очевидна, выберем их в качестве ФСР
уравнения (19) для рассматриваемого
случая. Тогда общее решение уравнения:
![]() =
=![]() =
=![]() . (24)
. (24)
Случай-3.
Корни![]() =
=![]() –
–
пара комплексно-сопряженных корней,![]() =
=![]() ,
,![]() =
=![]() .
.
Учитывая формулу
Эйлера:
![]() ,
,
для корня![]() =
=![]() запишем решение:
запишем решение:![]() =
=![]() =
=![]() ,
,
а для корня![]() =
=![]() решение:
решение:![]() =
=![]() =
=![]() .
.
Нетрудно проверить, что комплексные
функции-решения![]() и
и![]() независимы и могут использоваться для
независимы и могут использоваться для
построения ФСР… Возникает вопрос – А
нельзя ли составить два действительных
решения уравнения издействительныхполовинок:![]() =
=![]() и
и![]() =
=![]() ?..
?..
|
Теорема: (8.7) |
Если |
►Доказательство
теоремы:
1). Так
как (по условию) функция
![]()
является решением уравнения (19), подставив
её в это уравнение должны получить
тождество:
![]()
![]()
![]() . (25)
. (25)
2).
Учитывая правило дифференцирования
суммы функций, а также используя свойство
равенства двух комплексных чисел,
запишем:
![]()
![]() 0 и
0 и
![]()
![]() 0. (26)
0. (26)
3). Из
тождеств (26) следует, что функции
![]()
и
![]()
также являются решениями дифференциального
уравнения (19). ◄
Следствие:
Так как комплексная функция
![]() =
=![]()
является решением уравнения (19), то и
действительные функции ![]() =
=![]()
и ![]() =
=![]()
будут решениями этого уравнения.
Аналогично для
![]() =
=![]() .
.
Легко
заметить, что функции
![]()
и
![]()
линейно независимы. Это значит, что их
можно использовать в качестве ФСР.
Вывод.
Если пара комплексно-сопряжённых чисел
![]() =
=![]()
является характеристическими корнями
уравнения (19), то соответствующими им
функциями-решениями этого уравнения
будут независимые функции-решения:
![]() =
=![]()
и
![]() =
=![]() .
.
Учитывая все
рассмотренные Случаи характеристических
корней уравнения (19), запишем общий
алгоритм построения ФСР для этого
уравнения:
1). Корни
![]() и
и![]() – действительные и различные:
– действительные и различные:![]()
![]()
![]() .
.
Строим ФСР:![]() =
=![]() и
и![]() =
=![]() .
.
Записываем общее решение уравнения:![]() =
=![]() =
=![]() +
+![]() .
.
2). Корни
![]() и
и![]() – действительные и равные:
– действительные и равные:![]() =
=![]() .
.
Строим ФСР:![]() =
=![]() и
и![]() =
=![]() .
.
Записываем общее решение уравнения:![]() =
=![]() =
=![]() .
.
3). Корни
![]() =
=![]() – пара комплексно-сопряженных корней.
– пара комплексно-сопряженных корней.
Строим ФСР:![]() =
=![]() и
и![]() =
=![]() ,
,
а также общее решение уравнения:![]() =
=![]() =
=![]() .
.
Замечание:
Зная корни характеристического уравнения,
легко записать характеристическое
уравнение, определяющее эти корни:![]() .
.
☺☺
Пример 8–08: Имеем
фундаментальную систему решений (ФСР):
![]() ,
,
![]()
линейного однородного уравнения.
Составить это уравнение.
Решение:
1).
Имея решение уравнения:
![]() ,
,
учтем: 1 =![]()
→
![]() =0.
=0.
Также:
![]()
→
![]() =–1.
=–1.
2).
Имея корни
![]() ,
,
![]() ,
,
восстановим характеристический
многочлен:
![]() ,
,
или (после подстановки):
![]() .
.
3).
Имея характеристический многочлен,
восстановим ДУ:
![]() .
.
Ответ:
уравнение:
![]() .
.
Пример 8–09: Имеем
семейство прямых линий (не параллельны
оси
![]() ):
):
![]() .
.
Найти дифференциальное уравнение, для
которого заданное семейство является
решением.
Решение:
1).
Продифференцируем заданное выражение:
![]() =
=![]() ,
,
и далее
![]() =0.
=0.
2).
Уравнение
![]() =0:
=0:
и есть искомое ДУ.
3).
Имея характеристический многочлен,
восстановим ДУ:
![]() .
.
Ответ:
уравнение:
![]() =0.
=0.
Пример 8–10: По
данным корням:
![]() =3
=3
и
![]() =
=
–2 характеристического уравнения ЛОУ
с постоянными коэффициентами составить
ДУ и написать его общее решение.
Решение:
1). Учтем стандартную
запись уравнения 2-го порядка:
![]() .
.
2). В нашем случае
получим:
![]() .
.
3). Составляем ФСР:
![]() ,
,![]() .
.
Общее решение:![]() =
=![]() .
.
Ответ: дифференциальное
уравнение:![]() .
.
ФСР:![]() ,
,![]() .Общее решение уравнения:
.Общее решение уравнения:![]() .
.
Пример 8–11: По
данным корням:
![]() =
=![]()
характеристического уравнения ЛОУ с
постоянными коэффициентами составить
ДУ и написать его общее решение.
Решение:
1). Учтем стандартную
запись уравнения 2-го порядка:
![]() .
.
2). В нашем случае
получим:
![]() .
.
3). Составляем ФСР:
![]() ,
,![]() и общее решение:
и общее решение:![]() .
.
Ответ: уравнение:![]() .
.
ФСР:![]() ,
,![]() .Общее решение имеет вид:
.Общее решение имеет вид:![]() .
.
Пример 8–12: Найти
общее решение ДУ:
![]() .
.
Решение:
1). Характеристическое
уравнение:
![]() ,
,
его корни:![]() ,
,![]() .
.
2). Составляем ФСР:
![]() =
=![]() ,
,![]() =
=![]() и общее решение:
и общее решение:![]() .
.
Ответ: ФСР:![]() =
=![]() ,
,![]() =
=![]() .Общее решение:
.Общее решение:![]() .
.
☻
