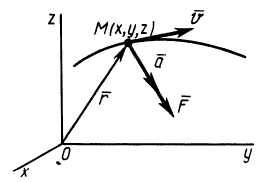
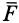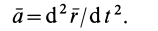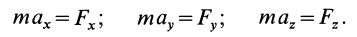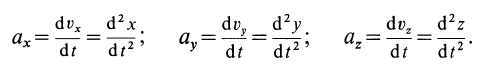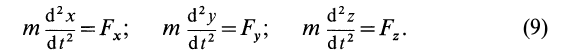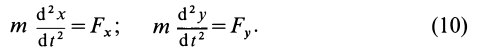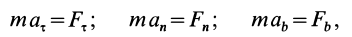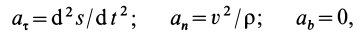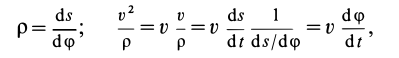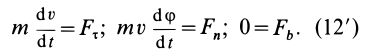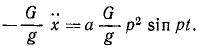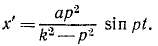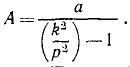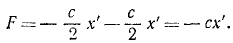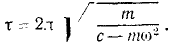Составление дифференциальных уравнений семейств линий
Пусть дано уравнение однопараметрического семейства плоских кривых
(1)
Дифференцируя (1) по , найдем
(2)
Исключая параметр из (1) и (2), получаем дифференциальное уравнение
(3)
выражающее свойство, общее всем кривым семейства (1). Уравнение (3) будет искомым дифференциальным уравнением семейства (1).
Если однопараметрическое семейство кривых определяется уравнением
то дифференциальное уравнение этого семейства получим, исключая параметр из уравнений
Пусть теперь имеем соотношение
(4)
где — параметры. Дифференцируя (4)
раз по
и исключая параметры
из (4) и полученных уравнений, приходим к соотношению вида
(5)
Это дифференциальное уравнение заданного n-параметрического семейства линий (4) в том смысле, что (4) есть общий интеграл уравнения (5).
Пример 1. Найти дифференциальное уравнение семейства гипербол .
Решение. Дифференцируя это уравнение по , получаем
или
Умножим обе части на , тогда
. Подставляя в уравнение семейства найдем
.
Пример 2. Найти дифференциальное уравнение семейства линий , где
— параметр.
Решение. Дифференцируем обе части уравнения по :
Из выражения для находим
и, подставляя это выражение для в уравнение семейства линий, получим
или
Пример 3. Составить дифференциальное уравнение семейства прямых, отстоящих от начала координат на расстояние, равное единице.
Решение. Будем исходить из нормального уравнения прямой
(6)
где — параметр.
Дифференцируя (6) по , найдем
, откуда
, следовательно,
Подставив и
в (6), получим
или
2°. Задачи на траектории
Пусть дано семейство плоских кривых, зависящее от одного параметра ,
(7)
Кривая, образующая в каждой своей точке постоянный угол с проходящей через эту точку кривой семейства (7), называется изогональной траекторией этого семейства; если, в частности,
, то — ортогональной траекторией.
Считая семейство (7) заданным, будем разыскивать его изогональные траектории.
А. Ортогональные траектории. Составляем дифференциальное уравнение данного семейства кривых (см. п. 1). Пусть оно имеет вид
Дифференциальное уравнение ортогональных траекторий имеет вид
Общий интеграл этого уравнения дает семейство ортогональных траекторий.
Пусть семейство плоских кривых задано уравнением в полярных координатах
(8)
где — параметр. Исключая параметр
из (8) и
, получаем дифференциальное уравнение семейства (8):
. Заменяя в нем
на
,
получаем дифференциальное уравнение семейства ортогональных траекторий
Б. Изогональные траектории. Пусть траектории пересекают кривые данного семейства под углом , причем
. Можно показать, что дифференциальное уравнение изогональных траекторий имеет вид
Пример 4. Найти ортогональные траектории семейства линий .
Решение. Семейство линий состоит из прямых, проходящих через начало координат. Для нахождения дифференциального уравнения данного семейства дифференцируем по
обе части уравнения
. Имеем
. Исключая параметр
из системы уравнений
будем иметь дифференциальное уравнение семейства
. Заменяя в нем
на
, получаем дифференциальное уравнение ортогональных траекторий
, или
. Полученное уравнение является уравнением с разделяющимися переменными; интегрируя его, найдем уравнение ортогональных траекторий
. Ортогональными траекториями являются окружности с центром в начале координат (рис. 15).
Пример 5. Найти уравнение семейства линий, ортогональных к семейству .
Решение. Данное семейство линий представляет собой семейство окружностей, центры которых находятся на оси и которые касаются оси
.
Дифференцируя по обе части уравнения данного семейства, найдем
. Исключая параметр
из уравнений
получаем дифференциальное уравнение данного семейства
. Дифференциальное уравнение ортогональных траекторий есть
или
Это уравнение является однородным. Интегрируя его, найдем . Интегральные кривые являются окружностями, центры которых расположены на оси
и которые касаются оси
(рис. 16).
Пример 6. Найти ортогональные траектории семейства парабол .
Решение. Составляем дифференциальное уравнение семейства парабол. Для этого дифференцируем обе части данного уравнения по . Исключая параметр
, найдем
, или
дифференциальное уравнение данного семейства. Заменяя в уравнении
на
, получим дифференциальное уравнение ортогональных траекторий
или
Интегрируя, найдем или
. Ортогональным семейством является семейство эллипсов (рис. 17).
Пример 7. Найти ортогональные траектории семейства лемнискат .
Решение. Имеем . Исключая параметр
, получим дифференциальное уравнение данного семейства кривых
Заменяя
на
, найдем дифференциальное уравнение семейства ортогональных траекторий
откуда
. Интегрируя, находим уравнение ортогональных траекторий
Ортогональными траекториями семейства лемнискат являются лемнискаты, ось симметрии которых образуют с полярной осью угол (рис. 18).
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Дифференциальные уравнения движения материальной точки в теоретической механике
Содержание:
Дифференциальные уравнения движения материальной точки:
Используя основной закон динамики, можно вывести дифференциальные уравнения движения материальной точки в различных системах координат. По аксиоме о связях и силах реакций связей можно получить дифференциальные уравнения движения и несвободной точки так же, как и для свободной, только ко всем приложенным к точке силам надо добавить силы реакций связей.
Силы реакций связей при движении точки могут зависеть в общем случае не только от вида наложенных на точку связей и приложенных к ней сил, но и от характера ее движения, например от ее скорости при движении в воздухе или в какой-либо другой сопротивляющейся среде. В дальнейшем не будем делать различия между свободной и несвободной материальными точками. Обозначая равнодействующую всех заданных сил и сил реакций связей
Из кинематики точки известно, что ускорение 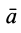
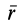
Дифференциальное уравнение движения материальной точки в векторной форме имеет вид
Если спроецировать обе части уравнений (7) или (8) на координатные оси, то можно получить дифференциальные уравнения движения точки в проекциях на эти оси.
В декартовой системе координат в общем случае
Проекции ускорения на координатные оси можно выразить через вторые производные по времени от координат движущейся точки:
Рис. 3
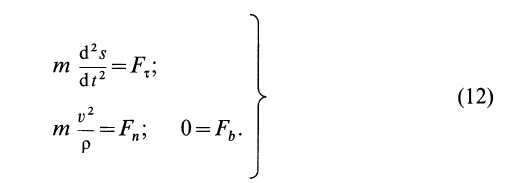
Дифференциальные уравнения движения материальной точки в прямоугольной декартовой системе координат имеют вид
Частные случаи дифференциального уравнения движения материальной точки
Если известно, что материальная точка движется в одной и той же плоскости, то, принимая ее за координатную плоскость 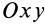
Так как 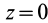
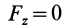
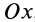
Так как при движении 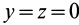
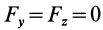
где 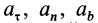
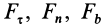
где 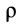
Второе уравнение из (12) можно преобразовать:
где 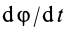
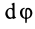
Дифференциальные уравнения (12) можно представить в виде
Рис. 4
Эта форма дифференциальных уравнений движения точки удобна при исследовании некоторых случаев полета снарядов и ракет, особенно по траектории, лежащей в плоскости. Тогда 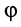
Дифференциальные уравнения движения точки можно представить в любой другой системе координат. Для этого надо знать выражения проекций ускорения на эти оси координат.
Дифференциальные уравнения относительного движения точки
Кориолисовыми силами инерции называют две векторные величины, имеющие размерность силы и добавляемые к силам, приложенным к материальной частице, для определения ее относительного ускорения
Все дифференциальные уравнения движения, с которыми мы ознакомились в этой главе, относятся к абсолютному движению, т. е. к движению по отношению к инерциальной системе отсчета. Для написания дифференциальных уравнений движения точки (или частицы) относительно подвижных осей подставим в основное уравнение динамики (123) вместо абсолютного ускорения точки его выражение (110):
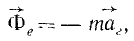
имеющую размерность силы, равную произведению массы материальной частицы на ее переносное ускорение и направленную противоположно этому ускорению, называют переносной силой инерции Кориолиса.
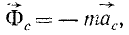
равную произведению массы материальной частицы на ее кориолисово ускорение и направленную противоположно этому ускорению, называют поворотной силой инерции Кориолиса.
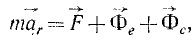
или в проекциях на оси координат:
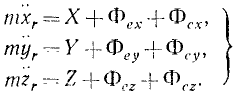
Таким образом, относительное движение материальной точки можно описать такими же (по форме) дифференциальными уравнениями, как и абсолютное, но к действующим на точку силам нужно прибавить две кориолисовы силы инерции: переносную и поворотную.
Эти величины следует отличать от даламберовых сил инерции (см. гл. XX), введение которых позволяет решать задачи динамики методом статики.
Пример решения задачи №1
Определить амплитуду вынужденных колебаний в относительном движении вибрографа для записи вертикальных колебаний фундамента (рис. 171), совершающего вместе с фундаментом колебания по закону χ = a sin pt, если вес груза равен G и жесткость пружины с.
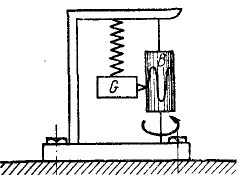
Рис. 171
Решение. Рама жестко соединена с фундаментом и участвует в его колебаниях, как и вращающийся барабан В, на котором груз G, перемещаясь вверх и вниз, записывает колебания фундамента. Вертикальные перемещения х’ груза G по отношению к раме являются относительными и по отношению к барабану, если пренебречь его вращением. Уравнение этих относительных перемещений можно составить как уравнение абсолютного движения, если к заданным силам добавить переносную кориолисову силу, равную и противоположную произведению вектора переносного ускорения на массу груза. Переносная сила инерции груза равна
Напишем дифференциальное уравнение относительных колебаний груза, сократив на m:
x’ + k 2 χ’ = ар 2 sin pt.
где 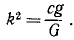
Амплитуда этих колебаний тем менее отличается от амплитуды колебаний фундамента, чем меньше собственная частота k прибора сравнительно с частотой р, т. е. чем меньше жесткость пружины и чем больше масса груза.
Ответ.
Пример решения задачи №2
Ползун G (рис. 172) может скользить по хорде AB равномерно вращающегося горизонтального диска, к точкам А и В которой он прикреплен двумя одинаковыми пружинами жесткостью 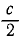
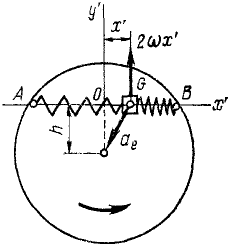
Рис. 172
Решение. Построим оси подвижной системы координат с началом в точке О (в положении относительного равновесия ползуна), направив Ox’ но хорде.
Определим силы, действующие на ползун. Если ползун отклонится от равновесного положения О на величину х’, то одна из пружин сожмется, а другая растянется. Согласно закону Гука сила каждой из пружин пропорциональна деформации х’ и направлена к точке О. Следовательно, на ползун действует активная сила
Кроме активной силы, надо учесть действие кориолисовых сил: Φe—переносной и Φc-поворотной.
Переносная сила инерции равна произведению массы т ползуна на его переносное ускорение: 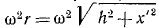
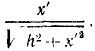
Поворотная сила Кориолиса равна произведению массы ползуна иа кориолисово ускорение 2ωx’ и направлена против этого ускорения. Таким образом, чтобы определить направление поворотной силы Кориолиса, надо вектор относительной скорости повернуть на 90° против переносного вращения. Находим, что поворотная сила инерции действует перпендикулярно AB и проекция ее на Ox’ равна нулю.
При найденных значениях активных сил и кориолисовых сил дифференциальное уравнение относительного движения ползуна по хорде имеет вид:
mх’ = — cx’ + mω 2 x’= — (с—mω 2 )x’.
Это уравнение выражает гармоническое колебание с периодом
Ответ. 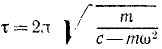
Пример решения задачи №3
Составить дифференциальное уравнение относительного движения ползуна, описанного в предыдущей задаче, считая, что при его движении вдоль хорды AB возникает трение, пропорциональное нормальному давлению на хорду.
Решение. Нормальное давление обусловлено поворотной силой инерции и нормальной составляющей переносной силы инерции.
Поворотная сила ползуна Φс=2mωx’ переменна по величине и направлению. Она направлена перпендикулярно к хорде AB, но в сторону положительных значений у’, если точка G движется в сторону отрицательных значений х’, т. е, если х’ 2 h. Эта составляющая в рассматриваемом механизме всегда направлена в сторону положительных у’, а потому в суммарном давлении обе кориолисовы силы складываются при х’ 0, и дифференциальное уравнение относительного движения точки имеет вид
mх’ =— (с—mω 2 ) x’ — fm (2ωx’ ± ω2h),
причем знак второго слагаемого в скобках надо брать положительным при х’ 0. Решение такого уравнения при движении точки G влево и вправо получается, конечно, различным. Если Л — 0 и хорда является диаметром, то вместо кулонова трения получается вязкое демпфирование, зависящее от скорости.
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Две основные задачи динамики точки
- Прямолинейное движение точки
- Криволинейное движение материальной точки
- Движение несвободной материальной точки
- Сложное движение точки
- Сложение движение твердого тела
- Кинематика сплошной среды
- Аксиомы классической механики
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Составление дифференциальных уравнений семейств линий
Пусть дано уравнение однопараметрического семейства плоских кривых
Дифференцируя (1) по , найдем
Исключая параметр из (1) и (2), получаем дифференциальное уравнение
выражающее свойство, общее всем кривым семейства (1). Уравнение (3) будет искомым дифференциальным уравнением семейства (1).
Если однопараметрическое семейство кривых определяется уравнением
то дифференциальное уравнение этого семейства получим, исключая параметр из уравнений
Пусть теперь имеем соотношение
где — параметры. Дифференцируя (4) раз по и исключая параметры из (4) и полученных уравнений, приходим к соотношению вида
Это дифференциальное уравнение заданного n-параметрического семейства линий (4) в том смысле, что (4) есть общий интеграл уравнения (5).
Пример 1. Найти дифференциальное уравнение семейства гипербол .
Решение. Дифференцируя это уравнение по , получаем
Умножим обе части на , тогда . Подставляя в уравнение семейства найдем .
Пример 2. Найти дифференциальное уравнение семейства линий , где — параметр.
Решение. Дифференцируем обе части уравнения по :
Из выражения для находим
и, подставляя это выражение для в уравнение семейства линий, получим
Пример 3. Составить дифференциальное уравнение семейства прямых, отстоящих от начала координат на расстояние, равное единице.
Решение. Будем исходить из нормального уравнения прямой
Дифференцируя (6) по , найдем , откуда , следовательно,
Подставив и в (6), получим
2°. Задачи на траектории
Пусть дано семейство плоских кривых, зависящее от одного параметра ,
Кривая, образующая в каждой своей точке постоянный угол с проходящей через эту точку кривой семейства (7), называется изогональной траекторией этого семейства; если, в частности, , то — ортогональной траекторией .
Считая семейство (7) заданным, будем разыскивать его изогональные траектории.
А. Ортогональные траектории . Составляем дифференциальное уравнение данного семейства кривых (см. п. 1). Пусть оно имеет вид
Дифференциальное уравнение ортогональных траекторий имеет вид
Общий интеграл этого уравнения дает семейство ортогональных траекторий.
Пусть семейство плоских кривых задано уравнением в полярных координатах
получаем дифференциальное уравнение семейства ортогональных траекторий
Б. Изогональные траектории . Пусть траектории пересекают кривые данного семейства под углом , причем . Можно показать, что дифференциальное уравнение изогональных траекторий имеет вид
Пример 4. Найти ортогональные траектории семейства линий .
Решение. Семейство линий состоит из прямых, проходящих через начало координат. Для нахождения дифференциального уравнения данного семейства дифференцируем по обе части уравнения . Имеем . Исключая параметр из системы уравнений будем иметь дифференциальное уравнение семейства . Заменяя в нем на , получаем дифференциальное уравнение ортогональных траекторий , или . Полученное уравнение является уравнением с разделяющимися переменными; интегрируя его, найдем уравнение ортогональных траекторий . Ортогональными траекториями являются окружности с центром в начале координат (рис. 15).
Пример 5. Найти уравнение семейства линий, ортогональных к семейству .
Решение. Данное семейство линий представляет собой семейство окружностей, центры которых находятся на оси и которые касаются оси .
Дифференцируя по обе части уравнения данного семейства, найдем . Исключая параметр из уравнений получаем дифференциальное уравнение данного семейства . Дифференциальное уравнение ортогональных траекторий есть
Это уравнение является однородным. Интегрируя его, найдем . Интегральные кривые являются окружностями, центры которых расположены на оси и которые касаются оси (рис. 16).
Пример 6. Найти ортогональные траектории семейства парабол .
Решение. Составляем дифференциальное уравнение семейства парабол. Для этого дифференцируем обе части данного уравнения по . Исключая параметр , найдем , или дифференциальное уравнение данного семейства. Заменяя в уравнении на , получим дифференциальное уравнение ортогональных траекторий
Интегрируя, найдем или 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAJUAAAAuBAMAAADTgUbKAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAD3RSTlMAmsOBAetBIBAxYUJRcbGvhmSvAAACYklEQVRIx2NgGOTgoNIEahnFrsEYQC2z2L6xfaOaHxN4vlMvwJgEqGfWReoZxSXQQZU4nMAxgWEygyUVjOJQVFz3kD3+/wcqmOU3IV8l3iMtLYEKZiUy5K/Qolq42xdQzSgWVQfcgWlMkte5OT4ylOGS7KsJJsUs+TN/GaxxSV4tsCfFLKEiZV+c+Wdew3osgeKC0xuSjfiiUQgzDBfFa3MtQBXzTiEmNMMxhI7qODTJo5acPIGi2OOIC5lT1IAuzfgXmO2+okZ96QGucOylD5I6DglmdMPuGwBDTA/I4BSHB6A8A8tHgmY1CZuie/oriNQFEUlww4IccCRSqFnsjyYwnFmkpIgm6/QLREJM2acNUcryyYFFH59ZfUUKLIGwYikNDEABPv8HktJCiGGcILMa8Jh1y/UB51+oEKcxGBwABZcCklKXwiiQYrZPDAz6GxgYFgrCAcjhXMbGpkBdQEtWnF/A+xNLQQBK1xxwbrEOKAwJmcUg38AUgsUsA5DT4SVLM8gsDkLhxRDE4P8Aix9B7poIDzAtkGIWQvHI8pkh/wIs7HeDASjs64H1O4c6zCgd4tIXMBLfY2lj8H50YJgEFd8ITRMM+xNwVPswPy4VCsXm7qWBRlBnJUnDs13s1QXw0tMci1ke2wOxFsN7j0MDURwhWLUcxpq0Vn8BRt4uVWAmp4kRydCKmZLyDfYvIKPi/t/A/BlDlFHpGTk1d2gD8ydMYReyajUXBsbP1GvmtEZQzyxRqrV8GbgiqeesqRM4qWUUpwYi51PsrGNpwlQyikP///8/1PKikpKSJuXGAACuZpWkdXHGfwAAAABJRU5ErkJggg==” style=”vertical-align: middle;” />. Ортогональным семейством является семейство эллипсов (рис. 17).
Пример 7. Найти ортогональные траектории семейства лемнискат .
Решение. Имеем . Исключая параметр , получим дифференциальное уравнение данного семейства кривых Заменяя на , найдем дифференциальное уравнение семейства ортогональных траекторий откуда . Интегрируя, находим уравнение ортогональных траекторий
Ортогональными траекториями семейства лемнискат являются лемнискаты, ось симметрии которых образуют с полярной осью угол (рис. 18).
Составление дифференциального уравнения семейства кривых
Составление уравнений семейства кривых
Чтобы построить дифференциальное уравнение, которому удовлетворяют кривые семейства:
φ 
необходимо продифференцировать равенство (1) n раз, считая y функцией от x, а затем из полученных уравнений и уравнения (1) исключить произвольные постоянные C1 … Cn.
Линии, пересекающие все кривые данного семейства под одним и тем же углом ϕ, называются изогональными траекториями . Углы β и α наклона траектории и кривой к оси Ox связаны соотношением β = α ± φ.


Тогда tg α = f (x,y), tg β = f1 (x,y).
Отсюда следует, что если дифференциальное уравнение семейства кривых написано и угол φ известен, то найти tg β не составит труда, а после также легко можно будет написать уравнение траекторий.
Частный случай:
Если уравнение семейства кривых записано в виде:

то при составлении уравнения траекторий можно обойтись без решения уравнения относительно y’, в этом случае будет достаточно y’ заменить на tg α = tg (β ± φ), где tg β = y’ — угловой коэффициент касательной к траектории.
Пример №1
Составить дифференциальное уравнение семейства кривых:
- Так как уравнение содержит два параметра (С1 и С2), то и дифференцировать будем два раза:
Первая производная:
Вторая производная:
- Дальше, чтобы составить дифференциальное уравнение семейства кривых необходимо избавиться от С1 , а для этого выведем его из уравнения первой производной С1 = -2(y — С2)y’ и подставим в наше уравнение:

- Теперь также нужно избавиться от параметра C2, а для этого выведем ее из второй производной: y — C2 = -y’ 2 / y» и подставим это в (2):
- Ну и наконец упростим полученное уравнение и получим:
Пример №2
Для закрепления составим еще одно уравнение:
Решение абсолютно идентично предыдущему, за исключением того, что вместо параметров С1 и С2 здесь представлены параметры a, b и с. Ну и, конечно, раз параметров три, то нам понадобятся производные первого, второго и третьего порядка.
Делать описание каждого шага я уже не буду, думаю вы уже сами разберетесь:
Первая производная:
Вторая производная:
Третья производная:
Ответ:
Ну, думаю, если вы разобрались в первыми двумя примерами, то все остальные вы решите без труда, а чтобы это проверить дам вам парочку заданий «на дом».
Пример №3
Выразим коэффициенты a и b через 1-ую и 2-ую производные:
Первая производная: 
Вторая производная: 
Подставим значение b второй производной в значение a первой производной:
А теперь подставим полученные значения a и b в исходное уравнение и упростим:

Ответ:
Пример №4
Ну а здесь все еще проще:
Возведем обе части уравнения в квадрат:
Чтобы воспользоваться основным тригонометрическим тождеством, вычтем из единицы обе части уравнения:
Ну и теперь как мы видим во второй части получилось исходное уравнение, только в квадрате, а значит оно будет равно:
Приведем к общему виду и запишем ответ:
Ответ:
Ну и на этой ноте мы с вами закончим данный урок, всем спасибо!
Если вам что-то непонятно (или нашли неточности в уроке) пишите в комментариях и мы вам обязательно ответим в ближайшее время.
[spoiler title=”источники:”]
http://mathhelpplanet.com/static.php?p=sostavlenie-differentsialnyh-uravnenii-semyeistv-linii-i-zadachi-na-traektorii
http://zadanonadom.ru/urok-1-sostavlenie-differentsialnogo-uravneniya-semejstva-krivyh/
[/spoiler]
Составление уравнений семейства кривых
Чтобы построить дифференциальное уравнение, которому удовлетворяют кривые семейства:
φ (1)
необходимо продифференцировать равенство (1) n раз, считая y функцией от x, а затем из полученных уравнений и уравнения (1) исключить произвольные постоянные C1 … Cn.
Линии, пересекающие все кривые данного семейства под одним и тем же углом ϕ, называются изогональными траекториями. Углы β и α наклона траектории и кривой к оси Ox связаны соотношением β = α ± φ.
Пусть
— дифференциальное уравнение данного семейства кривых, а
— уравнение семейства изогональных траекторий.
Тогда tg α = f (x,y), tg β = f1 (x,y).
Отсюда следует, что если дифференциальное уравнение семейства кривых написано и угол φ известен, то найти tg β не составит труда, а после также легко можно будет написать уравнение траекторий.
Частный случай:
Если уравнение семейства кривых записано в виде:
,
то при составлении уравнения траекторий можно обойтись без решения уравнения относительно y’, в этом случае будет достаточно y’ заменить на tg α = tg (β ± φ), где tg β = y’ — угловой коэффициент касательной к траектории.
Пример №1
Составить дифференциальное уравнение семейства кривых:
- Так как уравнение содержит два параметра (С1 и С2), то и дифференцировать будем два раза:
Первая производная:
Вторая производная:
- Дальше, чтобы составить дифференциальное уравнение семейства кривых необходимо избавиться от С1 , а для этого выведем его из уравнения первой производной С1 = -2(y — С2)y’ и подставим в наше уравнение:
(2)
- Теперь также нужно избавиться от параметра C2, а для этого выведем ее из второй производной: y — C2 = -y’2 / y» и подставим это в (2):
- Ну и наконец упростим полученное уравнение и получим:
Пример №2
Для закрепления составим еще одно уравнение:
Решение абсолютно идентично предыдущему, за исключением того, что вместо параметров С1 и С2 здесь представлены параметры a, b и с. Ну и, конечно, раз параметров три, то нам понадобятся производные первого, второго и третьего порядка.
Делать описание каждого шага я уже не буду, думаю вы уже сами разберетесь:
Первая производная:
Вторая производная:
Третья производная:
Ответ:
Ну, думаю, если вы разобрались в первыми двумя примерами, то все остальные вы решите без труда, а чтобы это проверить дам вам парочку заданий «на дом».
Пример №3
Выразим коэффициенты a и b через 1-ую и 2-ую производные:
Первая производная: , где
Вторая производная: , где
Подставим значение b второй производной в значение a первой производной:
А теперь подставим полученные значения a и b в исходное уравнение и упростим:
⇒
Ответ:
Пример №4
Ну а здесь все еще проще:
Найдем производную:
Возведем обе части уравнения в квадрат:
Чтобы воспользоваться основным тригонометрическим тождеством, вычтем из единицы обе части уравнения:
Ну и теперь как мы видим во второй части получилось исходное уравнение, только в квадрате, а значит оно будет равно:
И, следовательно,
Приведем к общему виду и запишем ответ:
Ответ:
Ну и на этой ноте мы с вами закончим данный урок, всем спасибо!
Если вам что-то непонятно (или нашли неточности в уроке) пишите в комментариях и мы вам обязательно ответим в ближайшее время.
Уроки по теории вероятности
Первая тема, которую я бы хотел рассмотреть на уроках элементарной алгебры — это выражения. Числовые выражения Числовые выражения — это выражения, состоящие только из цифр и знаков арифметических действий. Число, которое получается в результате выполнения действий в числовом выражении, называют значением выражения. Пример №1 Найти значение выражения: 12 * 6 — 16 : 4 Значение
Курс данного предмета мы начнем непосредственно с матриц, потому что именно они составляют основу данной дисциплины. Определение матрицы Матрицей размерности называется прямоугольная таблица чисел, содержащая — строк и — столбцов, число расположенное в -ой строке и -столбце обозначается и называется элементом матрицы , т. е. Операции над матрицами Рассмотрим основные операции, проводимые над матрицами: сумма матриц;
Данная статья занесена в архив так как написана новая, возможно более понятная статья, переходите по ссылке на нее http://mathcentr.ru/matritsa-i-operatsii-nad-nej/ Как вы, наверное, уже поняли матрицы ничем не отличаются от обычных чисел, по правде говоря — это просто много цифр в одном числе))) И разумеется, существуют такие же операции над матрицами, как и над числами, но не все и
Продолжаем изучать матрицы и сегодня на уроке мы научимся находить и вычислять обратную матрицу. Обратная матрица Матрица называется транспонированной к матрице , если выполняется условие: , для всех , где и — элементы матриц и соответственно. Проще говоря, транспонированная матрица — это перевернутая матрица, т.е. столбцы записаны строками, а строки столбцами. Пример №1 Транспонировать матрицу
Мы рассмотрели самые основные тригонометрические функции (не обольщайтесь помимо синуса, косинуса, тангенса и котангенса существует еще целое множество других функций, но о них позже), а пока рассмотрим некоторые основные свойства уже изученных функций. Тригонометрические функции числового аргумента Какое бы действительное число ни взять, ему можно поставить в соответствие однозначно определенное число . Правда, правило соответствия
Линию, пересекающую под определенным углом (varphi neq 90^o) каждую из кривых данного однопараметрического семейства (Phi(x,y,C)=0) (дифференциальное уравнение данного семейства кривых имеет вид (F(x,y,y’)=0)), называют изогональной траекторией этого семейства. Изогональные траектории данного семейства кривых образуют новое семейство линий.
В случае ортогональных траекторий, имеется всего одно семейство кривых. Но если (varphi neq 90^o), то можно построить два семейства кривых, в зависимости от того, как отсчитывать угол (varphi) (от исходной кривой к изогональной или наоборот).
Изогональные траектории находятся аналогично ортогональным, но в случае изогональных траекторий производные связаны следующим образом:
[frac{y_{изог}’-y’}{1+y’y_{изог}’}=tan varphi,]
где (varphi) отсчитывается от исходной кривой к изогональной кривой.
[frac{y’-y_{изог}’}{1+y’y_{изог}’}=tan varphi,]где (varphi) отсчитывается от изогональной кривой к исходной кривой.
Эти соотношения можно объединить в одно:
[y_{изог}’=frac{y’pm tan varphi}{1 mp y’ tan varphi}]
Соответственно уравнение изогональных траекторий будет иметь вид:
[F(x,y,dfrac{y’pm tan varphi}{1 mp y’ tan varphi})=0.]
Итак, чтобы найти уравнение семейства изогональных траекторий для данного однопараметрического семейства плоских кривых, нужно:
1) написать дифференциальное уравнение данного семейства кривых;
2) заменить в этом уравнении (y’) на (dfrac{y’pm tan varphi}{1 mp y’ tan varphi});
3) найти общее решение получившегося дифференциального уравнения.
При решении задач на нахождение изогональных траекторий обычно пользуются формулами для каждого отдельного семейства изогональных траекторий, или находят только одно уравнение:
[F(x,y,dfrac{y’- tan varphi}{1 + y’ tan varphi})=0.]
Пример. Составить дифференциальное уравнение изогональных траекторий, пересекающих семейство линий (x^2+y^2=a^2) под углом (varphi=45^o).
1. Найдем уравнение траекторий для которых где (varphi) отсчитывается от исходной кривой к искомой кривой:
[frac{y_1′-y’}{1+y’y_1′}=tan varphi]
[frac{y_1’+dfrac{x}{y}}{1-dfrac{x}{y}y_1′}=1]
Упрощая, получим:
[y_1’=frac{y-x}{y+x}]
2. Найдем уравнение траекторий для которых где (varphi) отсчитывается от искомой кривой к исходной кривой:
[frac{y’-y_2′}{1+y’y_2′}=tan varphi]
[frac{-dfrac{x}{y}-y_2′}{1-dfrac{x}{y}y_2′}=1]
Упрощая, получим:[y_2’=frac{y+x}{x-y}]
Таким образом, дифференциальные уравнения изогональных траекторий, пересекающих исходное семейство линий под углом (varphi=45^o) имеют вид:
[y’=frac{y-x}{y+x}; y’=frac{y+x}{x-y}.]
Результат построения семейства кривых и двух семейств изогональных траекторий:
Дифференциальные уравнения движения точки.
Основное уравнение
динамики
можно записать
так
или так
Проецируя уравнение
на оси координат получаем
так как ,
,
,
то
Частные случаи:
А) Точка движется
в плоскости. Выбираем в плоскости
координаты xOyполучаем
Б) Точка движется
по прямой. Выбираем на прямой координату
Oxполучаем
Основное уравнение
динамики
можно спроецировать на естественные
подвижные оси.
Эта форма уравнений
удобна для исследования некоторых
случаев полета снарядов и ракет.
Основные задачи динамики
Первая или прямая
задача:
Известна масса
точки и закон ее движения, необходимо
найти действующую на точку силу.
m
Вычисляем вторые
производные по времени от координат
точки, умножаем их на массу и получаем
проекции силы на оси координат
Зная проекции силы
на оси координат, определяем модуль
силы и ее направляющие косинусы:
Пример 1: Движение
точки в плоскости xOy
определяется уравнениями:
;
;
;
время.
Решение: ;

;
.
– Уравнение
траектории в координатной форме
(эллипс).
;
Пример 2: Точка,
имеющая массу
,
движется из состояния покоя по окружности
радиусас постоянным касательным ускорением
.
Определить действующую на точку силу
в момент, когда она пройдет по траектории
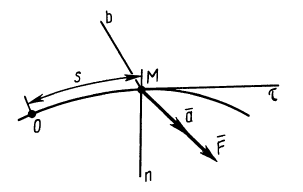
расстояние.
Решение: Применяя
дифференциальные уравнения движения
точки в проекциях на естественные оси,
имеем:

;
;
Так как
,
то,
;
;
; следовательно
;

следовательно
Вторая или
обратная задача:
Известна масса
точки и действующая на точку сила,
необходимо определить закон движение
этой точки.
Рассмотрим решение
этой задачи в декартовой системе
координат. Сила зависит от времени,
координат точки, ее скорости и других
причин.
,
,
Из теории обыкновенных
дифференциальных уравнений известно,
что решение одного дифференциального
уравнения второго порядка содержит две
произвольные постоянные. Для случая
системы трех обыкновенных дифференциальных
уравнений второго порядка имеется шесть
произвольных постоянных:
Каждая из координат
движущейся точки после интегрирования
системы уравнений зависит от времени
и всех шести произвольных постоянных,
т.е.
К этим уравнениям
необходимо добавить начальные условия:
,
,
Используя эти
начальные условия можно получить шесть
алгебраических уравнений для определения
шести произвольных постоянных
.
Основные виды прямолинейного движения точки
Дифференциальное
уравнение прямолинейного движения
точки вдоль оси Оx
имеет вид:
,
Начальные условия
,
.
Наиболее важные
случаи.
1. Сила постоянна.
Имеем равнопеременное
движение (движение с постоянным
ускорением)
2. Сила зависит от
времени.
3. Сила зависит от
координаты или скорости.
Силу, зависящую
от координаты х
,
создают упругие тела при их деформации
(например, сжатая или растянутая пружина).
Сила, зависящая
от скорости движения
,
это сила сопротивления (воздуха, воды
и т.д.)
В этих случаях
решение задачи упрощается.
Лекция 2
Краткое содержание:Свободные
колебания без сопротивления. Понятие
о фазовой плоскости. Свободные колебания
в поле постоянной силы. Параллельное
включение упругих элементов.
Последовательное включение упругих
элементов. Вынужденные колебания без
сопротивления. Резонанс. Свободные
колебания с вязким сопротивлением.
Вынужденные колебания с вязким
сопротивлением.