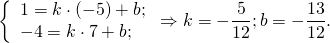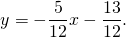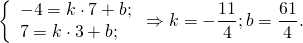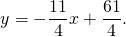Калькулятор длин сторон треугольника онлайн умеет вычислять длину сторон 14 способами.
Калькулятор может:
- Найти все стороны треугольника.
- Найти все углы треугольника.
- Найти площадь (S) и периметр (P) треугольника.
- Найти радиус (r) вписанной окружности.
- Найти радиус (R) описанной окружности.
- Найти высоту (h) треугольника.
Просто введите любые имеюшиеся данные и, если их достаточно, то калькулятор сам подберет нужные формулы для вычислений и покажет подробный расчет с выводом формул.
Сторона треугольника (или длина сторон) может быть найдена различными методами.
В большинстве случаев достаточно воспользоваться одной из ниже приведенных формул. Однако не редки случаи когда для нахождения искомой стороны понадобиться обратиться к дополнительным материалам или решения в два действия.
Как найти длину стороны треугольника?
Найти длину сторон треугольника очень просто на нашем онлайн калькуляторе. Так же длина может быть найдена самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.
Для прямоугольного треугольника:
1) Найти катет через гипотенузу и другой катет
где a и b – катеты, с – гипотенуза.
2) Найти гипотенузу по двум катетам
где a и b – катеты, с – гипотенуза.
3) Найти катет по гипотенузе и противолежащему углу
где a и b – катеты, с – гипотенуза,α° и β° – углы напротив катетов.
4) Найти гипотенузу через катет и противолежащий угол
где a и b – катеты, с – гипотенуза,α° и β°- углы напротив катетов.
Для равнобедренного треугольника:
1) Найти основание через боковые стороны и угол между ними
где a – искомое основание, b – известная боковая сторона,α° – угол между боковыми сторонами.
2) Найти основание через боковые стороны и угол при основании
где a – искомое основание,b – известная боковая сторона,β° – угол при осноавнии.
3) Найти боковые стороны по углу между ними
где b – искомая боковая сторона, a – основание,α° – угол между боковыми сторонами.
4) Найти боковые стороны по углу при основании
где b – искомая боковая сторона, a – основание,β° – угол при осноавнии.
Для равностороннего треугольника:
1) Найти сторону через площадь
где a – искомая сторона, S – площадь треугольника.
2) Найти сторону через высоту
где a – искомая сторона,h – высота треугольника.
3) Найти сторону через радиус вписанной окружности
где a – искомая сторона,r – радиус вписанной окружности.
4) Найти сторону через радиус описанной окружности
где a – искомая сторона,R – радиус описанной окружности.
Для произвольного треугольника:
1) Найти сторону через две известные стороны и один угол (теорема косинусов)
где a – искомая сторона, b и с – известные стороны, α° – угол напротив неизвестной стороны.
2) Найти сторону через одну известную сторону и два угла (теорема синусов)
где a – искомая сторона, b – известная сторона, α° и β° известные углы.
Скачать все формулы в формате Word
Решение треугольников онлайн
С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.
Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:
- Три стороны треугольника.
- Две стороны треугольника и угол между ними.
- Две стороны и угол противостоящий к одному из этих сторон треугольника.
- Одна сторона и любые два угла.
Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.
Решение треугольника по трем сторонам
Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем 
 |
(1) |
 |
(2) |
Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения

Пример 1. Известны стороны треугольника ABC: 

Решение. Из формул (1) и (2) находим:
И, наконец, находим угол C:
Решение треугольника по двум сторонам и углу между ними
Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.
Найдем сторону c используя теорему косинусов:


Далее, из формулы

 . . |
(3) |
Далее из (3) с помощью калькулятора находим угол A.
Поскольку уже нам известны два угла то находим третий:

Пример 2. Известны две стороны треугольника ABC: 

Решение. Иcпользуя теорму косинусов найдем сторону c:

Из формулы (3) найдем cosA:

Поскольку уже нам известны два угла то находим третий:
Решение треугольника по стороне и любым двум углам
Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.
Так как, уже известны два угла, то можно найти третий:

Далее, для находждения сторон b и c воспользуемся тероемой синусов:
Пример 3. Известна одна сторона треугольника ABC: 

Решение. Поскольку известны два угла, то легко можно найти третий угол С:
Найдем сторону b. Из теоремы синусов имеем:
Найдем сторону с. Из теоремы синусов имеем:
В треугольнике ABC длина стороны AB равна 5 сантиметров сторона BC длиннее стороны AB B на 8 см а длина стороны AC и меньше суммы длин его сторон A B и C на 6 сантиметров Найдите периметр треугольника?
Математика | 5 – 9 классы
В треугольнике ABC длина стороны AB равна 5 сантиметров сторона BC длиннее стороны AB B на 8 см а длина стороны AC и меньше суммы длин его сторон A B и C на 6 сантиметров Найдите периметр треугольника ответ.
5см + 8см = 13см – ВС
(5см + 13см) – 6см = 12см – АС
5см(АВ) + 13см(ВС) + 12см(АС) = 30см – Р.
Периметр треугольника ABC равен 50 сантиметрам?
Периметр треугольника ABC равен 50 сантиметрам.
Сторона AB равна 12 сантиметрам.
Сторона AC больше стороны AB на 10 сантиметров.
Найдите длину стороны BC.
Периметр треугольника abc равен 36 сантиметров?
Периметр треугольника abc равен 36 сантиметров.
Длина стороны ab равна 10 сантиметров, длина стороны bc на 4 сантиметра больше.
Чему равна длина стороны ac?
В треугольнике ABC длина стороны AB равна 5 см а сторона BC длинее стороны AB на 8 сантиметров, а длина стороны AC меньше суммы длин сторон AB и CD и на 6 см Найдите периметр треугольника?
В треугольнике ABC длина стороны AB равна 5 см а сторона BC длинее стороны AB на 8 сантиметров, а длина стороны AC меньше суммы длин сторон AB и CD и на 6 см Найдите периметр треугольника.
Составьте выражение для решения задачи и найдите его значение : “В треугольнике ABC длина стороны AB равна 5 сантиметров, сторона BC длиннее стороныABна 8 сантиметров, а длина стороны AC меньше суммы ?
Составьте выражение для решения задачи и найдите его значение : “В треугольнике ABC длина стороны AB равна 5 сантиметров, сторона BC длиннее стороныABна 8 сантиметров, а длина стороны AC меньше суммы длин сторон AB и BCа 6 сантиметров.
Найдите периметр треугольника.
Длина одной стороны треугольника равна 36 сантиметров что составляет 6 седьмых длины его 2 стороны длина третьей стороны равна 5 тринадцатых от суммы длин и первых двух сторон Найди периметр треугольн?
Длина одной стороны треугольника равна 36 сантиметров что составляет 6 седьмых длины его 2 стороны длина третьей стороны равна 5 тринадцатых от суммы длин и первых двух сторон Найди периметр треугольника.
Треугольник длина первой стороны треугольника равна 10 длина второй стороны на 2 сантиметра больше 11 стороны на 9 сантиметров меньше суммы длин первой и второй сторон Найдите длины сторон треугольник?
Треугольник длина первой стороны треугольника равна 10 длина второй стороны на 2 сантиметра бо
льше 11 стороны на 9 сантиметров меньше суммы длин первой и второй сторон Найдите длины сторон треугольника.
Периметр треугольника 20 сантиметров длины двух сторон 7 сантиметра и 8 сантиметра найди длина третьей стороны?
Периметр треугольника 20 сантиметров длины двух сторон 7 сантиметра и 8 сантиметра найди длина третьей стороны.
Составьте выражение для решения задачи и найдите его значение?
Составьте выражение для решения задачи и найдите его значение!
Треугольник ABC, длина стороны AB равна 5 сантиметров, сторона BC длиннее стороны AB на 8 сантиметров, а длина стороны АС меньше суммы длин сторон AB и BC 6 на сантиметров.
Найдите периметр треугольника.
В треугольнике a b c длины сторон a b равна 5 сантиметров сторона BC длиннее стороны AB 8 сантиметров а длина стороны АС и меньше суммы длин сторон AB и BC на 6 сантиметров Найди периметр треугольника?
В треугольнике a b c длины сторон a b равна 5 сантиметров сторона BC длиннее стороны AB 8 сантиметров а длина стороны АС и меньше суммы длин сторон AB и BC на 6 сантиметров Найди периметр треугольника.
В треугольнике a b c длины сторон a b равна 5 сантиметров сторона ABCD сторона BC 8 см а длина стороны AC меньше суммы длин сторон AB и BC на 6 сантиметров Найди периметр треугольника?
В треугольнике a b c длины сторон a b равна 5 сантиметров сторона ABCD сторона BC 8 см а длина стороны AC меньше суммы длин сторон AB и BC на 6 сантиметров Найди периметр треугольника.
На этой странице сайта размещен вопрос В треугольнике ABC длина стороны AB равна 5 сантиметров сторона BC длиннее стороны AB B на 8 см а длина стороны AC и меньше суммы длин его сторон A B и C на 6 сантиметров Найдите периметр треугольника? из категории Математика с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 5 – 9 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.
Точка с самым большим координатом находится правее, а с самым маленьким – левее а) В(200) б) А(7).
Путь = S (км) Формула определения S = v * t, где v – скорость, t – время в пути. Из этой формулы определяем время : t = S / v t = S / 65 (ч).
S = v * t t = S : v t = s : 65 (ч) Ответ : s : 65 часов.
Сначало узнаём сколько % мужчин 100 – 85 = 15% теперь узнаём сколько мужчин 48 * 0. 15 = 7(ч) учителя мужчины Ответ : 7 человек.
Умножаем первую дробь на два и получаем 28 / 30 (28 + 29) / 30 = 57 / 30 = 1, 9.
S = a * b = 32 P = 2 * (a + b) = 24 a = 8 длина b = 4 ширина.
Длина – 8 Ширина – 4 S = 8 × 4 = 32см ^ 2 – площадь P = 2 × (8 + 4) = 24см – периметр.
7. (148 + 148 + 125 + 126 + 112 + 115) : 6 = 774 : 6 = 129 кВт 8. 1 – а³ / 1 – а = 1 – ( – 0, 5)³ / 1 – ( – 0, 5) = 1 + 0, 125 / 1 + 0, 5 = 1, 125 / 1, 5 = 1125 / 1000 : 15 / 10 = 1125 / 1000 * 10 / 15 = 75 / 10 = 7, 5.
126 яблок в ящике так как в 3 кг 29 яблоко.
Составить уравнение стороны ab треугольника abc
Как составить уравнение сторон треугольника по координатам его вершин?
Зная координаты вершин треугольника, можно составить уравнение прямой, проходящей через 2 точки.
Дано: ΔABC, A(-5;1), B(7;-4), C(3;7)
Составить уравнения сторон треугольника.
1) Составим уравнение прямой AB, проходящей через 2 точки A и B.
Для этого в уравнение прямой y=kx+b подставляем координаты точек A(-5;1), B(7;-4) и из полученной системы уравнений находим k и b:
Таким образом, уравнение стороны AB
2) Прямая BC проходит через точки B(7;-4) и C(3;7):
Отсюда уравнение стороны BC —
3) Прямая AC проходит через точки A(-5;1) и C(3;7):
УСЛОВИЕ:
Даны вершины треугольника ABC. Найти: а) уравнение стороны AB; б) уравнение высоты CH; в) уравнение медианы AM; г) точку персечения медианы AM и высоты CH; д) уравнение прямой, проходящей через вершину C параллельно стороне AB; е) расстояние от точки C до прямой AB
A(-3,8); B(-6;2); C(0,-5)
РЕШЕНИЕ ОТ u821511235 ✪ ЛУЧШЕЕ РЕШЕНИЕ
Добавил vk247797756 , просмотры: ☺ 17346 ⌚ 2018-11-27 17:51:50. математика 1k класс
Решения пользователей
Написать комментарий
Делим обе части равенства на π
и умножаем на 4
+pi k, k in Z
Можно правую часть записать в виде двух ответов:
x=1+8n in Z : это . [b] -15; -7; 1; 9; 17; ..[/b].
x=3+ 8n, n in Z : это[b] -13; -5; 3; 11; . [/b]
[b]x=-5 – наибольшее отрицательное [/b]
О т в е т. x=1+8n in Z или x=3+ 8n, n in Z
корни чередуются так:
. -15;-13;-7;-5; 1;3; 9;11; 17; 19; .
[b]x=-5 – наибольшее отрицательное [/b] (прикреплено изображение)
a=1 – старший коэффициент
b=1 – средний коэффициент
с=-2 – свободный член
4.
x^2=a-5
При a-5=0 ⇒ при а=5
уравнение имеет один корень х=0
5.
Δ Прямоугольный, так как верно равенство: b^2=a^2+c^2
5^2=3^2+4^2
25=9+16
Значит, ∠ B=90 градусов и ∠ А+ ∠ С=90 градусов.
∠ А- ∠ С=36 градусов.
∠ А+ ∠ С=90 градусов.
складываем оба равенства:
2* ∠ А=126 градусов.
По формулам приведения:
sin^2x+sinx-2=0
D=9
sinx=-2 или sinx=1
sinx=-2 уравнение не имеет корней, -1 ≤ sinx ≤ 1
sinx=1 ⇒ x=(π/2)+2πk, k ∈ Z или х=90 ° +360 ° *k, k ∈ Z
Найдем корни, принадлежащие указанному отрезку с помощью неравенства:
-286 ° ≤ 90 ° +360 ° *k ≤ 204 °
-286 °-90 ° ≤ 360 ° *k ≤ 204 ° -90 °
-376 ° ≤ 360 ° *k ≤ 114 °
Неравенство верно при k=[green]-1[/green] и k=[red]0[/red]
Значит, указанному отрезку принадлежат два корня:
x=90 ° +360 °* ([green]-1[/green])=-270 °
x=90 ° +360 °*[red]0[/red]=90 °
7. KT- средняя линия трапеции:
Cредняя линия трапеции делит высоту трапеции пополам ( см. рис)
Высоты треугольников АКО и СОК равны половине высоты трапеции
S_( Δ АКО)+S_( Δ COK)=44
S_( Δ АКО)+S_( Δ COK)=KO*(h/4) +OT*(h/4)=
О т в е т. [b]176[/b]
B=-2
[i]l[/i]=8 – количество ребер четырехугольной пирамиды
Что ты хочешь узнать?
Ответ
Проверено экспертом
а) Длина стороны АВ:
б) Уравнение сторон АВ и ВС и их угловые коэффициенты: АВ : Х-Ха = У-Уа
Хв-Ха Ув-Уа
Получаем уравнение в общем виде:
АВ: 4х – 8 = 3у – 6 или
АВ: 4х – 3у – 2 = 0
Это же уравнение в виде у = кх + в:
у = (4/3)х – (2/3).
Угловой коэффициент к = 4/3.
ВС: 2х + у – 16 = 0.
ВС: у = -2х + 16.
Угловой коэффициент к = -2.
в) Внутренний угол В:Можно определить по теореме косинусов.
Находим длину стороны ВС аналогично стороне АВ:
BC = √((Хc-Хв)²+(Ус-Ув)²) = 2.236067977
cos В= ( АВ²+ВС²-АС²) / ( 2*АВ*ВС) = 0.447214
Угол B = 1.107149 радиан = 63.43495 градусов.
Можно определить векторным способом:
Пусть координаты точек
A: (Xa, Ya) = (2; 2) .
B: (Xb, Yb) = (5; 6).
С: (Xc, Yc) = (6; 4).
Находим координаты векторов AB и BС:
AB= (Xb-Xa; Yb-Ya) = ((5 – 2); (6 – 2)) = (3; 4);
BС= (Xc-Xв; Yс-Yв) = ((6 – 5); (4 – 6)) = (1; -2).
Находим длины векторов:
|AB|=√((Xb-Xa)² + (Yb-Ya)^2) = 5 ( по пункту а)
|ВС|=√((Xс-Xв)²+(Yс – Yв) = √(1²+(-2)²) = √5 = 2.236067977 .
b=cos α=(AB*ВС)/(|AB|*|ВС|
AB*ВC = (Xв – Xa)*(Xc – Xв) + (Yв – Ya)*(Yc – Yв) =
= 3*1 + 4*(-2) = 3 – 8 = -5.
b = cosα = |-5| / (5*2.236067977) = 5 / 11.18034 = 0.4472136 20
Угол α=arccos(b) = arc cos 0.4472136 = 1.1071487 радиан = 63.434949°.
г) Уравнение медианы АЕ.
Находим координаты точки Е (это основание медианы АЕ), которые равны полусумме координат точек стороны ВС.
3x – 6 = 3,5y – 7
3x – 3,5y + 1 =0, переведя в целые коэффициенты:
6х – 7у + 2 = 0,
С коэффициентом:
у = (6/7)х + (2/7) или
у = 0.85714 х + 0.28571.
[spoiler title=”источники:”]
http://matematika.my-dict.ru/q/4116646_v-treugolnike-abc-dlina-storony-ab/
http://4apple.org/sostavit-uravnenie-storony-ab-treugolnika-abc/
[/spoiler]
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a, b, c – стороны произвольного треугольника
α, β, γ – противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), (a):
* Внимательно, при подстановке в формулу, для тупого угла (α>90), cosα принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), (a):
Есть следующие формулы для определения катета или гипотенузы
a, b – катеты
c – гипотенуза
α, β – острые углы
Формулы для катета, (a):
Формулы для катета, (b):
Формулы для гипотенузы, (c):
Формулы сторон по теореме Пифагора, (a,b):
Вычислить длину неизвестной стороны через любые стороны и углы

b – сторона (основание)
a – равные стороны
α – углы при основании
β – угол образованный равными сторонами
Формулы длины стороны (основания), (b):
Формулы длины равных сторон , (a):
Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.

a – сторона, основание
b, c – стороны
β, γ – углы при основании
p – полупериметр, p=(a+b+c)/2
R – радиус описанной окружности
S – площадь треугольника
Формула длины высоты через стороны, (H):
Формула длины высоты через сторону и угол, (H):
Формула длины высоты через сторону и площадь, (H):
Формула длины высоты через стороны и радиус, (H):
В прямоугольном треугольнике катеты, являются высотами. Ортоцентр – точка пересечения высот, совпадает с вершиной прямого угла.
H – высота из прямого угла
a, b – катеты
с – гипотенуза
c1 , c2 – отрезки полученные от деления гипотенузы, высотой
α, β – углы при гипотенузе
Формула длины высоты через стороны, (H):
Формула длины высоты через гипотенузу и острые углы, (H):
Формула длины высоты через катет и угол, (H):
Формула длины высоты через составные отрезки гипотенузы , (H):
L– биссектриса, отрезок |OB|, который делит угол ABC пополам
a, b – стороны треугольника
с – сторона на которую опущена биссектриса
d, e – отрезки полученные делением биссектрисы
γ – угол ABC , разделенный биссектрисой пополам
p – полупериметр, p=(a+b+c)/2
Длина биссектрисы через две стороны и угол, (L):
Длина биссектрисы через полупериметр и стороны, (L):
Длина биссектрисы через три стороны, (L):
Длина биссектрисы через стороны и отрезки d, e, (L):
Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.
1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:
L – биссектриса, отрезок ME , исходящий из прямого угла (90 град)
a, b – катеты прямоугольного треугольника
с – гипотенуза
α – угол прилежащий к гипотенузе
Формула длины биссектрисы через катеты, ( L):
Формула длины биссектрисы через гипотенузу и угол, ( L):
2. Найти по формулам длину биссектрисы из острого угла на катет:
L – биссектриса, отрезок ME , исходящий из острого угла
a, b – катеты прямоугольного треугольника
с – гипотенуза
α, β – углы прилежащие к гипотенузе
Формулы длины биссектрисы через катет и угол, (L):
Формула длины биссектрисы через катет и гипотенузу, (L):
L – высота = биссектриса = медиана
a – одинаковые стороны треугольника
b – основание
α – равные углы при основании
β – угол образованный равными сторонами
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):
Формула высоты, биссектрисы и медианы, через стороны, (L):
Формула для вычисления высоты = биссектрисы = медианы.
В равностороннем треугольнике: все высоты, биссектрисы и медианы, равны. Точка их пересечения, является центром вписанной окружности.
L – высота=биссектриса=медиана
a – сторона треугольника
Формула длины высоты, биссектрисы и медианы равностороннего треугольника, (L):
Медиана – отрезок |AO|, который выходит из вершины A и делит противолежащею сторону c пополам.
Медиана делит треугольник ABC на два равных по площади треугольника AOC и ABO.
M – медиана, отрезок |AO|
c – сторона на которую ложится медиана
a, b – стороны треугольника
γ – угол CAB
Формула длины медианы через три стороны, (M):
Формула длины медианы через две стороны и угол между ними, (M):
Медиана, отрезок |CO|, исходящий из вершины прямого угла BCA и делящий гипотенузу c, пополам.
Медиана в прямоугольном треугольнике (M), равна, радиусу описанной окружности (R).

M – медиана
R – радиус описанной окружности
O – центр описанной окружности
с – гипотенуза
a, b – катеты
α – острый угол CAB
Медиана равна радиусу и половине гипотенузы, (M):
Формула длины через катеты, (M):
Формула длины через катет и острый угол, (M):
Геометрия 10-11 класс
10 баллов
Даны координаты вершин треугольника ABC :
A(−8;−3); B(4;−12); C(8;10) .
Необходимо найти:
1. длину стороны AB;
2. уравнение сторон AB и BC и их угловые коэффициенты;
3. угол ψ между прямыми AB и BC в радианах;
4. уравнение высоты CD и ее длину;
5. уравнение медианы AE и координаты точки K пересечения этой
медианы с высотой CD ;
6. уравнение прямой L, которая проходит через точку K
параллельно к стороне AB;
7. координаты точки ( , ) F F F x y , которая находится симметрично
точке A относительно прямой CD .
Ирина Каминкова
17.10.2020 15:19:31
Ответ эксперта
Ирина Каминкова
17.10.2020 15:19:56
Ответ эксперта
Ирина Каминкова
17.10.2020 15:20:20
Ответ эксперта
Ирина Каминкова
17.10.2020 15:20:40
Ответ эксперта
Все предметы
Рейтинг пользователей
Формул для нахождения стороны треугольника не так уж много, но главное не знать их – а успешно применять при решении задач, ведь далеко не каждую задачу можно решить в лоб.
Сейчас на примере я покажу, как нужно их применять.
Есть произвольный треугольник со стороной 18 см, один угол при нем равен 30 градусам, а площадь равна 36 см.кв. Нужно найти две другие стороны. Сделаем рисунок
Для решения задачи проведем к основанию (с=18см) высоту h и тем самым разделим наш треугольник на два прямоугольных.
Исходя из формулы площади, найдем высоту
S = 1/2h*c откуда h = 2S/c = 2*36/18 = 4 см
Теперь находим сторону b по синусу угла
sin = h/b (отношение противоположного катета к гипотенузе) откуда b = h/(sin 30) = 4/(1/2) = 8 см.
Мы уже знаем две стороны у угол между ними и третью сторону можно найти по формуле из теоремы косинусов, но к сожалению не всегда мы ее помним. В нашем случае ничего страшного – найдем сторону а по формуле Пифагора, но для начала нам нужно найти сторону х.
Можно по формуле Пифагора
откуда х = квадратный корень из (8*8 – 4*4), что равно 4*(кв.к3)
и находим последнюю сторону нашего треугольника
а = кв.к из (c-x)*(c-x) + h*h = кв.к из 18*18-2*18*4*(кв.к3)+4*(кв.к3)*4*(кв.к3)+4*4
здесь стоит обратить внимание, что
18*18 = с*с
4*(кв.к3)*4*(кв.к3)+4*4 = 4*4*3+4*4 = 4*4*4 = 4*2*2*2 = 8*8 = b*b
2*18*4*(кв.к3) = 2*18*4*2*(кв.к3/2) = 2*18*8*(кв.к3/2) = 2*с*b*cos30 и теперь можно записать
а = кв.к из с*с – 2*с*b*cos30 + b*b Что на самом деле есть формулой нахождения стороны треугольника по теореме косинусов (мы ее только что вывели)
Теперь посчитаем и найдем сторону а = 11,772 см.