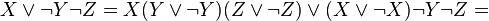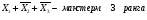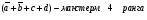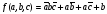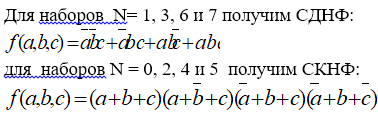Как составить днф по функции

ДНФ

Определение:

Простой конъюнкцией (англ. inclusive conjunction) или конъюнктом (англ. conjunct) называется конъюнкция одной или нескольких переменных или их отрицаний, причём каждая переменная встречается не более одного раза.

Простая конъюнкция

• полная, если в неё каждая переменная (или её отрицание) входит ровно раз;
• монотонная, если она не содержит отрицаний переменных.

Определение:

Дизъюнктивная нормальная форма, ДНФ (англ. disjunctive normal form, DNF) — нормальная форма, в которой булева функция имеет вид дизъюнкции нескольких простых конъюнктов.

Пример ДНФ:
.

СДНФ

Определение:

Совершенная дизъюнктивная нормальная форма, СДНФ (англ. perfect disjunctive normal form, PDNF) — ДНФ, удовлетворяющая условиям: в ней нет одинаковых простых конъюнкций, каждая простая конъюнкция полная.

Пример СДНФ:
.

Теорема:

Для любой булевой функции , не равной тождественному нулю, существует СДНФ, ее задающая.

Доказательство:

Для любой булевой функции выполняется следующее соотношение, называемое разложением Шеннона: . Данное соотношение легко проверить подстановкой возможных значений ( и ). Эта формула позволяет выносить за знак функции. Последовательно вынося , ,.., за знак , получаем следующую формулу: Так как применение данного соотношения к каждой из переменных увеличивает количество конъюнктов в два раза, то для функции от переменных мы имеем конъюнктов. Каждый из них соответствует значению функции на одном из возможных наборов значений переменных. Если на некотором наборе , то весь соответствующий конъюнкт также равен нулю и из представления данной функции его можно исключить. Если же , то в соответствующем конъюнкте само значение функции можно опустить. В результате для произвольной функции была построена СДНФ.

Алгоритм построения СДНФ по таблице истинности

1. В таблице истинности отмечаем те наборы переменных, на которых значение функции равно .
2. Для каждого отмеченного набора записываем конъюнкцию всех переменных по следующему правилу: если значение некоторой переменной есть , то в конъюнкцию включаем саму переменную, иначе ее отрицание.
3. Все полученные конъюнкции связываем операциями дизъюнкции.

Пример построения СДНФ для медианы

Построение СДНФ для медианы от трех аргументов

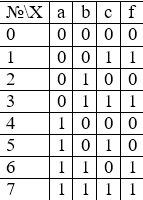
1. В таблице истинности отмечаем те наборы переменных, на которых значение функции равно .

0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

2. Для каждого отмеченного набора записываем конъюнкцию всех переменных по следующему правилу: если значение некоторой переменной есть , то в конъюнкцию включаем саму переменную, иначе ее отрицание.

0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

3. Все полученные конъюнкции связываем операциями дизъюнкции:

.

Построение СДНФ для медианы от пяти аргументов

0	0	0	0	0	0
0	0	0	0	1	0
0	0	0	1	0	0
0	0	0	1	1	0
0	0	1	0	0	0
0	0	1	0	1	0
0	0	1	1	0	0
0	0	1	1	1	1
0	1	0	0	0	0
0	1	0	0	1	0
0	1	0	1	0	0
0	1	0	1	1	1
0	1	1	0	0	0
0	1	1	0	1	1
0	1	1	1	0	1
0	1	1	1	1	1
1	0	0	0	0	0
1	0	0	0	1	0
1	0	0	1	0	0
1	0	0	1	1	1
1	0	1	0	0	0
1	0	1	0	1	1
1	0	1	1	0	1
1	0	1	1	1	1
1	1	0	0	0	0
1	1	0	0	1	1
1	1	0	1	0	1
1	1	0	1	1	1
1	1	1	0	0	1
1	1	1	0	1	1
1	1	1	1	0	1
1	1	1	1	1	1

.

Примеры СДНФ для некоторых функций

Стрелка Пирса: .

Исключающее или: .

См. также

• Сокращенная и минимальная ДНФ
• КНФ

Источники информации

• СДНФ — Википедия
• Е.Л Рабкин, Ю.Б. Фарфоровская — Дискретная математика

Алгоритм построения днф

1)
Избавиться от всех логических операций,
содержащихся в формуле, заменив их
основными: конъюнкцией, дизъюнкцией,
отрицанием. Это можно сделать, используя
равносильные формулы:

A→B=
ךAvB
A⇔B=(A^B)v(ךAvךB)

2)
Заменить знак отрицания, относящийся
ко всему выражению, знаками отрицания,
относящимися к отдельным переменным
высказываниям на основании формул:

ך(AvB)=
ךA^ךB
ך(A^B)=
ךAvךB

3)
Избавиться от знаков двойного отрицания.

4)
Применить, если нужно, к операциям
конъюнкции и дизъюнкции
свойства дистрибутивности и
формулы поглощения.

Пример построения днф

Приведем
к ДНФ формулу :F=((X→Y)↓
ך(Y→Z))

Выразим
логические операции → и ↓ через :v
^ ך

F=((
ךXvY)↓
ך(ךYvZ))=
ך
((ךXvY)v
ך
(ךYvZ))

В
полученной формуле перенесем отрицание
к переменным и сократим двойные отрицания:

F=
ך
((ךXvY)v
ך
(ךYvZ))=(
ך
ךX^
ךY)^(
ךYvZ)=(X^
ךY)^(
ךYvZ)

Используя
закон дистрибутивности,
приводим формулу к ДНФ:

F=(X^
ךY^
ךY)v(X^
ךY^Z)

Конъюнктивная
нормальная форма
(КНФ)
в булевой
логике —
нормальная
форма, в
которой булева
формула имеет
вид конъюнкции дизъюнкцийлитералов.
Конъюнктивная нормальная форма удобна
для автоматического
доказательства теорем.
Любая булева
формула может
быть приведена к КНФ. Для этого можно
использовать: Закон
двойного отрицания,
Закон
де Моргана,
Дистрибутивность.

Примеры и контр
примеры

Формулы в
КНФ:

ך
A^(BvC)
(AvB)^(
ך
BvCv
ך
D)^(Dv
ך
E)A^B

Формулы не
в КНФ:

ך
(BvC)
(A^B)vC
A^(Bv(D^E))

Но эти 3 формулы не
в КНФ эквивалентны следующим формулам
в КНФ:

ך
B^
ך
C
(AvC)^(BvC) A^(BvD)^(BvE)

Построение КНФ

Алгоритм построения
КНФ

1) Избавиться от
всех логических операций, содержащихся
в формуле, заменив их основными:
конъюнкцией, дизъюнкцией, отрицанием.
Это можно сделать, используя равносильные
формулы:

A→B=
ך
AvB
A↔B=(A^B)v(ך
A^
ך
B)

2) Заменить знак
отрицания, относящийся ко всему выражению,
знаками отрицания, относящимися к
отдельным переменным высказываниям на
основании формул:

ך
(AvB)=
ך
A^
ך
B
ך
(A^B)=
ך
Av
ך
B

3) Избавиться от
знаков двойного отрицания.

4) Применить, если
нужно, к операциям конъюнкции и дизъюнкции
свойства дистрибутивности
и формулы поглощения.

Пример построения
КНФ

Приведем к КНФ
формулу

F=(X→Y)^((
ך
Y→Z)
→
ך
X)

Преобразуем формулу
F к формуле не содержащей → :

F=(
ך
XvY)^(
ך
(ך
Y→Z)v
ך
X)=(
ך
XvY)^(
ך
(ך
ך
YvZ)v
ך
X)

В полученной формуле
перенесем отрицание к переменным и
сократим двойные отрицания:

F=(
ך
XvY)^((
ך
Y^
ך
Zv
ך
X)=(
ך
XvY)^((
ך
Y^
ך
Z)v
ך
X)

По закону
дистрибутивности
получим КНФ:

F=(
ך
XvY)^(
ך
Xv
ך
Y)^(
ך
Xv
ך
Z)

k-конъюнктивной
нормальной формой называют конъюнктивную
нормальную форму, в которой каждая
дизъюнкция содержит ровно kлитералов.

Например, следующая
формула записана в 2-КНФ:

(AvB)^(
ך
BvC)^(Bv
ך
C)

Переход от КНФ к
СКНФ

Если в простой
дизъюнкции не хватает какой-то переменной
(например, z), то добавляем в нее выражение
: (это не меняет самой дизъюнкции), после
чего раскрываем скобки с использованием
распределительного
закона:

(XvY)^(Xv
ך
Yv
ך
Z)=(XvYv(Z^
ך
Z))^(Xv
ך
Yv
ך
Z)=(XvYvZ)^(XvY
vך
Z)^(Xv
ךYv
ךZ)

Таким образом, из
КНФ получена СКНФ.

Переход от КНФ к
СКНФ

Если в простой
дизъюнкции не хватает какой-то переменной
(например, z), то добавляем в нее выражение
:Z^
ך
Z=0
(это не меняет самой дизъюнкции), после
чего раскрываем скобки с использованием
распределительного
закона:

(XvY)^(Xv
ךY
ךZ)=(XvYv(Zv
ךZ))^(Xv
ךYv
ךZ)=(XvYvZ)^(XvYv
ךZ)^(Xv
ךYv
ךZ)
Таким образом, из КНФ получена СКНФ.

25.
Совершенные дизъюнктивные и конъюнктивные
нормальные формы и алгоритмы приведения
к ним. Примеры.

Соверше́нная
конъюнкти́вная норма́льная фо́рма
(СКНФ) — это
такая конъюнктивная
нормальная форма,
которая удовлетворяет трём условиям:

в ней нет одинаковых
элементарных дизъюнкций

в каждой дизъюнкции
нет одинаковых пропозициональных
переменных

каждая элементарная
дизъюнкция содержит каждую пропозициональную
букву из входящих в данную КНФ
пропозициональных букв.

k-конъюнктивной
нормальной формой называют конъюнктивную
нормальную форму, в которой каждая
дизъюнкция содержит ровно k
литералов.

Например, следующая
формула записана в 2-КНФ:

Соверше́нная
дизъюнкти́вная норма́льная фо́рма
(СДНФ) —
это такая ДНФ,
которая удовлетворяет трём условиям:

в ней нет одинаковых
элементарных конъюнкций

в каждой конъюнкции
нет одинаковых пропозициональных букв

каждая элементарная
конъюнкция содержит каждую пропозициональную
букву из входящих в данную ДНФ
пропозициональных букв, причём в
одинаковом порядке.

Для любой функции
алгебры логики существует своя СДНФ,
причём единственная.

Для того, чтобы
получить СДНФ функции, требуется
составить её таблицу
истинности.
К примеру, возьмём одну из таблиц
истинности:

0	0	0	1
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	0
1	0	1	0
1	1	0	1
1	1	1	0

Совершенная ДНФэтой функции:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Дизъюнктивная нормальная форма

Дизъюнкти́вная норма́льная фо́рма (ДНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид дизъюнкции конъюнкций литералов. Любая булева формула может быть приведена к ДНФ.

Формулы в ДНФ:

Формулы не в ДНФ:

Алгоритм построения ДНФ

1) Избавиться от всех логических операций, содержащихся в формуле, заменив их основными: конъюнкцией, дизъюнкцией, отрицанием. Это можно сделать, используя равносильные формулы:

2) Заменить знак отрицания, относящийся ко всему выражению, знаками отрицания, относящимися к отдельным переменным высказываниям на основании формул:

3) Избавиться от знаков двойного отрицания.

4) Применить, если нужно, к операциям конъюнкции и дизъюнкции свойства дистрибутивности и формулы поглощения.

Пример построения ДНФ

Приведем к ДНФ формулу :

Выразим логические операции → и ↓ через :

В полученной формуле перенесем отрицание к переменным и сократим двойные отрицания:

Совершенная дизъюнктивная нормальная форма

Соверше́нная дизъюнкти́вная норма́льная фо́рма (СДНФ) — это такая ДНФ, которая удовлетворяет трём условиям:

• в ней нет одинаковых элементарных конъюнкций
• в каждой конъюнкции нет одинаковых пропозициональных букв
• каждая элементарная конъюнкция содержит каждую пропозициональную букву из входящих в данную ДНФ пропозициональных букв, причём в одинаковом порядке.

Для любой функции алгебры логики существует своя СДНФ, причём единственная.

Для того, чтобы получить СДНФ функции, требуется составить её таблицу истинности. К примеру, возьмём одну из таблиц истинности:

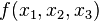0	0	0	1
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	0
1	0	1	0
1	1	0	1
1	1	1	0

В ячейках результата 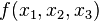 отмечаются лишь те комбинации, которые приводят логическое выражение в состояние единицы. Далее рассматриваются значения переменных при которых функция равна 1. Если значение переменной равно 0, то она записывается с инверсией. Если значение переменной равно 1, то без инверсии.

Первая строка содержит 1 в указанном поле. Отмечаются значения всех трёх переменных, это:

• 
• 
• 

Нулевые значения — тут все переменные представлены нулями — записываются в конечном выражении инверсией этой переменной. Первый член СДНФ рассматриваемой функции выглядит так: 

Переменные второго члена:

• 
• 
• 

 в этом случае будет представлен без инверсии: 

Таким образом анализируются все ячейки 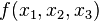. Совершенная ДНФ этой функции будет дизъюнкцией всех полученных членов (элементарных конъюнкций).

Совершенная ДНФ этой функции:

Переход от ДНФ к СДНФ

Если в какой-то простой конъюнкции недостаёт переменной, например, Z, вставляем в неё выражение

,

после чего раскрываем скобки (при этом повторяющиеся дизъюнктные слагаемые не пишем, так как  по закону идемпотентности). Например:

Таким образом, из ДНФ получили СДНФ.

Логические функции, СДНФ СКНФ

1.4 Формы представления функций алгебры логики

Функции алгебры логики могут быть заданы различными способами:

– таблицей истинности – в аналитической форме- в числовой форме..

Если функция имеет значения на всех наборах, то она называется полностью определенной.

элементарная дизъюнкция – дизъюнктивный терм или макстерм – это дизъюнктивный терм или макстерм – это дизъюнкция произв числа попарно независимых перем Например,

элементарная конъюнкция – конъюнктивный терм или минтерм – конъюнкция произв числа попарно независимых перем. Напр, Х ₁Х ₂ Х₃ – минтерм 3-его ранг

– это не минтерм, так как перем и зависимы.

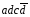
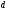
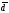
Для аналитической записи функций используют две формы:

1) Дизъюнктивную Нормальную Форму – ДНФ

2) Конъюнктивную Нормальную Форму – КНФ

ДНФ это дизъюнкция минтермов разл ранга

КНФ это конъюнкция макстермов различного ранга

Если все термы, входяшие в нормальную форму имеют одинаковый и максимальный ранг,= числу переменных функции – n, то такая форма называется совершенной. При этом, минтерм называют констинтуентой (составля) 1 (КЕ), а макстерм – конституентой 0 (КН).

– это СДНФ

– это СКНФ

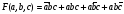
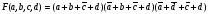
Т е СДНФ есть дизъюнкция конституент 1, а СКНФ – есть конъюнкция конституент 0

Составление совершенных форм по табл истинности

Совершенные формы составляют по табл истинности функции. СДНФ : для каждого набора переменных на которых функция=1, записывают минтерм ранга n , в которых с отрицанием берутся переменные = 0 на данном наборе. Все минтермы объединены дизъюнктивно.

СКНФ =для каждого набора переменных, на которых функция=0, записывают макстерм ранга n, в кот с отрицанием берутся переменные, имеющие значение=1 на данном наборе. Все макстермы объединены конъюнктивно

Для компактной записи функций исп числовую форму, в которой заданы только номера наборов. Числовая форма для СДНФ: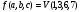

Числовая форма для СКНФ:

Алгоритм преобразованияя в ДНФ

1) Сначала избавляемся от операций импликации, эквивалентности и неравнозначности, выразив их через логические связки ¬, & и ∨ по законам:

2) Доводят знаки отрицания до независимых переменных, используя законы де Моргана:

3) Применяя з-н дистрибутивности

преобразуют формулу к дизъюнкции элементарных конъюнкций

4) 4) Постоянно избавляются от двойных отрицаний:
ДНФ A наз совершенной и обозн СДНФ, если каждая переменная формулы A входит с отрицанием или без отрицания в каждый конъюнкт точно 1 раз.

Алгебраическая форма представления булевых функций используется для минимизации (упрощения формулл) и для построения логических схем. Существукт 2 формы алгебраических функций – дизъюнктивная и конъюнктивн. Дизъюнктивная нормальная форма представляет сумму элементарных произведения аргументов, например

Если кажд слаг содер все арг или их отриц, то получ соверш дизъюнкт норм форму (СДФН), напр

Для перехода от табл истинн к СДНФ учит только те сост, для кот функц= 1. Для каждого такого сост запис элем произв всех ар. Если арг имеет зн “0”, то запис его отриц. Для привед примера СДНФ имеет вид   (17.4)

Совершенная конъюнктивная нормальная форма (СКНФ) представляет логическое произведение элементарных логических сумм, причем каждая сумма содержит все аргументы или их отрицания, например

ДНФ, но не СДНФ от 3 перем

-ДНФ от 2 перем

-представл импликации в виде ДНФ.

-СДНФ для импликации

-СДНФ для оп эквивалентности

-СДНФ для оп неравнозначности

Прим.1 Привести к ДНФ формулу

Реш.

2. Привести ту же формулу к СДНФ. Начав преобразования с ДНФ

Нахождение СДНФ по табл истинности функции	Нахождение СКНФ по табл истинности функции
1)Отметить те строки таблицы истинности, в последнем столбце которых стоят 1. 2)Выписать для каждой отмеченной строки конъюнкцию всех переменных так: если значение некоторой переменной в данной строке – 1, то в конъюнкцию включать саму эту переменную, если равно 1, то ее отрицание. 3)Все полученные конъюнкции связать в дизъюнкцию.	1)Отметить те строки таблицы истинности, в последнем столбце которых стоят 0. 2)Выписать для каждой отмеченной строки дизъюнкцию всех переменных так: если значение некоторой переменной в данной строке= 1, то в дизъюнкцию включать саму эту переменную, если равно 0, то ее отрицание. 3)Все полученные дизъюнкции связать в конъюнкцию.

Прим1

Прим 2

построение СДНФ:	построение СКНФ:

Для перехода от таблицы истинности к СКНФ учитывают только те состояния, для которых функция= “0”. Для каждого такого состояния записывается элементарная сумма аргументов. Если аргуент имеет значение “1”, то пишут его отрицание. Для примера СКНФ имеет вид

Примеры

1)Привести к КНФ и СКНФ.

Реш. упростим выражение, используя законы де Моргана и правило x y x y → = ∨

Теперь приводим к КНФ

Приведем к СКНФ:

2) С помощью эквивалентных преобразований построить д.н.ф. функции f (x):

Решение. Преобразуем функцию:

3) Используя СКНФ, найти наиболее простую формулу алгебры высказываний от 4 переменных, принимающую значение 0 на следующих наборах значений переменных, и только на них:

Решение. Запишем СКНФ функции по данным задачи

Получили

ЛИТЕРАТУРА и ССЫЛКИ

1)Курилова М.Н. Информатика-логика, СПБ Лес-техн ун-т им.Кирова

https://studfiles.net/preview/2069515/page:5/

2) http://ptca.narod.ru/lec/lec4_3.html

3) https://www.matburo.ru/ex_dm.php?p1=bfpg

Дизъюнкти́вная норма́льная фо́рма (ДНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид дизъюнкции конъюнкций литералов. Любая булева формула может быть приведена к ДНФ.^[1] Для этого можно использовать закон двойного отрицания, закон де Моргана, закон дистрибутивности. Дизъюнктивная нормальная форма удобна для автоматического доказательства теорем.

Примеры[править | править код]

Формулы в ДНФ:

Формулы не в ДНФ:

Но последние две формулы эквивалентны следующим формулам в ДНФ:

Построение ДНФ[править | править код]

Алгоритм построения ДНФ[править | править код]

1) Избавиться от всех логических операций, содержащихся в формуле, заменив их основными: конъюнкцией, дизъюнкцией, отрицанием. Это можно сделать, используя равносильные формулы:

2) Заменить знак отрицания, относящийся ко всему выражению, знаками отрицания, относящимися к отдельным переменным высказываниям на основании формул:

3) Избавиться от знаков двойного отрицания.

4) Применить, если нужно, к операциям конъюнкции и дизъюнкции свойства дистрибутивности и формулы поглощения.

Пример построения ДНФ[править | править код]

Приведем к ДНФ формулу

Выразим логическую операцию → через

В полученной формуле перенесем отрицание к переменным и сократим двойные отрицания:

Используя закон дистрибутивности, получаем:

Используя идемпотентность конъюкции, получаем ДНФ:

k-дизъюнктивная нормальная форма[править | править код]

k-дизъюнктивной нормальной формой называют дизъюнктивную нормальную форму, в которой каждая конъюнкция содержит ровно k литералов.

Например, следующая формула записана в 2-ДНФ:

Переход от ДНФ к СДНФ[править | править код]

Если в какой-то простой конъюнкции недостаёт переменной, например, Z, вставляем в неё выражение

,

после чего раскрываем скобки (при этом повторяющиеся дизъюнктные слагаемые не пишем, так как по закону идемпотентности). Например:

Таким образом, из ДНФ получили СДНФ.

Формальная грамматика, описывающая ДНФ[править | править код]

Следующая формальная грамматика описывает все формулы, приведенные к ДНФ:

<ДНФ> → <конъюнкт>

<ДНФ> → <ДНФ> ∨ <конъюнкт>

<конъюнкт> → <литерал>

<конъюнкт> → (<конъюнкт> ∧ <литерал>)

<литерал> → <терм>

<литерал> → ¬<терм>

где <терм> обозначает произвольную булеву переменную.

Особенности обозначений[править | править код]

Следует отметить, что для удобства восприятия в качестве обозначения конъюнкции и дизъюнкции часто используют символы арифметического умножения и сложения, при этом символ умножения часто опускается. В этом случае формулы булевой алгебры выглядят как алгебраические полиномы, что более привычно для глаза, однако иногда может привести к недоразумениям.

Например, следующие записи эквивалентны:

По этой причине ДНФ в русскоязычной литературе иногда называют «суммой произведений», что является калькой с английского термина «sum of products».

См. также[править | править код]

• Конъюнктивная нормальная форма
• Совершенная дизъюнктивная нормальная форма
• Совершенная конъюнктивная нормальная форма

• Конъюнктивный одночлен
• Дизъюнктивный одночлен

Примечания[править | править код]

Литература[править | править код]

• Ю.И. Галушкина, А.Н. Марьямов: Конспект лекций по дискретной математике – 2-е изд., испр. – М.: Айрис-пресс, 2008. – 176 с. – (Высшее образование).

Ссылки[править | править код]

• ДНФ, СДНФ, КНФ, СКНФ
• Disjunctive Normal Form
• Дизъюнктивная и Конъюнктивная нормальные формы
• Определение ДНФ и КНФ
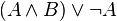
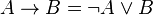
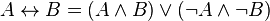
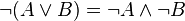
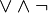
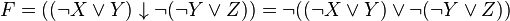
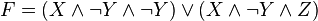
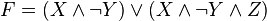
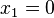
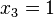
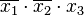
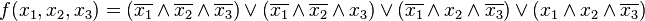
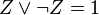