Как составить древо выбора

Рассказываем, как правильно использовать дерево решений для машинного обучения, визуализации данных и наглядной демонстрации процесса принятия решений. Пригодится не только аналитикам данных, но и тем, кто хочет найти методику, помогающую более взвешенно принимать решения в жизни и бизнесе.

Основные задачи, которые дерево решений решает в машинном обучении, анализе данных и статистике:

• Классификация — когда нужно отнести объект к конкретной категории, учитывая его признаки.
• Регрессия — использование данных для прогнозирования количественного признака с учетом влияния других признаков.

Деревья решений также могут помочь визуализировать процесс принятия решения и сделать правильный выбор в ситуациях, когда результаты одного решения влияют на результаты следующих решений. Попробуем объяснить, как это работает на простых примерах из жизни.

Что такое дерево решений

Визуально дерево решений можно представить как карту возможных результатов из ряда взаимосвязанных выборов. Это помогает сопоставить возможные действия, основываясь на их стоимости (затратах), вероятности и выгоде.

Как понятно из названия, для этого используют модель принятия решений в виде дерева. Такие древовидные схемы могут быть полезны и в процессе обсуждения чего-либо, и для составления алгоритма, который математически определяет наилучший выбор.

Обычно дерево решений начинается с одного узла, который разветвляется на возможные результаты. Каждый из них продолжает схему и создает дополнительные узлы, которые продолжают развиваться по тому же признаку. Это придает модели древовидную форму.

В дереве решений могут быть три разных типа узлов:

• Decision nodes — узлы решения, они показывают решение, которое нужно принять.
• Chance nodes — вероятностные узлы, демонстрируют вероятность определенных результатов.
• End nodes — замыкающие узлы, показывают конечный результат пути решения.

Преимущества и недостатки методики дерева решений

Преимущества метода:

1. Деревья решений создаются по понятным правилам, они просты в применении и интерпретации.
2. Можно обрабатывать как непрерывные, так и качественные (дискретные) переменные.
3. Можно работать с пропусками в данных, деревья решений позволяют заполнить пустое поле наиболее вероятным значением.
4. Помогают определить, какие поля больше важны для прогнозирования или классификации.

Недостатки метода:

1. Есть вероятность ошибок в задачах классификации с большим количеством классов и относительно небольшим числом примеров для обучения.
2. Нестабильность процесса: изменение в одном узле может привести к построению совсем другого дерева, что связано с иерархичностью его структуры.
3. Процесс «выращивания» дерева решений может быть довольно затратным с точки зрения вычислений, ведь в каждом узле каждый атрибут должен раскладываться до тех пор, пока не будет найден наилучший вариант решения или разветвления. В некоторых алгоритмах используются комбинации полей, в таком случае приходится искать оптимальную комбинацию по «весу» коэффициентов. Алгоритм отсечения (или «обрезки») также дорогостоящий, так как необходимо сформировать и сравнить большое количество потенциальных ветвей.

Как создать дерево решений

Для примера предлагаем сценарий, в котором группа астрономов изучает планету — нужно выяснить, сможет ли она стать новой Землей.

Существует N решающих факторов, которые нужно тщательно изучить, чтобы принять разумное решение. Этими факторами может быть наличие воды на планете, температурный диапазон, подвержена ли поверхность постоянным штормам, сможет ли выжить флора и фауна в этом климате и еще сотни других параметров.

Задачу будем исследовать через дерево решений.

1. Пригодная для обитания температура находится в диапазоне от 0 до 100 градусов Цельсия?

Таким образом, у нас получилось завершенное дерево решений.

Правила классификации

Сначала определимся с терминами и их значениями.

Правила классификации — это случаи, в которых учитываются все сценарии, и каждому присваивается переменная класса.

Переменная класса — это конечный результат, к которому приводит наше решение. Переменная класса присваивается каждому конечному, или листовому, узлу.

Вот правила классификации из примера дерева решений про исследование новой планеты:

1. Если температура не находится в диапазоне от -0,15 °C до 99,85 °C, то выживание затруднительно.
2. Если температура находится в диапазоне от -0,15 °C до 99,85 °C, но нет воды, то выживание затруднительно.
3. Если температура находится в диапазоне от -0,15 °C до 99,85 °C, есть вода, но нет флоры и фауны, то выживание затруднительно.
4. Если температура находится в диапазоне от -0,15 °C до 99,85 °C, есть вода, есть флора и фауна, поверхность не подвержена штормам, то выживание возможно.
5. Если температура находится в диапазоне от -0,15 °C до 99,85 °C, есть вода, есть флора и фауна, но поверхность подвержена штормам, то выживание затруднительно.

Почему сложно построить идеальное дерево решений

В структуре дерева решений выделяют следующие компоненты:

1. Root Node, или корневой узел — тот, с которого начинается дерево, в нашем примере в качестве корня рассматривается фактор «температура».
2. Internal Node, или внутренний узел — узлы с одним входящим и двумя или более исходящими соединениями.
3. Leaf Node, или листовой узел — это заключительный элемент без исходящих соединений.

Когда создается дерево решений, мы начинаем от корневого узла, проверяем условия тестирования и присваиваем элемент управления одному из исходящих соединений. Затем снова тестируем условия и назначаем следующий узел. Чтобы считать дерево законченным, нужно все условия привести к листовому узлу (Leaf Node). Листовой узел будет содержать все метки класса, которые влияют на «за» и «против» в принятии решения.

Обратите внимание — мы начали с признака «температура», посчитали его корнем. Если выбрать другой признак, то и дерево получится другим. В этом принцип метода — нужно выбрать оптимальный корень и с помощью него выстраивать дерево, решить, какое же дерево нужно для выполнения задачи.

Есть разные способы найти максимально подходящее дерево решений для конкретной ситуации. Ниже расскажем об одном из них.

Как использовать жадный алгоритм для построения дерева решений

Смысл подхода — принцип так называемой жадной максимизации прироста информации. Он основан на концепции эвристического решения проблем — делать оптимальный локальный выбор в каждом узле, так достигая решения, которое с высокой вероятностью будет самым оптимальным.

Упрощенно алгоритм можно объяснить так:

• На каждом узле выбирайте оптимальный способ проверки.
• После разбейте узел на все возможные результаты (внутренние узлы).
• Повторите шаги, пока все условия не приведут к конечным узлам.

Главный вопрос: «Как выбрать начальные условия для проверки?». Ответ заключается в значениях энтропии и прироста информации (информационном усилении). Рассказываем, что это и как они влияют на создание нашего дерева:

1. Энтропия — в дереве решений это означает однородность. Если данные полностью однородны, она равна 0; в противном случае, если данные разделены (50-50%), энтропия равна 1. Проще этот термин можно объяснить так — это то, как много информации, значимой для принятия решения, мы не знаем.
2. Прирост информации — величина обратная энтропии, чем выше прирост информации, тем меньше энтропия, меньше неучтенных данных и лучше решение.

Итого — мы выбираем атрибут, который имеет наибольший показатель прироста информации, чтобы пойти на следующий этап разделения. Это помогает выбрать лучшее решение на любом узле.

Смотрите на примере. У нас есть большое количество таких данных:

Здесь может быть n деревьев решений, которые формируются из этого набора атрибутов.

Ищем оптимальное решение с жадным алгоритмом

Первый шаг: создать два условных класса:

• «Да», человек может купить компьютер.
• «Нет», возможность отсутствует.

Второй шаг — вычислить значение вероятности для каждого из них.

1. Для результата «Да», «buys_computer=yes», формула выглядит так:

$$P(buys = yes) = {9 over 14}$$

2. Для результата «Нет», «buys_computer=no», вот так:

$$P(buys = no) = {5 over 14}$$

Третий шаг: вычисляем значение энтропии, поместив значения вероятности в формулу.

$$Info(D) = I(9,5) = -{9 over 14}log_{2}({9 over 14})-{5 over 14}log_{2}({5 over 14})=0,940$$

Это довольно высокий показатель энтропии.

Четвертый шаг: углубляемся и считаем прирост информации для каждого случая, чтобы вычислить подходящий корневой атрибут для дерева решения.

Здесь нужно пояснение. Например, что будет означать показатель прироста информации, если за основу взять атрибут «Возраст»? Эти данные показывают, сколько людей, попадающих в определенную возрастную группу, покупают и не покупают продукт.

Допустим, среди людей в возрасте 30 лет и младше покупают (Да) два человека, не покупают (Нет) три человека. Info(D) рассчитывается для последних трех категорий людей — соответственно, Info(D) будем считать по сумме этих трех диапазонов значений возраста.

В итоге разница между общей энтропией Info(D) и энтропией для возраста Info(D) age (пусть она равна 0,694) будет нужным значением прироста информации. Вот формула:

$$Gain(age)=Info(D)-Info_{age}(D)=0,246$$

Сравним показатели прироста информации для всех атрибутов:

• Возраст = 0,246.
• Доход = 0.029.
• Студент = 0,151.
• Кредитный рейтинг = 0,048.

Получается, что прирост информации для атрибута возраста является самым значимым — значит, стоит использовать его. Аналогично мы сравниваем прирост в информации при каждом разделении, чтобы выяснить, брать этот атрибут или нет.

Таким образом, оптимальное дерево выглядит так:

Правила классификации для этого дерева можно записать следующим образом:

• Если возраст человека меньше 30 лет и он не студент, то не будет покупать компьютер.
• Если возраст человека меньше 30 лет, и он студент, то купит компьютер.
• Если возраст человека составляет от 31 до 40 лет, он, скорее всего, купит компьютер.
• Если человек старше 40 лет и имеет отличный кредитный рейтинг, то не будет покупать компьютер.
• Если возраст человека превышает 40 лет, при среднем кредитном рейтинге он, вероятно, купит компьютер.

Вот мы и достигли оптимального дерева решений. Готово.

Что такое дерево решений и где его используют?

Ребята, привет! Сегодня команда ProductStar подготовила для вас статью, в которой мы рассмотрели общие принципы работы и области применения дерева решений. Материал подготовлен на основе работы Акобира Шахиди «Деревья решений: общие принципы»

Дерево решений — метод автоматического анализа больших массивов данных. В этой статье рассмотрим общие принципы работы и области применения.

Дерево решений — эффективный инструмент интеллектуального анализа данных и предсказательной аналитики. Он помогает в решении задач по классификации и регрессии.

Дерево решений представляет собой иерархическую древовидную структуру, состоящую из правила вида «Если …, то …». За счет обучающего множества правила генерируются автоматически в процессе обучения.

В отличие от нейронных сетей, деревья как аналитические модели проще, потому что правила генерируются на естественном языке: например, «Если реклама привела 1000 клиентов, то она настроена хорошо».

Правила генерируются за счет обобщения множества отдельных наблюдений (обучающих примеров), описывающих предметную область. Поэтому их называют индуктивными правилами, а сам процесс обучения — индукцией деревьев решений.

В обучающем множестве для примеров должно быть задано целевое значение, так как деревья решений — модели, создаваемые на основе обучения с учителем. По типу переменной выделяют два типа деревьев:

• дерево классификации — когда целевая переменная дискретная;

• дерево регрессии — когда целевая переменная непрерывная.

Развитие инструмента началось в 1950-х годах. Тогда были предложены основные идеи в области исследований моделирования человеческого поведения с помощью компьютерных систем.

Дальнейшее развитие деревьев решений как самообучающихся моделей для анализа данных связано с Джоном Р. Куинленом (автором алгоритма ID3 и последующих модификаций С4.5 и С5.0) и Лео Брейманом, предложившим алгоритм CART и метод случайного леса.

Структура дерева решений

Рассмотрим понятие более подробно. Дерево решений — метод представления решающих правил в определенной иерархии, включающей в себя элементы двух типов — узлов (node) и листьев (leaf). Узлы включают в себя решающие правила и производят проверку примеров на соответствие выбранного атрибута обучающего множества.

Простой случай: примеры попадают в узел, проходят проверку и разбиваются на два подмножества:

• первое — те, которые удовлетворяют установленное правило;

• второе — те, которые не удовлетворяют установленное правило.

Далее к каждому подмножеству снова применяется правило, процедура повторяется. Это продолжается, пока не будет достигнуто условие остановки алгоритма. Последний узел, когда не осуществляется проверка и разбиение, становится листом.

Лист определяет решение для каждого попавшего в него примера. Для дерева классификации — это класс, ассоциируемый с узлом, а для дерева регрессии — соответствующий листу модальный интервал целевой переменной. В листе содержится не правило, а подмножество объектов, удовлетворяющих всем правилам ветви, которая заканчивается этим листом.

Пример попадает в лист, если соответствует всем правилам на пути к нему. К каждому листу есть только один путь. Таким образом, пример может попасть только в один лист, что обеспечивает единственность решения.

Терминология

Изучите основные понятия, которые используются в теории деревьев решений, чтобы в дальнейшем было проще усваивать новый материал.

Какие задачи решает дерево решений?

Его применяют для поддержки процессов принятия управленческих решений, используемых в статистистике, анализе данных и машинном обучении. Инструмент помогает решать следующие задачи:

• Классификация. Отнесение объектов к одному из заранее известных классов. Целевая переменная должна иметь дискретные задачи.

• Регрессия (численное предсказание). Предсказание числового значения независимой переменной для заданного входного вектора.

• Описание объектов. Набор правил в дереве решений позволяет компактно описывать объекты. Поэтому вместо сложных структур, используемых для описания объектов, можно хранить деревья решений.

Процесс построения дерева решений

Основная задача при построении дерева решений — последовательно и рекурсивно разбить обучающее множество на подмножества с применением решающих правил в узлах. Но как долго надо разбивать? Этот процесс продолжают до того, пока все узлы в конце ветвей не станут листами.

Узел становится листом в двух случаях:

• естественным образом — когда он содержит единственный объект или объект только одного класса;

• после достижения заданного условия остановки алгоритм — например, минимально допустимое число примеров в узле или максимальная глубина дерева.

В основе построения лежат «жадные» алгоритмы, допускающие локально-оптимальные решения на каждом шаге (разбиения в узлах), которые приводят к оптимальному итоговому решению. То есть при выборе одного атрибута и произведении разбиения по нему на подмножества, алгоритм не может вернуться назад и выбрать другой атрибут, даже если это даст лучшее итоговое разбиение. Следовательно, на этапе построения дерева решений нельзя точно утверждать, что удастся добиться оптимального разбиения.

Популярные алгоритмы, используемых для обучения деревьев решений, строятся на базе принципа «разделяй и властвуй». Задают общее множество S, содержащее:

• n примеров, для каждого из которых задана метка класса Ci(i = 1..k);

• m атрибутов Aj(j = 1..m), которые определяют принадлежность объекта к тому или иному классу.

Тогда возможно три случая:

1. Примеры множества S имеют одинаковую метку Ci, следовательно, все обучающие примеры относятся к одному классу. В таком случае обучение не имеет смысла, потому что все примеры в модели будут одного класса, который и «научится» распознавать модель. Само дерево будет похоже на один большой лист, ассоциированный с классом Ci. Тогда его использование не будет иметь смысла, потому что все новые объекты будут относиться к одному классу.

2. Множество S — пустое множество без примеров. Для него сформируется лист, класс которого выберется из другого множества. Например, самый распространенный из родительского множества класс.

3. Множество S состоит из обучающих примеров всех классов Ck. В таком случае множество разбивается на подмножества в соответствии с классами. Для этого выбирают один из атрибутов Aj множества S, состоящий из двух и более уникальных значений: a1, a2, …, ap), где p — число уникальных значений признака. Множество S разбивают на p подмножеств (S1, S2, …, Sp), состоящих из примеров с соответствующим значением атрибута. Процесс разбиения продолжается, но уже со следующим атрибутом. Он будет повторяться, пока все примеры в результирующих подмножества не окажутся одного класса.

Третья применяется в большинстве алгоритмов, используемых для построения деревьев решений. Эта методика формирует дерево сверху вниз, то есть от корневого узла к листьям.

Сегодня существует много алгоритмов обучения: ID3, CART, C4.5, C5.0, NewId, ITrule, CHAID, CN2 и другие. Самыми популярными считаются:

• ID3 (Iterative Dichotomizer 3). Алгоритм позволяет работать только с дискретной целевой переменной. Деревья решений, построенные на основе ID3, получаются квалифицирующими. Число потомков в узле неограниченно. Алгоритм не работает с пропущенными данными.

• C4.5. «Продвинутая» версия ID3, дополненная возможностью работы с пропущенными значениями атрибутов. В 2008 году издание Spring Science провело исследование и выявило, что C4.5 — самый популярный алгоритм Data Mining.

• CART (Classification and Regression Tree). Алгоритм решает задачи классификации и регрессии, так как позволяет использовать дискретную и непрерывную целевые переменные. CART строит деревья, в каждом узле которых только два потомка.

Основные этапы построения дерева решений

Построение осуществляется в 4 этапа:

1. Выбрать атрибут для осуществления разбиения в данном узле.

2. Определить критерий остановки обучения.

3. Выбрать метод отсечения ветвей.

4. Оценить точность построенного дерева.

Далее рассмотрим каждый подробнее.

Выбор атрибута разбиения

Разбиение должно осуществляться по определенному правилу, для которого и выбирают атрибут. Причем выбранный атрибут должен разбить множество наблюдений в узле так, чтобы результирующие подмножества содержали примеры с одинаковыми метками класса или были максимально приближены к этому. Иными словами — количество объектов из других классов в каждом из этих множеств должно быть как можно меньше.

Критериев существует много, но наибольшей популярностью пользуются теоретико-информационный и статистический.

Теоретико-информационный критерий

В основе критерия лежит информационная энтропия:

где n — число классов в исходном подмножестве, Ni — число примеров i-го класса, N — общее число примеров в подмножестве.

Энтропия рассматривается как мера неоднородности подмножества по представленным в нем классам. И даже если классы представлены в равных долях, а неопределенность классификации наибольшая, то энтропия тоже максимальная. Логарифм от единицы будет обращать энтропию в ноль, если все примеры узла относятся к одному классу.

Если выбранный атрибут разбиения Aj обеспечивает максимальное снижение энтропии результирующего подмножества относительно родительского, его можно считать наилучшим.

Но на деле об энтропии говорят редко. Специалисты уделяют внимание обратной величине — информации. В таком случае лучшим атрибутом будет тот, который обеспечит максимальный прирост информации результирующего узла относительно исходного:

где Info(S) — информация, связанная с подмножеством S до разбиения, Info(Sa) — информация, связанная с подмножеством, полученным при разбиении атрибута A.

Задача выбора атрибута в такой ситуации заключается в максимизации величины Gain(A), которую называют приростом информации. Поэтому теоретико-информационный подход также известен под название «критерий прироста информации.

Статистический подход

В основе этого метода лежит использования индекса Джини. Он показывает, как часто случайно выбранный пример обучающего множества будет распознан неправильно. Важное условие — целевые значения должны браться из определенного статистического распределения.

Если говорить проще, то индекс Джини показывает расстояние между распределениями целевых значений и предсказаниями модели. Минимальное значение показателя говорит о хорошей работе модели.

Индекс Джини рассчитывается по формуле:

где Q — результирующее множество, n — число классов в нем, pi — вероятность i-го класса (выраженная как относительная частота примеров соответствующего класса).

Значение показателя меняется от 0 до 1. Если индекс равен 0, значит, все примеры результирующего множества относятся к одному классу. Если равен 1, значит, классы представлены в равных пропорциях и равновероятны. Оптимальным считают то разбиение, для которого значение индекса Джини минимально.

Критерий остановки алгоритма

Алгоритм обучения может работать до получения «чистых» подмножеств с примерами одного класса. В таком случае высока вероятность получить дерево, в котором для каждого примера будет создан отдельный лист. Такое дерево не получится применять на практике из-за переобученности. Каждому примеру будет соответствовать свой уникальный путь в дереве. Получится набор правил, актуальный только для данного примера.

Переобучение в случае дерева решений имеет схожие с нейронными сетями последствия. Оно будет точно распознавать примеры из обучения, но не сможет работать с новыми данными. Еще один минус — структура переобученного дерева сложна и плохо поддается интерпретации.

Специалисты решили принудительно останавливать строительство дерева, чтобы оно не становилось «переобученным».

Для этого используют несколько подходов:

• Ранняя остановка. Алгоритм останавливается после достижения заданного значения критерия (например, процентной доли правильно распознанных примеров). Преимущество метода — сокращение временных затрат на обучение. Главный недостаток — ранняя остановка негативно сказывается на точности дерева. Из-за этого многие специалисты советуют отдавать предпочтение отсечению ветей.

• Ограничение глубины дерева. Алгоритм останавливается после достижения установленного числа разбиений в ветвях. Этот подход также негативно сказывается на точности дерева.

• Задание минимально допустимого числа примеров в узле. Устанавливается ограничение на создание узлов с числом примером меньше заданного (например, 7). В таком случае не будут создаваться тривиальные разбиения и малозначимые правила.

Этими подходами пользуются редко, потому что они не гарантируют лучшего результата. Чаще всего, они работают только в каких-то определенных случаях. Рекомендаций по использованию какого-либо метода нет, поэтому аналитикам приходится набирать практический опыт путем проб и ошибок.

Отсечение ветвей

Без ограничения «роста» дерево решений станет слишком большим и сложным, что сделает невозможной дальнейшую интерпретацию. А если делать решающие правила для создания узлов, в которые будут попадать по 2-3 примера, они не лишатся практической ценности.

Поэтому многие специалисты отдают предпочтение альтернативному варианту — построить все возможные деревья, а потом выбрать те, которые при разумной глубине обеспечивают приемлемый уровень ошибки распознавания. Основная задача в такой ситуации — поиск наиболее выгодного баланса между сложностью и точностью дерева.

Но и тут есть проблема: такая задача относится к классу NP-полных задач, а они, как известно, эффективных решений не имеют. Поэтому прибегают к методу отсечения ветвей, который реализуется в 3 шага:

1. Строительство полного дерева, в котором листья содержат примеры одного класса.

2. Определение двух показателей: относительную точность модели (отношение числа правильно распознанных примеров к общему числу примеров) и абсолютную ошибку (число неправильно классифицированных примеров).

3. Удаление листов и узлов, потеря которых минимально скажется на точности модели и увеличении ошибки.

Отсечение ветвей проводят противоположно росту дерева, то есть снизу вверх, путем последовательного преобразования узлов в листья.

Главное отличие метода «отсечение ветвей» от преждевременной остановки — получается найти оптимальное соотношение между точностью и понятностью. При этом уходит больше времени на обучение, потому что в рамках этого подхода изначально строится полное дерево.

Извлечение правил

Иногда упрощения дерева недостаточно, чтобы оно легко воспринималось и интерпретировалось. Тогда специалисты извлекают из дерева решающие правила и составляют из них наборы, описывающие классы.

Для извлечения правил нужно отслеживать все пути от корневого узла к листьям дерева. Каждый путь дает правило с множеством условий, представляющих собой проверку в каждом узле пути.

Если представить сложное дерево решений в виде решающих правил (вместо иерархической структуры узлов), оно будет проще восприниматься и интерпретироваться.

Преимущества и недостатки дерева решений

Преимущества:

• Формируют четкие и понятные правила классификации. Например, «если возраст < 40 и нет имущества для залога, то отказать в кредите». То есть деревья решений хорошо и быстро интерпретируются.

• Способны генерировать правила в областях, где специалисту трудно формализовать свои знания.

• Легко визуализируются, то есть могут «интерпретироваться» не только как модель в целом, но и как прогноз для отдельного тестового субъекта (путь в дереве).

• Быстро обучаются и прогнозируют.

• Не требуется много параметров модели.

• Поддерживают как числовые, так и категориальные признаки.

Недостатки:

• Деревья решений чувствительны к шумам во входных данных. Небольшие изменения обучающей выборки могут привести к глобальным корректировкам модели, что скажется на смене правил классификации и интерпретируемости модели.

• Разделяющая граница имеет определенные ограничения, из-за чего дерево решений по качеству классификации уступает другим методам.

• Возможно переобучение дерева решений, из-за чего приходится прибегать к методу «отсечения ветвей», установке минимального числа элементов в листьях дерева или максимальной глубины дерева.

• Сложный поиск оптимального дерева решений: это приводит к необходимости использования эвристики типа жадного поиска признака с максимальным приростом информации, которые в конечном итоге не дают 100-процентной гарантии нахождения оптимального дерева.

• Дерево решений делает константный прогноз для объектов, находящихся в признаковом пространстве вне параллелепипеда, который охватывает не все объекты обучающей выборки.

Где применяют деревья решения?

Модули для построения и исследования деревьев решений входят в состав множества аналитических платформ. Это удобный инструмент, применяемый в системах поддержки принятия решений и интеллектуального анализа данных.

Успешнее всего деревья применяют в следующих областях:

• Банковское дело. Оценка кредитоспособности клиентов банка при выдаче кредитов.

• Промышленность. Контроль качества продукции (обнаружение дефектов в готовых товарах), испытания без нарушений (например, проверка качества сварки) и т.п.

• Медицина. Диагностика заболеваний разной сложности.

• Молекулярная биология. Анализ строения аминокислот.

• Торговля. Классификация клиентов и товар.

Это не исчерпывающий список областей применения дерева решений. Круг использования постоянно расширяется, а деревья решений постепенно становятся важным инструментом управления бизнес-процессами и поддержки принятия решений.

Надеемся, наша статья оказалась для вас полезной. Больше интересного контента от ProductStar вы найдёте в нашем блоге на vc и в аналитическом тг-канале.

Попробуйте применить дерево решений на практике для решения маленькой задачи. Постепенно, получая новый опыт, вы сможете использовать инструмент в крупном бизнесе и извлекать пользу от работы с ним.

Деревья решений — отличный способ отбросить эмоции при принятии важных решений. Используя деревья решений, вы можете сосредоточиться на важнейших решениях и возможностях, с которыми вы столкнетесь. Кроме того, с деревьями решений вы можете сосредоточиться на данных при принятии решения, чтобы сделать правильный выбор для своей организации или бизнеса. Более того, существует множество приложений и программного обеспечения, которые можно использовать для создания деревьев решений. А с Microsoft Word вы можете легко составить дерево решений. Поэтому, если вы хотите узнать больше о том, как составить дерево решений в Word, то дочитайте эту статью до конца.

• Часть 1. Шаги по созданию дерева решений в Word
• Часть 2. Плюсы и минусы использования Word для построения дерева решений
• Часть 3. Лучшая альтернатива Word для рисования дерева решений
• Часть 4. Часто задаваемые вопросы о том, как создать дерево решений в Word

Часть 1. Шаги по созданию дерева решений в Word

Microsoft Word — самый популярный коммерческий текстовый процессор, разработанный Microsoft. Первоначально он был запущен в 1983 году, и с тех пор он стал популярным приложением для обработки текстов и много раз пересматривался для улучшения его обслуживания. С Microsoft Word вы можете профессионально печатать документы. Но многие пользователи не знают, что с помощью Microsoft Word вы также можете создавать деревья решений, которые можно использовать в создаваемых вами документах. Итак, в этой части мы продемонстрируем, как построить дерево решений в Word. Обратите внимание, что в Microsoft Word вы можете создать дерево решений двумя способами. Вы можете использовать SmartArt или библиотеку фигур. Оба эти способа эффективны и отлично подходят для построения дерева решений. А ниже мы научим вас использовать эти два метода для построения дерева решений в Word.

Шаги по созданию дерева решений в Microsoft Word с использованием графики SmartArt

Шаги о том, как нарисовать дерево решений в Word с помощью библиотеки Shape

Часть 2. Плюсы и минусы использования Word для построения дерева решений

Microsoft Word действительно отличное приложение. Это не просто программа для создания документов. Кто бы мог подумать, что с помощью этого приложения вы можете создавать диаграммы, такие как дерево решений. Однако, как и другие инструменты, Microsoft Word также имеет ряд недостатков, которые необходимо учитывать. Прочтите ниже, чтобы узнать о преимуществах и недостатках использования Microsoft Word для построения дерева решений.

Часть 3. Лучшая альтернатива Word для рисования дерева решений

Поскольку Microsoft Word изначально не был приложением для создания диаграмм, многие люди ищут инструменты для создания диаграмм. Кроме того, люди не соглашаются использовать Microsoft Word для создания дерева решений, потому что в нем отсутствуют функции для его создания. Итак, вы можете использовать эту альтернативу, которую мы покажем ниже.

MindOnMap это приложение для создания диаграмм, которое позволяет вам создать дерево решений. Это безопасно для использования, и вы можете использовать его бесплатно. Вы можете использовать древовидную карту или правильную карту, чтобы составить дерево решений. MindOnMap — это удобное приложение, поскольку оно имеет интуитивно понятный пользовательский интерфейс. Кроме того, вы можете добавлять значки, наклейки, изображения и ссылки в свое дерево решений, если хотите, чтобы оно выглядело профессионально. Кроме того, вы можете легко экспортировать результат в различные форматы, такие как PNG, JPG, JPEG, PDF, SVG и DOC. Кроме того, MindoOnMap имеет функцию автоматического сохранения; поэтому, если вы случайно закроете приложение, вы всегда сможете продолжить работу, не перезапуская его.

Как составить дерево решений с помощью MindOnMap

Часть 4. Часто задаваемые вопросы о том, как сделать дерево решений в Word

Метод дерева решений – это прекрасный способ выбрать стратегию последовательных действий в условиях риска. Именно риск здесь выступает ключевым словом, поскольку при опасности принять рациональное решение очень сложно, а продуманный план помогает проанализировать сложившуюся ситуацию.

Дерево принятия решений подобно настоящему: у него есть ствол, ветви и листья. “Ствол” – основа всего – это главный вопрос, на который нужно ответить. Ветви – это стрелочки с несколькими вариантами ответов. А листья – это ситуации, к которым приведет нас выбранный ответ.

Самый простой пример

Любая теория воспринимается намного легче, если привести пример. Дерево решений “Пойти гулять?” – это самый простой алгоритм. В бизнесе все базируется на таких принципах. Кстати, в основе всех электронных программ тоже лежит алгоритм построения дерева.

Итак, стоит задача: решить, можно ли идти гулять. Наш ствол – первый вопрос – это ключевой фактор: “На улице солнечно?” От него зависит наш дальнейший путь. Если ответ положительный, двигаемся по направлению слова “Да”. Приходим к новому разветвлению. Если температура воздуха высокая, мы получаем окончательный ответ – “Не идти гулять”, в противном случае тоже получаем итог, но уже с результатом “Идти гулять”.

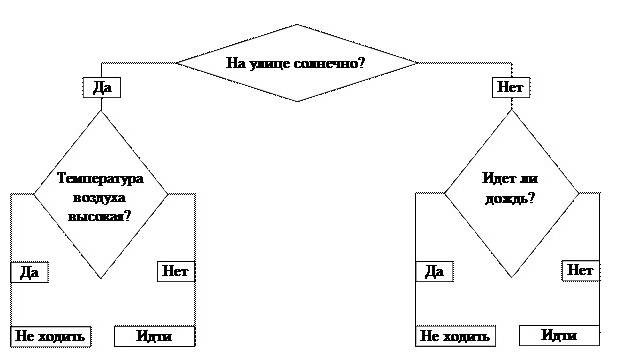
Можно было выбрать и другой путь. Дерево принятия решений подразумевает, что будут проанализированы все варианты движения и спрогнозированы результаты.

Почему следует выбирать этот метод

Преимущества дерева решений позволяют определить, почему данный метод является самым гибким из всех, что касаются вопроса о выборе решений.

• Это одномерная схема, которая наглядно показывает причинно-следственные связи. Что будет, если… И куда наш выбор приведет.
• Возможность одновременно рассматривать нетипичные ситуации и подбирать несколько вариантов их разрешения.
• Отсутствие каких-либо законов следствия.
• Простота в использовании.
• Работать над моделью может сразу несколько человек, что облегчает задачу.
• Дерево решений не ограничено во временных рамках.
• Подходит для большинства бизнес-ситуаций.

Область применения

Можно привести любой пример дерева решений. Это может быть вопрос о том, открывать ли новые производственные мощности, внедрять технологии, формировать новый ассортимент и т. д. Область применения данного метода невероятно широка.

Но можно выделить три большие группы, где дерево решений помогает выиграть время.

• Описание данных. Допустим, задача руководства – решить проблему расширения ассортимента. Схема данной задачи будет состоять из конкретных цифр возможных сумм прибыли и рентабельности. Структурировать такую информацию будет намного проще, если она будет храниться в виде схемы, а не в обширной таблице.
• Классификация. Появляется возможность сгруппировать исходные данные и сделать для них подборку.
• Регрессия. Дерево решений позволяет определить, как формируется целевая стратегия под воздействием независимых факторов. Например, на выбор стратегии формирования ассортимента будут влиять, кроме основных факторов производства, второстепенные, которые косвенно к этому относятся. Это может быть урожай какао-бобов из страны-экспортера или график движения транспортных судов. Вроде бы на выбор стратегии прямо не оказывают воздействия, но сбой их работы может помешать формированию ассортимента на кондитерской фабрике.

Алгоритмы

На сегодняшний день существует несколько известных алгоритмов, позволяющих создавать дерева решений (примеры мы уже рассмотрели).

• CART – аббревиатура слов Classificationand Regression Tree (классификация и регрессия). Согласно его принципам, каждый узел дерева может иметь только два ответвления.
• С4.5 – метод построения, при котором каждый узел может иметь неограниченное количество веток. В такой схеме тяжело делать прогнозы, поэтому ее используют для классификации.
• QUEST (Quick, Unbiased, Efficient Statistical Trees). Самая сложная из всех моделей, но очень достоверная. Позволяет создавать многомерное ветвление. Это значит, что в любом узле может создаваться не просто множество веток, а примеров действия.

Сбор данных

Метод дерева решений будет эффективен в том случае, если правильно подойти к вопросу сбора данных. Приведем характерную последовательность:

• Определение жизненного цикла проекта: сколько будет этапов и какова продолжительность каждого из них.
• Выделение ключевых событий, на этапе которых может возникнуть дилемма выбрать одно или другое.
• Описание каждого из возможных факторов, которые повлияют на наступление того или иного события, описанного в предыдущем шаге.
• Оценка вероятности принятия этих решений.
• Расчет стоимости всех этапов жизненного цикла (считается между ключевыми событиями).

Пример дерева решений

Рассмотрим типичную бизнес-ситуацию. Компании нужно выбрать выгодное инвестиционное вложение Ип1, Ип2, Ип3 с помощью дерева решений. Примеры решения задач формируются на основании исходных данных.

Первый проект требует вложения в размере 200 млн рублей и принесет прибыль 100 млн руб. Для второго необходимо 300 млн руб., но принесет 200 млн руб. Третий, самый прибыльный, – 300 млн руб., но вложить нужно 500. При этом есть риск потерять все. При первом варианте уровень риска – 10 %, при втором – 5 %, и при третьем – 20 %. Какой из проектов будет самый выгодный?

Провести математические расчеты довольно затруднительно. Поэтому нужно построить графическую схему. Правильное решение будет зависеть не только от того, насколько понятной будет модель, но и как будут расположены исходные данные.

Построение графика

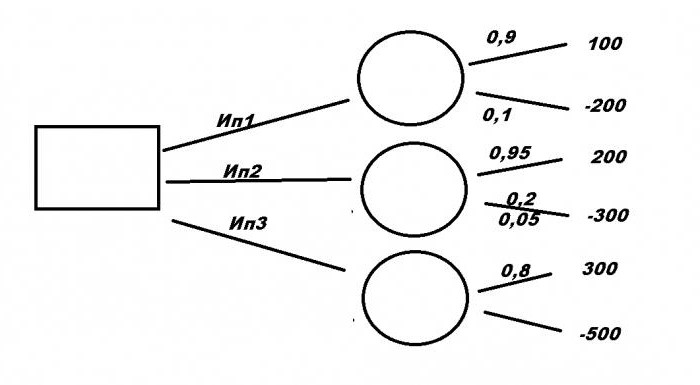
Итак, у нас есть три проекта: Ип1, Ип2 и Ип3. Рассмотрим, как составить дерево решений. Двигаться будем от первого ключевого момента, обозначенного большим квадратом. Здесь мы напишем конечный итог, а пока пускай сектор остается пустым. От него чертим три ответвления с именами проектов. Далее каждый вариант имеет свой уровень математических ожиданий, обозначенный кружочком. Пока они пустые, в них нужно будет написать полученный результат расчетов. От каждого из них будет еще два ответвления. Вверх – это доход и уровень его ожидания, вниз – затраты и риски потерь.

Математические расчеты

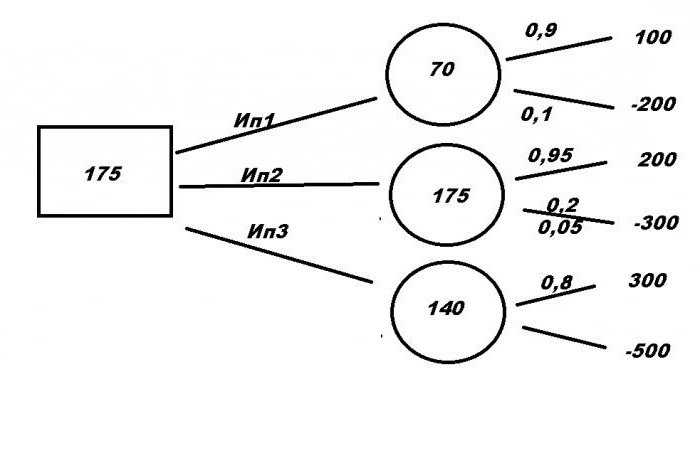
Пора приступать к поиску правильного решения. Для этого составим формулы:

• Ип1= 100 × 0.9 – 200 × 0.1 = 70
• Ип2 = 200× 0.95 – 300 × 0.05 = 175
• Ип3 = 300 × 0.8 – 500 × 0.2 = 140

Полученные данные записываем в кружочки. Выбираем наибольшее число – 175. И записываем его в квадрат. Это и есть математическое ожидание от проекта. И поскольку самое выгодное предложение – это Ип2, это и будет являться ответом на задачу.

Область применения

Казалось бы, что примеров дерева решений для бизнеса можно привести неограниченное количество. Действительно, чаще всего об этом методе говорят в контексте менеджмента. Но на самом деле область применения алгоритма намного больше. Приведем некоторые интересные факты:

• Дерево решений незаменимо в банковском деле. Его используют для оценки клиентов и принятия решения для выдачи кредита.
• Промышленность. Яркий пример – проверка качества. Поскольку на заводах не всегда есть возможность оценить все выпускаемые товары практическим методом, создают специальный алгоритм, с помощью которого брак отсекается на нескольких этапах проверки.
• Медицина. Для использования дерева решений в этой сфере не нужны листик и бумага. Любой врач делает это ежедневно при постановке диагноза. Доктор задает пациенту наводящие вопросы, ответы на которые приведут к единому правильному решению.
• Молекулярная биология. Даже в этой уникальной области есть где применить метод построения схем. Например, анализ строения аминокислот.
• Программирование. Любая программа или веб-страница построены по принципу алгоритма и движения от целого к множеству.

Пример использования алгоритма в банковской сфере

Попробуем построить дерево решений, представив, что мы сотрудники отдела кредитования любого банка. Обозначим ключевых факторы:

• возраст;
• уровень дохода;
• иждивенцы, семейное положение;
• кредиты в других организациях;
• наличие движимого и недвижимого имущества.

Теперь по каждой из ключевых веток необходимо составить примерный план возможных действий.

Начнем с возраста. Больше 21? Ответ “да” или “нет”. “Нет” сразу приводит нас к нулю. После ответа “Да” двигаемся к следующему вопросу.

Уровень дохода выше 50 000 руб. в месяц? “Нет” – это сразу ноль, “Да” – переходим к следующей ветке.

Семейное положение. В этом разделе могут появляться дополнительные ответвления, которые будут важными для нашего решения. Сколько человек в семье? Сколько из них иждивенцы, какой доход у супругисупруга. Если ответы нас удовлетворили, можно переходить к следующему сектору.

Кредиты в других организациях. Здесь рационально выделить: какую сумму брали, как быстро отдали, есть ли долги?

Наличие движимого и недвижимого имущества может стать дополнительной гарантией возврата средств, поэтому, если потенциальный заемщик дошел до этого этапа и положительно ответил на последний вопрос, то однозначно решение о выдаче ему денег будет позитивным.

Сократить путь к любому из решений “Выдать” или “Не выдать” можно на любом этапе.

Пример из медицины

Рассмотрим типичную ситуацию. К врачу пришел на осмотр пациент с кашлем. При постановке диагноза доктор оценивает человека по нескольким параметрам:

• как давно кашель;
• есть ли температура;
• заложен ли нос;
• как прослушиваются легкие, бронхи, наличие хрипов;
• сердечный ритм;
• возраст, наличие флюрографии и др. факторы.

Ответ на каждый из этих вопросов приведет доктора к постановке правильного диагноза.

Вывод

Пример дерева решений можно встретить в повседневной жизни. Люди сотни раз сталкиваются с дилеммой, решить которую можно, выбрав только самый короткий или самый выгодный путь. Точно так же и в бизнесе. Алгоритм помогает выбрать правильное решение, классифицировать и структурировать данные о вопросе, спрогнозировать исход. Важной задачей является выбор основных вопросов, которые составляют ключевые моменты, и ветвей с результатом. Существует множество моделей, компьютерных программ, позволяющих быстро и качественно построить дерево решений и облегчить поиск.

Возможности конструктора древовидных диаграмм

Визуализировать процессы принятия решений и создать дерево решений поможет программное обеспечение Visme. Используйте все возможные формы, линии и элементы дизайна, чтобы получить первоклассный результат.

Шаблоны дерева решений

Visme также предлагает красиво оформленные шаблоны древовидной диаграммы, которые помогут вам создать дизайн еще удобнее. Найдите базовый шаблон и скорректируйте диаграмму, чтобы она соответствовала вашим решениям.

Создать дерево решений

Постройте дерево решений онлайн

Редактор графиков Visme позволяет легко перемещать фигуры по холсту, соединять стрелками решения и результаты и построить иерархическую структуру так, чтобы она выглядела как вы задумаете.

Создать дерево решений

Настройте каждый аспект вашей древовидной диаграммы, чтобы визуализировать решения

Все разделы в конструкторе древовидных диаграмм можно настроить. Формы могут быть разного цвета или размера. Все линии взаимосвязаны, но при необходимости эту функцию можно отключить. “Ветви” и “листья” можно изменять, уменьшать и перемещать с помощью встроенных соединительных точек.

Создать дерево решений

ВСЕ, ЧТО ВАМ НУЖНО И ДАЖЕ БОЛЬШЕ

Больше, чем редактор графиков и диаграмм

Редактор графиков и диаграмм Visme позволяет вам невероятно легко настроить каждый аспект вашего дерева решений. Вы можете создать множество древовидных диаграмм, каждая из которых будет выглядеть по-разному, и вы можете настроить каждуюю из них в соответствии с вашим брендом. Настройте дизайн, линии, формы и анимацию в соответствии с вашим стилем.

ВПЕЧАТЛЯЙТЕ

Интерактивность

Создавайте интерактивные древовидные диаграммы со всплывающими окнами и эффектами анимации, которые позволяют зрителю взаимодействовать с вашим дизайном.

ВИЗУАЛИЗИРУЙТЕ ДАННЫЕ

Диаграммы и графики

Визуализируйте информацию красиво: используйте диаграммы, графики, элементы блок-схем, виджеты данных и другие настраиваемые ресурсы визуализации данных.

УКРАСЬТЕ СВОЙ КОНТЕНТ

Изображения и иконки

На ваш выбор более миллиона стоковых фотографий, иконки, иллюстрации, анимированная графика и другие элементы дизайна, чтобы создать совершенно уникальное дерево решений.

Вопросы про дерево решений

Для чего используется дерево решений?

Древовидная диаграмма или дерево решений используется для демонстрации последствий, которые могут иметь принятые решения. Они помогают найти и предпринять наиболее разумные действия в любой ситуации.

Сколько стоит создание древовидных диаграмм с помощью создателя древовидных диаграмм?

Создание древовидной диаграммы на 100 % бесплатно. Вы можете скачать диаграмму в виде файла JPEG или добавить дерево решений на веб-сайт. Если вы хотите скачать изображение в формате PNG, вам следует перейти на стандартный план.

Существуют ли какие-либо шаблоны древовидных диаграмм для использования?

Да, шаблоны древовидных диаграмм доступны в панели инструментов, и мы постоянно создаем новые. Тем не менее, редактор графиков и диаграмм настолько универсален, что вы сможете обойтись и без шаблонов.

Можно ли полностью настраивать шаблоны дерева решений?

Да! Конструктор древовидных диаграмм позволит вам нарисовать дерево решений именно так, как вам нужно. Каждая отдельная секция настраивается по форме, размеру и положению.

Могу ли я создать интерактивную древовидную диаграмму с помощью бесплатного онлайн-конструктора древовидных диаграмм?

Наверняка! Каждый раздел вашей иерархической структуры можно анимировать и добавить интерактивные элементы. Чтобы скачать дерево решений в виде файла HTML5, вам понадобится стандартный план, а добавить диаграмму на ваш сайт можно совершенно бесплатно.

Есть ли ограничение на размер моей древовидной диаграммы?

Нет. Если вы создаете древовидную диаграмму на чистом холсте или с использованием шаблона, вы можете изменить размер проекта и полностью отредактировать контент внутри него.