- Учебники
- 8 класс
- Алгебра 👍
- Макарычев
- №9

авторы: Макарычев, Миндюк, Нешков, Суворова.
издательство: “Просвещение” 2013 г
Раздел:
- ГЛАВА I. РАЦИОНАЛЬНЫЕ ДРОБИ
- §1. РАЦИОНАЛЬНЫЕ ДРОБИ И ИХ СВОЙСТВА
- 1. Рациональные выражения
ГДЗ учебник по алгебре 8 класс Макарычев. 1. Рациональные выражения. Номер №9
- Предыдущее
- Следующее
Составьте дробь:
а) числитель которой − произведение переменных x и y, а знаменатель − их сумма;
б) числитель которой − разность переменных a и b, а знаменатель − их произведение;
в) числитель которой − сумма переменных c и d, а знаменатель − их разность.

reshalka.com
ГДЗ учебник по алгебре 8 класс Макарычев. 1. Рациональные выражения. Номер №9
Решение а
Решение б
Решение в
- Предыдущее
- Следующее
![]()
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом
glogaresi115
Вопрос по алгебре:
Составьте дробь с переменной y, которая имеет смысл, при всех значениях y, кроме: а) y=8 б) y=0 и y=7
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!
Ответы и объяснения 1
rerilaicobo
А) 1/(у-8)
при у=8
у-8 = 0
на 0 делить нельзя
б)
1/(у (у-7))=1/(у²-7у)
при у=0 и 7 знаменатель = 0
вверху – не обязательно 1, может быть любая цифра и пр
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат – это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Алгебра.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!
Алгебра — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики.
Наталья Игоревна Восковская
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Уравнения, содержащие переменную в знаменателе можно решать двумя способами:
-
Приведя дроби к общему знаменателю
-
Используя основное свойство пропорции
Вне зависимости от выбранного способа необходимо после нахождения корней уравнения выбрать из найденных допустимые значения, т.е те, которые не обращают знаменатель в $0$.
1 способ. Приведение дробей к общему знаменателю.
Пример 1
$frac{2x+3}{2x-1}=frac{x-5}{x+3}$
Решение:
1.Перенесем дробь из правой части уравнения в левую
[frac{2x+3}{2x-1}-frac{x-5}{x+3}=0]
Для того чтобы правильно это сделать, вспомним, что при перенесении элементов в другую часть уравнения меняется знак перед выражениями на противоположный. Значит, если в правой части перед дробью был знак «+», то в левой перед ней будет знак «-».Тогда в левой части получим разность дробей.
2.Теперь отметим что у дробей разные знаменатели, значит для того, чтобы составить разность необходимо привести дроби к общему знаменателю. Общим знаменателем будет произведение многочленов, стоящих в знаменателях исходных дробей: $(2x-1)(x+3)$
Для того чтобы получить тождественное выражение, числитель и знаменатель первой дроби необходимо умножить на многочлен $(x+3)$, а второй на многочлен $(2x-1)$.
[frac{(2x+3)(х+3)}{(2x-1)(х+3)}-frac{(x-5)(2х-1)}{(x+3)(2х-1)}=0]
Выполним преобразование в числителе первой дроби-произведем умножение многочленов. Вспомним , что для этого необходимо умножить первое слагаемое первого многочлена умножить на каждое слагаемое второго многочлена, затем второе слагаемое первого многочлена умножить на каждое слагаемое второго многочлена и результаты сложить
[left(2x+3right)left(х+3right)=2хcdot х+2хcdot 3+3cdot х+3cdot 3={2х}^2+6х+3х+9]
Приведем подобные слагаемые в полученном выражении
[left(2x+3right)left(х+3right)=2хcdot х+2хcdot 3+3cdot х+3cdot 3={2х}^2+6х+3х+9=] [{=2х}^2+9х+9]
Выполним аналогично преобразование в числителе второй дроби-произведем умножение многочленов
$left(x-5right)left(2х-1right)=хcdot 2х-хcdot 1-5cdot 2х+5cdot 1={2х}^2-х-10х+5={2х}^2-11х+5$
Тогда уравнение примет вид:
[frac{{2х}^2+9х+9}{(2x-1)(х+3)}-frac{{2х}^2-11х+5}{(x+3)(2х-1)}=0]
Теперь дроби с одинаковым знаменателем, значит можно производить вычитание. Вспомним, что при вычитании дробей с одинаковым знаменателем из числителя первой дроби необходимо вычесть числитель второй дроби, знаменатель оставить прежним
[frac{{2х}^2+9х+9-({2х}^2-11х+5)}{(2x-1)(х+3)}=0]
Преобразуем выражение в числителе. Для того, чтобы раскрыть скобки, перед которыми стоит знак «-» надо изменить все знаки перед слагаемыми , стоящими в скобках на противоположные
[{2х}^2+9х+9-left({2х}^2-11х+5right)={2х}^2+9х+9-{2х}^2+11х-5]
Приведем подобные слагаемые
${2х}^2+9х+9-left({2х}^2-11х+5right)={2х}^2+9х+9-{2х}^2+11х-5=20х+4$
Тогда дробь примет вид
[frac{{rm 20х+4}}{(2x-1)(х+3)}=0]
3.Дробь равна $0$, если ее числитель равен 0. Поэтому мы приравниваем числитель дроби к $0$.
[{rm 20х+4=0}]
Решим линейное уравнение:
$20x=-4$
$X=-0,2$
4.Проведем выборку корней. Это значит, что необходимо проверить, не обращаются ли знаменатели исходных дробей в $0$ при найденных корнях.
Поставим условие, что знаменатели не равны $0$
[2x-1ne 0 x+3ne 0]
х$ne 0,5$ х$ne -3$
Значит допустимы все значения переменных, кроме $-3$ и $0,5$.
Найденный нами корень является допустимым значением, значит его смело можно считать корнем уравнения. Если бы найденный корень был бы не допустимым значением, то такой корень был бы посторонним и ,конечно, не был бы включен в ответ.
Ответ:$-0,2.$
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
Теперь можем составить алгоритм решения уравнения, которое содержит переменную в знаменателе
Алгоритм решения уравнения, которое содержит переменную в знаменателе
-
Перенести все элементы из правой части уравнения в левую. Для получения тождественного уравнения необходимо изменить все знаки, стоящие перед выражениями в правой части на противоположные
-
Если в левой части мы получим выражение с разными знаменателями, то приводим их к общему, используя основное свойство дроби. Выполнить преобразования, используя тождественные преобразования и получить итоговую дробь равную $0$.
-
Приравнять числитель к $0$ и найти корни получившегося уравнения.
-
Проведем выборку корней, т.е. найти допустимые значения переменных, которые не обращают знаменатель в $0$.
2 способ. Используем основное свойство пропорции
Основным свойством пропорции является то, что произведение крайних членов пропорции равно произведению средних членов.
Пример 2
Используем данное свойство для решения этого задания
[frac{2x+3}{2x-1}=frac{x-5}{x+3}]
1.Найдем и приравняем произведение крайних и средних членов пропорции.
$left(2x+3right)cdot( x+3)=left(x-5right)cdot(2x-1)$
[{2х}^2+3х+6х+9={2х}^2-10х-х+5]
$9x+11x=5-9$
$20x=-4$
$X=-0,2$
Решив полученное уравнение, мы найдем корни исходного
2.Найдем допустимые значения переменной .
Из предыдущего решения (1 способ) мы уже нашли , что допустимы любые значения, кроме $-3$ и $0,5$.
Тогда, установив что найденный корень является допустимым значением, мы выяснили, что $-0,2$ будет являться корнем.
Ответ:$-0,2.$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Составьте дробь с переменной y, которая имеет смысл, при всех значениях y, кроме : а) y = 8 б) y = 0 и y = 7.
На этой странице находится вопрос Составьте дробь с переменной y, которая имеет смысл, при всех значениях y, кроме : а) y = 8 б) y = 0 и y = 7?, относящийся к категории
Алгебра. По уровню сложности данный вопрос соответствует знаниям
учащихся 5 – 9 классов. Здесь вы найдете правильный ответ, сможете
обсудить и сверить свой вариант ответа с мнениями пользователями сайта. С
помощью автоматического поиска на этой же странице можно найти похожие
вопросы и ответы на них в категории Алгебра. Если ответы вызывают
сомнение, сформулируйте вопрос иначе. Для этого нажмите кнопку вверху.
Содержание:
Вы уже знакомы с целыми рациональными выражениями, то есть с выражениями, которые не содержат деления на выражение с переменной, например:
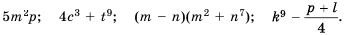
Любое целое выражение можно представить в виде многочлена стандартного вида, например:
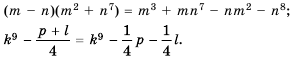
В отличие от целых выражений, выражения
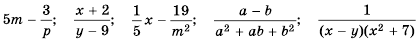
содержат деление на выражение с переменной. Такие выражения называют дробными рациональными выражениями. Целые рациональные и дробные рациональные выражения называют рациональными выражениями.
Рациональные выражения — это математические выражения, содержащие действии сложения, вычитания, умножения, деления и возведения в степень с целым показателем.
Определение рациональной дроби
Рациональное выражение вида 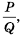 , где
, где 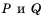 – выражения, содержащие числа или переменные, называют дробью. Выражение
– выражения, содержащие числа или переменные, называют дробью. Выражение 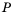 – ее числитель, a
– ее числитель, a 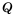 – знаменатель. Если
– знаменатель. Если 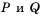 в дроби – многочлены, то дробь называют рациональной дробью.
в дроби – многочлены, то дробь называют рациональной дробью.
Целое рациональное выражение имеет смысл при любых значениях входящих в него переменных, так как при нахождении его значения выполняют действия сложения, вычитания, умножения и деления на число, отличное от нуля, что всегда выполнимо.
Рассмотрим дробное рациональное выражение — 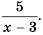 . Его значение можно найти для любого
. Его значение можно найти для любого 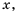 кроме
кроме 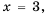 так как при
так как при 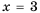 знаменатель дроби обращается в нуль. В этом случае говорят, что выражение
знаменатель дроби обращается в нуль. В этом случае говорят, что выражение 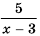 имеет смысл при всех значениях переменной
имеет смысл при всех значениях переменной 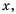 кроме
кроме 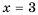 (или же при
(или же при 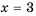 не имеет смысла).
не имеет смысла).
Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных в выражении.
Эти значения образуют область определения выражения, или область допустимых значений переменных в выражении.
Пример:
Найдите допустимые значения переменной в выражении:
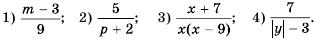
Решение:
1) Выражение имеет смысл при любых значениях переменной 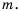 2) Допустимые значения переменной
2) Допустимые значения переменной 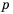 – все числа, кроме числа
– все числа, кроме числа 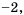 так как это число обращает знаменатель дроби в нуль. 3) Знаменатель дроби
так как это число обращает знаменатель дроби в нуль. 3) Знаменатель дроби 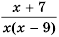 обращается в нуль при
обращается в нуль при 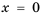 или
или 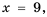 поэтому допустимые значения переменной
поэтому допустимые значения переменной 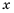 – все числа, кроме чисел 0 и 9. 4) Допустимые значения переменной
– все числа, кроме чисел 0 и 9. 4) Допустимые значения переменной 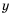 – все числа, кроме 3 и -3.
– все числа, кроме 3 и -3.
Кратко ответы можно записать следующим образом: 1) 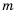 – любое число;
– любое число; 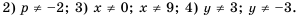
Рассмотрим условие равенства дроби нулю. Так как 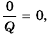 если
если 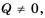 то можно сделать вывод, что дробь
то можно сделать вывод, что дробь 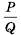 равна нулю тогда и только тогда, когда числитель
равна нулю тогда и только тогда, когда числитель 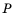 равен нулю, а знаменатель
равен нулю, а знаменатель 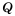 не равен нулю, то есть
не равен нулю, то есть 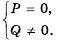
Пример:
При каких значениях переменной равно нулю значение дроби:
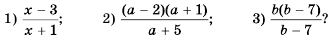
Решение:
1) Числитель дроби равен нулю при 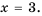 Это значение переменной не обращает знаменатель в нуль, поэтому число 3 является значением переменной, при котором данная дробь равна нулю. 2) Числитель дроби равен нулю при
Это значение переменной не обращает знаменатель в нуль, поэтому число 3 является значением переменной, при котором данная дробь равна нулю. 2) Числитель дроби равен нулю при 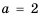 или
или  Для каждого из этих значений знаменатель дроби нулю не равен. Поэтому числа 2 и -1 – те значения переменной, при которых данная дробь равна нулю. 3) Числитель дроби равен нулю, если
Для каждого из этих значений знаменатель дроби нулю не равен. Поэтому числа 2 и -1 – те значения переменной, при которых данная дробь равна нулю. 3) Числитель дроби равен нулю, если 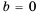 или
или 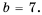 При
При 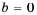 знаменатель дроби нулю не равен, а при
знаменатель дроби нулю не равен, а при 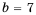 знаменатель дроби обращается в нуль, то есть такой дроби не существует. Следовательно, данная дробь равна нулю только при
знаменатель дроби обращается в нуль, то есть такой дроби не существует. Следовательно, данная дробь равна нулю только при 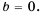
Ответ. 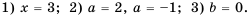
А еще раньше
Древнегреческий математик Диофант (прибл.  в. н. э.) рассмотрел рациональные дроби и действия с ними в своей работе «Арифметика». В частности, на страницах этой книги можно встретить доказательство тождеств
в. н. э.) рассмотрел рациональные дроби и действия с ними в своей работе «Арифметика». В частности, на страницах этой книги можно встретить доказательство тождеств
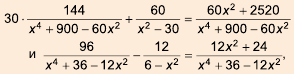
записанных символикой того времени.
Выдающийся английский ученый Исаак Ньютон (1643-1727) в своей монографии «Универсальная арифметика» (1707 г.) определяет дробь следующим образом: «Запись одной из двух величин под другой, ниже которой между ними проведена черта, означает часть или же величину, возникающую при делении верхней величины на нижнюю». В этой работе Ньютон рассматривает не топько обычные дроби, но и рациональные.
Определение: Дробь, числитель и знаменатель которой — многочлены, называется рациональной дробью.
Например, выражения 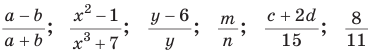
являются рациональными дробями.
Рациональная дробь является рациональным выражением. Выражения, составленные из чисел, переменных с помощью действий сложения, вычитания, умножения, деления, возведения в натуральную степень, называют рациональными выражениями.
Если рациональное выражение не содержит деления на выражение с переменными, то оно называется целым рациональным выражением.
Рассмотрим задачу: Туристы в первый день проплыли на лодке по течению реки 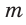 км, а во второй — на 6 км больше. Сколько времени продолжалось все путешествие, если собственная скорость лодки равна
км, а во второй — на 6 км больше. Сколько времени продолжалось все путешествие, если собственная скорость лодки равна 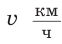 , а скорость течения реки —
, а скорость течения реки — 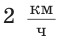 ?
?
Решение:
Так как за два дня туристы преодолели 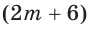 км по течению реки, а скорость движения лодки по течению реки равна
км по течению реки, а скорость движения лодки по течению реки равна 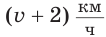 , то время, затраченное на весь путь, ч равно
, то время, затраченное на весь путь, ч равно 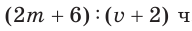 . Частное
. Частное 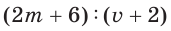 можно записать в виде дроби
можно записать в виде дроби 
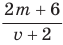 .
.
Ответ: 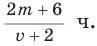
При решении этой задачи получили дробь, в числителе и знаменателе которой записаны многочлены. Такая дробь называется рациональной.
Целые рациональные выражения
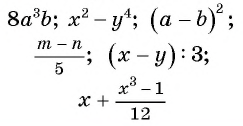
Например, выражения 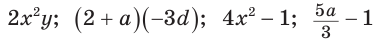 являются целыми рациональными выражениями.
являются целыми рациональными выражениями.
Рациональное выражение, содержащее деление на выражение с переменными, называют дробным рациональным выражением.
Дробные рациональные выражения
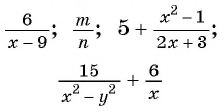
Например, выражения 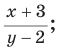
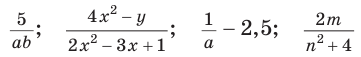 являются дробными рациональными выражениями, поскольку содержат (кроме действий сложения, вычитания, умножения) деление на выражение с переменными.
являются дробными рациональными выражениями, поскольку содержат (кроме действий сложения, вычитания, умножения) деление на выражение с переменными.
Связь между понятиями «рациональная дробь», «целое рациональное выражение» и «дробное рациональное выражение» иллюстрирует рисунок 1.
Целые рациональные выражения имеют смысл при любых значениях входящих в них переменных.
Например, областью определения выражения 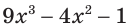 является множество всех действительных чисел.
является множество всех действительных чисел.
Рациональные выражения:
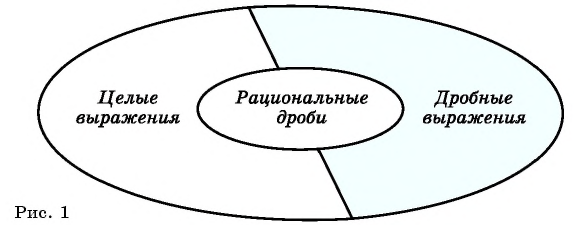
Дробные рациональные выражения имеют смысл при всех значениях переменных, кроме тех, которые обращают знаменатели дробей в нуль.
Например, выражение 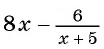 при
при 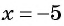 не имеет смысла, так как при
не имеет смысла, так как при 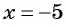 знаменатель дроби
знаменатель дроби 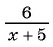 обращается в нуль. Значит, данное выражение имеет смысл при всех значениях переменной, кроме
обращается в нуль. Значит, данное выражение имеет смысл при всех значениях переменной, кроме 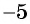 .
.
Рациональная дробь  имеет смысл при любых значениях переменной, кроме чисел
имеет смысл при любых значениях переменной, кроме чисел 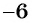 и
и 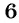 , так как при
, так как при 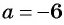 и при
и при 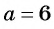 знаменатель дроби обращается в нуль.
знаменатель дроби обращается в нуль.
Областью определения рациональной дроби является множество всех значений входящих в нее переменных, кроме тех, которые обращают ее знаменатель в нуль.
Пример №1
Найдите область определения рациональной дроби:
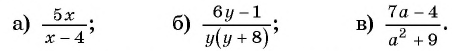
Решение:
а) Областью определения рациональной дроби 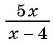 является множество всех действительных чисел, кроме числа
является множество всех действительных чисел, кроме числа 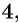 так как при
так как при 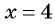 знаменатель дроби обращается в нуль. Можно записать:
знаменатель дроби обращается в нуль. Можно записать: 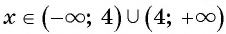 .
.
б) Найдем, при каких значениях переменной знаменатель дроби 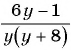 обращается в нуль. Для этого решим уравнение
обращается в нуль. Для этого решим уравнение 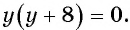 Корнями данного уравнения являются числа
Корнями данного уравнения являются числа 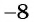 и
и 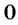 . Значит, областью определения дроби
. Значит, областью определения дроби 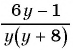 является множество всех действительных чисел, кроме чисел
является множество всех действительных чисел, кроме чисел 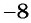 и
и 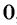 , т. е.
, т. е. 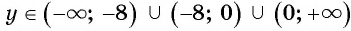 .
.
в) Поскольку выражение 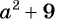 является положительным числом при любых значениях переменной, то нет таких значении переменной, при которых знаменатель дроби
является положительным числом при любых значениях переменной, то нет таких значении переменной, при которых знаменатель дроби 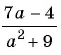 был бы равен нулю. Значит, рациональная дробь имеет смысл при любых значениях переменной, т. е. областью определения дроби является множество всех действительных чисел,
был бы равен нулю. Значит, рациональная дробь имеет смысл при любых значениях переменной, т. е. областью определения дроби является множество всех действительных чисел, 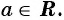
Рациональные выражения:
Пример №2
Какие из следующих выражений:
а) 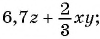
б) 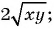
в) 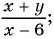
г) 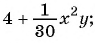
д) 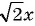 — являются рациональными?
— являются рациональными?
Решение:
Выражения а), в), г) и д) являются рациональными, так как составлены из чисел, переменных и содержат действия сложения, вычитания, умножения и деления. Выражение б) не является рациональным, так как содержит действие извлечения корня из выражения с переменными.
Пример №3
Какие из следующих выражений:
а) 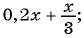
б) 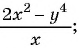
в) 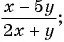
г) 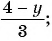
д) 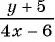 — являются дробными рациональными?
— являются дробными рациональными?
Решение:
Выражения б), в), д) являются дробными рациональными, так как составлены из чисел, переменных, натуральных степеней переменных с помощью действий сложения, вычитания, умножения и содержат действие деления на рациональное выражение с переменными.
Пример №4
Какие из следующих выражений:
а) 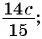
б) 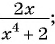
в) 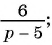
г) 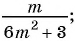
д) 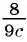 являются рациональными дробями?
являются рациональными дробями?
Решение:
Выражения а) — д) являются рациональными дробями, так как каждое из них представляет собой дробь, числитель и знаменатель которой являются многочленами.
Пример №5
Найдите значение выражения:
а) 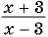 при
при 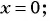
б) 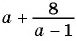 при
при 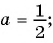
в) 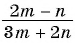 при
при 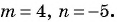
Решение:
а) Подставим 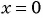 в выражение
в выражение 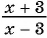 , и получим:
, и получим: 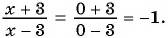
б) При 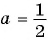 имеем:
имеем:
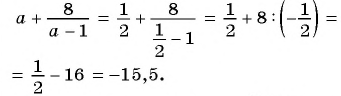
в) Если 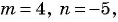 то
то 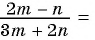
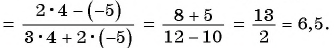
Область определения рациональной дроби
Пример №6
Найдите область определения рациональной дроби:
а) 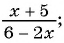
б) 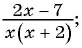
в) 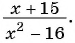
Решение:
а) Найдем, при каком значении переменной знаменатель дроби обращается в нуль. Для этого решим уравнение 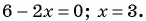 Областью определения данной дроби является множество всех действительных чисел, кроме числа 3, т. е.
Областью определения данной дроби является множество всех действительных чисел, кроме числа 3, т. е. 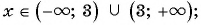
б) 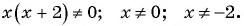 Областью определения данной дроби является множество всех действительных чисел, кроме чисел
Областью определения данной дроби является множество всех действительных чисел, кроме чисел 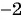 и
и 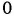 , т. е.
, т. е. 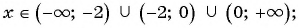
в) 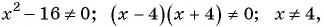
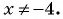 Областью определения данной дроби является множество всех действительных чисел, кроме чисел
Областью определения данной дроби является множество всех действительных чисел, кроме чисел 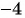 и
и 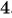 . Значит,
. Значит, 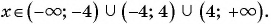
Пример №7
Найдите область определения рационального выражения:
а) 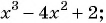
б) 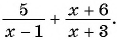
Решение:
а) Выражение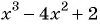 является целым рациональным, его областью определения является множество всех действительных чисел, т. е.
является целым рациональным, его областью определения является множество всех действительных чисел, т. е. 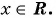
б) Знаменатель первой дроби обращается в нуль при 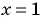 , а знаменатель второй дроби равен нулю при
, а знаменатель второй дроби равен нулю при 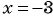 . Значит, областью определения данного выражения является множество всех действительных чисел, кроме чисел
. Значит, областью определения данного выражения является множество всех действительных чисел, кроме чисел 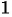 и
и 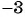 . Таким образом,
. Таким образом, 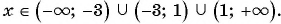
Основное свойство рациональной дроби
Действия с рациональными дробями выполняются по тем же правилам, что с обыкновенными дробями. Так, согласно основному свойству обыкновенных дробей, если числитель и знаменатель дроби умножить или разделить на одно и то же число, не равное нулю, то получится дробь, равная данной.
Например, 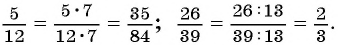
Аналогичное свойство можно сформулировать для рациональных дробей.
Если числитель и знаменатель дроби умножить или разделить на одно и то же выражение, не равное нулю, то получится дробь, тождественно равная данной.
Это свойство называют основным свойством дроби.
Для любой рациональной дроби 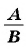 справедливо тождество
справедливо тождество 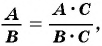 где
где 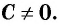
Умножим числитель и знаменатель дроби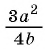 на одночлен
на одночлен 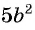 и получим:
и получим: 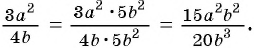 В этом случае говорят, что дробь
В этом случае говорят, что дробь 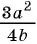 привели к новому знаменателю
привели к новому знаменателю 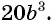
Пример №8
Приведите дробь:
а) 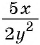 к знаменателю
к знаменателю 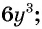
б) 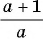 к знаменателю
к знаменателю 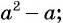
в) 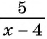 к знаменателю
к знаменателю 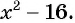
Решение:
а) 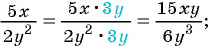
б) 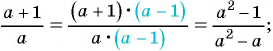
в) 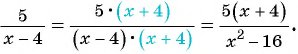
Если основное свойство дроби записать справа налево, то получится равенство
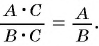
Это равенство позволяет дробь 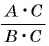 заменить на тождественно равную ей дробь
заменить на тождественно равную ей дробь 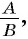 разделив числитель и знаменатель дроби
разделив числитель и знаменатель дроби 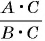 на множитель
на множитель 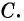
Например, разделим числитель и знаменатель дроби 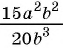 на одночлен
на одночлен 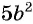 и получим:
и получим: 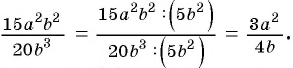 В этом случае говорят, что дробь
В этом случае говорят, что дробь 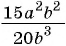 сократили на множитель
сократили на множитель 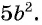 .
.
Сократить рациональную дробь — это значит числитель и знаменатель дроби разделить на их общий множитель.
Например, сократим дробь 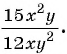 Для этого нужно найти множитель, на который можно разделить числитель и знаменатель дроби. Одночлены
Для этого нужно найти множитель, на который можно разделить числитель и знаменатель дроби. Одночлены 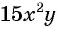 и
и 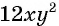 имеют общий множитель
имеют общий множитель 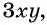 на который можно сократить данную дробь:
на который можно сократить данную дробь:
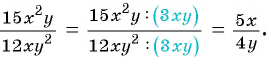
Чтобы сократить рациональную дробь, нужно:
- Разложить (если возможно) числитель и знаменатель дроби на множители.
- Определить общий множитель числителя и знаменателя дроби.
- Разделить числитель и знаменатель данной дроби на общий множитель.
Сократите дробь 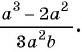
(1) 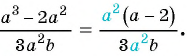
(2) 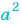 — общий множитель числителя и знаменателя дроби.
— общий множитель числителя и знаменателя дроби.
(3) 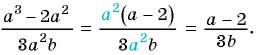
Пример №9
Сократите дробь:
а) 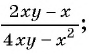
б) 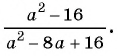
Решение:
а)
- (1) Разложим числитель и знаменатель дроби на множители:
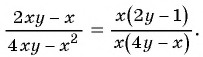
- (2) Числитель и знаменатель дроби имеют общий множитель
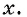
- (3) Разделим числитель и знаменатель данной дроби на общий множитель, т. е. сократим дробь:
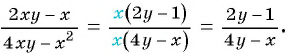
б)
Из основного свойства дроби следует, что 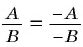 и
и 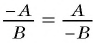 (и в том и в другом случае вторая дробь получена из первой умножением числителя и знаменателя на
(и в том и в другом случае вторая дробь получена из первой умножением числителя и знаменателя на 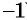 ).
).
Пример №10
Приведите дробь 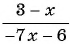 к знаменателю
к знаменателю 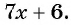
Решение:
Воспользуемся равенством 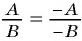 и получим:
и получим: 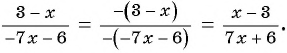
Пример №11
Сократите дробь:
а) 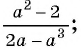
б) 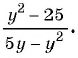
Решение:
а) Разложим знаменатель дроби на множители и получим:
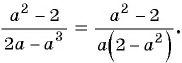
Выражения 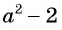 и
и 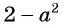 отличаются только знаками. Чтобы сократить дробь, поменяем знаки одного из множителей
отличаются только знаками. Чтобы сократить дробь, поменяем знаки одного из множителей 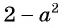 или
или 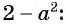
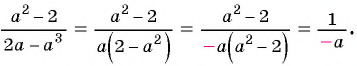
Полученный ответ можно записать в виде 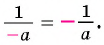 В этом случае говорят, что знак «минус» поставили перед дробью.
В этом случае говорят, что знак «минус» поставили перед дробью.
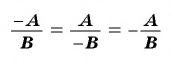
б) Разложим числитель и знаменатель дроби на множители и получим:
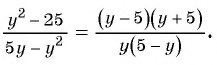
Поменяем знаки одного из множителей 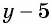 или
или 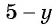 и поставим знак «минус» перед дробью:
и поставим знак «минус» перед дробью:
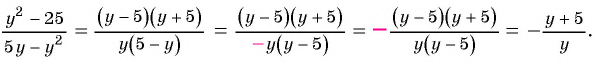
Пример №12
Приведите дробь 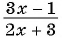 к знаменателю:
к знаменателю:
а) 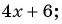
б) 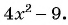
Решение:
а) Умножим числитель и знаменатель дроби на 2 и получим:
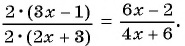
б) Умножим числитель и знаменатель дроби на 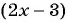 и получим:
и получим: 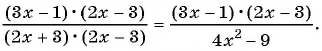
Разберём лекцию подробно:
Вспомним основное свойство обыкновенной дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получим дробь, равную данной. Иначе говоря, для любых натуральных чисел 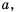
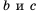 справедливо равенство:
справедливо равенство:
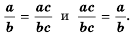
Докажем, что эти равенства являются верными не только для натуральных значений 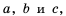 но и для любых других значений при условии
но и для любых других значений при условии 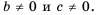
Докажем сначала, что 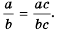
Пусть 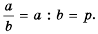 Тогда по определению частного
Тогда по определению частного 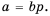 Умножим обе части этого равенства на
Умножим обе части этого равенства на 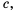 получим:
получим: 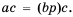 Используя переставное и сочетательное свойства умножения, приходим к равенству:
Используя переставное и сочетательное свойства умножения, приходим к равенству: 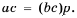 Так как
Так как 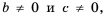 то и
то и 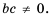 Из последнего равенства (по определению частного) имеем:
Из последнего равенства (по определению частного) имеем: 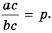 Поскольку
Поскольку 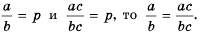
Это равенство является тождеством, следовательно, можем поменять в нем левую и правую части местами:
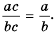
Это тождество дает возможность заменить дробь 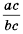 на дробь
на дробь 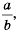 , то есть сократить дробь
, то есть сократить дробь 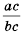 на общий множитель
на общий множитель 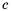 числителя и знаменателя.
числителя и знаменателя.
Свойство дроби, выраженное равенствами 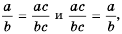 называют основным свойством рациональной дроби.
называют основным свойством рациональной дроби.
Если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля выражение, то получим дробь, равную данной.
Рассмотрим примеры применения этого свойства для дробей на их области допустимых значений переменной.
Пример №13
Сократите дробь 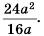
Решение:
Представим числитель и знаменатель этой дроби в виде произведений, содержащих одинаковый (общий) множитель 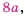 и сократим дробь на это выражение:
и сократим дробь на это выражение:
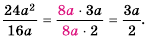
Ответ: 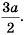
Пример №14
Сократите дробь 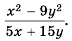
Решение:
Разложим на множители числитель и знаменатель дроби: 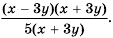 Сократим дробь на
Сократим дробь на 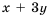 – общий множитель числителя и знаменателя:
– общий множитель числителя и знаменателя: 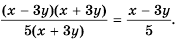
Ответ: 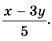
Таким образом, чтобы сократить дробь, нужно:
- разложить на множители числитель и знаменатель дроби, если это необходимо;
- выполнить деление числителя и знаменателя на их общий множитель и записать ответ.
Тождество 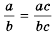 дает возможность приводить дроби к заданному другому (новому) знаменателю.
дает возможность приводить дроби к заданному другому (новому) знаменателю.
Пример №15
Приведите дробь 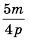 к знаменателю
к знаменателю 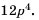
Решение:
Поскольку 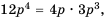 то, умножив числитель и знаменатель дроби
то, умножив числитель и знаменатель дроби 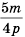 на
на 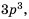 получим дробь со знаменателем
получим дробь со знаменателем 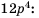
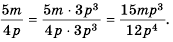
Множитель 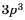 называют дополнительным множителем числителя и знаменателя дроби
называют дополнительным множителем числителя и знаменателя дроби 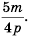
Ответ: 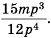
Пример №16
Приведите дробь 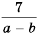 к знаменателю
к знаменателю 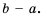
Решение:
Поскольку 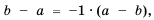 то, умножив числитель и знаменатель дроби
то, умножив числитель и знаменатель дроби 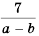 на -1, получим дробь со знаменателем
на -1, получим дробь со знаменателем 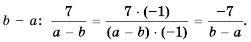
Дробь 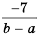 можно заменить тождественно равным ему выражением
можно заменить тождественно равным ему выражением 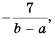 так как изменение знака перед дробью приводит к изменению знака в числителе или знаменателе.
так как изменение знака перед дробью приводит к изменению знака в числителе или знаменателе.
Поэтому 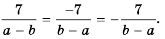
Ответ. 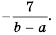
Аналогично, например, 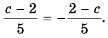 Следовательно,
Следовательно,
- если изменить знак в числителе (или знаменателе) дроби одновременно со знаком перед дробью, то получим дробь, тождественно равную данной.
Это правило можно записать с помощью тождества:
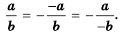
Пример №17
Найдите область определения функции 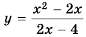 и постройте ее график.
и постройте ее график.
Решение:
Область определения функции – все числа, кроме тех, которые обращают знаменатель 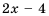 в нуль. Так как
в нуль. Так как 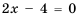 при
при 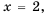 то область определения функции все числа, кроме числа 2. Упростим дробь
то область определения функции все числа, кроме числа 2. Упростим дробь 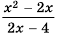 путем сокращения:
путем сокращения: 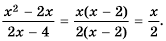 Следовательно, функция
Следовательно, функция 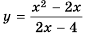 имеет вид
имеет вид 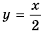 при условии
при условии 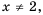 а ее графиком является прямая
а ее графиком является прямая 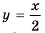 точки с абсциссой 2, то есть без точки (2; 1). Такую точку называют «выколотой» и обязательно исключают ее из графика, изображая «пустой».
точки с абсциссой 2, то есть без точки (2; 1). Такую точку называют «выколотой» и обязательно исключают ее из графика, изображая «пустой».
График функции 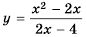 представлен на рисунке 1.
представлен на рисунке 1.
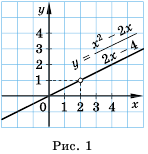
Сокращение рациональных дробей
Пример №18
Сократите дробь 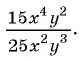
Решение:
Дробь можно сократить на 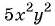 — общий множитель числителя и знаменателя дроби:
— общий множитель числителя и знаменателя дроби:
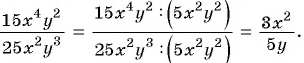
Пример №19
Сократите дробь:
а) 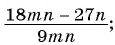
б) 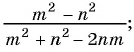
в) 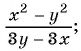
г) 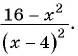
Решение:
а) Разложим на множители числитель дроби и сократим дробь:
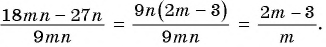
б) С помощью формул сокращенного умножения разложим на множители числитель и знаменатель дроби и получим:
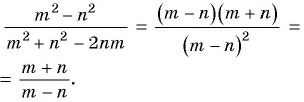
в) Разложим на множители числитель и знаменатель дроби:
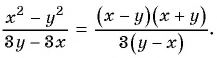
Множители 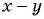 и
и 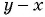 отличаются только знаками. Поменяем знаки одного из множителей
отличаются только знаками. Поменяем знаки одного из множителей 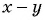 или
или 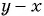 и поставим знак «минус» перед дробью:
и поставим знак «минус» перед дробью:
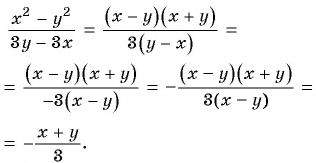
г) После разложения на множители числителя дроби имеем:
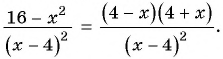
Воспользуемся тем, что 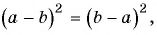 т. е.
т. е. 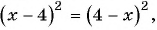 и получим:
и получим:
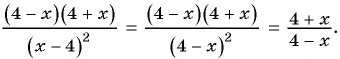
Пример №20
Сократите дробь:
а) 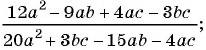
б) 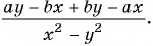
Решение:
а) С помощью способа группировки разложим числитель и знаменатель дроби на множители и сократим дробь:
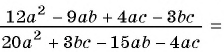
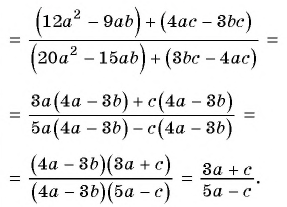
б) 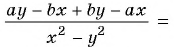
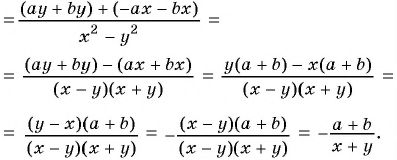
Пример №21
Сократите дробь:
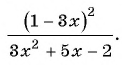
Решение:
Для разложения на множители знаменателя дроби воспользуемся формулой разложения квадратного трехчлена на множители: 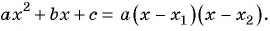 Найдем корни квадратного трехчлена
Найдем корни квадратного трехчлена 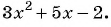 Для этого решим квадратное уравнение
Для этого решим квадратное уравнение 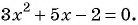
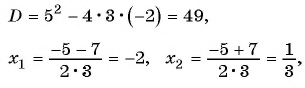
тогда 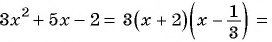
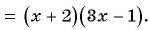
Сократим дробь:
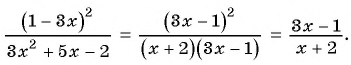
Пример №22
Упростите выражение 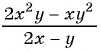 и найдите его значение при
и найдите его значение при 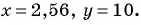
Решение:
Упростим выражение, сократив дробь:
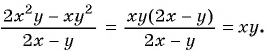
Подставим 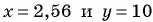 в выражение
в выражение 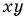 и получим
и получим 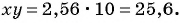
Пример №23
Из данных рациональных дробей выберите дробь, тождественно равную дроби 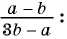
а) 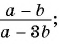
б) 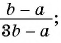
в) 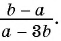
Решение:
Выполним преобразования:
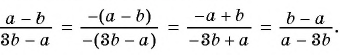
Дроби 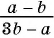 тождественно равна дробь в).
тождественно равна дробь в).
Пример №24
Приведите дробь:
а) 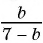 к знаменателю
к знаменателю 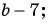
б) 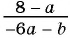 к знаменателю
к знаменателю 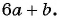
Решение:
Умножим числитель и знаменатель дроби на 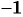 и получим:
и получим:
а) 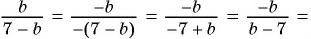
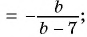
б) 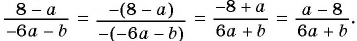
Пример №25
Постройте график функции 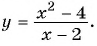
Решение:
Областью определения данной функции является множество всех действительных чисел, кроме числа 2.
Сократим дробь 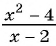 и получим:
и получим:
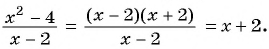
Необходимо построить график функции 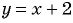 при
при 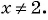 Графиком данной функции является прямая
Графиком данной функции является прямая 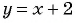 без точки (2; 4).
без точки (2; 4).
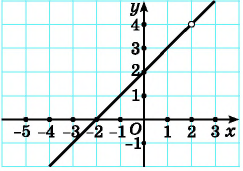
Сложение и вычитание рациональных дробей
Вспомним, как складывают и вычитают обыкновенные дроби. Например:
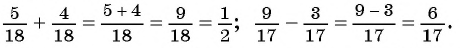
Сложение и вычитание рациональных дробей выполняются по таким же правилам, что сложение и вычитание обыкновенных дробей.
Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тем же.
Затем, если возможно, следует сократить полученную дробь.
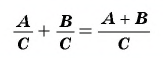
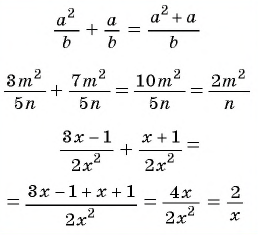
Пример №26
Найдите сумму рациональных дробей:
а) 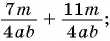
б) 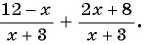
Решение:
а) 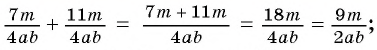
б) 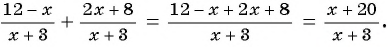
Чтобы вычесть дроби с одинаковыми знаменателями, нужно из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тем же. Затем, если возможно, следует сократить полученную дробь.
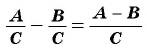
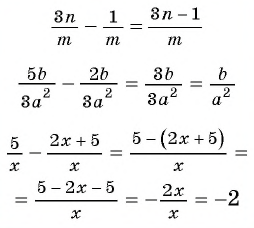
Пример №27
Найдите разность рациональных дробей:
а) 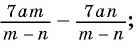
б) 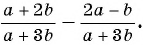
Решение:
а) 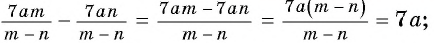
б) 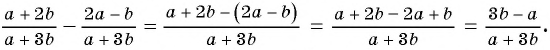
При сложении и вычитании обыкновенных дробей с разными знаменателями их приводят к общему знаменателю (например, 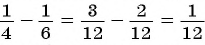 ).
).
Для того чтобы выполнить сложение или вычитание рациональных дробей с разными знаменателями, их также нужно привести к общему знаменателю.
Чтобы привести рациональные дроби к общему знаменателю, нужно:
- Разложить знаменатель каждой дроби на множители (если это необходимо) и определить общий знаменатель дробей.
- Умножить числитель и знаменатель каждой дроби на недостающие множители из общего знаменателя дробей.
Приведите к общему знаменателю рациональные дроби 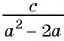 и
и 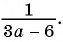
(1) 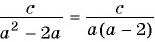 и
и 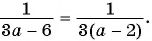
Общий знаменатель 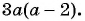
(2) 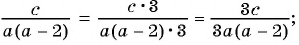
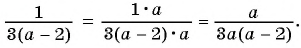
Пример №28
Приведите к общему знаменателю дроби: а) 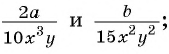
б) 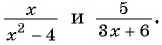
Решение:
а) Общим знаменателем данных дробей является одночлен 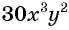 , поскольку НОК (10, 15) = 30 и переменные
, поскольку НОК (10, 15) = 30 и переменные 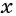 и
и 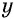 взяты с наибольшим показателем степени.
взяты с наибольшим показателем степени.
Умножим числитель и знаменатель первой дроби на 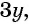 а числитель и знаменатель второй дроби на
а числитель и знаменатель второй дроби на 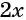 и приведем дроби к общему знаменателю:
и приведем дроби к общему знаменателю:
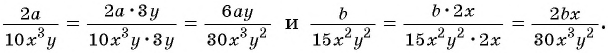
б) Разложим на множители знаменатель каждой дроби и получим:
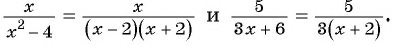
Умножим числитель и знаменатель первой дроби на 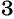 , а числитель и знаменатель второй дроби на
, а числитель и знаменатель второй дроби на 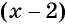 и приведем дроби к общему знаменателю:
и приведем дроби к общему знаменателю:
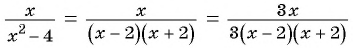
и
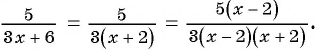
Чтобы выполнить сложение (вычитание) рациональных дробей с разными знаменателями, нужно:
- Привести дроби к общему знаменателю.
- Применить правила сложения (вычитания) дробей с одинаковыми знаменателями.
Найдите сумму рациональных дробей 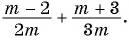
(1) 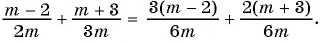
(2) 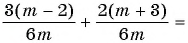
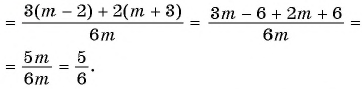
Пример №29
Найдите разность рациональных дробей
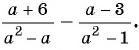
Решение:
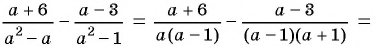
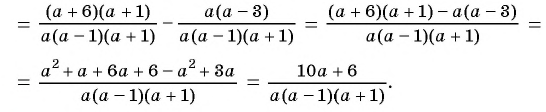
Сложение и вычитание дробей с одинаковыми знаменателями
Вспомним, как сложить дроби с одинаковыми знаменателями. Нужно сложить их числители, а знаменатель оставить тот же. Например:
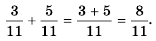
Запишем это правило в виде формулы:
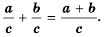
Это равенство справедливо для любых дробей. Докажем его (при условии 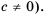
Пусть 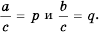 Тогда по определению частного
Тогда по определению частного 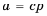
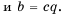 Имеем:
Имеем: 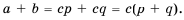 Поскольку
Поскольку 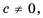 то по определению частного
то по определению частного 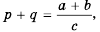
следовательно, 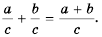
Сформулируем правило сложения дробей с одинаковыми знаменателями:
чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.
Пример №30
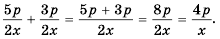
Аналогично можно доказать тождество
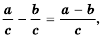
при помощи которого записывают правило вычитания дробей с одинаковыми знаменателями.
Сформулируем правило вычитания дробей с одинаковыми знаменателями:
чтобы вычесть дроби с одинаковыми знаменателями, нужно от числителя уменьшаемого отнять числитель вычитаемого, а знаменатель оставить тот же.
Пример №31
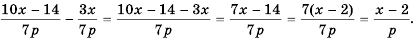
Рассмотрим еще несколько примеров.
Пример №32
Найдите сумму и разность дробей
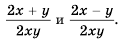
Решение:
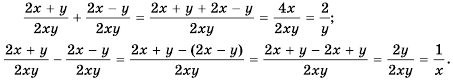
Ответ.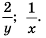
Пример №33
Упростите выражение
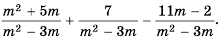
Решение:
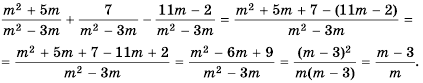
Ответ: 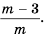
Пример №34
Найдите сумму 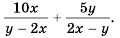
Решение:
Так как 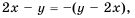 то второе слагаемое можно записать с тем же знаменателем, что и в первом слагаемом:
то второе слагаемое можно записать с тем же знаменателем, что и в первом слагаемом:
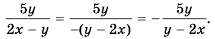
Тогда
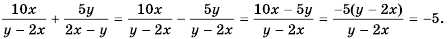
Ответ: 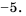
Если в тождествах 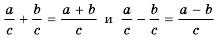 поменять местами левые и правые части, то получим тождества:
поменять местами левые и правые части, то получим тождества:
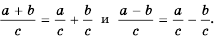
С помощью этих тождеств дробь, числитель которой является суммой или разностью нескольких выражений, можно записать в виде суммы или разности нескольких дробей.
Пример №35
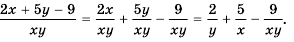
Пример №36
Запишите дробь в виде суммы или разности целого выражения и дроби: 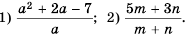
Решение:
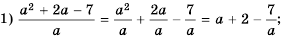
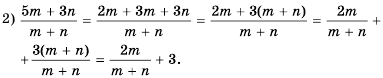
Ответ. 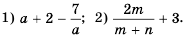
Пример №37
Выполните сложение рациональных дробей:
а) 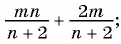
б) 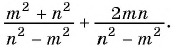
Решение:
а) 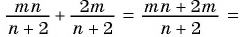
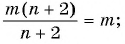
б) 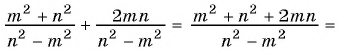
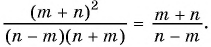
Пример №38
Найдите разность рациональных дробей:
а) 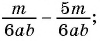
б) 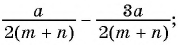
в) 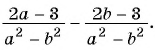
Решение:
а) 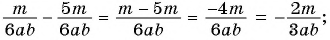
б) 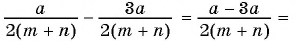
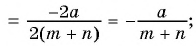
в) 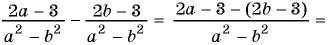
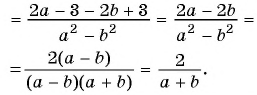
Пример №39
Выполните действия:
а) 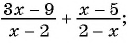
б) 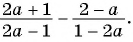
Решение:
а) Знаменатели дробей отличаются только знаком. Поменяем знак в знаменателе второй дроби и перед этой дробью и получим:
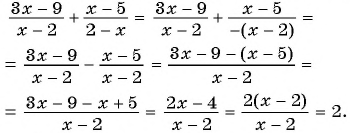
б) 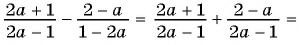
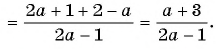
Пример №40
Выполните действия:
а) 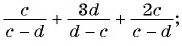
б) 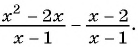
Решение:
а) 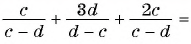
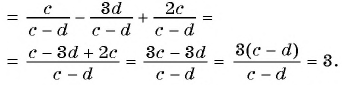
б) 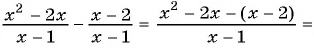
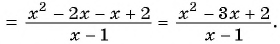
Разложим на множители квадратный трехчлен в числителе дроби и сократим дробь:
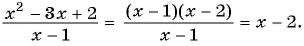
Сложение и вычитание дробей с разными знаменателями
Если дроби имеют разные знаменатели, то их, как и обычные дроби, сначала приводят к общему знаменателю, а потом складывают или вычитают по правилу сложения или вычитания дробей с одинаковыми знаменателями.
Рассмотрим, как прибавить дроби 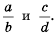 Приведем эти дроби к их общему знаменателю
Приведем эти дроби к их общему знаменателю 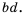 Для этого числитель и знаменатель дроби
Для этого числитель и знаменатель дроби 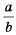 умножим на
умножим на 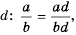 числитель и знаменатель дроби
числитель и знаменатель дроби 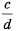 умножим на
умножим на 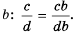 Дроби
Дроби 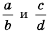 привели к общему знаменателю
привели к общему знаменателю 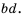 Напомним, что
Напомним, что 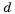 называют дополнительным множителем числителя и знаменателя дроби —
называют дополнительным множителем числителя и знаменателя дроби — 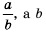 дополнительным множителем числителя и знаменателя дроби
дополнительным множителем числителя и знаменателя дроби 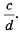
Описанную последовательность действий для сложения дробей с разными знаменателями можно записать так:
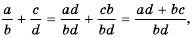
или сокращенно:
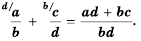
Аналогично выполняют и вычитание дробей с разными знаменателями:
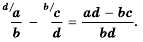
Пример №41
Выполните действие: 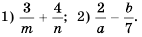
Решение:
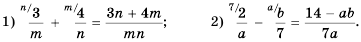
Общим знаменателем двух или более дробей может быть не только произведение их знаменателей. Вообще у дробей есть бесконечно много общих знаменателей. Часто при сложении и вычитании дробей с разными знаменателями удается найти более простой общий знаменатель, чем произведение знаменателей этих дробей. В таком случае говорят о простейшем общем знаменателе (аналогично наименьшему общему знаменателю числовых дробей).
Рассмотрим пример, где знаменатели дробей – одночлены.
Пример №42
Выполните сложение 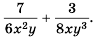
Решение. Общим знаменателем данных дробей можно считать одночлен 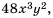 который является произведением знаменателей дробей, но в данном случае он не будет простейшим общим знаменателем. Попробуем найти простейший общий знаменатель, что для дробей, знаменатели которых являются одночленами, будет также одночленом. Коэффициент этого одночлена должен делиться и на 6, и на 8. Наименьшим из таких чисел будет 24. В общий знаменатель каждая из переменных должна входить с наибольшим из показателей степени, которые содержат знаменатели дробей. Таким образом, простейшим знаменателем будет одночлен
который является произведением знаменателей дробей, но в данном случае он не будет простейшим общим знаменателем. Попробуем найти простейший общий знаменатель, что для дробей, знаменатели которых являются одночленами, будет также одночленом. Коэффициент этого одночлена должен делиться и на 6, и на 8. Наименьшим из таких чисел будет 24. В общий знаменатель каждая из переменных должна входить с наибольшим из показателей степени, которые содержат знаменатели дробей. Таким образом, простейшим знаменателем будет одночлен 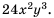 Тогда дополнительным множителем для первой дроби станет выражение
Тогда дополнительным множителем для первой дроби станет выражение 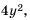 так как
так как 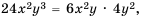 а для второй – выражение
а для второй – выражение 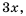 так как
так как 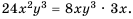 Следовательно, имеем:
Следовательно, имеем:
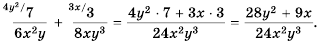
Ответ: 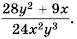
Обратите внимание, что в примере 2 при приведении дробей к общему знаменателю дополнительные множители 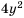 и
и 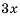 не содержали ни одного общего множителя, отличного от единицы. Это означает, что мы нашли простейший общий знаменатель дробей.
не содержали ни одного общего множителя, отличного от единицы. Это означает, что мы нашли простейший общий знаменатель дробей.
Рассмотрим пример, в котором знаменателями дробей являются многочлены.
Пример №43
Выполните вычитание
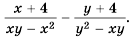
Решение:
Чтобы найти общий знаменатель, разложим знаменатели на множители:
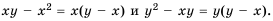
Простейшим общим знаменателем дробей будет выражение 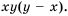 Тогда дополнительным множителем для первой дроби станет
Тогда дополнительным множителем для первой дроби станет 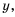 а для второй –
а для второй – 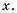 Выполним вычитание:
Выполним вычитание:
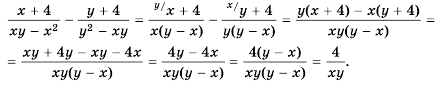
Ответ. 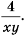
Таким образом, чтобы выполнить сложение или вычитание дробей с разными знаменателями, нужно:
- разложить на множители знаменатели дробей, если это необходимо;
- найти общий знаменатель, лучше простейший;
- записать дополнительные множители;
- найти дробь, которая является суммой или разницей данных дробей;
- упростить эту дробь и получить ответ.
Аналогично выполняют сложение и вычитание целого выражения и дроби.
Пример №44
Упростите выражение 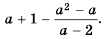
Решение:
Запишем выражение 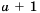 в виде дроби со знаменателем 1 и выполним вычитание:
в виде дроби со знаменателем 1 и выполним вычитание:
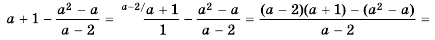
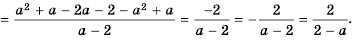
Ответ: 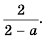
Пример №45
Выполните сложение рациональных дробей:
а) 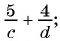
б) 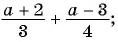
в) 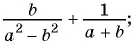
г) 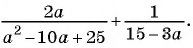
Решение:
а) 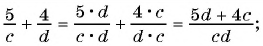
б) 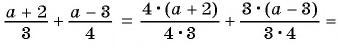
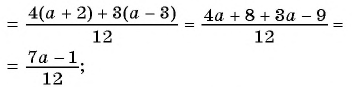
в) 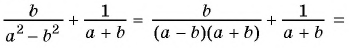
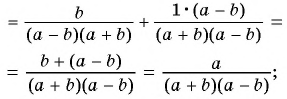
г) 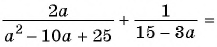
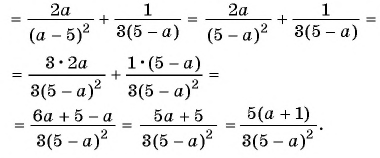
Пример №46
Выполните вычитание:
а) 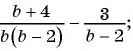
б) 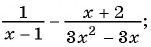
в) 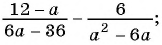
г) 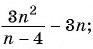
д) 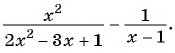
Решение:
а) 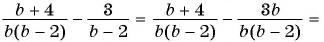
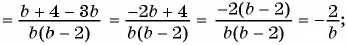
б) 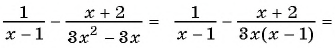
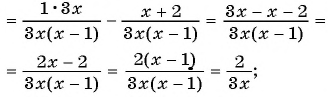
в) 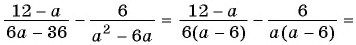
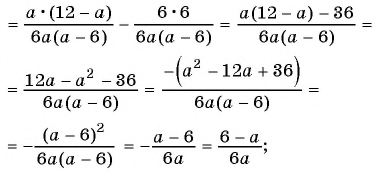
г) 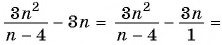
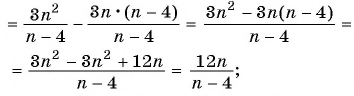
д) Разложим на множители квадратный трехчлен в знаменателе первой дроби и получим:
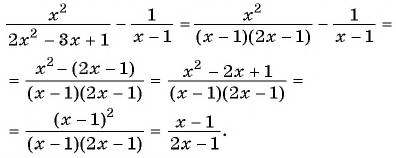
Пример №47
Представьте в виде дроби выражение
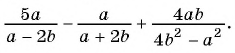
Решение:
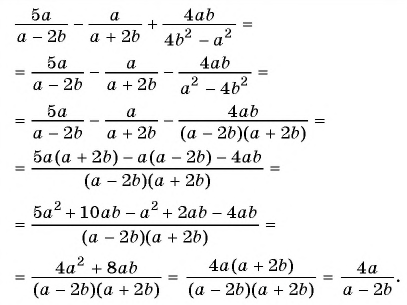
Умножение и деление рациональных дробей
Вспомним, как умножают и делят обыкновенные дроби.
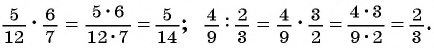
Правила умножения и деления рациональных дробей аналогичны правилам умножения и деления обыкновенных дробей.
Произведение рациональных дробей равно дроби, числитель которой равен произведению числителей данных дробей, а знаменатель равен произведению знаменателей данных дробей. 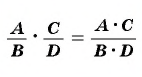
Чтобы найти произведение рациональных дробей, нужно:
- Произведение числителей данных дробей записать в числителе новой дроби, а произведение знаменателей данных дробей записать в знаменателе новой дроби.
- Сократить полученную дробь, если это возможно.
Найдите произведение рациональных дробей 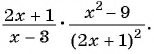
(1) 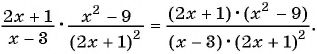
(2) 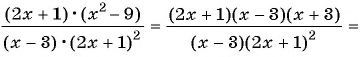
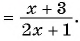
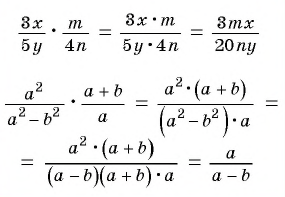
Пример №48
Найдите произведение рациональных дробей:
а) 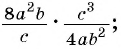
б) 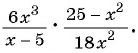
Решение:
а) 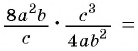
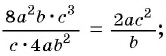
б) 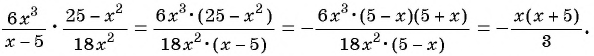
Правило умножения рациональных дробей можно использовать при возведении рациональной дроби в степень. Например:
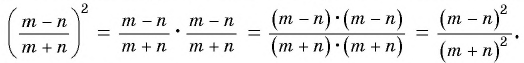
Обобщим этот прием и получим правило:
Чтобы возвести рациональную дробь в степень, нужно возвести в эту степень числитель дроби и полученный результат записать в числителе новой дроби, возвести в эту степень знаменатель дроби и полученный результат записать в знаменателе новой дроби.
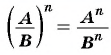
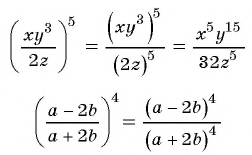
Пример №49
Возведите в степень дробь:
а) 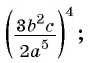
б) 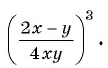
Решение:
а) 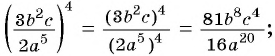
б) 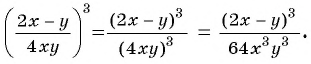
Чтобы разделить одну рациональную дробь на другую, нужно делимое умножить на дробь, обратную делителю.
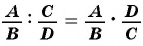
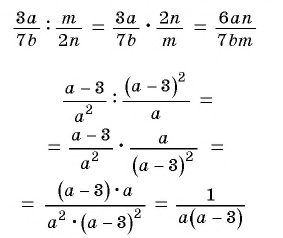
Пример №50
Найдите частное:
а) 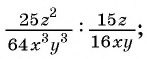
б) 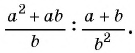
Решение:
а) 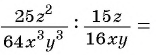
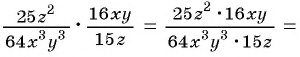
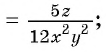
б) 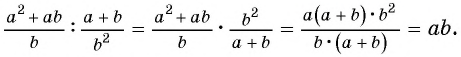
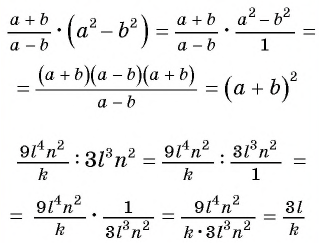
Пример №51
Представьте в виде дроби рациональное выражение:
а) 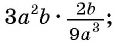
б) 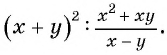
Решение:
а) Представим множитель 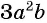 в виде рациональной дроби:
в виде рациональной дроби: 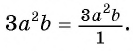
Выполним умножение дробей:
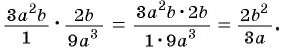
б) Представим выражение 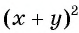 в виде рациональной дроби
в виде рациональной дроби 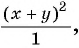 получим:
получим: 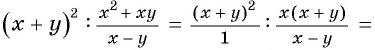
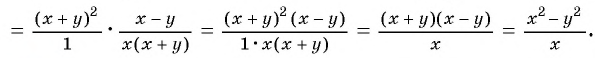
Пример №52
Выполните умножение рациональных дробей:
а) 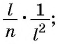
б) 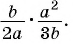
Решение:
а) 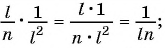
б) 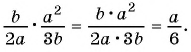
Пример №53
Представьте в виде рациональной дроби произведение:
а) 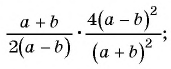
б) 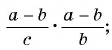
в) 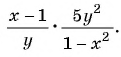
Решение:
а) 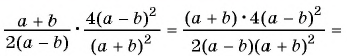
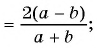
б) 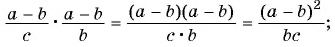
в) 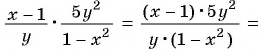
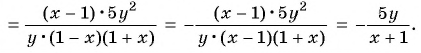
Пример №54
Представьте в виде рациональной дроби выражение:
а) 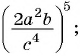
б) 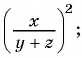
в) 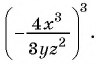
Решение:
а) 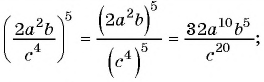
б) 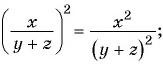
в) 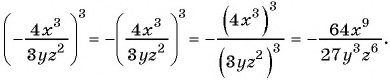
Пример №55
Представьте в виде степени рациональную дробь:
а) 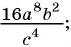
б) 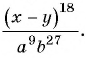
Решение:
а) 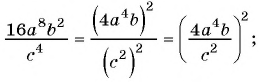
б) 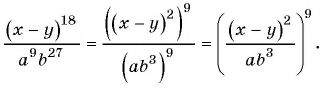
Пример №56
Выполните деление рациональных дробей:
а) 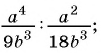
б) 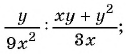
в) 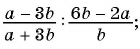
г) 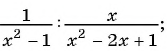
д) 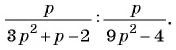
Решение:
а) 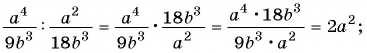
б) 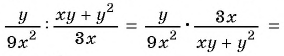
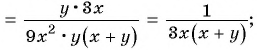
в) 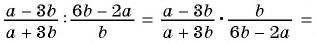
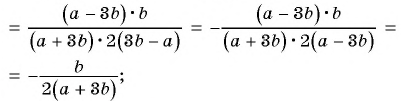
г) 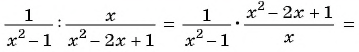
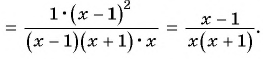
д) Воспользуемся формулой разложения квадратного трехчлена на множители и получим: 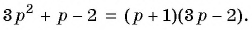
Тогда
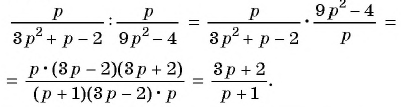
Пример №57
Выполните действия:
а) 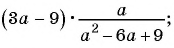
б) 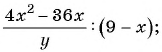
в) 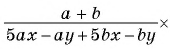
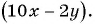
Решение:
а) 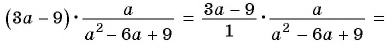
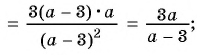
б) 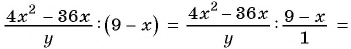
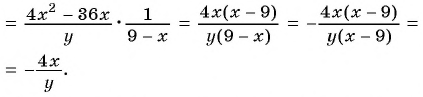
в) Разложим на множители многочлен, применив способ группировки:
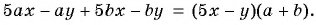
Тогда 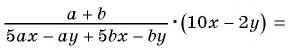
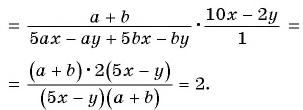
Пример №58
Найдите значение выражения
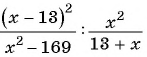
при 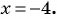
Решение:
Выполним деление:
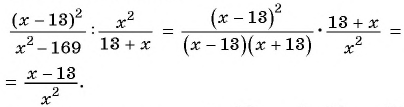
При 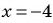 получим:
получим: 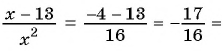
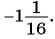
Пример №59
Найдите значение выражения 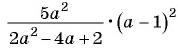
при 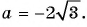
Решение:
Выполним умножение:
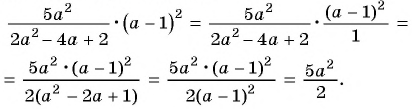
При 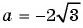 имеем:
имеем:
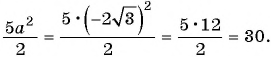
Умножение дробей
Напомним, что произведением двух обыкновенных дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей данных дробей:
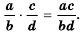
Докажем, что это равенство является тождеством для любых значений 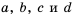 при условии, что
при условии, что 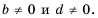
Пусть 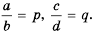 Тогда по определению частного
Тогда по определению частного 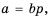
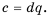 Поэтому
Поэтому 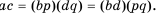 Так как
Так как 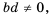 то, снова учитывая определение частного, получим:
то, снова учитывая определение частного, получим: 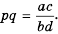 следовательно, если
следовательно, если 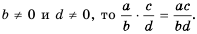
Сформулируем правило умножения дробей.
Чтобы умножить дробь на дробь, нужно перемножить отдельно числители и отдельно знаменатели сомножителей и записать первый результат в числителе, а второй – в знаменателе произведения дробей.
Пример №60
Выполните умножение 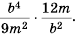
Решение:
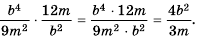
Ответ: 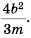
Пример №61
Найдите произведение
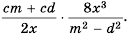
Решение.
Используем правило умножения дробей и разложим на множители числитель первой дроби и знаменатель второй:
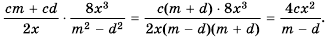
Ответ.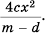
Обратите внимание, что в примерах 1 и 2 при умножении дробей мы не находили сразу же результат умножения числителей и знаменателей. Сначала мы записали произведения в числителе и в знаменателе по правилу умножения дробей, потом сократили полученную дробь, так как она оказалась сократимой, а уже затем выполнили умножение в числителе и в знаменателе и записали ответ. Целесообразно это учитывать и в дальнейшем.
Пример №62
Умножить дробь 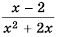 на многочлен
на многочлен 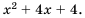
Решение:
учитывая, что 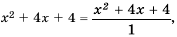 имеем:
имеем:
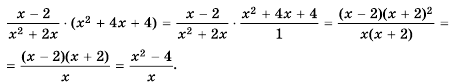
Ответ. 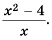
Правило умножения дробей можно распространить на произведение трех и более множителей.
Пример №63
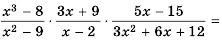
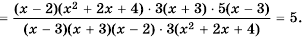
Возведение дроби в степень
Рассмотрим возведение дроби 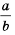 в степень
в степень 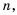 где
где 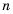 – натуральное число.
– натуральное число.
По определению степени и правилу умножения дробей имеем:
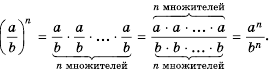
Следовательно:
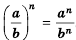
Сформулируем правило возведения дроби в степень.
Чтобы возвести дробь в степень, нужно возвести в эту степень числитель и знаменатель и первый результат записать в числитель, а второй – в знаменатель дроби.
Пример №64
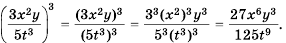
Пример №65
Представьте выражение 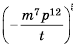 в виде дроби.
в виде дроби.
Решение:
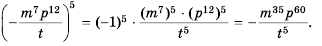
Ответ: 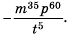
Деление дробей
Напомним, чтобы найти частное двух обыкновенных дробей, нужно делимое умножить на дробь, обратную делителю:
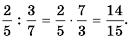
Формулой это можно записать так:
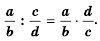
Докажем, что это равенство является тождеством для любых значений 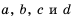 при условии, что
при условии, что 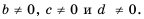
Так как: 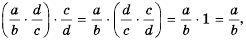
то по определению частного имеем: 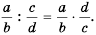
Следовательно, если 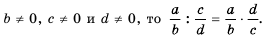
Дробь 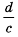 называют обратной дроби
называют обратной дроби 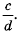
Сформулируем правило деления дробей.
Чтобы разделить одну дробь на другую, нужно первую дробь у множить на дробь, обратную второй.
Пример №66
Разделите дробь 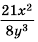 на дробь
на дробь 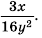
Решение:
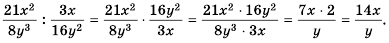
Ответ. 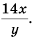
Пример №67
Выполните деление 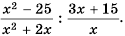
Решение:
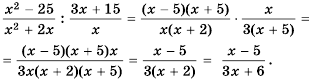
Ответ: 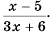
Пример №68
Упростите выражение: 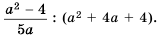
Решение:
Так как 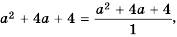 то:
то:
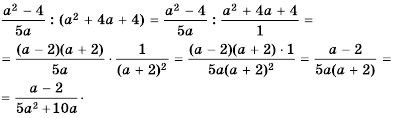
Ответ: 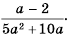
Преобразования рациональных выражений
При решении многих задач требуется упрощать рациональные выражения, приводя их к рациональным дробям. Для этого выполняют преобразования рациональных выражений.
Чтобы преобразовать рациональное выражение, нужно:
- Установить порядок действий в выражении.
- Выполнить действия по порядку, используя правила сложения, вычитания, умножения и деления рациональных дробей.
Упростите выражение:
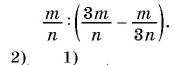
(1) 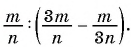
(2) 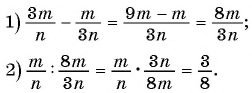
Пример №69
Представьте выражение 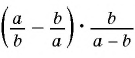 в виде рациональной дроби.
в виде рациональной дроби.
Решение:
(1) Сначала необходимо выполнить вычитание выражений, стоящих в скобках, а затем выполнить умножение.
(2) 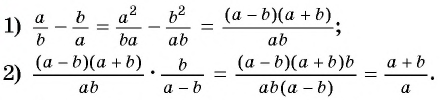
Преобразование рационального выражения можно выполнить не по действиям, а “цепочкой”. В данном случае получим:
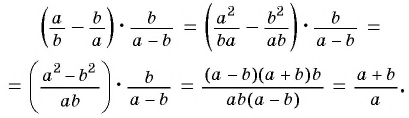
Пример №70
Найдите значение выражения
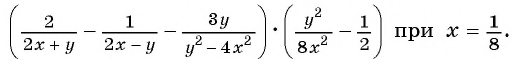
Решение:
Упростим выражение, выполнив действия по порядку:
1) 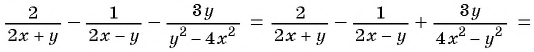
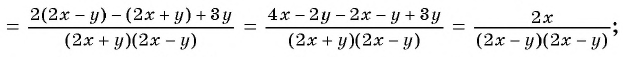
2) 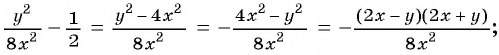
3) 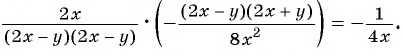
При 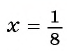 получим:
получим: 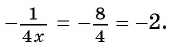
Преобразования рациональных выражений можно выполнять наряду с другими, ранее изученными преобразованиями.
Пример №71
Упростите выражение 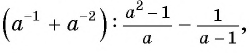 приведя его к рациональной дроби.
приведя его к рациональной дроби.
Решение:
1) 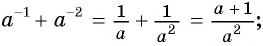
2) 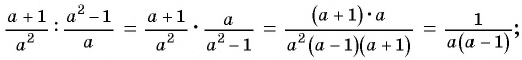
3) 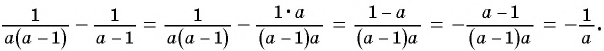
Правила преобразования рациональных выражений можно использовать и для преобразования выражений, содержащих корни.
Пример №72
Сократите дробь:
а) 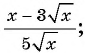
б) 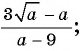
в) 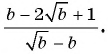
Решение:
а) 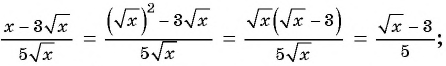
б) 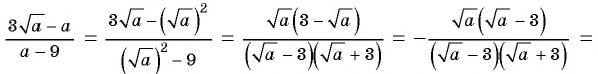
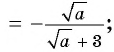
в) 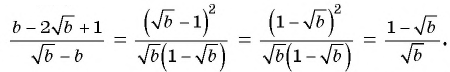
Пример №73
Упростите выражение 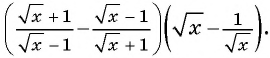
Решение:
1) 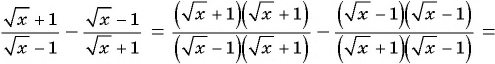
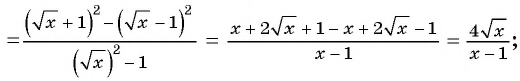
2) 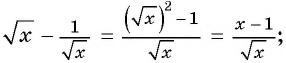
3) 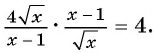
Пример №74
Представьте выражение 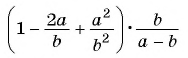 в виде дроби.
в виде дроби.
Решение:
1) 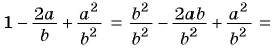
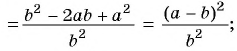
2) 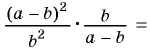
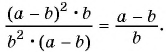
Пример №75
Найдите значение выражения 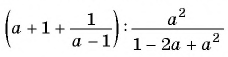 при
при 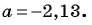
Решение:
Преобразуем данное выражение “цепочкой”:
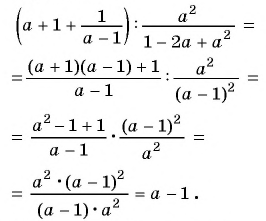
При 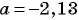 получим:
получим: 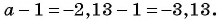
Пример №76
Упростите выражение
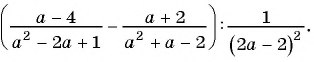
Решение:
1) Корнями квадратного трехчлена 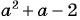 являются числа
являются числа 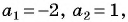 значит,
значит, 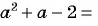
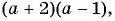 тогда:
тогда:
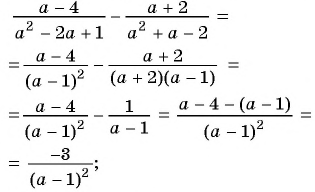
2) 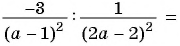
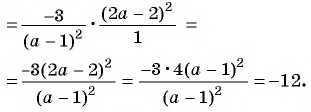
Пример №77
Докажите, что значение выражения
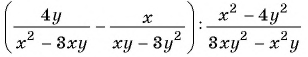
не зависит от значений переменных.
Решение:
Значение выражения при различных значениях переменных из области его определения можно найти, предварительно упростить его:
1) 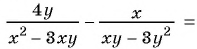
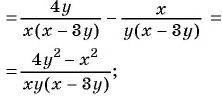
2) 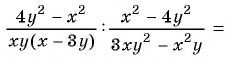
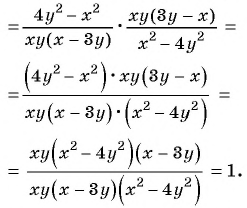
Получили, что результат упрощения равен числу 1, значит при любых значениях переменных из области определения значение данного выражения равно 1, т. е. не зависит от значений переменных.
Пример №78
Упростите выражение
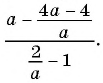
Решение:
Запишем дробь в виде частного и получим: 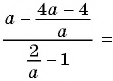
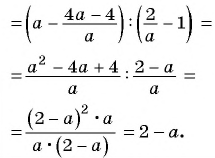
Пример №79
Упростите выражение
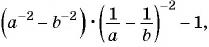 приведя его к несократимой дроби.
приведя его к несократимой дроби.
Решение:
1) 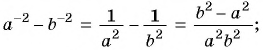
2) 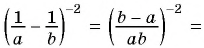
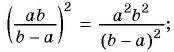
3) 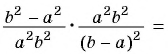
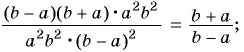
4) 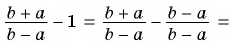
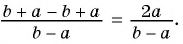
Пример №80
Примените к выражению алгоритм сокращения рациональной дроби:
а) 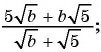
б) 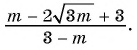
Решение:
а) 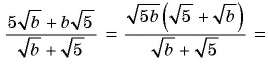
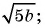
б) 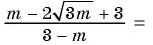
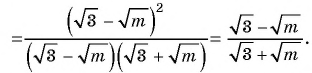
Пример №81
Упростите выражение
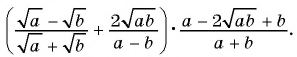
Решение:
1) 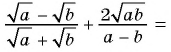
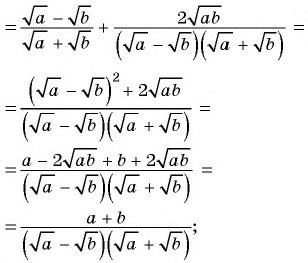
2) 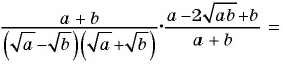
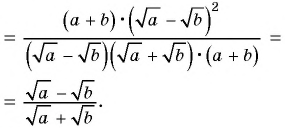
Пример №82
Найдите значение выражения 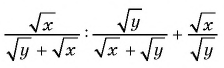 при
при 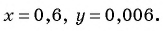
Решение:
Упростим данное выражение:
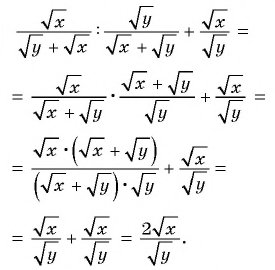
При 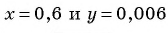 получим:
получим:
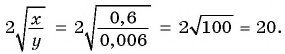
- Заказать решение задач по высшей математике
Тождественные преобразования рациональных выражений
Рассмотрим примеры преобразований рациональных выражений.
Пример №83
Докажите тождество 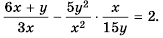
Решение:
Упростим левую часть равенства:
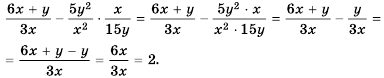
С помощью тождественных преобразований мы привели левую часть равенства к правой. Следовательно, равенство является тождеством.
Пример №84
Упростите выражение
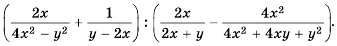
Решение:
Сначала выполним действие в каждой из скобок, а потом – действие деления:
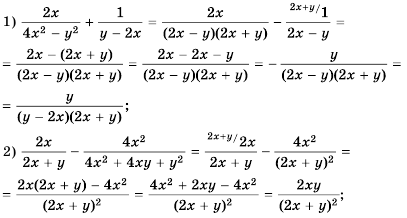
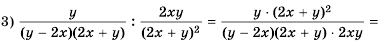
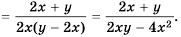
Ответ: 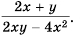
Решение можно было записать и в виде «цепочки»:
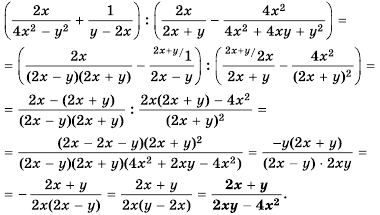
Каждое выражение, содержащее сумму, разность, произведение и частное рациональных дробей, можно представить в виде рациональной дроби.
Пример №85
Докажите, что при всех допустимых значениях переменных значение дроби 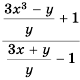 неотрицательно.
неотрицательно.
Решение:
Можно представить эту дробь в виде частного 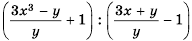 и далее преобразовать ее, как предложено в примере 2.
и далее преобразовать ее, как предложено в примере 2.
А можно, используя основное свойство дроби, умножить числитель и знаменатель данной дроби на их общий знаменатель, то есть на 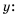
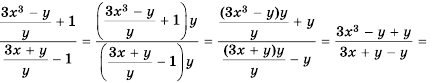
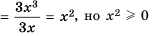 при любом значении
при любом значении 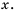
- Функция в математике
- Наибольшее и наименьшее значения функции
- Раскрытие неопределенностей
- Дробно-рациональные уравнения
- Система показательных уравнений
- Непрерывные функции и их свойства
- Правило Лопиталя
- Вычисления в Mathematica с примерами

