Математика в наши дни проникает во все сферы
жизни. Овладение практически любой профессией
требует тех или иных знаний по математике. Особое
значение в этом смысле имеет умение
смоделировать математически определённые
реальные ситуации. Данное умение интегрирует в
себе разнообразные специальные умения,
адекватные отдельным элементам математических
знаний, их системам, а также различные
мыслительные приёмы, характеризующие культуру
мышления.
В школьной математике знакомство с
математическим моделированием основано, прежде
всего, на решении текстовых задач. Текстовая
задача несет в себе важные элементы
математического моделирования. Решая ее,
учащийся некие производственные, экономические,
житейские связи зашифровывает с помощью
математических символов, придавая им
абстрактную математическую форму. Решая
уравнения, учащийся расшифровывает результат,
согласуя его со здравым смыслом. Вот почему
решению текстовых задач, этому важнейшему
мостику между математикой и ее приложениями
должно уделяться особое внимание. При этом
представляется, что техника решения текстовых
задач может отрабатываться на любых задачах.
Было бы наивным думать, что задача на движение,
начинающаяся словами “Два автомобиля:”
непременно предназначена для будущих водителей,
а для школы со спортивным уклоном она должна
начинаться словами “Два лыжника:”.
Применение на практике различных задач на
составление уравнений позволяет создавать такие
учебные ситуации, которые требуют от учащегося
умения смоделировать математически
определённые физические, химические,
экономические процессы и явления, составить план
действия в решении реальной проблемы. Практика
последних лет говорит о необходимости
формирования умений решения задач на
составление уравнений различных типов ещё и в
связи с включением их в содержание ГИА и ЕГЭ.
Однако, анализ образовательной практики по
данному направлению говорит о том, что
значительная часть учащихся испытывает
серьёзные затруднения при решении задач на
составление уравнений. В большей степени это
связано с недостаточной сформированностью у
учащихся умения составлять план действий,
алгоритм решения конкретной задачи, культурой
моделирования явлений и процессов. Большинство
учащихся решают такие задачи лишь на
репродуктивном уровне.
Решению текстовых задач предшествует
достаточно долгое время, отводимое на отработку решения уравнений.
Начиная с 8 класса, как только выучены дробные
рациональные выражения, решения задач
по алгебре практически все сводятся к решению
дробных рациональных уравнений, которые, в свою
очередь, включают чаще всего решение
квадратных уравнений.
В 8 классе решение задач с помощью дробных
рациональных уравнений как показывает опыт
эффективнее решать табличным методом, так как он
является более наглядным, что важно для
подготовки к ГИА в 9 классе.
Все задачи, решаемые с помощью дробных
рациональных уравнений, можно разделить на
несколько групп:
- Задачи на движение по местности.
- Задачи на движение по воде.
- Задачи на работу.
- Задачи на нахождение дробей и т.д.
Начинать обучение следует с простых задач,
условия которых полностью соответствуют
названиям основных типов, и сводящихся к решению
дробных рациональных уравнений. Затем можно
приступать к решению более сложных задач.
Рекомендуется подобрать разноуровневые задачи
по каждому типу, что дает возможность работать со
школьниками разных математических способностей.
Мы стараемся научить детей строить таблицы с
данными величинами задачи, слева обозначаются
объекты (автомобили, лодки, пешеходы, самолеты и
т.д.), сверху в колонках – величины,
характеризующие данную задачу, и обязательно
единицы их измерения. И дети понимают, что из трех
величин, зная две, всегда можно записать третью.
Приведем пример оформления задачи:
Автобус-экспресс отправился от вокзала в
аэропорт, находящийся на расстоянии 120км от
вокзала. Пассажир, опоздавший на 10 минут на
автобус, решил добраться до аэропорта на такси.
Скорость такси на 10км/ч больше скорости автобуса.
С какой скорость ехал автобус, если он приехал в
аэропорт одновременно с такси?
Пусть ![]() км/ч –
км/ч –
скорость автобуса, тогда составим и заполним
таблицу:
Т.к. по условию задачи пассажир опоздал на
автобус на 10 минут =![]() часа,
часа,
то составим и решим уравнение:
![]() , ОДЗ:
, ОДЗ: ![]() >0 (т.к. скорость
>0 (т.к. скорость
положительна)
720(х+10) – 720х= х (х+10),
х2+10х-7200=0,
Далее решая квадратное уравнение, получаем:
х1=80,
х2=-90,
-90 – не входит в ОДЗ, значит, скорость автобуса
равна 80 км/ч.
Ответ: 80км/ч.
Основная часть класса уверенно заполняет
таблицу и составляет уравнение.
В зависимости от выделенного времени,
обучаемым может быть предложен широкий спектр
мероприятий – семинары, кружки, факультативы,
индивидуальные и групповые консультации и т.д., в
рамках которых обучаемые более глубоко
осваивают решение задач с помощью уравнений.
Практикум по решению задач табличным методом с
помощью дробных рациональных уравнений можно
провести во второй половине дня на групповой
консультации по математике, что целесообразно в
рамках школы полного дня.
Список предлагаемых задач:
Числитель обыкновенной дроби на 4 меньше ее
знаменателя. Если к числителю этой дроби
прибавить 19, а к знаменателю 28, то она увеличится
на ![]() . Найдите
. Найдите
эту дробь.
Теплоход, собственная скорость которого 18 км/ч,
прошел 50 км по течению реки и 8 км против течения,
затратив на весь путь 3 часа. Какова скорость
течения реки?
Два комбайна убрали поле за 4 дня. За сколько
дней мог убрать поле каждый комбайн, если одному
из них для выполнения этой работы потребовалось
бы на 6 дней меньше, чем другому?
Моторная лодка прошла против течения 8 км и
вернулась обратно, затратив на обратный путь на 30
мин меньше, чем при движении против течения.
Найдите скорость лодки в неподвижной воде, если
скорость течения равна 4 км/ч.
Расстояние 700 км экспресс проходит на 4 часа
быстрее товарного поезда, так как его скорость
больше скорости товарного поезда на 20 км/ч.
Определите скорость каждого из поездов, если
известно, что они движутся с постоянной
скоростью без остановок.
Мастеру на выполнение заказа потребуется на 5
дней меньше, чем его ученику, но при совместной
работе они выполнят заказ на 4 дня быстрее, чем
мастер, работающий в одиночку. За сколько дней
выполнит заказ мастер, работая в одиночку?
На участке пути длиной 300 км поезд увеличил
скорость на 10 км/ч, в результате чего прибыл на
конечную станцию на 1 час раньше, чем
планировалось по расписанию. С какой скоростью
должен был идти поезд по расписанию?
Прозаик хочет набрать на компьютере рукопись
объемом 450 страниц. Если он будет набирать на 5
страниц в день больше, чем запланировал, то
закончит работу на 3 дня раньше. Сколько страниц в
день планирует набирать прозаик?
Дорога между пунктами А и В состоит из подъема и
спуска, а ее длина равна 19 км. Пешеход прошел путь
из А в В за 5 часов. Время его движения на спуске
составило 4 часа. С какой скоростью пешеход шел на
спуске, если скорость его движения на подъеме
меньше скорости движения на спуске на 1 км/ч?
Велосипедист отправился с некоторой скоростью
из города А в город В, расстояние между которыми
равно 88 км. Возвращаясь из В в А, он ехал поначалу
с той же скоростью, но через 2 часа пути вынужден
был сделать остановку на 10 минут. После этого он
продолжил путь в А, увеличив скорость на 2 км/ч, и в
результате затратил на обратный путь столько же
времени, сколько на путь из А в В. Найдите
скорость велосипедиста на пути из А в В.
Количество решаемых задач может меняться в
зависимости от отводимого на это время.
Используемая литература:
- И.Л.Бродский, А.М.Видус, А.Б.Коротаев “Сборник
текстовых задач по математике для профильных
классов”. - В.И. Жохов, Ю.Н.Макарычев, Н.Г.Миндюк
“Дидактические материалы по алгебре 8 класс”. - Сборник задач для подготовки и проведения
письменного экзамена по алгебре за курс основной
школы под редакцией С.А.Шестакова. - Ш.А.Алимов, М.Ю.Колягин и др. “Алгебра 8 класс”.
- А.П.Ершова, В.В.Голобородько, А.С.Ершова
“Самостоятельные и контрольные работы по
алгебре и геометрии для 8 класса”.
Примеры
Об общем алгоритме решения задач с помощью уравнений, см. §31 данного справочника.
Пример 1. От посёлка до речки 60 км. Утром турист на скутере отправился на речку. Вечером он возвратился в посёлок, но при этом ехал со скоростью на 10 км/ч меньшей и потратил на дорогу на 18 мин больше. Сколько времени ехал турист от речки к посёлку?
Пусть t – время вечером, на дорогу от речки к посёлку.
Тогда время утром, на дорогу от посёлка к речке t- $frac{18}{60}$ = t-0,3 (ч)
Заполним таблицу:
Скорость, км/ч
Время, ч
Расстояние, км
Утром
$frac{60}{t-0,3}$
t-0,3
60
Вечером
$frac{60}{t}$
t
60
По условию разность скоростей равна 10:
$$ frac{60}{t-0,3} – frac{60}{t} = =10 |:10 $$
$$ frac{6}{t-0,3} – frac{6}{t} = 1 Rightarrow frac{6(t-(t-0,3) )}{t(t-0,3)} = 1 $$
$$1,8=t(t-0,3), t neq 0, t neq 0,3$$
$$ t^2-0,3t-1,8 = 0 $$
$$ D = 0,3^2-4 cdot (-1,8) = 0,09+7,2=7,29 = 2,7^2 $$
$$ t = frac{0,3 pm 2,7}{2} = left[ begin{array}{cc} t_1 = -1,1 \ t_2 = 1,5 end{array} right. $$
Выбираем положительный корень, t = 1,5 ч
Ответ: 1,5 ч
Пример 2. Катер прошёл по течению 120 км. На этот же путь против течения от тратит времени в 1,5 раза больше. Найдите скорость течения, если скорость катера в стоячей воде 20 км/ч.
Пусть u – скорость течения
Заполним таблицу:
Скорость, км/ч
Время, ч
Расстояние, км
По течению
20+u
$frac{120}{20+u}$
120
Против течения
20-u
$frac{120}{20-u}$
120
По условию время против течения в 1,5 раз больше:
$$ 1,5 cdot frac{120}{20+u} = frac{120}{20-u} |:120 $$
$$ frac{1,5}{20+u} = frac{1}{20-u}$$
$$ 1,5(20-u) = 20+u, u neq pm 20 $$
$$ 30-1,5u = 20+u $$
$$ 2,5u = 10 $$
$$ u = 4 $$
Ответ: 4 км/ч
Пример 3. В раствор, содержащий 50 г соли, добавили 150 г воды. В результате концентрация соли уменьшилась на 7,5%. Найдите первоначальную массу раствора.
Пусть x – масса воды в первоначальном растворе, в граммах.
Заполним таблицу:
Раствор после
50
x+150
x+200
По условию разность концентраций:
$$ frac{50}{x+50} – frac{50}{x+200} = 0,075 $$
$$ frac{50(x+200-x-50)}{(x+50)(x+200)} = 0,075 $$
$$ 50 cdot 150 = frac{75}{1000} (x+50)(x+200), x neq -50, x neq -200 $$
Сократим дробь:
$$ frac{50 cdot 150 cdot 1000}{75} = frac{50}{5} cdot frac{150}{15} cdot 1000 = 100000 $$
Получаем:
$$ (x+50)(x+200) = 100000 $$
$$ x^2+250x+10000 = 100000 $$
$$ x^2+250x-90000 = 0 $$
$$ D = 250^2-4 cdot (-90000) = 62500+360000 = 100(625+3600) = $$
$$ = 100 cdot 4225 = 650^2 $$
$$ x = frac{-250 pm 650}{2} = left[ begin{array}{cc} x_1 = -450 \ x_2 = 200 end{array} right. $$
Выбираем положительный корень x=200 г – начальное количество воды в растворе. Начальная масса всего раствора: 50+200 = 250 г.
Ответ: 250 г
Пример 4. Мастер и его ученик, работая вместе, выполняют норму на 8 ч. Если каждый работает самостоятельно, то мастер тратит на выполнение нормы на 12 ч меньше, чем ученик. Сколько часов тратит каждый из них на выполнении нормы?
Пусть N изделий – это норма, t – время, потраченное мастером.
Заполним таблицу:
Производительность, изделий/ч
Время, ч
Результат, изделий
Ученик
$frac{N}{t+12}$
t+12
N
Вместе
$frac{N}{t}+frac{N}{t+12}$
8
N
Из последней строки таблицы получаем:
$$ frac{N}{t}+frac{N}{t+12} = frac{N}{8} |:N $$
$$ frac{1}{t}+frac{1}{t+12} = frac{1}{8} $$
$$ frac{t+12+t}{t(t+12)} = frac{1}{8} $$
$$ 8(2t+12) = t(t+12), t neq 0, t neq -12$$
$$ 16t+96 = t^2+12t $$
$$ t^2-4t-96 = 0 Rightarrow (t-12)(t+8) = 0 Rightarrow left[ begin{array}{cc} t_1 = -8 \ t_2 = 12 end{array} right. $$
Выбираем положительный корень, t=12 ч – время, которое мастер потратит самостоятельно. Ученик потратит 12+12=24 ч.
Ответ: 12 ч и 24 ч
Пример 5*. Один фрилансер может выполнить проект на 12 дней быстрее, чем второй. Над новым проектом первый фрилансер сначала проработал самостоятельно 6 дней, а затем к нему присоединился второй. Через 3 дня совместной работы frac{3}{5} проекта было готово.
За сколько дней каждый из фрилансеров может выполнить проект самостоятельно? За сколько дней проект был фактически выполнен?
Пусть d – количество дней первого фрилансера при самостоятельной работе.
Заполним таблицу:
Производительность, проект/день
Время, дни
Результат, проект
Фрилансер 1
$frac{1}{d}$
d
1
Фрилансер 2
$frac{1}{d+12}$
d+12
1
Первые 6 дней
$frac{1}{d}$
6
$frac{6}{d}$
Совместные 3 дня
$frac{1}{d} + frac{1}{d+12}$
3
$frac{3}{5}-frac{6}{d}$
Из последней строки таблицы получаем:
$$ 3 Biggl(frac{1}{d} + frac{1}{d+12}Biggr) = frac{3}{5}-frac{6}{d} |:3 $$
$$ frac{1}{d} + frac{1}{d+12} = frac{1}{5}-frac{2}{d} $$
$$ frac{d+12+d}{d(d+12)} = frac{d-10}{5d} | times 5d(d+12), d neq 0, d neq -12 $$
$$ 5(2d+12) = (d-10)(d+12) Rightarrow 10d+60 = d^2+2d-120 $$
$$ d^2-8d-180 = 0 Rightarrow (d-18)(d+10) = 0 Rightarrow left[ begin{array}{cc} d_1 = -10 \ d_2 = 18 end{array} right. $$
Выбираем положительный корень, d=18 дней – время самостоятельной работы 1-го фрилансера. 2-й фрилансер будет самостоятельно работать 18+12 = 30 дней.
Найдём фактически потраченное время.
3/5 проекта было сделано за 9 дней. Осталось 2/5, которые выполнялись совместно:
$$ frac{2}{5}: Biggl( frac{1}{18}+ frac{1}{30} Biggr) = frac{2}{5}: frac{5+3}{90} = frac{2}{5} cdot frac{45}{4} = frac{9}{2} = 4,5 $$
Всего было потрачено 9+4,5 = 13,5 дней.
Ответ: 18 дней 1-й фрилансер; 30 дней 2-й фрилансер; 13,5 дней фактически.
Мы с вами уже научились решать рациональные уравнения.
Напомним, что рациональные уравнения
– это уравнения, у которых левая и правая части являются рациональными
выражениями. Рациональное уравнение, в котором левая или правая части
являются дробными выражениями, называют дробным.
Очень часто решение задач сводится к решению
дробных рациональных уравнений. Решим несколько задач, которые сводятся к
решению таких уравнений.
Задача 1. Числитель дроби на меньше её знаменателя.
Сумма дроби и обратной ей дроби в раза больше исходной
дроби. Найти исходную дробь.
Решение:
Обозначим за – знаменатель дроби. Тогда
– числитель этой дроби. Значит,
исходная дробь имеет вид . Так как по условию
задачи сумма дроби и обратной ей дроби
в
раза больше исходной
дроби, то можем составить уравнение:
Задача 2. Велосипедисту надо проехать 15 км. Он
выехал на 15 минут позже намеченного срока и, чтобы приехать вовремя, увеличил
скорость на 2 км/ч. С какой скоростью ехал велосипедист?
Решение:
Пусть (км/ч) – скорость
велосипедиста. Тогда расстояние в км велосипедист проедет
за часов. Если бы велосипедист
выехал вовремя, то его скорость была бы равна км/ч. И тогда расстояние
в км он проехал бы за
часов. По условию
задачи, велосипедист выехал на минут позже намеченного
срока, или, что тоже самое, на часа позже. Составим
уравнение:
Задача 3. Моторная лодка прошла вниз по реке 14 км, а
затем 9 км против течения, затратив на весь путь 5 часов. Найти скорость
течения реки, если скорость моторной лодки в стоячей воде равна 5 км/ч.
Решение:
Пусть (км/ч) – скорость
течения реки. Тогда расстояние в км/ч скорость моторной
лодки по течению реки и км/ч скорость моторной
лодки против течения. Известно, что моторная лодка прошла по течению реки км, а значит, затратила
на это расстояние часов. Затем против
течения лодка прошла км, затратив на это
расстояние часов. По условию
известно, что на весь путь моторная лодка затратила часов. Составим уравнение:
Задача 4. Вело эквилибрист, проектируя своё
оборудование для выступления в цирке, рассчитал, что если длину окружности
колеса его одноколёсного велосипеда увеличить на один метр, то на расстоянии
990 м оно сделает на 40 оборотов меньше. Найти длину окружности велосипедного
колеса эквилибриста.
Решение:
Пусть метров – длина
окружности колеса. Тогда на расстоянии в метров это колесо делает
оборотов.
И тогда на расстоянии метров такое колесо
сделает оборотов. По условию
задачи известно, что после увеличения длины окружности колеса, оно делает на
расстоянии метров на
оборотов меньше. Составим
уравнение:
Итоги:
Итак, сегодня на уроке мы с вами познакомились с задачами,
решение которых предполагает составление и решение дробных рациональных
уравнений, и научились решать такие задачи.
Дробно-рациональные уравнения — это уравнения c одной переменной.
Содержание:
Определение дробно-рационального уравнения
Определение дробно-рационального уравнения:
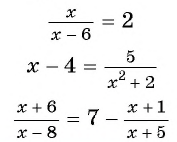
Например, уравнения
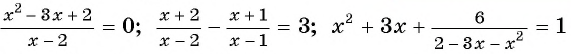
являются дробно-рациональными.
Рассмотрим дробно-рациональное уравнение 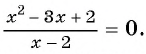 Это уравнение можно решить, используя условие равенства рациональной дроби нулю.
Это уравнение можно решить, используя условие равенства рациональной дроби нулю.
Рациональная дробь равна нулю тогда и только тогда, когда числитель дроби равен нулю, а знаменатель не равен нулю.
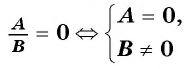
Таким образом, получим:
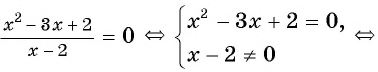
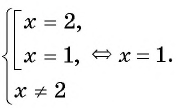
Ответ: 1.
Вернемся к уравнению 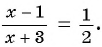 Выполним тождественные преобразования уравнения.
Выполним тождественные преобразования уравнения.
1) Перенесем все слагаемые из правой части уравнения в левую: 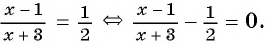
2) Преобразуем левую часть уравнения к рациональной дроби:
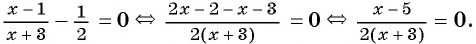
3) Применим условие равенства дроби нулю:
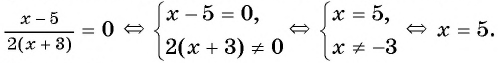
Ответ: 5.
Что нужно для решения дробно-рационального уравнения
Чтобы решить дробно-рациональное уравнение, нужно:
- Перенести все слагаемые из правой части уравнения в левую.
- Преобразовать левую часть уравнения к рациональной дроби.
- Применить условие равенства дроби нулю.
- Записать ответ.
Рассмотрим задачу: В дроби числитель на 2 больше знаменателя. Если числитель этой дроби уменьшить на 3, а знаменатель увеличить на 3, то новая дробь будет равна 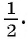 Найдите знаменатель первоначальной дроби.
Найдите знаменатель первоначальной дроби.
Решение:
Обозначим знаменатель первоначальной дроби через х, тогда ее числитель равен 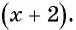
Если числитель дроби уменьшить на 3, то получится числитель новой дроби: 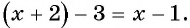 Знаменатель новой дроби после увеличения на 3 будет равен
Знаменатель новой дроби после увеличения на 3 будет равен 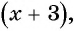 а новая дробь будет иметь вид
а новая дробь будет иметь вид 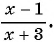 Так как по условию задачи она равна
Так как по условию задачи она равна 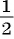 , то получим уравнение
, то получим уравнение 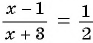 . В левой части этого уравнения записано дробное рациональное выражение.
. В левой части этого уравнения записано дробное рациональное выражение.
Решение многих задач приводит к уравнениям, у которых в левой или правой (или в той и другой) частях записаны дробные рациональные выражения. Такие уравнения называют дробно-рациональными уравнениями.
Пример №1
Решите уравнение 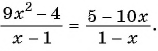
Решение:
(1) 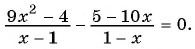
(2) 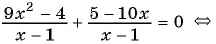
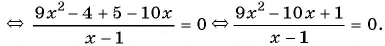
(3) 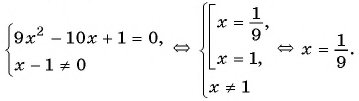
(4) Ответ: 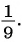
Пример №2
Решите уравнение
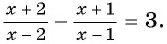
Решение:
(1) 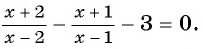
(2) 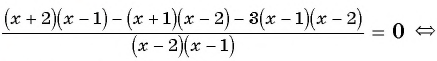
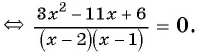
(3) 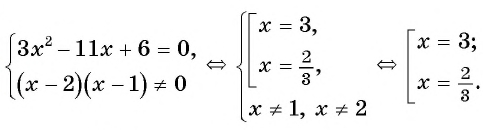
(4) Ответ: 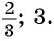
Пример №3
Решите уравнение
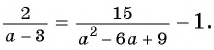
Решение:
(1) 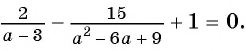
(2) 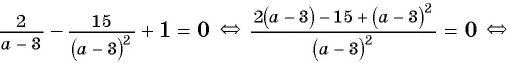
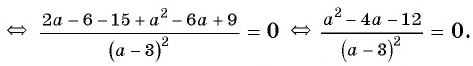
(3) 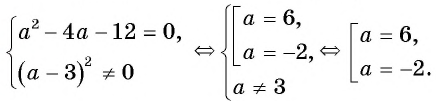
(4) Ответ: -2; 6.
Пример №4
Решите уравнение 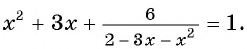
Решение:
Выполним замену переменной 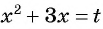 и получим уравнение
и получим уравнение 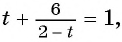 которое является дробно-рациональным. Решим его, применив алгоритм:
которое является дробно-рациональным. Решим его, применив алгоритм:
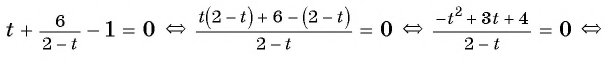
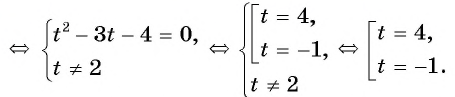
Подставим найденные значения 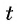 в равенство
в равенство 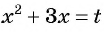 и получим:
и получим:
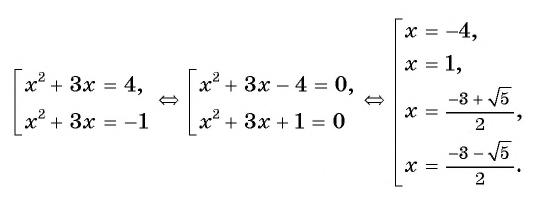
Ответ: 
Дробно-рациональные уравнения используются как математические модели для решения задач, описывающих реальные ситуации.
Например, рассмотрим задачу. На тушение лесных пожаров площадью 200 га отправлено несколько вертолетов с водосливными устройствами. По информации метеорологов предполагается усиление ветра, поэтому было выделено еще 5 вертолетов, в связи с чем площадь для сброса воды каждым вертолетом уменьшилась на 20 га. Сколько вертолетов участвовало в тушении пожаров первоначально?
Решение:
(1) Выясним, о каких величинах и зависимостях между ними в задаче идет речь. В задаче речь идет о площади лесных пожаров и количестве вертолетов для тушения пожаров.
(2) Выясним, какие значения, величин и зависимости между ними, известны. Известна зависимость между количеством вертолетов и площадью для сброса воды.
(3) Выясним, какие значения величин и зависимости между ними не известны. Неизвестно, сколько потребовалось вертолетов.
(4) Обозначим неизвестное значение одной величины через х, а остальные выразим через х и зависимости между величинами. Обозначим через 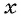 первоначальное количество вертолетов и получим, что
первоначальное количество вертолетов и получим, что 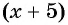 вертолетов направлено на тушение пожаров после сообщения метеорологов. Составим таблицу зависимостей между величинами.
вертолетов направлено на тушение пожаров после сообщения метеорологов. Составим таблицу зависимостей между величинами.
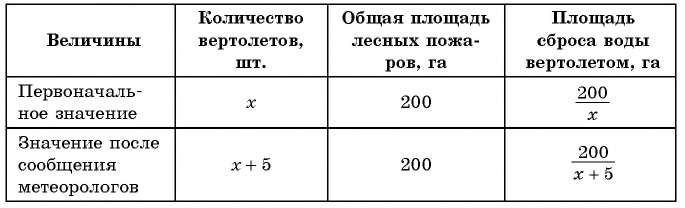
(5) Используя зависимости между известными и неизвестными значениями величин, составим уравнение (математическую модель задачи) и решим его.
По условию задачи 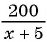 га на 20 га меньше, чем
га на 20 га меньше, чем 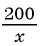 га. Значит, разность между большим и меньшим числом равна 20, т. е.
га. Значит, разность между большим и меньшим числом равна 20, т. е.
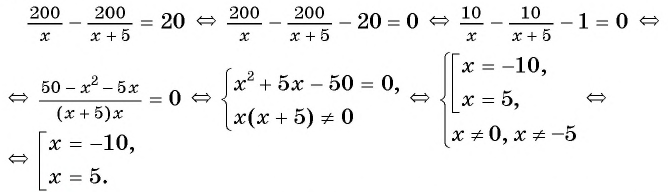
(6) Запишем ответ в соответствии со смыслом задачи. Поскольку 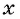 — число вертолетов, то выбираем число 5.
— число вертолетов, то выбираем число 5.
Ответ: 5 вертолетов.
Многие задачи, описывающие реальные процессы, имеют одну и ту же математическую модель. К таким относятся, например, задачи на движение, работу и т. п.
Рассмотрим две задачи:
Задача 1. Два велосипедиста выехали одновременно из поселка 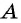 в поселок
в поселок 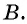 Скорость первого велосипедиста на
Скорость первого велосипедиста на 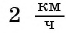 больше скорости второго, поэтому он прибыл в поселок
больше скорости второго, поэтому он прибыл в поселок 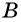 на 0,5 ч раньше. С какими скоростями двигались велосипедисты, если расстояние между поселками равно 30 км?
на 0,5 ч раньше. С какими скоростями двигались велосипедисты, если расстояние между поселками равно 30 км?
Задача 2. Для заполнения водой резервуара объемом 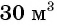 используют два крана: первый кран заполняет резервуар на 0,5 ч быстрее второго, так как в час через него наливается на
используют два крана: первый кран заполняет резервуар на 0,5 ч быстрее второго, так как в час через него наливается на 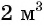 больше, чем через второй. Найдите скорость заполнения резервуара водой через каждый кран.
больше, чем через второй. Найдите скорость заполнения резервуара водой через каждый кран.
В обеих задачах речь идет о процессах: в первой — о процессе движения, во второй — о процессе заполнения резервуара водой.
Составим таблицу зависимостей между величинами.
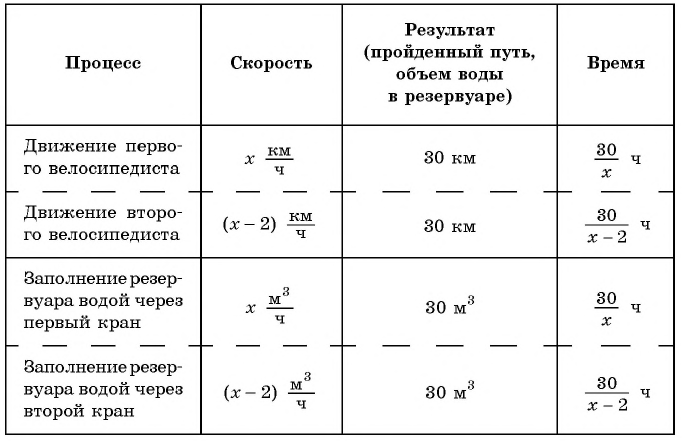
Поскольку первый велосипедист прибыл в поселок на 0,5 ч раньше второго, а один кран заполняет резервуар на 0,5 ч быстрее другого, то уравнение 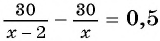 является математической моделью каждой из предложенных задач.
является математической моделью каждой из предложенных задач.
Решим полученное уравнение:
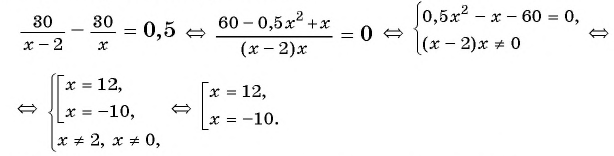
По условию каждой задачи подходит число 12.
Ответ задачи 1: скорость первого велосипедиста 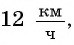 скорость второго велосипедиста
скорость второго велосипедиста 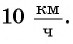 Ответ задачи 2: скорость заполнения резервуара водой через первый кран
Ответ задачи 2: скорость заполнения резервуара водой через первый кран 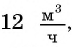 через второй кран —
через второй кран — 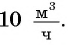
Пример №5
Является ли дробно-рациональным уравнение:
а) 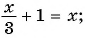
б) 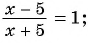
в) 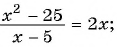
г) 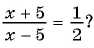
Решение:
Уравнение а) не является дробно-рациональным, так как его левая и правая части — целые рациональные выражения. Уравнения б)—г) являются дробно-рациональными, так как левые части этих уравнений — дробно-рациональные выражения.
Пример №6
Решите уравнение, используя условие равенства дроби нулю:
а) 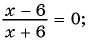
б) 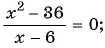
в) 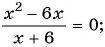
г) 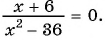
Решение:
а) 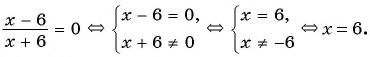
Ответ: 6.
б) 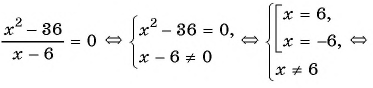
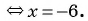
Ответ: -6.
в) 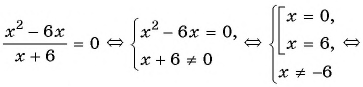
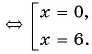
Ответ: 0; 6.
г) 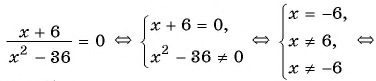
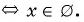
Ответ: нет корней.
Пример №7
Какие из уравнений:
а) 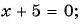
б) 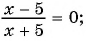
в) 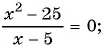
г) 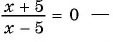 равносильны?
равносильны?
Решение:
а) 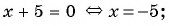
б) 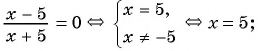
в) 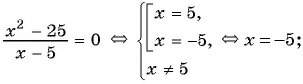
г) 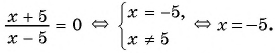
Ответ: уравнения а), в), г) имеют один и тот же корень (уравнения равносильны).
Пример №8
Решите уравнение:
а) 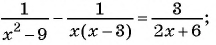
б) 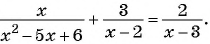
Решение:
а) (1) 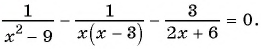
(2) 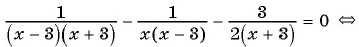
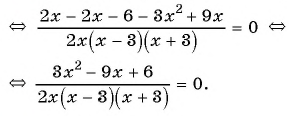
(3) 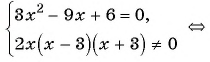
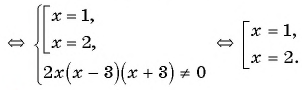
(4) Ответ: 1; 2.
б) 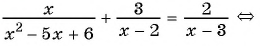
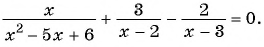
Разложим на множители квадратный трехчлен в знаменателе первой дроби и получим:
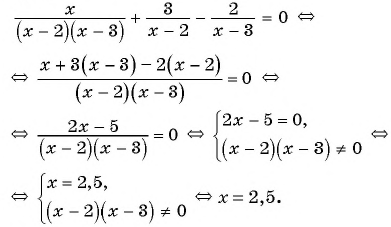
Ответ: 2,5.
Пример №9
Найдите нули функции
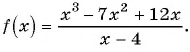
Решение:
Так как нули функции – это значения аргумента, при которых значение функции равно нулю, то для решения задачи нужно решить уравнение 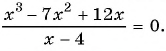
Используем условие равенства дроби нулю:
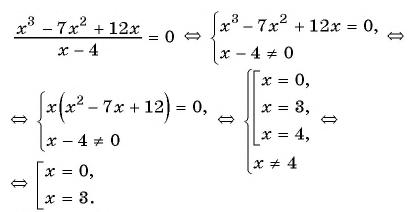
Ответ: 0; 3.
Пример №10
Найдите корни уравнения
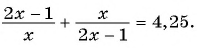
Решение:
Выполним замену переменной в данном уравнении: 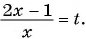 Получим уравнение
Получим уравнение 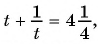 которое является дробно-рациональным.
которое является дробно-рациональным.
Решим его:
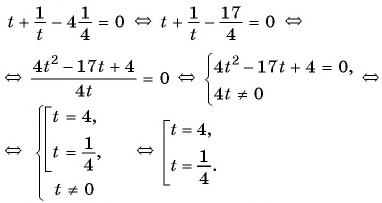
Выполним подстановку найденных значений переменной 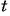 и получим:
и получим:
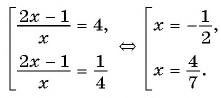
Ответ: 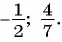
Моделирование реальных процессов с помощью дробно-рациональных уравнении
Задача:
Катер прошел 15 км по течению реки и 4 км по озеру, затратив на весь путь 1 ч. Чему равна скорость катера при движении по озеру, если скорость течения реки 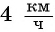 ?
?
Решение:
В задаче идет речь о процессах движения катера по реке и по озеру. Составим таблицу зависимостей между величинами.

Так как по условию задачи на весь путь затрачен 1 ч, то составим уравнение: 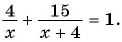 Решим его:
Решим его: 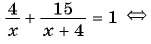
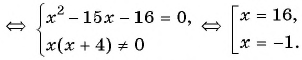
По условию подходит число 16.
Ответ: 16 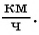
Системы нелинейных уравнений для решения дробно-рациональных уравнений
Рассмотрим задачу. Из листа картона прямоугольной формы нужно изготовить коробку без крышки, сделав надрезы в углах длиной 4 см (рис. 67). Найдите длину и ширину листа, зная, что его периметр равен 60 см, а объем коробки должен быть равен 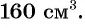
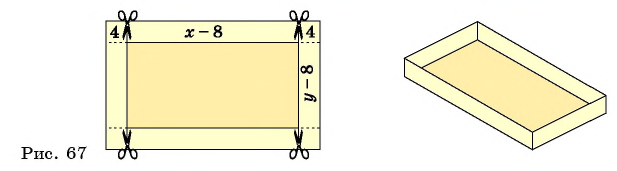
Решение:
Обозначим длину и ширину листа соответственно 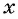 см и
см и 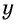 см. Так как в углах листа сделаны надрезы длиной 4 см, то высота коробки равна 4 см, а длина и ширина коробки равны
см. Так как в углах листа сделаны надрезы длиной 4 см, то высота коробки равна 4 см, а длина и ширина коробки равны 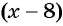 см и
см и  см соответственно.
см соответственно.
По условию задачи периметр листа прямоугольной формы равен 60 см, а объем коробки равен 160 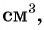 значит,
значит, 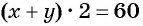 и
и 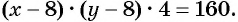 Оба полученных условия должны быть выполнены, поэтому объединим их в систему уравнений
Оба полученных условия должны быть выполнены, поэтому объединим их в систему уравнений 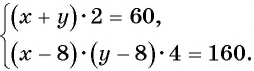
Полученная система уравнений содержит нелинейное рациональное уравнение 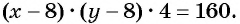 Такие системы называют системами нелинейных уравнений. Рассмотрим способы решения систем нелинейных уравнений.
Такие системы называют системами нелинейных уравнений. Рассмотрим способы решения систем нелинейных уравнений.
Способ подстановки
Решим полученную в задаче систему уравнений способом подстановки:
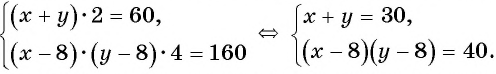
Из первого уравнения системы выразим переменную 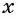 и получим
и получим 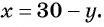
Заменим во втором уравнении переменную 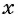 на
на 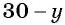 и получим уравнение
и получим уравнение 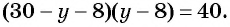 Решим это уравнение:
Решим это уравнение:
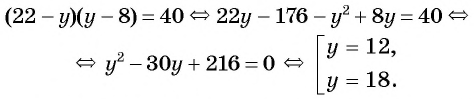
Найденные значения 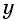 подставим в выражение
подставим в выражение 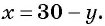 Тогда если
Тогда если 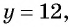 то
то 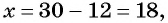 а если
а если 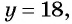 то
то 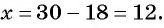
Решениями системы уравнений являются пары чисел 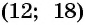 и
и 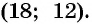 Таким образом, размер прямоугольного листа картона
Таким образом, размер прямоугольного листа картона 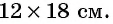
Чтобы решить систему уравнений способом подстановки, нужно:
- Из одного уравнения системы выразить одну из переменных.
- Заменить в другом уравнении эту переменную на ее выражение.
- Решить полученное уравнение.
- Найденные значения одной переменной подставить в выражение для другой переменной и найти значение другой переменной.
- В виде упорядоченных пар чисел записать ответ.
Решите систему уравнений
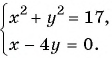
Решение:
(1) Из второго уравнения системы выразим переменную 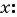
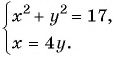
(2) Заменим в первом уравнении переменную 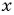 на
на 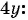
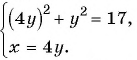
(3) Решим уравнение 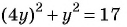 и получим:
и получим: 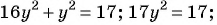
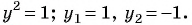
(4) Найденные значения 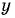 подставим в выражение
подставим в выражение 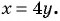
Если 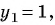 то
то 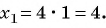
Если 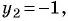 то
то 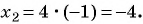
(5) Ответ: (4; 1), (-4; -1).
Способ сложения
Чтобы решить систему уравнений способом сложения, нужно:
- Одно из уравнений системы оставить без изменения, а другое заменить суммой уравнений системы.
- Из полученного уравнения (суммы) найти значения одной из переменных.
- Подставить эти значения переменной в оставленное без изменения уравнение системы и найти значения другой переменной.
- Записать ответ.
Решите систему уравнений
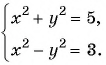
Решение:
(1) 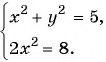
(2) 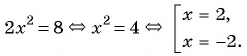
(3) При 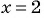 получим:
получим:
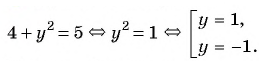
При 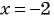 получим:
получим:
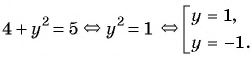
(4) Ответ: (2;1), (2;-1), (-2;1), (-2;-1).
- Заказать решение задач по высшей математике
Графический метод решения систем нелинейных уравнений
Решим систему уравнений 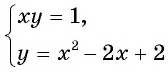 графическим методом. Для этого построим в одной системе координат графики каждого из уравнений системы.
графическим методом. Для этого построим в одной системе координат графики каждого из уравнений системы.
Первое уравнение системы равносильно уравнению 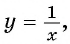 графиком которого является гипербола, проходящая через точки (1; 1), (0,5; 2) (рис. 68).
графиком которого является гипербола, проходящая через точки (1; 1), (0,5; 2) (рис. 68).
Графиком второго уравнения системы 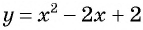 является парабола с вершиной в точке (1; 1), пересекающая ось ординат в точке (0; 2).
является парабола с вершиной в точке (1; 1), пересекающая ось ординат в точке (0; 2).
Единственная точка пересечения гиперболы 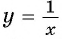 и параболы
и параболы 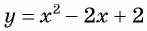 имеет координаты (1; 1).
имеет координаты (1; 1).
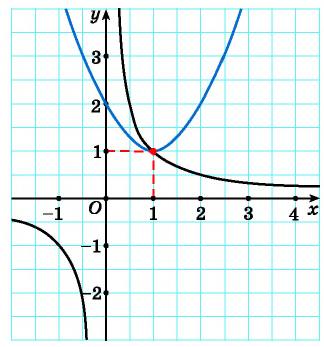
Рис. 68
Поскольку графический метод решения систем уравнений не является точным, то полученный результат необходимо проверить.
Подставим пару чисел (1; 1) в каждое из уравнений системы 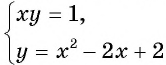 , и получим верные равенства. Таким образом, данная система имеет единственное решение (1; 1).
, и получим верные равенства. Таким образом, данная система имеет единственное решение (1; 1).
В рассмотренной системе решением оказалась пара целых чисел, которую легко было найти с помощью построенных графиков. В других случаях найти точные значения переменных по графику может оказаться затруднительно. Но, как правило, с помощью графического метода можно определить число решений системы уравнений.
Например, определим число решений системы уравнений 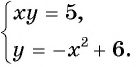 Построим в одной системе координат графики каждого из уравнений системы (рис. 69). Графиком первого уравнения системы является гипербола, проходящая через точки (1; 5), (5; 1). Графиком второго уравнения – парабола, ветви которой направлены вниз, с вершиной в точке (0; 6). Графики пересекаются в трех точках, значит, система уравнений имеет три решения.
Построим в одной системе координат графики каждого из уравнений системы (рис. 69). Графиком первого уравнения системы является гипербола, проходящая через точки (1; 5), (5; 1). Графиком второго уравнения – парабола, ветви которой направлены вниз, с вершиной в точке (0; 6). Графики пересекаются в трех точках, значит, система уравнений имеет три решения.
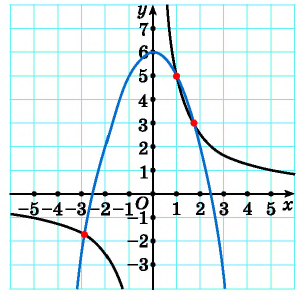
Рис. 69
Моделирование реальных процессов с помощью систем нелинейных уравнений
Системы нелинейных уравнений также являются математическими моделями при решении задач.
Задача:
Лечебными травами было решено засеять прямоугольный участок площадью 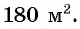 При вспашке участка одну его сторону уменьшили на 3 м, а другую — на 2 м. Его площадь стала равна
При вспашке участка одну его сторону уменьшили на 3 м, а другую — на 2 м. Его площадь стала равна 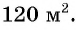 Какими были первоначальные размеры участка?
Какими были первоначальные размеры участка?
Решение:
В задаче речь идет о длине и ширине прямоугольного участка и его площади.
Если одну сторону участка обозначить через 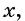 а другую — через
а другую — через 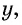 то планируемая площадь участка равна
то планируемая площадь участка равна 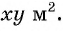 По условию она равна
По условию она равна 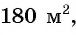 значит, получится уравнение
значит, получится уравнение 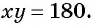
После уменьшения размеров участка площадь станет равной 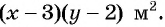 По условию задачи составим уравнение
По условию задачи составим уравнение 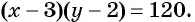
Объединим оба уравнения в систему 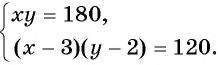
Получили математическую модель задачи в виде системы нелинейных уравнений. Решим ее, используя способ подстановки.
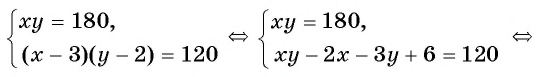
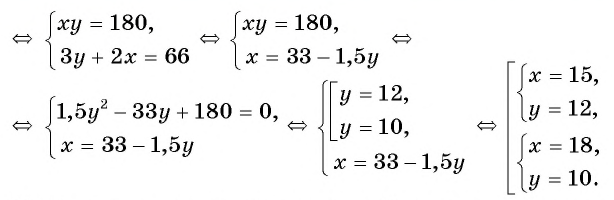
Условию задачи удовлетворяют найденные решения системы: стороны участка равны либо 15 м и 12 м, либо 18 м и 10 м.
Ответ: 15 м, 12 м или 18 м, 10 м.
Пример №11
Решите систему уравнений:
а) 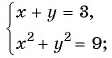
б) 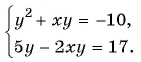
Решение:
а) Решим систему способом подстановки:
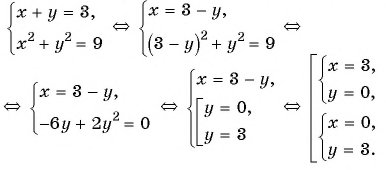
Ответ: (3; 0), (0; 3).
б) Применим способ сложения. Умножим первое уравнение на 2, сложим со вторым и получим:
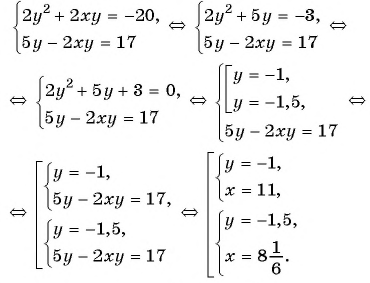
Ответ: 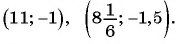
Пример №12
Решите графически систему уравнений
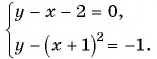
Решение:
Построим графики уравнений системы
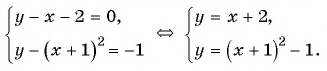
График первого уравнения — прямая, проходящая через точки (-2; 0), (1; 3). График второго уравнения — парабола с вершиной в точке (-1; -1), пересекающая ось абсцисс в точках (-2; 0) и (0; 0), проходящая через точку (1; 3). 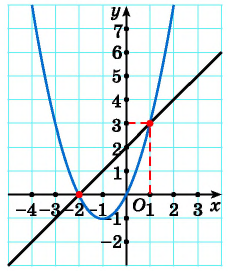
Прямая пересекается с параболой в точках с координатами (-2; 0), (1; 3). С помощью проверки убеждаемся, что пары чисел (-2; 0) и (1; 3) являются решениями данной системы.
Ответ: (-2; 0), (1; 3).
Пример №13
Сколько решений имеет система уравнений 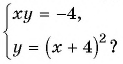
Решение:
Построим в одной системе координат графики уравнений системы. Графиком первого уравнения системы является гипербола, проходящая через точки (-1; 4), (-4; 1). График второго уравнения — парабола с вершиной в точке (-4; 0), пересекающая ось ординат в точке (0; 16).
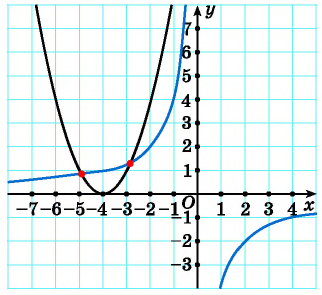
На рисунке видны только две точки пересечения графиков. Но, учитывая то, что парабола пересекает ось ординат, а гипербола не пересекает, делаем вывод, что графики пересекаются еще в одной точке. Таким образом, графики пересекаются в трех точках, а, значит, система имеет три решения.
Пример №14
Решите систему уравнений
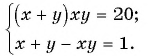
Решение:
Решим систему методом замены переменных. Введем новые переменные: 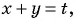
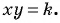
Тогда система примет вид 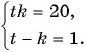
Решим ее способом подстановки:
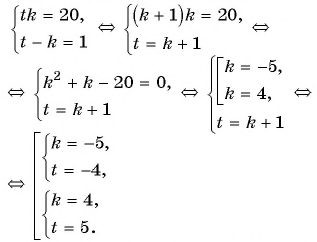
Подставим 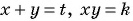 и получим:
и получим:
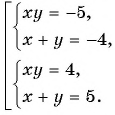
Решив каждую из двух систем совокупности способом подстановки, получим следующие решения исходной системы уравнений: (-5; 1); (1; -5); (4; 1); (1; 4).
Ответ: (-5; 1); (1; -5); (4; 1); (1; 4).
Задача:
Сумма квадратов цифр двузначного числа равна 13. Если из этого числа вычесть 9, то получится число, записанное теми же цифрами, но в обратном порядке. Найдите данное число.
Решение:
Обозначим цифру десятков данного числа через 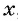 , а цифру единиц через
, а цифру единиц через 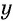 , тогда данное число будет иметь вид
, тогда данное число будет иметь вид 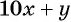 . Числом, записанным теми же цифрами, но в обратном порядке, будет
. Числом, записанным теми же цифрами, но в обратном порядке, будет 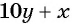 . По условию задачи:
. По условию задачи: 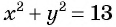 и
и 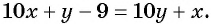 Составим и решим систему уравнений:
Составим и решим систему уравнений:
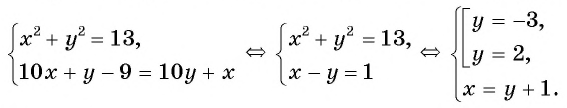
По условию задачи подходит только 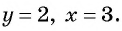
Ответ: 32.
Задача:
Из поселка 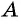 в поселок
в поселок 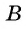 вышел пешеход. Одновременно с ним из поселка
вышел пешеход. Одновременно с ним из поселка 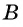 в поселок
в поселок 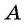 выехал велосипедист. Через 50 мин они встретились. Сколько времени потребовалось бы пешеходу для того, чтобы пройти весь путь из
выехал велосипедист. Через 50 мин они встретились. Сколько времени потребовалось бы пешеходу для того, чтобы пройти весь путь из 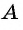 в
в 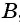 , если известно, что велосипедист проделал бы тот же путь на 4 ч быстрее пешехода?
, если известно, что велосипедист проделал бы тот же путь на 4 ч быстрее пешехода?
Решение:
Составим таблицу зависимостей между величинами.
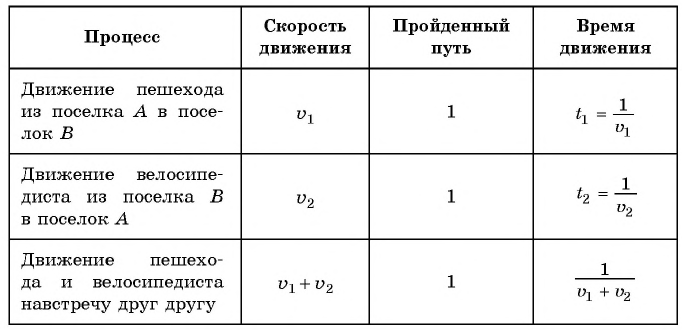
По условию задачи велосипедист проделал бы тот же путь на 4 ч быстрее пешехода, поэтому получим уравнение 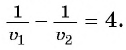
При движении навстречу друг другу пешеход и велосипедист встретились через 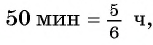 т. е.
т. е. 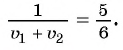
Составим и решим систему уравнений:
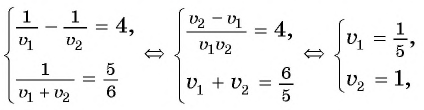 откуда
откуда 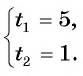
Ответ: 5 ч.
Задача:
Две бригады, работая вместе, ремонтировали дорогу в течение б дней, а затем одна вторая бригада закончила ремонт за 10 дней. За сколько дней могла бы отремонтировать дорогу одна первая бригада, если она может выполнить эту работу на б дней быстрее, чем одна вторая?
Решение:
Составим таблицу зависимостей между величинами.
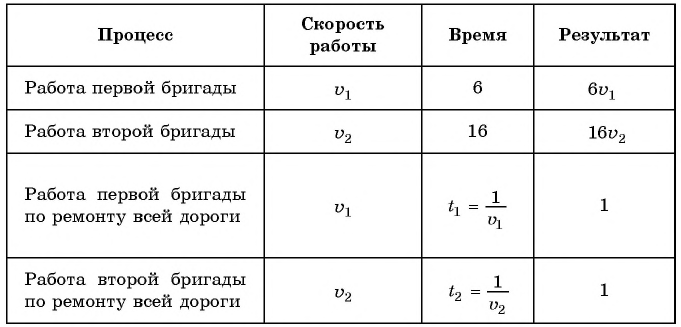
Обозначим объем всей работы через 1, тогда получим уравнение 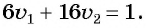
Зная, что одна первая бригада может выполнить эту работу на б дней быстрее, чем одна вторая, составим уравнение 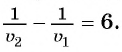
Составим и решим систему уравнений: 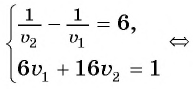
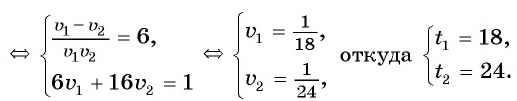
Ответ: 18 ч.
Формула длины отрезка с заданными координатами его концов. Уравнение окружности
Для применения графического метода решения систем необходимо знать графики различных уравнений. Многие из них вам уже знакомы. Это, например, прямая, гипербола, парабола.
Расширим возможности использования графического метода решения систем нелинейных уравнений и выведем уравнение окружности с центром в заданной точке с заданным радиусом. Для этого сначала выведем формулу для вычисления длины отрезка с заданными координатами его концов, т. е. для вычисления расстояния между двумя точками, заданными своими координатами.
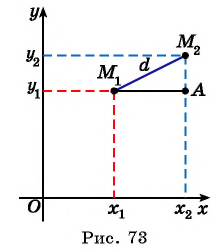
Рассмотрим точки 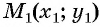 и
и 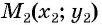 (рис. 73). Найдем расстояние
(рис. 73). Найдем расстояние 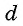 между этими точками (длину отрезка
между этими точками (длину отрезка 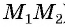 ). Рассмотрим прямоугольный треугольник
). Рассмотрим прямоугольный треугольник 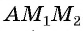 , в котором
, в котором 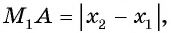
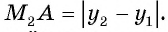 По теореме Пифагора найдем гипотенузу треугольника
По теореме Пифагора найдем гипотенузу треугольника 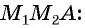
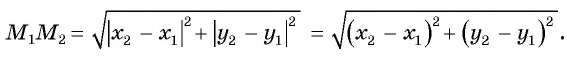
Получили формулу длины отрезка с заданными координатами его концов, или формулу расстояния между двумя точками с координатами 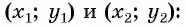
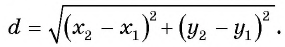
Пример №15
Найдите расстояние между точками А(-1; 3) и В(2; 5).
Решение:
Подставим координаты точек А(-1; 3) и В(2; 5) в формулу расстояния между двумя точками 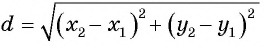 и получим, что
и получим, что
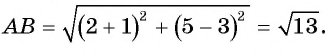
Рассмотрим окружность на координатной плоскости. Окружность — это множество точек плоскости, расстояние от каждой из которых до одной данной точки (центра окружности) является величиной постоянной, равной радиусу окружности 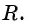
По формуле расстояния между двумя точками найдем расстояние от данной точки 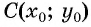 (центра окружности) до произвольной точки окружности
(центра окружности) до произвольной точки окружности 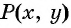 (рис. 74):
(рис. 74):
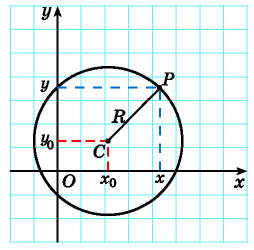
Рис. 74
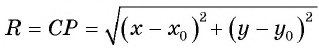 или
или 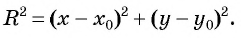
Таким образом, если точка принадлежит окружности с центром 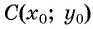 и радиусом
и радиусом 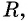 то ее координаты удовлетворяют уравнению
то ее координаты удовлетворяют уравнению 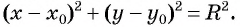
Уравнение 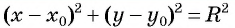 является уравнением окружности с центром в точке
является уравнением окружности с центром в точке 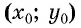 и радиусом
и радиусом 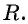
Если координаты точки удовлетворяют уравнению 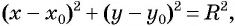 то эта точка принадлежит окружности с центром
то эта точка принадлежит окружности с центром 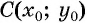 и радиусом
и радиусом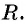
Покажем, что если точка 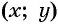 не принадлежит окружности с центром
не принадлежит окружности с центром 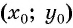 и радиусом
и радиусом 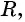 то ее координаты не удовлетворяют уравнению
то ее координаты не удовлетворяют уравнению 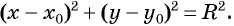 Действительно, если точка лежит вне окружности, то расстояние от нее до центра окружности больше радиуса, т. е.
Действительно, если точка лежит вне окружности, то расстояние от нее до центра окружности больше радиуса, т. е. 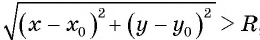 , а если точка лежит внутри окружности, то меньше,
, а если точка лежит внутри окружности, то меньше,
т. е. 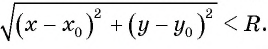
Чтобы составить уравнение окружности, нужно:
- Определить координаты центра окружности
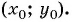
- Определить радиус окружности
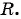
- Подставить найденные значения
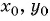 и
и 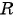 в уравнение окружности
в уравнение окружности 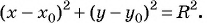
Составьте уравнение окружности с центром в точке (-8; 2) и радиусом 5.
Решение:
(1) 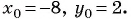
(2) 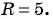
(3) 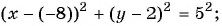
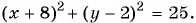
Пример №16
Составьте уравнение окружности:
а) с центром в точке (4; -1) и радиусом 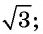
б) с центром в точке (0; 0) и радиусом 4.
Решение:
а) Подставим координаты центра окружности 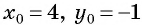 и значение радиуса
и значение радиуса 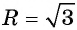 в уравнение окружности
в уравнение окружности 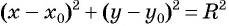 и получим
и получим 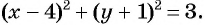
б) Координаты центра окружности: 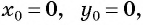 радиус окружности
радиус окружности 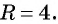 Тогда уравнение данной окружности
Тогда уравнение данной окружности 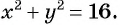
Если центром окружности радиуса 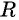 является начало координат, то ее уравнение имеет вид
является начало координат, то ее уравнение имеет вид 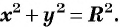
Пример №17
Определите количество решений системы уравнений 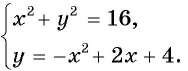
Решение:
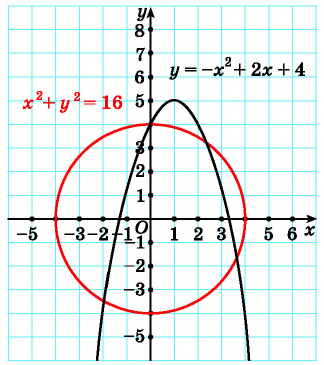
Рис. 75
Построим графики уравнений системы. Первое уравнение — это уравнение окружности с центром в начале координат и радиусом, равным 4. Графиком второго уравнения является парабола с вершиной в точке (1; 5), пересекающая ось ординат в точке (0; 4).
Построенные графики пересекаются в четырех точках (рис. 75). Значит, данная система уравнений имеет 4 решения.
Ответ: 4 решения.
Пример №18
Найдите длину отрезка 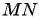 , если
, если 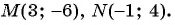
Решение:
По формуле длины отрезка 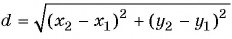 получим:
получим: 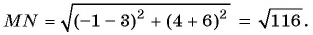
Пример №19
Найдите длину диагонали прямоугольника, если заданы его вершина 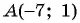 и точка пересечения его диагоналей
и точка пересечения его диагоналей 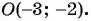
Решение:
Найдем длину отрезка 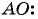
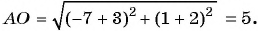
Длина отрезка 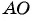 равна половине диагонали прямоугольника, следовательно, длина диагонали равна 10.
равна половине диагонали прямоугольника, следовательно, длина диагонали равна 10.
Пример №20
Определите координаты центра и радиус окружности:
а) 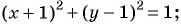
б) 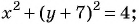
в) 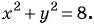
Решение:
а) 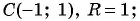
б) 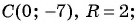
в) 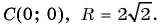
Пример №21
Какие из данных точек лежат на окружности 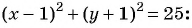
а) 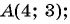
б) 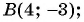
в) 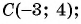
г) 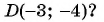
Решение:
Подставим координаты точек в уравнение окружности:
а) 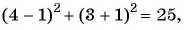 равенство верное, значит, точка
равенство верное, значит, точка 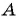 лежит на окружности; б)
лежит на окружности; б) 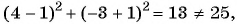 значит, точка
значит, точка 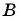 не лежит на окружности;
не лежит на окружности;
в) 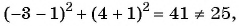 значит, точка
значит, точка 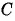 не лежит на окружности;
не лежит на окружности;
г) 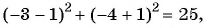 равенство верное, значит, точка
равенство верное, значит, точка 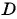 лежит на окружности.
лежит на окружности.
Пример №22
Запишите уравнение окружности с центром в точке (-1; 1) и радиусом 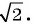
Решение:
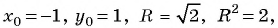
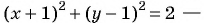 уравнение окружности.
уравнение окружности.
Пример №23
Запишите уравнение окружности с центром в точке 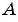 , для которой отрезок
, для которой отрезок 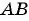 является радиусом, если А(2; 4), В(5; 7).
является радиусом, если А(2; 4), В(5; 7).
Решение:
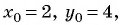 радиус найдем по формуле расстояния между двумя точками:
радиус найдем по формуле расстояния между двумя точками: 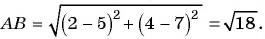
Уравнение окружности 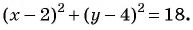
Пример №24
Решите систему уравнений 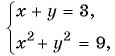 используя графический метод.
используя графический метод.
Решение:
График первого уравнения — прямая, проходящая через точки (3; 0), (0; 3). График второго уравнения — окружность с центром в начале координат и радиусом, равным 3.
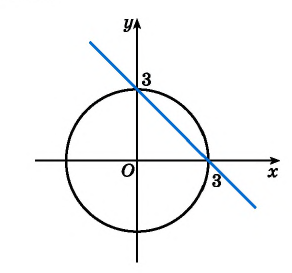
Координаты точек пересечения (3; 0), (0; 3) — решения системы.
- Дробно-рациональные неравенства
- Прогрессии в математике – арифметическая, геометрическая
- Единичная окружность – в тригонометрии
- Определение синуса и косинуса произвольного угла
- Рациональная дробь
- Функция в математике
- Наибольшее и наименьшее значения функции
- Раскрытие неопределенностей
Михеева Светлана Юрьевна
учитель математики
МБОУ МПЛ
Г. Димитровграда, Ульяновской обл.
Класс: 8
Тема урока: Решение задач с помощью дробно-рациональных уравнений.
Урок обобщения знаний.
Деятельностная цель: формирование способности учащихся обобщать и систематизировать знания при решении задач с помощью рациональных уравнений.
Образовательная цель: отработка навыков работы составления уравнений по условию задач.
Задачи:
Образовательные: выработать умение решать задачи с помощью дробно – рациональных уравнений.
Развивающие: вовлечь в активную практическую деятельность, совершенствовать навыки общения.
Воспитательные: формирование уважительного отношения к малой Родине, чувства патриотизма к родной земле, желания трудиться на ней и приносить пользу.
Личностные УУД: ценностное отношение к умению удерживать учебную задачу, осознание учащимися практической и личностной значимости результатов каждого этапа урока, ответственное отношение к результатам своей деятельности.
Регулятивные УУД: умение принимать и сохранять цель урока, умение планировать, контролировать и оценивать свои действия, умение провести рефлексию своих действий на уроке.
Коммуникативные УУД: умение слушать собеседника и вести диалог, высказывать свою точку зрения, правильно говорить, умение преодолевать трудности в учении, используя для этого проблемную ситуацию, умение анализировать, сравнивать, обобщать изучаемый материал.
Ход урока.
-
Вступительное слово учителя. Здравствуйте, коллеги, ребята! Я рада видеть Вас. А чем мы будем заниматься на занятие, вы сможете ответить, решив ребус. Слово задача (Слайд 1). Когда есть задача, должно быть и решение. Решать их можно разными способами. Мы сегодня будем решать задачи с помощью составления дробно-рациональных уравнений (Слайд2)
-
Актуализация знаний. Работа с шестиугольниками -классификация задач.
Работают в группах.
-
Что лежит у вас на столах? Тексты математических задач и шестиугольники. Необходимо быстро и внимательно прочитать задачи и произвести их классификацию с помощью имеющихся шестиугольников. 5 мин
Что вы создали? (кластер) Озвучьте и покажите, что у вас получилось. Есть ли что лишнее? Что вы еще добавили? (Слайд3)
-
Чтобы успешно решать задачи, нужно знать этапы ее решения. Попрошу вас опять составить кластер, используя шестиугольники. Если вы хотите еще что-то добавить, то вписывайте необходимое вам в чистые шестиугольники и используйте их. Заслушать полученные алгоритмы решения задач. 5 мин. Подвести итог. (Слайд 4)
-
Мы сегодня несколько раз применяли слово кластер. Ассоциируется ли оно у вас с нашим городом? В 2010 году в нашем городе начал создаваться …? Ядерно-инновационный кластер.
Что входит в кластер? Центральное место в ядерно-инновационном кластере занимает ядерная наука, а именно с научно исследовательским институтом атомных реакторов. Инновационная медицина, связанная с центром медицинской радиологии (радиологический центр). Мы являемся участниками этого кластера?….????(инновационные кадры) (Слайды 5-7)
-
Давайте вспомним, какие величины содержаться в задачах на движение:
t– время, v – скорость, s– расстояние. Формулы, связывающие их.
Почему задачи на движение по реке выделяют отдельно? (добавляются формулы скорости по течению и против течения реки)(Слайд8)
-
Решение задач
-
Предлагаю решить задачу на движение
Два пациента медицинского радиологического центра выехали на автомобилях одновременно из Екатеринбурга и Минска . Скорость первого на 15 км/ч меньше, чем скорость второго. Найдите скорости автомобилей, если известно, что пациент из Минска приехал в центр на 6 ч 40 мин позже.
–Внимательно прочитали задачу? Ничего не смущает? Важно ли нам названия городов при решении задач? Что необходимо знать?(Расстояние между городами). Екатеренбург-Димитровград-750 км, Минск-Димитровград-1500 км.
-Что еще хочется сделать? (перевести время в часы)
Составьте таблицу и уравнение к решению задачи. Изобразите на листах. (Слайд 9,10,11)
Обсуждение решения
-
Специалисты какого профиля будут востребованы с вашей точки зрения? ВСЕ. На данный момент времени это строители, специалисты внутренней отделки помещений и т.п
Задачи на работу содержат какие величины?:
t– время, в течение которого производится работа,
p – производительность труда, работа, произведенная в единицу времени (возможны и другие обозначения N, W);
A– работа, произведенная за время t(Слайд 12)
3) Две бригады, работая вместе, могут выполнить задание по внутренней отделке радиологического центра за 20 дней. За сколько дней может выполнить задание каждая из них, работая самостоятельно, если одной из них для этого надо на 9 дней больше, чем другой?(Слайд 13, 14)Обсуждение решения
-
Придумать задачу по таблице
|
А=vt |
v |
t |
A |
|
I |
|
x-6 |
1 |
|
II |
|
x |
1 |
|
Вместе |
|
4 |
1 |
-
Придумать задачу по уравнению
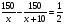 . (Слайд 15)
. (Слайд 15) -
Рефлексия.
Для детей:
+,-,затрудняюсь ответить:
1.Своей работой на занятии в целом я доволен;
2.Своей работой в группе я доволен;
3.Для меня не было подходящего задания;
4.Занятие для меня показалось коротким;
5.За занятие я устал;
6.Мое настроение улучшилось;
7.Материал занятия мне был интересен;
8.Материал занятия мне был полезен;
9.Сегодня на занятии мне было комфортно
Для учителей:
-
Что ожидали увидеть?
-
Я возьму в свою методическую копилку…
-
Мне хочется отметить…
-
Ваши пожелания и рекомендации.
-
Резерв. Два пешехода вышли одновременно навстречу друг другу. Один из НИИАРа, а другой из радиологического центра. Расстояние между этими объектами 6 км. Скорость первого на 1 км/ч больше скорости второго, поэтому он прибыл в радиологический центр на 1 час раньше, чем второй в НИИАР. Определите скорость каждого пешехода.
Для группы взрослых заготовка таблицы.