Правильно сформулированная цель — это половина успеха на пути к её достижению. Часто бывает так: человек или компания ставят вдохновляющие и значимые цели, а спустя время оказывается, что ни одна из них не реализована на 100%. Притом, что усилия для их достижения были существенны. При повторной попытке добиться желаемого результата получается то же самое: цели выбраны, но не достигнуты.
Пример: девушка хочет освоить английский язык. Это откроет для неё новые карьерные перспективы. Из года в год она ставит перед собой цель — выучить английский. Но у неё ничего не получается, хотя она мотивирована и регулярно посещает языковые курсы. Другой пример — компания включает в число своих приоритетных целей рост прибыли, но также не добивается этого.
Почему так происходит? Потому что в обоих случаях нарушена или не выполнена технология постановки целей. Мы привыкли, что технологии применяются в производстве, но они так же работают и в области целеполагания. Когда их нарушаешь, ничего не получается.
В этой статье мы пошагово и подробно расскажем о том, как правильно ставить цели, чтобы они становились достижимыми.
Как правильно поставить цель: важные моменты
Технологии постановки целей относятся к сфере управления, при этом не важно чем и кем 😉 Это может быть управление проектом, бизнесом или своей жизнью. Существует большое количество методик целеполагания, рассказывающих, как формулировать цели и расставлять приоритеты в личной жизни и бизнесе.
Эта статья посвящена одной конкретной проблеме – как правильно поставить цель, чтобы она наконец-то покорилась. Прежде, чем перейти непосредственно к теме, расскажем об основных принципах постановки целей:
1. Конкретность и измеримость. Ваша цель должна быть предельна конкретна. Это касается и бизнеса, и здоровья, и личной жизни. Её нужно сформулировать максимально точно, без витиеватых формулировок, неясных моментов и двойственных трактовок. Она должна быть понятна всем, кто участвует в процессе её реализации.
| Плохо | Хорошо |
| Хорошо знать английский язык. | Свободное общение с носителями английского языка — «продвинутый уровень». |
2. Актуальность. Цель должна быть по-настоящему значима для вас или вашей организации. В необходимость её реализации нужно верить и желать этого.
| Плохо | Хорошо |
|
Мне нужно выучить английский, потому что, не зная его, я не смогу вырасти в должности. |
Я хочу выучить английский, потому что это откроет для меня новые горизонты, изменит мою жизнь. С помощью языка я получу новую интересную работу с высоким статусом, заведу новые знакомства, смогу путешествовать. Мои родители будут мной гордиться. |
3. Определённость во времени. Даже самая масштабная цель должна иметь конкретную дату реализации. Определение срока, когда вы должны добиться желаемого результата, поможет точнее определить и управлять необходимыми ресурсами.
| Плохо | Хорошо |
| Выучить английский к 2020 году | К 31 декабря 2019 года я сдала экзамен по курсу В1. |
4. Достижимость. В момент формулирования цель может казаться недостижимой, однако это не должно быть препятствием. Формулируя свою цель или цели, Вы делаете первый шаг. Следующие шаги – это определение необходимых ресурсов и действий, ведущих к её достижению.
При этом следует учитывать, что есть граница между тем, что возможно достичь, и фантазиями, оторванными от реальности. Допустим, Вы решили поставить перед собой цель в области изучения английского языка. Срок достижения этой цели – 1 год. Она может быть сформулирована следующим образом:
| Плохо | Хорошо |
|
Владеть языком на уровне тех, кто родился и вырос в этой стране. |
Способен поддерживать разговор на бытовом уровне, не совершая лексических и грамматических ошибок. |
Первая формулировка точно не достижима за 1 год, даже если Вы будете учить язык каждый день.
Пошаговый алгоритм постановки целей
Прежде, чем рассмотреть пошаговый алгоритм постановки целей, условимся, что у нас уже есть желание, которое мы хотим реализовать. Например, мы хотим, чтобы наш бизнес вырос в этом году. То есть — Рост бизнеса — это область, в которой мы хотим сформулировать цель, к которой будем стремиться.
Сразу договоримся, что такое Цель?
Цель — это мысленно полученный образ желаемого результата. Другими словами, этот результат уже достигнут в Вашей голове!
Все Ваши последующие шаги будут направлены на то, чтобы превратить мысленный результат в физический аналог.
Итак, вот какие шаги нужно осуществить, чтобы правильно поставить цель. Эти шаги соответствуют критериям правильно сформулированной цели – SMART:
1. Актуальность. Почему для нас актуальна цель в этой области? Например: за последние 3 года рост рынка был выше, чем рост компании и топ-менеджмент осознает, что бизнес теряет свои позиции. Поэтому выбрана область — «Рост бизнеса».
2. Конкретность. Чётко сформулировать то, чего мы хотим. Этот шаг кажется банальным и очевидным, но именно с него всё начинается. Пропускать его нельзя. Пример: мы хотим, чтобы наш бизнес развивался и показывал устойчивый рост. А что такое рост бизнеса в Вашем понимании? Нам надо придумать такую формулировку, чтобы она была понятна всем сотрудникам компании и актуальна на данный момент времени.
Важный момент: в каких показателях может выражаться рост бизнеса? Какие из этих показателей наиболее адекватны в существующей ситуации? Например: открытие новых филиалов, рост численности сотрудников, увеличение физических объемов производства или объема продаж в денежном выражении? А может быть увеличение объема чистой прибыли? Или увеличение количества новых клиентов, с которыми компания начнет работать?
Допустим, что в результате этих размышлений принято решение, что рост бизнеса будем определять через количество новых клиентов, с которыми компания начнет работать в текущем году и увеличение чистой прибыли.
3. Измеримость. Следующий шаг — это сформулировать цели таким образом, чтобы можно было однозначно понимать всем участникам, какой результат мы хотим получить в итоге нашей деятельности.
Сразу стоит отметить, что измеримость формулировки проверяется очень просто: при подведении итогов мы сможем, сравнивая запланированную цель и полученный результат, ответить кратко: Да, достигнута/Нет, не достигнута? Без дополнительных пояснений, что имелось ввиду, когда цель была сформулирована.
Рассмотрим наш пример. Мы выбрали 2 формулировки и теперь опишем их в измеримом виде.
| Можно толковать по разному | Однозначное толкование |
|
Доля продаж по новым клиентам в общем объеме продаж компании составила не менее 25% |
Чистая прибыль по итогам года увеличена не менее, чем на 30 процентов по сравнению с достигнутым значением за предыдущий год. |
Первую формулировку можно толковать по разному: непонятно, объём продаж фиксируется по подписанным контрактам или объём продаж фиксируется по приходу денежных средств на р/счет компании.
4. Достижимость. Далее необходимо определить уровень сложности цели — цель должна быть сложной, но достижимой. Допустим, что компания по итогам прошлого года получила приемлемый размер чистой прибыли.
| Недостижимая | Достижимая |
| По итогам следующего года увеличить размер чистой прибыли в 3 раза. | По итогам следующего года увеличить размер чистой прибыли на 30 процентов. |
Первый вариант выглядит существенно менее достижимым за 1 год, чем второй вариант.
5. Определены сроки достижения цели. В нашем примере срок исполнения выбранных целей – это 31.12.2019
6. Цель необходимо записать. Это очень важный момент, хотя, кажется, простым. Во-первых, мы можем забыть к концу года, какие формулировки выбрали. Во-вторых, когда цель записывается, возникает ощущение обязательства. То есть не просто поговорили на тему целей, а договорились о том, что именно мы хотим получить в итоге нашей совместной деятельности.
Заключение
Первый шаг в реализации целей — это их правильная постановка. Следуя предложенному алгоритму, можно сформулировать цели, как в области бизнеса, так и в области личной жизни.
Второй важный шаг: в момент постановки целей не думать насколько вероятно её достижение. Не стремиться сразу подводить итоги: можем мы её выполнить или нет? Сформулированная цель – это точка, к которой Вам нужно придти через некоторый период времени. И это время Вы потратите на выбор задач и действий, которые необходимо совершить для достижения этой цели.
Поэтому итоги: достигнута или нет, нужно подводить в конце выбранного временного промежутка. При этом, есть некоторая граница между фантазиями и реальностью, однако эту грань Вы проводите сами. Здесь нет четких критериев.
Содержание
- Решение одной задачи несколькими способами алгоритмы
- Алгоритмы
- Алгоритмы. Разработка алгоритма решения задачи
- Базовые алгоритмические конструкции
- Линейные алгоритмы
- Пример
- Разветвляющиеся алгоритмы
- Пример
- Циклические алгоритмы
- Пример
- От сложного к простому: алгоритм гарантированного решения любой задачи
- Система с одинарной петлей
- Петля двойная
- Определение сложных точек
- Пример решения задачи в написании
Решение одной задачи несколькими способами алгоритмы
Всего учащихся в классе : 30
Выполнили верно: 5 чел. – около 17%
Продолжив решать задачи, я погрузилась в поиски других способов решения и вот какие из них мне удалось найти.
Составим уравнение по меди: в куске в 2 кг 100-20=80% меди, т.е. 0.8, а масса меди в этом куске (0,8*2)кг. В куске в 6 кг 100-40=60% меди,т.е. 0.6, масса меди в этом куске (0,6*6) кг. Масса всего сплава 2+6=8 кг.
Пусть х — процентное содержание меди в сплаве.
Составим и решим уравнение:
II способ. Квадрат Пирсона.
Карл Пи́рсон — английский математик, статистик, биолог и философ; основатель математической статистики, один из основоположников биометрики. Автор свыше 650 опубликованных научных работ. В русскоязычных источниках его иногда называют Чарлз Пирсон. Родился 27 марта 1857 г. в Уитбеке, графство Камберленд. После окончания гимназии в Хоуксхеде, Пирсон некоторое время работал школьным учителем в Хоуксхеде, после чего окончил школу в Линкольне. С юных лет увлёкся астрономией, самостоятельно сконструировал астрономические часы и модель Солнечной системы , которую использовал для публичных лекций. Пирсон в 1793 году поступил в Клэр-колледж Кембриджского университета, где из-за материальных трудностей получил статус sizar (студент, который получает определенную форму помощи, такие как питание, более низкие ставки сборов или жилье во время своего периода обучения), но, по-видимому, университет не окончил.
В 1817 году лорд-канцлер Элдон предоставил Пирсону должность пастора в Саут-Килворте, графство Лестершир.
С 1810 года У.Пирсон преподавал в частной школе для мальчиков в лондонском районе Ист-Шин, где создал астрономическую обсерваторию, в которой, в частности, измерил диаметры Солнца и Луны во время частного солнечного затмения 7 сентября 1820 года, с помощью одного из микрометров, изготовленных Д.Доллондом. Основание астрономического общества в Лондоне (позже — Королевского астрономического общества) во многом осуществилось благодаря усилиям У.Пирсона. Пирсон участвовал в разработке Устава и служил его казначеем в течение первых десяти лет существования общества. В 1819 году он был избран членом Королевского общества и получил степень Legum Doctor (почётного доктора права).
В 1821 году У. Пирсон оставил работу в школе в Ист-Шин и организовал постройку обсерватории в Саут-Килворте, графство Лестершир.
В обсерватории в Саут-Килворте Пирсон наблюдал покрытие Плеяд в июле и октябре 1821 года. В 1824 и 1829 он опубликовал 2-томный труд Введение в практическую астрономию ( Introduction to Practical Astronomy ). В первом томе в основном содержатся таблицы редукции . Во втором томе представлены сложные описания и изображения различных астрономических инструментов (рисунки Дж. Фарея и гравюры Э.Террела) с инструкциями по их использованию. Пирсон получил золотую медаль Королевского астрономического общества 13 февраля 1829 за публикацию, которую сэр Джон Гершель называл «одной из самых важных и обширных работ по этому вопросу, который когда-либо был опубликован».
В 1830 году Пирсон был назначен в состав совета Королевской обсерватории в Гринвиче. В том же году при содействии деревенского математика Амвросия Кларка, Пирсон начал наблюдения и расчет покрытий 520 звезд. Он представил полученный каталог Королевскому астрономическому обществу 11 июня 1841 года.
Пирсон наблюдал комету Галлея 29 октября 1835 года, а в 1839 году он вывел значение величины наклонения эклиптики на основе собственных наблюдений.
У.Пирсон умер 6 сентября 1847 года в Саут-Килворте, в его честь установлена мемориальная табличка на местной церкви.
Как составить Квадрат Пирсона? Нужно записать массовые доли вещества в исходных растворах одну под другой (их обозначают ɷ1 и ɷ2). Справа от них записывают их массовую долю (ɷ3) в растворе, который нужно получить и вычитают по диагонали из большего числа меньшее. Еще правее записывают исходную массу каждого раствора ( m 1 — масса первого раствора, m 2 — масса второго раствора).
Теперь по этому алгоритму записываем наше условие:
Пусть х % — концентрация конечного сплава, тогда
Источник
Алгоритмы
Алгоритмы. Разработка алгоритма решения задачи
Исключительно важно использовать язык блок-схем при разработке алгоритма решения задачи. Решение одной и той же задачи может быть реализовано с помощью различных алгоритмов, отличающихся друг от друга как по времени счета и объему вычислений, так и по своей сложности. Запись этих алгоритмов с помощью блок-схем позволяет сравнивать их, выбирать наилучший алгоритм, упрощать, находить и устранять ошибки.
Отказ от языка блок-схем при разработке алгоритма и разработка алгоритма сразу на языке программирования приводит к значительным потерям времени, к выбору неоптимального алгоритма. Поэтому необходимо изначально разработать алгоритм решения задачи на языке блок-схем, после чего алгоритм перевести на язык программирования.
При разработке алгоритма сложной задачи используется метод пошаговой детализации. На первом шаге продумывается общая структура алгоритма без детальной проработки отдельных его частей. Блоки, требующие детализации, обводятся пунктирной линией и на последующих шагах разработки алгоритма продумываются и детализируются.
В процессе разработки алгоритма решения задачи можно выделить следующие этапы:
- Этап 1 . Математическое описание решения задачи.
- Этап 2 . Определение входных и выходных данных.
- Этап 3 . Разработка алгоритма решения задачи.
Базовые алгоритмические конструкции
В теории программирования доказано, что для записи любого, сколь угодно сложного алгоритма достаточно трех базовых структур:
- следование (линейный алгоритм);
- ветвление (разветвляющийся алгоритм);
- цикл-пока (циклический алгоритм).
Линейные алгоритмы
Линейный алгоритм образуется из последовательности действий, следующих одно за другим. Например, для определения площади прямоугольника необходимо сначала задать длину первой стороны, затем задать длину второй стороны, а уже затем по формуле вычислить его площадь.
Пример
ЗАДАЧА. Разработать алгоритм вычисления гипотенузы прямоугольного треугольника по известным значениям длин его катетов a и b.
На примере данной задачи рассмотрим все три этапа разработки алгоритма решения задачи:
Этап 1. Математическое описание решения задачи.
Математическим решением задачи является известная формула:

где с-длина гипотенузы, a, b – длины катетов.
Этап 2. Определение входных и выходных данных.
Входными данными являются значения катетов a и b. Выходными данными является длина гипотенузы – c.
Этап 3. Разработка алгоритма решения задачи.
На данной схеме цифрами указаны номера элементов алгоритма, которые соответствуют номерам пунктов словесного описания алгоритма.
Разветвляющиеся алгоритмы
Алгоритм ветвления содержит условие, в зависимости от которого выполняется та или иная последовательность действий.
Пример
ЗАДАЧА. Разработать алгоритм вычисления наибольшего числа из двух чисел x и y.
Этап 1. Математическое описание решения задачи.
Из курса математики известно, если x > y, то наибольшее число x, если x y, то переход к шагу 6, иначе к шагу 7.
В схеме алгоритма решения задачи цифрами указаны номера элементов алгоритма, которые соответствуют номерам шагов словесного описания алгоритма
В рассматриваемом алгоритме (рис.3) имеются три ветви решения задачи:
- первая: это элементы 1, 2, 3, 4, 8.
- вторая: это элементы 1, 2, 3, 5, 6, 8
- третья: это элементы 1, 2, 3, 5, 7, 8.
Выбор ветви определяется значениями x и y в элементах 3 и 5, которые являются условиями, определяющими порядок выполнения элементов алгоритма. Если условие (равенство), записанное внутри символа «решение», выполняется при введенных значениях x и y, то следующими выполняется элементы 4 и 8. Это следует из того, что они соединены линией с надписью «да» и направление (последовательность) вычислений обозначена стрелочкой.
Если условие в элементе 3 не выполняется, то следующим выполняется элемент 5. Он соединен с элементом 3 линией с надписью «нет». Если условие, записанное в элементе 5, выполняется, то выполняется элементы 6 и 8, в противном случае выполняются элементы 7 и 8.
Циклические алгоритмы
Циклический алгоритм – определяет повторение некоторой части действий (операций), пока не будет нарушено условие, выполнение которого проверяется в начале цикла. Совокупность операций, выполняемых многократно, называется телом цикла.
Алгоритмы, отдельные действия в которых многократно повторяются, называются циклическими алгоритмами, Совокупность действий, связанную с повторениями, называют циклом.
При разработке алгоритма циклической структуры выделяют следующие понятия:
- параметр цикла – величина, с изменением значения которой связано многократное выполнение цикла;
- начальное и конечное значения параметров цикла;
- шаг цикла – значение, на которое изменяется параметр цикла при каждом повторении.
Цикл организован по определенным правилам. Циклический алгоритм состоит из подготовки цикла, тела цикла и условия продолжения цикла.
В подготовку цикла входят действия, связанные с заданием исходных значений для параметров цикла:
- начальные значения цикла;
- конечные значения цикла;
- шаг цикла.
В тело цикла входят:
- многократно повторяющиеся действия для вычисления искомых величин;
- подготовка следующего значения параметра цикла;
- подготовка других значений, необходимых для повторного выполнения действий в теле цикла.
В условии продолжения цикла определяется допустимость выполнения повторяющихся действий. Если параметр цикла равен или превысил конечное значение цикла, то выполнение цикла должно быть прекращено.
Пример
ЗАДАЧА. Разработать алгоритм вычисления суммы натуральных чисел от 1 до 100.
Этап 1. Математическое описание решения задачи.
Обозначим сумму натуральных чисел через S. Тогда формула вычисления суммы натуральных чисел от 1 до 100 может быть записана так:
где Xi – натуральное число X c номером i, который изменяется от 1 до n, n=100 – количество натуральных чисел.
Этап 2. Определение входных и выходных данных.
Входными данными являются натуральные числа: 1, 2, 3, 4, 5, …, 98, 99, 100.
Выходные данные – значение суммы членов последовательности натуральных чисел.
Параметр цикла – величина, определяющая количество повторений цикла. В нашем случае i – номер натурального числа.
Подготовка цикла заключается в задании начального и конечного значений параметра цикла.
- начальное значение параметра цикла равно 1,
- конечное значение параметра цикла равно n,
- шаг цикла равен 1.
Для корректного суммирования необходимо предварительно задать начальное значение суммы, равное 0.
Тело цикла. В теле цикла будет выполняться накопление значения суммы чисел, а также вычисляться следующее значение параметра цикла по формулам:
Условие продолжения цикла: цикл должен повторяться до тех пор, пока не будет добавлен последний член последовательности натуральных чисел, т.е. пока параметр цикла будет меньше или равен конечному значению параметра цикла.
Этап 3. Разработка алгоритма решения задачи.
Введем обозначения: S – сумма последовательности, i – значение натурального числа.
Начальное значение цикла i=1, конечное значение цикла i =100, шаг цикла 1.
Источник
От сложного к простому: алгоритм гарантированного решения любой задачи
Достаточно часто люди ставят перед собой задачи, но при этом не знают, как их решить. Каждый человек пытается самостоятельно найти решение данной проблемы. Программист Дэвид Макайвер делится своими методами решения сложных задач.

По мнению Макайвера, его система позволяет освоить то, что на первый взгляд является сложным. Для того чтобы добиться успеха в чем-либо Дэвид часто использует свою систему, но не всегда придерживается всех правил. Его система является беспроигрышной в любом случае, но время на выполнение задачи зависит от многих факторов. Суть данной системы заключается в том, что вы в любом случае получите определенную выгоду, даже если не достигнете конечной цели.
Система с одинарной петлей
Эта система подойдет тем, кто знает, что такое успех, но на данный момент он его не достиг. Как это работает:
- Найдите легкую задачу, которая на первый взгляд кажется трудной.
- Найдите что-то общее между легкой и трудной схожей задачей.
- Продолжайте видоизменять задачу до тех пор, пока она не станет максимально простой.
- Если вам не удалось превратить сложную задачу в простую, постарайтесь рассмотреть ее под другим углом. Также можно воспользоваться советом специалиста в определенной отрасли.
- Если вам не удалось достичь желаемого, просто вернитесь ко второму пункту.
Данная система прекрасно работает благодаря отличному видению всего процесса обратной связи. Для того, чтобы становиться лучше в каком-то деле, необходимо сосредоточиться на одном аспекте, откинув все остальное. Обращая внимание сразу на несколько аспектов, вы упускаете возможность достичь успеха.
Петля двойная
В случае невозможности представления окончательного результата придется копнуть несколько глубже и провести двойную работу:
- Сразу вам нужно воспользоваться предыдущей системой, чтобы лучше понять суть проблемы.
- Примените одну петлю по отношению к проблеме, воспользовавшись своим чувством вкуса.
- Обязательно получите отзыв со стороны о вашей проделанной работе.
Определение сложных точек
Часто понять то, что нужно улучшить, просто, однако, бывают ситуации, когда человек не может разобраться в данном вопросе. Чтобы лучше сориентироваться и увидеть очевидное, вам потребуется:
- Максимально приложить усилия, чтобы выполнить задачу наилучшим образом. Не переживайте, если вас настигнет неудача, так как подобное явление бывает часто во многих начинаниях. В решении данного вопроса вам поможет список, где вы сможете указать, что сделали хорошо и плохо. Если вы не можете решить проблему, значит вам надо ознакомиться со списком и понять, где именно вы совершили ошибку.
- Не пренебрегайте упражнениями в той области, которую вы начали изучать. Обратите внимание на то, что вам дается очень сложно.
- Обратитесь за помощью к специалисту, который поможет вам разобраться с тем, в чем следует потренироваться.
- Не стоит тратить время на простые задачи, лучше выбирайте сложные и старайтесь максимально их облегчить. Не бойтесь мыслить от простого к сложному и наоборот.
Пример решения задачи в написании
Научиться хорошо писать сложно, ведь этот процесс подразумевает множество пунктов, среди которых:
- процесс написания;
- поиск своего собственного стиля;
- невозможность начать из-за боязни насмешек со стороны окружающих;
- редактирование написанного.
Уже после упоминания этих основных моментов можно подумать и о менее важных. Что вам нужно:
- научиться печатать вслепую;
- использовать свой собственный голос, например, для записи текста на диктофон;
- не ожидать изначально от своих тестов высочайшего качества;
- не стараться отредактировать текст в целом, а лучше обращать внимание на конкретные вещи.
Существует немало примеров того, что следует попробовать, однако, для начала вам нужно выбрать исходную точку и следовать к своим целям. Четко поставленные цели и осознание необходимости их достижения – залог решения даже самых сложных задач. Курс Викиум «Целеполагание» как раз эффективно обучает постановке целей.
Источник
Adblock
detector
| Словесное описание алгоритма | Запись алгоритма на языке блок-схем |
|
#статьи
- 7 дек 2022
-
0
Что такое алгоритмы и какими они бывают
Ты можешь разрабатывать микросервисы и знать все уровни модели OSI, но какой ты программист, если не можешь объяснить ребёнку, что такое алгоритм?
Иллюстрация: Катя Павловская для Skillbox Media
Пишет об истории IT, разработке и советской кибернетике. Знает Python, JavaScript и немного C++, но предпочитает писать на русском.
Ведущий бэкенд-разработчик мобильного приложения «Альфа-Банка».
Иногда совсем простые вопросы о профессии вводят в ступор даже опытных специалистов. Примерно так происходит, когда у разработчика с 5–10-летним стажем спрашивают: «Что такое алгоритм?»
Но для того мы здесь и собрались, чтобы дать понятные ответы на «глупые» вопросы. В этой статье расскажем, что такое алгоритмы, для чего они нужны и какими бывают.
Вы узнаете:
- Что такое алгоритмы
- Для чего их используют
- Какие у них есть свойства
- Что такое псевдокод
- Что такое блок-схемы и как их рисовать
- Примеры линейных, ветвящихся, циклических и рекурсивных алгоритмов и блок-схем
В широком смысле алгоритм — это последовательность действий, которые нужно выполнить, чтобы получить определённый результат.
Слово «алгоритм» произошло от имени персидского математика Абу Абдуллаха аль-Хорезми. В своём труде «Китаб аль-джебр валь-мукабала» учёный впервые дал описание десятичной системы счисления. А наука алгебра получила своё название в честь его книги.
Мы часто пользуемся алгоритмами в повседневной жизни. Например, когда хотим приготовить кофе в капсульной кофемашине, руководствуемся примерно таким алгоритмом:
1. Устанавливаем капсулу.
2. Проверяем уровень воды в специальном отсеке.
3. Если воды недостаточно — доливаем.
4. Ставим чашку под кран кофемашины.
5. Запускаем кофемашину.
6. Выключаем кофемашину, когда чашка наполнилась.
7. Достаём кружку.
Если не перепутать порядок шагов, то с помощью такой инструкции любой сможет порадовать себя чашкой горячего кофе. Достаточно лишь знать, как установить капсулу и включить/выключить кофемашину.
С компьютерами намного сложнее. Им неизвестно, что значит «установить капсулу», «долить воду», «запустить кофемашину» и так далее. Чтобы запрограммировать робота-баристу под определённую модель бытовой техники, алгоритм придётся расписать более детально:
1. Возьми штепсельную вилку шнура питания кофемашины.
2. Вставь штепсельную вилку в розетку.
3. Проверь, есть ли вода в отсеке для воды.
4. Если воды недостаточно:
4.1. Подними крышку отсека.
4.2. Возьми кувшин с водой.
4.3. Лей воду из кувшина в отсек, пока он не заполнится.
4.4. Закрой крышку отсека.
4.5. Поставь кувшин с водой на стол.
5. Открой крышку кофемашины.
6. Возьми из коробки капсулу с кофе.
7. Вставь капсулу в отсек для капсулы.
8. Закрой крышку кофемашины.
9. Поверни рычаг кофемашины вправо.
10. Когда чашка наполнится, поверни рычаг кофемашины влево.
11. Возьми кружку.
12. Принеси кружку хозяину.
Конечно, если мы собираем робота с нуля, то даже такой детализации будет недостаточно. Каждую процедуру ещё нужно будет реализовать на языке программирования (например, на C++ или Python), что само по себе — нетривиальная задача. Тем не менее описание стало более точным и формальным.
C научной точки зрения определение алгоритма, которое мы дали выше, не совсем точное. Ведь не всякую последовательность действий, приводящую к результату, можно назвать алгоритмом.
Алгоритм в информатике — это понятный исполнителю набор правил для решения конкретного множества задач, который получает входные данные и возвращает результат за конечное время.
У алгоритмов есть два замечательных качества: они позволяют эффективно решать задачи и не изобретать решения, которые кто-то уже придумал до нас. Это справедливо как для повседневной жизни, так и для IT.
Представьте, что оформляете загранпаспорт. Если будете всё делать сами и без инструкции, около 40 минут потратите только на выяснение необходимых справок и порядка оформления. Куда проще воспользоваться «Госуслугами», потому что алгоритм там уже составлен — делаете, что вам говорят, и ждёте результат. А ещё проще — обратиться к посреднику, который подготовит все справки и оформит паспорт за неделю.
Это очень бытовой пример, но программирование примерно так и работает. Разработчики изучают алгоритмы, чтобы писать быстрый и эффективный код, — распознают типовую задачу и подбирают для неё оптимальный алгоритм.
Допустим, нужно отсортировать в порядке возрастания числа в списке из 1000 элементов. Можно пройтись по списку 1000 раз: на каждой итерации находить наименьшее число и переставлять его в начало списка. В этом случае общее количество шагов будет равно 1 000 000 — современный компьютер справится с этим за секунду.
А если нужно упорядочить массив из 10 000 000 элементов? Тогда компьютеру придётся выполнить 1014 шагов, что потребует гораздо больше времени. Надо оптимизировать!
Разработчик, не сведущий в computer science, начнёт ломать голову над более эффективным решением. А опытный специалист применит алгоритм быстрой сортировки, который в среднем случае даст «время» 16 × 107 шагов.
Знатоки скажут, что ещё проще было бы воспользоваться библиотечной функцией сортировки (например, sorted() в Python). Тем не менее даже встроенные алгоритмы бывают недостаточно эффективными и разработчикам приходится писать собственные функции для сортировки. Но это уже совсем другая история 🙂
Теперь представьте: вы живёте в XX веке где-нибудь в США и зарабатываете тем, что ездите по городам и продаёте мультимиксеры. Чтобы сэкономить время и деньги, вам нужно придумать кратчайший маршрут, который позволит заехать в каждый город хотя бы один раз и вернуться обратно.
Это знаменитая задача коммивояжёра, для которой практически невозможно подобрать лучшее решение. Простой перебор здесь не поможет. Уже при 10 городах количество возможных маршрутов будет равно 3,6 млн, а при 26 — даже самым мощным компьютерам понадобится несколько миллиардов лет, чтобы перебрать все варианты.
Тем не менее каждый день миллионы устройств решают эту задачу: смартфоны строят маршруты между городами, а маршрутизаторы рассчитывают оптимальный путь для пакетов в сети. Дело в том, что существуют специальные алгоритмы, которые дают неидеальный, но достаточно эффективный результат. И их нужно знать, если вы хотите работать в компаниях, которые создают сложные, интересные проекты.
Информатик и автор классических учебников по программированию Дональд Кнут выделял следующие свойства алгоритмов:
- конечность,
- определённость,
- наличие ввода,
- наличие вывода, или результативность,
- универсальность,
- эффективность.
Рассмотрим каждое подробно.
Конечность. Алгоритм должен решать задачу за конечное число шагов. Необходимость этого критерия очевидна: программа, которая решает задачу бесконечно долго, никогда не приведёт к результату.
Определённость. Исполнитель (компьютер, операционная система) должен однозначно и верно интерпретировать каждый шаг алгоритма.
Наличие ввода. Как и у математической функции, результат работы алгоритма зависит от входных данных. Например, на вход алгоритма сортировки подаётся массив чисел. А функция, рассчитывающая факториал, принимает натуральное число.
Наличие вывода, или результативность. Алгоритм должен выдавать конкретный результат. Например, если мы ищем подстроку в строке и такая подстрока в ней присутствует, то на выходе мы должны получить позицию этой строки. Если такой подстроки нет — алгоритм должен вернуть соответствующее значение, например -1.
Универсальность. Алгоритм должен решать задачи с разными входными данными. Например, хорошая функция для сортировки массивов должна одинаково хорошо справляться с массивами из 10, 100 и 1 000 000 элементов.
Эффективность. Это требование продиктовано ограниченными ресурсами компьютеров. На заре развития вычислительной техники каждая секунда работы процессора, каждый байт памяти были на счету. И хотя современные компьютеры гораздо мощнее своих предшественников, они тоже могут «тормозить» из-за неэффективных алгоритмов.
Представьте, что вы изучили какой-нибудь язык программирования, например Go, и устроились бэкенд-разработчиком в IT-компанию. В вашей команде, помимо бэкендеров, есть фронтенд-разработчики, которые пишут код на JavaScript.
Вы придумали крутой алгоритм, который ускорит работу приложения, и хотите рассказать о нём коллегам. Но как это сделать, если они программируют на другом языке?
Для таких ситуаций есть псевдокод. Он позволяет изложить логику программы с помощью понятных для всех команд, не углубляясь в детали реализации конкретного языка. В учебной литературе алгоритмы описывают в основном с помощью псевдокода.
У псевдокода нет общепринятых стандартов, и авторы используют собственные оригинальные нотации. Хотя часто они заимствуют названия операций из Python, Pascal и Java. Например, код ниже напоминает программу на Python:
int linear_search(int[] arr, int x): if arr is empty: return -1 for i in 0..n: if arr[i] == x: return i return -1
Также псевдокод можно писать на русском языке, как в школьных учебниках по информатике:
ФУНКЦИЯ линейный_поиск(целое[] массив, целое x):
ЕСЛИ массив ПУСТОЙ:
ВЕРНУТЬ -1
ДЛЯ i В ДИАПАЗОНЕ ОТ 0 ДО ДЛИНА(массив):
ЕСЛИ массив[x] РАВНО x:
ВЕРНУТЬ i
ВЕРНУТЬ -1
Главное — чтобы тот, кто читает ваш алгоритм, понял его и воспроизвёл на своём языке программирования.
Если у вас в школе были уроки по информатике, то вы наверняка рисовали и читали блок-схемы. Если нет, то знайте: алгоритмы можно описывать не только словесно, но и графически.
Блок-схемы — это геометрические фигуры, соединённые между собой стрелками. Овалы, прямоугольники, ромбы и другие фигуры обозначают отдельные шаги алгоритма, а стрелки указывают направление потока данных. При этом в каждый блок записывается команда в виде логического или математического выражения.
В таблице ниже представлены основные элементы блок-схем:
Графическое изображение
Значение
Элемент кода в Python
Начало/конец программы
Никак не обозначается
или обозначается как начало функции:
def foo(x): #код
Конец функции обозначается словом return
Ввод/вывод данных
Операторы ввода и вывода:
print("Hello!")
word = input()
Арифметические операции
Арифметические операторы:
100 - 10 25 + 100 6 * 12.0
Условие
Условный оператор:
if n < 5: sum += 10
Цикл со счётчиком
Цикл for:
for k,v in enumerate(arr): print(k, v)
Ввод/вывод в файл
Функции для работы с файлами:
f = open("text.txt", 'r') f.close()
С помощью этого нехитрого набора фигур можно нарисовать схему практически любого алгоритма. Другие фигуры блок-схем вы найдёте в документации к ГОСТ 19.701-90.
Блок-схемы можно рисовать в Microsoft Visio и в Google Docs (Вставка → Рисунок → Новый +). Также есть специальные сервисы: например, облачный Draw.io и десктопные Dia и yEd.
А теперь разберёмся, какими бывают алгоритмы, напишем примеры на Python и нарисуем для них блок-схемы.
По конструкции алгоритмы можно разделить на несколько групп.
В линейных алгоритмах действия идут последовательно, одно за другим. Такие программы — самые простые, но на практике они встречаются редко.
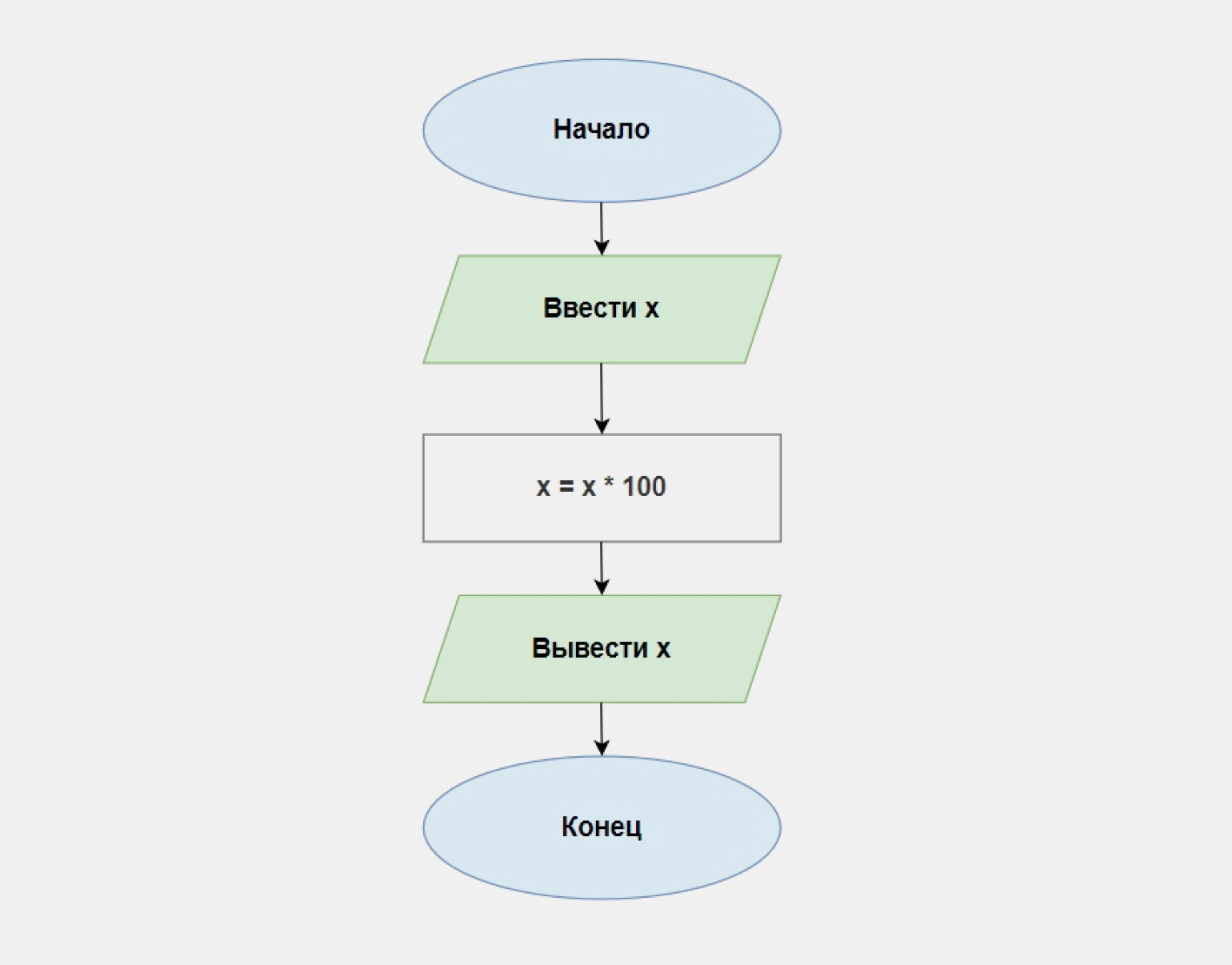
Пример. Напишите программу, которая умножает число, введённое пользователем, на 100 и выводит результат на экран.
Последовательность действий уже изложена в задании: ввести число → умножить на 100 → вывести результат. Переведём это на язык блок-схем:
Ниже приведена реализация алгоритма на языке Python:
x = int(input()) x = x * 100 print(x) >>> 5 >>> 500
В ветвящихся алгоритмах ход программы зависит от значения логического выражения в блоке «Условие». По большому счёту, любое логическое выражение сводится к выбору между истиной (True, «1») или ложью (False, «0»).
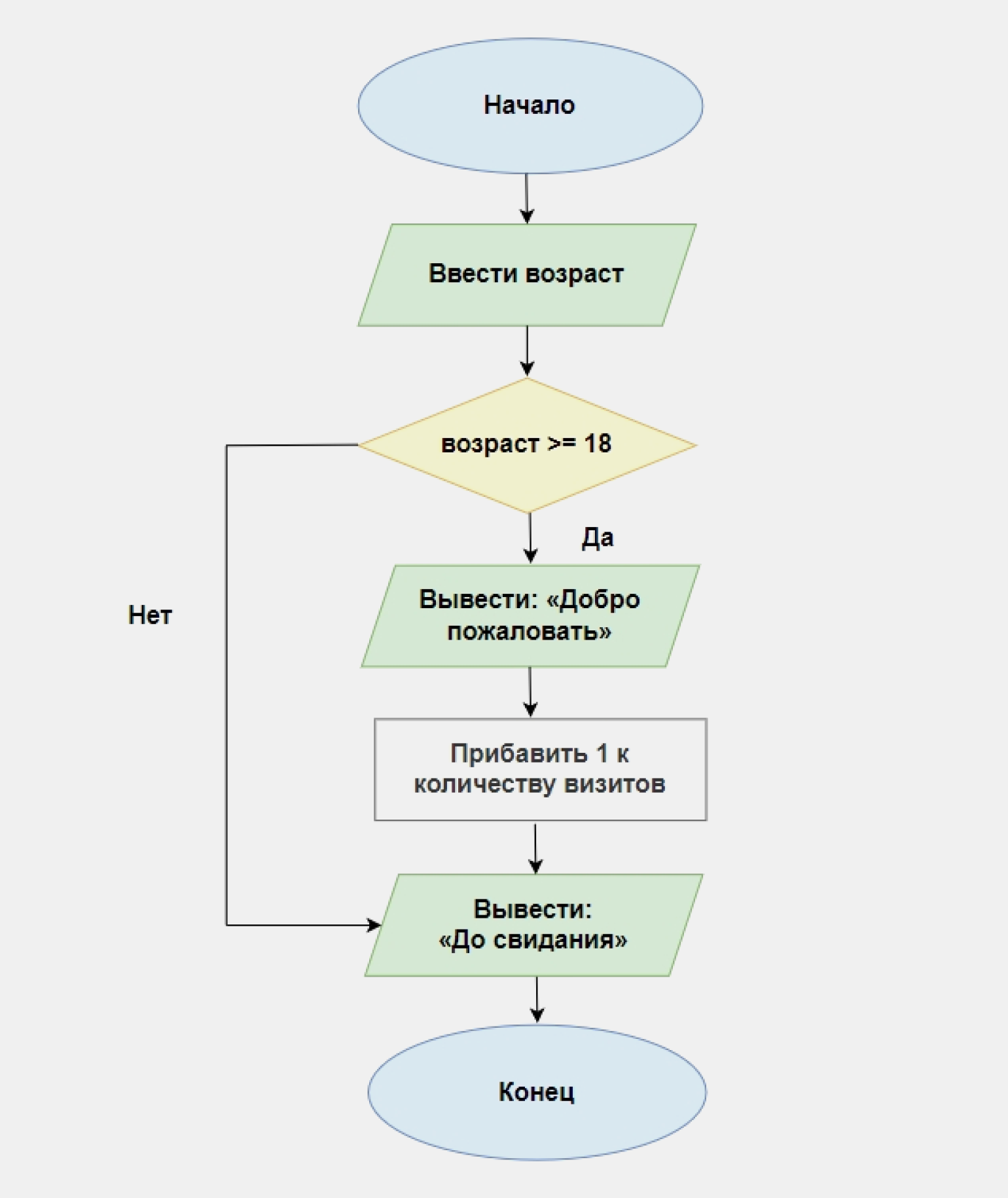
Пример. Напишите программу, которая запрашивает у пользователя возраст. Если он равен или больше 18, программа выводит приветствие, увеличивает значения счётчика посетителей на 1 и прощается, а если меньше — сразу прощается и завершает работу.
Чтобы изобразить ход решения, воспользуемся условным блоком. Во всех схемах его обозначают ромбом с вписанным условием:
То же самое на Python:
visits_counter = 0 answer = int(input("Сколько вам лет? ")) if answer >= 18: print("Добро пожаловать!") visits_counter += 1 else: print("Доступ запрещён")
Когда пользователь вводит 18 или больше, программа выполняет часть кода, которая записана под оператором if. Если же возраст меньше 18, то на экран выводится сообщение «Доступ запрещён» и программа завершает работу.
Такие алгоритмы содержат циклы — наборы действий, которые выполняются несколько раз. Количество повторений может задаваться целым числом или условием. В некоторых случаях, например, в операционных системах и прошивках микроконтроллеров, используются бесконечные циклы.
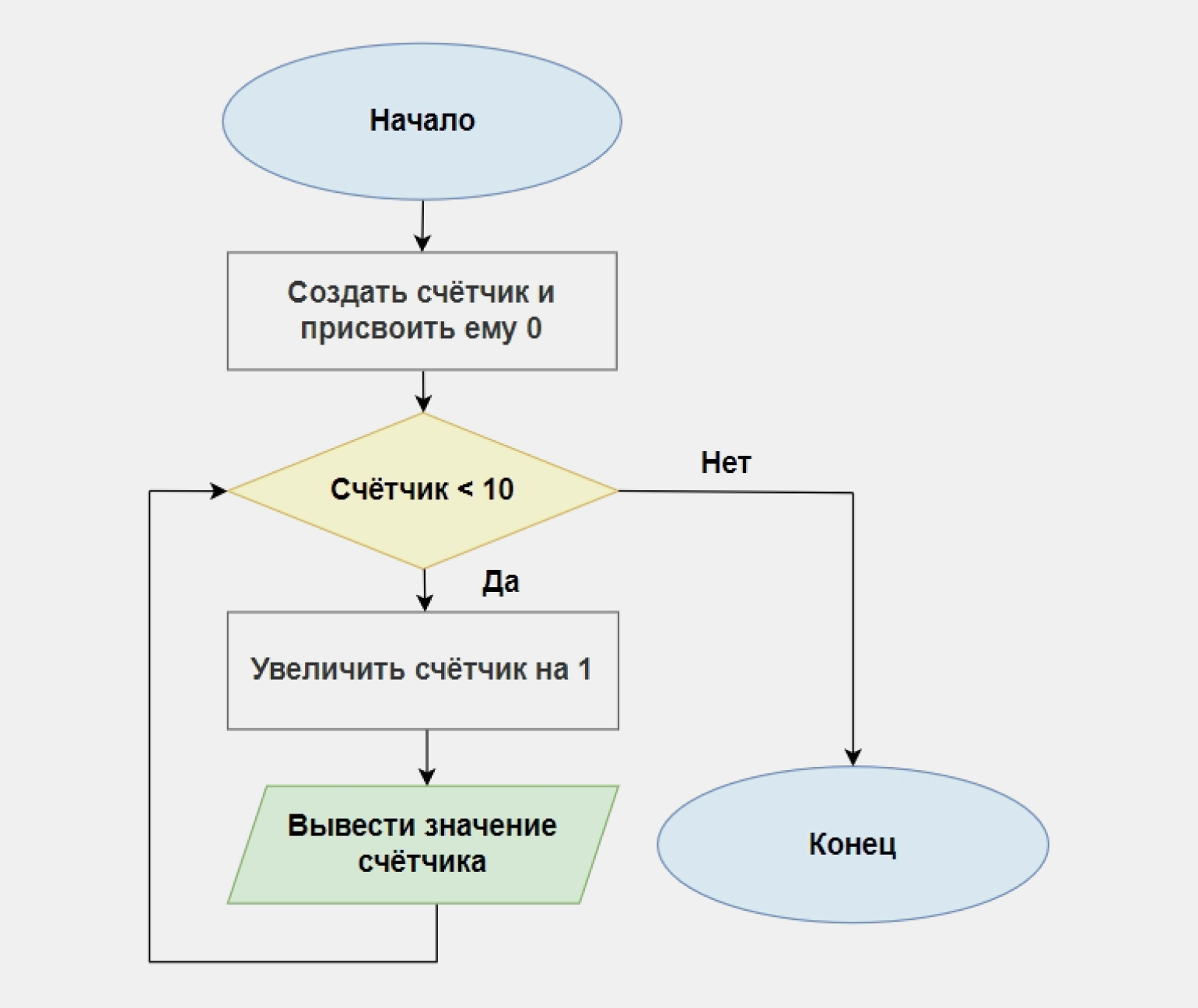
Пример. Напишите программу, которая циклично увеличивает значения счётчика на 1 и на каждом шаге выводит его значение. Когда значение счётчика достигнет 10, программа должна завершиться.
В основе нашего решения будет лежать следующее условие: если значение счётчика меньше 10 — прибавить 1, иначе — завершить работу. Вот как это выглядит в виде блок-схемы:
Переведём это в код на Python. Обратите внимание, что мы не прописываем отдельную ветвь для случая «Нет»:
count = 0 #прибавлять 1 к count, пока count меньше 10 while count < 10: count += 1 print(count) print("Переменная count равна 10!")
Результат работы программы:
1 2 3 4 5 6 7 8 9 10
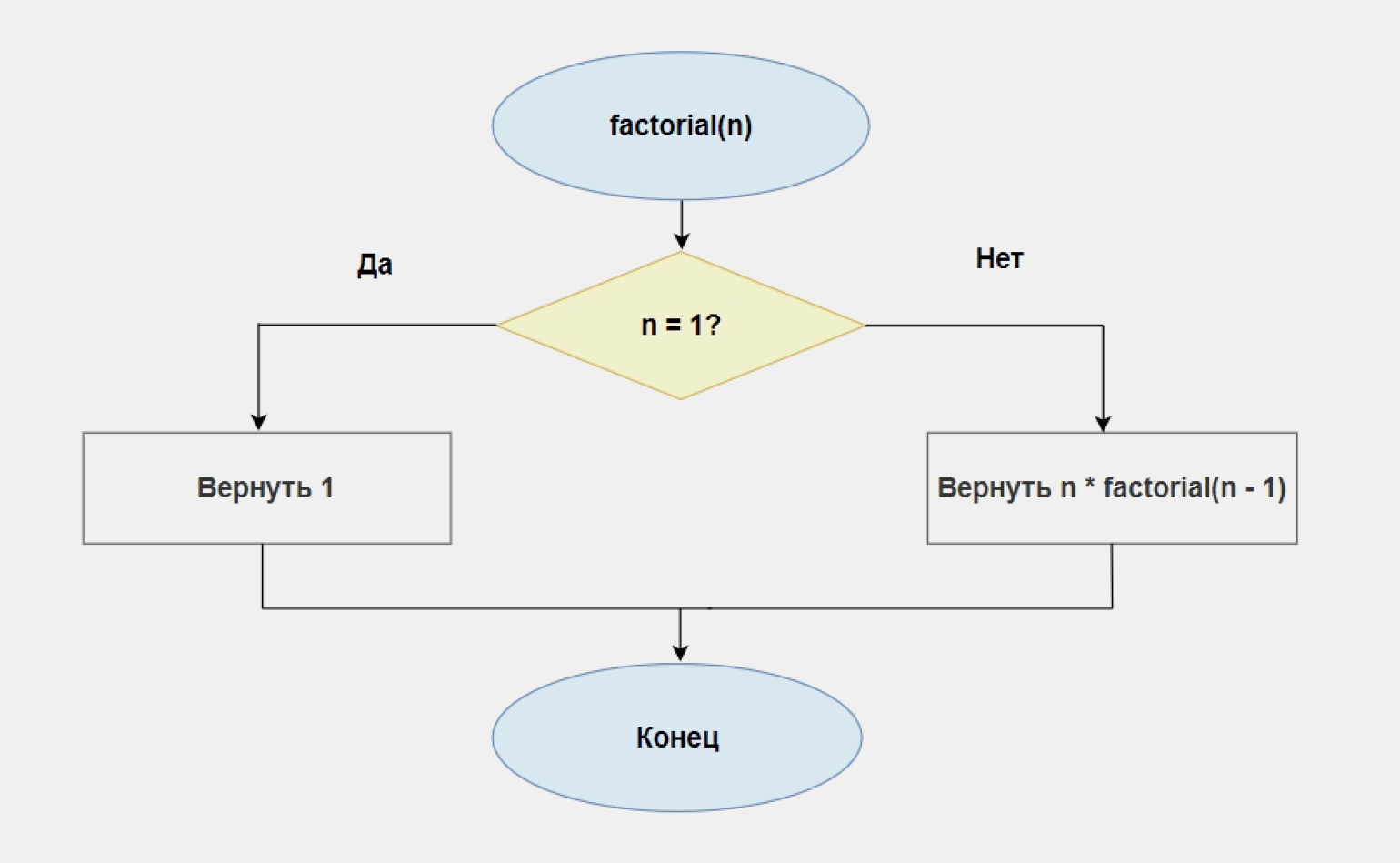
Рекурсия — это явление, при котором система вызывает саму себя, но с другими входными данными. Такие алгоритмы используют для обхода словарей в глубину, вычисления факториала, расчёта степеней и других практических задач. В целом всё это можно сделать с помощью циклов, но код рекурсивных функций более лаконичен и удобочитаем.
Пример. Пользователь вводит число n. Посчитайте его факториал и выведите результат на экран.
#функция, которая вызывает саму себя def factorial(n): if n == 1: return 1 #когда функция возвращает значение, #она вызывает себя, но с аргументом n - 1 return n * factorial(n - 1)
Вот как выглядит блок-схема рекурсивного алгоритма:
На практике чисто последовательные, условные или циклические алгоритмы встречаются редко, но вместе они позволяют создать решение любой сложности.
Есть и другие классификации алгоритмов. Например, по множеству решаемых задач их можно разделить на численные, поисковые, сортировочные, строковые, сетевые и криптографические. А по точности получаемых результатов — на нормальные и стохастические (вероятностные).
Если хотите изучить алгоритмы более подробно, начните с простых и увлекательных книг по computer science:
- «Грокаем алгоритмы», Адитья Бхаргава;
- «Теоретический минимум по Computer Science», Владстон Фило;
- «Гид по Computer Science», Вильям Спрингер.
Когда познакомитесь с основными алгоритмами и научитесь решать с их помощью стандартные задачи, переходите к более серьёзной литературе. Например, прочитайте Computer Science Роберта Седжвика и «Алгоритмы» Рода Стивенса.
У «Яндекса» есть бесплатные тренировки с разбором алгоритмических задач и распространённых ошибок. А попрактиковаться, закрепить теорию и подготовиться к техническому интервью можно на LeetCode — там есть сотни задач разной сложности и для разных языков программирования.

Научитесь: Профессия Python-разработчик
Узнать больше
Алгоритм достижения цели

Думаю, многие из вас знают такую методику постановки целей, как SMART. Согласно ей, цель должна быть:
- Specific (Конкретной) – что необходимо достигнуть;
- Measurable (Измеримый) – в чем будет измеряться результат;
- Achievable (Достижимый) – за счет чего планируется достичь цели;
- Relevant (Актуальный) – действительно ли выполнение этой задачи позволит добиться желаемого результата;
- Time-bound (Ограниченный во времени) – определение временного промежутка, по наступлению / окончанию которого должна быть достигнута цель.
Но, чтобы достигнуть цели, используя SMART, одних правильных формулировок не достаточно. Нужна еще четко прописанная последовательность шагов. Объясним на примерах.
Предположим, вы поставили перед собой главную (долгосрочную) цель – стать руководителем отдела перспективных IT-разработок компании. А в среднесрочной перспективе еще хотите, реализуя личные цели, съездить в отпуск на Алтай и сплавиться на плоте по горной реке.
Обе эти цели анализируем по следующей схеме:
- Средства;
- Имеется;
- Не хватает;
- Делается;
- Улучшить (идеи).
Итак, цель – стать руководителем отдела перспективных IT-разработок компании. Для достижения цели необходимо:
Средства:
- Заявить о себе. Успешно управлять проектной командой по разработке продукта X.
- Наладить отношения с NN.
- Иметь опыт работы от … лет.
- Иметь высшее образование и обучение по работе с удаленными командами.
Имеется:
- Исследования по результатам тестирования продукта X – есть перспективы.
- Чаще общаюсь с NN и получил возможность присутствовать на совещаниях топ-менеджмента.
- Опыт работы 2 года.
- Высшее образование есть, начато обучение по работе с удаленными командами (20 часов из 72).
Не хватает:
- Поддержки коллег.
- Доверия со стороны NN.
- 1-го года опыта работы.
- Свидетельства об окончании курсов управления удаленной командой.
Делается:
- Агитирую коллег на участие в новом суперпроекте.
- Делаю доклады по итогам работы NN каждые 2 недели.
Улучшить (идеи):
- Заинтересовать всех проектом по разработке продукта X. Сделать презентацию, акцентировать внимание на планерках.
Для достижения цели личной – съездить в отпуск на Алтай и сплавиться по горной реке – необходимо:
Средства:
- XXX рублей.
- Купить билеты и забронировать гостиницу.
- Приобрести туристическое снаряжение.
- Найти единомышленников, желающих присоединиться.
- 28 дней отпуска.
Имеется:
- XX рублей.
- Контакты приличного хостела.
- Адрес пункта проката туристического оборудования и снаряжения.
- Две недели законного отпуска.
Не хватает:
- XXX рублей.
- Бабушкиного согласия остаться с ребенком.
- Единомышленников, желающих присоединиться к этой авантюре.
- Свободного времени.
Делается:
- Откладываются деньги.
- Ведутся переговоры с бабушкой.
Улучшить (идеи):
- Найти компанию, организующие туры на Алтай и присоединиться к группе туристов.
- Уточнить у бывалых туристов, какое снаряжение и оборудование может понадобиться.
После того, как вы пропишите свою цель в соответствии с этим алгоритмом, вам будет легче перейти к календарному планированию, распределяя цели и задачи по времени.
Читайте также:
- Ключевые навыки современного лидера
- Bullet Journal: управлять временем проще, чем кажется
- Основные ошибки в планировании рабочего дня
- Chronodex: визуализируйте свое время и задачи
- Прокрастинация и как с ней справиться
— У тебя есть план?
Помню именно этот вопрос, задал мне
мой знакомый, который собственно и вложил
в меня азы нестандартного мышления.
-План? ответил я.
-Да план, хотя бы на ближайший год;
Я, не задумываясь — ответил:
-Ну конечно же!
На самом деле плана у меня не было даже на завтрашний день. А быстрота моего ответа была обусловлена тем, что мне казалось, что написание плана не самая тяжелая задача, просто у меня на это не было времени. Сам себе я мог сказать, что мол вот выдастся свободный часок и я смогу всю свою жизнь распланировать. В общем самоуверенности было хоть отбавляй.
Про план меня мой знакомый спрашивал регулярно, такое ощущение, что ему нравилось наблюдать за скоростью моей реакции ответа на этот вопрос. Меня же это уже начало понемногу выводить из себя! И в один прекрасный день, я все-таки выделил «часок», чтобы написать заветный план и предоставить его затем моему знакомому на обозрение.
Что я вам могу сказать, посидев за работой «часок», с горем пополам смог накропать только кажущиеся на тот момент для меня главные цели. Ими оказались:
1. Здоровье;
2. Отношения;
3. Образование;
4. Карьера.
Я думаю, этот список совпал бы со списком большинства людей и как на мой взгляд это замечательные цели, заслуживающие того чтобы потратить на их реализацию максимум сил, энергии и времени! Так то оно так, но я столкнулся с проблемой, дело в том, что все эти цели казались для меня абстрактными. Лично у меня сложилось впечатление, что я стою на краю обрыва, вижу пред собой все эти четыре цели, причем так четко и ясно, но самое главное, что я не вижу мостов к этим целям. Увидеть эти мосты, именно это, на мой взгляд, и есть важнейший момент в достижение своих запланированных целей. Ясно было одно, что для достижения каждой конкретной цели, необходим алгоритм, то есть четкая последовательность действий. Эта логическая структура не терпит приближенностей и случайностей. Теперь хотелось бы представить непосредственно алгоритм, который я так и назвал – алгоритм достижения поставленных целей.
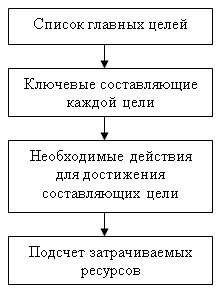
Теперь позвольте мне объяснить эту логическую схему словами.
Как видите, алгоритм строится из четырех блоков, эти блоки я буду называть этапами.
1-й этап алгоритма достижения целей
Это базовый этап, на котором мы определяемся со своими самыми главными целями, составляя из них список. Свой ранний список целей я вверху приводил уже.
2-й этап алгоритма достижения целей
На втором этапе необходимо выделить ключевые составляющие каждой из главных целей.
3-й этап алгоритма достижения целей
Внимание! Этот этап требует максимального внимания, потому как он является самой главной деталью в механизме достижения целей. На этом этапе требуется составить список действий необходимых для достижения всех составляющих, каждого базового пункта плана.
4-й этап алгоритма достижения целей
И наконец заключительный этап, он носит арифметический характер. Именно на этом этапе просчитываются все затрачиваемые ресурсы, выражаемые во временном диапазоне и в денежном эквиваленте, либо еще в каком-нибудь.
Я рассказал о четырех этапов направленных на реализацию ваших планов, но хочу отметить, что могут быть алгоритмы, состоящие из пяти и более этапов. Алгоритм с пятью этапами может быть применим, скажем, для промежуточных целей, с которыми нам все приходится сталкиваться на протяжении всей жизни очень часто. Примером для иллюстрирования алгоритма из четырех блоком может стать стандартная бытовая ситуация. Допустим, вы нуждаетесь в таких вещах как холодильник и мягкая мебель. Вы согласно алгоритму определились с моделью, просчитали стоимость и знаете, каким путем вы получите деньги на покупку одной из этих вещей. И вот тут как раз и появляется пятый этап, целью которого, как вы уже догадались, будет «взвешивания» по принципу первой необходимости.
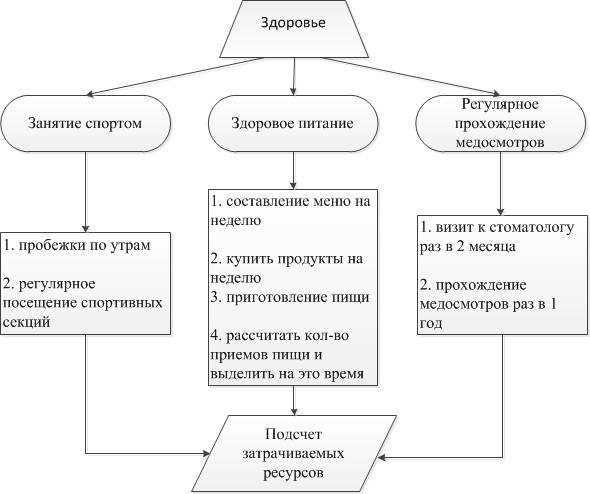
Теперь для наглядности, я бы хотел изобразить пример алгоритма, который я создал. Так как первой целью в моем жизненном план, я думаю как и у многих, стоит пункт Здоровье, то я изображу его:
Каждому этапу соответствует своя геометрическая фигура. В заключение хотелось бы дать последний совет, при составлении подобных алгоритмов, старайтесь не увеличивать количество блоков, без явной на то необходимости, это может привести к эффекту «далекой цели». Сядьте, спокойно выделите все ключевые блоки и уже в этих блоках можете составлять список из мелких деталей. Именно это и даст положительный эффект, так как вы будете знать, что для достижения цели у вас всего два-три шага (кол-во блоков), составленных из множества маленьких шажков. А ввиду того, что эти шажки вы будете преодолевать легко, каждый раз вычеркивая уже пройденный пункт, все это будет вас мотивировать идти дальше маленькими, но уверенными шажками.
Автор: Станислав Плюваченко
Все права защищены. При перепечатке ссылка на блог Мотивация к успеху обязательна.