Как составить два числовых выражения задач

Чтобы составить задачу, которая приведёт к этим выражениям, например, с двумя неизвестными, нужно сначала поиграться с числами.

Берём две машины. Одна движется со скоростью 60 км/час, а вторая на 20 быстрее 80 км/час. У этих скоростей оптимальный общий множитель 48. Увеличиваем его в 10 раз получится 480 км.

Первой машине потребуется 8 часов, для преодоления этого расстояния, а второй 6 на 2 часа меньше. 480 км – это известное расстояние. Неизвестные величины — это скорость и время.

Напускаем туману. Определяемся, что скорость 1-й машины на 20 км/час меньше второй машины. Но вторая выехала на 2 часа позже и догнала первую на расстоянии 480 км. Задача готова. Нужно хитро задать вопрос. Например: Через какое время 2-я машина будет на расстоянии в 100 км от первой после из встречи.

Чтобы решить такую задачу потребуется составлять выражение. Принимать за “х” скорость первой или второй машины до встречи. За “у” время первой или второй машины также до встречи. Или обходиться одним “х”, а можно и просто обойтись числами. Но это не для составителя. Составитель оперирует известными ему числами, а “решала” составляет выражения.

Конечно это интересно. Составить хитрую математическую задачку, и чтобы её не быстро решили. А выдёргивать с интернета любой может. Я составляю сама. Бывает до взрыва мозга, а не такую легкотню, как написала выше. Например вот эта: про курагу, чернослив и инжир.

Числовые и буквенные выражения

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Числовые выражения: что это

Числовое выражение — это запись, которая состоит из чисел и знаков арифметического действия между ними.

Именно числовые выражения окружают нас повсюду — не только на уроках математики, но и в магазине, на кухне или когда мы считаем время. Простые примеры, в которых нужно вычислить разность, сумму, получить результат умножения или деления — это все числовые выражения.

Например:

• 23 + 5 = 28
• 5 — 2 = 3
• 52 * 3 = 156
• 28 : 7 = 4

Это простые числовые выражения.

Чтобы получить сложное числовое выражение, нужно к простому выражению присоединить знаком арифметического действия еще одно простое числовое выражение. Вот так:

• (5 * 3) — (5 * 2) = 5
• 6 : (7 — 4) = 2
• (45 + 45) : 9 = 10
• 11 * (5 * 5) = 275

Это сложные числовые выражения.

Знать, где простое выражение, а где сложное — нужно, но называть оба типа выражений следует просто «числовое выражение».

Число, которое мы получаем после выполнения всех арифметических действий в числовом выражении, называют значением этого выражения.

Вспомним, какие виды арифметических действий есть.
+ — знак сложения, найти сумму.
— — знак вычитания, найти разность.
* — знак умножения, найти произведение.
: — знак деления, найти частное.

11 — значение числового выражения.
6 * 8 = 48
48 — значение числового выражения.

При вычислении сложных числовых выражений нужно строго соблюдать очередность выполнения арифметических действий:

• Сначала выполняется действие, записанное в скобках.
• Затем выполняется деление/умножение.
• В последнюю очередь выполняется сложение/вычитание.

Пример 1. Найдите значение числового выражения: 3 * (2 + 8) — 4

Пример 2. Найдите значение числового выражения: (6 + 7) * (13 + 2)

(6 + 7) * (13 + 2) = 195

Часто бывает нужно сравнить два числовых выражения.

Сравнить числовые выражения — значит найти значения каждого выражения и сравнить их.

Пример 1. Сравните два числовых выражения: 6 + 8 и 2 * 2

Сначала находим значение первого выражения:

14 больше 4
14 > 4
6 + 8 > 2 * 2

Пример 2. Сравните следующие числовые выражения:
5 * (12 — 2) — 7 и (115 + 9) — (7 — 3)

Находим значение первого выражения, соблюдая порядок выполнения арифметических действий:

43 меньше 120
43

Буквенные выражения

Кажется, с числовыми выражениями все достаточно просто. Буквенные выражения немногим сложнее.

В буквенном выражение есть цифры, знаки арифметических действия и буквы.

Получается, что буквенное выражение — это числовое выражение, в котором есть не только числа, но и буквы.

Это буквенные выражения. Для записи буквенных выражений используют буквы латинского алфавита.

У буквенных выражений, как и у числовых, есть определенный алгоритм вычисления:

• Сначала следует прочитать его полностью.
• Затем оно записывается.
• Третьим шагом идет подстановка значения неизвестного в выражение.
• А затем производится вычисление, согласно очередности выполнения арифметических действий.

Пример 1. Найдите значение выражения: 5 + x.

1. Читаем: найдите сумму числа 5 и x.
2. Подставляем вместо неизвестного x число 4.
3. Вычисляем: 5 + 4 = 9.

Пример 2. Найдите значение выражения: (4 + a) * (2 + x).

1. Читаем: найдите произведение суммы числа 4 и а и суммы числа 2 и x.
2. Подставляем вместо неизвестного a число 2.
3. Вычисляем 4 + 2 = 6.
4. Подставляем вместо неизвестного x число 5.
5. Вычисляем 2 + 5 = 10.
6. Находим произведение 6 * 10 = 60.
7. Записываем результат: (4 + 2) * (2 + 5) = 60.

Выражения с переменными

Переменная — это значение буквы в буквенном выражении.

• Например, в выражении x + a — 8
  x — переменная
  a — переменная

Если вместо переменных подставить числа, то буквенное выражение x + a — 8 станет числовым выражением. Вот так:

• подставляем вместо переменной x число 5, а вместо переменной a — число 10, получаем 5 + 10 — 8.

Числа, которые подставляют вместо переменных — это значения переменных. В нашем примере это числа 5 и 10.

После подстановки значения переменных находим значение x + a — 8 = 5 + 10 — 8 = 7.

Часто можно встретить буквенные выражения, записанные следующим образом:
5x — 4a

Число и переменная записаны без знака арифметического действия. Так коротко записывается умножение.

5x — это произведение числа 5 и переменной x
4a — это произведение числа 4 и переменной a

Числа 4 и 5 называют коэффициентами.
Коэффициент показывает, во сколько раз будет увеличена переменная.

Теперь вы вооружены всеми необходимыми теоретическими знаниями о числовых и буквенных выражениях. Давайте немного поупражняемся в решении задачек и примеров, чтобы научиться применять полученные знания на практике.

Задание раз.

1. Сумма 6 и a.
2. Разность 8 и x.
3. Сумма x — 2 и 6
4. Разность 15 и x — y
5. Сумма 45 + 5 и 12 — 6

Задание два.

Составьте буквенное выражение:

Сумма разности b и 345 и суммы 180 и x.

Ответ: (b — 345) + (180 + x).

Задание три.
Составьте буквенное выражение:
Разность разности 30 и y и разности a и b.
Ответ: (30 — y) — (a — b).

Задание четыре.
Составьте выражение для решения задачи и найдите его значение.
Ролл «Калифорния» стоит 480 рублей — это на 40 рублей меньше, чем ролл «Филадельфия». Сколько будут стоить оба ролла?
Как решаем:
Калифорния — 480 рублей.
Филадельфия — 480 + 40.
Калифорния + Филадельфия = ?
480 + (480 + 40).
Мы помним, что выполнение арифметических действий в числовом выражении имеет строгую последовательность. Сначала — действие в скобках:
480 + 520 = 1 000.

Ответ: роллы “Калифорния” и “Филадельфия” вместе стоят 1 000 рублей.

Задание пять.
Составьте выражение для решения задачи и найдите его значение.
Маша посмотрела за день 150 видео в ТикТок, а Лена — на 13 видео больше. Сколько всего видео было просмотрено обеими девочками?

Маша — 150 видео.
Лена — 150 + 13 видео.
Маша + Лена = ? видео.

150 + (150 + 13)
Выполняем сначала действие в скобках: 150 + 13 = 163.
150 + 163 = 313.

Ответ: Маша и Лена посмотрели всего 313 видео.

Задание шесть.
Вычислите:
(500 + 300) : a — 15,
при условии, что a = 10.

Подставляем число 10 (значение переменной) вместо переменной
(500 + 300) : 10 — 15

Затем выполняем сначала арифметическое действие в скобках: 500 + 300 = 800.
Затем выполняем деление 800 : 10 = 80.
Выполняем вычитание 80 — 15 = 65.

Ответ: (500 + 300) : 10 — 15 = 65.

Задание семь.
Вычислите:
(270 — 120) * (x — 10),
при условии, что x = 45.

Как решаем: подставляем число 45 (значение переменной) вместо переменной x
(270 — 120) * (45 — 10).

Затем выполняем сначала арифметическое действие в скобках: 270 — 120 = 150.
Выполняем арифметическое действие во вторых скобках: 45 — 10 = 35.
Затем выполняем умножение 150 * 35 = 5 250

Ответ: (270 — 120) * (45 — 10) = 5 250.

Задание восемь.
Вычислите:
(50 * x) — (3 * y)
при условии, что x = 2; y = 10

Подставляем число 2 вместо переменной x
(50 * 2) — (3 * y).

Подставляем число 10 вместо переменной y
(50 * 2) — (3 * 10).

Затем выполняем сначала арифметическое действие в скобках: 50 * 2 = 100.
Выполняем арифметическое действие во вторых скобках: 3 * 10 = 30.
Затем выполняем вычитание 100 — 30 = 70

Источник

Запись решения задачи выражением

Урок 15. Математика 2 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Запись решения задачи выражением»

— Плюс. Плююююс! Ты где?

Привет, Плюс! Чего так долго? Включай скорее компьютер. Сейчас у нас будет в скайпе разговор с царицей Математикой.

— Здравствуй, Минус. Как это я забыл! Включаю.

— Здравствуйте, Дорогие Плюс и Минус!

Сегодня я хочу проверить, как вы умеете решать задачи. Я дам несколько задач и предлагаю вам устроить соревнование — кто сможет их решить быстрее, но при этом, конечно, правильно.

— Да, царица, мы Вас внимательно слушаем.

— Мы очень внимательно слушаем.

— Ну что же, приступим. Итак, вот первая задача:

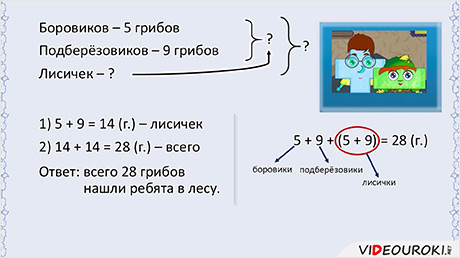
Ребята в лесу собирали грибы. Они нашли 5 боровиков, 9 подберёзовиков, а лисичек столько, сколько боровиков и подберёзовиков вместе. Сколько всего грибов нашли ребята в лесу?

Ну, Плюс и Минус, я жду вашего решения. Может быть и ребята, которые на вас смотрят, попробуют решить эту задачу.

— Всё, я готов! Могу даже объяснить, как я решал эту задачу.

Нам даны два числа: количество боровиков — их 5, и количество подберёзовиков — их 9. Но неизвестно количество лисичек. Про них сказано, что их столько, сколько боровиков и подберёзовиков вместе. А ещё неизвестно, сколько всего грибов.

В задаче два неизвестных, значит, задача составная, то есть в ней не одно действие, а два. В первом действии я узнаю, сколько лисичек.

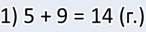
А так как боровиков и подберёзовиков вместе столько же, сколько и лисичек, то общее количество грибов я нашёл вот так:

Ответ: всего 28 грибов нашли ребята в лесу.

— А я решал задачу другим способом. Вот посмотрите:

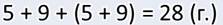
— Да, Минус, чувствуется, что сложение — это не твой конёк. Конечно, задачу ты решил правильно. Но при этом у тебя получилось не два, а три действия. При этом первое и второе действия повторяются. Для этой задачи такой способ записи не очень удобен. Хотя некоторые задачи действительно удобно записывать не по действиям, как это сделал я, а числовым выражением. А вот, кстати, царица Математика уже даёт нам новую задачу.

— Тихо, Плюс, слушаем!

— На уроке физкультуры присутствовало 14 мальчиков. А девочек — на 5 меньше. Сколько всего учащихся присутствовало на уроке физкультуры?

— Ну что же, начинаем решать. Ребята, и вы попробуйте с нами решать!

— Я уже решил. Вот посмотрите, в задаче известно количество мальчиков, Их 14. Но неизвестно количество девочек. Ведь сказано, что их на 5 меньше, чем мальчиков.

А в задаче надо узнать количество девочек, и только потом — сколько всего детей. Я так и узнавал:

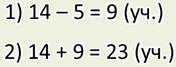
Ответ: всего 23 учащихся присутствовало на уроке физкультуры.

— А вот я записал решение этой задачи по-другому:

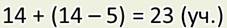
И ещё можно вот так:

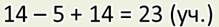
— Но ведь ты мне только что говорил, что такой способ решения неудобен! Зачем же ты решил задачу другим способом — записью выражения.

— В первой задаче он действительно был неудобен, а в этой — очень даже удобен. Во-первых, это не другой способ решения задачи. Посмотри, в моём решении есть те же действия, что и в твоём, и даже в той же последовательности.

Ты первым действием узнаёшь, сколько девочек, и я тоже. Ведь это действие я записал в скобках. А то, что записано в скобках, всегда выполняется первым.

Во втором действии к 14 прибавляем полученное в первом действии число 9. А в этой записи слагаемые меняются местами — к 9 прибавляется 14.

И получается, что это не другой способ решения задачи — ведь все действия одинаковы, а другой способ записи решения. Ты решал по действиям, а я — выражением. Способ решения одинаковый, а способ записи этого решения — разный. Но посмотри, моя запись получилась короче. В ней нет номеров действий и пояснений. Поэтому такая запись помогает экономить и время, и бумагу.

— Ты, Плюс, как всегда. Все тебе надо складывать да экономить. Хотя, наверное, ты прав. Эта запись действительно удобная. А хотелось бы и мне попробовать такую запись задачи выражением.

Ваше величество, госпожа королева. Не могли бы Вы задать нам ещё одну задачу?

— Ну что же, слушайте:

В моём саду растёт 6 яблонь. А груш на 2больше. Сколько всего яблонь и груш растёт в моём саду?

Я хочу видеть у вас оба способа записи решения — и по действиям, и выражением.

— Ну вот что у меня получилось. Прежде, чем узнать, сколько всего яблонь и груш, необходимо узнать, сколько груш. Ведь нам это неизвестно. Сказано, что их на 2 больше, чем яблонь.

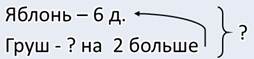
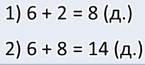
Значит, в саду царицы растёт 14 яблонь и груш.

А вот как получилась запись выражением:

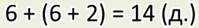
Сначала я нашёл, количество груш. Но, так как это действие стоит не в начале записи, я выделил его скобками. А потом нашёл сумму чисел. Ответ такой же, как и при записи по действиям — 14.

— Хорошо. Задача решена, верно. А теперь расскажите, чему вы научились.

— Можно я начну первый.

Записывать решение задачи можно по действиям и выражением.

— При записи по действиям мы пишем номер действия и пояснения к каждому действию, а при записи выражением только пояснение к значению записанного выражения.

— При записи выражения первое действие часто записываем в скобках, и конечно, не забываем записать ответ задачи.

— Ну что же, молодцы, Плюс и Минус. Вы справились с заданием. И сейчас вы можете пойти погулять в мой сад и полакомиться яблоками и грушами.

Источник

Есть в задачах (для второго класса) на умножение небольшой подвох. Скажу честно, пока не поняла сути, сама делала подобные ошибки.

Доброго всем времени суток!

Разберем на примерах:

Задача 1.

В трех вазах лежит по два апельсина. Сколько всего апельсинов в трех вазах?

Задача 2.

Катя читала книгу три часа. За один час она прочитывала пять страниц. Сколько страниц прочла Катя за три часа?

Задача 3.

В магазин привезли шесть коробок конфет. В каждой коробке пять килограмм конфет. Сколько всего килограмм конфет привезли в магазин ?

Также во втором классе встречаются задания с формулировкой «составить выражение». Что же это значит? А это значит, что необходимо составить решение задачи в одно действие.

Пример 1.

Составь выражение и вычисли.

Катя купила три набора карандашей по шесть штук в каждом. Из всех наборов восемь карандашей она отдала брату. Сколько карандашей у Кати осталось ?

Пример2.

Составь выражение и вычисли.

У Вани было 30 рублей. Он купил два ластика по 3 рубля каждый. Сколько денег осталось у Вани?

! Иногда требуется просто составить выражение, иногда пишут составь и вычисли.

На этом у меня всё. Возможно мои маленькие заметки стали полезными для Вас.

С уважением Tasha.I

Спасибо за лайки и отзывы.

РЕШЕНИЕ ЗАДАЧ В ДВА ДЕЙСТВИЯ ВЫРАЖЕНИЕМ. РЕШЕНИЕ ВЫРАЖЕНИЙ СО СКОБКАМИ

Цели: дать понятие числовые выражения, формировать умение учащихся решать задачи в два действия и выражения со скобками; сравнивать именованные числа; развивать вычислительные навыки; прививать интерес к предмету.

Ход урока

I. Организационный момент.

II. Каллиграфическая минутка.

6 9 6 9 6 9 6 9

III. Устный счет.

А)Индив.задания- карточки с дифференцированными заданиями

Б)М.диктант (если считаете высказывание верным –кв., неверно-кр.

Однозн.числа-красным цветом раскрашиваем, двузн.числа-синим

(с.15,в рабочей тетради Т.Н.Ситникова,2012)

В)Сравните величины

IV. Составление и решение выражений.

Прочитайте записи

9+7          30+6+1

23-3          18-(4+6)

Это числовые выражения. Если в выражении выполнить действие ,то мы найдем значение выражения

Разбирается задание 2 (с. 34 учебника, часть 1). Учащиеся составляют выражения, определяют порядок действий в них и находят значения.

V. Работа над задачами.

Учитель просит учащихся прочитать задачу  из задания 4 (с. 34 учебника, часть 1), внимательно рассмотреть выражения, записанные ниже, и выбрать то выражение, которое соответствует задаче.

– Какое из записанных ниже выражений соответствует задаче? (6 + 3 – 2.)

– Объясните, почему так считаете. (Сначала в мастерской было 6 машин, затем поставили ещё 3, значит, машин в мастерской стало больше, это можно записать выражением  6 + 3. Потом две машины забрали из ремонта, значит, машин в мастерской стало меньше, следовательно, можно дописать предыдущее выражение 6 + 3 – 2.)

Далее дети составляют задачи по оставшимся выражениям.

Н а п р и м е р:

6 – 3 + 2

∙ В гараже стояло 6 машин. 3 машины выехали из гаража, а 2 вернулись. Сколько машин стало в гараже?

6 + 3 + 2

∙ На стоянке стояло 6 машин. Приехало 3 машины, а затем ещё 2. Сколько машин стало на стоянке?

6 – 3 – 2

∙ Во дворе было 6 машин. Сначала уехало 3 машины, а потом ещё 2. Сколько машин осталось во дворе?

VI. Сравнение именованных чисел.

С этой целью учитель может использовать задание 5 (с. 34 учебника, часть 1), а также подобрать свои аналогичные задания.

Н а п р и м е р:

Сравните: 1 дм и 1 см;

   1 ч и 60 мин;

   10 мм и 1 см;

   1 м и 15 дм.

Задание может быть выполнено детьми как самостоятельно с последующей фронтальной проверкой, так и фронтально, с объяснением.

VIIСамостоятельная работа

Проверочные работы с.20-21 по вариантам

VIII. Итог урока.

– Что нового узнали на уроке?

– Для чего нужны эти знания?

– Какую работу вам хотелось бы выполнить ещё?

– Каков ваш вклад в этот урок?

IX.Д/З: №3,№5 с.40

Тема: Что такое корень слова? Что такое однокоренные слова?

Цель: познакомить с понятиями корень, однокоренные слова; развивать речь; пополнять словарный запас учащихся.

Планируемые результаты: учащиеся научатся находить в словах корень и образовывать однокоренные слова, употреблять их в речи; анализировать, делать выводы, сравнивать.

Формирование универсальных учебных действий на уроках:

Личностные:

1. Овладение начальными навыками адаптации в динамично изменяющемся и развивающемся мире.
2. Формирование чувства гордости за свою Родину, российский народ и историю России;
3. Принятие и освоение социальной роли обучающегося, развитие мотивов учебной деятельности и формирование личностного смысла учения.
4. Формирование установки на безопасный, здоровый образ жизни, мотивации к творческому труду, к работе на результат.

Регулятивные:

1. Овладение способностью принимать и сохранять цели и задачи учебной деятельности, поиска средств её осуществления.
2. Формирование умения планировать, контролировать и оценивать учебные действия в соответствии с поставленной задачей и условиями её реализации, определять наиболее эффективные способы достижения результата.
3. Использование знаково-символических средств представления информации.

Познавательные:

1. Активное использование речевых средств и средств для решения коммуникативных и познавательных задач.
2. Использование различных способов поиска (в справочных источниках), сбора, обработки, анализа, организации, передачи и интерпретации информации.

3.Овладение навыками смыслового чтения текстов различных стилей и жанров в соответствии с целями и задачами: осознанно строить речевое высказывание в соответствии с задачами коммуникации и составлять тексты в устной и письменной формах.

1. Овладение логическими действиями сравнения, анализа, синтеза, обобщения, классификации по родовидовым признакам, установления аналогий и причинно-следственных связей, построения рассуждений, отнесения к известным понятиям.

Коммуникативные:

1. Готовность слушать собеседника и вести диалог, признавать возможность существования различных точек зрения и права каждого иметь свою, излагать своё мнение и аргументировать свою точку зрения и оценки событий.
2. Работать в паре и группе           

       Межпредметные связи: Чтение. ИЗО. Музыка (умение работать с текстом, развитие моторики руки; развитие фонематического слуха).

Ресурсы: методическое пособие; Учебник; тетрадь с печатной основой; тетрадь для учащихся в узкую линейку.

Организация пространства: фронтальная, в парах, самостоятельная.

Ход урока:

Этап урока	Содержание учебного материала и деятельности учителя. Форма организации.	ФУУД у учащихся
Мобилизующее начало	Учитель настраивает детей на работу. Самостоятельная работа Минутка чистописания Бб	Л1. Ученики проверяют готовность к уроку. презентация Повторяют написание элементов букв, букв, слогов.
Актуализация знаний	Самостоятельная работа Словарная работа Б.реза,л.пата в.терок,скор..,пр.щай, ..сина, р.сунок. .	Л4; Р1, 2; П1, 3; К1. Сверка с записью на доске.
Самоопределение к деятельности	Фронтальная работа (Презентация) На доске записаны слова: часовщик, часто, часы, часики, часовой, часть. – Выпишите только однокоренные слова. – Выделите общую часть родственных слов. – Как называется общая часть родственных слов? – Это тема нашего сегодняшнего урока.	Л4; Р1, 2; П1, 3; К1. Часовщик, часы, часики, часовой. Час- Корень.
4. Работа по теме урока	Фронтальная работа Работа по учебнику, с. 61 Упр. 84 – по заданиям учебника	Л4; Р1, 2; П1, 3; К1. Дети подбирают родственные слова, выделяют корень в словах.
Физминутка
5. Продолжение работы по теме	Самостоятельная работа Работа по учебнику, с. 61 – 62   Упр. 85 – по заданиям учебника Фронтальная работа) Упр. 86 – устно Работа в парах Упр. 87	Л4; Р1, 2; П1, 3; К1 Умение находить однокоренные слова. Закройте пальчиком общую часть слова и прочитайте то,что осталось незакрытым. -Можно ли назвать то,что вы прочитали,словами? Убедились ,что в слове обязательно должен быть корень.Он «хранит»общее значение всех однокоренных слов.
6.Рефлексия	Самостоятельная работа Текст в рабочей тетради с корнем –кур-	Р2. Оценивать свои достижения. Дети выписывают только однокоренные слова. Сверка с образцом с доски. Ученики оценивают свою работу с помощью светофоров-«смайликов».
7.Итог урока	Фронтальная работа – Что такое корень? – Назовите синоним слову родственные. – Кто может сказать, что уже понял, что такое корень слова? – Кому нужно время, чтобы разобраться в этой теме?	К2. Отвечать на итоговые вопросы урока. Ответы детей. Однокоренные.
8.Домашнее задание	С. 63 упр.88  (уч.)	Л3, 4; Р2; П3.

–
Плюс!….. Плююююс! Ты где?

Привет,
Плюс! Чего так долго? Включай скорее компьютер. Сейчас у нас будет в скайпе разговор
с царицей Математикой.

–
Здравствуй, Минус. Как это я забыл! Включаю.

–
Здравствуйте, Дорогие Плюс и Минус!

Сегодня
я хочу проверить, как вы умеете решать задачи. Я дам несколько задач и предлагаю
вам устроить соревнование – кто сможет их решить быстрее, но при этом, конечно,
правильно.

–
Да, царица, мы Вас внимательно слушаем.

–
Мы очень внимательно слушаем.

–
Ну что же, приступим. Итак, вот первая задача:

Ребята
в лесу собирали грибы. Они нашли 5 боровиков, 9 подберёзовиков, а лисичек
столько, сколько боровиков и подберёзовиков вместе. Сколько всего грибов нашли
ребята в лесу?

Ну,
Плюс и Минус, я жду вашего решения. Может быть и ребята, которые на вас
смотрят, попробуют решить эту задачу.

–
Всё, я готов! Могу даже объяснить, как я решал эту задачу.

Нам
даны два числа: количество боровиков – их 5, и количество подберёзовиков – их 9.
Но неизвестно количество лисичек. Про них сказано, что их столько, сколько
боровиков и подберёзовиков вместе. А ещё неизвестно, сколько всего грибов.

В
задаче два неизвестных, значит, задача составная, то есть в ней не одно
действие, а два. В первом действии я узнаю, сколько лисичек.

А
так как боровиков и подберёзовиков вместе столько же, сколько и лисичек, то
общее количество грибов я нашёл вот так:

Ответ:
всего 28 грибов нашли ребята в лесу.

–
А я решал задачу другим способом. Вот посмотрите:

–
Да, Минус, чувствуется, что сложение – это не твой конёк. Конечно, задачу ты
решил правильно. Но при этом у тебя получилось не два, а три действия. При этом
первое и второе действия повторяются. Для этой задачи такой способ записи не
очень удобен. Хотя некоторые задачи действительно удобно записывать не по
действиям, как это сделал я, а числовым выражением. А вот, кстати,
царица Математика уже даёт нам новую задачу.

–
Тихо, Плюс, слушаем!

–
На уроке физкультуры присутствовало 14 мальчиков. А девочек – на 5 меньше.
Сколько всего учащихся присутствовало на уроке физкультуры?

–
Ну что же, начинаем решать. Ребята, и вы попробуйте с нами решать!

–
Я уже решил. Вот посмотрите, в задаче известно количество мальчиков, Их 14. Но
неизвестно количество девочек. Ведь сказано, что их на 5 меньше, чем мальчиков.

А
в задаче надо узнать количество девочек, и только потом – сколько всего детей. Я
так и узнавал:

Ответ:
всего 23 учащихся присутствовало на уроке физкультуры.

–
А вот я записал решение этой задачи по-другому:

И
ещё можно вот так:

–
Но ведь ты мне только что говорил, что такой способ решения неудобен! Зачем же
ты решил задачу другим способом – записью выражения.

–
В первой задаче он действительно был неудобен, а в этой – очень даже удобен.
Во-первых, это не другой способ решения задачи. Посмотри, в моём решении есть
те же действия, что и в твоём, и даже в той же последовательности.

Ты
первым действием узнаёшь, сколько девочек, и я тоже. Ведь это действие я
записал в скобках. А то, что записано в скобках, всегда выполняется первым.

Во
втором действии к 14 прибавляем полученное в первом действии число 9. А в этой
записи слагаемые меняются местами – к 9 прибавляется 14.

И
получается, что это не другой способ решения задачи – ведь все действия
одинаковы, а другой способ записи решения. Ты решал по действиям, а я –
выражением. Способ решения одинаковый, а способ записи этого решения –
разный. Но посмотри, моя запись получилась короче. В ней нет номеров действий и
пояснений. Поэтому такая запись помогает экономить и время, и бумагу.

–
Ты, Плюс, как всегда. Все тебе надо складывать да экономить. Хотя, наверное, ты
прав. Эта запись действительно удобная. А хотелось бы и мне попробовать такую
запись задачи выражением.

Ваше
величество, госпожа королева. Не могли бы Вы задать нам ещё одну задачу?

–
Ну что же, слушайте:

В
моём саду растёт 6 яблонь. А груш на 2больше. Сколько всего яблонь и груш
растёт в моём саду?

Я
хочу видеть у вас оба способа записи решения – и по действиям, и выражением.

–
Хорошо.

–
Хорошо.

–
Ну вот что у меня получилось. Прежде, чем узнать, сколько всего яблонь и груш,
необходимо узнать, сколько груш. Ведь нам это неизвестно. Сказано, что их на 2
больше, чем яблонь.

Получаем:

Значит,
в саду царицы растёт 14 яблонь и груш.

А
вот как получилась запись выражением:

Сначала
я нашёл, количество груш. Но, так как это действие стоит не в начале записи, я
выделил его скобками. А потом нашёл сумму чисел. Ответ такой же, как и при
записи по действиям – 14.

–
Хорошо. Задача решена, верно. А теперь расскажите, чему вы научились.

–
Можно я начну первый.

Записывать
решение задачи можно по действиям и выражением.

–
При записи по действиям мы пишем номер действия и пояснения к каждому действию,
а при записи выражением только пояснение к значению записанного выражения.

–
При записи выражения первое действие часто записываем в скобках, и конечно, не
забываем записать ответ задачи.

–
Ну что же, молодцы, Плюс и Минус. Вы справились с заданием. И сейчас вы можете
пойти погулять в мой сад и полакомиться яблоками и грушами.

–
Ура!!!