Содержание
- Что такое пропорция
- Что такое пропорция
- Основное свойство пропорции
- Примеры решения задач с пропорцией
- Что такое равноправие между мужчиной и женщиной
- Что такое равноправие между мужчиной и женщиной
- Когда возможно равноправие
- Кому не подходят партнерские отношения
- Как построить равноправные отношения
- Равенство (математика)
- Определения равенства
- Связанные определения
- См. также
- Полезное
- Смотреть что такое «Равенство (математика)» в других словарях:
- Равенство (математика)
- СОДЕРЖАНИЕ
- Этимология [ править ]
- Основные свойства [ править ]
- Равенство как предикат [ править ]
- Личности [ править ]
- Уравнения [ править ]
- Конгруэнции [ править ]
- Примерное равенство [ править ]
- Связь с эквивалентностью и изоморфизмом [ править ]
- Логические определения [ править ]
- Равенство в теории множеств [ править ]
- Установите равенство на основе логики первого порядка с помощью равенства [ править ]
- Установите равенство на основе логики первого порядка без равенства [ править ]
Что такое пропорция

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Что такое пропорция
Пропорция — это равенство двух отношения.
Пропорциональный — это такой, который находится в определенном отношении к какой-либо величине.
Пропорция всегда содержит равные коэффициенты.
Если выразить определение формулой, то выглядеть оно будет так:
a и d — крайние члены пропорции
Читается это выражение так: a так относится к b, как c относится к d
Например:

Это равенство двух отношений: 15 так относится к 5, как 9 относится к 3.
15 и 3 — крайние члены пропорции.
5 и 9 — средние члены пропорции.

Наглядный пример для понимания:
У нас есть восемь кусочков аппетитной пиццы и, предположим, четыре голодных друга.
Это значит, что 8 аппетитных кусочков пиццы будут так относиться к 4 голодным друзьям, что каждому голодающему достанется по 2 кусочка. Прекрасно!
А теперь представим, ситуацию, в которой есть только половина аппетитной пиццы, но при этом и голодных друга — всего два.

Что мы имеем: 4 кусочка и 2 друга, претендующих на них.
Это значит, что 4 аппетитных кусочка будут так относиться к 2 голодным друзьям, что каждому из них достанется по 2 кусочка.
Оценив обе ситуации, делаем вывод, что отношение 8/4 пропорционально отношению 4/2. Отношения в пропорции — равные.
Вывод: знание математических пропорций пригодится при заказе пиццы. Быстренько прикидываем отношение количества человек, претендующих на пиццу, и число кусочков — и сразу заказываем побольше пиццы, чтобы никто не остался голодным😉
Основное свойство пропорции
Запомните основное свойство пропорции:
Произведение крайних членов пропорции равно произведению средних членов этой пропорции.
В виде формулы свойство выглядит так:

a : b = c : d = a * d = b * c
Мы знаем, что a и d — крайние члены пропорции, b и c — средние.
Это свойство следует применять, чтобы проверить пропорцию. Если все сходится согласно формулировке — пропорция составлена верно, и отношения в пропорции являются равными друг другу.
Давайте проверим несколько пропорций.
Пример 1. Дана пропорция:6/2 = 12/4
Делаем вывод, что пропорция 6/2 = 12/4 составлена верно.
Пример 2. Дана пропорция: 10/2 = 16/4
Отсюда делаем вывод, что отношения в пропорции 10/2 ≠ 16/4 не являются равными.
Примеры решения задач с пропорцией
Чтобы потренироваться в составлении пропорций, решим вместе несколько задачек.
Задачка 1. Дана математическая пропорция: 15/3 = x/4
Ответ: в пропорции 15/3 = x/4, x = 20
Задачка 2. Найдите четвертый член пропорции: 18, 9 и 24.
Ответ: четвертый член пропорции — 12.
Задачка 3. 18 человек могут съесть пять килограммов суши за 8 часов, сколько часов понадобится 9 людям?
Ответ: 16 часов понадобится 9 людям, чтобы съесть все суши.
Задачка 4. Дана пропорция: 20/2 = y/4
Источник
Что такое равноправие между мужчиной и женщиной
Равноправные отношения между мужчиной и женщиной – все еще редкость. Для многих равноправие между полами и вовсе воспринимается как миф, поскольку оно не сочетается с привычными шаблонами о роли мужчины и женщины в отношениях и семье. Более того, зачастую само понятие равноправных отношений искажается. Построить такие отношения можно, но стоит понимать, что подходят они не всем.
Что такое равноправие между мужчиной и женщиной
Равноправные отношения — это партнерские отношения, в которых мужчина и женщина отказываются от своих предубеждений о том, как все должно быть в семье, любые вопросы решают вдвоем, обо всем договариваются на равных.
И у мужчины, и у женщины есть свои планы, свои убеждения, свое видение отношений. Но равноправие означает, что люди договариваются обо всех аспектах семейных отношений, а потом живут по этим договоренностям.
Каждый должен четко понимать: за любыми партнерскими отношениями стоят не только равные права, но и обязательства
Важно и то, что равный брак возможен в том случае, когда социальный статус, а также вложения партнеров примерно одинаковы.
Равноправие противостоит понятию традиционной семьи, где мужчина и женщина советуются друг с другом, но окончательное решение по основным вопросам принадлежит мужчине. В традиционных отношениях имеется вертикаль власти, равноправные отношения строятся по принципу демократии.
 Равноправие в отношениях — это равные права и возможности
Равноправие в отношениях — это равные права и возможности
Когда возможно равноправие
«Равноправие» звучит красиво, но в реальности все может быть сложнее. Партнеры должны уметь договариваться, а для этого нужно не только говорить самому, но и выслушивать другого, не перебивать, сдерживать свои эмоции. Нужно уметь придерживаться правил и договоренностей, а для этого человек должен иметь внутреннюю дисциплину. Не каждый готов выстраивать такие отношения.
Возможность партнерства зависит от того, есть ли у партнера умение и желание быть дисциплинированным и ответственным:
Если речь идет о семье, то равноправие в партнерских семьях касается даже детей: родители, которые выстраивают между собой равные отношения, стараются также выслушивать и мнение ребенка.
 Равноправие возможно между людьми с внутренней дисциплиной
Равноправие возможно между людьми с внутренней дисциплиной
Кому не подходят партнерские отношения
Равноправие означает равные права и возможности у обоих партнеров. Партнерские отношения не подойдут тем, кто привык к традиционным отношениям. Например, равноправие предполагает, что семейные расходы делятся поровну. Если мужчина и женщина живут на принципах равенства, то в общий бюджет они должны вкладывать одинаковую сумму. Хорошо, если зарплата у обоих партнеров примерно на одном уровне. Но если зарплата женщина в два, три, а то и более раз меньше зарплаты мужчины, то ей придется вложить половину своей заработной платы, тогда как ему — только небольшую часть.
 Партнерские отношения подходят не всем
Партнерские отношения подходят не всем
Таким образом, партнерские отношения могут быть не очень выгодны, когда у мужчины и женщины разный социальный статус. Не устроят они и людей, которые зависимы от партнера. Например, женщина рассчитывала в браке быть домохозяйкой, а мужчина, который предпочитает партнерские отношения, предполагает, что и она будет работать.
Партнерский тип отношений не подойдет эмоциональным людям без внутренней дисциплины: такие люди попросту не смогут длительное время придерживаться договоренностей
А вот кому идеально подойдет партнерство, так это людям, которые хотят быть уверены, что их интересы будут защищены договоренностями. Привлекательны они для женщин, который строят карьеру, ведут активный образ жизни и не хотят быть ограничены тесными семейными рамками.
 Партнерские отношения могут не подойти людям с разным социальным статусом
Партнерские отношения могут не подойти людям с разным социальным статусом
Как построить равноправные отношения
Равноправные отношения — это не только равный заработок, но и взаимное уважение партнеров, общие культурные ценности и интересы. Главное — открытость и готовность обсуждать любые проблемы.
Источник
Равенство (математика)
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0 | • | × | × | × | × | × | × | × | × | × |
| 1 | × | • | × | × | × | × | × | × | × | × |
| 2 | × | × | • | × | × | × | × | × | × | × |
| 3 | × | × | × | • | × | × | × | × | × | × |
| 4 | × | × | × | × | • | × | × | × | × | × |
| 5 | × | × | × | × | × | • | × | × | × | × |
| 6 | × | × | × | × | × | × | • | × | × | × |
| 7 | × | × | × | × | × | × | × | • | × | × |
| 8 | × | × | × | × | × | × | × | × | • | × |
| 9 | × | × | × | × | × | × | × | × | × | • |
| Равенство десятичных цифр как бинарное отношение: • истина, × ложь |
Ра́венство (отношение равенства) в математике — бинарное отношение, наиболее логически сильная разновидность отношений эквивалентности.
Определения равенства
Равенство является интуитивно очевидным отношением: значение двух выражений одно и то же. При его формальном определении возникает разнобой.
Теория множеств, по определению, считает два объекта (то есть, два множества) равными, если они состоят из одних и тех же элементов:

В теориях с типизацией объектов отношение равенства имеет смысл лишь между элементами одного типа (попросту говоря, внутри определённого множества). Логицисты (сначала в логике предикатов Фреге, затем в рамках теории типов) опирались на определение равенства, похожее на теоретико-множественное, но рассматривающее отношения с другой стороны:

То есть, для равенства двух объектов необходимо и достаточно, чтобы любой предикат, который может быть построен на данном типе, давал на них одинаковое логическое значение. Впрочем, не логицисты это определение придумали — оно было известно ещё Лейбницу.
Некоторые формальные теории уклоняются от определения равенства, считая его изначально заданным отношением эквивалентности.

Связанные определения
Формальное определение и интуитивное понимание равенства иногда конфликтуют. Равно ли (целое) число 1 (действительному) числу  ? С точки зрения интуиции — да, а с точки зрения теории типов вопрос неверно поставлен (ср. с проблемой приведения типов в программировании). В математике в подобных случаях подразумевается каноническое вложение одного множества (пространства, типа) в другое, большее. Вопрос о равенстве целого числа действительному можно понимать как равенство собственно действительного и другого действительного числа, соответствующего нашему целому. То есть, работа с интуитивно «очевидными» фактами типа всякое целое число является рациональным, а рациональное — действительным, требует в рамках некоторых формальных подходов специальных оговорок.
? С точки зрения интуиции — да, а с точки зрения теории типов вопрос неверно поставлен (ср. с проблемой приведения типов в программировании). В математике в подобных случаях подразумевается каноническое вложение одного множества (пространства, типа) в другое, большее. Вопрос о равенстве целого числа действительному можно понимать как равенство собственно действительного и другого действительного числа, соответствующего нашему целому. То есть, работа с интуитивно «очевидными» фактами типа всякое целое число является рациональным, а рациональное — действительным, требует в рамках некоторых формальных подходов специальных оговорок.
Уравнение — построенное при помощи равенства логическое высказывание, в которое входит переменная. Оно задаёт подмножество предметной области переменной — множество корней уравнения.
Определение величины или переменной записывается с помощью равенства: Пусть переменная равна выражению.
Тождество — высказывание, верное при любых значениях переменных. Оно часто (хотя вовсе не обязательно) строится на основе отношения равенства.
См. также

Полезное
Смотреть что такое «Равенство (математика)» в других словарях:
Равенство — может означать: Равенство в Викисловаре … Википедия
МАТЕМАТИКА — Математику обычно определяют, перечисляя названия некоторых из ее традиционных разделов. Прежде всего, это арифметика, которая занимается изучением чисел, отношений между ними и правил действий над числами. Факты арифметики допускают различные… … Энциклопедия Кольера
Равенство классов P и NP — Задачи тысячелетия Равенство классов P и NP Гипотеза Ходжа Гипотеза Пуанкаре Гипотеза Римана Квантовая теория Янга Миллса Существование и гладкость решений уравнений Навье Стокса Гипотеза Бёрча Свиннертон Дайера В теории алгоритмов… … Википедия
Функция (математика) — У этого термина существуют и другие значения, см. функция. Запрос «Отображение» перенаправляется сюда; см. также другие значения … Википедия
Пропорция (математика) — Пропорция (лат. proportio соразмерность, выровненность частей), равенство двух отношений, т. е. равенство вида a : b = c : d, или, в других обозначениях, равенство (часто читается как: «a относится к b так же, как c относится к d») … Википедия
Портал:Математика — Начинающим · Сообщество · Порталы · Награды · Проекты · Запросы · Оценивание География · История · Общество · Персоналии · Религия · Спорт · Техника · Наука · Искусство · Философия … Википедия
Конструктивная математика — абстрактная наука о конструктивных процессах, человеческой способности осуществлять их и о их результатах конструктивных объектах. Абстрактность К. м. проявляется прежде всего в том, что в ней систематически применяются две абстракции:… … Большая советская энциклопедия
Ротор (математика) — У этого термина существуют и другие значения, см. Ротор. Ротор, или вихрь векторный дифференциальный оператор над векторным полем. Обозначается (в русскоязычной[1] литературе) или (в англоязычной литературе), а также как векторное умножение … Википедия
Группа (математика) — Теория групп … Википедия
Источник
Равенство (математика)

СОДЕРЖАНИЕ
Этимология [ править ]
Этимологию этого слова от латинского aequālis ( «равно», «как», «сопоставимы», «подобные») от aequus ( «равный», «уровень», «ярмарка», «просто»).
Основные свойства [ править ]
Вот некоторые конкретные примеры этого:
Равенство как предикат [ править ]
Личности [ править ]
Уравнения [ править ]
Не существует стандартной нотации, которая отличает уравнение от тождества или другого использования отношения равенства: нужно угадывать подходящую интерпретацию из семантики выражений и контекста. Утверждается, что идентичность истинна для всех значений переменных в данной области. «Уравнение» иногда может означать идентичность, но чаще всего оно определяет подмножество пространства переменных как подмножество, в котором уравнение истинно.
Конгруэнции [ править ]
Примерное равенство [ править ]
Проверяемое сомнительное равенство можно обозначить символом.
Связь с эквивалентностью и изоморфизмом [ править ]
Однако есть и другие варианты изоморфизма, например
Логические определения [ править ]
Лейбниц охарактеризовал понятие равенства следующим образом:
Равенство в теории множеств [ править ]
Равенство множеств аксиоматизируется в теории множеств двумя разными способами, в зависимости от того, основаны ли аксиомы на языке первого порядка с равенством или без него.
Установите равенство на основе логики первого порядка с помощью равенства [ править ]
В логике первого порядка с равенством аксиома протяженности утверждает, что два набора, содержащие одинаковые элементы, являются одним и тем же набором. [8]
Включение половины работы в логику первого порядка можно рассматривать как простое удобство, как отмечает Леви.
«Причина, по которой мы беремся за исчисление предикатов первого порядка с равенством, заключается в удобстве; тем самым мы экономим труд по определению равенства и доказательству всех его свойств; теперь это бремя ложится на логику». [9]
Установите равенство на основе логики первого порядка без равенства [ править ]
Источник
Отношения и пропорции
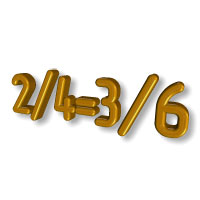
В математике отношением называется то частное, которое получается при делении одного числа на другое. Ранее сам этот термин использовался только в тех случаях, когда было необходимо выражение какой-либо одной величины в долях другой, причем такой, которая однородна первой. К примеру, отношения использовались при выражении площади в долях другой площади, длины в долях другой длины и т.п. Решение этой задачи производилось с помощью деления.
Таким образом, сам смысл термина «отношение» был несколько иной, чем термина «деление»: дело в том, что второй означал разделение определенной именованной величины на любое совершенно отвлеченное абстрактное число. В современной математике понятия «деление» и «отношение» по своему смыслу абсолютно идентичны и являются синонимами. Например, и тот, и другой термин с одинаковым успехом применяют для отношения величин, являющихся неоднородными: массы и объема, расстояния и времени и т.п. При этом многие отношения величин однородных принято выражать в процентах.
Пример
В супермаркете насчитывается четыреста наименований различных товаров. Из них двести произведено на территории Российской Федерации. Определить, каково отношение отечественных товаров к общему числу товаров, продаваемых в супермаркете?
400 – общее число товара
200 – РФ
Ответ: двести разделить на четыреста равняется ноль целых пять десятых, то есть пятьдесят процентов.
200 : 400 = 0,5 или 50%
В математике делимым принято называть предыдущий член отношения, а делителем – последующий член отношения. В приведенном выше примере предыдущим членом являлось число двести, а последующим – число четыреста.
Два равных отношения образуют пропорцию
В современной математике принято считать, что пропорцией является два равным между собой отношения. К примеру, если общее количество наименований товаров, продаваемых в одном супермаркете, – четыреста, а в России из них произведено двести, а те же значения для другого супермаркета составляют шестьсот и триста, то соотношение количества российских товаров к общему их числу, реализовываемых в обеих торговых предприятиях, одинаково:
1.Двести разделить на четыреста равняется ноль целых пять десятых, то есть пятьдесят процентов
200 : 400 = 0,5 или 50%
2.Триста разделить на шестьсот равняется ноль целых пять десятых, то есть пятьдесят процентов
300 : 600 = 0,5 или 50%
В данном случае имеется пропорция, которую можно записать следующим образом:
Если формулировать это выражение так, как это принято делать в математике, то говорится, что двести относится к четыремстам так же, как триста относится к шестистам. При этом двести и шестьсот называются крайними членами пропорции, а четыреста и триста – средними членами пропорции.
Произведение средних членов пропорции
Согласно одному из законов математики, произведение средних членов любой пропорции равняется произведению ее крайних членов. Если возвратиться к приведенным выше примерам, то проиллюстрировать это можно следующим образом:
Двести умноженное на шестьсот равняется сто двадцать тысяч;
200 × 600 = 120 000
Триста умноженное на четыреста равняется сто двадцать тысяч.
300 × 400 = 120 000
Из этого следует, что любой из крайних членов пропорции равен произведению ее средних членов, деленному на другой крайний член. По тому же самому принципу каждый из средних членов пропорции равен крайних ее членов, деленному на другой средний член.
Если вернуться к приведенному выше примеру пропорции, то:
Двести равняется четыреста умноженное на триста и деленное на шестьсот.
Эти свойства широко используются в практических математических вычислениях тогда, когда требуется найти значение неизвестного члена пропорции при известных значениях трех членов остальных.
Продолжаем изучать соотношения. В данном уроке мы познакомимся с пропорцией.
Что такое пропорция?
Пропорцией называют равенство двух отношений. Например, отношение ![]() равно отношению
равно отношению ![]()
![]()
Данная пропорция читается следующим образом:
Десять так относится к пяти, как два относится к одному
Дроби, из которых составлена пропорция, всегда равны. Например, если в пропорции ![]() выполнить деление в обеих дробях, то получится число 2 в обеих частях:
выполнить деление в обеих дробях, то получится число 2 в обеих частях:
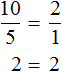
Предположим, что в классе 10 девочек и 5 мальчиков

Запишем отношение десяти девочек к пяти мальчикам:
10 : 5
Преобразуем данное отношение в дробь
![]()
Выполнив деление в этой дроби, мы получим 2. То есть десять девочек так будут относиться к пяти мальчикам, что на одного мальчика будет приходиться две девочки

Теперь рассмотрим другой класс в котором две девочки и один мальчик

Запишем отношение двух девочек к одному мальчику:
2 : 1
Преобразуем данное отношение в дробь:
![]()
Выполнив деление в этой дроби, мы снова получим 2. То есть две девочки так будут относиться к одному мальчику, что на этого одного мальчика будут приходиться две девочки:

Можно сделать вывод, что отношение ![]() пропорционально отношению
пропорционально отношению ![]() . Поэтому оно и читалось как «десять так относится к пяти, как два относится к одному».
. Поэтому оно и читалось как «десять так относится к пяти, как два относится к одному».
В нашем примере десять девочек так относятся к пяти мальчикам, как и две девочки относятся к одному мальчику.
Пример 2. Рассмотрим отношение 12 девочек к 3 мальчикам

а также отношение 12 девочек к 2 мальчикам

Данные отношения не являются пропорциональными. Другими словами, мы не можем записать, что ![]() , поскольку первое отношение, как видно на рисунке показывает, что на одного мальчика приходятся четыре девочки, а второе отношение показывает, что на одного мальчика приходятся шесть девочек.
, поскольку первое отношение, как видно на рисунке показывает, что на одного мальчика приходятся четыре девочки, а второе отношение показывает, что на одного мальчика приходятся шесть девочек.
Поэтому отношение ![]() не пропорционально отношению
не пропорционально отношению ![]() .
.
![]()
Из рассмотренных примеров видно, что пропорция составляется из дробей. Первая рассмотренная нами пропорция ![]() состоит из двух дробей. Если выполнить деление в этих дробях, то получим, что 2=2. Понятно, что 2 равно 2.
состоит из двух дробей. Если выполнить деление в этих дробях, то получим, что 2=2. Понятно, что 2 равно 2.
Вторая рассмотренная нами пропорция была ![]() . Мы пришли к выводу, что она составлена неправильно, поэтому поставили между дробями
. Мы пришли к выводу, что она составлена неправильно, поэтому поставили между дробями ![]() и
и ![]() знак не равно (≠). Если выполнить деление в этих дробях, получим числа 4 и 6. Понятно, что 4 не равно 6.
знак не равно (≠). Если выполнить деление в этих дробях, получим числа 4 и 6. Понятно, что 4 не равно 6.
Рассмотрим пропорцию . Данная пропорция составлена правильно, поскольку отношения
и
равны между собой:
Можно проверить это, выполнив деление в этих дробях, то есть разделить 4 на 2, а 8 на 4. В результате с двух сторон получатся двойки. А 2 равно 2
![]()
2 = 2
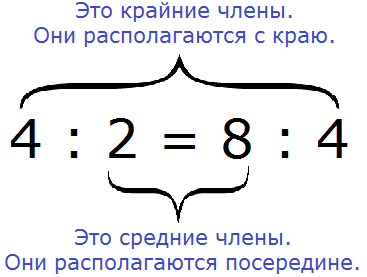
Все числа, находящиеся в пропорции (числители и знаменатели обеих дробей) называются членами пропорции. Эти члены подразделяются на два вида: крайние члены и средние члены.
В нашей пропорции ![]() крайние члены это 4 и 4, а средние члены это 2 и 8
крайние члены это 4 и 4, а средние члены это 2 и 8
Почему крайние члены называют крайними, а средние средними? Если записать пропорцию не в дробном, а в обычном виде, то сразу станет всё понятно:
4 : 2 = 8 : 4
Числа 4 и 4 располагаются с краю, поэтому их назвали крайними, а числа 2 и 8 располагаются посередине, поэтому их назвали средними:
С помощью переменных пропорцию можно записать так:
![]()
Данное выражение можно прочесть следующим образом:
a так относится к b, как c относится к d
Смысл данного предложения уже понятен. Речь идет о членах, участвующих в соотношении. a и d — это крайние члены пропорции, b и c — средние члены пропорции.
Основное свойство пропорции
Основное свойство пропорции выглядит следующим образом:
Произведение крайних членов пропорции равно произведению её средних членов.
Мы знаем, что произведение это ни что иное, как обычное умножение. Чтобы проверить правильно ли составлена пропорция, нужно перемножить её крайние и средние члены. Если произведение крайних членов будет равно произведению средних членов, то такая пропорция составлена правильно.
Например, проверим правильно ли составлена пропорция ![]() . Для этого перемножим её крайние и средние члены. Легко заметить, что крайние и средние члены пропорции располагаются «крест-накрест», поэтому в умножении нет ничего сложного. Перемножаем члены пропорции «крест-накрест»:
. Для этого перемножим её крайние и средние члены. Легко заметить, что крайние и средние члены пропорции располагаются «крест-накрест», поэтому в умножении нет ничего сложного. Перемножаем члены пропорции «крест-накрест»:
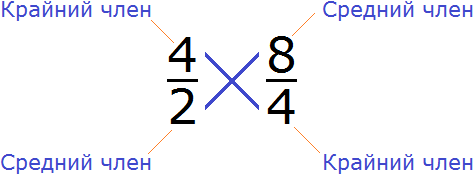
4 × 4 = 16 — произведение крайних членов пропорции равно 16.
2 × 8 = 16 — произведение средних членов пропорции так же равно 16.
4 × 4 = 2 × 8
16 = 16
4 × 4 = 2 × 8 — произведение крайних членов равно произведению средних членов. Значит пропорция ![]() составлена правильно.
составлена правильно.
Пример 2. Проверить правильно ли составлена пропорция ![]()
Проверим равно ли произведение крайних членов пропорции произведению её средних членов. Перемножим члены пропорции крест-накрест:
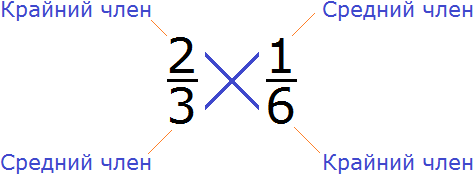
2 × 6 = 12 — произведение крайних членов пропорции равно 12
3 × 1 = 3 — произведение средних членов пропорции равно 3
2 × 6 ≠ 3 × 1
12 ≠ 3
2 × 6 ≠ 3 × 1 — произведение крайних членов пропорции НЕ равно произведению её средних членов. Значит пропорция ![]() составлена неправильно.
составлена неправильно.
Поэтому в пропорции ![]() разумнее заменить знак равенства (=) на знак не равно (≠)
разумнее заменить знак равенства (=) на знак не равно (≠)
![]()
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже


Запомните!
![]()
Пропорция — это равенство двух отношений.
Рассмотрим два равных отношения:
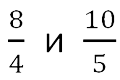
Соединив их знаком равенства, мы получим пропорцию.
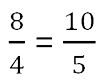
В пропорции различают крайние и средние члены.

- 8 и
5 называют крайними членами. - 4 и 10 — средние члены.
Основное свойство пропорции
Если пропорция составлена верно, то есть отношения, составляющие эту пропорцию действительно равны,
то для пропорции верно следующее:
Запомните!
![]()
Произведение крайних членов пропорции равно произведению средних.
Правило выше и называется основным свойством пропорции.
Чтобы правильно применять правило, мы предлагаем вам запомнить правило (креста) «X».
Рассмотрим его на примере пропорции.
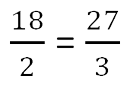
Убедимся, что пропорция составлена верно.
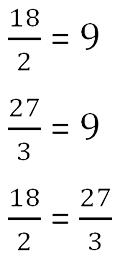
Теперь запишем пропорцию и нарисуем карандашом поверх знака равенства крест.
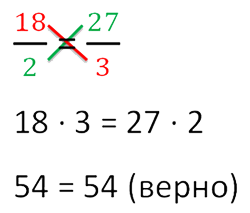
Нарисовав крест, гораздо легче составить нужное произведение (выполнить основное свойство пропорции).
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
2 января 2020 в 11:01
Sergei Mixailov

Профиль
Благодарили: 0
Сообщений: 1

Sergei Mixailov
Профиль
Благодарили: 0
Сообщений: 1
Можно ли менять местами неизвестный множитель буквы например в пропорции например в пропорции крайний член A D= C B средний
0
Спасибо
Ответить
5 января 2020 в 14:18
Ответ для Sergei Mixailov
Эмма Аддамс

Профиль
Благодарили: 0
Сообщений: 2

Эмма Аддамс
Профиль
Благодарили: 0
Сообщений: 2
Если дана пропорция = , то верно следующее: = и
= . Таким образом, мы можем менять местами крайние и средние члены пропорции.
А вот здесь видео-уроки по математике:
https://www.youtube.com/channel/UChuPWiMp13sUQ6G6oPTjzag?disable_polymer=true
0
Спасибо
Ответить
17 ноября 2016 в 21:51
Саша Икс

Профиль
Благодарили: 0
Сообщений: 1

Саша Икс
Профиль
Благодарили: 0
Сообщений: 1
Всем привет! Задача не сложная, но что то не до конца понимаю, поэтму ищу у Вас помощи. Задача такая:
Мужу с женой пришёл счёт за оплату электричество 2500 рублей. Они договорились вместе оплатить этот счёт, но каждый вносит равную долю по отношению к своей зарплате. Сколько внесёт в счёт за электричество муж и сколько жена, при условии, что зарплата мужа 15000 рублей, а зарплата жены 12000 рублей.
0
Спасибо
Ответить
21 ноября 2016 в 13:21
Ответ для Саша Икс
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Необходимо определить долю, которую каждый из них приносит в общий бюджет. Т.е. 12000+15000 = 27000(общий бюджет). 12000/27000 = 0,44; 15000/27000=0,56. Т.е. Жена должна оплатить 44%, а муж 56% от счета. Находим проценты и считаем:
2500 · 0,44 = 1100 — должна внести жена
2500 · 0,56 = 1400 — должен внести муж
1
Спасибо
Ответить
27 октября 2016 в 20:26
Анастасия Чакиева

Профиль
Благодарили: 0
Сообщений: 1

Анастасия Чакиева
Профиль
Благодарили: 0
Сообщений: 1
Помогите пожалуйста ребёнок болел, а теперь нужно срочно сдавать доклад поматематике на темуосновное свойство пропорций
0
Спасибо
Ответить
28 октября 2016 в 8:39
Ответ для Анастасия Чакиева
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Думаю для доклада, этого будет маловато, но как основа вполне подойдёт.
0
Спасибо
Ответить
5 ноября 2016 в 21:48
Ответ для Анастасия Чакиева
София Деревянко

Профиль
Благодарили: 0
Сообщений: 2

София Деревянко
Профиль
Благодарили: 0
Сообщений: 2
Я нашла на YuoTube ролик, в котором очень понятно разясняют https://www.youtube.com/watch?v=AWO4ISLFAaw, удачи
0
Спасибо
Ответить
4 февраля 2016 в 16:30
Павел Жердев

Профиль
Благодарили: 0
Сообщений: 1

Павел Жердев
Профиль
Благодарили: 0
Сообщений: 1
Подскажите пожалуйста при составлении пропорции, как понять в отношениях какую величину нужно делить.Например в 20л.керосина весят 10кг, а 40л. 20кг.Что должно в отношении быть в числители, а что в знаменатели и почему?
0
Спасибо
Ответить
19 сентября 2016 в 11:47
Ответ для Павел Жердев
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
В этой теме есть примеры на решение задач с пропорциями.
В конкретном случае:
20л — весят 10кг, а 20л -весят 40 кг.
Находим соотвествующие параметры. А именно. л и л, кг и кг. Проверяем логику. Она не нарушена. Значит в числитель ставим л, а в знаменатель кг. 20/10=40/20. Если сократим обе части, то увидим: 2=2, а значит пропорция составлена верно.
0
Спасибо
Ответить
26 января 2016 в 6:15
Егор Король

Профиль
Благодарили: 0
Сообщений: 1

Егор Король
Профиль
Благодарили: 0
Сообщений: 1
Найдите отношения: 8 целых 2/13 к 15/13 желательно с решением
6 целых 5/6 к 8,2 тоже с решением
1,35 к 5 целых 5/8 Помогите очень прошу!!!
0
Спасибо
Ответить
3 февраля 2016 в 21:41
Ответ для Егор Король
Сергей Аколоцев

Профиль
Благодарили: 0
Сообщений: 3

Сергей Аколоцев
Профиль
Благодарили: 0
Сообщений: 3
8*13+2=106/13 больше 15/13
6*6+5=41/6 и 82/10сокращаем, приводим к общему знаменателю 30, получаем 205/30 меньше 246/30
1целая 35/100 сокращаем получается 1 целая 7/10 или 17/10
5целых 5/8 получается 45/8
опять же приводим к общему знаменателю 40 получаем 68/40 меньше 225/40
0
Спасибо
Ответить
15 января 2016 в 7:37
Артем Зурлов

Профиль
Благодарили: 0
Сообщений: 1

Артем Зурлов
Профиль
Благодарили: 0
Сообщений: 1
Мне не понятно пропорция и отношение объясните пожалуста кратно
0
Спасибо
Ответить
21 января 2016 в 20:51
Ответ для Артем Зурлов
Ангелина Дмитриева

Профиль
Благодарили: 0
Сообщений: 2

Ангелина Дмитриева
Профиль
Благодарили: 0
Сообщений: 2
Отношение — это просто частное двух чисел. Например 3:4, 6:13 и т. д. В записи отношения важна именно связь между двумя числами, а не результат, полученный при вычислении частного, что отличает отношение от деления.
Равенство двух отношений называют пропорцией.
12: 16 = 18: 24 (например)
![]()
0
Спасибо
Ответить
19 сентября 2016 в 10:48
Ответ для Артем Зурлов
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Вот здесь подробно описаны пропорции.
0
Спасибо
Ответить
24 сентября 2015 в 13:12
Андрей Валах

Профиль
Благодарили: 0
Сообщений: 1

Андрей Валах
Профиль
Благодарили: 0
Сообщений: 1
Выберете из отношений из которых можно составить пропорцию состовте прпорцию 14* 21,8*14,15*10,27**18,18*24,36*54,20*35,6*8 *это разделить
0
Спасибо
Ответить
12 сентября 2016 в 11:37
Ответ для Андрей Валах
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
На сайте имеется возможность ставить знак “: “.
Чтобы составить пропорции, предлагаю сократить обыкновенные дроби и увидеть, что может стать пропорцией.
=; =; =; =; =; =; =; =.
Отсюда видно, что пропорцию составляют: 1) и 6); 2) и 7); 3) и 4); 5) и 8).
0
Спасибо
Ответить
16 сентября 2015 в 20:43
Альфия Абдалимова

Профиль
Благодарили: 0
Сообщений: 1

Альфия Абдалимова
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
8 сентября 2016 в 16:40
Ответ для Альфия Абдалимова
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Воспользуемся свойством пропорции: произведение крайних членов пропорции равно произведению средних членов (правило креста).
1,8 · (6x + 1) = 2,5 · 7,2
1,8 · 6x + 1,8 = 18
10,8x=18 ?1,8
10,8x=16,2
x=1,5
0
Спасибо
Ответить
6 сентября 2015 в 20:45
Кристина Папина

Профиль
Благодарили: 0
Сообщений: 1

Кристина Папина
Профиль
Благодарили: 0
Сообщений: 1
я взела у 1 друга 100 рублей и пошла в магазин по дороге всретила 2 друга и взяла у его взаймы 50 рублей пошла в магази и купила там 2 шоколадки по 10 рублей штука, у меня осталось 30 рублей их я оддала 1 другу и в сумме у меня получилось 70 рублей должна первому другу 50 руб. 2 другу и 20 рублей купила шоколадку и полус=чилось 140 рублей где 10 рублей?
0
Спасибо
Ответить
2 сентября 2016 в 15:12
Ответ для Кристина Папина
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Считаем финальную сумму долга с твоей стороны: 100 (заняла у первого друга) ? 30 (вернула первому другу) + 50 (заняла у второго друга) = 120;
Считаем потраченные деньги: 100 (потеряные) + 20 (потрачено на шоколад) = 120.
120=120 — ничего не потеряно. Попытка запутать здесь, ведёт к нарушению логики.
0
Спасибо
Ответить
19 мая 2015 в 4:26
Даша Казанцева

Профиль
Благодарили: 0
Сообщений: 1

Даша Казанцева
Профиль
Благодарили: 0
Сообщений: 1
Правило нахождение элементов пропорции
0
Спасибо
Ответить
19 мая 2015 в 20:30
Ответ для Даша Казанцева
Леся Деркачева

Профиль
Благодарили: 0
Сообщений: 1

Леся Деркачева
Профиль
Благодарили: 0
Сообщений: 1
Произведение крайник членов равно произведению средних членов!
0
Спасибо
Ответить
- Учебники
- 6 класс
- Математика 👍
- Бунимович
- №323

авторы: Бунимович, Кузнецова, Минаева.
издательство: “Просвещение”
Раздел:
- ГЛАВА 6. ОТНОШЕНИЯ И ПРОЦЕНТЫ
- 21. Что такое отношение
- Упражнения
ГДЗ учебник по математике 6 класс Бунимович. 21. Что такое отношение. Номер №323
- Предыдущее
- Следующее
Напишите несколько отношений, равных:
а) 10;
б) 0,1;
в)
2
3
;
г)
3
2
.

reshalka.com
ГДЗ учебник по математике 6 класс Бунимович. 21. Что такое отношение. Номер №323
Решение а
100 : 10 = 10;
30 : 3 = 10;
80 : 8 = 10.
Решение б
10 : 100 = 0,1;
300 : 3000 = 0,1;
5 : 50 = 0,1.
Решение в
4
6
=
2
3
;
8
12
=
2
3
;
20
30
=
2
3
.
Решение г
6
4
=
3
2
;
12
8
=
3
2
;
30
20
=
3
2
.
- Предыдущее
- Следующее
![]()
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом
