Что такое двойной интеграл
Двойной интеграл обобщает понятие определенного интеграла на случай функций двух переменных:
z=f(x,y)z=f(x,y)
и записывается так:I=∬Df(x,y) dx dyI=iint limits_{D}f(x,y), dx,dy
где DD-двумерная область, по которой происходит интегрирование функции f(x,y).f(x,y).
Для того чтобы вычислить двойной интеграл, переходят к повторному:
∬Df(x,y) dx dy=∫abdx∫c(x)d(x)f(x,y) dy=∫a1b1dy∫c1(y)d1(y)f(x,y) dxiint limits_{D}f(x,y), dx,dy=int_a^b dxint_{c(x)}^{d(x)}f(x,y) dy
=int_{a_1}^{b_1} dyint_{c_1(y)}^{d_1(y)}f(x,y) dx
Вычисляется повторный интеграл также, как и определенный, но поочередно: сначала внутренний, затем внешний.
Пределы интегрирования: a,ba,b – числа; c,dc,d – функции зависят от области DD. Подробнее рассмотрим на примере.
Вычисление двойного интеграла: пример
Рассмотрим пример.
Задача: вычислить двойной интеграл функции z=x2yz=x^2y по обласли D:x=1,y=x2,y=3D:x=1,y=x^2,y=3}
Сначала нарисуем область:
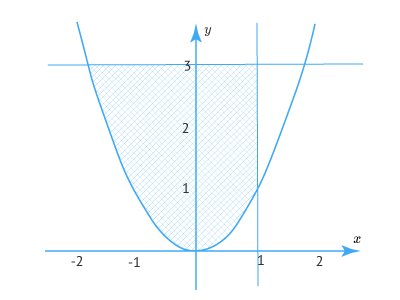
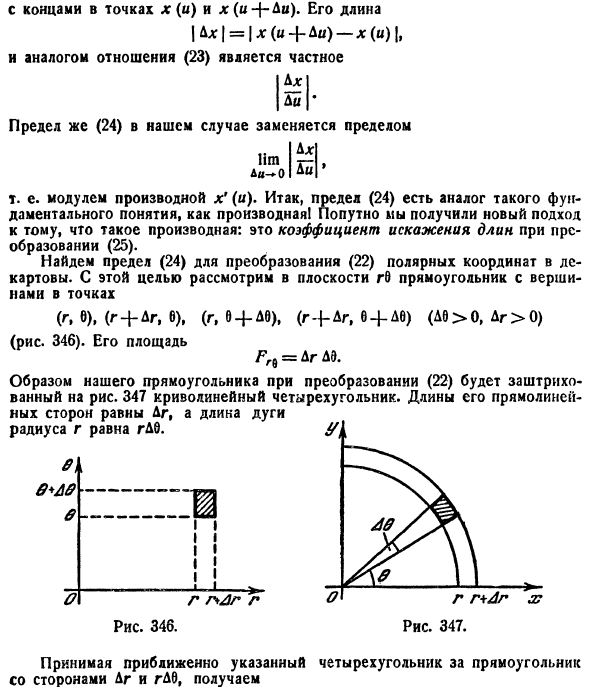
Теперь запишем двойной интеграл через повторный, интегрируя сначала по yy, потом по xx:
∬Dx2y dx dy=∫a1b1dx∫c1(x)d1(x)x2y dyiint limits_{D}x^2y, dx,dy=int_{a_1}^{b_1} dxint_{c_1(x)}^{d_1(x)}x^2y dy
Посмотрим на нашу область и найдем границы изменения xx:
y=x2y=x^2 и y=3y=3 пересекаются в точках x1=−3,x2=3x_1=-sqrt{3}, x_2=sqrt{3}.
Тогда xx лежит в пределах от −3-sqrt{3} до 1: −3≤x≤1-sqrt{3}leq xleq 1
Теперь нам нужно найти границы изменения yy, в зависимости от xx.
Видно, что yy изменятется от параболы до прямой y=3y=3. Или:
x2≤y≤3x^2leq yleq 3
Подставляем найденные пределы интегрирования в повторный интеграл и вычисляем его:
∫−31dx∫x23x2y dy=∫−31(x2y22∣x23)dx=∫−31(9×22−x62)dx=3×32−x714∣−31=10+1837int_{-sqrt{3}}^{1} dxint_{x^2}^{3}x^2y dy=int_{-sqrt{3}}^{1} (frac {x^2y^2}{2}|_{x^2}^3)dx=int_{-sqrt{3}}^{1} (frac {9x^2}{2}-frac{x^6}{2})dx=frac {3x^3}{2}-frac{x^7}{14}|_{-sqrt{3}}^1=frac{10+18sqrt{3}}{7}
Геометрическим смыслом вычисленного интеграла является объем фигуры с площадью основания – областью DD и высотой h=z(x,y)=x2yh=z(x,y)=x^2y.
Посчитаем этот же интеграл, изменив порядок интегрирования:
∬Dx2y dx dy=∫a1b1dy∫c1(y)d1(y)x2y dxiint limits_{D}x^2y, dx,dy=int_{a_1}^{b_1} dyint_{c_1(y)}^{d_1(y)}x^2y dx
При 0≤y≤1,−y≤x≤y0leq y leq 1, -sqrt{y}leq x leq sqrt{y}
При 1≤y≤3,−y≤x≤11leq y leq 3, -sqrt{y}leq x leq 1
Имеем разные пределы интегрирования для разных частей области DD.
Используя свойства двойного интеграла, можно разбить эту область на две:
∬Dx2y dx dy=∬D1x2y dx dy+∬D2x2y dx dyiint limits_{D}x^2y, dx,dy=iint limits_{D_1}x^2y, dx,dy+iint limits_{D_2}x^2y, dx,dy
Переходим к повторным интегралам и вычисляем их:
I1=∫01dy∫−yyx2y dx=∫01(x3y3∣−yy)dy=∫01(y2y3+y2y3)dy=4y3y21∣01=421I_1=int_0^{1} dyint_{-sqrt{y}}^{sqrt{y}}x^2y dx=int_0^{1} (frac {x^3y}{3}|_{-sqrt{y}}^{sqrt{y}})dy=int_0^1 (frac {y^2sqrt{y}}{3}+frac{y^2sqrt{y}}{3})dy=frac {4y^{3}sqrt{y}}{21}|_0^1=frac{4}{21}
I2=∫13dy∫−y1x2y dx=∫13(x3y3∣−y1)dy=∫13(y2y3+y3)dy=2y3y21+y26∣13=1837+32−221−13=2621+1837I_2=int_1^{3} dyint_{-sqrt{y}}^1x^2y dx=int_1^{3} (frac {x^3y}{3}|_{-sqrt{y}}^1)dy=int_1^3 (frac {y^2sqrt{y}}{3}+frac{y}{3})dy=frac {2y^{3}sqrt{y}}{21}+frac{y^2}{6}|_1^3=
frac{18sqrt{3}}{7}+frac{3}{2}-frac{2}{21}-frac{1}{3}=frac{26}{21}+frac{18sqrt{3}}{7}
I=I1+I2=10+1837I=I_1+I_2=frac{10+18sqrt{3}}{7}
Как мы убедились, результат не зависит от порядка интегрирования.
- Построить область интегрирования.
- При необходимости разбить её на несколько областей.
- Выбрать порядок интегрирования и перейти к повторному интегралу.
- Найти пределы интегрирования и вычислить полученные интегралы.
Тест по теме «Вычисление двойных интегралов»
Вычисление двойных интегралов с помощью повторного интегрирования
Пусть
функция
определена в области
![]()
,
где![]()
и
![]()
–
непрерывные функции на отрезке
![]()
.
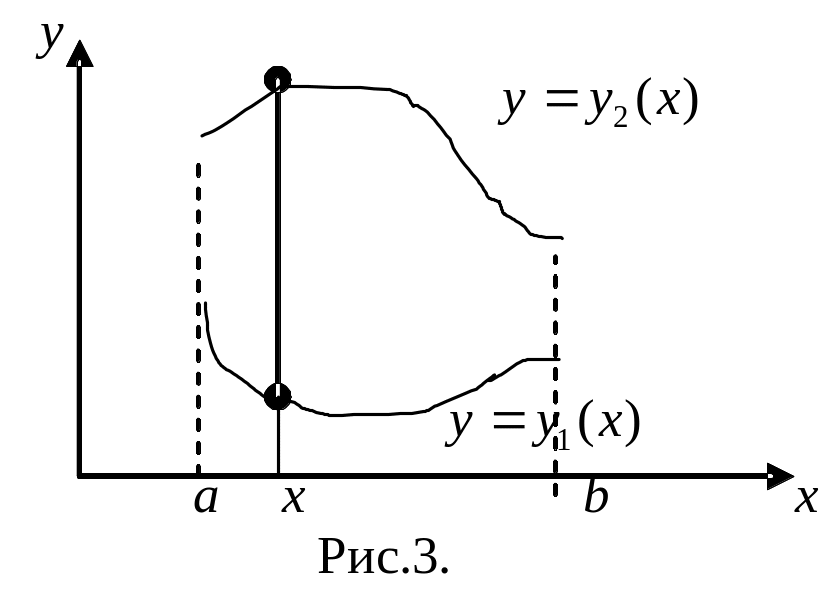
Область, в которой
всякая прямая параллельная оси![]()
,
проходящая через внутреннюю точку
области, пересекает ее границы в двух
точках, называется правильной
относительно
оси
(рис.3).
Аналогично
определяется о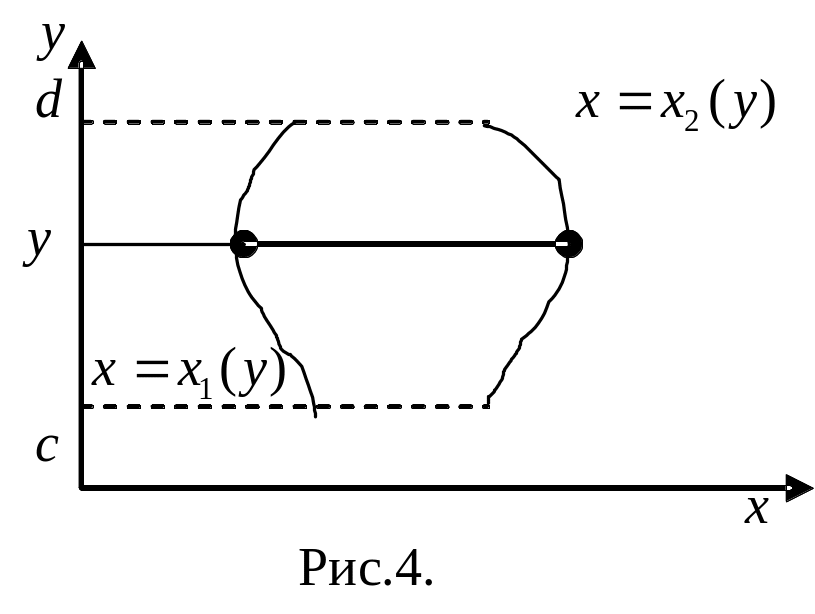
бласть
правильная
относительно оси![]()
:
![]()
где
функции
![]()
и
![]()
–
непрерывные функции на отрезке
![]()
(рис.4).
Выражения
вида
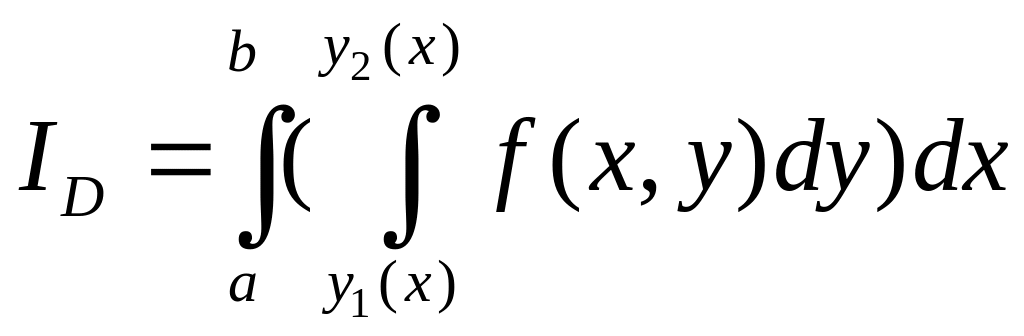
,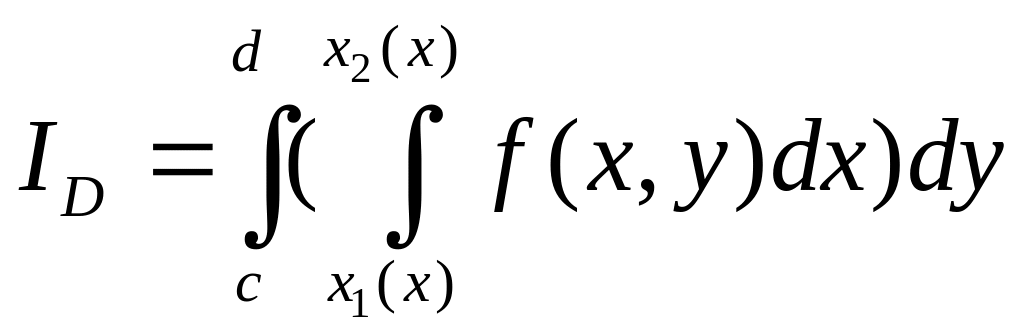
называются
повторными
интегралами
от функции
по
области
.
Теорема.
Двойной интеграл от непрерывной функции
по
правильной области
равен повторному интегралу от этой
функции по области
.
![]()
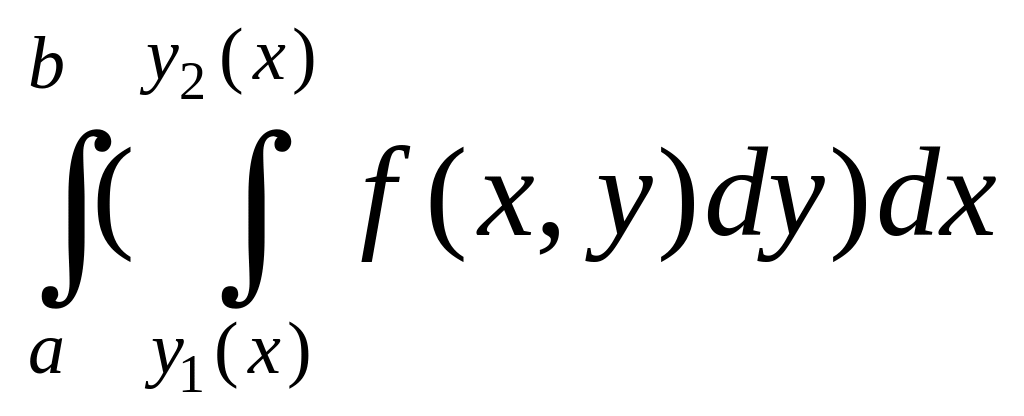
=
.
Если
область правильная относительно оси
,
то двойной интеграл вычисляется как
повторный вида
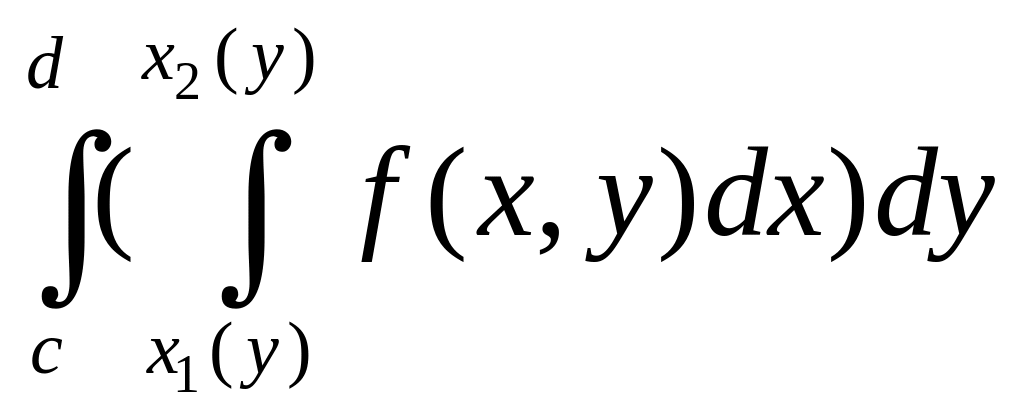
=
В
случае, когда область
не является правильной, ее разбивают
на части, каждая из которых является
правильной.
Частный
случай. Если
область интегрирования есть прямоугольник,
ограниченный прямыми
![]()
![]()
то
формула преобразования двойного
интеграла в повторный имеет вид
![]()
.
Если
кроме того, в подынтегральной функции
переменные разделены, то есть![]()
,
то двойной интеграл превращается в
произведение двух определенных
интегралов:
![]()
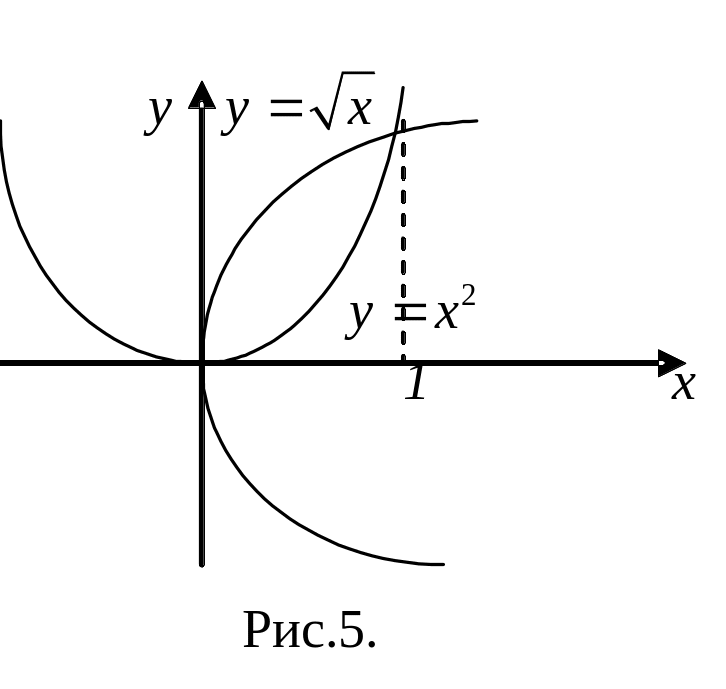
![]()
.
Пример.
Найти![]()
,
где
–
область, ограниченная линиями
![]()
(рис.5).
Решение.
=
=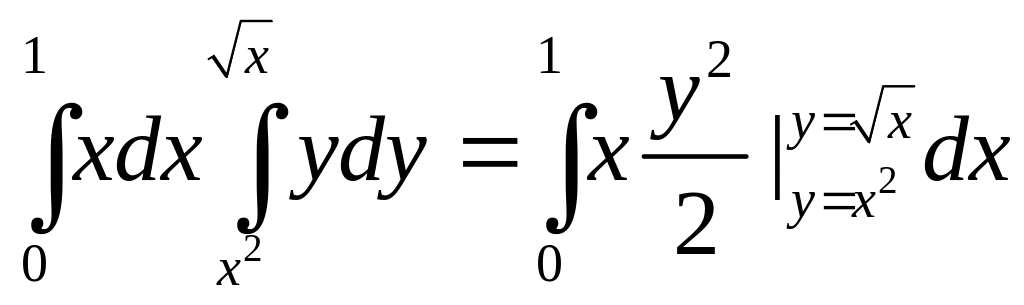
![]()
Пример.
Найти![]()
,
где
–
квадрат
![]()
(рис.6).

Решение.
=
=
![]()
![]()
Представление
двойного интеграла в виде повторного
=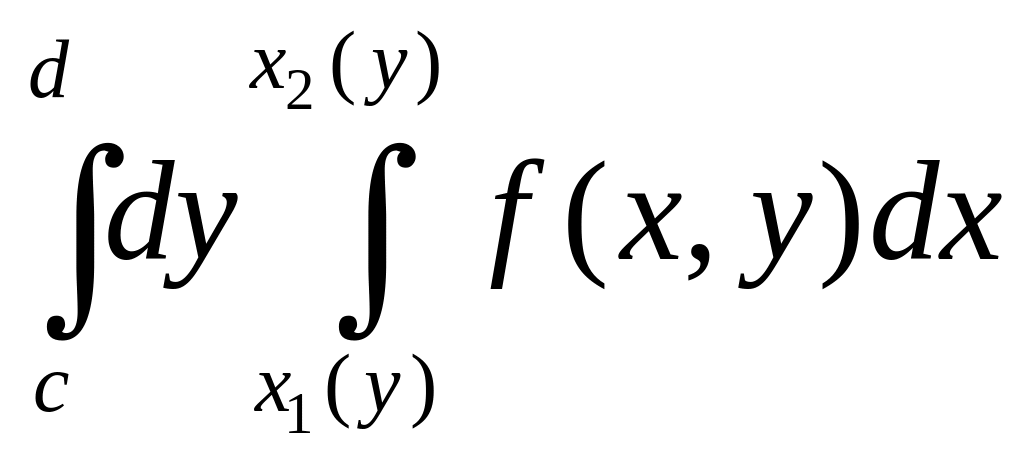
называют
расстановкой пределов интегрирования
в определенном порядке. Задача расстановки
пределов интегрирования допускает
несколько вариантов.
1.
Задан двойной интеграл по области
.
Расставить пределы интегрирования в
том и другом порядке.
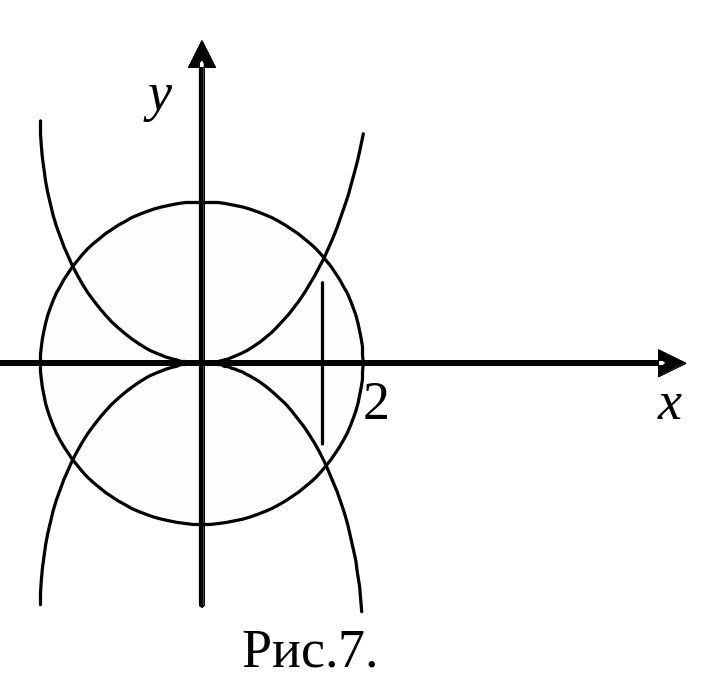
Пример. Область
лежит в правой полуплоскости (т.е.
![]()
и
ограничена
кривыми:
![]()
(рис.7). В двойном интеграле
расставить пределы интегрирования в
одном и другом порядке.
Решение.
Запишем неравенства, которым должны
удовлетворять координаты точек области
:
![]()
![]()
или
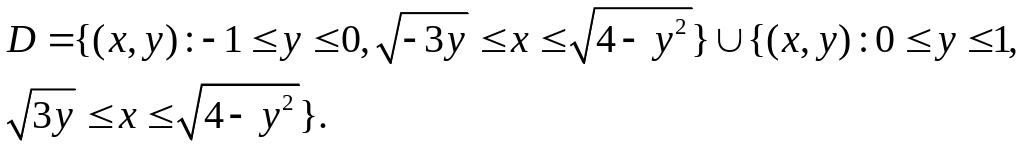
Расставим
пределы интегрирования
=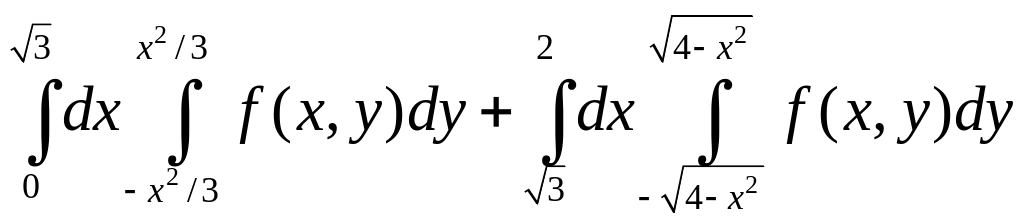
=

2.
Задан двойной интеграл по области
.
Расставить пределы интегрирования в
каком-либо порядке.
В
этом случае выбирают порядок
интегрирования, при котором интеграл
имеет наиболее простое представление.
Выбор может определяться как видом
области интегрирования, так и свойствами
подынтегральной функции. Например,
расстановка пределов в одном порядке
требует разбиения множества
на меньшее число составляющих, чем
расстановка в другом порядке.

Пример. Расставить
пределы интегрирования в интеграле
,
где
–
область ограниченная линиями:![]()
,
![]()
,![]()
(рис.8).
Решение.
Для расстановки пределов интегрирования
в порядке
![]()
можно не разбивать
на составляющие области, а для другого
порядка расстановки пределов такое
разбиение необходимо. Исходя из этого
выбираем порядок
.
Решая систему
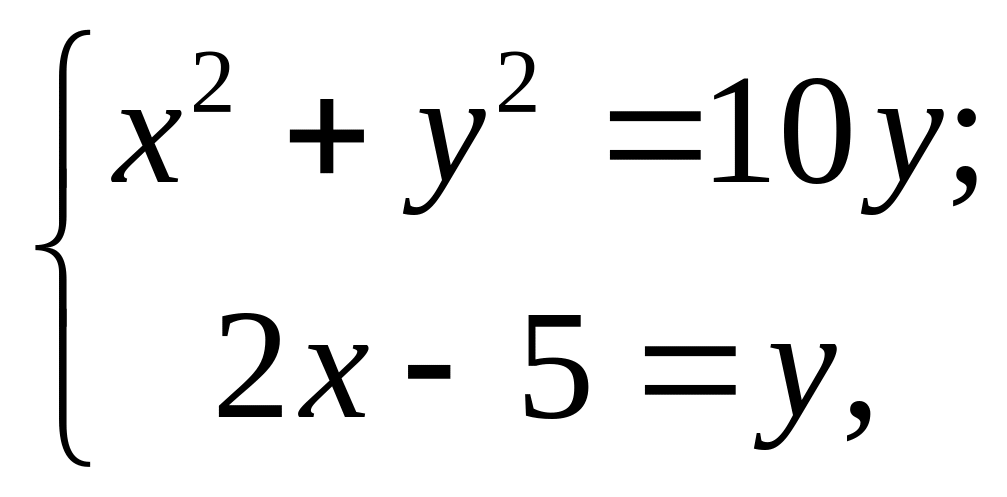
получаем координаты точек пересечения:![]()
.
Следовательно,
![]()
и
=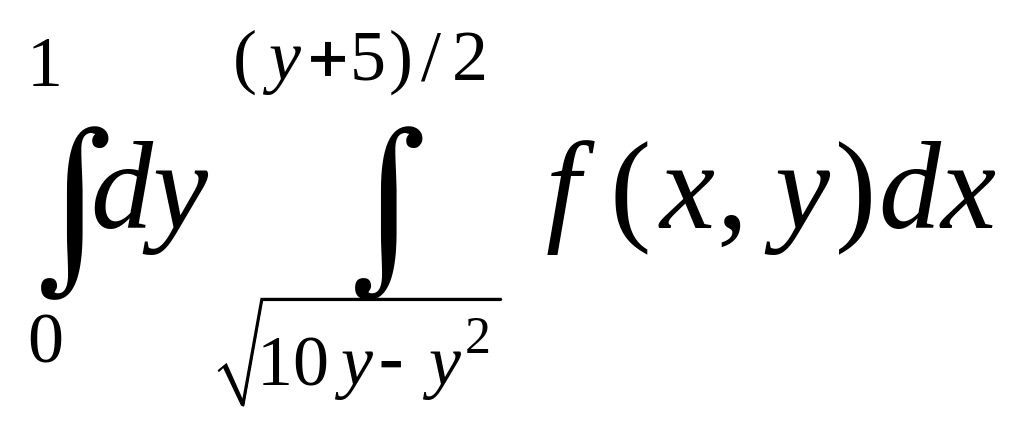
.
3.Задан
повторный интеграл
.
Поменять порядок интегрирования.
Для
решения такой задачи сначала делают
переход от заданного повторного интеграла
к двойному, то есть восстанавливают по
данным пределам область интегрирования
:
=
.
Условия на координаты точек (![]()
множества
получаем исходя из заданного повторного
интеграла
![]()
![]()
.
В полученном двойном интеграле проведем
расстановку пределов интегрирования
в требуемом порядке. Таким образом,
считая область
правильной относительно обеих осей
и
,
получаем цепочку равенств
=
=
.

Пример. Изменить
порядок интегрирования в повторном
интеграле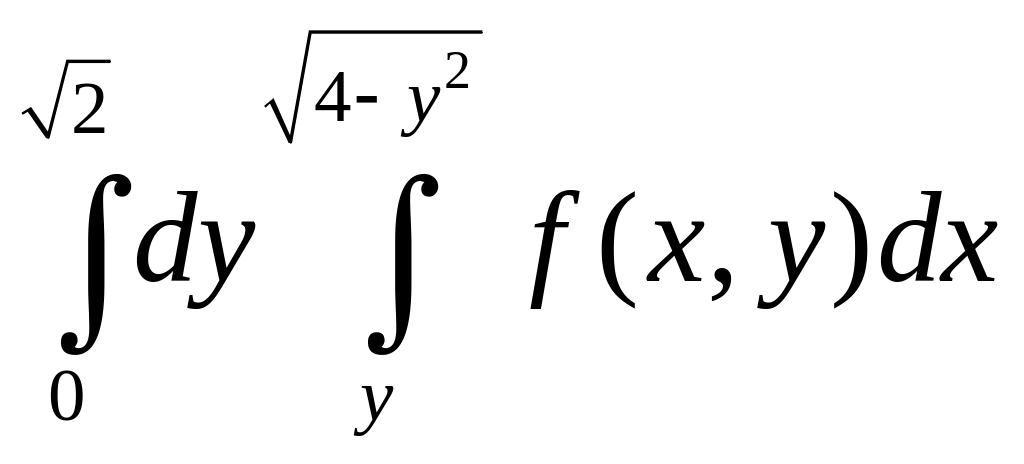
.
Решение.
Запишем условие на координаты точек
![]()
из множества
,
по которому берется
интеграл:
![]()
(рис.9).
Область
правильная как относительно оси
,
так и относительно оси
.
Так как при интегрировании в порядке
![]()
верхняя граница области
задается двумя различными функциями,
представим множество
в виде![]()
,
где

Итак,
=
.
Двойной
интеграл в полярной системе координат
Выведем
формулу перехода от декартовых координат
к полярным в двойном интеграле.
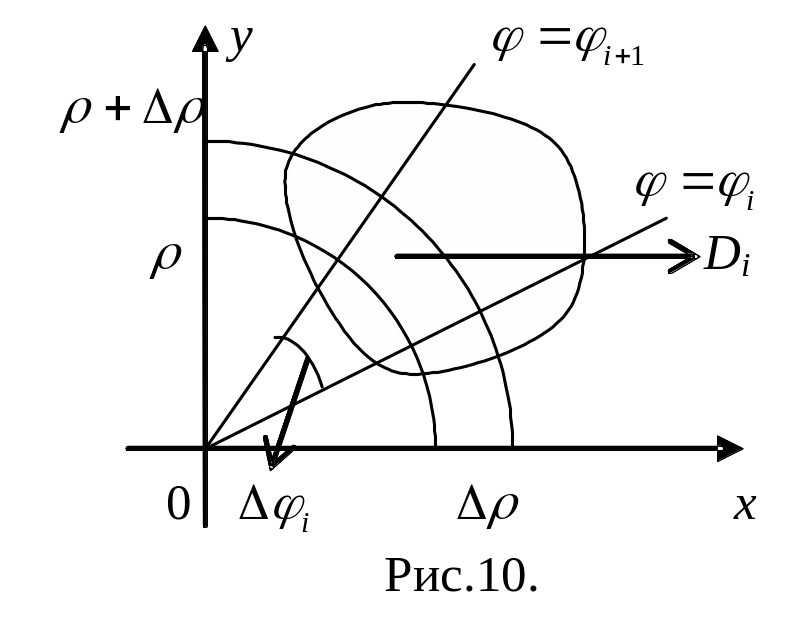
Пусть
– непрерывная функция на ограниченной
замкнутой области
.
Так как при определении двойного
интеграла предел последовательности
интегральных сумм не зависел от способа
разбиения области
на
части
,
то разобьем область
на
концентрическими окружностями
![]()
и лучами
![]()
(рис.10). Тогда площадь
![]()
с
точностью до бесконечно малых более
высокого порядка малости чем
![]()
.
Таким образом, двумерный элемент
площади в полярных координатах
запишется в виде
![]()
.

Пусть теперь
область
правильная относительно![]()
,
то есть любой луч, исходящий из полюса
и проходящий через внутреннюю точку
области пересекает границу области
только в двух точках. В этом случае
область
можно задать множеством
![]()
(рис.11).
Тогда повторный интеграл по области
представим в виде

Е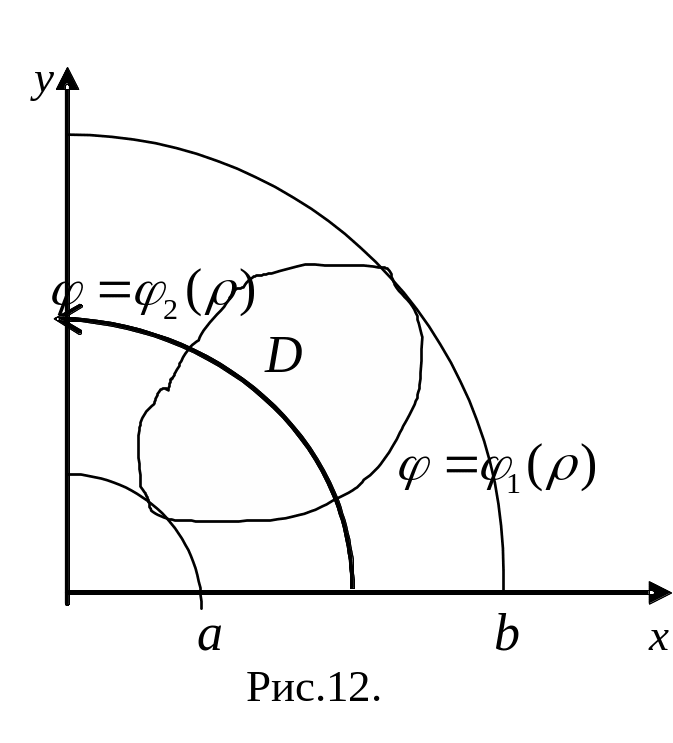
сли
любая окружность с центром в начале
координат, проходящая через внутреннюю
точку области пересекает линию границы
в двух точках, то есть область
есть множество:
![]()

,
(рис.12), то повторный интеграл примет
вид
![]()
=
В
случае, когда полюс лежит внутри области
и любой луч пересекает границу не более
чем в одной точке (рис.13), для вычисления
удобно использовать формулу

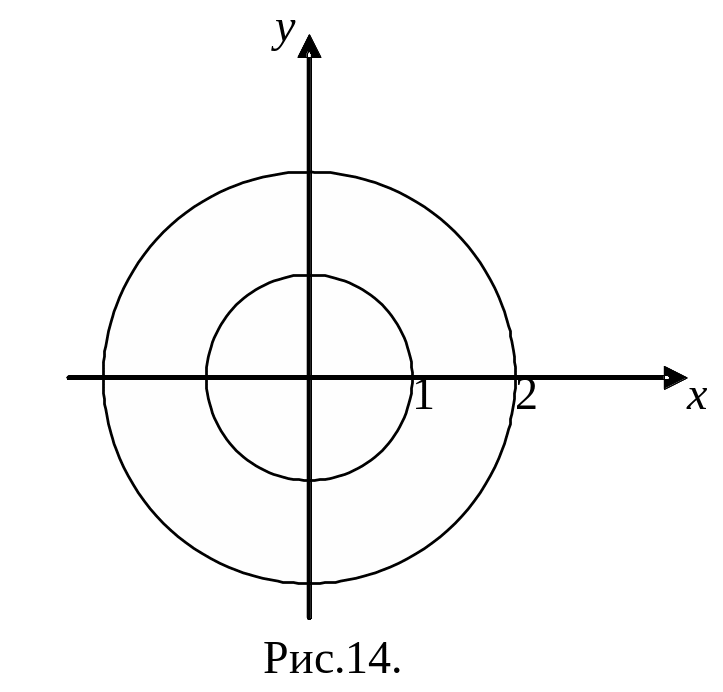
Пример.
Вычислить двойной интеграл
![]()
в
полярной
системе координат по области
,
ограниченной линиями![]()
,
расположенной в I
квадранте (рис.14).
Решение.
![]()
![]()
![]()
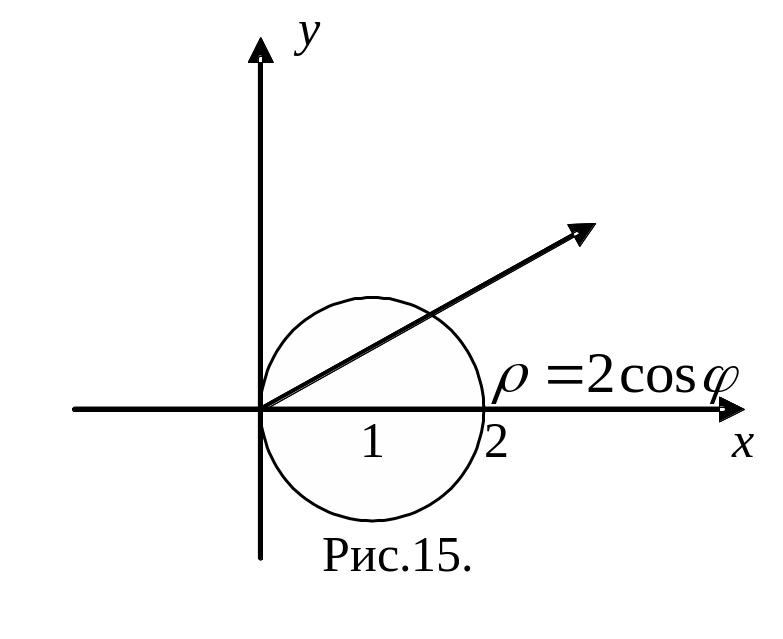
Пример. Вычислить
двойной интеграл
![]()
в полярной системе координат по области
,
ограниченной окружностью![]()
(рис.15).
Решение.
Перейдем к полярным координатам c
полюсом в точке
![]()
:![]()
Угол
![]()
изменяется от
![]()
до
![]()
Подставляя полярные
координаты
в уравнение окружности, получим![]()
,
откуда
![]()
или
![]()
– уравнение окружности в полярных
координатах. Двойной интеграл по области
сводится повторному
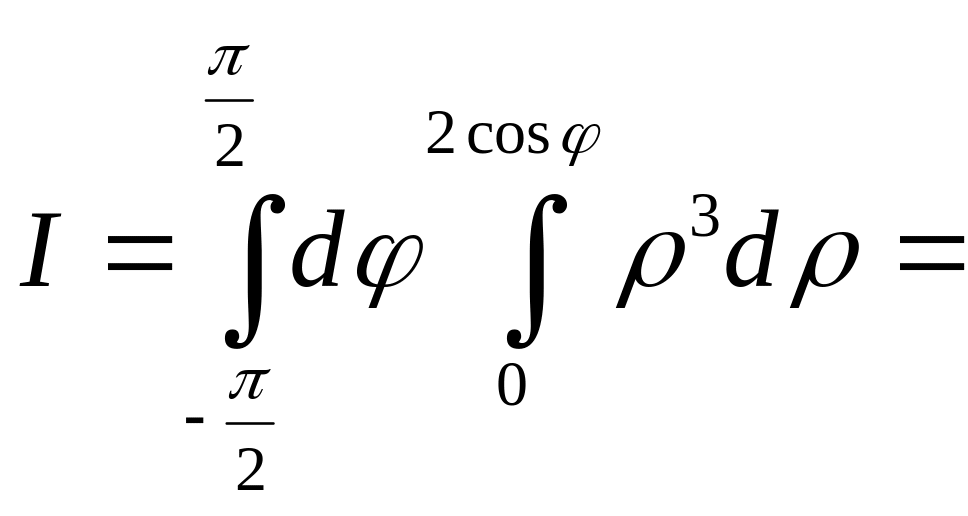

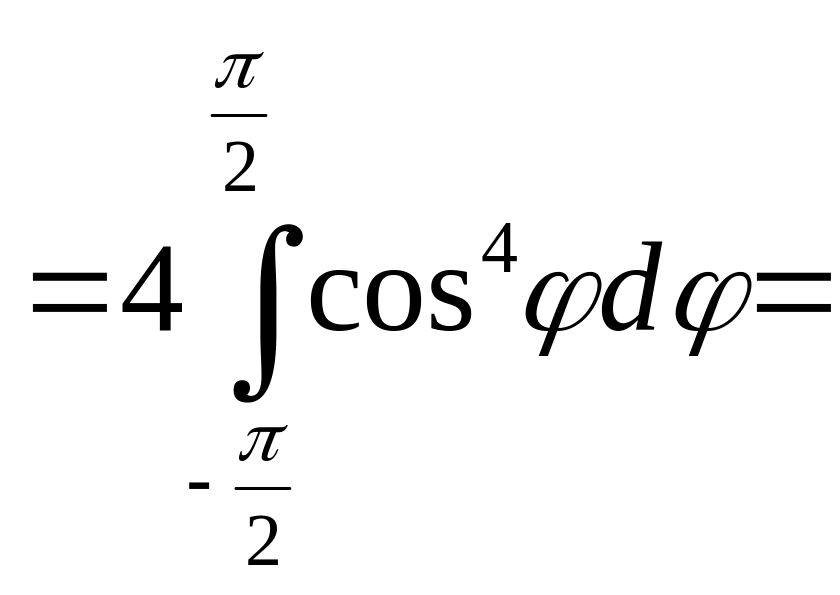
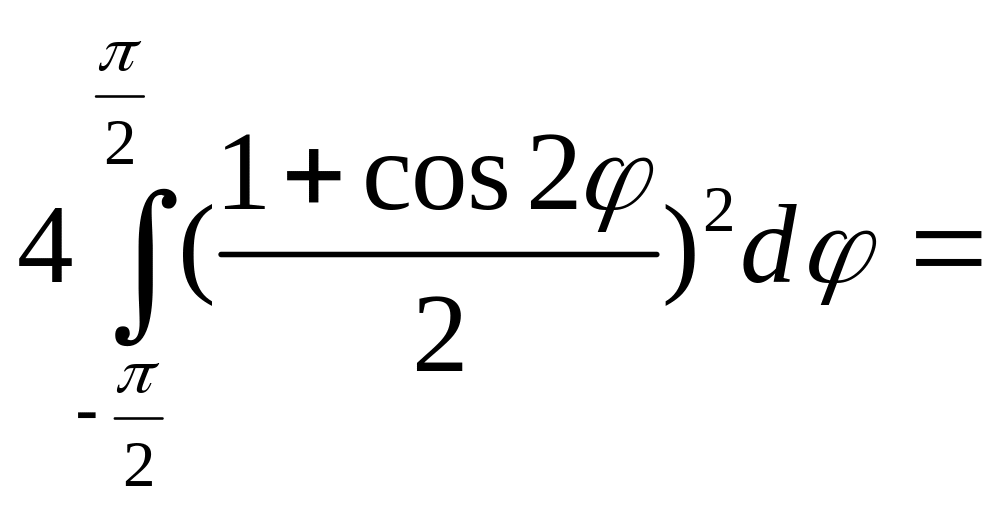

=![]()
![]()
![]()
Замена
переменных в двойном интеграле.
Рассмотрим
двойной интеграл вида
.
Замена переменных в двойном интеграле
состоит в переходе от
переменных
![]()
и
![]()
к новым переменным
![]()
и
![]()
по формулам
![]()
,![]()
.
При этом каждая точка
области
соответствует некоторой точке
![]()
области![]()
,
а каждая точка
области
переходит в некоторую точку
области
![]()
Функции
называют также отображением области
плоскости
на область
плоскости
.
Пусть отображение удовлетворяет
следующим условиям:
1.
Отображение взаимно однозначно, то есть
различным точкам
![]()
области
соответствуют различные точки
![]()
области
.
2.Функции
имеют
в области
непрерывные частные производные первого
порядка.
3.
Якобиан отображения![]()
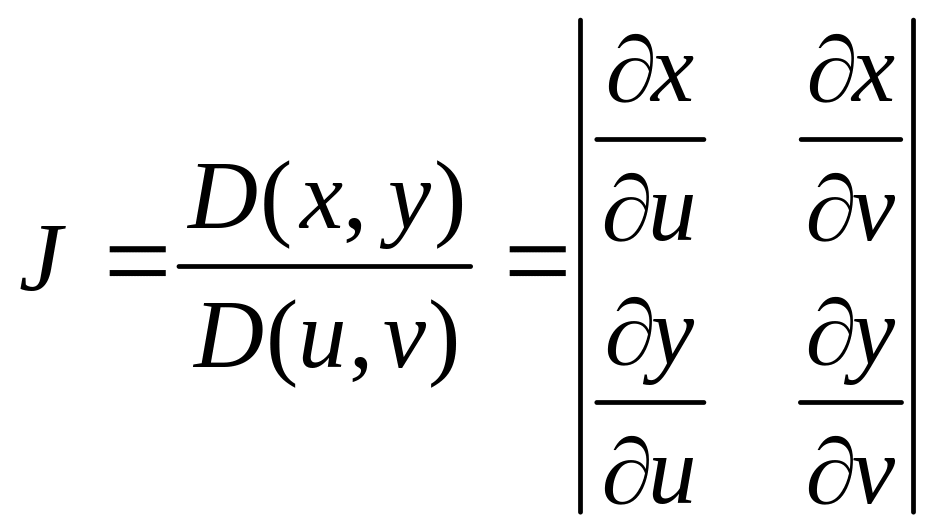
отличен от нуля во всех точках области
.
Тогда
справедливо равенство
=![]()
Эта
формула называется формулой замены
переменных в
двойном
интеграле.
Замечание.
При переходе к полярной системе координат
якобиан перехода имеет вид
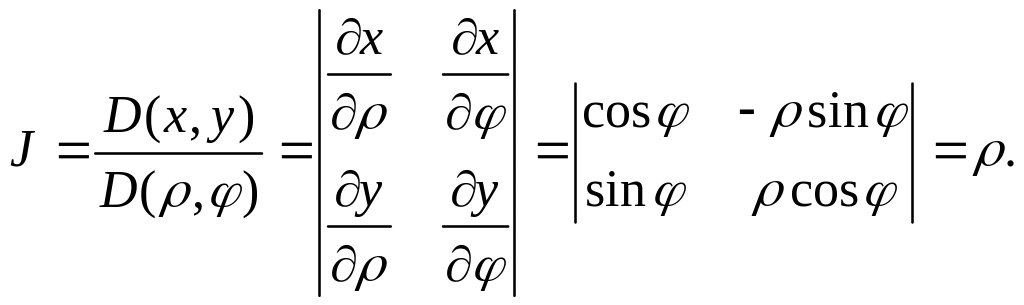
Приложения
двойных интегралов.
Двойные
интегралы применяются для вычисления
площадей плоских фигур и поверхностей,
объемов пространственных тел, механических
величин связанных с непрерывным
распределением массы в плоской области,
а также для решения многих других задач.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Обобщением определенного интеграла на случай функций двух переменных является так называемый двойной интеграл.
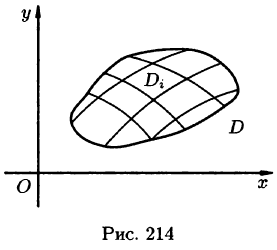
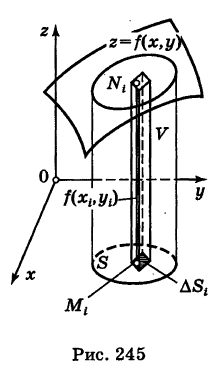
Пусть в замкнутой облас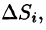 ти D плоскости Оху задана непрерывная функция z = f(x;y). Разобьем область D на п «элементарных областей»
ти D плоскости Оху задана непрерывная функция z = f(x;y). Разобьем область D на п «элементарных областей» 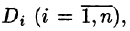 площади которых обозначим через
площади которых обозначим через 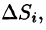 а диаметры (наибольшее расстояние между точками области) — через
а диаметры (наибольшее расстояние между точками области) — через 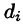 (см. рис. 214).
(см. рис. 214).
В каждой области  выберем произвольную точку
выберем произвольную точку 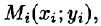 умножим значение
умножим значение 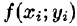 функции в этой точке на
функции в этой точке на 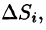 и составим сумму всех таких произведений:
и составим сумму всех таких произведений:
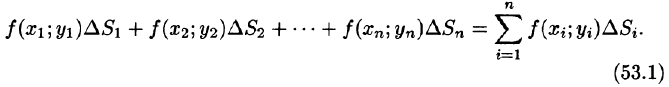
Эта сумма называется интегральной суммой функции f(x; у) в области D.
Рассмотрим предел интегральной суммы (53.1), когда п стремится к бесконечности таким образом, что 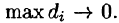 Если этот предел существует и не зависит ни от способа разбиения области D на части, ни от выбора точек в них, то он называется двойным интегралом от функции f(x;y) по области D и обозначается
Если этот предел существует и не зависит ни от способа разбиения области D на части, ни от выбора точек в них, то он называется двойным интегралом от функции f(x;y) по области D и обозначается
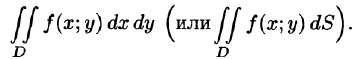
Таким образом, двойной интеграл определяется равенством
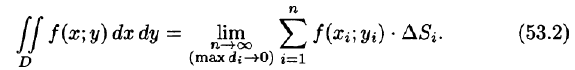
В этом случае функция f(x;y) называется интегрируемой в области D; D — область интегрирования; х и у — переменные интегрирования; dx dy (или dS) — элемент площади.
Для всякой ли функции f(x; у) существует двойной интеграл? На этот вопрос отвечает следующая теорема, которую мы приведем здесь без доказательства.
Теорема:
Достаточное условие интегрируемости функции. Если функция z = f(x;y) непрерывна в замкнутой области D, то она интегрируема в этой области.
Замечания:
- Далее будем рассматривать только функции, непрерывные в области интегрирования, хотя двойной интеграл может существовать не только для непрерывных функций.
- Из определения двойного интеграла следует, что для интегрируемой в области D функции предел интегральных сумм существует и не зависит от способа разбиения области. Таким образом, мы можем разбивать область D на площадки прямыми, параллельными координатным осям (см. рис. 215). При этом
 равенство (53.2) можно записать в виде
равенство (53.2) можно записать в виде
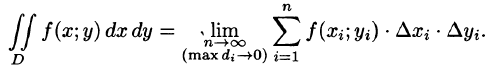
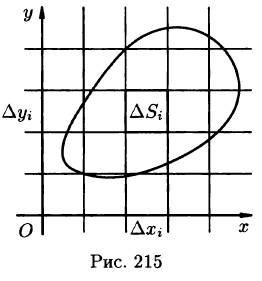

Геометрический и физический смысл двойного интеграла
Рассмотрим две задачи, приводящие к двойному интегралу. Объем цилиндрического тела
Рассмотрим тело, ограниченное сверху поверхностью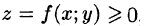 , снизу — замкнутой областью D плоскости Оху, с боков — цилиндрической поверхностью, образующая которой параллельна оси Oz, а направляющей служит граница области D (см. рис. 216). Такое тело называется цилиндрическим. Найдем его объем V. Для этого разобьем область D (проекция поверхности z = f(x; у) на плоскость Оху) произвольным образом на п областей
, снизу — замкнутой областью D плоскости Оху, с боков — цилиндрической поверхностью, образующая которой параллельна оси Oz, а направляющей служит граница области D (см. рис. 216). Такое тело называется цилиндрическим. Найдем его объем V. Для этого разобьем область D (проекция поверхности z = f(x; у) на плоскость Оху) произвольным образом на п областей  , площади которых равны A
, площади которых равны A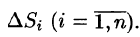 Рассмотрим цилиндрические столбики с основаниями ограниченные сверху кусками поверхности z = f(x;y) (на рис. 216 один из них выделен). В своей совокупности они составляют тело V. Обозначив объем столбика с основанием
Рассмотрим цилиндрические столбики с основаниями ограниченные сверху кусками поверхности z = f(x;y) (на рис. 216 один из них выделен). В своей совокупности они составляют тело V. Обозначив объем столбика с основанием  через
через 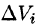 , получим
, получим
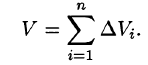
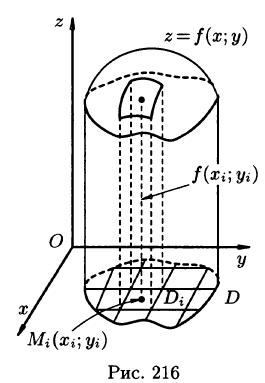
Возьмем на каждой площадке Di произвольную точку 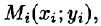 и заменим каждый столбик прямым цилиндром с тем же основанием
и заменим каждый столбик прямым цилиндром с тем же основанием  и высотой
и высотой 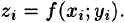 Объем этого цилиндра приближенно равен объему
Объем этого цилиндра приближенно равен объему 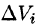 цилиндрического столбика, т. е.
цилиндрического столбика, т. е. 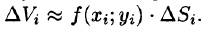 Тогда получаем:
Тогда получаем:
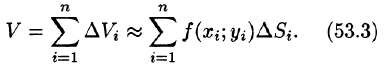
Это равенство тем точнее, чем больше число п и чем меньше размеры «элементарных областей»  ,. Естественно принять предел суммы (53.3) при условии, что число площадок
,. Естественно принять предел суммы (53.3) при условии, что число площадок  неограниченно увеличивается
неограниченно увеличивается 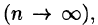 а каждая площадка стягивается в точку
а каждая площадка стягивается в точку 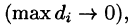 за объем V цилиндрического тела, т. е.
за объем V цилиндрического тела, т. е.
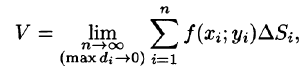
или, согласно равенству (53.2),
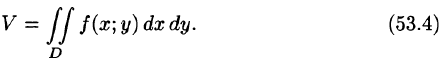
Итак, величина двойного интеграла от неотрицательной функции равна объему цилиндрического тела. В этом состоит геометрический смысл двойного интеграла.
Масса плоской пластинки
Требуется найти массу m плоской пластинки D. зная, что ее поверхностная плотность 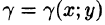 есть непрерывная функция координат точки (х; у). Разобьем пластинку D на п элементарных частей
есть непрерывная функция координат точки (х; у). Разобьем пластинку D на п элементарных частей 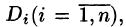 площади которых обозначим через
площади которых обозначим через 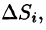 . В каждой области
. В каждой области  возьмем произвольную точку
возьмем произвольную точку 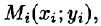 и вычислим плотность в ней:
и вычислим плотность в ней: 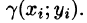
Если области D, достаточно малы, то плотность в каждой точке 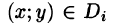 мало отличается от значения
мало отличается от значения 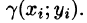 Считая приближенно плотность в каждой точке области
Считая приближенно плотность в каждой точке области  постоянной, равной
постоянной, равной 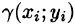 , можно найти ее массу
, можно найти ее массу 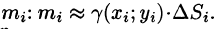 Так как масса m всей пластинки D равна
Так как масса m всей пластинки D равна 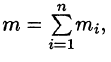 Для ее вычисления имеем приближенное равенство
Для ее вычисления имеем приближенное равенство
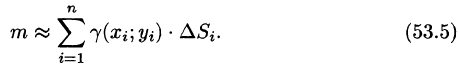
Точное значение массы получим как предел суммы (53.5) при условии 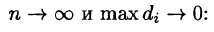
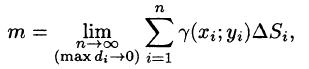
или, согласно равенству (53.2),
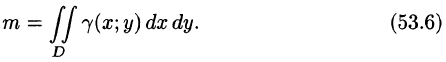
Итак, двойной интеграл от функции 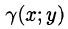 численно равен массе пластинки, если подынтегральную функцию
численно равен массе пластинки, если подынтегральную функцию 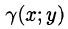 считать плотностью этой пластинки в точке (х; у). В этом состоит физический смысл двойного интеграла.
считать плотностью этой пластинки в точке (х; у). В этом состоит физический смысл двойного интеграла.
Основные свойства двойного интеграла
Можно заметить, что процесс построения интеграла в области D дословно повторяет уже знакомую нам процедуру определения интеграла функции одной переменной на отрезке (см. § 35). Аналогичны и свойства этих интегралов и их доказательства (см. § 38). Поэтому перечислим основные свойства двойного интеграла, считая подынтегральные функции интегрируемыми.
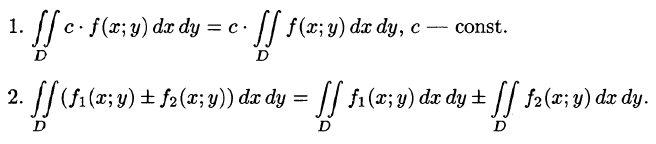
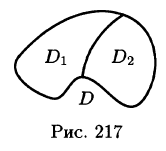
3.Если область D разбить линией на две области  такие, что
такие, что 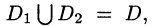 а пересечение
а пересечение 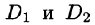 состоит лишь из линии, их разделяющей (см. рис. 217), то
состоит лишь из линии, их разделяющей (см. рис. 217), то
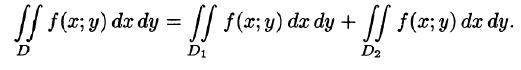
4.Если в области D имеет место неравенство 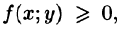 то и
то и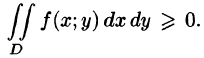 Если в области D функции f(x;y) и
Если в области D функции f(x;y) и 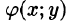 удовлетворяют неравенству
удовлетворяют неравенству 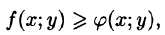 то и
то и
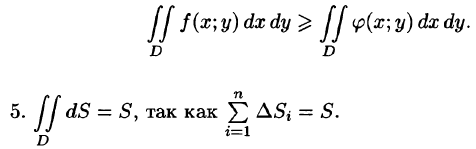
6.Если функция f(x;y) непрерывна в замкнутой области D, площадь которой 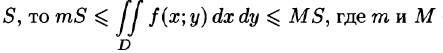 — соответственно наименьшее и наибольшее значения подынтегральной функции в области D.
— соответственно наименьшее и наибольшее значения подынтегральной функции в области D.
7.Если функция f(x;y) непрерывна в замкнутой области D, площадь которой S, то в этой области существует такая точка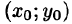 , что
, что 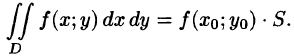 Величину
Величину
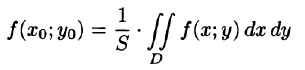
называют средним значением функции f(x; у) в области D.
Вычисление двойного интеграла в декартовых координатах
Покажем, что вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов.
Пусть требуется вычислить двойной интеграл 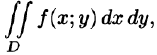 где функция
где функция 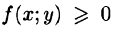 непрерывна в области D. Тогда, как это было показано в п. 53.2, двойной интеграл выражает объем цилиндрического тела, ограниченного сверху поверхностью z = f(x;y). Найдем этот объем, используя метод параллельных сечений. Ранее (см. (41.6)) было показано, что
непрерывна в области D. Тогда, как это было показано в п. 53.2, двойной интеграл выражает объем цилиндрического тела, ограниченного сверху поверхностью z = f(x;y). Найдем этот объем, используя метод параллельных сечений. Ранее (см. (41.6)) было показано, что
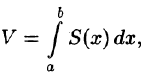
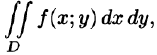
где S(x) — площадь сечения плоскостью, перпендикулярной оси Ох, а х = а, х = b — уравнения плоскостей, ограничивающих данное тело.
Положим сначала, что область D представляет собой криволинейную трапецию, ограниченную прямыми x = a и x = b и кривыми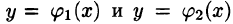 , причем функции
, причем функции 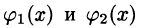 непрерывны и таковы, что
непрерывны и таковы, что 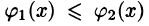 для всех
для всех 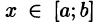 (см. рис. 218). Такая область называется правильной в направлении оси Оу: любая прямая, параллельная оси Оу, пересекает границу области не более чем в двух точках.
(см. рис. 218). Такая область называется правильной в направлении оси Оу: любая прямая, параллельная оси Оу, пересекает границу области не более чем в двух точках.
Построим сечение цилиндрического тела плоскостью, перпендикулярной оси 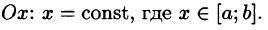
В сечении получим криволинейную трапецию ABCD, ограниченную линиями
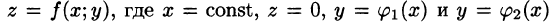
(см. рис. 219).
Площадь S(x) этой трапеции находим с помощью определенного интеграла
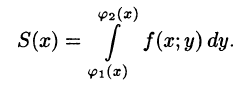
Теперь, согласно методу параллельных сечений, искомый объем цилиндрического тела может быть найден так:
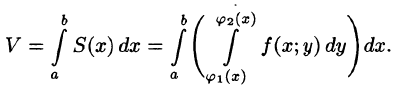
С другой стороны, в п. 53.2 было доказано, что объем цилиндрического тела определяется как двойной интеграл от функции 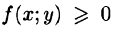 по области D. Следовательно,
по области D. Следовательно,
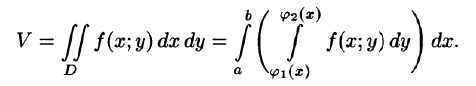
Это равенство обычно записывается в виде
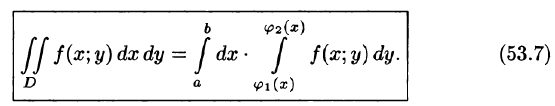
Формула (53.7) представляет собой способ вычисления двойного интеграла в декартовых координатах. Правую часть формулы (53.7) называют двукратным (или повторным) интегралом от функции f(x;y) по области D. При этом 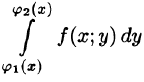 называется внутренним интегралом.
называется внутренним интегралом.
Для вычисления двукратного интеграла сначала берем внутренний интеграл, считая х постоянным, затем берем внешний интеграл, т. е. результат первого интегрирования интегрируем по х в пределах от а до b.
Если же область D ограничена прямыми 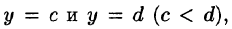 кривыми
кривыми
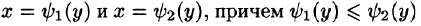
для всех 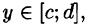 т. е. область D — правильная в направлении оси Ох, то, рассекая тело плоскостью у = const, аналогично получим:
т. е. область D — правильная в направлении оси Ох, то, рассекая тело плоскостью у = const, аналогично получим:
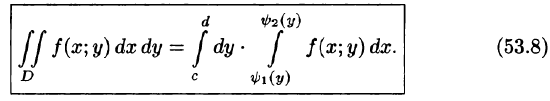
Здесь, при вычислении внутреннего интеграла, считаем у постоянным.
Замечания:
- Формулы (53.7) и (53.8) справедливы и в случае, когда
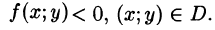
- Если область D правильная в обоих направлениях, то двойной интеграл можно вычислять как по формуле (53.7), так и по формуле (53.8).
- Если область D не является правильной ни «по x», ни «по у», то для сведения двойного интеграла к повторным ее следует разбить на части, правильные в направлении оси Ох или оси Оу.
- Полезно помнить, что внешние пределы в двукратном интеграле всегда постоянны, а внутренние, как правило, переменные.
Пример:
Вычислить 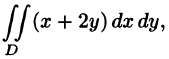 где область D ограничена линиями у
где область D ограничена линиями у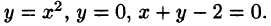
Решение:
На рисунке 220 изображена область интегрирования D. Она правильная в направлении оси Ох. Для вычисления данного двойного интеграла воспользуемся формулой (53.8):
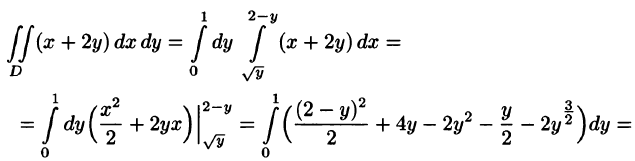
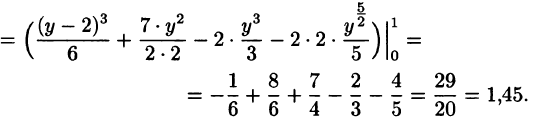
Отметим, что для вычисления данного двойного интеграла можно воспользоваться формулой (53.7). Но для этого область D следует разбить на две области: 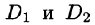 . Получаем:
. Получаем:
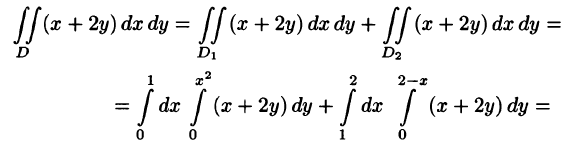
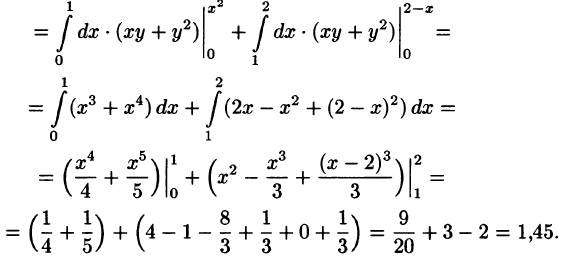
Ответ, разумеется, один и тот же.
Вычисление двойного интеграла в полярных координатах
Для упрощения вычисления двойного интеграла часто применяют метод подстановки (как это делалось и при вычислении определенного интеграла), т. е. вводят новые переменные под знаком двойного интеграла.
Определим преобразование независимых переменных х и у (замену переменных) как
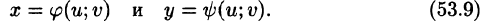
Если функции (53.9) имеют в некоторой области D* плоскости Ouv непрерывные частные производные первого порядка и отличный от нуля определитель

а функция f(х; у) непрерывна в области D, то справедлива формула замены переменных в двойном интеграле:
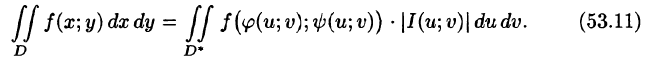
Функциональный определитель (53.10) называется определителем Якоби или якобианом (Г. Якоби — немецкий математик). Доказательство формулы (53.11) не приводим.
Рассмотрим частный случай замены переменных, часто используемый при вычислении двойного интеграла, а именно замену декартовых координат х и у полярными координатами 
В качестве инь возьмем полярные координаты  Они связаны с декартовыми координатами формулами
Они связаны с декартовыми координатами формулами 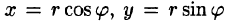 (см. п. 9.1).
(см. п. 9.1).
Правые части в этих равенствах — непрерывно дифференцируемые функции. Якобиан преобразования определяется из (53.10) как
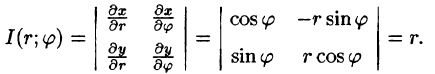
Формула замены переменных (53.11) принимает вид:
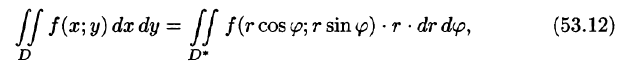
где D* — область в полярной системе координат, соответствующая области D в декартовой системе координат.
Для вычисления двойного интеграла в полярных координатах применяют то же правило сведения его к двукратному интегралу. Так, если
область D* имеет вид, изображенный на рисунке 221 (ограничена лучами и кривыми
и кривыми  где
где 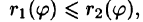 т. е. область D* правильная: луч, выходящий из полюса, пересекает ее границу не более чем в двух точках), то правую часть формулы (53.12) можно записать в виде
т. е. область D* правильная: луч, выходящий из полюса, пересекает ее границу не более чем в двух точках), то правую часть формулы (53.12) можно записать в виде
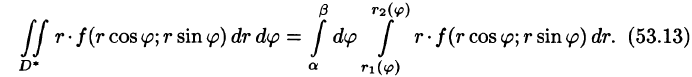
Внутренний интеграл берется при постоянном 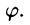
Замечания:
- Переход к полярным координатам полезен, когда подынтегральная функция имеет вид
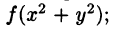 область D есть круг, кольцо или часть таковых.
область D есть круг, кольцо или часть таковых. - На практике переход к полярным координатам осуществляется путем замены
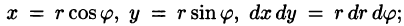 уравнения линий, ограничивающих область D, также преобразуются к полярным координатам. Преобразование области D в область D* не выполняют, а, совместив декартову и полярную системы координат, находят нужные пределы интегрирования по
уравнения линий, ограничивающих область D, также преобразуются к полярным координатам. Преобразование области D в область D* не выполняют, а, совместив декартову и полярную системы координат, находят нужные пределы интегрирования по  (исследуя закон изменения
(исследуя закон изменения  точки
точки 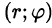 при ее отождествлении с точкой (х; у) области D).
при ее отождествлении с точкой (х; у) области D).
Пример:
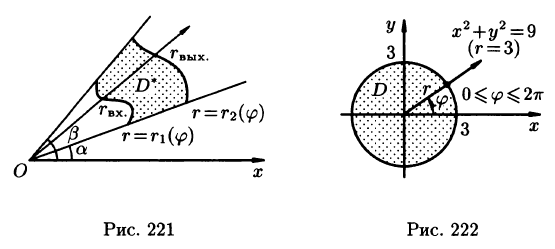
Вычислить 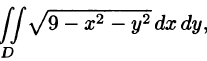 где область D — круг
где область D — круг 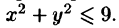
Решение: Применив формулу (53.12), перейдем к полярным координатам:
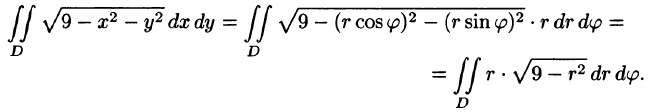
Область D в полярной системе координат определяется неравенствами (см. рис. 222) 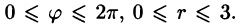 Заметим: область D —круг — преобразуется в область D* — прямоугольник. Поэтому, согласно формуле (53.13), имеем:
Заметим: область D —круг — преобразуется в область D* — прямоугольник. Поэтому, согласно формуле (53.13), имеем:
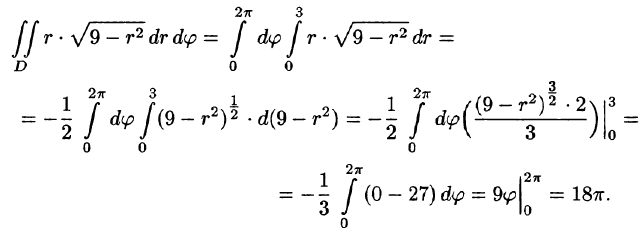
Приложения двойного интеграла
Приведем некоторые примеры применения двойного интеграла.
Объем тела
Как уже показано (п. 53.2), объем цилиндрического тела находится по формуле
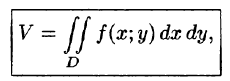
где z = f(x;y) — уравнение поверхности, ограничивающей тело сверху.
Площадь плоской фигуры
Если положить в формуле (53.4) f(x;y) = 1, то цилиндрическое тело «превратится» в прямой цилиндр с высотой Н = 1. Объем такого цилиндра, как известно, численно равен площади S основания D. Получаем формулу для вычисления площади S области D:
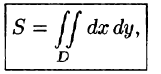
или, в полярных координатах,
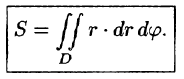
Масса плоской фигуры
Как уже показано (п. 53.2), масса плоской пластинки D с переменной плотностью 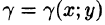 находится по формуле
находится по формуле
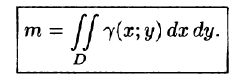
Статические моменты и координаты центра тяжести плоской фигуры
Статические моменты фигуры D относительно осей Ох и Оу (см. п. 41.6) могут быть вычислены по формулам
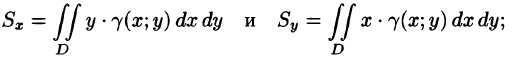
а координаты центра масс фигуры по формулам
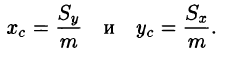
Моменты инерции плоской фигуры
Моментом инерции материальной точки массы m относительно оси l называется произведение массы m на квадрат расстояния d точки до оси, т. е. 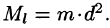 Моменты инерции плоской фигуры относительно осей Ох и Оу могут быть вычислены по формулам:
Моменты инерции плоской фигуры относительно осей Ох и Оу могут быть вычислены по формулам:
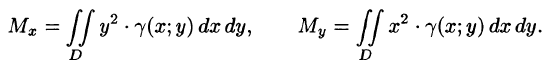
Момент инерции фигуры относительно начала координат — по формуле 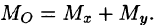
Замечание:
Приведенными примерами не исчерпывается применение двойного интеграла. Далее мы встретим приложение двойного интеграла к вычислению площадей поверхностей фигур (п. 57.3).
Пример:
Найти объем тела, ограниченного поверхностями
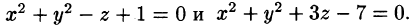
Решение: Данное тело ограничено двумя параболоидами (см. рис. 223). Решая систему
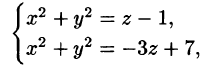
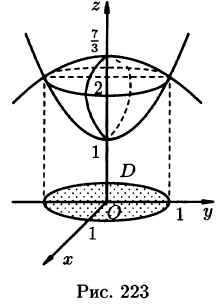
находим уравнение линии их пересечения:
Искомый объем равен разности объемов двух цилиндрических тел с одним основанием (круг 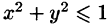 ) и ограниченных сверху соответственно поверхностями
) и ограниченных сверху соответственно поверхностями 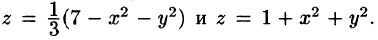 Используя формулу (53.4), имеем
Используя формулу (53.4), имеем
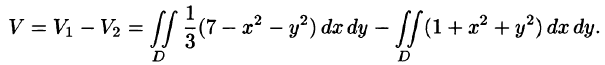
Переходя к полярным координатам, находим:
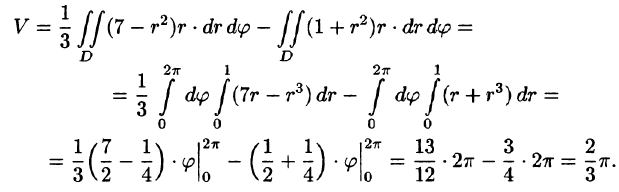
Пример:
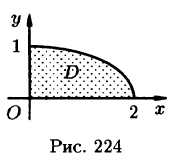
Найти массу, статические моменты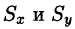 и координаты центра тяжести фигуры, лежащей в первой четверти, ограниченной эллипсом
и координаты центра тяжести фигуры, лежащей в первой четверти, ограниченной эллипсом 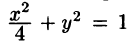 и координатными осями (см. рис. 224). Поверхностная плотность в каждой точке фигуры пропорциональна произведению координат точки.
и координатными осями (см. рис. 224). Поверхностная плотность в каждой точке фигуры пропорциональна произведению координат точки.
Решение: По формуле (53.6) находим массу пластинки. По условию, 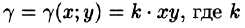 — коэффициент пропорциональности.
— коэффициент пропорциональности.
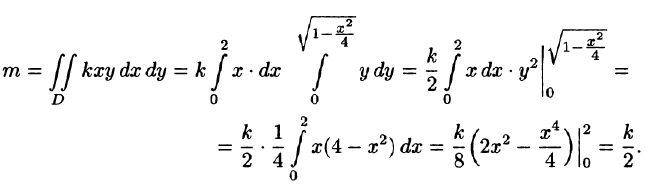
Находим статические моменты пластинки:
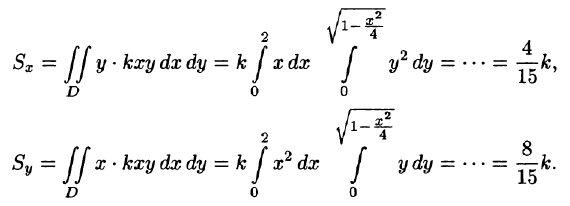
Находим координаты центра тяжести пластинки, используя формулы
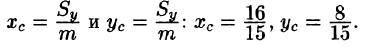
Двойной интеграл












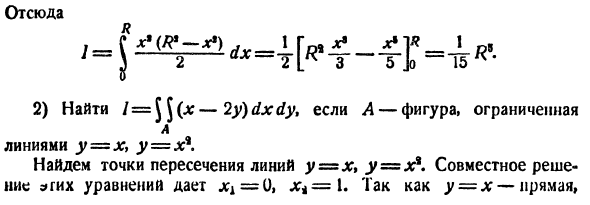

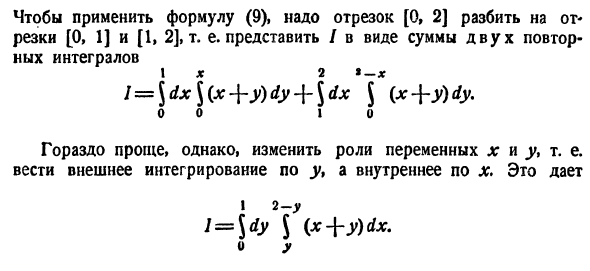

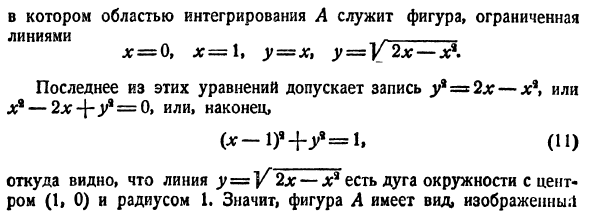














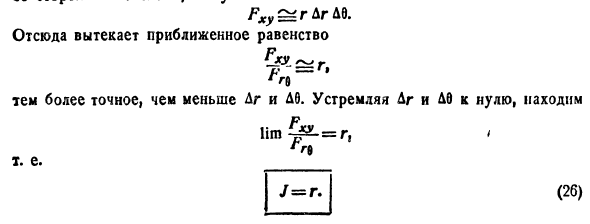












Смотрите также:
Предмет высшая математика
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат

Содержание:
Двойные и тройные интегралы
Понятие двойного интеграла
В теории определенного интеграла для нахождения площади криволинейной трапеции было введено понятие интегральной суммы, пределом которой является определенный интеграл. На основе задачи об определении объема тела мы придем к понятию двумерной интегральной суммы, предел которой называется двойным интегралом.
Пример:
Найти объем тела, ограниченного сверху непрерывной поверхностью z = f(x, у) (f(x, у) 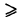
Тело указанного вида для краткости называется цилиндроидом. В частном случае, когда верхнее основание цилиндроида есть плоскость, параллельная нижнему основанию его, то цилиндроид называется цилиндром. Примером цилиндра служит круговой цилиндр, рассматриваемый в средней школе. Обобщая рассуждение, обычно применяемое для нахождения объема кругового цилиндра, нетрудно доказать, что объем V цилиндра с площадью основания S и высотой Н равен V = SH.
Для вычисления объема V данного цилиндроида разобьем основание его S на конечное число элементарных ячеек  (вообще говоря, криволинейных). В каждой из этих ячеек
(вообще говоря, криволинейных). В каждой из этих ячеек  выберем точку
выберем точку  и построим прямой цилиндрический столбик с основанием
и построим прямой цилиндрический столбик с основанием 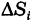 и высотой
и высотой 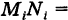
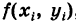 , равной аппликате поверхности в выбранной точке.
, равной аппликате поверхности в выбранной точке.
Объем такого столбика на основании формулы объема цилиндра, очевидно, равен

где 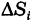 — площадь соответствующей ячейки. Сумма объемов этих цилиндрических столбиков представляет собой объем ступенчатого тела, приближенно заменяющего данное криволинейное тело, причем аппроксимация является, вообще говоря, тем более точной, чем меньше диаметры ячеек
— площадь соответствующей ячейки. Сумма объемов этих цилиндрических столбиков представляет собой объем ступенчатого тела, приближенно заменяющего данное криволинейное тело, причем аппроксимация является, вообще говоря, тем более точной, чем меньше диаметры ячеек 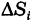 . Поэтому объем нашего цилиндроида приближенно выразится суммой
. Поэтому объем нашего цилиндроида приближенно выразится суммой
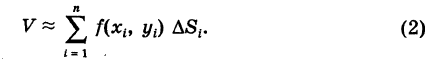
Формула (2) дает возможность найти объем V с любой степенью точности, если число ячеек 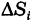 достаточно велико и линейные размеры их весьма малы. Обозначим через d1 диаметр ячейки
достаточно велико и линейные размеры их весьма малы. Обозначим через d1 диаметр ячейки 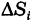 т. е. наибольший линейный размер ее. Точнее говоря, под диаметром d ограниченной замкнутой (т. е. с присоединенной границей) фигуры Ф (дуги, площадки и т. п.) понимается длина наибольшей ее хорды АВ, где
т. е. наибольший линейный размер ее. Точнее говоря, под диаметром d ограниченной замкнутой (т. е. с присоединенной границей) фигуры Ф (дуги, площадки и т. п.) понимается длина наибольшей ее хорды АВ, где 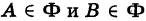 (рис. 246).
(рис. 246).
Из данного определения следует, что фигура Ф, имеющая диаметр d, целиком помещается внутри круга радиуса d, описанного из любой ее точки С как из центра. Поэтому если 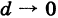 , то фигура Ф «стягивается в точку». Аналогично определяется диаметр пространственного тела.
, то фигура Ф «стягивается в точку». Аналогично определяется диаметр пространственного тела.
Пусть
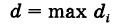
— наибольший из диаметров ячеек 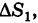
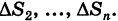 Предполагая, что в формуле (2) число ячеек п неограниченно возрастает
Предполагая, что в формуле (2) число ячеек п неограниченно возрастает 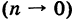 , причем диаметр наибольшей из них становится сколь угодно малым
, причем диаметр наибольшей из них становится сколь угодно малым 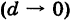 , в пределе получаем точную формулу для объема цилиндроида
, в пределе получаем точную формулу для объема цилиндроида
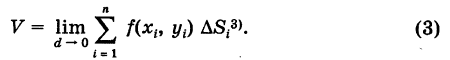
Здесь мы для удобства ячейки и их площади обозначаем одинаковыми буквами. Разница между ними видна из контекста.
Ячейки 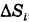 можно предполагать замкнутыми.
можно предполагать замкнутыми.
Точнее говоря, по определению под объемом цилиндроида понимается предел (3), если он существует.
Выражение, стоящее в правой части формулы (3), называется двойным интегралом от функции f(x, у), распространенным на область S, и обозначается следующим образом:
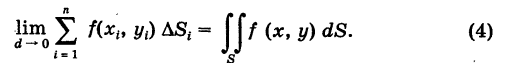
Поэтому для объема цилиндроида окончательно имеем
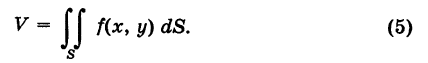
Обобщая конструкцию, примененную для вычисления объема цилиндроида, приходим к следующим определениям.
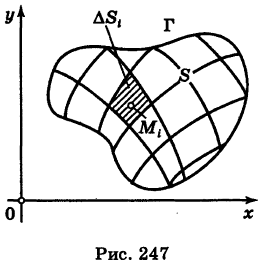
Определение: Двумерной интегральной суммой (2) от данной функции f(x9 у)> распространенной на данную область S, называется сумма парных произведений площадей элементарных ячеек 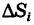 области S на значения
области S на значения 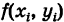 функции f(x, у) в выделенных точках этих ячеек (рис. 247).
функции f(x, у) в выделенных точках этих ячеек (рис. 247).
Определение: Двойным интегралом (4) от функции f(x, у), распространенным на данную область S, называется предел соответствующей двумерной интегральной суммы (2) при неограниченном возрастании числа п элементарных ячеек 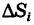 и стремлении к нулю их наибольшего диаметра d при условии, что этот предел существует и не зависит от способа дробления области S на элементарные ячейки
и стремлении к нулю их наибольшего диаметра d при условии, что этот предел существует и не зависит от способа дробления области S на элементарные ячейки  и выбора точек в них.
и выбора точек в них.
В формуле (4) у) называется подынтегральной функцией, S — областью интегрирования, a dS — элементом площади. Справедлива следующая теорема:
Теорема: Если область S с кусочно-гладкой границей Г ограничена и замкнута, а функция f(x, у) непрерывна в области S, то двойной интеграл
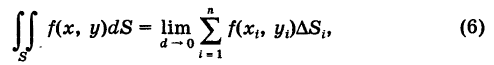
существует, т. е. предел соответствующей двумерной интегральной суммы существует и не зависит от способа дробления области S на элементарные ячейки  , и выбора точек в них.
, и выбора точек в них.
В дальнейшем мы будем предполагать, что условия этой теоремы выполнены.
В формуле (6) нет необходимости указывать, что 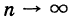 , так как из
, так как из 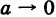 , очевидно, следует
, очевидно, следует 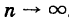 .
.
Если f(x, у) 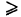 0, то двойной интеграл (6) представляет собой объем прямого цилиндроида, построенного на области S как на основании и ограниченного сверху поверхностью z = f(x, у) (геометрический смысл двойного интеграла).
0, то двойной интеграл (6) представляет собой объем прямого цилиндроида, построенного на области S как на основании и ограниченного сверху поверхностью z = f(x, у) (геометрический смысл двойного интеграла).
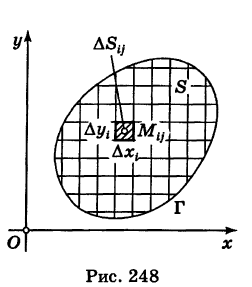
Так как значение двойного интеграла не зависит от вида элементарных ячеек, то в дальнейшем при решении задач мы будем использовать это обстоятельство, выбирая наиболее подходящие сетки. Весьма часто удобной оказывается прямоугольная сетка, образованная пересечением двух систем прямых, параллельных соответственно координатным осям Ох и Оу (рис. 248). В этом случае элементарными ячейками 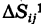 являются прямоугольники со сторонами, равными
являются прямоугольники со сторонами, равными 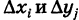 , за исключением, возможно, ячеек, примыкающих к границе Г.
, за исключением, возможно, ячеек, примыкающих к границе Г.
Чтобы подчеркнуть использование прямоугольной сетки, в обозначении интеграла (4) полагают
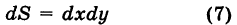
(двумерный элемент площади в прямоугольных координатах), причем
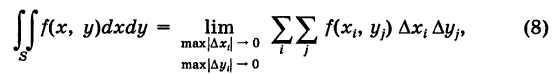
где 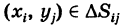 и сумма (8) распространяется на все значения i и для которых
и сумма (8) распространяется на все значения i и для которых 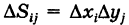 (можно показать, что непрямоугольные ячейки, примыкающие к кусочно-гладкой границе Г, не влияют на значение предела (8)).
(можно показать, что непрямоугольные ячейки, примыкающие к кусочно-гладкой границе Г, не влияют на значение предела (8)).
В следующих параграфах мы рассмотрим основные способы вычисления двойного интеграла.
Здесь мы применяем двойную индексацию ячеек, указывая отдельно номер i вертикальной полосы и номер j горизонтальной полосы, содержащих данную ячейку, подобно тому, как на билете в кино отмечается номер ряда и номер места.
Двойной интеграл в прямоугольных декартовых координатах
Предположим для определенности, что область интегрирования S представляет собой криволинейную трапецию (рис. 249);
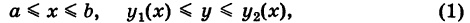
где 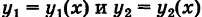 — однозначные непрерывные функции на отрезке
— однозначные непрерывные функции на отрезке 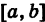 . Такую область будем называть стандартной относительно оси Оу. Заметим, что вертикаль, проходящая через точку х оси Ох при а < х < Ь, пересекает границу Г области S только в двух точках
. Такую область будем называть стандартной относительно оси Оу. Заметим, что вертикаль, проходящая через точку х оси Ох при а < х < Ь, пересекает границу Г области S только в двух точках 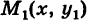 («точка входа») и
(«точка входа») и 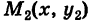 («точка выхода»).
(«точка выхода»).
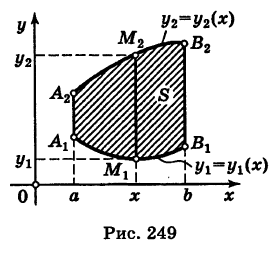
Пусть f(x, у) — функция, непрерывная в области S, и
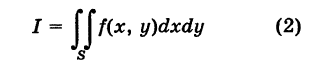
— ее двойной интеграл.
1) Предположим сначала, что 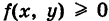 в области S. Тогда двойной интеграл I представляет собой объем цилиндроида (рис. 250), ограниченного снизу областью S, сверху поверхностью z = f(x, у) и с боков прямой цилиндрической поверхностью.
в области S. Тогда двойной интеграл I представляет собой объем цилиндроида (рис. 250), ограниченного снизу областью S, сверху поверхностью z = f(x, у) и с боков прямой цилиндрической поверхностью.
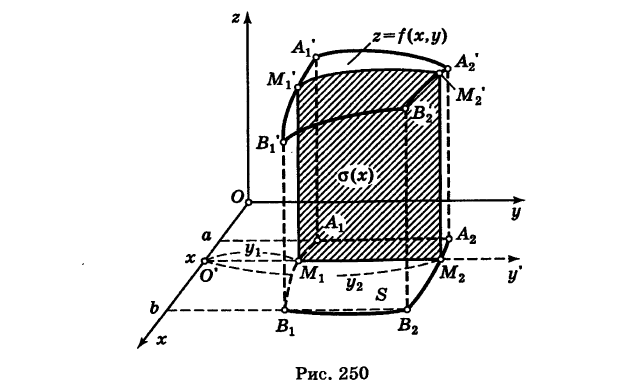
Для вычисления объема I применим метод сечений. А именно, пусть а(х) — площадь сечения цилиндроида плоскостью  перпендикулярной оси Ох в точке ее
перпендикулярной оси Ох в точке ее 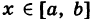 (рис. 250).
(рис. 250).
Тогда имеем

Но а(х) представляет собой площадь криволинейной трапеции, ограниченной снизу отрезком 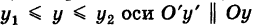 и сверху кривой z = f(x, у) х = const. Поэтому
и сверху кривой z = f(x, у) х = const. Поэтому
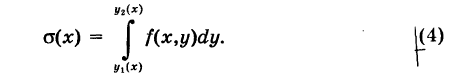
Можно доказать, что при наших условиях а(х) непрерывна при 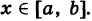
Подставляя выражение (4) в формулу (3), получим окончательно
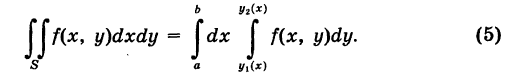
Таким образом, двойной интеграл равен соответствующему повторному интегралу (5), т. е. вычисление двойного интеграла сводится к двум квадратурам. Заметим, что при вычислении внутреннего интеграла в формуле (5) х рассматривается как постоянная величина.
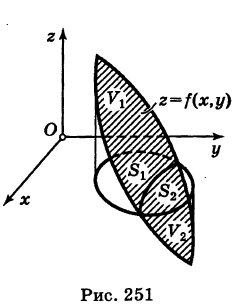
2) В случае знакопеременной функции z = f(x, у), например, если 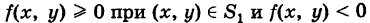
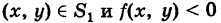 , двойной интеграл (2) равен алгебраической сумме объемов
, двойной интеграл (2) равен алгебраической сумме объемов  цилиндроидов, построенных соответственно на основаниях
цилиндроидов, построенных соответственно на основаниях  (рис. 251), т. е.
(рис. 251), т. е.
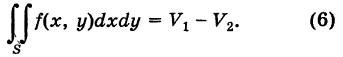
Можно доказать, что формула (5) справедлива и в этом случае.
Отметим один важный случай: пусть S — прямоугольник  (рис. 252) и
(рис. 252) и 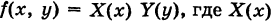 — функция, непрерывная на
— функция, непрерывная на 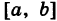 и зависящая только от х, и
и зависящая только от х, и 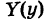 — функция, непрерывная на [А, Б] и зависящая только от у. В силу формулы (5) имеем
— функция, непрерывная на [А, Б] и зависящая только от у. В силу формулы (5) имеем
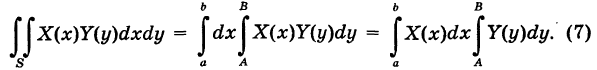
Но внутренний интеграл в формуле (7) есть постоянное число, поэтому его можно вынести за знак внешнего интеграла и мы получим
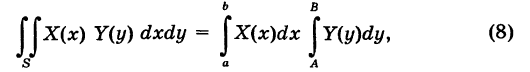
т. е. двойной интеграл (8) равен произведению двух однократных интегралов.
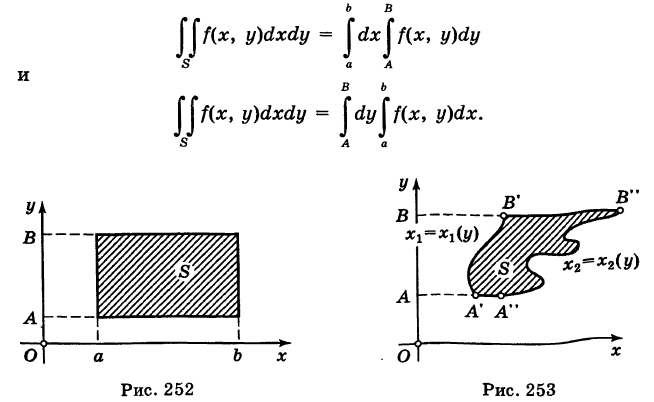
Замечание 1. Если область S — стандартная относительно оси Ох, т. е. (рис. 253)
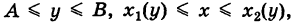
то по аналогии с формулой (5) получаем
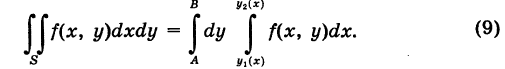
В частности, если область S есть прямоугольник: 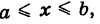
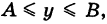 то имеем
то имеем
Отсюда получаем
т е. если пределы интегрирования в повторном интеграле от непрерывной функции конечны и постоянны, то результат интегрирования не зависит от порядка интегрирования.
Замечание 2. Если область S нестандартная, то ее разбивают (если это возможно) на конечное число областей  стандартных относительно осей координат Ох или Оу и на основании свойства пределов полагают
стандартных относительно осей координат Ох или Оу и на основании свойства пределов полагают
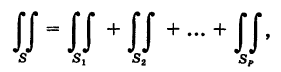
а затем применяют соответственно формулы (5) или (9).
Пример:
Найти
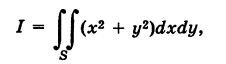
где S — квадрат 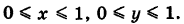
Решение:
Расставляя пределы интегрирования, будем иметь
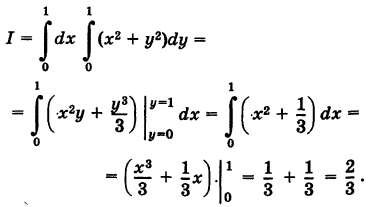
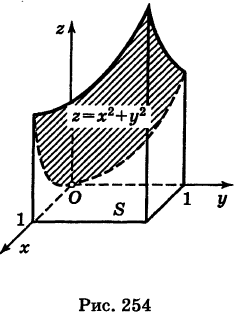
Геометрически / представляет собой объем цилиндроида с квадратным нижним основанием, ограниченного сверху параболоидом вращения 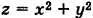 (рис. 254).
(рис. 254).
Пример:
Вычислить двойной интеграл
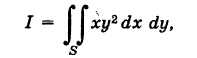
где S — прямоугольник 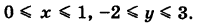
Решение:
Расставляя пределы интегрирования и разделяя переменные, будем иметь
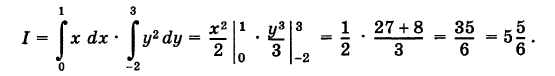
Пример:
Вычислить

где S — треугольник с вершинами О (0, 0), А (2, 0) и В (2, 1) (рис. 255).
Решение:
Область S ограничена прямыми у = 0, у = х/2, х = 2 и является стандартной как относительно оси Оу, так и оси Ох.
Для вертикали MN «точка входа» в область S есть М(х, 0), «точка выхода» — N(x, х/2) (0 < х < 2). Таким образом, при фиксированном х переменная у для точек области S меняется от 0 до х/2. Поэтому, интегрируя в двойном интеграле (10) сначала по у при х = const, а затем по x, согласно формуле (5) будем иметь
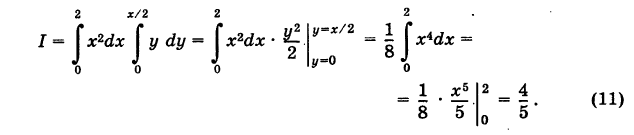
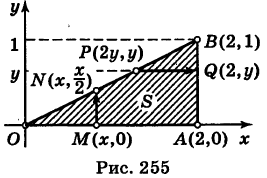
Аналогично, для горизонтали PQ «точка входа» в область есть Р{2у, у) и «точка выхода» — Q (2, у) (0 < у < 1). Следовательно, при фиксированном у переменная х для точек области S меняется от 2у до 2. Произведя в двойном интеграле (10) интегрирование сначала по х при у = const, а затем по у, на основании формулы (9) получаем
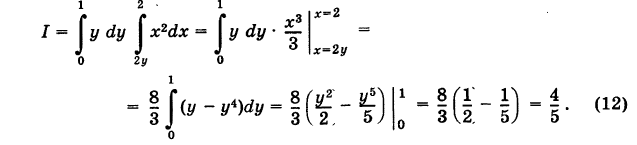
Мы пришли, как и следовало ожидать, к тому же самому результату, причем второй способ вычисления оказался несколько более сложным.
Пример:
Изменить порядок интегрирования в повторном интег- рале
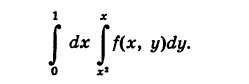
Область интегрирования S ограничена кривыми у= х2, у = х и х = 0, х = 1 (рис. 256). Отсюда, изменяя роли осей координат, получаем
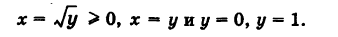
Следовательно,
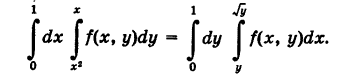
Пример:
Расставить пределы интегрирования в двойном интеграле
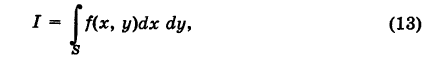
если область интегрирования 5 есть круговое кольцо, ограниченное окружностями 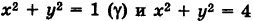 (Г) (рис. 257). Область S не является стандартной. Для расстановки пределов интегрирования в интервале (13) разбиваем область S на четыре стандартные относительно оси OY области
(Г) (рис. 257). Область S не является стандартной. Для расстановки пределов интегрирования в интервале (13) разбиваем область S на четыре стандартные относительно оси OY области  как указано на рисунке. Используя уравнение окружностей
как указано на рисунке. Используя уравнение окружностей
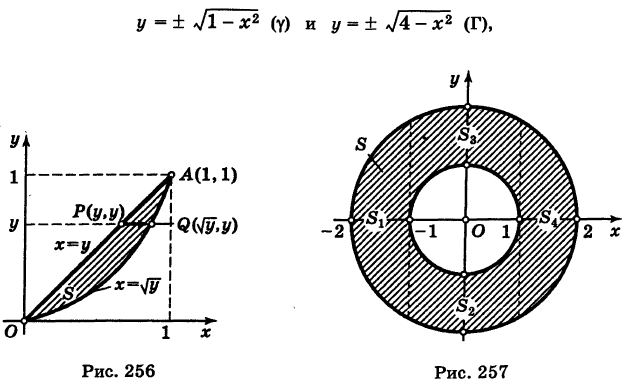
имеем
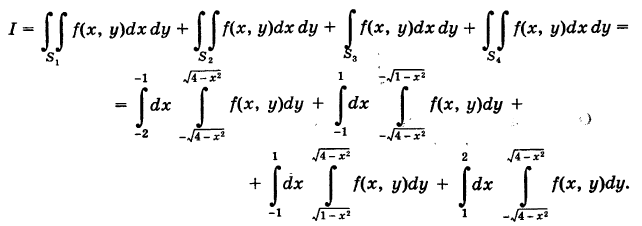
Аналогичная формула получится, если мы будем расставлять пределы интегрирования в другом порядке.
Двойной интеграл в полярных координатах
Пусть в двойном интеграле
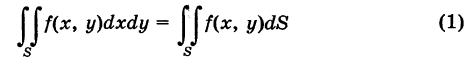
при обычных предположениях мы желаем перейти к полярным координатам г и ф, полагая
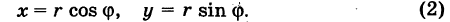
Область интегрирования S разобьем на элементарные ячейки  с помощью координатных линий
с помощью координатных линий  (окружности) и ф
(окружности) и ф 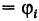 (лучи) (рис. 258).
(лучи) (рис. 258).
Введем обозначения
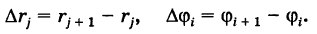
Так как окружность перпендикулярна (ортогональна) радиусам, то внутренние ячейки 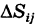 с точностью до бесконечно малых высшего порядка малости относительно их площади можно рассматривать как прямоугольники с измерениями
с точностью до бесконечно малых высшего порядка малости относительно их площади можно рассматривать как прямоугольники с измерениями 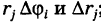 ; поэтому площадь каждой такой ячейки будет равна
; поэтому площадь каждой такой ячейки будет равна
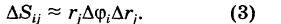
Что касается ячеек AS^ неправильной формы, примыкающих к границе Г
области интегрирования S, то эти ячейки не повлияют на значение двойного интеграла и мы их будем игнорировать.
В качестве точки  для простоты выберем вершину ячейки
для простоты выберем вершину ячейки  с полярными координатами
с полярными координатами 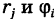 . Тогда декартовы координаты точки
. Тогда декартовы координаты точки 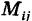 равны
равны
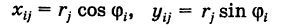
и, следовательно,
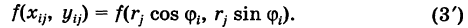
Двойной интеграл (1) представляет собой предел двумерной интегральной суммы, причем можно показать, что на значение этого предела не влияют добавки к слагаемым интегральной суммы, являющиеся бесконечно малыми высшего порядка малости. Поэтому, учитывая формулы (3) и (3′), получаем
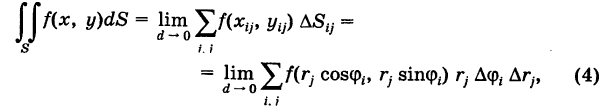
где d — максимальный диаметр ячеек 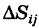 и сумма распространена на все ячейки указанного выше вида, целиком содержащиеся в области S. С другой стороны, величины суть числа и их можно рассматривать как прямоугольные декартовы координаты некоторых точек плоскости
и сумма распространена на все ячейки указанного выше вида, целиком содержащиеся в области S. С другой стороны, величины суть числа и их можно рассматривать как прямоугольные декартовы координаты некоторых точек плоскости 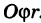 . Таким образом, сумма (4) является интегральной суммой для функции
. Таким образом, сумма (4) является интегральной суммой для функции
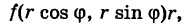
соответствующая прямоугольной сетке с линейными элементами 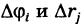 . Следовательно,
. Следовательно,
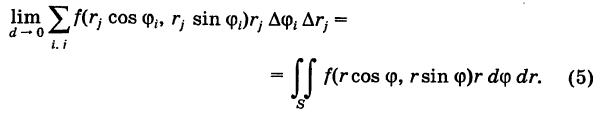
Выравнивая формулы (4) и (5), получаем окончательно
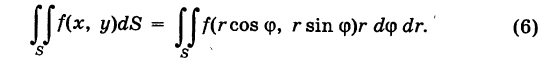
Выражение

называется двумерным элементом площади в полярных координатах. Итак, чтобы в двойном интеграле (1) перейти к полярным координатам, достаточно координаты х и у заменить по формулам (2), а вместо элемента площади dS подставить выражение (7).
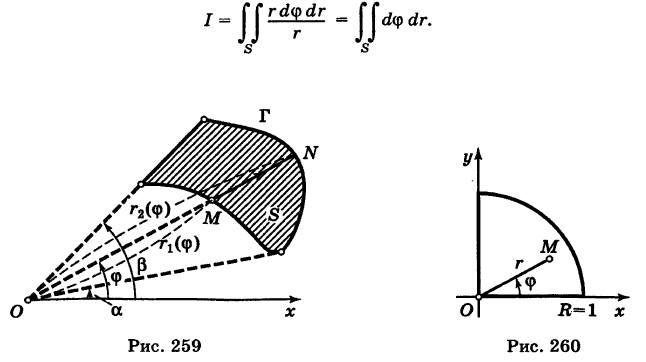
Для вычисления двойного интеграла (6) его нужно заменить повторным. Пусть область интегрирования S определяется неравенствами
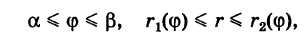
где 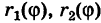 — однозначные непрерывные функции на отрезке
— однозначные непрерывные функции на отрезке 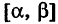 (рис. 259). Тогда по аналогии с прямоугольными координатами имеем
(рис. 259). Тогда по аналогии с прямоугольными координатами имеем
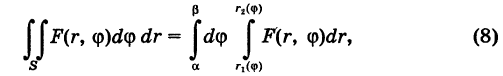
где
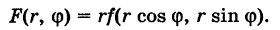
Пример:
Переходя к полярным координатам  , вычислить двойной интеграл
, вычислить двойной интеграл
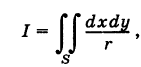
где S — первая четверть круга радиуса R = 1 с центром в точке О (0, 0) (рис. 260).
Так как  , то, применяя формулу (6), получаем
, то, применяя формулу (6), получаем
Область S определяется неравенствами 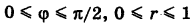 . Поэтому на основании формулы (8) имеем
. Поэтому на основании формулы (8) имеем
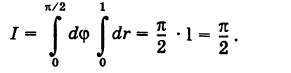
Пример:
В интеграле
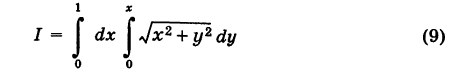
перейти к полярным координатам.
Область интегрирования здесь есть треугольник S, ограниченный прямыми у=0, у = х, х = 1 (рис. 261).
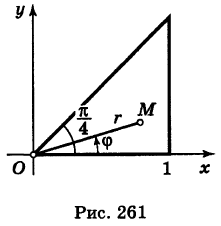
В полярных координатах уравнения этих прямых записываются следующим образом: 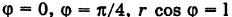 и, следовательно, область S определяется неравенствами
и, следовательно, область S определяется неравенствами
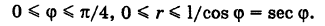
Отсюда на основании формул (6) и (8), учитывая, что 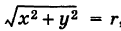 , имеем
, имеем
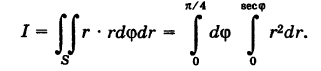
Интеграл Эйлера—Пуассона
С помощью полярных координат можно просто вычислить важный для теории вероятностей интеграл Эйлера— Пуассона

Так как определенный интеграл не зависит от обозначения переменной интегрирования, то, очевидно, можно также записать

Перемножая формулы (1) и (2) и учитывая, что произведение этих однократных интегралов можно рассматривать как двойной интеграл от произведения подынтегральных функций, будем иметь
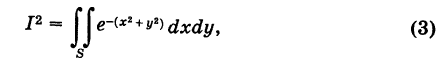
где область S определяется неравенствами
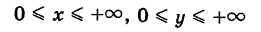
и, следовательно, представляет собой первый квадрант координатной плоскости Оху (рис. 262).
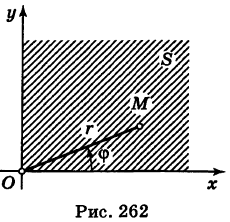
Переходя в интеграле (3) к полярным координатам, получим
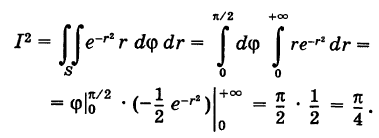
Отсюда, учитывая положительность числа 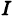 , находим
, находим
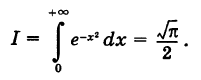
В силу четности функции 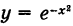 имеем также
имеем также
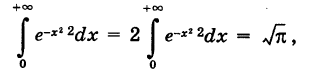
что представляет собой площадь, ограниченную осью Ох и кривой Гаусса 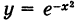 (см, рис. 120).
(см, рис. 120).
Теорема о среднем
Пусть функция f(x, у) непрерывна в ограниченной замкнутой области 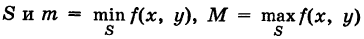 — соответственно наименьшее и наибольшее значения функции f(x, у) в области S.
— соответственно наименьшее и наибольшее значения функции f(x, у) в области S.
Для двумерной интегральной суммы этой функции, распространенной на область S, имеем оценки
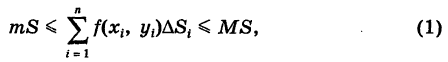
где 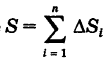 — площадь области S. Отсюда, переходя к пределу при
— площадь области S. Отсюда, переходя к пределу при 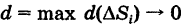 в неравенствах (1) и учитывая существование двойного интеграла, получаем
в неравенствах (1) и учитывая существование двойного интеграла, получаем
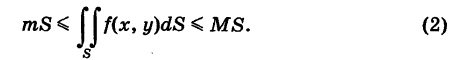
Число

называется средним значением функции 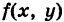 в области S. Из неравенств (2) вытекает, что
в области S. Из неравенств (2) вытекает, что 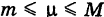 .
.
Формулу (3) можно переписать в следующем виде:

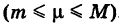 . Таким образом, двойной интеграл равен среднему значению подынтегральной функции, умноженной на площадь области интегрирования.
. Таким образом, двойной интеграл равен среднему значению подынтегральной функции, умноженной на площадь области интегрирования.
Не нужно думать, что формула (4) дает универсальный способ вычисления двойного интеграла. Дело в том, что, как правило, среднее значение функции определяется через двойной интеграл. Поэтому реальный смысл здесь имеет оценка (2).
Пример:
Оценить интеграл
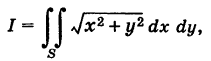
где S — квадрат 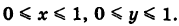
Для функции f(x, у) = 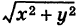 имеем
имеем
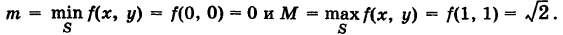
Так как S = 1, то 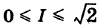 = 1,41. Можно принять
= 1,41. Можно принять
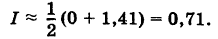
Эта оценка грубая, так как точное значение интеграла есть
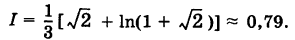
Более точное значение интеграла I получится, если область интегрирования S разбить на достаточно мелкие части и к каждой из них применить теорему о среднем.
Геометрические приложения двойного интеграла
Прямой цилиндроид, построенный на основании S в координатной плоскости Оху и ограниченный сверху непрерывной поверхностью z = f(x, у), имеет объем, равный
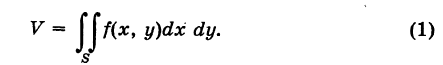
Пример:
Найти объем 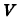 тела, ограниченного поверхностями
тела, ограниченного поверхностями
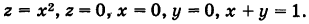
Решение:
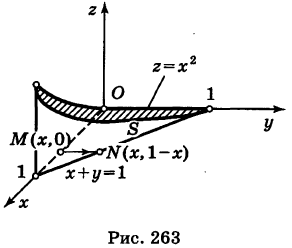
Искомое тело имеет своим основанием треугольник S на плоскости Оху у образованный линиями 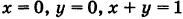 ,и ограничено сверху параболическим цилиндром
,и ограничено сверху параболическим цилиндром 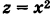 (рис. 263). Отсюда на основании формулы (1) получим
(рис. 263). Отсюда на основании формулы (1) получим
Если в формуле (1) положить
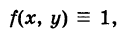
то получим объем прямого цилиндра с высотой 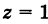 , численно равный площади S его основания. Поэтому площадь плоской области S равна
, численно равный площади S его основания. Поэтому площадь плоской области S равна

Формулу (2) можно записать также в виде

- Заказать решение задач по высшей математике
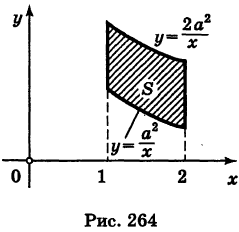
Пример:
Найти площадь, ограниченную гиперболами 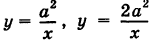 (а > 0) и прямыми х = 1, х = 2 (рис. 264).
(а > 0) и прямыми х = 1, х = 2 (рис. 264).
Решение:
На основании формулы (2) получим, что площадь S равна
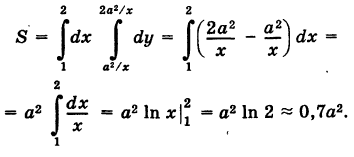
Физические приложения двойного интеграла
Пусть S — материальная пластинка. Если  есть часть пластинки S, содержащая точку М и имеющая массу
есть часть пластинки S, содержащая точку М и имеющая массу  , то отношение
, то отношение
называется средней поверхностной плотностью куска 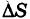 а предел этого отношения при условии, что диаметр
а предел этого отношения при условии, что диаметр 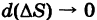 , называется поверхностной плотностью р(М) пластинки S в точке М:
, называется поверхностной плотностью р(М) пластинки S в точке М:
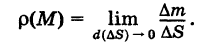
Очевидно, поверхностная плотность р(М) пластинки S есть функция точки М. Понятия средней поверхностной плотности пластинки и поверхностной плотности пластинки в данной точке
вполне аналогичны понятиям средней линейной плотности дуги и линейной плотности дуги в точке, введенным.
Положим, что поверхностная плотность пластинки S в текущей точке М(х, у) равна 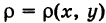 , где
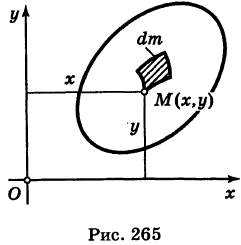
, где 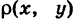 — известная непрерывная функция. Рассмотрим бесконечно малый элемент dS пластинки, содержащий точку М (рис. 265). Так как в пределах этого элемента пластинку можно считать однородной с плотностью р, то масса элемента dS (элементарная масса) равна
— известная непрерывная функция. Рассмотрим бесконечно малый элемент dS пластинки, содержащий точку М (рис. 265). Так как в пределах этого элемента пластинку можно считать однородной с плотностью р, то масса элемента dS (элементарная масса) равна

Интегрируя выражение (1) по всей пластинке S, находим массу пластинки

Рассматривая dm как материальную точку, удаленную от осей координат Ох и Оу на расстояния у их, получим элементарные статические моменты пластинки
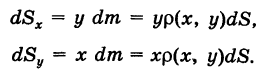
Отсюда, интегрируя эти выражения по всей пластинке S, находим статические моменты пластинки S относительно координатных осей
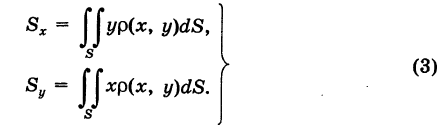
В механике доказывается, что статический момент пластинки относительно какой-нибудь оси совпадает со статическим моментом точечной массы, равной массе пластинки, сосредоточенной в центре масс ее относительно той же оси (теорема Вариньона). Отсюда, обозначая через (х0, у0) координаты центра масс пластинки S, будем иметь
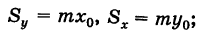
следовательно,
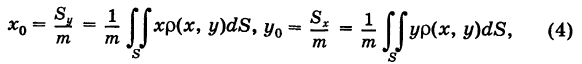
где 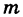 — масса (2) пластинки.
— масса (2) пластинки.
Аналогично, для элементарных моментов инерции пластинки S относительно осей координат Ох и Оу получаем выражения
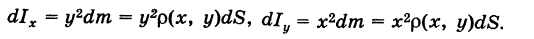
Отсюда после интегрирования по пластинке S будем иметь моменты инерции пластинки S относительно координатных осей
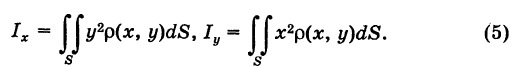
Элементарный полярный момент инерции определяется формулой
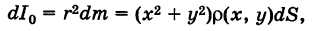
где 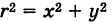 — квадрат расстояния массы dm от начала координат. Интегрируя последнее выражение по пластинке S, получаем полярный момент пластинки
— квадрат расстояния массы dm от начала координат. Интегрируя последнее выражение по пластинке S, получаем полярный момент пластинки
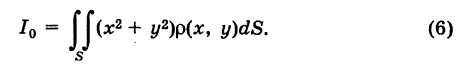
Из формул (5) и (6) следует, что

Полагая 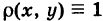 в формулах моментов, получим соответствующие моменты инерции геометрической фигуры S. Напомним, что при вычислении в декартовых прямоугольных координатах, как обычно, принимается dS = dx dy, а в случае полярных координат имеем
в формулах моментов, получим соответствующие моменты инерции геометрической фигуры S. Напомним, что при вычислении в декартовых прямоугольных координатах, как обычно, принимается dS = dx dy, а в случае полярных координат имеем 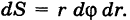
Пример:
Определить координаты центра масс квадратной пластинки S: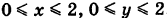 , поверхностная плотность которой в точке
, поверхностная плотность которой в точке 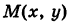 равна р = х + у.
равна р = х + у.
Решение:
Пользуясь формулой (2), находим массу пластинки
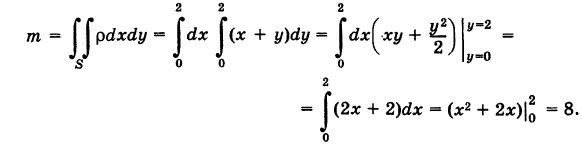
По формуле (3) определяем статические моменты пластинки S относительно координатных осей:
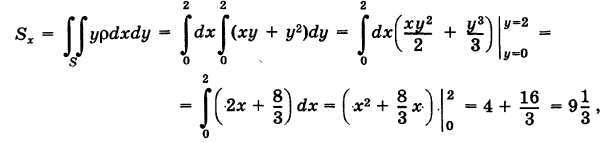
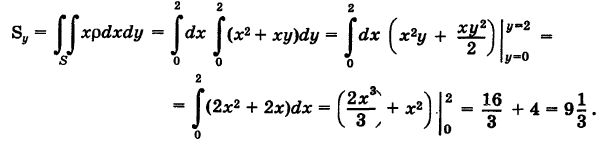
Равенство моментов  можно было предвидеть ввиду симметрии задачи.
можно было предвидеть ввиду симметрии задачи.
На основании формул (4) центр масс пластинки S имеет координаты
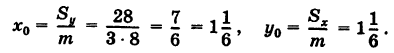
Пример:
Найти момент инерции 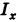 круга S:
круга S: 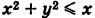 (рис. 266) относительно оси Ох.
(рис. 266) относительно оси Ох.
Решение:
Полагая р = 1, на основании первой формулы (5) имеем

Задачу будем решать в полярных координатах. Имеем
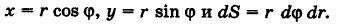
Уравнение границы Г области S есть
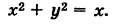
Отсюда, переходя к полярным координатам, получаем 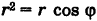 . Следовательно, после сокращения на несущественный множитель г имеем
. Следовательно, после сокращения на несущественный множитель г имеем
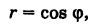
причем так как 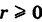 , то
, то 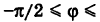
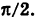 Таким образом, при каждом фиксированном
Таким образом, при каждом фиксированном 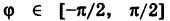 радиус г меняется в пределах О
радиус г меняется в пределах О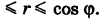 Переходя к полярным координатам в формуле (8), получаем
Переходя к полярным координатам в формуле (8), получаем
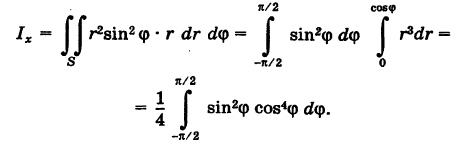
Как известно, 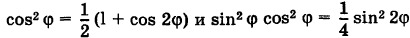 поэтому
поэтому
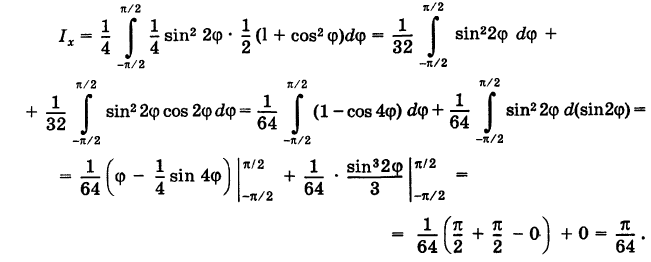
Понятие о тройном интеграле
По аналогии с двойным интегралом определяется так называемый тройной интеграл. Пусть в декартовом пространстве Охуz задана конечная замкнутая область V и f(x, у, z) — ограниченная функция, определенная в V. Разобьем область V на конечное число ячеек 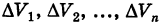 и в каждой из них выберем точку
и в каждой из них выберем точку
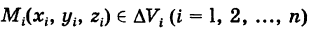
(рис. 267). Сумма
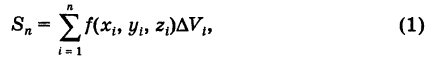
где 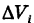 — объем i-й ячейки, называется трехмерной интегральной суммой.
— объем i-й ячейки, называется трехмерной интегральной суммой.
Обозначим через d наибольший из диаметров ячеек 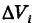 . Будем произвольным способом неограниченно измельчать ячейки
. Будем произвольным способом неограниченно измельчать ячейки 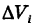 . Тогда предел интегральной суммы (1) при
. Тогда предел интегральной суммы (1) при 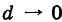 , если этот предел существует и не зависит от формы ячеек
, если этот предел существует и не зависит от формы ячеек 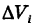 и выбора точек
и выбора точек 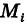 в них, называется тройным интегралом
в них, называется тройным интегралом
от функции 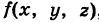 , распространенным на область V, и обозначается следующим образом:
, распространенным на область V, и обозначается следующим образом:
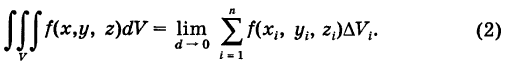
Доказывается, что если подынтегральная функция 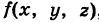 непрерывна в замкнутой ограниченной области интегрирования V с кусочно-гладкой границей, то тройной интеграл (2) существует.
непрерывна в замкнутой ограниченной области интегрирования V с кусочно-гладкой границей, то тройной интеграл (2) существует.
Если область V заполнена массой и 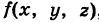 представляет собой непрерывно распределенную объемную плотность в текущей точке
представляет собой непрерывно распределенную объемную плотность в текущей точке 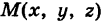 , то
, то 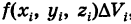 где
где 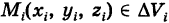 с точностью до бесконечно малой высшего порядка малости относительно максимального объема ячеек
с точностью до бесконечно малой высшего порядка малости относительно максимального объема ячеек 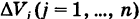 есть масса ячейки
есть масса ячейки 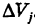 . Следовательно, интегральная сумма (1) приближенно равна массе т, заполняющей область V. При
. Следовательно, интегральная сумма (1) приближенно равна массе т, заполняющей область V. При 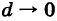 получаем, что предел суммы Sn будет равен массе т. Отсюда выводим физический смысл тройного интеграла: если
получаем, что предел суммы Sn будет равен массе т. Отсюда выводим физический смысл тройного интеграла: если 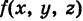 есть непрерывная плотность распределения массы в пространстве Oxyz, то тройной интеграл
есть непрерывная плотность распределения массы в пространстве Oxyz, то тройной интеграл
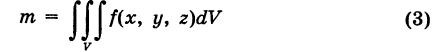
представляет собой массу, заполняющую область интегрирования V. В частности, если плотность f(x, у, z) 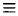 1, то масса области V численно равна ее объему. Поэтому объем области V выражается тройным интегралом
1, то масса области V численно равна ее объему. Поэтому объем области V выражается тройным интегралом

Если вычисление тройного интеграла (2) ведется в прямоугольных координатах х, у, z, то в качестве ячеек 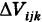 выбирают прямоугольные параллелепипеды с измерениями
выбирают прямоугольные параллелепипеды с измерениями 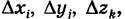 грани которых параллельны координатным плоскостям, т. е. полагают
грани которых параллельны координатным плоскостям, т. е. полагают
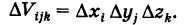
В этом случае элемент объема dV считают равным

(элемент объема в прямоугольных координатах) и тройной интеграл (2) записывают в следующем виде:
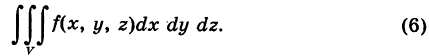
В частности, для объема тела получаем формулу
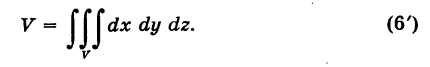
В простейшем случае вычисление тройного интеграла (6) сводится к трем квадратурам. А именно, пусть область интегрирования Г стандартна относительно оси Oz, т. е. ограничена снизу и сверху соответственно однозначными непрерывными поверхностями
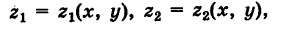
причем проекция области V на координатную плоскость Оху есть плоская область S (рис. 268).
Отсюда следует, что при фиксированных значениях (х, у) 6 S соответствующие аппликаты z точек области V изменяются в пределах 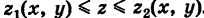 По аналогии с двойным интегралом будем иметь
По аналогии с двойным интегралом будем иметь
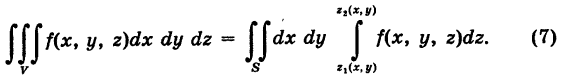
Если, кроме того, проекция S стандартна относительно оси Оу и определяется неравенствами
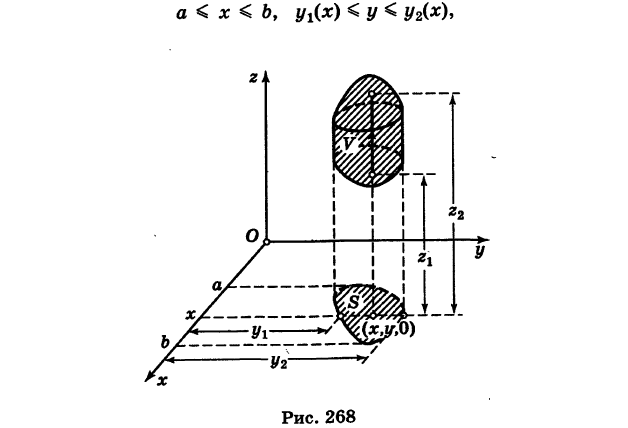
где 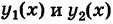 — однозначные непрерывные функции на отрезке
— однозначные непрерывные функции на отрезке 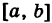 , то
, то
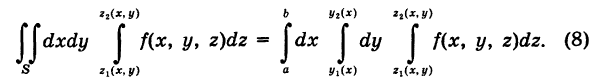
Из формул (7) и (8) получаем окончательно
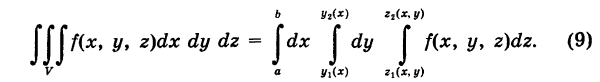
Таким образом, вычисление тройного интеграла сводится к трем квадратурам.
Заметим, что если область интегрирования V стандартна относительно всех трех координатных осей Ох, Оу и Oz, то пределы интегрирования для тройного интеграла (6) можно расставить 3! = 6 различными способами.
Пример:
Вычислить
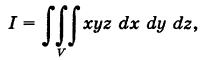
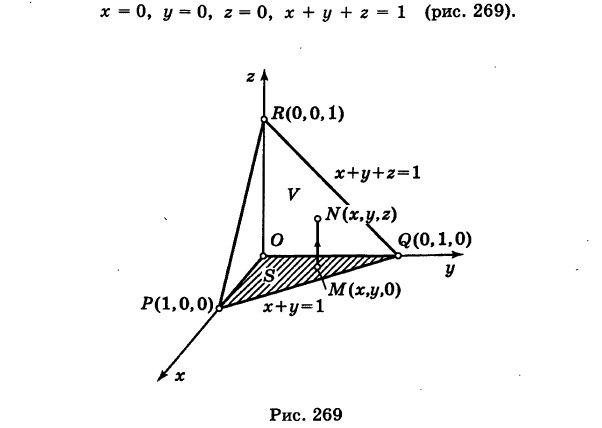
где V — пирамида OPQR, ограниченная следующими плоскостями:
Решение:
Проекция области V на координатную плоскость Оху есть треугольник S, ограниченный прямыми
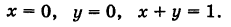
При 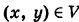 аппликаты точек
аппликаты точек 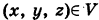 удовлетворяют неравенству
удовлетворяют неравенству 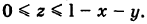 Поэтому
Поэтому
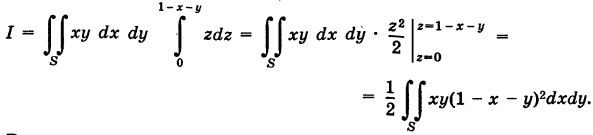
Расставляя пределы интегрирования для треугольника S, получаем
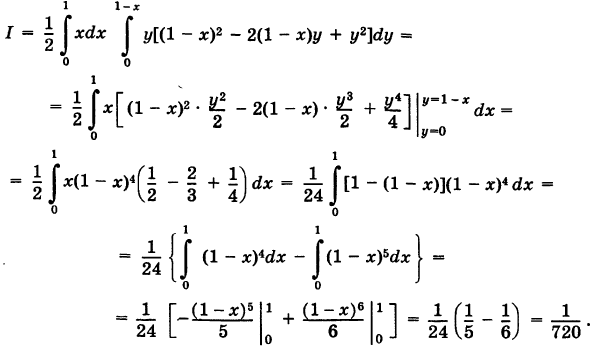
Число I представляет собой массу пирамиды V, если плотность ее в текущей точке 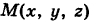 равна
равна 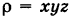 .
.
- Делимость чисел в математике
- Обыкновенные дроби
- Отношения и пропорции
- Рациональные числа и действия над ними
- Общее уравнение плоскости
- Угол между плоскостями
- Понятие о производной вектор-функции
- Криволинейные интегралы
Вычисление двойного интеграла. Двукратный { повторный } интеграл
Определение простой { правильной } области
Область $ mathbf { textit { D } } $ на плоскости $mathbf { textit { Oxy } } $будем называть $textbf { простой { правильной } в направлении оси } quad mathbf { textit { Oy } } $, если любая прямая, проходящая через внутреннюю точку области $mathbf { textit { D } } $ и параллельная оси $mathbf { textit { Oy } } $, пересекает границу $mathbf { textit { D } } $ в двух точках.
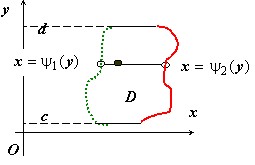
Аналогично определяется область, $textbf { простая { правильная } в направлении оси } mathbf { textit { Ox } } $: любая прямая, проходящая через внутреннюю точку области $mathbf { textit { D } } $ и параллельная оси $mathbf { textit { Oх } } $, пересекает границу $mathbf { textit { D } } $ в двух точках.
Область, правильную { простую } в направлении обеих осей, будем называть $textbf { правильной } $.

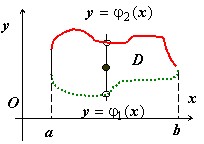
$y=varphi _1 (x) y=varphi _2 (x)$ Ограниченную замкнутую область $mathbf { textit { D } } $, правильную в направлении оси $mathbf { textit { Oy } } $, можно описать неравенствами
$D:left[ begin{array} { l } aleqslant xleqslant b, newline varphi _1 (x)leqslant yleqslant varphi _2 (x) newline end{array} right].$
Числа $mathbf { textit { a } } $ и $mathbf { textit { b } } $ существуют вследствие ограниченности области $mathbf { textit { D } } $, функция $varphi _1 (x)$ образована нижними точками пересечения прямой $mathbf { textit { x } } =mathbf { textit { x } } _ { 0 } $ при $a<x_0 <b$ с границей области $mathbf { textit { D } } $, функция $varphi _2 (x)$ – верхними точками пересечения этой прямой с границей области $mathbf { textit { D } } $.
Аналогичным образом область $mathbf { textit { D } } $, ограниченную, замкнутую и правильную в направлении оси $mathbf { textit { Oх } } $, можно описать неравенствами
$D:left[ begin{array} { l } cleqslant yleqslant d, newline psi _1 (y)leqslant xleqslant psi _2 (y) newline end{array} right].$
Функция $psi _1 (y)$ образована левыми точками пересечения прямой $mathbf { textit { y } } =mathbf { textit { y } } _ { 0 } $ при $c<y_0 <d$ с границей области $mathbf { textit { D } } $, функция $psi _2 (y)$ – правыми точками пересечения этой прямой с границей области $mathbf { textit { D } } $.
$x=psi _2 (y) x=psi _1 (y)$ Для правильной области { т.е. области, правильной в направлении обеих осей } существуют оба способа представления:
$D:left[ begin{array} { l } aleqslant xleqslant b, newline varphi _1 (x)leqslant yleqslant varphi _2 (x) newline end{array} right]$ и $D:left[ begin{array} { l } cleqslant yleqslant d, newline psi _1 (y)leqslant xleqslant psi _2 (y) newline end{array} right].$
Двукратный { повторный } интеграл
Пусть $mathbf { textit { D } } $ – область, простая в направлении оси $mathbf { textit { Oy } } $. Рассмотрим выражение $J(D)=intlimits_a^b { left( { intlimits_ { varphi _1 (x) } ^ { varphi _2 (x) } { f(x,y)dy } }right)dx } $. Эта конструкция определяется через два обычных определённых интеграла. После интегрирования по $mathbf { textit { у } } $ во внутреннем интеграле { переменная $mathbf { textit { х } } $ при этом рассматривается как постоянная } и подстановки по $mathbf { textit { у } } $ в пределах от $varphi _1 (x)$ до $varphi _2 (x)$ получается функция, зависящая только от $mathbf { textit { х } } $, которая интегрируется в пределах от $mathbf { textit { a } } $ до $mathbf { textit { b } } $. В дальнейшем мы будем обычно записывать этот объект без внутренних скобок:
$$ J(D)=intlimits_a^b { dxintlimits_ { varphi _1 (x) } ^ { varphi _2 (x) } { f(x,y)dy } } . $$
Можно показать, что двукратный интеграл обладает всеми свойствами двойного интеграла:
Свойства линейности и интегрирования неравенств следуют из этих свойств определённого интеграла; интеграл от единичной функции даёт площадь области $mathbf { textit { D } } $: $intlimits_a^b { dxintlimits_ { varphi _1 (x) } ^ { varphi _2 (x) } { dy } } =intlimits_a^b { dxcdot left. y right|_ { varphi _1 (x) } ^ { varphi _2 (x) } } =intlimits_a^b { left[ { varphi _2 (x)-varphi _1 (x) }right]dx } =s(D)$;
$y=varphi _1 (x) y=varphi _2 (x)$ теоремы об оценке и о среднем следуют из перечисленных свойств. Единственное свойство, с которым придётся повозиться – это свойство аддитивности. Мы докажем его в простой, но достаточной для нас форме: если область $mathbf { textit { D } } $ разбита на две подобласти $mathbf { textit { D } } _ { 1 } $ и $mathbf { textit { D } } _ { 2 } $ прямой, параллельной одной из координатных осей, то двукратный интеграл по области $mathbf { textit { D } } $ равен сумме интегралов по $mathbf { textit { D } } _ { 1 } $ и $mathbf { textit { D } } _ { 2 } $: $mathbf { textit { J } } (mathbf { textit { D } } )=mathbf { textit { J } } (mathbf { textit { D } } _ { 1 } )+mathbf { textit { J } } (mathbf { textit { D } } _ { 2 } )$.
Первый случай:
прямая $mathbf { textit { x } } =mathbf { textit { a } } _ { 1 } $ параллельна оси $mathbf { textit { Oy } } $. Тогда $J(D)=intlimits_a^b { dxintlimits_ { varphi _1 (x) } ^ { varphi _2 (x) } { f(x,y)dy } } =intlimits_a^ { a_1 } { dxintlimits_ { varphi _1 (x) } ^ { varphi _2 (x) } { f(x,y)dy } } +intlimits_ { a_1 } ^b { dxintlimits_ { varphi _1 (x) } ^ { varphi _2 (x) } { f(x,y)dy } } $ { аддитивность внешнего интеграла } = $mathbf { textit { J } } (mathbf { textit { D } } _ { 1 } )+mathbf { textit { J } } (mathbf { textit { D } } _ { 2 } )$.
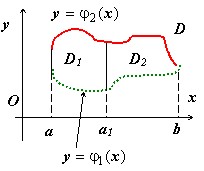
$y=varphi _2 (x) y=varphi _2 (x)$
Второй случай:
прямая $mathbf { textit { y } } =mathbf { textit { c } } _ { 1 } $ параллельна оси $mathbf { textit { Oх } } $. Воспользуемся сначала аддитивностью внешнего интеграла: $J(D)=intlimits_a^b { dxintlimits_ { varphi _1 (x) } ^ { varphi _2 (x) } { f(x,y)dy } } = y=varphi _1 (x) =intlimits_a^ { a_1 } { dxintlimits_ { varphi _1 (x) } ^ { varphi _2 (x) } { f(x,y)dy } } +intlimits_ { a_1 } ^ { b_1 } { dxintlimits_ { varphi _1 (x) } ^ { varphi _2 (x) } { f(x,y)dy } } +intlimits_ { b_1 } ^b { dxintlimits_ { varphi _1 (x) } ^ { varphi _2 (x) } { f(x,y)dy } } =$ { теперь применим свойство аддитивности для внутреннего интеграла в среднем слагаемом } $textbf { = } intlimits_a^ { a_1 } { dxintlimits_ { varphi _1 (x) } ^ { varphi _2 (x) } { f(x,y)dy } } +intlimits_ { a_1 } ^ { b_1 } { dxleft[ { intlimits_ { varphi _1 (x) } ^ { с_1 } { f(x,y)dy } +intlimits_ { с_1 } ^ { varphi _2 (x) } { f(x,y)dy } }right] } +intlimits_ { b_1 } ^b { dxintlimits_ { varphi _1 (x) } ^ { varphi _2 (x) } { f(x,y)dy } } = $ { применяем свойство линейности для внешнего интеграла в среднем слагаемом и перегруппировываем сумму } =$ =intlimits_a^ { a_1 } { dxintlimits_ { varphi _1 (x) } ^ { varphi _2 (x) } { f(x,y)dy } } +intlimits_ { a_1 } ^ { b_1 } { dxintlimits_ { varphi _1 (x) } ^ { с_1 } { f(x,y)dy } } +intlimits_ { a_1 } ^ { b_1 } { dxintlimits_ { с_1 } ^ { varphi _2 (x) } { f(x,y)dy } } +intlimits_ { b_1 } ^b { dxintlimits_ { varphi _1 (x) } ^ { varphi _2 (x) } { f(x,y)dy } } =$ $ =left [ { intlimits_a^ { a_1 } { dxintlimits_ { varphi _1 (x) } ^ { varphi _2 (x) } { f(x,y)dy } } +intlimits_ { a_1 } ^ { b_1 } { dxintlimits_ { с_1 } ^ { varphi _2 (x) } { f(x,y)dy } + } intlimits_ { b_1 } ^b { dxintlimits_ { varphi _1 (x) } ^ { varphi _2 (x) } { f(x,y)dy } } }right ]+ left [ { intlimits_ { a_1 } ^ { b_1 } { dxintlimits_ { varphi _1 (x) } ^ { с_1 } { f(x,y)dy } } }right ] $
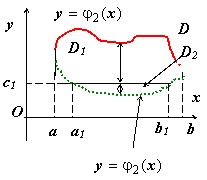
первая скобка даёт повторный интеграл по $mathbf { textit { D } } _ { 1 } $, вторая – по $_ { } mathbf { textit { D } } _ { 2 } =mathbf { textit { J } } (mathbf { textit { D } } _ { 1 } )+mathbf { textit { J } } (mathbf { textit { D } } _ { 2 } )$.
Понятно, что возможны различные случаи взаимного расположения прямых $mathbf { textit { y } } =mathbf { textit { c } } _ { 1 } $, $mathbf { textit { x } } =mathbf { textit { a } } _ { 1 } $, $mathbf { textit { x } } =mathbf { textit { a } } _ { 2 } $ и функций $y=varphi _1 (x)$, $y=varphi _2 (x)$, но логика доказательства во всех случаях такая же.
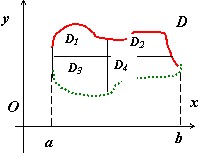
Обобщим доказанное свойство. Пусть прямая разбивает область $mathbf { textit { D } } $ на две подобласти $mathbf { textit { D } } _ { 1,1 } $ и $mathbf { textit { D } } _ { 1,2 } $. Проведём ещё одну прямую, параллельную какой-либо координатной оси. Пусть эта прямая разбивает $mathbf { textit { D } } _ { 1,1 } $ на $mathbf { textit { D } } _ { 1 } $ и$mathbf { textit { D } } _ { 2 } $; $mathbf { textit { D } } _ { 1,2 } $ – на $mathbf { textit { D } } _ { 3 } $ и $mathbf { textit { D } } _ { 4 } $. По доказанному, $mathbf { textit { J } } (mathbf { textit { D } } _ { 1,1 } )=mathbf { textit { J } } (mathbf { textit { D } } _ { 1 } )+mathbf { textit { J } } (mathbf { textit { D } } _ { 2 } )$, $mathbf { textit { J } } (mathbf { textit { D } } _ { 1,2 } )=mathbf { textit { J } } (mathbf { textit { D } } _ { 3 } )+mathbf { textit { J } } (mathbf { textit { D } } _ { 4 } )$, поэтому $mathbf { textit { J } } (mathbf { textit { D } } )=mathbf { textit { J } } (mathbf { textit { D } } _ { 1,1 } )+mathbf { textit { J } } (mathbf { textit { D } } _ { 1,2 } )=mathbf { textit { J } } (mathbf { textit { D } } _ { 1 } )+mathbf { textit { J } } (mathbf { textit { D } } _ { 2 } )+mathbf { textit { J } } (mathbf { textit { D } } _ { 3 } )+mathbf { textit { J } } (mathbf { textit { D } } _ { 4 } )$. Продолжая рассуждать также, убеждаемся в справедливости следующего утверждения: если область $mathbf { textit { D } } $ с помощью прямых, параллельных координатным осям, разбита на подобласти $mathbf { textit { D } } _ { 1 } $, $mathbf { textit { D } } _ { 2 } , { ldots } , mathbf { textit { D } } _ { n } $, то $J(D)=J(D_1 )+J(D_2 )+ldots +J(D_n )=sumlimits_ { i=1 } ^n { J(D_i ) } $.
Теорема о переходе от двойного интеграла к повторному
Пусть $mathbf { textit { D } } $ – простая в направлении оси $mathbf { textit { Oy } } $ область. Тогда двойной интеграл от непрерывной функции по области $mathbf { textit { D } } $ равен повторному интегралу от той же функции по области $mathbf { textit { D } } $: $iintlimits_D { f(x,y)dxdy } =intlimits_a^b { dxintlimits_ { varphi _1 (x) } ^ { varphi _2 (x) } { f(x,y)dy } } $.
Док-во: Разобьём область $mathbf { textit { D } } $ с помощью прямых, параллельных координатным осям, на подобласти $mathbf { textit { D } } _ { 1 } $, $mathbf { textit { D } } _ { 2 } $, { ldots } , $mathbf { textit { D } } _ { n } $. По доказанному выше, $J(D)=intlimits_a^b { dxintlimits_ { varphi _1 (x) } ^ { varphi _2 (x) } { f(x,y)dy } } =sumlimits_ { i=1 } ^n { J(D_i ) } $. К каждому из интегралов $mathbf { textit { J } } (mathbf { textit { D } } _ { i } )$ применим теорему о среднем: в любой области $mathbf { textit { D } } _ { i } $ найдётся точка $mathbf { textit { P } } _ { i } $ такая, что $mathbf { textit { J } } (mathbf { textit { D } } _ { i } )=mathbf { textit { f } } (mathbf { textit { P } } _ { i } ) quad mathbf { textit { s } } (mathbf { textit { D } } _ { i } )$. Следовательно, $J(D)=sumlimits_ { i=1 } ^n { f(P_i )s(D_i ) } $. В последнем равенстве справа стоит интегральная сумма для двойного интеграла $iintlimits_D { f(x,y)dxdy } $. Будем мельчить разбиение области так, чтобы $d=mathop { max } limits_ { i=1,2,ldots ,n } diam(D_i )to 0$. Вследствие непрерывности функции $mathbf { textit { f } } (mathbf { textit { x } } $, $mathbf { textit { y } } )$ по теореме существования интегральная сумма при этом стремится к двойному интегралу $iintlimits_D { f(x,y)dxdy } $, т.е. в пределе получим $intlimits_a^b { dxintlimits_ { varphi _1 (x) } ^ { varphi _2 (x) } { f(x,y)dy } } =iintlimits_D { f(x,y)dxdy } $, что и требовалось доказать.
Если область $mathbf { textit { D } } $ правильная в направлении оси $mathbf { textit { Oх } } $, то аналогично доказывается формула $iintlimits_D { f(x,y)dxdy } =intlimits_с^d { dyintlimits_ { psi _1 (y) } ^ { psi _2 (y) } { f(x,y)dx } } $. Если $mathbf { textit { D } } $ правильна в направлении обеих осей, то для вычисления двойного интеграла можно применять любую из эти формул: $iintlimits_D { f(x,y)dxdy } =intlimits_a^b { dxintlimits_ { varphi _1 (x) } ^ { varphi _2 (x) } { f(x,y)dy } } =intlimits_с^d { dyintlimits_ { psi _1 (y) } ^ { psi _2 (y) } { f(x,y)dx } } $.
Если область не является правильной, её разбивают на правильные подобласти.
