Как составить единичную матрицу - Сайт, где вы сможете решить свои вопросы

Единичная матрица

Формула

Единичная матрица – это квадратная матрица, расположенные элементы которой по главной диагонали равны единице, а оставшиеся равны нулю. Обозначается символом $ E $.

Общая формула единичной матрицы имеет вид: $$ E = begin{pmatrix} 1&0&0&text{…}&0 \ 0&1&0&text{…}&0 \ 0&0&1&text{…}&0 \ text{…}&text{…}&text{…}&text{…}&text{…} \ 0&0&0&text{…}&1 end{pmatrix} $$

Свойства

При умножении матрицы на единичную матрицу получается та же самая матрица:
$$ A cdot E = E cdot A = A $$
Любая квадратная матрица в нулевой степени равна единичной матрице:
$$ A^0 = E $$
При умножении матрицы на обратную её матрицу получается единичная матрица:
$$ A cdot A^{-1} = E $$
При умножении матрицы на транспонированную к ней матрицу получается единичная матрица:
$$ A cdot A^T = E $$
Определитель единичной матрицы $ E $ равен единице:
$$ Delta = det E = 1 $$

Свойства единичной матрицы подразумеваются для квадратных матриц.

Примеры

Пример

Составить единичную матрицу второго, третьего и четвертого порядка

Решение

По определению единичная матрица является квадратной, главная диагональ заполнена единицами, а остальные элементы равны нулю:

$$ E = begin{pmatrix} 1&0 \ 0&1 end{pmatrix}; E = begin{pmatrix} 1&0&0 \ 0&1&0 \ 0&0&1 end{pmatrix}; E = begin{pmatrix} 1&0&0&0 \ 0&1&0&0 \ 0&0&1&0 \ 0&0&0&1 end{pmatrix} $$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

Аналогичным способом составляются матрицы более высокого порядка

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 6 декабря 2021 года; проверки требует 1 правка.

Едини́чная ма́трица — квадратная матрица, элементы главной диагонали которой равны единице поля, а остальные равны нулю.

Определение[править | править код]

Квадратная матрица $E_{n}=(e_{{ij}})$ размера (порядка) , где $e_{{ii}}=1$ для всякого , и $e_{{ij}}=0$ для всяких ineq j , называется единичной матрицей порядка ^[1].

Единичную матрицу можно также определить как матрицу $(e_{{ij}})$ , у которой $e_{{ij}}=delta _{{ij}}$ , где $delta _{{ij}}$ — символ Кронекера^[1].

Единичная матрица является частным случаем скалярной матрицы.

Обозначение[править | править код]

Единичная матрица размера обычно обозначается $E_{n}$ и имеет вид:

$E_{n}={begin{bmatrix}1&0&cdots &0\0&1&cdots &0\cdots &cdots &cdots &cdots \0&0&cdots &1end{bmatrix}},$

Так же используется и другое обозначение: $I_{n}$ .

Если из контекста ясно, какого размера матрица, то нижний индекс (указывающий порядок) опускается: , ^[1].

Свойства[править | править код]

Произведение любой матрицы и единичной матрицы подходящего размера равно самой матрице^[1]:

Квадратная матрица в нулевой степени дает единичную матрицу того же размера^[1]:

$A^{0}=E$

При умножении матрицы на обратную ей, тоже получается единичная матрица^[2]:

${displaystyle AA^{-1}=A^{-1}A=E}$

Единичная матрица получается при умножении ортогональной матрицы на её транспонированную матрицу^[3]:

$AA^{T}=E$

Определитель единичной матрицы равен единице:

Примеры[править | править код]

Единичные матрицы первых порядков имеют вид

$E_{1}={begin{pmatrix}1end{pmatrix}}, E_{2}={begin{pmatrix}1&0\0&1end{pmatrix}}, E_{3}={begin{pmatrix}1&0&0\0&1&0\0&0&1end{pmatrix}}$

Примечания[править | править код]

↑ ¹ ² ³ ⁴ ⁵ Гантмахер, 1966, с. 24.
↑ Гантмахер, 1966, с. 27.
↑ Гантмахер, 1966, с. 238.

Литература[править | править код]

Гантмахер, Ф. Р. Теория матриц. — 2-е изд., доп.. — М.: Наука, 1966. — 576 с.
См. список литературы по линейной алгебре

См. также[править | править код]

Нулевая матрица

Источник

Перед тем как перейти к знакомству с единичной и нулевой матрицей, вспомним, что такое матрица, а также ее основные типы. Особое внимание при повторении следует уделить квадратной матрице и ее подтипам — диагональной, симметричной и кососимметричной матрицам.

Итак, среди квадратных матриц можно выделить класс диагональных матриц, у которых все элементы кроме элементов главной диагонали равны нулю. Рассмотрим два вида матриц с совпадающими элементами на главной диагонали. К таким матрицам относят нулевую и единичную. Рассмотрим каждую более подробно.

Нулевая матрица

Матрица, у которой все элементы равны нулю.

Ее принято обозначать как ZZ или OO или OmnO_{mn}.

Общий вид нулевой матрицы:

O=(00…000…0…………00…0)O=begin{pmatrix}0&0&…&0\0&0&…&0\…&…&…&…\0&0&…&0end{pmatrix}

Как различать: все элементы матрицы — нули.

Пример 1

O1=(0000)O_{1}=begin{pmatrix}0&0\0&0end{pmatrix} — квадратная нулевая матрица 2-го порядка поскольку имеет размер 2×22times 2.

Нулевая матрица существует для любого размера m×nmtimes n.

Пример 2

O2=(00000000000000000000)O_{2}=begin{pmatrix}0&0&0&0\0&0&0&0\0&0&0&0\0&0&0&0\0&0&0&0end{pmatrix} — нулевая матрица размера 5×45times 4.

Свойства нулевой матрицы

Нулевая матрица играет такую же роль при выполнении действий над матрицами, как число нуль при соответствующих арифметических операциях.

При умножении нулевой матрицы на число, получаем ту же нулевую матрицу: k⋅O=O⋅k=Okcdot O=Ocdot k=O.
Важно понимать, что на какое бы число мы ни умножили нулевую матрицу любого размера, всегда получим ту же нулевую матрицу.

Пример 1

152⋅(0000)=(0000)152cdot begin{pmatrix}0&0\0&0end{pmatrix}=begin{pmatrix}0&0\0&0end{pmatrix}

Пример 2

73⋅(000000000)=(000000000)73cdot begin{pmatrix}0&0&0\0&0&0\0&0&0end{pmatrix}=begin{pmatrix}0&0&0\0&0&0\0&0&0end{pmatrix}

Сумма произвольной матрицы и нулевой матрицы того же размера есть произвольная матрица: A+O=O+A=AA+O=O+A=A.

Складывая произвольную ненулевую матрицу с нулевой матрицей того же размера, получаем исходную ненулевую матрицу.

Пример 1

(39672548)+(0000)=(39672548)begin{pmatrix}39&67\25&48end{pmatrix}+begin{pmatrix}0&0\0&0end{pmatrix}=begin{pmatrix}39&67\25&48end{pmatrix}

Пример 2

(9678354927781014567)+(000000000)=(9678354927781014567)begin{pmatrix}96&78&35\49&27&78\101&45&67end{pmatrix}+begin{pmatrix}0&0&0\0&0&0\0&0&0end{pmatrix}=begin{pmatrix}96&78&35\49&27&78\101&45&67end{pmatrix}

С правилами сложения произвольных матриц вы можете ознакомиться в теме «Как складывать матрицы».

Разность произвольной матрицы и нулевой матрицы того же размера есть произвольная матрица.
Вычитая из матрицы любого порядка нулевую матрицу такого же порядка, получим исходную ненулевую матрицу.

Пример 1

(48362954)−(0000)=(48362954)begin{pmatrix}48&36\29&54end{pmatrix}-begin{pmatrix}0&0\0&0end{pmatrix}=begin{pmatrix}48&36\29&54end{pmatrix}

Если же мы вычтем из нулевой матрицы произвольную матрицу такого же порядка, получим исходную ненулевую матрицу со знаком «минус» (с противоположным знаком): O−A=−AO-A=-A.

Пример 2

(0000)−(57342019)=−(57342019)begin{pmatrix}0&0\0&0end{pmatrix}-begin{pmatrix}57&34\20&19end{pmatrix}=-begin{pmatrix}57&34\20&19end{pmatrix}

С правилами вычитания матриц вы можете ознакомиться здесь.

Произведение произвольной матрицы размера k×lktimes l и нулевой матрицы размера l×mltimes m есть нулевая матрица размера k×mktimes m.

Правила, существующие при умножении произвольных матриц, выполняются и в данном случае. Ознакомиться с ними вы можете тут.

Пример 1

(54762453)⋅(0000)=(0000)begin{pmatrix}54&76\24&53end{pmatrix}cdot begin{pmatrix}0&0\0&0end{pmatrix}=begin{pmatrix}0&0\0&0end{pmatrix}

Пример 2

(91195736)⋅(000000)=(000000)begin{pmatrix}91&19\57&36end{pmatrix}cdot begin{pmatrix}0&0&0\0&0&0end{pmatrix}=begin{pmatrix}0&0&0\0&0&0end{pmatrix}

Возможен случай, когда произведение двух ненулевых матриц дает нулевую матрицу:

(025010)⋅(607300)=(0000)begin{pmatrix}0&25\0&10end{pmatrix}cdot begin{pmatrix}60&73\0&0end{pmatrix}=begin{pmatrix}0&0\0&0end{pmatrix}

Также нулевая матрица является симметричной и кососимметричной.

Единичная матрица

Матрица, каждый элемент главной диагонали которой равен единице, а все остальные — нулю.

Общий вид единичной матрицы:

E=(10…001…0…………00…1)E=begin{pmatrix}1&0&…&0\0&1&…&0\…&…&…&…\0&0&…&1end{pmatrix}

Пример 1

E1=(1001)E_{1}=begin{pmatrix}1&0\0&1end{pmatrix}

Пример 2

E2=(100010001)E_{2}=begin{pmatrix}1&0&0\0&1&0\0&0&1end{pmatrix}

Свойство единичной матрицы

Произведение произвольной матрицы и единичной матрицы соответствующего размера (её порядок равен числу столбцов исходной ненулевой матрицы) есть исходная матрица: AE=EA=AAE=EA=A.

Пример 1

(253741173619)⋅(100010001)=(253741173619)begin{pmatrix}25&37&41\17&36&19end{pmatrix}cdot begin{pmatrix}1&0&0\0&1&0\0&0&1end{pmatrix}=begin{pmatrix}25&37&41\17&36&19end{pmatrix}

Пример 2

(2579)⋅(1001)=(2579)begin{pmatrix}25&79end{pmatrix}cdot begin{pmatrix}1&0\0&1end{pmatrix}=begin{pmatrix}25&79end{pmatrix}

С действиями над произвольными матрицами мы познакомимся на следующих уроках.

Помощь с решением задач по математике от специалистов на Студворк!

Тест по теме «Единичная и нулевая матрица»

Источник

Единичная матрица

Содержание:

Примеры с решением

Диагональная матрица, все диагональные элементы которой равны единице , называется единичной матрицей и обозначается символом .

Элементы единичной матрицы могут быть представлены с помощью дельта-символа Кронекера:

В матричной алгебре матрица играет ту же роль, что число единица в системе вещественных чисел, а именно – при умножении на единичную матрицу (справа или слева) исходная матрица не изменяется:

(2)

Единичная матрица представляет собой квадратную матрицу, элементы которой находятся на главной диагонали, а остальные элементы равны нулю. Обозначается символом Е.

Действительно, пусть – произвольная матрица размера. Рассмотрим -ый элемент матричного произведения АЕ, где Е – единичная матрица -го порядка.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Согласно определению матричного произведения и с учетом свойств дельта-символа,

(3)

для любых допустимых значений индексов , следовательно, АЕ = А.

Рассмотрим теперь -ый элемент матричного произведения ЕА. где Е – единичная матрица -го порядка.

Умножение матрицы на единичную матрицу дает ту же матрицу.

Примеры с решением

Пример 1

диагональная матрица второго порядка,

диагональная матрица третьего порядка.

Определение Если у диагональной матрицы -го порядка Е все диагональные элементы равны единице, то такая матрица называется единичной матрицей -го порядка.

Возможно вам будут полезны данные страницы:

Пример 2

— единичная матрица третьего порядка.

Определение Матрица любого размера называется нулевой, или нуль-матрицей, если все ее элементы равны нулю: В отличие от чисел, где число 0 единственно, нулевых матриц бесконечно много, т. к. каждому размеру матриц соответствует нулевая матрица этого размера.

Нетрудно убедиться, что при умножении единичная матрица играет ту же роль, что и число 1 при умножении чисел: единичная матрица -го порядка перестановочна с любой квадратной матрицей А того же порядка, причем

АЕ = ЕА = А. (2.12)

Чтобы доказать это, введем обозначения: АЕ = F, ЕА = G. Используя правило умножения матриц и определение единичной матрицы

(2.13)

находим, что для всех

Определение Под нулевой степенью квадратной матрицы А понимается единичная матрица того же порядка что и А, т. е. .. Целой положительной степенью квадратной матрицы А называется произведение матриц, равных А, т. е.

Лекции:

Таблица производных
Диаграмма “ящик с усами”
Объём тела вращения
Фигуры вращения
Признаки сходимости рядов
Определение предела функции
Вычисление пределов
Формулы сокращенного умножения
Прямоугольная система координат в пространстве
Производная и экономические задачи

Источник

A unit matrix, or identity matrix, is a square matrix whose all elements are zeros except the main diagonal elements which are ones. A matrix is defined as a rectangular array of numbers that are arranged in rows and columns. The size of a matrix can be determined by the number of rows and columns in it. A matrix is said to be an “m by n” matrix when it has “m” rows and “n” columns and is written as an “m × n” matrix. For example, the matrix given below is a “3 × 4” matrix, i.e., a matrix that has three rows and four columns. We have different types of matrices, such as rectangular matrices, square matrices, triangular matrices, symmetric matrices, etc.

Identity Matrix Definition (Unit Matrix)

A unit matrix, or identity matrix, is a square matrix whose principal diagonal elements are ones, and the rest of the elements of the matrix are zeros. An identity matrix is always a square matrix and is expressed as “I.” For example, “I_n” is the identity matrix of order n, i.e., it has “n” rows and columns. It is a scalar matrix. When the product of any two square matrices is an identity matrix, then the matrices are said to be inverses of each other. The rank of an identity matrix of order “n × n” is n, as it has “n” linearly independent rows (or columns). The matrix given below represents an identity matrix of order “n by n.”

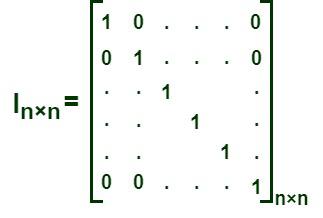
Unit matrix of order n × n

Examples of an Identity Matrix

A square matrix P = [a_ij] is said to be an identity matrix when a_ij = 1 for i = j and a_ij = 0 for i ≠ j.

⇒ The matrix given below is an identity matrix of order “2 × 2.”

⇒ The matrix given below is an identity matrix of order “3 × 3.”

Properties of an Identity Matrix

The properties mentioned below are some important properties of an Identity Matrix:

An identity matrix is always a square matrix, i.e., a matrix that has an equal number of rows and columns.
The determinant of an identity matrix or unit matrix is always equal to 1, i.e., |I| = 1.

|I| = 1

The inverse of an identity matrix or unit matrix is the identity matrix itself.

I^-1 = I

If an identity matrix of order “n” is multiplied by itself n times, then the resultant matrix will also be a unit matrix of order n.

Iⁿ = I

If any matrix A is multiplied by an identity matrix, then the resultant matrix is A.

AI = IA = A

The product of two inverse matrices is an identity matrix.

AA^-1 = A^-1A = I

Solved Examples on Identity Matrix

Example 1: Determine whether the given matrices are identity matrices or not.

a) A = $left[begin{array}{cc} 1 & 1\ 1 & 1 end{array}right]$

b) B= $left[begin{array}{ccc} 1 & 0 & 0\ 0 & 1 & 0\ 0 & 0 & 1 end{array}right]$

Solution:

a) In matrix A, all the principal diagonal elements are ones, and the rest of the elements are also equal to 1. We know that a unit matrix, or identity matrix, is a square matrix whose all elements are zeros except the main diagonal elements, which are ones. Hence, matrix A is not an identity matrix.

b) In matrix B, all the principal diagonal elements are ones, and the rest of the elements are zeros. So, from the definition of an identity matrix, the given matrix B is an identity matrix.

Example 2: Give an example of an identity matrix that has four rows and four columns.

Solution:

The order of an identity matrix that has four rows and four columns is “4 × 4.” The matrix given below represents an identity matrix of order “4 × 4,” where all the principal diagonal elements are ones, and the rest of the elements are zeros.

I_4×4 = $left[begin{array}{cccc} 1 & 0 & 0 & 0\ 0 & 1 & 0 & 0\ 0 & 0 & 1 & 0\ 0 & 0 & 0 & 1 end{array}right]$

Example 3: Find the value of (p − q + r) if the matrix given below is an identity matrix.

Solution:

If the given matrix is an identity matrix, then all its principal diagonal elements are ones, and the rest of the elements are zeros.

So, p = 1

q + 1 = 0 ⇒ q = -1

r – 2 = 0 ⇒ r = 2

Now, p − q + r = 1 −(−1) + 2

= 1 + 1 + 2 = 4

Hence, the value of (p − q + r) is 4 if matrix A is an identity matrix.

Example 4: Prove that the inverse of the identity matrix is the identity matrix itself.

Solution:

Let’s consider an identity matrix of order “2 × 2” to prove that the inverse of the identity matrix is the identity matrix itself.

I_{2 × 2} = $left[begin{array}{cc} 1 & 0\ 0 & 1 end{array}right]$

We know that the inverse of a matrix A $left[begin{array}{cc} a & b\ c & d end{array}right]$ = Adj A/ (ad – bc)

where Adj A = $left[begin{array}{cc} d & -b\ -c & a end{array}right]$

I^-1 = 1/ (1 – 0) $left[begin{array}{cc} 1 & 0\ 0 & 1 end{array}right]$

I^-1 = $left[begin{array}{cc} 1 & 0\ 0 & 1 end{array}right]$ = I

Hence proved.

Example 5: For a given matrix A, prove that AI = A.

Solution:

Let’s consider a square matrix A = $left[begin{array}{cc} a & b\ c & d end{array}right]$ to prove that AI = A.

AI = $left[begin{array}{cc} a & b\ c & d end{array}right]$ $left[begin{array}{cc} 1 & 0\ 0 & 1 end{array}right]$

= $left[begin{array}{cc} (atimes1+btimes0) & (0times a+btimes1)\ (ctimes1+dtimes0) & (0times c+dtimes1) end{array}right]$

= $left[begin{array}{cc} (a+0) & (0+b)\ (c+0) & (0+d) end{array}right]$

= $left[begin{array}{cc} a & b\ c & d end{array}right]$ = A

Hence, proved.

FAQs on Identity Matrix

Question 1: What is an identity matrix?

Answer:

A unit matrix, or identity matrix, is a square matrix whose all elements are zeros except the main diagonal elements which are ones. A square matrix P = [a_ij] is said to be an identity matrix when a_ij = 1 for i = j and a_ij= 0 for i ≠ j.

Question 2: Is an identity matrix a scalar matrix?

Answer:

A scalar matrix is a square matrix whose principal diagonal elements are equal, and the rest of the elements of the matrix are zeros. We know that an identity matrix is a square matrix whose principal diagonal elements are ones, and the rest of the elements of the matrix are zeros. So, an identity matrix or a unit matrix is a scalar matrix.

Question 3: What is the determinant of an identity matrix?

Answer:

The determinant of an identity matrix or unit matrix is always equal to 1, i.e., |I| = 1.

Question 4: What is the rank of an identity matrix of order n?

Answer:

As the identity matrix of order “n × n” has “n” linearly independent rows (or columns), its rank is n.

Last Updated :
02 Feb, 2023

Like Article

Save Article

Источник

Единичная матрица

Формула

Свойства

Примеры

Определение[править | править код]

Обозначение[править | править код]

Свойства[править | править код]

Примеры[править | править код]

Примечания[править | править код]

Литература[править | править код]

См. также[править | править код]

Нулевая матрица

Свойства нулевой матрицы

Единичная матрица

Свойство единичной матрицы

Тест по теме «Единичная и нулевая матрица»

Единичная матрица

Примеры с решением

Пример 1

Пример 2

Identity Matrix Definition (Unit Matrix)

Examples of an Identity Matrix

Properties of an Identity Matrix

Solved Examples on Identity Matrix

FAQs on Identity Matrix

Question 1: What is an identity matrix?

Question 2: Is an identity matrix a scalar matrix?

Question 3: What is the determinant of an identity matrix?

Question 4: What is the rank of an identity matrix of order n?

Вам также может понравиться

Как найти своего ребенка после развода

Как найти точки пересечения двух сфер

Как составить таблицу по оплате зарплаты

Добавить комментарий Отменить ответ