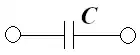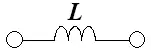Эквивалентная схема замещения конденсатора.
Эквивалентная
схема замещения конденсатора представлена
на рис 1 и представляет собой последовательное
соединение собственной емкости
конденсатора С,
индуктивности пластин и выводов
конденсатора
и активного сопротивления выводов,
контактного узла и сопротивления
обкладок конденсатора
Рис.1.
Упрощенная эквивалентная схема замещения
конденсатора.
Модуль
полного сопротивления
–
цепи
определяется по формуле
4
где С собственная
емкость конденсатора;
индуктивность
пластин и выводов конденсатора;
активное
сопротивление выводов контактного узла
и сопротивление обкладок конденсатора;
рабочая
частота
Из
формулы (4) видно, что модуль полного
сопротивления такой цепи зависит от
частоты, на которой работает конденсатор.
На рис.2 представлена зависимость полного
сопротивления RLC
–
цепи от частоты.
Рис.
2 Зависимость модуля полного сопротивления
RLC
-цепи
от частоты.
Из
формулы (4) и рис.2 видно, что модуль
полного сопротивления на резонансной
частоте имеет минимальное значение и
носит шюто активный характер. Резонансная
частота такой цепи определяется по
формуле
5
На
частоте ниже резонансной модуль полного
сопротивления RLC
цепи носит емкостный характер, а на
частоте выше резонансной – индуктивный.
Это приводит к изменению эквивалентной
схемы замещения для различных частот.
Достаточно рассмотреть три случая когда
конденсатор используется на резрнансной
частоте
,
и
чтобы представить переходные процессы,
происходящие в нем.
Для
случая, когда рабочая частота совпадает
с резонансной, т.е.
емкостная и индуктивные составляющие
в выражении (4) равны и модуль полного
сопротивления носит чисто активный
характер, причем это сопротивление
минимально и определяется из выражения
6
Резонансная
частота такого контура без учета потерь
определяется формулой (5), а добротность
контура равна

где волновое
сопротивление контура;
сопротивление
контура на резонансной частоте.
Полоса
пропускания такого контура находится
из следующего выражения
8
В
полосе пропускания контура, с достаточной
степенью точности, можно считать,
что эквивалентная схема замещения
конденсатора состоит из чисто активного
сопротивления, поэтому переходные
процессы, происходящие в активном
сопротивлении, от частоты не зависят.
Для
случая когда рабочая частота больше
резонансной частоты контура (),
т.е. когдасоставляющая в выражении (4) стремится
к нулю. Модуль полного сопротивления
конденсатора носит индуктивный характер
и, соответственно, эквивалентная
схема замещения конденсатора для
рассматриваемого случая, несколько
видоизменяется.. Она представлена на
рис. 3.
Рис.3.
Эквивалентная схема замещения конденсатора
для частот выше резонансной частоты.
Модуль
полного сопротивления RLC
– цепи, представленной на рис.3, определяется
выражением
9
Наличие
индуктивности в рассматриваемой цепи
приводит к частотной зависимости
модуля полного сопротивления конденсатора
на частотах
.
Переходные процессы происходящие вRL
–
цепи при коммутации подробно рассмотрены
в лабораторной работе №1,
поэтому здесь не рассматриваются.
Для
случая когда рабочая частота ниже
резонансной
,
т.е. когдаиндуктивная составляющая в выражении
(4) стремится к нулю ()
поэтому модуль полного сопротивления
конденсатора носит емкостный характер
и, соответственно, эквивалентная схема
замещения конденсатора для рассмотриваемого
случая несколько видоизменяется. Она
представлена на рис.4.
Рис.
4. Эквивалентная схема замещения
конденсатора для частот ниже резонансной
частоты.
Модуль
полного сопротивления RC
– цепи, представленной на рис.4, определяется
выражением
10
Наличие
емкости в
рассматриваемой
цепи приводит к частотной зависимости
модуля полного сопротивления конденсатора
на частотах
.
Рассмотрим
переходные процессы, происходящие в RC
– цепи при подключении её к источнику
постоянной э.д.с. Схема включения RC
– цепи к источнику постоянной э.д.с.
представлена на рис.5.
Рис.
5.
В
RC
– цепях рекомендуется вначале найти
напряжение на конденсаторе, а затем
ток е
цепи.
Из рис.5 видно, что при замыкании
выключателя В
в момент
источник
постоянной э.д.с. подключается к RC
– цепи. В момент скачка входного напряжения
сопротивления конденсатора равно
нулю, так как согласно второму закону
коммутации напряжение на нем мгновенно
измениться не может, поэтому в
начальный момент напряжение источника
целиком оказывается приложенным к
резистору
.
Затем конденсатор начинает заряжаться,
на его обкладках накапливается заряд
и напряжение между ними постепенно
возрастает. В соответствии со вторым
законом Кирхгофа (сумма падений напряжений
на резистореи конденсатораС
уравновешивается внешней э.д.с.) и для
запишем уравнение
11
Учитывая
уравнение (11), можно утверждать, что при
увеличении напряжения
падение напряжения на резисторе
уменьшается,
а, следовательно, ток в RC
– цепи уменьшается. Наконец, напряжение
на конденсаторе
становится
равным з.д.с. источника
и процесс заряда конденсатора
заканчивается, ток вRC
– цепи становится равным нулю. Очевидно,
что напряжение на конденсаторе изменяется
от нуля до Е. Для определения переходного
процесса RC
– цепи выразим напряжение на резисторе
через
.
Учитывая,
что при последовательном соединении R
и С
ток в любом участке RС
– цепи одинаков и равен
можно записать
12
подставляя
значение
из (12) в уравнение (11) получим
13
Это
выражение представляет собой
дифференциальное уравнение первого
порядка, в котором неизвестной функцией
является напряжение
.
При использовании “классического”
метода решения напряжениеследует искать в виде суммы вынужденной
и свободной
составляющих. Исходя из этого запишем
14
Вынужденная
составляющая напряжения, очевидно,
равна
,
поскольку в установившимся режиме
конденсатор заряжен до э.д.с. внешнего
источника питания.
Тогда
согласно выражению (14) можно записать
15
Чтобы
определить постоянную А,
воспользуемся начальными условиями,
состоящими в том, что к моменту коммутации
конденсатор был разряжен, т.е.
.
Из выражения (15) для моментаимеем
.
С другой стороны, согласно второму
закону коммутации напряжение. Из этих двух отношений находим
.
Таким образом, свободная составляющая
напряжения на конденсаторе равна,
а полное напряжение на конденсаторе в
процессе его заряда изменяется во
времени согласно выражению
16
по
экспоненциальному закону, стремясь к
Е.
На
рис. 6а. приведены графики полного
напряжения на конденсаторе, а также
вынужденной и свободной составляющих.
Обратим внимание, что в момент
сумма напряжений
,
чем обеспечивается выполнение начальных
условий. При значенияхт.е. начальном этапе переходного процесса,
функцияс удовлетворительной для практических
целей точностью приможет быть аппроксимирована рядом
разложения
Тогда
для напряжения
получим выражение
17
из
которого следует, что нарастание
напряжения на конденсаторе в начале
процесса происходит по линейному закону.
Ток
в RC-цепи
(ток заряда конденсатора) может быть
найден дифференцированием выражения
(16) для
.
Очевидно,
он должен содержать только свободную
составляющую, так как в установившемся
режиме ток в цепи равен нулю.

Падение
напряжения на резисторе
19
Ток
в RC
–
цепи и напряжение на
с течением времени убывают по одинаковому
экспоненциальному закону. Этот ток
максимален в начальный момент, причем
его начальная величина ограничена
только сопротивлением.
График кривой тока показан на рис. 6.б.
Заметим,
что в момент включения ток конденсатора
изменяется скачком от нуля до максимального
значения; это физически возможно,
так
как скачек тока в RC
– цепи не приводит к скачкообразному
изменению запаса энергии в электрическом
поле конденсатора.
Произведение
RC
для данной цепи постоянно (поскольку
значения
и
С
не изменяются). Это произведение
обозначается буквой
и называется постоянной времениRC
– цепи.
Длительность
переходного процесса зависит от
постоянной времени. Чем больше
сопротивление
,
тем медленнее заряжается конденсаторС.
Чем больше емкость конденсатора С,
тем больше заряд надо .накопить на
пластинах конденсатора для получения
напряжения Е.
Таким образом, чем больше постоянная
времени цепи, тем больше продолжительность
переходного процесса. Величина
позволяет сравнивать между собой
различные конденсаторы в отношении
времени установления стационарного
режима. Физически постоянная времени
представляет время, в течение которого
свободные составляющие тока и напряжения
в цепи уменьшаются вe
раз.
По
истечении времени
,
которое называется временем установления,
переходной процесс принято считать
закончившимся, напряжение на
конденсаторе становится равным0,95E,
а ток в цепи уменьшается до 0,05Е.
Чтобы
получить представление о скорости
нарастания напряжения
нa
конденсаторе, из уравнения (13) найдем
производную
20
Рис.6.
Кривые изменения напряжения на
конденсаторе (а) и тока (б) в RC-цепи
при включении постоянной э.д.с.
Величина
обратно
пропорциональна постоянной времени
RC-цепи.
Скорость нарастаний напряжения уменьшения
по мере того, как само напряжение
увеличивается, т.е. по мере заряда
конденсатора, в начальный момент,
когда
,
имеет максимальное значение
Такие
выводы не являются неожиданными и
вытекают из свойств экспоненциальной
функции, которая в данном случае
определяет закон нарастания напряжения
на конденсаторе.
Во
время переходного процесса в электрическом
поле конденсатора происходит
непрерывное накопление энергии, которая
в установившемся режиме
равна
.
Одновременно часть энергии, отдаваемой
источником, выделяется в виде тепла в
резисторе. Эта энергия может быть
вычислена по формуле
Энергия
,
теряемая в,
не
зависит от величины сопротивления и
равна энергии, запасаемой в электрическом
поле конденсатора. Таким образом, к.п.д.
процесса заряда конденсатора от источника
постоянного напряжения равен 50%.
Рассмотрим
переходные процессы, происходящие в RC
– цепи, при ее закорачивании (конденсатор
заряжен).
На
рис.7 представлена RC
– цепь, которая закорачивается при
замыкании выключателя В.
Рис.7.
На
рис. 7 представлена RC
– цепь, в которой ток отсутствует, а
конденсатор С
заряжен до напряжения Е.
Если в момент
перевести выключательВ
во включенное состояние, то конденсатор
окажется замкнутым на резистор и в
RС
– цепи возникнет ток, который будет
поддерживаться за счет запаса энергии,
накопленной в электрическом поле
конденсатора. С
течением времени энергия электрического
поля рассеивается, превращаясь в
тепло е
резисторе,
ток разряда уменьшается и со временем
становится равным нулю. Эта задача с не
нулевыми начальными условиями.
Полагая в выражении (13), что его правая
часть равна нулю, получим однородное
дифференциальное уравнение для напряжения
на конденсаторе
21
Внешнее
воздействие в цепи отсутствует, поэтому
искомое решение для напряжения
в выражении (14) будет иметь только
свободную составляющую.
22
Для
определения постоянной А
воспользуемся начальными условиями.
Из уравнения (22) при
,
.
Кроме того, согласно второму закону
коммутации,
так как конденсатор к моменту коммутации
был заряжен до напряженияЕ.
Следовательно, А
= Е
и напряжение на конденсаторе согласно
уравнению (22)
23
изменяется
по экспоненциональному закону.
Величина
разрядного тока равна

Падение
напряжения на резисторе равно
25
Отрицательный
знак в выражении (24) для
указывает на то, что направление
разрядного тока противоположно
направлению зарядного тока, условно
принятому за положительное (рис.5).
Максимальная величина разрядного токаограничивается лишь активным сопротивлениемRС
–
цепи. Если сравнить выражения (24) и (18)
для разрядного и зарядного токов, то
можно заключить, что оба тока в RС
–
цепи изменяются одинаково, но имеют
противоположные направления.
Продолжительность
переходного процесса определяется
постоянной времени
.
Чем больше емкость конденсатора и
сопротивление резистора, тем,
соответственно, больше накопленный
заряд на пластинах и меньше разрядный
ток и тем медленнее разряжается
конденсатор.
С
энергетической точки зрения процесс
короткого замыкания RС-цепи
характеризуется тем, что энергия, которая
до коммутации была запасена в электрическом
поле конденсатора, целиком превращается
в тепло в резисторе.
При
проектировании приборных устройств
весьма часто возникает необходимость
передавать через RС
– цепи импульсный сигнал.
Рассмотрим
воздействие импульсного сигнала на
RC-цепь.
Предположим, что на RC
– цепь воздействует сигнал, представляющий
прямоугольный импульс напряжения
.
Его можно представить следующим
соотношением:

Схема
включения RС
– цепи к генератору импульсов представлена
на рис.8.
Рис.8.
В
интервале времени
RC-цепь
подвергается воздействию ступенчатого
напряжения, поэтому ток в RС
– цепи, падение напряжения на резисторе
и конденсаторе изменяются по тем же
законам, как и при воздействии на RС
– цепь постоянной э.д.с.
При
конденсатор за время действия импульса
почти не заряжается (рис.9.а). Напряжение
на выходеRС
– цепи (падение напряжения на резисторе)
в соответствии со вторым законом Кирхгофа
равно.
27
В
течение действия импульса в электрическом
поле конденсатора накапливается
незначительное количество знергии,
поэтому после окончания действия
импульса при
вRC
– цепи практически не возникает переходный
процесс (рис.9.а).
Когда
постоянная времени RС-цепи
соизмерена с длительностью импульса,
т.е.
(рис.9.б), то за время действия импульса
конденсатор успевает зарядиться до
величины.
Поэтому выходное напряжение в течение
длительности непрерывно уменьшается
и в конце импульса определяется следующим
выражением
28
После
окончания действия входного импульса
при
вRC
– цепи возникает переходной процесс,
обусловленный рассеянием энергии,
запасенной в электрическом поле
конденсатора. В RC
– цепи появляется разрядный ток
конденсатора, направление которого
противоположно зарядному току, а на
выходе возникает отрицательный импульс
(рис.9.б).
В
случае когда постоянная времени RС
– цепи значительно меньше длительности
импульса ()
конденсатор успевает полностью разрядится
в
самом
начале импульса
.
После чего выходное напряжение (падение
напряжения на резисторе) станет равным
нулю, т.е..
На выходе появится короткий импульс
положительной полярности (см.рис.9.в)
обусловленный
протеканием зарядного тока, с
амплитудой равной
.
В
момент окончания входного импульса,
т.е.
,
вRC
– цепи возникает ток разряда конденсатора
и на выходе RC
– цепи появляется короткий отрицательный
импульс с амплитудой равной
(рис.9.в).
Рис.9.
Прохождение импульса через RC
– цепь:
а
– эпьюры напряжений при
б
– тоже при
в
– тоже при

С помощью ёмкостного элемента в эквивалентной схеме замещения учитывают накопление в электрическом поле энергии и протекание токов смещения в реальном элементе цепи. С помощью индуктивного элемента учитывают накопление в магнитном поле энергии и наведение ЭДС. При помощи резистивного элемента в эквивалентной схеме учитывают выделение тепла.
Любой элемент реально существующей электрической цепи может быть представлен на эквивалентной схеме в виде нескольких идеальных элементов.
Эквивалентная схема замещения резистора
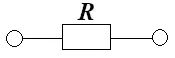
Постоянный резистор, используемый в схеме с низкими частотами может быть представлен в виде одного резистивного элемента R.
Эквивалентная схема того же самого резистора, работающего в схеме на высоких частотах, кроме резистивного элемента включает также индуктивность и ёмкость. С помощью паразитной ёмкости Cп учитывается ток смещения на зажимах элемента. С помощью паразитной индуктивности Lп учитывается сцепленный с резистором магнитный поток.
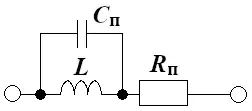
Эквивалентная схема замещения конденсатора
Конденсатор, который работает в схеме на низких частотах представляют, как один ёмкостной элемент C.
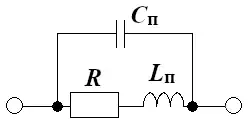
Конденсатор, который работает на высоких частотах в эквивалентной схеме представляется ёмкостным элементом, резистором и индуктивностью. С помощью резистора Rп учитывают потери тепла в диэлектрике конденсатора. Паразитной индуктивность Lп учитывается магнитный поток в подводящих контактах.
Эквивалентная схема замещения катушки индуктивности
Катушку индуктивности, работающую на низких частотах, представляют в виде индуктивного элемента L.
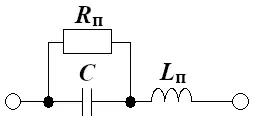
Схема замещения катушки индуктивности, кроме индуктивного элемента, включает также резистор и ёмкость. Резистивный элемент Rп учитывает потери на выделение тепла в сердечнике и сопротивлении обмотки. При помощи паразитной ёмкости Cп учитываются токи смещения, существующие между витками катушки.
В случае составления эквивалентной схемы для реальных элементов цепи в неё включают такие идеальные элементы, которые могут описать основные процессы, протекающие в этих реальных элементах. При этом второстепенными процессами, как правило, пренебрегают.
Представленную как совокупность идеализированных элементов схемы реальную электрическую цепь называют схемой замещения, эквивалентной схемой или эквивалентной схемой замещения.
Если ток и напряжение на всех элементах в реальной электрической цепи никак не зависят от координат в пространстве, то такую цепь называют цепью с сосредоточенными параметрами. Если же ток и напряжение зависят от координат в пространстве, то это цепь с распределёнными параметрами.
Процессы, которые происходят в цепи с сосредоточенными параметрами описывают при помощи дифференциальных или алгебраических уравнений. Процессы, происходящие в цепях с распределёнными параметрами, описывают с помощью уравнений в частных производных.
Расчётную модель реальной электрической цепи сопоставляют с экспериментальными данными. В случае больших расхождений модель необходимо будет уточнить.
Практические аспекты применения конденсаторов
Добавлено 11 декабря 2019 в 00:19
Конденсаторы, как и все электрические компоненты, имеют ограничения, которые необходимо учитывать для надежности и правильной работы схемы.
Рабочее напряжение конденсатора
Рабочее напряжение: поскольку конденсаторы представляют собой не более чем два проводника, разделенных изолятором (диэлектриком), вы должны обратить внимание на максимально допустимое на нем напряжение. Если приложено слишком высокое напряжение, номинальное значение «пробоя» диэлектрического материала может быть превышено, что приведет к внутреннему короткому замыканию конденсатора.
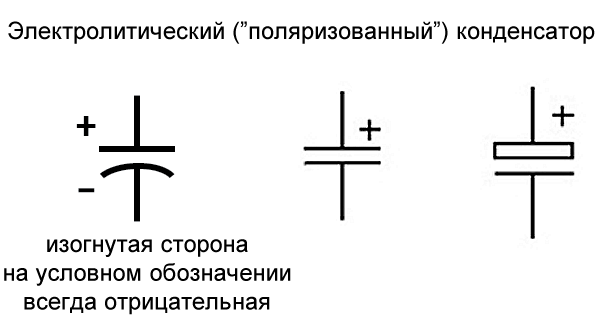
Полярность конденсатора
Полярность: некоторые конденсаторы изготавливаются таким образом, что они могут выдерживать приложенное напряжение только одной полярности, но не другой. Это связано с их конструкцией: диэлектрик представляет собой микроскопически тонкий слой изоляции, нанесенный во время изготовления на одну из пластин с помощью постоянного напряжения. Они называются электролитическими конденсаторами, и их полярность четко обозначена.
Изменение полярности напряжения на электролитическом конденсаторе может привести к разрушению этого сверхтонкого диэлектрического слоя, что приведет к разрушению устройства. Однако толщина этого диэлектрика позволяет получать чрезвычайно высокие значения емкости при относительно небольшом размере корпуса. По той же причине электролитические конденсаторы имеют тенденцию иметь низкое номинальное напряжение по сравнению с другими типами конструкций конденсаторов.
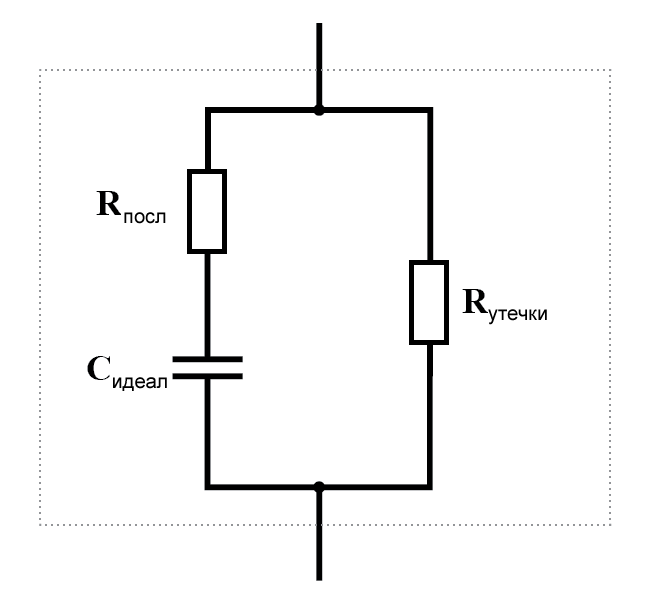
Эквивалентная схема конденсатора
Эквивалентная схема: поскольку пластины в конденсаторе имеют некоторое сопротивление, и поскольку ни один диэлектрик не является идеальным изолятором, не существует такой вещи, как «идеальный» конденсатор. В реальной жизни конденсатор имеет как последовательное сопротивление, так и параллельное сопротивление (сопротивление утечки), взаимодействующие с его чисто емкостными характеристиками:
К счастью, относительно легко изготовить конденсаторы с очень маленьким последовательным сопротивлением и очень высоким сопротивлением утечки!
Физические размеры конденсатора
Для большинства применений в электронике минимальный размер является целью для разработки компонентов. Чем меньшие по размеру компоненты можно изготовить, тем большая схема может быть встроена в меньший корпус, при этом, как правило, также уменьшается вес. В случае конденсаторов существуют два основных ограничивающих фактора для минимального размера устройства: рабочее напряжение и емкость. И эти два фактора, как правило, противоречат друг другу. Для любого конкретного выбранного диэлектрического материала единственный способ увеличить номинальное напряжение конденсатора – это увеличить толщину диэлектрика. Однако, как мы видели, это приводит к уменьшению емкости. Емкость можно восстановить, увеличив площадь пластины, но это делает компонент больше. Вот почему вы не можете судить о емкости конденсатора в фарадах просто по размеру. Конденсатор любого заданного размера может быть относительно высоким по емкости и с низким рабочим напряжением, или наоборот, или иметь некоторый компромисс между двумя этими крайностями. Посмотрим для примера следующие две фотографии:
Это довольно большой конденсатор по физическим размерам, но он имеет довольно низкое значение емкости: всего 2 мкФ. Тем не менее, его рабочее напряжение довольно высокое: 2000 вольт! Если бы этот конденсатор был перепроектирован так, чтобы между его пластинами был более тонкий слой диэлектрика, то могло бы быть достигнуто, по крайней мере, стократное увеличение емкости, но за счет значительного снижения его рабочего напряжения. Сравните приведенную выше фотографию с приведенной ниже. Конденсатор, показанный на нижнем рисунке, представляет собой электролитический компонент, по размерам подобный приведенному выше, но с очень отличающимися значениями емкости и рабочего напряжения:
Более тонкий слой диэлектрика дает ему гораздо большую емкость (20000 мкФ) и резко снижает рабочее напряжение (постоянное напряжение 35 В, напряжение 45 В в пике).
Вот некоторые образцы конденсаторов разных типов, все по размеру меньше, чем показанные ранее:
Электролитические и танталовые конденсаторы являются полярными (чувствительны к полярности) и всегда помечаются как таковые. У электролитических конденсаторов отрицательные (-) выводы отмечаются стрелками на корпусе. У некоторых полярных конденсаторов полярность обозначена на положительном выводе. У большого электролитического конденсатора на 20 000 мкФ, показанного выше, положительный (+) вывод помечен знаком «плюс». Керамические, майларовые, пленочные и воздушные конденсаторы не имеют маркировки полярности, потому что эти типы являются неполярными (они не чувствительны к полярности).
Конденсаторы являются очень распространенными компонентами в электронных схемах. Внимательно посмотрите на следующую фотографию – каждый компонент, обозначенный на печатной плате буквой «С», является конденсатором:
Некоторые конденсаторы на плате – это стандартные электролитические конденсаторы: C30 (верхняя часть платы, в центре) и C36 (левая сторона, 1/3 от вершины). Некоторые другие представляют собой особый вид электролитических конденсаторов, называемый танталовым, потому что именно этот тип металла используется для изготовления пластин. Танталовые конденсаторы имеют относительно высокую емкость для своих физических размеров. На плате, показанной выше, танталовые конденсаторы: C14 (чуть ниже слева от C30), C19 (непосредственно под R10, который ниже C30), C24 (нижний левый угол платы) и C22 (внизу справа).
Примеры еще меньших по размеру конденсаторов можно увидеть на этой фотографии:
Конденсаторы на этой печатной плате из соображений экономии места являются «устройствами поверхностного монтажа», как и все резисторы. В соответствии с соглашением о маркировке компонентов конденсаторы могут быть идентифицированы по меткам, начинающимся с буквы «C».
Теги
Алюминиевый электролитический конденсаторКерамический конденсаторКонденсаторТипы конденсаторовЭлектролитический конденсаторЭлектронные компоненты
При низких частотах конденсаторы можно рассматривать как емкостные элементы. При высоких частотах играют существенную роль потери энергии в изоляции. Эти потери растут с увеличением частоты тока и зависят от материала изоляции. Например, бумажная изоляция, которая применяется для конденсаторов, устанавливаемых в цепях низких и звуковых частот, оказывается непригодной при высоких частотах, так как потери энергии в ней приводят к недопустимому нагреву.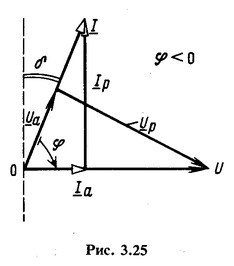
Для конденсатора, как и для любого двухполюсника, можно составить две схемы замещения (рис. 3.26), в которых g и r учитывают потери энергии в диэлектрике.
Обычно угол потерь δ очень мал. Величина для различных частот и диэлектриков лежит в пределах от
. При таких условиях
Поэтому практически можно считать
и так как yz = 1, то С = С1 т. е. емкости С и С1 обеих схем практически одинаковы.
Связь между r и g найдем из общих соотношений между сопротивлениями и проводимостями (3.36):
На практике конденсатор характеризуют параметрами С и tgδ. Для параллельной эквивалентной схемы (рис. 3.26, а)
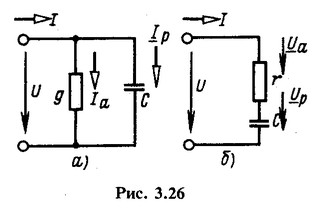
Величину, обратную tgδ, называют добротностью конденсатора:
Смешанное соединение конденсаторов

4.2
Средняя оценка: 4.2
Всего получено оценок: 141.
4.2
Средняя оценка: 4.2
Всего получено оценок: 141.
Основными типами соединений в электротехнике являются последовательные и параллельные соединения. Если элементы схемы соединены одновременно обоими типами соединений, говорят о смешанном соединении. Найдем электрические характеристики смешанного соединения конденсаторов.
Соединение конденсаторов в батарею
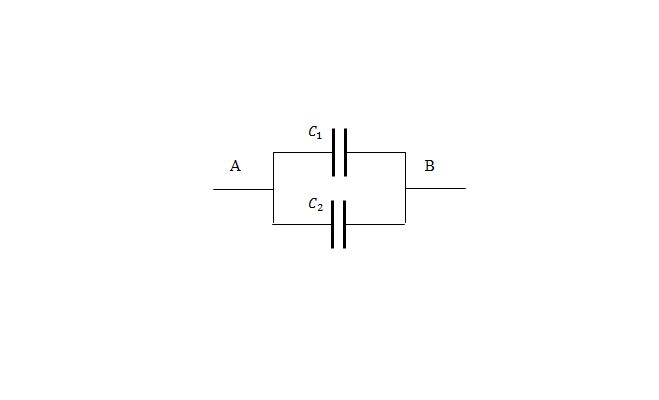
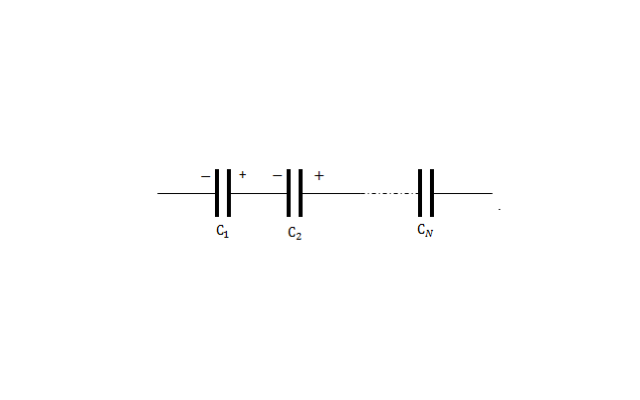
В электротехнике иногда требуется соединение нескольких конденсаторов. При параллельном соединении выводы каждого конденсатора присоединяются к выводам цепи. При последовательном соединении к выводам цепи подсоединяются только выводы первого и последнего конденсаторов. Из остальных же конденсаторов создается «цепочка», так, чтобы первый вывод очередного конденсатора подсоединялся ко второму выходу предыдущего.
Большое число конденсаторов можно соединить в несколько последовательных цепей, эти цепи могут быть соединены параллельно, образующиеся новые цепи можно опять соединять последовательно — и так из большого числа конденсаторов можно создать большую параллельно-последовательную батарею. Как найти характеристики такой батареи?
Поскольку в такой батарее существуют только конденсаторы, следовательно, в ней не происходит ни потерь энергии, ни ее преобразования. Электрический заряд, проходящий по батарее, лишь распределяется между ее элементами. То есть батарея, состоящая из одних конденсаторов, с точки зрения внешней цепи представляет собой конденсатор некоторой емкости.
Найдем ее.
Емкость соединенных конденсаторов
Для расчета смешанного соединения конденсаторов требуется знать две формулы: емкость чисто параллельного и чисто последовательного соединения. При чисто параллельном соединении конденсаторов их емкость складывается:
$$C_{пар}=C_1+C_2+…+C_n$$
Если конденсаторы соединяются последовательно, то складывается напряжение на них, зарядить их труднее, следовательно, емкость уменьшается. Величина, обратная суммарной емкости, равна сумме обратных величин отдельных емкостей конденсаторов:
$${1over C_{посл}}={{1over C_1}+{1over C_1}+…{1over C_n}}$$
Анализ схемы смешанного соединения
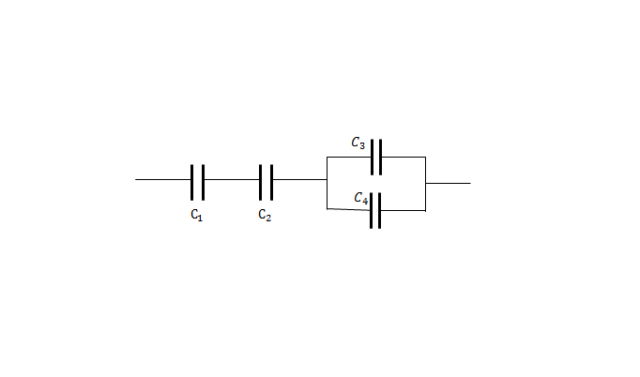
Теперь можно приступать к анализу схемы смешанного соединения.
В схеме необходимо выделить узлы — точки цепи, к которым присоединены три и более звеньев. Даже в очень сложной схеме найдутся такие узлы, между которыми соединение конденсаторов будет только последовательным или только параллельным. Эти конденсаторы в схеме заменяются одним эквивалентным, имеющим емкость, для определения которой используется соответствующая формула.
После замены схема снова анализируется. В ней снова выделяются узлы, между которыми конденсаторы соединены только одним из двух способов. Снова проводится замена конденсаторов эквивалентом.
Так делается до тех пор, пока схема максимально не упростится. Чаще всего при этом остается только один эквивалентный конденсатор, емкость которого и будет равна емкости всей батареи конденсаторов в смешанном соединении.
Иногда, в сложных случаях, невозможно упростить схему до одного эквивалентного конденсатора с помощью указанных двух преобразований. В этом случае для расчета смешанного соединения конденсаторов используются более сложные методы, например, метод узловых потенциалов. Кроме того, существуют особые эквивалентные преобразования, например, преобразование треугольника конденсаторов в трехлучевую звезду и обратно. Все эти методы изучаются в вузовском курсе теории цепей.
Что мы узнали?
Для нахождения эквивалентной емкости смешанного соединения конденсаторов в схеме выделяются узлы, звенья между соседними узлами заменяются эквивалентными элементами с помощью формул последовательного или параллельного соединения. В результате схема упрощается. Такие упрощения проводятся, пока не останется один эквивалентный конденсатор, имеющий емкость, равную емкости исходного соединения.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.2
Средняя оценка: 4.2
Всего получено оценок: 141.
А какая ваша оценка?