интервал дан для x, а для abc надо завести 3 ячейки сверху.
Примерно так:
a: b: c:
x y
-5 тут формула =$b$1*c1*c1+$d$1*c1+$f$1 вотом её тянем вниз и строим график по таблице
-4.8
-4.6
-4.4
-4.2
и т. к. до +5
Теперь играя параметрами abc можно смотреть как меняется график
RetroBatonПрофи (805)
11 лет назад
Получается Х будет лежать в интервале А1:А50, У в интервале В1:В50, а значения А Б С, будут изначально пустыми?
RetroBatonПрофи (805)
11 лет назад
Я изменил формулу на =A$2^2*C1+A$2*D1+E1 так как у меня в графе А1 стоит Х, В2 – У, С1 – А, D1 – В, Е1 – С.
В ячейке В2 получилось вывести правильное значение 18, при а-1 в-2 с-3, а в других ячейках не получается(
|
Время |
Задачи лабораторной После
|
|
Цель работы Освоение |
|
|
Перечень обеспечивающих Для |
Задание 1.
Составить таблицу
расчета доходов фирмы в абсолютном и
процентном отношении и диаграмму роста
доходов на основе данных о доходах
фирмы.

Выполнение.
-
Составить таблицу
расчета доходов фирмы: определить тип,
размер и стиль шрифтов для заголовков
строк и столбцов: Times New Roman Cyr, размер
12, стиль полужирный; для остального
текста – Times New Roman Cyr, размер 10, стиль
обычный; -
Вычислить рост уровня
доходов фирмы в процентном отношении
в каждом месяце 1999 года по отношению к
январю 1999 года (3-й столбец таблицы);
=(Ci-C$3)/C$3
где Сi
– адрес ячейки i-го
месяца графы Уровень доходов фирмы в
2009 году, С$3 – абсолютный адрес ячейки
Уровень доходов фирмы за январь 2009 года;
-
Вычислить суммарный
уровень доходов фирмы за 2009 и 2010 годы,
результаты поместить в последней строке
второго и третьего столбца соответственно;
-
Вычислить среднее
значение роста уровня доходов в
процентах, результат поместить в
последней строке четвертого столбца; -
Построить диаграмму
зависимости уровня доходов фирмы за
2009 и 2010 годы по месяцам в виде гистограммы; -
Построить диаграмму
зависимости уровня доходов фирмы в
процентном отношении в виде линейного
графика; -
Построить совмещенную
диаграмму (тип нестандартная/график|гистограмма
2) по данным
полученной таблицы (второй, третий и
четвертый столбцы); -
Рассмотреть другие
типы диаграмм, освоить редактирование
элементов диаграмм.
Задание 2.
Составить круговую диаграмму с
отображением среднего балла по предметам
на основании таблицы “Итоги
экзаменационной сессии” Лабораторной
работы №3_3.
Итоги экзаменационной сессии
|
№ п/п |
Ф. |
Математика |
Эконом. |
Информатика |
|
1. |
Макаров |
8 |
7 |
6 |
|
2. |
… |
… |
||
|
3. |
||||
|
… |
||||
|
Средний |
Задание 3.
Построить график функции y=sin
x.
Значение аргумента х выбрать в пределах
от –6 до 6 с шагом 0,5.
Выполнение.
Построим таблицу
следующего вида
-
X
-6,0
-5,5
-5,0
…
Y
0,28
0,71
0,96
…
Для чего заполним
значениями строку Х путем протягивания.
В строку Y
вставим формулу =Sin(B2)
и протянем до конца таблицы.
Затем выделим построенный
диапазон и на панели стандартная нажмем
кнопку Мастер диаграмм. Выберем тип
диаграммы – график.
Задание 4.
Составьте электронную таблицу для
вывода графика квадратичной функции
![]() ,
,
считая a,
b и с
параметрами на интервале [-5;5] с шагом
0.2.
Задание 5. Составьте
электронную таблицу для вывода графика
![]() ,
,
считая a,
b и с
параметрами на интервале [n1;n2]
с шагом h=(n2-n1)/30.
Задание 6. Составьте
электронную таблицу для вывода графика
функции
![]()
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание статьи (кликните для открытия/закрытия)
- Построение графика линейной функции в Excel
- Подготовка расчетной таблицы
- Построение графика функции
- Построение графиков других функций
- Квадратичная функция y=ax2+bx+c
- Кубическая парабола y=ax3
- Гипербола y=k/x
- Построение тригонометрических функций sin(x) и cos(x)
Построение графика зависимости функции является характерной математической задачей. Все, кто хотя бы на уровне школы знаком с математикой, выполняли построение таких зависимостей на бумаге. В графике отображается изменение функции в зависимости от значения аргумента. Современные электронные приложения позволяют осуществить эту процедуру за несколько кликов мышью. Microsoft Excel поможет вам в построении точного графика для любой математической функции. Давайте разберем по шагам, как построить график функции в excel по её формуле
Построение графиков в Excel 2016 значительно улучшилось и стало еще проще чем в предыдущих версиях. Разберем пример построения графика линейной функции y=kx+b на небольшом интервале [-4;4].
Подготовка расчетной таблицы
В таблицу заносим имена постоянных k и b в нашей функции. Это необходимо для быстрого изменения графика без переделки расчетных формул.
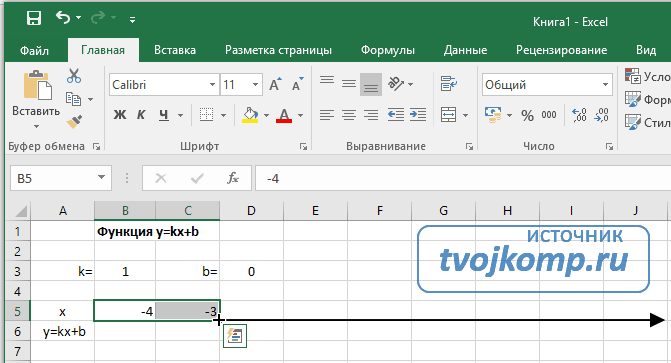
Далее строим таблицу значений линейной функции:
- В ячейки A5 и A6 вводим соответственно обозначения аргумента и саму функцию. Запись в виде формулы будет использована в качестве названия диаграммы.
- Вводим в ячейки B5 и С5 два значения аргумента функции с заданным шагом (в нашем примере шаг равен единице).
- Выделяем эти ячейки.
- Наводим указатель мыши на нижний правый угол выделения. При появлении крестика (смотри рисунок выше), зажимаем левую кнопку мыши и протягиваем вправо до столбца J.
Ячейки автоматически будут заполнены числами, значения которых различаются заданным шагом.

Далее в строку значений функции в ячейку B6 записываем формулу =$B3*B5+$D3
Внимание! Запись формулы начинается со знака равно(=). Адреса ячеек записываются на английской раскладке. Обратите внимание на абсолютные адреса со знаком доллара.
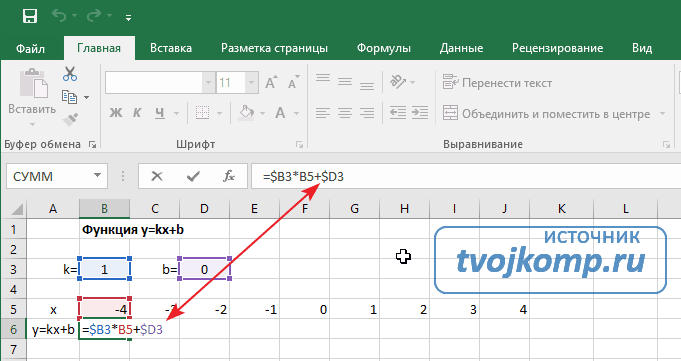
Чтобы завершить ввод формулы нажмите клавишу Enter или галочку слева от строки формул вверху над таблицей.
Копируем эту формулу для всех значений аргумента. Протягиваем вправо рамку от ячейки с формулой до столбца с конечными значениями аргумента функции.
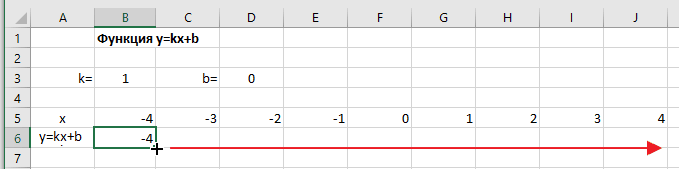
Построение графика функции
Выделяем прямоугольный диапазон ячеек A5:J6.
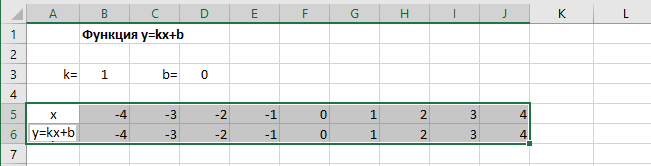
Переходим на вкладку Вставка в ленте инструментов. В разделе Диаграмма выбираем Точечная с гладкими кривыми (см. рисунок ниже).Получим диаграмму.
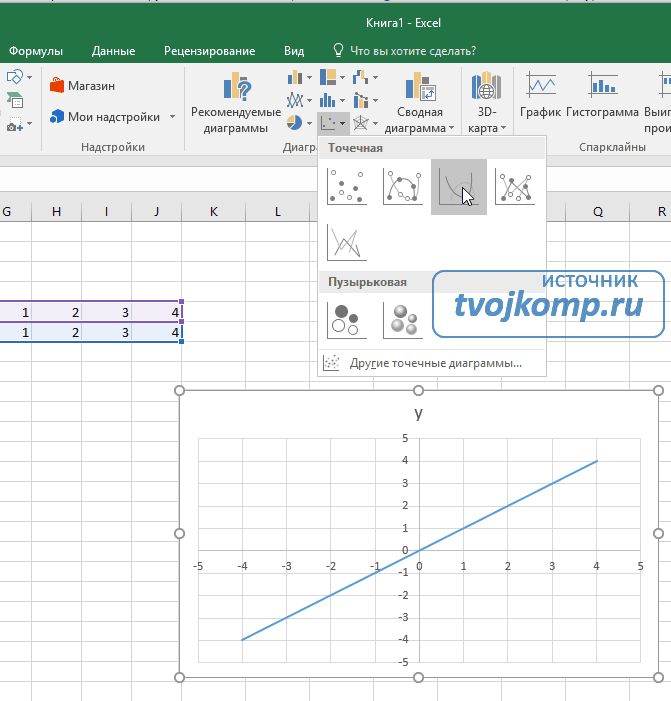
После построения координатная сетка имеет разные по длине единичные отрезки. Изменим ее перетягивая боковые маркеры до получения квадратных клеток.
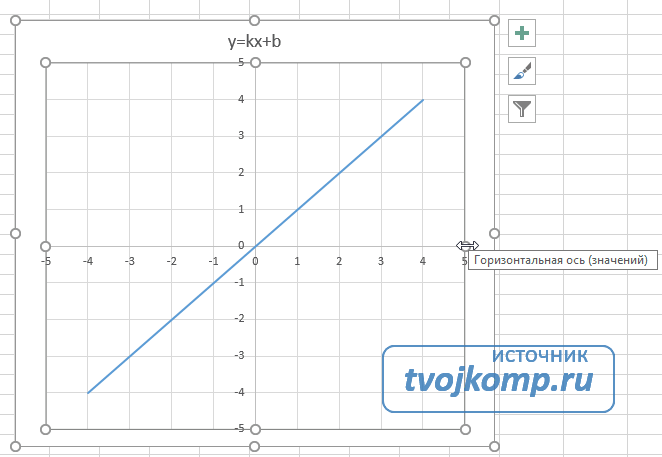
Теперь можно ввести новые значения постоянных k и b для изменения графика. И видим, что при попытке изменить коэффициент график остается неизменным, а меняются значения на оси. Исправляем. Кликните на диаграмме, чтобы ее активировать. Далее на ленте инструментов во вкладке Работа с диаграммами на вкладке Конструктор выбираем Добавить элемент диаграммы – Оси – Дополнительные параметры оси..
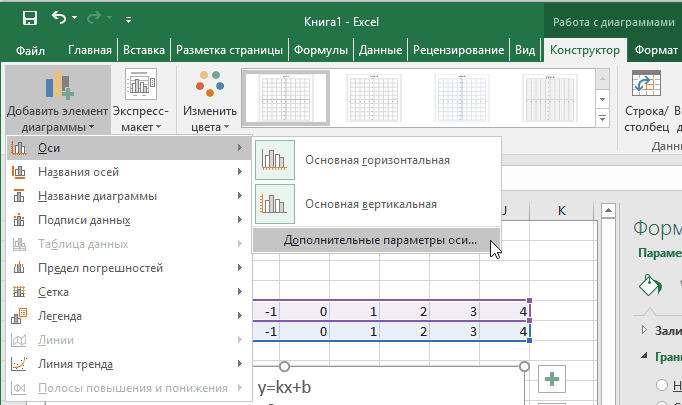
В правой части окна появиться боковая панель настроек Формат оси.
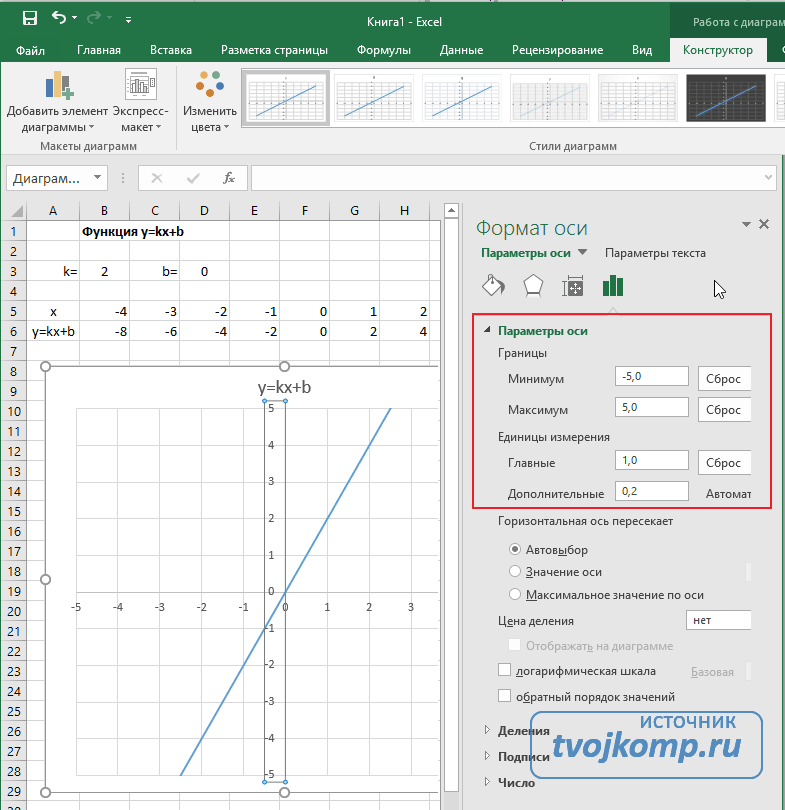
- Кликните на раскрывающийся список Параметры оси.
- Выберите Вертикальная ось (значений).
- Кликните зеленый значок диаграммы.
- Задайте интервал значений оси и единицы измерения (обведено красной рамкой). Ставим единицы измерения Максимум и минимум (Желательно симметричные) и одинаковые для вертикальной и горизонтальной осей. Таким образом, мы делаем мельче единичный отрезок и соответственно наблюдаем больший диапазон графика на диаграмме.И главную единицу измерения – значение 1.
- Повторите тоже для горизонтальной оси.
Теперь, если поменять значения K и b , то получим новый график с фиксированной сеткой координат.
Построение графиков других функций
Теперь, когда у нас есть основа в виде таблицы и диаграммы, можно строить графики других функций, внося небольшие корректировки в нашу таблицу.
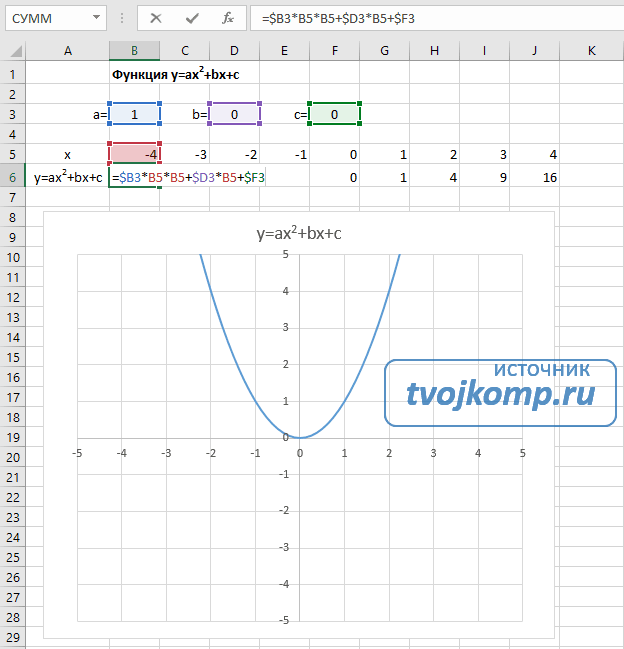
Квадратичная функция y=ax2+bx+c
Выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3
- Копируем её на весь диапазон значений аргумента вправо
Получаем результат
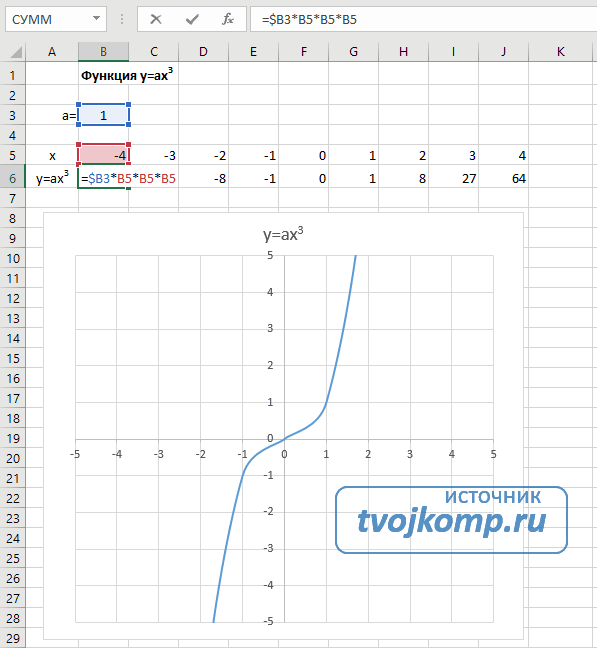
Кубическая парабола y=ax3
Для построения выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5*B5
- Копируем её на весь диапазон значений аргумента вправо
Получаем результат
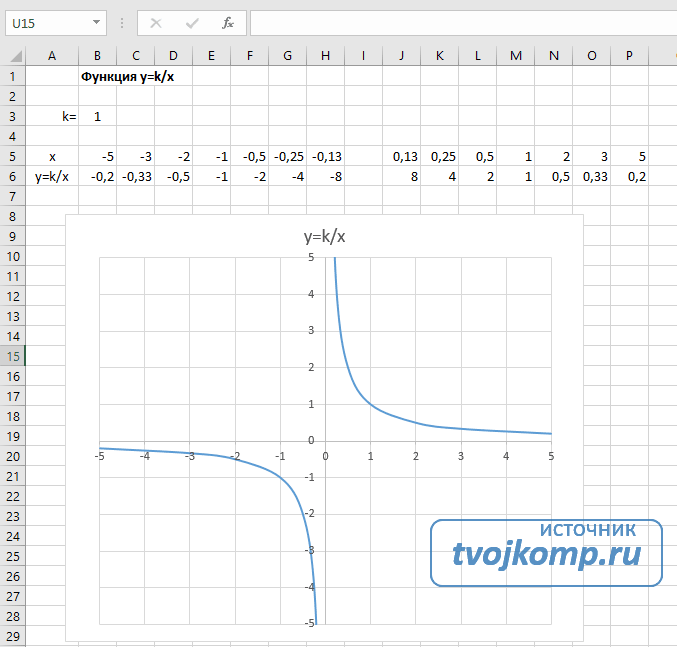
Гипербола y=k/x
Для построения гиперболы заполните таблицу вручную (смотри рисунок ниже). Там где раньше было нулевое значение аргумента оставляем пустую ячейку.
Далее выполните действия:
- В первой строке меняем заголовок.
- В третьей строке указываем коэффициенты и их значения.
- В ячейку A6 записываем обозначение функции.
- В ячейку B6 вписываем формулу =$B3/B5
- Копируем её на весь диапазон значений аргумента вправо.
- Удаляем формулу из ячейки I6.
Для корректного отображения графика нужно поменять для диаграммы диапазон исходных данных, так как в этом примере он больше чем в предыдущих.
- Кликните диаграмму
- На вкладке Работа с диаграммами перейдите в Конструктор и в разделе Данные нажмите Выбрать данные.
- Откроется окно мастера ввода данных
- Выделите мышкой прямоугольный диапазон ячеек A5:P6
- Нажмите ОК в окне мастера.
Получаем результат
Построение тригонометрических функций sin(x) и cos(x)
Рассмотрим пример построения графика тригонометрической функции y=a*sin(b*x).
Сначала заполните таблицу как на рисунке ниже
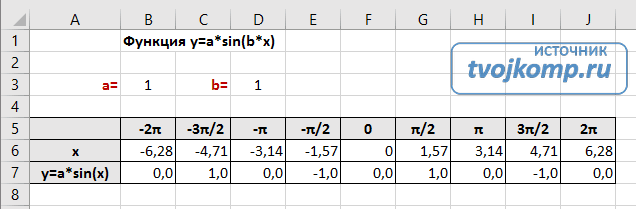
В первой строке записано название тригонометрической функции.
В третьей строке прописаны коэффициенты и их значения. Обратите внимание на ячейки, в которые вписаны значения коэффициентов.
В пятой строке таблицы прописываются значения углов в радианах. Эти значения будут использоваться для подписей на графике.
В шестой строке записаны числовые значения углов в радианах. Их можно прописать вручную или используя формулы соответствующего вида =-2*ПИ(); =-3/2*ПИ(); =-ПИ(); =-ПИ()/2; …
В седьмой строке записываются расчетные формулы тригонометрической функции.
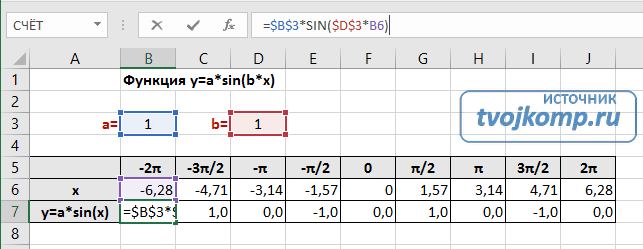
В нашем примере =$B$3*SIN($D$3*B6). Адреса B3 и D3 являются абсолютными. Их значения – коэффициенты a и b, которые по умолчанию устанавливаются равными единице.
После заполнения таблицы приступаем к построению графика.
Выделяем диапазон ячеек А6:J7. В ленте выбираем вкладку Вставка в разделе Диаграммы указываем тип Точечная и вид Точечная с гладкими кривыми и маркерами.
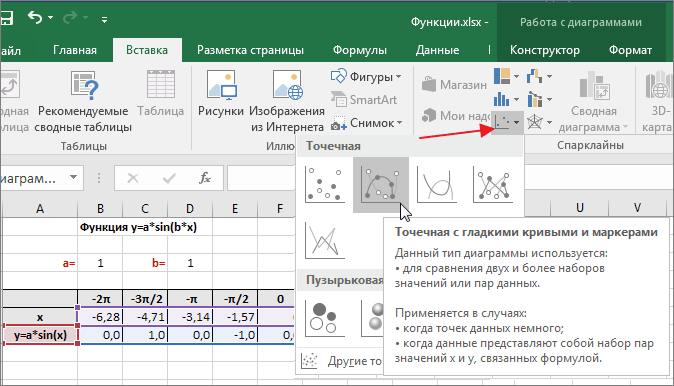
В итоге получим диаграмму.
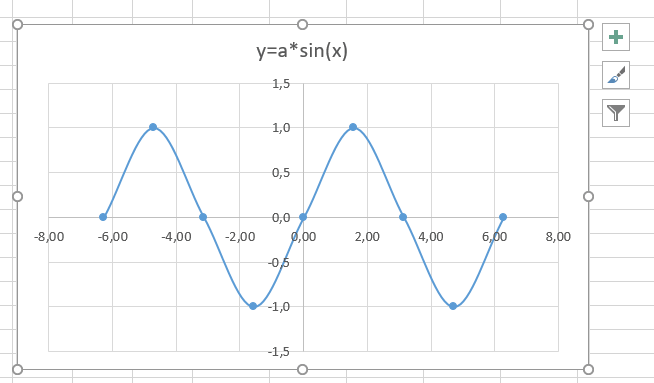
Теперь настроим правильное отображение сетки, так чтобы точки графика лежали на пересечении линий сетки. Выполните последовательность действий Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Сетка и включите три режима отображения линий как на рисунке.
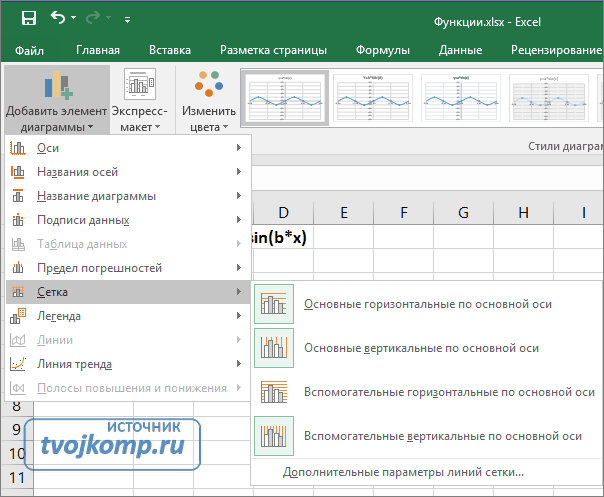
Теперь зайдите в пункт Дополнительные параметры линий сетки. У вас появится боковая панель Формат области построения. Произведем настройки здесь.
Кликните в диаграмме на главную вертикальную ось Y (должна выделится рамкой). В боковой панели настройте формат оси как на рисунке.
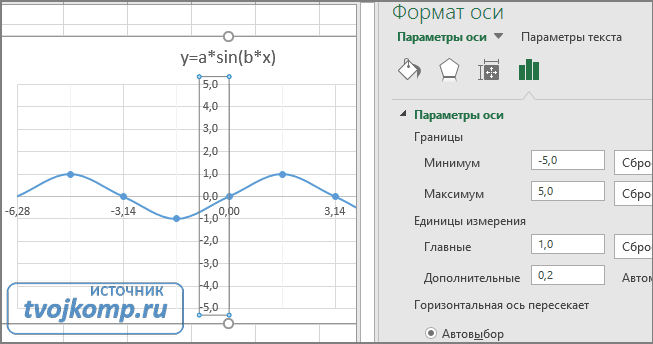
Кликните главную горизонтальную ось Х (должна выделится) и также произведите настройки согласно рисунку.
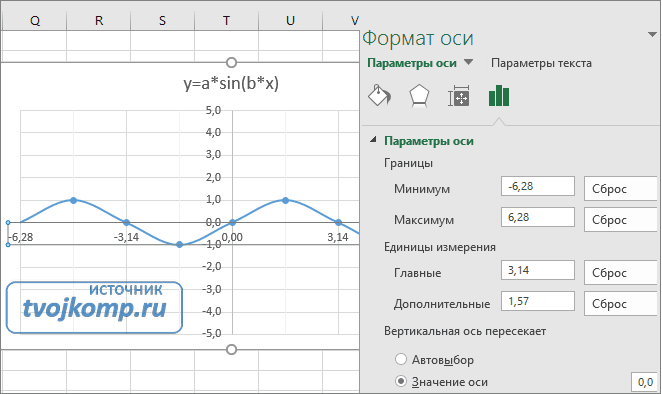
Теперь сделаем подписи данных над точками. Снова выполняем Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Подписи данных – Сверху. У вас подставятся значения числами 1 и 0, но мы заменим их значениями из диапазона B5:J5.
Кликните на любом значении 1 или 0 (рисунок шаг 1) и в параметрах подписи поставьте галочку Значения из ячеек (рисунок шаг 2). Вам будет сразу же предложено указать диапазон с новыми значениями (рисунок шаг 3). Указываем B5:J5.
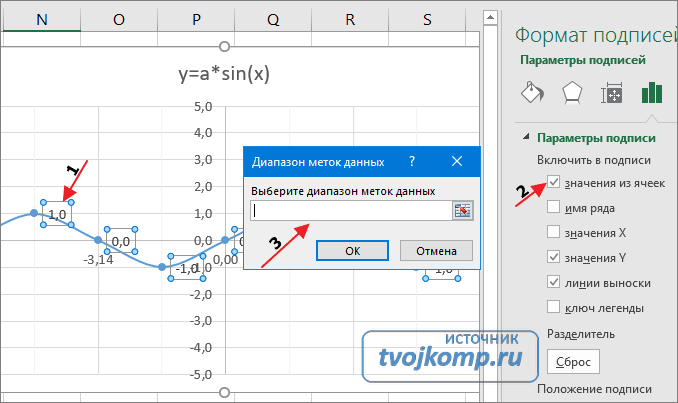
Вот и все. Если сделали правильно, то и график будет замечательным. Вот такой.
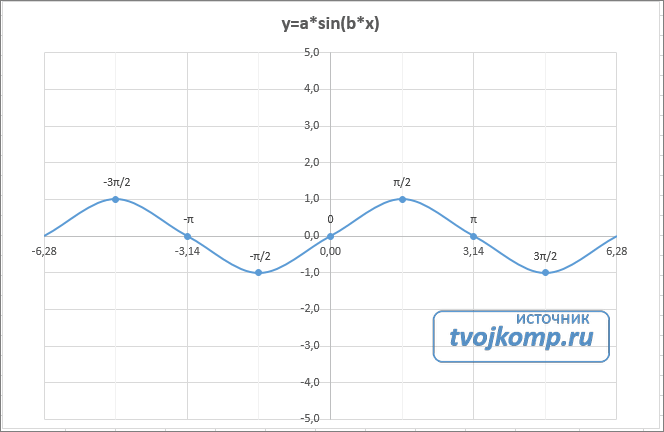
Чтобы получить график функции cos(x), замените в расчетной формуле и в названии sin(x) на cos(x).
Аналогичным способом можно строить графики других функций. Главное правильно записать вычислительные формулы и построить таблицу значений функции. Надеюсь, что вам была полезна данная информация.
Дополнительные статьи по теме:
- Знакомство с таблицами в Excel
- Изменение строк и столбцов в Excel
- Работа с ячейками: объединение, изменение, защита…
- Ошибки в формулах: почему excel не считает
- Использования условий в формулах Excel
- Функция CЧЕТЕСЛИМН
- Работа с текстовыми функциями Excel
- Все уроки по Microsoft Excel
Дорогой читатель! Вы посмотрели статью до конца.
Получили вы ответ на свой вопрос? Напишите в комментариях пару слов. Если ответа не нашли, укажите что искали или откройте содержание блога.

ОЧЕНЬ ВАЖНО! Оцени лайком или дизлайком статью!


квадратичная функция.doc
Войти
Файл
Правка
Вид
Инструменты
Справка
Цели:
- формирование умений и навыков практического
применения программы MS Excel при решении задач и
построении графиков; - развитие мышления; навыков работы на ПК,
- воспитание бережного отношения к
вычислительной технике.
Оборудование: доска, ПК, карточки с заданием
практической работы.
Ход урока
Организационный момент (постановка целей).
Начинаем наш урок информатики. Сегодня у нас
практическое занятие на тему: “MS Excel. Построение
графиков”, на котором мы будем строить графики
функций и траекторию движения тел. А именно,
рассмотрим задачу на построение графика
линейной и квадратичной функций и задачу по
физике на тему: “Криволинейное движение тел”.
Актуализация знаний.
Мы начали работать с электронными таблицами MS
Excel.
Скажите, что мы научились выполнять в программе
MS Excel.
- Составлять последовательность чисел;
- Присваивать имена ячейкам;
- Записывать относительные и абсолютные ссылки;
- Вставлять функцию;
- Записывать формулы и вычислять значения по
формулам; - Копировать значения ячеек;
- Строить графики функций.
Фронтальный опрос:
Как составить последовательность чисел в
отдельных ячейках? (Чтобы создать возрастающую
последовательность с постоянным шагом, следует
ввести в две соседние ячейки первые два значения
последовательности. Excel использует эти два
значения для определения шага и исходного
значения последовательности. Затем, выделить эти
две ячейки и перетащить маркер заполнения вниз
(курсор при этом приобретает форму плюса).
Как ввести формулу в ячейку? (Формулу можно
ввести в строке формул или в ячейке. Все формулы в
Excel должны начинаться со знака равенства и не
должны содержать пробелов. После завершения
ввода формулы следует нажать клавишу Enter или
щелкнуть по кнопке в строке формул.)
Как скопировать формулу в другие ячейки? (Для
этого необходимо выделить ячейку и перетащить
маркер заполнения вниз, курсор при этом
приобретает форму плюса.)
Для записи формулы мы используем ссылки. А
какие виды ссылок вы знаете? Приведите примеры. (Ссылки
бывают относительные, абсолютные и смешанные.
Ссылка $A$1 абсолютной. Ссылка A3 или B5 являются
относительными.)
Назовите отличие относительной и абсолютной
ссылок. (При копировании адрес относительной
ячейки меняется в соответствии с новым
положением ячейки, адрес абсолютной ячейки не
изменяется.)
Формирование УН:
На прошлом уроке мы научились строить графики и
диаграммы, редактировать их. А сейчас с помощью
графиков найдем точку пересечения двух функций.
Но сначала вспомним, какие функции являются
линейными и квадратичными?
(Ответы учащихся).
Итак, линейную функцию можно записать в виде
y=ax+b, где a и b – некоторые числа, а? 0. Квадратичная
функция записывается в виде y=ax2+bx+c, где a, b, с
– некоторые числа, а? 0.
Частный вид квадратичной функции y=x2.
Задача 1. Даны две функции y=x2 и y=ax+b. В
формуле значения a и b задайте самостоятельно.
Постройте графики этих функций и найдите точки
пересечения графиков, если таковы имеются.
Пример: y=ax+b, a=5, b=-4.
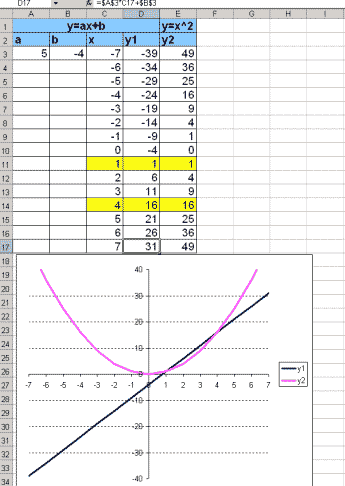
Рисунок 1.
Физкультминутка. Гимнастика для глаз.
Задача 2. Один мяч подбросили вертикально
вверх с высоты 10 м. Второй мяч подбросили с земли
со скоростью 10 м/с. Как будет изменяться значение
высоты с изменением времени, если высота
вычисляется по формуле: h=h0+v0t-gt2/2,
где h0 – начальная высота, v0 –
начальная скорость, g – ускорение свободного
падения.
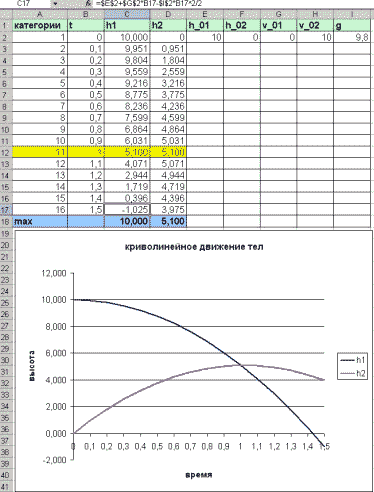
Рисунок 2.
Ответьте на вопросы:
Найдите, на какую максимальную высоту
подбросили второй мяч?
Через сколько секунд два мяча будут на одной
высоте и какое значение этой высоты?
Подберите свои начальные условия для задачи и
постройте траектории движения тел при новых
условиях.
Рефлексия и итог урока:
Сохраните свои работы.
Подведем итог.
Какие необходимы исходные данные для того,
чтобы построить график функции в электронных
таблицах?
Как осуществить быстрый переход от
относительной ссылки к абсолютной или смешанным
ссылкам. (Нажатием на клавишу F4).
Домашнее задание.
Повторить основные понятия темы: “Принцип
адресации в электронных таблицах MS Excel”.
