2.2.3. Эмпирическая функция распределения интервального ряда
Она определяется точно так же, как в дискретном случае:
![]() , где
, где ![]() – количество вариант СТРОГО МЕНЬШИХ, чем «икс», который
– количество вариант СТРОГО МЕНЬШИХ, чем «икс», который
«пробегает» все значения от «минус» до «плюс» бесконечности.
Но вот построить её для интервального ряда намного проще. Находим накопленные относительные частоты:
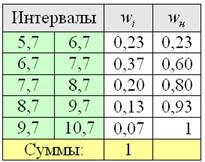
И строим кусочно-ломаную линию, с промежуточными точками ![]() , где
, где ![]() – правые концы интервалов, а
– правые концы интервалов, а ![]() – относительная частота, которая успела накопиться на всех «пройденных»
– относительная частота, которая успела накопиться на всех «пройденных»
интервалах:
При этом ![]() если
если ![]() и
и ![]() если
если ![]() .
.
Напоминаю, что данная функция не убывает, принимает значения из промежутка ![]() и, кроме того, для ИВР она ещё и непрерывна.
и, кроме того, для ИВР она ещё и непрерывна.
Эмпирическая функция является аналогом функции распределения НСВ и
приближает теоретическую функцию ![]() , которую теоретически, а иногда и практически можно построить по всей
, которую теоретически, а иногда и практически можно построить по всей
генеральной совокупности.
Помимо перечисленных графиков, вариационные ряды также можно представить с помощью кумуляты и
огивычастот либо относительных частот, но в классическом учебном курсе эта дичь редкая, и
поэтому я не буду останавливаться на ней этой книге. Скажу только, что у вас вряд ли возникнут проблемы с их построением в
случае такой необходимости.
Теперь что касаемо объёма выборки. Хорошо, если в вашей задаче всего лишь 20-30-50 вариант, но что делать,
если их 100-200 и больше? В моей практике встречались десятки таких задач, и ручной подсчёт здесь уже не торт. Никаких
проблем:
Как быстро составить ИВР при большом объёме выборки?
(Ютуб)
Но не всё так сурово. Во многих задачах вам будет дан готовый вариационный ряд:
Пример 7
Выборочная проверка партии чая, поступившего в торговую сеть, дала следующие результаты:

Требуется построить гистограмму и полигон относительных частот, эмпирическую функцию распределения
Проверяем свои навыки работы в Экселе! (исходные числа и краткая инструкция прилагается)
И на всякий случай краткое решение для сверки есть в конце книги.
Иногда встречаются ИВР с открытыми крайними интервалами, например:
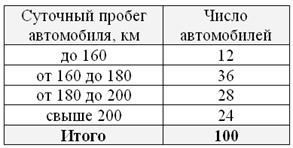
В таких случаях интервалы «закрывают». Обычно поступают так: сначала смотрим на средние интервалы и выясняем длину
частичного интервала: ![]() км. И для
км. И для
дальнейшего решения можно считать, что крайние интервалы имеют такую же длину: от 140 до 160 и от 200 до 220 км.
Соответственно, середины интервалов: 150 и 210 км.
И самое важное по главе, обязательно прочитайте, тут немного:)
 2.3. Вариационные ряды – главное
2.3. Вариационные ряды – главное
 2.2.2. Гистограммы
2.2.2. Гистограммы
| Оглавление |
Интервальный вариационный ряд и его характеристики
- Построение интервального вариационного ряда по данным эксперимента
- Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения
- Выборочная средняя, мода и медиана. Симметрия ряда
- Выборочная дисперсия и СКО
- Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
- Алгоритм исследования интервального вариационного ряда
- Примеры
п.1. Построение интервального вариационного ряда по данным эксперимента
Интервальный вариационный ряд – это ряд распределения, в котором однородные группы составлены по признаку, меняющемуся непрерывно или принимающему слишком много значений.
Общий вид интервального вариационного ряда
| Интервалы, (left.left[a_{i-1},a_iright.right)) | (left.left[a_{0},a_1right.right)) | (left.left[a_{1},a_2right.right)) | … | (left.left[a_{k-1},a_kright.right)) |
| Частоты, (f_i) | (f_1) | (f_2) | … | (f_k) |
Здесь k – число интервалов, на которые разбивается ряд.
Размах вариации – это длина интервала, в пределах которой изменяется исследуемый признак: $$ F=x_{max}-x_{min} $$
Правило Стерджеса
Эмпирическое правило определения оптимального количества интервалов k, на которые следует разбить ряд из N чисел: $$ k=1+lfloorlog_2 Nrfloor $$ или, через десятичный логарифм: $$ k=1+lfloor 3,322cdotlg Nrfloor $$
Скобка (lfloor rfloor) означает целую часть (округление вниз до целого числа).
Шаг интервального ряда – это отношение размаха вариации к количеству интервалов, округленное вверх до определенной точности: $$ h=leftlceilfrac Rkrightrceil $$
Скобка (lceil rceil) означает округление вверх, в данном случае не обязательно до целого числа.
Алгоритм построения интервального ряда
На входе: все значения признака (left{x_jright}, j=overline{1,N})
Шаг 1. Найти размах вариации (R=x_{max}-x_{min})
Шаг 2. Найти оптимальное количество интервалов (k=1+lfloorlog_2 Nrfloor)
Шаг 3. Найти шаг интервального ряда (h=leftlceilfrac{R}{k}rightrceil)
Шаг 4. Найти узлы ряда: $$ a_0=x_{min}, a_i=1_0+ih, i=overline{1,k} $$ Шаг 5. Найти частоты (f_i) – число попаданий значений признака в каждый из интервалов (left.left[a_{i-1},a_iright.right)).
На выходе: интервальный ряд с интервалами (left.left[a_{i-1},a_iright.right)) и частотами (f_i, i=overline{1,k})
Заметим, что поскольку шаг h находится с округлением вверх, последний узел (a_kgeq x_{max}).
Например:
Проведено 100 измерений роста учеников старших классов.
Минимальный рост составляет 142 см, максимальный – 197 см.
Найдем узлы для построения соответствующего интервального ряда.
По условию: (N=100, x_{min}=142 см, x_{max}=197 см).
Размах вариации: (R=197-142=55) (см)
Оптимальное число интервалов: (k=1+lfloor 3,322cdotlg 100rfloor=1+lfloor 6,644rfloor=1+6=7)
Шаг интервального ряда: (h=lceilfrac{55}{5}rceil=lceil 7,85rceil=8) (см)
Получаем узлы ряда: $$ a_0=x_{min}=142, a_i=142+icdot 8, i=overline{1,7} $$
| (left.left[a_{i-1},a_iright.right)) cм | (left.left[142;150right.right)) | (left.left[150;158right.right)) | (left.left[158;166right.right)) | (left.left[166;174right.right)) | (left.left[174;182right.right)) | (left.left[182;190right.right)) | (left[190;198right]) |
п.2. Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения
Относительная частота интервала (left.left[a_{i-1},a_iright.right)) – это отношение частоты (f_i) к общему количеству исходов: $$ w_i=frac{f_i}{N}, i=overline{1,k} $$
Гистограмма относительных частот интервального ряда – это фигура, состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – относительным частотам каждого из интервалов.
Площадь гистограммы равна 1 (с точностью до округлений), и она является эмпирическим законом распределения исследуемого признака.
Полигон относительных частот интервального ряда – это ломаная, соединяющая точки ((x_i,w_i)), где (x_i) – середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Накопленные относительные частоты – это суммы: $$ S_1=w_1, S_i=S_{i-1}+w_i, i=overline{2,k} $$ Ступенчатая кривая (F(x)), состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – накопленным относительным частотам, является эмпирической функцией распределения исследуемого признака.
Кумулята – это ломаная, которая соединяет точки ((x_i,S_i)), где (x_i) – середины интервалов.
Например:
Продолжим анализ распределения учеников по росту.
Выше мы уже нашли узлы интервалов. Пусть, после распределения всех 100 измерений по этим интервалам, мы получили следующий интервальный ряд:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| (left.left[a_{i-1},a_iright.right)) cм | (left.left[142;150right.right)) | (left.left[150;158right.right)) | (left.left[158;166right.right)) | (left.left[166;174right.right)) | (left.left[174;182right.right)) | (left.left[182;190right.right)) | (left[190;198right]) |
| (f_i) | 4 | 7 | 11 | 34 | 33 | 8 | 3 |
Найдем середины интервалов, относительные частоты и накопленные относительные частоты:
| (x_i) | 146 | 154 | 162 | 170 | 178 | 186 | 194 |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 |
| (S_i) | 0,04 | 0,11 | 0,22 | 0,56 | 0,89 | 0,97 | 1 |
Построим гистограмму и полигон:

Построим кумуляту и эмпирическую функцию распределения: 

Эмпирическая функция распределения (относительно середин интервалов): $$ F(x)= begin{cases} 0, xleq 146\ 0,04, 146lt xleq 154\ 0,11, 154lt xleq 162\ 0,22, 162lt xleq 170\ 0,56, 170lt xleq 178\ 0,89, 178lt xleq 186\ 0,97, 186lt xleq 194\ 1, xgt 194 end{cases} $$
п.3. Выборочная средняя, мода и медиана. Симметрия ряда
Выборочная средняя интервального вариационного ряда определяется как средняя взвешенная по частотам: $$ X_{cp}=frac{x_1f_1+x_2f_2+…+x_kf_k}{N}=frac1Nsum_{i=1}^k x_if_i $$ где (x_i) – середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Или, через относительные частоты: $$ X_{cp}=sum_{i=1}^k x_iw_i $$
Модальным интервалом называют интервал с максимальной частотой: $$ f_m=max f_i $$ Мода интервального вариационного ряда определяется по формуле: $$ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h $$ где
(h) – шаг интервального ряда;
(x_o) – нижняя граница модального интервала;
(f_m,f_{m-1},f_{m+1}) – соответственно, частоты модального интервала, интервала слева от модального и интервала справа.
Медианным интервалом называют первый интервал слева, на котором кумулята превысила значение 0,5. Медиана интервального вариационного ряда определяется по формуле: $$ M_e=x_o+frac{0,5-S_{me-1}}{w_{me}}h $$ где
(h) – шаг интервального ряда;
(x_o) – нижняя граница медианного интервала;
(S_{me-1}) накопленная относительная частота для интервала слева от медианного;
(w_{me}) относительная частота медианного интервала.
Расположение выборочной средней, моды и медианы в зависимости от симметрии ряда аналогично их расположению в дискретном ряду (см. §65 данного справочника).
Например:
Для распределения учеников по росту получаем:
| (x_i) | 146 | 154 | 162 | 170 | 178 | 186 | 194 | ∑ |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 | 1 |
| (x_iw_i) | 5,84 | 10,78 | 17,82 | 57,80 | 58,74 | 14,88 | 5,82 | 171,68 |
$$ X_{cp}=sum_{i=1}^k x_iw_i=171,68approx 171,7 text{(см)} $$ На гистограмме (или полигоне) относительных частот максимальная частота приходится на 4й интервал [166;174). Это модальный интервал.
Данные для расчета моды: begin{gather*} x_o=166, f_m=34, f_{m-1}=11, f_{m+1}=33, h=8\ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\ =166+frac{34-11}{(34-11)+(34-33)}cdot 8approx 173,7 text{(см)} end{gather*} На кумуляте значение 0,5 пересекается на 4м интервале. Это – медианный интервал.
Данные для расчета медианы: begin{gather*} x_o=166, w_m=0,34, S_{me-1}=0,22, h=8\ \ M_e=x_o+frac{0,5-S_{me-1}}{w_me}h=166+frac{0,5-0,22}{0,34}cdot 8approx 172,6 text{(см)} end{gather*} begin{gather*} \ X_{cp}=171,7; M_o=173,7; M_e=172,6\ X_{cp}lt M_elt M_o end{gather*} Ряд асимметричный с левосторонней асимметрией.
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|}=frac{2,0}{0,9}approx 2,2lt 3), т.е. распределение умеренно асимметрично.
п.4. Выборочная дисперсия и СКО
Выборочная дисперсия интервального вариационного ряда определяется как средняя взвешенная для квадрата отклонения от средней: begin{gather*} D=frac1Nsum_{i=1}^k(x_i-X_{cp})^2 f_i=frac1Nsum_{i=1}^k x_i^2 f_i-X_{cp}^2 end{gather*} где (x_i) – середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Или, через относительные частоты: $$ D=sum_{i=1}^k(x_i-X_{cp})^2 w_i=sum_{i=1}^k x_i^2 w_i-X_{cp}^2 $$
Выборочное среднее квадратичное отклонение (СКО) определяется как корень квадратный из выборочной дисперсии: $$ sigma=sqrt{D} $$
Например:
Для распределения учеников по росту получаем:
| $x_i$ | 146 | 154 | 162 | 170 | 178 | 186 | 194 | ∑ |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 | 1 |
| (x_iw_i) | 5,84 | 10,78 | 17,82 | 57,80 | 58,74 | 14,88 | 5,82 | 171,68 |
| (x_i^2w_i) – результат | 852,64 | 1660,12 | 2886,84 | 9826 | 10455,72 | 2767,68 | 1129,08 | 29578,08 |
$$ D=sum_{i=1}^k x_i^2 w_i-X_{cp}^2=29578,08-171,7^2approx 104,1 $$ $$ sigma=sqrt{D}approx 10,2 $$
п.5. Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
Исправленная выборочная дисперсия интервального вариационного ряда определяется как: begin{gather*} S^2=frac{N}{N-1}D end{gather*}
Стандартное отклонение выборки определяется как корень квадратный из исправленной выборочной дисперсии: $$ s=sqrt{S^2} $$
Коэффициент вариации это отношение стандартного отклонения выборки к выборочной средней, выраженное в процентах: $$ V=frac{s}{X_{cp}}cdot 100text{%} $$
Подробней о том, почему и когда нужно «исправлять» дисперсию, и для чего использовать коэффициент вариации – см. §65 данного справочника.
Например:
Для распределения учеников по росту получаем: begin{gather*} S^2=frac{100}{99}cdot 104,1approx 105,1\ sapprox 10,3 end{gather*} Коэффициент вариации: $$ V=frac{10,3}{171,7}cdot 100text{%}approx 6,0text{%}lt 33text{%} $$ Выборка однородна. Найденное значение среднего роста (X_{cp})=171,7 см можно распространить на всю генеральную совокупность (старшеклассников из других школ).
п.6. Алгоритм исследования интервального вариационного ряда
На входе: все значения признака (left{x_jright}, j=overline{1,N})
Шаг 1. Построить интервальный ряд с интервалами (left.right[a_{i-1}, a_ileft.right)) и частотами (f_i, i=overline{1,k}) (см. алгоритм выше).
Шаг 2. Составить расчетную таблицу. Найти (x_i,w_i,S_i,x_iw_i,x_i^2w_i)
Шаг 3. Построить гистограмму (и/или полигон) относительных частот, эмпирическую функцию распределения (и/или кумуляту). Записать эмпирическую функцию распределения.
Шаг 4. Найти выборочную среднюю, моду и медиану. Проанализировать симметрию распределения.
Шаг 5. Найти выборочную дисперсию и СКО.
Шаг 6. Найти исправленную выборочную дисперсию, стандартное отклонение и коэффициент вариации. Сделать вывод об однородности выборки.
п.7. Примеры
Пример 1. При изучении возраста пользователей коворкинга выбрали 30 человек.
Получили следующий набор данных:
18,38,28,29,26,38,34,22,28,30,22,23,35,33,27,24,30,32,28,25,29,26,31,24,29,27,32,24,29,29
Постройте интервальный ряд и исследуйте его.
1) Построим интервальный ряд. В наборе данных: $$ x_{min}=18, x_{max}=38, N=30 $$ Размах вариации: (R=38-18=20)
Оптимальное число интервалов: (k=1+lfloorlog_2 30rfloor=1+4=5)
Шаг интервального ряда: (h=lceilfrac{20}{5}rceil=4)
Получаем узлы ряда: $$ a_0=x_{min}=18, a_i=18+icdot 4, i=overline{1,5} $$
| (left.left[a_{i-1},a_iright.right)) лет | (left.left[18;22right.right)) | (left.left[22;26right.right)) | (left.left[26;30right.right)) | (left.left[30;34right.right)) | (left.left[34;38right.right)) |
Считаем частоты для каждого интервала. Получаем интервальный ряд:
| (left.left[a_{i-1},a_iright.right)) лет | (left.left[18;22right.right)) | (left.left[22;26right.right)) | (left.left[26;30right.right)) | (left.left[30;34right.right)) | (left.left[34;38right.right)) |
| (f_i) | 1 | 7 | 12 | 6 | 4 |
2) Составляем расчетную таблицу:
| (x_i) | 20 | 24 | 28 | 32 | 36 | ∑ |
| (f_i) | 1 | 7 | 12 | 6 | 4 | 30 |
| (w_i) | 0,033 | 0,233 | 0,4 | 0,2 | 0,133 | 1 |
| (S_i) | 0,033 | 0,267 | 0,667 | 0,867 | 1 | – |
| (x_iw_i) | 0,667 | 5,6 | 11,2 | 6,4 | 4,8 | 28,67 |
| (x_i^2w_i) | 13,333 | 134,4 | 313,6 | 204,8 | 172,8 | 838,93 |
3) Строим полигон и кумуляту

Эмпирическая функция распределения: $$ F(x)= begin{cases} 0, xleq 20\ 0,033, 20lt xleq 24\ 0,267, 24lt xleq 28\ 0,667, 28lt xleq 32\ 0,867, 32lt xleq 36\ 1, xgt 36 end{cases} $$ 4) Находим выборочную среднюю, моду и медиану $$ X_{cp}=sum_{i=1}^k x_iw_iapprox 28,7 text{(лет)} $$ На полигоне модальным является 3й интервал (самая высокая точка).
Данные для расчета моды: begin{gather*} x_0=26, f_m=12, f_{m-1}=7, f_{m+1}=6, h=4\ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\ =26+frac{12-7}{(12-7)+(12-6)}cdot 4approx 27,8 text{(лет)} end{gather*}
На кумуляте медианным является 3й интервал (преодолевает уровень 0,5).
Данные для расчета медианы: begin{gather*} x_0=26, w_m=0,4, S_{me-1}=0,267, h=4\ M_e=x_o+frac{0,5-S_{me-1}}{w_{me}}h=26+frac{0,5-0,4}{0,267}cdot 4approx 28,3 text{(лет)} end{gather*} Получаем: begin{gather*} X_{cp}=28,7; M_o=27,8; M_e=28,6\ X_{cp}gt M_egt M_0 end{gather*} Ряд асимметричный с правосторонней асимметрией.
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|} =frac{0,9}{0,1}=9gt 3), т.е. распределение сильно асимметрично.
5) Находим выборочную дисперсию и СКО: begin{gather*} D=sum_{i=1}^k x_i^2w_i-X_{cp}^2=838,93-28,7^2approx 17,2\ sigma=sqrt{D}approx 4,1 end{gather*}
6) Исправленная выборочная дисперсия: $$ S^2=frac{N}{N-1}D=frac{30}{29}cdot 17,2approx 17,7 $$ Стандартное отклонение (s=sqrt{S^2}approx 4,2)
Коэффициент вариации: (V=frac{4,2}{28,7}cdot 100text{%}approx 14,7text{%}lt 33text{%})
Выборка однородна. Найденное значение среднего возраста (X_{cp}=28,7) лет можно распространить на всю генеральную совокупность (пользователей коворкинга).
Комментарий
1.4: При
построении интервального вариационного
ряда в качестве частот используют как
числа значений варианты ni,
так и относительные ча-
стоты
νi
= ni/n,
причём относительные величины обычно
употребляются при больших объёмах
выборок n.
В данном случае n
= 100 – выборка
достаточно большого объёма; будем
пользоваться относительными частотами.
Порядок построения
интервального вариационного ряда таков:
1.
Определим размах
вариаций значения признака
R
= xmax
– xmin
= 14,51 – 12,01 ≈
14,6 – 12,0 = 2,6 –
Комментарий
1.5: Граничнае
значения признака обычно округляют и
подправляют так, чтобы все выборочные
значения лежали внутри интервала R.
2.
Определим число
частичных интервалов:
если обозначить k
– число этих
интервалов, то, при объёме выборки n,
хорошее приближение для числа k
можно найти
по формуле
k
= [2 ln(n)],
где
[…] означает целую часть числа. В данном
случае получаем k
= 9
Комментарий
1.6: Ширина
hi
i–го
частичного интервала выбирается
достаточно произвольно. Обычно это
определяется структурой вариационного
ряда. Во многих случаях эта структура
не проявляется и у нас нет никаких других
априорных данных. В таком случае
естественным является выбор одинаковой
ширины всех интервалов (поправки в
дальнейшем – возмржны).
Поправим,
в соответствии с комментарием 4, границы
интервала R,
чтобы было
удобно делить его на
9 одинаковых
интервала:
R
=14,7 – 12,0 =
2,7;
i
hi
= R/k
= 0,3.
3.
Определим границы
частичных интервалов: [12,0;12,3); [12,3;12,6);
[12,6;12,9); [12.9;13,2); [13,2;13,5); [13,5;13,8); [13,8;14,1);
[14,1;14,4); [14,4;14,7].
4.
Составим таблицу 3 для интервального
вариационногоряда.
|
Интервал |
12,0-12,3 |
12,3-12,6 |
12,6-12,9 |
12,9-13,2 |
13,2-13,5 |
13,5-13,8 |
13.8-14,1 |
14,1-144 |
14,4-14,7 |
|
Середина интервала |
12,15 |
12,45 |
12,75 |
13,05 |
13,35 |
13,65 |
13,95 |
14,25 |
14,55 |
|
Частота |
2 |
6 |
8 |
10 |
35 |
21 |
9 |
7 |
2 |
|
Относитель ноя |
0,02 |
0,06 |
0,08 |
0,1 |
0,35 |
0,21 |
0,09 |
0,07 |
0,02 |
|
Накоплен- ные |
0,02 |
0,08 |
0,16 |
0,26 |
0,61 |
0,82 |
0,91 |
0,98 |
1 |
Замечание:
как обычно
– начало интервала включается,
а конец – не включается в интервал
(исключая последний)
3. Эмпирическая функция распределения и графическое преставление распеделения частот
Эмпирической
(статистической)
функцией
распределения
назывыется функция F
*(x),
равная относительной частоте события
X
< x:
![]() ,
,
где
nx
– число вариант, меньших x;
n
– объём выборки.
Для нахождения
эмпирической функции распределения
воспользуемся формулой
 .
.
Значениями
эмпирической функции распределения
являются, таким образом, накопленные
частоты, поэтому используем четвёртую
строку таблицы 3:

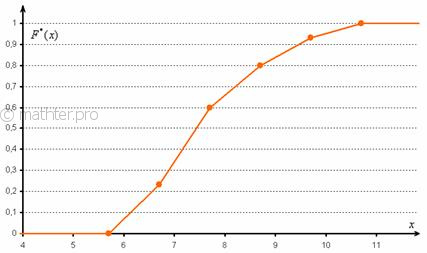
Изобразим
функцию F*(x)
графически (рис. 1): вдоль оси абсцисс x
откладываем значения середин частичных
интервалов; вдоль оси ординат – накопленные
частоты.
На
этом же рисунке построим кумулянту
– график
накопленных частот; в данном случае это
ломанная линия, состоящая из отрезков
прямых, соединяющих точки с координатами
(xi,
Σνi).
Кумулянта является довольно хорошим
приближением графика функции распределения
непрерывной случайной величины X.
Комментарий
1.7: График
кумулянты точно совпадает с графиком
функции
распределения,
если все значения варианты в каждом
интервале, как и вся генральная
совокупность, распределены равномерно.
F
*(x)




 1,0
1,0



 0,98
0,98
0,92







 0,82
0,82


 0,61
0,61



 0,26
0,26


 0,16
0,16



 0,08
0,08


 0,02
0,02
 0
0
 12,15 12,45 12,75 13,05 13,35 13,65 13,95 14,25 14,55x
12,15 12,45 12,75 13,05 13,35 13,65 13,95 14,25 14,55x
Р
ис.
1
Существует
два общих метода графического представления
частот: гистограмма
и
полигон распределения.
Полигон
распределеня
строят из отрезков, соединяющих точки,
координатами которых являюься значения
признака xi
(середины частичных интервалов) и
соответствующие им частоты ni
или относительные частоты ni/n.
Гистограмма
– это последовательность столбцов,
каждый из которых опирается на один
частичный интервал, а высота его равна
частоте (или относительной частоте) в
этом интервале.
Оба
графика являются выборочным аналогом
плотности распределения непрерывной
случайной величины и обычно изображают
лишь один из них. Но здесь, в порядке
исключения, изобразим оба: рис.2 и рис.
3.
Комментарий
1.7: Следует
обратить внимание на то, что
суммарная площадь под гистограммой
всегда равна единице
 νi
νi
= ni/n
0


 ,35
,35
`
0

 ,21
,21
0

 ,10
,10
0

 ,09
,09
0
 ,08
,08
0

 ,07
,07
0
 ,06
,06


 0,02
0,02
0
 12,15 12,45 12,75 13,05 13,35 13,65 13,95 14,25 14,55
12,15 12,45 12,75 13,05 13,35 13,65 13,95 14,25 14,55
Рис. 2 Полигон распределения
ν i
i
= ni/n
0


 ,35
,35
`
0

 ,21
,21
0

 ,10
,10
0


 ,09
,09
0

 ,08
,08
0

 ,07
,07
0

 ,06
,06




 0,02
0,02
 0
0
12,0 12,3 12,6 12,9 13,2 13,5 13,8 14,1 14,4 14,7 x
Рис. 3. Гистограмма
План:
1. Задачи математической статистики.
2. Виды выборок.
3. Способы отбора.
4. Статистическое распределение выборки.
5. Эмпирическая функция распределения.
6. Полигон и гистограмма.
7. Числовые характеристики вариационного ряда.
8. Статистические оценки параметров
распределения.
9. Интервальные оценки параметров распределения.
1.
Задачи и методы математической статистики
Математическая статистика– это раздел математики, посвященный методам
сбора, анализа и обработки результатов статистических данных наблюдений для
научных и практических целей.
Пусть требуется
изучить совокупность однородных объектов относительно некоторого качественного
или количественного признака, характеризующего эти объекты. Например, если
имеется партия деталей, то качественным признаком может служить стандартность детали,
а количественным- контролируемый размер детали.
Иногда проводят
сплошное исследование, т.е. обследуют каждый объект относительно нужного
признака. На практике сплошное обследование применяется редко. Например, если
совокупность содержит очень большое число объектов, то провести сплошное
обследование физически невозможно. Если обследование объекта связано с его
уничтожением или требует больших материальных затрат, то проводить сплошное
обследование не имеет смысла. В таких случаях случайно отбирают из всей
совокупности ограниченное число объектов (выборочную совокупность) и подвергают
их изучению.
Основная задача
математической статистики заключается в исследовании всей совокупности по
выборочным данным в зависимости от поставленной цели, т.е. изучение
вероятностных свойств совокупности: закона распределения, числовых
характеристик и т.д. для принятия управленческих решений в условиях
неопределенности.
2.
Виды выборок
Генеральная совокупность – это совокупность объектов, из которой производится выборка.
Выборочная совокупность (выборка) – это совокупность случайно отобранных
объектов.
Объем совокупности –
это число объектов этой совокупности. Объем генеральной совокупности
обозначается N,
выборочной – n.
Пример:
Если из 1000
деталей отобрано для обследования 100 деталей, то объем генеральной
совокупности N =
1000, а объем выборки n =
100.
При составлении выборки можно поступить двумя
способами: после того, как объект отобран и над ним произведено наблюдение, он
может быть возвращен либо не возвращен в генеральную совокупность. Т.о. выборки
делятся на повторные и бесповторные.
Повторной называют выборку, при которой
отобранный объект (перед отбором следующего) возвращается в генеральную
совокупность.
Бесповторной называют выборку, при которой отобранный
объект в генеральную совокупность не возвращается.
На практике обычно
пользуются бесповторным случайным отбором.
Для того, чтобы по
данным выборки можно было достаточно уверенно судить об интересующем признаке
генеральной совокупности, необходимо, чтобы объекты выборки правильно его
представляли. Выборка должна правильно представлять пропорции генеральной
совокупности. Выборка должна быть репрезентативной (представительной).
В силу закона больших чисел можно утверждать,
что выборка будет репрезентативной, если ее осуществлять случайно.
Если объем
генеральной совокупности достаточно велик, а выборка составляет лишь
незначительную часть этой совокупности, то различие между повторной и
бесповторной выборками стирается; в предельном случае, когда рассматривается
бесконечная генеральная совокупность, а выборка имеет конечный объем, это
различие исчезает.
Пример:
В американском журнале
«Литературное обозрение» с помощью статистических методов было проведено исследование прогнозов
относительно исхода предстоящих выборов президента США в 1936 году.
Претендентами на этот пост были Ф.Д. Рузвельт и А. М. Ландон. В качестве
источника для генеральной совокупности исследуемых американцев были взяты
справочники телефонных абонентов. Из них случайным образом были выбраны 4
миллиона адресов., по которым редакция журнала разослала открытки с просьбой
высказать свое отношение к кандидатам на пост президента. Обработав результаты
опроса, журнал опубликовал социологический прогноз о том, что на предстоящих
выборах с большим перевесом победит Ландон. И … ошибся: победу одержал
Рузвельт.
Этот пример можно рассматривать, как пример нерепрезентативной выборки. Дело в
том, что в США в первой половине двадцатого века телефоны имела лишь зажиточная
часть населения, которые поддерживали взгляды Ландона.
3.
Способы отбора
На практике
применяются различные способы отбора, которые можно разделить на 2 вида:
1. Отбор не требует
расчленения генеральной совокупности на части (а) простой случайный
бесповторный; б) простой случайный повторный).
2. Отбор, при
котором генеральная совокупность разбивается на части. (а) типичный отбор;
б) механический отбор; в) серийный отбор).
Простым случайным
называют такой отбор, при котором объекты извлекаются по одному из всей
генеральной совокупности (случайно).
Типичным называют отбор, при котором объекты
отбираются не из всей генеральной совокупности, а из каждой ее «типичной»
части. Например, если деталь изготавливают на нескольких станках, то отбор
производят не из всей совокупности деталей, произведенных всеми станками, а из
продукции каждого станка в отдельности. Таким отбором пользуются тогда, когда
обследуемый признак заметно колеблется в различных «типичных» частях
генеральной совокупности.
Механическим называют отбор, при котором
генеральную совокупность «механически» делят на столько групп, сколько объектов
должно войти в выборку, а из каждой группы отбирают один объект. Например, если
нужно отобрать 20 % изготовленных станком деталей, то отбирают каждую 5-ую
деталь; если требуется отобрать 5 % деталей- каждую 20-ую и т.д. Иногда такой
отбор может не обеспечивать репрезентативность выборки (если отбирают каждый
20-ый обтачиваемый валик, причем сразу же после отбора производится замена
резца, то отобранными окажутся все валики, обточенные затупленными резцами).
Серийным называют отбор, при котором объекты
отбирают из генеральной совокупности не по одному, а «сериями», которые
подвергают сплошному обследованию. Например, если изделия изготавливаются
большой группой станков-автоматов, то подвергают сплошному обследованию
продукцию только нескольких станков.
На практике часто
применяют комбинированный отбор, при котором сочетаются указанные выше способы.
4.
Статистическое распределение выборки
Пусть из генеральной совокупности извлечена выборка, причем значение x1–наблюдалось
раз,
x2-n2
раз,… xk – nk
раз. n =
n1+n2+…+nk– объем
выборки. Наблюдаемые значения
называются вариантами, а
последовательность вариант, записанных в возрастающем порядке- вариационным
рядом. Числа наблюдений
называются
частотами (абсолютными частотами), а их отношения к объему выборки
– относительными частотами или статистическими вероятностями.
Если количество
вариант велико или выборка производится из непрерывной генеральной
совокупности, то вариационный ряд составляется не по отдельным точечным
значениям, а по интервалам значений генеральной совокупности. Такой
вариационный ряд называется интервальным.
Длины интервалов при этом должны быть равны.
Статистическим
распределением выборки
называется перечень вариант и соответствующих им частот или относительных
частот.
Статистическое
распределение можно задать также в виде последовательности интервалов и
соответствующих им частот (суммы частот, попавших в этот интервал значений)
Точечный
вариационный ряд частот может быть представлен таблицей:
|
xi |
x1 |
x2 |
… |
xk |
|
ni |
n1 |
n2 |
… |
nk |
Аналогично можно
представить точечный вариационный ряд относительных частот.
Причем:
Пример:
Число букв в
некотором тексте Х оказалось равным 1000. Первой встретилась буква «я», второй- буква «и», третьей- буква
«а», четвертой- «ю». Затем шли буквы
«о», «е», «у», «э», «ы».
Выпишем места,
которые они занимают в алфавите, соответственно имеем: 33, 10, 1, 32, 16, 6,
21, 31, 29.
После упорядочения
этих чисел по возрастанию получаем вариационный ряд: 1, 6, 10, 16, 21, 29, 31,
32, 33.
Частоты появления
букв в тексте: «а» – 75, «е» -87, «и»- 75, «о»- 110, «у»- 25, «ы»- 8, «э»- 3,
«ю»- 7, «я»- 22.
Составим точечный
вариационный ряд частот:

Пример:
Задано
распределение частот выборки объема n
= 20.
Составьте точечный
вариационный ряд относительных частот.
Решение:
Найдем
относительные частоты:
|
xi |
2 |
6 |
12 |
|
wi |
0,15 |
0,5 |
0,35 |
При построении интервального
распределения существуют правила выбора
числа интервалов или величины каждого интервала. Критерием здесь служит
оптимальное соотношение: при увеличении числа интервалов улучшается репрезентативность,
но увеличивается объем данных и время на их обработку. Разность
xmax – xmin между наибольшим и наименьшим значениями
вариант называют размахом выборки.
Для подсчета числа
интервалов k
обычно применяют эмпирическую формулу Стреджесса (подразумевая округление до
ближайшего удобного целого): k
= 1 + 3.322 lg n.
Соответственно,
величину каждого интервала h
можно вычислить по формуле
:
5.
Эмпирическая
функция распределения
Рассмотрим некоторую
выборку из генеральной совокупности. Пусть известно статистическое
распределение частот количественного признака Х. Введем обозначения: nx
– число наблюдений, при которых
наблюдалось значение признака, меньшее х; n – общее число наблюдений (объем
выборки). Относительная частота события Х<х равна
nx/n. Если х изменяется, то изменяется и относительная частота, т.е.
относительная частота nx/n–
есть функция от х. Т.к. она находится эмпирическим путем, то она называется
эмпирической.
Эмпирической функцией распределения
(функцией распределения выборки) называют функцию
,
определяющую для каждого х относительную частоту события Х<х.
где
число вариант, меньших х,
n– объем выборки.
В отличие от эмпирической функции
распределения выборки, функцию распределения F(x)
генеральной совокупности называют теоретической функцией распределения.
Различие между эмпирической и
теоретической функциями распределения состоит в том, что теоретическая функция F(x) определяет вероятность события Х<x , а эмпирическая
функция
F*(x) -относительную
частоту этого же события. Из теоремы Бернулли следует, что относительная
частота события Х<х , т.е
F*(x) стремится
по вероятности к вероятности F(x) этого события. Т.е.при
большом n F*(x)
и
F(x) мало отличаются друг от друга.
Т.о. целесообразно использовать
эмпирическую функцию распределения выборки для приближенного представления
теоретической (интегральной) функции распределения генеральной совокупности.
F*(x) обладает всеми свойствами F(x).
1. Значения
F*(x)
принадлежат
интервалу [0; 1].
2.
F*(x)
– неубывающая
функция.
3. Если
– наименьшая варианта, то
F*(x)= 0, при х
< x1
; если xk
– наибольшая варианта, то
F*(x)= 1, при х
> xk
.
Т.е.
F*(x) служит для
оценки F(x).
Если выборка задана вариационным рядом, то эмпирическая
функция имеет вид:
График эмпирической функции называется кумулятой.
Пример:
Постройте эмпирическую функцию по данному распределению
выборки.
Решение:
Объем выборки n = 12 + 18 +30 = 60. Наименьшая
варианта 2, т.е.
при х <
2. Событие X<6,
( x1= 2) наблюдалось 12 раз, т.е.
F*(x)=12/60=0,2 при 2 < x <
6. Событие Х<10, (
x1=2,
x2= 6) наблюдалось 12 + 18 = 30 раз, т.е. F*(x)=30/60=0,5
при 6 < x <
10. Т.к. х=10 наибольшая варианта, то F*(x) = 1
при х>10. Искомая эмпирическая функция имеет вид:
Кумулята:
Кумулята дает возможность
понимать графически представленную информацию, например, ответить на вопросы:
«Определите число наблюдений, при которых значение признака было меньше 6 или
не меньше 6. F*(6)=0,2
» Тогда число наблюдений, при которых
значение наблюдаемого признака было меньше 6 равно 0,2*n = 0,2*60 = 12. Число наблюдений, при
которых значение наблюдаемого признака было не меньше 6 равно (1-0,2)*n = 0,8*60 = 48.
Если задан интервальный вариационный
ряд, то для составления эмпирической функции распределения находят середины
интервалов и по ним получают эмпирическую функцию распределения аналогично
точечному вариационному ряду.
6. Полигон и гистограмма
Для наглядности строят различные графики
статистического распределения: полином и гистограммы
Полигон
частот- это ломаная, отрезки которой соединяют точки (
x1
;n1
), (
x2
;n2
),…, (
xk
; nk
), где
– варианты,
–
соответствующие им частоты.
Полигон
относительных частот- это ломаная, отрезки которой соединяют точки (
x1
;w1
), (x2
;w2
),…, (
xk
;wk
), где
xi–варианты,
wi –
соответствующие им относительные частоты.
Пример:
Постройте полином относительных
частот по данному распределению выборки:
Решение:
В случае
непрерывного признака целесообразно строить гистограмму, для чего интервал, в
котором заключены все наблюдаемые значения признака, разбивают на несколько
частичных интервалов длиной h
и находят для каждого частичного интервала ni – сумму частот вариант,
попавших в i-ый
интервал. (Например, при измерении роста человека или веса, мы имеем дело с
непрерывным признаком).
Гистограмма
частот- это ступенчатая фигура, состоящая из прямоугольников, основаниями
которых служат частичные интервалы длиною h, а высоты равны отношению
(плотность
частот).
Площадь i-го частичного
прямоугольника равна– сумме частот вариант i– го интервала, т.е. площадь
гистограммы частот равна сумме всех частот, т.е. объему выборки.
Пример:
Даны результаты изменения напряжения
(в вольтах) в электросети. Составьте вариационный ряд, постройте полигон и
гистограмму частот, если значения напряжения следующие: 227, 215, 230, 232,
223, 220, 228, 222, 221, 226, 226, 215, 218, 220, 216, 220, 225, 212, 217, 220.
Решение:
Составим вариационный ряд. Имеем n = 20, xmin=212
, xmax=232
.
Применим формулу
Стреджесса для подсчета числа интервалов.
.
Интервальный вариационный ряд
частот имеет вид:
|
|
|
Плотность частот |
|
212-216 |
3 |
0,75 |
|
216-220 |
3 |
0,75 |
|
220-224 |
7 |
1,75 |
|
224-228 |
4 |
1 |
|
228-232 |
3 |
0,75 |
Построим гистограмму частот:
Построим полигон частот, найдя предварительно середины
интервалов:
Гистограммой относительных
частот называют ступенчатую фигуру, состоящую из прямоугольников ,
основаниями которых служат частичные
интервалы длиною h, а
высоты равны отношению wi/h
(плотность
относительной частоты).
Площадь i-го частичного прямоугольника равна
– относительной частоте вариант, попавших в i– ый интервал. Т.е. площадь
гистограммы относительных частот равна сумме всех относительных частот, т.е.
единице.
7.
Числовые
характеристики вариационного ряда
Рассмотрим основные характеристики генеральной и выборочной
совокупностей.
Генеральным средним
называется среднее
арифметическое значений признака генеральной совокупности.
Для различных значений x1, x2
, x3
, …, xn.
признака
генеральной совокупности объема N
имеем:
Если
значения признака имеют соответствующие частоты N1
+N2
+…+Nk
=N,
то
Выборочным средним называется среднее арифметическое значений
признака выборочной совокупности.
Для различных значений x1, x2
, x3, …, xn
признака выборочной
совокупности объема n
имеем:
Если
значения признака имеют соответствующие частоты n1+n2+…+nk
= n,
то
Пример:
Вычислите выборочное среднее для выборки :
x1= 51,12;
x2= 51,07;
x3= 52,95; x4
=52,93;
x5= 51,1;x6
= 52,98; x7
= 52,29; x8
= 51,23; x9
= 51,07; x10
= 51,04.
Решение:
Генеральной дисперсией называется среднее арифметическое квадратов отклонений
значений признака Х генеральной совокупности от генерального среднего .
Для различных значений x1, x2, x3, …, xN
признака
генеральной совокупности объема N
имеем:
Если
значения признака имеют соответствующие частоты
N1+N2+…+Nk
=N,
то
Генеральным среднеквадратическим отклонением (стандартом)
называют квадратный корень из генеральной дисперсии
Выборочной дисперсией называется среднее
арифметическое квадратов отклонений наблюдаемых значений признака от среднего
значения.
Для различных значений
x1, x2, x3, …, xn
признака выборочной
совокупности объема n
имеем:
Если
значения признака имеют соответствующие частоты n1+n2+…+nk
= n,
то
Выборочным среднеквадратическим
отклонением (стандартом) называется квадратный корень из выборочной
дисперсии.
Пример:
Выборочная совокупность задана таблицей распределения. Найдите
выборочную дисперсию.
Решение:
Теорема: Дисперсия
равна разности среднего квадратов значений признака и квадрата общего среднего.
Пример:
Найдите дисперсию по данному распределению.
Решение:
8. Статистические оценки параметров распределения
Пусть генеральная совокупность исследуется по некоторой
выборке. При этом можно получить лишь приближенное значение неизвестного
параметра Q, который
служит его оценкой. Очевидно, что оценки могут изменяться от одной выборки к
другой.
Статистической
оценкой Q* неизвестного параметра
теоретического распределения называется функция f, зависящая от наблюдаемых значений
выборки. Задачей статистического оценивания неизвестных параметров по выборке
заключается в построении такой функции от имеющихся данных статистических
наблюдений, которая давала бы наиболее точные приближенные значения реальных,
не известных исследователю, значений этих параметров.
Статистические оценки делятся на
точечные и интервальные, в зависимости от способа их предоставления (числом или
интервалом).
Точечной
называют статистическую оценку параметра Q теоретического распределения определяемую одним значением
параметра Q*=f(x1, x2, …, xn), где x1, x2, …, xn – результаты эмпирических наблюдений над
количественным признаком Х некоторой выборки.
Такие оценки параметров, полученные по
разным выборкам, чаще всего отличаются друг от друга. Абсолютная разность /Q*-Q/ называют ошибкой выборки (оценивания).
Для того, чтобы статистические оценки
давали достоверные результаты об оцениваемых параметрах, необходимо, чтобы они
были несмещенными, эффективными и состоятельными.
Точечная
оценка, математическое ожидание которой равно (не равно) оцениваемому
параметру, называется несмещенной
(смещенной). М(Q*)=Q.
Разность М(Q*)-Q называют смещением или
систематической ошибкой. Для несмещенных оценок систематическая ошибка
равна 0.
Эффективной
называют такую статистическую оценку
Q*, которая при
заданном объеме выборки n
имеет наименьшую возможную дисперсию: D[Q*]min
(n=const). Эффективная оценка
имеет наименьший разброс по сравнению с другими несмещенными и состоятельными
оценками.
Состоятельной
называют такую статистическую оценку
Q*,
которая при n стремится по вероятности к оцениваемому
параметру Q,
т.е. при увеличении объема выборки n
оценка стремится по вероятности к истинному значению параметра Q.
Требование состоятельности
согласуется с законом больших числе: чем больше исходной информации об
исследуемом объекте, тем точнее результат. Если объем выборки мал, то точечная
оценка параметра может привести к серьезным ошибкам.
Любую выборку (объема n) можно рассматривать
как упорядоченный набор
x1, x2, …, xn независимых
одинаково распределенных случайных величин.
Выборочные средние для
различных выборок объема n из одной и той же генеральной
совокупности будут различны. Т. е. выборочное среднее можно рассматривать как
случайную величину, а значит, можно говорить о распределении выборочного
среднего и его числовых характеристиках.
Выборочное среднее
удовлетворяет всем накладываемым к статистическим оценкам требованиям, т.е.
дает несмещенную, эффективную и состоятельную оценку генерального среднего.
Можно доказать, что. Таким образом, выборочная дисперсия
является смещенной оценкой генеральной дисперсии, давая ее заниженное значение.
Т. е. при небольшом объеме выборки она будет давать систематическую ошибку. Для
несмещенной, состоятельной оценки достаточно взять величину
, которую называют исправленной
дисперсией. Т. е.
На практике для оценки генеральной дисперсии применяют исправленную
дисперсию при n
< 30. В остальных случаях (n>30) отклонение
от
малозаметно. Поэтому при больших значениях n
ошибкой смещения можно пренебречь.
Можно
так же доказать, что относительная
частота
ni / n является
несмещенной и состоятельной оценкой вероятности P(X=xi). Эмпирическая функция распределения F*(x) является несмещенной
и состоятельной оценкой теоретической функции распределения F(x)=P(X<x).
Пример:
Найдите
несмещенные оценки математического ожидания
и дисперсии по таблице выборки.
Решение:
Объем выборки n=20.
Несмещенной оценкой математического
ожидания является выборочное среднее.
Для вычисления несмещенной оценки
дисперсии сначала найдем выборочную дисперсию:
Теперь найдем
несмещенную оценку:
9.
Интервальные
оценки параметров распределения
Интервальной называется статистическая
оценка, определяемая двумя числовыми значениями- концами исследуемого
интервала.
Число> 0, при котором |Q–Q*|<
, характеризует точность интервальной
оценки.
Доверительным
называется интервал
, который с заданной вероятностью
покрывает неизвестное значение параметра Q. Дополнение
доверительного интервала до множества всех возможных значений параметра Q называется критической областью. Если критическая
область расположена только с одной стороны от доверительного интервала, то
доверительный интервал называется односторонним:
левосторонним, если критическая область существует только слева, и правосторонним- если только справа. В
противном случае, доверительный интервал называется двусторонним.
Надежностью,
или доверительной вероятностью, оценки Q (с помощью Q*) называют вероятность,
с которой выполняется следующее неравенство: |Q–Q*|<
.
Чаще всего доверительную вероятность
задают заранее (0,95; 0,99; 0,999) и на нее накладывают требование быть близкой
к единице.
Вероятность
называют вероятностью
ошибки, или уровнем значимости.
Пусть |Q–Q*|<
, тогда
. Это означает, что с вероятностью
можно утверждать, что истинное значение
параметра Q
принадлежит интервалу. Чем меньше величина отклонения
, тем точнее оценка.
Границы (концы) доверительного интервала
называют доверительными границами, или
критическими границами.
Значения границ доверительного интервала
зависят от закона распределения параметра Q*.
Величину отклонения
равную половине ширины доверительного
интервала, называют точностью оценки.
Методы построения доверительных
интервалов впервые были разработаны американским статистом Ю. Нейманом.
Точность оценки
, доверительная вероятность
и
объем выборки n связаны между собой. Поэтому, зная
конкретные значения двух величин, всегда можно вычислить третью.
Нахождение
доверительного интервала для оценки математического ожидания нормального
распределения, если известно среднеквадратическое отклонение.
Пусть произведена выборка из генеральной
совокупности, подчиненной закону нормального распределения. Пусть известно
генеральное среднеквадратическое отклонение
, но неизвестно математическое ожидание
теоретического распределения a
().
Справедлива следующая формула:
Т.е.
по заданному значению отклонения
можно найти, с какой вероятностью неизвестное
генеральное среднее принадлежит интервалу. И наоборот. Из формулы видно, что при
возрастании объема выборки и фиксированной величине доверительной вероятности
величина
–
уменьшается, т.е. точность оценки увеличивается. С увеличением надежности
(доверительной вероятности), величина
-увеличивается,
т.е. точность оценки уменьшается.
Пример:
В результате испытаний
были получены следующие значения -25, 34, -20, 10, 21. Известно, что они
подчиняются закону нормального распределения с среднеквадратическим отклонением
2. Найдите оценку а* для математического ожидания а. Постройте для него 90%-ый
доверительный интервал.
Решение:
Найдем несмещенную
оценку
Тогда
Доверительный интервал
для а имеет вид: 4 – 1,47< a
< 4+ 1,47 или 2,53 < a
< 5, 47
Нахождение
доверительного интервала для оценки математического ожидания нормального
распределения, если неизвестно среднеквадратическое отклонение.
Пусть известно, что генеральная
совокупность подчинена закону нормального распределения, где неизвестны а и
. Точность доверительного интервала,
покрывающего с надежностью
истинное значение параметра а, в данном случае вычисляется по формуле:
, где n– объем выборки,
,
– коэффициент Стьюдента (его следует
находить по заданным значениям n и
из
таблицы «Критические точки распределения Стьюдента»).
Пример:
В результате испытаний были получены
следующие значения -35, -32, -26, -35, -30, -17. Известно, что они подчиняются
закону нормального распределения. Найдите доверительный интервал для
математического ожидания а генеральной совокупности с доверительной вероятностью
0,9.
Решение:
Найдем несмещенную оценку
.
Найдем
.
Далее найдем
.
Тогда
Доверительный интервал примет вида (-29,2
– 5,62; -29,2 + 5,62) или (-34,82; -23,58).
Нахождение
доверительного интерла для дисперсии и среднеквадратического отклонения
нормального распределения
Пусть из некоторой генеральной
совокупности значений, распределенной по нормальному закону, взята случайная
выборка объема n <
30, для которой вычислены выборочные
дисперсии: смещенная
и
исправленная s2
. Тогда для нахождения интервальных
оценок с заданной надежностью
для генеральной дисперсии D генерального
среднеквадратического отклонения
используются следующие формулы.
или
,
Значения
– находят с помощью таблицы значений
критических точек распределения
Пирсона.
Доверительный интервал для дисперсии
находится из этих неравенств путем возведения всех частей неравенства в
квадрат.
Пример:
Было проверено качество 15 болтов.
Предполагая, что ошибка при их изготовлении подчинена нормальному закону
распределения, причем выборочное среднеквадратическое отклонение
равно 5 мм, определить с надежностью
доверительный интервал для неизвестного
параметра
.
Решение:
Т. к. n = 15 <30, то воспользуемся формулой
.
Найдем пограничные значения вероятности
для .
Тогда:
Границы интервала представим в виде двойного неравенства:
Концы двустороннего доверительного
интервала для дисперсии можно определить и без выполнения арифметических
действий по заданному уровню доверия и объему выборки с помощью соответствующей
таблицы (Границы доверительных интервалов для дисперсии в зависимости от числа
степеней свободы и надежности). Для этого полученные из таблицы концы интервала
умножают на исправленную дисперсию s2
.
Пример:
Решим предыдущую задачу другим способом.
Решение:
Найдем исправленную
дисперсию:
По таблице «Границы
доверительных интервалов для дисперсии в зависимости от числа степеней свободы
и надежности» найдем границы доверительного интервала для дисперсии при k=14 и
: нижняя граница 0,513 и верхняя 2,354.
Умножим полученные
границы на
s2 и
извлечем корень (т.к. нам нужен доверительный интервал не для дисперсии, а для
среднеквадратического отклонения).
Как видно из примеров,
величина доверительного интервала зависит от способа его построения и дает
близкие между собой, но неодинаковые результаты.
При выборках достаточно
большого объема (n>30)
границы доверительного интервала для генерального среднеквадратического
отклонения можно определить по формуле:
Существует и другой
способ определения границы доверительного интервала для дисперсии, в основе
которого лежит выбор интервала, симметричного относительно
:
Причем
–
некоторое число, которое табулировано и приводится в соответствующей справочной
таблице.
Если 1- q<1, то формула имеет
вид:
Пример:
Решим предыдущую задачу третьим способом.
Решение:
Ранее было найдено s
= 5,17. q(0,95;
15) = 0,46 – находим по таблице.
Тогда:
